Đề chọn đội tuyển HSG Toán năm 2020 sở GD&ĐT Khánh Hòa (vòng 1).

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN ĐỘI TUYỂN KHÁNH HÒA
THI HSG THPT CẤP QUỐC GIA NĂM 2020 Môn thi: TOÁN (Vòng 1) ĐỀ THI CHÍNH THỨC Ngày thi: 19/9/2019 (Đề thi có 01 trang)
Thời gian làm bài: 180 phút (không kể thời gian phát đề) Bài 1. (4,0 điểm)  3 3
x  4x  2   4 6  2 y  y  4   3 Giải hệ phương trình: 3
 y  4 y  2 
 4 6  2z (x, y, z  ). z  4   3 3
z  4z  2   4 6  2x  x  4  Bài 2. (6,0 điểm)
a) Chứng minh rằng với mỗi số nguyên dương n, tồn tại duy nhất một cặp số nguyên dương  ; a b 1 sao cho n 
(a  b 1)(a  b  2)  . a 2 1
b) Cho dãy số u xác định bởi u  5, u  u  với mọi n  1. n  1 n 1  n un
Tìm phần nguyên của u . 209 Bài 3. (4,0 điểm)
Một nhóm phượt có n thành viên. Năm 2018, họ thực hiện sáu chuyến du lịch mà mỗi chuyến có
đúng 5 thành viên tham gia. Biết rằng hai chuyến du lịch bất kì chung nhau không quá 2 thành viên.
Tìm giá trị nhỏ nhất của n. Bài 4. (4,0 điểm)
Cho tam giác ABC nhọn không cân có đường trung tuyến AM và đường phân giác trong AD. Qua
điểm N thuộc đoạn thẳng AD (N không trùng với A và D), kẻ NP vuông góc với AB (P thuộc cạnh
AB). Đường thẳng qua P vuông góc với AD cắt đoạn thẳng AM tại Q. Chứng minh rằng QN vuông góc với BC. Bài 5. (2,0 điểm)
Cho x, y, z là các số thực dương thỏa mãn xy  yz  zx  xyz(x  y  z). 1 1 1 Chứng minh rằng    1. 2x 1 2 y 1 2z 1
--------------- HẾT ---------------
SỞ GIÁO DỤC VÀ ĐÀO TẠO KHÁNH HOÀ
GIẢI ĐỀ THI CHỌN ĐỘI TUYỂN HỌC SINH GIỎI QUỐC GIA
NĂM HỌC 2019 – 2020
MÔN THI: TOÁN (ngày 1)
Thời gian: 180 phút (Không kể thời gian phát đề) ĐÈ CHÍNH THỨC  3 3 x + 4x + 2 = + 4 6 − 2y  y − 4   3 Bài 1.
(3 điểm) Giải hệ phương trình 3 y + 4y + 2 = + 4 6 − 2z . z − 4   3 3 z + 4z + 2 = + 4 6 − 2x  x − 4  Lời giải x ≤ 3 
Điều kiện:  y ≤ 3 . z ≤ 3  Xét hàm f (t ) 3
= t + 4t + 2 và g (t) 3 =
+ 4 6 − 2t trên (− ; ∞ ] 3 . t − 4
 f (x) = g ( y) ( ) 1 
Hệ phương trình trở thành  f ( y) = g ( z) (2)  f
 ( z) = g ( x) (3) Ta có f ′(t ) 2
= 3t + 4 > 0 t ∀ ∈(− ; ∞ ]
3 ⇒ Hàm số f (t ) 3
= t + 4t + 2 đồng biến trên (− ; ∞ ] 3 . g′(t ) 3 4 = − − < 0 t ∀ ∈(− ; ∞ 3) ⇒ g (t) 3 =
+ 4 6 − 2t nghịch biến trên (t − 4)2 6 − 2t t − 4 (− ; ∞ ] 3 .
Không mất tính tổng quát ta giả sử x = max{ ; x ; y }
z . Khi đó ta có x ≥ y ; x ≥ z .
x ≥ y (*) ⇒ f ( x) ≥ f ( y) (vì hàm f (t ) đồng biến), kết hợp với hệ phương trình
⇒ g ( y) ≥ g ( z) (vì hàm g (t) nghịch biến), kết hợp hệ phương trình ⇒ y ≤ z ⇒ f ( y) ≤ f ( z)
⇒ g ( z) ≤ g ( x) ⇒ z ≥ x (**).
Từ (*) và (**) ta suy ra x = z ⇒ f ( x) = f ( z) ⇒ g ( y) = g ( x) ⇒ y = x .
Vậy ta có x = y = z . 3
Từ hệ phương trình ta suy ra f ( x) = g ( x) 3 ⇔ x + 4x + 2 = + 4 6 − 2x x − 4 3 3
⇔ x + 4x + 2 − − 4 6 − 2x = 0 . x − 4 3 Xét hàm h ( x) 3 = x + 4x + 2 −
− 4 6 − 2x trên (− ; ∞ ] 3 . x − 4
Trang 2/8 – Diễn đàn giáo viên Toán 3 4 Ta có h′( x) 2 = 3x + 4 + + > 0 x ∀ ∈(− ; ∞ 3) (x − 4)2 6 − 2x ⇒ 3 hàm số h ( x) 3 = x + 4x + 2 −
− 4 6 − 2x đồng biến trên (− ; ∞ ] 3 . x − 4
⇒ Phương trình h( x) = 0 có nhiều nhất một nghiệm. Ta có h ( )
1 = 0 nên phương trình h ( x) = 0 có nghiệm duy nhất x = 1.
Vậy hệ phương trình đã cho có nghiệm duy nhất (1;1; ) 1 Bài 2.
a. Chứng minh rằng với mỗi số nguyên dương n , tồn tại duy nhất một cặp số nguyên dương ( 1
a ;b) sao cho n = (a + b − )
1 (a + b − 2) + a . 2 1
b. Cho dãy số xác định bởi u = 5;u = u +
với mọi n ≥ 1. Tìm phần (u nguyên của n ) 1 n 1 + n un u . 209 Lời giải a.
Cách 1. Đặt m = a + b ⇒ m ≥ 2 .
Phương trình trên trở thành: 1 1 1 n = (m − )
1 (m − 2) + m − b 2 2
⇔ m − m +1− b − n = 0 ⇔ m − m + 2(1− b − n) = 0 (1). 2 2 2
Để tồn tại cặp số nguyên dương (a;b) thì (1) phải có nghiệm nguyên dương lớn hơn hoặc bằng 2.
Do đó, điều kiện cần là ∆
> 0 và phải chính phương. (1)
∆ =1− 8 1− b − n = 8 b + n − 7 (1) ( ) ( ) Dễ thấy ∆ = (2k + )2 1 , k ∈ ℕ (1) 2
Khi đó (b + n) − = ( k + ) ⇔ (b + n) 2 8 7 2 1 2 = k + k + 2 . 2 k + k ⇔ b = +1− n . 2 1+ 2k +1 Khi này, ∆
= 2k +1 và nghiệm nguyên dương duy nhất của (1) là m = = k +1. (1) 2 2 2  k + k  k − k
Thay vào được a = m − b = k +1− +1− n = n −   . 2 2  
Sử dụng các điều kiện a ≥ 1;b ≥ 1 được hệ Trang 3/8 – HSG-WT 2
k + k +1−n ≥1 2 
k + k ≥ 2 2 n  ⇔  (2). 2 2 k − k 
k − k + 2 ≤ 2n  n − ≥ 1  2
Việc còn lại là chỉ ra (2) chỉ có nghiệm duy nhất với k ∈ ℕ .
Gọi k là số nguyên không âm lớn nhất sao cho 2
k − k + 2 ≤ 2n , lúc này k luôn tồn tại và duy 0 0 0 0 nhất. 2 Khi đó (k + ) 1 − (k + ) 2
1 + 2 > 2n ⇔ k + k > 2n − 2 . 0 0 0 0 Vì 2
k + k ≥ 2n (đpcm). 0 0
Vậy với mỗi số nguyên dương n , tồn tại duy nhất một cặp số nguyên dương (a;b) sao cho 1 n = (a + b − )
1 (a + b − 2) + a . 2 Cách 2. l (l + ) 1
Rõ ràng với n cho trước, tồn tại số tự nhiên l để ≥ n . 2
Ta gọi l là giá trị nhỏ nhất của n thoả mãn bất phương trình trên. 0 l l −1 l l +1 l l +1 0 ( 0 ) 0 ( 0 ) 0 ( 0 ) Khi đó hiển nhiên < n < , ta chọn b =
+1− n , với cách chọn này b 2 2 2 xác định và duy nhất. 1
Ta đặt X = a + b − 2 ⇒ a = X − b + 2 nên ta có: n = X ( X + ) 1 + X − b + 2 2  l l +1  2 n 2 0 ( 0 )
⇔ X + 3X − 2b + 4 − 2 = 0 ⇔ X + 3X − 2
+1− n  + 4 − 2n = 0 2   2
⇔ X + 3X + 2 − l l +1 = 0 * . 0 ( 0 ) ( )
Ta có: ∆ = 3 − 4 (2 − l (l + ) 1 ) = (1+ 2l )2 2
, do đó phương trình (*) có hai nghiệm * 0 0 0  3 − +1+ 2l0 X = = l −1 0  2 
. Do vậy phương trình (*) có nghiệm dương duy nhất là 3 − −1− 2l  0 X = = −l −1 < 0 0  2 X = l −1 0 l l +1  l l −1 0 ( 0 ) 0 ( 0 )
⇔ a + b − 2 = l −1 ⇔ a = 1+ l − b = 1+ l − +1− n = n − . 0 0 0   2 2   l l −1 0 ( 0 )
Theo trên thì a = n − > 0 . 2
Vì vậy, các yêu cầu của bài toán đều thoả mãn. Ta có điều phải chứng minh.
Trang 4/8 – Diễn đàn giáo viên Toán Cách 3
Ta cần chứng minh rằng * * *
f : ℕ × ℕ → ℕ được cho bởi f (a b) 1 ; = (a + b − )
1 (a + b − 2) + a , ( *
∀a,b ∈ ℕ ) là một song ánh. 2
Chứng minh được f là một ánh xạ.
Ta chứng minh f là một đơn ánh. Thật vậy, giả sử (a ;b ),(a ;b ) * * ∈ℕ × ℕ thỏa mãn 1 1 2 2
f (a ;b = f a ;b 1 1 ) ( 2 2 ) n n +1 Đặt T (n) ( ) * =
, n ∈ ℕ . Ta có f ( ;
a b) −T (a + b − 2) = a > 0 2
a + b −1 a + b
a + b −1 a + b − 2
Và T (a + b − ) 1 − f ( ; a b) ( )( ) ( )( ) = −
− a = b −1 ≥ 0. 2 2
Do đó T (a + b − 2) < f ( ;
a b) ≤ T (a + b − ) 1 .
Khi đó T (a + b − 2 < f a ;b ≤ T a + b −1 , ... 1 1 ) ( 1 1) ( 1 1 )
Kết hợp với dãy (T (n)) là dãy tăng ngặt ta chứng minh được f là một đơn ánh.
Ta chứng minh f là một toàn ánh.
Thật vậy, với n là một số nguyên dương tùy ý, vì dãy (T (n)) tăng ngặt nên luôn tồn tại một số
nguyên dương k thỏa − +
T (k − ) < n ≤ T (k ) (k ) 1 k k (k ) 1 1 ⇔ < n ≤ . 2 2 (k − ) 1 k Đặt a = n −
và b = k − a +1. 2
Chứng minh được a và b là các số nguyên dương và ( − b) 1 k k f a; = (a + b − ) 1 (a + b − 2) ( ) 1 + a = + a = . n 2 2
Vậy f là một song ánh, suy ra điều phải chứng minh. 1
b. Cho dãy số (u xác định bởi u = 5;u = u +
với mọi n ≥ 1. Tìm phần nguyên của n ) 1 n 1 + n un u . 209
Nhận xét: (u là dãy tăng và u ≥ u > 0, n ∀ . n ) n 1 2 n 1 − n 1 − n 1  1   1 −  1 Ta có: 2 2 2 2 2 u = u +
 ⇒ ∑u = ∑u +
+ 2 ⇒ u = u + 2 n −1 + ∑ . k 1 + k k 1 + k 2 n 1 ( ) 2 u   = = u   = u k k 1 k 1 k k 1 k Suy ra: 2
u > u + 2 n −1 , n
∀ ≥ 2 , hay u ≥ 25 + 2 n − n ∀ ≥ . n ( ) 1 , 1 n 1 ( ) 1 1 1 1  1 1  Mặt khác, 2 2
u ≥ u + 2 k −1 ⇒ ≤ ⇒ <  − . k 1 ( )  2 2 u u + 2 k − u u + k − u + k − k ( ) 4 2 2 1 2 2 3 2 1 1 k  1 1  n 1 − 1 1 1 1 1 Suy ra: ∑ < − < = . 4 2 2 = u u − u + n − − k 1 2 3 u k 2( 2 1 48 1 1 1 1 ) Từ đó ta có n 1 − 1 n −1 2 2
u = u + 2 n − + < u + n − + n ∀ ≥ ∑ . n ( ) 2 1 2 1 , 2 1 2 1 ( ) = u k 48 1 k n − Suy ra u < + n − + n ∀ ≥ . n ( ) 1 25 2 1 , 2 48 Trang 5/8 – HSG-WT n − Hay u ≤ + n − + n ∀ ≥ . n ( ) 1 25 2 1 , 1 48 208 Khi đó 441 ≤ u ≤ 441+ . Hay 21 ≤ u
< 21,5 nên phần nguyên của u bằng 21. 209 48 209 209 Bài 3.
Một nhóm phượt có n thành viên. Năm 2018 , họ thực hiện sáu chiến du lịch mà mỗi chuyến
có đúng 5 thành viên tham gia. Biết rằng hai chuyến du lịch bất kì chung nhau không quá 2
thành viên . Tìm giá trị nhỏ nhất của n . Lời giải
Ta xác định bảng ô vuông với cột là thành vượt nhóm phượt được đánh số từ 1 đến n , dòng là
các chuyến du lịch A , A ,..., A . Điền số 1 vào ô (i, A nếu người thứ i tham gia chuyến du i ) 1 2 6
lịch A , điền số 0 vào ô tương ứng trong trường hợp ngược lại. i 1 2 … n A1 A2 … A6
Gọi c là số chuyến du lịch người thứ i tham gia, tức là trên cột i có c số 1. i i n
Gọi S là tổng số các cặp số 1 trong bảng. Ta có c = 30 ∑ . i i 1 = n
Vì trên cột i có c số 1, suy ra có 2
C cặp số 1 trên cột i . Suy ra 2 S = C ∑ . i i c i c i 1 =
Mặt khác, xét 2 hàng i ≠ j bất kì, do A ∩ A ≤ 2 nên hai hàng này có nhiều nhất là 2 cặp số i j 1, suy ra 2
S ≤ 2C ≤ 30 . i c 2 n   ∑c  i  n n n n   Từ đó ta có 2 i 1 = 2 S = C ≤ 30 ⇒ − c ≤ c − c ≤ 60 ∑ ∑ ∑ ∑ . i c i i i i 1 = n i 1 = i 1 = i 1 = 900 ⇒ ≤ 90 ⇔ n ≥ 10 . n Xét n = 10 1 2 3 4 5 6 7 8 9 10 A 1 1 1 1 1 0 0 0 0 0 1 A 1 1 0 0 0 1 1 1 0 0 2 A 1 0 1 0 0 1 0 0 1 1 3 A 0 1 0 1 0 0 1 0 1 1 4 A 0 0 1 0 1 1 0 1 1 0 5 A 0 0 0 1 1 0 1 1 0 1 6
Vậy giá trị nhỏ nhất của n bằng 10 , khi mỗi chuyến có đúng 5 thành viên tham gia và mỗi cặp
thành viên cùng tham gia không quá 2 chuyến. Bài 4.
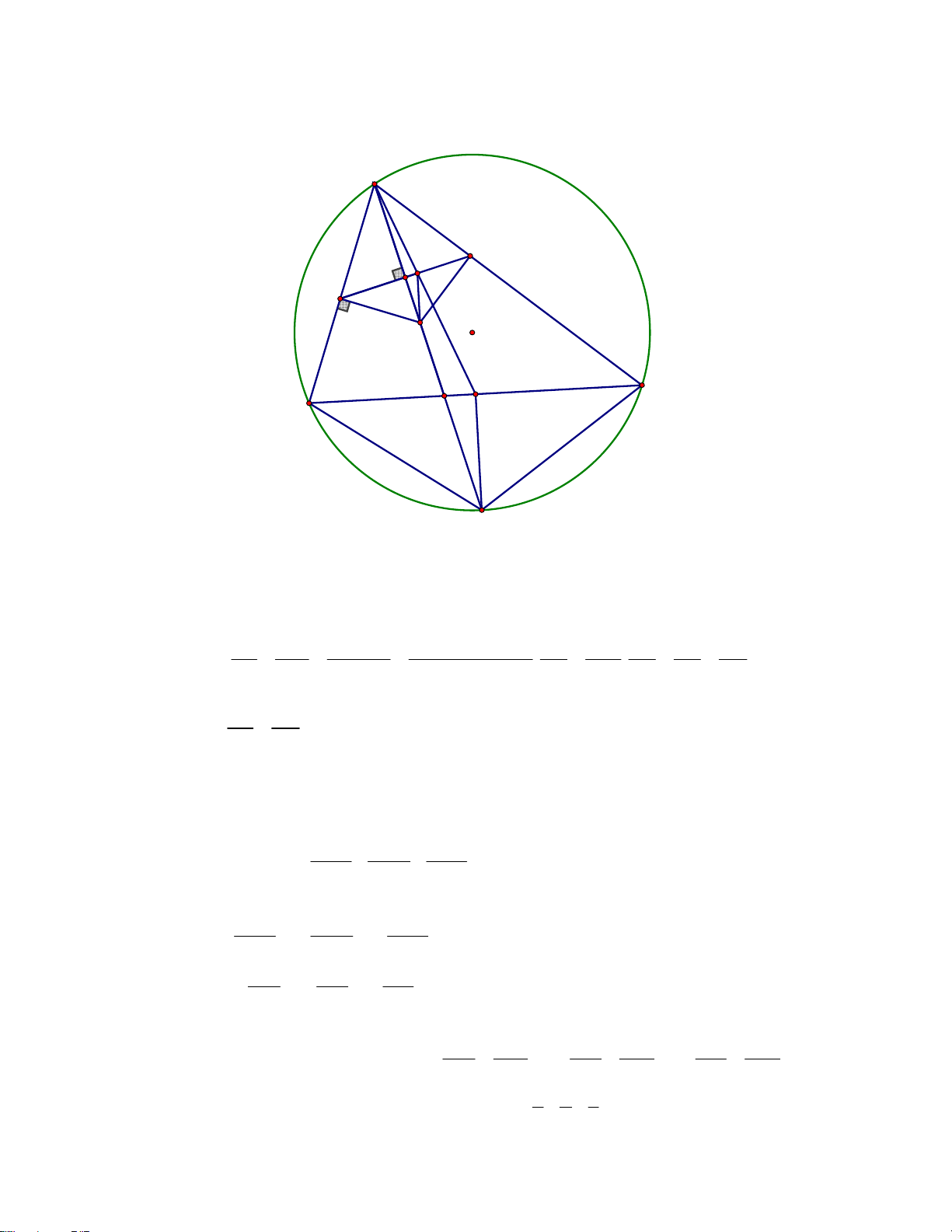
Cho tam giác ABC nhọn không cân có đường trung tuyến AM và đường phân giác trong AD.
Qua điểm N thuộc đoạn thẳng AD (N không trùng với A và D), kẻ NP vuông góc với AB (P
Trang 6/8 – Diễn đàn giáo viên Toán
thuộc cạnh AB). Đường thẳng qua P vuông góc với AD cắt đoạn thẳng AM tại Q. Chứng minh
rằng QN vuông góc với BC. Lời giải A E Q I P N O C D M B K
Có PQ ∩ AD = I; AD ∩ (O) = K; PQ ∩ AC = E .
Dễ chứng minh các tam giác cân NPE và KBC đồng dạng. QE SQAE sin MAC
sin MAC.AM .AC AB S AB AB DB Lại có: = = = . MAC = . = = QP S MAB MAB AM AB AC S AC AC DC QAP sin sin . . MAB QE DB Suy ra =
lại có M, Q lần lượt là trung điểm của BC, PE và N ∆ PE ∼ C ∆ KB nên: QP DC
∆QIE ∼ ∆DMK (c g c) . .
⇒ QNI = DKM ⇒ QN // MK ⇒ QN ⊥ BC . Bài 5.
Cho x, y, z là các số thực dương thỏa mãn xy + yz + zx = xyz ( x + y + z) . 1 1 1 Chứng minh rằng: + + ≥ 1. 2x +1 2 y +1 2z +1 Lời giải 1 1 1 Đặt a = , b = , c =
thì 0 < a, b, c < 1. 2x +1 2 y +1 2z +1 1 − a 1− b 1− c Ta có x = , y = , z = . 2a 2b 2c
Ta cần chứng minh a + b + c ≥ 1 (Chứng minh bằng phản chứng). 1− a b + c 1− b c + a 1− c a + b
Giả sử a + b + c < 1. Khi đó, ta có x = > , y = > , z = > . 2a 2a 2b 2b 2c 2c
Ta có: xy + yz + zx = xyz ( x + y + 1 1 1
z) ⇔ x + y + z = + + x y z Trang 7/8 – HSG-WT 1 1 1 b + c 2a c + a 2b a + b 2c
⇔ 0 = x − + y + + z + > − + − + − x y z 2a b + c 2b c + a 2c a + b b + c c + a a + b  a b c  ⇔ + + < 4 + +  ( ) 1 . a b c
 b + c c + a a + b  Ta chứng minh được:  a b c   1 1   1 1 
 1 1  b + c c + a a + b 4 + + ≤ a + + b + + c + = + +         (2).
 b + c c + a a + b   b c   c a   a b  a b c Từ ( )
1 và (2) ta có điều mâu thuẫn nên ta có điều phải chứng minh. 1
Đẳng thức xảy ra khi và chỉ khi a = b = c =
⇔ x = y = z = 1. 3 ---HẾT---
Trang 8/8 – Diễn đàn giáo viên Toán
Document Outline

• de-chon-doi-tuyen-hsg-toan-nam-2020-so-gddt-khanh-hoa-vong-1
• 1570504670_WT.CHỌN HSG QG-KHÁNH HOÀ NĂM 2019-2020D1