Đề chọn đội tuyển Toán 8 vòng 2 năm 2024 – 2025 trường THCS Trần Mai Ninh – Thanh Hóa

PGD&ĐT TP THANH HOÁ
TRƯỜNG THCS TRẦN MAI NINH ĐỀ KHẢO SÁT CHỌN ĐỘI TUYỂN
TOÁN 8 NĂM HỌC 2024 – 2025 (VÒNG II)
ĐỀ THI CHÍNH THỨC
Ngày thi 29 tháng 11 năm 2024 Đề thi có 01 trang
Thời gian làm bài 120 phút, không kể thời gian giao đề
Bài 1: (4,0 điểm) 4 2 2 2 2 2 2 1. Rút gọn biểu thức x − (x −1) x − (x −1) x (x −1) −1 A = + + 2 2 2 2 2 4 2 (x +1) − x
x (x +1) −1 x − (x +1)
2. Với các số thực x, y, z thỏa mãn xyz =−1; x + y + z = 4 và x y z 4 + +
= . Tính giá trị của biểu thức 2 2 2
P = x + y + z . 2 2 2
x − 3x −1 y − 3y −1 z − 3z −1 9
Bài 2: (4,0 điểm)
1. Tìm x biết x −1 x − 2 x −3 x − 2025 + + + ...+ = 2025 2025 2024 2023 1
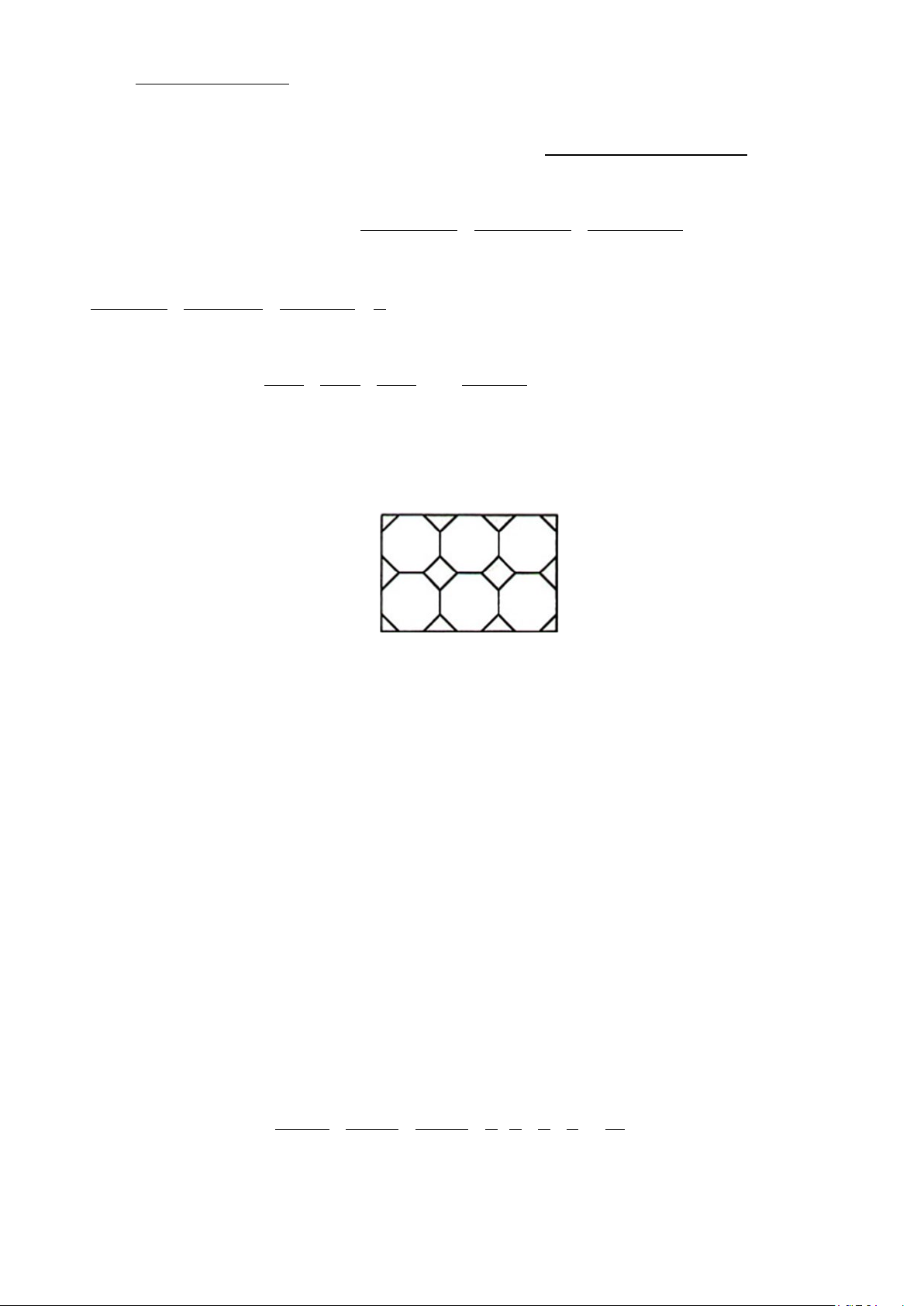
2. Một sân vườn hình chữ nhật được lát bởi các viên gạch hình bát giác đều và các
viên gạch hình vuông hoặc hình tam giác vuông cân (hình vẽ minh họa). Biết cạnh bát
giác đều bằng 2dm và số gạch hình bát giác đều là 500 viên. Tính diện tích phần sân
vườn được lát bởi những viên gạch không phải là hình bát giác đều.
Bài 3: (4,0 điểm)
1. Tìm tất cả các cặp số nguyên ( ;x y) thỏa mãn: 2
x(1+ x + x ) = 4y(y −1).
2. Cho hai số nguyên dương x, y thỏa mãn 4 2 2 4
x + x y + y chia hết cho 11. Chứng minh rằng 4 2 2 4
x + x y + y chia hết cho 4 11 .
Bài 4: (6,0 điểm)
1. Cho hình bình hành ABCD có O là giao điểm của hai đường chéo AC và BD,
góc A tù và AB > A .
D Gọi H là hình chiếu vuông góc của B trên AC. Trên tia BH lấy
điểm E sao cho H là trung điểm của BE.
a) Chứng minh rằng ADEC là hình thang cân.
b) Gọi I là giao điểm của AE và CD, K là hình chiếu vuông góc của O trên CD,
J là trung điểm của OK. Chứng minh rằng IJ vuông góc với AK.
2. Cho hình vuông ABCD, E là một điểm trên cạnh .
CD Tia phân giác góc BAE cắt
BC tại M. Chứng minh rằng AM ≤ 2ME.
Bài 5: (2,0 điểm)
1. Bạn Tú có một hộp bút trong đó có 5 chiếc bút bi mực xanh, 7 chiếc bút bi mực đen
và 3 chiếc bút chì. Bạn lấy ngẫu nhiên hai chiếc bút. Xác suất của biến cố: “Bạn Tú lấy được 1
chiếc bút chì và 1 chiếc bút mực”.
2. Cho a,b,c là các số dương thảo mãn a +b + c =1. Chứng minh rằng: ab bc ca 1  1 1 1  15 + + + + + ≥   . 2 2 2 2 2 2 a + b b + c c + a 4  a b c  4
--------------- Hết ---------------
Cán bộ coi thi không giải thích gì thêm. 1 PGD&ĐT TP THANH HOÁ
TRƯỜNG THCS TRẦN MAI NINH HƯỚNG DẪN VÀ BIỂU CHẤM
Biểu chấm gồm 05 trang
KHẢO SÁT CHỌN ĐỘI TUYỂN TOÁN 8 - VÒNG II
NĂM HỌC 2024 – 2025 Bài
Nội dung cần đạt Điểm 4 2 2 2 2 2 2
1. Rút gọn biểu thức x − (x −1) x − (x −1) x (x −1) −1 A = + + 2,0 2 2 2 2 2 4 2 (x +1) − x
x (x +1) −1 x − (x +1) 2 2 2 2 2 2
(x + x −1)(x − x +1) (x + x −1)(x − x +1) (x − x +1)(x − x −1) A = + + 2 2 2 2 2 2
(x +1+ x)(x +1− x) (x + x +1)(x + x −1) (x − x −1)(x + x +1) 1,0 2 2 2 2
x + x −1 x − x +1 x − x +1 x + x +1 = + + = = 1. 1,0 2 2 2 2
x + x +1 x + x +1 x + x +1 x + x +1
2. Với các số thực x, y, z thỏa mãn xyz =−1; x + y + z = 4 và x y z 4 + +
= . Tính giá trị của biểu thức 2 2 2
x − 3x −1 y − 3y −1 z − 3z −1 9 2,0 2 2 2
P = x + y + z . Ta có: x x 1 1 1 = = = = 2 2
x − 3x −1 x − 3x + xyz x − 3+ yz 1− y − z + yz (y −1)(z −1) 0,25 Bài 1 Tương tự y 1 = ; 4,0đ 2
y − 3y −1 (x −1)(z −1) z 1 = . 2
z − 3z −1 (x −1)(y −1) 0,5 Suy ra 1 1 1 4 + + =
(y −1)(z −1) (x −1)(z −1) (x −1)(y −1) 9
x −1+ y −1+ z −1 4 9
= ⇒ (x −1)(y −1)(z −1) =
(x −1)(y −1)(z −1) 9 4 9
⇒1− (x + y + z) + (xy + yz + zx) = 0,5 4 1 xy yz zx − ⇒ + + = 4 2 2 2 2 33
⇒ x + y + z = (x + y + z) − 2(xy + yz + zx) = 2 Vậy 2 2 2 33
x + y + z = . 0,5 2
1. Tìm x biết x −1 x − 2 x −3 x − 2025 + + + ...+ = 2025 2,0 2025 2024 2023 1
Ta có: x −1 x − 2 x −3 x − 2025 + + + ...+ = 2025 0,75 2025 2024 2023 1
Bài 2 x − 2026 x − 2026 x − 2026 x − 2026 4.0đ + + + ...+ = 0 2025 2024 2023 1 (x ) 1 1 1 1 2026 ...  − + + + + = 0,75   0  2025 2024 2023 1 x = 2026 Vậy x = 2026 . 0,5 2
2. Một sân vườn hình chữ nhật được lát bởi các viên gạch hình bát 2,0
giác đều và các viên gạch hình vuông hoặc hình tam giác vuông cân
(hình vẽ minh họa). Biết cạnh bát giác đều bằng 2dm và số gạch hình
bát giác đều là 500 viên. Tính diện tích phần sân vườn được lát bởi
những viên gạch không phải là hình bát giác đều.
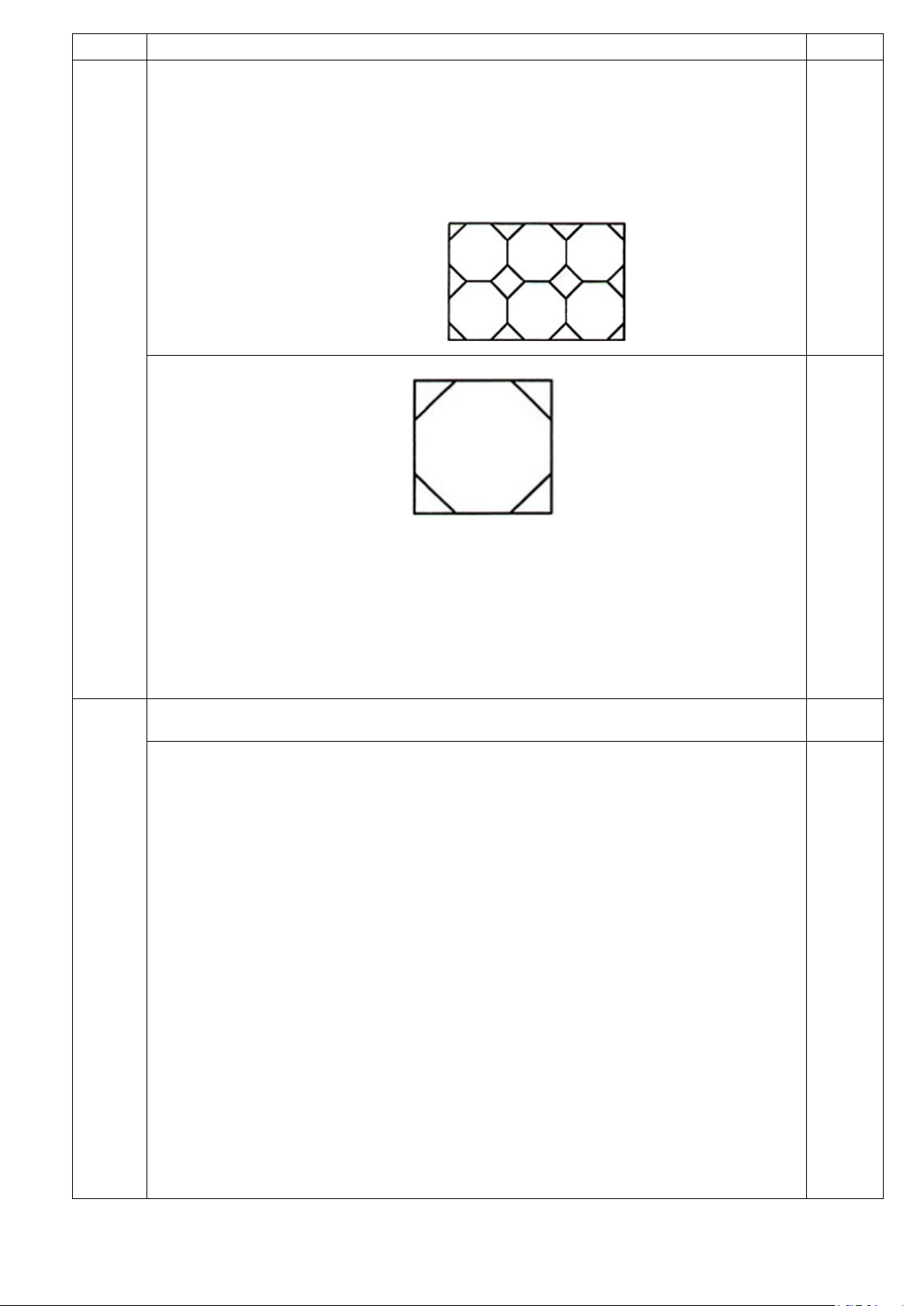
Xét một hình vuông chứa viên gạch hình bát giác đều cạnh 2 dm. 0,75
Bốn tam giác vuông cân nằm ngoài viên gạch hình bát giác đều ghép lại
được một hình vuông cạnh 2 dm có diện tích bằng 4 dm2.
Như vậy ứng với mỗi viên gạch hình bát giác đều, có diện tích 4 dm2 0,5
được lát bởi các viên gạch không phải là hình bát giác đều. 0,75
Vậy diện tích phải tìm là 500 x 4 = 2000 (dm2) = 20 (m2).
1. Tìm tất cả các cặp số nguyên ( ;x y) thỏa mãn: 2
x(1+ x + x ) = 4y(y −1). 2,0 Ta có 2
x(1+ x + x ) = 4y(y −1) 0,5 3 2 2
(x + x ) + (x +1) = 4y − 4y +1 2 2
(x +1)(x +1) = (2y −1) ( ) 1 0,5 Vì
x, y ∈ ⇒ ( y − )2 2 1 > 0 nên từ ( )
1 ⇒ x ≥ 0 và x chẵn. Bài 3 Giả sử 2
(x +1, x +1) = d ⇒ d lẻ và 2 x −1d; 2
x +1d ⇒ 2d ⇒ d =1 4,0đ Vì 2
(x +1)(x +1) là số chính phương và 2
(x +1, x +1) =1 nên (x +1) và 2 (x +1) 0,5
cũng là hai số chính phương. Do x ≥ 0 2 2 2
⇒ x < x +1≤ (x +1) 2 2
⇒ x +1= (x +1) ⇒ x = 0 Khi  y = t m
x = 0 , ta có 4y(y −1) = 0 0( / ) ⇒ 0,25  .
 y = 1(t / m) 0,25
Vậy (x, y)∈{(0;0);(0;1 }) 3
2. Cho hai số nguyên dương x, y thỏa mãn 4 2 2 4
x + x y + y chia hết cho11 2,0
Chứng minh rằng: 4 2 2 4
x + x y + y chia hết cho 4 11 . Ta có: 4 2 2 4 2 2 2 2 2 2 2 2
x + x y + y = (x + y ) − (xy) = (x + y + xy)(x + y − xy) 1  1 2 2
⇒ x + y + xy 11  hoặc 2 2
x + y − xy 11  +) Nếu 0,25 2 2 3 3 3 3
x + y + xy 11
 ⇒ x − y 11
 ⇒ x ≡ y (mod11) ⇒ x ≡ y(mod11) 4 4 2 2 4 4
⇒ x + y + x y ≡ 3x (mod11) ⇒ x ≡ 0(mod11) (vì (3,4) =1) ⇒ x 11  ⇒ y 11  0,5 Do đó 4 4 2 2 4
x + y + x y 11  +) Nếu 2 2 3 3 3 3
x + y − xy 11  ⇒ x + y 11
 ⇒ x ≡ −y (mod11) ⇒ x ≡ −y(mod11) 0,5 4 4 2 2 4 4
⇒ x + y + x y ≡ 3x (mod11) ⇒ x ≡ 0(mod11) (vì (3,4) =1) ⇒ x 11  ⇒ y 11  Do đó 4 4 2 2 4
x + y + x y 11  0,5
Vậy với x, y nguyên dương thỏa mãn 4 2 2 4
x + x y + y chia hết cho 11 thì 4 2 2 4
x + x y + y chia hết cho 4 11 . 0,25
1. Cho hình bình hành ABCD có O là giao điểm của hai đường chéo
AC và BD , góc A tù và AB > AD . Gọi H là hình chiếu vuông góc của
Bài 4.1 B trên AC . Trên tia BH lấy điểm E sao cho H là trung điểm của BE.
4,0đ a) Chứng minh rằng AEDC là hình thang cân. 4,0
b) Gọi I là giao điểm của AE và CD, K là hình chiếu vuông góc của
O trên CD, J là trung điểm của OK. Chứng minh rằng IJ vuông góc với AK. A B O J H D I K M C E 4
a) Ta có: OH là đường trung trực của BE=> OB = OE , mà OB = OD 0,5
Suy ra OB = OD = OE ⇒ B
∆ DE vuông tại E ⇒ ED ⊥ BE 0,5
Chứng minh DE / /AC ⇒tứ giác ADEC là hình thang (1) Chứng minh A
∆ BE cân⇒ AB = AE mà AB = CD ⇒ DC = AE (2) 0,5
Từ (1) và (2) suy ra tứ giác ADEC là hình thang cân. 0,5
b) Gọi M là trung điểm của KC.
Câu 1 + Chứng minh JM là đường trung bình của OK ∆
C nên JM / /OC (3) 0,5
4,0đ + Chứng minh IA
∆ C cân tại I có IO là đường trung tuyến đồng thời là đường 0,5
cao nên IO ⊥ AC (4)
Từ (3) và (4) suy ra MJ ⊥ . IO + Xét IMO ∆
có OK ⊥ IM; JM ⊥ OI mà OK cắt MJ tại J ⇒ J là trực tâm của 0,5 IMO ∆
⇒ JI ⊥ OM (5)
+ Chứng minh MO là đường trung bình của A
∆ KC ⇒ OM / / AK (6) 0,5
Từ (5) và (6) suy ra AK ⊥ IJ.
2. Cho hình vuông ABCD, E là một điểm trên cạnh .
CD Tia phân giác 2,0
góc BAE cắt BC tại M . Chứng minh rằng: AM ≤ 2ME. F M B C G E Bài 4.2 2,0đ A D
Vẽ EF ⊥ AM (F ∈ AB), EG ⊥ AB (G∈ AB)
+ Chứng minh tứ giác AGED là hình chữ nhật ⇒ GE = A . D 0,5 + Xét ∆ ∆  =  0 = = =  = 
ABM và EGF có : ABM EGF ( 90 ); AB EG ( AD);MAB GEF 0,5 Do đó A ∆ BM = E ∆ GF ( .
G C.G) ⇒ AM = EF. + Xét A
∆ EF có AM là đường phân giác đồng thời là đường cao nên 0,5 A ∆ EF cân tại A
⇒ AM là đường trung trực của EF.
+ Xét ba điểm M,E,F ta có EF ≤ ME + MF ⇒ AM ≤ 2.ME. 0,5
Dấu “=” xảy ra khi M là trung điểm của BC.
1. Bạn Tú có một hộp bút trong đó có 5 chiếc bút bi mực xanh, 7
chiếc bút bi mực đen và 3chiếc bút chì. Bạn lấy ngẫu nhiên hai chiếc 1,0
bút. Xác suất của biến cố:“Bạn Tú lấy được 1 chiếc bút chì và 1 chiếc bút mực”.
+ Chiếc bút thứ nhất chọn 1 trong số 15 chiếc bút nên có 15 cách. 0,25
Bài 5 Chiếc bút thứ hai chọn 1 trong 14 chiếc bút còn lại nên có 14 cách. 5
2,0đ Số cách chọn 2 chiếc bút là 15.14:2 =105 cách. (Cứ mỗi cặp bị lăp lại 2 0,25 lần).
+ Chiếc bút chì chọn 1 trong 3 chiếc nên có 3 cách.
+ Chiếc thứ hai chọn 1 trong 12 chiếc bút mực nên có 12 cách. 0,25
Số cách chọn ra 2 chiếc bút trong đó có 1 chiếc bút chì và một chiếc bút mực là 3.12 = 36 cách.
Xác suất của biến cố: “Bạn Tú lấy được 1 chiếc bút chì và 1 chiếc bút 0,25 mực” là 36 12 = . 105 35
2. Cho a,b,c là các số dương thảo mãn a +b + c =1. Chứng minh rằng: 1,0 ab bc ca 1  1 1 1  15 + + + + + ≥   . 2 2 2 2 2 2 a + b b + c c + a 4  a b c  4 Vì 1 1 1 + + =1
a + b + c a + b + c a + b + c a b c nên + + = + + a b c a b c 0,25 2 2 2 2 2 2
3  a b   b c   c a  + + + = + + + + + + a b b c c a  = 3+ + + .
b a   c b   a c        ab bc ca Do đó: ab bc ca 1  1 1 1  + + + + + = 2 2 2 2 2 2 a b b c c a 4  a b c  + + +   2 2 2 2 2 2  ab
a + b   bc
b + c   ca c + a  3 =  +  +  +  +  +  + 0,25 2 2 2 2 2 2  a + b
4ab   b + c
4bc   c + a 4ca  4 2 2 2 2 2 2 ab a + b bc b + c ca c + a 3 ≥ 2 . + 2 . + 2 . + 2 2 2 2 2 2 a + b 4ab b + c 4bc c + a 4ca 4 0,25 1 1 1 3 15 = 2. + 2. + 2. + = 2 2 2 4 4 Dấu “=” xảy ra khi 1
a = b = c = . 0,25 3
Lưu ý: - Trên đây chỉ là hướng dẫn chấm, giám khảo căn cứ vào bài làm của học sinh,
linh hoạt cho điểm.
- Học sinh làm cách khác đúng vẫn cho điểm tối đa.
- Bài hình vẽ hình sai hoặc không vẽ hình thì không chấm. 6
Xem thêm: ĐỀ THI HSG TOÁN 8
https://thcs.toanmath.com/de-thi-hsg-toan-8
Document Outline

• ĐỀ THI HSG TOÁN 8 VÒNG II - TMN NĂM 2024 - 2025 CHUẨN (18-11-2024)
• HSG 8