PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI CHỌN ĐỘI DỰ TUYỂN HSG TỈNH TRIỆU SƠN Năm học 2022 - 2023 Môn: Toán …………………
Thời gian: 150 phút (không kể thời gian giao đề) Số báo danh Ngày 17 tháng 3 năm 2023
.....................................
(Đề có 01 trang, gồm 05 câu) Câu 1: (4,0 điểm) 2 2  x  3x  2 x  x   1 1  1. Cho biểu thức: P   :  .  2 2    x  x  2 x 1    x 1 x 1  1 x 1
a) Rút gọn P. b. Tìm x để   1. P 8  1 1   1 1   1 1 
2. Cho ba số thực a, b, c khác không thỏa mãn a   b   c   2        và  b c   c a   a b  1 1 1 3 3 3
a  b  c  1. Chứng minh rằng    1. a b c Câu 2: (4,0 điểm) 3 2  x  x 1. Giải phương trình: 3 x   3  28   .  x 1 x 1 1 2
2. Tìm các cặp số (x; y) thỏa mãn các điều kiện: 2x  y    6 và y x 1 x y xy     4 . xy y x Câu 3: (4,0 điểm)
1. Tìm nghiệm nguyên (x; y) của phương trình:  xy  x  2 2
1  xy  x  3x . 1 1 1
2. Cho a, b là các số tự nhiên lớn hơn 2 và p là số tự nhiên thỏa mãn   . 2 2 p a b
Chứng minh rằng p là hợp số. Câu 4: (6,0 điểm)
1. Cho đoạn thẳng AB = 2a. Gọi O là trung điểm của AB. Dựng các tia Ax, By về cùng
một phía của AB sao cho Ax, By lần lượt vuông góc với AB. Trên tia Ax lấy điểm C, trên tia By
lấy điểm D sao cho 0 ˆ COD  90 . a. Chứng minh 2
AC.BD  a và CD  AC  . BD
b. Kẻ OM vuông góc với CD tại M, gọi N là giao điểm của AD và BC. Chứng minh rằng MN // AC.
2. Cho hình thang ABCD có đáy lớn là CD. Gọi O là giao điểm của AC và BD. Một
đường thẳng cắt các đoạn AD, OD, OC, BC lần lượt tại M, N, P, Q sao cho MN=NP=PQ.
Chứng minh rằng CD=2AB. Câu 5: (2,0 điểm)
Cho các số thực dương x, y, z thoả mãn: xy  yz  xz  3xyz . Tìm giá trị nhỏ nhất của 2 2 2 y z x biểu thức A    . x  2 y   y  2
z   z  2 1 1 x   1
---------------- Hết ---------------
Thí sinh không sử dụng tài liệu. Giám thị không giải thích gì thêm.
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT ĐỘI DỰ TUYỂN HSG TỈNH LỚP 8 TRIỆU SƠN Năm học 2022 - 2023 Môn thi: Toán Hướng dẫn chấm Ngày 17 tháng 3 năm 2023
(Hướng dẫn chấm có 05 trang, gồm 05 câu) Câu Nội dung Điểm 1. 2,5đ * ĐKXĐ: x  2  , x  1.  Ta có: 0.25 2 2      x 3x 2 x x  1 1  P   :  .  2 2    x  x  2 x 1    x 1 x 1    x   1  x  2 x(x 1)   x 1 x 1      :    0.25
 (x 1)(x 2) x  1  x  1      (x 1)(x 1) (x 1)(x 1)      x 1 x  2x =  :    x 1
x 1  (x 1)(x 1) 0.5 1 (x 1)(x 1) = . x 1 2x x 1 = 0.25 2x x 1 Vậy với x  2  , x  1  thì P = . 0.25 2x 1 x 1 2x x 1 + Ta có:   1   1  0 P 8 x 1 8 2 16x (x 1) 8(x 1)     0 1 8(x 1) 8(x 1) 8(x 1) (4,0đ)
x   x  2   x   2 16 1 8 1 (x  3)   0   0   1 0.5 8(x 1) x 1
+ Nếu: x  3  0  x  3  (1) luôn đúng với x  2  , x  1  . 0.25
+ Nếu: x    x    x  2 3 0 3 3  0  . x  x  2 3 
 0  x 1  0  x  1.  0.25 x 1 1 x 1 Vậy với x  1   x  3 thì   1. P 8 2. 1,5đ  1 1   1 1   1 1 Ta có:  a   b   c   2         b c   c a   a b  2
a b  c 2
 b c  a 2
 c a  b   2 0,25 abc 2 2 2 2 2 2
 a b  a c  b c  b a  c a  c b  2abc  0
 aba  b  ca  b2 2
 c a  b  0  a  b 2
ab  ac  bc  c   0
 a  bb  cc  a  0 0,5 0,25 2 1 1 1
 Xét a  b . Từ 3 3 3
a  b  c  1  c  1. Suy ra:    1. a b c 0,25 1 1 1
 Xét b  c . Từ 3 3 3
a  b  c  1  a  1. Suy ra:    1 a b c 1 1 1
 Xét c  a .Từ 3 3 3
a  b  c  1  b  1 . Suy ra:    1 a b c 1 1 1 Vậy  
 1 khi a, b, c khác không thỏa mãn: a b c 0,25  1 1   1 1   1 1  a   b   c   2       và 3 3 3
a  b  c  1.  b c   c a   a b  1. 2đ + Điều kiện: x   1 0,25 + Ta có: 3 2 3 3 2 2  x   x  x  x   x   x  3 x   x   3 . x x    3 0,5            x 1  x 1  x 1 x 1 x 1 x 1    
Khi đó phương trình đã cho trở thành 0,5 3 2 3 2 2 2 2  x   x  x  x  3  3  3 1  27  1  3       x 1 x 1 x 1 x 1       2 2 x x     
 x  x     x  2 2 1 3 4 4 4 0 2  0  x  2 x 1 x 1 0,5 0,25 KL: x=2 2. 2đ + Ta có: 2  2 1 (4,0đ) 2 2
2x y  y x  x  2 y  6xy   1 2x  y    6    x y  1 x y   xy     4  2 1 x y  xy     4 xy y x   xy y x  .   1   1  2 x   y   6        x  y     0,5  1   1  x  y   4      x   y    1 x   a   x
2a  b  6 + Đặt    1 ab  4  y   b   y  3 a  2 0,5 b  2
+ Giải hệ trên ta có:   a 1  0,5  b  4   1 x   2   x x  1 + Với    1 y  1  y   2   y  0,5  1 x   1  + Với  x  VN ( ) 1  y   4  y 
KL Cặp số  x; y  1;  1 1. 2đ + Biến đổi
 xy  x  2 2
1  xy  x  3x
  xy  x  2 2
1  xy  x 1  x  2x 1 0,25
  xy  x  
1  xy  x  
1 1   x  2 1
  xy  x  
1  xy  x  2   x  2 1 (1) 0.5  
+ Nếu x 1  0  x  1 thay vào (1) tìm được y  2  ; y  3  0,25
+ Nếu x 1  0  x  1
 : Khi đó VT(1) là tích hai số nguyên liên tiếp, VP(1)
là bình phương của số nguyên khác 0. Nên phương trình vô nghiệm. 0,5
KL : Các số x, y nguyên thoả mãn điều kiện bài toán là:  ; x y    1, 2  ;1, 3  . 0,5 2. 2đ
+ Giả sử p là số nguyên tố. 3 (4,0đ) a p
Từ: a2b2= p(a2+b2) 0.5  (1) b p
 a2b2 p2  p(a2+b2)p2  a2+b2p (2) 0.5
+ Từ (1) và (2)  ap và bp 1 1 2 1 2
+ Từ a ≥ p, b ≥ p       p≤2 (3) 0.5 2 2 2 a b p 2 p p 1 1 1 1 1
+ Từ a > 2, b > 2       p  2 (4) 0.25 2 2 a b 4 4 2
+ Từ (3), (4)  mâu thuẫn, chứng tỏ p là hợp số. 0.25 4 1. y x a.  ACO và  BOD có: D  CAO =  OBD (= 900)
 AOC = BDO (cùng phụ với 0,25 M BOD) C
Do đó:  ACO ~  BOD (g.g) 0,25 N AC AO 2  
 AC.BD  A . O BO  a 0,5 BO BD A B O E
* Kéo dài CO cắt tia đối của By tại E. 0,25  AOC =  BOE (g.c.g ) 0,25
=> CO = EO; AC = BE (các cạnh tương ứng)
=> tam giác DCE cân tại D (vì có đường cao DO đồng thời là trung tuyến) 0,25  DC= DE 4
+ Mà DE = BE + BD = AC + BD hay CD = AC + BD. (6,0đ) 0,25
b. Ta có:  ODM ~  ODB (g.g)  MO = BO  MO = AO 0,25
  ACO =  MCO (cạnh huyền - cạnh góc vuông)  MC = CA 0,5
+ Chứng minh tương tự ta có: MD = BD.
+ Xét hai tam giác CAN và BDN.
Có AC//BD (cùng vuông góc với AB ) 0,25 AN AC => 
(Hệ quả Định lí Ta-let) ND BD 0,5 AN CM hay  (MC= CA; MD = BD ) ND MD
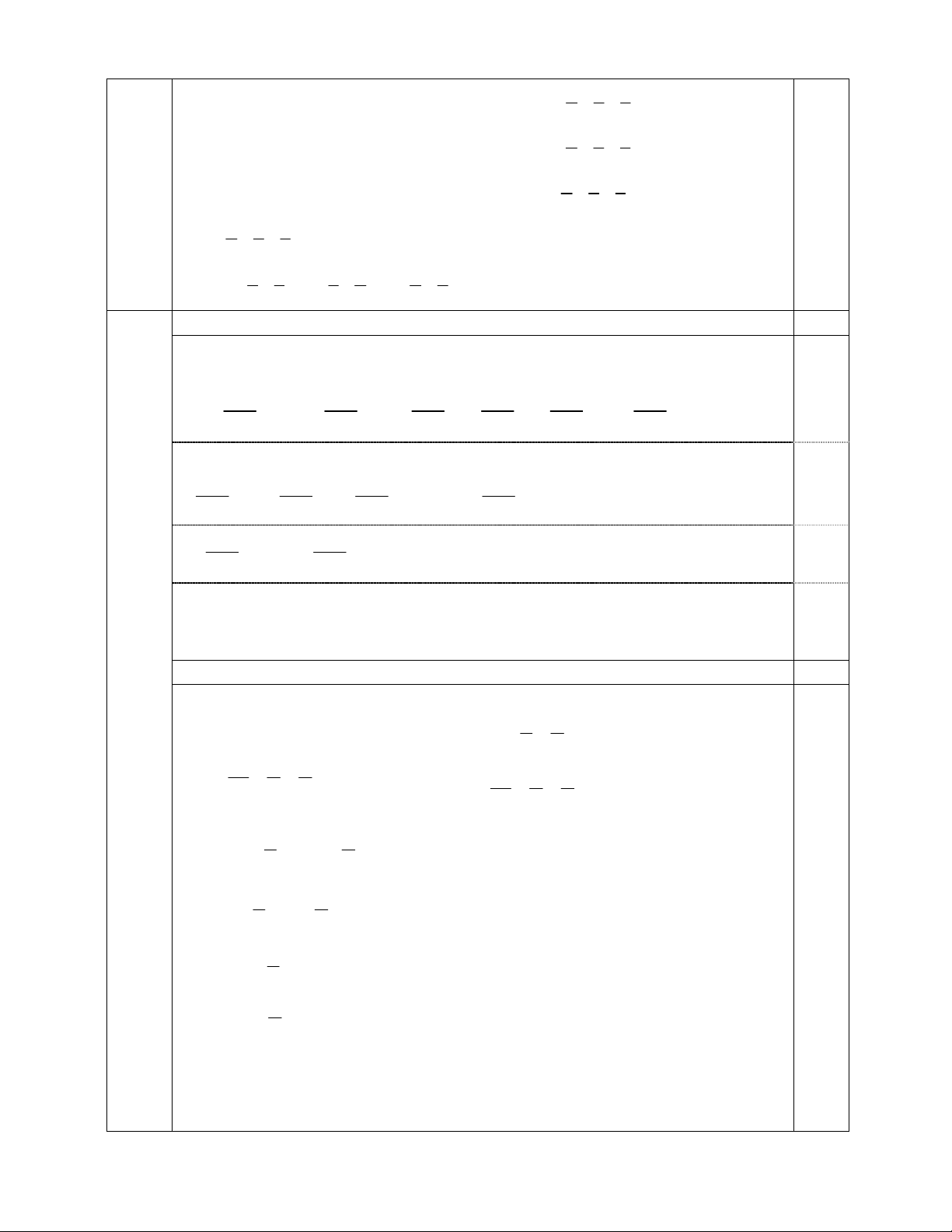
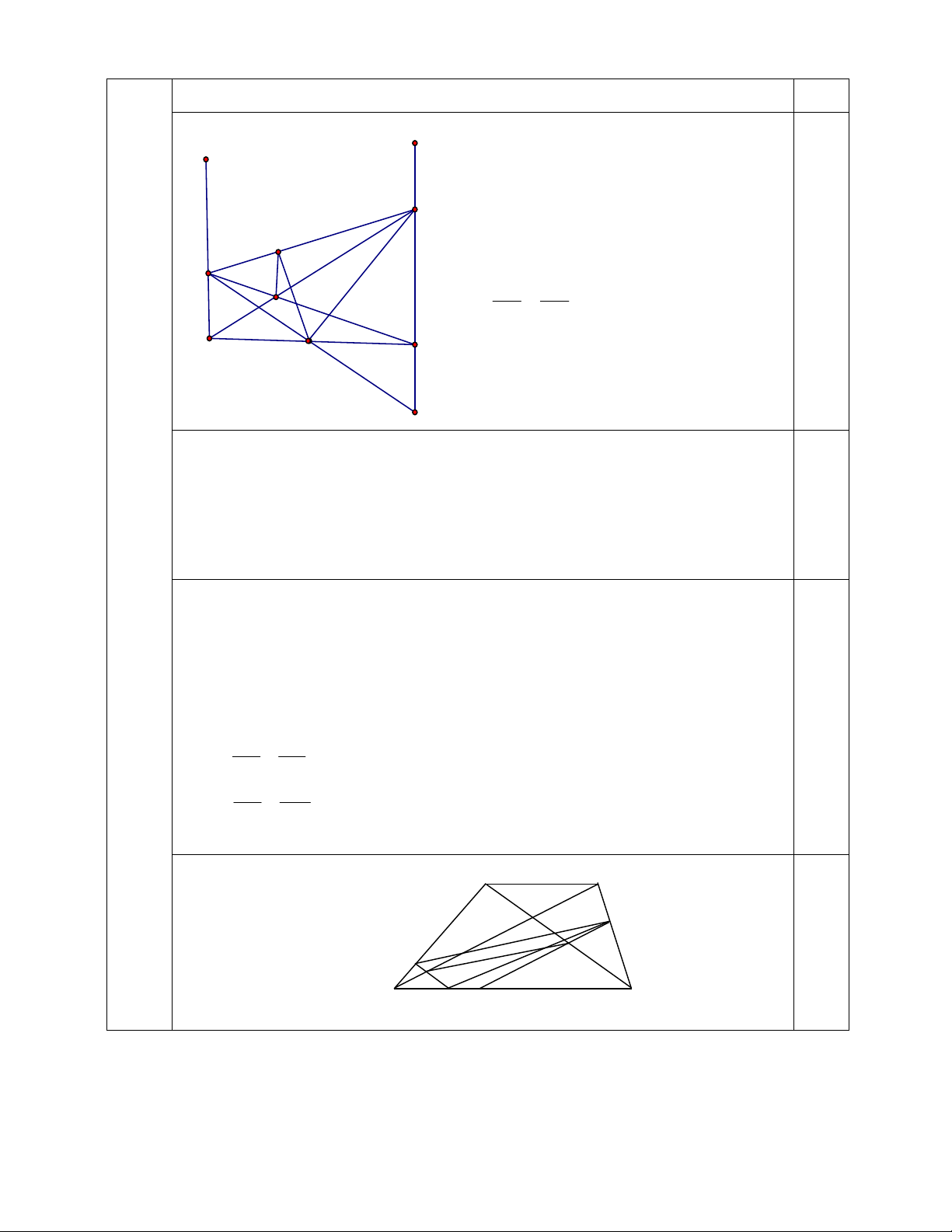
=> MN//AC (Định lí Ta-let đảo). 0,5 2. A B O Q P N I M K J D C E F 5
+ Gọi O là giao điểm của AC và BD.
+ Qua M kẻ đường thẳng song song với AC cắt DC tại E.
+ Qua Q kẻ đường thẳng song song với BD cắt DC tại F.
+ ME cắt BD tại J, QF cắt CA tại K. - Ta có: MJ DJ JE MJ OA     AO DO OC JE OC KQ CK KF QK OB     OB CO OD KF OD OA OB MJ QK    OC OD JE KF 0.5 NM NJ PK PQ + Mặt khác:   1;   1 NP NO PO PN
=> N, P lần lượt là trung điểm của OJ và OK => NP//JK. 0.5
+ Nếu E không trùng với F. Nối QE cắt JK tại I, ta có: KQ JM IQ  
 KI / /EF  MQ//DC (không đúng với gt) KF JE IE 1
=> E trùng với F  I  K  NP  .IJ. 2 0.5 2 JE OC
+ Ta có:  I  K  IJ  MQ   2 
 2  CD  2 A . B 0.5 3 JM OA 1 1 1 Đặt  a,  , b
 c ; ta có: a, ,
b c là các số dương và a  b  c  3 . x y z a b c Khi đó: A    2 2 2 1 b 1 c 1 a 0,25 2 2 a ab ab ab a ab Ta có:  a   a   a    a  (1) 2 2 2 1 b 1 b 2b 2 1 b 2 b bc c ac Tương tự:  b  (2);  c  (3). 0,5 2 1 c 2 2 1 a 2 5
Cộng vế tương ứng của (1), (2) và (3), ta được: (2,0đ) a b c
ab  bc  ca 0,25 A   
 a  b  c  2 2 2 1 b 1 c 1 a 2 Ta lại có:  2 2 2
a  b  c   3ab  bc  ca  3  ab  bc  ca . 0,25 3 3 Từ đó A  3   A  2 2 0,5
Dấu “=” xảy ra, khi và chỉ khi: a  b  c  1  x  y  z  1 3 Vậy, min A 
khi x  y  z  1 2 0,25 Chú ý:
1. Thí sinh có thể làm bài bằng cách khác, nếu đúng vẫn được điểm tối đa.
2. Nếu thí sinh chứng minh bài hình mà không vẽ hình thì không chấm điểm bài hình. 6