Đề chọn học sinh giỏi tỉnh Toán THPT năm 2024 – 2025 sở GD&ĐT Khánh Hòa

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI THPT CẤP TỈNH KHÁNH HÒA NĂM HỌC 2024 - 2025 Môn thi: TOÁN
ĐỀ THI CHÍNH THỨC Ngày thi: 06/12/2024
(Đề thi có 02 trang)
Thời gian: 180 phút (không kể thời gian phát đề) Câu 1 (3,50 điểm):
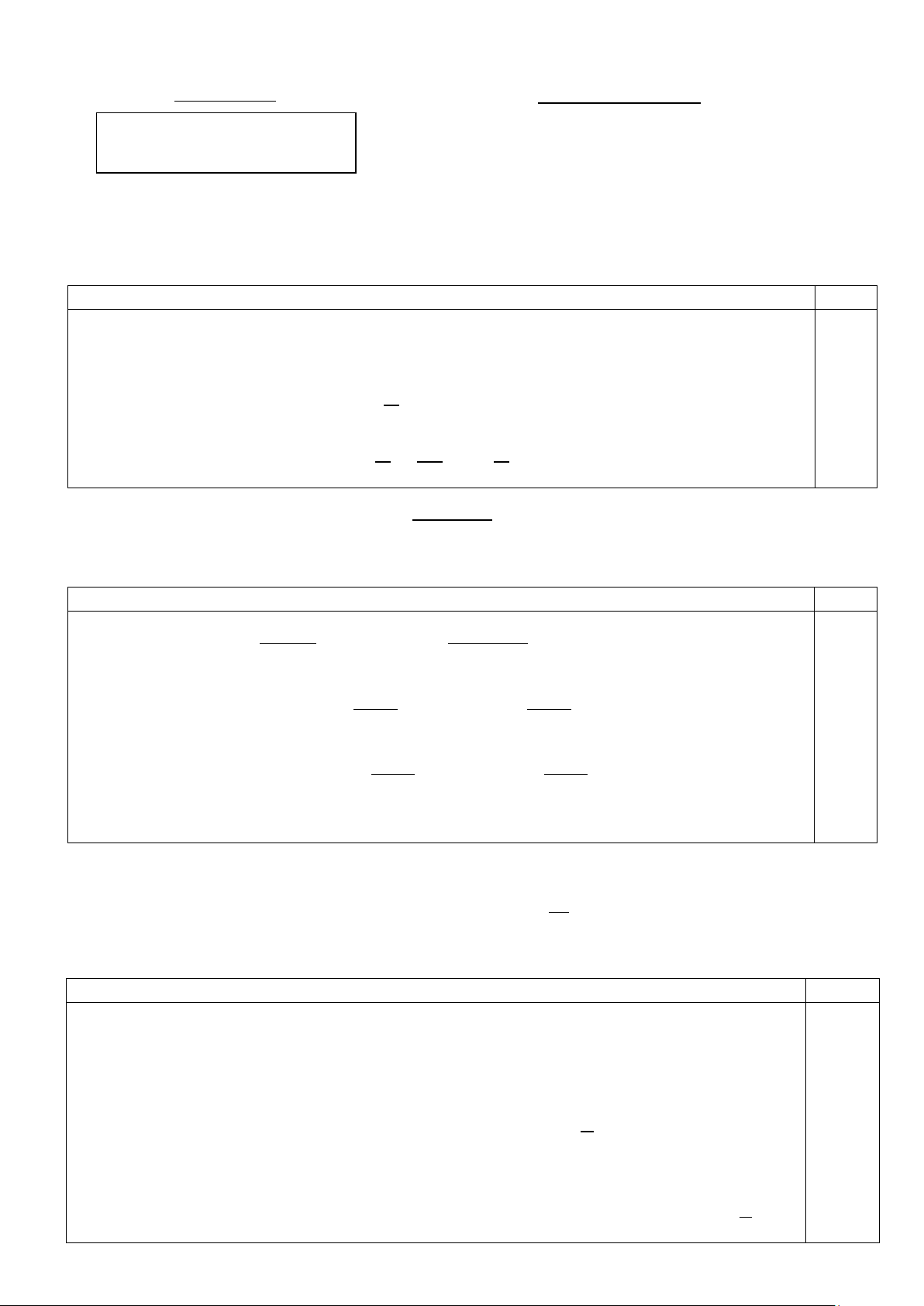
a) Giải phương trình cosx(sinx  cosx  sin 3x)  sinx sin 3x .  
b) Cho dãy số hữu hạn 2025n u  log   
, với n  {1; 2; 3; ...; 2024}. n
2025 2025  n 
Hãy tính tổng tất cả các số hạng của dãy số trên. Câu 2 (3,50 điểm): a) Cho hàm số 3 2 m
y  2(1  m)x  3(m  1)x  x 
 1 (1), (với m là tham số). 2
Chứng minh rằng đồ thị của hàm số (1) luôn đi qua 3 điểm cố định thẳng hàng với mọi m .
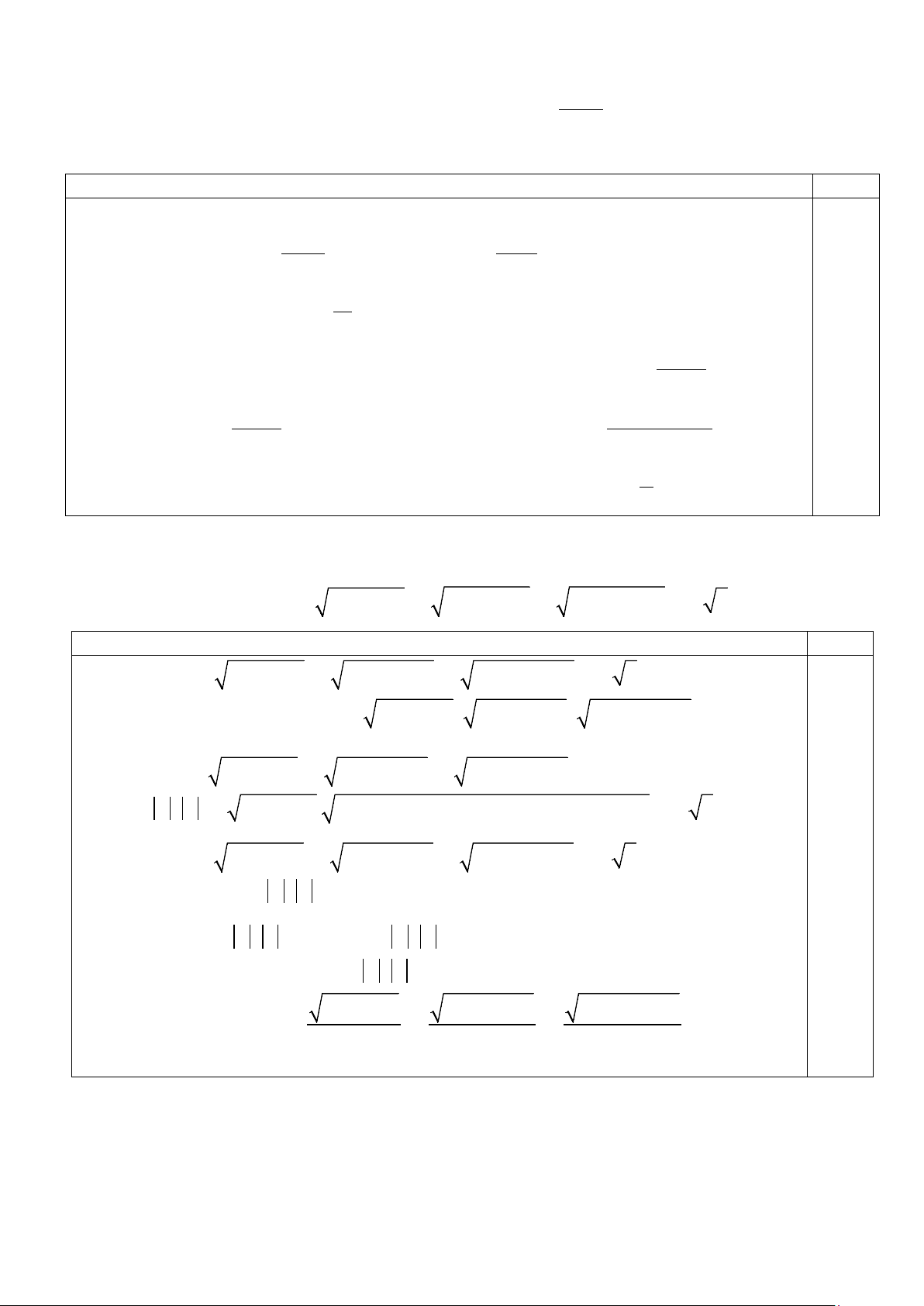
b) Cho các số thực x,y thỏa mãn: x 3y 1 xy  xy 1  1 e e
 x(1  y)  1  e 
 3y , (với x  0). x 3y e
Tìm giá trị nhỏ nhất của biểu thức T  x  2y  3 . Câu 3 (4,00 điểm):
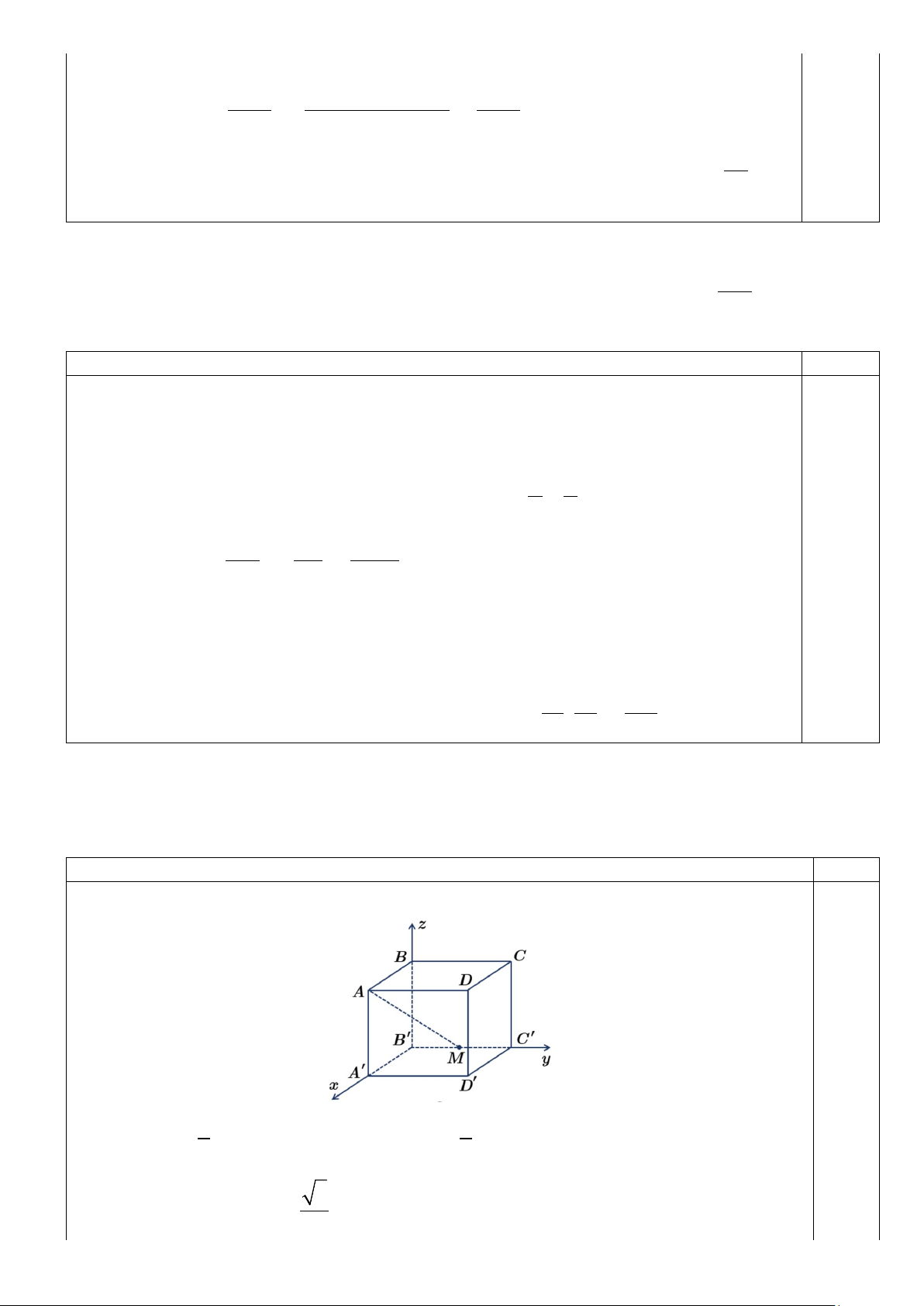
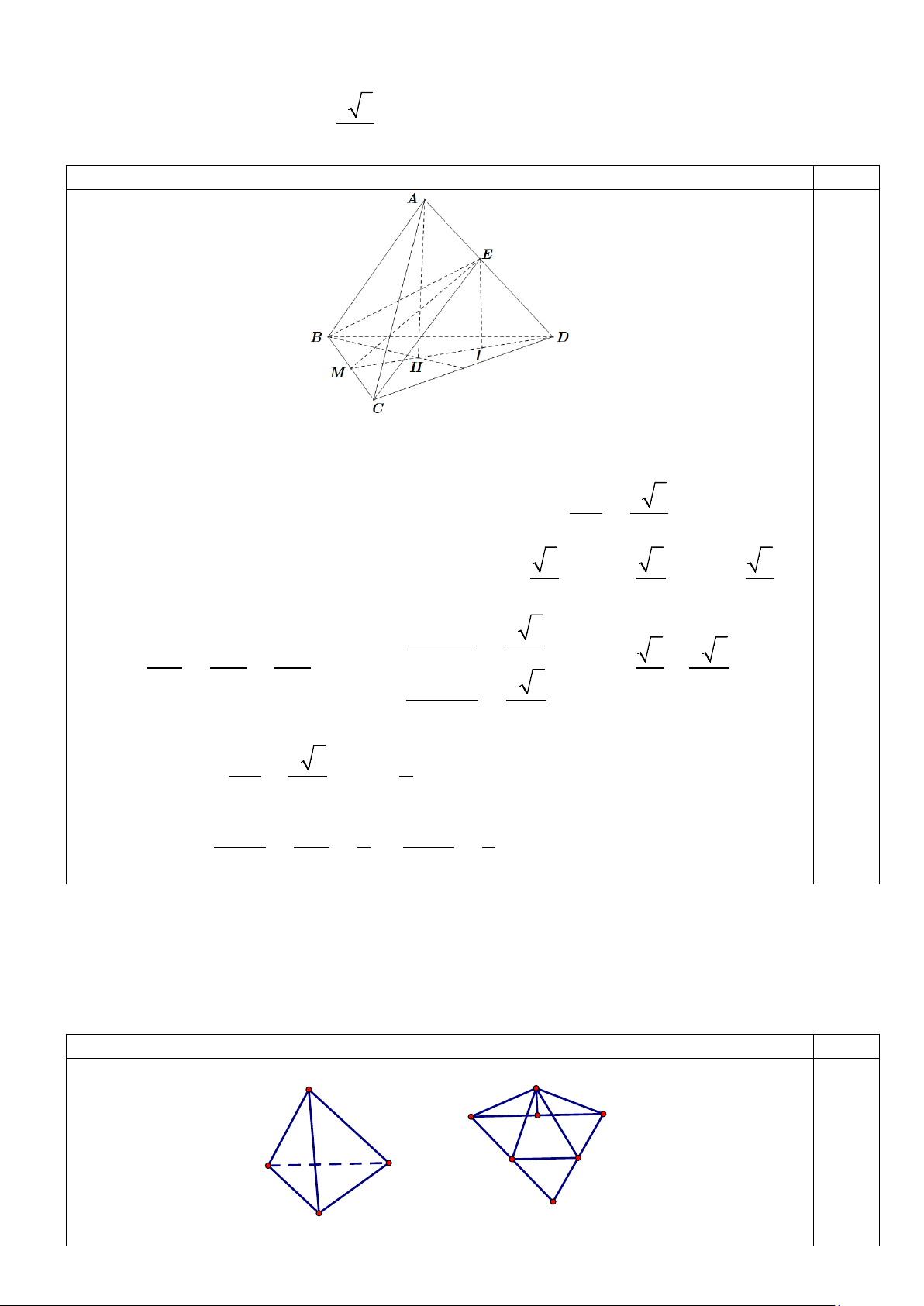
a) Giải bất phương trình x   2 x    3 log 1 log 3 17 log x  3 5 .  2 2 x   3y  27  b) Cho x, ,
y z là các số thực dương thỏa mãn  2 2 y
  yz  z  16 .  2 2 x
  3xz  3z  75 
Tính giá trị của biểu thức P  2xy  3yz  zx . Câu 4 (3,00 điểm):
a) Một lớp học có (2n  3) học sinh (với *
n   ), trong đó có ba em , , A B C . Xếp ngẫu
nhiên các học sinh của lớp học vào ngồi một dãy ghế có đánh số thứ tự từ 1 đến (2n  3),
mỗi em ngồi một ghế. Biết xác suất để số ghế của ba em , ,
A B C theo thứ tự đó tạo thành
cấp số cộng là 17 . Tìm số học sinh của lớp học. 1155
b) Có 35 con thỏ (bao gồm thỏ trắng và thỏ đen) được nhốt vào hai chuồng. Bắt ngẫu nhiên
mỗi chuồng một con thỏ. Biết xác suất để bắt được hai con thỏ đen là 247 , hãy tính xác 300
suất để bắt được hai con thỏ trắng. Trang 1/2 Câu 5 (6,00 điểm):
a) Cho hình lập phương ABCD.AB C  D
  và M là trung điểm của B C   . Tìm số đo góc
giữa hai đường thẳng AM và BC  .
b) Cho tứ diện đều ABCD và điểm E trên cạnh AD sao cho tan của góc giữa hai mặt phẳng 5 2
(BCD) và (BCE) bằng
. Tính tỷ số thể tích của hai khối tứ diện ABCE và EBCD . 7
c) Cho tứ diện ABCD có  o ACB  60 và         o
ACD  BCD  CAD  BAD  BAC  CBD  ABD  ABC  180 .
Gọi S là diện tích toàn phần của hình tứ diện ABCD . Hãy tìm giá trị lớn nhất của S , biết
chu vi tam giác ABC bằng 3.
 HẾT 
- Cán bộ coi thi không giải thích gì thêm.
- Họ và tên thí sinh:……………………………. SBD:……………/Phòng:………………...
- Cán bộ coi thi 1:……………………………… Chữ ký:……………………………………
- Cán bộ coi thi 2:……………………………… Chữ ký:…………………………………… Trang 2/2
SỞ GIÁO DỤC VÀ ĐÀO TẠO KỲ THI CHỌN HỌC SINH GIỎI THPT CẤP TỈNH KHÁNH HÒA NĂM HỌC 2024 - 2025 HƯỚNG DẪN CHẤM Môn thi: TOÁN ĐỀ THI C HÍNH THỨC Ngày thi: 06/12/2024
(H ướng dẫn chấm có 06 trang) Câu 1 (3,50 điểm):
a) Giải phương trình cosx(sinx  cosx  sin 3x)  sinx sin 3x . Hướng dẫn chấm Điểm Pt 2
 cos x  (sin x  sin 3x)cos x  sin x sin 3x  0 0,50
 (cosx  sin x)(cosx  sin 3x)  0 0,50 • 
cos x  sin x  0  x    k , (với k   ); 0,50 4 •  k 
cos x  sin 3x  0  x   ; x 
 k , (với k   ). 0,50 8 2 4  
b) Cho dãy số hữu hạn 2025n u  log   
, với n  {1; 2; 3; ...; 2024}. n
2025 2025  n 
Hãy tính tổng tất cả các số hạng của dãy số trên. Hướng dẫn chấm Điểm     • 2025n   n u  log    1  log     0,50 n 2025   2025 2025n    2025  n      • 1   2024 u  u  1  log    1  log      2 ;… 1 2024 2025   2025 2024    1      0,50 • 1012   1013 u  u  1  log    1  log      2 1012 1013 2025   2025 1013   1012
• u  u  u    u  10122  2024 . 0,50 1 2 3 2024 Câu 2 (3,50 điểm): a) Cho hàm số 3 2 m
y  2(1  m)x  3(m  1)x  x 
 1 (1), (với m là tham số). 2
Chứng minh rằng đồ thị của hàm số (1) luôn đi qua 3 điểm cố định thẳng hàng với mọi m . Hướng dẫn chấm Điểm
• Hàm số được viết lại 3 2 3 2
(4x  6x  1)m  4x  6x  2x  2  2y  0 . 0,50
• Tọa độ điểm cố định (nếu có) của họ đồ thị đã cho thỏa mãn 3 2  3 2  4
 x  6x  1  0 4
 x  6x  1  0       0,50 3 2 3 4
 x  6x  2x  2  2y  0  y     x    2
• Hệ trên có ba nghiệm phân biệt nên đồ thị của hàm số đã cho luôn đi qua ba
điểm cố định và các điểm cố định này nằm trên đường thẳng 3
(d) : y  x  . 0,50 2 Trang 1/6
b) Cho các số thực x,y thỏa mãn: x 3y 1 xy  xy 1  1 e e
 x(1  y)  1  e 
 3y , (với x  0). x 3y e
Tìm giá trị nhỏ nhất của biểu thức T  x  2y  3 . Hướng dẫn chấm Điểm
• Biến đổi giả thiết bài toán x 3y 1 xy 1  1 e 
 x  3y  e   xy  1 (*) 0,50 x 3y xy 1 e e  • Vì hàm số 1 f (t) t  e 
 t đồng biến trên  nên t e 0,50 x  1
(*)  f (x  3y)  f (xy  1)  x  3y  xy  1  y  x  3 2    • Thay x 1 x 4x 7 y 
vào biểu thức T , ta được T  h(x)  . 0,50 x  3 x  3 • Khảo sát hàm 7
h(x) , với x  0 cho ta minT  min h(x)  . 0,50 x 0  3 Câu 3 (4,00 điểm):
a) Giải bất phương trình x   2 x    3 log 1 log 3 17 log x  3 5 . Hướng dẫn chấm Điểm
• Bpt  logx  1  2 logx  3  17  3 logx  3 5 0,50 Đặt  
u  (1; 1; 1) và v   logx 1; 2logx  3; 17  3logx , ta có •  
u.v  log x  1  2 log x  3  17  3 log x 0,50  
u . v  1  1  1. log x  1  2 log x  3  17  3 log x  3 5
• Bpt  logx  1  2 logx  3  17  3 logx  3 5 0,50    
 u.v  u . v (*)        
• Vì u.v  u . v .cos(u; v)  u . v nên      
(*)  u.v  u . v  u và v cùng hướng 0,50 log x  1 2 log x  3 17  3 log x    1 1 1
 logx  4  x  10 000 .  2 2 x   3y  27  b) Cho x, ,
y z là các số thực dương thỏa mãn  2 2 y
  yz  z  16 .  2 2 x
  3xz  3z  75 
Tính giá trị của biểu thức P  2xy  3yz  zx . Trang 2/6 Hướng dẫn chấm Điểm
• Trong mặt phẳng lấy điểm x
O tùy ý, vẽ OA  , 3
OB  y , OC  z sao cho 0,50  o  o  o AOB  90 , 120 BOC  , AOC  150  2  2 x 2 AB    y  9  3 • Ta có  2 2 2 BC 
 y  yz  z  16  A
 BC vuông tại B .  0,50  2  2 x 2 A
 C   xz  z  25  3 • xy yz 3 xz S  S  S  S     6 0,50 OAB OBC OAC ABC 2 3 4 4 3
 2xy  3yz  xz  24 3  P  24 3 0,50 Câu 4 (3,00 điểm):
a) Một lớp học có (2n  3) học sinh (với *
n   ), trong đó có ba em , , A B C . Xếp ngẫu
nhiên các học sinh của lớp học vào ngồi một dãy ghế có đánh số thứ tự từ 1 đến (2n  3),
mỗi em ngồi một ghế. Biết xác suất để số ghế của ba em , ,
A B C theo thứ tự đó tạo thành
cấp số cộng là 17 . Tìm số học sinh của lớp học. 1155 Hướng dẫn chấm Điểm
• Tính số cách xếp ba học sinh A, B, C theo thứ tự lập thành cấp số cộng.
Xếp B vào ghế số 2 thì có 2! cách xếp ghế cho A và C .
Xếp B vào ghế số 3 thì có 2.2! cách xếp ghế cho A và C .
Xếp B vào ghế số 4 thì có 3.2! cách xếp ghế cho A và C ;…
Xếp B vào ghế số n thì có (n 1).2! cách xếp ghế cho A và C .
Xếp B vào ghế số (n  1) thì có n.2! cách xếp ghế cho A và C . 0,50
Xếp B vào ghế số (n  2) thì có (n  1).2! cách xếp ghế cho A và C .
Xếp B vào ghế số (n  3) thì có n.2! cách xếp ghế cho A và C ; …
Xếp B vào ghế số (2n  2) thì có 2! cách xếp ghế cho A và C .
Vậy số cách xếp ba học sinh , ,
A B C theo thứ tự tạo thành cấp số cộng là 2
2.2!.(1 2 ... n) (n 1).2! 2! n
 (n 1) (n 1)           2!(n  1)  
• Tính xác suất:
Với mỗi cách xếp ba em , ,
A B C như trên, có (2n)! cách xếp các em còn lại.
Số cách xếp các học sinh của lớp thỏa mãn số ghế của ba em , , A B C theo thứ
tự tạo thành cấp số cộng là 2
n(X)  (2n)!.2!.(n  1) . Ta có 0,50 2 (2n)!2!(n  1) n( )
  (2n  3)!  P(X)  . (2n  3)! Trang 3/6
• Tính số học sinh của lớp: 17 (n  1) 17 P(X)    1155
(2n  1)(2n  3) 1155 0,50 2
 68n  1019n  1104  0  n  16 (loại 69 n   ). 68
Số học sinh của lớp là 2n  3  2.16  3  35 học sinh.
b) Có 35 con thỏ (bao gồm thỏ trắng và thỏ đen) được nhốt vào hai chuồng. Bắt ngẫu nhiên
mỗi chuồng một con thỏ. Biết xác suất để bắt được hai con thỏ đen là 247 , hãy tính xác 300
suất để bắt được hai con thỏ trắng. Hướng dẫn chấm Điểm
• Giả sử chuồng thứ nhất có x con thỏ, trong đó có a con thỏ đen,
chuồng thứ hai có y con thỏ, trong đó có b con thỏ đen. 0,50
Ta có x  y  35 , (với * a, ,
b x, y   ; a  x, b  y ).
• Xác suất bắt được hai con thỏ màu đen là a b P   . x y Ta có 247 a.b 13.19 0,50 P     a  13; 19 b  300 x.y 300
(vì 13; 19 là các số nguyên tố và không mất tổng quát, giả sử a  b ).
• Khi đó x  15; 20 y  .
Số thỏ trắng ở mỗi chuồng thứ nhất và chuồng thứ hai tương ứng là 2 và 1. 0,50
Vậy xác suất để bắt được hai con thỏ màu trắng là 2 1 1 .  15 20 150 Câu 5 (6,00 điểm):
a) Cho hình lập phương ABCD.AB C  D
  và M là trung điểm của B C   . Tìm số đo góc
giữa hai đường thẳng AM và BC  . Hướng dẫn chấm Điểm
• Chọn hệ trục tọa độ Oxyz sao cho B (0; 0; 0), A (1
 ; 0; 0), C (0; 1; 0), B(0; 0; 1). 0,50       • 1   1 M 0; ; 0, (1 A ; 0; 1)  AM   
 1; ;  1, BC   (0; 1;  1)  .  0,50  2     2 
 
  • 2 o o cos(AM; ) BC    (AM; )
BC   45  (AM; ) BC   45 . 0,50 2 Trang 4/6
b) Cho tứ diện đều ABCD và điểm E trên cạnh AD sao cho tan của góc giữa hai mặt phẳng 5 2
(BCD) và (BCE) bằng
. Tính tỷ số thể tích của hai khối tứ diện ABCE và EBCD . 7 Hướng dẫn chấm Điểm 0,50
• Gọi H , I lần lượt là hình chiếu vuông góc của A và E trên mặt phẳng (BCD).
Khi đó H , I  DM (với M là trung điểm của BC ). Ta có  BCD BCE    EI 5 2 ( ); (
)  DME  tan DME   . MI 7
• Đặt AB  1 và DE  x , ta tính được 6 AH  , 3 DH  , 3 MH  . 0,50 3 3 6  DE.AH x 6 EI     • DE EI DI 3 x 3  AD 3      MI   . 0,50 AD AH DH  DE.DH x 3 2 3 DI     AD 3 EI 5 2 5 tan     x  . 0,50 MI 7 8 V V Khi đó DE 5 DBCE   3 ABCE   . 0,50 V AD 8 V 5 ABCD BCDE
c) Cho tứ diện ABCD có  o ACB  60 và         o
ACD  BCD  CAD  BAD  BAC  CBD  ABD  ABC  180 .
Gọi S là diện tích toàn phần của hình tứ diện ABCD . Hãy tìm giá trị lớn nhất của S ,
biết chu vi tam giác ABC bằng 3. Hướng dẫn chấm Điểm D D C2 C3 H A B A B C1 C Trang 5/6
• Cắt tứ diện ABCD theo các cạnh , ,
CA CB CD và trải xuống mặt phẳng (ABD). Khi đó A
 DC  A  DC ; B
 DC  B  DC ; A
 BC  A  BC . 0,50 2 3 1 Ta có       o
CBD  ABD  ABC  C BD  ABD  ABC  180 3 1  C , , B C thẳng hàng. 3 1       o
CAD  BAD  BAC  C AD  BAD  BAC  180 2 1  C , , A C thẳng hàng. 2 1      o
ACD  BCD  BAC  AC D  BC D  180 . 2 1  C C DC  o C DC  120 , (vì   o
ACB  AC B  60 ) 1 2
3 là tứ giác nội tiếp, do đó 2 3 1
• Diện tích toàn phần của tứ diện ABCD là diện tích tứ giác C C DC . Ta có 1 2 3 S  S  S C C DC C C C C DC 1 2 3 1 2 3 2 3 Đặt 2 2
CA  x; CB  y  AB  x  y  xy Chu vi A  BC bằng 2 2
x  y  x  y  xy  3 . 0,50 Ta có 2 2
C C  2CA  2x;
C C  2CB  2y;
C C  2AB  2 x  y  xy . 1 2 1 3 2 3 2 2 C H C C   o x y xy 3 2 3 tan 60   DH   . DH 2. 3 3 • Ta có 1 o 1 S  S  S
 .C C .C C .sin 60  .DH.C C C C DC C C C C DC 1 2 1 3 2 3 1 2 3 1 2 3 2 3 2 2 0,50 2 2 2
x  y  xy (x  y)  3xy   3 3 2 
• Áp dụng bất đẳng thức (x y) xy  , ta có 4 2 2 2
3  x  y  x  y  xy  x  y  (x  y)  3xy 2 3 2 3
 x  y  (x  y)  (x  y)  (x  y) 0,50 4 2
 x  y  2 2 Vậy (x  y) 4 4 S    S 
(khi x  y  1). max 3 3 3
Chú ý: Học sinh giải cách khác, giám khảo căn cứ các ý trong đáp án để cho điểm.
 HẾT  Trang 6/6
Xem thêm: ĐỀ THI HSG TOÁN 12
https://toanmath.com/de-thi-hsg-toan-12
Document Outline

• De chinh thuc THPT-B (2024-2025)
  • ĐỀ THI CHÍNH THỨC
• HD cham chinh thuc THPT-B (2024-2025)
  • HƯỚNG DẪN CHẤM
  • ĐỀ THI CHÍNH THỨC
• HSG 12