Đề chọn học sinh giỏi tỉnh Toán THPT năm 2024 – 2025 sở GD&ĐT Long An

SỞ GIÁO DỤC VÀ ĐÀO TẠO KỲ THI CHỌN HỌC SINH GIỎI CÁC MÔN VĂN HÓA CẤP TỈNH LONG AN NĂM HỌC 2024-2025
MÔN THI: TOÁN-CẤP THPT ĐỀ CHÍ NH THỨC NGÀY THI: 23/3/2025
(Đề có 02 trang , gồm 05 câu)
Thời gian làm bài: 180 phút (không kể thời gian phát đề)
Lưu ý: Thí sinh không được phép sử dụng máy tính cầm tay.
Câu 1 (5,0 điểm).
a) Giải phương trình sau trên tập số thực: 2
x − 2x − 3 = x + 3 . 3
 xy + y +1 = 21x
b) Giải hệ phương trình 
(x, y∈). 2 2 2 9
 x y + 3xy +1 = 117x
Câu 2 (5,0 điểm).
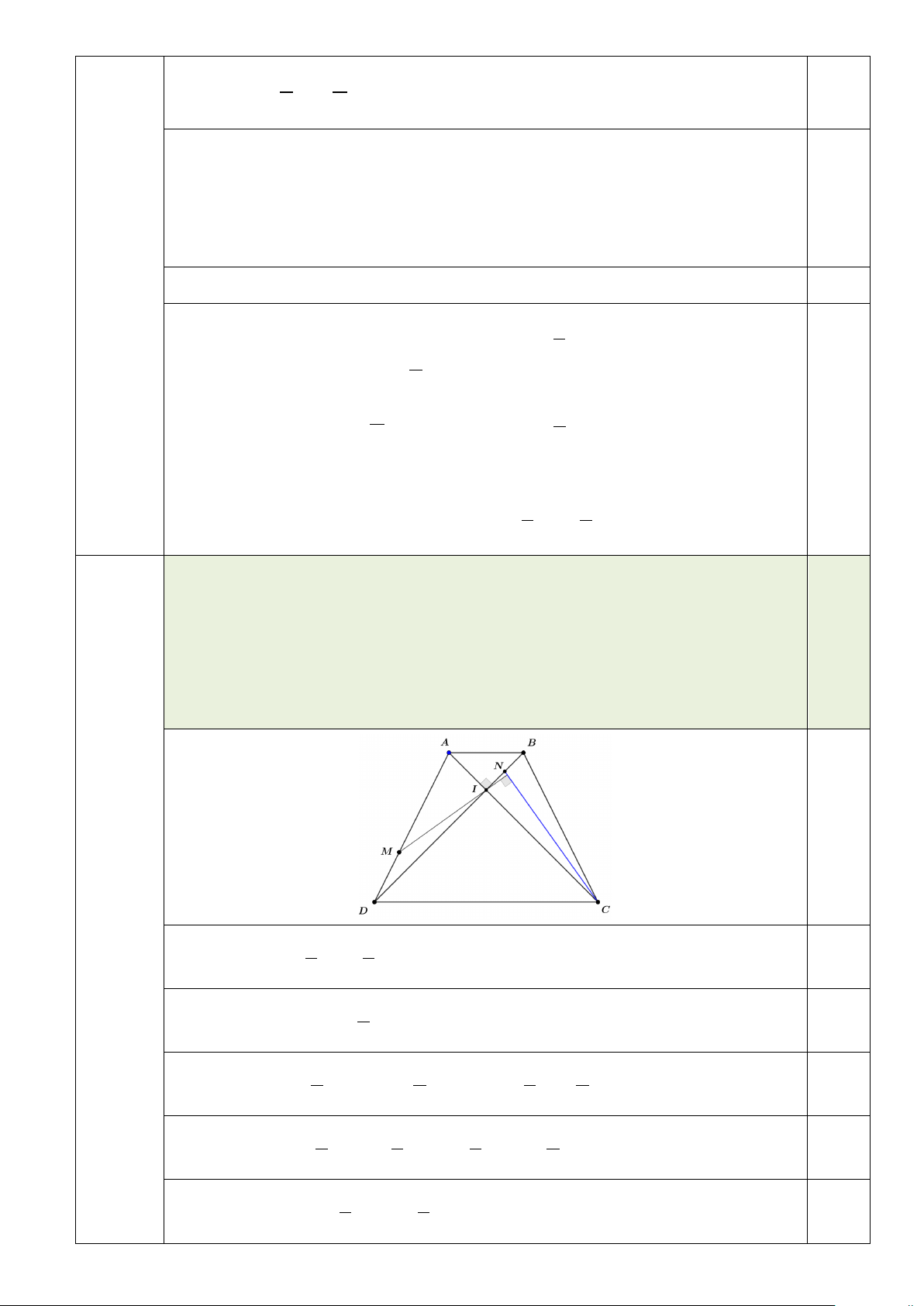
a) Trong mặt phẳng toạ độ Oxy , cho hình thang cân ABCD có hai đáy là AB và
CD với CD = 3AB , hai đường chéo AC, BD vuông góc nhau tại I . Lấy điểm M
thuộc cạnh AD sao cho DA = 3DM và điểm N là trung điểm của đoạn thẳng IB .
Đường thẳng IM đi qua điểm P(10;7) và đường thẳng CN có phương trình là
7x + 5y − 37 = 0 . Chứng minh rằng IM vuông góc với CN và tìm toạ độ điểm C ,
điểm D biết A(2;3).
b) Cho tam giác ABC có AD là đường phân giác trong góc A và BM là đường
trung tuyến kẻ từ đỉnh B (với D thuộc cạnh BC và M thuộc cạnh AC ). Biết rằng
hai đường thẳng AD và BM vuông góc với nhau và 3 BM = 5 − 2 5.AD . Tính 2 cos A.
Câu 3 (4,0 điểm).
a) Cho dãy số (a xác định bởi a = 0 và a = − + + , với mọi n ≥1. + a n n n 2 1 n ) 1 1
Chứng minh rằng a = (− )
1 n + n với mọi n ≥1 và tính tổng 2025 số hạng đầu tiên n của dãy số (a . n )
b) Cho dãy số (u xác định bởi u = 4 và 2 u = −
+ , với mọi n ≥1. + u u n n 5 n 9 n ) 1 1 Chứng minh rằng 1 1 1 + + ...+ < 1. u − 2 u − 2 u − 2 1 2 2025
Câu 4 (3,0 điểm).
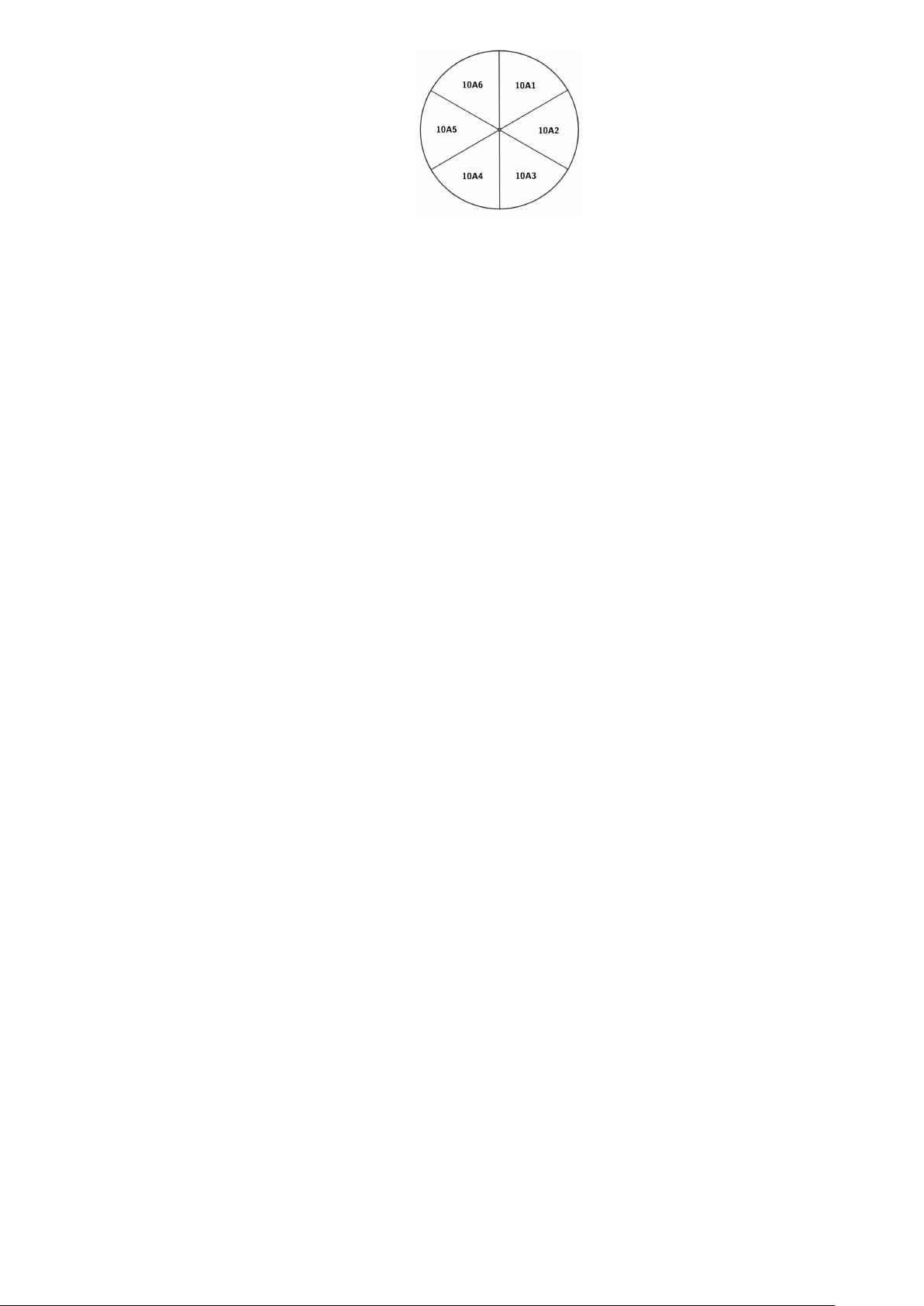
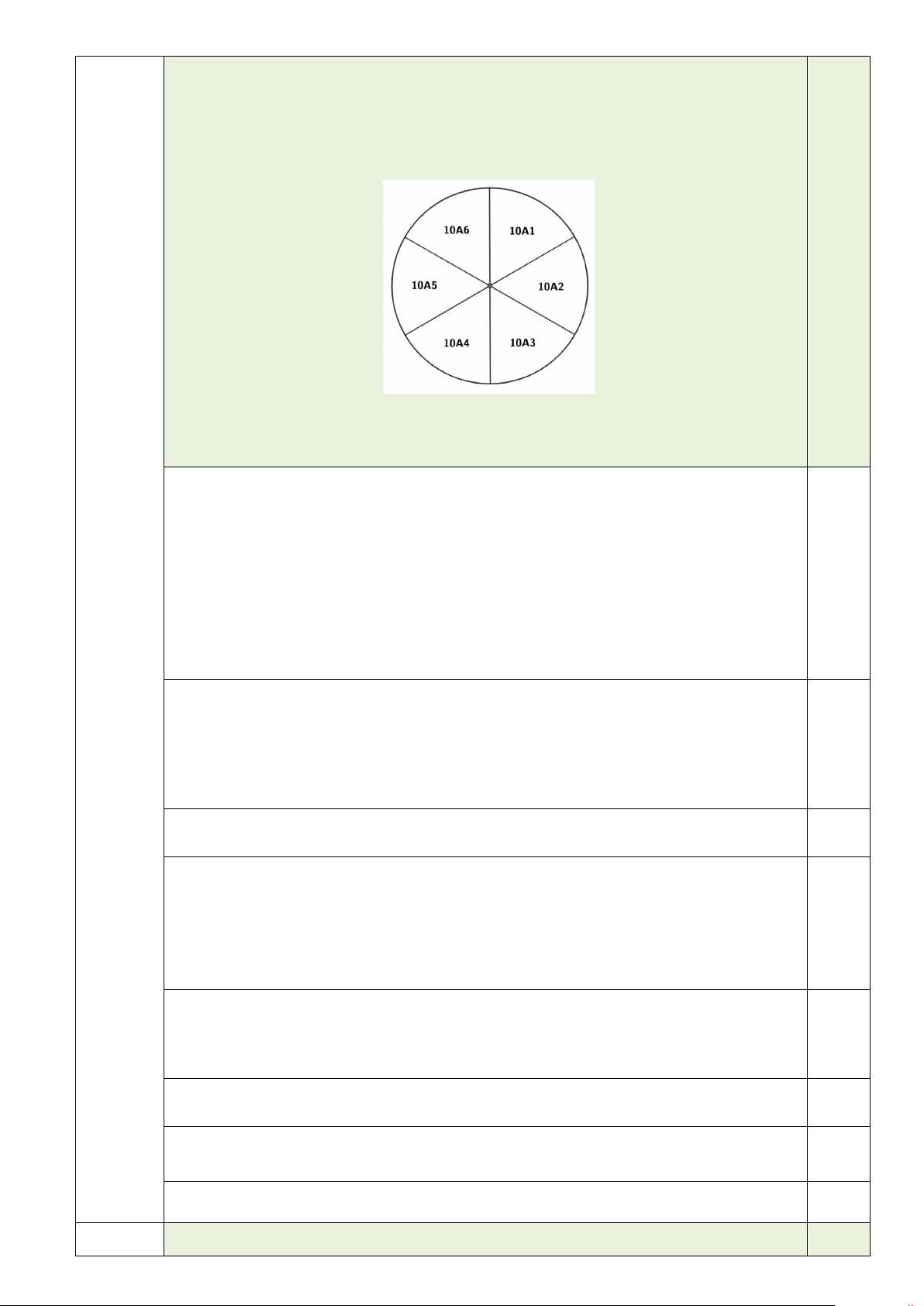
Một bồn hoa hình tròn ở giữa sân trường được chia thành 6 phần bằng nhau và
giao nhiệm vụ cho 6 lớp 10 chọn trồng một trong 4 loại hoa là hoa cúc, hoa hồng,
hoa lan, hoa hướng dương theo các khu vực hình quạt được phân công cụ thể như hình vẽ. Trang 1/2
Hỏi có tất cả bao nhiêu phương án trồng hoa của các lớp sao cho hai lớp được phân
công hai khu vực cạnh nhau thì không cùng trồng một loại hoa?
Câu 5 (3,0 điểm).
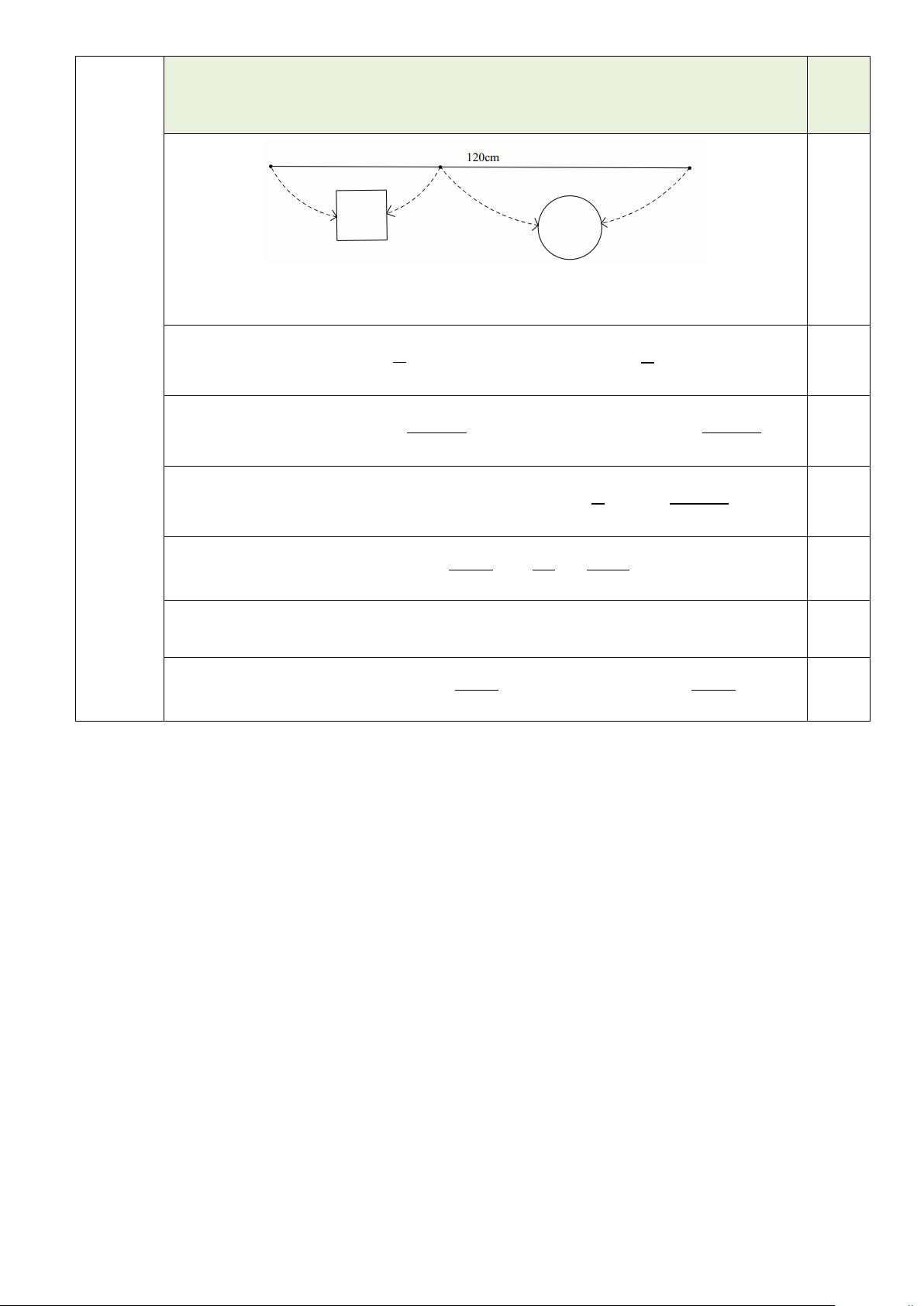
Một sợi dây kim loại dài 120 cm được cắt thành hai đoạn: đoạn dây thứ nhất
được uốn thành hình vuông, đoạn dây thứ hai được uốn thành vòng tròn. Tổng diện
tích của hình vuông và hình tròn đạt giá trị nhỏ nhất bằng bao nhiêu 2 cm ?
……………… HẾT ………………
- Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh:………………………………….. Số báo danh:…………………...
Chữ ký cán bộ coi thi 1:………………….. Chữ ký cán bộ coi thi 2:………………….. Trang 2/2
SỞ GIÁO DỤC VÀ ĐÀO TẠO KỲ THI CHỌN HỌC SINH GIỎI CÁC MÔN VĂN HÓA CẤP TỈNH LONG AN NĂM HỌC 2024-2025
MÔN THI: TOÁN-CẤP THPT NGÀY THI: 23/3/2025
Thời gian làm bài: 180 phút (không kể thời gian phát đề)
HƯỚNG DẪN CHẤM THI ĐỀ CHÍNH THỨC
(Hướng dẫn chấm gồm 06 trang) Câu Hướng dẫn chấm Điểm
Câu 1a Giải phương trình sau trên tập số thực: 2x − 2x −3 = x + 3 ( )1.
(3,0đ) Điều kiện: x ≥ 3−. 0,25 ( ) 2 1
⇔ x − x + = (x + ) 1 1 3 + x + 3 + 0,5 4 4 2 2  1   1 x   x 3  ⇔ − = + +  0,25 2 2     
 x + 3 = x −1 ⇔  . 0,5
 x + 3 = −x 3 17 x 3 x 1 x ± + = − ⇒ = . 0,5 2 1 13 x 3 x x ± + = − ⇒ = . 0,5 2  + − 
Thử lại, ta có tập nghiệm 3 17 1 13 S ;  =  . 0,5  2 2    Câu 1b 3
 xy + y +1 = 21x
(2,0đ) Giải hệ phương trình  (x, y∈). 2 2 2 9
 x y + 3xy +1 = 117x
Dễ thấy x = 0 không thỏa mãn hệ phương trình. 0,25  y 1 3y + + = 21 
Với x ≠ 0, ta có  x x  0,25  2 y 1 9y + 3 + = 117 2  x x  1  3  y y + + =   21   x  x ⇔  . 2 0,25   1 3  + − 3 y y =   117   x  x Trang 1/6 a + b = 21 Đặt 1 = 3 + , y a y b = ta có . x x  0,25 2
a − 3b = 117 a = 15 −  b   = 36 ⇔  . 0,25 a = 12   b   = 9 Với a = 15
− ,b = 36 ta có hệ vô nghiệm. 0,25  1 x =  1  3 3y + =12    y = 3 Với 
a =12,b = 9 ta có x  ⇔ . y   = 9  1   x =  x  9 0,5  y = 1
Vậy hệ phương trình có nghiệm (x y)  1   1
; ∈  ;3; ;1 .   3   9  
Câu 2a Trong mặt phẳng toạ độ Oxy , cho hình thang cân ABCD có hai đáy là AB ,
(3,0đ) CD với CD = 3AB , hai đường chéo AC, BD vuông góc nhau tại I . Lấy
điểm M thuộc cạnh AD sao cho DA = 3DM và điểm N là trung điểm của
đoạn thẳng IB . Đường thẳng IM đi qua điểm P(10;7) và đường thẳng CN
có phương trình là 7x + 5y − 37 = 0 . Chứng minh rằng IM vuông góc với
CN và tìm toạ độ điểm C , điểm D biết A(2;3). Ta có 1 1
IA = IB = IC = ID 0,25 3 3
     Ta có 1
CN = IN − IC = IB − IC 0,25 2         2 2
IM = IA + AD = IA + (ID − IA) 1 2 = IA + ID 0,25 3 3 3 3           Khi đó 1 1 1 2 CN.IM = . IB IA + . IB ID − .
IA IC − IC.ID . 0,25 6 3 3 3 1 1 = 0 − . IB ID + .
IA IC − 0 = 0 . Vậy IM ⊥ CN . 0,25 3 3 Trang 2/6
Đường thẳng IM có phương trình 5x − 7y −1 = 0 . 0,25  −    − Ta có 5t 1 I IM I t;  ∈ ⇒ t   ; 20 67 IC = 3
− .IA ⇒ C 4t −  6; . 0,25 7      7 
C ∈CN ⇒ ( t − ) 20t − 67 7. 4 6 + 5.
− 37 = 0 ⇒ t = 3 ⇒ I (3;2);C (6;− ) 1 . 0,25 7
Đường thẳng BD có phương trình x − y −1 = 0 . 0,25
7x + 5y − 37 = 0 Toạ độ điểm  7 5 N ( ; x y) thoả hệ:  N  ;  ⇒ . 0,25 x y 1 0 2 2  − − =     
Ta có DI = 3.IB = 6.IN , do đó tìm được điểm D(0;− ) 1 . 0,5
Câu 2b Cho tam giác ABC có AD là đường phân giác trong góc A và BM là
(2,0đ) đường trung tuyến kẻ từ đỉnh B (với D thuộc cạnh BC và M thuộc cạnh
AC ). Biết hai đường thẳng AD, BM vuông góc nhau, 3 BM = 5 − 2 5.AD 2 Tính cos A.
Kí hiệu BC = a,CA = b, AB = c. 2  2 2 2 2 2 2 2 2. . .cos  b  = + − = + − b c b a BM AB AM AB AM BAC c   2 . c . + −  2  2 2bc 0,25 2( 2 2 a + c ) 2 − b 2 ⇒ BM = 4
Gọi H là giao điểm của AD, BM . Xét tam giác ABM có AH là đường cao
cũng là đường phân giác nên tam giác ABM cân tại A. 0,25
⇒ b = 2AM = 2c .
Gọi N là giao điểm của BC và đường thẳng song song với AD qua M . 0,25 Ta có 4
AD = 2MN = 4HD ⇒ AD = AH . 3 2 2 2 2 2 2 2 Ta có 2 a c BM − = và 2 2 2 b 1 a c 9 . c a AH AM HM − − = − = − = . 0,25 2 4 4 2 8 1 ( 2 2 2 a − c ) 2 2 2 − −
Khi đó 9 (5− 2 5) BM 2 9 a c a 23 9 5 = = = . ⇒ = 2 4 AD 16 1 0,5 ( c −a ) 2 2 2 2 2 4 9c − a c 3 − 5 . 9 9 8 2 2 2 2 2 Ta có
b + c − a 5c − a 5 1 23 − 9 5 5 −1 cos A = = = − . = . 0,5 2 2bc 4c 4 4 3− 5 4 Trang 3/6
Câu 3a Cho dãy số (a xác định bởi a = 0 và a = − + + , với mọi n ≥1. + a n n n 2 1 n ) 1 1
(2,0đ) Chứng minh rằng a = (− )1n + n với mọi n ≥1 và tính tổng 2025 số hạng đầu n
tiên của dãy số (a . n )
Ta chứng minh a = (− )
1 n + n với mọi n ≥1 bằng quy nạp. n 0,25 Ta có a = 0 = (− )1 1 +1 (đúng) 1 Giả sử a = (− )
1 k + k với k ≥1. Ta chứng minh a = 1 k+ − + + . 0,5 + k k 1 1 ( ) 1 k
Thật vậy, a = −a + k + = − − + k + k + + = − + + . + k k k 2 1
( )1k ) 2 1 ( )k 1 1 1 1 0,5
Vậy theo nguyên lí chứng minh quy nạp, ta có a = (− )
1 n + n với mọi n ≥1. n
Ta có S = a + a + ...+ a 1 2 2025 0,25
= (− ) + (− )2 + + (− )2025 1 1 ... 1  + (1+ 2 +...+ 2025)   2025 1− 1 − = (− ) ( ) 2025 1 . . 0,5 − (− ) + (1+ 2025) = 2051324 1 1 2
Câu 3b Cho dãy số (u xác định bởi u = 4 và 2 u = −
+ , với mọi n ≥ 1. + u u n n 5 n 9 n ) 1 1
(2,0đ) Chứng minh rằng 1 1 1 + + ...+ < 1. u − 2 u − 2 u − 2 1 2 2025
Ta chứng minh u > với mọi n ≥1 bằng quy nạp. n 3 0,25
Ta có u = 4 > 3 (đúng). 1
Giả sử u > với k ≥1. Ta chứng minh u > . k+ 3 k 3 1 0,25 Thật vậy, 2 u > ⇔ − + > ⇔ − − > (luôn đúng) + u u u u k 3 k 5 k 9 3 k 2 k 3 0 1 ( )( ) 0,25
Vậy theo nguyên lí chứng minh quy nạp, ta có u > với mọi n ≥1. n 3 Ta có u − = − − + u u n 3 n 2 n 3 1 ( )( ) 0,25 1 1 1 1 1 1 1 ⇒ = = − ⇒ = − u − − − − − u − u − u − 0,25 n 2 n 3 n+ 3 + u u u u n 3 n 2 n 3 n 3 n 2 1 ( )( ) 1 Ta có 1 1 1 + + ...+ u − 2 u − 2 u − 2 1 2 2025 0,25       1 1 1 1 1 1 =  −  +  −  + ... +  − u − 3 u − 3 u − 3 u − 3 u − 3 u −      3  1 2 2 3 2025 2026  1 1 1 = − = 1− u − 3 u − 3 u − 3 0,25 1 2026 2026 Ta có 1 1 1 1 u > 3 nên − < 0 , do đó + + ...+ < 1. 2026 u − 3 u − 2 u − 2 u − 2 0,25 2026 1 2 2025 Trang 4/6
Câu 4 Một bồn hoa hình tròn ở giữa sân trường được chia thành 6 phần bằng nhau
(3,0đ) và giao nhiệm vụ cho 6 lớp 10 chọn trồng một trong 4 loại hoa là hoa cúc,
hoa hồng, hoa lan, hoa hướng dương theo các khu vực hình quạt được phân
công cụ thể như hình vẽ.
Hỏi có tất cả bao nhiêu phương án trồng hoa của các lớp sao cho hai lớp
được phân công hai khu vực cạnh nhau thì không cùng trồng một loại hoa?
Gọi số phương án trồng hoa cần tìm là a (ứng với 6 lớp). 6
Lớp 10A1 có 4 cách chọn hoa để trồng.
Lớp 10A2 có 3 cách chọn hoa để trồng khác với hoa mà lớp 10A1 đã chọn. 0,5
Tương tự cho các lớp 10A3, 10A4, 10A5, 10A6 cũng có 3 cách chọn. Vậy có tất cả 5
4.3 cách mà các lớp chọn hoa để trồng, tính luôn trường hợp
lớp 10A6 và 10A1 chọn cùng loại hoa để trồng.
Ta xét trường hợp: lớp 10A6 và 10A1 chọn cùng loại hoa. Ta xem khu vực
trồng hoa của 2 lớp này là một nhóm và xem như chỉ còn 5 khu vực (nhóm
này và 4 khu vực của các lớp 10A2, 10A3, 10A4 và 10A5). Khi đó sẽ có a 0,5 5 cách trồng. Ta có 5 a = 4.3 − a . 6 5 0,25
Lớp 10A6 và 10A1 có 4 cách. Lớp 10A2 có 3 cách, lớp 10A3 có 3 cách, lớp
10A4 có 3 cách và lớp 10A5 có 3 cách. 0,5 Do đó có tất cả 4
4.3 cách mà các lớp chọn hoa để trồng, tính luôn trường hợp
lớp 10A5, 10A6 và 10A1 chọn cùng loại hoa để trồng. Ta có 4 a = 4.3 − a . 5 4 0,5 3
a = 4.3 − a . 4 3
Với a là số phương án trồng hoa ứng với 3 khu vực nên 3 a = A = 24 . 3 3 4 0,25 Do đó 5 5
a = 4.3 − a = 4.3 − ( 4 4.3 − a ) 5 4 3
= 4.3 − 4.3 + 4.3 − a . 6 5 4 3 0,25
Vậy có tất cả 732 phương án trồng hoa cho các lớp. 0,25
Câu 5 Một sợi dây kim loại dài 120 cm được cắt thành hai đoạn: đoạn dây thứ nhất Trang 5/6
(3,0đ) được uốn thành hình vuông, đoạn dây thứ hai được uốn thành vòng tròn.
Tổng diện tích của hình vuông và hình tròn đạt giá trị nhỏ nhất bằng bao nhiêu 2 cm ?
Gọi x cm (với 0 < x <120 ) là độ dài đoạn dây thứ nhất. Khi đó, độ dài đoạn 0,25
dây thứ hai là 120 − x . 2
Độ dài cạnh hình vuông là x và diện tích hình vuông là  x  . 0,5 4  4   − 2
Độ dài bán kính hình tròn là 120 x và diện tích hình tròn là 120 . − x π  . 0,5 2π  2π    2 2
Tổng diện tích của hình vuông và hình tròn là  x  120  . − x S π  = +  . 0,25 4  2π      π +
Biến đổi, rút gọn ta thu được 4 2 60 3600 S = x − x + . 0,5 16π π π
Ta thấy S là một hàm số bậc hai theo biến x có đồ thị là một parabol có bề lõm hướng lên. 0,5 Vậy tổng 3600
S đạt giá trị nhỏ nhất là 2 cm khi và chỉ khi 480 x = cm . 0,5 π + 4 π + 4
Lưu ý: Nếu thí sinh làm bài không theo cách nêu trong hướng dẫn chấm mà đúng thì vẫn cho đủ
điểm từng phần như hướng dẫn quy định.
…………..HẾT………….. Trang 6/6
Xem thêm: ĐỀ THI HSG TOÁN 12
https://toanmath.com/de-thi-hsg-toan-12
Document Outline

• Đề chính thức HSG vòng 1 môn Toán THPT năm 2025
• HDC chính thức HSG vòng 1 môn Toán THPT năm 2025
• HSG 12