Đề chọn học sinh giỏi tỉnh Toán THPT năm 2024 – 2025 sở GD&ĐT Thanh Hóa
Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề thi chọn học sinh giỏi cấp tỉnh môn Toán THPT năm học 2024 – 2025 sở Giáo dục và Đào tạo tỉnh Thanh Hóa. Đề thi gồm 20 câu trắc nghiệm nhiều phương án lựa chọn + 06 câu trắc nghiệm đúng sai + 06 câu trắc nghiệm trả lời ngắn, thời gian làm bài 90 phút. Đề thi có đáp án và lời giải chi tiết mã đề GỐC.
Chủ đề: Đề HSG Toán 12 360 tài liệu
Môn: Toán 12 4.3 K tài liệu
Tác giả:
Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH THANH HOÁ NĂM HỌC 2024 - 2025
ĐÁP ÁN CHÍNH THỨC
MÔN THI: TOÁN – THPT Mã đề thi: GỐC
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 20. Mỗi câu hỏi
thí sinh chỉ chọn một phương án.
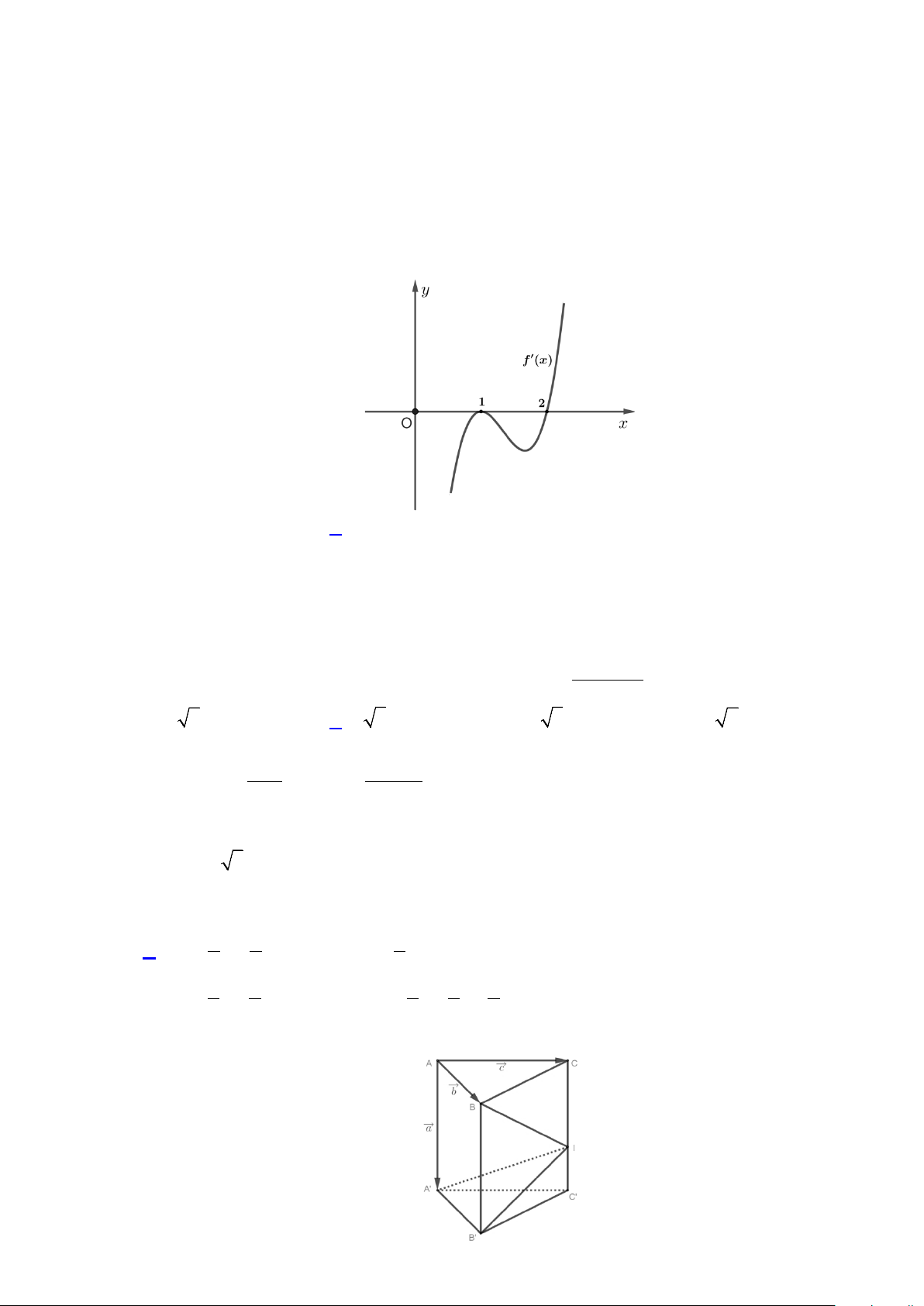
Câu 1: Cho hàm số y = f (x) liên tục trên . Hình bên là đồ thị của hàm số y = f ′(x). Hỏi hàm số
y = f (x) nghịch biến trên khoảng nào dưới đây? A. (1;3) . B. ( ;2 −∞ ) . C. (0; )
1 và (2;+∞) . D. (0;+∞). Lời giải x =
Dựa vào đồ thị hàm số y = f ′(x) ta thấy f ′(x) ≤ 0, x
∀ ≤ 2 , f ′(x) 1 = 0 ⇔ x = 2
Vậy hàm số y = f (x) nghịch biến trên khoảng ( ;2 −∞ ) . 2
Câu 2: Khoảng cách giữa hai điểm cực trị của đồ thị hàm số x + x + 9 y = bằng x +1 A. 2 2 . B. 6 5 . C. 4 5 . D. 3 2 . Lời giải 9 9 x = 2 y = 5 Ta có y = x + ⇒ y ' =1− = 0 ⇔ ⇒ x +1 (x + )2 1 x 4 = − y = 7 −
Khi đó đồ thị hàm số có 2 điểm cực trị là: A(2;5); B( 4; − 7 − ) . ⇒ AB = 6 5 .
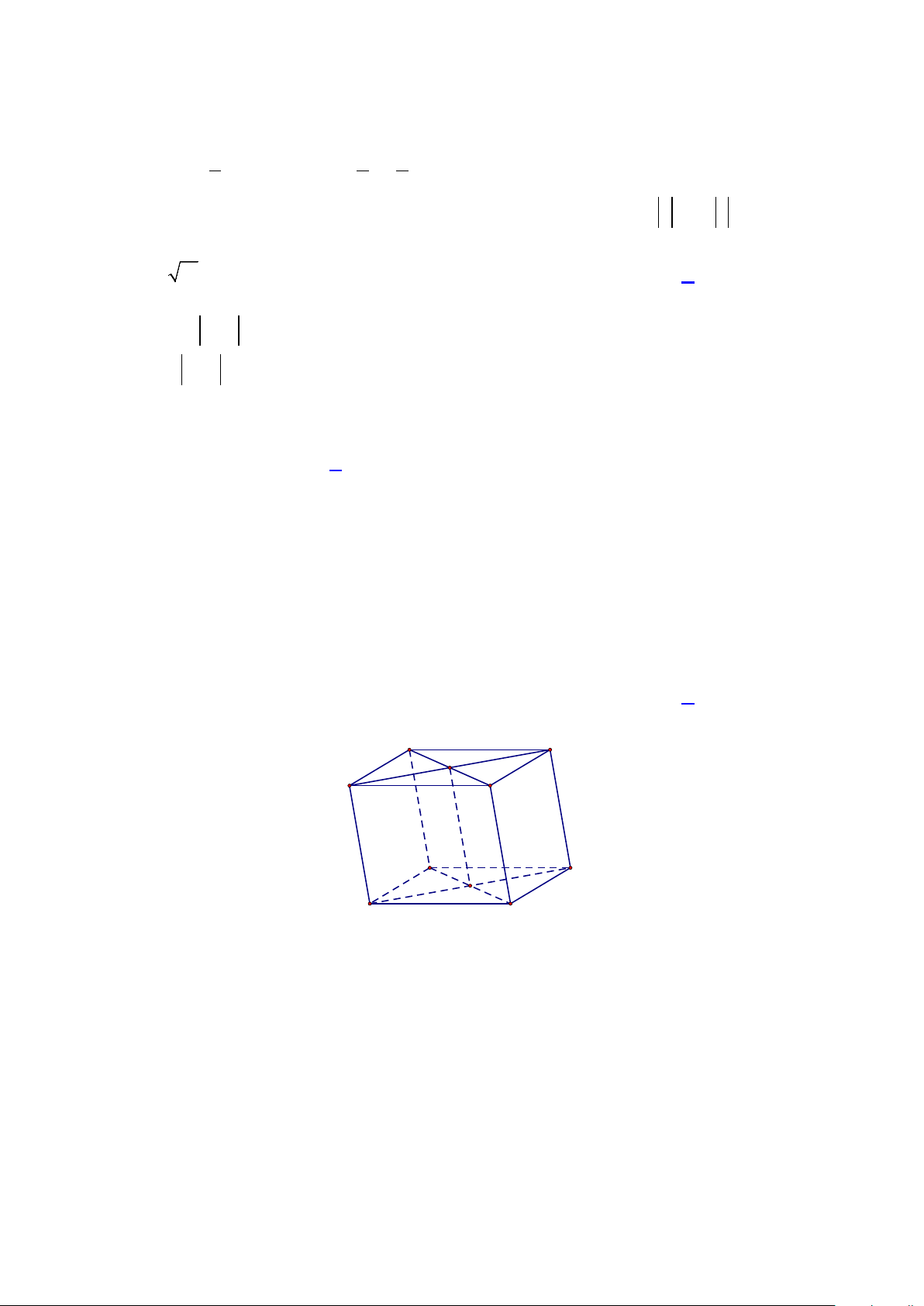
Câu 3: Cho lăng trụ tam giác ABC.A′B C
′ ′. Đặt AA′ = a, AB = b, AC = c . Gọi I là điểm thuộc đoạn
CC′ thỏa mãn IC = 3.IC′ , G là trọng tâm tứ diện BA′B C
′ ′ . Khẳng định nào sau đây là đúng? A. 1 3
IG = b − c . B. 1
IG = (a +b + 2c) . 2 4 4 C. 1 3
IG = a + c . D. 1 3 1
IG = − a + b + c . 4 4 2 4 4 Lời giải Trang 1/18 - Mã đề GỐC
Ta có: GB + GA′ + GB′ + GC′ = 0 ⇔ 4IG = IB + IA′ + IB′ + IC′
⇔ 4IG = (IC +CB)+(IC′+C A′′)+(IC′+C B′′)+ IC′
⇔ 4IG = (IC +3IC′)+ 2CB +C A′′ ⇔ 4IG = 2( AB − AC)− AC 1
⇔ IG = ( b − c) 1 3 2
3 ⇔ IG = b − c 4 2 4
Câu 4: Trong không gian, cho hai vectơ a và b tạo với nhau góc o
120 và a = 3, b = 5 . Tính độ dài
của vectơ a − b . A. 19 . B. 49 . C. 19. D. 7 . Lời giải 2
Ta có ( a −b ) = (a −b)2 2 2 2 o 2 = a − 2 .
a b + b = 3 − 2.3.5.cos120 + 5 = 49 .
Nên a − b = 7 .
Câu 5: Trong không gian Oxyz , cho A(1; − 2; 3), B(0; 2; − ) 1 , C ( 2; − 0; )
1 . Xác định tọa độ của
vectơ u = 2.AB − AC
A. u = (7; 2; − 2).
B. u = (1; 6; − 6) .
C. u = (1; 6; − 2) .
D. u = (4; 14; −14) . Lời giải Ta có: +) AB = ( 1;
− 4; − 4) ⇒ 2.AB = ( 2 − ; 8; −8) ; +) AC = ( 3;
− 2; − 2) ⇒ −AC = (3; − 2;2) .
Suy ra u = 2.AB − AC = (1; 6; − 6) .
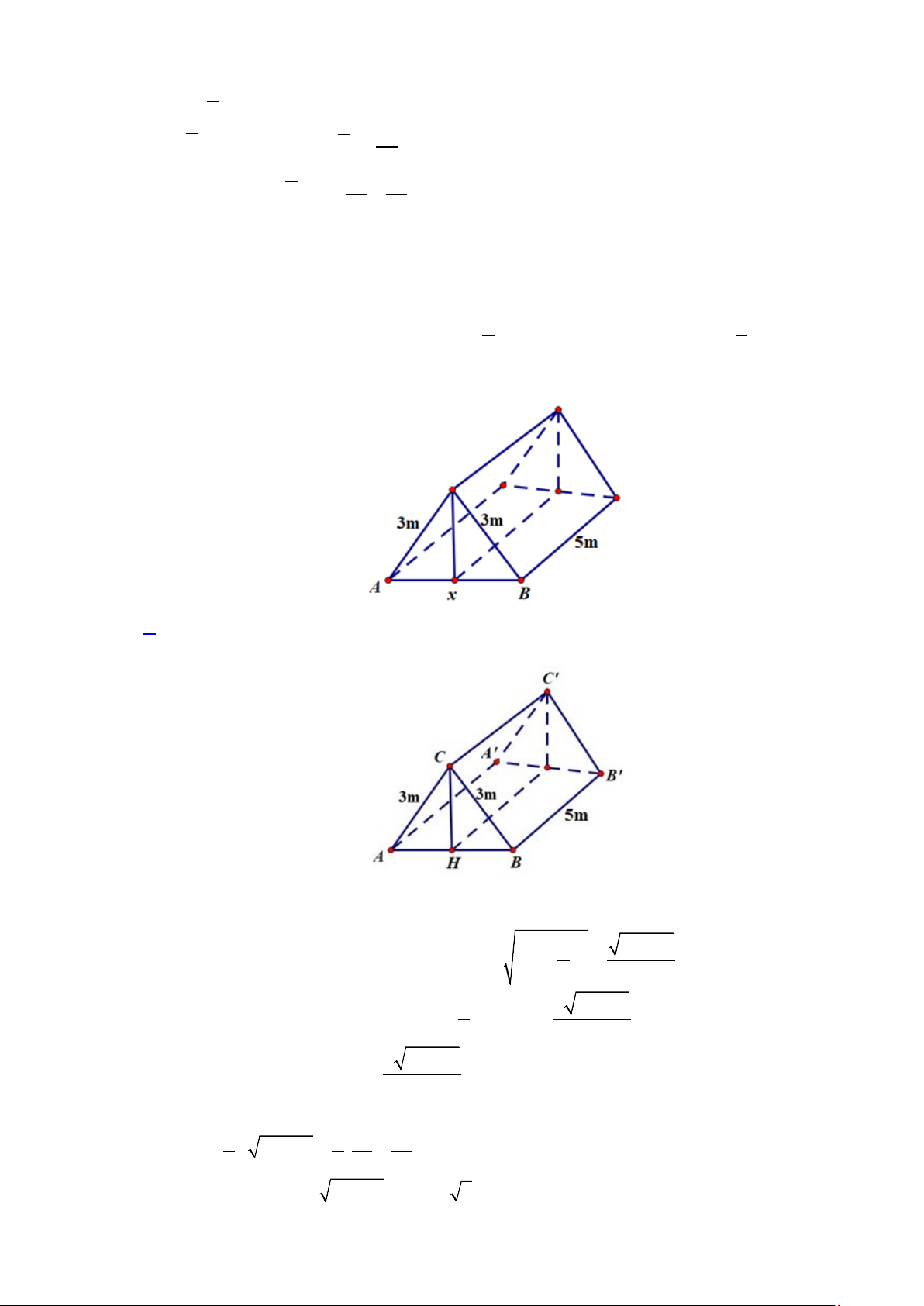
Câu 6: Trong không gian với hệ tọa độ Oxyz , cho hình hộp ABC . D A′B C ′ D
′ ′ có các đỉnh A′( 1; − 2;3) ,
C′(1;4;5), B( 3 − ;3; 2
− ) , D(5;3;2) . Tìm tọa độ đỉnh D′ .
A. D′(0;2;− ) 1 . B. D′( 4 − ;3;2) . C. D′(2;4; ) 1 .
D. D′(4;3;6) . Lời giải B C I D A C' B' I' A' D'
Gọi I, I′ lần lượt là tâm của các hình bình hành ABCD và A′B C ′ D ′ ′ .
Khi đó: I là trung điểm của BD ⇒ I (1;3;0) .
Và I′ là trung điểm của A′C′ ⇒ I′(0;3;4) ⇒ II′ = ( 1; − 0;4) .
Gọi D′(x, y, z) ⇒ DD′ = (x −5; y −3; z − 2). x − 5 = 1 − x = 4 Do D I′ ID
′ là hình bình hành ⇒ DD = II ⇔ y −3 = 0 ′ ′ ⇔ y = 3 . z 2 4 − = z = 6 Vậy D′(4;3;6) .
Câu 7: Khảo sát thu nhập theo tháng của người lao động ở một công ty thu được mẫu số liệu ghép nhóm sau: Trang 2/18 - Mã đề GỐC
Tính mức thu nhập trung bình của người lao động ở công ty trên (đơn vị: triệu đồng). A. 11,75. B. 12,5. C. 11. D. 10,5. Lời giải
6,5 30 9,5 55 12,5 45 15,5 30 18,5 20 x × + × + × + × + × = =11,75. 180
Câu 8: Bạn Chi rất thích nhảy hiện đại. Thời gian tập nhảy mỗi ngày trong thời gian gần đây của bạn
Chi được thống kê lại ở bảng sau:
Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên là A. 12,2 . B. 27,5. C. 155 . D. 165 . 13 14 Lời giải Cỡ mẫu n = 28 Gọi x ; x ; ;
… x là mẫu số liệu gốc về thời gian tập nhảy mỗi ngày của bạn Chi được xếp theo 1 2 28 thứ tự không giảm.
Ta có: x ;…; x ∈ 20;25 ; x ;…; x ∈ 25;30 ; x ;…; x ∈ 30;35 ; 1 6 [ ) 7 13 [ ) 14 18 [ )
x ;...; x ∈ 35;40 ; x ;...; x ∈ 40;45 . 19 24 [ ) 25 28 [ )
Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm thuộc nhóm [25;30) , do đó tứ phân vị thứ nhất 28 −6
của mẫu số liệu ghép nhóm là: 4 180 Q = 25 + 30 − 25 = 1 ( ) 7 7
Tứ phân vị thứ ba của mẫu số liệu ghép nhóm thuộc nhóm [35;40) , do đó, tứ phân vị thứ ba 3.28 −18
của mẫu số liệu ghép nhóm là: 4 75 Q = 35 + 40 − 35 = 3 ( ) 6 2
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là: 165 ∆ = Q − Q = . Q 3 1 14 Câu 9: π
Nghiệm của phương trình 2cos x + − 2 = 0 là: 4 x = k2π x = kπ A. π (k ∈). B. π (k ∈). x = − + kπ x = − + kπ 2 2 x = kπ x = k2π C. π (k ∈) . D. π (k ∈) .
x = − + k2π
x = − + k2π 2 2 Lời giải π 2 π π pt ⇔ cos x + = ⇔ cos x + = cos 4 2 4 4 π π x + = + k2π x = k2π 4 4 ⇔ ⇔ π −
;(k ∈) π π − x = + k2 x + = + k2 π π 2 4 4 Trang 3/18 - Mã đề GỐC
Câu 10: Gọi giá trị nhỏ nhất và giá trị lớn nhất của hàm số
sin x + 2cos x +1 y = lần lượt là , m M . Khi
sin x + cos x + 2
đó 2M + m bằng A. 1. B. 2 . C. 0 . D. 1 − . Lời giải Ta có
sin x + 2cos x +1 y = ⇔ ( y − )
1 sin x + ( y − 2)cos x =1− 2y (*)
sin x + cos x + 2
Phương trình (*) có nghiệm ⇔ ( y − )2 + ( y − )2 ≥ ( − y)2 2 1 2 1 2
⇔ y + y − 2 ≤ 0 ⇔ 2 − ≤ y ≤1. Do đó m = 2 − ; M =1.
Vậy 2M + m = 0. a(m + nb)
Câu 11: Đặt a = log 3 , b = log 3 . Nếu biểu diễn (với 2 5 log 45 = , m , n p ∈ 6 ) thì b(a + p)
13m +12n + 2024 p bằng: A. 3012. B. 1024. C. 2028 . D. 2061. Lời giải Ta có: 2 1 1 log 3 + log 45 log 9 + log 5 3 2 log 3 + a 1+ 2b 5 ( ) 3 3 3 log 45 = = b = = = . 6 log 6 log 2 + log 3 1 1 b(a + ) 1 3 3 3 log 3+ 1+ 3 log 3 a 2 a(m + nb) Theo bài ra: log 45 = , do đó: = = = . 6
m 1 , n 2 , p 1 b(a + p)
Vậy 13m +12n + 2024 p = 2061. Câu 12: Biết − + − + = với a,b∈ .
Tính a + 8b ta được →+∞ ( 2
lim 4x 3x 1 (ax b)) 0 x A. 1 − . B. 5. C. 4 − . D. 2 . Lời giải Ta có − + − + = ⇔
x − x + − ax − b = x→+∞ ( 2 lim 4 3 1 ) ) 0 →+∞ ( 2
lim 4x 3x 1 (ax b)) 0 x 2 2 2
4x −3x +1− ( 2 4 − a ) 2 x − 3x +1 ⇔ lim a x
− b = 0 ⇔ lim − b = 0 x→+∞ 2
4x − 3x +1 + ax x→+∞ 2
4x 3x 1 ax − + + 2 4 − a = 0 a = 2 ⇔ a > 0 ⇔ 3 . = − 3 b − − b = 0 4 2 + a Vậy a + 8b = 4 − .
Câu 13: Một cấp số cộng (u có tổng của n số hạng đầu là S được tính theo công thức n ) n 2 S n n n ∗ = + ∈ u và công sai n 3 5 ,
. Tìm số hạng đầu 1
d của cấp số cộng đó. A. u = 8; − d = 6 .
B. u = 8; d = 6 − .
C. u = 8; d = 6 .
D. u = 6; d = 8. 1 1 1 1 Lời giải Ta có: 2
S = 3.1 + 5.1 = 8 = u 1 1
Lại có S = u + u ⇔ 2u + d = 22 ⇒ d = 6. 2 1 2 1
Câu 14: Gieo đồng thời hai con xúc xắc I và II cân đối, đồng chất một lần. Ta gọi biến cố A : “Có ít
nhất một con xúc xắc xuất hiện mặt 6 chấm”. Khi đó xác suất P( A) của biến cố A là
A. P( A) 25 = .
B. P( A) 11 = .
C. P( A) 1 = .
D. P( A) 15 = . 36 36 36 36 Trang 4/18 - Mã đề GỐC Lời giải
Nhận thấy: n(Ω) = 6.6 = 36.
Biến cố A : “không có con xúc xắc nào xuất hiện mặt 6 chấm”
⇒ n( A) = 5.5 = 25 ⇒ P( A) 25 = 36
Vậy P( A) = − P( A) 25 11 1 = 1− = . 36 36
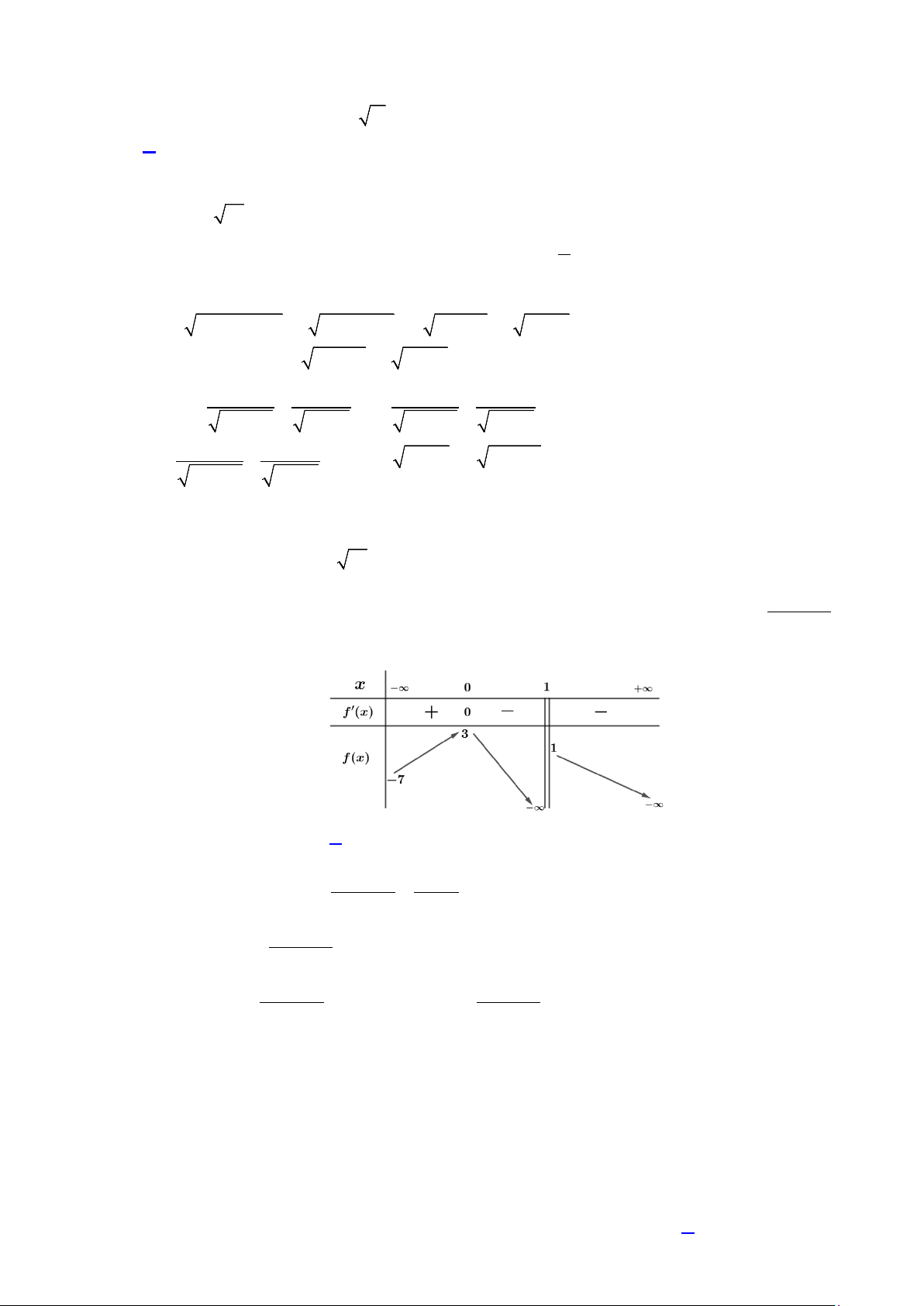
Câu 15: Người ta dựng trên mặt đất bằng phẳng một chiếc lều từ một tấm bạt hình chữ nhật có chiều dài
6 m và chiều rộng 5 m bằng cách: Gập đôi tấm bạt lại theo đoạn nối trung điểm hai cạnh
chiều dài của tấm bạt sao cho hai mép cạnh chiều rộng của tấm bạt sát đất và cách nhau x(m) ,
hai đầu hồi của lều được thiết kế cửa ra, vào và có thể khép kín (tham khảo hình vẽ dưới). Thể
tích không gian phía trong lều lớn nhất bằng a ( 3 m ) với a,b ∗
∈ và phân số a tối giản. Tính b b
giá trị a + b ? A. 47 . B. 27 . C. 35. D. 28 . Lời giải
Xét hình lăng trụ đứng ABC.A′B C
′ ′ có đáy là tam giác cân với hai cạnh bên có độ dài bằng
3 m , chiều cao lăng trụ bằng 5m . 2 2
Gọi H là trung điểm AB thì 2 x 36 ⊥ , = 3 x CH AB CH − − = . 2 2 2 −
Do đó diện tích tam giác ABC là 1 x 36 x S = ⋅ = . ∆ CH AB ABC 2 4 2
Suy ra thể tích của lều là x 36 5 x V − = ⋅ . 4
Để không gian phía trong lều lớn nhất thì V . max Ta có 5 2 5 36 45
V = x 36 − x ≤ . = ( 3
m ) với mọi x∈(0;6). 4 4 2 2 Dấu "=" xảy ra khi 2
x = 36 − x ⇔ x = 3 2 .
Vậy a = 45, b = 2 ⇒ a + b = 47 . Trang 5/18 - Mã đề GỐC
Câu 16: Trong không gian Oxyz , cho các điểm A(5; 3 − ;2) , B(2;1; 2
− ). Gọi M , N là hai điểm phân
biệt thay đổi thoả mãn BM = BN = 2 và ,
A M , N thẳng hàng. Giá trị nhỏ nhất của biểu thức
S = 2.AM + 5.AN có dạng 7 m − n với ,
m n là số tự nhiên. Tính giá trị 5m + n . A. 211. B. 161. C. 215 . D. 169. Lời giải
Ta có: M , N nằm trên mặt cầu tâm B , bán kính R = 2 .
Do BA = 41 > R = 2 ⇒ A nằm ngoài đoạn MN . Để S nhỏ nhất thì N phải nằm giữa , A M
Gọi H là trung điểm MN 1
⇒ BH ⊥ MN, HM = HN = MN 2
Khi đó: S = 2( AH + HM ) + 5( AH − NH ) = 7.AH −3.NH 2 2 2 2 2 2
S = 7 AB − BH − 3 R − BH = 7 41− x − 3 4 − x với BH = x, 0 ≤ x < 2
Xét hàm số f (x) 2 2
= 7 41− x − 3 4 − x ,(0 ≤ x < 2) − − f ′(x) 7x 3x 7 3 = + = x + . 2 2 2 2 41− x 4 − x 41− x 4 − x Xét 7 − 3 + > 0 2 2
⇔ 7 4 − x < 3 41− x 2 2 41− x 4 − x 2 2 2
⇔ 196 − 49x < 369 − 9x ⇔ 40x +173 > 0 (luôn đúng )
Suy ra f ′(x) ≥ 0, x
∀ ∈[0;2), f ′(x) = 0 ⇔ x = 0 ⇒ f (x) đồng biến trên [0;2)
Vậy min f (x) = f (0) = 7 41 − 6 ⇒ m = 41, n = 6 ⇒ 5m + n = 211 [0;2)
Câu 17: Cho hàm số y = f (x) có bảng biến thiên như hình vẽ. Đồ thị hàm số y = g (x) 2024 = có f (x) −1
tất cả bao nhiêu đường tiệm cận đứng và tiệm cận ngang? A. 4 . B. 5. C. 8 . D. 6 . Lời giải - Ta có: g (x) 2024 2024 lim = lim = = − ⇒ y = 253 − là tiệm cận ngang. x→−∞
x→−∞ f ( x) 253 −1 7 − −1 g (x) 2024 lim = lim
= ⇒ y = là tiệm cận ngang. x→+∞
x→+∞ f ( x) 0 0 −1 g (x) 2024 2024 lim = lim = 0; lim g x = lim = −∞ x 1−
x 1− f ( x) ( ) − x 1+ x 1 1 + → → → → f (x) −1
⇒ x =1 là tiệm cận đứng.
- Lại thấy: phương trình f (x) −1= 0 có 2 nghiệm x < 0 < x <1 nên đồ thị hàm số y = g (x) 1 2
có 2 tiệm cận đứng là x = x , x = x . 1 2
Vậy đồ thị hàm số y = g (x) có tất cả 5 đường tiệm cận (đứng và ngang).
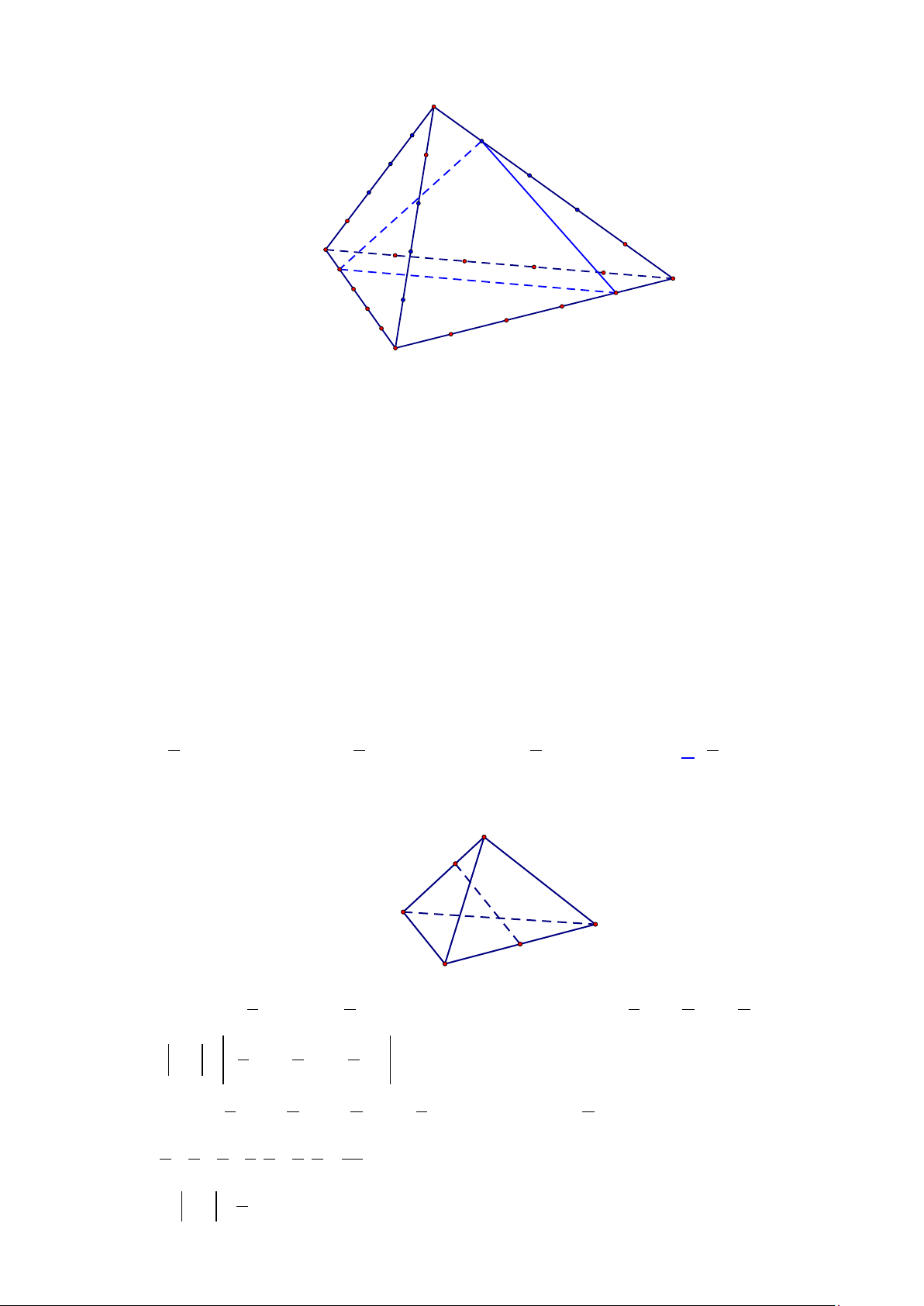
Câu 18: Cho tứ diện ABCD . Trên mỗi cạnh của tứ diện, ta đánh dấu 4 điểm chia đều cạnh đó thành các
phần bằng nhau. Hỏi có thể lập được bao nhiêu tam giác mà ba đỉnh lấy từ 24 điểm đánh dấu
sao cho mặt phẳng chứa tam giác đó song song với đúng một cạnh của tứ diện đã cho. A. 336. B. 216 . C. 288 . D. 432 . Trang 6/18 - Mã đề GỐC Lời giải A H C E D F B
Nhận thấy, nếu một đoạn thẳng có hai đầu mút nằm trên hai cạnh chéo nhau của tứ diện thì nó
không thể song song với bất kỳ cạnh nào của tứ diện. Xét tam giác HEF có 3 đỉnh thuộc 24 đỉnh đã đánh dấu. Giả sử HE ∆
F thỏa mãn điều kiện đề bài. Khi đó một trong các cạnh của nó, giả sử là EF
song song với CD . Ta có hai trường hợp là X ∈ BC, F ∈ BD hoặc E ∈ AC, F ∈ AD
Trường hợp 1: Nếu E ∈ BC, F ∈ BD thì H ∉(BCD) , chỉ còn 12 điểm có thể chọn làm H .
Ta thấy có 4 cặp E, F thỏa mãn. Theo định lý Talet vì có các đoạn tỉ lệ và ứng với mỗi cặp như
vậy, trên các cạnh AB, AC, AD ta lại loại bớt 3 điểm nữa (vì khi đó (HEF ) song song với
nhiều hơn một cạnh của tứ diện). Suy ra có 9 cách chọn H . Do đó, có 4.9 = 36 tam giác thỏa mãn bài toán.
Trường hợp 2: Nếu E ∈ AC, F ∈ AD tương tự có 36 tam giác thỏa mãn.
Do các cạnh của tứ diện bình đẳng nên có 6.(2.36) = 432 tam giác.
Câu 19: Cho tứ diện OABC có = = °
AOB BOC 60 ; AOC = 90°; OA = OB = OC =1. M là điểm thuộc
cạnh OA sao cho AM = 2.MO ; N là trung điểm BC . Tính độ dài vectơ MN . A. 2 . B. 3 . C. 4 . D. 5 . 3 4 5 6 Lời giải Chọn D O M A C N B
Ta có: 1 1 OM = ,
OA ON = (OB +OC) 1 1 1
⇒ MN = ON − OM = − OA + OB + OC . 3 2 3 2 2
1 1 1
⇒ MN = − OA + OB + OC 3 2 2
2 1 2 1 2 1 2 1
⇒ MN = OA + OB + OC − (OAOB + OAOC) 1 . . + . OB OC 9 4 4 3 2 1 1 1 1 1 1 1 25 = + + − . + . = 9 4 4 3 2 2 2 36 Vậy 5 MN = . 6 Trang 7/18 - Mã đề GỐC
Câu 20: Cho a, b là các số thực thỏa mãn 4
1< a ≤ b ≤ a . Tìm giá trị nhỏ nhất của biểu thức: 3 2 log a b P = − . a 3log a b a A. 18 − . B. 6 . C. 26 − . D. 4 . Lời giải 3 2 Ta có: a b P = − = − b − b − . a ( a a )3 log 3log 2 log 6(loga ) 1 b a Do 4
1< a ≤ b ≤ a ⇒1≤ log b ≤ . a 4 Đặt 3 2
t = log b ⇒ P = t − + t − t + t ∈ . a 6 18 14, [1;4] Ta có: 2 P′ = 3
− t +12t −18 < 0, t
∀ ∈[1;4], do đó hàm P(t) nghịch biến trên đoạn [1;4]
Vậy P = P 4 = 26 − . min ( )
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 6. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai.
Câu 1: Trong không gian Oxyz , cho tam giác ABC có A(2; 1; − 2) , B(4;3; 2 − ) và C (5; 1; − 6).
Xét tính đúng sai của các mệnh đề sau:
a) Chu vi tam giác ABC là 20 .
b) Độ dài đường cao AH của tam giác ABC là 10 2 . 3
c) Tọa độ chân đường phân giác trong góc B của tam giác ABC là 16 18 ; 1; − . 5 5
d) Điểm M (a; ;0
b ) thuộc mặt phẳng (Oxy) sao cho biểu thức 2 2 2
2MA − 3MB + 4MC đạt giá
trị nhỏ nhất thỏa mãn a + b =1. Lời giải a) Ta có AB = ( − ) 2 2
2;4; 4 ⇒ AB = 2 + 4 + ( 4 − )2 = 6 .
AC = (3;0;4) ⇒ AC = 5 ; BC = (1; 4 − ;8) ⇒ BC = 9 .
Do đó chu vi tam giác ABC là 2 p = AB + BC + CA = 20. Vậy a) đúng.
b) Diện tích tam giác ABC là S
= p p − BC p − CA p − AB = ABC ( )( )( ) 10 2 2SABC 20 2 ⇒ AH = = . BC 9 Vậy b) sai.
c) Ta có BA = 6, BC = 9 . Gọi D( ;
x y; z) là chân đường phân giác trong hạ từ B xuống AC . Khi đó BA 6 2 DA = −
.DC ⇔ DA = − .DC ⇔ DA = − DC . BC 9 3 Mà DA = (2 − ; x 1
− − y;2 − z) và DC = (5 − ; x 1
− − y;6 − z) nên 16 18 D ; 1; − . 5 5 Vậy c) đúng.
d) Gọi I là điểm thỏa mãn 2IA −3IB + 4IC = 0 . Suy ra 34 I 4; 5; = − . 3 Khi đó: 2 2 2 2 2 2
MA − MB + MC = IA − IB + IC + MI ( IA− IB + IC) 2 2 3 4 2. 3. 4. 2. . 2. 3. 4. + 3MI 2 2 2 2
= 2.IA − 3.IB + 4.IC + 3.MI Do đó 2 2 2
2MA − 3MB + 4MC đạt giá trị nhỏ nhất khi MI đạt giá trị nhỏ nhất. Trang 8/18 - Mã đề GỐC
Do M thuộc mặt phẳng (Oxy) nên M là hình chiếu vuông góc của I trên (Oxy) hay M (4; 5; − 0).
Suy ra a = 4; b = 5 − ⇒ a + b = 1 − . Vậy d) sai.
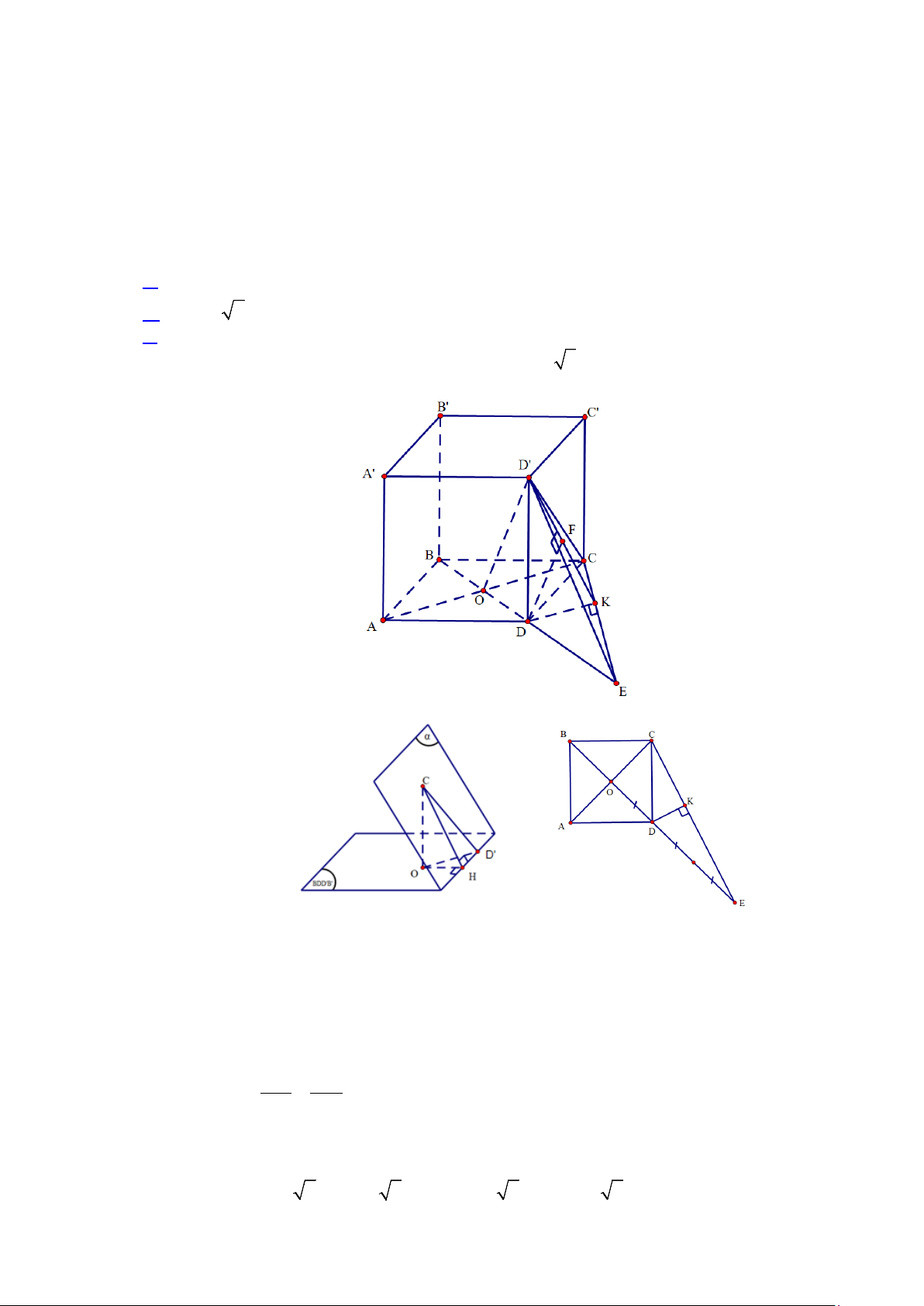
Câu 2: Cho hình lập phương ABC . D A′B C ′ D
′ ′ cạnh bằng 6 và O là giao điểm của AC và BD . Trong
các mặt phẳng chứa đường thẳng CD′ , gọi (α ) là mặt phẳng tạo với mp(BDD B ′ ′) một góc
nhỏ nhất; đường thẳng ∆ = (α ) ∩(BDD B
′ ′); điểm E = ∆ ∩ BD . Kẻ OH ⊥ ∆ tại H . Xét tính
đúng sai của các mệnh đề sau:
a) Góc giữa (α ) và (BDD B ′ ′) là góc OHC . b) DE = 6 2 .
c) Thể tích tứ diện C B
′ CE là V = 72 .
d) Khoảng cách từ điểm A đến mặt phẳng (α ) bằng 2 6 . Lời giải
a) ∆ = (α ) ∩(BDD B ′ ′).
Ta có CO ⊥ (BDD B ′ ′) ⇒ CO ⊥ . ∆
Kẻ OH ⊥ ∆ ⇒ CH ⊥ ∆ ⇒ ϕ = ((α ) (BDD B ′ ′)) = (OH CH ) = , ,
OHC là góc giữa (α ) và (BDD B ′ ′) . Vậy a) đúng. * Ta có: OC OC ϕ = ≥ = ′ ⇒ ϕ = sin sin OD C min OD C
′ , đạt được khi ∆ ⊥ OD′ . CH CD′
Gọi E = ∆ ∩ BD ⇒ D ∆ OE ′
vuông tại D′ và (α ) ≡ (ED C ′ ) . b) Do D ∆ OE ′
vuông tại D và có đường cao D D ′ nên
OD OE = OD′ ⇒ OE = ( )2 2 . 3 2.
3 6 ⇒ OE = 9 2 ⇒ DE = 6 2 . Vậy b) đúng. Trang 9/18 - Mã đề GỐC
c) Do E đối xứng với B qua D nên S = = ∆ S∆ S BCE 2. BCD ABCD 3 1 1 6 ⇒ V = ′ = ′ = = . ′ CC S∆ CC S C BCE . BCE . ABCD 72 3 3 3 Vậy c) đúng.
d) Có d ( A (α )) = d (O (α )) 3 , 2 ;
= 2. d (D,(α )) = 3d ( ; D (α )) . 2
Kẻ DK ⊥ CE ,(K ∈CE) ; kẻ DF ⊥ D K ′ , (F ∈ D K
′ ) ⇒ DF ⊥ (α ) ⇒ d (D,(α )) = DF . Ta có 6 DK =
; DD′ = 6 ⇒ DF = 6 ⇒ d ( ,
A (α )) = 3.DF = 3 6 . 5 Vậy d) sai.
Câu 3: Một hộp chứa 45 quả cầu có cùng kích thước và khối lượng được đánh số từ 1 đến 45 . Lấy
ngẫu nhiên 3 quả cầu từ hộp đó. Xét tính đúng sai của các mệnh đề sau:
a) Số cách lấy được cả 3 quả cầu đánh số chẵn bằng 1540.
b) Xác suất để tổng 3 số ghi trên 3 quả cầu là số lẻ bằng 1 . 2
c) Xác suất để tổng 3 số ghi trên 3 quả cầu là số chia hết cho 4 bằng 323 . 1290
d) Xác suất để tích 3 số ghi trên 3 quả cầu là một số chia hết cho 8 bằng 523 . 1290 Lời giải
Trong 45 quả cầu có 22 quả cầu đánh số chẵn và 23 quả cầu đánh số lẻ.
a) Số cách lấy ra cả 3 quả cầu đánh số chẵn từ trong hộp: 3 C =1540. 22 Vậy a) đúng.
b) Để tổng của 3 số ghi trên 3 quả cầu là số lẻ thì cả 3 số ghi trên 3 quả cầu đều là lẻ hoặc có 2
quả ghi số chẵn và 1 quả ghi số lẻ.
+) Cả 3 quả ghi số lẻ: có 3 C cách chọn 23
+) Có 2 quả ghi số chẵn và 1 quả ghi số lẻ: có 2 1
C .C cách chọn 22 23 3 2 1 +
Vậy xác suất để tổng 3 số là số lẻ bằng: C C .C 322 23 22 23 = . 3 C 645 45 Vậy b) sai.
c) Nhận thấy: trong các số từ 1 đến 45 có: 11 số chia hết cho 4, 12 số chia 4 dư 1, 11 số chia 4
dư 2 và 11 số chia 4 dư 3.
Để chọn được 3 quả cầu mà tổng của 3 số ghi trên đó là số chia hết cho 4 ta có các trường hợp sau:
TH1: Chọn cả 3 quả cầu đều ghi số chia hết cho 4, có: 3 C . 11
TH2: Chọn 1 quả ghi số chia hết cho 4, 1 quả ghi số chia 4 dư 1 và 1 quả ghi số chia 4 dư 3: có 1 1 1
C .C .C . 11 12 11
TH3: Chọn 1 quả ghi số chia hết cho 4, 2 quả ghi số chia 4 dư 2: có 1 2 C .C . 11 11
TH4: Chọn 2 quả ghi số chia 4 dư 1 và 1 quả ghi số chia 4 dư 2: có 2 1 C .C . 12 11
TH5: Chọn 2 quả ghi số chia 4 dư 3 và 1 quả ghi số chia 4 dư 2: có 2 1 C .C . 11 11
Vậy xác suất chọn được 3 quả cầu mà tổng của 3 số là số chia hết cho 4 là 3 1 1 1 1 2 2 1 2 1
C + C .C .C + C .C + C .C + C .C 323 11 11 12 11 11 11 12 11 11 11 = . 3 C 1290 45 Vậy c) đúng.
d) Chia 45 quả cầu thành 4 nhóm:
Nhóm 1: Gồm 23 quả cầu mang số lẻ.
Nhóm 2 : Gồm 11 quả cầu mang số chia hết cho 2 mà không chia hết cho 4 .
Nhóm 3: Gồm 6 quả cầu mang số chia hết cho 4 mà không chia hết cho 8 .
Nhóm 4 : Gồm 5 quả cầu mang số chia hết cho 8 .
Trang 10/18 - Mã đề GỐC
Để tích 3 số ghi trên 3 quả cầu lấy được là một số không chia hết cho 8 thì có 4 trường hợp sau:
TH1: 1 quả nhóm 1 và 2 quả nhóm 2 có: 1 2
C .C cách lấy. 23 11
TH 2 : 2 quả nhóm 1 và 1 quả nhóm 2 có: 2 1
C .C cách lấy. 23 11
TH3: 2 quả nhóm 1 và 1 quả nhóm 3 có: 2 1
C .C cách lấy. 23 6
TH 4 : 3 quả nhóm 1: 3 C cách lấy. 23 1 2 2 1 2 1 3 + + + Vậy xác suất cần tính: C .C C .C C .C C 623 23 11 23 11 23 6 23 P =1− = . 3 C 1290 45 Vậy d) sai. 2 Câu 4: Cho hàm số x + x − 6 y =
có đồ thị là đường cong (C). Giả sử ,
A B là 2 điểm thuộc 2 nhánh x +1
của đồ thị (C) sao cho AB song song với trục hoành. Xét tính đúng sai của các mệnh đề sau:
a) Trên đồ thị (C) của hàm số có 8 điểm mà hoành độ và tung độ đều là số nguyên.
b) Có 2 tiếp tuyến của đồ thị (C) song song với đường thẳng d : y = 7x +18.
c) Giá trị nhỏ nhất của đoạn thẳng AB bằng 2 5 .
d) Đường tròn (T ) (x + )2 + ( y + )2 2 : 1
1 = R cắt (C) tại 4 điểm phân biệt khi và chỉ khi 2 R >12( 2 − )1 . Lời giải 2 a) Ta có x + x − 6 6 y = = x − x +1 x +1 Khi đó
x∈, y ∈ ⇔ 6(x + ) 1 ⇔ x +1∈{ 6; − 3 − ; 2; − 1 − ;1;2;3; } 6 ⇔ x∈{ 7 − ; 4; − 3 − ; 2; − 0;1;2; } 5
Vậy có 8 điểm mà toạ độ là những số nguyên. Vậy a) đúng.
b) Hệ số góc của tiếp tuyến là k = 7 .
Giả sử M (a;b) là tiếp điểm. Khi đó 6 a = 0 M (0; 6 − )
y′(a) = 7 ⇔ 1+ = 7 ⇔ ⇒ ( a + )2 1 a = 2 − M ( 2; − 4)
+ Phương trình tiếp tuyến tại M (0; 6
− ) : y = 7x − 6 .
+ Phương trình tiếp tuyến tại M ( 2;
− 4) : y = 7(x + 2) + 4 = 7x +18 (loại)
Hay có 1 tiếp tuyến thỏa mãn. Vậy b) sai.
c) Giả sử phương trình AB là y = a . Hoành độ ,
A B là nghiệm của phương trình 2 x + x − 6 x ≠ 1 − = a ⇔ 2 x +1 x − (a − )
1 x − a − 6 = ( ) 0 1 2
∆ = a + 2a + 25 > 0 Vì ( − )2 1 + (a − ) 1 − a − 6 = 6 − ≠ 0 nên phương trình ( )
1 luôn có 2 nghiệm phân biệt x ; x khác 1 − 1 2 Khi đó 2
AB = x − x = ∆ = a + 2a + 25 = a +1 + 24 ≥ 2 6 , a ∀ ∈ . 1 2 ( )2
Hay giá trị nhỏ nhất của AB bằng 2 6 khi a = 1 − . Vậy c) sai.
Trang 11/18 - Mã đề GỐC
d) Đường tròn (T ) có tâm I ( 1; − − )
1 là giao của 2 đường tiệm cận của đồ thị (C). Nên I là
tâm đối xứng của (C). Gọi 6 A 1 a;a 1 − + − − ;a >
0 là điểm thuộc nhánh bên phải tiệm cận a đứng của (C).
(T ) cắt (C) tại 4 điểm phân biệt khi và chỉ khi R > IA min. 2 Ta có: 2 6 2 36 2 36
IA = a + a − = 2a + −12 ≥ 2 2a . −12 = 2 3 2 − 3 2 2 a a a 2 36 4
IA = 2 3 2 − 3 ⇔ 2a = ⇔ a = 18. min 2 a 2
⇒ R > 2 3 2 − 3 ⇔ R >12( 2 − )1 thì đường tròn (T ) cắt đồ thị (C) tại 4 điểm phân biệt. Vậy d) đúng.
Câu 5: Tại một trường THPT, để khảo sát năng lực học môn Toán của hai lớp 12E và 12F, giáo viên
đã cho học sinh ở hai lớp làm bài kiểm tra khảo sát đầu năm, thống kê điểm của học sinh được cho trong bảng sau:
Xét tính đúng sai của các mệnh đề sau:
a) Dựa vào điểm trung bình môn Toán ta đánh giá được lớp 12E học tốt môn Toán hơn lớp 12F.
b) Khoảng tứ phân vị của mẫu số liệu thống kê điểm của lớp 12F nhỏ hơn 2,9 .
c) Điểm thi có số học sinh đạt được nhiều nhất ở lớp 12E nhỏ hơn ở lớp 12F.
d) Dựa vào độ lệch chuẩn của mẫu số liệu thống kê ghép nhóm, ta thấy rằng lớp 12E học đều hơn lớp 12F. Lời giải
a) Điểm trung bình của lớp 12E: 1 x = + + + + = . E (3.1 6.3 12.5 24.7 5.9) 5,88 50
Điểm trung bình của lớp 12F: 1 x = + + + + = . F (4.1 5.3 16.5 18.7 7.9) 5,76 50 ⇒ x > x E F
Do đó dựa vào điểm trung bình ta thấy học sinh lớp 12E học tốt hơn học sinh lớp 12F. Vậy a) đúng.
b) Tìm khoảng tứ phân vị của MSLGN lớp 12F:
- Nhóm chứa tứ phân vị thứ nhất là nhóm [4;6), do đó: 50 −9 4 71 Q = 4 + . 6 − 4 = . 1 ( ) 16 16
- Nhóm chứa tứ phân vị thứ 3 là nhóm [6;8) , do đó: 50 3. − 25 4 133 Q = 6 + . 8 − 6 = . 3 ( ) 18 18 Khoảng tứ phân vị là 133 71 425 ∆ = Q − Q = − = ≈ . Q 2,95 3 1 18 16 144 Vậy b) sai.
c) Điểm học sinh đạt được nhiều nhất ở mỗi lớp là mốt của mẫu số liệu ghép nhóm của mỗi lớp được cho bảng trên.
- Nhóm chứa mốt của mẫu số liệu thống kê ghép nhóm ở lớp 12E là nhóm [6;8)
Trang 12/18 - Mã đề GỐC 24 12 M − = + − = ≈ . o ( ) 210 6 . 8 6 6,77 24 −12 + 24 − 5 31
- Nhóm chứa mốt của mẫu số liệu thống kê ghép nhóm ở lớp 12F là nhóm [6;8) 18 16 M − = + − = ≈ . o ( ) 82 6 . 8 6 6,31 18 −16 +18 − 7 13 Vậy c) sai.
d) - Độ lệch chuẩn của mẫu số liệu ghép nhóm của lớp 12E: 2 1 s = S = + + + + − ≈ E E ( 2 2 2 2 2 3.1 6.3 12.5 24.7 5.9 ) 2 5,88 2,05 50
- Độ lệch chuẩn của mẫu số liệu ghép nhóm của lớp 12F: 2 1 s = S = + + + + − ≈ F F ( 2 2 2 2 2 4.1 5.3 16.5 18.7 7.9 ) 2 5,76 2,19 50
Ta thấy độ lệch chuẩn ở mẫu số liệu lớp 12E nhỏ hơn độ lệch chuẩn của mẫu số liệu lớp 12F.
Do đó lớp 12E học đều môn Toán hơn lớp 12F. Vậy d) đúng.
Câu 6: Huyết áp là áp lực cần thiết tác động lên thành của động mạch để đưa máu từ tim đến nuôi
dưỡng cơ thể. Huyết áp được tạo ra do lực co bóp của cơ tim và sức cản của thành động mạch.
Mỗi lần tim đập, huyết áp của chúng ta tăng rồi giảm giữa các nhịp. Huyết áp tối đa và huyết áp
tối thiểu gọi là huyết áp tâm thu và huyết áp tâm trương, tương ứng. Chỉ số huyết áp của chúng
ta được viết là tâm thu/tâm trương. Chỉ số huyết áp 120 / 80 là bình thường. Giả sử huyết áp của
một người nào đó được mô hình hoá bởi hàm số P(t) =115 + 20sin (180πt) ở đó P(t) là
huyết áp tính theo đơn vị mmHg (milimét thuỷ ngân) và thời gian t tính theo phút.
Xét tính đúng, sai của các mệnh đề sau:
a) Chu kỳ của hàm P(t) là 90.
b) Số lần huyết áp tâm thu xảy ra trong khoảng thời gian một giờ đồng hồ là 5000.
c) Chỉ số huyết áp là 135 / 95 .
d) Trong một phút, số lần mà tốc độ thay đổi huyết áp bằng 1800π (mmHg/phút) là 180. Lời giải
a) Chu kỳ của hàm số P(t) là 2π 1 = . 180π 90 Vậy a) sai.
b) Dựa vào hàm số P(t) ta thấy: huyết áp cao nhất là 135 mmHg
hay P(t) =135 ⇔ 115 + 20sin (180πt) =135 ⇔ sin (180πt) =1 π 1 ⇔ 180π = + 2 k t k π ⇔ t = + (k ∈) 2 360 90 Xét 1 k 1 1
0 ≤ t ≤ 60 ⇔ 0 ≤ +
≤ 60 ⇔ − ≤ k ≤ 5400 − ⇔ k ∈{0;1;2; } ...5399 vì k ∈ . 360 90 4 4
Vậy trong khoảng 1 giờ đồng hồ số lần huyết áp cao nhất (huyết áp tâm thu) là 5400 lần. Vậy b) sai. c) Vì 1
− ≤ sin (180πt) ≤1 nên 95 ≤115 + 20sin (180πt) ≤135.
P(t) lớn nhất bằng 135; P(t) nhỏ nhất bằng 95 nên chỉ số huyết áp là 135 / 95 . Vậy c) đúng.
d) Yêu cầu bài toán ⇔ P′(t) =1800π ⇔ 3600π.cos(180πt) =1800π ⇔ ( π ) 1 π 1 cos 180 = ⇔ 180π = ± + 2 k t t k π ⇔ t = ± + (k ∈) 2 3 540 90 1 0 k ≤ + ≤ 1
k∈ k ∈{0;1; 2;...; } 89 Do 540 90 0 ≤ t ≤1⇒ ⇒
⇒ có 180 giá trị của t . Vậy d) đúng. 1 k k ∈ ≤ − + ≤ {1;2;3;...; } 90 0 1 540 90
Trang 13/18 - Mã đề GỐC
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh làm từ câu 1 đến câu 6.
Câu 1: Cho hàm số f (x) 3 2
= x + 3x + 4x + 3. Có tất cả bao nhiêu giá trị nguyên không âm của tham số
m để phương trình f ( 3f (x)+ f (x)+ m) 3 2 3
= −x + 3x − 4x + 3 có nghiệm x ∈[ 2; − ] 1 ? Lời giải TL: 11.
Xét hàm số f (t) 3 2
= t + 3t + 4t + 3 , ta có f ′(t) 2
= 3t + 6t + 4 > 0, t ∀ ∈ .
Do đó hàm số f đồng biến trên . Ta có: PT ⇔ ( 3 3 f
f (x) + f (x) + m ) = f (−x) 3
⇔ −x = f (x) + f (x) 3
+ m ⇔ f (x) + f (x) 3 3 + x + m = 0 (1) Xét hàm số ( ) 3 = ( )+ ( ) 3 h x f x
f x + x + m trên đoạn [ 2; − ] 1 .
Ta có: h′ x = f ′(x) 2
⋅ f (x) + f ′(x) 2
+ x = f ′(x) 2 f (x) 2 ( ) 3 3 3 +1 + 3x Ta có f ′(x) 2
= 3x + 4x + 6 > 0, x ∀ ∈[ 2; − ]
1 ⇒ h′(x) > 0, x ∀ ∈[ 2; − ] 1 .
⇒ hàm số h( x) đồng biến trên [ 2; − ] 1 nên
min h(x) = h( 2
− ) = m −10, max h(x) = h( ) 1 = m +1343 [ 2 − ] ;1 [ 2 − ] ;1
Phương trình (1) có nghiệm khi và chỉ khi
min h(x).max h(x) ≤ 0 ⇔ h(− )
1 ⋅h(2) ≤ 0 ⇔ (m −10)(m +1343) ≤ 0 ⇔ 134 − 3 ≤ m ≤10 [ 2 − ] ;1 [ 2 − ] ;1
Do m nguyên không âm nên tập các giá trị m thỏa mãn là S = {0;1;2;...; } 10 .
Vậy có tất cả 11 giá trị nguyên không âm của m thỏa mãn.
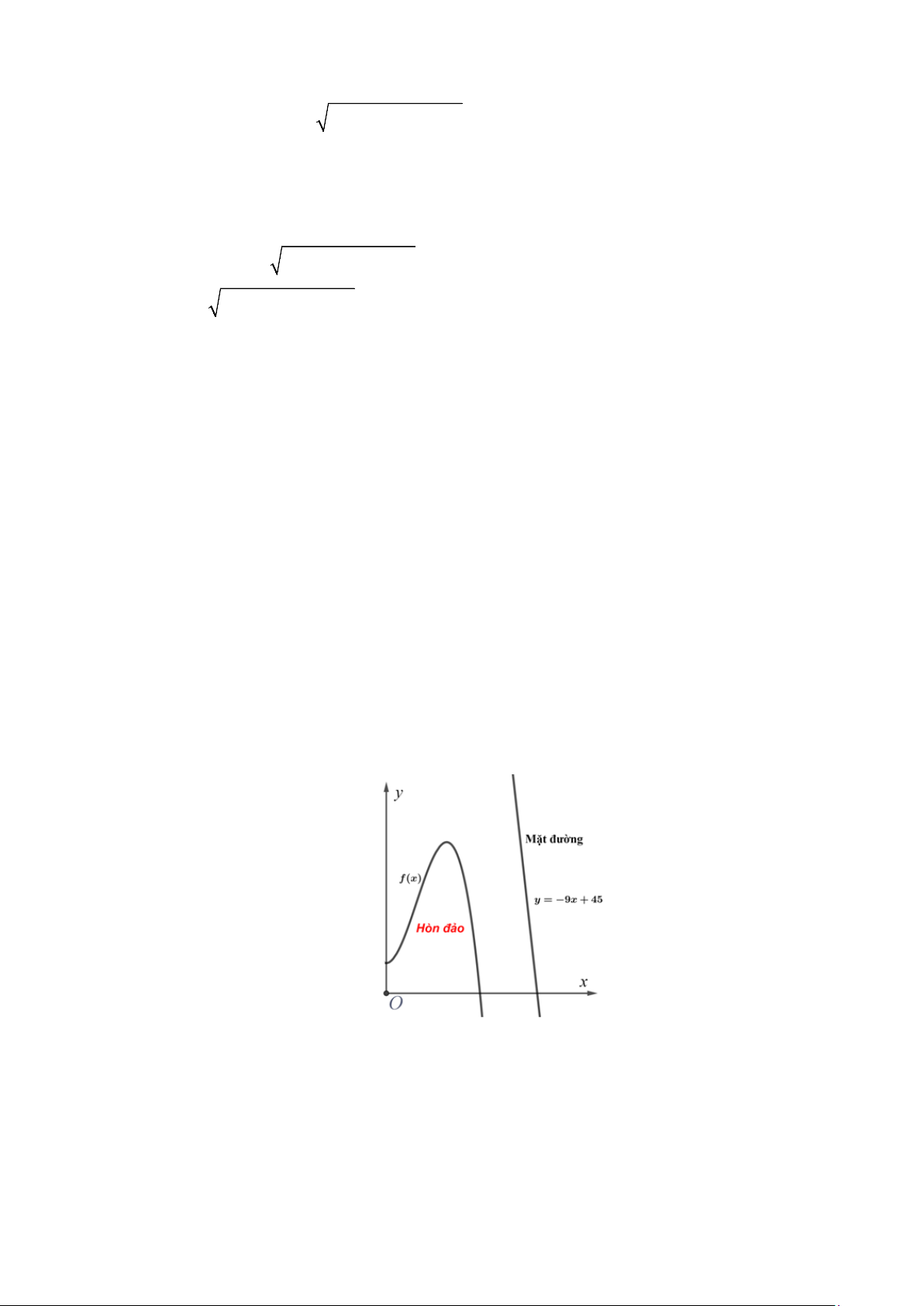
Câu 2: Có một hòn đảo nằm trong một vịnh biển, giả sử rằng đường bao sát biển của hòn đảo được mô
hình hóa vào hệ trục tọa độ Oxy là một phần bên phải trục tung của đồ thị hàm số bậc ba y = f (x) 3 2
= −x + 3x +1 và giả sử một con đường trong đất liền chạy trên một đường thẳng có phương trình y = 9
− x + 45 như hình vẽ, với đơn vị của hệ trục là 100m . Tập đoàn đầu tư du
lịch S muốn làm một cây cầu vượt biển có dạng một đoạn thẳng nối từ con đường trong đất
liền ra hòn đảo để khai thác du lịch sinh thái. Tính độ dài ngắn nhất (đơn vị: mét) của cây cầu
cần làm với kết quả làm tròn đến hàng đơn vị. Lời giải TL: 188
Gọi M (x ; y , x > 0, là điểm nằm trên đường bao sát biển của hòn đảo (thuộc đồ thị hàm số 0 0 ) 0
bậc ba đã cho) để từ đó xây dựng cây cầu nối với con đường trong đất liền.
Gọi ∆ là tiếp tuyến của đồ thị hàm số y = f (x) tại điểm M , khi đó, để độ dài của cây cầu
ngắn nhất thì ∆ phải song song với con đường trong đất liền.
Đường thẳng y = 45 − 9x có hệ số góc k = 9
− , do đó tiếp tuyến ∆ có hệ số góc k = 9 −
Trang 14/18 - Mã đề GỐC = ⇒ f ′( x 3 x = 9 − ⇔ 3 − x + 6x = 9 − ⇔ ⇒ M 3;1 . 0 ) 2 0 0 0 ( ) x = 1 − 0
Nhận thấy: độ dài ngắn nhất của cây cầu bằng khoảng cách từ điểm M đến đường thẳng
(d ):9x + y − 45 = 0 . + −
d (M d ) 9.3 1 45 289 ; = = . 2 2 9 +1 82
Vì đơn vị của hệ trục là 100m nên độ dài ngắn nhất của cây cầu là 289 100. ≈188 (m) 82
Câu 3: Cho hai số thực x, y thỏa mãn y
x > > 0 và 3x + y + 3xy ≥ 7 . Biết giá trị nhỏ nhất của biểu 3 thức 2 1
P = 9x + (3x + 5y)2 − 2ln ( 2
1+ 30xy − 5y ) bằng a − lnb với a,b là các số tự nhiên. 4
Tính giá trị a − . b Lời giải TL: -651
- Đặt z = 3x , ta được: z > y > 0 và z + y + zy ≥ 7 . Khi đó: 2 2 2 2 2
1+ 30xy − 5y =1+10zy − 5y >1+10y − 5y = 5y +1 >1 và 2 1
P = z + (z + 5y)2 − 2ln ( 2
1+10zy − 5y ) . 4
Theo giả thiết ta được: 7 − y z ≥ . y +1 1
5 z + 2zy + 5y 2 ( 2 2 2 )
Ta có: z + (z + 5y) = 4 4 Mà 2 2
z + zy + y = (z + y)2 2 2 5 + 4y ≥ 8
(z + y) −16 +
[8y − 4] = 8( z + 2y) − 20 7 − y 8 ≥ 8 + 2y − 20 = 8 + 2( y + ) 1 − 44 ≥ 64 − 44 = 20 y +1 y +1 z + 5y 2 ( )2 Nên z +
≥ 25, dấu "=" xảy ra khi z = 3, y =1 hay x = y =1. 4 Mặt khác ta có 5( 2 2
z + 2zy + 5y 5 − z − 3y 2 ) ( )2 10zy − 5y − = ≤ 0 4 4
(dấu "=" xảy ra khi z = 3, y =1 hay x = y =1) (z +5y)2 2 2
⇒1+10zy − 5y ≤ z + +1. 4 z + 5y 2 ( )2 Đặt t = z + +1≥ 26 ⇒ ln ( 2
1+10zy − 5y ) ≤ lnt ⇒ P ≥ t −1− 2lnt 4
Xét hàm số f (t) = t −1− 2ln t với t ≥ 26 . Có: f ′(t) 2 t − 2 = 1− = > 0, t
∀ ≥ 26 ⇒ f (t) đồng biến trên [26;+∞) t t
⇒ P ≥ f (t) ≥ f (26) = 25− 2ln 26 = 25− ln 676 .
Do đó P = 25 − ln 676 khi z = 3, y =1 hay x = y =1 min
Vậy a = 25, b = 676 ⇒ a − b = 651 − .
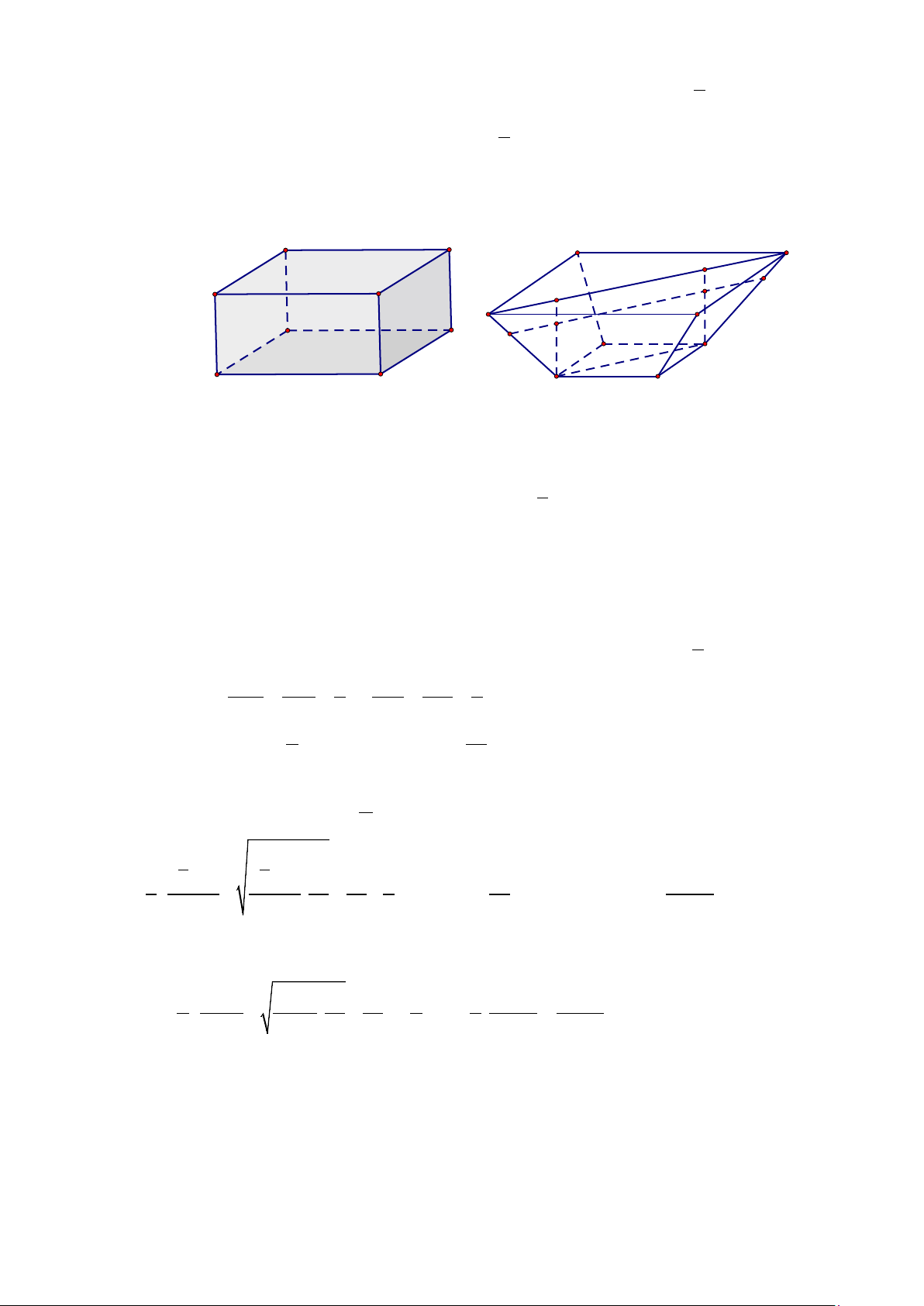
Câu 4: Một chiếc khay đựng đầy nước có dạng hình hộp chữ nhật với kích thước: chiều dài 30cm,
chiều rộng 20cm , chiều cao 10cm. Để san bớt nước cho đỡ đầy, người ta đổ nước từ chiếc
khay thứ nhất đó sang chiếc khay thứ hai (không có nước) có dạng hình chóp cụt tứ giác đều
Trang 15/18 - Mã đề GỐC
với đáy khay là hình vuông nhỏ có đường chéo dài x (cm), miệng khay là hình vuông lớn có
đường chéo dài 2x (cm). Sau khi đổ, mực nước ở khay thứ hai cao bằng 2 chiều cao của khay 3
đó và lượng nước trong khay thứ nhất giảm đi 1 so với lượng nước ban đầu. Tính thể tích của 5
chiếc khay thứ hai (đơn vị 3
cm ) với kết quả làm tròn đến hàng đơn vị. Lời giải TL: 2314 A2 D2 D C K 2x N H B Q 2 C2 A B A1 D P 1 M D' C' x B1 C1 A' B' Hình 4a Hình 4b
- Ta có: 2 khay nước được mô hình hóa thành hình 4a và hình 4b
Thể tích nước ở khay thứ nhất trước khi đổ bằng: = ( 3 30.20.10 6000 cm )
Sau khi đổ, thể tích nước ở khay thứ hai bằng: 1 6000. =1200 ( 3 cm ) 5
- Xét khay thứ 2 (hình 4b).
Gọi chiều cao của khay thứ hai là: h (cm) . Xét hình thang ACC A
′ ′, lấy MN //AC , MN là vị trí mực nước trong khay; H, K lần lượt là
hình chiếu của A ,′ C′ trên AC ; P, Q lần lượt là giao điểm của A′H và MN , C K ′ và MN .
Theo giả thiết, mực nước (ngang với MN ) trong khay thứ hai cao bằng 2 chiều cao của khay 3 ′ ′ đó, suy ra: A P C Q 2 MP NQ 2 = = ⇒ = = . A′H C K ′ 3 AH CK 3 Ta có: x
AH = CK = , HK = x , nên 5x MN =
. Thể tích của nước trong khay thứ hai bằng thể 2 3
tích khối chóp cụt tứ giác đều với đáy lớn nhận MN là đường chéo và đáy nhỏ nhận A′C′ là
đường chéo, chiều cao bằng 2 h . Vì thể tích nước trong khay thứ hai bằng 3 1200 cm nên ta có 3 2 2 5 5 x x 2 2 1 3 3 x x 2 49 2 2 97200 + . + . h =1200 ⇔
hx =1200 ⇔ x h = 3 2 2 2 2 3 81 49
Thể tích của chiếc khay thứ hai bằng h (2x)2 (2x)2 2 2 x x 7 2 7 97200 16200 V = + . + = x h = . = ≈ 2314 ( 3 cm ) . 3 2 2 2 2 6 6 49 7 Vậy 3 V ≈ 2314 cm .
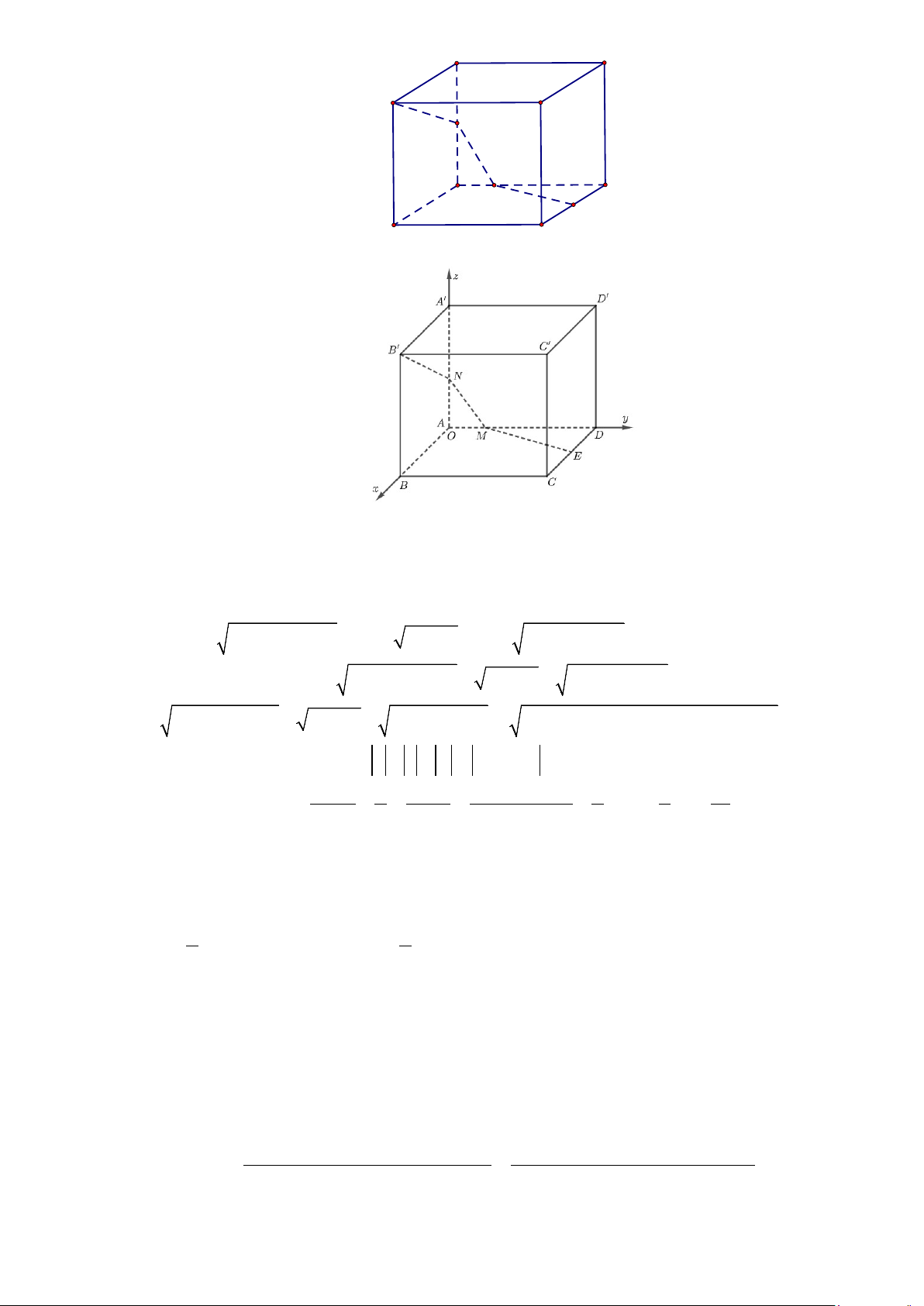
Câu 5: Một mô hình trang trí có dạng là hình lập phương ABC . D A′B C ′ D
′ ', cạnh bằng 10dm (như hình
vẽ). Người ta cần nối một đường dây điện đi từ điểm E (là trung điểm của CD ) đi qua điểm
M thuộc cạnh AD , đi tiếp qua điểm N thuộc cạnh AA′ rồi tới điểm B′. Độ dài đoạn dây
điện ngắn nhất bằng bao nhiêu dm ?
Trang 16/18 - Mã đề GỐC A' D' C' B' N A D M E B C Lời giải TL: 25
Chọn hệ toạ độ Oxyz sao cho O trùng với A ; các tia Ox,Oy,Oz lần lượt trùng với các tia AB
, AD và AA′ (như hình vẽ). Ta có: B′(10;0;10) và E (5;10;0).
N ∈Oz ⇒ N (0;0;a) ; M ∈Oy ⇒ M (0; ;
b 0) , ( điều kiện 0 ≤ a,b ≤10). ⇒ B N ′ = + (a − )2 2 2 100
10 ;MN = a + b ;ME = 25 + (b −10)2 . Ta có: B N ′ + MN + ME = + (a − )2 2 2 100
10 + a + b + 25 + (b −10)2 . = ( − a)2 2 2 2 2 10
+10 + a + b + 5 + (10 −b)2 ≥ ( − a + a + )2 + ( + b + −b)2 10 5 10 10 = 25 .
(Áp dụng bất đẳng thức vectơ u + v + w ≥ u + v + w ).
Dấu “=” xảy ra khi: 10 − a a 5
10 − a + a + 5 3 5 10 = = = = ⇒ a = ; b = (thoả mãn điều 10
b 10 − b 10 + b +10 − b 4 2 3 kiện).
Vậy độ dài đoạn dây điện ngắn nhất bằng 25 dm .
Câu 6: Cho dãy gồm 2021 số được sắp thứ tự tăng dần như sau: 4 4 4 4
C ; C ; ...; C ; C . Lấy ngẫu 4 5 2023 2024
nhiên ba số hạng liên tiếp từ dãy số đã cho, biết xác suất để tổng của ba số này là một số lẻ
bằng a , với a,b ∗
∈ và phân số a tối giản. Tính giá trị a + b . b b Lời giải TL: 3029 Với mỗi số hạng 4
C của dãy đã cho ta xét n thuộc một trong hai nhóm số sau: n
- Nhóm 1: 8p + 4; 8p + 5; 8p + 6; 8p + 7 với p ≥ 0 . - Nhóm 2: 8 ;
q 8q +1; 8q + 2; 8q + 3 với q ≥1.
a/ Xét n thuộc nhóm 1, chẳng hạn n = 8p + 4 (xét tương tự cho các số còn lại trong nhóm 1) Ta có:
8p + 4 8p + 3 8p + 2 8p +1
2 p +1 8p + 3 4 p +1 8p +1 4 4 ( )( )( )( ) ( )( )( )( ) C = C = = , n 8 p+4 1.2.3.4 3
đây là số lẻ (tử số là tích của 4 số lẻ, mẫu số là số lẻ).
b/ Xét n thuộc nhóm 2, chẳng hạn n = 8q +1(xét tương tự cho các số còn lại trong nhóm 2)
Trang 17/18 - Mã đề GỐC
8q +1 8q 8q −1 8q − 2 4 4 ( ) ( )( ) Ta có C = C = n 8q 1 + 1.2.3.4 8
q(8q − ) 1 (8q − 2)3 Do
nên 8q(8q − ) 1 (8q − 2)48 4
⇒ C là số chẵn. 8 q n (8q − )
1 (8q − 2) =16q(8q − ) 1 (4q − ) 1 16
Từ những điều ở trên ta thấy 4 số hạng đầu của dãy là các số lẻ, 4 số hạng kế tiếp là các số chẵn
và cứ liên tiếp như thế.
- Ta thấy: trong 2021 số đã cho:
+) có 253 nhóm gồm các số lẻ (nhóm đầu tiên 4 4 4 4
C ,C ,C ,C là nhóm các số lẻ và nhóm 4 5 6 7 4 4 4 4
C ,C ,C ,C là nhóm các số lẻ); 2020 2021 2022 2023
+) có 252 nhóm các số chẵn (nhóm thứ hai 4 4 4 4
C ,C ,C ,C và nhóm gần cuối 8 9 10 11 4 4 4 4
C ,C ,C ,C ) 2016 2017 2018 2019 +) và số 4 C là số chẵn. 2024
- Ta có số cách lấy 3 số hạng liên tiếp trong dãy 2021 số hạng bằng 2019 cách nên số phần tử
của không gian mẫu là: n(Ω) = 2019 .
- Gọi A là biến cố đề bài nêu, ta có các nhóm ba số hạng liên tiếp thỏa mãn biến cố A là:
+) 3 số liên tiếp thuộc 1 nhóm các số lẻ: mỗi nhóm có 2 cách chọn, nên có 253× 2 = 506 cách
+) 1 số lẻ ở đầu (từ nhóm số lẻ thứ 2) hoặc cuối nhóm các số lẻ và 2 số chẵn liên tiếp ở cuối
hoặc đầu nhóm các số chẵn, tương ứng: có 504 cách (3 số liên tiếp cuối cùng 4 4 4 C ,C ,C 2022 2023 2024 không thoả mãn).
Do đó n( A) = 506 + 504 =1010.
Suy ra: xác suất cần tính là P( A) 1010 =
hay a =1010, b = 2019 2019
Vậy a + b = 3029 . HẾT
Trang 18/18 - Mã đề GỐC