12 trang 2 lượt tải

Đề chọn học sinh giỏi Toán 12 năm 2024 – 2025 trường THPT Kon Tum

4

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề thi chọn học sinh giỏi cấp trường môn Toán 12 năm học 2024 – 2025 trường THPT Kon Tum, tỉnh Kon Tum. Kỳ thi được diễn ra vào ngày 04 tháng 01 năm 2025. Đề thi có đáp án chi tiết và hướng dẫn chấm điểm.

Chủ đề: Đề HSG Toán 12 360 tài liệu

Môn: Toán 12 4.3 K tài liệu

Tác giả:

Profile

Linh Đan

1 tuần trước
Danh sách Quiz
/12
Trang 1/2
TRƯỜNG THPT KON TUM
ĐỀ THI CHỌN HỌC SINH GIỎI CẤP TRƯỜNG
NĂM HỌC 2024 – 2025
(Đề thi gồm 02 trang)
Môn: Toán, LỚP 12
Thời gian: 180 phút (không kể thời gian giao đề)
Ngày thi: 04/01/2025
Câu 1 (4,0 điểm).
1) Cho hàm số
(
)
322
1
31
32
= − − −+
m
y x x m xm
. Tìm tất cả các giá trị của tham số
m
để hàm số
đã cho đạt cực trị tại hai điểm
12
,xx
thỏa mãn
( )
12 1 2
2 40+ + +=xx x x
.
2) Hai con tàu
A
và
B
đang ở cùng một vĩ tuyến và cách nhau 5 hải lí. Cả hai tàu đồng thời cùng
khởi hành. Tàu
A
chạy về hướng Nam với vận tốc 6 hải lí/giờ, còn tàu
B
chạy về vị trí hiện tại của tàu
A
với vận tốc 7 hải lí/giờ. Hỏi sau bao nhiêu phút thì khoảng cách giữa hai tàu là ngắn nhất (làm tròn kết
quả đến hàng đơn vị)?
Câu 2 (3,0 điểm).
1) Giải hệ phương trình
2) Cho dãy số
( )
n
a
xác định bởi
(
) ( ) ( )
12
21
20; 24
32 2 1 *
++
= =
=+ −+ ∈
n nn
aa
na n a n a n
.
Tìm
1
lim
+
→+∞
n
n
n
a
a
.
Câu 3 (3,0 điểm).
1) Từ các chữ số 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, ta lập được bao nhiêu số tự nhiên có 6 chữ số, mà các
chữ số đôi một khác nhau và trong đó hai chữ số kề nhau không cùng là số lẻ?
2) Trong một đề thi trắc nghiệm môn Toán có loại câu hỏi trả lời Đúng/ Sai. Mỗi câu hỏi có 4 ý,
tại mỗi ý học sinh lựa chọn đúng hoặc sai. Cách thức tính điểm cho mỗi câu hỏi như sau:
• Học sinh chọn chính xác 01 ý được 0,1 điểm.
• Học sinh chọn chính xác 02 ý được 0,25 điểm.
• Học sinh chọn chính xác 03 ý được 0,5 điểm.
• Học sinh chọn chính xác 04 ý được 1,0 điểm.
Giả sử một thí sinh làm bài bằng cách chọn phương án ngẫu nhiên để trả lời cho 2 câu hỏi loại Đúng/ Sai
này. Tính xác suất để học sinh đó được 0,5 điểm ở phần trả lời 2 câu hỏi này.
Câu 4 (4,0 điểm).
1) Cho tứ diện
ABCD
có
AB
vuông góc với
CD
,
6= =AB CD
.
M
là điểm thuộc cạnh
BC
sao
cho
( )
01= <<MC xBC x
. Mặt phẳng
( )
P
song song với
AB
và
CD
lần lượt cắt
,,,BC DB AD AC
tại
, ,,M N PQ
. Diện tích lớn nhất của tứ giác
MNPQ
bằng bao nhiêu?
ĐỀ CHÍNH THỨC
Trang 2/2
2) Cho khối chóp
.
S ABCD
có đáy
ABCD
là hình chữ nhật,
=AB a
,
SA
vuông góc với mặt
phẳng đáy và
=SA a
. Góc giữa hai mặt phẳng
(
)
SBC
và
( )
SCD
bằng
ϕ
, với
1
cos
3
ϕ
=
. Tính thể
tích của khối chóp
.
S ABCD
.
Câu 5 (3,0 điểm). Cho hình chóp
.S ABC
, mặt bên
SBC
là tam giác đều và nằm trong mặt phẳng vuông
góc với mặt đáy,
60 , 1= =°=ASB ASC SB
. Tính khoảng cách từ
C
đến mặt phẳng
(
)
SAB
.
Câu 6 (1,5 điểm). Một chiếc máy bay đang bay trên không trung. Xét hệ trục tọa độ
Oxyz
được gắn như
hình vẽ, trong đó gốc
O
là vị trí của trạm kiểm soát không lưu và
( )
;;
M xyz
(km) biểu thị vị trí máy bay
trên không trung. Tại thời điểm 9 giờ, máy bay đang ở vị trí
( )
50;120;4
và chuyển động với vận tốc
( )
1
300;400;3=

v
( )
km/h
. Khi máy bay đạt độ cao 10 km so với mặt đất, máy bay đổi vận tốc mới
( )
2
400;300; 5= −

v
( )
km/h
để hướng đến sân bay
A
. Tìm tọa độ máy bay khi vừa đáp xuống sân bay
A
Câu 7 (1,5 điểm). Cho
,,xyz
là các số thực dương thoả mãn điều kiện
111
4++=
xyz
. Chứng minh rằng
111
1
222
++≤
++ + + ++xyz x yz xy z
.
HẾT
Thí sinh không được sử dụng tài liệu, giám thị không giải thích gì thêm.
Trang 1/9
TRƯỜNG THPT KON TUM
ĐỀ THI CHỌN HỌC SINH GIỎI CẤP TRƯỜNG
NĂM HỌC 2024 – 2025
Môn: Toán, LỚP 12
HƯỚNG DẪN CHẤM THI
(Hướng dẫn gồm 09 trang)
I. HƯỚNG DẪN CHUNG
- Các cách giải khác đúng thì cho điểm tương ứng với biểu điểm đã cho.
- Điểm chấm của từng phần được chia nhỏ đến 0,25 điểm. Điểm của toàn bài là tổng điểm của các phần
và không làm tròn số.
II. ĐÁP ÁN VÀ THANG ĐIỂM
Câu 1 (4,0 điểm).
1) Cho hàm số
( )
322
1
31
32
= − − −+
m
y x x m xm
. Tìm tất cả các giá trị của tham số
m
để hàm số
đã cho đạt cực trị tại hai điểm
12
,xx
thỏa mãn
( )
12 1 2
2 40+ + +=xx x x
.
2) Hai con tàu
A
và
B
đang ở cùng một vĩ tuyến và cách nhau 5 hải lí. Cả hai tàu đồng thời cùng
khởi hành. Tàu
A
chạy về hướng Nam với vận tốc 6 hải lí/giờ, còn tàu
B
chạy về vị trí hiện tại của tàu
A
với vận tốc 7 hải lí/giờ. Hỏi sau bao nhiêu phút thì khoảng cách giữa hai tàu là ngắn nhất? (làm tròn
kết quả đến hàng đơn vị).
CÂU
Ý
NỘI DUNG
ĐIỂM
Câu 1
1)
(2,0)
Ta có:
22
31
′
=−− +y x mx m
.
0,25
Hàm số
(
)
322
1
31
32
= − − −+
m
y x x m xm
đạt cực trị tại hai điểm
12
,xx
khi
phương trình
0
′
=y
có hai nghiệm phân biệt
12
,xx
.
( )
22 2
4 3 1 0 13 4 0⇔ − − + >⇔ −>mm m
(*).
0,5
Theo định lí Vi-et ta có:
12
2
12
31
+=
=−+
xx m
xx m
.
0,25
Do đó
( )
12 1 2
2 40+ + +=xx x x
22
3 12 4 0 3 2 5 0⇔− + + + = ⇔− + + =
m m mm
1
5
3
= −
⇔
=
m
m
.
0,5
Đối chiếu với điều kiện (*), giá trị của
m
cần tìm là
5
1;
3
=−=mm
.
0,5
2)
(2,0)
Gọi
d
là khoảng cách giữa hai tàu sau khi xuất phát
t
giờ,
0>t
. Khi đó tàu
A
đang ở vị trí
1
A
và tàu
B
đang ở vị trí
1
B
như hình vẽ sau
0,5
HƯỚNG DẪN CHÍNH THỨC
Trang 2/9
Quãng đường tàu
A
đi được là
1
.6= =
A
AA v t t
.
Quãng đường tàu
B
đi được là
1
7= ⋅=
B
BB v t t
.
Ta có
( )
2
2 22 2 2 2
11 1 1
5
,0 .5 (5 7 ) (6 )
7
=+=− +=− <+ ≤d AB AA B t
tB AA t
Vậy
2
085 7
5
,.
7
0 25= −+ <≤td tt
0,5
Đặt
2
( ) 85 70 25
= −+ft t t
(với
5
0.
7
<≤t
Bài toán trở thành tìm
5
0;
7
min ( )


ft
.
Ta có
(
)
(
)
2
170 70 7
,0 .
17
2 85 70 25
′
−
= = ⇔=
−+
′
t
t
t
tt
ft f
0,5
Lập bảng biến thiên
Từ bảng biến thiên, ta có
5
0;
7
7 6 85
min ( ) 3,524
17 17



= = ≈


ft f
(hải lí)
0,25
Vậy
7
25
17
= ≈
th
phút.
0,25
Trang 3/9
Câu 2 (3,0 điểm).
1) Giải hệ phương trình
( )
(
) (
)
33 3 3
4 3 41
.
log log 1 log 4 log 2
++=+ −
+ − += + +
xy x x y
x xy y xy
2) Cho dãy số
( )
n
a
xác định bởi
( )
(
) (
)
12
21
20; 24
32 2 1 *
++
= =
=+ −+ ∈
n nn
aa
na n a n a n
.
Tìm
1
lim
+
→+∞
n
n
n
a
a
.
CÂU
Ý
NỘI DUNG
ĐIỂM
Câu 2
1)
(1,5)
Điều kiện
0
0
0
20
4 30
>
>
−>
+>
++≥
x
y
xy
xy
xy x
( )
*
0,25
( ) ( ) ( )
33 3 3
log log 1 log 4 log 2+ − += + +x xy y xy
( )
1
⇔
( ) ( )
33
log 3 log 4 2−= +


xx y y x y
⇔
( )
(
)
3 42
−= +xx y y x y
⇔
22
3 11 4 0− −=x xy y
⇔
( )( )
3 40+ −=xyx y
⇔
3
4
= −
=
yx
xy
0,5
Xét phương trình
4 3 41++=+ −xy x x y
( )
2
Với
3= −yx
,
( )
2
trở thành
2
12 3 11 1 (3)− ++=− −xx x
.
Theo điều kiện trên,
0>x
nên phương trình
(3)
vô nghiệm.
0,25
Với
4=xy
,
( )
2
trở thành
2
32 1++= −xx x
⇔
2
1
2
3 5 20
≥
− −=
x
xx
⇔
1
2
2
1
3
2
≥
⇔=
= −
=
x
x
x
x
0,25
Kết hợp với điều kiện
( )
*
, suy ra hệ phương trình có duy nhất một nghiệm
là
( )
1
; 2;
2

=


xy
.
0,25
Trang 4/9
2)
(1,5)
Từ hệ thức truy hồi ta suy ra
( ) ( )
( ) ( )( )
21
21 1
21 1
32 2 1
21
2. .
1
++
++ +
++ +
=+ −+
⇔ −=+ −
−−
⇔=
+
n nn
n n nn
n n nn
na n a n a
na a n a a
aa aa
nn
Đặt
1+
−
=
nn
n
aa
b
n
, ta được
1
2
+
=
nn
bb
*∀∈n
Suy ra
( )
n
b
là một cấp số nhân có công bội bằng 2.
Do đó
11 1
1
11
1
1
.2 2 .2 .
2 22
−+ +
+
+
+
= = ⇒ −= ⇒ − =
nn n
nn
n nn
nn
aa
bb a an n
(
)
(
)
1
1
1
2 14 . 2 4
2 22
+
+

⇒ − +− = − −




nn
nn
aa
nn
.
0,5
Đặt
(
)
1
1
24 *
22
+
= − − ⇒ = ∀∈
n
n nn
n
a
c n c cn
, do đó
( )
n
c
là một cấp số
nhân có công bội bằng
1
2
( )
1
1
1 24
. 2 4 2 24
22
−

⇒= = ⇒= − +


n
n
nn
n
cc a n
*∀∈n
.
0,5
Ta có
( )
( )
( )
( )
1
1
24
2
2 22 24 2 22
lim lim lim 2
2 4 24
2 4 2 24
22222
+
+
→+∞ →+∞ →+∞
+
−+ −
= = =
−
−+
+
−−
nn
n
n
nn n
n
n
nn
a
n
an
nn
.
0,5
Câu 3 (3,0 điểm).
1) Từ các chữ số 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, ta lập được bao nhiêu số tự nhiên có 6 chữ số, mà các
chữ số đôi một khác nhau và trong đó hai chữ số kề nhau không cùng là số lẻ?
2) Trong một đề thi trắc nghiệm môn Toán có loại câu hỏi trả lời Đúng/ Sai. Mỗi câu hỏi có 4 ý,
tại mỗi ý học sinh lựa chọn đúng hoặc sai. Cách thức tính điểm cho mỗi câu hỏi như sau:
• Học sinh chọn chính xác 01 ý được 0,1 điểm.
• Học sinh chọn chính xác 02 ý được 0,25 điểm.
• Học sinh chọn chính xác 03 ý được 0,5 điểm.
• Học sinh chọn chính xác 04 ý được 1,0 điểm.
Giả sử một thí sinh làm bài bằng cách chọn phương án ngẫu nhiên để trả lời cho 2 câu hỏi loại Đúng/ Sai
này. Tính xác suất để học sinh đó được 0,5 điểm ở phần trả lời 2 câu hỏi này.
CÂU
Ý
NỘI DUNG
ĐIỂM
Câu 3
1)
(1,5)
Gọi số đó là
123456
A aaaaaa=
. Từ giả thiết suy ra A có 1 hoặc 2 hoặc 3 chữ
số lẻ lấy từ
{ }
1; 3; 5; 7; 9
.
0,25
Trường hợp 1: A có 1 chữ số lẻ.
0,25
Trang 5/9
+)
1
a
lẻ: Số các số A là
1
55
600CP=
+)
1
a
chẵn: Có 4 cách chọn
1
a
. Số các số A là
14
54 5
4.( ) 2400CC P =
Tổng có: 600 + 2400 = 3000 số các số A trong đó có đúng một chữ số lẻ.
Trường hợp 2: A có 2 chữ số lẻ.
+)
1
a
lẻ: Có 5 cách chọn
1
a
. Có 5 cách chọn
2
a
chẵn.
Vậy số các số A là
13
44 4
5.5.( ) 9600CC P
=
+)
1
a
chẵn: Có 4 cách chọn
1
a
. Có 6 cách chọn hai vị trí không kề nhau
của hai số lẻ trong
2
a
3
a
4
a
5
a
6
a
. Vậy số các số A là
23
5 24
4.( .6. ). 11520C PA=
Tổng có: 9600 + 11520 = 21120 số các số A.
0,25
Trường hợp 3: A có 3 chữ số lẻ
+)
1
a
lẻ: Có 5 cách chọn
1
a
. Có 5 cách chọn
2
a
. Có 3 cách chọn hai vị trí
không kề nhau của hai số lẻ trong
3
a
4
a
5
a
6
a
. Vậy số các số A là
22
4 24
5.5.( .3. ). 10800
C PA=
+)
1
a
chẵn: Có 4 cách chọn
1
a
. Có 1 cách chọn 3 vị trí không kề nhau của
3 số lẻ trong
2
a
3
a
4
a
5
a
6
a
. Vậy số các số A là:
32
5 34
4.( .1. ). 2880
C PA=
.
Tổng có: 10800 + 2880 = 13680 số các số A.
0,25
Vậy có: 3000 + 21120 + 13680 = 37800 số các số A.
0,5
2)
(1,5)
Số phần tử không gian mẫu là
( )
8
2 256Ω= =n
.
0,25
Để đạt 0,5 điểm sẽ có các trường hợp sau xảy ra:
Trường hợp 1. Mỗi câu hỏi học sinh trả lời đúng 2 ý và sai 2 ý, khi đó số
điểm đạt được mỗi câu hỏi là 0,25 điểm.
Trường hợp 2. Một câu hỏi trong hai câu học sinh trả lời đúng 3 ý, sai 1 ý,
câu hỏi còn lại trong hai câu đó học sinh trả lời sai cả 4 ý.
0,5
Gọi A là biến cố học sinh đó được 0,5 điểm. Khi đó
( )
22 34
44 44
. 2 . 44=+=nA CC CC
.
0,5
Vậy xác suất để học sinh đó được 0,5 điểm là
(
)
( )
( )
44 11
256 64
= = =
Ω
nA
PA
n
.
0,25
Câu 4 (4,0 điểm).
1) Cho tứ diện
ABCD
có
AB
vuông góc với
CD
,
6= =AB CD
. Gọi
M
là điểm thuộc cạnh
BC
sao cho
( )
01= <<MC xBC x
. Mặt phẳng
( )
P
song song với
AB
và
CD
lần lượt cắt
,,,BC DB AD AC
tại
, ,,M N PQ
. Diện tích lớn nhất của tứ giác
MNPQ
bằng bao nhiêu?
2) Cho khối chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật,
=AB a
,
SA
vuông góc với mặt phẳng
đáy và
=SA a
. Góc giữa hai mặt phẳng
( )
SBC
và
( )
SCD
bằng
ϕ
, với
1
cos
3
ϕ
=
. Tính thể tích của
khối chóp
.S ABCD
.
Trang 6/9
CÂU
Ý
NỘI DUNG
ĐIỂM
Câu 4
1)
(2,0)
Xét tứ giác
MNPQ
có
// //
// //
MQ NP AB
MN PQ CD
⇒ MNPQ
là hình bình hành.
Mặt khác,
⊥⇒ ⊥AB CD MQ MN
. Do đó,
MNPQ
là hình chữ nhật.
0,5
Vì
//MQ AB
nên
.6= =⇒= =
MQ CM
x MQ x AB x
AB CB
.
Theo giả thiết
( )
.1= ⇒=−MC x BC BM x BC
.
Vì
//MN CD
nên
( ) ( )
1 1 . 61= =−⇒ = − = −
MN BM
x MN x CD x
CD BC
.
0,5
Diện tích hình chữ nhật
MNPQ
là
( ) ( )
2
1
. 6 1 .6 36. . 1 36 9
2
+−

= = − = −≤ =


xx
S MN MQ x x x x
MNPQ
.
0,5
Ta có
9=S
MNPQ
khi
1
1
2
=−⇔=x xx
.
Vậy diện tích tứ giác
MNPQ
lớn nhất bằng 9 khi
M
là trung điểm của
BC
.
0,5
2)
(2,0)
+ Gọi
H
là trung điểm
SB
, vì
∆SAB
vuông cân tại
A
nên
( )
1⊥AH SB
.
0,5
6
6
P
N
Q
B
A
C
D
M
Trang 7/9
+ Lại có
( ) ( )
2
⊥
⇒⊥ ⇒⊥
⊥
BC AB
BC SAB BC SB
BC SA
.
Từ
( ) ( ) ( ) ( )
31, 2
⇒⊥AH SBC
.
+ Gọi
K
là hình chiếu của
A
lên
SD
, chứng minh tương tự ta có
(
) (
)
4⊥AK SCD
.
+ Vì
(
) (
)
SBC SCD SC∩=
nên từ
(
)
( )
3, 4
suy ra
( ) ( )
(
)
( )
,,
ϕ
= =SBC SCD AH AK
.
+ Gọi
,
MN
lần lượt là trung điểm
,SC AD
, dễ dàng chứng minh được
AHMN
là hình bình hành, suy ra
//
MN AH
+ Kẻ
( )
// ∈NP AK P SD
, vì
( )
//
⇒⊥ ⇒⊥NP AK NP SCD NP MP
.
+ Ta có
( )
( )
,,
ϕ
= = =AH AK MN NP MNP
(vì
∆
MNP
vuông tại
P
).
0,5
+ Đặt
=
AD x
, dễ thấy
22
.
= =
+
SA AD ax
AK
SD
ax
22
2
⇒=
+
ax
NP
ax
.
+ Xét
∆
MNP
vuông tại
P
, ta có
22
1
cos
32
+
= = =
ax
NP
ax
MNP
MN
a
2
⇒=xa
.
0,5
Vậy
3
2
.
11 2
. .. 2
33 3
= = =
S ABCD ABCD
a
V SA S a a
.
0,5
Câu 5 (3,0 điểm). Cho hình chóp
.S ABC
, mặt bên
SBC
là tam giác đều và nằm trong mặt phẳng vuông
góc với mặt đáy,
60 , 1
= =°=
ASB ASC SB
. Tính khoảng cách từ
C
đến mặt phẳng
( )
SAB
.
CÂU
Ý
NỘI DUNG
ĐIỂM
Câu 5
Gọi
H
là trung điểm của
BC
suy ra
( )
⊥SH ABC
.
Ta có
( )
( )
( )
( )
, 2,=d C SAB d H SAB
.
Kẻ
;⊥⊥HI AB HK SI
suy ra
( )
( )
, =d H SAB HK
.
0,5
Trang 8/9
Vì
∆SBC
đều,
1=
SB
suy ra
3
2
=SH
.
Đặt
=SA x
.
22 2
2. . .cos 1
⇒ = + − = −+AB SA SB SA SB ASB x x
(do
60= °
ASB
).
Ta lại có
∆=∆ASB ASC
.
2 22
3
4
⇒=⇒⊥⇒= − =−+AB AC AH BC AH AB BH x x
1,0
Mà tam giác
SHA
vuông tại
H
nên
2 2 22 2
3 33
4 42
= + ⇔ = + −+ ⇔ =
SA SH HA x x x x
.
Suy ra
7 6 . 42
;
2 2 14
= = ⇒= =
BH AH
AB AH HI
AB
.
1,0
Từ đó ta có
22
.6
6
= =
+
SH HI
HK
SH HI
.
Suy ra
(
)
(
)
6
,.
3
=
d C SAB
0,5
Câu 6 (1,5 điểm). Một chiếc máy bay đang bay trên không trung. Xét hệ trục tọa độ
Oxyz
được gắn như
hình vẽ, trong đó gốc
O
là vị trí của trạm kiểm soát không lưu và
( )
;;M xyz
(km) biểu thị vị trí máy bay
trên không trung. Tại thời điểm 9 giờ, máy bay đang ở vị trí
( )
50;120;4
và chuyển động với vận tốc
( )
1
300;400;3=

v
(
)
km/h
. Khi máy bay đạt độ cao 10 km so với mặt đất, máy bay đổi vận tốc mới
( )
2
400;300; 5
= −

v
(
)
km/h
để hướng đến sân bay
A
. Tìm tọa độ máy bay khi vừa đáp xuống sân bay
A
.
CÂU
Ý
NỘI DUNG
ĐIỂM
Câu 6
Tại thời điểm 11 giờ, máy bay ở điểm có tọa độ:
( )
50 300.2;120 400.2;4 3.2+ ++
hay
(
)
650;920;10
Suy ra, khi đạt độ cao 10 km so với mặt đất, máy bay ở điểm có tọa độ:
( )
650;920;10
.
0,5
Máy bay đổi vận tốc mới
( )
2
400;300; 5= −

v
thì sau một khoảng thời gian
t
(h) máy bay ở điểm có tọa độ
( )
650 400 ;920 300 ;10 5+ +−t tt
.
0,5
Trang 9/9
Khi máy bay đáp xuống sân bay
A
thì độ cao của máy bay so với mặt đất
bằng
0
nên
10 5 0 2− = ⇔=tt
.
0,25
Tọa độ máy bay khi vừa đáp xuống sân bay
A
là
( )
1450;1520;0
.
0,25
Câu 7 (1,5 điểm). Cho
,,xyz
là các số thực dương thoả mãn điều kiện
111
4++=
xyz
. Chứng minh rằng
111
1
222
++≤
++ + + ++
xyz x yz xy z
.
CÂU
Ý
NỘI DUNG
ĐIỂM
Câu 6
Chứng minh BĐT:
11 4
+≥
+a b ab
,0∀>ab
(*).
Thật vậy
,0∀>
ab
ta có:
( )
11 4 11
4

+≥ ⇔ + + ≥

+

ab
abab ab
Theo BĐT CÔSI cho các số dương a, b;
11
,
ab
ta có
( )
20
11
4
11 1
20
+≥ >

⇒+ + ≥


+≥ >
a b ab
ab
ab
a b ab
.
Dấu bằng khi
=
ab
.
0,25
Áp dụng (*)
1 11 1
4

⇔ ≤+

+

ab a b
, ta có
( ) ( )
1 1 11 1
24
111 1 11 1
44 4

= ≤+

++ + + + + +




≤ ++ +






xyz xy xz xy xz
xy xz
1 1211
2 16

⇒ ≤ ++

++

xyz x y z
(1)
0,5
Chứng minh tương tự ta có
1 11 21
2 16

≤ ++

++

x yz x y z
(2)
1 111 2
2 16

≤ ++

++

xy z x y z
(3)
0,25
Cộng vế với vế của (1), (2), (3) ta được
1111111
41
2 2 2 16


+ + ≤ ++ =


++ + + ++


xyz x yz xy z x y z
.
Dấu bằng xảy ra khi
3
4
= = =xyz
.
0,5
HẾT
Xem thêm: ĐỀ THI HSG TOÁN 12
https://toanmath.com/de-thi-hsg-toan-12

Tài liệu khác của Toán 12

Preview text:

TRƯỜNG THPT KON TUM
ĐỀ THI CHỌN HỌC SINH GIỎI CẤP TRƯỜNG
NĂM HỌC 2024 – 2025
Môn: Toán, LỚP 12 ĐỀ CHÍNH THỨC
Thời gian: 180 phút (không kể thời gian giao đề)
(Đề thi gồm 02 trang) Ngày thi: 04/01/2025 Câu 1 (4,0 điểm). 1) Cho hàm số 1 3 m 2
y = x − x − ( 2 3m − )
1 x + m . Tìm tất cả các giá trị của tham số m để hàm số 3 2
đã cho đạt cực trị tại hai điểm x , x thỏa mãn x x + 2 x + x + 4 = 0. 1 2 ( 1 2) 1 2
2) Hai con tàu A và B đang ở cùng một vĩ tuyến và cách nhau 5 hải lí. Cả hai tàu đồng thời cùng
khởi hành. Tàu A chạy về hướng Nam với vận tốc 6 hải lí/giờ, còn tàu B chạy về vị trí hiện tại của tàu
A với vận tốc 7 hải lí/giờ. Hỏi sau bao nhiêu phút thì khoảng cách giữa hai tàu là ngắn nhất (làm tròn kết
quả đến hàng đơn vị)? Câu 2 (3,0 điểm).
 4xy + x + 3 = x + 4y −1
1) Giải hệ phương trình  .
log x + log x − y +1 = log 4y + log 2x +  y 3 3 ( ) 3 ( ) 3 ( ) a =  20;a = 24
2) Cho dãy số (a xác định bởi 1 2 . n )  na
= n + a − n + a n∈  n+ 3 2 n+ 2 1 n * 2 ( ) 1 ( ) ( ) Tìm an 1 lim + . n→+∞ an Câu 3 (3,0 điểm).
1) Từ các chữ số 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, ta lập được bao nhiêu số tự nhiên có 6 chữ số, mà các
chữ số đôi một khác nhau và trong đó hai chữ số kề nhau không cùng là số lẻ?
2) Trong một đề thi trắc nghiệm môn Toán có loại câu hỏi trả lời Đúng/ Sai. Mỗi câu hỏi có 4 ý,
tại mỗi ý học sinh lựa chọn đúng hoặc sai. Cách thức tính điểm cho mỗi câu hỏi như sau:
• Học sinh chọn chính xác 01 ý được 0,1 điểm.
• Học sinh chọn chính xác 02 ý được 0,25 điểm.
• Học sinh chọn chính xác 03 ý được 0,5 điểm.
• Học sinh chọn chính xác 04 ý được 1,0 điểm.
Giả sử một thí sinh làm bài bằng cách chọn phương án ngẫu nhiên để trả lời cho 2 câu hỏi loại Đúng/ Sai
này. Tính xác suất để học sinh đó được 0,5 điểm ở phần trả lời 2 câu hỏi này. Câu 4 (4,0 điểm).
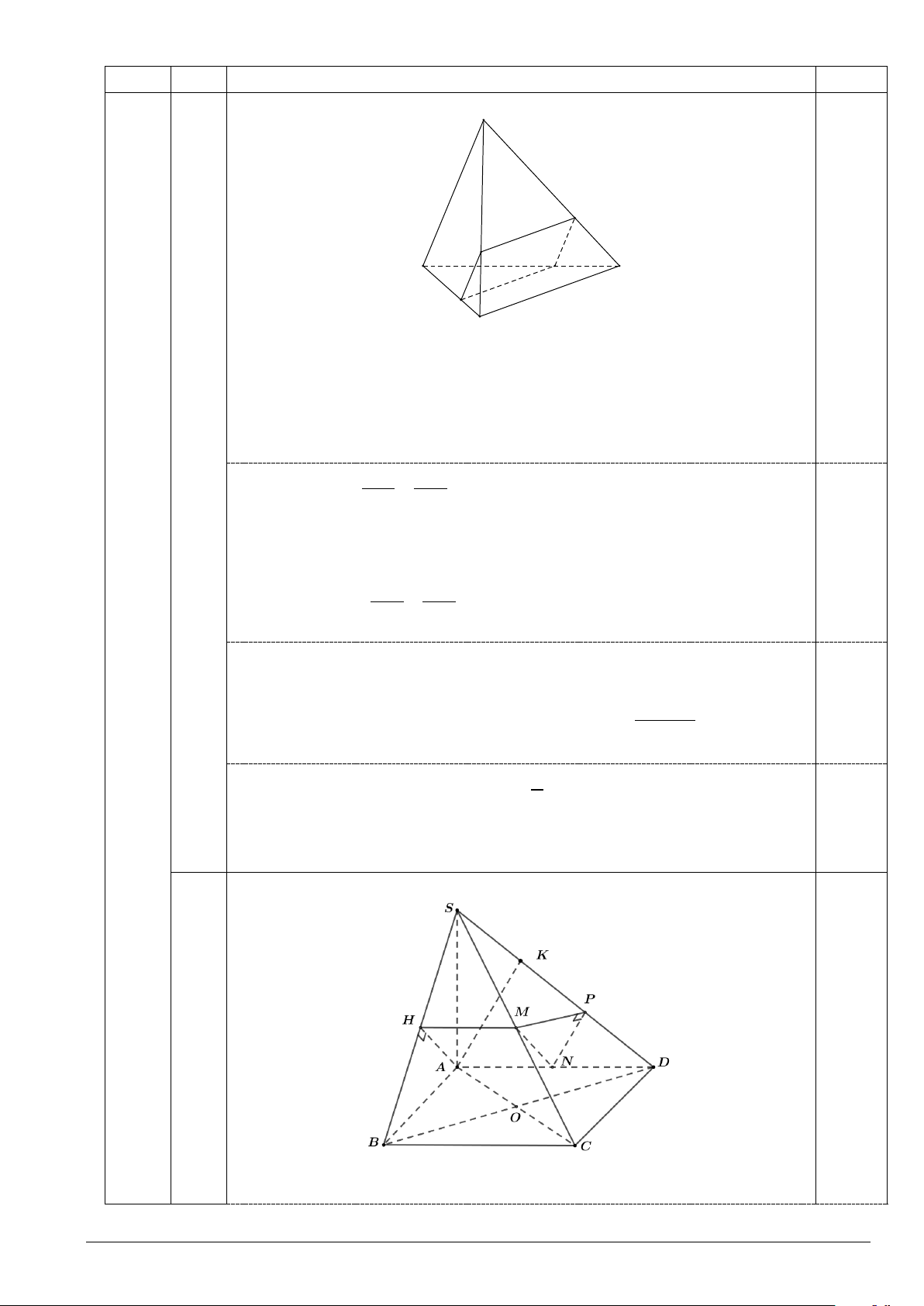
1) Cho tứ diện ABCD có AB vuông góc với CD , AB = CD = 6 . M là điểm thuộc cạnh BC sao
cho MC = xBC (0 < x < )
1 . Mặt phẳng (P) song song với AB và CD lần lượt cắt BC, DB, AD, AC tại
M , N, P,Q . Diện tích lớn nhất của tứ giác MNPQ bằng bao nhiêu? Trang 1/2
2) Cho khối chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a , SA vuông góc với mặt
phẳng đáy và SA = a . Góc giữa hai mặt phẳng (SBC) và (SCD) bằng ϕ , với 1 cosϕ = . Tính thể 3
tích của khối chóp S.ABCD .
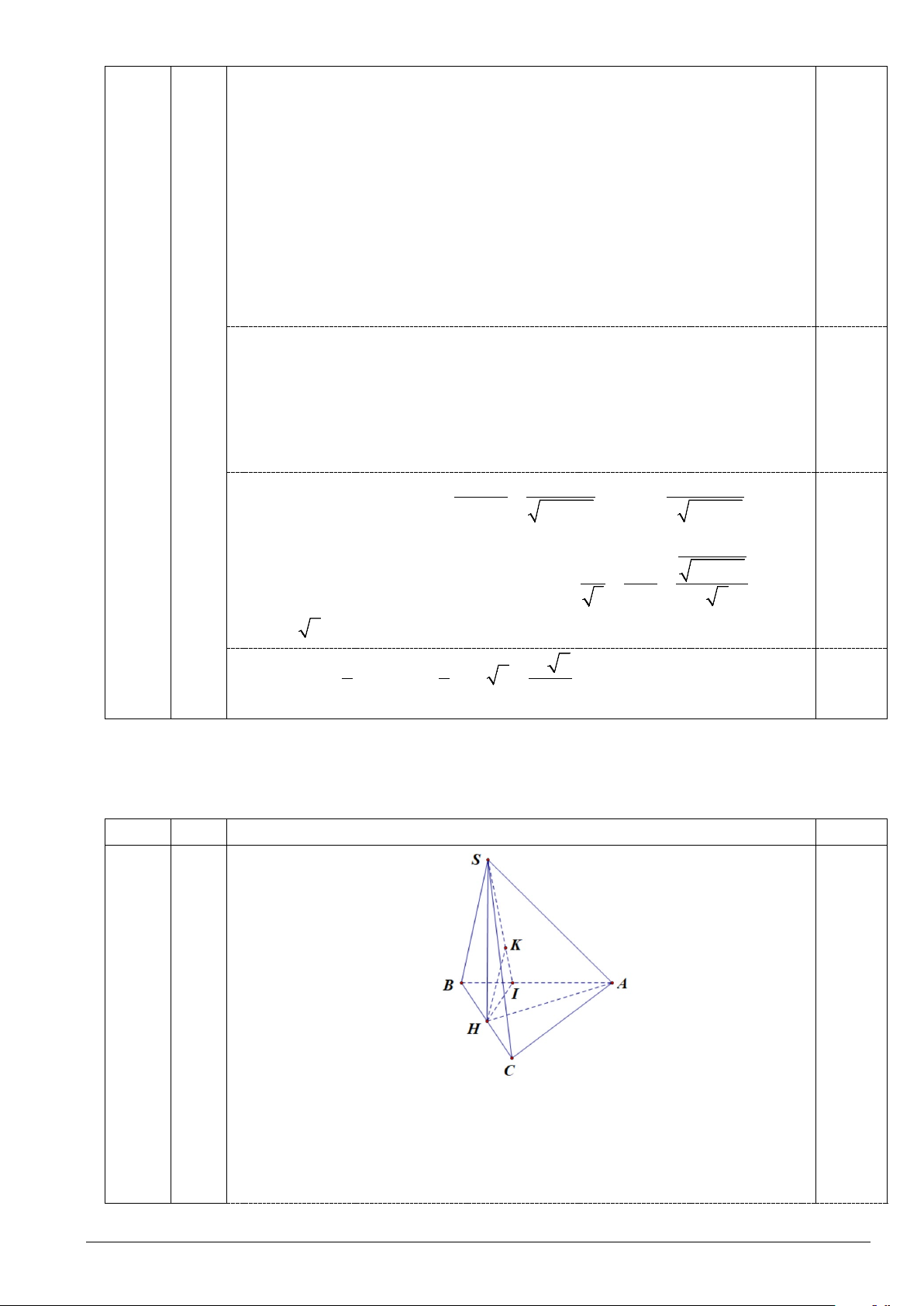
Câu 5 (3,0 điểm). Cho hình chóp S.ABC , mặt bên SBC là tam giác đều và nằm trong mặt phẳng vuông góc với mặt đáy,  ASB = 
ASC = 60 ,° SB =1. Tính khoảng cách từ C đến mặt phẳng (SAB) .
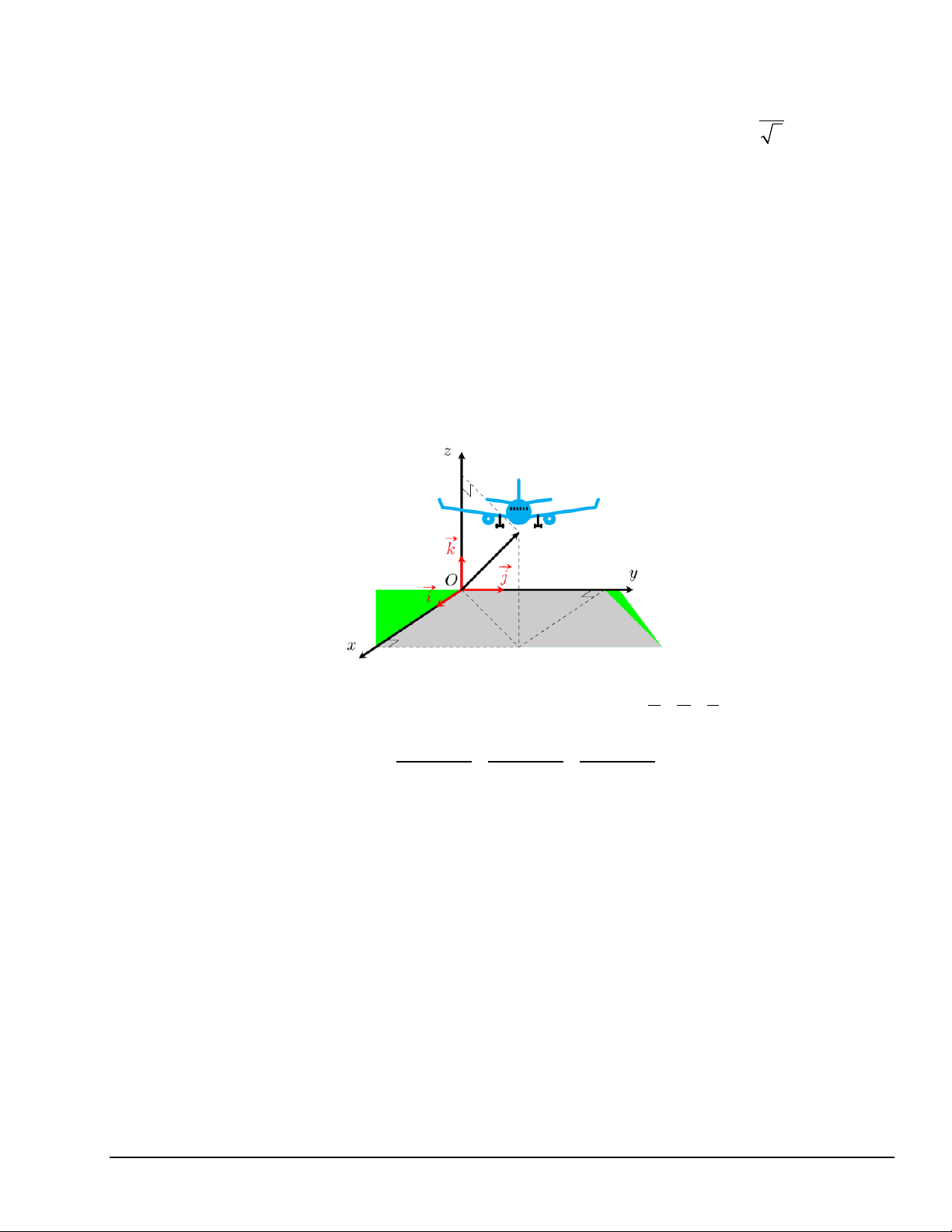
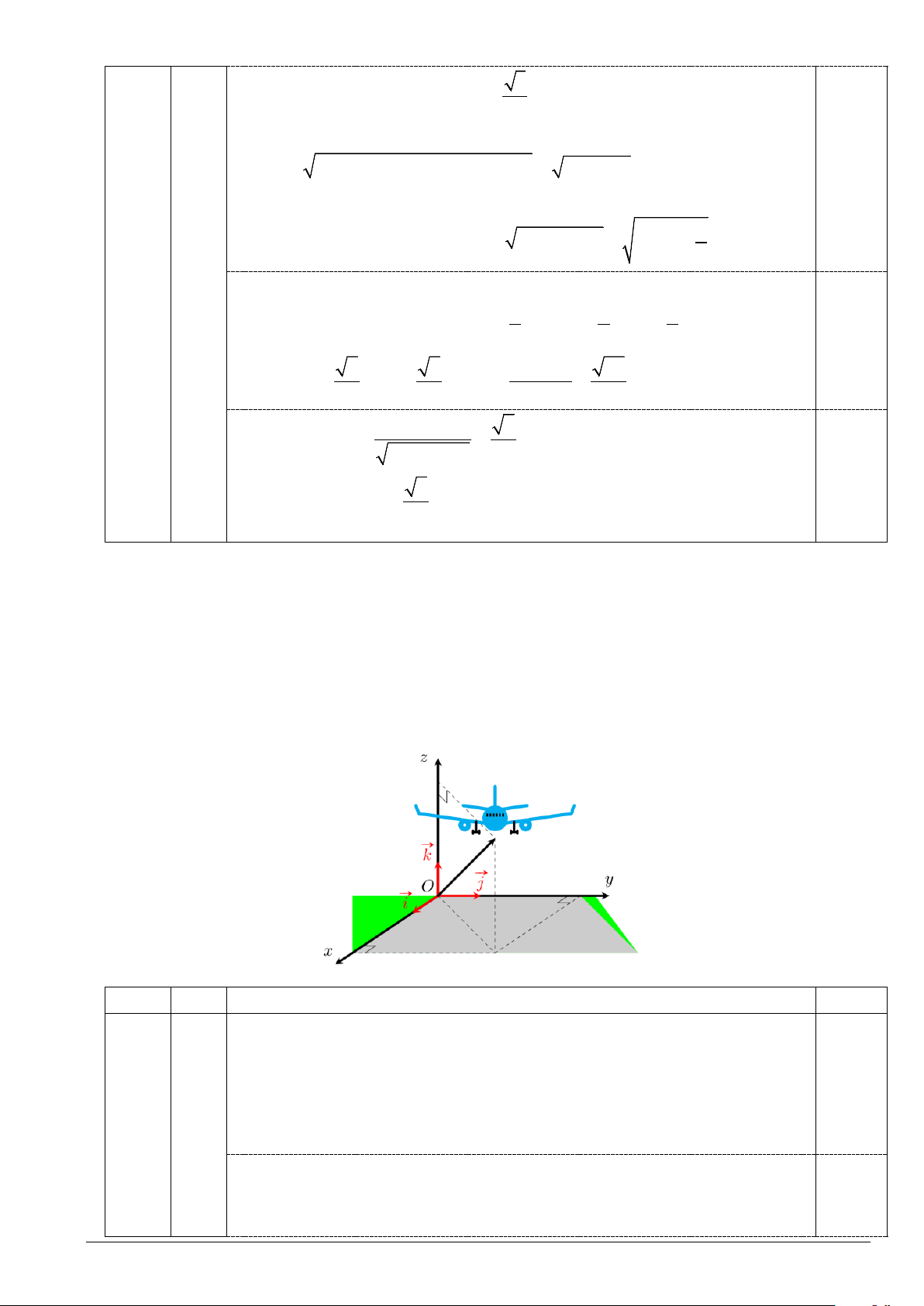
Câu 6 (1,5 điểm). Một chiếc máy bay đang bay trên không trung. Xét hệ trục tọa độ Oxyz được gắn như
hình vẽ, trong đó gốc O là vị trí của trạm kiểm soát không lưu và M ( ;
x y; z) (km) biểu thị vị trí máy bay
trên không trung. Tại thời điểm 9 giờ, máy bay đang ở vị trí (50;120;4) và chuyển động với vận tốc 
v = 300;400;3 (km/h) . Khi máy bay đạt độ cao 10 km so với mặt đất, máy bay đổi vận tốc mới 1 ( ) 
v = 400;300;− 5 (km/h) để hướng đến sân bay A . Tìm tọa độ máy bay khi vừa đáp xuống sân bay A 2 ( )
Câu 7 (1,5 điểm). Cho x, y, z là các số thực dương thoả mãn điều kiện 1 1 1 + + = 4 . Chứng minh rằng x y z 1 1 1 + + ≤ 1.
2x + y + z x + 2y + z x + y + 2zHẾT
Thí sinh không được sử dụng tài liệu, giám thị không giải thích gì thêm. Trang 2/2 TRƯỜNG THPT KON TUM
ĐỀ THI CHỌN HỌC SINH GIỎI CẤP TRƯỜNG
NĂM HỌC 2024 – 2025
Môn: Toán, LỚP 12
HƯỚNG DẪN CHÍNH THỨC
HƯỚNG DẪN CHẤM THI
(Hướng dẫn gồm 09 trang) I. HƯỚNG DẪN CHUNG
- Các cách giải khác đúng thì cho điểm tương ứng với biểu điểm đã cho.
- Điểm chấm của từng phần được chia nhỏ đến 0,25 điểm. Điểm của toàn bài là tổng điểm của các phần
và không làm tròn số.
II. ĐÁP ÁN VÀ THANG ĐIỂM Câu 1 (4,0 điểm). 1) Cho hàm số 1 3 m 2
y = x − x − ( 2 3m − )
1 x + m . Tìm tất cả các giá trị của tham số m để hàm số 3 2
đã cho đạt cực trị tại hai điểm x , x thỏa mãn x x + 2 x + x + 4 = 0. 1 2 ( 1 2) 1 2
2) Hai con tàu A và B đang ở cùng một vĩ tuyến và cách nhau 5 hải lí. Cả hai tàu đồng thời cùng
khởi hành. Tàu A chạy về hướng Nam với vận tốc 6 hải lí/giờ, còn tàu B chạy về vị trí hiện tại của tàu
A với vận tốc 7 hải lí/giờ. Hỏi sau bao nhiêu phút thì khoảng cách giữa hai tàu là ngắn nhất? (làm tròn
kết quả đến hàng đơn vị). CÂU Ý NỘI DUNG ĐIỂM Ta có: 2 2
y′ = x − mx − 3m +1. 0,25 Hàm số 1 3 m 2
y = x − x − ( 2 3m − )
1 x + m đạt cực trị tại hai điểm x , x khi 3 2 1 2 phương trình
y′ = 0 có hai nghiệm phân biệt x , x . 0,5 1 2 2 ⇔ m − ( 2 − m + ) 2 4 3
1 > 0 ⇔ 13m − 4 > 0 (*).
x + x = m
1) Theo định lí Vi-et ta có: 1 2  . 0,25 2 (2,0) x x = 3 − m +  1 1 2 Câu 1
Do đó x x + 2 x + x + 4 = 0 1 2 ( 1 2) m = 1 − 0,5 2 2 ⇔ 3
− m +1+ 2m + 4 = 0 ⇔ 3
− m + 2m + 5 = 0  ⇔ 5 . m =  3
Đối chiếu với điều kiện (*), giá trị của m cần tìm là 5 m = 1; − m = . 0,5 3
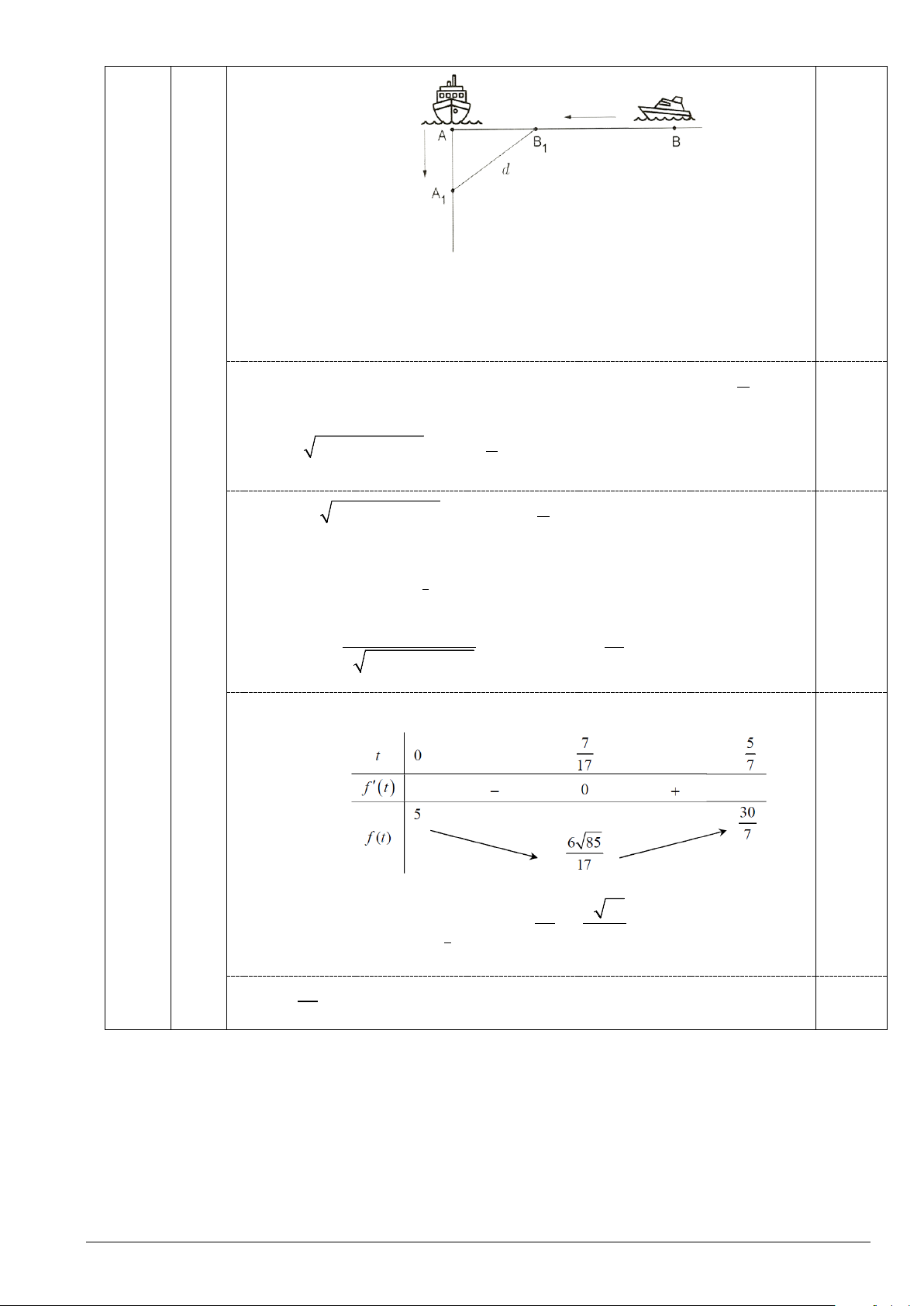
2) Gọi d là khoảng cách giữa hai tàu sau khi xuất phát t giờ, t > 0. Khi đó tàu
(2,0) A đang ở vị trí A và tàu B đang ở vị trí B như hình vẽ sau 0,5 1 1 Trang 1/9
Quãng đường tàu A đi được là AA = v .t = t . A 6 1
Quãng đường tàu B đi được là BB = v ⋅t = t . B 7 1 Ta có 2 2 2
d = AB + AA = (5 − BB )2 2 2 2 5
+ AA = (5 − 7t) + (6t) , 0 < t ≤ . 1 1 1 1 7 0,5 Vậy 2
d = 85t − 70t + 25 0 5 , < t ≤ . 7 Đặt 2
f (t) = 85t − 70t + 25 (với 5 0 < t ≤ . 7
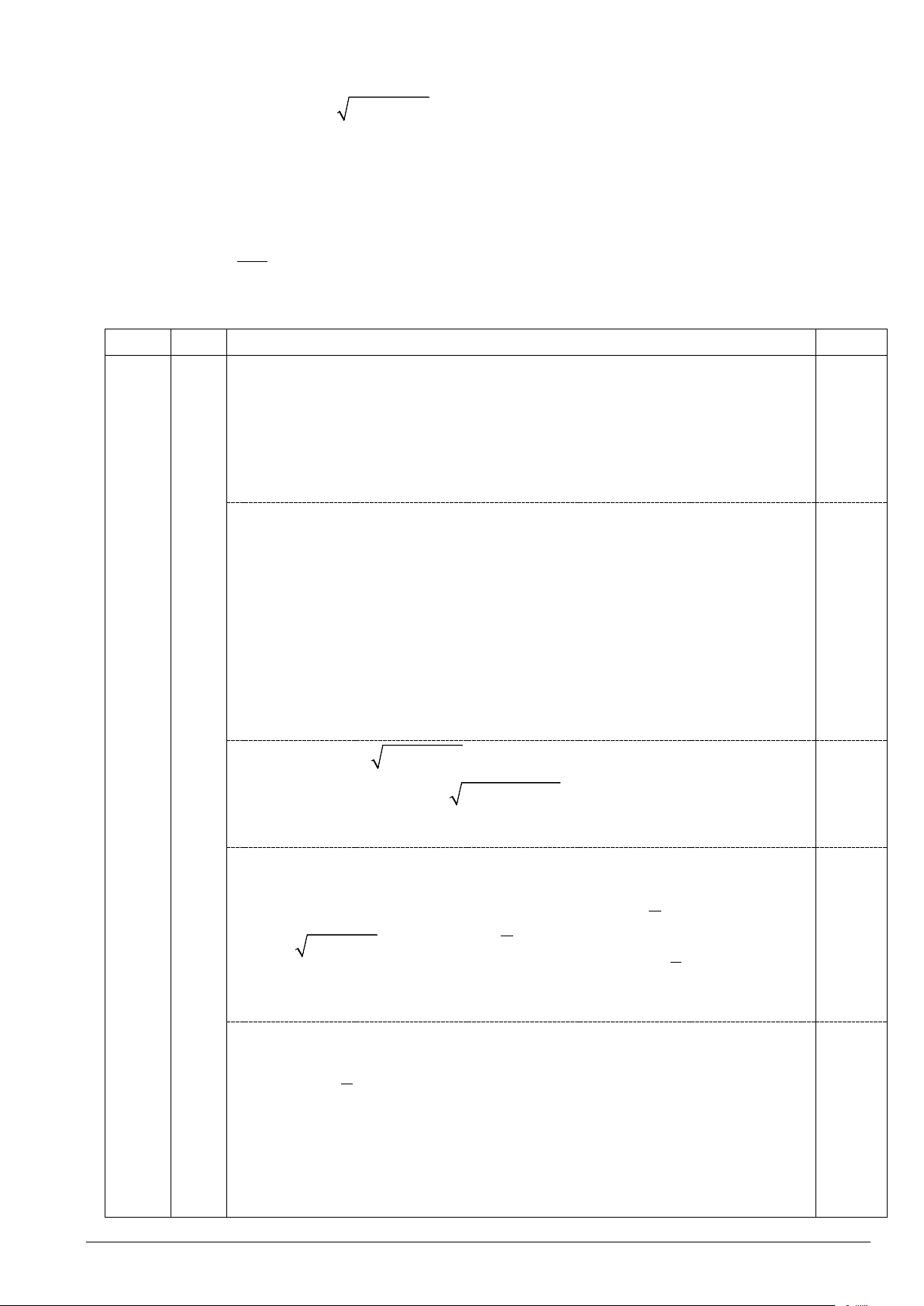
Bài toán trở thành tìm min f (t) .  5 0;   7 0,5   Ta có f ′(t) 170t − 70 = f ′(t) 7 , = 0 ⇔ t = . 2
2 85t − 70t + 25 17 Lập bảng biến thiên 0,25
Từ bảng biến thiên, ta có  7  6 85
min f (t) = f = ≈   3,524 (hải lí)  5 0;   17  17 7   Vậy 7 t = h ≈ 25 phút. 0,25 17 Trang 2/9 Câu 2 (3,0 điểm).
 4xy + x + 3 = x + 4y −1
1) Giải hệ phương trình  .
log x + log x − y +1 = log 4y + log 2x +  y 3 3 ( ) 3 ( ) 3 ( ) a =  20;a = 24
2) Cho dãy số (a xác định bởi 1 2 . n )  na
= n + a − n + a n∈  n+ 3 2 n+ 2 1 n * 2 ( ) 1 ( ) ( ) Tìm an 1 lim + . n→+∞ an CÂU Ý NỘI DUNG ĐIỂM x > 0 y > 0 
Điều kiện x − y > 0 (*) 0,25 2x + y > 0 
4xy + x + 3 ≥ 0
log x + log x − y +1 = log 4y + log 2x + y ( ) 1 3 3 ( ) 3 ( ) 3 ( )
⇔ log 3x x − y  = log 4y 2x + y  3  ( ) 3  ( )
⇔3x(x − y) = 4y(2x + y) ⇔ 2 2
3x −11xy − 4y = 0 0,5
⇔(3x + y)(x − 4y) = 0  y = 3 − x ⇔  x = 4y
Xét phương trình 4xy + x + 3 = x + 4y −1 (2) 1)
Câu 2 (1,5) Với y = 3
− x , (2) trở thành 2 12
− x + x + 3 = 11 − x −1 (3) . 0,25
Theo điều kiện trên, x > 0 nên phương trình (3) vô nghiệm.
Với x = 4y , (2) trở thành  1 x ≥  1  2 x ≥  0,25 2
x + x + 3 = 2x −1⇔  2 ⇔  1 ⇔ x = 2  x = − 2 3
x − 5x − 2 = 0  3  x = 2
Kết hợp với điều kiện (*) , suy ra hệ phương trình có duy nhất một nghiệm là (x y)  1 ; 2;  =  . 2    0,25 Trang 3/9
Từ hệ thức truy hồi ta suy ra
na = n + a − n + a n+ 3 2 n+ 2 1 2 ( ) 1 ( ) n
⇔ n(a − a = n + a − a n+ n+ 2 1 2 1 ) ( )( n 1+ n ) a − a a − a n+2 n 1 + n 1 ⇔ = 2. + n . n +1 n Đặt a − a 1 + b = n
n , ta được b = b ∀n∈ * n+ 2 n n 1 n 0,5
Suy ra (b là một cấp số nhân có công bội bằng 2. n ) Do đó n 1 − n 1 + n 1 + a a n+ 1 1 b = b a a n n n .2 = 2 ⇒ − = ⇒ − n = n+ n .2 . 1 1 n 1 2 + 2 2n 2) a a n+ 1 1 2 n 1 4 . n 2n 4  ⇒ − + − = − − . n 1 +  ( )  n ( ) (1,5) 2 2 2   
Đặt c = an − n c c n
, do đó (c là một cấp số n ) n n ( − ) 1 2 4 ⇒ = ∀ ∈ n+ n * 1 2 2
nhân có công bội bằng 1 2 0,5 n 1 −  1  24 ⇒ c = c a n ∀n∈*. n . = ⇒ = n n 2 − 4 2n +   24 1 ( )  2  2 24 + a n − n + n − n n+ (2 2) + 2 1 2 24 2 2 2 1 ( ) Ta có lim = lim = = . →+∞ →+∞ a n n 0,5 n (2 − 4) lim 2 2n n n + 24 n→+∞ 2 − 4 24 +
2n − 2 (2n − 2)2n Câu 3 (3,0 điểm).
1) Từ các chữ số 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, ta lập được bao nhiêu số tự nhiên có 6 chữ số, mà các
chữ số đôi một khác nhau và trong đó hai chữ số kề nhau không cùng là số lẻ?
2) Trong một đề thi trắc nghiệm môn Toán có loại câu hỏi trả lời Đúng/ Sai. Mỗi câu hỏi có 4 ý,
tại mỗi ý học sinh lựa chọn đúng hoặc sai. Cách thức tính điểm cho mỗi câu hỏi như sau:
• Học sinh chọn chính xác 01 ý được 0,1 điểm.
• Học sinh chọn chính xác 02 ý được 0,25 điểm.
• Học sinh chọn chính xác 03 ý được 0,5 điểm.
• Học sinh chọn chính xác 04 ý được 1,0 điểm.
Giả sử một thí sinh làm bài bằng cách chọn phương án ngẫu nhiên để trả lời cho 2 câu hỏi loại Đúng/ Sai
này. Tính xác suất để học sinh đó được 0,5 điểm ở phần trả lời 2 câu hỏi này. CÂU Ý NỘI DUNG ĐIỂM
Gọi số đó là A = a a a a a a . Từ giả thiết suy ra A có 1 hoặc 2 hoặc 3 chữ 1) 1 2 3 4 5 6 0,25
Câu 3 (1,5) số lẻ lấy từ {1;3;5;7; }9.
Trường hợp 1: A có 1 chữ số lẻ. 0,25 Trang 4/9
+) a lẻ: Số các số A là 1 C P = 600 1 5 5
+) a chẵn: Có 4 cách chọn a . Số các số
4.(C C )P = 2400 1 1 A là 1 4 5 4 5
Tổng có: 600 + 2400 = 3000 số các số A trong đó có đúng một chữ số lẻ.
Trường hợp 2: A có 2 chữ số lẻ.
+) a lẻ: Có 5 cách chọn a . Có 5 cách chọn a chẵn. 1 1 2
Vậy số các số A là 1 3
5.5.(C C )P = 9600 4 4 4 0,25
+) a chẵn: Có 4 cách chọn a . Có 6 cách chọn hai vị trí không kề nhau 1 1
của hai số lẻ trong a a a a a . Vậy số các số
4.(C .6.P ).A = 11520 2 3 4 5 6 A là 2 3 5 2 4
Tổng có: 9600 + 11520 = 21120 số các số A.
Trường hợp 3: A có 3 chữ số lẻ
+) a lẻ: Có 5 cách chọn a . Có 5 cách chọn a . Có 3 cách chọn hai vị trí 1 1 2
không kề nhau của hai số lẻ trong a a a a . Vậy số các số 3 4 5 6 A là 2 2
5.5.(C .3.P ).A = 10800 4 2 4 0,25
+) a chẵn: Có 4 cách chọn a . Có 1 cách chọn 3 vị trí không kề nhau của 1 1
3 số lẻ trong a a a a a . Vậy số các số
4.(C .1.P ).A = 2880 . 2 3 4 5 6 A là: 3 2 5 3 4
Tổng có: 10800 + 2880 = 13680 số các số A.
Vậy có: 3000 + 21120 + 13680 = 37800 số các số A. 0,5
Số phần tử không gian mẫu là n(Ω) 8 = 2 = 256. 0,25
Để đạt 0,5 điểm sẽ có các trường hợp sau xảy ra:
Trường hợp 1. Mỗi câu hỏi học sinh trả lời đúng 2 ý và sai 2 ý, khi đó số
điểm đạt được mỗi câu hỏi là 0,25 điểm. 0,5
2) Trường hợp 2. Một câu hỏi trong hai câu học sinh trả lời đúng 3 ý, sai 1 ý,
(1,5) câu hỏi còn lại trong hai câu đó học sinh trả lời sai cả 4 ý.
Gọi A là biến cố học sinh đó được 0,5 điểm. Khi đó n( A) 2 2 3 4
= C .C + 2C .C = 44. 0,5 4 4 4 4 n A
Vậy xác suất để học sinh đó được 0,5 điểm là P( A) ( ) 44 11 = . n( ) = = Ω 256 64 0,25 Câu 4 (4,0 điểm).
1) Cho tứ diện ABCD có AB vuông góc với CD , AB = CD = 6 . Gọi M là điểm thuộc cạnh BC
sao cho MC = xBC (0 < x < )
1 . Mặt phẳng (P) song song với AB và CD lần lượt cắt BC, DB, AD, AC
tại M , N, P,Q . Diện tích lớn nhất của tứ giác MNPQ bằng bao nhiêu?
2) Cho khối chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a , SA vuông góc với mặt phẳng
đáy và SA = a . Góc giữa hai mặt phẳng (SBC) và (SCD) bằng ϕ , với 1 cosϕ = . Tính thể tích của 3
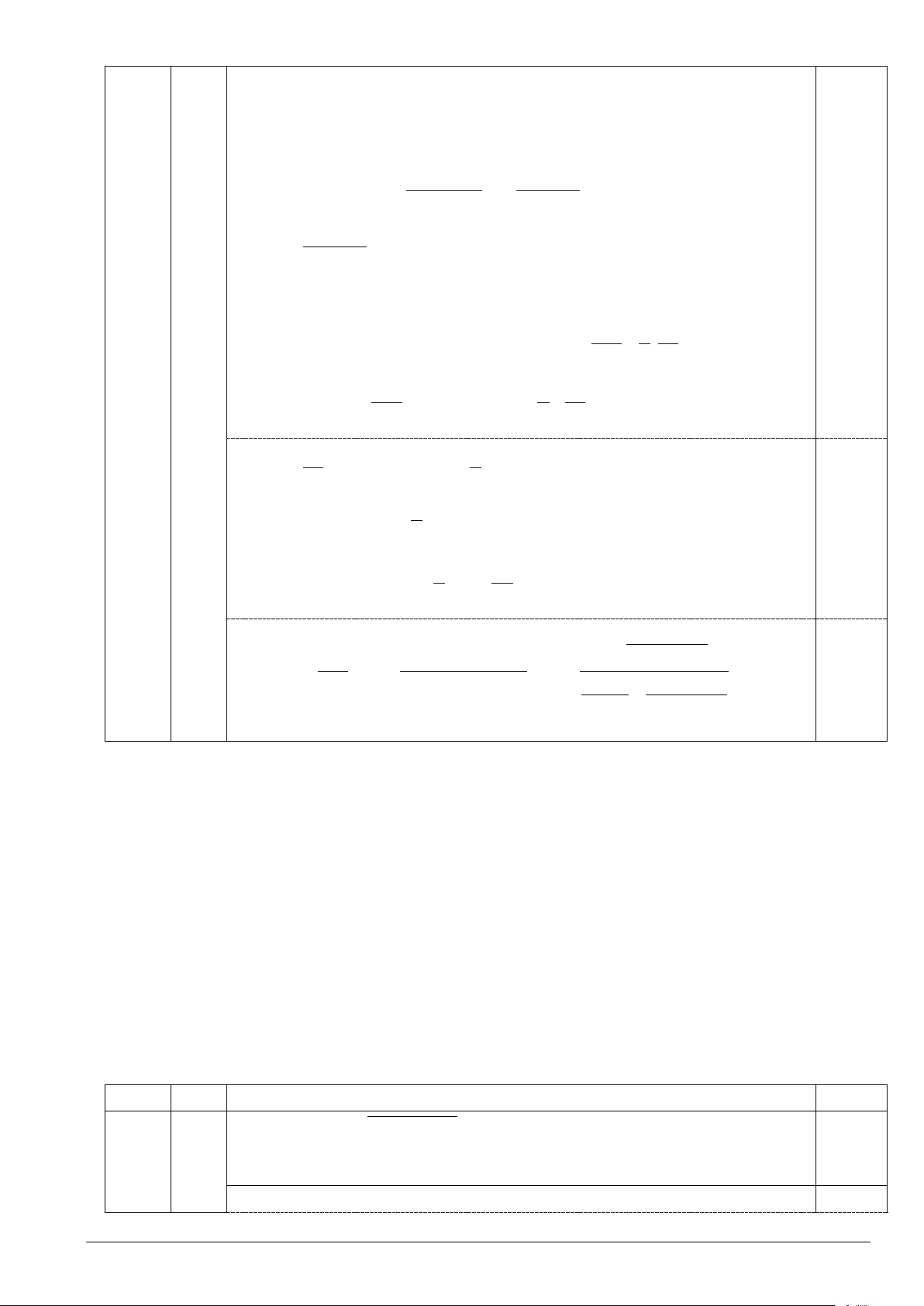
khối chóp S.ABCD . Trang 5/9 CÂU Ý NỘI DUNG ĐIỂM A 6 P Q B D N 0,5 6 M C
MQ//NP//AB
Xét tứ giác MNPQ có 
⇒ MNPQ là hình bình hành.
MN //PQ//CD
Mặt khác, AB ⊥ CD ⇒ MQ ⊥ MN . Do đó, MNPQ là hình chữ nhật. 1) MQ CM
(2,0) Vì MQ//AB nên = = x ⇒ MQ = . x AB = 6x . AB CB
Theo giả thiết MC = .xBC ⇒ BM = (1− x) BC . 0,5
Vì MN //CD nên MN = BM =1− x ⇒ MN = (1− x).CD = 6(1− x) . CD BC Câu 4
Diện tích hình chữ nhật MNPQ là 2 0,5 S MN MQ ( x) x x ( x)  x +1 . 6 1 .6 36. . 1 36 − x  = = − = − ≤ =   9 MNPQ .  2  Ta có S = 9 MNPQ khi 1
x =1− x ⇔ x = . 2 0,5
Vậy diện tích tứ giác MNPQ lớn nhất bằng 9 khi M là trung điểm của BC . 2) 0,5 (2,0)
+ Gọi H là trung điểm SB , vì ∆SAB vuông cân tại A nên AH ⊥ SB ( ) 1 . Trang 6/9 BC ⊥ AB + Lại có 
⇒ BC ⊥ (SAB) ⇒ BC ⊥ SB (2). BC ⊥ SA Từ ( )
1 , (2) ⇒ AH ⊥ (SBC) (3) .
+ Gọi K là hình chiếu của A lên SD , chứng minh tương tự ta có
AK ⊥ (SCD) (4) .
+ Vì (SBC)∩(SCD) = SC nên từ (3), (4) suy ra (SBC),(SCD)  ( )=  (AH,AK)=ϕ.
+ Gọi M , N lần lượt là trung điểm SC, AD , dễ dàng chứng minh được
AHMN là hình bình hành, suy ra MN //AH
+ Kẻ NP // AK (P∈ SD) , vì NP // AK ⇒ NP ⊥ (SCD) ⇒ NP ⊥ MP . 0,5 + Ta có  (AH AK)=  (MN NP)=  , ,
MNP = ϕ (vì ∆MNP vuông tại P ).
+ Đặt AD = x , dễ thấy . = SA AD = ax AK ⇒ = ax NP . 2 2 SD a + x 2 2 2 a + x ax 0,5
+ Xét ∆MNP vuông tại P , ta có  2 2 1 cos NP a + = = = x MNP 3 MN a 2 ⇒ x = a 2 . 3 Vậy 1 1 2 a 2 V = SA S a a . ABCD . = ABCD . . 2 = S. 3 3 3 0,5
Câu 5 (3,0 điểm). Cho hình chóp S.ABC , mặt bên SBC là tam giác đều và nằm trong mặt phẳng vuông góc với mặt đáy,  ASB = 
ASC = 60 ,° SB =1. Tính khoảng cách từ C đến mặt phẳng (SAB) . CÂU Ý NỘI DUNG ĐIỂM Câu 5 0,5
Gọi H là trung điểm của BC suy ra SH ⊥ ( ABC) .
Ta có d (C,(SAB)) = 2d (H,(SAB)).
Kẻ HI ⊥ AB; HK ⊥ SI suy ra d (H,(SAB)) = HK . Trang 7/9
Vì ∆SBC đều, SB =1 suy ra 3 SH = . 2 Đặt SA = x . 2 2
⇒ AB = SA + SB −  2 2. . SA .
SB cos ASB = x − x +1 (do  ASB = 60° ). 1,0
Ta lại có ∆ASB = ∆ASC . 2 2 2 3
⇒ AB = AC ⇒ AH ⊥ BC ⇒ AH = AB − BH = x − x + 4
Mà tam giác SHA vuông tại H nên 2 2 2 2 3 2 3 3
SA = SH + HA ⇔ x = + x − x + ⇔ x = . 4 4 2 1,0 Suy ra 7 6 BH.AH 42 AB = ; AH = ⇒ HI = = . 2 2 AB 14 Từ đó ta có SH.HI 6 HK = = . 2 2 SH + HI 6 0,5
Suy ra d (C (SAB)) 6 , = . 3
Câu 6 (1,5 điểm). Một chiếc máy bay đang bay trên không trung. Xét hệ trục tọa độ Oxyz được gắn như
hình vẽ, trong đó gốc O là vị trí của trạm kiểm soát không lưu và M ( ;
x y; z) (km) biểu thị vị trí máy bay
trên không trung. Tại thời điểm 9 giờ, máy bay đang ở vị trí (50;120;4) và chuyển động với vận tốc 
v = 300;400;3 (km/h) . Khi máy bay đạt độ cao 10 km so với mặt đất, máy bay đổi vận tốc mới 1 ( ) 
v = 400;300;− 5 (km/h) để hướng đến sân bay A . Tìm tọa độ máy bay khi vừa đáp xuống sân bay A 2 ( ) . CÂU Ý NỘI DUNG ĐIỂM
Tại thời điểm 11 giờ, máy bay ở điểm có tọa độ:
(50+300.2;120+ 400.2;4+3.2) hay (650;920;10) 0,5
Suy ra, khi đạt độ cao 10 km so với mặt đất, máy bay ở điểm có tọa độ: Câu 6 (650;920;10) . 
Máy bay đổi vận tốc mới v = 400;300; 5
− thì sau một khoảng thời gian t 2 ( ) 0,5
(h) máy bay ở điểm có tọa độ (650 + 400t;920 + 300t;10 −5t). Trang 8/9
Khi máy bay đáp xuống sân bay A thì độ cao của máy bay so với mặt đất 0,25
bằng 0 nên 10 − 5t = 0 ⇔ t = 2 .
Tọa độ máy bay khi vừa đáp xuống sân bay A là (1450;1520;0) . 0,25
Câu 7 (1,5 điểm). Cho x, y, z là các số thực dương thoả mãn điều kiện 1 1 1 + + = 4 . Chứng minh rằng x y z 1 1 1 + + ≤ 1.
2x + y + z x + 2y + z x + y + 2z CÂU Ý NỘI DUNG ĐIỂM Chứng minh BĐT: 1 1 4 + ≥
∀a, b > 0 (*). a b a + b
Thật vậy ∀a, b > 0 ta có: 1 1 4 (a b) 1 1  + ≥ ⇔ + + ≥   4 a b a + ba b
Theo BĐT CÔSI cho các số dương a, b; 1 1 , ta có a b 0,25
a + b ≥ 2 ab > 0  (a b)1 1 ⇒ + + ≥   4 1 1 1 . + ≥ 2 > 0  a b a b ab
Dấu bằng khi a = b . Áp dụng (*) 1 1  1 1  ⇔ ≤ + , ta có a b 4   +  a b  1 1 1  1 1  = ≤ +   Câu 6
2x + y + z (x + y) + (x + z) 4  x + y x + z 0,5
1  1  1 1  1  1 1  ≤  + + + 4  4    x y  4    x z  1 1  2 1 1  ⇒ ≤ + + (1) 2x y z 16   + +  x y z   
Chứng minh tương tự ta có 1 1 1 2 1 ≤ + + (2) x 2y z 16   + +  x y z 0,25 1 1  1 1 2  ≤ + + (3) x y 2z 16   + +  x y z
Cộng vế với vế của (1), (2), (3) ta được 1 1 1 1   1 1 1  + + ≤  4 + +   = 1.
2x + y + z x + 2y + z x + y + 2z 16   x y z  0,5 Dấu bằng xảy ra khi 3
x = y = z = . 4  HẾT  Trang 9/9
Xem thêm: ĐỀ THI HSG TOÁN 12
https://toanmath.com/de-thi-hsg-toan-12
Document Outline

  • Đề chính thức 12 24-25
  • HDC ĐỀ HSG 12 CẤP TRƯỜNG 2024-2025
  • HSG 12

Tài liệu liên quan: