Đề chọn HSG thành phố Toán 12 năm 2019 – 2020 sở GD&ĐT Hải Phòng

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI THÀNH PHỐ LỚP 12 HẢI PHÒNG Năm học 2019 – 2020 ĐỀ CHÍNH THỨC
ĐỀ THI MÔN:TOÁN – BẢNG KHÔNG CHUYÊN
(Đề thi gồm 01 trang)
Thời gian: 180 phút (không kể thời gian giao đề) Ngày thi: 19/9/2019 Bài 1 (2,0 điểm) 1 a) Cho hàm số 3 2 y 
x  x  m  2 2
x  m  2019. Tìm điều kiện của tham số m để hàm số đã 3
cho đồng biến trên khoảng 0; . 2mx  3  2m b) Cho hàm số y 
có đồ thị là C  . Tìm tất cả các giá trị thực của tham số m để x  2
đường thẳng d : y  x  2 cắt C  tại hai điểm phân biệt ,
A B sao cho góc giữa hai đường
thẳng OA và OB bằng 0 45 . Bài 2 (2,0 điểm)
1 2sin xcos x
a) Giải phương trình lượng giác sau  3.
1 2sin x1 sin x 2 2
x  3y  2 x y  2y  2  0 
b) Giải hệ phương trình sau trên tập số thực  2 3
 x  4x  y 1  2x 1  1 
Bài 3 (2,0 điểm) Cho hình lăng trụ đứng ABC.A' B 'C ' có AB  a; AC  2a; AA'  2a 5 và góc  BAC bằng 0
120 . Gọi M là trung điểm của cạnh CC ' .
a) Chứng minh rằng MB vuông góc với A' M.
b) Tính khoảng cách từ điểm A đến mặt phẳng  A' BM  theo . a
Bài 4 (1,0 điểm) Từ tập hợp tất cả các số tự nhiên có 5 chữ số mà các chữ số đều khác 0 , lấy ngẫu
nhiên một số. Tính xác suất để trong số tự nhiên được lấy ra có mặt đúng ba chữ số khác nhau.
Bài 5 (1,0 điểm) Trong mặt phẳng với hệ tọa độ Oxy cho tứ giác ABCD nội tiếp đường tròn đường
kính BD . Gọi H , K lần lượt là hình chiếu vuông góc của A trên các đường thẳng BD và C . D Biết
A4;6; đường thẳng HK có phương trình 3x  4 y  4  0; điểm C thuộc đường thẳng
d : x  y  2  0 và điểm B thuộc đường thẳng d : x  2 y  2  0; điểm K có hoành độ nhỏ hơn 1. 1 2
Tìm tọa độ các điểm B và C. u   2 1 1 
Bài 6 (1,0 điểm) Cho dãy số u xác định bởi  . n  1 un u   , n   , n  1 n 1   2
Hai dãy số v , w xác định như sau: v  4n  u w  u u u u n    n  Tìm các giới n 1 n  ; . . ... , , 1. n  n  n 1 2 3 n
hạn lim v ; lim w . n n
Bài 7 (1,0 điểm) Cho các số thực dương a, b, .
c Tìm giá trị nhỏ nhất của biểu thức 3 3 3 2
4a  3b  2c  3b c P 
a  b  c3
……………HẾT……………
(Cán bộ coi thi không giải thích gì thêm)
Họ và tên thí sinh:…………………………………….. Số báo danh:………………………….…………….
Cán bộ coi thi 1:……………………………............... Cán bộ coi thi 2:…………………………………… Trang 1/1
SỞ GIÁO DỤC VÀ ĐÀO TẠO ĐÁP ÁN KỲ THI CHỌN HỌC SINH GIỎI THÀNH PHỐ LỚP 12 HẢI PHÒNG Năm học 2019 – 2020 ĐỀ CHÍNH THỨC
ĐỀ THI MÔN:TOÁN – BẢNG KHÔNG CHUYÊN
(Đáp án gồm 06 trang)
Thời gian: 180 phút (không kể thời gian giao đề) Ngày thi: 19/9/2019 BÀI Ý ĐÁP ÁN ĐIỂM 1 3 2 2 Bài 1 Cho hàm số y 
x  x  m  2 x  m  2019. Tìm điều kiện của a 3 (1,0đ) (2,0 điểm)
tham số m để hàm số đã cho đồng biến trên khoảng 0; . TXĐ: D  .  ; 2
y '  x  2x  m  2 0,25
Hàm số đồng biến trên khoảng 0;   y '  0, x  0;  2
 x  x  m   x    2 2 2 0, 0;
 m  x  2x  2, x  0;  0,25
Xét hàm số g  x 2
 x  2x  2; g ' x  2
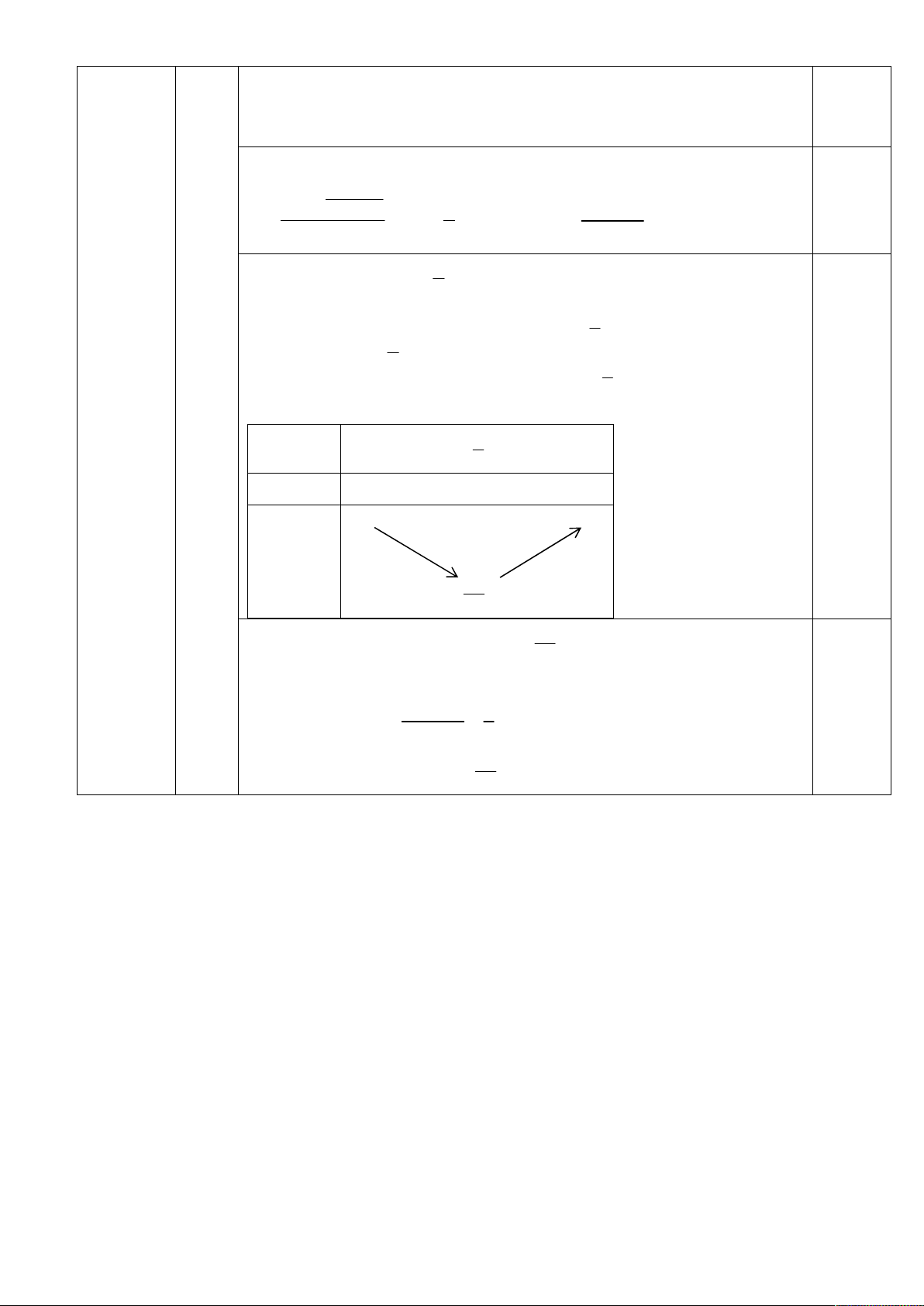
 x  2; g ' x  0  x  1 x 0 1 
g ' x + 0 - 0,25 3 g  x Từ bảng biến thiên
 m  g  x, x
 0;   m  Max g  x  m  3   0,25 x   0; 2mx  3  2m Cho hàm số y 
có đồ thị là C  . Tìm tất cả các giá trị x  2 b
thực của tham số m để đường thẳng d : y  x  2 cắt C  tại hai điểm (1,0đ) phân biệt ,
A B sao cho góc giữa hai đường thẳng OA và OB bằng 0 45 .
Phương trình hoành độ giao điểm:
2mx  3  2m  x  2, x  2 x  2 2
 x  2mx  2m 1  0 ,  x  2   0,25  x  1   x  2m 1  m  1 2m 1  1 
d cắt C  tại hai điểm phân biệt     1 0,25 2m 1  2  m      2   Gọi A1;  
1 ; B 2m 1; 2m  3  OA1;  
1 ;OB 2m 1; 2m  3   0 . OA OB  . OA . OB cos 45 2 2
 2  8m 16m 10  8m 16m  6  0  3 0,25 m   2   1 m   2 3 1
Kết hợp điều kiện, ta được m  hoặc m  . 0,25 2 2 Bài 2
1 2sin xcos x a
Giải phương trình lượng giác sau  3. (1,0đ) (2,0 điểm)
1 2sin x1 sin x   x    k 2  6   7 ĐK: x   m2 , k, , m n  .  0,25 6    x   n2   2 Pt  x  x   2 cos sin 2
3 1 sin x  2 sin x 0,25
 cos x  3 sin x  sin 2x  3 cos 2x   2 x    k        18 3  sin
 x  sin 2x    , k       0,25  6   3  
x   k2  2  2
Kết hợp điều kiện  Pt có nghiệm x    k , k   . 0,25 18 3
Giải hệ phương trình sau trên tập số thực 2 2  b
x  3y  2 x y  2 y  2  0 (1)  (1,0đ)  2 3
 x  4x  y 1  2x 1  1 (2)  ĐK: 2
y  0; x  4x  y 1  0 Từ phương trình   1 ta có 3y y 2
x  2  3y  2 y  2 x  2   2  1 0,5 2 2 x  2 x  2 y Suy ra 2
 1  y  x  2 2 x  2
Thay vào phương trình 2 ta có 3
4x  1  2x  1  1 u    4x  1 Đặt  u  0 3 v  2x  1  0,25
Hệ phương trình đã cho trở thành u   v  1 u   1    2 3 u  2v  1 v  0    1 x    4x  1  1   2 Ta có:    (Thỏa mãn điều kiện) 3 9  2x  1  0   y  0,25   4  1 9  Vậy hệ có nghiệm ;    2 4 
Cho hình lăng trụ đứng ABC.A' B 'C ' có AB  a; AC  2a; AA '  2a 5 Bài 3 a  (1,0đ) (2,0 điểm) và góc BAC bằng 0
120 . Gọi M là trung điểm của cạnh CC ' .
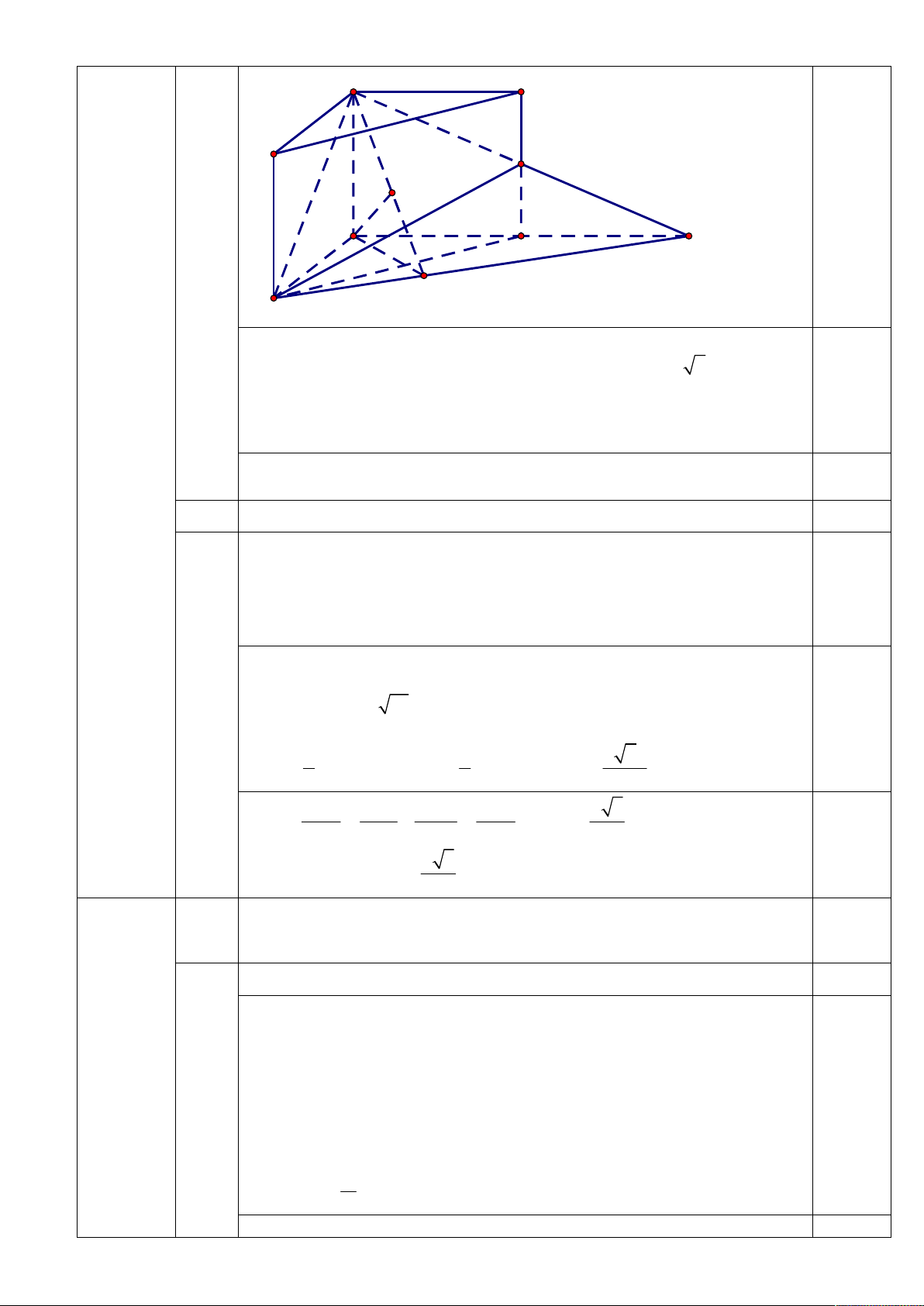
a) Chứng minh rằng MB vuông góc với A' M . A' C' B' M H A N C K B
Áp dụng định lí cosin trong tam giác ABC 2 2 2  2
 BC  AB  AC  2 A .
B AC.cos BAC  7a  BC  a 7 Trong tam giác 2 2 2 2
A 'C ' M : A ' M  A 'C '  C ' M  9a 0,5 Trong tam giác 2 2 2 2
BAA ' : A ' B  AB  A ' A  21a Trong tam giác 2 2 2 2
BCM : BM  BC  CM  12a Ta có: 2 2 2
A ' M  MB  A ' B  tam giác A ' BM vuông tại M 0,5
hay MB  A' M . b
Tính khoảng cách từ điểm A đến mặt phẳng  A' BM . (1,0đ)
Gọi A' M  AC  N  d  ,
A  A' BM   d  ,
A  A' BN 
Kẻ AK  BN , K  BN 0,5
Kẻ AH  A ' K , H  A ' K  d  ,
A  A' BN   AH
Chứng minh được CM là đường trung bình của tam giác A' AN
 A' M  MN và có BM  A' N  tam giác A' BN cân tại B
 BN  A' B  a 21 0,25
Diện tích tam giác ABN là: 1  1 2 7a S  .
AB AN.sin BAN 
AK.BN  AK  ABN 2 2 7 1 1 1 36 a 5 Ta có:     AH  2 2 2 2 AH AK A ' A 20a 3 0,25 a
Vậy: d  A  A BM  5 , '  3
Từ tập hợp tất cả các số tự nhiên có 5 chữ số mà các chữ số đều khác
0 , lẫy ngẫu nhiên một số. Tính xác suất để trong số tự nhiên được lấy (1,0đ)
ra có mặt đúng ba chữ số khác nhau.
Ta có: Số phần tử của không gian mẫu  là: n  5  9 0,25
Gọi A là biến cố: “Trong số tự nhiên được lấy ra chỉ có mặt ba chữ số khác nhau” Bài 4
Số cách chọn 3 chữ số phân biệt a, b, c từ 9 chữ số 1; 2;3; 4;5;6;7;8;  9 là (1,0 điểm) 3 C . 9
Xét các số thỏa mãn yêu cầu bài toán được tạo thành từ 3 chữ số a; ; b c ở 0,25
trên. Có hai trường hợp sau xảy ra
TH1: Một chữ số có mặt 3 lần; các chữ số còn lại có mặt đúng 1 lần: 5! Có tất cả: 3.  60 số. 3!
TH2: Hai chữ số có mặt hai lần, chữ số còn lại có mặt 1 lần: 0,25 5! Có tất cả: 3.  90 số. 2!.2!
Số kết quả thuận lợi của biến cố A là: n  A  60  90 3 .C  12600 9 n  A 1400 0,25
Xác suất của biến cố A là: p  A    0, 2134 n  6561
Trong mặt phẳng với hệ tọa độ Oxy cho tứ giác ABCD nội tiếp
đường tròn đường kính BD . Gọi H , K lần lượt là hình chiếu vuông
góc của A trên các đường thẳng BD và C .
D Biết A4;6; đường Bài 5
thẳng HK có phương trình 3x  4 y  4  0; điểm C thuộc đường (1,0đ) (1,0 điểm) thẳng
d : x  y  2  0 và điểm B thuộc đường thẳng 1
d : x  2 y  2  0; điểm K có hoành độ nhỏ hơn 1. Tìm tọa độ các 2
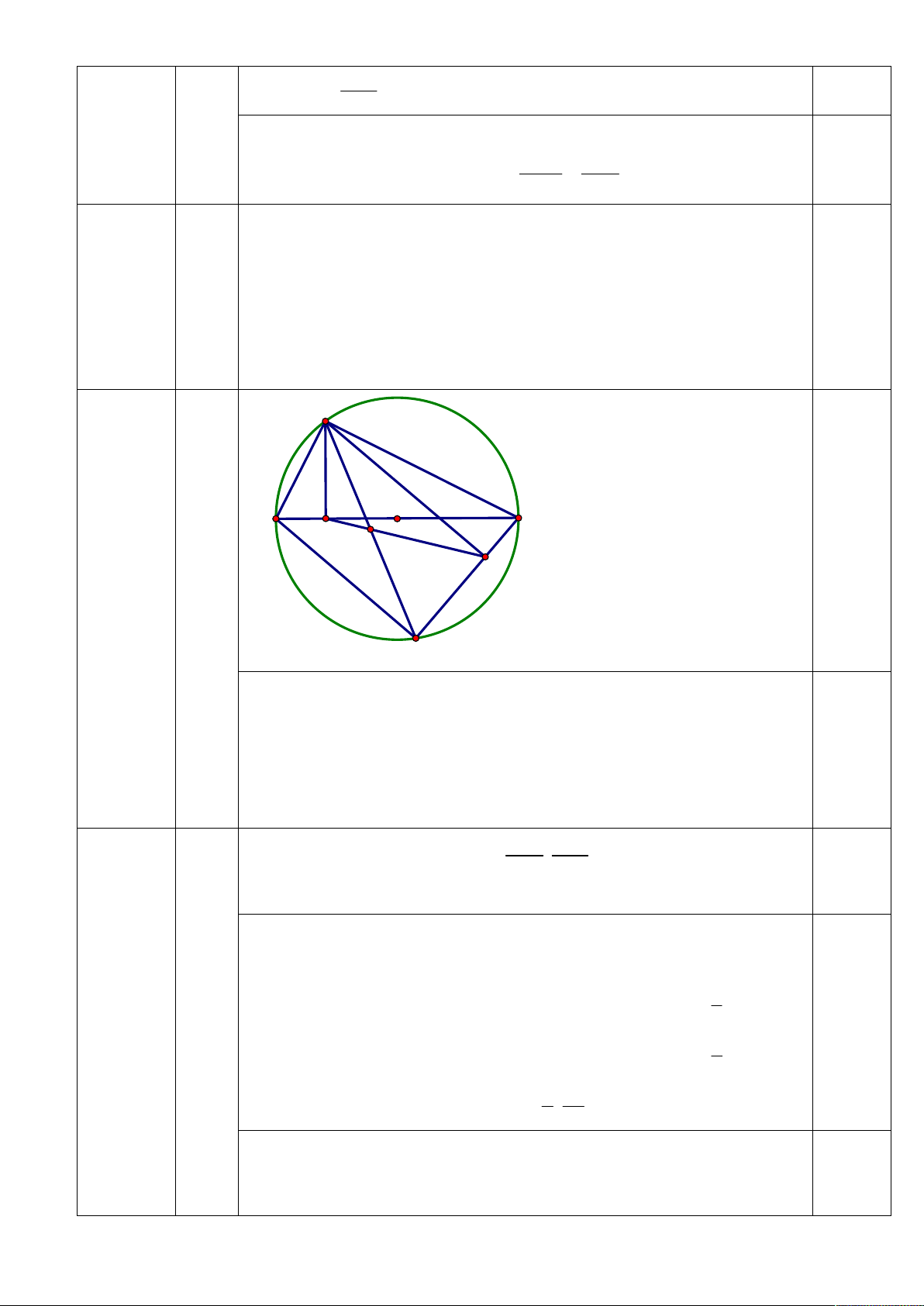
điểm B và C. A B D H E K C
Gọi E  AC  HK
Tứ giác AHKD nội tiếp  
 HAD  HKC.
Tứ giác ABCD nội tiếp  
 ABD  ACD . 0,25 Tam giác  
ABD vuông tại A  ABD  HAD Vậy  
HKC  ACD hay tam giác ECK cân tại E .
Vì tam giác ACK vuông tại K nên E là trung điểm của AC .
 c  4 8  c 
Ta có C  d  C ;
c 2  c  E ; 1      2 2  0,25
Vì E  HK nên tìm được c  4  C 4; 2  .
K  HK : 3x  4 y  4  0 nên gọi K 4t;3t   1  
 AK 4t  4;3t  7 ; CK (4t  4;3t  1) .  1   t   5
Ta có: AK  CK  AK.CK  0 2
 25t  50t  9  0   . 0,25 9 t   5 4 2 
Vì hoành độ điểm K nhỏ hơn 1  K ( ; ) 5 5
BC có phương trình: 2x  y  10  0.
B  BC  d  B(6; 2) . 2 0,25
Kết luận: B 6; 2;C 4; 2   u   2 1 1 
Cho dãy số u xác định bởi  . n  1 un u   , n   , n  1 n 1  Bài 6  2 (1,0đ) (1,0 điểm)
Hai dãy số v , w xác định như sau: n  n  v  4n  u w  u u u u n    n  Tìm các giới hạn n 1 n  ; . . ... , , 1. n 1 2 3 n lim v ; lim w . n n    Chọn   0;   sao cho cos  2 1  2  1  cos 
Khi đó ta có u  cos u   cos 1 2 2 2     ( Do   0;   nên cos  0 ).  2  2 0,25  1  cos  Tương tự ta sẽ có 2 u   cos 3 2 4  1  cos n 1  
Bằng quy nạp ta chứng minh được 2 u   cos n n 1  2 2     Suy ra n n n 2
v  4 (1  u )  4 1  os c  4 .2sin n n  n 1   2   2n 2    sin 0,25  n     Vậy n 2 2 2 2 lim v  lim 4 .2sin  lim     .2  2 n  2n      2n    
Ta có w  u u ...u  cos .cos    cos  o c s n 1 2 n n 1  n2 2 2 2     2n sin . os c . os c ... os c .c os 0,25 n 1  n 1  n 2 sin 2 2 2 2 2      2n sin 2n sin n 1  n 1 2 2          sin 2 sin 2 1 sin 2 Suy ra lim w lim lim      n 0,25     n 2  2 2 sin sin n 1   n 1 2 2        n 1  2  
Cho các số thực dương a, b, .
c Tìm giá trị nhỏ nhất của biểu thức: Bài 7 3 3 3 2
4a  3b  2c  3b c (1,0 điểm) P  (1,0đ)
a  b  c3
Áp dụng BĐT Cauchy, ta có: 2 3 3
3b c  2b  c , dấu “=” xảy ra  b  . c 0,25 b  c 3 3  3
Ta chứng minh: b  c  (1) , b   0, c  0. 4 Thật vậy:
   b  c   b  b c  bc  c  b  cb  c2 3 3 3 2 2 3 1 4 3 3
 0, b  0, c  0
Dấu “=” xảy ra  b  . c
Áp dụng các BĐT trên ta được: b  c3 3 4a  1 0,25 4 a P   4t  1 t , với t  , t  0  ;1 3  3 3
a  b  c 4
a  b  c 1
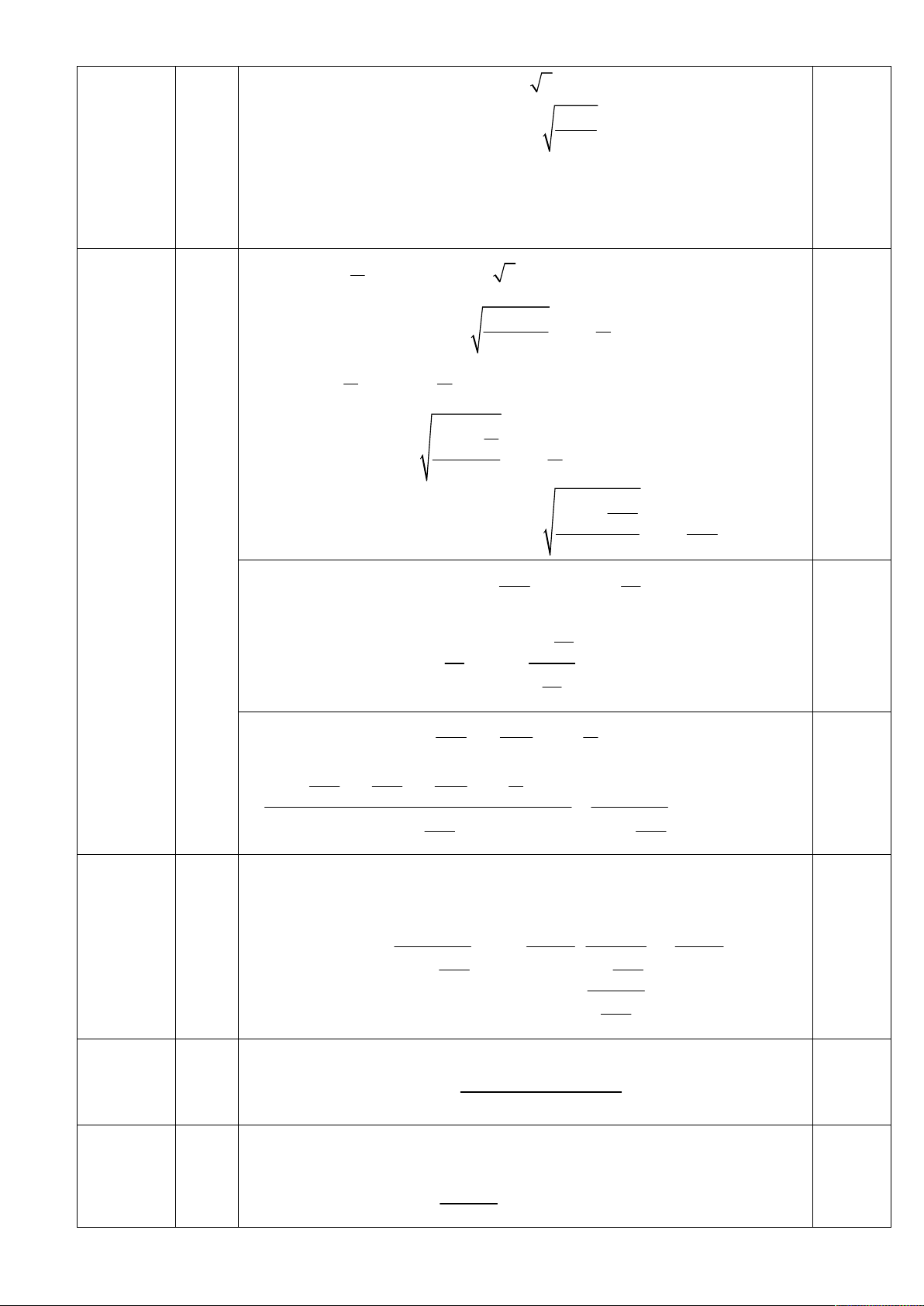
Xét hàm số f t   4t  1 t 3 3 với t  0  ;1 4  1 t  3  2 5 Có: f 't  2  12t 
1 t ; f 't  0   4 1 t    3 Bảng biến thiên: 1 0,25 t 0 1 5 f 't  - 0 + f t  4 25 4
Từ bảng biến thiên suy ra: P  f t   . 25 b   c  Dấu “=” xảy ra   a
1  2a  b  . c 0,25  
 a  b  c 5 4
Vậy giá trị nhỏ nhất của P là
khi 2a  b  . c 25
Lưu ý: Học sinh làm theo cách khác mà đúng thì vẫn cho điểm tối đa.
Document Outline

• ĐỀ TOÁN CHÍNH THỨC 2019-2020
• ĐÁP ÁN ĐỀ TOÁN CHÍNH THỨC 2019-2020