Đề chọn lớp chất lượng cao Toán 10 năm 2020 – 2021 trường Yên Phong 2 – Bắc Ninh

SỞ GD&ĐT BẮC NINH
THI CHỌN LỚP CHẤT LƯỢNG CAO
TRƯỜNG THPT YÊN PHONG SỐ 2
Năm học : 2020 – 2021 Môn: Toán Lớp: 10 ĐỀ CHÍNH THỨC
Thời gian làm bài: 90 phút ( Không kể thời gian phát đề)
Đề gồm có : 02 trang
Phần I. Trắc nghiệm (3điểm)
Câu 1. Tìm tập xác định D của hàm số 2
y  3x  4x 1 . A. 1     1  1
D   ; 1 . B. 1   C.       D.    D   ; 1. D ;  1 ;   D    ;     1 ;    .      . 3      3   3    3
Câu 2. Tìm tọa độ giao điểm của đồ thị hàm số 2
y  x  2021x  2020 với trục hoành.
A. M(1;0) và N(2020;0) .B. P(0;1)và Q(0;2020). C. O(0;0)và M(1;2020). D. N(2020;0)và O(0;0).
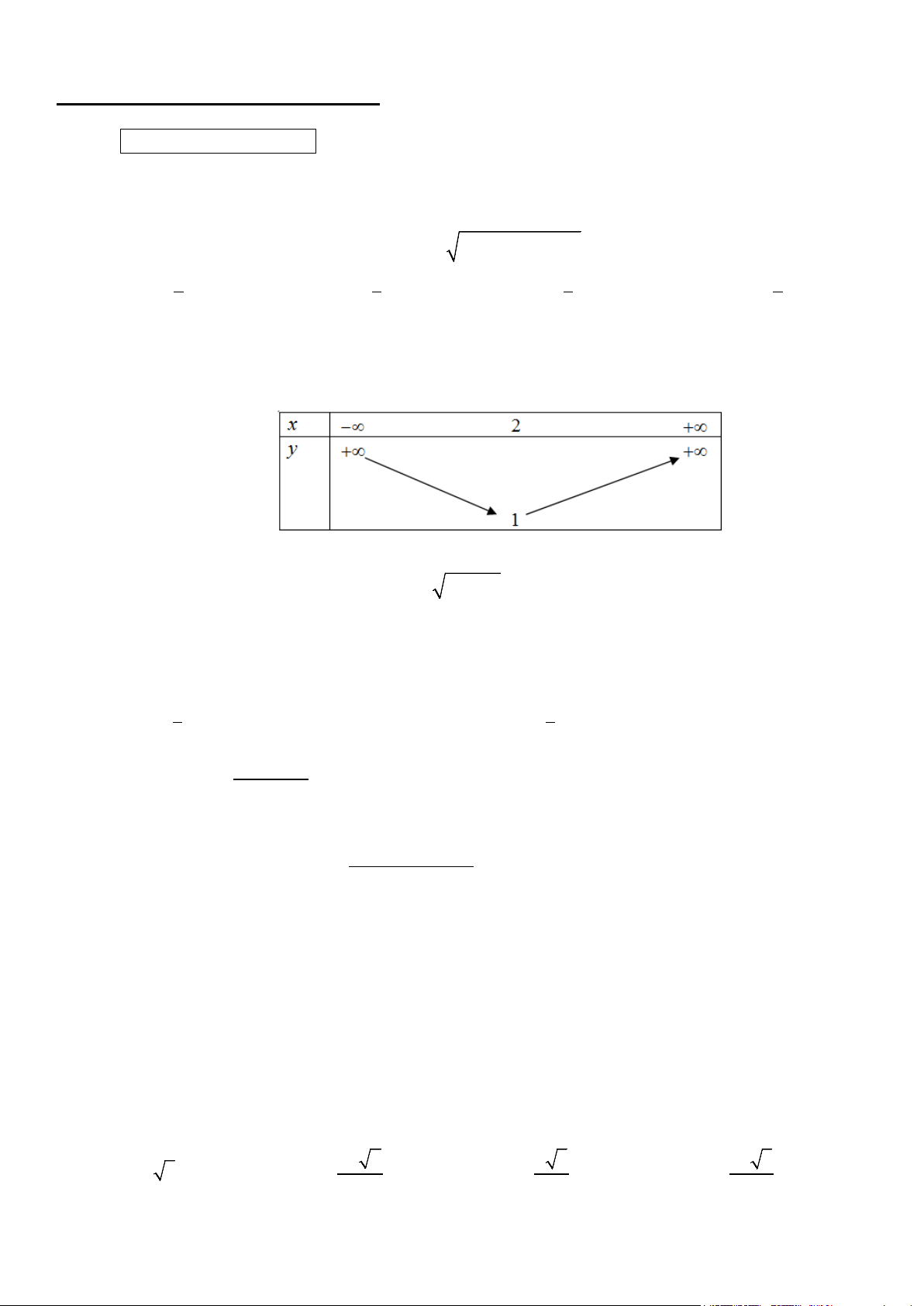
Câu 3. Tìm hàm số bậc hai có bảng biến thiên như hình vẽ dưới đây. A. 2 y  x
  4x  3. B. 2
y  x  2x  1. C. 2
y  x  4x  5 . D. 2
y  x  4x  5.
Câu 4. Tập hợp nghiệm của phương trình 5x  6  x  6. A. {2}. B. { 2, 15}. C. {15}. D. {6}.
Câu 5. Gọi S là tập nghiệm của bất phương trình 2x 1  0, S là tập nghiệm của bất phương 1 2 trình 2
x  5x  6  0 . Tìm S  S  S . 1 2 A. 1  1  S    ;     .        B. S   2 ; 3 . C. S ; 2  3 ;  
D. S   ;    .      . 2    2   Câu 6.  Cho 2019  
. Khi đó  thuộc góc phần tư nào? 4
A. Thứ I. B. Thứ II. C. Thứ III. D. Thứ IV. 4 4
Câu 7. Rút gọn biểu thức sin x  cos x M   1 2 cos x A. 2 M  tan x . B. 2
M  2  tan x . C. 2 sin x . D. 2 2
sin x  tan x .
Câu 8. Tính giá trị biểu thức A 
 0   0   0   0 cos 90 sin 180 sin 90 cos 180  . A. A  1 . B. A  0 . C. A  2 . D. A  1 .
Câu 9. Trong hệ tọa độ Oxy, cho ba điểm A1;  1 B , 3;2 C  , 6; 
5 . Tìm tọa độ điểm D để ABCD là hình bình hành. A. 4;  3 . B. 3;4. C. 8;6. D. 4;4.
Câu 10. Tam giác ABC đều, cạnh 2a, nội tiếp đường tròn bán kính R. Khi đó bán kính đường tròn
ngoại tiếp tam giác ABC là: A. a 3 . B. 2a 2 . C. a 3 . D. 2a 3 . 3 2 3
Câu 11. Cho tam giác ABC có AB = 17 , BC = 21, CA = 10. Góc lớn nhất của tam giác ABC là A. ˆ A. B. ˆ B . C. ˆ C . D. ˆ ˆ ˆ
A  B  C .
Câu 12. Khoảng cách từ điểm O(0;0) tới đường thẳng : x y ∆ + = 1 bằng 6 8 A. 1 . B. 24 . C. 48 . D. 1 . 8 5 14 6
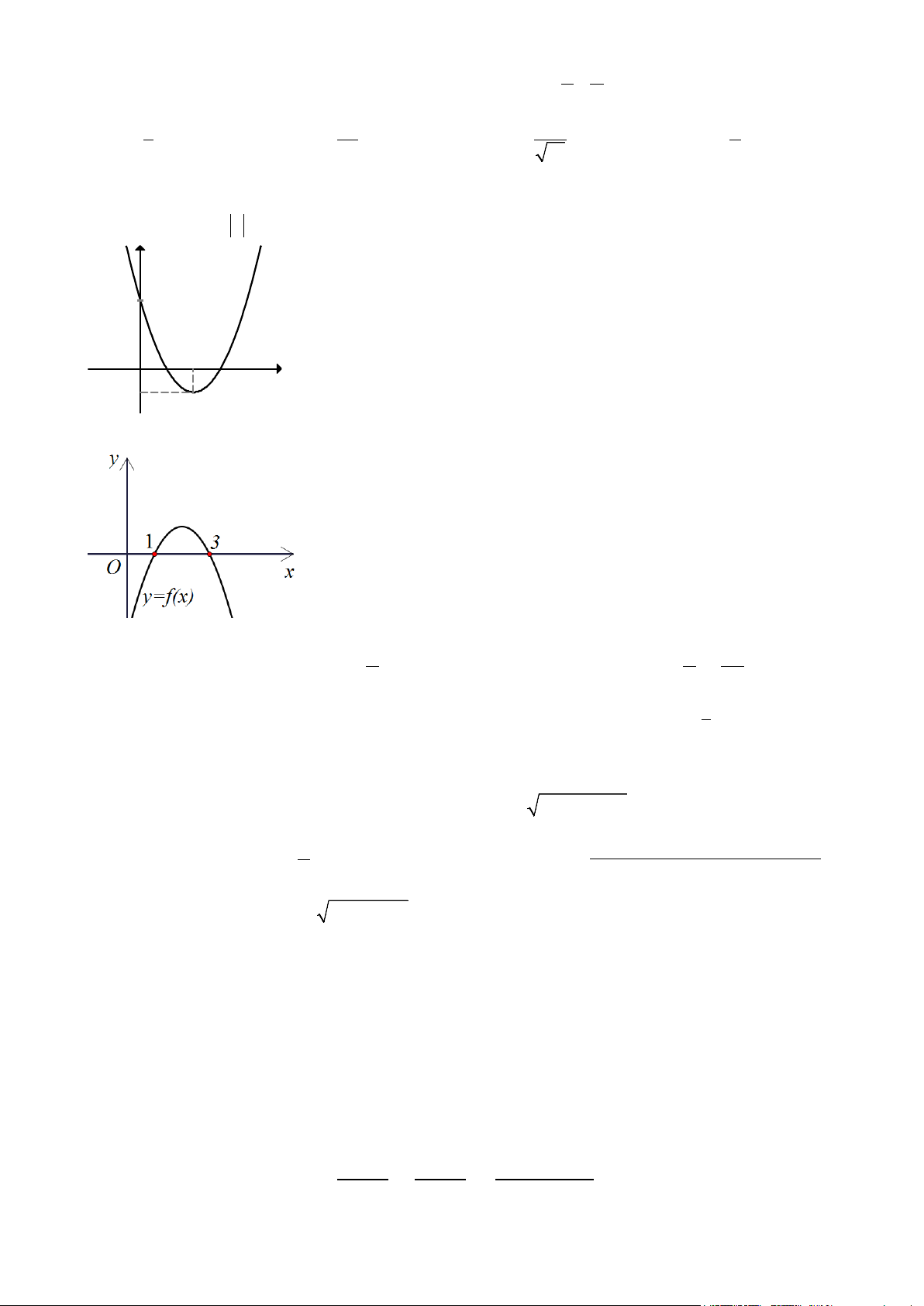
Câu 13. Cho hàm số ( ) 2
f x = ax + bx + c đồ thị như hình. Hỏi với những giá trị nào của m thì phương
trình f ( x ) −1= m có đúng 3nghiệm phân biệt. y A. m = 3 . B. m > 3 . 3 C. m = 2 . D. 2 − < m < 2 . x O 2 1
Câu 14. Cho hàm số y  f x có đồ thị như hình vẽ. Hãy so sánh f 2020 với số 0.
A. Không so sánh được f 2020 với số 0.
B. f 2020  0.
C. f 2020  0.
D. f 2020  0.
Câu 15. Chox,y  0 và 5
x  y  . Giá trị nhỏ nhất của biểu thức 4 1 B   . 4 x 4y A. 5. B. 0 . C. 2. D. 5 . 2
Phần II. Tự luận ( 7 điểm)
Câu 16(1đ). Giải bất phương trình sau a) 4 2
x  2x  3  0 . b) 2 2
(x − 3x) 2x − 3x − 2 ≥ 0. 2 2 Câu 17 (1đ). Biết 1 + − tan x
2sin x 3sin .xcos x 4cos x
= . Tính giá trị của biểu thức M = 2 2 2 5cos x − sin x
Câu 18 (1đ). Tìm m để 2 2
x + 5 + 4x − x = 4x + m −103 có nghiệm.
Câu 19 (2đ). Trên mặt phẳng Oxy, cho A(2;2), B(5; )
1 và đường thẳng ∆ : x – 2y +8 = 0.
a) Viết PTTQ của d đi qua A và vuông góc với ∆ . Tìm H là hình chiếu của A lên ∆.
b) Tìm điểm C ∈∆ , C có hoành độ dương sao cho diện tích tam giác ABC bằng 17.
Câu 20(1đ). Trên mặt phẳng Oxy, cho tam giác ABC có A(2; 1), đường cao BH: x – 3y – 7 = 0,
đường trung tuyến CM: x + y + 1 = 0. Tìm B, C. Câu 21(1đ). b c a
a) Cho tam giác ABC thoả mãn:   . Chứng minh ΔABC vuoâng. cos B cosC sin B sinC
b) Chox,y,z  [0; 2],x  y  z  3 . Tìm GTLN của 2 2 2
S  x  y  z .
--------------------- Hết --------------------- SỞ GD&ĐT BẮC NINH
HƯỚNG DẪN CHẤM THI CHỌN LỚP CHẤT
TRƯỜNG THPT YÊN PHONG SỐ LƯỢNG CAO 2
Năm học : 2020 – 2021 Môn: Toán Lớp: 10
Phần I. Trắc nghiệm(3đ) 1A 2A 3C 4C 5B 6B 7A 8A 9D 10D 11A 12B 13C 14D 15C
Phần II. Tự luận (7đ) Câu Nội dung Điểm  2  x  1(L) x  3 a) 4 2 x  
 2x  3  0     2 x   3 x    3 0.5 16(1đ)   2  x ≥ 3 b)
x − 3x ≥ 0 2 2
(x − 3x) 2x − 3x − 2 ≥ 0 ⇔   ⇔ 1 2  0.5
2x − 3x − 2 ≥ 0 x ≤ −  2 Biết 1 tan x = . Tính giá trị của biểu thức 2 2 2
2sin x + 3sin .xcos x − 4cos x M = 2 2 5cos x − sin x 1.0 17(1đ) LG:
Chia cả tử và mẫu của M cho 2 cos x ta có: 2 sin x sin .xcos x 1 1 2 + 3 − 4 2. + 3. − 4 2 2 cos x cos x 4 2 8 M = = = − . 2 sin x 1 19 5 − 5 − 2 cos x 4 Tìm m để 2 2
x + 5 + 4x − x = 4x + m −103 có nghiệm. LG: Đặt 2
t = 5 + 4x - x = 9 -(x - 2)2 nên 0 ≤ t ≤ 3hay t ∈[0; ] 3 Ta được PT 2t
− + t +108 = m
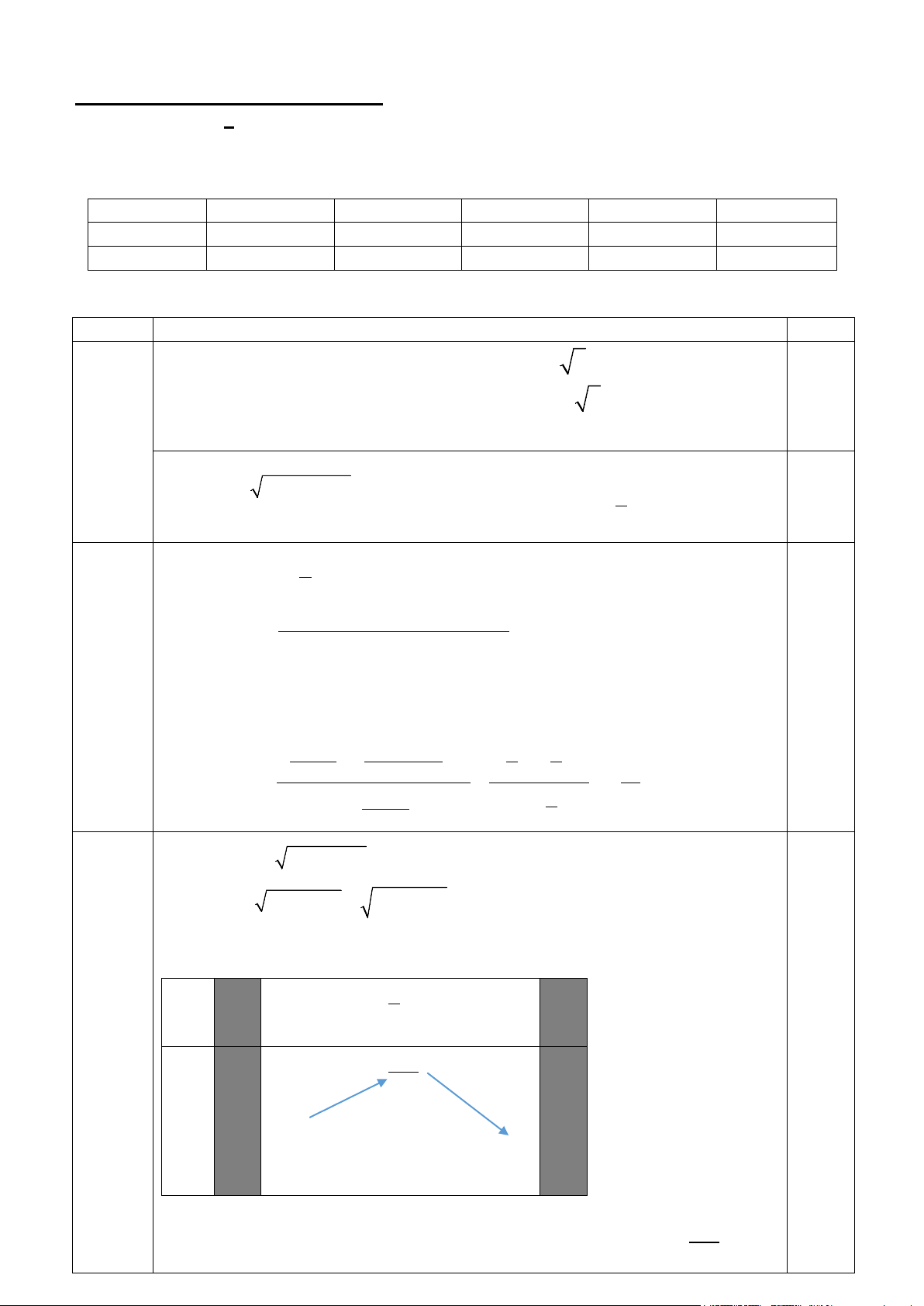
Khi đó xét y = f (t) 2
= − t + t +108với t ∈[0; ] 3 0.5 18(1đ) t 0 1 3 2 f(t) 433 4 108 102
Từ bảng biến thiên trên ta thấy PT có nghiệm khi và chỉ khi 433 102 ≤ m ≤ . 4 0.5
Trên mặt phẳng Oxy, cho A(2;2), B(5; )
1 và đường thẳng ∆ : x – 2y +8 = 0.
a) d   : x  2y  8  0  d : 2x  y  m  0 0.5 (
A 2;2)  d  m  6. Vậy d : 2x  y  6  0 . 0.5
H là hình chiếu của A lên . Ta có 4 22
H  d    H( ; ) 19(2đ) 5 5
Phương trình đường thẳng AB : x +3y −8 = 0. Điểm C ∈∆ ⇒ C (2t −8;t)
Diện tích tam giác ABC : 1.0 t = 10 1 t − A .
B d (C; AB) 1 5 16 17 10. 17  = ⇒ = ⇒ 18 ⇒ C (12;10) 2 2 10 t = −  5
Đường AC đi qua A vuông góc BH có phương trình là: 3x + y – 7 = 0.
C  AC CM  C(4; 5).
B  BH : x  3y  7  0  B(3a  7;a). 20.(1đ) 1.0   M là trung điểm AB 3a 9 a 1  M( ;
).Do M  CM  a  3 2 2 Vậy B ( - 2; - 3) b c a
a) Cho tam giác ABC thoả mãn:   . Chứng cos B cosC sin B sinC minh ΔABC vuông. Ta có : b c a   cos B cosC sin B sinC 2R sin B 2R sinC 2R sin A    cos B cosC sin B sinC 21(1đ)
sin B cosC  cos B sinC sin A   0.5 cos B cosC sin B sinC sin(B C ) sin A  
, do sin(B C )  sin A  0 cos B cosC sin B sinC
 cosB.cosC  sin B sinC  0  o
c s(B C )  0   B C  2 Vậy ΔABC vuông tại A.
b) Chox,y,z  [0; 2].Tìm GTNN của 2 2 2
S  x  y  z . Ta có 2 2 2 2
S  x  y  z  (x  y  z)  2(xy  yz  zx)  9  2 . A
(Với A=xy  yz  zx ) Lại có:          
0 (2 x)(2 y)(2 z) 8 4(x y z) 2A xyz
 0  8 12  2A  xyz  2A  4  xyz  A  2
Vậy S  9  2A  9  2.2  5 . GTLN của S là 5. Khi x
 y  z  3   x  yz  0  (2
 x)(2y)(2z)  0  0.5
Ta đc (x;y;z)  (0;1;2),(0;2;1),(1;0;2),(1;2;0),(2;1;0),(2;0;1  ) .
Lưu ý: Học sinh làm theo cách khác đúng vẫn cho điểm tối đa.
Document Outline

• De thi chon lop CLC ngay 472020 Toan hoc 10 THPT Yen Phong so 2