Đề cuối học kì 1 Toán 10 năm 2022 – 2023 trường THPT Trần Quốc Tuấn – TP HCM

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 10 đề kiểm tra cuối học kì 1 môn Toán 10 năm học 2022 – 2023 trường THPT Trần Quốc Tuấn, thành phố Hồ Chí Minh, mời bạn đọc đón xem

33 17 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK1 Toán 10

Môn: Toán 10

Thông tin:

5 trang 9 tháng trước

Tác giả:

Profile Thanh Tâm
SỞ GD&ĐT TP HỒ CHÍ MINH
TRƯỜNG THPT TRẦN QUỐC TUẤN
ĐỀ KIỂM TRA CUỐI HỌC KÌ 1
Môn: TOÁN 10
Năm học: 2022 - 2023
Thời gian làm bài: 90 phút
(Không k
ể
th
ờ
i gian phát đ
ề
)
Câu 1: (2,0 điểm) Tìm tập xác định của các hàm số sau:
a)
2
1
x
y
x
b)
2
3 9
5 4
x
y
x x
Câu 2: (2,0 điểm)
a) Vẽ đồ thị hàm số
2
( ): 2 4 1P y x x
b) Xác định hàm số
2
: 4P y ax bx
. Biết đồ thị hàm số (P) đi qua hai điểm
1;12M
và
3;4N
.
Câu 3: (1,0 điểm) Điểm kiểm tra học kì I môn Toán của các bạn tổ 1 lớp 10A như sau:
5; 8; 8; 6; 7; 4; 9; 3; 7; 8.
Tính điểm trung bình và tìm khoảng biến thiên của mẫu số liệu trên.
Câu 4: (1,0 điểm) Cho
1
cos
2
x
. Tính giá trị của biểu thức
2 2
3sin 4cosP x x
Câu 5: (2,0 điểm)
a) Cho 4 điểm
, , ,M N P Q
bất kỳ. Chứng minh rằng:
0MN NP PQ QM
   
b) Cho tam giác
ABC
. Gọi I là trung điểm của AB, M là trung điểm của IC. Chứng
minh rằng:
2 0MA MB MC
 
Câu 6: (1,0 điểm) Cho tam giác đều
ABC
có cạnh bằng a. Tính
.AC CB

Câu 7: (1,0 điểm) Hai người đứng trên bờ biển ở hai vị
trí A, B cách nhau 500
m
cùng nhìn thấy mép một hòn
đảo ở vị trí C trên đảo với các góc so với bờ biển lần
lượt là 60
0
và 70
0
. Tính khoảng cách
d
từ mép hòn đảo
đến bờ biển (làm tròn kết quả đến phần nguyên).
---------Hết--------
(Giám thị coi kiểm tra không giải thích gì thêm)
Đề chính thức
HƯỚNG DẪN CHẤM – TOÁN 10 (CUỐI HK1)
CÂU LỜI GIẢI ĐIỂM
1
Tìm tập xác định của các hàm số sau:
a)
2
1
x
y
x
Điều kiện:
1 0x
0,5
1x
0,25
Vậy: TXĐ của hàm số là:
\ 1D
0,25
b)
2
3 9
5 4
x
y
x x
Điều kiện:
2
3 9 0
5 4 0
x
x x
0,5
3
3
1
4
4
x
x
x
x
x
0,25
Vậy: TXĐ của hàm số là:
3; \ 4D 
0,25
2
a) Vẽ đồ thị hàm số
2
( ) : 2 4 1P y x x
Tọa độ đỉnh
1; 3S
0,25
2 0a
Bề lõm của (P) quay lên
BBT:
0,25
0,5
b) Xác định hàm số
2
: 4P y ax bx
. Biết đồ thị hàm số (P)
đi qua hai điểm
1;12M
và
3;4N
.
1;12 ( ) 8M P a b
0,25
3;4 ( ) 3 0N P a b
0,25
Ta có hpt:
8 2
3 0 6
a b a
a b b
0,25
Vậy: Hàm số
2
: 2 6 4P y x x
.
0,25
3
Điểm kiểm tra học kì I môn Toán của các bạn tổ 1 lớp 10A như
sau:
5; 8; 8; 6; 7; 4; 9; 3; 7; 8.
Tính điểm trung bình và tìm khoảng
biến thiên của mẫu số liệu trên.
Sắp xếp dãy số liệu:
3;4;5;6;7;7;8;8;8;9.
0,5
Điểm trung bình là: 6,5
0,25
Khoảng biến thiên của mẫu số liệu là:
9 3 6R
0,25
4
Cho
1
cos
2
x
. Tính giá trị của biểu thức
2 2
3sin 4cosP x x
2 2 2 2
3sin 4cos 3 1 cos 4cosP x x x x
0,25
2
3 cos x
0,25
2
1
3
2
0,25
13
4
0,25
5
a) Cho 4 điểm
, , ,M N P Q
bất kỳ. Chứng minh rằng:
0MN NP PQ QM
   
MN NP PQ QM MN NP PQ QM
      
0,5
MP PM
 
0,25
0MM

0,25
b) Cho tam giác
ABC
. Gọi I là trung điểm của AB, M là trung
điểm của IC. Chứng minh rằng:
2 0MA MB MC
  
Do I là trung điểm của AB nên
2MA MB MI
 
0,5
2 2 2MA MB MC MI MC

0,25
2 2.0 0MI MC
(vì M là trung điểm của IC
0MI MC
)
0,25
6
Cho tam giác đều
ABC
có cạnh bằng a. Tính
.AC CB

Xác định được góc
,AC CB
là góc ngoài của góc
C
nên
0
, 120AC CB
0,25
Do đó
. . .cos ,AC CB AC CB AC CB
0,25
0
. .cos , . .cos120AC CB AC CB a a
0,25
2
2
a
0,25
7
Hai người đứng trên bờ biển ở hai
vị trí A, B cách nhau 500
m
cùng
nhìn thấy mép một hòn đảo ở vị trí
C trên đảo với các góc so với bờ
biển lần lượt là 60
0
và 70
0
. Tính
khoảng cách
d
từ mép hòn đảo
đến bờ biển (làm tròn kết quả đến phần nguyên).
Ta có:
0 0 0 0 0
180 180 60 70 50
C A B
0,25
Áp dụng định lý sin trong tam giác ABC:
sin A sin
BC AB
C
0,25
0
0
.sin A 500.sin 60
565
sin sin 50
AB
BC
C
0,25
0
565.sin 70 531( )
d m
0,25
(Lưu ý: Học sinh giải cách khác đúng vẫn chấm điểm tối đa)
| 1/5
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GD&ĐT TP HỒ CHÍ MINH
ĐỀ KIỂM TRA CUỐI HỌC KÌ 1
TRƯỜNG THPT TRẦN QUỐC TUẤN Môn: TOÁN 10 Năm học: 2022 - 2023 Đề chính thức
Thời gian làm bài: 90 phút
(Không kể thời gian phát đề)
Câu 1: (2,0 điểm) Tìm tập xác định của các hàm số sau: 2x 3x  9 a) y  b) y  x 1 2 x  5x  4 Câu 2: (2,0 điểm) a) Vẽ đồ thị hàm số 2 ( ) P : y  2x  4x 1
b) Xác định hàm số P 2
: y  ax  bx  4 . Biết đồ thị hàm số (P) đi qua hai điểm M 1;12 và N  3  ;4 .
Câu 3: (1,0 điểm) Điểm kiểm tra học kì I môn Toán của các bạn tổ 1 lớp 10A như sau: 5; 8; 8; 6; 7; 4; 9; 3; 7; 8.
Tính điểm trung bình và tìm khoảng biến thiên của mẫu số liệu trên. 1
Câu 4: (1,0 điểm) Cho cos x  . Tính giá trị của biểu thức 2 2 P  3sin x  4cos x 2 Câu 5: (2,0 điểm)
    
a) Cho 4 điểm M , N, P, Q bất kỳ. Chứng minh rằng: MN  NP  PQ  QM  0
b) Cho tam giác ABC . Gọi I là trung điểm của AB, M là trung điểm của IC. Chứng    
minh rằng: MA  MB  2MC  0  
Câu 6: (1,0 điểm) Cho tam giác đều ABC có cạnh bằng a. Tính AC.CB
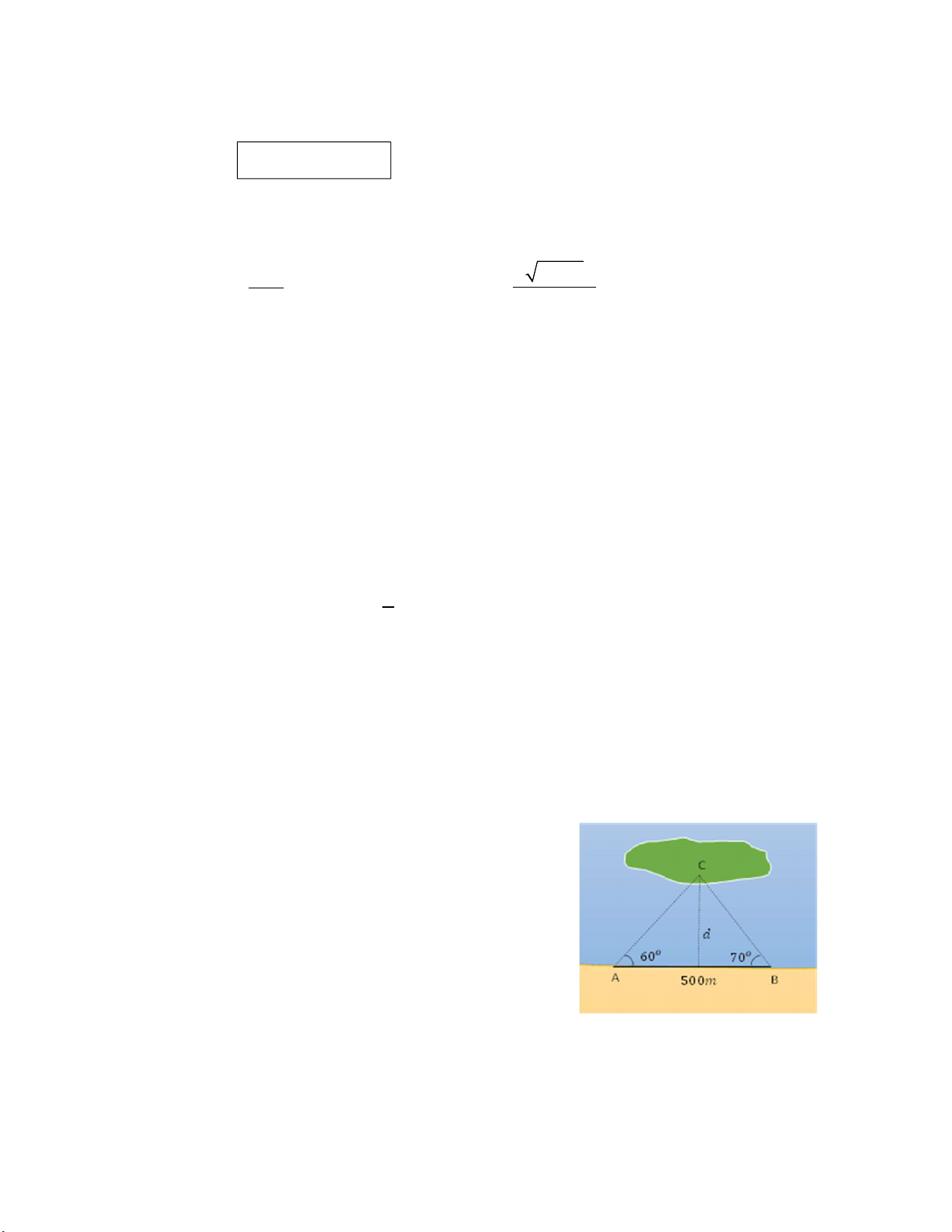
Câu 7: (1,0 điểm) Hai người đứng trên bờ biển ở hai vị
trí A, B cách nhau 500 m cùng nhìn thấy mép một hòn
đảo ở vị trí C trên đảo với các góc so với bờ biển lần
lượt là 600 và 700. Tính khoảng cách d từ mép hòn đảo
đến bờ biển (làm tròn kết quả đến phần nguyên). ---------Hết--------
(Giám thị coi kiểm tra không giải thích gì thêm)
HƯỚNG DẪN CHẤM – TOÁN 10 (CUỐI HK1) CÂU LỜI GIẢI ĐIỂM
Tìm tập xác định của các hàm số sau: 2x a) y  x 1 Điều kiện: x 1  0 0,5  x  1 0,25
Vậy: TXĐ của hàm số là: D   \  1 0,25 3x  9 1 b) y  2 x  5x  4 3x  9  0 Điều kiện:  0,5 2 x  5x  4  0 x  3  x  3  x  1   0,25  x  4 x  4 
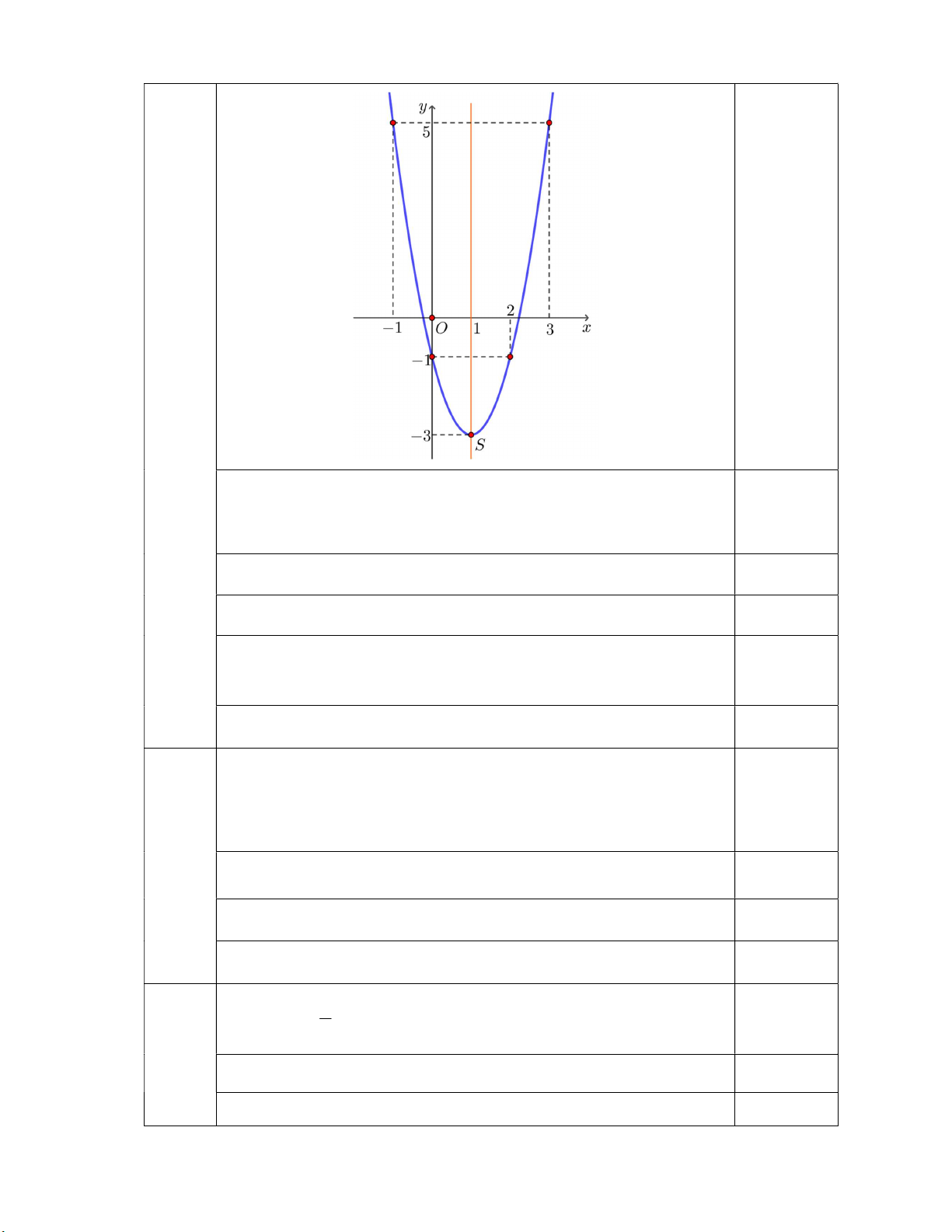
Vậy: TXĐ của hàm số là: D  3; \  4 0,25 a) Vẽ đồ thị hàm số 2 (P) : y  2x  4x 1
Tọa độ đỉnh S 1;3 0,25
a  2  0  Bề lõm của (P) quay lên BBT: 2 0,25 0,5
b) Xác định hàm số P 2
: y  ax  bx  4 . Biết đồ thị hàm số (P)
đi qua hai điểm M 1;12 và N  3  ;4.
M 1;12(P)  a  b  8 0,25
N 3;4(P)  3a  b  0 0,25 a  b  8 a  2 Ta có hpt:    0,25 3  a  b  0 b  6 Vậy: Hàm số P 2 : y  2x  6x  4 . 0,25
Điểm kiểm tra học kì I môn Toán của các bạn tổ 1 lớp 10A như
sau: 5; 8; 8; 6; 7; 4; 9; 3; 7; 8. Tính điểm trung bình và tìm khoảng
biến thiên của mẫu số liệu trên. 3
Sắp xếp dãy số liệu: 3;4;5;6;7;7;8;8;8;9. 0,5 Điểm trung bình là: 6,5 0,25
Khoảng biến thiên của mẫu số liệu là: R  9  3  6 0,25 1
Cho cos x  . Tính giá trị của biểu thức 2 2 P  3sin x  4cos x 2 4 2 2 P  x  x   2  x 2 3sin 4cos 3 1 cos  4cos x 0,25 2  3  cos x 0,25 2  1   3    0,25  2  13  0,25 4
a) Cho 4 điểm M , N, P, Q bất kỳ. Chứng minh rằng:
     MN  NP  PQ  QM  0
       
MN  NP  PQ  QM  MN  NP  PQ  QM  0,5    MP  PM 0,25    MM  0 0,25 5
b) Cho tam giác ABC . Gọi I là trung điểm của AB, M là trung    
điểm của IC. Chứng minh rằng: MA  MB  2MC  0   
Do I là trung điểm của AB nên MA  MB  2MI 0,5     
MA  MB  2MC  2MI  2MC 0,25    
 2MI  MC  2.0  0    0,25
(vì M là trung điểm của IC  MI  MC  0 )  
Cho tam giác đều ABC có cạnh bằng a. Tính AC.CB  
Xác định được góc  AC,CB là góc ngoài của góc C nên 0,25   AC CB 0 , 120 6
     
Do đó AC.CB  AC . CB .cos AC,CB 0,25    AC CB AC CB 0 . .cos ,  a.a.cos120 0,25 2 a   0,25 2
Hai người đứng trên bờ biển ở hai
vị trí A, B cách nhau 500 m cùng
nhìn thấy mép một hòn đảo ở vị trí 7
C trên đảo với các góc so với bờ
biển lần lượt là 600 và 700. Tính
khoảng cách d từ mép hòn đảo
đến bờ biển (làm tròn kết quả đến phần nguyên). Ta có:  0,25 0 C   A    B 0    0 0   0 180 180 60 70  50 BC AB
Áp dụng định lý sin trong tam giác ABC:  0,25 sin A sin C 0 A . B sin A 500.sin 60  BC    565 0,25 0 sin C sin 50 0
 d  565.sin 70  531(m) 0,25
(Lưu ý: Học sinh giải cách khác đúng vẫn chấm điểm tối đa)