UBND THÀNH PHỐ SƠN LA
ĐỀ KIỂM TRA, ĐÁNH GIÁ CUỐI HỌC KI I
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
NĂM HỌC: 2023 – 2024 Môn: Toán 8 ĐỀ CHÍNH THỨC
Ngày kiểm tra: Ngày 03 tháng 01 năm 2024
Thời gian làm bài 90 phút không kể thời gian phát đề
(Đề kiểm tra có 04 trang)
I. PHẦN TRẮC NGHIỆM (3 ĐIỂM)
Chọn chữ cái đứng trước câu trả lời đúng nhất. MÃ ĐỀ 01
Câu 1. Trong những biểu thức sau, biểu thức nào là đơn thức? A. 3 − 2xy . x B. 1 2 3
− x (y − z ) . C. 1 2 5 − xy z . D. 2 . 4 2 3yz Câu 2. Biểu thức 2 2
4x − 25y được viết dưới dạng tích là
A. (2x − 5y)(2x + 5y).
B. (4x − 5y)(4x + 5y).
C. (4x − 25y)(4x + 25y).
D. (2x − 25y)(2x + 25y) .
Câu 3. Điều kiện xác định của phân thức M là N A. M ≠ 0. B. N ≥ 0.
C. N ≤ 0.
D. N ≠ 0.
Câu 4. Giá trị của phân thức 16 tại x =1 là 2 x − 2x + 5 A. 2. B. 4. C. 8. D. 16.
Câu 5. Công thức biểu thị số tiền phải trả y đồng khi mua 15 quyển vở, giá của một
quyển vở là x đồng là
A. y =15 .x
B. y =15: .x
C. x =15 .y D. 15 x = . y
Câu 6. Hệ số góc của đường thẳng y = 3 − x + 2 là A. 2 . B. 3 -2. C. -3. D. 2.
Câu 7. Hình chóp tứ giác đều có các mặt bên là hình gì? A. Tam giác đều.
B. Tam giác vuông cân
C. Tam giác vuông.
D. Tam giác cân.
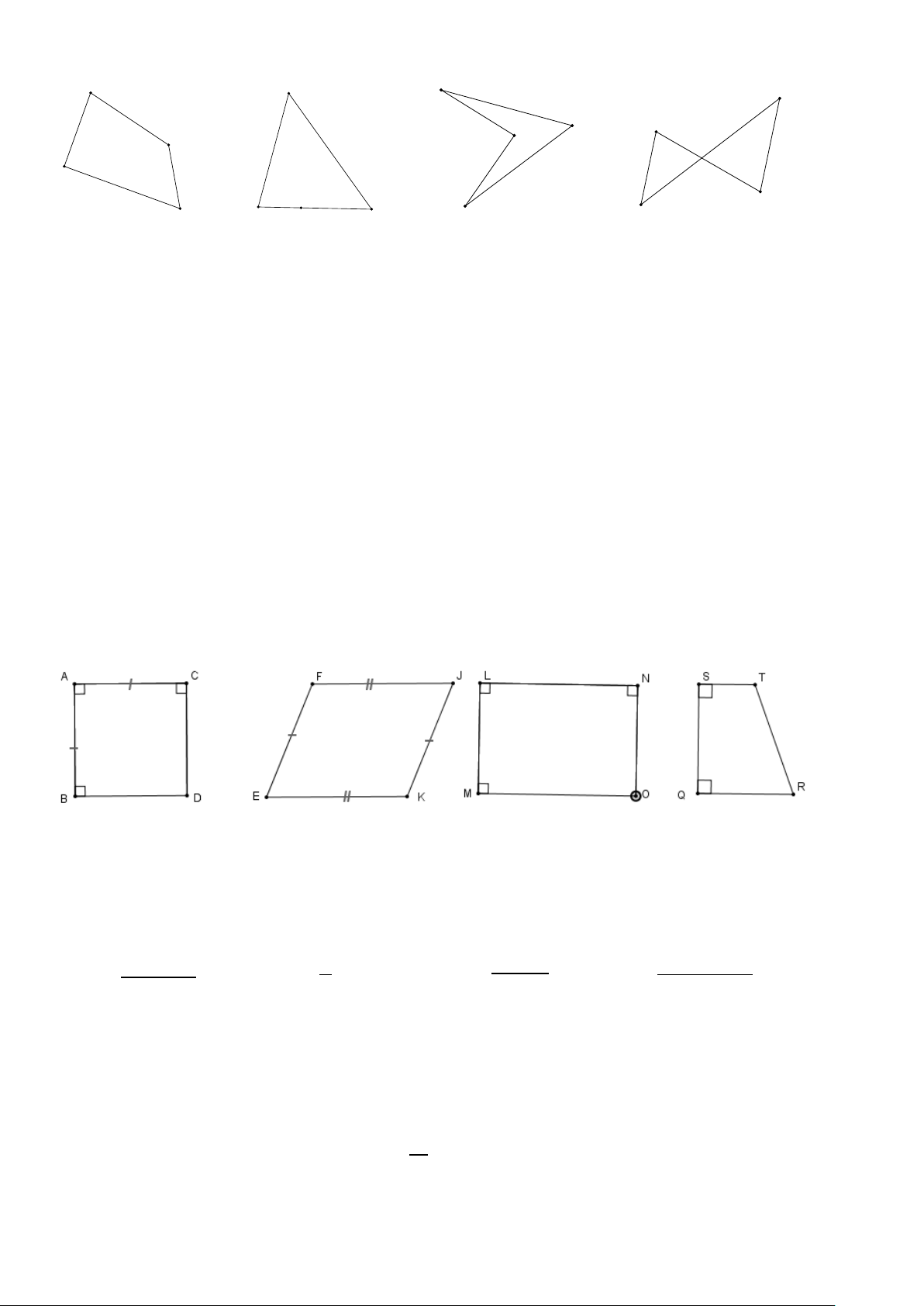
Câu 8. Trong các hình vẽ dưới đây, hình nào không phải là tứ giác? Trang 01/ 0 9 M A E O F D N G Q R P B D C H S Hình 1 Hình 2 Hình 3 Hình 4 A. Hình 1. B. Hình 2. C. Hình 3. D. Hình 4.
Câu 9. Khẳng định nào sau đây là đúng?
A. Tứ giác có hai cạnh đối song song là hình bình hành.
B. Tứ giác có hai cạnh đối bằng nhau là hình bình hành.
C. Tứ giác có hai góc đối bằng nhau là hình bình hành.
D. Tứ giác có các cạnh đối song song là hình bình hành.
Câu 10. Hình thang cân ABCD (AB//CD) có  0
A = 90 thì ABCD là A. Hình vuông. B. Hình bình hành.
C. Hình chữ nhật. D. Hình thoi.
Câu 11. Tứ giác ABCD có  =   = 
A C;D B và AC ⊥ BD thì tứ giác ABCD là A. Hình bình hành. B. Hình thoi. C. Hình vuông. D. Hình thang.
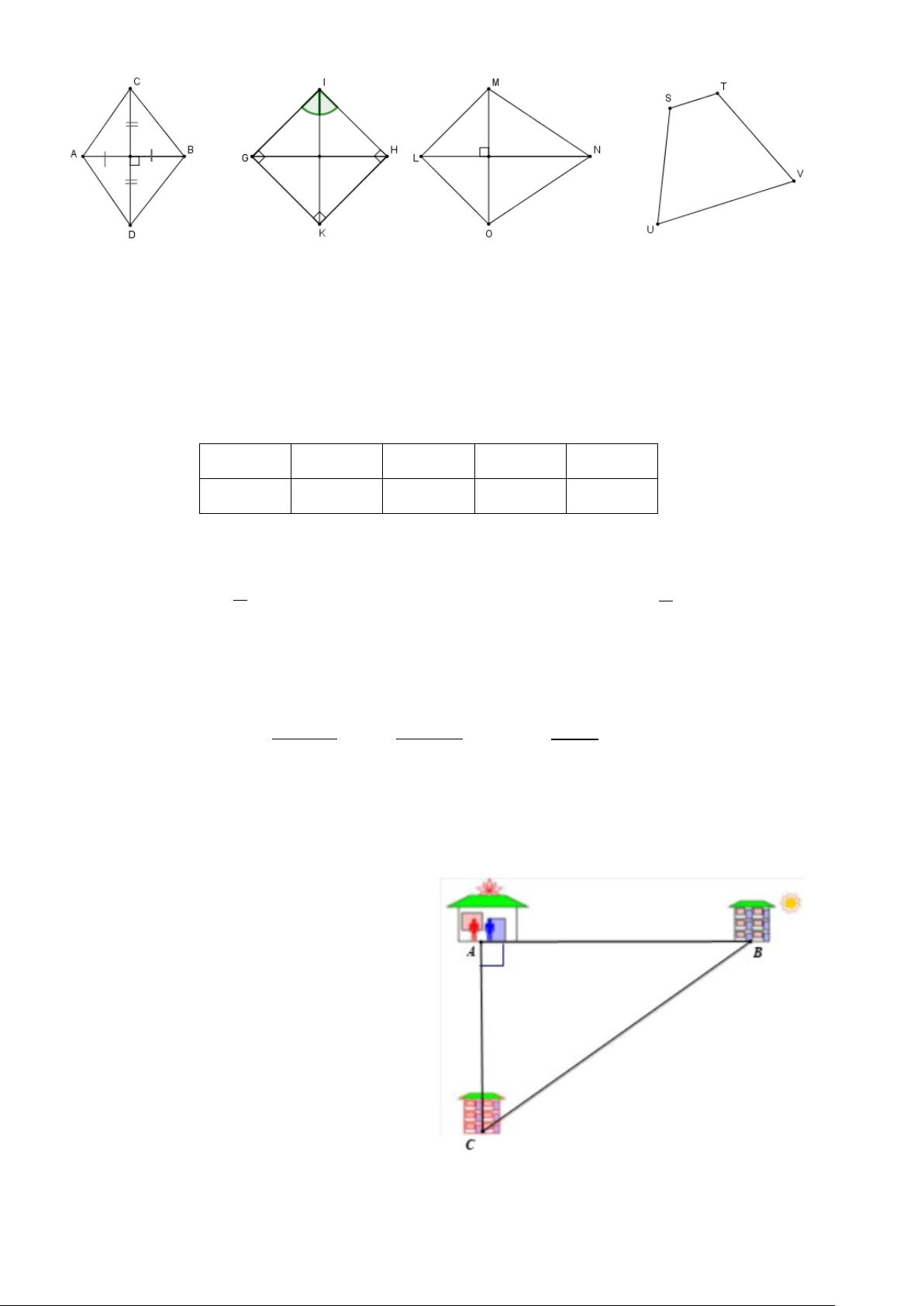
Câu 12. Trong các hình sau, tứ giác nào là hình vuông
A. Tứ giác ABDC.
B. Tứ giác EFJK.
C. Tứ giác LMON.
D. Tứ giác QST . R MÃ ĐỀ 02.
Câu 1. Trong những biểu thức sau, biểu thức nào là đa thức? 2 3 3 − xy z 1 x + y 2 x − 2x +1 A. . B. 2
xy − x yz + 2. C. − . D. . 2x −1 3 2x − y 2 xy −1 Câu 2. Biểu thức 2 2
9x −16y được viết dưới dạng tích là
A. (3x −16y)(3x +16y) .
B. (9x − 4y)(9x + 4y) .
C. (3x − 4y)(3x + 4y).
D. (9x −16y)(9x +16y).
Câu 3. Điều kiện xác định của phân thức P là Q Trang 02/ 0 9 A. P ≠ 0. B. Q ≠ 0.
C. Q ≥ 0.
D. Q ≤ 0.
Câu 4. Giá trị của phân thức 25 tại y = 2 là 2 y − 4y + 9 A. 5. B. -5. C. 7. D. -7.
Câu 5. Một người đi xe đạp được y km với vận tốc x km/h trong 2 giờ. Công thức biểu
thị quãng đường đi được của người đó là A. x y = . B. 2 y = .
C. x = 2y .
D. y = 2 .x 2 x
Câu 6. Hệ số góc của đường thẳng y = 2x +1 là A. 1. B. 2. C. -2. D. 1 . 2
Câu 7. Hình chóp tứ giác đều có mặt đáy là hình gì? A. Hình thang cân. B. Hình bình hành.
C. Hình vuông.
D. Hình chữ nhật.
Câu 8. Trong các hình vẽ dưới đây, hình nào không phải là tứ giác lồi? A R S M N E F G D B C N M Q P H Hình 1 Hình 2 Hình 3 Hình 4
A. Hình 1. B. Hình 2. C. Hình 3. D. Hình 4.
Câu 9. Khẳng định nào sau đây là sai?
A. Tứ giác có hai cặp cạnh đối song song là hình bình hành.
B. Hình thang có hai góc kề một đáy bằng nhau là hình bình hành.
C. Tứ giác có hai cặp cạnh đối bằng nhau là hình bình hành.
D. Tứ giác có hai cặp góc đối bằng nhau là hình bình hành.
Câu 10. Hình bình hành ABCD có  0
A = 90 thì ABCD là A. Hình vuông. B. Hình bình hành. C. Hình thoi.
D. Hình chữ nhật.
Câu 11. Cho tứ giác MNPQ là hình bình hành, có MPlà tia phân giác của  NMQ .
Tứ giác MNPQ là hình gì? A. Hình thoi. B. Hình thang. C. Hình vuông. D. Hình bình hành.
Câu 12. Với mỗi hình dưới đây, tứ giác nào là hình vuông Trang 03/ 0 9
A. Tứ giác ABC . D
B. Tứ giác STVU.
C. Tứ giác LMN . O
D. Tứ giác GIHK.
II. PHẦN TỰ LUẬN (7,0 điểm) Câu 13 (0,5 điểm)
Đại lượng y có phải là hàm số của đại lượng x hay không nếu các giá trị tương ứng
của chúng được cho bởi bảng sau? x 0 6 8 12 y 18 19 21 23 Câu 14 (1,0 điểm)
1) Thực hiện phép tính a) 3 5 5 2 3 3
5x y − y (4x y +1); b) 3 2 2  1 (x 2x y 3xy ) : x − + − 4 2   
2) Tính giá trị của đa thức 2 2
A = 36x + y −12xy tại x = 7; 3 y = − . Câu 15 (1,5 điểm) 3 3  +  Cho biểu thức x y 1 M =  − xy . = 2 2 và 2y N . x + y x −   y x + y
a) Viết điều kiện xác định của các biểu thức M, N.
b) Rút gọn biểu thức M.
c) Chứng tỏ giá trị của biểu thức P = M + N không phụ thuộc vào giá trị của biến x, y? Câu 16 (0,5 điểm)
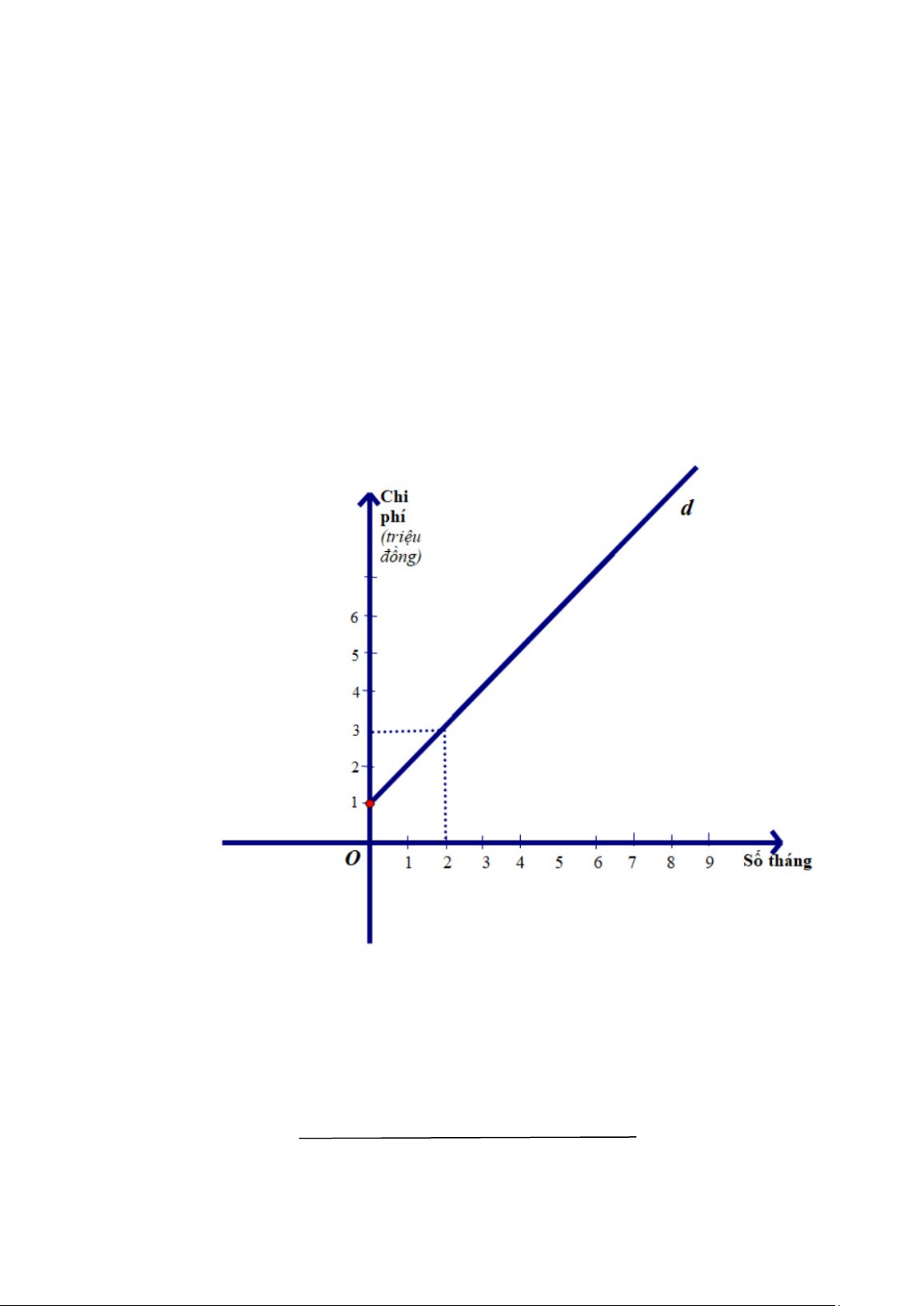
Hai anh em An và Bình cùng đi bộ
từ nhà ở vị trí A đến trường, biết khoảng
cách từ trường của An ở vị trí B đến nhà là
1,5 km , khoảng cách từ trường của Bình ở
vị trí C đến nhà là 1,2 km (Hình 5). Hỏi
trường của An và Bình cách nhau bao
nhiêu ki-lô-mét? (kết quả làm tròn đến hàng phần mười). Hình 5 Trang 04/ 0 9
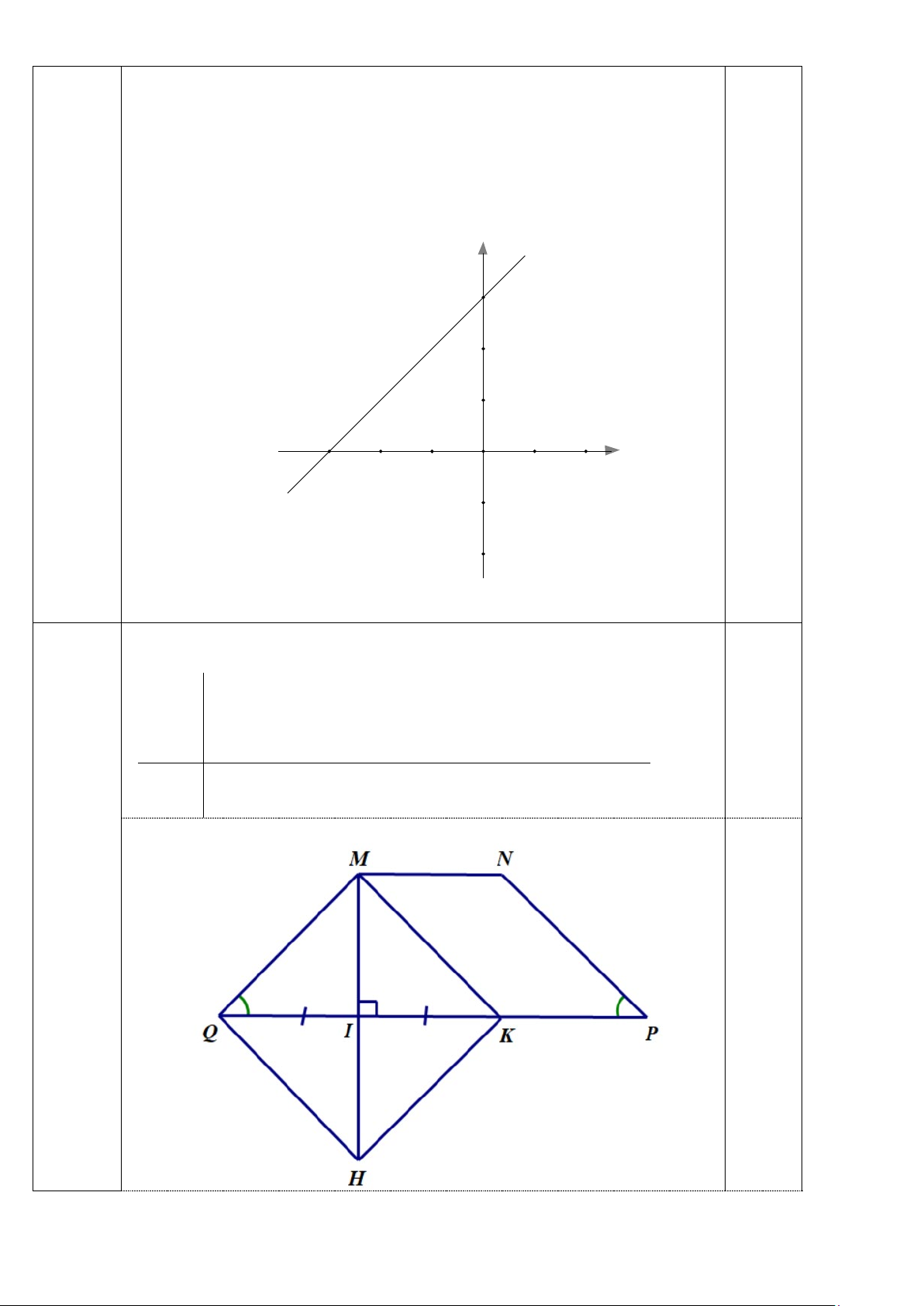
Câu 17 (1,0 điểm). Vẽ đồ thị hàm số y = x + 3. Câu 18 (1,5 điểm)
Cho hình thang cân MNPQ có MN / /PQ ,  =  0
P Q = 45 . Kẻ MI vuông góc với PQ
tại I. Lấy điểm K thuộc cạnh PQ sao cho IK = QI.
a) Giải thích vì sao tứ giác MNPK là hình bình hành.
b) Đường thẳng qua Q và song song với MK cắt MI tại H. Tứ giác MQHK là hình gì? Vì sao? Câu 19 (1,0 điểm)
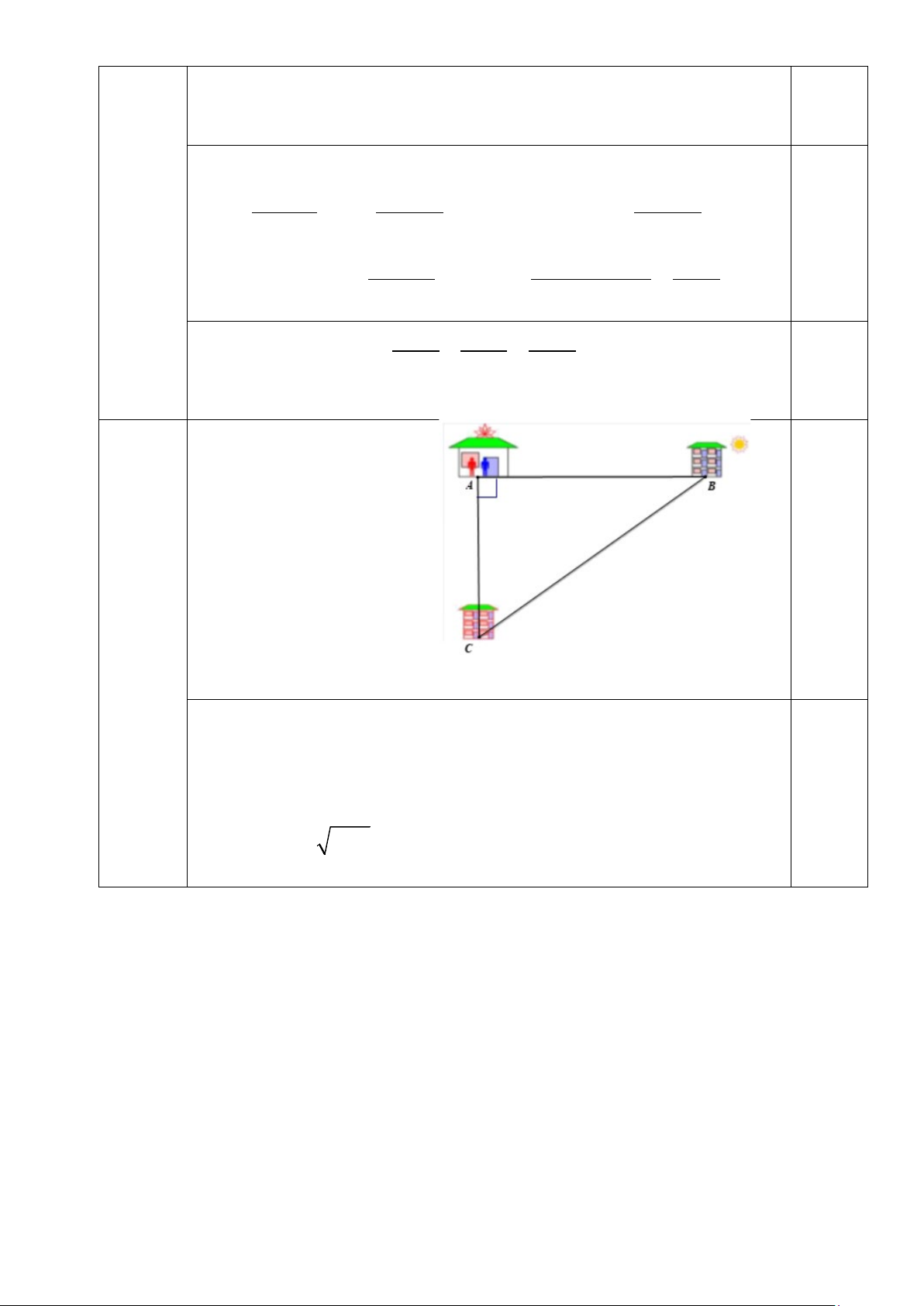
Để sử dụng thẻ dịch vụ học lớp chất lượng cao tại trường X, phụ huynh phải trả phí
thuê dịch vụ theo tháng và một khoản phí ban đầu gọi là phí duy trì thẻ. Một phần đường
thẳng d ở (Hình 6) biểu thị tổng chi phí (đơn vị: triệu đồng) mà phụ huynh đó phải trả để
sử dụng dịch vụ chất lượng cao của nhà trường theo thời gian học tập (đơn vị: tháng). Hình 6
a) Tìm hàm số bậc nhất sao cho đồ thị của hàm số là đường thẳng d.
b) Giao điểm của đường thẳng d với trục Oy trong tình huống này có ý nghĩa gì?
c) Tính tổng chi phí mà phụ huynh phải trả khi sử dụng thẻ dịch vụ học lớp chất
lượng cao của nhà trường trong thời gian 9 tháng. HẾT
Thí sinh không sử dụng tài liệu. Cán bộ coi kiểm tra không giải thích gì thêm. Trang 05/ 0 9 UBND THÀNH PHỐ SƠN LA HƯỚNG DẪN CHẤM
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KIỂM TRA, ĐÁNH GIÁ CUỐI HỌC KÌ I
NĂM HỌC: 2023 – 2024 ĐỀ CHÍNH THỨC Môn: Toán 8
(Hướng dẫn chấm gồm 04 trang)
I. PHẦN TRẮC NGHIỆM ( 3 điểm) Mỗi ý trả lời đúng được 0,25 điểm MÃ ĐỀ 01 Câu 1 2 3 4 5 6 7 8 9 10 11 12 Đáp án C A D B A C D B D C B A MÃ ĐỀ 02 Câu 1 2 3 4 5 6 7 8 9 10 11 12 Đáp B C B A D B C D B D A D án
II. PHẦN TỰ LUẬN (7,0 điểm) Câu Nội dung Thang điểm
Câu 13 Đại lượng y là hàm số của đại lượng x, vì mỗi giá trị của x chỉ xác 0,5 (0,5
định đúng một giá trị của y. điểm)
Câu 14 1) Thực hiện phép tính (1,0 3 5 5 2 3 3 3 5 3 5 5 2 5 2 0, 25
điểm) a) 5x y − y (4x y +1) = 5x y − 5x y − y = − y 4 4 4 3 2 2  1 b) (x 2x y 3xy ) : x − + −  2    0,25 3  1  2  1  2  1 x : x 2x y : x 3xy : x = − − − + −  2 2 2        2 2 = 2
− x + 4xy − 6y 2) Ta có: 2 2
A = 36x + y −12xy = 2 (6x − y) . Thay x = 7; 3
y = − vào biểu thức A, ta được: 0,5 [6.7 – (-3)]2 = 452 = 2025
Vậy giá trị của biểu thức A = 2025 tại x = 7, y = -3. 3 3  x + y  1
Câu 15 Biểu thức M =  − xy . và 2y N = 2 2 (1,5 x + y x −   y x + y điểm) 0,25 Trang 06/ 0 9
a) Điều kiện xác định của các biểu thức M là 2 2
x + y ≠ 0, x − y ≠ 0 0,25
Điều kiện xác định của các biểu thức N x + y ≠ 0 b) Ta có: 3 3  x + y  1 M =  − xy  = ( 2 2 1 .
x − xy + y − xy . 2 2 ) 2 2 x + y x − y x −   y 0,25 2 2 1 2 1 =( − 2 + ). = ( − ) . x − y x xy y x y = 2 2 x − y
(x + y)(x − y) x + y 0,25 c) Ta có: x − y 2y x + y P = M + N = + = =1
x + y x + y x + y 0,5
Vậy giá trị của biểu thức P không phụ thuộc vào giá trị của biến x, y. Câu 16 (0,5 điểm)
Ta có: AB =1,5 km; AC =1,2 km Xét A
∆ BC vuông tại A có: 2 2 2
BC = AB + AC (định lí Pythagore) 2 2 2 BC =1,5 +1,2 0,25 2 BC = 3,69
Suy ra: BC = 3,69 ≈1,9 (km) (vì BC > 0) 0,25
Vậy trường của Bình và An cách nhau khoảng 1,9 km. Trang 07/ 0 9
Câu 17 a) Xét hàm số y = x + 3. (1,0
Với x = 0 thì y = 3, ta được điểm P(0;3) thuộc đồ thị hàm số điểm) 0,25 y = x + 3.
Với y = 0 thì x = 3
− , ta được điểm Q( 3
− ;0) thuộc đồ thị hàm số y = x + 3. 0,25 y y = x + 3 P 3 2 1 0,25 Q O 1 x -3 -2 -1 2 -1 -2
Vậy đồ thị hàm số y = x + 3là đường thẳng đi quan hai điểm P, Q. 0,25 Câu 18
Giả thiết, kết luận 0,25 (1,5
Hình vẽ 0,25 điểm) GT
Hình thang cân MNPQ , MN / /PQ ,  =  0 P Q = 45
MI ⊥ PQ tại I. IK = QI , K ∈ PQ, QH //MK, QH cắt MI tại H. KL
a) MNPK là hình bình hành.
b) MQHK là hình gì? Vì sao? Trang 08/ 0 9 a)Xét tam giác MQ ∆ I và MK ∆ I có:
QI = KI (giả thiết);  =  0
MIQ MIK = 90 (giả thiết); MI cạnh chung. Do đó: MQ ∆ I = MK ∆
I (c.g.c). Suy ra:  = 
MQI MKI (hai góc tương 0,25 ứng). Hay  =  MQP MKQ Mà  = 
MQP NPQ (do MNPQ là hình thang cân). Suy ra:  =  MKQ NPQ . Mà   M ;
KQ NPQ nằm ở vị trí đồng vị, suy
ra: MK//NP (dấu hiệu nhận biết). 0,25
Xét tứ giác MNPK có: MN //PK, MK // NP nên MNPK là hình bình
hành (dấu hiệu nhận biết). b) Xét tam giác Q ∆ IH và K ∆ IM có:  =  0
MIQ MIK = 90 (giả thiết); QI = KI (giả thiết);  =  HQI MKI (hai
góc so le trong, QH//MK). Do đó: Q ∆ IH = K
∆ IM (g.c.g). Suy ra: IH = IM (hai cạnh tương ứng).
Xét tứ giác MQHK có hai đường chéo MH và QK cắt nhau tại trung 0,25
điểm I của mỗi đường nên MQHK là hình bình hành (dấu hiệu nhận biết).
Mặt khác, tam giác MQK có  =  0
MQK MKQ = 45 , MQ = MK nên
tam giác MQK vuông cân tại M, hay  0 QMK = 90 Hình bình hành MQHK có  0
QMK = 90 nên MQHK là hình chữ nhật (dấu hiệu nhân biết) 0,25
Hình chữ nhật MQHK có MQ = MK nên MQHK là hình vuông (dấu hiệu nhận biết)
Câu 19 a) Giả sử hàm số y = ax + b (a ≠ 0)có đồ thị của hàm số là đường (1,0 thẳng d. điểm)
Do đường thẳng d đi qua điểm (0; 1) nên ta có: 1 = a. 0 + b. Suy ra: b = 1 (1)
Do đường thẳng d cũng đi qua điểm (2; 3) nên ta có: 3 = a.2 + b (2)
Từ (1) và (2) suy ra: a = 1 (thỏa mãn điều kiện)
Vậy hàm số y = x + 1 có đồ thị hàm số là đường thẳng d. 0,25
b) Giao điểm của đường thẳng d với trục Oy trong tình huống này 0,25
có nghĩa là phụ huynh phải trả phí duy trì thẻ 1 triệu đồng.
c) Tổng chi phí mà phụ huynh phải trả khi học lớp chất lượng cao 0,5
trong thời gian 9 tháng là: 9 + 1 = 10 (triệu đồng)
(Lưu ý: HS có cách làm khác đúng được tính điểm tương đương) Trang 09/ 0 9