Đề cuối học kỳ 1 Toán 10 năm 2022 – 2023 trường THPT Hùng Vương – Quảng Nam

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 10 đề kiểm tra đánh giá cuối học kỳ 1 môn Toán 10 năm học 2022 – 2023 trường THPT Hùng Vương, tỉnh Quảng Nam, mời bạn đọc đón xem

20 10 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK1 Toán 10

Môn: Toán 10

Thông tin:

11 trang 8 tháng trước

Tác giả:

Profile Thanh Tâm
SỞ GD-ĐT QUẢNG NAM
TRƯỜNG THPT HÙNG VƯƠNG
KIỂM TRA CUỐI KỲ I NĂM HỌC 2022-2023
Môn: TOÁN – KHỐI 10
Thời gian: 60 phút (không kể thời gian giao đề)
MÃ ĐỀ 101
(Đề này gồm có 2 trang)
I - PHẦN TRẮC NGHIỆM (5.0 điểm)
Câu 1. Cho hình bình hành
ABCD
. Vectơ tổng
CB CD+
bằng
A.
CA
. B.
BD
. C.
. D.
DB
.
Câu 2. Trong mặt phẳng
Oxy
cho
( ) ( )
4;2 , 1; 5 .AB−
Tìm tọa độ trọng tâm G của tam giác
OAB
.
A.
51
;
33
G



. B.
5
;2
3
G



. C.
( )
1;3G
. D.
5
;1
3
G

−


.
Câu 3. Cho hai vectơ
(2;3)u =
,
(0;5)v =
. Tích
.uv
bằng
A.
11.
B.
10.−
C.
15.
D.
2.−
Câu 4. Trong mặt phẳng tọa độ
,Oxy
cho hai vectơ
( )
4;3a =
và
( )
1;7b =
. Góc
giữa hai vectơ
a
và
b
bằng
A.
O
90 .
=
B.
O
45 .
=
C.
O
60 .
=
D.
O
30 .
=
Câu 5. Cho tam giác ABC. Khẳng định nào sau đây đúng?
A.
1
. .sin
2
S AC AB A=
. B.
1
. .sin
2
S BC AB A=
. C.
1
. .sin
2
S AC AB B=
. D.
1
. .sin
2
S BC AB C=
.
Câu 6. Cho hình bình hành
MNPQ
. Khẳng định nào sau đây sai?
A.
MN PQ=
. B.
MQ PN=
. C.
MN QP=
. D.
MQ PN=
.
Câu 7. Cho hình bình hành MNPQ. Mệnh đề nào dưới đây đúng?
A.
MN MQ MP+=
. B.
MN MQ PQ+=
. C.
MN MQ NP+=
. D.
MN MQ NQ+=
.
Câu 8. Cho đoạn thẳng
AB
. Điều kiện cần và đủ để điểm
I
là trung điểm của đoạn thẳng
AB
là
A.
IA IB=
. B.
AI BI=
. C.
2AB AI=
. D.
0IA IB+=
.
Câu 9. Trên mặt phẳng với hệ tọa độ
Oxy
cho vectơ
2022 2023u i j=−
. Tọa độ của vectơ
u
là
A.
( )
2022; 2023u = − −
. B.
( )
2022;2023u =
. C.
( )
2022; 2023u =−
. D.
( )
2022;2023u =−
.
Câu 10. Trong mặt phẳng với hệ tọa độ Oxy, cho
( ) ( )
10;0 , 0;2022AB
. Tọa độ trung điểm I của đoạn
thẳng AB là
A.
( )
5; 1011I −
. B.
( )
5;1011I −
. C.
( )
10;2022I −
. D.
( )
5;1011I
.
Câu 11. Kí hiệu nào sau đây dùng để viết đúng mệnh đề “
2
không phải là số hữu tỉ”
A.
2
. B.
2
. C.
2
. D.
2
.
Câu 12. Cho tập hợp
1; 2; 3; 4A =
. Số tập hợp con gồm hai phần tử của tập hợp A là
A. 4. B. 8. C. 16. D. 6.
Câu 13. Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn
,xy
?
A.
2
3 5 .xy−
B.
2
3 4.xy+
C.
2 5 0.x xy−
D.
3 0.x y z xyz+ + −
Câu 14. Miền nghiệm của hệ bất phương trình
10
23
0
13
2
22
xy
x
y
x
+ −
+ −
chứa điểm nào trong các điểm sau
đây?
A.
( )
.0;0O
B.
( )
.1;1N
C.
( )
.2;1M
D.
( )
.5;1P
Câu 15. Cho
và
là hai góc khác nhau và bù nhau, trong các đẳng thức sau đây đẳng thức nào
sai?
A.
sin sin

=
. B.
cos cos

=−
. C.
tan tan

=−
. D.
cot cot

=
.
II - PHẦN TỰ LUẬN (5.0 điểm)
Câu 1. (1 điểm). Cho hai tập hợp
1;4A=
và
( )
3;6B =
.
)a
Dùng các ký hiệu đoạn, nửa khoảng, khoảng để biểu diễn tập
A
và tập
B
trên từng trục số.
)b
Xác định các tập hợp
AB
;
.AB
Câu 2. (1 điểm). Cho tam giác
ABC
. Xác định vị trí điểm M trong mặt phẳng chứa
ABC
sao cho
MA MC MB=−
(có vẽ hình minh họa vị trí điểm M).
Câu 3. (1 điểm). Cho tam giác
ABC
có các cạnh
6b cm=
,
7c cm=
và
3
cos
4
A =
.
)a
Tính
sin .A
)b
Tính diện tích tam giác
.ABC
Câu 4. (1 điểm). Cho tứ giác
ABCD
. Chứng minh rằng
.AC BD BC AD+ = +
Câu 5. (1 điểm). Trong mặt phẳng với hệ tọa độ
Oxy
cho
( ) ( )
1;2 ; 3;4AB−
và
( )
0; 1 .C −
Tìm tọa độ
điểm
D
là hình chiếu vuông góc của điểm
A
trên đường thẳng đi qua hai điểm
B
và
C
?
………….…….Hết……………
SỞ GD-ĐT QUẢNG NAM
TRƯỜNG THPT HÙNG VƯƠNG
KIỂM TRA CUỐI KỲ I NĂM HỌC 2022-2023
Môn: TOÁN – KHỐI 10
Thời gian: 60 phút (không kể thời gian giao đề)
MÃ ĐỀ 102
(Đề này gồm có 2 trang)
I - PHẦN TRẮC NGHIỆM (5.0 điểm)
Câu 1. Cho hình bình hành
ABCD
. Vectơ tổng
BA BC+
bằng
A.
CA
. B.
BD
. C.
. D.
DB
.
Câu 2. Trong mặt phẳng
Oxy
cho
( ) ( )
4;2 , 1;4 .AB
Tìm tọa độ trọng tâm G của tam giác
OAB
.
A.
51
;
33
G



. B.
5
;2
3
G



. C.
( )
1;3G
. D.
5
;1
3
G

−


.
Câu 3. Cho hai vectơ
(2;3)u =
,
( 5;0)v =−
. Tích
.uv
bằng
A.
11.
B.
10.−
C.
15.
D.
2.−
Câu 4. Trong mặt phẳng tọa độ
,Oxy
cho hai vectơ
( )
4;3a =
và
( )
1;7b =
. Góc
giữa hai vectơ
a
và
b
bằng
A.
O
90 .
=
B.
O
60 .
=
C.
O
45 .
=
D.
O
30 .
=
Câu 5. Cho tam giác ABC. Khẳng định nào sau đây đúng?
A.
1
. .sin
2
S BC AB C=
. B.
1
. .sin
2
S BC AB A=
. C.
1
. .sin
2
S AC AB B=
. D.
1
. .sin
2
S AC AB A=
.
Câu 6. Cho hình bình hành
MNPQ
. Khẳng định nào sau đây sai?
A.
MN PQ=
. B.
MQ PN=
. C.
MN QP=
. D.
MQ PN=
.
Câu 7. Cho hình bình hành MNPQ. Mệnh đề nào dưới đây đúng?
A.
MN MQ MP+=
. B.
MN MQ PQ+=
. C.
MN MQ NP+=
. D.
MN MQ NQ+=
.
Câu 8. Cho đoạn thẳng
AB
. Điều kiện cần và đủ để điểm
I
là trung điểm của đoạn thẳng
AB
là
A.
IA IB=
. B.
AI BI=
. C.
2AB AI=
. D.
0IA IB+=
.
Câu 9. Trên mặt phẳng với hệ tọa độ
Oxy
cho vectơ
2022 2023u i j= − +
. Tọa độ của vectơ
u
là
A.
( )
2022; 2023u = − −
. B.
( )
2022;2023u =
. C.
( )
2022; 2023u =−
. D.
( )
2022;2023u =−
.
Câu 10. Trong mặt phẳng với hệ tọa độ Oxy, cho
( ) ( )
10;0 , 0;2022AB−
. Tọa độ trung điểm I của đoạn
thẳng AB là
A.
( )
5; 1011I −
. B.
( )
5;1011I −
. C.
( )
10;2022I −
. D.
( )
5;1011I
.
Câu 11. Kí hiệu nào sau đây dùng để viết đúng mệnh đề “
2
là số hữu tỉ”
A.
2
. B.
2
. C.
2
. D.
2
.
Câu 12. Cho tập hợp
1; 2;3; 4A =
. Số tập hợp con gồm hai phần tử của tập hợp A là
A. 4. B. 8. C. 16. D. 6.
Câu 13. Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn
,xy
?
A.
2 5 0.x xy−
B.
2
3 4.xy+
C.
2
2 5 3 .xy−
D.
3 0.x y z xyz+ − +
Câu 14. Miền nghiệm của hệ bất phương trình
10
23
0
13
2
22
xy
x
y
x
+ −
+ −
chứa điểm nào trong các điểm sau đây?
A.
( )
.0;0O
B.
( )
.2;1M
C.
( )
.1;1N
D.
( )
.5;1P
Câu 15. Cho
và
là hai góc khác nhau và bù nhau, trong các đẳng thức sau đây đẳng thức nào sai?
A.
sin sin

=
. B.
cos cos

=−
. C.
tan tan

=
. D.
cot cot

=−
.
II - PHẦN TỰ LUẬN (5.0 điểm)
Câu 1. (1 điểm). Cho hai tập hợp
1;4A=
và
( )
2;6B =
.
)a
Dùng các ký hiệu đoạn, nửa khoảng, khoảng để biểu diễn tập
A
và tập
B
trên từng trục số.
)b
Xác định các tập hợp
AB
;
.AB
Câu 2. (1 điểm). Cho tam giác
ABC
. Xác định vị trí điểm M trong mặt phẳng chứa
ABC
sao cho
MA MB MC=−
(có vẽ hình minh họa vị trí điểm M).
Câu 3. (1 điểm). Cho tam giác
ABC
có các cạnh
6b cm=
,
7c cm=
và
3
cos
4
A =
.
)a
Tính
sin .A
)b
Tính diện tích tam giác
.ABC
Câu 4. (1 điểm). Cho tứ giác
ABCD
. Chứng minh rằng
.AC BD BC AD+ = +
Câu 5. (1 điểm). Trong mặt phẳng với hệ tọa độ
Oxy
cho
( ) ( )
1;2 ; 3;4AB−
và
( )
0; 1 .C −
Tìm tọa độ
điểm
D
là hình chiếu vuông góc của điểm
A
trên đường thẳng đi qua hai điểm
B
và
C
?
………….…….Hết……………
SỞ GD-ĐT QUẢNG NAM
TRƯỜNG THPT HÙNG VƯƠNG
KIỂM TRA CUỐI KỲ I NĂM HỌC 2022-2023
Môn: TOÁN – KHỐI 10
Thời gian: 60 phút (không kể thời gian giao đề)
MÃ ĐỀ 103
(Đề này gồm có 2 trang)
I - PHẦN TRẮC NGHIỆM (5.0 điểm)
Câu 1. Kí hiệu nào sau đây dùng để viết đúng mệnh đề “
2
không phải là số hữu tỉ”
A.
2
. B.
2
. C.
2
. D.
2
.
Câu 2. Cho hai vectơ
(2;3)u =
,
(0;5)v =
. Tích
.uv
bằng
A.
11.
B.
10.−
C.
15.
D.
2.−
Câu 3. Cho tập hợp
1; 2;3; 4A =
. Số tập hợp con gồm hai phần tử của tập hợp A là
A.4. B. 8. C. 6. D. 16.
Câu 4. Trong mặt phẳng tọa độ
,Oxy
cho hai vectơ
( )
4;3a =
và
( )
1;7b =
. Góc
giữa hai vectơ
a
và
b
bằng
A.
O
45 .
=
B.
O
90 .
=
C.
O
60 .
=
D.
O
30 .
=
Câu 5. Cho hình bình hành
MNPQ
. Khẳng định nào sau đây sai?
A.
MN PQ=
. B.
MN QP=
. C.
MQ PN=
. D.
MQ PN=
.
Câu 6. Trong mặt phẳng với hệ tọa độ Oxy, cho
( ) ( )
10;0 , 0;2022AB
. Tọa độ trung điểm I của đoạn
thẳng AB là
A.
( )
5; 1011I −
. B.
( )
5;1011I
. C.
( )
10;2022I −
. D.
( )
5;1011I −
.
Câu 7. Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn
,xy
?
A.
2
3 5 .xy−
B.
2
3 4.xy+
C.
2 5 0.x xy−
D.
3 0.x y z xyz+ + −
Câu 8. Cho hình bình hành
ABCD
. Vectơ tổng
CB CD+
bằng
A.
CA
. B.
BD
. C.
. D.
DB
.
Câu 9. Cho hình bình hành MNPQ. Mệnh đề nào dưới đây đúng?
A.
MN MQ NQ+=
. B.
MN MQ PQ+=
. C.
MN MQ NP+=
. D.
MN MQ MP+=
.
Câu 10. Trong mặt phẳng
Oxy
cho
( ) ( )
4;2 , 1; 5 .AB−
Tìm tọa độ trọng tâm G của tam giác
OAB
.
A.
51
;
33
G



. B.
5
;2
3
G



. C.
5
;1
3
G

−


. D.
( )
1;3G
.
Câu 11. Miền nghiệm của hệ bất phương trình
10
23
0
13
2
22
xy
x
y
x
+ −
+ −
chứa điểm nào trong các điểm sau
đây?
A.
( )
.0;0O
B.
( )
.1;1N
C.
( )
.2;1M
D.
( )
.5;1P
Câu 12. Cho đoạn thẳng
AB
. Điều kiện cần và đủ để điểm
I
là trung điểm của đoạn thẳng
AB
là
A.
IA IB=
. B.
AI BI=
. C.
2AB AI=
. D.
0IA IB+=
.
Câu 13. Cho tam giác ABC. Khẳng định nào sau đây đúng?
A.
1
. .sin
2
S AC AB A=
. B.
1
. .sin
2
S BC AB A=
. C.
1
. .sin
2
S AC AB B=
. D.
1
. .sin
2
S BC AB C=
.
Câu 14. Trên mặt phẳng với hệ tọa độ
Oxy
cho vectơ
2022 2023u i j=−
. Tọa độ của vectơ
u
là
A.
( )
2022; 2023u = − −
. B.
( )
2022;2023u =
. C.
( )
2022; 2023u =−
. D.
( )
2022;2023u =−
.
Câu 15. Cho
và
là hai góc khác nhau và bù nhau, trong các đẳng thức sau đây đẳng thức nào
sai?
A.
sin sin

=
. B.
cot cot

=
. C.
tan tan

=−
. D.
cos cos

=−
.
II - PHẦN TỰ LUẬN (5.0 điểm)
Câu 1. (1 điểm). Cho hai tập hợp
1;4A =
và
( )
3;6B =
.
)a
Dùng các ký hiệu đoạn, nửa khoảng, khoảng để biểu diễn tập
A
và tập
B
trên từng trục số.
)b
Xác định các tập hợp
AB
;
.AB
Câu 2. (1 điểm). Cho tam giác
ABC
. Xác định vị trí điểm M trong mặt phẳng chứa
ABC
sao cho
MA MC MB=−
(có vẽ hình minh họa vị trí điểm M).
Câu 3. (1 điểm). Cho tam giác
ABC
có các cạnh
6b cm=
,
7c cm=
và
3
cos
4
A =
.
)a
Tính
sin .A
)b
Tính diện tích tam giác
.ABC
Câu 4. (1 điểm). Cho tứ giác
ABCD
. Chứng minh rằng
.AC BD BC AD+ = +
Câu 5. (1 điểm). Trong mặt phẳng với hệ tọa độ
Oxy
cho
( ) ( )
1;2 ; 3;4AB−
và
( )
0; 1 .C −
Tìm tọa độ
điểm
D
là hình chiếu vuông góc của điểm
A
trên đường thẳng đi qua hai điểm
B
và
C
?
……….…….Hết……………
SỞ GD-ĐT QUẢNG NAM
TRƯỜNG THPT HÙNG VƯƠNG
KIỂM TRA CUỐI KỲ I NĂM HỌC 2022-2023
Môn: TOÁN – KHỐI 10
Thời gian: 60 phút (không kể thời gian giao đề)
MÃ ĐỀ 104
(Đề này gồm có 2 trang)
I - PHẦN TRẮC NGHIỆM (5.0 điểm)
Câu 1. Cho tập hợp
1; 2;3; 4A =
. Số tập hợp con gồm hai phần tử của tập hợp A là
A. 4. B. 8. C. 16. D. 6.
Câu 2. Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn
,xy
?
A.
2 5 0.x xy−
B.
2
3 4.xy+
C.
2
2 5 3 .xy−
D.
3 0.x y z xyz+ − +
Câu 3. Cho hình bình hành
ABCD
. Vectơ tổng
BA BC+
bằng
A.
CA
. B.
BD
. C.
. D.
DB
.
Câu 4. Cho hai vectơ
(2;3)u =
,
( 5;0)v =−
. Tích
.uv
bằng
A.
11.
B.
10.−
C.
15.
D.
2.−
Câu 5. Cho tam giác ABC. Khẳng định nào sau đây đúng?
A.
1
. .sin
2
S BC AB C=
. B.
1
. .sin
2
S BC AB A=
. C.
1
. .sin
2
S AC AB B=
. D.
1
. .sin
2
S AC AB A=
.
Câu 6. Trong mặt phẳng với hệ tọa độ Oxy, cho
( ) ( )
10;0 , 0;2022AB−
. Tọa độ trung điểm I của đoạn
thẳng AB là
A.
( )
5; 1011I −
. B.
( )
5;1011I −
. C.
( )
10;2022I −
. D.
( )
5;1011I
.
Câu 7. Cho hình bình hành
MNPQ
. Khẳng định nào sau đây sai?
A.
MN PQ=
. B.
MQ PN=
. C.
MN QP=
. D.
MQ PN=
.
Câu 8. Trong mặt phẳng
Oxy
cho
( ) ( )
4;2 , 1;4 .AB
Tìm tọa độ trọng tâm G của tam giác
OAB
.
A.
51
;
33
G



. B.
5
;2
3
G



. C.
( )
1;3G
. D.
5
;1
3
G

−


.
Câu 9. Cho
và
là hai góc khác nhau và bù nhau, trong các đẳng thức sau đây đẳng thức nào sai?
A.
sin sin

=
. B.
cos cos

=−
. C.
tan tan

=
. D.
cot cot

=−
.
Câu 10. Cho hình bình hành MNPQ. Mệnh đề nào dưới đây đúng?
A.
MN MQ MP+=
. B.
MN MQ PQ+=
. C.
MN MQ NP+=
. D.
MN MQ NQ+=
.
Câu 11. Trên mặt phẳng với hệ tọa độ
Oxy
cho vectơ
2022 2023u i j= − +
. Tọa độ của vectơ
u
là
A.
( )
2022; 2023u = − −
. B.
( )
2022;2023u =
. C.
( )
2022; 2023u =−
. D.
( )
2022;2023u =−
.
Câu 12. Trong mặt phẳng tọa độ
,Oxy
cho hai vectơ
( )
4;3a =
và
( )
1;7b =
. Góc
giữa hai vectơ
a
và
b
bằng
A.
O
90 .
=
B.
O
60 .
=
C.
O
45 .
=
D.
O
30 .
=
Câu 13. Kí hiệu nào sau đây dùng để viết đúng mệnh đề “
2
là số hữu tỉ”
A.
2
. B.
2
. C.
2
. D.
2
.
Câu 14. Cho đoạn thẳng
AB
. Điều kiện cần và đủ để điểm
I
là trung điểm của đoạn thẳng
AB
là
A.
IA IB=
. B.
AI BI=
. C.
2AB AI=
. D.
0IA IB+=
.
Câu 15. Miền nghiệm của hệ bất phương trình
10
23
0
13
2
22
xy
x
y
x
+ −
+ −
chứa điểm nào trong các điểm sau đây?
A.
( )
.0;0O
B.
( )
.2;1M
C.
( )
.1;1N
D.
( )
.5;1P
II - PHẦN TỰ LUẬN (5.0 điểm)
Câu 1. (1 điểm). Cho hai tập hợp
1;4A =
và
( )
2;6B =
.
)a
Dùng các ký hiệu đoạn, nửa khoảng, khoảng để biểu diễn tập
A
và tập
B
trên từng trục số.
)b
Xác định các tập hợp
AB
;
.AB
Câu 2. (1 điểm). Cho tam giác
ABC
. Xác định vị trí điểm M trong mặt phẳng chứa
ABC
sao cho
MA MB MC=−
(có vẽ hình minh họa vị trí điểm M).
Câu 3. (1 điểm). Cho tam giác
ABC
có các cạnh
6b cm=
,
7c cm=
và
3
cos
4
A =
.
)a
Tính
sin .A
)b
Tính diện tích tam giác
.ABC
Câu 4. (1 điểm). Cho tứ giác
ABCD
. Chứng minh rằng
.AC BD BC AD+ = +
Câu 5. (1 điểm). Trong mặt phẳng với hệ tọa độ
Oxy
cho
( ) ( )
1;2 ; 3;4AB−
và
( )
0; 1 .C −
Tìm tọa độ
điểm
D
là hình chiếu vuông góc của điểm
A
trên đường thẳng đi qua hai điểm
B
và
C
?
………….…….Hết……………
ĐÁP ÁN TOÁN 10 CUỐI KỲ 1 NĂM HỌC 2022-2023
TRẮC NGHIỆM:
TỰ LUẬN:
MÃ
NỘI DUNG CÂU HỎI
ĐIỂM
(101
và
103)
Câu 1. (1 điểm). Cho hai tập hợp
1;4A =
và
( )
3;6B =
.
)a
Dùng các ký hiệu đoạn, nửa khoảng, khoảng để biểu diễn tập
A
và tập
B
trên từng trục số.
1)a
Mỗi cách biểu diễn đúng được 0,25
1)b
Xác định các tập hợp;
;.A B A B
1)b
)
1;6AB=
và
(
3;4AB=
0,5
0,5
(101
và
103)
Câu 2. (1 điểm). Cho tam giác
ABC
. Xác định vị trí điểm M trong mặt phẳng chứa
ABC
sao cho
MA MC MB=−
(có vẽ hình minh họa vị trí điểm M).
Biến đổi:
MA MC MB MA BC= − =
hoặc
AM CB=
Dựng đúng điểm M (như hình vẽ)
0,5
0,5
(102
và
104)
Câu 1. (1 điểm). Cho hai tập hợp
1;4A =
và
( )
2;6B =
.
)a
Dùng các ký hiệu đoạn, nửa khoảng, khoảng để biểu diễn tập
A
và tập
B
trên từng trục số.
1)a
Mỗi cách biểu diễn đúng được 0,25
1)b
Xác định các tập hợp;
;.A B A B
1)b
)
1;6AB=
và
(
2;4AB=
0,5
0,5
(102
và
104)
Câu 2. (1 điểm). Cho tam giác
ABC
. Xác định vị trí điểm M trong mặt phẳng chứa
ABC
sao cho
MA MB MC=−
(có vẽ hình minh họa vị trí điểm M).
Biến đổi:
MA MB MC MA CB= − =
hoặc
AM BC=
Dựng đúng điểm M (hình vẽ)
0,5
0,5
Câu
Mã 101
Mã 102
Mã 103
Mã 104
1
A
B
B
D
2
D
B
C
C
3
C
B
C
B
4
B
C
A
B
5
A
D
C
D
6
B
B
B
B
7
A
A
A
B
8
D
D
A
B
9
C
D
D
C
10
D
B
C
A
11
C
D
C
D
12
D
D
D
C
13
A
C
A
D
14
C
B
C
D
15
D
C
B
B
A
B
C
M
A
M
C
B
(101
102
103
và
104)
Câu 3. (1 điểm). Cho tam giác
ABC
có các cạnh
6b cm=
,
7c cm=
và
3
cos
4
A =
.
)a
Tính
sin .A
)b
Tính diện tích tam giác
.ABC
)a
Tính
2
0,25
sin 1 cosAA=−
0,25
9 7 7
1
16 16 4
= − = =
)b
Tính diện tích tam giác
.ABC
( )
2
0,25
0,25
1 1 7 21 7
. .sin .6.7.
2 2 4 4
ABC
S bc A cm
= = =
Lưu ý: Học sinh có thể tích cạnh
a
và dung CT Hêrong để tính diện tích tam giác.
2 2 2 2 2
3
2 cosA 6 7 2.6.7. 22 22( )
4
a b c bc a cm= + − = + − = =
6 7 22 13 22
22
p
+ + +
= =
2
0,25
0,25
21 7
( )( )( ) ( )
4
S p p a p b p c cm = − − − =
;
0,5
0,5
0,25
0,25
0,5
(101
102
103
và
104)
Câu 4. (1 điểm). Cho tứ giác
ABCD
. Chứng minh rằng
.AC BD BC AD+ = +
C1:
0,25 0,25 0,25
0,25
( ) ( ) 0VT AC BD AD DC BC CD AD BC DC CD AD BC AD BC VP= + = + + + = + + + = + + = + =
C2: (biến đổi tương đương)
( ) ( )
0,25
0,25
0,5
0 0,( )AC BD BC AD AC AD BD BC DC CD doi nhau dpcm+ = + − + − = + =
1,0
1,0
(101
102
103
và
104)
Câu 5. (1 điểm). Trong mặt phẳng với hệ tọa độ
Oxy
cho
( ) ( )
1;2 ; 3;4AB−
và
( )
0; 1 .C −
Tìm tọa độ điểm
D
là hình chiếu vuông góc của điểm
A
trên đường thẳng đi qua hai điểm
B
và
C
?
( )
( )
0,5
0,25
0,25
18
. 0 *
3 5 7(***)
17
5 3 3 13
; **
17
x
AD BC
xy
ycbt
xy
CD BCcung phuong
y
=−
=
− = −

+ = −

=
trong đó:
( )
( 1; 2)
3; 5
( ; 1)
AD x y
BC
CD x y
= − −
=−
=+
Lưu ý: Nếu làm được (*) và (***) thì cho 0,25.
1,0
| 1/11
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GD-ĐT QUẢNG NAM
KIỂM TRA CUỐI KỲ I NĂM HỌC 2022-2023
TRƯỜNG THPT HÙNG VƯƠNG
Môn: TOÁN – KHỐI 10
Thời gian: 60 phút (không kể thời gian giao đề) MÃ ĐỀ 101
(Đề này gồm có 2 trang)
I - PHẦN TRẮC NGHIỆM (5.0 điểm)
Câu 1. Cho hình bình hành ABCD. Vectơ tổng CB +CD bằng A. CA . B. BD . C. AC . D. DB .
Câu 2. Trong mặt phẳng Oxy cho A(4;2), B(1; 5
− ). Tìm tọa độ trọng tâm G của tam giác OAB .  5 1   5   5  A. G ;   . B. G ; 2   . C. G(1; ) 3 . D. G ; 1 −   .  3 3  3   3 
Câu 3. Cho hai vectơ u = (2;3) , v = (0;5) . Tích u.v bằng A. 11. B. 10. − C. 15. D. 2. −
Câu 4. Trong mặt phẳng tọa độ Oxy, cho hai vectơ a = (4; )
3 và b = (1;7) . Góc  giữa hai vectơ a và b bằng A. O  = 90 . B. O  = 45 . C. O  = 60 . D. O  = 30 .
Câu 5. Cho tam giác ABC. Khẳng định nào sau đây đúng? 1 1 1 1 A. S = AC.A .
B sin A . B. S = BC.A . B sin A . C. S = AC.A .
B sin B . D. S = BC.A . B sin C . 2 2 2 2
Câu 6. Cho hình bình hành MNPQ . Khẳng định nào sau đây sai?
A. MN = PQ .
B. MQ = PN .
C. MN = QP .
D. MQ = PN .
Câu 7. Cho hình bình hành MNPQ. Mệnh đề nào dưới đây đúng?
A. MN + MQ = MP . B. MN + MQ = PQ .
C. MN + MQ = NP . D. MN + MQ = NQ .
Câu 8. Cho đoạn thẳng AB . Điều kiện cần và đủ để điểm I là trung điểm của đoạn thẳng AB là
A. IA = IB .
B. AI = BI .
C. AB = 2AI .
D. IA + IB = 0 .
Câu 9. Trên mặt phẳng với hệ tọa độ Oxy cho vectơ u = 2022i − 2023 j . Tọa độ của vectơ u là A. u = ( 2 − 022; 2 − 02 )
3 . B. u = (2022;202 )
3 . C. u = (2022; 2 − 02 ) 3 . D. u = ( 2 − 022;202 ) 3 .
Câu 10. Trong mặt phẳng với hệ tọa độ Oxy, cho A(10;0), B(0;2022) . Tọa độ trung điểm I của đoạn thẳng AB là A. I (5; 1 − 01 ) 1 . B. I ( 5 − ;101 ) 1 . C. I ( 1 − 0;2022) . D. I (5;101 ) 1 .
Câu 11. Kí hiệu nào sau đây dùng để viết đúng mệnh đề “ 2 không phải là số hữu tỉ” A. 2  . B. 2  . C. 2  . D. 2  .
Câu 12. Cho tập hợp A = 1; 2; 3; 
4 . Số tập hợp con gồm hai phần tử của tập hợp A là A. 4. B. 8. C. 16. D. 6.
Câu 13. Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn , x y ? A. 2 3x − y  5 . 2 +  −  + + − 
B. x 3y 4. C. 2x 5xy 0.
D. x 3y z xyz 0. x y + −1 0 2 3 
Câu 14. Miền nghiệm của hệ bất phương trình x  0
chứa điểm nào trong các điểm sau  1 3yx + −  2  2 2 đây?
A. O(0;0). B. N (1; ) 1 . C. M (2; ) 1 . D. P(5; ) 1 .
Câu 15. Cho  và  là hai góc khác nhau và bù nhau, trong các đẳng thức sau đây đẳng thức nào sai?
A. sin = sin  .
B. cos = − cos  . C. tan = − tan  .
D. cot = cot  .
II - PHẦN TỰ LUẬN (5.0 điểm)
Câu 1. (1 điểm). Cho hai tập hợp A = 1;  4 và B = (3;6) .
a) Dùng các ký hiệu đoạn, nửa khoảng, khoảng để biểu diễn tập A và tập B trên từng trục số. )
b Xác định các tập hợp A B ; A . B
Câu 2. (1 điểm). Cho tam giác ABC . Xác định vị trí điểm M trong mặt phẳng chứa ABC  sao cho
MA = MC − MB (có vẽ hình minh họa vị trí điểm M). 3
Câu 3. (1 điểm). Cho tam giác ABC có các cạnh b = 6cm , c = 7cm và cos A = . 4 a) Tính sin . A )
b Tính diện tích tam giác . ABC
Câu 4. (1 điểm). Cho tứ giác ABCD . Chứng minh rằng AC + BD = BC + A . D
Câu 5. (1 điểm). Trong mặt phẳng với hệ tọa độ Oxy cho A(1;2); B( 3 − ;4) và C(0;− ) 1 . Tìm tọa độ
điểm D là hình chiếu vuông góc của điểm A trên đường thẳng đi qua hai điểm B và C ?
………….…….Hết……………
SỞ GD-ĐT QUẢNG NAM
KIỂM TRA CUỐI KỲ I NĂM HỌC 2022-2023
TRƯỜNG THPT HÙNG VƯƠNG
Môn: TOÁN – KHỐI 10
Thời gian: 60 phút (không kể thời gian giao đề) MÃ ĐỀ 102
(Đề này gồm có 2 trang)
I - PHẦN TRẮC NGHIỆM (5.0 điểm)
Câu 1. Cho hình bình hành ABCD. Vectơ tổng BA+ BC bằng A. CA . B. BD . C. AC . D. DB .
Câu 2. Trong mặt phẳng Oxy cho A(4;2), B(1;4). Tìm tọa độ trọng tâm G của tam giác OAB .  5 1   5   5  A. G ;   . B. G ; 2   . C. G(1; ) 3 . D. G ; 1 −   .  3 3  3   3 
Câu 3. Cho hai vectơ u = (2;3) , v = ( 5
− ;0) . Tích u.v bằng A. 11. B. 10. − C. 15. D. 2. −
Câu 4. Trong mặt phẳng tọa độ Oxy, cho hai vectơ a = (4; )
3 và b = (1;7) . Góc  giữa hai vectơ a và b bằng A. O  = 90 . B. O  = 60 . C. O  = 45 . D. O  = 30 .
Câu 5. Cho tam giác ABC. Khẳng định nào sau đây đúng? 1 1 1 1 A. S = BC.A .
B sin C . B. S = BC.A . B sin A . C. S = AC.A .
B sin B . D. S = AC.A . B sin A . 2 2 2 2
Câu 6. Cho hình bình hành MNPQ . Khẳng định nào sau đây sai?
A. MN = PQ .
B. MQ = PN .
C. MN = QP .
D. MQ = PN .
Câu 7. Cho hình bình hành MNPQ. Mệnh đề nào dưới đây đúng?
A. MN + MQ = MP . B. MN + MQ = PQ .
C. MN + MQ = NP . D. MN + MQ = NQ .
Câu 8. Cho đoạn thẳng AB . Điều kiện cần và đủ để điểm I là trung điểm của đoạn thẳng AB là
A. IA = IB .
B. AI = BI .
C. AB = 2AI .
D. IA + IB = 0 .
Câu 9. Trên mặt phẳng với hệ tọa độ Oxy cho vectơ u = 2
− 022i + 2023 j . Tọa độ của vectơ u là A. u = ( 2 − 022; 2 − 02 )
3 . B. u = (2022;202 )
3 . C. u = (2022; 2 − 02 ) 3 . D. u = ( 2 − 022;202 ) 3 .
Câu 10. Trong mặt phẳng với hệ tọa độ Oxy, cho A( 1
− 0;0),B(0;2022). Tọa độ trung điểm I của đoạn thẳng AB là A. I (5; 1 − 01 ) 1 . B. I ( 5 − ;101 ) 1 . C. I ( 1 − 0;2022) . D. I (5;101 ) 1 .
Câu 11. Kí hiệu nào sau đây dùng để viết đúng mệnh đề “ 2 là số hữu tỉ” A. 2  . B. 2  . C. 2  . D. 2  .
Câu 12. Cho tập hợp A = 1; 2; 3; 
4 . Số tập hợp con gồm hai phần tử của tập hợp A là A. 4. B. 8. C. 16. D. 6.
Câu 13. Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn , x y ?
A. 2x − 5xy  0. 2 +  2 −  + − +  B. x 3y 4.
C. 2x 5y 3 .
D. x 3y z xyz 0. x y + −1 0 2 3 
Câu 14. Miền nghiệm của hệ bất phương trình x  0
chứa điểm nào trong các điểm sau đây?  1 3yx + −  2  2 2
A. O(0;0). B. M (2; ) 1 . C. N (1; ) 1 . D. P(5; ) 1 .
Câu 15. Cho  và  là hai góc khác nhau và bù nhau, trong các đẳng thức sau đây đẳng thức nào sai?
A. sin = sin  .
B. cos = − cos  . C. tan = tan  . D. cot = −cot  .
II - PHẦN TỰ LUẬN (5.0 điểm)
Câu 1. (1 điểm). Cho hai tập hợp A = 1;  4 và B = (2;6) .
a) Dùng các ký hiệu đoạn, nửa khoảng, khoảng để biểu diễn tập A và tập B trên từng trục số. )
b Xác định các tập hợp A B ; A . B
Câu 2. (1 điểm). Cho tam giác ABC . Xác định vị trí điểm M trong mặt phẳng chứa ABC  sao cho
MA = MB − MC (có vẽ hình minh họa vị trí điểm M). 3
Câu 3. (1 điểm). Cho tam giác ABC có các cạnh b = 6cm , c = 7cm và cos A = . 4 a) Tính sin . A )
b Tính diện tích tam giác . ABC
Câu 4. (1 điểm). Cho tứ giác ABCD . Chứng minh rằng AC + BD = BC + A . D
Câu 5. (1 điểm). Trong mặt phẳng với hệ tọa độ Oxy cho A(1;2); B( 3 − ;4) và C(0;− ) 1 . Tìm tọa độ
điểm D là hình chiếu vuông góc của điểm A trên đường thẳng đi qua hai điểm B và C ?
………….…….Hết……………
SỞ GD-ĐT QUẢNG NAM
KIỂM TRA CUỐI KỲ I NĂM HỌC 2022-2023
TRƯỜNG THPT HÙNG VƯƠNG
Môn: TOÁN – KHỐI 10
Thời gian: 60 phút (không kể thời gian giao đề) MÃ ĐỀ 103
(Đề này gồm có 2 trang)
I - PHẦN TRẮC NGHIỆM (5.0 điểm)
Câu 1. Kí hiệu nào sau đây dùng để viết đúng mệnh đề “ 2 không phải là số hữu tỉ” A. 2  . B. 2  . C. 2  . D. 2  .
Câu 2. Cho hai vectơ u = (2;3) , v = (0;5) . Tích u.v bằng A. 11. B. 10. − C. 15. D. 2. −
Câu 3. Cho tập hợp A = 1; 2; 3; 
4 . Số tập hợp con gồm hai phần tử của tập hợp A là A.4. B. 8. C. 6. D. 16.
Câu 4. Trong mặt phẳng tọa độ Oxy, cho hai vectơ a = (4; )
3 và b = (1;7) . Góc  giữa hai vectơ a và b bằng A. O  = 45 . B. O  = 90 . C. O  = 60 . D. O  = 30 .
Câu 5. Cho hình bình hành MNPQ . Khẳng định nào sau đây sai?
A. MN = PQ .
B. MN = QP .
C. MQ = PN .
D. MQ = PN .
Câu 6. Trong mặt phẳng với hệ tọa độ Oxy, cho A(10;0), B(0;2022) . Tọa độ trung điểm I của đoạn thẳng AB là A. I (5; 1 − 01 ) 1 . B. I (5;101 ) 1 . C. I ( 1 − 0;2022) . D. I ( 5 − ;101 ) 1 .
Câu 7. Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn , x y ? A. 2 3x − y  5 . 2 +  −  + + − 
B. x 3y 4. C. 2x 5xy 0.
D. x 3y z xyz 0.
Câu 8. Cho hình bình hành ABCD. Vectơ tổng CB +CD bằng A. CA . B. BD . C. AC . D. DB .
Câu 9. Cho hình bình hành MNPQ. Mệnh đề nào dưới đây đúng?
A. MN + MQ = NQ . B. MN + MQ = PQ .
C. MN + MQ = NP . D. MN + MQ = MP .
Câu 10. Trong mặt phẳng Oxy cho A(4;2), B(1; 5
− ). Tìm tọa độ trọng tâm G của tam giác OAB.  5 1   5   5  A. G ;   . B. G ; 2   . C. G ; 1 −  . D. G(1; ) 3 .  3 3  3   3   x y + −1 0 2 3 
Câu 11. Miền nghiệm của hệ bất phương trình x  0
chứa điểm nào trong các điểm sau  1 3yx + −  2  2 2 đây?
A. O(0;0). B. N (1; ) 1 . C. M (2; ) 1 . D. P(5; ) 1 .
Câu 12. Cho đoạn thẳng AB . Điều kiện cần và đủ để điểm I là trung điểm của đoạn thẳng AB là
A. IA = IB .
B. AI = BI .
C. AB = 2AI .
D. IA + IB = 0 .
Câu 13. Cho tam giác ABC. Khẳng định nào sau đây đúng? 1 1 1 1 A. S = AC.A .
B sin A . B. S = BC.A . B sin A . C. S = AC.A .
B sin B . D. S = BC.A . B sin C . 2 2 2 2
Câu 14. Trên mặt phẳng với hệ tọa độ Oxy cho vectơ u = 2022i − 2023 j . Tọa độ của vectơ u là A. u = ( 2 − 022; 2 − 02 )
3 . B. u = (2022;202 )
3 . C. u = (2022; 2 − 02 ) 3 . D. u = ( 2 − 022;202 ) 3 .
Câu 15. Cho  và  là hai góc khác nhau và bù nhau, trong các đẳng thức sau đây đẳng thức nào sai?
A. sin = sin  .
B. cot = cot  .
C. tan = − tan  .
D. cos = − cos  .
II - PHẦN TỰ LUẬN (5.0 điểm)
Câu 1. (1 điểm). Cho hai tập hợp A = 1;  4 và B = (3;6) .
a) Dùng các ký hiệu đoạn, nửa khoảng, khoảng để biểu diễn tập A và tập B trên từng trục số. )
b Xác định các tập hợp A B ; A . B
Câu 2. (1 điểm). Cho tam giác ABC . Xác định vị trí điểm M trong mặt phẳng chứa ABC  sao cho
MA = MC − MB (có vẽ hình minh họa vị trí điểm M). 3
Câu 3. (1 điểm). Cho tam giác ABC có các cạnh b = 6cm , c = 7cm và cos A = . 4 a) Tính sin . A )
b Tính diện tích tam giác . ABC
Câu 4. (1 điểm). Cho tứ giác ABCD . Chứng minh rằng AC + BD = BC + A . D
Câu 5. (1 điểm). Trong mặt phẳng với hệ tọa độ Oxy cho A(1;2); B( 3 − ;4) và C(0;− ) 1 . Tìm tọa độ
điểm D là hình chiếu vuông góc của điểm A trên đường thẳng đi qua hai điểm B và C ?
……….…….Hết……………
SỞ GD-ĐT QUẢNG NAM
KIỂM TRA CUỐI KỲ I NĂM HỌC 2022-2023
TRƯỜNG THPT HÙNG VƯƠNG
Môn: TOÁN – KHỐI 10
Thời gian: 60 phút (không kể thời gian giao đề) MÃ ĐỀ 104
(Đề này gồm có 2 trang)
I - PHẦN TRẮC NGHIỆM (5.0 điểm)
Câu 1. Cho tập hợp A = 1; 2; 3; 
4 . Số tập hợp con gồm hai phần tử của tập hợp A là A. 4. B. 8. C. 16. D. 6.
Câu 2. Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn , x y ?
A. 2x − 5xy  0. 2 +  2 −  + − +  B. x 3y 4.
C. 2x 5y 3 . D. x 3y z xyz 0.
Câu 3. Cho hình bình hành ABCD. Vectơ tổng BA+ BC bằng A. CA . B. BD . C. AC . D. DB .
Câu 4. Cho hai vectơ u = (2;3) , v = ( 5
− ;0) . Tích u.v bằng A. 11. B. 10. − C. 15. D. 2. −
Câu 5. Cho tam giác ABC. Khẳng định nào sau đây đúng? 1 1 1 1 A. S = BC.A .
B sin C . B. S = BC.A . B sin A . C. S = AC.A .
B sin B . D. S = AC.A . B sin A . 2 2 2 2
Câu 6. Trong mặt phẳng với hệ tọa độ Oxy, cho A( 1
− 0;0),B(0;2022). Tọa độ trung điểm I của đoạn thẳng AB là A. I (5; 1 − 01 ) 1 . B. I ( 5 − ;101 ) 1 . C. I ( 1 − 0;2022) . D. I (5;101 ) 1 .
Câu 7. Cho hình bình hành MNPQ . Khẳng định nào sau đây sai?
A. MN = PQ .
B. MQ = PN .
C. MN = QP .
D. MQ = PN .
Câu 8. Trong mặt phẳng Oxy cho A(4;2), B(1;4). Tìm tọa độ trọng tâm G của tam giác OAB .  5 1   5   5  A. G ;   . B. G ; 2   . C. G(1; ) 3 . D. G ; 1 −   .  3 3  3   3 
Câu 9. Cho  và  là hai góc khác nhau và bù nhau, trong các đẳng thức sau đây đẳng thức nào sai?
A. sin = sin  .
B. cos = − cos  . C. tan = tan  . D. cot = −cot  .
Câu 10. Cho hình bình hành MNPQ. Mệnh đề nào dưới đây đúng?
A. MN + MQ = MP . B. MN + MQ = PQ .
C. MN + MQ = NP . D. MN + MQ = NQ .
Câu 11. Trên mặt phẳng với hệ tọa độ Oxy cho vectơ u = 2
− 022i + 2023 j . Tọa độ của vectơ u là A. u = ( 2 − 022; 2 − 02 )
3 . B. u = (2022;202 )
3 . C. u = (2022; 2 − 02 ) 3 . D. u = ( 2 − 022;202 ) 3 .
Câu 12. Trong mặt phẳng tọa độ Oxy, cho hai vectơ a = (4; )
3 và b = (1;7) . Góc  giữa hai vectơ a và b bằng A. O  = 90 . B. O  = 60 . C. O  = 45 . D. O  = 30 .
Câu 13. Kí hiệu nào sau đây dùng để viết đúng mệnh đề “ 2 là số hữu tỉ” A. 2  . B. 2  . C. 2  . D. 2  .
Câu 14. Cho đoạn thẳng AB . Điều kiện cần và đủ để điểm I là trung điểm của đoạn thẳng AB là
A. IA = IB .
B. AI = BI .
C. AB = 2AI .
D. IA + IB = 0 . x y + −1 0 2 3 
Câu 15. Miền nghiệm của hệ bất phương trình x  0
chứa điểm nào trong các điểm sau đây?  1 3yx + −  2  2 2
A. O(0;0). B. M (2; ) 1 . C. N (1; ) 1 . D. P(5; ) 1 .
II - PHẦN TỰ LUẬN (5.0 điểm)
Câu 1. (1 điểm). Cho hai tập hợp A = 1;  4 và B = (2;6) .
a) Dùng các ký hiệu đoạn, nửa khoảng, khoảng để biểu diễn tập A và tập B trên từng trục số. )
b Xác định các tập hợp A B ; A . B
Câu 2. (1 điểm). Cho tam giác ABC . Xác định vị trí điểm M trong mặt phẳng chứa ABC  sao cho
MA = MB − MC (có vẽ hình minh họa vị trí điểm M). 3
Câu 3. (1 điểm). Cho tam giác ABC có các cạnh b = 6cm , c = 7cm và cos A = . 4 a) Tính sin . A )
b Tính diện tích tam giác . ABC
Câu 4. (1 điểm). Cho tứ giác ABCD . Chứng minh rằng AC + BD = BC + A . D
Câu 5. (1 điểm). Trong mặt phẳng với hệ tọa độ Oxy cho A(1;2); B( 3 − ;4) và C(0;− ) 1 . Tìm tọa độ
điểm D là hình chiếu vuông góc của điểm A trên đường thẳng đi qua hai điểm B và C ?
………….…….Hết……………
ĐÁP ÁN TOÁN 10 CUỐI KỲ 1 NĂM HỌC 2022-2023 TRẮC NGHIỆM: Câu Mã 101 Mã 102 Mã 103 Mã 104 1 A B B D 2 D B C C 3 C B C B 4 B C A B 5 A D C D 6 B B B B 7 A A A B 8 D D A B 9 C D D C 10 D B C A 11 C D C D 12 D D D C 13 A C A D 14 C B C D 15 D C B B TỰ LUẬN: MÃ NỘI DUNG CÂU HỎI ĐIỂM
Câu 1. (1 điểm). Cho hai tập hợp A = 1;  4 và B = (3;6) .
a) Dùng các ký hiệu đoạn, nửa khoảng, khoảng để biểu diễn tập A và tập B trên từng trục số. (101
1a) Mỗi cách biểu diễn đúng được 0,25 0,5 và
1b) Xác định các tập hợp; A  ; B A  . B 103) 0,5
1b) A B = 1;6) và AB = (3;  4
Câu 2. (1 điểm). Cho tam giác ABC . Xác định vị trí điểm M trong mặt phẳng chứa ABC
(101 sao cho MA = MC − MB (có vẽ hình minh họa vị trí điểm M). M A và 0,5
Biến đổi: MA = MC − MB MA = BC hoặc AM = CB
103) Dựng đúng điểm M (như hình vẽ) 0,5 B C
Câu 1. (1 điểm). Cho hai tập hợp A = 1;  4 và B = (2;6) . (102
a) Dùng các ký hiệu đoạn, nửa khoảng, khoảng để biểu diễn tập A và tập B trên từng trục số. và
1a) Mỗi cách biểu diễn đúng được 0,25 0,5
104) 1b) Xác định các tập hợp; A ; B A  . B 0,5
1b) A B = 1;6) và AB = (2;  4
Câu 2. (1 điểm). Cho tam giác ABC . Xác định vị trí điểm M trong mặt phẳng chứa ABC
(102 sao cho MA = MB − MC (có vẽ hình minh họa vị trí điểm M). A M và 0,5
Biến đổi: MA = MB − MC MA = CB hoặc AM = BC
104) Dựng đúng điểm M (hình vẽ) 0,5 B C 3 = = cos A =
Câu 3. (1 điểm). Cho tam giác ABC có các cạnh b 6cm , c 7cm và . 4 a) Tính sin . A )
b Tính diện tích tam giác . ABC 9 7 7 0,5 a) Tính 2
sin A = 1− cos A = 1− = = 16 16 4 0,25 0,25 )
b Tính diện tích tam giác . ABC 1 1 7 21 7 (101 S = . b . c sin A = .6.7. = cm ABC  ( 2) 0,5 102 2 2 4 4 0,25 0,25
103 Lưu ý: Học sinh có thể tích cạnh a và dung CT Hêrong để tính diện tích tam giác. và 3 2 2 2 2 2
104) a = b + c − 2bccosA = 6 + 7 − 2.6.7. = 22  a = 22(c ) m 4 0,25 6 + 7 + 22 13 + 22  0,25 p = = 2 2 21 7 2  0,5 S =
p( p − a)( p − b)( p − c) = (cm ) ; 4 0,25 0,25
Câu 4. (1 điểm). Cho tứ giác ABCD . Chứng minh rằng AC + BD = BC + A . D (101 C1: 102 1,0
VT = AC + BD = AD + DC + BC + CD = (AD + BC) + (DC + CD) = AD + BC + 0 = AD + BC = VP 103 0,25 0,25 0,25 0,25 và
C2: (biến đổi tương đương)
104) AC + BD = BC + AD  (AC − AD)+(BD − BC) = 0  DC +CD = 0,(doi nhau)  dpcm 1,0 0,25 0,25 0,5
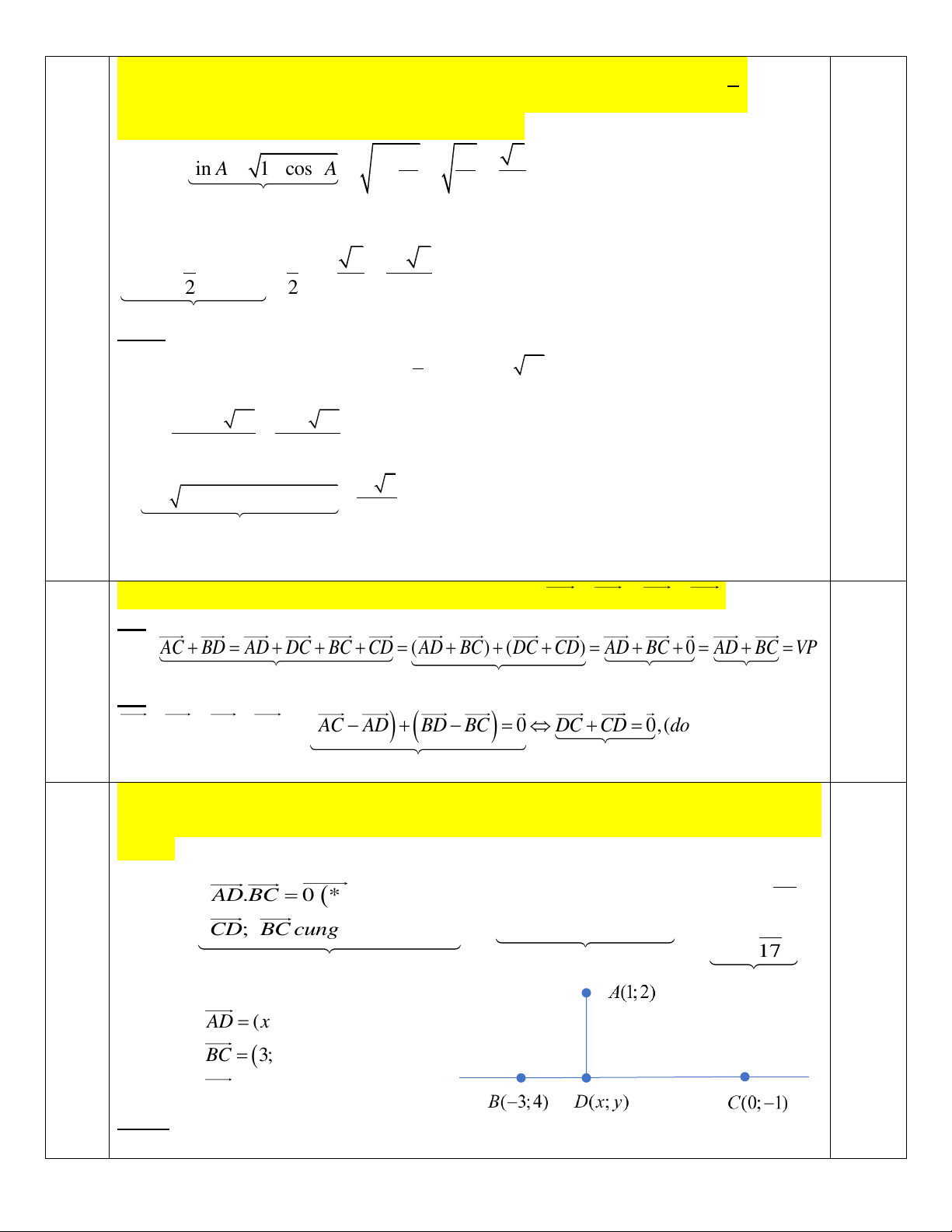
Câu 5. (1 điểm). Trong mặt phẳng với hệ tọa độ Oxy cho A(1;2); B( 3 − ;4) và C(0;− ) 1 . Tìm tọa độ điểm
D là hình chiếu vuông góc của điểm A trên đường thẳng đi qua hai điểm B và C ?  18 x = −  A . D BC = 0 ( ) * 3
x − 5y = 7( − ***)   17 ycbt       (101 CD BC cung phuong  ( ) 5  x + 3y = 3 − 13 ; **  y = 102 0,5  17 0,25 103 0,25 và 1,0 104)
AD = (x −1; y − 2)  
trong đó: BC = (3; 5 − ) CD = ( ; x y +1) 
Lưu ý: Nếu làm được (*) và (***) thì cho 0,25.
Document Outline

  • ma 101
  • ma 102
  • ma 103
  • ma 104
  • đáp án toán 10 cuối kỳ 1 năm 2022-2023