Đề cuối học kỳ 1 Toán 10 năm 2023 – 2024 trường THPT Cù Huy Cận – Hà Tĩnh

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 10 đề kiểm tra cuối học kỳ 1 môn Toán 10 năm học 2023 – 2024 trường THPT Cù Huy Cận, huyện Vũ Quang, tỉnh Hà Tĩnh, mời bạn đọc đón xem

39 20 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 10

Môn: Toán 10

Thông tin:

18 trang 9 tháng trước

Tác giả:

Profile Thanh Tâm
MA TRẬN KIỂM TRA CUỐI HỌC KÌ I MÔN TOÁN – LỚP 10.CHC
TT
(1)
Chương/Chủ đề
(2)
Nội dung/đơn vị kiến thức
(3)
Mức độ đánh giá
(4-11)
Tổng % điểm
(12)
Nhận biết
Thông hiểu
Vận dụng
Vận dụng cao
TNKQ
TL
TL
TNKQ
TL
TNKQ
TL
1
Tập hợp. Mệnh
đề (7 tiết)
Mệnh đề toán học. Mệnh đề
phủ định. Mệnh đề đảo.
Mệnh đề tương đương.
Điều kiện cần và đủ.
(3,5
tiết)
1 0 0 0 0 0 0 0 2%
Tập hợ
p. Các phép toán
trên tập hợp (3,5 tiết)
2 0 3 0 0 0 0 0 4%
2
Bất phương
trình và hệ bất
phương trình
bậc nhất hai ẩn
(6 tiết)
Bất phương trình, hệ bất
phương trình bậc nhất hai
ẩn và ứng dụng (6 tiết)
4-5 0 6 0 0 0 0 0 6%
3
Hàm số và đồ
thi (18 tiết)
Hàm số và đồ thị (5 tiết)
7-8 0 9 0 0
TL4
0 0
19%
Hàm số bậc hai. Đồ thị hàm
số bậc hai và ứng dụng (2,5
tiết)
10 0 11-13 0 0 0 0
Dấu của tam thức bậc hai
Bất phương trình bậc hai
một ẩn (7 tiết)
14-16 0 17-19 0 0 TL2 0 0
17%
Hai dạng phương trình vô
tỷ (2,5 tiết)
20-21 0 22 0 0 TL1 0 TL5 16%
4
Hệ thức lượng trong tam
giác. Định lí côsin. Định lí
23-24 0 25 0 0 0 0 0 6%
Hệ thức lượng
trong tam giác.
Vectơ (16 tiết)
sin. Công thức tính diện
tích tam giác. Giải tam giác
(6 ,5 tiết)
Vectơ, các phép toán (tổng
và hiệu hai vectơ, tích một
số với một vectơ, tích vô
hướng của hai vectơ
) và
một số ứng dụng trong Vật
lí
(9,5 tiết)
26-31 0 32-35 0 0 TL3 0 TL6 30%
Tổng 20 0 15 0 0 4 0 2
Tỉ lệ % 40% 30% 20% 10% 100%
Tỉ lệ chung 70% 30% 100%
Mã đề 101 Trang 1/4
SỞ GD-ĐT HÀ TĨNH
TRƯỜNG THPT CÙ HUY CẬN
ĐỀ CHÍNH THỨC
ĐỀ KIỂM TRA CUỐI HỌC KỲ I, NĂM HỌC 2023- 2024
Môn:Toán-Lớp 10
Thời gian làm bài: 90 phút; Không kể giao đề
(35 câu trắc nghiệm và 05 câu tự luận)
Mã đề: 101
Họ và tên thí sinh:............................................ SBD..............Lớp..........
I.Phần trắc nghiệm khách quan:( 7.0 điểm)
Câu 1. Cho hai vectơ
a
và
b
khác
0
. Xác định góc
α
giữa hai vectơ
a
và
b
khi
. ..
ab a b= −

A.
o
45
α
=
. B.
o
90
α
=
. C.
o
0
α
=
. D.
o
180
α
=
.
Câu 2. Cho parabol
()
P
có phương trình
2
34yx x= ++
. Số giao điểm của
()P
với trục hoành là
A.
0
. B.
2
. C.
3
. D.
1
.
Câu 3. Cho tam giác
ABC
vuông tại
A
có
3, 5
AB cm BC cm= =
. Khi đó
AB BC+
 
là:
A.
4
. B.
8
. C.
13
. D.
2 13
.
Câu 4. Bảng xét dấu nào sau đây là của tam thức
( )
2
43fx x x=++
.
A.
B.
C.
D.
Câu 5. Cho hàm số
4yx= −
. Điểm nào sau đây thuộc đồ thị hàm số đã cho?
A.
( )
2; 2
. B.
( )
1; 3−
. C.
(
)
1; 3
. D.
( )
2; 2−
.
Câu 6. Gọi
O
là giao điểm hai đường chéo
AC
và
BD
của hình bình hành
ABCD
. Đẳng thức nào sau
đây là đẳng thức sai?
A.
OA OC=
 
. B.
AB DC=
 
. C.
CB DA=
 
. D.
OB DO=
 
.
Câu 7. Cho tam giác
ABC
có
00
3, 30 , 120AB A B
= = =
. Chọn khẳng định đúng.
A.
33AC =
. B.
3
AC =
. C.
23AC =
. D.
43AC =
.
Câu 8. Cho parabol có phương trình
2
62yx x=−+
. Trục đối xứng của Parabol là đường thẳng
A.
7x = −
. B.
3
2
x =
. C.
3x = −
. D.
3x =
.
Mã đề 101 Trang 2/4
Câu 9. Số nghiệm của phương trình
2
45 1xx x
− += +
là
A.
1
. B.
0
. C.
2
. D.
3
.
Câu 10. Cho tam giác
ABC
,
G
là trọng tâm của tam giác
ABC
,
M
là điểm bất kì. Đẳng thức vectơ nào
sau đây đúng?
A.
3GA GB GC GM
++ =
   
. B.
0
MA MB MC
++ =
  
.
C.
3MA MB MC MG++ =
   
. D.
2MA MB MC MG++ =
   
.
Câu 11. Cho tam giác đều
ABC
có cạnh bằng
.a
Tính tích vô hướng
..AB AC
 
A.
2
3
.
2
a
AB AC = −
 
B.
2
.
2
a
AB AC =
 
C.
2
. 2.AB AC a=
 
D.
2
.
2
a
AB AC = −
 
Câu 12. Cho tam giác
ABC
, gọi
M
là trung điểm của
BC
và
G
là trọng tâm của tam giác
ABC
. Mệnh
đề nào sau đây đúng?
A.
AB AC AM+=
  
. B.
( )
1
3
AG AB AC= +
  
. C.
( )
3
4
AG AB AC= +
  
. D.
1
3
AG AM=
 
.
Câu 13. Cho tam giác
ABC
. Tập hợp các điểm
M
thỏa mãn
.0MA BC =
 
là:
A. đoạn thẳng. B. một điểm. C. đường thẳng. D. đường tròn.
Câu 14. Cho hàm số
( )
2
y f x ax bx c= = ++
có đồ thị như hình vẽ. Đặt
2
4
b ac∆= −
, tìm dấu của
a
và
∆
A.
0a >
,
0∆=
. B.
0a <
,
0
∆>
. C.
0a
>
,
0∆>
. D.
0a <
,
, 0∆=
.
Câu 15. Parabol
2
2y ax bx= ++
đi qua hai điểm
( )
1; 5M
và
( )
2;8N −
có phương trình là
A.
2
2yx x= +
. B.
2
2 22yx x= ++
. C.
2
22y xx= ++
. D.
2
2yx x= ++
.
Câu 16. Cho tam giác
ABC
. Mệnh đề nào dưới đây sai ?.
A.
222
cos
2
acb
B
ac
+−
=
. B.
2 22
2 cos
a b c bc A=+−
.
C.
2 22
2 cos
a b c bc A=++
. D.
222
cos
2
bca
A
bc
+−
=
.
Câu 17. Cặp số nào sau đây là nghiệm của bất phương trình
2xy+<
A.
(0; 5)
. B.
(2;3)
. C.
( 3;1)−
. D.
(5; 0)
.
Câu 18. Parabol
2
44yx x=−+
có đỉnh là:
A.
( )
1;1I
. B.
(
)
1; 2
I −
. C.
( )
1;1
I −
. D.
( )
2; 0I
.
Câu 19. Với
x
thuộc tập hợp nào dưới đây thì
( )
2
–4 3fx x x= +
luôn âm?
A.
( ) ( )
;1 4;−∞ ∪ +∞
. B.
( )
1; 3
. C.
( )
[
)
;1 3;−∞ ∪ +∞
. D.
[ ]
1; 3
.
Câu 20. Cho tập hợp
{ }
1; 2;3; 4;5A =
,
{ }
2;3; 5;6; 7B =
. Khi đó
?AB∩=
A.
{ }
2;3AB∩=
. B.
{ }
3AB∩=
. C.
{ }
3; 5
AB∩=
. D.
{ }
2;3;5AB∩=
.
Câu 21. Tập xác định của hàm số
2
2 273yx x
=−+
là
A.
( )
1;D = − +∞
. B.
( )
0;D = +∞
. C.
D =
. D.
( )
;0D = −∞
.
O
x
y
4
4
1
( )
y fx=
Mã đề 101 Trang 3/4
Câu 22. Cho tam thức bậc hai
2
( ) ( 0)f x ax bx c a= ++ ≠
. Mệnh đề nào sau đây đúng?
A. Nếu
0∆=
thì
(
)
fx
luôn cùng dấu với hệ số
a
, với mọi
\
2
b
x
a

∈−


.
B. Nếu
0∆>
thì
( )
fx
luôn cùng dấu với hệ số
a
, với mọi
x ∈
.
C. Nếu
0∆<
thì
( )
fx
luôn cùng dấu với hệ số
b
, với mọi
x
∈
.
D. Nếu
0∆<
thì
( )
fx
luôn trái dấu với hệ số
a
, với mọi
x ∈
.
Câu 23. Tìm khẳng định đúng trong các khẳng định sau?
A.
( )
27fx x= −
là tam thức bậc hai.
B.
( )
3
24fx x x=+−
là tam thức bậc hai.
C.
( )
42
21fx x x=−+
là tam thức bậc hai.
D.
( )
2
25
fx x x
=+−
là tam thức bậc hai.
Câu 24. Trong các mệnh đề toán học sau, mệnh đề nào sai?
A.
22
chia hết cho
11
. B.
10
là số nguyên tố.
C.
25
là ước của
125
. D.
49
là số chính phương.
Câu 25. Điều kiện xác định của phương trình
24xx−=
là
A.
0x ≥
. B.
0x <
. C.
2x ≥
. D.
2x >
.
Câu 26. Tìm tập xác định
D
của hàm số
31
22
x
y
x
.
A.
D 1; 
. B.
D 1; 
. C.
D
. D.
D \1
.
Câu 27. Cho bốn điểm bất kì A, B, C, O. Đẳng thức nào sau đây đúng?
A.
.OA OB AB= +
  
B.
.AB OB OA= +
  
C.
.OA OC CA
= +
  
D.
.
AB AC BC= +
  
Câu 28. Bất phương trình nào sau đây không phải là bất phương trình bậc nhất hai ẩn?
A.
2 3 20xy− +≤
. B.
10 0
23
xy
−+ <
. C.
5 10xy− −≥
. D.
2
3 2 10
xy x
+ − +≤
.
Câu 29. Nghiệm của phương trình
3 63x +=
là
A.
1x = −
. B.
0x =
. C.
5x =
. D.
1x =
.
Câu 30. Miền nghiệm của bất phương trình
32 6xy
− ≥−
là:
A. B. .
C. . D.
O
x
y
2−
3
O
x
y
2−
3
O
2
3
y
x
O
x
2−
3
y
Mã đề 101 Trang 4/4
Câu 31. Cho tập hợp
(
]
(
]
;3 ; 1;5AB= −∞ =
. Khi đó, tập
AB∪
là
A.
( ;5]−∞
. B.
(1; 3]
. C.
(3; 5 ]
. D.
( ;1)−∞
.
Câu 32. Cho tam giác
ABC
. Mệnh đề nào dưới đây đúng ?.
A.
.sinaR A=
. B.
2 .sin
aR A=
. C.
2 .cosaR A=
. D.
2 .sinaRA=
.
Câu 33. Cho tam thức bậc hai
2
( ) ( 0)
f x ax bx c a

. Điều kiện cần và đủ để
( ) 0,fx x 
là:
A.
0
0
a

. B.
0
0
a

. C.
0
0
a

. D.
0
0
a

.
Câu 34. Cho hình vuông
ABCD
có cạnh bằng
a
. Tính độ dài vectơ
AB

.
A.
2a
. B.
2a
. C.
a
. D.
3a
.
Câu 35. Gọi O là tâm hình bình hành ABCD. Đằng thức nào sau đây sai?
A.
.OB OC OD OA−=−
   
B.
.AB AD DB−=
  
C.
.BC BA DC DA−= −
   
D.
.OA OB CD−=
  
II.Phần tự luận:(3.0 điểm)
Câu 1. Giải phương trình
72 1xx+= −
.
Câu 2. Cho tam thức
( )
2
2 45f x x mx m=− −+
. Tìm tất cả các giá trị nguyên của
m
để
( )
0
fx x> ∀∈
.
Câu 3. Cho tam giác
ABC
có
M
là điểm thuộc cạnh
BC
sao cho
2
MB MC=
,
N
là trung điểm của cạnh
AC
. Giả sử
,AB a AC b= =
 
. Biểu diễn các vectơ
,AM MN
 
theo hai vectơ
a
và
b
.
Câu 4. Thầy Nam được bố chia cho một miếng đất để xây nhà, biết miếng đất được chọn là hình chữ nhật
có chu vi
400 ( )m
. Hỏi thầy Nam chọn mỗi kích thước của miếng đất bằng bao nhiêu để diện
tích đất dùng để xây nhà là lớn nhất.
Câu 5. Tìm
m
để phương trình
( )
22
25 1 24 0x xm x x xm
− ++− − + =
có hai nghiệm thực phân
biệt.
Câu 6. Cho tam giác
ABC
,
M
là điểm di động trên đường tròn ngoại tiếp tam giác
ABC
. Tìm vị trí
điểm
M
để
22 2
2MB MC MA+−
đạt giá trị nhỏ nhất.
------ HẾT ------
Mã đề 102 Trang 1/4
SỞ GD-ĐT HÀ TĨNH
TRƯỜNG THPT CÙ HUY CẬN
ĐỀ CHÍNH THỨC
ĐỀ KIỂM TRA CUỐI HỌC KỲ I, NĂM HỌC 2023- 2024
Môn:Toán-Lớp 10
Thời gian làm bài: 90 phút; Không kể giao đề
(35 câu trắc nghiệm và 05 câu tự luận)
Mã đề: 102
Họ và tên thí sinh:............................................ SBD..............Lớp..........
I.Phần trắc nghiệm khách quan:( 7.0 điểm)
Câu 1. Parabol
2
44
yx x=++
có đỉnh là:
A.
(
)
2; 0
I −
. B.
( )
2;16I
. C.
( )
1; 2I −
. D.
(
)
1;1
I −
.
Câu 2. Cặp số nào sau đây là nghiệm của bất phương trình
23xy−<
A.
(0; 5)
−
. B.
(5; 0)
. C.
(2;3)
. D.
(3; 1)−
.
Câu 3. Cho parabol có phương trình
2
82yx x= −+
. Trục đối xứng của Parabol là đường thẳng
A.
8x = −
. B.
4
x = −
. C.
2x = −
. D.
4x =
.
Câu 4. Nghiệm của phương trình
5 14x +=
là
A.
3
x =
. B.
1
5
x
−
=
. C.
3x = −
. D.
3
5
x =
.
Câu 5. Miền nghiệm của bất phương trình
32 6xy+≥
là:
A. B. .
C. . D.
Câu 6. Cho bốn điểm bất kì A, B, C, O. Đẳng thức nào sau đây đúng?
A.
.OA OC AC= +
  
B.
.AB AO OB= +
  
C.
.AB AC BC= +
  
D.
AB OA OB= +
  
.
Câu 7. Cho parabol
()P
có phương trình
2
65yx x= +−
. Số giao điểm của
()P
với trục hoành là
A.
1
. B.
3
. C.
2
. D.
0
.
Câu 8. Cho hình vuông
ABCD
có cạnh bằng
2a
. Tính độ dài vectơ
BC

.
A.
2a
. B.
3a
. C.
22a
. D.
2a
.
Câu 9. Tìm tập xác định
D
của hàm số
31
22
x
y
x
.
A.
D 1; 
. B.
D
. C.
D \1
. D.
D 1; 
.
O
x
y
2−
3
O
2
3
y
x
O
x
y
2−
3
O
x
2
−
3
y
Mã đề 102 Trang 2/4
Câu 10. Tìm khẳng định đúng trong các khẳng định sau?
A.
( )
3
24fx x x=−+ +
là tam thức bậc hai.
B.
( )
31fx x= +
là tam thức bậc hai.
C.
( )
2
3 25fx x x= −+
là tam thức bậc hai.
D.
( )
42
21
fx x x
=++
là tam thức bậc hai.
Câu 11. Cho tam giác
ABC
. Mệnh đề nào dưới đây đúng ?.
A.
2 .cosbR B=
. B.
2 .sinbRB=
. C.
.sinbR B=
. D.
2 .sin
bR B=
.
Câu 12. Cho hai vectơ
a
và
b
khác
0
. Xác định góc
α
giữa hai vectơ
a
và
b
khi
. ..ab a b=

A.
o
45
α
=
. B.
o
90
α
=
. C.
o
180
α
=
. D.
o
0
α
=
.
Câu 13. Bảng xét dấu nào sau đây là của tam thức
( )
2
54fx x x=−+
.
A.
B.
C.
D.
Câu 14. Số nghiệm của phương trình
2
52 2xx x
− −= −
là
A.
0
. B.
3
. C.
2
. D.
1
.
Câu 15. Cho tam giác
ABC
,
G
là trọng tâm của tam giác
ABC
,
M
là điểm bất kì. Đẳng thức vectơ nào
sau đây đúng?
A.
0MA MB MC
++ =
  
. B.
3GA GB GC GM++ =
   
.
C.
2MA MB MC MG++ =
   
. D.
3MA MB MC MG++ =
   
.
Câu 16. Tập xác định của hàm số
2
2 2023yx x=++
là
A.
( )
1;D = − +∞
. B.
D =
. C.
( )
0;D = +∞
. D.
( )
;0D = −∞
.
Câu 17. Với
x
thuộc tập hợp nào dưới đây thì
( )
2
–4 3fx x x= +
luôn dương?
A.
( ) ( )
;1 3;−∞ ∪ +∞
. B.
( )
1; 3
. C.
[
]
1; 3
. D.
(
] [
)
;1 3;−∞ ∪ +∞
.
Câu 18. Cho tam thức bậc hai
2
( ) ( 0)f x ax bx c a 
. Điều kiện cần và đủ để
( ) 0,fx x
là:
A.
0
0
a

. B.
0
0
a

. C.
0
0
a

. D.

0
0
a
.
Câu 19. Trong các mệnh đề toán học sau, mệnh đề nào sai?
A.
25
là ước của
125
. B.
16
là số lẻ .
C.
20
chia hết cho
5
. D.
36
là số chính phương.
Mã đề 102 Trang 3/4
Câu 20. Gọi
O
là giao điểm hai đường chéo
AC
và
BD
của hình bình hành
ABCD
. Đẳng thức nào sau
đây là đẳng thức sai?
A.
OA CO=
 
. B.
DO BO
=
 
. C.
AB DC=
 
. D.
AD BC
=
 
.
Câu 21. Cho tam thức bậc hai
2
( ) ( 0)
f x ax bx c a
= ++ ≠
. Mệnh đề nào sau đây đúng?
A. Nếu
0∆=
thì
( )
fx
luôn cùng dấu với hệ số
a
, với mọi
x ∈
B. Nếu
0
∆<
thì
( )
fx
luôn cùng dấu với hệ số
a
, với mọi
x ∈
.
C. Nếu
0∆<
thì
( )
fx
luôn cùng dấu với hệ số
b
, với mọi
x ∈
.
D. Nếu
0∆>
thì
( )
fx
luôn trái dấu với hệ số
a
, với mọi
x ∈
.
Câu 22. Gọi O là tâm hình bình hành ABCD. Đằng thức nào sau đây sai?
A.
.BC BA DA DC−=−
   
B.
.AB AD DB−=
  
C.
.OB OC OA OD−=−
   
D.
.DA DB BA−=
  
Câu 23. Parabol
2
2y ax bx= ++
đi qua hai điểm
(
)
1; 2A
và
( )
2; 0B
có phương trình là
A.
2
22yx x=−+ +
. B.
2
2y xx
=− ++
. C.
2
2yx x= ++
. D.
2
22yx x=−− +
.
Câu 24. Cho tam giác
ABC
, gọi
M
là trung điểm của
BC
và
G
là trọng tâm của tam giác
ABC
. Mệnh
đề nào sau đây đúng?
A.
3AG AM=
 
. B.
( )
1
6
GM AB AC= +
  
. C.
( )
1
2
AG AB AC= +
  
. D.
AB AC AM+=
  
.
Câu 25. Cho tam giác đều
ABC
có cạnh bằng
2.a
Tính tích vô hướng
..BA BC
 
A.
2
. 23
BA BC a
=
 
B.
2
. 2.
BA BC a=
 
C.
2
.2BA BC a= −
 
D.
2
. 23BA BC a
= −
 
Câu 26. Cho hàm số
6yx= −
. Điểm nào sau đây thuộc đồ thị hàm số đã cho?
A.
( )
2; 4
. B.
( )
1; 5
−−
. C.
( )
2; 4−−
. D.
( )
1; 5−
.
Câu 27. Cho tam giác
ABC
vuông tại
A
có
3, 4AB cm AC cm
= =
. Khi đó
AC AB
−
 
là:
A.
5
. B.
5
. C.
2 13
. D.
4
.
Câu 28. Cho tập hợp
(
]
(
]
; 2 ; 1; 8AB= −∞ =
. Khi đó, tập
AB∪
là
A.
( ;1)
−∞
. B.
(1; 2 ]
. C.
( ;8]−∞
. D.
(2; 8 ]
.
Câu 29. Cho tam giác
ABC
có
00
6, 120 , 30BC A B= = =
. Chọn khẳng định đúng.
A.
43AB =
. B.
23AB =
. C.
3AB =
. D.
33AB =
.
Câu 30. Cho hàm số
( )
2
y f x ax bx c= = ++
có đồ thị như hình vẽ . Đặt
2
4b ac
∆= −
, hãy xác định
dấu của hệ số a và
∆
.
A.
0a
>
,
0∆<
. B.
0a
>
,
0∆>
. C.
0a <
,
0∆>
. D.
0a >
,
0∆=
.
Câu 31. Bất phương trình nào sau đây không phải là bất phương trình bậc nhất hai ẩn?
A.
2 3 20xy+ +≤
. B.
2
3 10x yx+ + +≥
. C.
5 10xy− +<
. D.
10 0
23
xy
−+ <
.
Câu 32. Cho tam giác
ABC
. Tập hợp các điểm
M
thỏa mãn
.0MB AC =
 
là:
A. đường thẳng. B. đoạn thẳng. C. một điểm. D. đường tròn.
Câu 33. Điều kiện xác định của phương trình
24 2xx+=−
là
A.
2x <−
. B.
2x ≥
. C.
2x ≥−
. D.
2x <
.
Mã đề 102 Trang 4/4
Câu 34. Cho tam giác
ABC
. Mệnh đề nào dưới đây sai ?.
A.
222
cos
2
abc
C
ab
+−
=
. B.
2 22
2 cos
b a c ac B
=+−
.
C.
2 22
cos
c abab C=+−
. D.
222
cos
2
bca
A
bc
+−
=
.
Câu 35. Cho tập hợp
{ }
1; 2;3; 4;5;8A =
,
{ }
2;5; 6; 7B =
. Khi đó
?AB∩=
A.
{ }
2;3AB∩=
. B.
{
}
2AB∩=
. C.
{ }
3; 5AB∩=
. D.
{
}
2;5AB∩=
.
II.Phần tự luận:(3.0 điểm)
Câu 1. Giải phương trình
52 4xx
+= +
.
Câu 2. Cho tam thức
( )
2
2 56f x x mx m=−+ + −
.Tìm tất cả các giá trị nguyên của
m
để
( )
0 .fx x< ∀∈
Câu 3. Cho tam giác
ABC
có
M
là điểm thuộc cạnh
BC
sao cho
2MB MC=
,
N
là trung điểm của cạnh
AB
. Giả sử
,AB a AC b= =
 
. Biểu diễn các vectơ
,AM MN
 
theo hai vectơ
a
và
b
.
Câu 4. Thầy Hùng muốn làm một cái sân hình chữ nhật có chu vi
240 ( )m
. Hỏi thầy Hùng chọn mỗi kích
thước của cái sân bằng bao nhiêu để diện tích sân là lớn nhất.
Câu 5. Tìm
m
để phương trình
(
)
22
5 8 12 5 6 0
x xm x x xm− −+− − − =
có hai nghiệm thực phân
biệt.
Câu 6. Cho tam giác
ABC
,
M
là điểm di động trên đường tròn ngoại tiếp tam giác
ABC
. Tìm vị trí
điểm
M
để
22 2
2MA MC MB+−
đạt giá trị nhỏ nhất.
------ HẾT ------
Đề\câu 1 2 3 4 5 6 7 8
9 10
11
12 13
14 15 16 17 18 19 20 21 22 23 24 25 26 27 28
000 C
A C
D C
A
D D C B B A C A A B B A B A A A D
A
C D
B D
101 A C B A C B C A
C
C B D D D D B A D B B B A B B B D B C
102
D
D D
A
B A
C C D A A B C A D B A C C B
B
C D
D B
C
D A
29 30 31 32 33 34 35
D C B A B A B
B C B A C C D
D D B A D A B
ĐÁP ÁN TỰ LUẬN MÃ ĐỀ 101 VÀ 103
Câu
Nội dung
Điểm
Câu 1
Giải phương trình
72 1xx+= −
.
Giải:
2
2
2 10
72 1
74 4 1
1
1
2
2
2
2
4 5 60
3
()
4
x
xx
x xx
x
x
x
x
xx
xL
−≥
+ = −⇔
+= − +
≥
≥
⇔ ⇔ ⇔=
=


− −=
−
=
Chú ý: HS có thể giải bằng cách bình phương hai vế rồi thử nghiệm
0.25
0.25
Câu 2
Cho tam thức
( )
2
2 45f x x mx m=− −+
. Tìm tất cả các giá trị nguyên của
m
để
( )
0 fx x> ∀∈
Giải:
( )
2
10
0
0 5 1
0
4 50
a
a
fx x m
mm
= >
>
> ∀ ∈ ⇔ ⇔ ⇔− < <

∆<
′
∆= + − <
0.25
Vì
m
nguyên nên
{ }
4;3;2;1;0m
∈−−−−
Vậy có
5
giá trị nguyên của
m
thỏa mãn điều kiện bài toán
0.25
Câu 3
Cho tam giác
ABC
có
M
là điểm thuộc cạnh
BC
sao cho
2MB MC=
,
N
là trung điểm của
cạnh
AC
. Giả sử
,AB a AC b
= =
 
. Biểu diễn các vectơ
,AM MN
 
theo hai vectơ
a
và
b
.
Giải:
Ta có
( )
( )
1
2 2 22
BM AM AB
CM AM AC CM AM AC
= −
= −⇒ = −
  
     
Lấy
(
) ( )
12+
vế theo vế ta có
12
3 20
33
12
33
AM AB AC AM AB AC
ab
−− =⇒ = +
= +
     

0.25
Lại có
1 12
2 33
1 1 11
3 6 36
MN AN AM AC AB AC
MN AB AC a b

=−= − +


⇒ =− − =−−
     
  
0.25
Câu 4
Thầy Nam được bố chia cho một miếng đất để xây nhà, biết miếng đất được chọn là hình chữ
nhật có chu vi
400 ( )m
. Hỏi thầy Nam chọn mỗi kích thước của miếng đất bằng bao
nhiêu để diện tích đất dùng để xây nhà là lớn nhất.
Giải:
Gọi chiều dài của miếng đất là
x
, chiều rộng của miếng đất là
( )
, 0; , :
y xy xy m
>
Theo bài ra ta có
( )
( )
2 400 200
200 200
xy xy
y xx
+ = ⇒+=
⇒= − <
Khi đó diện tích miếng đất là:
(
)
200Sx x= −
Xét hàm số
( ) (
)
2
200 200
fx x x x x= − =−+
0.25
Lập bảng biến thiên suy ra
Miếng đất có diện tích lớn nhất là
2
10000( )m
Khi
( )
100
xy m= =
Vậy miếng đất là hình vuông cạnh
100m
0.25
Câu 5
Tìm
m
để phương trình
( )
22
25 1 24 0x xm x x xm− ++− − + =
có hai nghiệm thực phân
biệt.
Giải: Điều kiện
2
24 0x xm− +≥
PT đã cho
(
)
(
)
(
)
(
)
( )
22 2
2 22
22 2
22
2
22
2
2
22
25 24 24 0
4 24 24 0
24 24 24 0
24 24 1
24 0
24 0 24
2 4 1 0
0
0
4*
24
x xm x xmx x xm
x xmx x xm x xmx
x xm x xmx x xmx
x xmx x xm
x xmx
x xmx x xm x
x x m VN
x
x
x xm
x xm x
⇔ −++ −+− −+=
⇔−+− −++ −+−=
⇔ −+ −+−+ −+−=
− +− − ++
− + −=
⇔ ⇔ −+−=⇔ −+=
− + +=
≥
≥
⇔⇔
−=−
− +=
0.25
Đặt
( )
2
4
fx x x
= −
. Ta có BBT:
Yêu cầu bài toán suy ra PT(*) phải có
Hai nghiệm phân biệt thỏa mãn
12
0 xx≤<
Dựa vào bảng biến thiên suy ra
4 00 4mm− <− ≤ ⇔ ≤ <
Vậy
[
)
0; 4m∈
0.25
Câu 6
Cho tam giác
ABC
,
M
là điểm di động trên đường tròn ngoại tiếp tam giác
ABC
. Tìm vị trí
điểm
M
để
22 2
2MB MC MA
+−
đạt giá trị nhỏ nhất.
Giải:
Gọi
O
là tâm đường tròn ngoại tiếp tam giác
ABC
,
I
là trung điểm
BC
.
Theo đề bài suy ra
2 2 2 22
OM OA OB OC R= = = =
Ta có
( ) ( ) (
)
22 2
22 2
2
2
MB MC MA
OB OM OC OM OA OM
+−
=−+−−−
     
2. 2. 4.
OM OB OM OC OM OA=−− +
     
2 (2 )OM OA OB OC= −−
   
2( )OM BA CA= +
  
4.OM AI
= −
 
( )
4..cos , 4.OM AI OM AI OM AI=− ≥−
 
Vì
OM
và
AI
không đổi. Do đó
22 2
2MB MC MA+−
đạt giá trị nhỏ nhất khi
(
)
cos , 1OM AI
=
 
. Khi đó
M
thuộc đường tròn
( )
O
sao có
OM

và
AI

cùng hướng.
0.25
0.25
I
O
A
B
C
M
ĐÁP ÁN TỰ LUẬN MÃ ĐỀ 102 VÀ 104
Câu
Nội dung
Điểm
Câu 1
Giải phương trình
52 4xx+= +
.
Giải:
2
2
2 40
52 4
5 4 16 16
2
2
1
1
4 15 11 0
11
()
4
x
xx
x xx
x
x
x
x
xx
xL
+≥
+= +⇔
+= + +
≥−
≥−
= −
⇔ ⇔ ⇔=−

+ +=
−
=
Chú ý: HS có thể giải bằng cách bình phương hai vế rồi thử nghiệm
0.25
0.25
Câu 2
Cho tam thức
( )
2
2 56f x x mx m=−+ + −
.Tìm tất cả các giá trị nguyên của
m
để
( )
0 .fx x< ∀∈
Giải:
(
)
2
10
0
0 6 1
0
5 60
a
a
fx x m
mm
=−<
<
< ∀ ∈ ⇔ ⇔ ⇔− < <

∆<
′
∆= + − <
0.25
Vì
m
nguyên nên
{
}
5;4;3;2;1;0m ∈−−−−−
Vậy có
6
giá trị nguyên của
m
thỏa mãn điều kiện bài toán
0.25
Câu 3
Cho tam giác
ABC
có
M
là điểm thuộc cạnh
BC
sao cho
2MB MC=
,
N
là trung điểm của
cạnh
AB
. Giả sử
,AB a AC b= =
 
. Biểu diễn các vectơ
,AM MN
 
theo hai vectơ
a
và
b
.
Giải:
Ta có
( )
( )
2 2 21
2
BM AM AB BM AM AB
CM AM AC
= −⇒ = −
= −
     
  
Lấy
( ) (
)
12+
vế theo vế ta có
21
32 0
33
21
33
AM AB AC AM AB AC
AM a b
− −=⇒ = +
⇒=+
     

0.25
Lại có
1 21
2 33
1 1 11
6 3 63
MN AN AM AB AB AC
MN AB AC a b

=−= − +


⇒ =− − =−−
     
  
0.25
Câu 4
Thầy Hùng muốn làm một cái sân hình chữ nhật có chu vi
240 ( )m
. Hỏi thầy Hùng chọn mỗi
kích thước của cái sân bằng bao nhiêu để diện tích sân là lớn nhất.
Giải:
Gọi chiều dài của cái sân là
x
, chiều rộng của cái sân là
( )
, 0; , :y xy xy m>
Theo bài ra ta có
( )
( )
2 240 120
120 120
xy xy
y xx
+ = ⇒+=
⇒= − <
Khi đó diện tích cái sân là:
(
)
120Sx x
= −
Xét hàm số
( ) (
)
2
120 120
fx x x x x= − =−+
0.25
Lập bảng biến thiên suy ra
Cái sân có diện tích lớn nhất là
2
3600( )m
Khi
( )
60
xy m= =
Vậy miếng đất là hình vuông cạnh
60m
0.25
Câu 5
Tìm
m
để phương trình
( )
22
5 8 12 5 6 0x xm x x xm− −+− − − =
có hai nghiệm thực
phân biệt.
Giải: Điều kiện
2
24 0x xm− +≥
PT đã cho
( )
(
)
(
)
(
)
( )
22
22 2
2 22
22 2
22
2
22
2
5 8 12 5 6 0
58 56 256 0
56 256 56 20
56 56 2 56 20
56 2 56 1
5 6 20
56 20 56
5 6 1 0
x xm x x xm
x xm x xm x x xm
x xm x x xm x xm x
x xm x xm x x xm x
x xm x x xm
x xm x
x xm x x xm
x x m VN
− −+− − − =
⇔ −−+ −−− −−=
⇔ −−− −−+ −−−=
⇔ −− −−− + −−−=
− −− − −+
− −− =
⇔ ⇔ −−−=⇔ −−=
− − +=
( )
2
22
2
0
20
6*
56 4
x
x
x
x xm
x xm x
≥
≥
⇔⇔

−=
− −=
0.25
Đặt
( )
2
6fx x x= −
. Ta có BBT:
Yêu cầu bài toán suy ra PT(*) phải có
Hai nghiệm phân biệt thỏa mãn
12
0 xx≤<
Dựa vào bảng biến thiên suy ra
90m−< ≤
Vậy
(
]
9; 0
m ∈−
0.25
Câu 6
Cho tam giác
ABC
,
M
là điểm di động trên đường tròn ngoại tiếp tam giác
ABC
. Tìm vị trí
điểm
M
để
22 2
2MA MC MB+−
đạt giá trị nhỏ nhất.
Giải:
Gọi
O
là tâm đường tròn ngoại tiếp tam giác
ABC
,
I
là trung điểm
AC
.
Theo đề bài suy ra
2 2 2 22
OM OA OB OC R= = = =
Ta có
( ) ( ) (
)
22 2
22 2
2
2
MA MC MB
OA OM OC OM OB OM
+−
=−+−−−
     
2. 2. 4.
OM OA OM OC OM OB=−− +
     
( )
2 (2 )
2
OM OB OA OC
OM OB OA OB OC
= −−
= −+−
   
    
2( )2( )OM AB CB OM BA BC= + = −−
     
4.OM BI= −
 
(
)
4..cos , 4.
OM BI OM BI OM BI
=− ≥−
 
Vì
OM
và
BI
không đổi. Do đó
22 2
2MA MC MB+−
đạt giá trị nhỏ nhất khi
( )
cos , 1OM BI =
 
. Khi đó
M
thuộc đường tròn
( )
O
sao có
OM

và
BI

cùng hướng.
0.25
0.25
I
O
A
B
C
M
| 1/18
| | Tải xuống

Có thể bạn quan tâm:

Preview text:


MA TRẬN KIỂM TRA CUỐI HỌC KÌ I MÔN TOÁN – LỚP 10.CHC
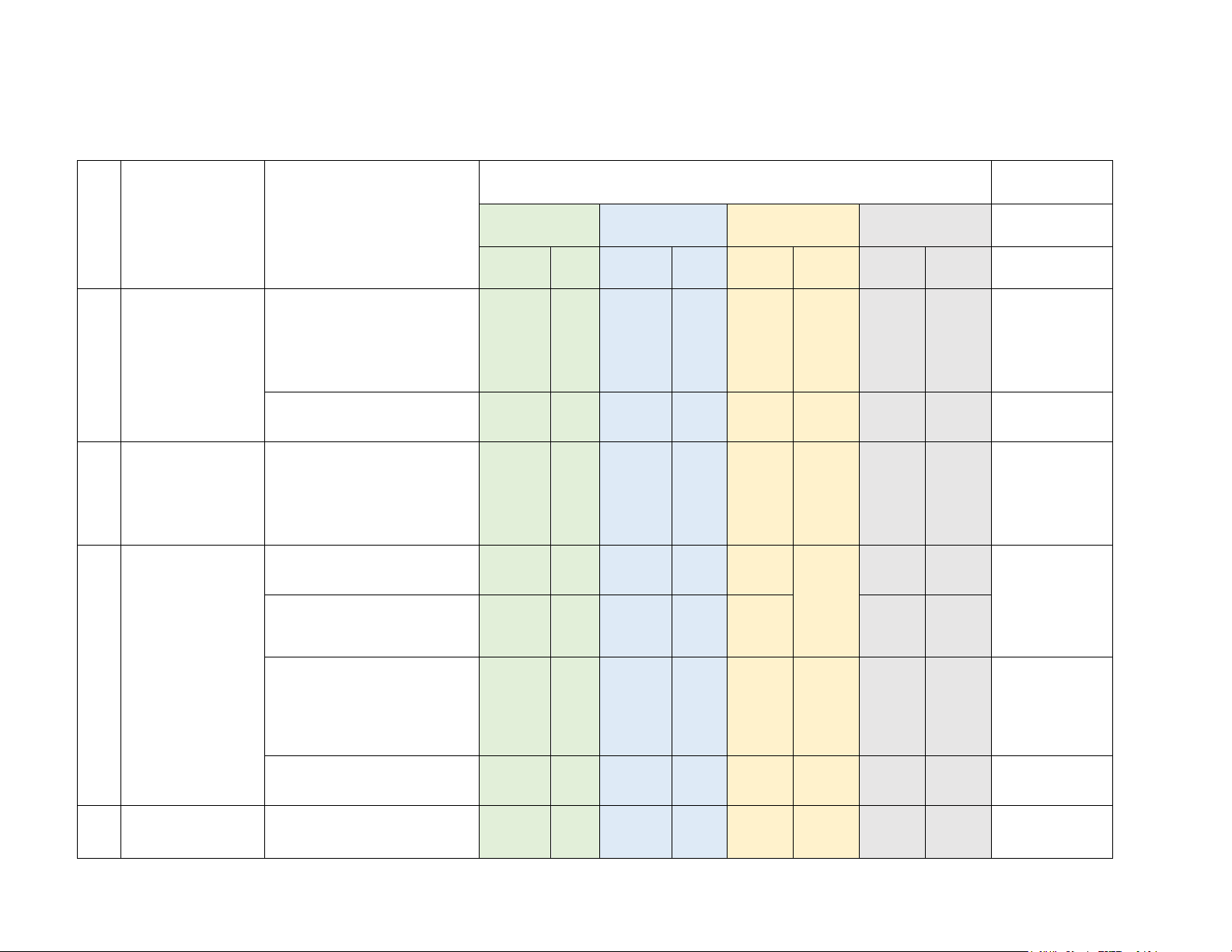
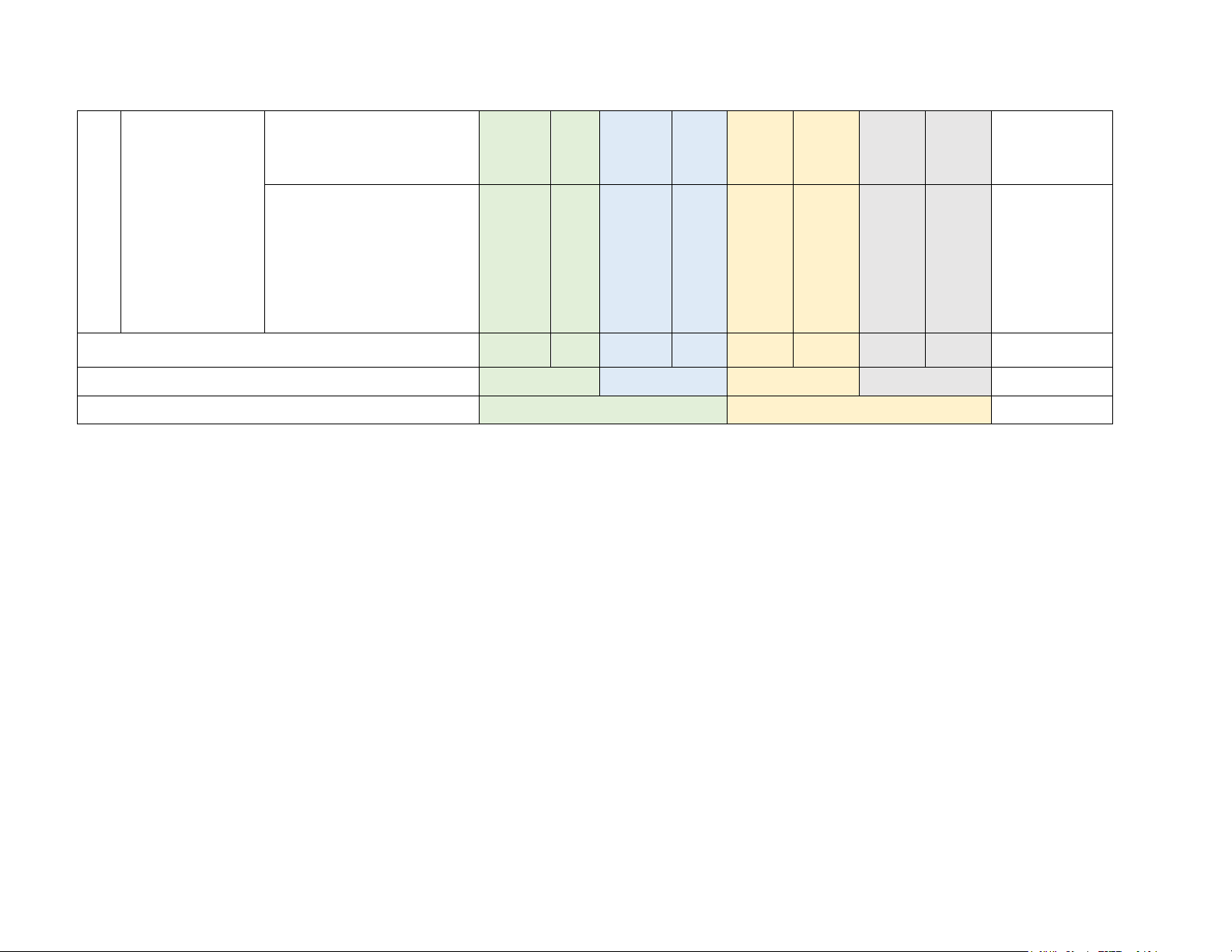
Mức độ đánh giá Tổng % điểm (4-11) (12)
TT Chương/Chủ đề Nội dung/đơn vị kiến thức Nhận biết Thông hiểu Vận dụng Vận dụng cao (1) (2) (3) TNKQ TL TNKQ TL TNKQ TL TNKQ TL
Mệnh đề toán học. Mệnh đề
phủ định. Mệnh đề đảo.
Mệnh đề tương đương. 1 0 0 0 0 0 0 0 2%
1 Tập hợp. Mệnh Điều kiện cần và đủ. (3,5 đề (7 tiết) tiết)
Tập hợp. Các phép toán
trên tập hợp (3,5 tiết) 2 0 3 0 0 0 0 0 4% Bất phương 2
trình và hệ bất Bất phương trình, hệ bất
phương trình phương trình bậc nhất hai 4-5 0 6 0 0 0 0 0 6%
bậc nhất hai ẩn ẩn và ứng dụng (6 tiết) (6 tiết)
Hàm số và đồ thị (5 tiết) 7-8 0 9 0 0 0 0
Hàm số bậc hai. Đồ thị hàm TL4 19%
số bậc hai và ứng dụng (2,5 10 0 11-13 0 0 0 0 tiết) 3 Hàm số và đồ thi (18 tiết)
Dấu của tam thức bậc hai
Bất phương trình bậc hai 14-16 0 17-19 0 0 TL2 0 0 17% một ẩn (7 tiết)
Hai dạng phương trình vô tỷ (2,5 tiết) 20-21 0 22 0 0 TL1 0 TL5 16% 4
Hệ thức lượng trong tam 23-24 0 25 0 0 0 0 0 6%
giác. Định lí côsin. Định lí
sin. Công thức tính diện
tích tam giác. Giải tam giác (6 ,5 tiết)
Hệ thức lượng Vectơ, các phép toán (tổng
trong tam giác. và hiệu hai vectơ, tích một Vectơ (16 tiết)
số với một vectơ, tích vô
hướng của hai vectơ) và 26-31 0 32-35 0 0 TL3 0 TL6 30%
một số ứng dụng trong Vật lí (9,5 tiết) Tổng 20 0 15 0 0 4 0 2 Tỉ lệ % 40% 30% 20% 10% 100% Tỉ lệ chung 70% 30% 100% SỞ GD-ĐT HÀ TĨNH
ĐỀ KIỂM TRA CUỐI HỌC KỲ I, NĂM HỌC 2023- 2024
TRƯỜNG THPT CÙ HUY CẬN Môn:Toán-Lớp 10
Thời gian làm bài: 90 phút; Không kể giao đề ĐỀ CHÍNH THỨC
(35 câu trắc nghiệm và 05 câu tự luận) Mã đề: 101
Họ và tên thí sinh:............................................ SBD..............Lớp..........
I.Phần trắc nghiệm khách quan:( 7.0 điểm)       
Câu 1. Cho hai vectơ a và b khác 0 . Xác định góc α giữa hai vectơ a và b khi .
a b = − a . b . A. o α = 45 . B. o α = 90 . C. o α = 0 . D. o α =180 .
Câu 2. Cho parabol (P) có phương trình 2
y = x + 4x + 3. Số giao điểm của (P) với trục hoành là A. 0 . B. 2. C. 3. D. 1.  
Câu 3. Cho tam giác ABC vuông tại A có AB = 3c ,
m BC = 5cm . Khi đó AB + BC là: A. 4. B. 8. C. 13 . D. 2 13 .
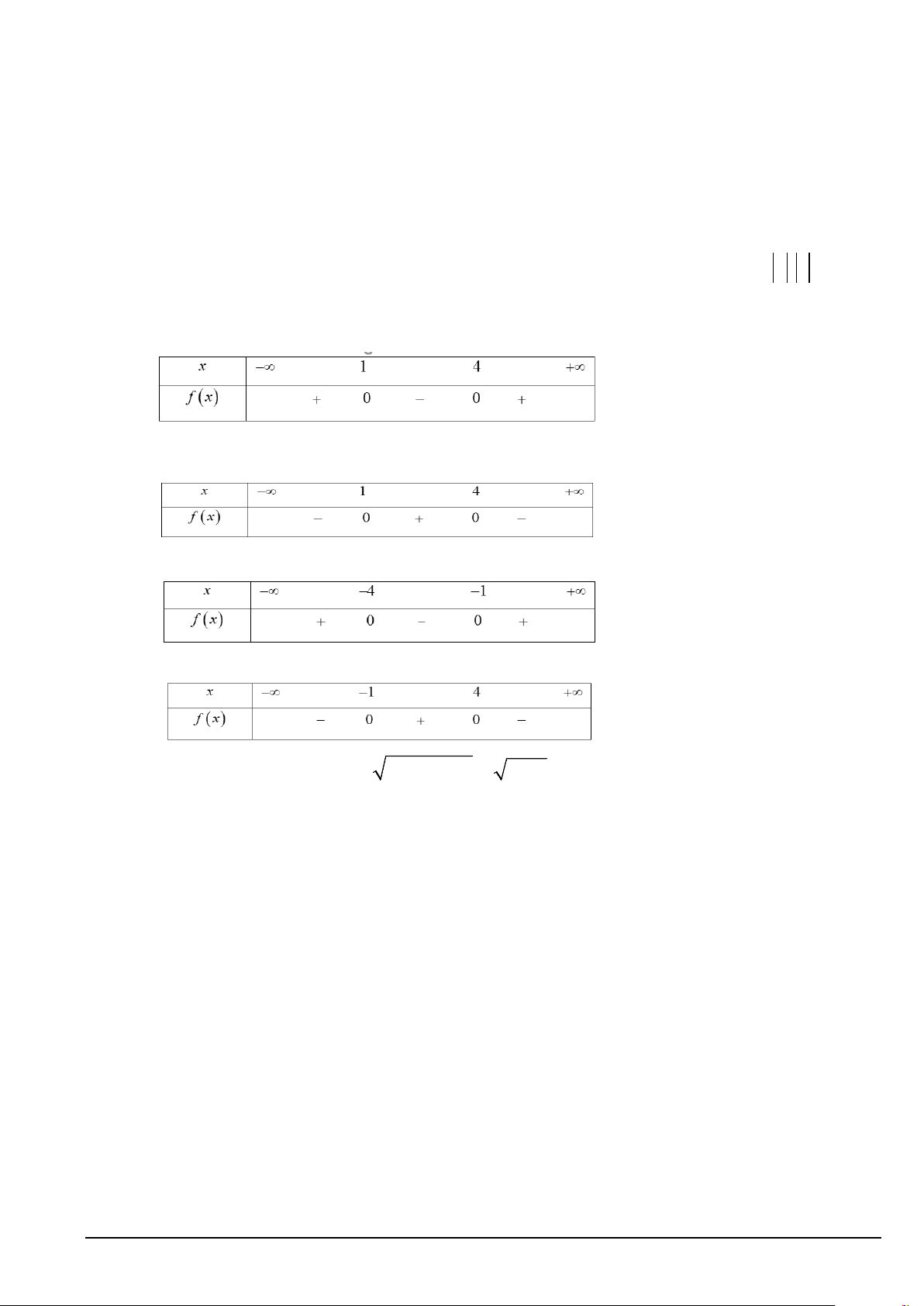
Câu 4. Bảng xét dấu nào sau đây là của tam thức f (x) 2 = x + 4x + 3. A. B. C. D.
Câu 5. Cho hàm số y = x − 4. Điểm nào sau đây thuộc đồ thị hàm số đã cho? A. (2;2). B. (1; 3 − ). C. (1;3) . D. ( 2; − 2).
Câu 6. GọiO là giao điểm hai đường chéo AC và BD của hình bình hành ABCD . Đẳng thức nào sau
đây là đẳng thức sai?        
A. OA = OC .
B. AB = DC .
C. CB = DA.
D. OB = DO .
Câu 7. Cho tam giác ABC có =  0 =  0
AB 3, A 30 , B =120 . Chọn khẳng định đúng.
A. AC = 3 3 .
B. AC = 3 .
C. AC = 2 3 . D. AC = 4 3 .
Câu 8. Cho parabol có phương trình 2
y = x − 6x + 2 . Trục đối xứng của Parabol là đường thẳng 3 A. x = 7 − . B. x = . C. x = 3 − . D. x = 3. 2 Mã đề 101 Trang 1/4
Câu 9. Số nghiệm của phương trình 2
x − 4x + 5 = x +1 là A. 1. B. 0 . C. 2. D. 3.
Câu 10. Cho tam giác ABC ,G là trọng tâm của tam giác ABC , M là điểm bất kì. Đẳng thức vectơ nào
sau đây đúng?
   
   
A. GA + GB + GC = 3GM .
B. MA + MB + MC = 0.
   
   
C. MA + MB + MC = 3MG .
D. MA + MB + MC = 2MG .  
Câu 11. Cho tam giác đều ABC có cạnh bằng .
a Tính tích vô hướng A . B AC. 2   2     2   A. a 3 A . B AC = − B. . a AB AC = C. 2 A .
B AC = 2a . D. . a AB AC = − 2 2 2
Câu 12. Cho tam giác ABC , gọi M là trung điểm của BC và G là trọng tâm của tam giác ABC . Mệnh
đề nào sau đây đúng?
  
 1  
 3    1 
A. AB + AC = AM .
B. AG = ( AB + AC). C. AG = ( AB + AC). D. AG = AM . 3 4 3  
Câu 13. Cho tam giác ABC . Tập hợp các điểm M thỏa mãn . MA BC = 0 là:
A. đoạn thẳng.
B. một điểm.
C. đường thẳng. D. đường tròn.
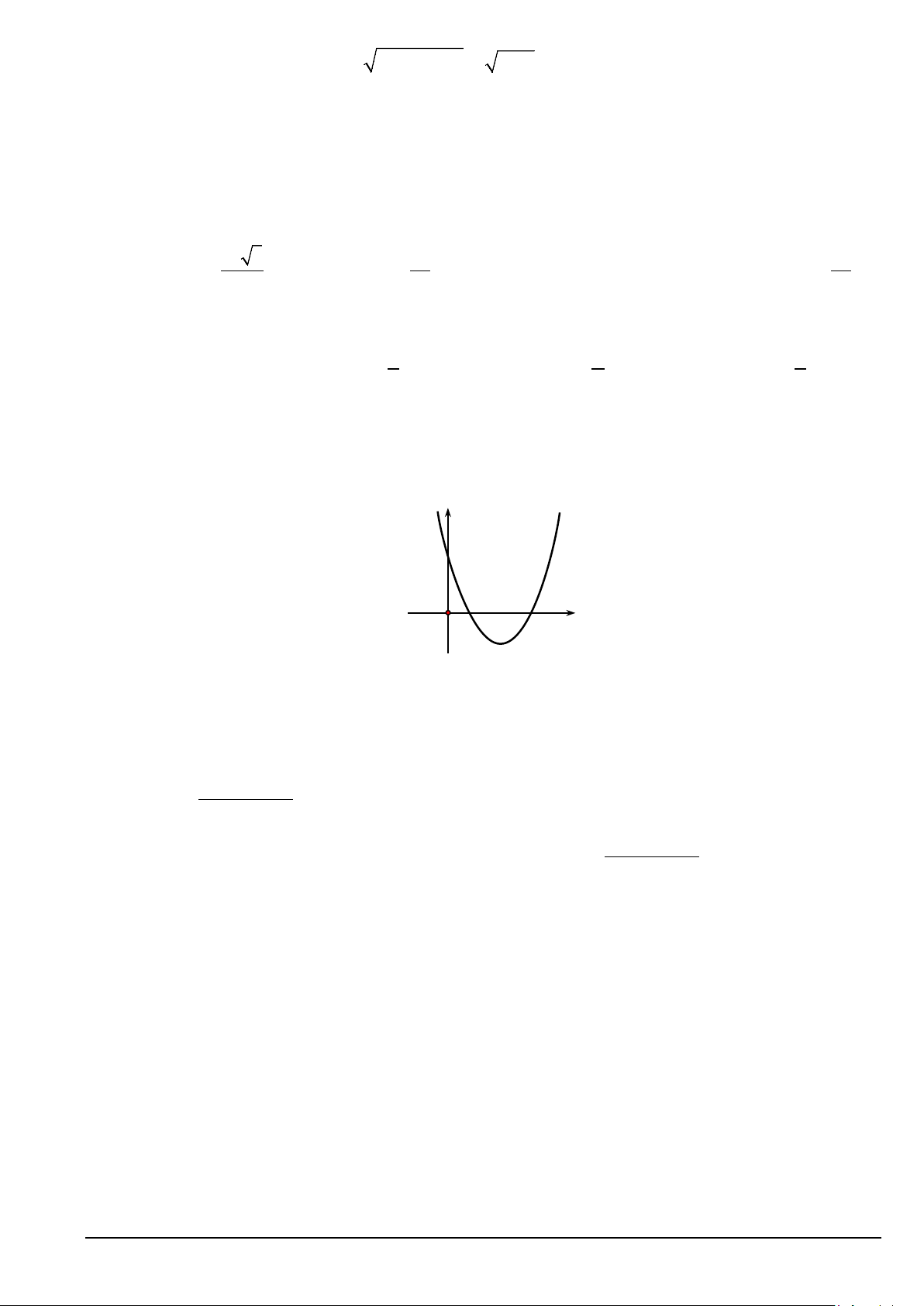
Câu 14. Cho hàm số = ( ) 2
y f x = ax + bx + c có đồ thị như hình vẽ. Đặt 2
∆ = b − 4ac , tìm dấu của a và ∆ y y = f (x) 4 O 1 4 x
A. a > 0 , ∆ = 0.
B. a < 0 , ∆ > 0.
C. a > 0 , ∆ > 0.
D. a < 0 , , 0 ∆ = . Câu 15. Parabol 2
y = ax + bx + 2 đi qua hai điểm M (1;5) và N ( 2;
− 8) có phương trình là A. 2
y = x + 2x . B. 2
y = 2x + 2x + 2 . C. 2
y = 2x + x + 2 . D. 2
y = x + x + 2 .
Câu 16. Cho tam giác ABC . Mệnh đề nào dưới đây sai ?. 2 2 2
a + c − b A. cos B = . B. 2 2 2
a = b + c − 2bccos A . 2ac 2 2 2
b + c − a C. 2 2 2
a = b + c + 2bccos A. D. cos A = . 2bc
Câu 17. Cặp số nào sau đây là nghiệm của bất phương trình x + y < 2 A. (0;5) . B. (2;3) . C. ( 3 − ;1). D. (5;0) . Câu 18. Parabol 2
y = x − 4x + 4 có đỉnh là: A. I (1; ) 1 . B. I ( 1; − 2). C. I ( 1; − ) 1 . D. I (2;0).
Câu 19. Với x thuộc tập hợp nào dưới đây thì f (x) 2
= x – 4x + 3 luôn âm? A. ( ; −∞ ) 1 ∪(4;+∞) . B. (1;3). C. ( ; −∞ ) 1 ∪[3;+∞). D. [1; ] 3 .
Câu 20. Cho tập hợp A = {1;2;3;4; } 5 , B = {2;3;5;6; }
7 . Khi đó A∩ B = ?
A. A ∩ B = {2; } 3 .
B. A ∩ B = { } 3 .
C. A ∩ B = {3; } 5 .
D. A ∩ B = {2;3 } ;5 .
Câu 21. Tập xác định của hàm số 2
y = x − 2x + 273 là A. D = ( 1; − + ∞).
B. D = (0;+ ∞) .
C. D =  . D. D = ( ;0 −∞ ). Mã đề 101 Trang 2/4
Câu 22. Cho tam thức bậc hai 2
f (x) = ax + bx + c (a ≠ 0). Mệnh đề nào sau đây đúng?  b
A. Nếu ∆ = 0 thì f (x) luôn cùng dấu với hệ số a , với mọi x  \  ∈ − . 2a   
B. Nếu ∆ > 0 thì f (x) luôn cùng dấu với hệ số a , với mọi x ∈  .
C. Nếu ∆ < 0 thì f (x) luôn cùng dấu với hệ số b , với mọi x ∈  .
D. Nếu ∆ < 0 thì f (x) luôn trái dấu với hệ số a , với mọi x ∈  .
Câu 23. Tìm khẳng định đúng trong các khẳng định sau?
A. f (x) = 2x − 7 là tam thức bậc hai. B. f (x) 3
= x + 2x − 4 là tam thức bậc hai. C. f (x) 4 2
= x − 2x +1 là tam thức bậc hai. D. f (x) 2
= x + 2x − 5 là tam thức bậc hai.
Câu 24. Trong các mệnh đề toán học sau, mệnh đề nào sai?
A. 22 chia hết cho 11.
B. 10 là số nguyên tố.
C. 25 là ước của 125 .
D. 49 là số chính phương.
Câu 25. Điều kiện xác định của phương trình 2x − 4 = x là
A. x ≥ 0 .
B. x < 0 .
C. x ≥ 2 . D. x > 2 . 3x 1
Câu 26. Tìm tập xác định D của hàm số y  . 2x 2
A. D 1;.
B. D 1;. C. D   . D. D   \  1 .
Câu 27. Cho bốn điểm bất kì A, B, C, O. Đẳng thức nào sau đây đúng?
  
  
  
  
A. OA = OB + . AB
B. AB = OB + . OA
C. OA = OC + C . A
D. AB = AC + BC.
Câu 28. Bất phương trình nào sau đây không phải là bất phương trình bậc nhất hai ẩn? x y
A. 2x − 3y + 2 ≤ 0 .
B. − +10 < 0.
C. x − 5y −1 ≥ 0 . D. 2
x + 3y − 2x +1≤ 0. 2 3
Câu 29. Nghiệm của phương trình 3x + 6 = 3là A. x = 1 − .
B. x = 0 .
C. x = 5. D. x = 1.
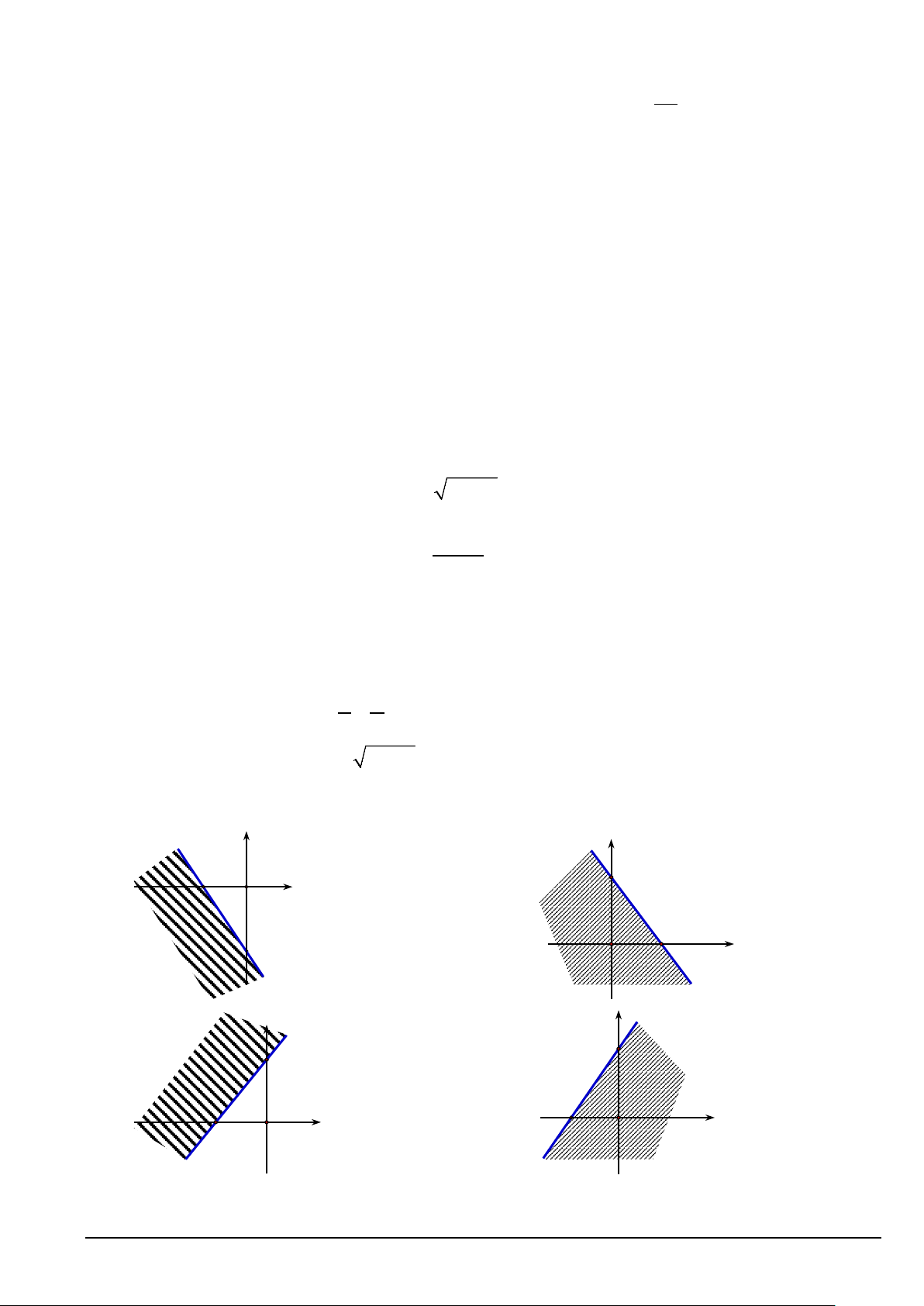
Câu 30. Miền nghiệm của bất phương trình 3x − 2y ≥ 6 − là: y y 3 2 − O x 2 x 3 O A. B. . y y 3 3 2 − 2 − O x O x C. . D. Mã đề 101 Trang 3/4
Câu 31. Cho tập hợp A = ( ; −∞ ]
3 ; B = (1;5]. Khi đó, tập A∪ B là A. ( ; −∞ 5] . B. (1;3]. C. (3;5 ] . D. ( ; −∞ 1) .
Câu 32. Cho tam giác ABC . Mệnh đề nào dưới đây đúng ?. A. a = .
R sin A . B. 2a = . R sin A. C. a = 2 . R cos A. D. a = 2 . R sin A.
Câu 33. Cho tam thức bậc hai 2
f (x)  ax bx c (a  0). Điều kiện cần và đủ để f (x)  0, x   là: a   0 a   0 a   0 a   0 A.  . B.  . C.  . D.  .      0        0    0    0  
Câu 34. Cho hình vuông ABCD có cạnh bằng a . Tính độ dài vectơ AB .
A. a 2 . B. 2a . C. a . D. a 3 .
Câu 35. Gọi O là tâm hình bình hành ABCD. Đằng thức nào sau đây sai?
   
  
   
  
A. OB − OC = OD − .
OA B. AB − AD = . DB
C. BC − BA = DC − .
DA D. OA − OB = C . D
II.Phần tự luận:(3.0 điểm)
Câu 1. Giải phương trình x + 7 = 2x −1.
Câu 2. Cho tam thức f (x) 2
= x − 2mx − 4m + 5 . Tìm tất cả các giá trị nguyên của m để f (x) > 0 x ∀ ∈  .
Câu 3. Cho tam giác ABC có M là điểm thuộc cạnh BC sao cho MB = 2MC , N là trung điểm của cạnh
   
   
AC . Giả sử AB = a, AC = b . Biểu diễn các vectơ AM , MN theo hai vectơ a và b .
Câu 4. Thầy Nam được bố chia cho một miếng đất để xây nhà, biết miếng đất được chọn là hình chữ nhật
có chu vi 400 (m) . Hỏi thầy Nam chọn mỗi kích thước của miếng đất bằng bao nhiêu để diện
tích đất dùng để xây nhà là lớn nhất.
Câu 5. Tìm m để phương trình 2
x − x + m + ( − x) 2 2 5 1
2x − 4x + m = 0 có hai nghiệm thực phân biệt.
Câu 6. Cho tam giác ABC , M là điểm di động trên đường tròn ngoại tiếp tam giác ABC . Tìm vị trí điểm M để 2 2 2
MB + MC − 2MA đạt giá trị nhỏ nhất.
------ HẾT ------ Mã đề 101 Trang 4/4 SỞ GD-ĐT HÀ TĨNH
ĐỀ KIỂM TRA CUỐI HỌC KỲ I, NĂM HỌC 2023- 2024
TRƯỜNG THPT CÙ HUY CẬN Môn:Toán-Lớp 10
Thời gian làm bài: 90 phút; Không kể giao đề ĐỀ CHÍNH THỨC
(35 câu trắc nghiệm và 05 câu tự luận) Mã đề: 102
Họ và tên thí sinh:............................................ SBD..............Lớp..........
I.Phần trắc nghiệm khách quan:( 7.0 điểm) Câu 1. Parabol 2
y = x + 4x + 4 có đỉnh là: A. I ( 2; − 0) .
B. I (2;16). C. I ( 1; − 2) . D. I ( 1; − ) 1 .
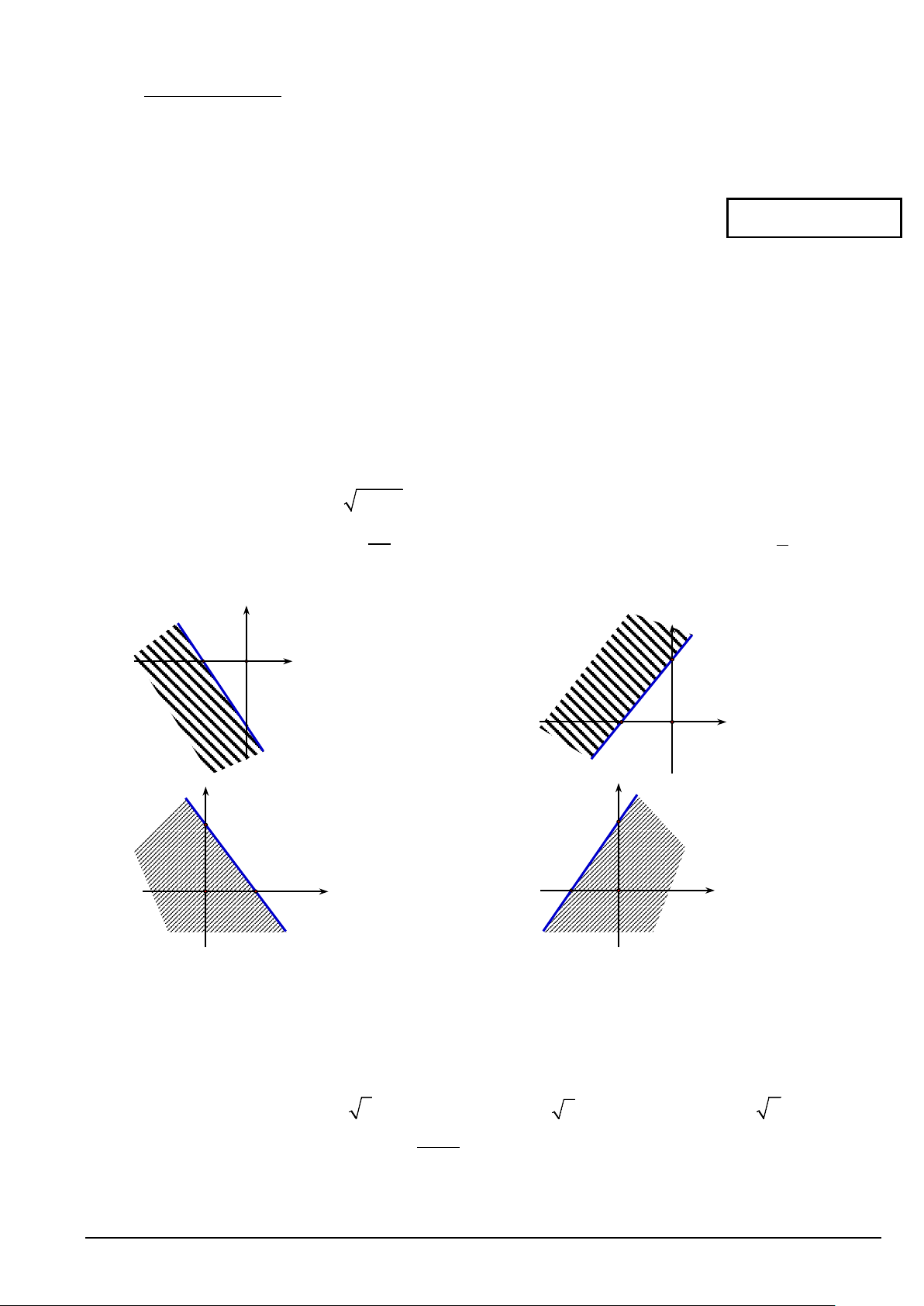
Câu 2. Cặp số nào sau đây là nghiệm của bất phương trình x − 2y < 3 A. (0; 5 − ) . B. (5;0) . C. (2;3) . D. (3; 1) − .
Câu 3. Cho parabol có phương trình 2
y = x + 8x − 2. Trục đối xứng của Parabol là đường thẳng A. x = 8 − . B. x = 4 − . C. x = 2 − . D. x = 4 .
Câu 4. Nghiệm của phương trình 5x +1 = 4 là 1 3
A. x = 3. B. x − = . C. x = 3 − . D. x = . 5 5
Câu 5. Miền nghiệm của bất phương trình 3x + 2y ≥ 6 là: y y 2 − 3 O x 3 2 − O x A. B. . y y 3 3 2 x 2 − O O x C. . D.
Câu 6. Cho bốn điểm bất kì A, B, C, O. Đẳng thức nào sau đây đúng?
  
  
  
  
A. OA = OC + AC.
B. AB = AO + . OB
C. AB = AC + BC.
D. AB = OA + OB .
Câu 7. Cho parabol (P) có phương trình 2
y = x − 5x + 6. Số giao điểm của (P) với trục hoành là A. 1. B. 3. C. 2. D. 0 . 
Câu 8. Cho hình vuông ABCD có cạnh bằng 2a . Tính độ dài vectơ BC . A. 2a . B. a 3 .
C. 2 2a . D. a 2 .
Câu 9. Tìm tập xác định x  D của hàm số 3 1 y  . 2x  2
A. D 1;. B. D   .
C. D   \  1 .
D. D 1;. Mã đề 102 Trang 1/4
Câu 10. Tìm khẳng định đúng trong các khẳng định sau? A. f (x) 3
= −x + 2x + 4 là tam thức bậc hai.
B. f (x) = 3x +1 là tam thức bậc hai. C. f (x) 2
= 3x − 2x + 5 là tam thức bậc hai. D. f (x) 4 2
= x + 2x +1 là tam thức bậc hai.
Câu 11. Cho tam giác ABC . Mệnh đề nào dưới đây đúng ?. A. b = 2 .
R cos B . B. b = 2 .
R sin B . C. b = .
R sin B . D. 2b = . R sin B .       
Câu 12. Cho hai vectơ a và b khác 0 . Xác định góc α giữa hai vectơ a và b khi .
a b = a . b . A. o α = 45 . B. o α = 90 . C. o α =180 . D. o α = 0 .
Câu 13. Bảng xét dấu nào sau đây là của tam thức f (x) 2 = x − 5x + 4. A. B. C. D.
Câu 14. Số nghiệm của phương trình 2
x − 5x − 2 = x − 2 là A. 0 . B. 3. C. 2. D. 1.
Câu 15. Cho tam giác ABC ,G là trọng tâm của tam giác ABC , M là điểm bất kì. Đẳng thức vectơ nào
sau đây đúng?
   
   
A. MA + MB + MC = 0.
B. GA + GB + GC = 3GM .
   
   
C. MA + MB + MC = 2MG .
D. MA + MB + MC = 3MG .
Câu 16. Tập xác định của hàm số 2
y = x + 2x + 2023 là A. D = ( 1; − + ∞).
B. D =  .
C. D = (0;+ ∞) . D. D = ( ;0 −∞ ).
Câu 17. Với x thuộc tập hợp nào dưới đây thì f (x) 2
= x – 4x + 3 luôn dương? A. ( ; −∞ ) 1 ∪(3;+∞). B. (1;3). C. [1; ] 3 . D. ( ; −∞ ] 1 ∪[3;+∞) .
Câu 18. Cho tam thức bậc hai 2
f (x)  ax bx c (a  0). Điều kiện cần và đủ để f (x)  0, x   là: a   0 a   0 a   0 a  0 A.  . B.  . C.  . D.  .      0        0    0     0
Câu 19. Trong các mệnh đề toán học sau, mệnh đề nào sai?
A. 25 là ước của 125 . B. 16 là số lẻ .
C. 20 chia hết cho 5 .
D. 36 là số chính phương. Mã đề 102 Trang 2/4
Câu 20. GọiO là giao điểm hai đường chéo AC và BD của hình bình hành ABCD . Đẳng thức nào sau
đây là đẳng thức sai?        
A. OA = CO .
B. DO = BO .
C. AB = DC .
D. AD = BC .
Câu 21. Cho tam thức bậc hai 2
f (x) = ax + bx + c (a ≠ 0). Mệnh đề nào sau đây đúng?
A. Nếu ∆ = 0 thì f (x) luôn cùng dấu với hệ số a , với mọi x ∈ 
B. Nếu ∆ < 0 thì f (x) luôn cùng dấu với hệ số a , với mọi x ∈  .
C. Nếu ∆ < 0 thì f (x) luôn cùng dấu với hệ số b , với mọi x ∈  .
D. Nếu ∆ > 0 thì f (x) luôn trái dấu với hệ số a , với mọi x ∈  .
Câu 22. Gọi O là tâm hình bình hành ABCD. Đằng thức nào sau đây sai?
   
  
   
  
A. BC − BA = DA − DC. B. AB − AD = . DB
C. OB − OC = OA − .
OD D. DA − DB = . BA Câu 23. Parabol 2
y = ax + bx + 2 đi qua hai điểm A(1;2) và B(2;0) có phương trình là A. 2
y = −x + 2x + 2 . B. 2
y = −x + x + 2 . C. 2
y = x + x + 2 . D. 2
y = −x − 2x + 2.
Câu 24. Cho tam giác ABC , gọi M là trung điểm của BC và G là trọng tâm của tam giác ABC . Mệnh
đề nào sau đây đúng?  
 1  
 1  
  
A. 3AG = AM . B. GM = ( AB + AC). C. AG = ( AB + AC). D. AB + AC = AM . 6 2  
Câu 25. Cho tam giác đều ABC có cạnh bằng 2 .
a Tính tích vô hướng B . A BC.         A. 2 B .
A BC = 2 3a B. 2 B .
A BC = 2a . C. 2 B . A BC = 2 − a D. 2 B . A BC = 2 − 3a
Câu 26. Cho hàm số y = x − 6 . Điểm nào sau đây thuộc đồ thị hàm số đã cho? A. (2;4). B. ( 1; − 5 − ). C. ( 2; − 4 − ). D. (1; 5 − ) .  
Câu 27. Cho tam giác ABC vuông tại A có AB = 3c ,
m AC = 4cm . Khi đó AC − AB là: A. 5 . B. 5 . C. 2 13 . D. 4.
Câu 28. Cho tập hợp A = ( ;
−∞ 2] ; B = (1;8]. Khi đó, tập A∪ B là A. ( ; −∞ 1) . B. (1;2]. C. ( ; −∞ 8]. D. (2;8 ] .
Câu 29. Cho tam giác ABC có =  0 =  0
BC 6, A 120 , B = 30 . Chọn khẳng định đúng.
A. AB = 4 3 .
B. AB = 2 3 .
C. AB = 3 . D. AB = 3 3 .
Câu 30. Cho hàm số = ( ) 2
y f x = ax + bx + c có đồ thị như hình vẽ . Đặt 2
∆ = b − 4ac , hãy xác định
dấu của hệ số a và ∆ .
A. a > 0 , ∆ < 0.
B. a > 0 , ∆ > 0.
C. a < 0 , ∆ > 0 .
D. a > 0 , ∆ = 0.
Câu 31. Bất phương trình nào sau đây không phải là bất phương trình bậc nhất hai ẩn? x y
A. 2x + 3y + 2 ≤ 0 . B. 2
x + 3y + x +1≥ 0.
C. x − 5y +1 < 0 . D. − +10 < 0. 2 3  
Câu 32. Cho tam giác ABC . Tập hợp các điểm M thỏa mãn . MB AC = 0 là:
A. đường thẳng.
B. đoạn thẳng.
C. một điểm. D. đường tròn.
Câu 33. Điều kiện xác định của phương trình 2x + 4 = x − 2 là A. x < 2 − .
B. x ≥ 2 . C. x ≥ 2 − . D. x < 2 . Mã đề 102 Trang 3/4
Câu 34. Cho tam giác ABC . Mệnh đề nào dưới đây sai ?. 2 2 2
a + b − c A. cosC = . B. 2 2 2
b = a + c − 2accos B . 2ab 2 2 2
b + c − a C. 2 2 2
c = a + b − abcosC . D. cos A = . 2bc
Câu 35. Cho tập hợp A = {1;2;3;4;5; } 8 , B = {2;5;6; }
7 . Khi đó A∩ B = ?
A. A ∩ B = {2; } 3 .
B. A ∩ B = { } 2 .
C. A ∩ B = {3; } 5 .
D. A ∩ B = {2; } 5 .
II.Phần tự luận:(3.0 điểm)
Câu 1. Giải phương trình x + 5 = 2x + 4 .
Câu 2. Cho tam thức f (x) 2
= −x + 2mx + 5m − 6 .Tìm tất cả các giá trị nguyên của m để f (x) < 0 . x ∀ ∈ 
Câu 3. Cho tam giác ABC có M là điểm thuộc cạnh BC sao cho 2MB = MC , N là trung điểm của cạnh
   
   
AB . Giả sử AB = a, AC = b . Biểu diễn các vectơ AM , MN theo hai vectơ a và b .
Câu 4. Thầy Hùng muốn làm một cái sân hình chữ nhật có chu vi 240 (m) . Hỏi thầy Hùng chọn mỗi kích
thước của cái sân bằng bao nhiêu để diện tích sân là lớn nhất.
Câu 5. Tìm m để phương trình 2
x − x − m + ( − x) 2 5 8 1 2
5x − 6x − m = 0 có hai nghiệm thực phân biệt.
Câu 6. Cho tam giác ABC , M là điểm di động trên đường tròn ngoại tiếp tam giác ABC . Tìm vị trí điểm M để 2 2 2
MA + MC − 2MB đạt giá trị nhỏ nhất.
------ HẾT ------ Mã đề 102 Trang 4/4
Đề\câu 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28
000 C A C D C A D D C B B A C A A B B A B A A A D A C D B D
101 A C B A C B C A C C B D D D D B A D B B B A B B B D B C
102 D D D A B A C C D A A B C A D B A C C B B C D D B C D A 29 30 31 32 33 34 35 D C B A B A B B C B A C C D D D B A D A B
ĐÁP ÁN TỰ LUẬN MÃ ĐỀ 101 VÀ 103 Câu Nội dung Điểm Câu 1
Giải phương trình x + 7 = 2x −1. Giải: 2x −1 ≥ 0
x + 7 = 2x −1 ⇔  2 0.25
x + 7 = 4x − 4x +1  1 x ≥ 1   2 x ≥  ⇔  2 ⇔ x = 2 ⇔ x = 2  2 0.25
4x − 5x − 6 = 0  3 x − = (L)  4
Chú ý: HS có thể giải bằng cách bình phương hai vế rồi thử nghiệm
f x = x − mx − m + Câu 2 Cho tam thức ( ) 2 2 4
5 . Tìm tất cả các giá trị nguyên của m để
f (x) > 0 x ∀ ∈  Giải:  >  = > 0.25 f (x) a 0 a 1 0 > 0 x ∀ ∈  ⇔  ⇔  ⇔ 5 − < m <1 2 ∆ < 0
∆′ = m + 4m − 5 < 0
Vì m nguyên nên m∈{ 4 − ; 3 − ; 2 − ; 1 − ; } 0
Vậy có 5 giá trị nguyên của m thỏa mãn điều kiện bài toán 0.25 Câu 3
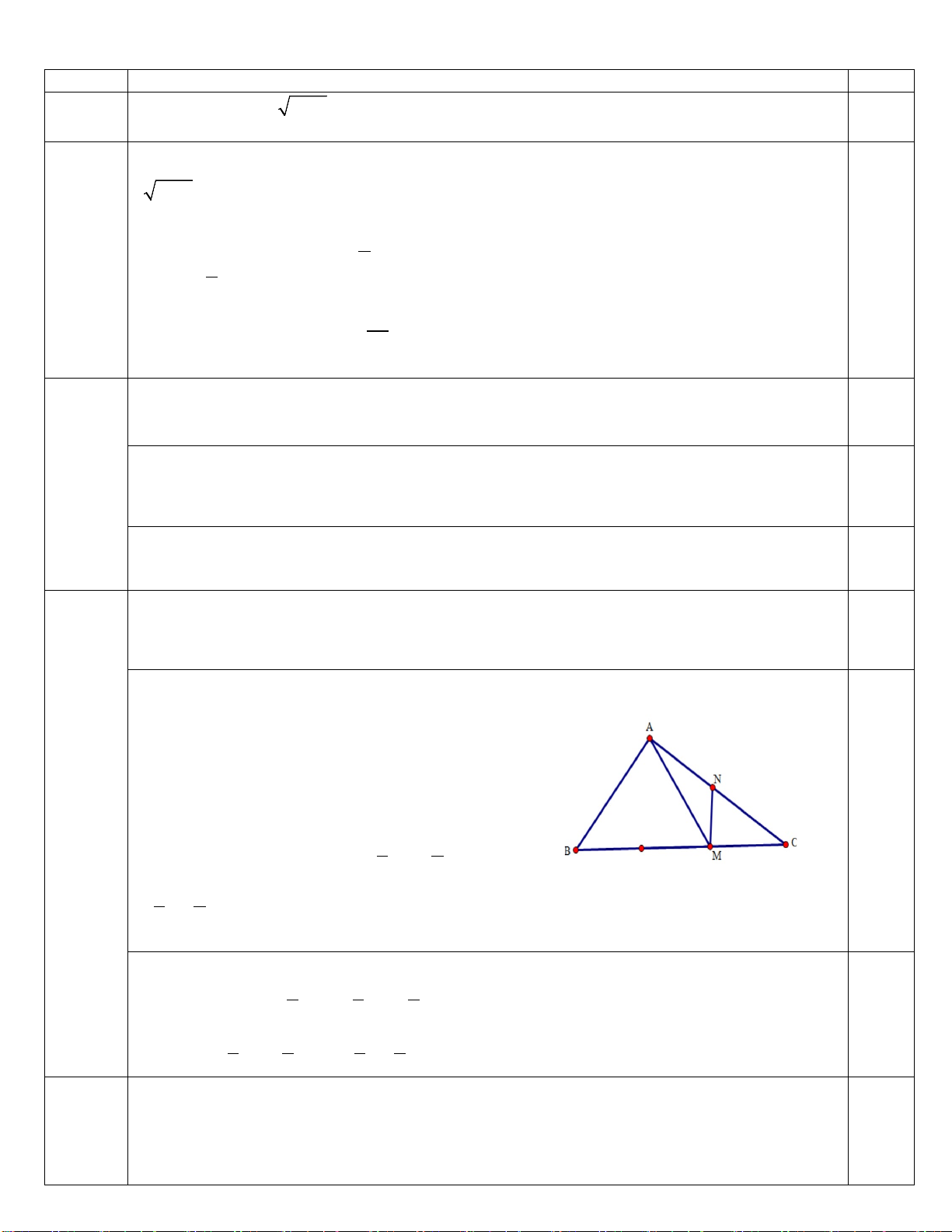
Cho tam giác ABC có M là điểm thuộc cạnh BC sao cho MB = 2MC , N là trung điểm của
   
  
cạnh AC . Giả sử AB = a, AC = b . Biểu diễn các vectơ AM , MN theo hai vectơ a  và b . Giải: Ta có
  
BM = AM − AB( ) 1
  
   0.25
CM = AM − AC ⇒ 2CM = 2AM − 2AC (2) Lấy ( ) 1 + (2) vế theo vế ta có    
 1  2 
3AM − AB − 2AC = 0 ⇒ AM = AB + AC 3 3 1  2  = a + b 3 3 Lại có
   1   1  2  MN AN AM AC AB AC  = − = − +   0.25 2  3 3   1  1  1  1 
⇒ MN = − AB − AC = − a − b 3 6 3 6 Câu 4
Thầy Nam được bố chia cho một miếng đất để xây nhà, biết miếng đất được chọn là hình chữ
nhật có chu vi 400 (m) . Hỏi thầy Nam chọn mỗi kích thước của miếng đất bằng bao
nhiêu để diện tích đất dùng để xây nhà là lớn nhất. Giải:
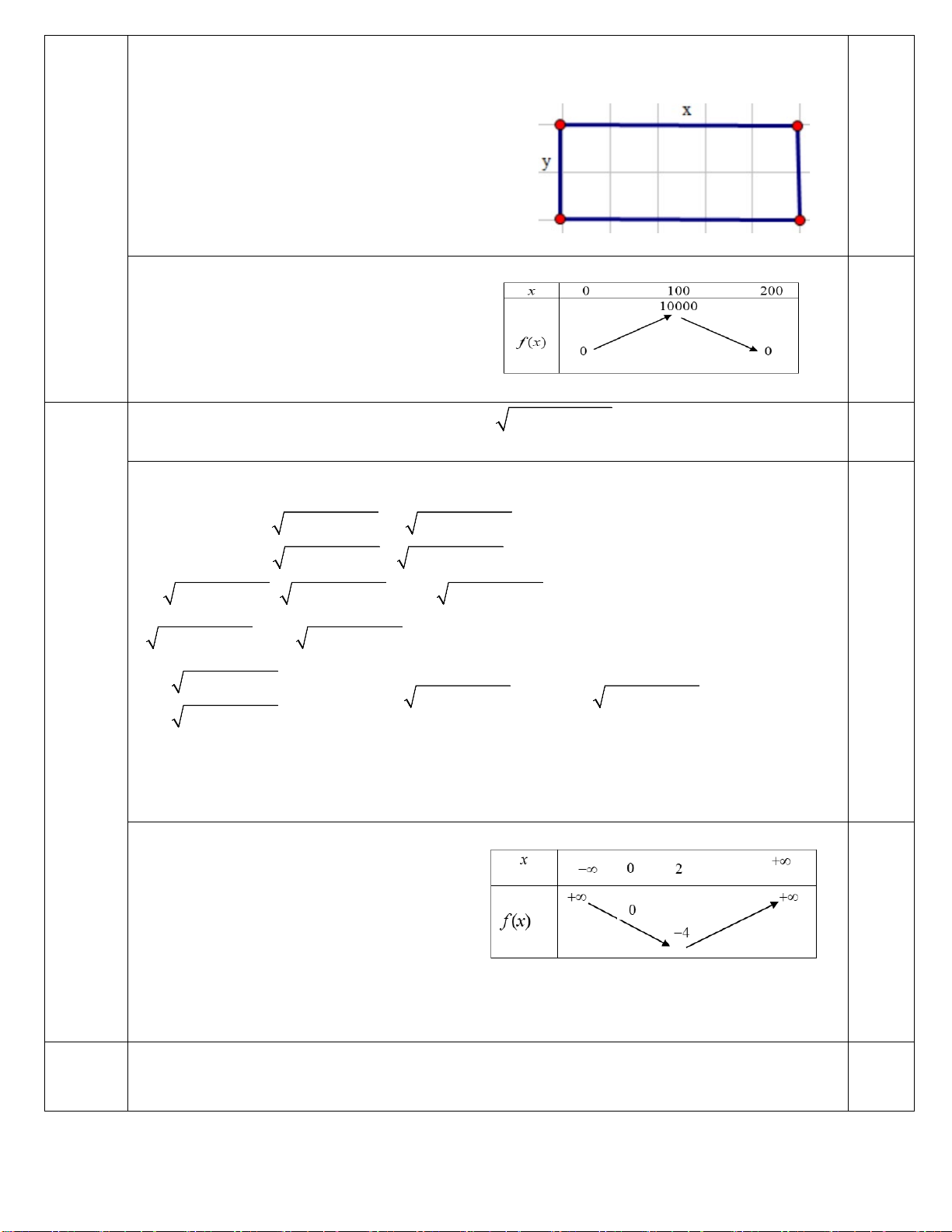
Gọi chiều dài của miếng đất là x , chiều rộng của miếng đất là y(x, y > 0; x, y : m) Theo bài ra ta có
2(x + y) = 400 ⇒ x + y = 200
⇒ y = 200 − x(x < 200)
Khi đó diện tích miếng đất là: S = x(200 − x) 0.25
Xét hàm số f (x) = x( − x) 2 200 = −x + 200x
Lập bảng biến thiên suy ra
Miếng đất có diện tích lớn nhất là 2 10000(m )
Khi x = y =100(m) 0.25
Vậy miếng đất là hình vuông cạnh 100m Câu 5
Tìm m để phương trình 2
x − x + m + ( − x) 2 2 5 1
2x − 4x + m = 0 có hai nghiệm thực phân biệt.
Giải: Điều kiện 2
2x − 4x + m ≥ 0 PT đã cho 2 2 2
⇔ 2x − 5x + m + 2x − 4x + m − x 2x − 4x + m = 0 2 2 2
⇔ x − 4x + m − x 2x − 4x + m + 2x − 4x + m − x = 0 2
⇔ 2x − 4x + m ( 2
2x − 4x + m − x) 2
+ 2x − 4x + m − x = 0 ( 2
2x − 4x + m − x)( 2
2x − 4x + m + )1  2
2x − 4x + m − x = 0 2 2 ⇔ 
⇔ 2x − 4x + m − x = 0 ⇔ 2x − 4x + m = x 2
 2x − 4x + m +1= 0  (VN ) x ≥ 0 x ≥ 0 ⇔  ⇔ 2 2  2 0.25
2x − 4x + m = x
x − 4x = −m  (*) Đặt f (x) 2
= x − 4x . Ta có BBT:
Yêu cầu bài toán suy ra PT(*) phải có
Hai nghiệm phân biệt thỏa mãn 0 ≤ x < x 1 2
Dựa vào bảng biến thiên suy ra 0.25 4
− < −m ≤ 0 ⇔ 0 ≤ m < 4 Vậy m∈[0;4) Câu 6
Cho tam giác ABC , M là điểm di động trên đường tròn ngoại tiếp tam giác ABC . Tìm vị trí điểm M để 2 2 2
MB + MC − 2MA đạt giá trị nhỏ nhất. Giải:
Gọi O là tâm đường tròn ngoại tiếp tam giác ABC , I là trung điểm BC . Theo đề bài suy ra 2 2 2 2 2
OM = OA = OB = OC = R Ta có 2 2 2
MB + MC − 2MA       A
= (OB −OM )2 +(OC −OM )2 − 2(OA−OM )2       = 2
− OM.OB − 2OM.OC + 4OM.OA
    M 0.25
= 2OM (2OA − OB − OC) O
    
= 2OM (BA + C ) A = 4 − OM.AI   B C = 4
− OM.AI.cos(OM, AI ) ≥ 4 − OM.AI I  
Vì OM và AI không đổi. Do đó 2 2 2
MB + MC − 2MA đạt giá trị nhỏ nhất khi cos(OM, AI ) =1   0.25
. Khi đó M thuộc đường tròn (O) sao có OM và AI cùng hướng.
ĐÁP ÁN TỰ LUẬN MÃ ĐỀ 102 VÀ 104 Câu Nội dung Điểm Câu 1
Giải phương trình x + 5 = 2x + 4 . Giải: 2x + 4 ≥ 0
x + 5 = 2x + 4 ⇔  2 0.25
x + 5 = 4x +16x +16 x ≥ 2 − x 2  ≥ − x = 1 − ⇔  ⇔  ⇔ x = 1 − 2 4x 15x 11 0  + + =  11 x − = (L) 0.25  4
Chú ý: HS có thể giải bằng cách bình phương hai vế rồi thử nghiệm
Cho tam thức f (x) 2
= −x + 2mx + 5m − 6 .Tìm tất cả các giá trị nguyên của m để Câu 2
f (x) < 0 x ∀ ∈ .  Giải:  <  = − < 0.25 f (x) a 0 a 1 0 < 0 x ∀ ∈  ⇔  ⇔  ⇔ 6 − < m <1 2 ∆ < 0
∆′ = m + 5m − 6 < 0
Vì m nguyên nên m∈{ 5 − ; 4 − ; 3 − ; 2 − ; 1 − ; } 0
Vậy có 6 giá trị nguyên của m thỏa mãn điều kiện bài toán 0.25 Câu 3
Cho tam giác ABC có M là điểm thuộc cạnh BC sao cho 2MB = MC , N là trung điểm của
   
  
cạnh AB . Giả sử AB = a, AC = b . Biểu diễn các vectơ AM , MN theo hai vectơ a  và b . Giải: Ta có
  
  
BM = AM − AB ⇒ 2BM = 2AM − 2AB( ) 1
   0.25
CM = AM − AC (2) Lấy ( ) 1 + (2) vế theo vế ta có
   
 2  1 
3AM − 2AB − AC = 0 ⇒ AM = AB + AC 3 3  2  1 
⇒ AM = a + b 3 3 Lại có
   1   2  1  MN AN AM AB AB AC  = − = − +   0.25 2  3 3   1  1  1  1 
⇒ MN = − AB − AC = − a − b 6 3 6 3 Câu 4
Thầy Hùng muốn làm một cái sân hình chữ nhật có chu vi 240 (m) . Hỏi thầy Hùng chọn mỗi
kích thước của cái sân bằng bao nhiêu để diện tích sân là lớn nhất. Giải:
Gọi chiều dài của cái sân là x , chiều rộng của cái sân là y(x, y > 0; x, y : m) Theo bài ra ta có
2(x + y) = 240 ⇒ x + y =120
⇒ y =120 − x(x <120)
Khi đó diện tích cái sân là: S = x(120 − x) 0.25
Xét hàm số f (x) = x( − x) 2 120 = −x +120x
Lập bảng biến thiên suy ra
Cái sân có diện tích lớn nhất là 2 3600(m )
Khi x = y = 60(m) 0.25
Vậy miếng đất là hình vuông cạnh 60m Câu 5
Tìm m để phương trình 2
x − x − m + ( − x) 2 5 8 1 2
5x − 6x − m = 0 có hai nghiệm thực phân biệt.
Giải: Điều kiện 2
2x − 4x + m ≥ 0 PT đã cho 2
5x −8x − m + (1− 2x) 2
5x − 6x − m = 0 2 2 2
⇔ 5x −8x − m + 5x − 6x − m − 2x 5x − 6x − m = 0 2 2 2
⇔ 5x − 6x − m − 2x 5x − 6x − m + 5x − 6x − m − 2x = 0 2
⇔ 5x − 6x − m ( 2
5x − 6x − m − 2x) 2
+ 5x − 6x − m − 2x = 0 ( 2
5x − 6x − m − 2x)( 2
5x − 6x − m + )1  2 5x
− 6x − m − 2x = 0 2 2 ⇔ 
⇔ 5x − 6x − m − 2x = 0 ⇔ 5x − 6x − m = 2x 2
 5x − 6x − m +1= 0  (VN ) 0.25 2x ≥ 0 x ≥ 0 ⇔  ⇔ 2 2  2 5
x − 6x − m = 4x
x − 6x = m  (*) Đặt f (x) 2
= x − 6x . Ta có BBT:
Yêu cầu bài toán suy ra PT(*) phải có
Hai nghiệm phân biệt thỏa mãn 0 ≤ x < x 1 2
Dựa vào bảng biến thiên suy ra 0.25 9 − < m ≤ 0 Vậy m∈( 9; − 0] Câu 6
Cho tam giác ABC , M là điểm di động trên đường tròn ngoại tiếp tam giác ABC . Tìm vị trí điểm M để 2 2 2
MA + MC − 2MB đạt giá trị nhỏ nhất. Giải:
Gọi O là tâm đường tròn ngoại tiếp tam giác ABC , I là trung điểm AC . Theo đề bài suy ra 2 2 2 2 2
OM = OA = OB = OC = R Ta có 2 2 2
MA + MC − 2MB       A
= (OA−OM )2 +(OC −OM )2 − 2(OB −OM )2       = 2
− OM.OA − 2OM.OC + 4OM.OB
    M 0.25
= 2OM (2OB − OA − OC) O
    
= 2OM (OB −OA+OB −OC)
  
     B C I
= 2OM (AB + CB) = 2OM (−BA − BC) = 4 − OM.BI   = 4
− OM.BI.cos(OM, BI ) ≥ 4 − OM.BI 0.25  
Vì OM và BI không đổi. Do đó 2 2 2
MA + MC − 2MB đạt giá trị nhỏ nhất khi cos(OM,BI ) =1  
. Khi đó M thuộc đường tròn (O) sao có OM và BI cùng hướng.
Document Outline

  • MA TRẬN KT CUỐI HKI TOÁN 10.CHC
  • Ma_de_101
  • Ma_de_102
  • Dap_an_excel_app_QM
    • Sheet1
  • ĐÁP ÁN TỰ LUẬN MÃ ĐỀ 101 VÀ 103. CUỐI HK1 TOÁN 10
  • ĐÁP ÁN TỰ LUẬN MÃ ĐỀ 102 VÀ 104. CUỐI HK1 TOÁN 10