Đề cuối học kỳ 2 Toán 11 năm 2022 – 2023 trường PTDL Hermann Gmeiner – TP HCM
Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 11 đề kiểm tra cuối học kỳ 2 môn Toán 11 năm học 2022 – 2023 trường PTDL Hermann Gmeiner, thành phố Hồ Chí Minh; đề thi có đáp án và thang điểm.
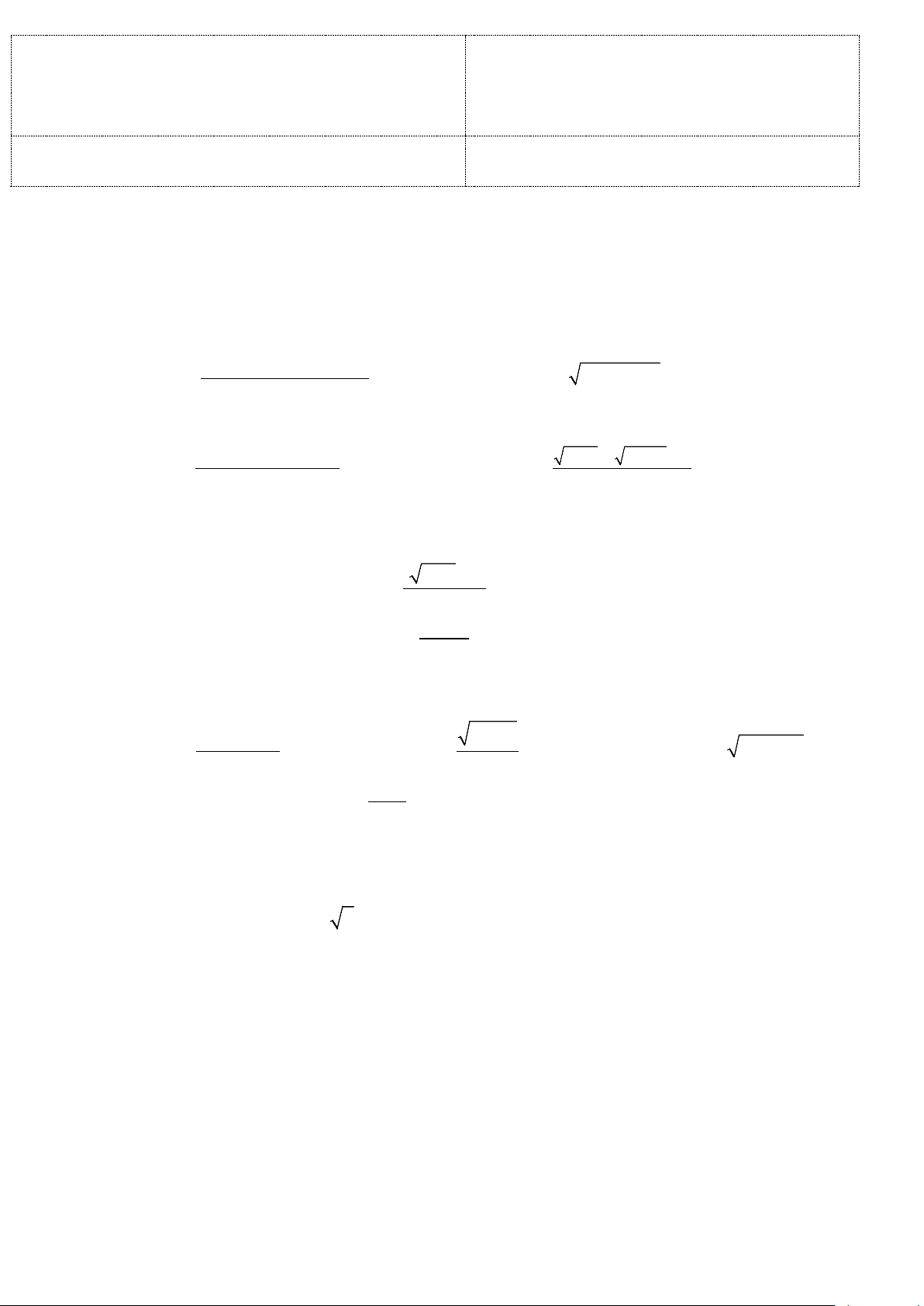
Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KIỂM TRA CUỐI HỌC KỲ II THÀNH PHỐ HỒ CHÍ MINH
NĂM HỌC 2022 – 2023
TRƯỜNG PTDL HERMANN GMEINER Môn:Toán. Lớp: 11
Thời gian làm bài: 90 phút ĐỀ CHÍNH THỨC
(Đề thi có 01 trang)
Họ và tên thí sinh:……………………………………………
Số báo danh:………………………………………………….
ĐỀ THI GỒM CÓ 05 CÂU
Câu 1: ( 2 điểm): Tính các giới hạn sau: (x −8)2.( 2 − x + 5)3 3 2 a. lim b. 2
lim ( x − 2x + 5 − x). .
x→−∞ (4 −3x )3 2 .( 3 2 −x + 2x ) x→+∞ 3 2 c.
x + 2x −12x − 9 lim . d.
x 4 4x 9 5 lim . 2 x→3 2x − 3x − 9 x0 2x
Câu 2: (1,25 điểm) Giá trị của m để hàm số liên tục tại x = 2. x −1 −1 khi x ≠ 2 f (x) 2 x − 3x + 2 = 2m+ 1 khi x = 2 6
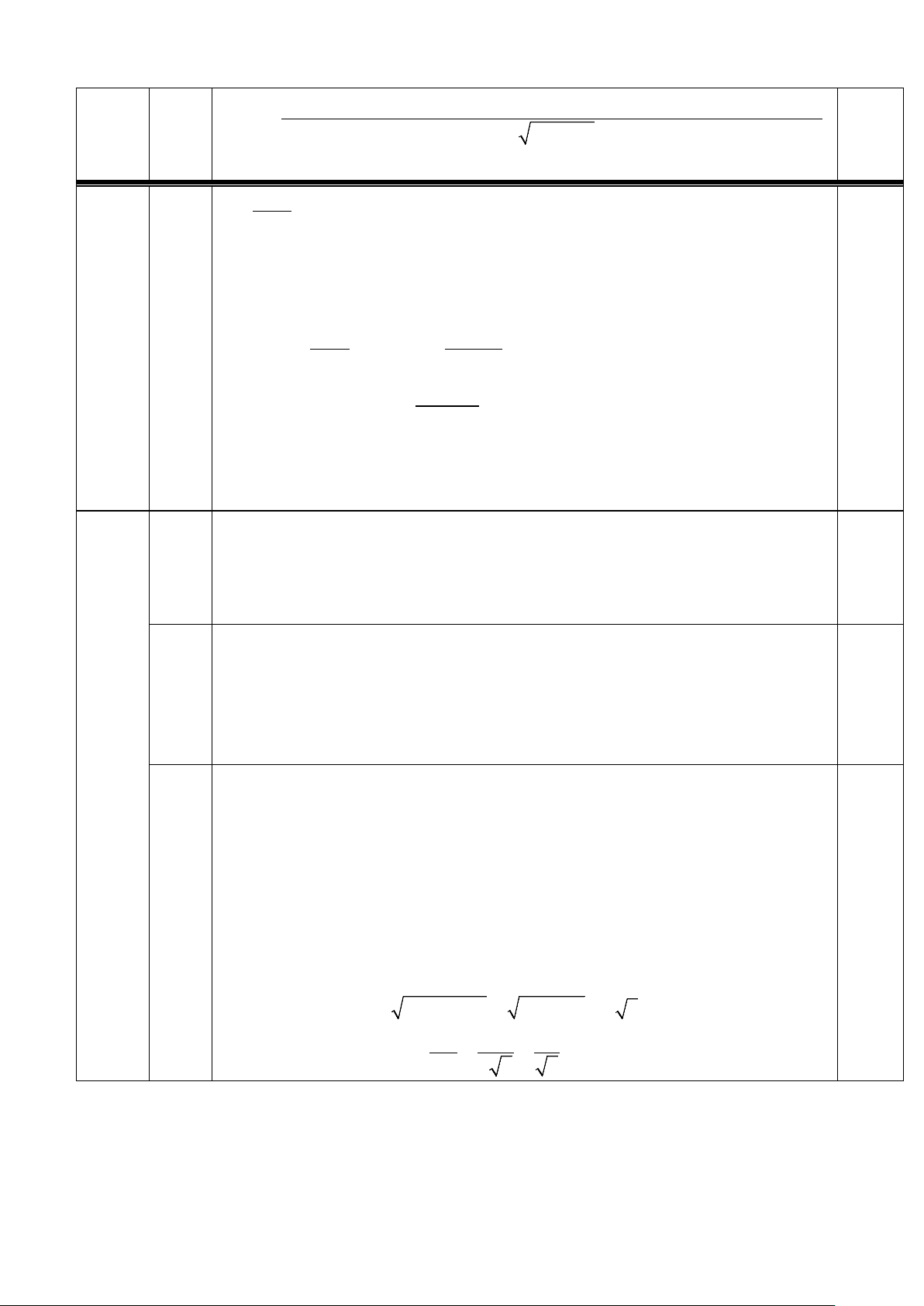
Câu 3: (2,25 điểm) Tính đạo hàm của các hàm số sau: 2 2 a. 2 − 2x + x y + =
. b. y = x 2 c. 3 y = ( x) 3 2
sin cos5 . x − 4x . x2 −1 4x +1
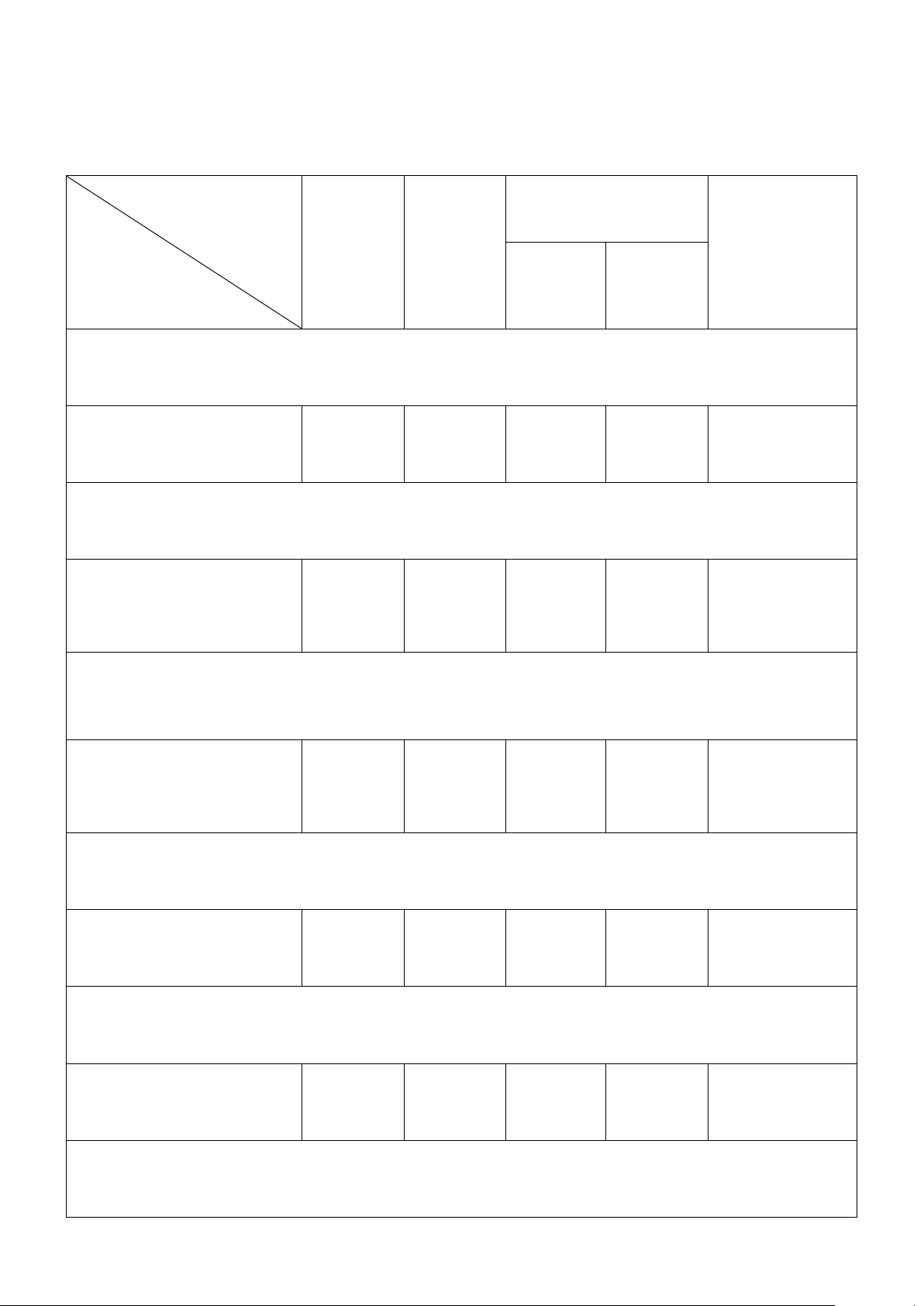
Câu 4: (1,5 điểm) Cho hàm số x + 2 y =
có đồ thị (C). Viết phương trình tiếp tuyến của x −1
(C) biết tiếp tuyến song song với đường thẳng (d ) : 3x + y − 4 = 0 .
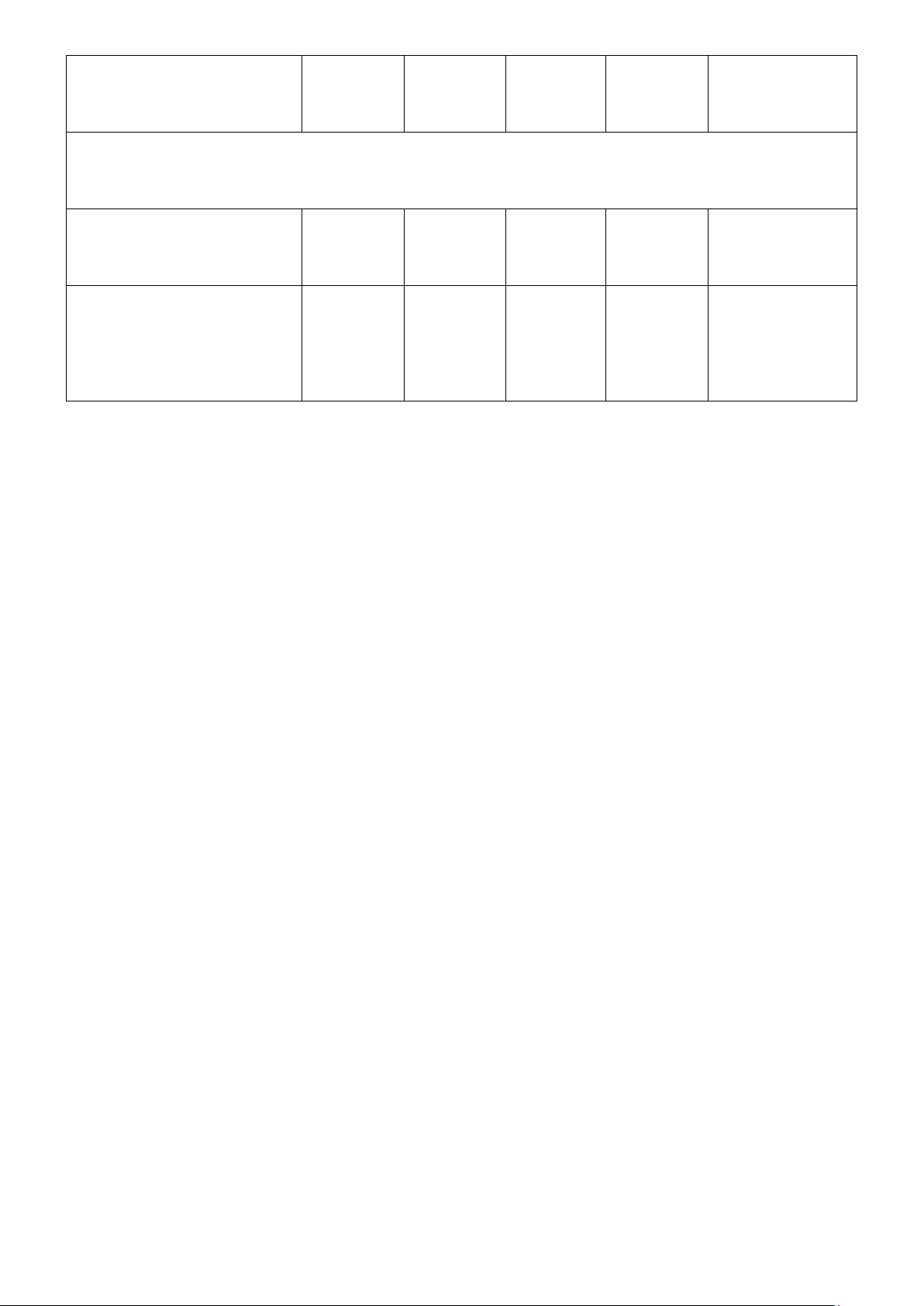
Câu 5: (3 điểm) Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Biết
SA ⊥ (ABCD) , SA = a 6 .
a. Chứng minh : BC ⊥ (SAB)
b. Chứng minh: (SAC) ⊥ (SBD)
c. Tính góc giữa đường thẳng SC và mặt phẳng (SAD)
---------- HẾT ----------
Thí sinh không được sử dụng tài liệu. Giám thị không giải thích gì thêm.
Họ và tên giám thị 1: ….……………………Chữ ký: …………………………..
Họ và tên giám thị 2: ….……………………Chữ ký: …………………………..
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KIỂM TRA CUỐI HỌC KỲ II THÀNH PHỐ HỒ CHÍ MINH
NĂM HỌC 2022 – 2023
TRƯỜNG PTDL HERMANN GMEINER Môn:Toán. Lớp: 11
Thời gian làm bài: 90 phút
ĐÁP ÁN CHÍNH THỨC
ĐÁP ÁN-THANG ĐIỀM TOÁN 11 HK2 (2022-2023) Câu Nội dung Điểm 2 3 8 5 ( x − 8) .( 2 − x + 5) 3 2 3 3 2 x 1− . 2 − + 3 2 lim x x = = +∞
x→−∞ (4 − 3x ) lim 3 .(−x + 2x ) 3 2 3 2 x→−∞ 4 2 0,25 − 3 1 − + 2 x x a) 0.5 điểm 3 lim x = −∞ x→−∞ 2 3 8 5 vì 1− . 2 − + 3 2 x x 8 0,25 lim − = < 0 3 x→−∞ 4 2 27 − 3 1 − + 2 x x Câu 1 (2đ) 2 2 − x + 5
lim ( x − 2x + 5 − x) = lim x→+∞ x→+∞ 2
x − 2x + 5 + x 0,25 b) 0.5 5 điểm 2 − + = lim x = 1 − 0,25 x→+∞ 2 5 1− + +1 2 x x 3 2 2
x + 2x −12x − 9
(x − 3)(x + 5x + 3) lim = lim 0,25 2 x→3 x→3 2x − 3x − 9 3 2(x − 3)(x + ) c) 0.5 2 điểm 2 (x + 5x + 3) = lim = 3 0,25 x→3 3 2(x + ) 2
x 4 4x 9 5 x 4 2 4x 9 3 lim lim lim x0 2x x0 2x x0 2x 0.25 d) 0.5 x 4 lim lim x điểm x0 x0 2 ( x x 4 2) 2 (
x 4x 9 3) 1 2 11 lim lim x0 x0 2( x 4 2) ( 4x 9 3) 24 0.25
Giá trị của m để hàm số liên tục tại . x −1 −1 khi x ≠ 2 f (x) 2 x − 3x + 2 = 2m + 1 khi x = 2 6 x −1 −1 x − 2 1 lim = lim = . 2 x→2 x→2 x − 3x + 2
(x − 2)(x − ) 1 ( x −1+ )1 2 0.5 Câu 2: m + (1,25 f ( ) 2 1 2 = 0.25 6 điểm)
Hàm số liên tục tại x = 2 ⇔ lim f (x) = f (2) 0.25 x→2 2a +1 1 ⇔ = ⇔ a = 1 0.25 6 2 a) 2 − 2x + x2
(2x − 2)(x2 −1) − 2x(x2 − 2x + y 2) = ⇒ y′ = 0,75 0,5 x2 − 2 1 điểm (x2 − )1 2x2 − 6x y + 2 ′ ⇒ = 0,25 (x2 2 −1) 2 2 2 Câu 3: y = x + 2
( x + 2)'(4 x+1) − x + 2(4 x+1)' ⇒ y' = (2,25 4x +1 2 (4 x+1) 0,25 điểm) b) 2x 2 0,75 (4 x+1) − 4 x + 2 2 0,25 điểm = 2 x + 2 2 (4 x+1) = x−8 2 2 (4 x+1) x + 2 0,25 3 y = sin (cos5x) 3 2 . x − 4x 2 3 2 3 2 3 0.25
⇒ y ' = 3sin (cos5x)(sin( os
c 5x))'. x − 4x + ( x − 4x )'.sin (cos5x) c) 0,75 3 2 (x − 4x )'. điểm 2
⇒ y ' = 3sin (cos5x) 3 2 3 . os c ( os c 5x).( os
c (5x)).' x − 4x + sin (cos5x) 3 2 2 x − 4x 0.25 2 30 − sin (cos5x) 3 2 2 3 . os c ( os
c 5x).sin (5x).(x − 4x ) + (3x − 8x)sin (cos5x) ⇒ y ' = 3 2 2 x − 4x 0.25 x + 2 y =
(C), biết tiếp tuyến song song với đường thẳng x −1 (
d ) : 3x + y − 4 = 0 ⇒ y = 3 − x + 4 .
Gọi (∆) là tiếp tuyến của (C), M (x ; y )là tiếp điểm 0 0 Ta có: k = = = − 0,25 ∆
f '(x ) kd 3 Câu 4: 0 x + 2 3 − (1,5
y = f (x) = ⇒ f '(x ) = 0,25 0 2 điểm) x −1 (x −1) 0.25 Suy ra : 3 −
x = 0 ⇒ y = 2 − 0 0 f '(x ) = 3 − ⇒ = 3 − ⇒ 0 2 (x −1)
x = 2 ⇒ y = 4 0 0 0 0.25
Pt tiếp tuyến: ∆ y = 3 − x − 2 0.25 1 0.25
Pt tiếp tuyến : ∆ y = 3 − x +10 2 BC ⊥ SA a) BC ⊥ AB ⇒ BC ⊥ (SAB) 1.0 đ 0,25x4 S , A AB ⊂ (SAB)
SA∩ AB = A BD ⊥ SA BD ⊥ AC b) ⇒ BD ⊥ (SAC) ⊂ 1.0 đ S , A AC (SAC) 0,25x4
SA∩ AC = A Câu 5
BD ⊂ (SBD) ⇒ (SBD) ⊥ (SAC) (3điểm) (SC,(SAD)) = ?
SC ∩ (SAD) = S CD ⊥ AD 0,25 CD ⊥ SA ⇒ CD ⊥ (SAD) c)
AD, SA ⊂ (SAD) 1.0 đ
AD ∩ SA = A
D là hình chiếu của C lên mp (SAD) 0,25 SC (SAD) = = ( ,
) (SC, SD) CSD 0,25 2 2 2 2
SD = SA + AD = 7a + a = a 7 SA
∆ D ⊥ tai A , 0,25 CD a 1 = = = ⇒ 0 tan CSD CSD = 20,7 SD a 7 7
KHUNG MA TRẬN ĐỀ KIỂM TRA HỌC KỲ II TOÁN 11 Năm học: 2022 - 2023 Cấp độ Vận dụng Tên
Nhận biết Thông hiểu Cộng Chủ đề Cấp độ thấp Cấp độ cao (nội dung, chương…) Chủ đề 1:
Tính giới hạn của hàm số Số câu: 4 Số câu: 1 Số câu: 1 Số câu: 2 Số câu: 4
Số điểm : 2 Tỉ lệ 20 % Số điểm: 0.5
Số điểm: 0.5 Số điểm: 1.0 2 điểm=20% Chủ đề 2: Hàm số liên tục Số câu: 1 Số câu: 1 Số câu: 1
Số điểm :1.25 Tỉ lệ 12.5 % Số điểm: 1.25 điểm=12.5% 1.25 Chủ đề 3: Tính đạo hàm Số câu: 3 Số câu: 1 Số câu: 1 Số câu: 1 Số câu: 3
Số điểm 2.250 Tỉ lệ 22.5 % Số điểm: Số điểm: Số điểm: 2.250 điểm=22.5% 0.75 0.75 0.75 Chủ đề 4:
Phương trình tiếp tuyến của đồ thị hàm số. Số câu: 1 Số câu:1 Số câu:1
Số điểm 1.50 Tỉ lệ 15% Số điểm:1.5 1.5 điểm=15% Chủ đề 5:
Chứng minh đường thẳng vuông góc với mặt phẳng. Số câu: 1 Số câu:1 Số câu:1
Số điểm 1.0 Tỉ lệ 10% Số điểm:1.0 1.0điểm=10% Chủ đề 6:
Chứng minh hai mặt phẳng vuông góc. Số câu: 1 Số câu:1 Số câu:1
Số điểm 1.0 Tỉ lệ 10% Số điểm:1.0 1.0 điểm=10% Chủ đề 7:
Tính góc giữa đường thẳng và mặt phẳng. Số câu: 1 Số câu:1 Số câu:1
Số điểm 1.0 Tỉ lệ 10% Số điểm:1.0 1.0 điểm=10% Tổng số câu: 12 Số câu: 3 Số câu: 5 Số câu: 3 Số câu: 1 Số câu: 12
Tổng số điểm:10.0
Số điểm:2.25 Số điểm:5.0
Số điểm:1.75 Số điểm:1.00 Số điểm: 10.0=100% Tỉ lệ 22.5% Tỉ lệ 50% Tỉ lệ 17.5% Tỉ lệ 10% Tỉ lệ 100%
Document Outline
- Toan 11 hk2 - Hermann Gmeiner - 2023
- ĐÁ HK2 TOÁN 11-2023
- Matran-Toan11-HK2 (1)