Đề cuối kì 1 Toán 9 năm 2024 – 2025 phòng GD&ĐT Gia Lâm – Hà Nội

PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
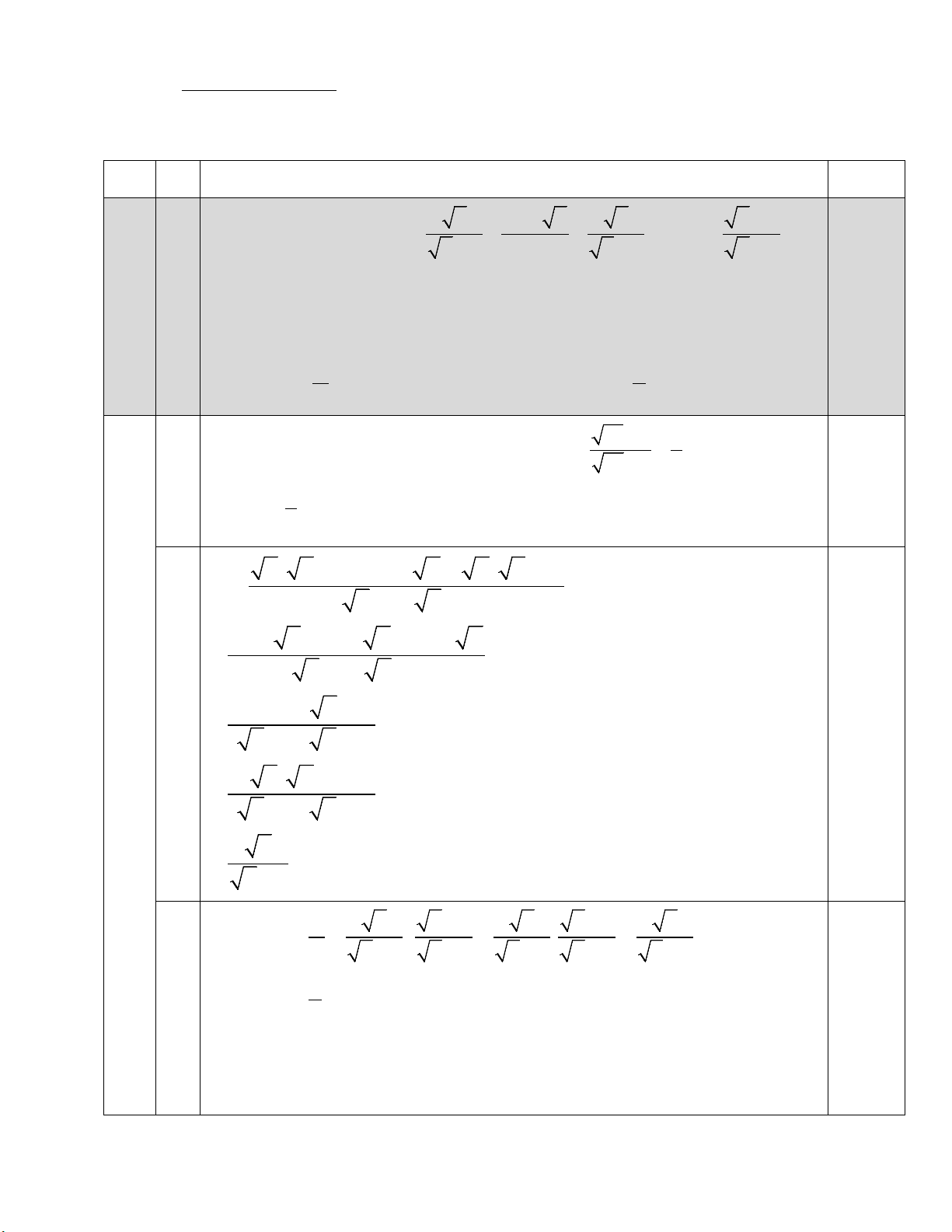
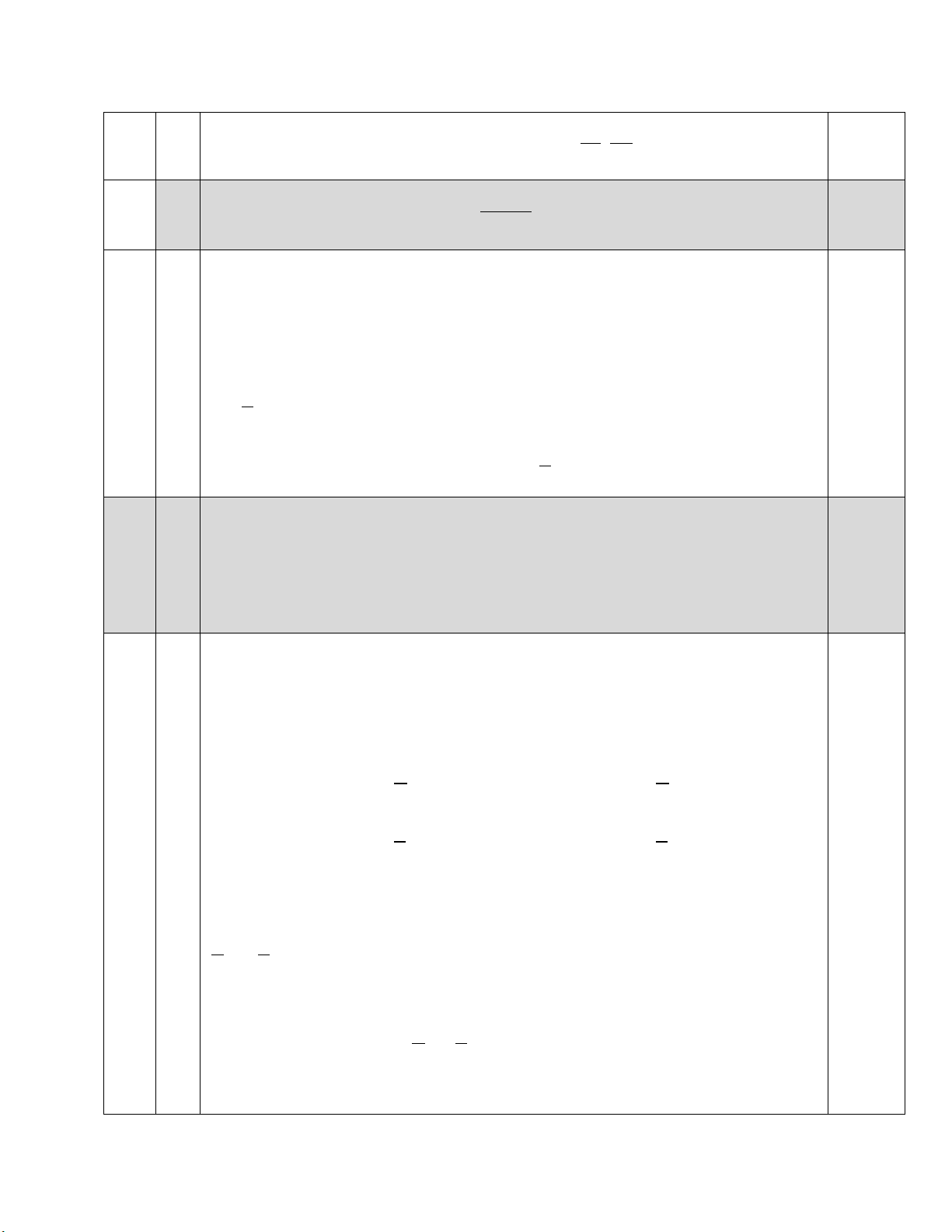
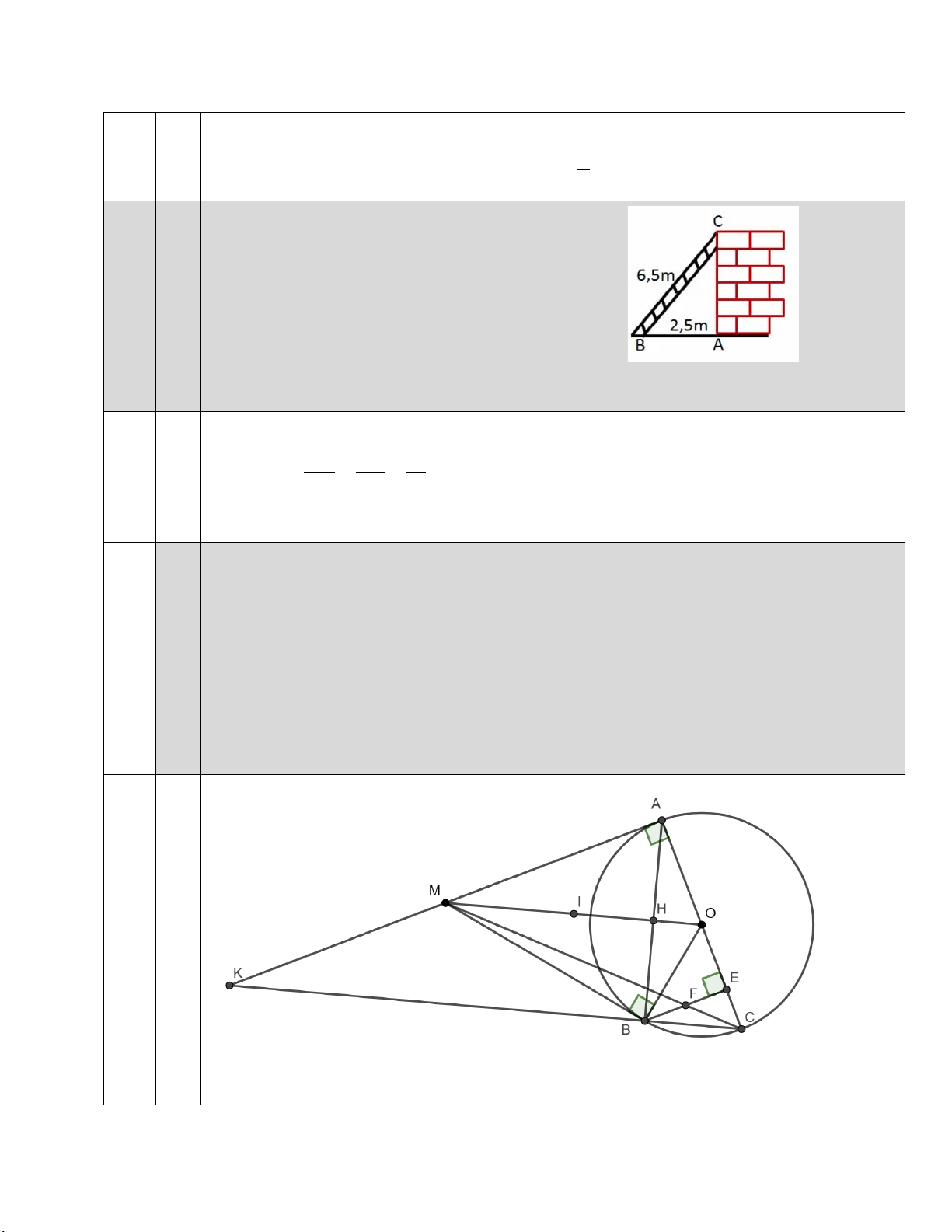
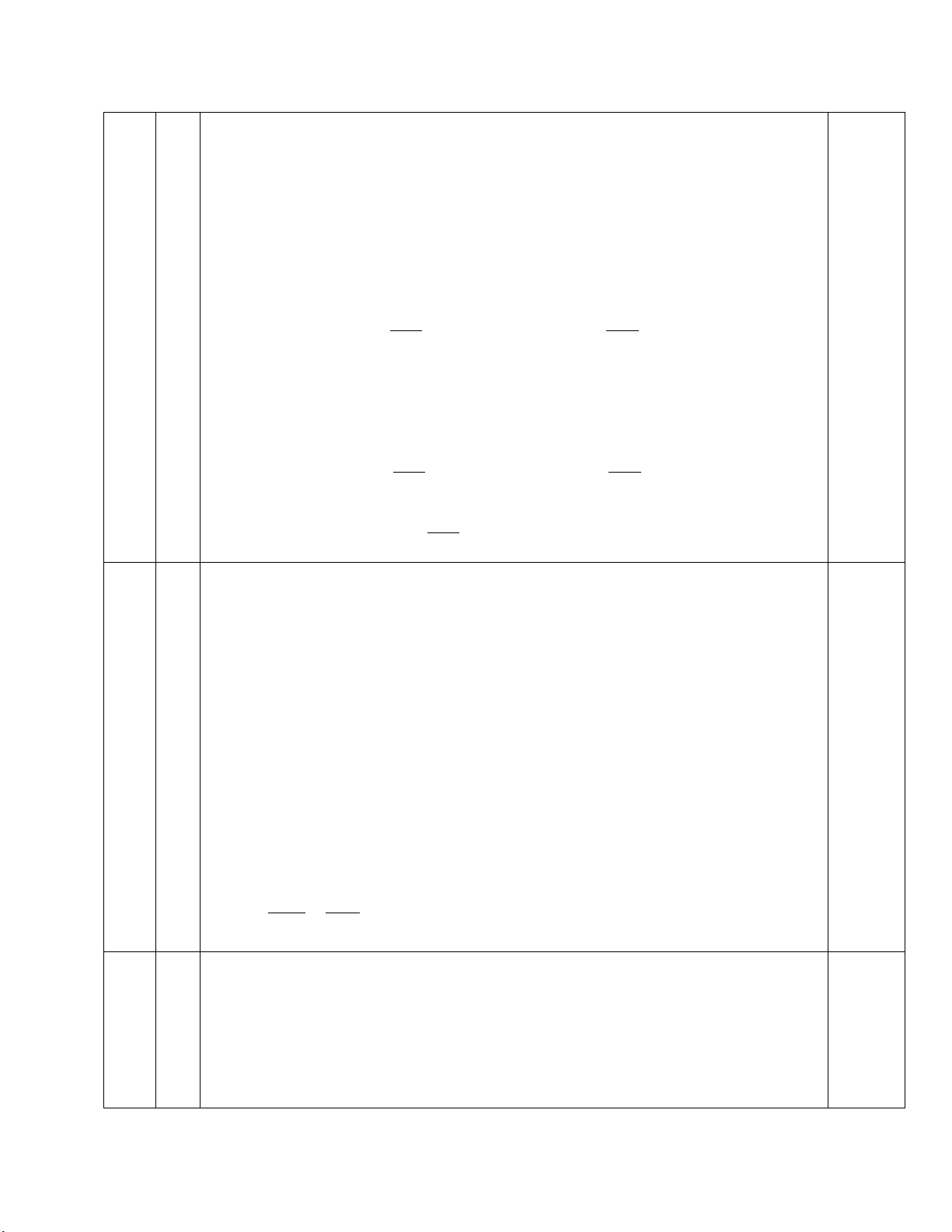
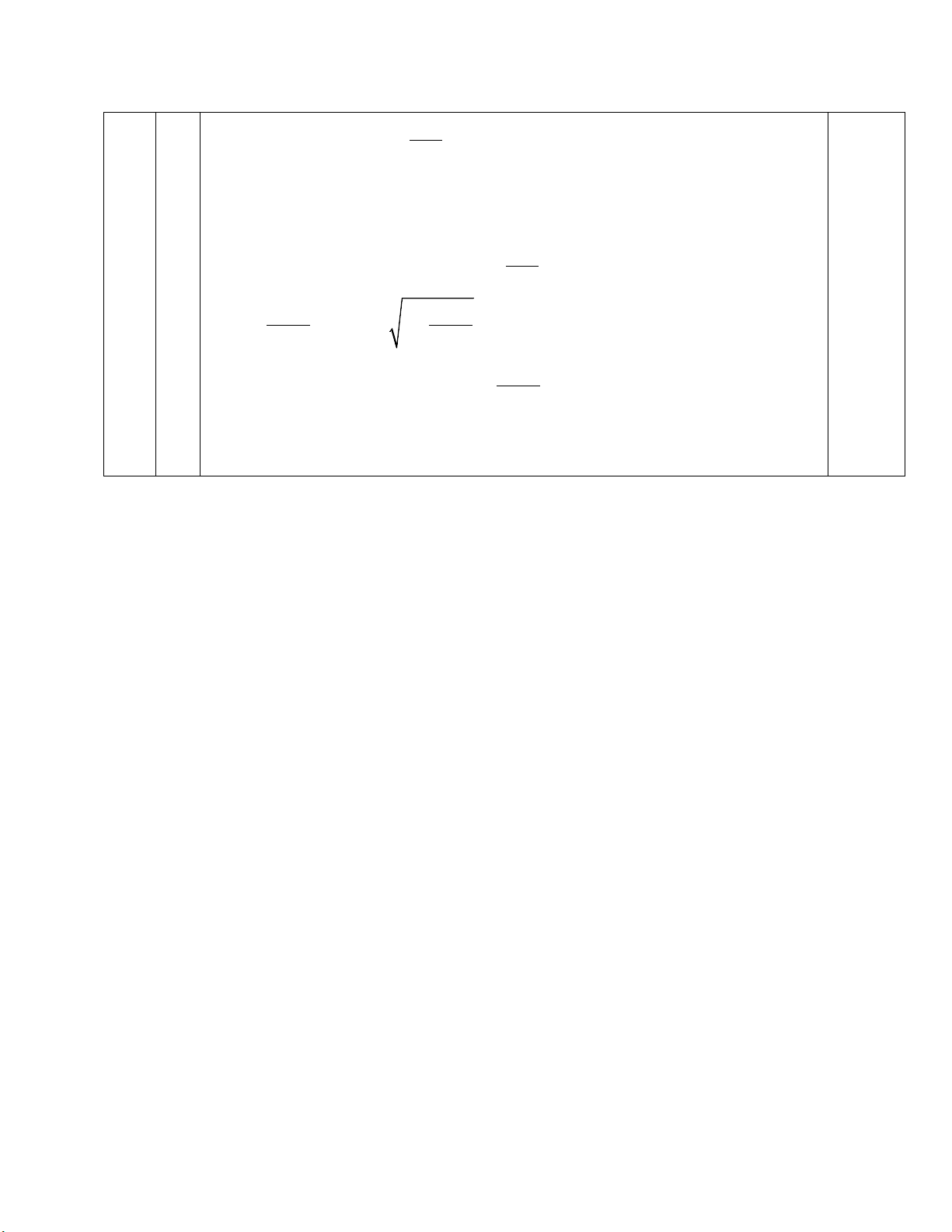
HƯỚNG DẪN CHẤM ĐỀ KIỂM TRA CUỐI KÌ I HUYỆN GIA LÂ M NĂM HỌC 2024-2025 MÔN: TO ÁN 9 Bài ý Nội dung Điểm 1 − + 2.0 Cho hai biểu thức: x x 2 x x A = + + và x 2 B = với x − 2 4 − x x + 2 x − 2
x ≥ 0; x ≠ 4
a) Tính giá trị của biểu thức B khi x = 25
b) Rút gọn biểu thức A c) Biết A
M = . Tìm giá trị nguyên của x để 1 M < B 2 1 1.a
Thay x = 25 (tmđk) vào biểu thức B ta có: 25 2 7 B + = = 25 − 2 3
Vậy B = 7 tại x = 25 0.5 3 1.b
x( x + 2) − x + 2 x + x( x − 2) A = ( x + 2)( x − 2)
x + 2 x − x + 2 x + x − 2 x = ( x + 2)( x − 2) 0.25 x + 2 x = ( x + 2)( x − 2) 0.25 x( x + 2) = ( x + 2)( x − 2) 0.25 x = x − 2 0.25 1.c + − Ta có: A x x 2 x x 2 = = : = . x M = B x − 2 x − 2 x − 2 x + 2 x + 2 Ta có: 1 M < 2 Do đó x 1 < x + 2 2 2 x − x − 2 ( < x + ) 0 2 2 x − 2 ( < x + ) 0 2 2 Do 2( x + 2) > 0 Suy ra x − 2 < 0 0.25 x < 2 x < 4 Kết hợp ĐKXĐ ta có: 0 0.25
≤ x < 4 và x nguyên x ∈{0;1;2; } 3 2
2.a Giải phương trình: 2x−5 3x−5 1+ −
= 0 (với x ≠ 1; x ≠ 2 ) 1.0 x − 2 x −1
(x − 2)(x − ) 1 + (x − )
1 (2x − 5) − (x − 2)(3x − 5) ( = x − )(x − ) 0 2 1 2 2 2
x − 3x + 2 + 2x − 7x + 5 − 3x +11x −10 = 0 x − 3 = 0 0.5 x = 3 (TM) Vậy x = 3 0.5 2.b 3  x + y = 7 1.0
Giải hệ phương trình: 
x − 7 y = 13 − 3  x + y = 7 3 
 x − 21y = 39 − 3  x + y = 7
Trừ 2 vế của phương trình ta được  0.5 22y = 46 3  18  x + y = 7 x =  Khi đó   11  23 giải được  0.25 y =  23  11  y =   11
Vậy nghiệm của hệ phương trình là (x y) 18 23 ; ;  = 11 11   0.25
2.c Giải bất phương trình: 6 9 3 2 x 0.5 x + − − > 0 3
3− 2x − (2 + 3x) > 0
3 − 2x − 2 − 3x > 0 1− 5x > 0 5 − x > 1 − 1 0.25 x < 5
Vậy nghiệm của bất phương trình là 1 x < 5 0.25 3
Hai xe máy cùng xuất phát đi quãng đường từ Hà Nội đến Thái 1.0
Nguyên. Xe máy thứ nhất đi hết 2 giờ 20 phút. Xe máy thứ hai đi hết 2
giờ 40 phút. Mỗi giờ xe máy thứ nhất đi nhanh hơn xe máy thứ hai là 5
km. Tính vận tốc của mỗi xe máy và quãng đường từ Hà Nội đến Thái
Nguyên (kết quả làm tròn đến hàng đơn vị).
Gọi vận tốc của xe máy thứ nhất và xe máy thứ hai lần lượt là x, y
(km/h), x > 5, y > 0
Vì xe máy thứ nhất đi nhanh hơn xe máy thứ hai là 5 km/h nên ta có: x − y = 5 Trong 2 giờ 20 phút 7
= giờ, xe máy thứ nhất đi được 7 x (km) 3 3 0.25 Trong 2 giờ 40 phút 8
= giờ, xe máy thứ nhất đi được 8 y (km) 3 3
Vì hai xe máy cùng xuất phát đi quãng đường từ Hà Nội về Thái Nguyên nên ta có: 7 8 x = y 3 3 x − y = 5 x = 40
Ta có hệ phương trình: 7 8 giải được  x − y =  0 y = 35 0.25 3 3
Vậy vận tốc của xe máy thứ nhất và xe máy thứ hai lần lượt là 40 km/h và 0.25 35 km/h
Quãng đường từ Hà Nội đến Thái Nguyên là 7 .40 0.25 ≈ 93 km 3
4 1) Một chiếc thang dài 6,5m được đặt 1.0
dựa vào tường, biết khoảng cách từ
chân thang đến chân tường là 2,5m
(như hình vẽ). Tính góc tạo bởi chiếc
thang với mặt đất ? (làm tròn kết quả
đến hàng đơn vị của độ). Biết rằng
tường được xây vuông góc với mặt đất.
Xét tam giác ABC vuông tại A ta có: AB 2,5 5 cos ABC = = = 0.5 BC 6,5 13 Vậy  0 ABC ≈ 67 0.5
2) Từ điểm M nằm ngoài đường tròn ( O;R ) với OM > 2R, kẻ các tiếp 3.0
tuyến MA, MB của đường tròn ( O ) ( A, B là các tiếp điểm). Gọi H là
giao điểm của AB và OM, vẽ đường kính AC.
a) Chứng minh bốn điểm O, A, M, B cùng nằm trên một đường tròn.
b) Chứng minh: AB ⊥ OM tại H và 2
OA = OH.OM
c) Vẽ BE ⊥ AC tại E, BE cắt MC tại F. Chứng minh: F là trung điểm EB 0.25
a Gọi I là trung điểm MO , ta có:
+ I là tâm đường tròn đường kính MO
+ AI là đường trung tuyến OA ∆ M
+ BI là đường trung tuyến OB ∆ M - OA ∆
M vuông tại A ( do MA là tiếp tuyến của (O;R)) 0.5
có AI là đường trung tuyến Suy ra MO
AI = OI = MI =
nên ta có , , ∈( ; MO O M A I ) (1) 2 2 0.5 - OB ∆
M vuông tại B ( do MB là tiếp tuyến của (O;R))
có BI là đường trung tuyến 0.25 Suy ra MO
BI = MI = OI =
nên ta có , , ∈( ; MO O M B I ) (2) 2 2
(1)(2) suy ra , , , ∈( ; MO O A M B I ) 2
b + Ta có: MA = MB ( Tính chất của hai tiếp tuyến cắt nhau) OA = OB = R
Suy ra OM là đường trung trực của AB 0.5
Khi đó OM ⊥ AB tại H
+ Xét hai tam giác OAH và OMA ta có:  O chung  =  0 OHA OAM = 90 0.5 Do đó OAH ∆ ∽ O ∆ MA (g.g) Suy ra OA OH = hay 2
OA = OM.OH OM OA
c Chứng minh được ABC ∆ vuông tại B ⇒ AB ⊥ BC Mà OM ⊥ AB (cmt) Suy ra OM // BC
Gọi K là giao điểm AM và BC Xét AK ∆
C ta có: O là trung điểm của AC và OM // KC (vì OM // BC) 0.25
nên M là trung điểm của AK nên MA=MK (3) Chứng minh được C ∆ EF ∽ C ∆ AM (g.g) Suy ra EF CF = AM CM 0.25 Chứng minh được C ∆ FB ∽ C ∆ MK (g.g) Suy ra BF CF = MK CM Khi đó EF FB = (4) AM MK
Từ (3) và (4) suy ra F là trung điểm của EB 5
Cho một trang giấy biết phần màu xám trong hình vẽ dưới đây 0.5
chứa một đoạn văn bản có diện tích 2
384cm . Biết rằng trang giấy được
căn lề trái 2cm, lề phải 2cm, lề trên 3cm và lề dưới 3c .
m Tìm chiều dài
và chiều rộng của trang giấy để trang giấy có diện tích nhỏ nhất.
Gọi chiều dài và chiều rộng của phần màu xám chứa đoạn văn bản lần lượt
là x, y(cm)(x, y > 0) Ta có xy = 384 hay 384 y = x
Theo bài ta có diện tích của trang giấy là S = (x + 6)( y + 4) Ta có: 384
S = xy + 4x + 6y + 24 = 408 + 4x + 6. x 2304 2304 = 4x + + 408 ≥ 2 4 . x + 408 = 600 x x
Dấu “=” xảy ra khi và chỉ khi 2304 4x =
hay x = 24 suy ra y =16 x 0.25
Vậy trang giấy có diện tích nhỏ nhất là 2
600cm khi chiều dài là 30cm và
chiều rộng là 20cm 0.25
Document Outline

• Doc1
• Hướng dẫn chấm môn Toán CK I GIA LÂM 24-25