Đề cuối kỳ 1 Toán 10 năm 2022 – 2023 trường THPT Lương Thế Vinh – Quảng Nam

SỞ GD & ĐT QUẢNG NAM
KIỂM TRA CUỐI KỲ I NĂM HỌC 2022-2023
TRƯỜNG THPT LƯƠNG THẾ VINH Môn: Toán – Lớp 10
Thời gian: 60 phút (không kể thời gian giao đề) ĐỀ CHÍNH THỨC (Đề gồm có 02 trang) MÃ ĐỀ 101
Họ và tên học sinh:……………………………………Số báo danh:………………......Lớp…………
A/ TRẮC NGHIỆM (5.0 điểm).
Câu 1. Phát biểu nào sau đây là một mệnh đề?
A. Mùa thu Hà Nội đẹp quá!
B. Bạn có đi học không?
C. Đề thi môn Toán khó quá!
D. Hà Nội là thủ đô của Việt Nam.
Câu 2. Trong các cặp số sau đây, cặp nào không là nghiệm của bất phương trình 2x  y  1? A.  2  ;  1 . B. 3; 7   . C. 0;  1 . D. 0;0 .  x  y  0 
Câu 3. Miền nghiệm của hệ bất phương trình x 3y  3  0 là phần mặt phẳng chứa điểm  x y 5  0  A. 5;  3 . B. 0;  0 . C. 1;  1  . D.  2  ;2 .
Câu 4. Khẳng định nào sau đây là khẳng định đúng?
A. cos   cos180   .
B. cot  cot 180   .
C. tan  tan 180   .
D. sin  sin 180   .
Câu 5. Trong tam giác ABC có: A. 2 2 2 a  b  c bc cos A. B. 2 2 2 a  b  c  bccos A. C. 2 2 2 a  b  c  2bc cos A. D. 2 2 2 a  b  c  2bc cos A.
Câu 6. Cho hình bình hành ABCD với I là giao điểm của hai đường chéo. Khẳng định nào sau đây là khẳng định sai?   
       A. IA  IC  0 . B. AB  AD  AC . C. AB  DC . D. AC  BD .
   
Câu 7. Véctơ tổng MN  PQ  NP  QR bằng     A. MR . B. MN . C. PR . D. MP .   
Câu 8. Cho tam giác ABC . Điểm M thỏa mãn AB  AC  2AM . Chọn khẳng định đúng.
A. M là trọng tâm tam giác ABC .
B. M là trung điểm của BC .
C. M trùng với B hoặc C . D. M trùng với A .  
Câu 9. Cho hình vuông ABCD có cạnh bằng a . Độ dài AD  AB bằng a 2 a 3 A. 2a B. . C. . D. a 2 . 2 2 
Câu 10. Trong mặt phẳng tọa độ Oxy , cho hai điểm ( A 2  ;3), B(1; 6
 ) . Tọa độ của véctơ AB bằng     A. AB  3;9 . B. AB  1;3 . C. AB  3;9 . D. AB  1;9 .
Câu 11. Trong mặt phẳng tọa độ Oxy , cho A x ; y và B x ; y . Tọa độ trung điểm I của đoạn thẳng 2 2  1 1  AB là Mã đề 101 Trang 1/2  x  y x  y   x  x y  y  A. 1 1 2 2 I ;   . B. 1 2 1 2 I ;   .  2 2   3 3   x  x y  y   x  x y  y  C. 2 1 2 1 I ;   . D. 1 2 1 2 I ;   .  2 2   2 2    
Câu 12. Cho hai vectơ a và b đều khác 0 . Khẳng định nào sau đây đúng?           A. . a b  a . b . B. . a b  a . b .cos a,b.             C. . a b  . a b .cos a,b . D. .
a b  a . b .sin a,b .    
Câu 13. Trong mặt phẳng tọa độ Oxy , cho hai véc tơ a   1  ;  1 ; b  2; 0
  . Góc giữa hai véc tơ a , b là A. 45 . B. 60 . C. 90 . D. 135 .
Câu 14. Cho số gần đúng a  367 653 964 với độ chính xác d  213 . Hãy viết số quy tròn của số a . A. 367 653 960 . B. 367 653 000 . C. 367 654 000 . D. 367 653 970 .
Câu 15. Đo độ cao một ngọn cây là h  17,14 m  0,3m . Hãy viết số quy tròn của số 17,14 ? A. 17,1 . B. 17,15 . C. 17, 2 . D. 17 .
B/ TỰ LUẬN ( 5.0 điểm).
Câu 1. (1 điểm). Cho các tập hợp A  x  | 3   x   2 ;   * B x  N | 4  x   0 . Tìm A  B ; B \ A
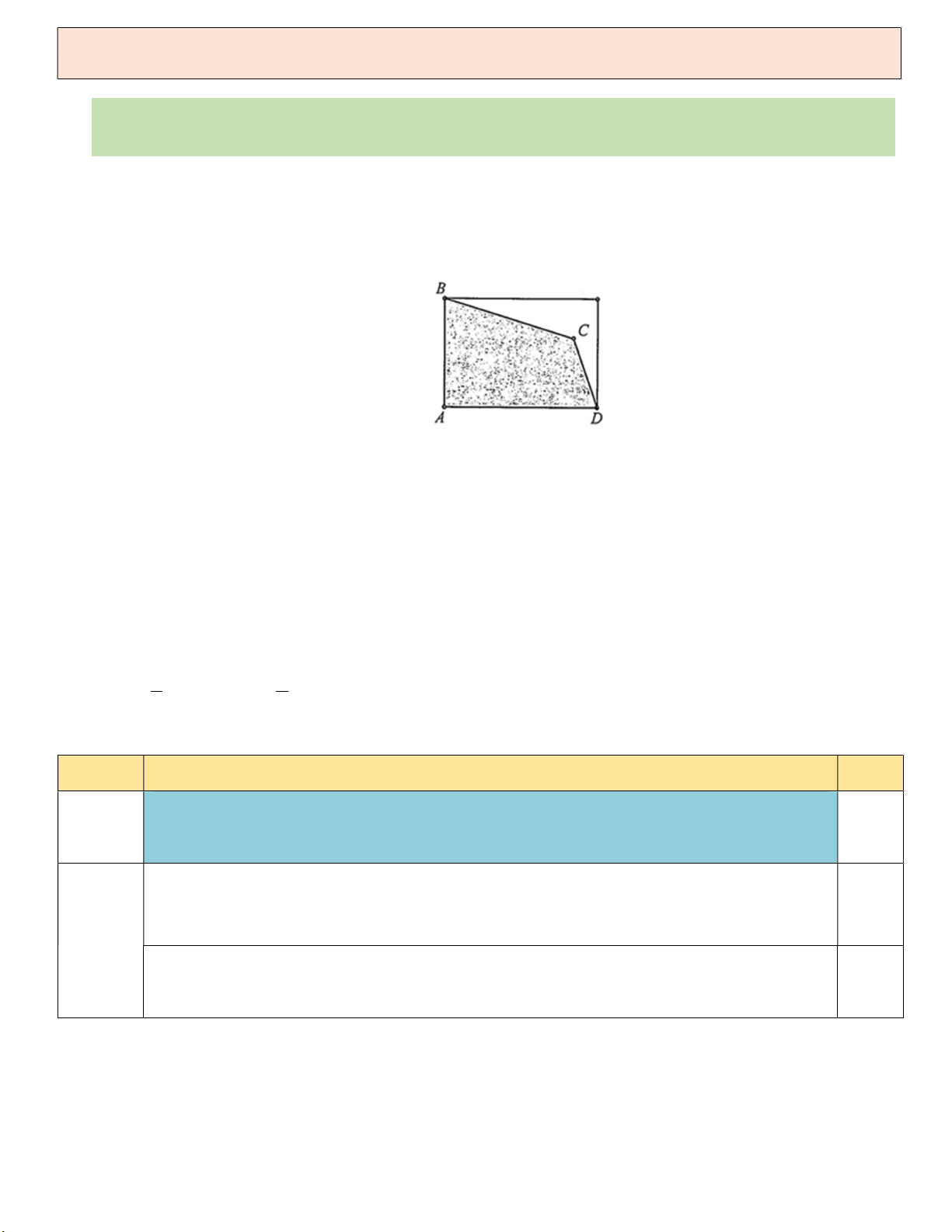
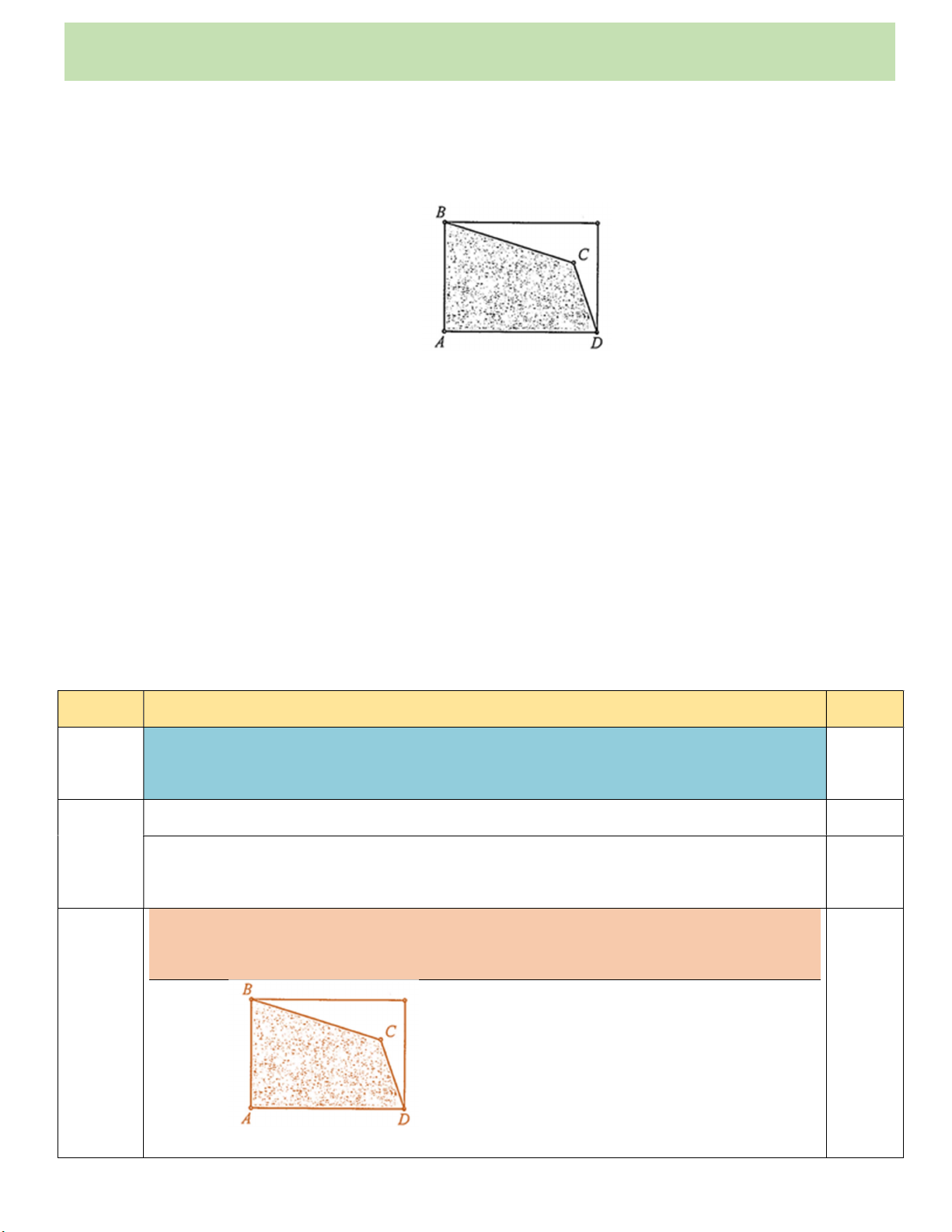
Câu 2. (1điểm). Một mảnh đất hình chữ nhật bị xén đi một góc (Hình), phần còn lại có dạng hình tứ giác
ABCD với độ dài các cạnh là AB  15 , m BC  19 ,
m CD  10 m , DA  20 m . Diện tích mảnh đất
ABCD bằng bao nhiêu mét vuông (làm tròn kết quả đến hàng đơn vị)?
Câu 3. (1,5 điểm). Trong mặt phẳng với hệ trục tọa độ Oxy ; cho tam giác ABC có ( A 1  ;2), B(1;3) và trọng tâm là G 2; 
1 . Tìm tọa độ đỉnh C còn lại của tam giác ABC và tọa độ điểm M trên tia Oy (khác gốc tọa
độ) sao cho tam giác MBC vuông tại M . Câu 4. (1,5 điểm) .
    a) Cho 4 điểm ,
A B,C, D tùy ý. Chứng minh AD  BC  AC  BD .
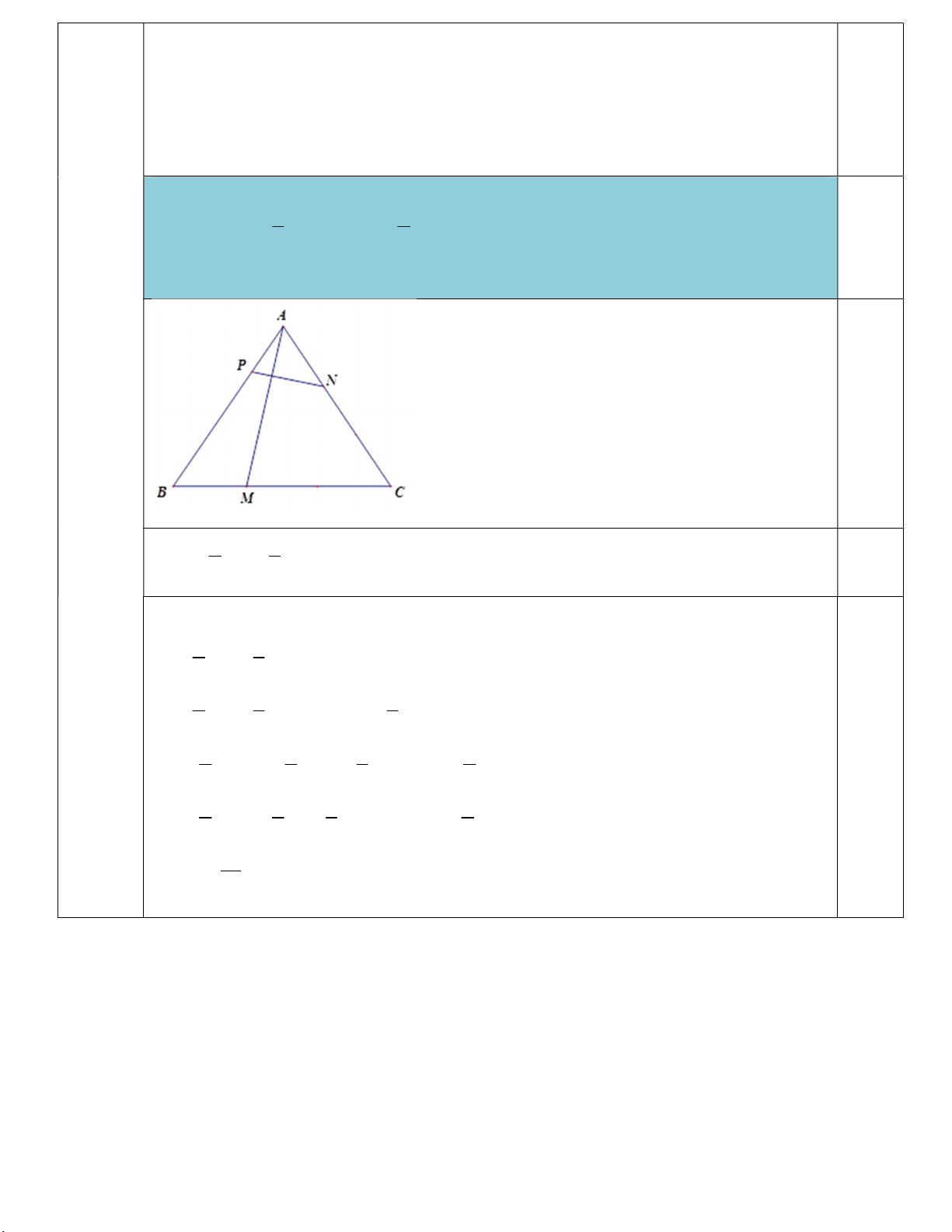
b) Cho tam giác đều ABC cạnh a , trên các cạnh BC,C ,
A AB lấy các điểm M , N, P sao cho
 1   1      
BM  BC ; AN   CN , AP  m AB 0  m  a . Hãy phân tích vectơ AM theo A , B AC và tìm 3 2
m biết AM vuông góc với PN. -----------HẾT---------- Mã đề 101 Trang 2/2 CÂU HỎI 101 102 103 104 105 106 107 108 1 D B D D C D D D 2 C B B C A A B A 3 A C D A B B A A 4 A D B D A A D A 5 C B A A B B D C 6 D D C D A D A D 7 A C B A C C B B 8 B B C C A B A B 9 D A A B C A D B 10 C A A A C A B D 11 D D D B D D D C 12 B A A A D A C B 13 D A A B A B B D 14 C D B C B A C A 15 D A B A A A D A
KIỂM TRA CUỐI KỲ I NĂM HỌC 2022-2023 Môn: Toán – Lớp 10 ĐÁP ÁN ĐỀ 1.
(Gồm các mã đề 101, 103, 105, 107)
Câu 1. (1 điểm). Cho các tập hợp A  x  | 3  x   2 ;   * B x  N | 4  x   0 . Tìm A  B ; B \ A
Câu 2. (1điểm). Một mảnh đất hình chữ nhật bị xén đi một góc (Hình), phần còn lại có dạng hình tứ giác
ABCD với độ dài các cạnh là AB  15 , m BC  19 ,
m CD 10 m , DA  20 m . Diện tích mảnh đất
ABCD bằng bao nhiêu mét vuông (làm tròn kết quả đến hàng đơn vị)?
Câu 3. (1,5 điểm). Trong mặt phẳng với hệ trục tọa độ Oxy ; cho tam giác ABC có ( A 1  ;2), B(1;3) và trọng tâm là G 2; 
1 . Tìm tọa độ đỉnh C còn lại của tam giác ABC và tọa độ điểm M trên tia Oy ( khác gốc tọa
độ) sao cho tam giác MBC vuông tại M . Câu 4. (1,5 điểm) .
    a) Cho 4 điểm , A ,
B C, D tùy ý. Chứng minh AD  BC  AC  BD .
b) Cho tam giác đều ABC cạnh a , trên các cạnh BC,C ,
A AB lấy các điểm M , N, P sao cho
 1   1      
BM  BC ; AN   CN , AP  m AB 0  m  a . Hãy phân tích vectơ AM theo AB, AC và tìm 3 2
m biết AM vuông góc với PN. Câu Nội dung Điểm 1
Cho các tập hợp; A  x  | 3  x   2   * B x  N | 4  x   0 . Tìm A  B ; B \ A (1,0đ)
Liệt kê các phần tử của tập A,B 0,5 A   2  ; 1  ;0;  1 ; B  1;2;3;  4 Tìm A  B ; B \ A 0,5 (mỗi ý 0,25) 1
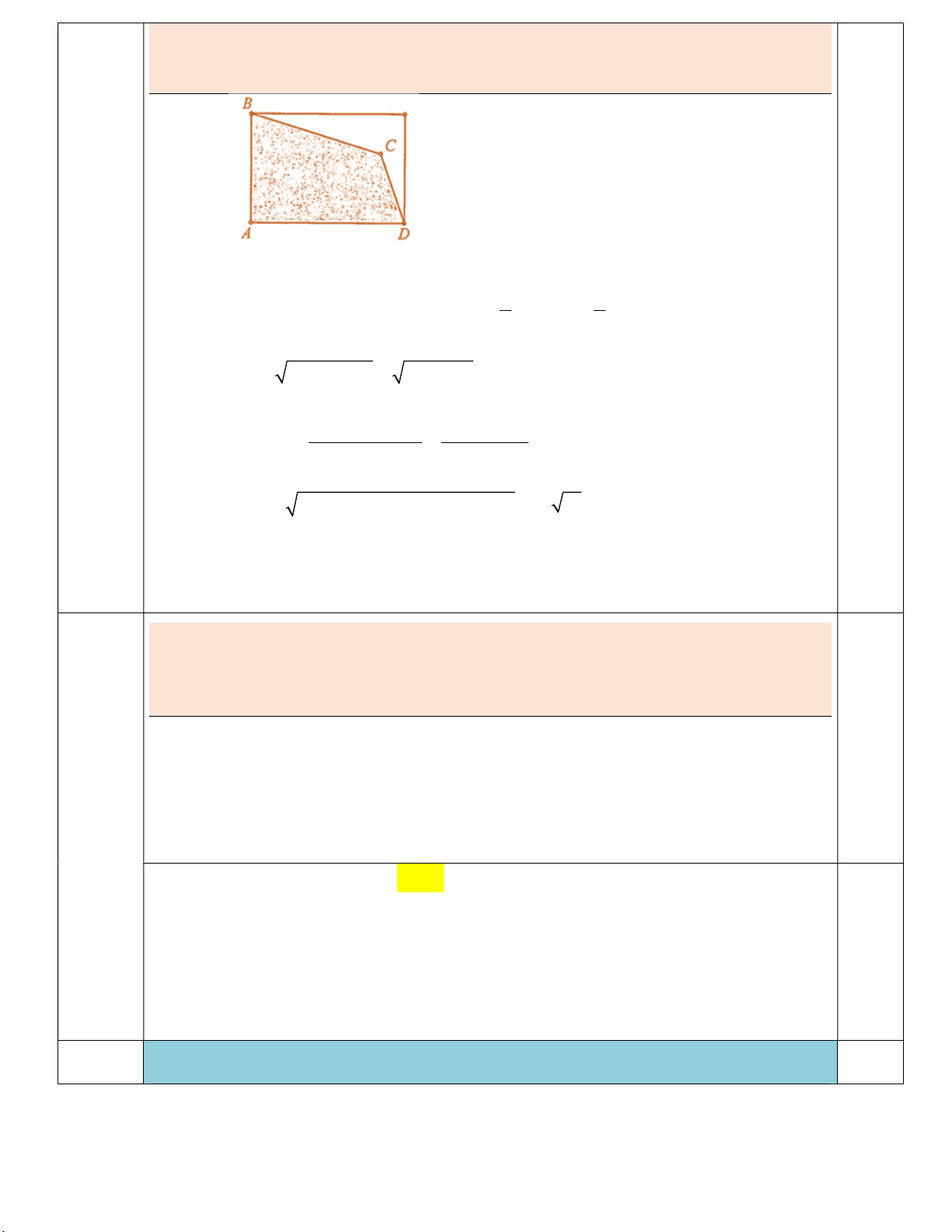
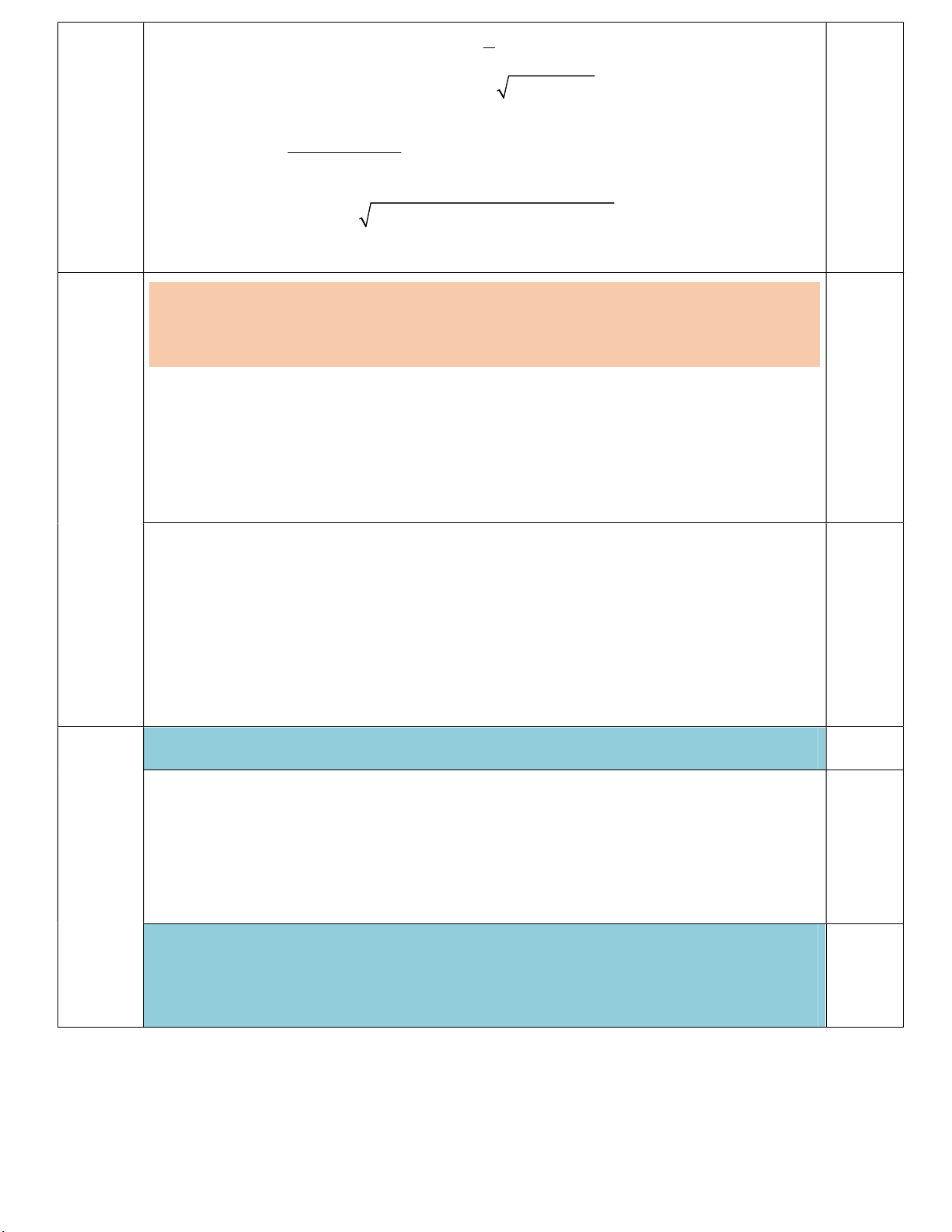
Một mảnh đất hình chữ nhật bị xén đi một góc (Hình), phần còn lại có dạng hình tứ giác
ABCD với độ dài các cạnh là AB  15 , m BC  19 ,
m CD 10 m , DA  20 m . Diện tích
mảnh đất ABCD bằng bao nhiêu mét vuông (làm tròn kết quả đến hàng đơn vị)? Giải Câu 2
 Xét tam giác ABD vuông tại A , ta có: 1 1 0,25 (1,0đ)
Diện tích tam giác ABD là: S
 AB  AD  15 20 150 m  . ABD  2  2 2
 Áp dụng định lí Pythagore ta có: 2 2 2 2 0,25
BD  AB  AD  15  20  25( m) .  Xét tam giác BCD :
BC  CD  DB 19 10  25 Ta có: p    27( m) . 2 2
Áp dụng công thức Heron, ta có diện tích tam giác BCD là: S  p  p   p   p      2 ( 19) ( 10) ( 25) 12 51 86 m . BCD  0,25
 Vậy diện tích mảnh đất ABCD là: 0,25 S  S  S    m . ABD BCD  2 150 86 236   
Trong mặt phẳng với hệ trục tọa độ Oxy ; cho tam giác ABC có ( A 1  ;2), B(1;3) và trọng tâm là G 2; 
1 . Tìm tọa độ đỉnh C còn lại của tam giác ABC và tọa độ điểm M trên tia
Oy ( khác gốc O) sao cho tam giác MBC vuông tại M . x  3x  (x  x ) C( ; x y) : G A B  y  3y  ( y  y )  G A B 0,25 Câu 3 x  6    C(6; 2) (1,5 đ)  y  2  0,25  
 M thuộc tia Oy  M (0;m) ( m  0 ), BM  (1;m  3); CM  (6;m  2) (0,25)
  0,25  M
 BC vuông tại M  BM  CM  BM .CM  0  1.6  (m  3)(m  2)  0 (0,25) 0,25   2 m 4 (n)
 m  m 12  0   0,25 m  3  (l) . (0,25) 0,25  Vậy M (0;4) (0,25)
    4
a) Cho 4 điểm A, B, C, D tùy ý. Chứng minh AD  BC  AC  BD 2
   
     (1,5đ)
AD  BC  AC  BD  AD  BC  AC  BD  0
    AD  BC  AC  BD
     AD  BC  CA  DB 0,25
     
 AD  DB  BC  CA  AA  0 0,25
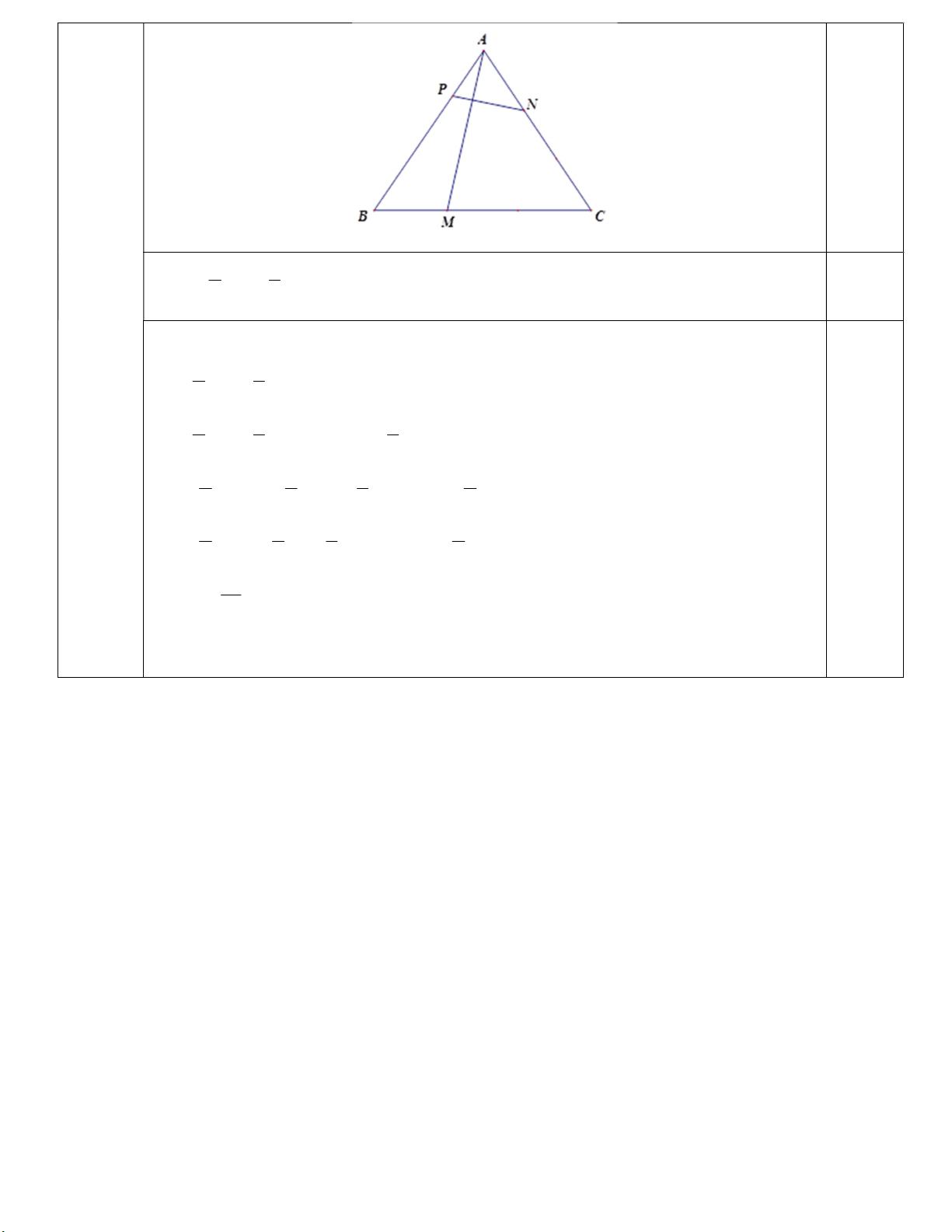
b) Cho tam giác đều ABC cạnh a, trên các cạnh BC, CA, AB lấy các điểm M, N, P sao
 1   1   
cho BM  BC ; AN   CN , AP  m AB 0  m  a . Hãy phân tích vectơ 3 2   
AM theo AB, AC và tìm m biết AM vuông góc với PN.
 2  1  AM  AB  AC 0,5 3 3   AM .PN  0 0,25
2  1    
( AB  AC).(PA  AN )  0 3 3 2  1   1 
 ( AB  AC).(m AB  AC)  0 3 3 3
2 2 1 2 1   2    
m AB  AC  m AB.AC  A . B AC  0 3 9 3 9 2 2 1 2 1 2 0 2 2 0   . m a  a  .
m a .cos 60  .a .cos 60  0 3 9 3 9 4  0,25 m  15 3 ĐÁP ÁN ĐỀ 2
(Gồm các mã đề 102, 104, 106, 108)
Câu 1. (1 điểm). Cho các tập hợp A  x  | 2  x   3 ;   * B x  N | 5  x   0 . Tìm A  B ; B \ A
Câu 2. (1điểm). Một mảnh đất hình chữ nhật bị xén đi một góc (Hình), phần còn lại có dạng hình tứ giác
ABCD với độ dài các cạnh là AB  12 m, BC  18 ,
m CD 10 m , DA  16m . Diện tích mảnh đất
ABCD bằng bao nhiêu mét vuông (làm tròn kết quả đến hàng đơn vị)?
Câu 3. (1,5 điểm). Trong mặt phẳng với hệ trục tọa độ Oxy ; cho tam giác ABC có ( A 0; 2  ), B(1; 3  ) và trọng tâm là G 1  ; 
1 . Tìm tọa độ đỉnh C còn lại của tam giác ABC và tọa độ điểm M trên tia Ox (khác
gốc tọa độ) sao cho tam giác MBC vuông tại M . Câu 4. (1,5 điểm) .
   
a) Cho 4 điểm A, B, C, D tùy ý. Chứng minh DC  BA  BC  DA .
b) Cho tam giác đều ABC cạnh a, trên các cạnh BC, CA, AB lấy các điểm M, N, P sao cho          MC  2MB ; CN  2N ,
A AP  m AB 0  m  a . Hãy phân tích vectơ AM theo AB, AC và tìm
m biết AM vuông góc với PN. ----------- HẾT ---------- Câu Nội dung Điểm 1
Cho các tập hợp A  x  | 2  x   3 ;   * B x  N | 5  x   0 . Tìm A  B ; B \ A (1,0đ)
Liệt kê các phần tử của tập A,B 0,5 Tìm A  B ; B \ A 0,5 (mỗi ý 0,25)
Một mảnh đất hình chữ nhật bị xén đi một góc (Hình), phần còn lại có dạng hình tứ giác
ABCD với độ dài các cạnh là AB  12 m, BC  18 ,
m CD 10 m , DA  16m . Diện tích
mảnh đất ABCD bằng bao nhiêu mét vuông (làm tròn kết quả đến hàng đơn vị)? Câu 2 (1,0đ)
 Xét tam giác ABD vuông tại A , ta có: 4 1 0,25
Diện tích tam giác ABD là: S  AB  AD  96 m . A  BD  2  2
 Áp dụng định lí Pythagore ta có: 2 2 BD  AB  AD  20( m) . 0,25  Xét tam giác BCD : BC  CD  DB Ta có: p  . 2
Áp dụng công thức Heron, ta có diện tích tam giác BCD là: S
 p  p  BC  p  CD  p  BD  0,25   2 ( ) ( ) ( ) 90 m . BCD 
 Vậy diện tích mảnh đất ABCD là: S  S  S    0,25    2 96 90 186 m ABD BCD 
Trong mặt phẳng với hệ trục tọa độ Oxy ; cho tam giác ABC có ( A 0; 2  ), B(1; 3  )và trọng tâm là G 1  ; 
1 . Tìm tọa độ đỉnh C còn lại của tam giác ABC và tọa độ điểm
M trên tia Ox (khác gốc tọa độ) sao cho tam giác MBC vuông tại M . x  3x  (x  x ) C( ; x y) : G A B  0,25 y  3y  ( y  y )  G A B    Câu 3 x 4   C(4; 2) 0,25 y  2 (1,5 đ)   M thuộc tia Ox  M ( ;
m 0), m  0 , BM  (m 1;3) ; CM  (m  4; 2  )
  0,25
MBC vuông tại M  BM  CM  BM.CM  0  m  1 m  4 3 2    0 0,25 m  5  l 2
 m  3m 10  0   . 0,25 m  2  n 0,25 Vậy M (2;0)
   
a) Cho 4 điểm A, B, C, D tùy ý. Chứng minh DC  BA  BC  DA
   
    
Ta xét: DC  BA  BC  DA  DC  BA  BC  DA  0
    DC  BA  BC  DA 4
     DC  BA  CB  AD 0,25 (1,5đ)
     
 AD  DC  CB  BA  AA  0 0,25
b) Cho tam giác đều ABC cạnh a, trên các cạnh BC, CA, AB lấy các điểm M, N, P      
sao cho MC  2MB ; CN  2N ,
A AP  m AB 0  m  a . Hãy phân tích   
vectơ AM theo AB, AC và tìm m biết AM vuông góc với PN. 5
 2  1  AM  AB  AC 0,5 3 3   AM .PN  0
2  1     0,25
( AB  AC).(PA  AN )  0 3 3 2  1   1 
 ( AB  AC).(mAB  AC)  0 3 3 3
2 2 1 2 1   2    
m AB  AC  m AB.AC  AB.AC  0 3 9 3 9 2 2 1 2 1 2 2 2   . m a  a  .
m a .cos 60  .a .cos 60  0 3 9 3 9 4  m  15 0,25 6 TT 5 4 3 2 1 T ỉ lệ T chu 5. Các và h ph N ỉ l T m l 1. M tr ượ 3. H ộ ệ ổ 4. Véc t tam giác nh ẫ ươ T i dung k ( ng ư n u s ng trong % ng c ấ ệ 2. B ậ th g ệ t 2 bp ng trìn p h ệ (%) ) ố s th nh ứ li ố ấ ủ ệ đặ ơ ứ ẩ t t ợ c a n b p đề u c ậ iế c c h . n 5.3.Các s tâm 5.2.Các s 5.1.S 4.4.Tíc 4.3.V 4.2.Tíc T 4.1.Các kh 3.2. H t 3.1. G hai N 2.2. H Nn 2.1. B 1.2. T 1.1. M ừ 0° ố ổ n e g n đế h ct ệ i ệ ấ ậ h g th á tr b t ph p h ệ ầ vô ơ v và n 18 nh ố ố n ấ t e ứ Đơ ị đặ đặ đ r ái n ct c l l t ph ợ ươ đề úng và sai s h on p hi 0° ượ n v c t c tr ư ơ ớ g v ệ ượ i ươ ng u c ệ ng g r ng c ư ư m ớ m m ng trong t ị ng t ki ng ng i m r ặ ủ ình b t ph a h i ế ủ ác đ đ ộ ở r n th a h ìn o o xu t s a ẳ đầ c i độ ố a ng t ố ủ h ậ MÔ v i v u tam c nh ứ a m b e phân tá ậ c th c ect ọ c nh N t ế a ơ ộ ấ trung giác t gó t h : MA TOÁN ơ độ ấ a t c i TR n , L Ậ CH 12 S N 2 1 2 1 1 1 1 1 1 1 ố Nh Ớ ĐỀ P 1 40% ận b KI (ph 0 gian Th – TH i ế Ể ú ờ t Thôn M TRA t) i Ờ I 1+1 CH GIA S 5 1 1 1 ố CU 30% M N g Ố (p ứ LÀM BÀI: gian Th hi c I H hút ể độ ờ u V Ọ i ) nh C K ậ CH n t S Ỳ 2 1 1 ố 60 ph 20% ậ h 1 n d ứ c T (p gian Th ụ út ) hút ng ời CH S 1 1 ố V ậ 10 cao n d % (phú gi Th ụ a ng n ờ t) i TN TL S ố CH ổ ng (p gi Th hú an ờ t) i đ t i ổ % ể ng m TT 3 2 1 tron 3. H nh trình tr ph ph T M ki N l ình 2. B giác ượ ậ ệ ế ộ ẩ ấ g tam ệ ươ b ươ p h nh n th i dun 1. ng th n. t hai ấ b t - ng H ng ấ ứ ậ t ợ đề ứ p c c ệ . c g l 3.2. c b ph b ph Đơ ượ t ủ l 3.1 2.2. ượ ậ ậ ừ a m c nh ươ c nh ươ 2.1. T M n 180 0 g H ng giác . ậ n v 0 Giá t N ng trìn H N ng trìn p h 1.2. ệ 1.1. th nh tron ệ ộ n. n. ứ th 0 đế ấ t góc ệ ấ B ị . t h b t h ấ ợ c ki đề ứ n r ấ t p ế g c ị a i h t a i h n Tính di Câu 5 T d Câ Xác m Xác tr Xác Câu 3 T N N Câu 2 T h Xác Câ hi Câ N N ấu các ộ ướ ợ h h ệ u 4 t h ậ ậ p. h h u 16 TL-TH u t u đị c. n bi n b ậ ậ đị đị n bi n b 1 TN ệ đị ồ nh h ệ TN-NB4 b nh nh i nh t n t n tích N g ế ế i ấ N i t t N ế ế -NB5: á t t p ạ đượ t t ệ đư -NB3 đư đư -NB2: ậ i ( -NB1: đượ đư r b h p h ị l ấ ươ ợ ợ ợ  c mi ta ượ t ph c m c nghi c b ). ợ M ợ m : nh ng trì : 4 c m c th công ấ p b ứ M ng c g ươ ộ ề t ph ệ ế Ô iác g ậ t n ng ệ ằ nh nà độ N n b ng n đ m c ng cách th i ươ ki t ác h iể đề o : TOÁN B ừ ứ i trình khi cho . ế b m ch hi ủ ng trình b l ph à ế Ả g c d t công ậ ệ a m n t c nh i m c m NG ả ủ th i ộ h ệ o ộ l n tích, ấ ủ i đị t m ứ i tr t b ệ c, k 10 – T ĐẶ ế t h a m t k nh c t th ướ ệ cho ấ ứ a t p ậ nh c l i c thu c n ê ĩ C T ộ n ủ đị N bi t h h cá a m đề n cho ă tr ượ ươ h H nh l ế ệ ấ c ng c Ả , m Ờ ư t m ộ ớ ng b t h ng trìn ph ệ ĐỀ c hay I nh c. ý ấ a ệ sin, giác i ầ ầ GIA ề tr t ph i nh n t n k KI n ướ N đề ngh n. đị c. không t ươ h ử đề ch i N . Th ể Ể cung bù, b ph m tr M TR nh lý i ng ậ ứ LÀ ệ c n a ủ m trì ự kí h c hi đị a, M BÀI c h n ấ hi nh, m A GI o u h t h đ sin ph ộ ệ ệ á c m b a n c u p nh giá . ụ ậ i : c nh , h N ệ Ữ 60 ph ác ph h n. nh i ổ A K ề ệ bi n th ấ đề ng t ha ế Ỳ é ứ n ( ch út p 1 c c hi i to  ứ ệ ơ m c N án t ) và a bi n c b ả ế n, ủ ho ậ kí n. a p Nh S bi ố 1 1 1 1 1 1 ế ậ câu t n h Th ỏ hi i theo m ể ông u d ứ V ụ c 1 ng ận độ nh ậ d cao V n t ụ ng ậ h n ứ c TT đặ c 5. Các s 4. V ki N s ủ ố a m c tr ế ộ n th i dun li é ệ ư c T u ẫ t ng ứ u ố ơ ổ c g n g p vect ni 4.1.Các kh đ 5.1.S h 4.4.Tíc hi h T Đơ úng và sai ha t 4.3.V ệ ướ ẳ r 4. ệ m m tam n on i ơ 2.Tích vec u c n v th s vec ng c g ố ố t g m s v ổ ố g h ọ e ớ ủ gi t ng và ứ ở ị ầ tơ ủ vô a ct i m ơ a h c ki ặ đầ ác n a độ ơ t a ái ế ộ i u n t Câ Câ + Ch + Bi Câ Câ vect Câ Câ Câ Câ Câu 9 T Câu 8 T + Ch Câ Câu 7 T Câu 6 T - Á Câ Tính m u 15 T u 14 T u 20 TL. V u 13 T u 12 TN u 19 TL: v u 11 T u 10 T u 18.TL-TH p u 17 TL. V ế ơ ứ t b , cá ứ d ng m ng m ụ i n ộ ể c N N N N g t c N N u d N tí N N -TH2: -NB7: -TH1: -NB6: cá -NB12 -NB11 inh -TH3: nh -NB10: -NB9 -NB8: i ạ nh nh, tính gó i c ễ hai n m ậ ậ h M ậ ch n d n d ba 5 ệ n d ứ Tìm ấ : : l l đư ộ Tí : Đị Xác Đị th T t. đ c ụ t v ụ T đị à à n n ọ nh ngh iể nh ngh ứ ụ độ m m ờ n ọ ng e g h nh ngh g a a m t c l ng đ đị ki c cao: 2. Tìm t độ tròn s tròn s t tích vô h độ i ư 1 c ể h nh t t ợ c ế ơ c m, ẳ h the t n ủ n t ĩ ng h ĩ ẳ r ủ ng vuô ĩ ung x a, t ổ a, t g a t a tr ố ố a, vect ng h h o á a h bi c í í nh ch à nh ch o m ứ ọ ướ a a đ đị ng+ Ch n c, k g ể i vect i i g u t ng n độ ể ơ nh ệ ta i m, tr , c u c á ĩ c n g h v ấ ấ m góc , góc gi ứ đ ủ t t ủ t ơ c t i a e ừ ă ể ọ c ứ a hai ho g gi ng c không m th đ t ng iá ng tâm ọ i ơ c ả ể , tính a thi ầ m để m ữ n k độ a hai ỏ i c c a m n ặ g ế , t cho ù ủ độ h c n i i ả ể đỉ n a đẳ i b m tr ã g v nh h dài v h tích n ph ect ng th i à ề i tr đ u v to ướ a, ươ ơ vô h i ì ề nh b e , g u ki c ứ e án th c. đ ng t ó ơ c ct á nh giá v ơ c t ướ ì , t ệ nh hành ect ự n c ỷ r c t o ng, s ơ ng ta h ố ế góc gi o . độ t m giác r dà ướ i. ữ c a hai Nh S bi 12 5 ố 2 1 1 2 1 1 1 2 ế ậ câu t n h Th ỏ hi i theo m ể ông u d ứ V ụ c 2 1 ng ận độ nh ậ d cao V n t ụ 1 1 ng ậ h n ứ c
Document Outline

• TOAN 10-HKI-Ma_de_101
• DAP AN TN TOAN 10-HKI-2022_23
• DAP AN TL TOAN 10-HKI-2022_23-MOI
• [LTV]-Ma-tran-de-Cuối-ky-1-Toan-10-KNTT-DIEU CHINH