Đề cuối kỳ 1 Toán 10 năm 2023 – 2024 trường THPT Nguyễn Trãi – Khánh Hòa

SỞ GIÁO DỤC & ĐÀO TẠO KHÁNH HÒA
ĐỀ KIỂM TRA CUỐI KỲ 1 TOÁN 10
TRƯỜNG THPT NGUYỄN TRÃI NĂM HỌC 2023-2024 Mã đề thi: 101
Thời gian làm bài: 90 phút;
Họ, tên thí sinh:..................................................................... Lớp: ............................. A. TRẮC NGHIÊM
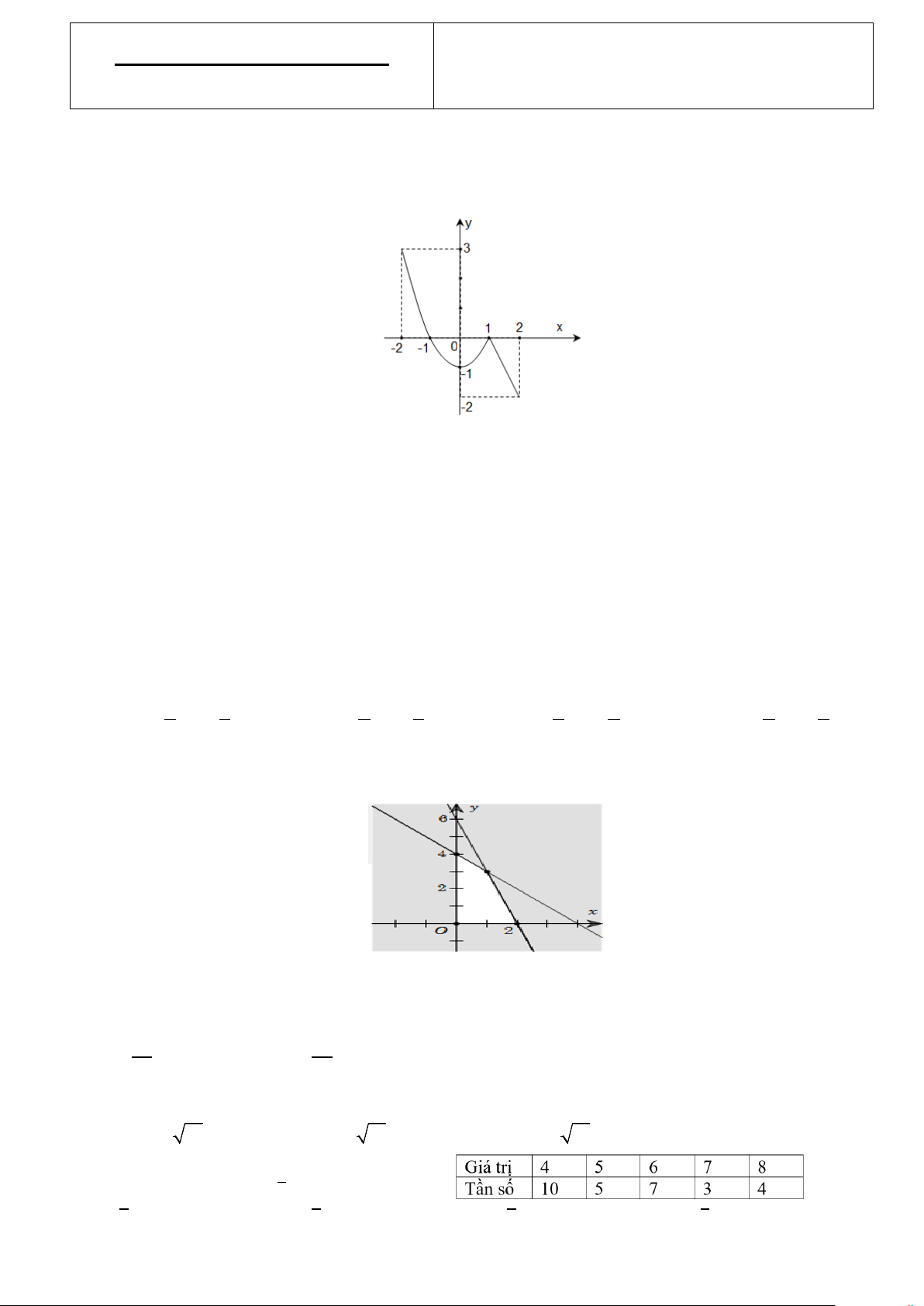
Câu 1: Cho đồ thị hàm số như hình vẽ, hãy chọn khẳng định đúng?
A. Hàm số đồng biến trên khoảng (0; )
1 và nghịch biến trên khoảng ( 2; − 2).
B. Hàm số đồng biến trên khoảng (0; )
1 và nghịch biến trên khoảng ( 1; − 2).
C. Hàm số đồng biến trên khoảng ( 1; − )
1 và nghịch biến trên khoảng (1;2) .
D. Hàm số đồng biến trên khoảng (0; )
1 và nghịch biến trên khoảng (1;2) .
Câu 2: Cho tam giác ABC có M là trung điểm BC và G là trọng tâm của tam giác ABC . Khẳng định nào
sau đây là khẳng định sai ?     
  
   
A. GA = 2GM. B. AB + AC = 2AM.
C. MB + MC = 0. D. GA + GB + GC = 0.  
Câu 3: Cho tam giác ABC . Gọi M là trung điểm của AB , N là điểm thuộc AC sao cho CN = 2NA và   
K là trung điểm của MN . .Biểu diễn AK theo hai vectơ ABvà AC.             A. 1 1
AK = AB + AC. B. 1 1
AK = AB + AC. C. 1 2
AK = AB + AC. D. 1 1
AK = AB + AC. 2 3 4 3 2 3 4 6
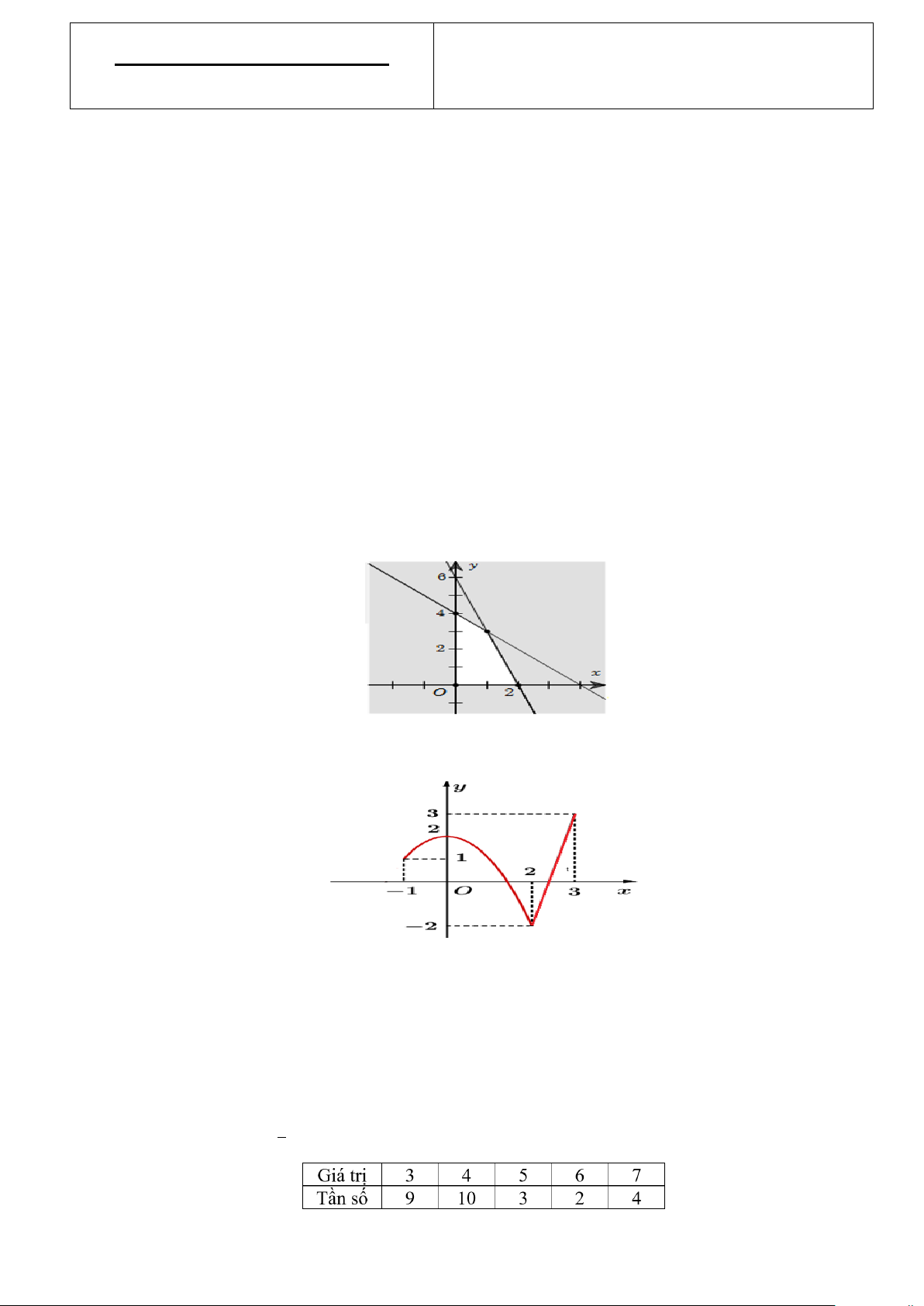
Câu 4: Biểu thức F = 2x − 5y đạt giá trị nhỏ nhất bằng bao nhiêu trên miền đa giác không bị tô đậm trong hình bên? A. 0. B. -20. C. -13. D. 4.
   
Câu 5: Cho tam giác đều ABC có cạnh bằng .
a Tính tích vô hướng A . B AC − A . B BC 2 2 A. a − B. a C. 2 a D. 0 2 2
Câu 6: Cho tam giác ABC có  +  0
B C =120 , AB = 6, AC = 8.Tính BC. A. BC = 2 19. B. BC = 13. C. BC = 2 13. D. BC = 52.
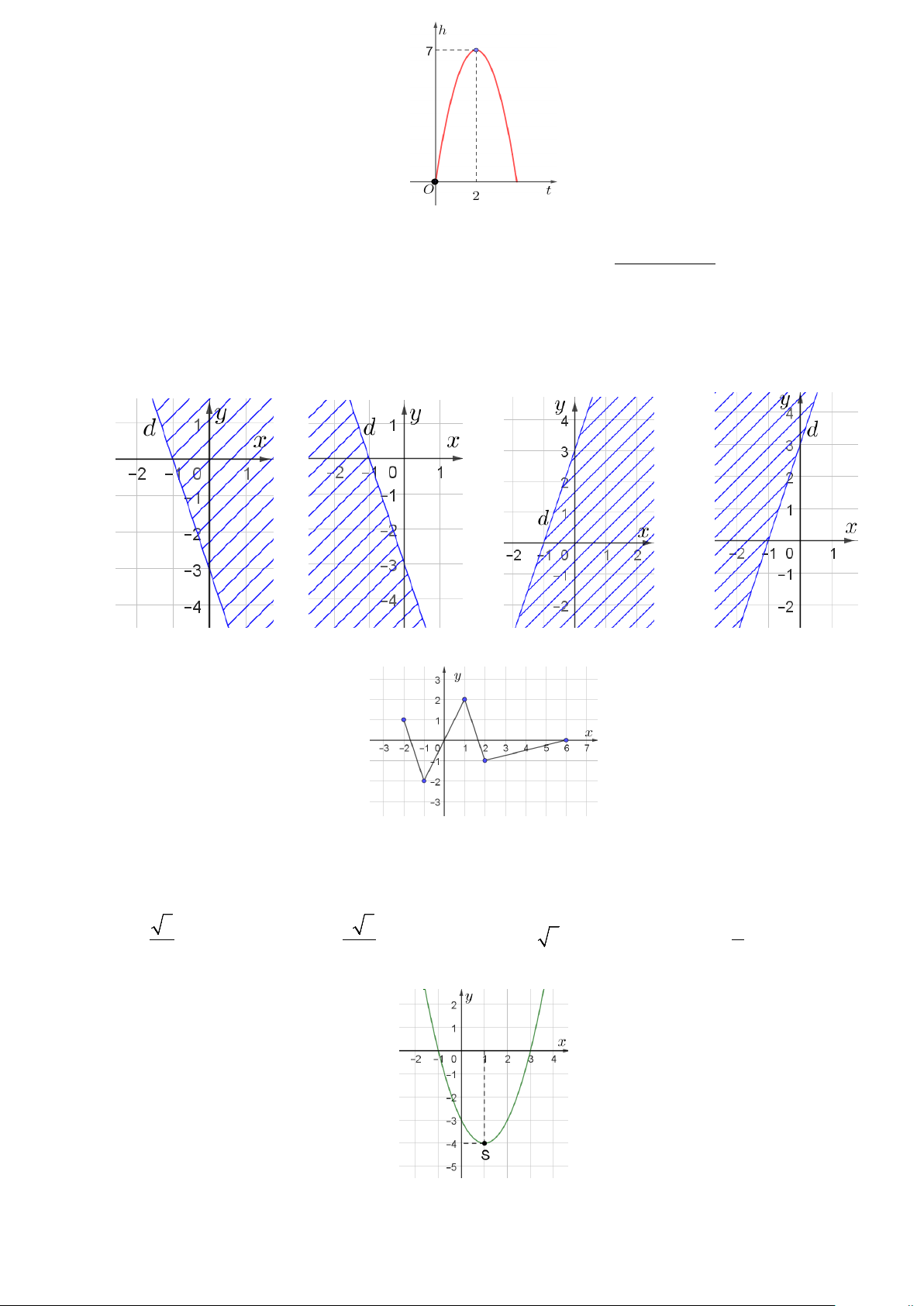
Câu 7: Tìm số trung bình x của mẫu số liệu sau:
A. x ≈ 6,07 . B. x ≈ 6,83. C. x ≈ 5,33. D. x ≈ 5,52.
Trang 1/4 - Mã đề thi 101
Câu 8: Hàm số nào sau đây có giá trị lớn nhất bằng 19? A. 2
y = −x − 6x +10 . B. 2 y = 2
− x + 4x +19 . C. 2
y = 2x − 4x + 21. D. 2
y = x −8x +19.
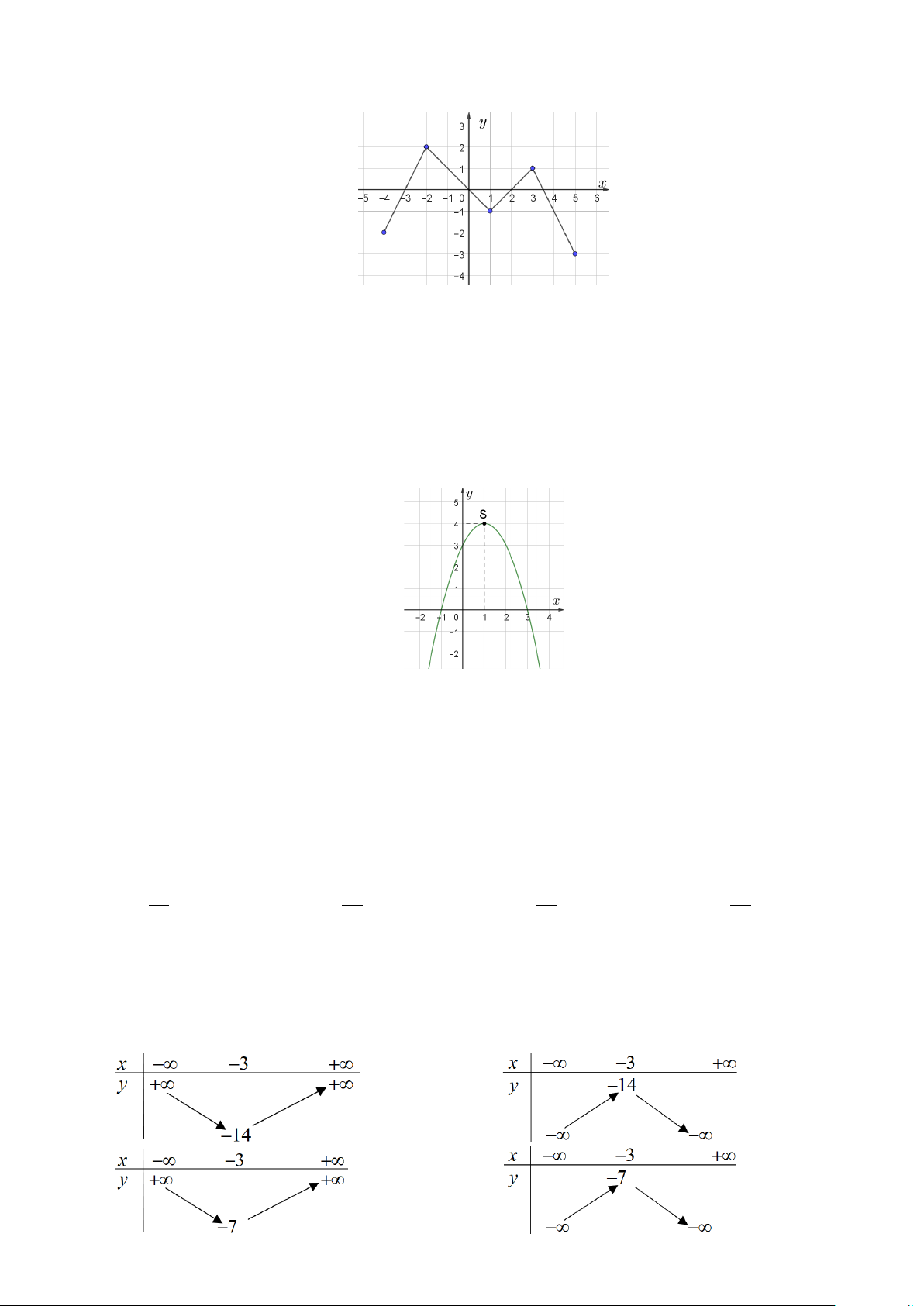
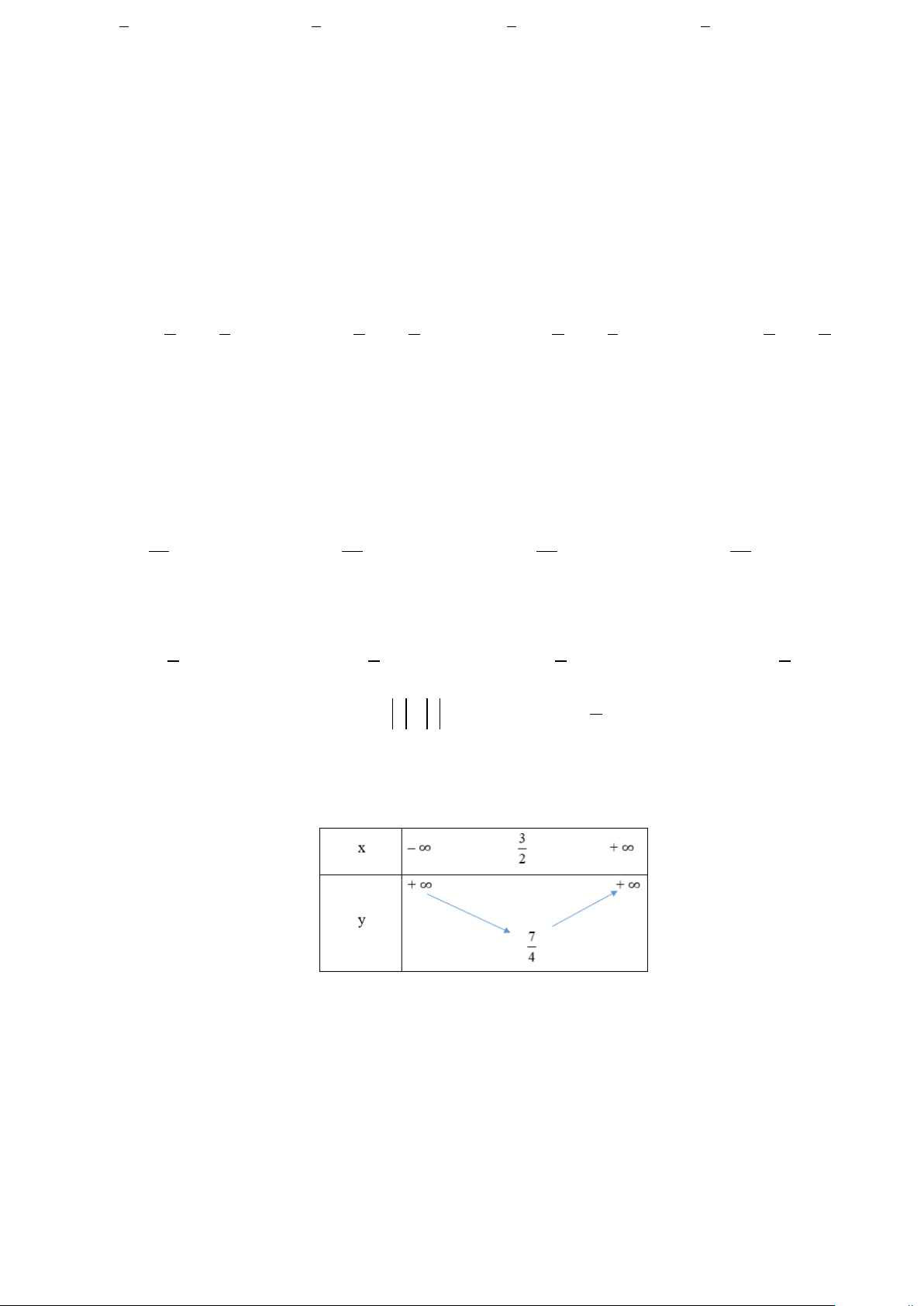
Câu 9: Cho hàm số y = f (x) có tập xác định D = [ 4;
− 5] và có đồ thị như hình vẽ sau:
Tập giá trị của hàm số y = f (x) là: A. [0;2] B. [ −1;2] C. [ − 4;5] D. [ −3;2]
Câu 10: Cặp số nào sau đây là một nghiệm của bất phương trình x − 2y +1 > 0 ? A. (3;1) . B. (1;1) . C. (2;3) . D. (0;2) .
    
Câu 11: Thu gọn u = AB + CA − AD − CB , ta được       
A. u = DA
B. u = DB
C. u = AD
D. u = DA
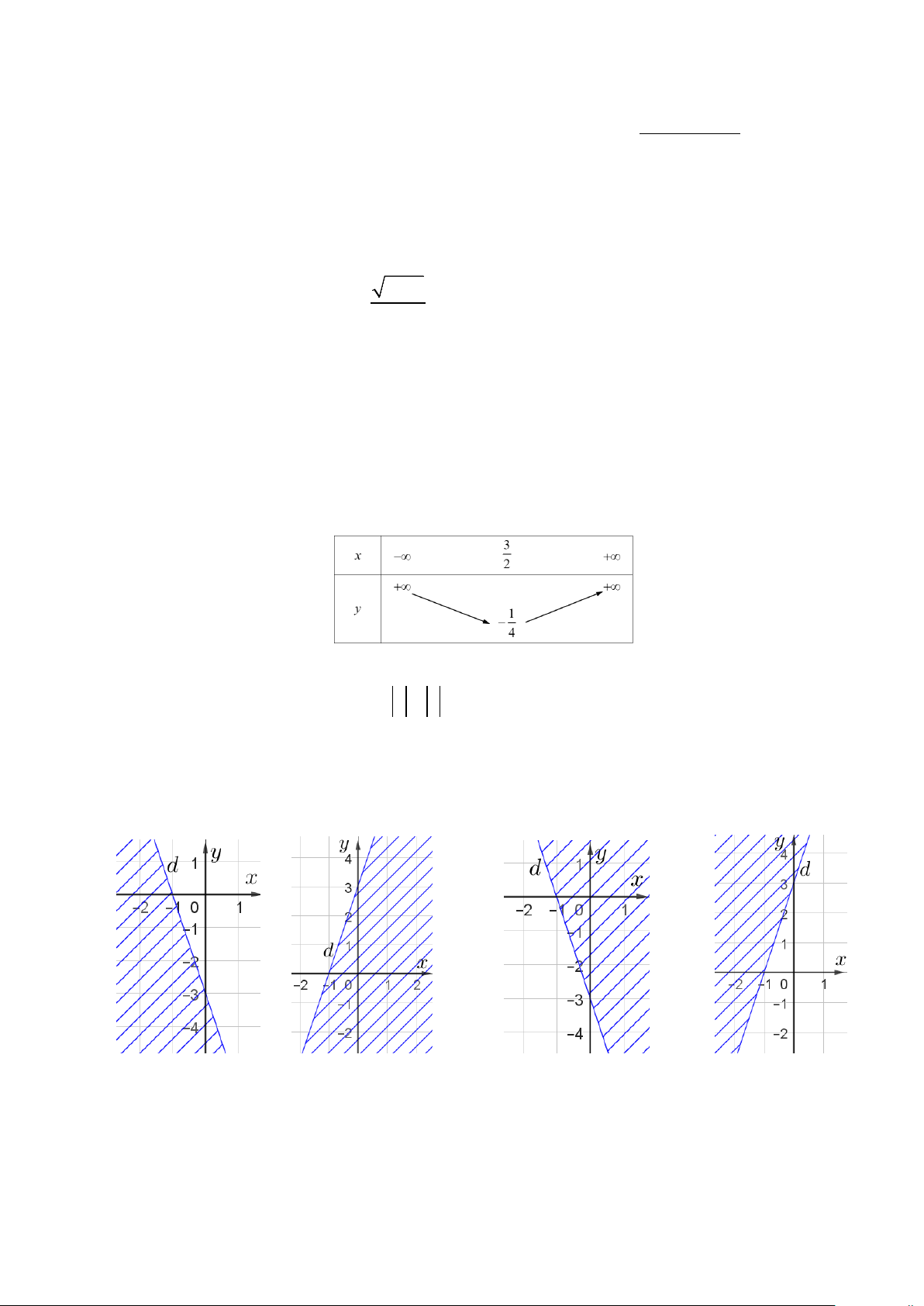
Câu 12: Parabol ở hình bên dưới là đồ thị của hàm số bậc hai nào sau đây? A. 2
y = −x + 2x + 3. B. 2
y = −x + x − 3 . C. 2
y = x − 2x − 3 . D. 2
y = x − 4x + 3 .
Câu 13: Cho hai tập hợp A = {x∈ | 3 − < x ≤ } 4 và B = { 2; − 0;2;4; }
6 . Tìm A∪ B .
A. A∪ B = [ − 2;6].
B. A∪ B = [ − 2;4].
C. A∪ B = { 2; − 1 − ;0;1;2;3;4; } 6 .
D. A∪ B = { 2; − 0;2; } 4 .
Câu 14: Cho hàm số bậc hai 2
y = ax + bx + c có đồ thị (P) . Cho biết (P) cắt trục tung tại điểm A có tung
độ bằng 4 và tiếp xúc với trục hoành tại điểm B có hoành độ âm sao cho tam giác OAB (O là gốc tọa độ)
có diện tích bằng 12. Tính tổng S = a + b + c . A. 75 S = . B. 27 S = . C. 49 S = D. 25 S = . 8 8 9 9 Câu 15: Cho hàm số 2
y = f (x) = ax + bx + c(a ≠ 0) có đồ thị là parabol có đỉnh S(-2;1) và đi qua gốc tọa
độ. Khi đó giá trị của 4a + b + c là? A. 1. B. -2. C. 2. D. 0. Câu 16: Hàm số 2
y = x + 6x − 5 có bảng biến thiên là A. B. C. D.
Trang 2/4 - Mã đề thi 101
Câu 17: Cho mẫu số liệu: 5;13;5;7;11;2;3. Khi đó tứ phân vị của mẫu số liệu này là?
A. Q = 3; Q = 7; Q = 11. Q = 2; Q = 5; Q =11. 1 2 3 B. 1 2 3 C. Q = 3; Q = 5; Q =11 .
Q = 3; Q = 5; Q = 7 . 1 2 3 D. 1 2 3
Câu 18: Có bao nhiêu giá trị nguyên dương của tham số m để hàm số 2x −1 y = luôn xác định với 2
x + x − m + 5 mọi số thực x? A. 4 . B. 5 C. 6 . D. 3.
Câu 19: Tính góc A của tam giác ABC biết BC = 7, AB = 3, AC = 8 A.  0 A =120 B.  0 A = 60 C.  0 A = 90 D.  0 A = 30 3 − x
Câu 20: Tập xác định của hàm số y = là? x − 2 A. ( ; −∞ 2] \{− } 3 . B. [2;3) . C. (−∞ ] ;3 \{ } 2 . D.  \{ } 2 .
Câu 21: Tọa độ đỉnh của đồ thị hàm số 2
y = −x + 4x − 3 là? A. S(2;1). B. S(-2;-1). C. S(-2;1). D. S(2;-1).  
Câu 22: Cho tam giác đều ABC. Tính góc ( AB,CA) A. 0 60 B. 0 120 C. 0 90 D. 0 30 Câu 23: Cho hàm số 2
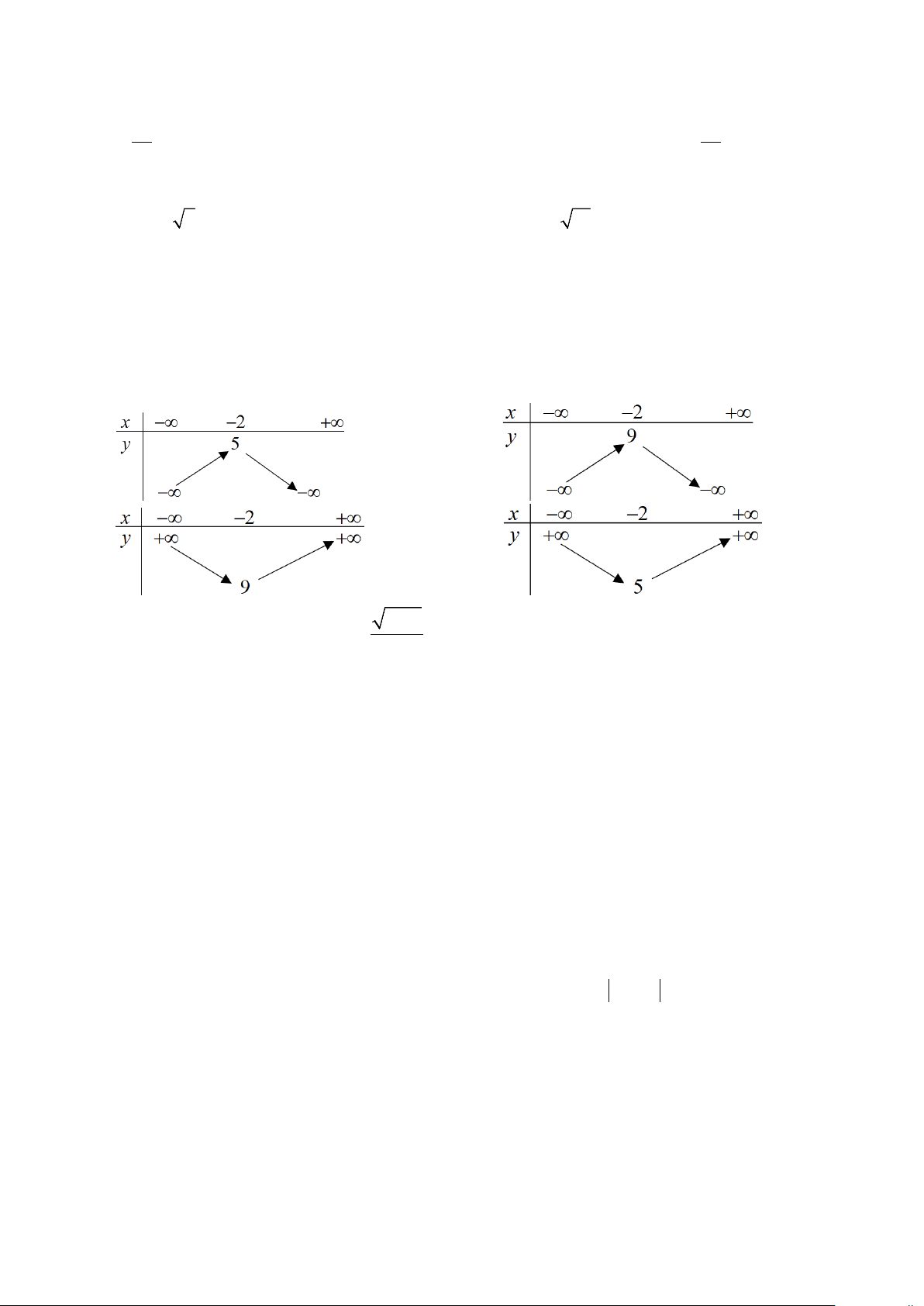
y = x + bx + c có bảng biến thiên như hình vẽ. Tìm hai hệ số b,c?
A. b = 3, c = 2 − . B. b = 3, − c = 2. C. b = 3, − c = 2 − .
D. b = 3, c = 2.       
Câu 24: Cho hai vectơ a và b thỏa mãn a = b =1. Biết vectơ x = a + 2b vuông góc với vectơ      y = 5a − 4 .
b Góc giữa hai vectơ a và b bằng: A. 0 60 B. 0 120 C. 0 90 D. 0 30
Câu 25: Miền không bị gạch chéo (kể cả bờ d ) nào sau đây là miền nghiệm của bất phương trình
3x − y + 3 ≤ 0? A. B. C. D.
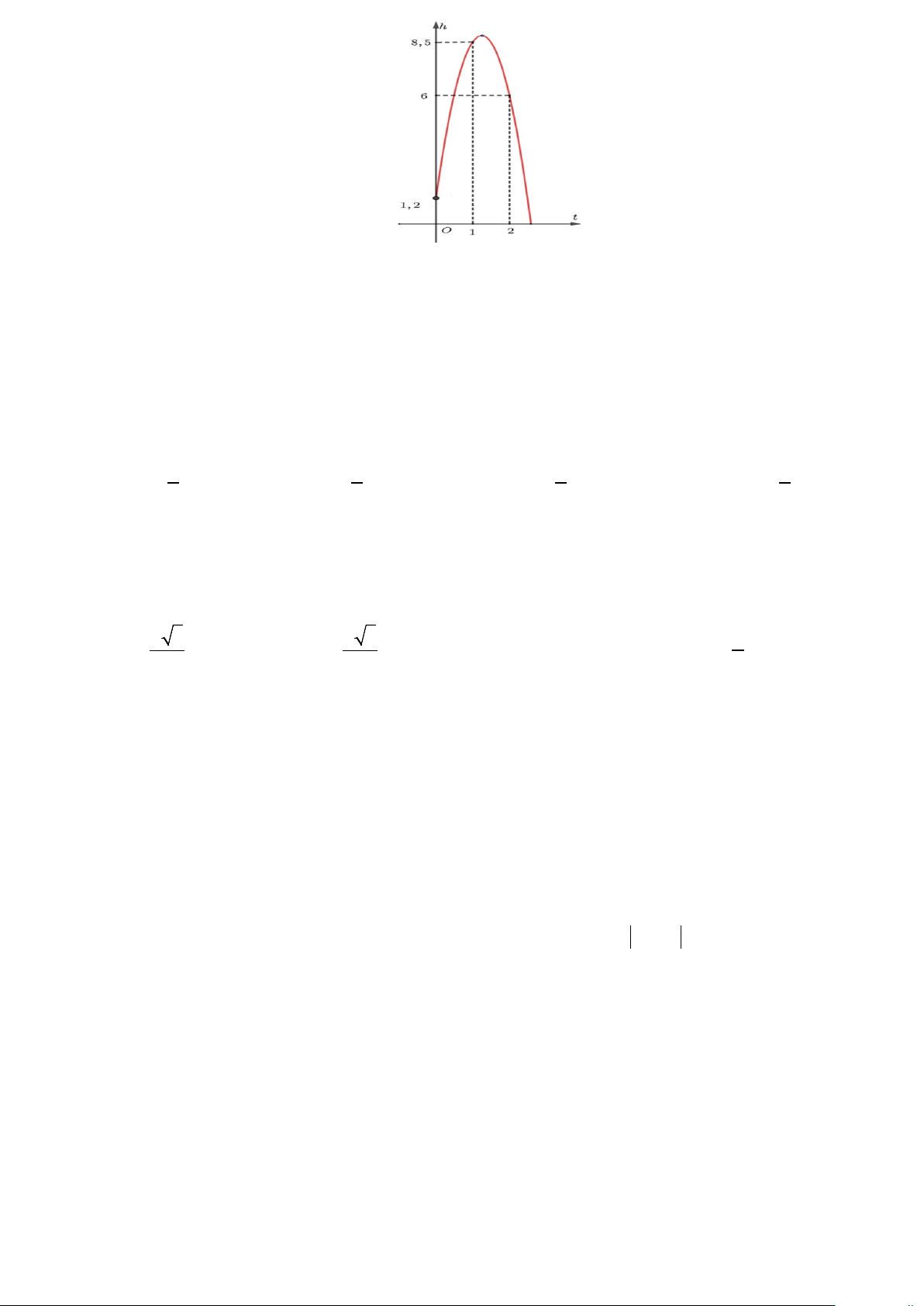
Câu 26: Khi một quả bóng được đá lên, nó sẽ đạt độ cao nào đó rồi rơi xuống đất. Biết rằng quỹ đạo của
quả bóng là một cung parabol 2
h = at + bt + c trong mặt phẳng với hệ tọa độ Oth được minh họa như hình
vẽ phía dưới, trong đó t là thời gian (tính bằng giây) kể từ khi quả bóng được đá lên; h là độ cao (tính bằng
mét) của quả bóng. Giả thiết rằng quả bóng được đá lên từ độ cao1,2 mét. Sau đó 1 giây, nó đạt độ cao 8,5
mét và 2 giây sau khi đá lên, nó ở độ cao 6 mét. Hỏi sau khi đá bao nhiêu giây thì quả bóng chạm đất lần đầu tiên?
Trang 3/4 - Mã đề thi 101 A. 2,458 . B. 2,585. C. 2,476 . D. 2,574 . Câu 27: Cho hàm số 2
y = x + 2x + 2, hãy chọn khẳng định đúng?
A. Hàm số cắt trục tung tại điểm có tung độ bằng 2, giá trị nhỏ nhất của hàm số bằng -1.
B. Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng 2, giá trị lớn nhất của hàm số bằng 1.
C. Hàm số cắt trục tung tại điểm có tung độ bằng 2, giá trị nhỏ nhất của hàm số bằng 1.
D. Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng 2, giá trị nhỏ nhất của hàm số bằng 1.
Câu 28: Cho hình bình hành ABCD .Gọi N là trung điểm DC và M là điểm trên cạnh AB sao cho   
AB = 3AM. Biểu diễn MN theo hai vectơ AB và A . D             A. 1
MN = AB + A . D B. 1
MN = AB + A . D C. 1
MN = AB − A . D D. 1
MN = − AB + A . D 6 2 6 6
Câu 29: Cho A = C ( ;
−∞ 2), B = (−∞ . Tìm A \ B ?  ] ;3 A. [3;+∞) . B. [2;+∞). C. (3;+∞) . D. (2;+∞).
Câu 30: Cho tam giác ABC có  0
BAC =120 , BC = a.Tính bán kính đường tròn ngoại tiếp tam giác ABC . A. a 3 R = . B. a 3 R = . C. R = . a D. a R = . 3 2 2 B. TỰ LUẬN
Bài 1. Tìm phương trình parabol (P) 2
: y = x + bx + c biết (P) đi qua điểm A(2; 3 − ), B(1; ) 1 .
  
Bài 2. Cho hình vuông ABCD có cạnh bằng 2. Tính tích vô hướng AC.(BC + BD)
Bài 3. Hai chiếc tàu thuỷ cùng xuất phát từ vị trí A, đi thẳng theo hai hướng tạo với nhau một góc 0 60 . Tàu
thứ nhất chạy với tốc độ 30km / h , tàu thứ hai chạy với tốc độ 40km / h . Sau 2 giờ hai tàu lần lượt tới điểm
B và C. Tính khoảng cách BC?
Bài 4. Cho parabol (P) 2
: y = x + 2mx +1 và đường thẳng (d ) 2
: y = −x − m . Tìm tất cả các giá trị của tham
số m để (P) cắt (d ) tại hai điểm phân biệt có hoành độ x , x thỏa mãn x − x = 3. 1 2 1 2 ----------- HẾT ----------
Trang 4/4 - Mã đề thi 101
SỞ GIÁO DỤC & ĐÀO TẠO KHÁNH HÒA
ĐỀ KIỂM TRA CUỐI KỲ 1 TOÁN 10
TRƯỜNG THPT NGUYỄN TRÃI NĂM HỌC 2023-2024 Mã đề thi: 241
Thời gian làm bài: 90 phút;
Họ, tên thí sinh:..................................................................... Lớp: ............................. A. TRẮC NGHIÊM Câu 1: Cho hàm số 2
y = −x + 2x + 3, hãy chọn khẳng định đúng?
A. Hàm số cắt trục tung tại điểm có tung độ bằng 3, giá trị lớn nhất của hàm số bằng -1.
B. Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng 3, giá trị nhỏ nhất của hàm số bằng 4.
C. Hàm số cắt trục tung tại điểm có tung độ bằng 3, giá trị lớn nhất của hàm số bằng 4.
D. Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng 3, giá trị lớn nhất của hàm số bằng 4.
Câu 2: Cho hai tập hợp A = {x∈ | 3 − < x ≤ } 4 và B = { 2; − 0;2;4; }
6 . Tìm A∩ B .
A. A∩ B = { 2; − 1 − ;0;1;2;3;4; } 6 .
B. A∩ B = { 2; − 0;2; } 4 .
C. A∩ B = [ − 2;6].
D. A∩ B = [ − 2;4].
    
Câu 3: Thu gọn u = AM + NA − AD − NM , ta được       
A. u = DA
B. u = AD
C. u = DA
D. u = DM
Câu 4: Biểu thức F = 3x − 4y đạt giá trị lớn nhất bằng bao nhiêu trên miền đa giác không bị tô đậm trong hình bên? A. 0. B. 9. C. 6. D. -16.
Câu 5: Cho đồ thị hàm số như hình vẽ, hãy chọn khẳng định đúng?
A. Hàm số đồng biến trên khoảng ( 1;
− 0) và nghịch biến trên khoảng (0;3).
B. Hàm số đồng biến trên khoảng (0; )
1 và nghịch biến trên khoảng ( 2; − 2).
C. Hàm số đồng biến trên khoảng (0; )
1 và nghịch biến trên khoảng (0;2) .
D. Hàm số đồng biến trên khoảng (2;3) và nghịch biến trên khoảng (0;2) .
Câu 6: Tọa độ đỉnh của đồ thị hàm số 2
y = −x − 4x −1 là? A. S(-2;1). B. S(2;-3). C. S(-2;3). D. S(-2;-3).
Câu 7: Tìm số trung bình x của mẫu số liệu sau:
Trang 1/4 - Mã đề thi 241
A. x ≈ 4,78 . B. x ≈ 5,73. C. x ≈ 5,49 . D. x ≈ 4,36 .
Câu 8: Hàm số nào sau đây có giá trị nhỏ nhất bằng 19? A. 2
y = 2x − 4x + 21. B. 2 y = 2
− x + 4x +19 . C. 2
y = −x − 6x +10 . D. 2
y = x −8x +19.  
Câu 9: Cho tam giác đều ABC. Tính góc (B , A CB) A. 0 30 B. 0 60 C. 0 90 D. 0 120
Câu 10: Tính góc A của tam giác ABC biết BC = 7, AB = 5, AC = 8 A.  0 A = 60 B.  0 A =120 C.  0 A = 90 D.  0
A = 30  
Câu 11: Cho tam giác ABC . Gọi M là trung điểm của AB , N là điểm thuộc AC sao cho CN = 3NA và   
K là trung điểm của MN . .Biểu diễn AK theo hai vectơ ABvà AC.             A. 1 1
AK = AB + AC. B. 1 1
AK = AB + AC. C. 1 1
AK = AB + AC. D. 1 2
AK = AB + AC. 4 8 2 4 4 3 2 3 Câu 12: Cho hàm số 2
y = f (x) = ax + bx + c(a ≠ 0) có đồ thị là parabol có đỉnh S(-4;-4) và đi qua gốc
tọa độ. Khi đó giá trị của 4a + b + c là? A. 3. B. 2. C. 1. D. -3.
Câu 13: Cho hàm số bậc hai 2
y = ax + bx + c có đồ thị (P) . Cho biết (P) cắt trục tung tại điểm M có tung
độ bằng 6 và tiếp xúc với trục hoành tại điểm E có hoành độ âm sao cho tam giác OME (O là gốc tọa độ)
có diện tích bằng 12. Tính tổng S = a + b + c . A. 75 S = . B. 27 S = . C. 49 S = D. 25 S = . 8 8 9 9
Câu 14: Cho hình bình hành ABCD .Gọi N là trung điểm DC và M là điểm trên cạnh AB sao cho   
AB = 4AM. Biểu diễn MN theo hai vectơ AB và A . D             A. 1
MN = AB − A . D B. 1
MN = − AB + A . D C. 1
MN = AB + A . D D. 1
MN = − AB + A . D 6 4 4 6          
Câu 15: Cho hai vectơ a và b thỏa mãn a = b =1. Biết vectơ 2
u = a − 3b vuông góc với vectơ v = a + b 5  
. Góc giữa hai vectơ a và b bằng: A. 0 0 B. 0 120 C. 0 90 D. 0 180 Câu 16: Cho hàm số 2
y = x + bx + c có bảng biến thiên như hình vẽ. Tìm hai hệ số b,c? A. b = 3, − c = 2 − . B. b = 3, − c = 4.
C. b = 3, c = 2.
D. b = 3, c = 4.
Câu 17: Cho tam giác ABC có M là trung điểm AB và G là trọng tâm của tam giác ABC . Khẳng định nào
sau đây là khẳng định sai ?  
         
A. GC = 2GM. B. GA + GB + GC = 0.
C. MA + MB = 0. D. CA + CB = 2CM.
Câu 18: Khi một quả bóng được đá lên, nó sẽ đạt độ cao nào đó rồi rơi xuống đất. Biết rằng quỹ đạo của
quả bóng là một cung parabol 2
h = at + bt + c trong mặt phẳng với hệ tọa độ Oth được minh họa như hình
vẽ phía dưới, trong đó t là thời gian (tính bằng giây) kể từ khi quả bóng được đá lên; h là độ cao (tính bằng
mét) của quả bóng. Giả thiết rằng quả bóng được đá lên từ mặt đất và sau 2 giây quả bóng đạt đến độ cao
lớn nhất là 7 mét. Hỏi sau khi đá 3 giây thì quả bóng đạt được độ cao bao nhiêu mét so với mặt đất?
Trang 2/4 - Mã đề thi 241 A. 5,25. B. 6,15. C. 5,75. D. 6,85.
Câu 19: Có bao nhiêu giá trị nguyên âm của tham số m để hàm số 2x −1 y =
luôn xác định với mọi 2
x − x + m + 8 số thực x? A. 8 . B. 6 . C. 9 D. 7 .
Câu 20: Miền không bị gạch chéo (không kể cả bờ d ) nào sau đây là miền nghiệm của bất phương trình
3x + y + 3 > 0 ? A. B. C. D.
Câu 21: Cho hàm số y = f (x) có tập xác định D = [ 2;
− 6] và có đồ thị như hình vẽ sau:
Tập giá trị của hàm số y = f (x) là: A. [ − 2;2] B. [ −1;1] C. [0;2] D. [ −1;2]
Câu 22: Cho tam giác ABC có  0
BAC =120 , BC = 3.Tính bán kính đường tròn ngoại tiếp tam giác ABC . A. 3 R = . B. 3 3 R = . C. R = 3. D. 3 R = . 3 2 2
Câu 23: Parabol ở hình bên dưới là đồ thị của hàm số bậc hai nào sau đây? A. 2
y = x − 4x + 3 . B. 2
y = x − 2x − 3 . C. 2
y = −x + x − 3 . D. 2
y = −x + 2x + 3.
Câu 24: Cho mẫu số liệu: 2;3;10;13;5;15;4. Khi đó tứ phân vị của mẫu số liệu này là?
Trang 3/4 - Mã đề thi 241 A. Q = 3; Q = 5; Q =13 . Q = 3; Q =13; Q =11. 1 2 3 B. 1 2 3 C. Q = 3; Q = 4; Q =13. Q = 2; Q = 5; Q =11. 1 2 3 D. 1 2 3
   
Câu 25: Cho tam giác đều ABC có cạnh bằng .
a Tính tích vô hướng AC.AB − AC.CB 2 2 A. a − B. 0 C. 2 a D. a 2 2
Câu 26: Cho tam giác ABC có  +  0
B C =120 , AB = 4, AC = 6. Tính BC. A. BC = 2 7. B. BC = 28. C. BC = 2 10. D. BC = 40.
Câu 27: Cho A = C (2;+∞), B = [1;+∞ . Tìm A \ B ?  ) A. (1;2]. B. [1;+∞) . C. (2; ) 1 . D. ( ) ;1 −∞ .
Câu 28: Cặp số nào sau đây là một nghiệm của bất phương trình 2x − y +1≤ 0 ? A. (2;3) . B. (2;0) . C. (1;3) . D. (1;1) . Câu 29: Hàm số 2 y = 2
− x −8x +1 có bảng biến thiên là A. B. C. D. 1− x
Câu 30: Tập xác định của hàm số y = là? x + 2 A.  \{ } 2 − . B. (−∞ ] ;1 \{− } 2 . C. [ 2; − ) 1 . D. ( ; −∞ 2] \{− } 2 . B. TỰ LUẬN
Bài 1. Tìm phương trình parabol (P) 2
: y = −x + bx + c biết (P) đi qua điểm A(1;2), B(2; ) 1 .
  
Bài 2. Cho hình vuông ABCD có cạnh bằng 2. Tính tích vô hướng B .
D ( AC + AD)
Bài 3. Hai chiếc tàu thuỷ cùng xuất phát từ vị trí A, đi thẳng theo hai hướng tạo với nhau một góc 0 60 .
Tàu thứ nhất chạy với tốc độ 30km / h , tàu thứ hai chạy với tốc độ 40km / h . Sau 3 giờ hai tàu lần lượt tới
điểm B và C. Tính khoảng cách BC?
Bài 4. Cho parabol (P) 2
: y = x − 2mx −1 và đường thẳng (d ) 2
: y = x − m . Tìm tất cả các giá trị của tham số
m để (P) cắt (d ) tại hai điểm phân biệt có hoành độ x , x thỏa mãn x − x =1. 1 2 1 2 ----------- HẾT ----------
Trang 4/4 - Mã đề thi 241 mamon made cautron dapan T10 101 1 D T10 101 2 D T10 101 3 D T10 101 4 B T10 101 5 C T10 101 6 C T10 101 7 D T10 101 8 A T10 101 9 D T10 101 10 A T10 101 11 D T10 101 12 A T10 101 13 C T10 101 14 C T10 101 15 B T10 101 16 A T10 101 17 C T10 101 18 A T10 101 19 B T10 101 20 C T10 101 21 A T10 101 22 B T10 101 23 B T10 101 24 A T10 101 25 B T10 101 26 B T10 101 27 D T10 101 28 A T10 101 29 C T10 101 30 A mamon made cautron dapan T10 241 1 D T10 241 2 B T10 241 3 C T10 241 4 C T10 241 5 D T10 241 6 C T10 241 7 D T10 241 8 A T10 241 9 D T10 241 10 A T10 241 11 A T10 241 12 A T10 241 13 A T10 241 14 C T10 241 15 D T10 241 16 B T10 241 17 B T10 241 18 A T10 241 19 D T10 241 20 B T10 241 21 A T10 241 22 C T10 241 23 B T10 241 24 A T10 241 25 C T10 241 26 A T10 241 27 D T10 241 28 C T10 241 29 B T10 241 30 B
Xem thêm: ĐỀ THI HK1 TOÁN 10
https://toanmath.com/de-thi-hk1-toan-10 B. TỰ LUẬN
Bài 1. Tìm phương trình parabol (P) 2
: y = x + bx + c biết (P) đi qua điểm A(2; 3 − ), B(1; ) 1 .
  
Bài 2. Cho hình vuông ABCD có cạnh bằng 2. Tính tích vô hướng AC.(BC + BD)
Bài 3. Hai chiếc tàu thuỷ cùng xuất phát từ vị trí A, đi thẳng theo hai hướng tạo với nhau một góc 0 60 . Tàu
thứ nhất chạy với tốc độ 30km / h , tàu thứ hai chạy với tốc độ 40km / h . Sau 2 giờ hai tàu lần lượt tới điểm B
và C. Tính khoảng cách BC?
Bài 4. Cho parabol (P) 2
: y = x + 2mx +1 và đường thẳng (d ) 2
: y = −x − m . Tìm tất cả các giá trị của tham số m
để (P) cắt (d ) tại hai điểm phân biệt có hoành độ x , x thỏa mãn x − x = 3. 1 2 1 2 B. TỰ LUẬN
Bài 1. Tìm phương trình parabol (P) 2
: y = −x + bx + c biết (P) đi qua điểm A(1;2), B(2; ) 1 .
  
Bài 2. Cho hình vuông ABCD có cạnh bằng 2. Tính tích vô hướng B .
D ( AC + AD)
Bài 3. Hai chiếc tàu thuỷ cùng xuất phát từ vị trí A, đi thẳng theo hai hướng tạo với nhau một góc 0 60 . Tàu
thứ nhất chạy với tốc độ 30km / h , tàu thứ hai chạy với tốc độ 40km / h . Sau 3 giờ hai tàu lần lượt tới điểm B và C. Tính khoảng cách BC?
Bài 4. Cho parabol (P) 2
: y = x − 2mx −1 và đường thẳng (d ) 2
: y = x − m . Tìm tất cả các giá trị của tham số m
để (P) cắt (d ) tại hai điểm phân biệt có hoành độ x , x thỏa mãn x − x =1. 1 2 1 2
ĐÁP ÁN PHẦN TỰ LUẬN
KIỂM TRA HỌC KỲ 1 – MÔN TOÁN 10 – NĂM HỌC 2023-2024 Nguồn 1 Điể m Nguồn 2
Bài 1. Tìm phương trình parabol
Bài 1. Tìm phương trình parabol (P) 2
: y = x + bx + c biết (P) đi qua điểm 1 (P) 2
: y = −x + bx + c biết (P) đi qua điểm A(2; 3 − ), B(1; ) 1 . A(1;2), B(2; ) 1 .
Parabol đi qua điểm A(2; 3
− ) nên 2b + c = 7 − .
0.25 Parabol đi qua điểm A(1;2) nên b + c = 3.
Parabol đi qua điểm B(1; )
1 nên b + c = 0.
0.25 Parabol đi qua điểm B(2; )
1 nên 2b + c = 5. 2b + c = 7 − b  = 7 − b  + c = 3 b  = 2
Ta có hệ phương trình  ⇔ .  ⇔ . b   c 0  + = c = 7
0.25 Ta có hệ phương trình 2b+c = 5 c =1
Vậy phương trình (P) 2
: y = x − 7x + 7
0,25 Vậy phương trình (P) 2
: y = −x + 2x +1
Bài 2. Cho hình vuông ABCD có cạnh bằng 2.
  
Bài 2. Cho hình vuông ABCD có cạnh bằng 2.
  
Tính tích vô hướng AC.(BC + BD) 1
Tính tích vô hướng B .
D ( AC + AD)
   
    Viết được = =  AC.BC C .
ACB AC.BC.cos ACB 0.25 Viết được = =  B . D AD D . B DA B . D A . D cos ADB  
Tính ra AC.BC = 4 0.25 Tính ra . DB AD = 4    
Lập luận AC ⊥ BD ⇒ AC.BD = 0
0.25 Lập luận AC ⊥ BD ⇒ AC.BD = 0
  
  
Kết luận : AC.(BC + BD) = 4 0.25 Kết luận : B .
D ( AC + AD) = 4
Bài 3. Hai chiếc tàu thuỷ cùng xuất phát từ vị trí
Bài 3. Hai chiếc tàu thuỷ cùng xuất phát từ vị trí
A , đi thẳng theo hai hướng tạo với nhau một góc
A , đi thẳng theo hai hướng tạo với nhau một góc 0
60 . Tàu thứ nhất chạy với tốc độ 30km / h , tàu 0
60 . Tàu thứ nhất chạy với tốc độ 30km / h , tàu 1
thứ hai chạy với tốc độ 40km / h . Sau 2 giờ hai
thứ hai chạy với tốc độ 40km / h . Sau 3 giờ hai
tàu lần lượt tới điểm B và C. Tính khoảng cách
tàu lần lượt tới điểm B và C. Tính khoảng cách BC? BC?
Quảng đường tàu thứ nhất chạy được sau 2 giờ:
Quảng đường tàu thứ nhất chạy được sau 2 giờ: AB=60km 0.25 AB=90km
Quảng đường tàu thứ hai chạy được sau 2 giờ:
Quảng đường tàu thứ hai chạy được sau 2 giờ: AC=80km 0.25 AC=120km
Áp dụng định lý cos vào ∆ABC, ta có:
Áp dụng định lý cos vào ∆ABC, ta có: 2 2 2
BC = AB + AC − 2A .
B AC.cos A ⇒ BC = 20 13 0.25 2 2 2
BC = AB + AC − 2A .
B AC.cos A ⇒ BC = 30 13
Kết luận : sau 2 giờ, hai tàu cách nhau khoảng
Kết luận : sau 3 giờ, hai tàu cách nhau khoảng 20 13 km 0.25 30 13 km
Bài 4. Cho parabol (P) 2
: y = x + 2mx +1 và
Bài 4. Cho parabol (P) 2
: y = x − 2mx −1 và đường thẳng (d ) 2
: y = −x − m . Tìm tất cả các giá đường thẳng (d ) 2
: y = x − m . Tìm tất cả các giá
trị của tham số m để (P) cắt (d ) tại hai điểm 1
trị của tham số m để (P) cắt (d ) tại hai điểm
phân biệt có hoành độ x , x thỏa mãn x − x = 3.
phân biệt có hoành độ x , x thỏa mãn x − x =1 1 2 1 2 1 2 1 2 . Pt hđộ giao điểm: 2 x + ( m + ) 2 2
1 x + m +1 = 0( ) 1 Pt hđộ giao điểm: 2 x − ( m + ) 2 2
1 x + m −1 = 0( ) 1
+) (P) cắt (d ) tại hai điểm phân biệt có hoành độ
+) (P) cắt (d ) tại hai điểm phân biệt có hoành
x , x ⇔ 1 có hai nghiệm phân biệt x ,
0.25 độ x , x ⇔ 1 có hai nghiệm phân biệt x , 1 2 ( ) 1 2 ( ) x x 1 2 1 2 ∆ = ( m + )2 − ( 2 m + ) 3 2 1 4
1 = 4m − 3 > 0 ⇔ m > ∆ = ( m + )2 − ( 2 m − ) 5 2 1 4
1 = 4m + 5 > 0 ⇔ m > − 4 4
+) x − x = 3 ⇔ (x + x )2 − 4x .x = 9
0.25 +) x − x =1 ⇔ x + x − 4x .x =1 1 2 ( 1 2)2 1 2 1 2 1 2 1 2 +) ( m + )2 2 2
1 − 4(m +1) = 9 ⇔ m = 3 0.25 +) ( m + )2 2 2
1 − 4(m −1) =1 ⇔ m = 1 −
Kết luận : m = 3 là giá trị cần tìm.
0.25 Kết luận : m = 1
− là giá trị cần tìm.
Các cách giải khác, trình bày khác, nếu đúng vẫn được điểm tối đa
Document Outline