ỦY BAN NHÂN DÂN QUẬN 10
KIỂM TRA CUỐI KÌ 1
TRƯỜNG THCS NGUYỄN TRI PHƯƠNG
NĂM HỌC: 2023 – 2024 ĐỀ CHÍNH THỨC Môn: TOÁN
A. PHẦN TRẮC NGHIỆM (3,0 điểm)
Học sinh đọc kĩ câu hỏi và chọn 1 đáp án đúng nhất.
Vẽ lại bảng sau vào bài kiểm tra và điền đáp án (A,B,C hoặc D) theo đúng thứ tự câu hỏi. Câu 1 2 3 4 5 6 7 8 9 10 11 12 Đáp án Câu 1.
Trong các biểu thức sau, biểu thức nào là đơn thức? 5 A. 2 3x y B. ( x y +1)
C. 1− 2x D. 2x 1 2 3 Câu 2.
Đơn thức đồng dạng với đơn thức x y z là 2 2 3 3 2 . A 5x y z 2 3 . B 7 y x z C. − 2x y z 2 3 . D 15x z y 13 −1 3 2 = Câu 3.
Giá trị của đa thức 2x + 3x − x − 2 tại x là 5 2 −1 −17 1 17 A. B. C. D. 5 10 5 10 2 2 6 4 Câu 4.
Bậc của đa thức 9x y + 2x + 3x y −18xyz −15 là A. 4 B. 5 C. 6 D. 7 Câu 5.
Tích (2x + 9)(2x - 9) có kết quả bằng A. 2x2 – 81 B. 4x2 + 81 C. (2x +9)2 D. 4x2 – 81 2  1  Câu 6. Biểu thức 3x − 
 được viết dưới dạng đa thức là  6  1 1 1 1 1 2 A. 3x − x + 2 B. 9x − x − 2 C. 9x − x + 2 D. 9x − x + 36 36 2 36 36 x + 2 Câu 7.
Với điều kiện nào của x thì phân thức 5x − xác định? 5 A. x  0 B. x  1 C. x  2 D. x  1 − Câu 8.
Kết luận nào sau đây đúng?
A. Hình chóp tứ giác đều có 1 đỉnh, 6 mặt, 8 cạnh.
B. Hình chóp tam giác đều có 1 đỉnh, 4 mặt, 8 cạnh.
C. Hình chóp tứ giác đều có 1 đỉnh, 5 mặt, 8 cạnh.
D. Hình chóp tam giác đều có 1 đỉnh, 4 mặt, 8 cạnh.
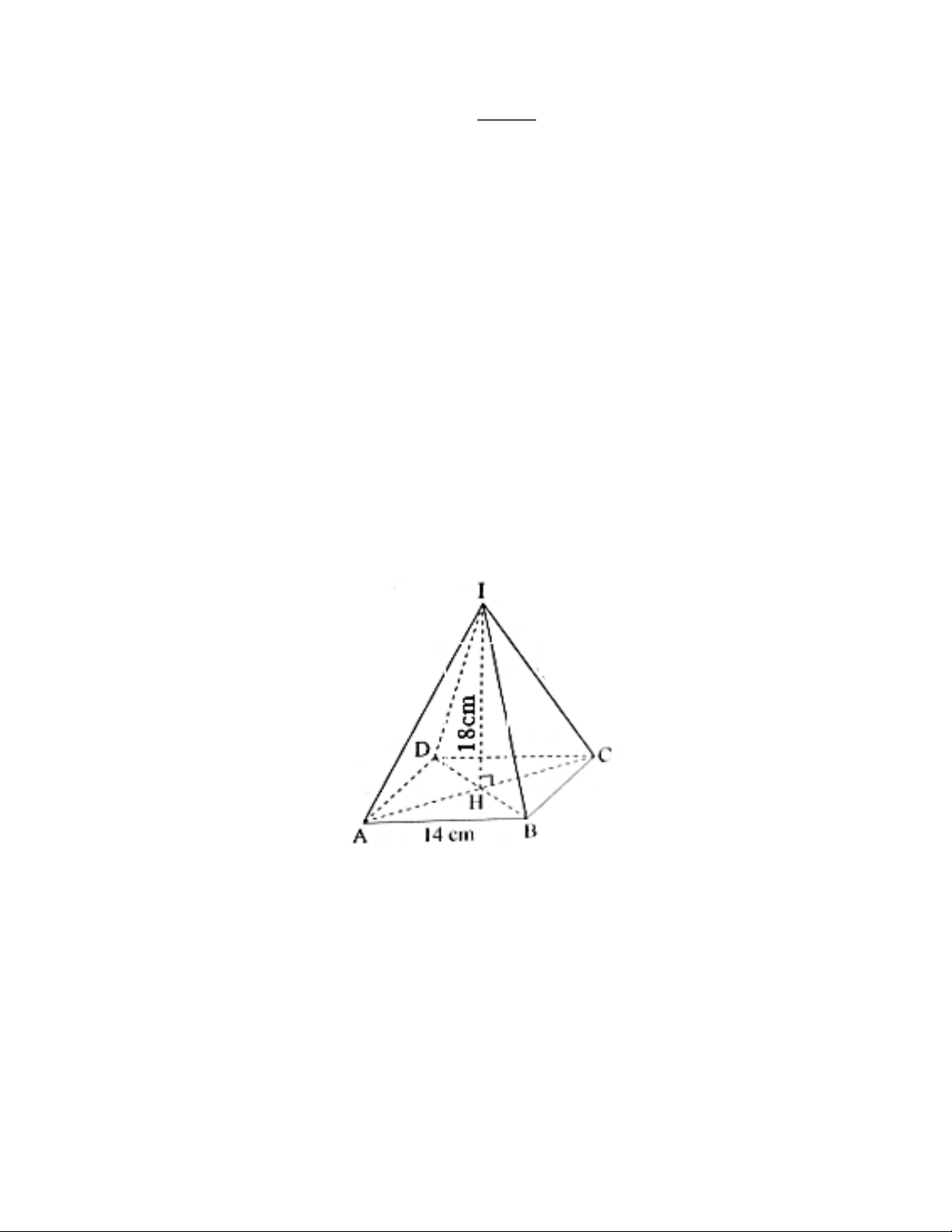
Câu 9. Cho hình chóp tứ giác đều I.ABCD có độ dài cạnh đáy là 14cm và chiều cao là 18cm.
Thể tích của hình chóp tứ giác đều I.ABCD là: A. 3 196cm 3 B. 1176cm 3 C. 168cm 3
D. 3528cm
Câu 10. Trong các khẳng định sau, khẳng định nào sai?
A. Tứ giác có 3 góc vuông là hình chữ nhật.
B. Hình bình hành có 1 góc vuông là hình chữ nhật.
C. Tứ giác có các cạnh đối bằng nhau là hình bình hành.
D. Hình bình hành có 2 đường chéo cắt nhau tại trung điểm mỗi đường là hình chữ nhật.
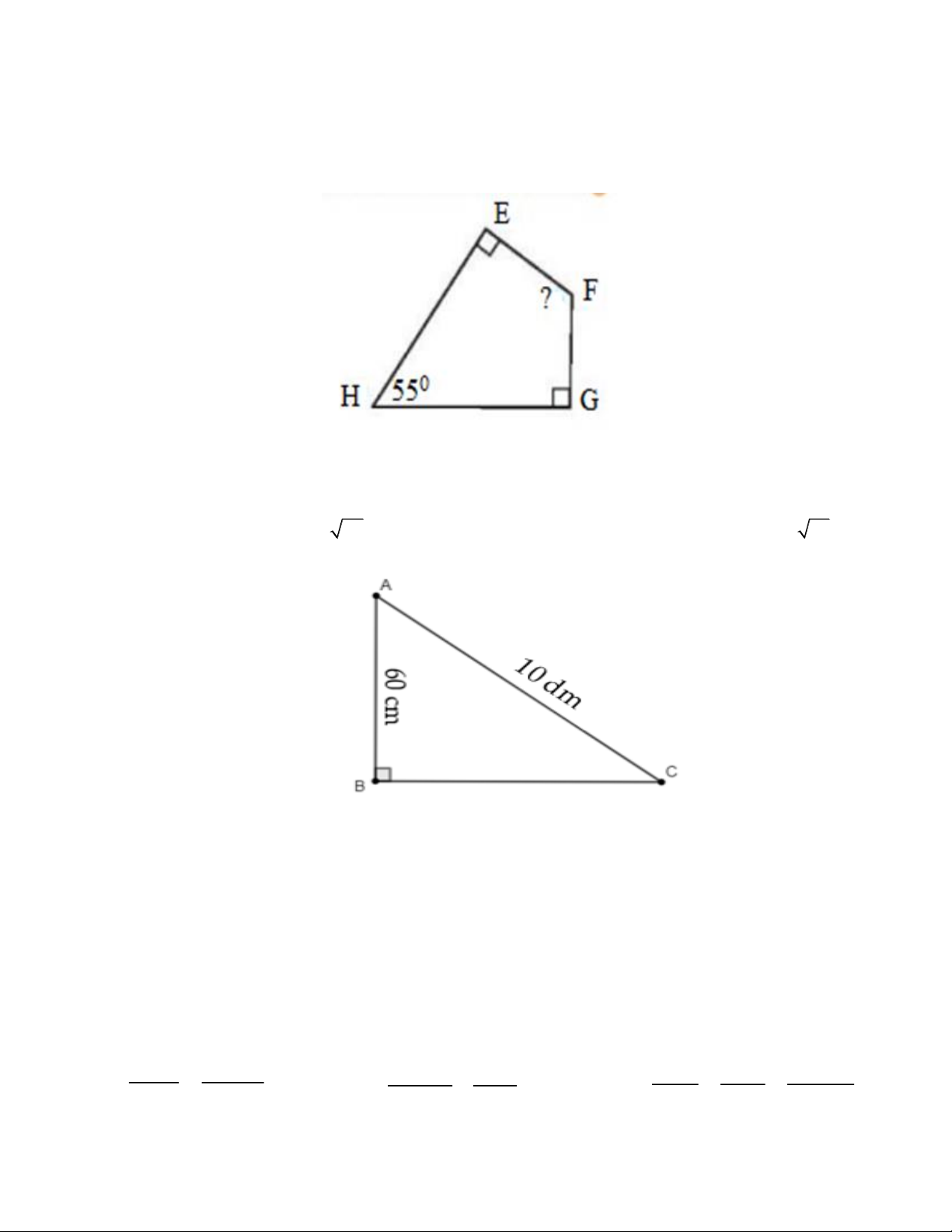
Câu 11. Cho tứ giác EFGH như hình bên. Số đo F bằng: A. 1150 B. 1250 C. 550 D. 900
Câu 12. Cho tam giác ABC vuông tại B có AB = 60 cm; AC = 10 dm. Độ dài đoạn BC là: A. 80 dm B. 10 37 cm C. 8 dm D. 2 (20 34 ) cm
B. PHẦN TỰ LUẬN (7,0 điểm)
Bài 1. (1,0 điểm) Thực hiện phép tính
a) 3x(x − 2 y) + 2xy b) 2
(2x + y) − 3x(x − y)
Bài 2. (2,0 điểm) Thực hiện phép tính x + y 2x − y 2 2 x − 5x x − 9 x + 2 2 3x + x a) + b) − c) + + 2 y 2 y x − 3 x − 3 2 x − 3 x + 3 9 − x
Bài 3. (1,0 điểm) Phân tích đa thức thành nhân tử: 2 2 a) 4x y + 8x
b) 9x – 6x + 1 c) 2 2
y + 2xy − 4 + x
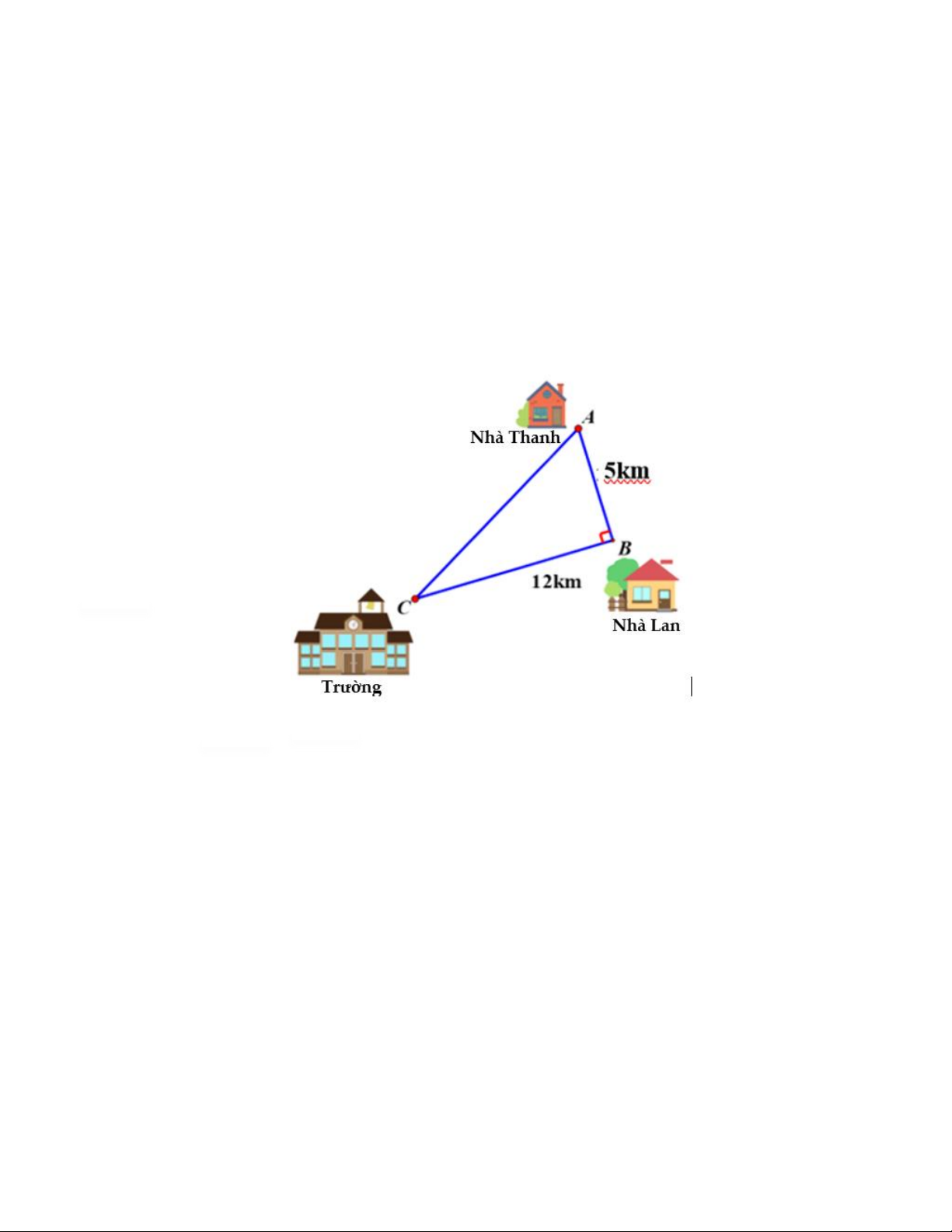
Bài 4. (0,5 điểm) Nhà bạn Lan cách nhà bạn Thanh 5 km và cách trường học 12 km. Biết rằng
nhà bạn Thanh, nhà bạn Lan và trường học tạo thành 3 đỉnh của một tam giác vuông như hình
vẽ bên dưới. Hỏi quãng đường từ nhà đến trường của bạn Thanh dài hơn quãng đường từ nhà
đến trường của bạn Lan bao nhiêu km?
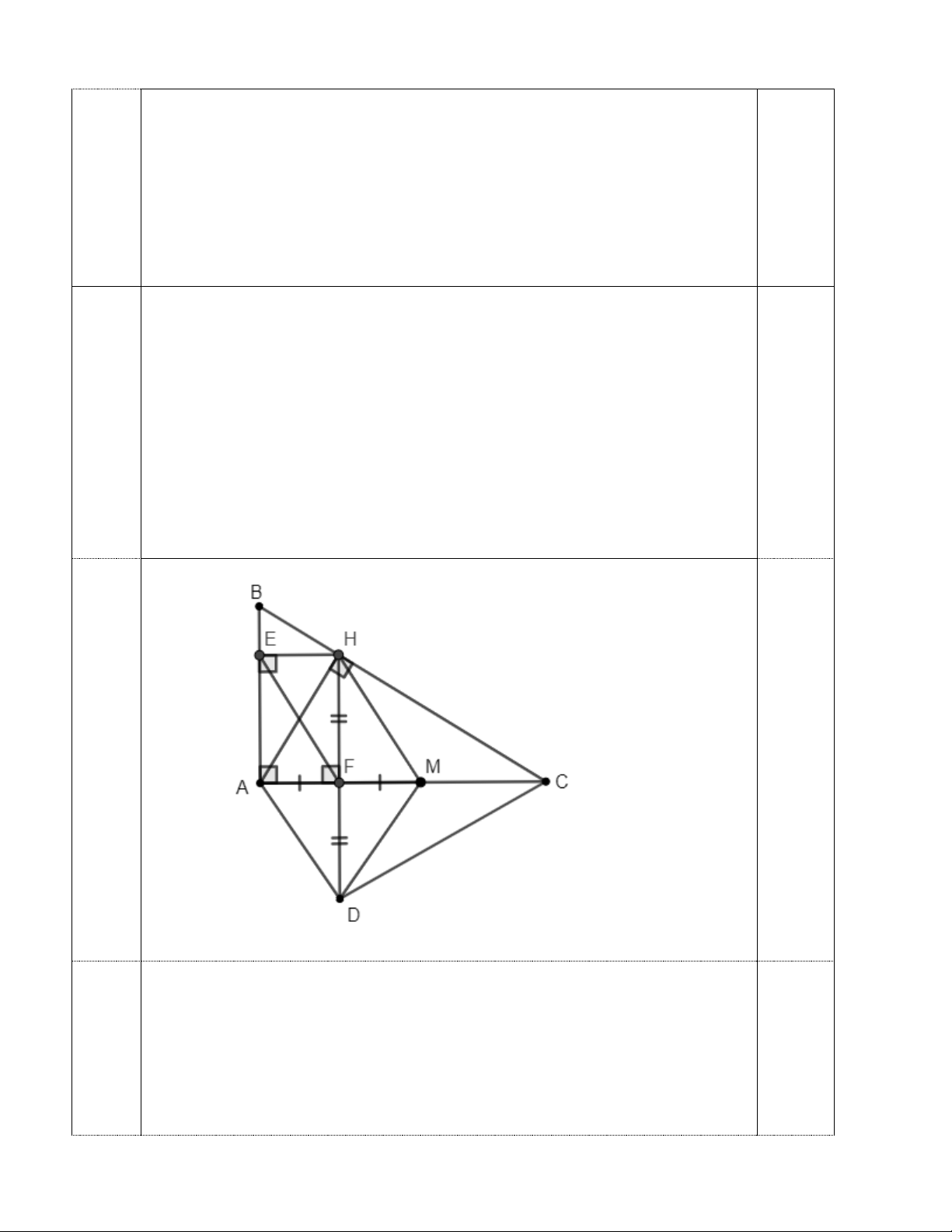
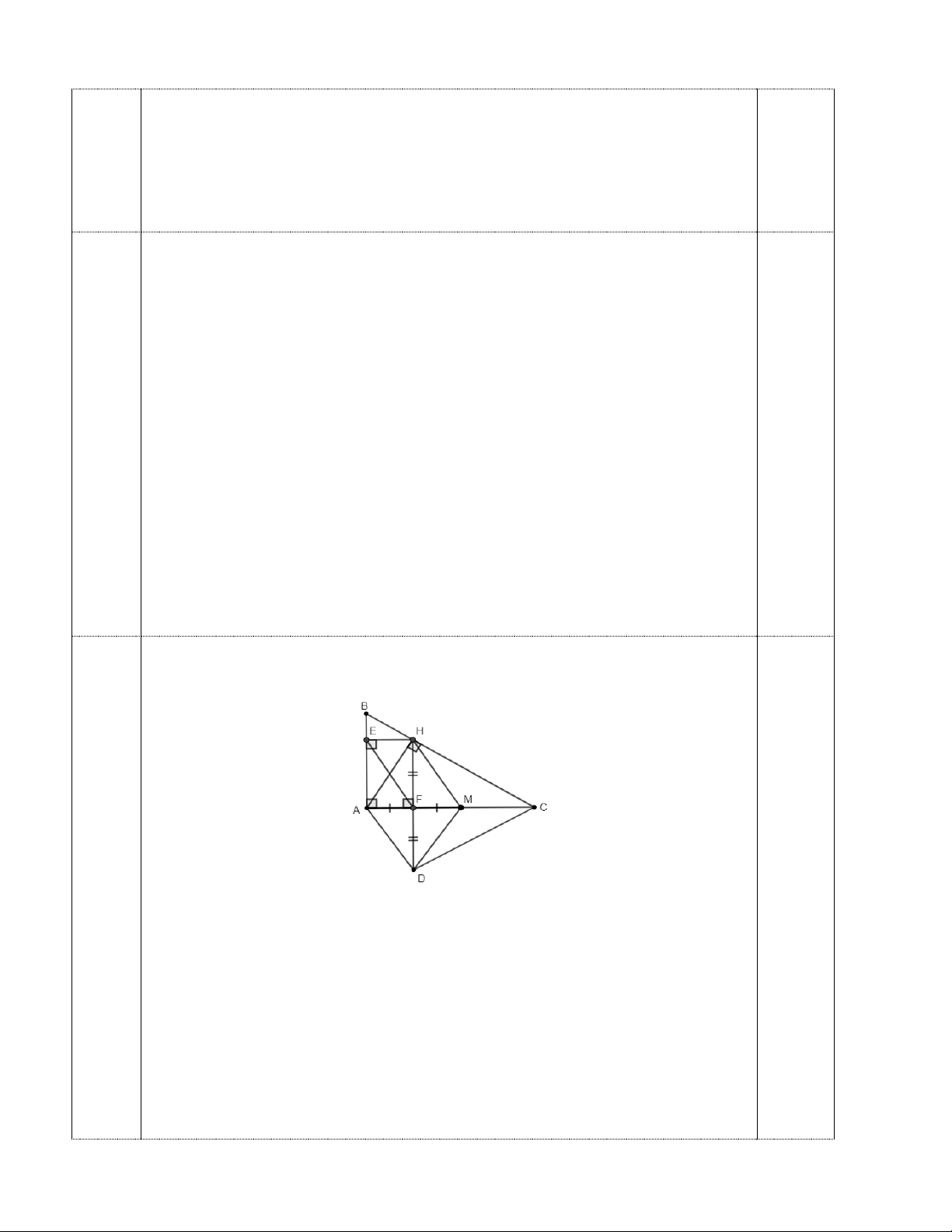
Bài 5. (2,5 điểm) Cho ΔABC vuông tại A (AB < AC) có AH là đường cao. Kẻ HE ⊥ AB tại E, kẻ HF ⊥ AC tại F.
a) Chứng minh tứ giác AEHF là hình chữ nhật.
b) Lấy điểm M đối xứng với điểm A qua điểm F. Chứng minh tứ giác EFMH là hình bình hành.
c) Lấy điểm D đối xứng với H qua F. Chứng minh tứ giác AHMD là hình thoi và EF ⊥ DC . --- Hết ---
ĐÁP ÁN VÀ THANG ĐIỂM ĐỀ CH ÍNH THỨC - A
ĐÁP ÁN & HƯỚNG DẪN CHẤM
Môn : Toán – Lớp: 8
I.TRẮC NGHIỆM: (3,0 điểm) Mỗi phương án chọn đúng 0,25 điểm. Câu 1 2 3 4 5 6 7 8 9 10 11 12 Đ/án A C A C D D B C B D B C
II. TỰ LUẬN: (7,0 điểm) Câu Lời giải Điểm 1a 2 2
3x(x − 2 y) + 2xy = 3x − 6xy + 2xy = 3x − 4xy 0.25x2 (0,5đ) 1b 2 2 2 2 2 2
(2x + y) − 3x(x − y) = 4x + 4xy + y − 3x + 3xy = x + 7xy + y 0.25x2 (0,5đ) 2 x + y 2x − y
x + y + 2x − y 3x 0,5 a) + = = 2 y 2 y 2 y 2 y (2,0đ) 2 2 2 2 x − 5x x − 9
x − 5x − x + 9 x − 6x + 9 (x − 3) b) − = = = = x − 3 x − 3 x − 3 x − 3 x − 3 x − 3 0,5 2 x + 2 2 3x + x c) + + 2 x − 3 x + 3 9 − x 2 0,5 (x + 2)(x + 3) 2(x − 3) 3x + x = + − (x − 3)(x + 3) (x + 3)(x − 3)
(x − 3)(x + 3) 0,5 2 2 2
x + 5x + 6 + 2x − 6 − 3x − x 2 − x + 6x = = (x − 3)(x + 3) (x − 3)(x + 3) 2 − x(x − 3) 2 − x = = (x − 3)(x + 3) x + 3 3 2
a) 4x y + 8x = 4x(xy + 2) 0,25 (1,0đ) 2 2 )
b 9x – 6x + 1 = (3x −1) 0,25 2 2
c y + xy − + x = ( 2
x + xy + y ) − = ( x + y)2 2 2 ) 2 4 2 4 − 2 0,25x2
= (x + y − 2)(x + y + 2) 4
Xét △ 𝐴𝐵𝐶 vuông tại B: (1,0đ)
𝐴𝐶2 = 𝐵𝐶2 + 𝐴𝐵2 (đị𝑛ℎ 𝑙ý 𝑃𝑦𝑡ℎ𝑎𝑔𝑜𝑟𝑒𝑠) 0,25 𝐴𝐶2 = 122 + 52 𝐴𝐶2 = 169 𝐴𝐶 = 13km
Vậy quãng đường từ nhà đến trường của bạn Thanh xa hơn quãng 0,25
đường từ nhà đến trường của bạn Lan là 13 – 12 = 1 (km). 5 (2.5đ) a
Chứng minh tứ giác AEHF là hình chữ nhật 0,75
- Xét tứ giác AEHF có µ 0
A = 90 (  ABC vuông tại A) µ 0
E = 90 (HE ⊥ AB tại E) µ 0
F = 90 (HF ⊥ AC tại F)
Suy ra tứ giác AEHF là hình chữ nhật (tứ giác có 3 góc vuông)
Vẽ hình và ghi đầy đủ các yếu tố có trên hình 0,25 b
Chứng minh tứ giác EFMH là hình bình hành 0,5
- Ta có : EH = AF (EFMH là hình chữ nhật)
AF = FM (M đối xứng A qua F) Suy ra EH = FM
- Ta có EH // AF (EFMH là hình chữ nhật)
Do đó EH // FM (M thuộc AF) - Xét tứ giác EFMH có: EH = FM (cmt), EH // FM (cmt)
Vậy tứ giác EFMH là hình bình hành (tứ giác có 2 cạnh
đối song song và bằng nhau c
Chứng minh tứ giác AHMD là hình thoi và EF ⊥ DC .
- Chứng minh tứ giác AHMD là hình thoi 0,5
Chứng minh tứ giác AHMD là hình bình hành Có AM ⊥ HD
- Chứng minh M là trung trực của △ HDC
Chứng minh EF ⊥ DC 0,5
Mỗi ý 0,5 điểm và ý 2 không chia nhỏ điểm