lOMoARcPSD| 36067889
CHƯƠNG 1: CƠ SỞ ĐẠI SỐ LOGIC
Câu 1: Khi khoanh 2n ô kề hoặc đối nhau trên bìa Karnaugh, số biến được loại đi là: A. 1 biến C. (n-1) biến
B. 2 biến D. n biến
Câu 7: Với mọi phần tử x thuộc tập hợp B={0,1}, tồn tại các hằng số 0 và 1 sao cho:
A. x + 1 = x ; x.0 = x C. x + 1 = x ; x.0 = 0
B. x + 1 = 1 ; x.0 = x D. x + 1 = 1 ; x.0 = 0
Câu 8: Trên tập hợp đại số Boole, cổng OR có giá trị là 1 khi: A. Có 1 đầu vào bằng 1
C. Tất cả các đầu vào đều bằng 1 B. Có 1 đầu vào bằng 0
D. Có ít nhất 1 đầu vào bằng 1 A. D.
Câu 11: Cho x, y, z là 3 đầu vào thuộc tập hợp đại số Boole, phép toán (x + y.z) có giá trị bằng: A. x.(y + z) C. y + x.z B. (x+y).(x+z) D. (x+y).z
Câu 12: Trên tập hợp đại số Boole, giá trị đầu ra cổng XOR có 2 đầu vào a, b là 1 khi: A. a = 0, b tùy ý C. a = b
B. a = 1, b tùy ý D. a ≠ b
Câu 13: Loại mã nào dùng 4 bít nhị phân để mã hóa cho các số hệ thập phân: a. Mã BCD (Đ) b. Mã Gray c. Mã vòng d. Mã ASCII lOMoARcPSD| 36067889
Câu 14: Loại mã nào dùng 8 bít nhị phân để mã hóa cho các ký tự và số trên bàn phím máy tính: a. Mã BCD b. Mã Gray c. Mã vòng d. Mã ASCII (Đ)
Câu 15: Loại mã nào có các từ mã kế tiếp nhau chỉ khác nhau một vị trí: a. Mã BCD b. Mã Gray (Đ) c. Mã vòng d. Mã ASCII
Câu 16: Loại mã nào dùng để phát hiện lỗi sai 1 bít trong hệ thống thông tin: a. Mã BCD b. Mã Gray c. Mã Parity (Đ) d. Mã ASCII
Câu 17: Những tổ hợp mã nào không phải là mã BCD: a. 1001 b. 1010 (Đ) c. 1000 d. 0111
Câu 18: Những tổ hợp mã nào là mã BCD: a. 1001 (Đ) b. 1110 c. 1101 d. 1111
Câu 19: Chuyển số (345)8 sang hệ đếm cơ số 9: a. 229 lOMoARcPSD| 36067889 b. 274 (Đ) c. 472 d. 922
Câu 20: Chuyển số (700)10 sang hệ đếm cơ số 16: a. 21112 b. 12112 c. 2BC (Đ) d. CB2
Câu 21: Chuyển số (11110011,00101001)2 sang hệ đếm cơ số 16: a. F3,29 (Đ) b. 564,25 c. 363,121 d. 456,34
Câu 22: Số (142)7 chuyển sang hệ đếm 5 là: a. (204)5 b. (104)5 c. (304)5 (Đ) d. (404)5
Câu 23: Số (0.8125)10 chuyển sang hệ nhị phân là: a. 0.8125 = (0.0010)2 b. 0.8125 = (0.1101)2 (Đ) c. 0.8125 = (0.1100)2 d. 0.8125 = (0.0100)2
Câu 24: Mã Gray của số 14 là: a. 10101 b. 00010100 c. 1110 lOMoARcPSD| 36067889 d. 1001 (Đ)
Câu 25: Cách biểu diễn nào sau đây là đúng: a. 43,5 = 4.102+3.101+5.100
b. 43,5 = 4.101+3.100+5.10-1 (Đ) c. 43,5 = 4.22+3.21+5.20 d. 43,5 = 4.21+3.20+5.2-1
Câu 26: Chỉ ra phép toán cơ bản của đại số logic a. Khai căn bậc 2 b. Trừ c. Bù (Đ) d. Logarit
Câu 27 : Mã Gray có đặc điểm:
a. Hai từ mã kề nhau luôn khác nhau 2 bít
b. Trong một từ mã chỉ có duy nhất 1 bít bằng 1 các bít còn lại bằng 0
c. Hai từ mã kề nhau chỉ khác nhau duy nhất 1 bít (Đ)
d. Mỗi từ mã của nó được cấu tạo bằng cách lấy từ mã NBCD tương ứngcộng thêm
Câu 28: Mạch số có ưu điểm là: (Chọn phương án sai) a. Dễ thiết kế
b. Lưu trữ thông tin dễ dàng
c. Ít chịu ảnh hưởng của nhiễu
d. Mật độ tích hợp thấp (Đ)
Câu 29: Mạch số có nhược điểm là: (Chọn phương án đúng)
1. Phải có các bộ chuyển đổi từ tín hiệu tương tự thành tín hiệu số và ngượclại (Đ) 2. Không thể lập trình
3. Mật độ tích hợp thấp lOMoARcPSD| 36067889
4. Chịu ảnh hưởng của nhiễu lớn
Câu 30: Khi các con số, các chữ cái, các từ được biểu diễn bởi một nhóm các
ký hiệu đặc biệt, ta gọi đây là: a. Từ mã b. Mã hóa (Đ) c. Giải mã d.
Điều chế và giải điều chếCâu 31: Mã Parity dùng để: a. Phát hiện lỗi (Đ) b. Sửa lỗi
c. Mã hóa số thập phân cơ bản
d. Mã hóa cho các ký tự trên bàn phím
Câu 32: Hàm Boole có thể nhận các giá trị:
a. Các số hệ nhị phân 0 và 1 (Đ)
b. Tất cả các giá trị dạng số thực
c. Các số hệ thập phân từ 0 đến 9
d. Các số nguyên âm và nguyên dương
Câu 33: Loại mạch nào mà các tín hiệu đầu ra chỉ phụ thuộc vào các tín hiệu đầu
vào tại thời điểm đang xét, không phụ thuộc vào trạng thái trước đó của mạch: a. Mạch khuếch đại
b. Mạch logic tổ hợp (Đ) c. Mạch vi phân
d. Mạch dãy (hệ logic có nhớ)
Câu 34 : Loại mạch nào mà các tín hiệu đầu ra ngoài phụ thuộc vào các tín hiệu
đầu vào tại thời điểm đang xét còn phụ thuộc vào trạng thái trước đó của mạch: a. Mạch khuếch đại b. Mạch logic tổ hợp c. Mạch vi phân d.
Mạch dãy (hệ logic có nhớ) (Đ) Câu 35: Nói 1+1 = 1 khi thực hiện: lOMoARcPSD| 36067889 a. Phép cộng logic (Đ)
b. Phép cộng số nhị phân c. Phép cộng Module
d. Phép cộng số thập phân
Câu 36: Nói 1+1 = 0 khi thực hiện: a. Phép cộng logic
b. Phép cộng số nhị phân c. Phép cộng Module (Đ)
d. Phép cộng số thập phân
Câu 37: Cổng logic nào có đầu ra là 1 khi tất cả các đầu vào đều bằng 1: a. NOT b. AND (Đ) c. NAND d. OR
Câu 38: Cổng logic nào có đầu ra là 0 khi ít nhất 1 đầu vào bằng 0 a. XOR b. NOR c. AND (Đ) d. NAND
Câu 39: Trong kỹ thuật số mức logic 0 tương ứng với mức điện áp qui ước: a. 2V đến 5V b. 0V đến 0,8V (Đ) c. 2V đến 3V d. 3V đến 5V
Câu 40: Trong kỹ thuật số mức logic 1 tương ứng với mức điện áp qui ước: a. 2V đến 5V (Đ) b. 0V đến 0,8V c. 2V đến 3V lOMoARcPSD| 36067889 d. 3V đến 5V
Câu 41: Biến đổi các mã nào đó về dạng mã ban đâu là bộ: a. Bộ mã hóa b. Bộ giải mã (Đ) c. Bộ so sánh d. Bộ cộng
Câu 41: Biểu diễn hàm logic có n biến về dạng chuẩn tắc tuyển đầy đủ là:
a. Hàm logic gồm tích các thừa số trong đó mỗi thừa số là tổng của đầy đủ nbiến
b. Hàm logic gồm tổng của các số hạng, trong đó mỗi số hạng là tích của đầyđủ n biến (Đ)
c. Hàm logic gồm tích các thừa số trong đó mỗi thừa số là tổng của (n- 1)biến
d. Hàm logic gồm tổng của các số hạng, trong đó mỗi số hạng là tích của (n- 1) biến
Câu 42: Biểu diễn hàm logic có n biến dạng chuẩn tắc hội đầy đủ là:
a. Hàm logic gồm tích các thừa số, trong đó mỗi thừa số là tổng của đầy đủ nbiến (Đ)
b. Hàm logic gồm tổng của các số hạng, trong đó mỗi số hạng là tích của đầyđủ n biến
c. Hàm logic gồm tích các thừa số trong đó mỗi thừa số là tổng của (n- 1)biến
d. Hàm logic gồm tổng của các số hạng, trong đó mỗi số hạng là tích của (n- 1) biến
Câu 43: Cho một đầu vào x thuộc tập hợp đại số Boole, phép toán (x + 1) có giá trị là: lOMoARcPSD| 36067889 a. x b. 1 (Đ) c. 0 d.
Không xác định được Câu 44: Rút gọn hàm logic: b. A c. (Đ) d. B d.
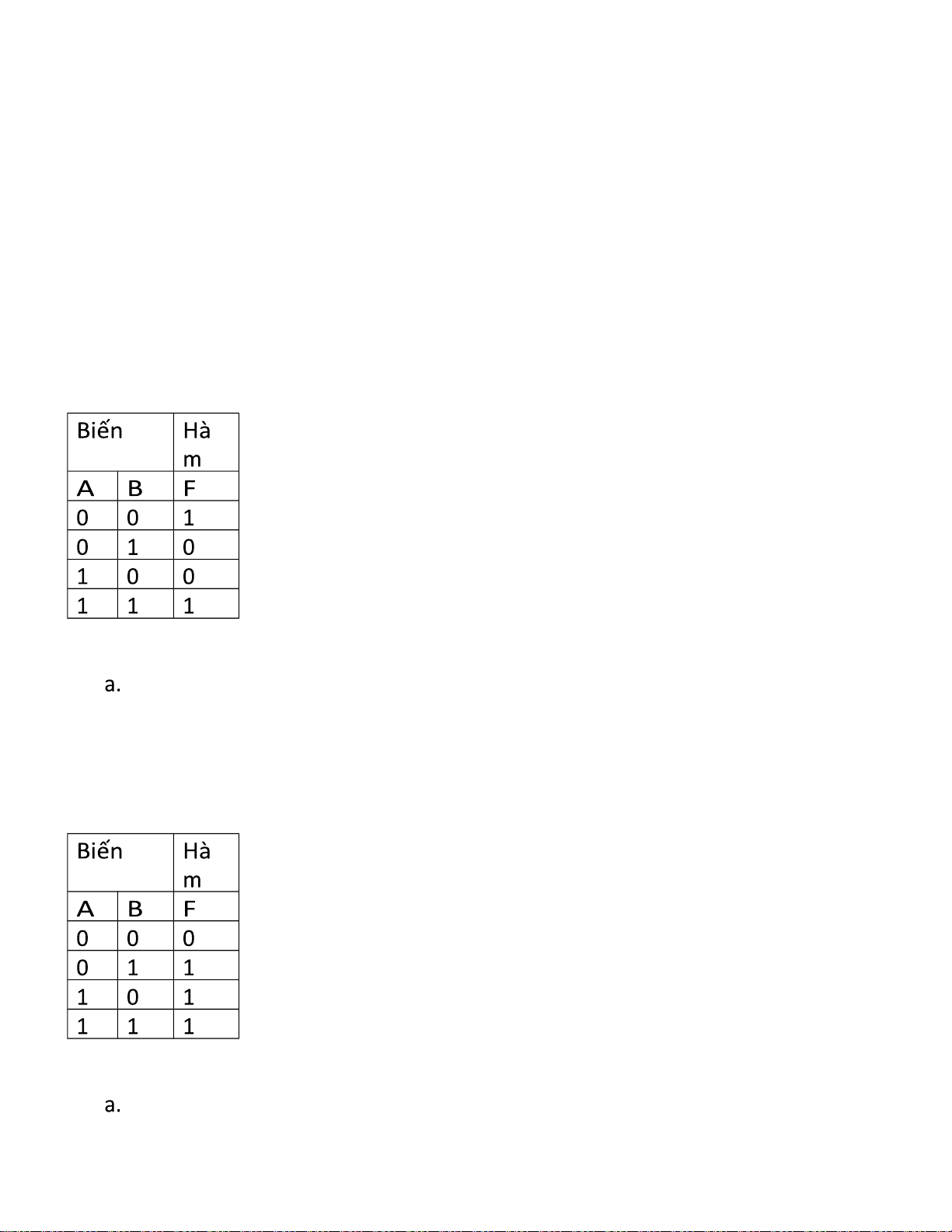
Câu 45: Bảng chân lý sau thực hiện phép toán logic nào? b. (Đ) c. d.
Câu 46: Bảng chân lý sau thực hiện phép toán logic nào? lOMoARcPSD| 36067889 b. c. e. (Đ)
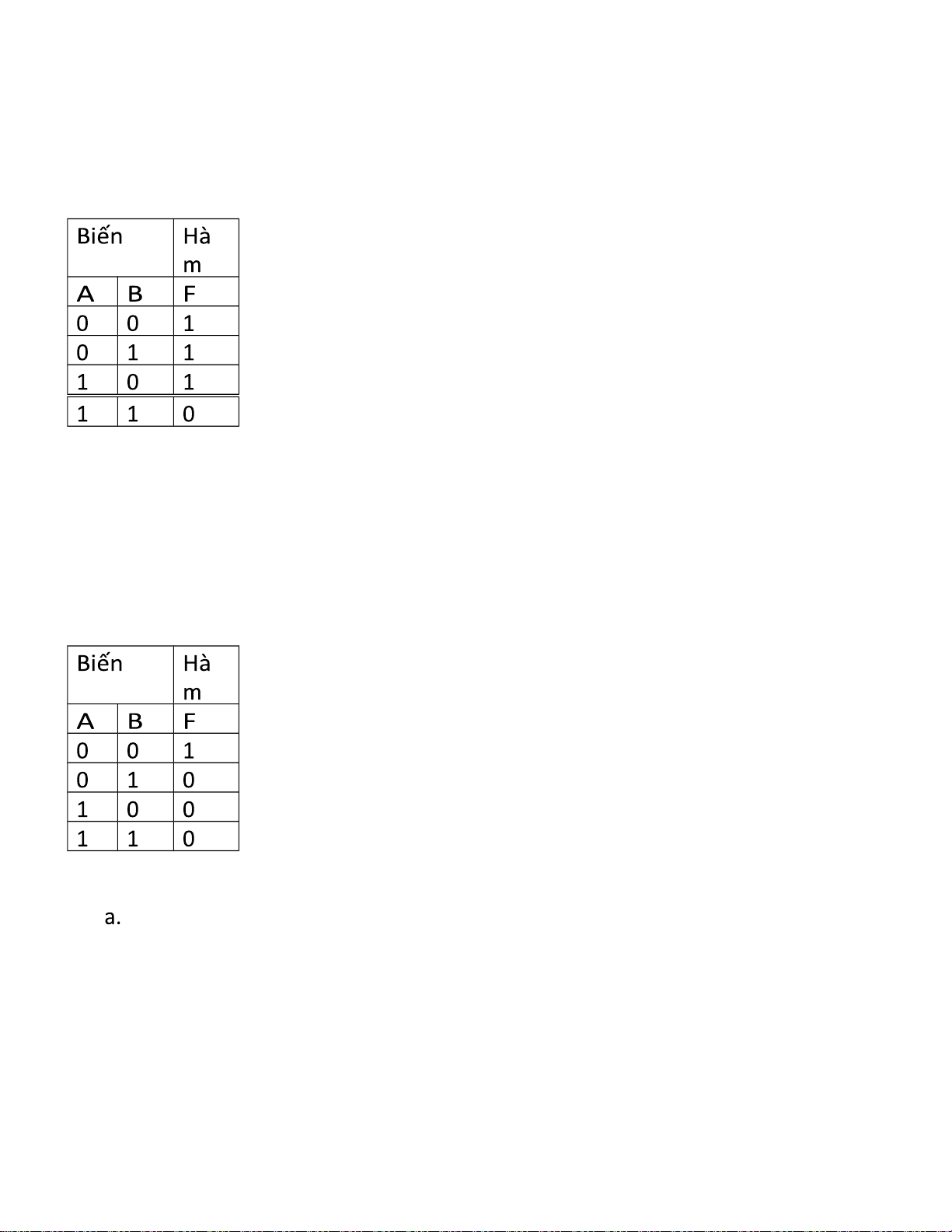
Câu 47: Bảng chân lý sau thực hiện phép toán logic nào? a. b. c. (Đ) d.
Câu 48: Bảng chân lý sau thực hiện phép toán logic nào? b. (Đ) c. d.
Câu 49: Rút gọn biểu thức được kết quả là: a. Y lOMoARcPSD| 36067889 b. c. X (Đ) d.
Câu 50: Rút gọn biểu thức được kết quả là: a. b. (Đ) c. d.
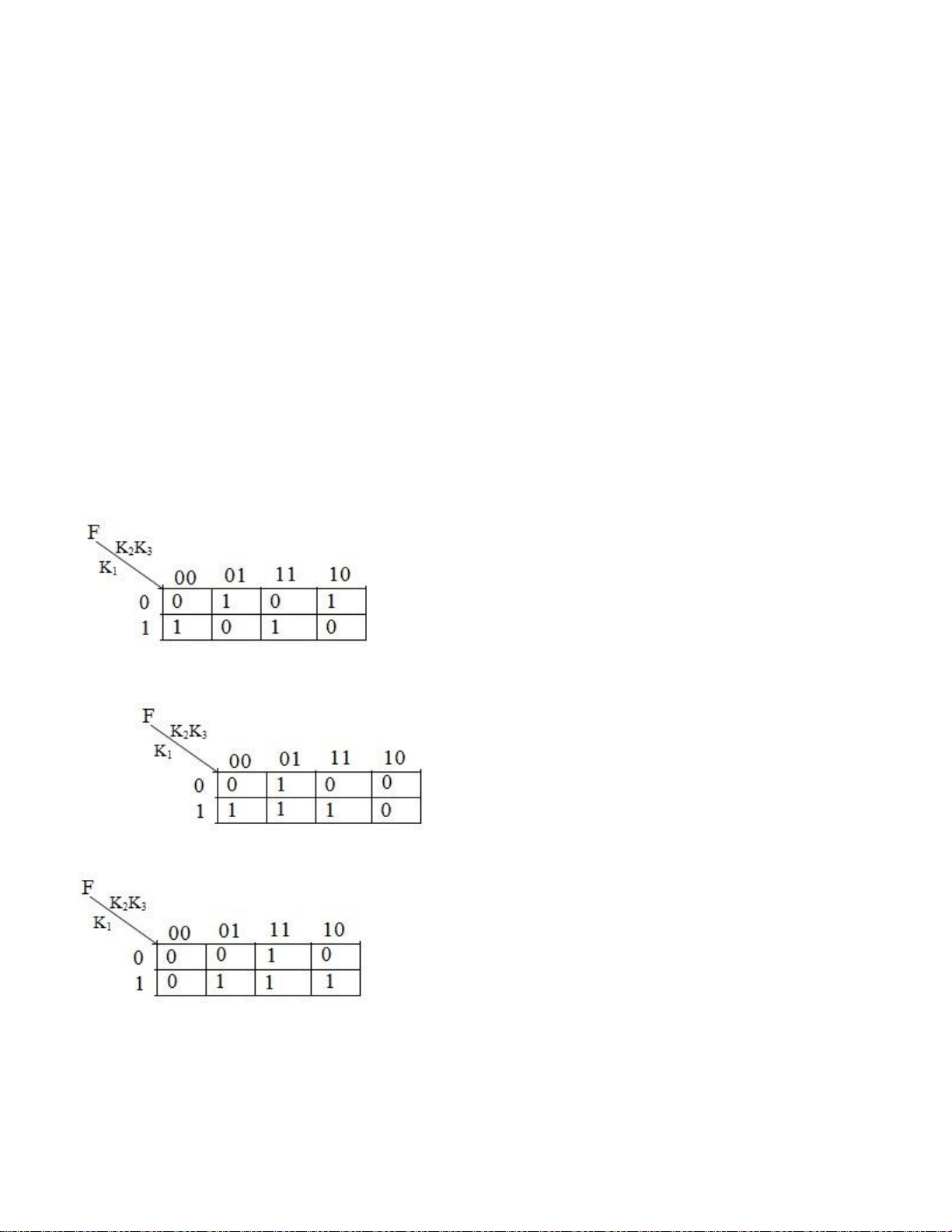
Câu 51: Một bóng đèn được điều khiển với 3 công tắc K1, K2, K3. Đèn chỉ sáng
khi có ít nhất 2 công tắc đóng. Chọn bảng Karnaught cho hàm điều khiển nói trên. a. (Đ) b. c. d. lOMoARcPSD| 36067889
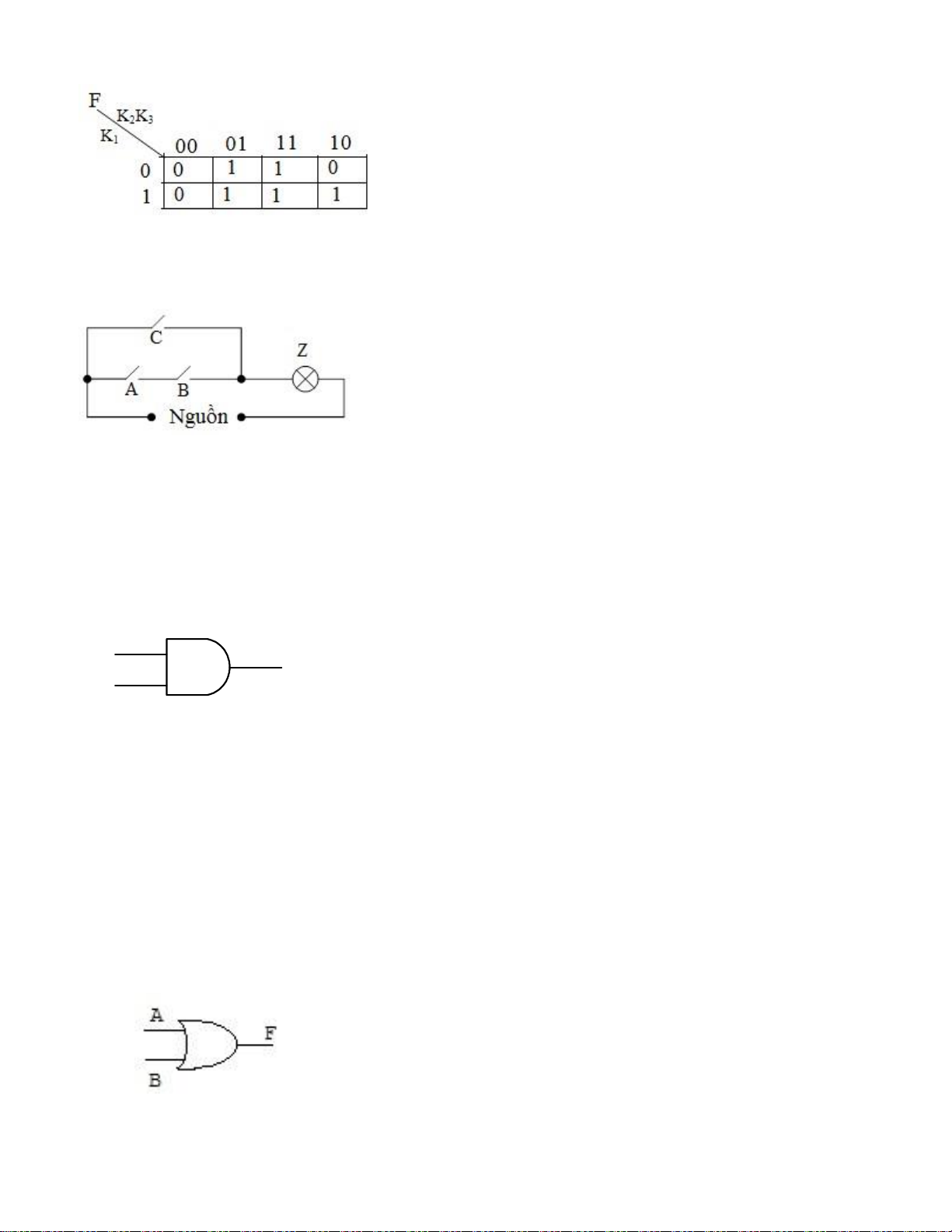
Câu 52: Viết phương trình trạng thái cho hàm số thực hiện điều khiển mạch
điện sau để đèn Z sáng. (Coi A, B, C là biến logic và Z là hàm logic): a. AB + C (Đ) b. A + B + C c. A.B.C d. A + BC
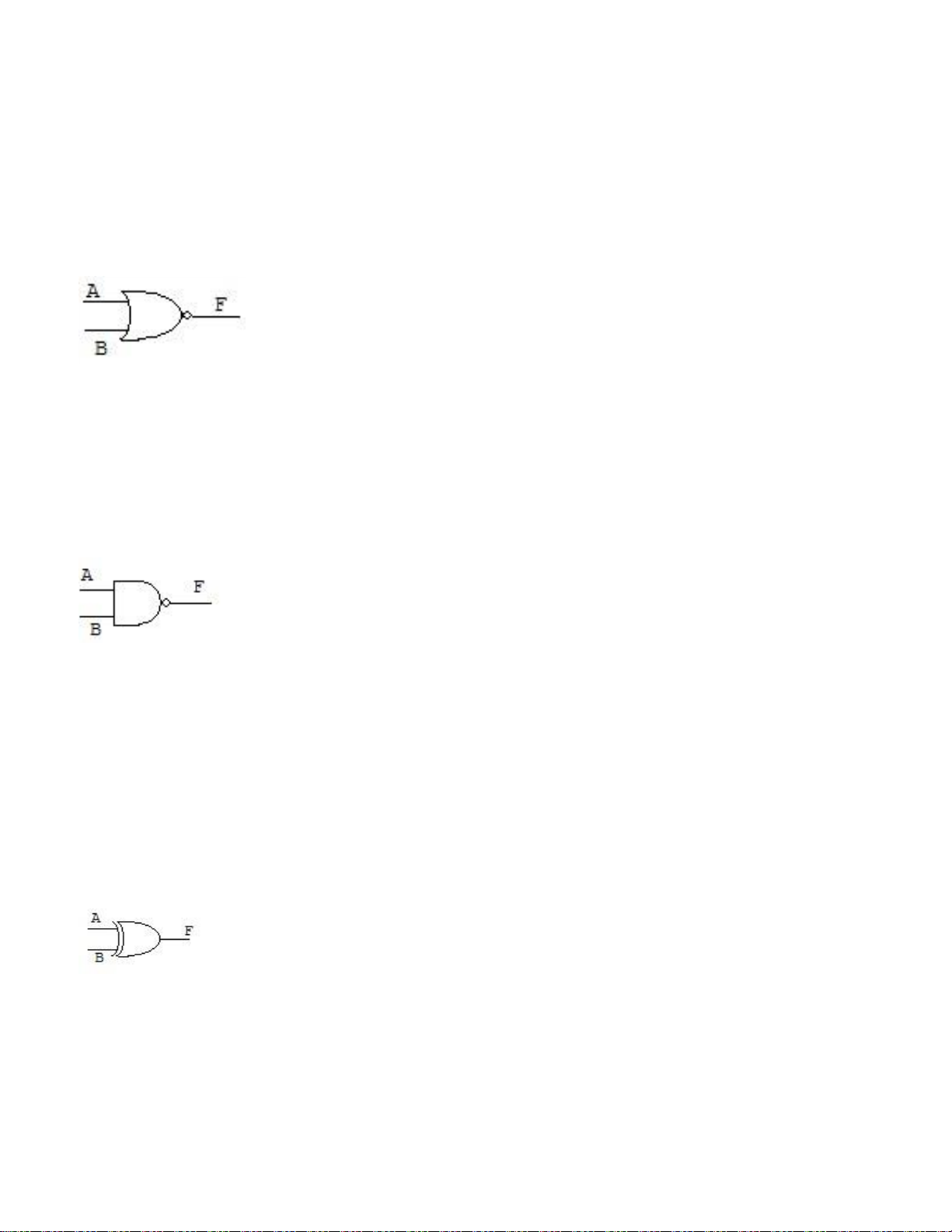
Câu 53: Cho biết cổng logic sau thực hiện phép toán nào: X 1 F X 2 a. F = X1 + X2 b. F = X1 . X2 (Đ) c. d.
Câu 54: Cho biết cổng logic sau thực hiện phép toán nào: lOMoARcPSD| 36067889 a. F = A + B (Đ) b. F = A.B c. d.
Câu 55: Cho biết cổng logic sau thực hiện phép toán nào: a. F = A + B b. F = A.B c. d. (Đ)
Câu 56: Cho biết cổng logic sau thực hiện phép toán nào: a. F = A + B b. F = A.B c. (Đ) d.
Câu 57: Cho biết cổng logic sau thực hiện phép toán nào: a. F = (Đ) b. F = A.B c. lOMoARcPSD| 36067889 d.
Câu 58: Cho biết cổng logic sau thực hiện phép toán nào: a. F = b. (Đ) c. d.
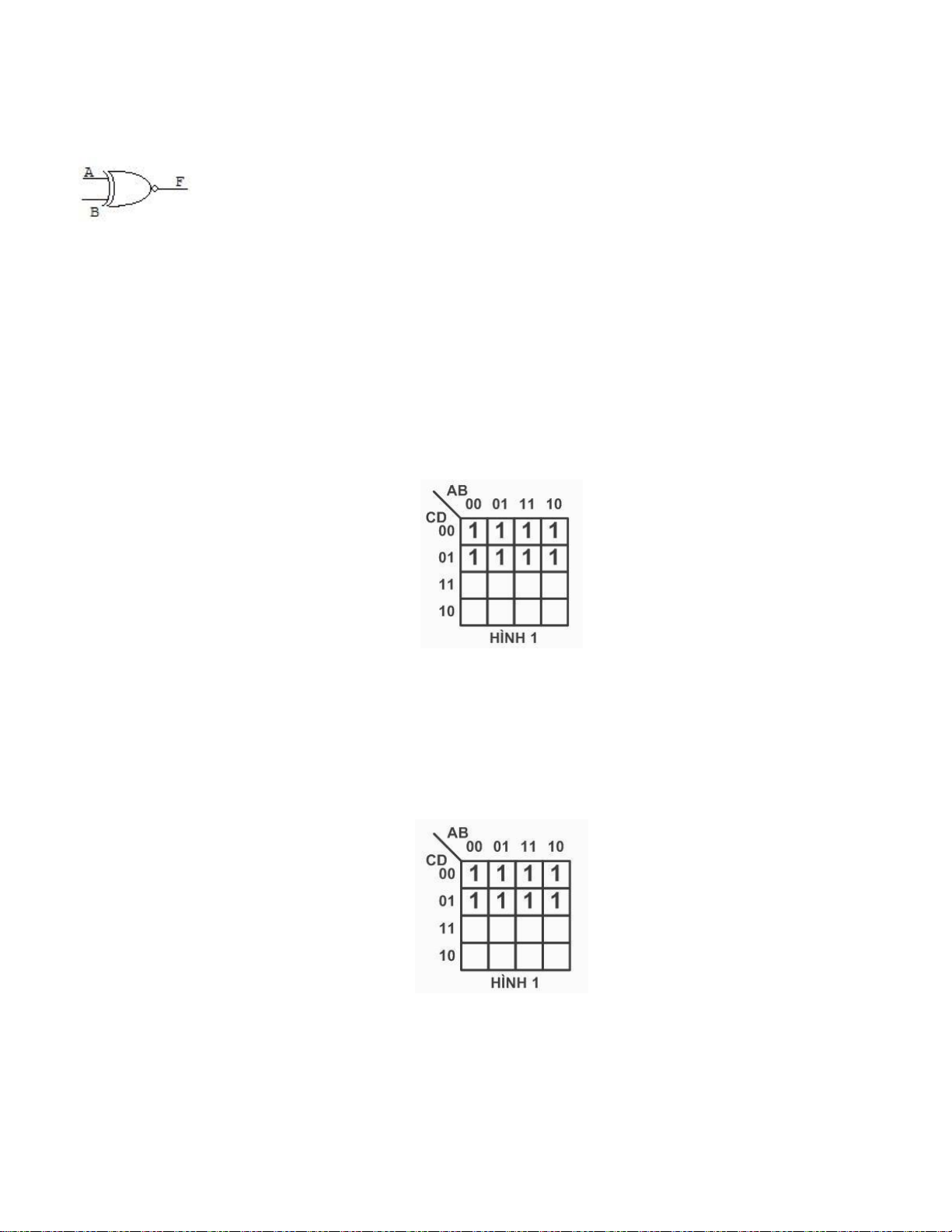
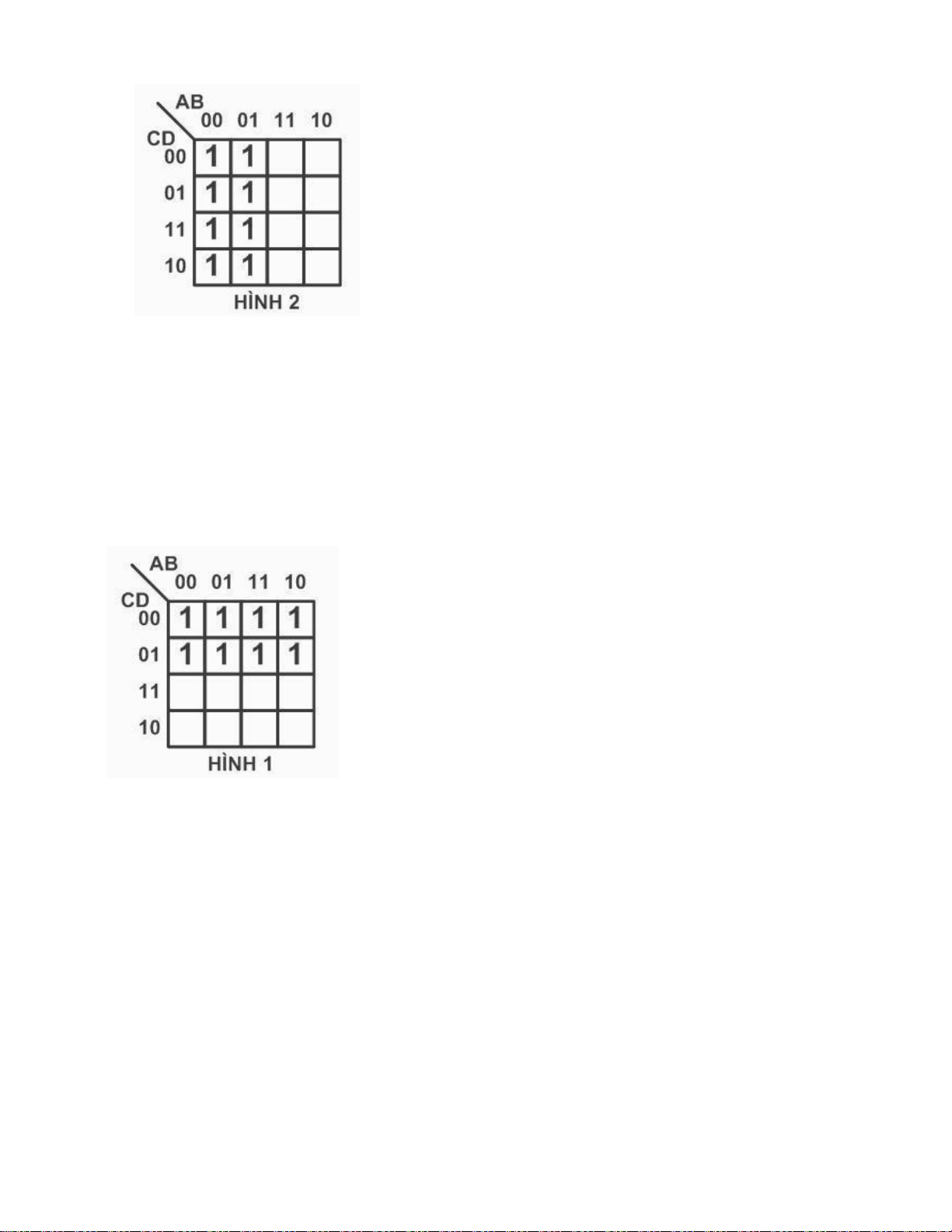
Câu 59: Hàm F được biểu diễn bằng bìa Karnaugh như hình 1, dạng rút gọn của hàm F là: A. C. B. D.
Câu 60: Hàm F được biểu diễn bằng bìa Karnaugh như hình 1, biểu diễn dạng đại số của hàm F là:
A. F (A , B , C , D) = ∑ (0 , 1 , 5 , 6 , 8 , 9 , 12 , 13)
B. F (A , B , C , D) = ∑ (0 , 1 , 4 , 5 , 8 , 9 , 12 , 13) lOMoARcPSD| 36067889
C. F (A , B , C , D) = ∏ (0 , 1 , 5 , 6 , 8 , 9 , 12 , 13) D. F (A , B , C , D) = ∏ (0 , 1 , 4 , 5 , 8 , 9 , 12 , 13)
Câu 61: Hàm F được biểu diễn bằng bìa Karnaugh như hình 2, dạng rút gọn của hàm F là: A. C. B. D.
Câu 62: Mã Gray tương đương của số nhị phân 110010 là: a. 111100 b. 101010 c. 101101 d. 101011 (Đ)
Câu 63: Số thập phân tương đương của số nhị phân 10000001 là: a. 129 (Đ) b. 128 c. 127 d. 126
Câu 64: Trên tập hợp đại số Boole, cổng NOR có giá trị là 1 khi: a. Có 1 ngõ vào bằng 0 b. Có 1 ngõ vào bằng 1
c. Có ít nhất 1 ngõ vào bằng 0 lOMoARcPSD| 36067889
d. Tất cả các ngõ vào đều bằng 0 (Đ)
Câu 65: Trên tập hợp đại số Boole, cổng NAND có giá trị là 1 khi:
a. Có ít nhất 1 ngõ vào bằng 0 (Đ)
b. Có ít nhất 1 ngõ vào bằng 1
c. Tất cả các ngõ vào đều bằng 0
d. Tất cả các ngõ vào đều bằng 1
Câu 66: Trên tập hợp đại số Boole, cổng OR có giá trị là 1 khi: a. Có 1 ngõ vào bằng 0 b. Có 1 ngõ vào bằng 1
c. Có ít nhất 1 ngõ vào bằng 1 (Đ)
d. Tất cả các ngõ vào đều bằng 1
Câu 67: Trên tập hợp đại số Boole, cổng AND có giá trị là 1 khi:
a. Có ít nhất 1 ngõ vào bằng 1
b. Tất cả các ngõ vào đều bằng 1 (Đ) c. Có 1 ngõ vào bằng 1 d. Có 1 ngõ vào bằng 0
Câu 68: Trên tập hợp đại số Boole, cổng NOR có giá trị là 0 khi: a. Có 1 ngõ vào bằng 1 b. Có 1 ngõ vào bằng 0
c. Có ít nhất 1 ngõ vào bằng 1 (Đ)
d. Tất cả các ngõ vào đều bằng 0
Câu 69 : Trên tập hợp đại số Boole, cổng NAND có giá trị là 0 khi:
a. Có ít nhất 1 ngõ vào bằng 0
b. Có ít nhất 1 ngõ vào bằng 1
c. Tất cả các ngõ vào đều bằng 0
d. Tất cả các ngõ vào đều bằng 1 (Đ)
Câu 70 : Trên tập hợp đại số Boole, cổng OR có giá trị là 0 khi: lOMoARcPSD| 36067889 a. Có 1 ngõ vào bằng 1 b. Có 1 ngõ vào bằng 0
c. Có ít nhất 1 ngõ vào bằng 0
d. Tất cả các ngõ vào đều bằng 0 (Đ)
Câu 71: Trên tập hợp đại số Boole, cổng AND có giá trị là 0 khi:
a. Có ít nhất 1 ngõ vào bằng 0 (Đ)
b. Tất cả các ngõ vào đều bằng 0 c. Có 1 ngõ vào bằng 0
d. Tất cả các ngõ vào đều bằng 1
Câu 72 : Cho F là một hàm 4 biến A, B, C, D.
F=1 nếu trị thập phân tương ứng với các biến của hàm chia hết cho 3 hoặc 5 F=0: Ngược lại
Biểu thức của hàm F là :
a. F (A , B , C , D) = ∑ (1 , 2 , 4 , 7 , 8 , 11 , 13 , 14)
b. F (A , B , C , D) = ∑ (3 , 5 , 6 , 9 , 10 , 12 , 15) (Đ)
c. F (A , B , C , D) = ∏ (1 , 2 , 4 , 7 , 8 , 11 , 13 , 14)
d. F (A , B , C , D) = ∏ (1 , 2 , 4 , 5 , 7 , 8 , 11 , 13 , 14)
Câu 73 : Cho hàm F với 4 biến A, B, C, D.
F = 1: nếu số lượng biến vào có trị bằng 1 nhiều hơn hoặc bằng số lượng biến có trị bằng 0. F = 0: Ngược lại.
Biểu thức của hàm F là:
a. F (A , B , C , D) = ∑ (0 , 1 , 2 , 4 , 8) và d (3 , 5 , 6 , 9 , 10 , 12)
b. F (A , B , C , D) = ∑( 0 , 1 , 2 , 4 , 8 , 3 , 5 , 6 , 9 , 10 , 12)
c. F (A , B , C , D) = ∑(3 , 5 , 6 , 7 , 9 , 10 , 11 , 12 , 13 , 14 , 15) (Đ)
d. F (A , B , C , D) = ∑ (0 , 1 , 2 , 4 , 8 , 3 , 5 , 6 , 9 , 10 , 12)
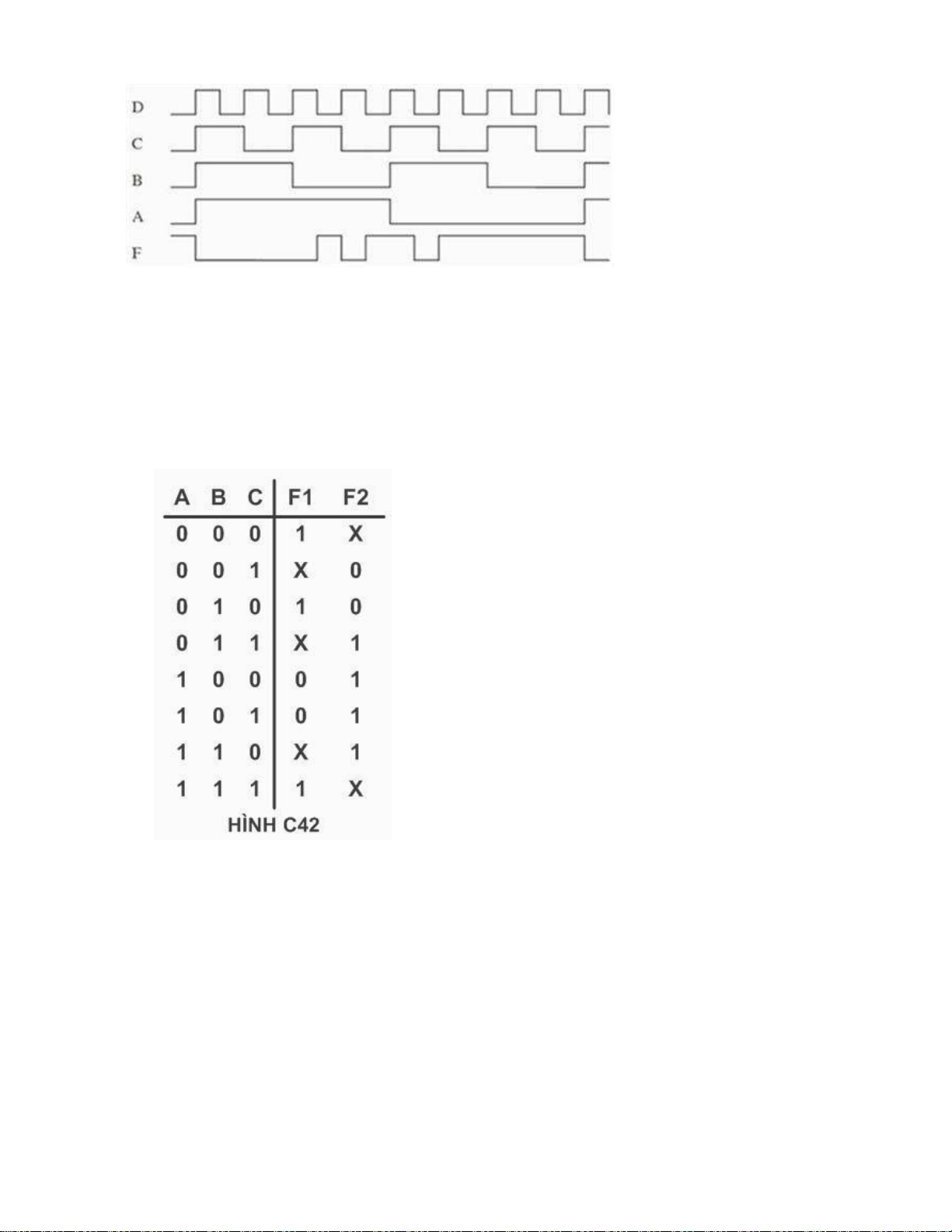
Câu 74 : Cho hàm F(A,B,C,D) biểu diễn trên giản đồ xung như sau. Xác định biểu thức của hàm F lOMoARcPSD| 36067889
a. F(A, B, C, D) = ∑ (1 , 2 , 3 , 4 , 5 , 7 , 8 , 10)
b. F(A, B, C, D) = ∏ (6 , 9 , 11 , 12 , 13 , 14 , 15) (Đ)
c. F(A, B, C, D) = ∑ (6 , 9 , 11 , 12 , 13 , 14 , 15)
d. F(A, B, C, D) = ∏ (1 , 2 , 3 , 4 , 5 , 7 , 8 , 10)
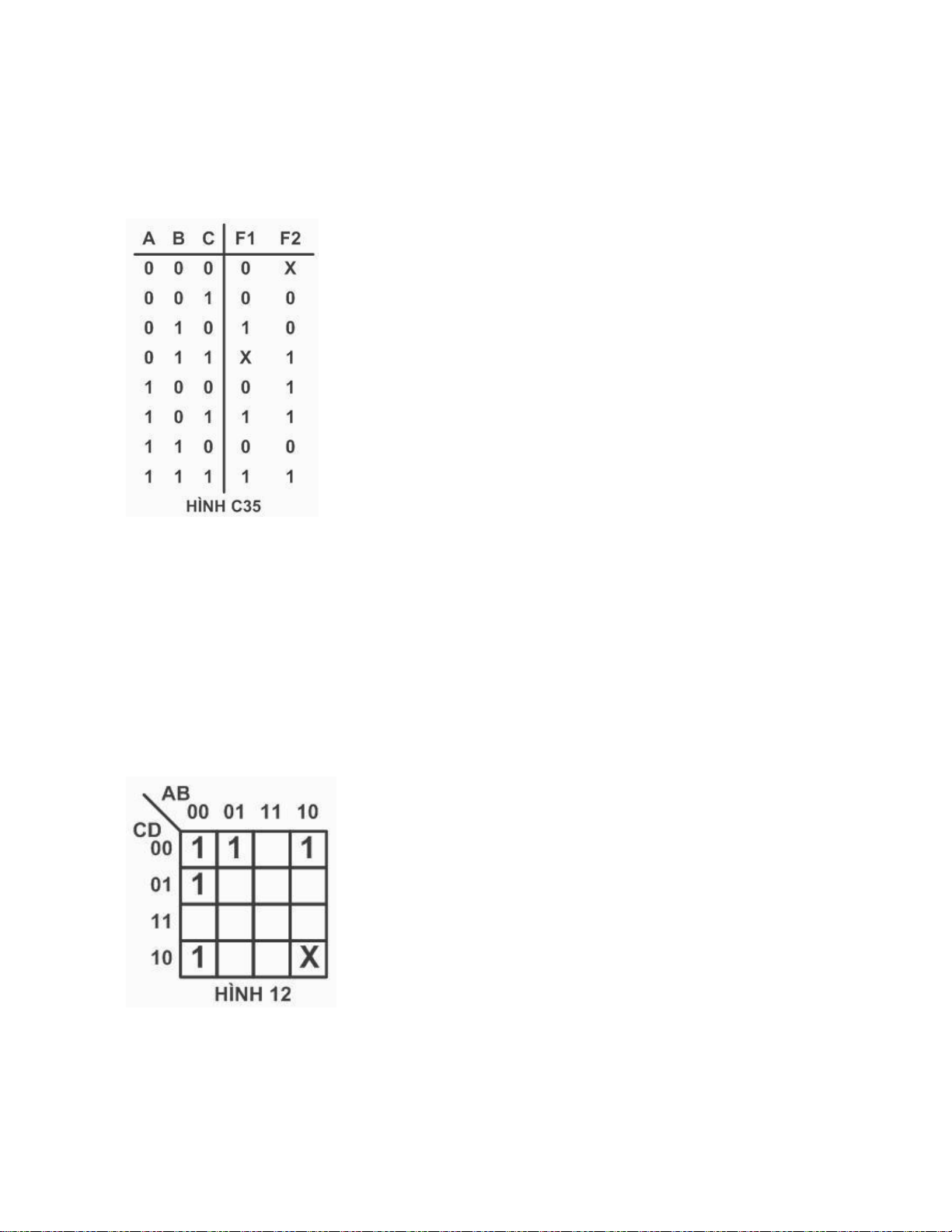
Câu 75: Cho bảng giá trị sau. Xác định biểu thức của hàm F2:
a. F (A , B , C) = ∑ (1 , 2) N=(0,3,5)
b. F (A , B , C) = ∏ (1 , 2) N=(0,7) (Đ)
c. F (A , B , C) = ∑( 0 , 1 , 2 , 7)
d. F (A , B , C) = ∏ (0 , 1 , 2 , 7)
Câu 76: Cho bảng giá trị sau. Xác định biểu thức của hàm F1: lOMoARcPSD| 36067889
a. F (A , B , C) = ∑ (0, 2,7) N=(1,3,6) (Đ)
b. F (A , B , C) = ∏ (1 , 3 , 4 , 5) N=(6)
c. F (A , B , C) = ∑( 0 , 1 , 2 , 3 , 7)
d. F (A , B , C) = ∏ (1 , 3 , 4 , 5 , 6)
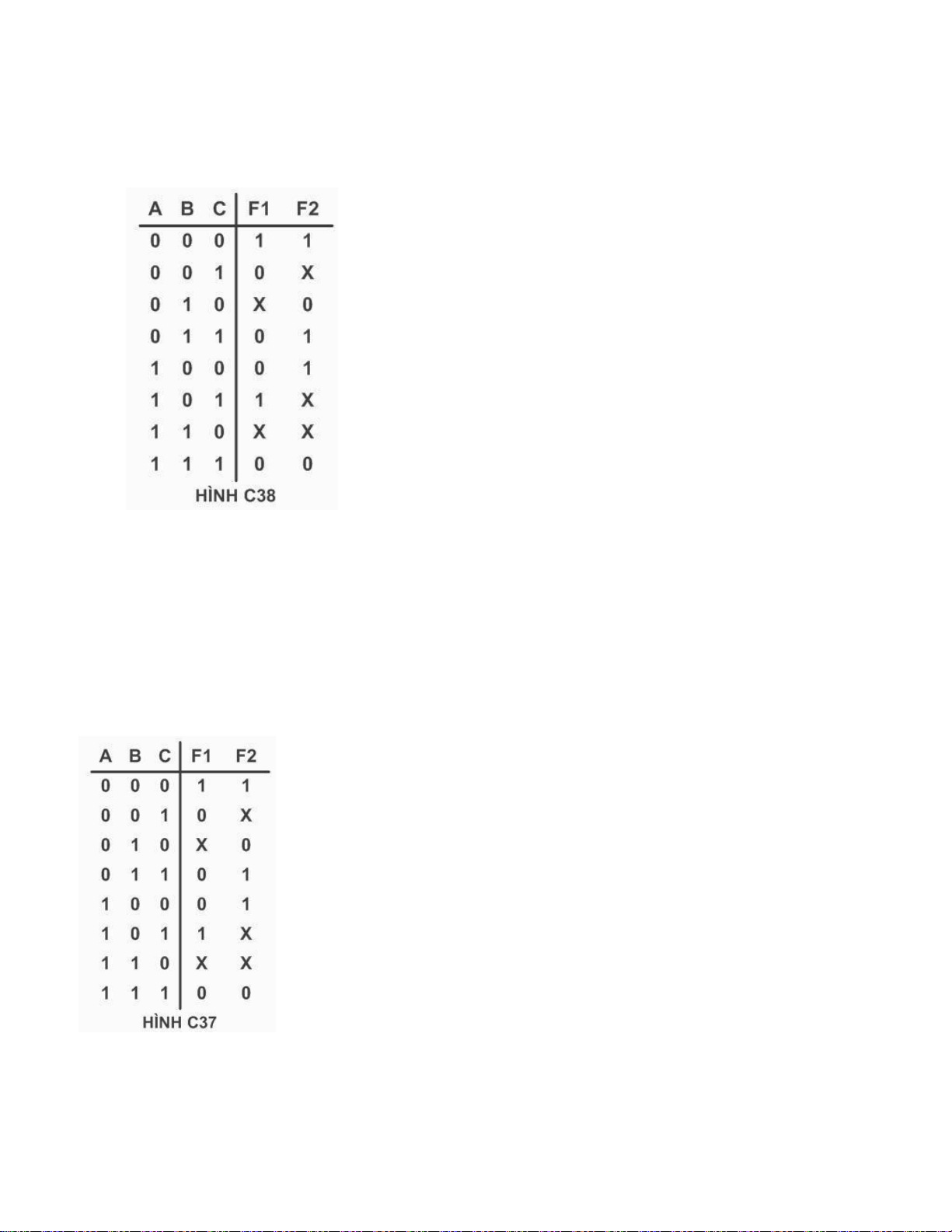
Câu 77: Cho bảng giá trị sau. Xác định biểu thức của hàm F2:
a. F (A , B , C) = ∑ (0 , 1 , 2 , 7)
b. F (A , B , C) = ∏ (0 , 1 , 2 , 7) lOMoARcPSD| 36067889
c. F (A , B , C) = ∑( 3 , 4 , 5 , 6 ) N = (0) (Đ)
d. F (A , B , C) = ∏ (0 , 1 , 2 , 7)
Câu 78: Cho bảng giá trị sau. Xác định biểu thức của hàm F2:
a. F (A , B , C) = ∑ (0 , 1 , 3 , 4 , 5 , 6)
b. F (A , B , C) = ∏ (1 , 2 , 5 , 6 , 7)
c. F (A , B , C) = ∑( 0 , 3 , 4) N=(1,5,6) (Đ)
d. F (A , B , C) = ∏ (1 , 2 , 7)
Câu 79: Cho bảng giá trị sau. Xác định biểu thức của hàm F1:
a. F (A , B , C) = ∑ (0 , 2 , 5 , 6) lOMoARcPSD| 36067889
b. F (A , B , C) = ∏ (1 , 2 , 3 , 4 , 6 , 7)
c. F (A , B , C) = ∑( 0 , 2 , 5 , 6) N=(2,6)
d. F (A , B , C) = ∏ (1 , 3 , 4 , 7) d = (2,6) (Đ)
Câu 80: Cho bảng giá trị sau. Xác định biểu thức của hàm F1:
a. F (A , B , C) = ∑ (0 , 1 , 4 , 6)
b. F (A , B , C) = ∏ (0 , 3 , 4 , 5 , 6)
c. F (A , B , C) = ∑( 2 , 3 , 5 , 7)
d. F (A , B , C) = ∏ (0 , 1 , 4 , 6) N = (3) (Đ)
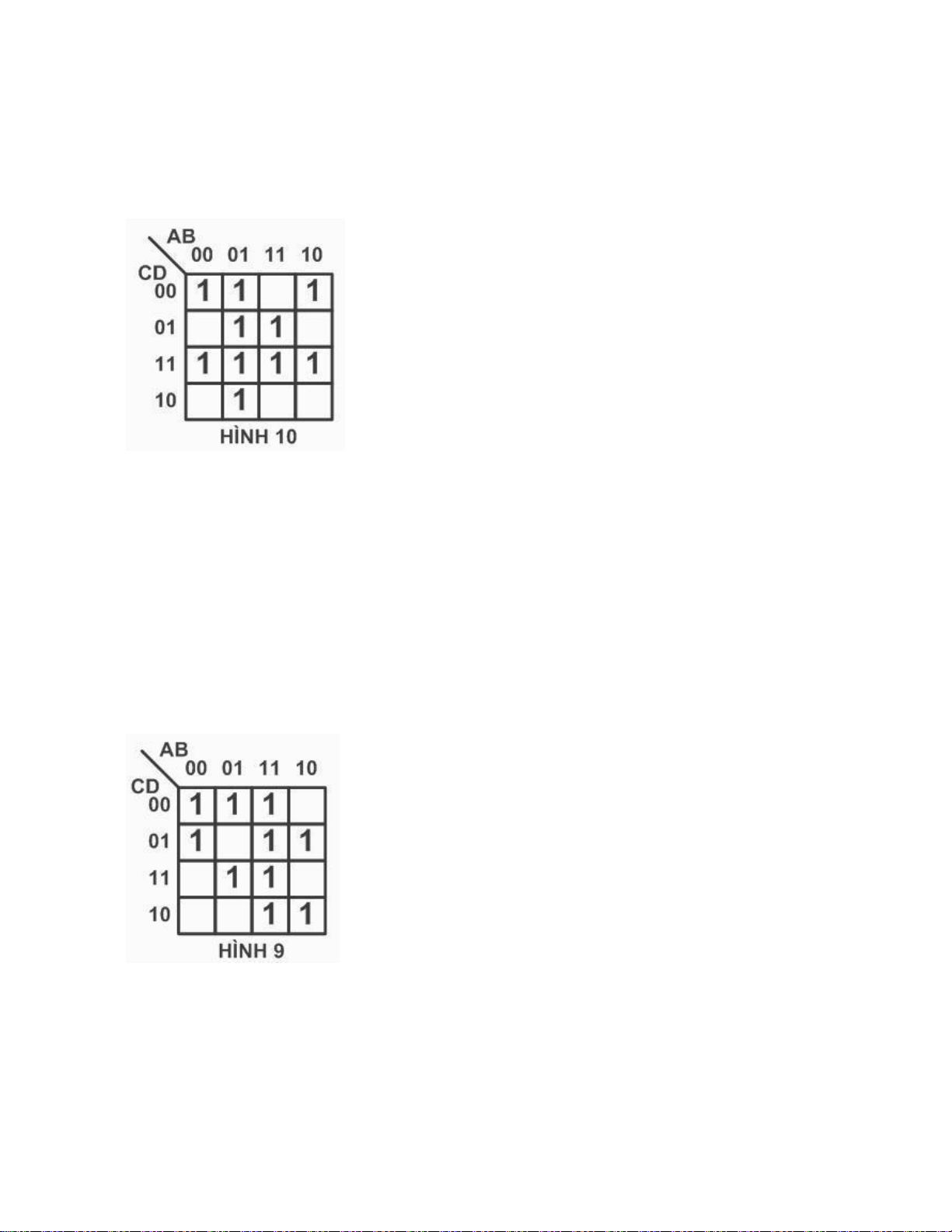
Câu 81: Hàm F được biểu diễn bằng bìa Karnaugh như hình 12, biểu diễn dạng đại số của hàm F là:
a. F (A, B, C, D) = ∑ (0, 1, 2, 4, 8) N = (10) (Đ)
b. F (A, B, C, D) = ∑ (0, 1, 2, 4, 8 , 10) lOMoARcPSD| 36067889
c. F (A ,B ,C, D) = ∏ (0 ,1 ,2 ,4 ,8) d = (10)
d. F (A ,B ,C, D) = ∏ (3, 5 ,6 ,7 ,9 ,11 ,12 ,13 ,14 ,15)
Câu 82: Hàm F được biểu diễn bằng bìa Karnaugh như hình 10, biểu diễn dạng đại số của hàm F là:
a. F (A, B, C, D) = ∑ (1, 2, 9, 10, 12, 14)
b. F (A, B, C, D) = ∑ (0 , 2 , 4 , 5 , 6 , 7 , 8 , 10 , 13 , 15)
c. F (A ,B ,C, D) = ∏ (1 , 2 , 9 , 10 , 12 , 14) (Đ)
d. F (A ,B ,C, D) = ∏ (0 , 3 , 4 , 5 , 6 , 7 , 8 , 11 , 13 , 15)
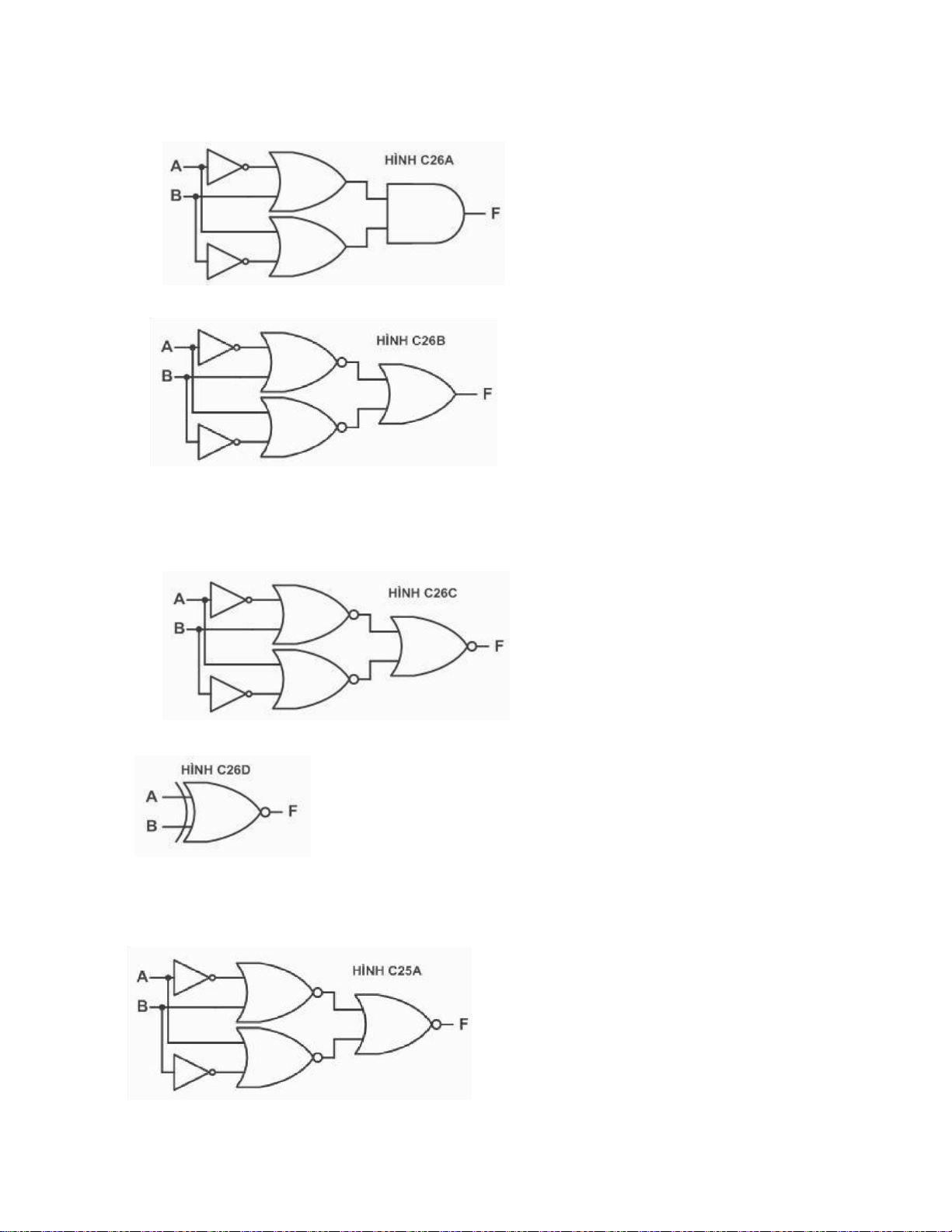
Câu 83: Hàm F được biểu diễn bằng bìa Karnaugh như hình 9, biểu diễn dạng đại số của hàm F là:
a. F (A, B, C, D) = ∑ (0, 1, 4, 6, 9, 11, 12, 13, 14, 15)
b. F (A, B, C, D) = ∑ (2, 3, 5 ,6 ,8 ,11)
c. F (A ,B ,C, D) = ∏ (3 ,5 ,6 ,9 ,11) d = (0,2)
d. F (A ,B ,C, D) = ∏ (2 ,3 ,5 ,6 ,8 ,11) (Đ) lOMoARcPSD| 36067889
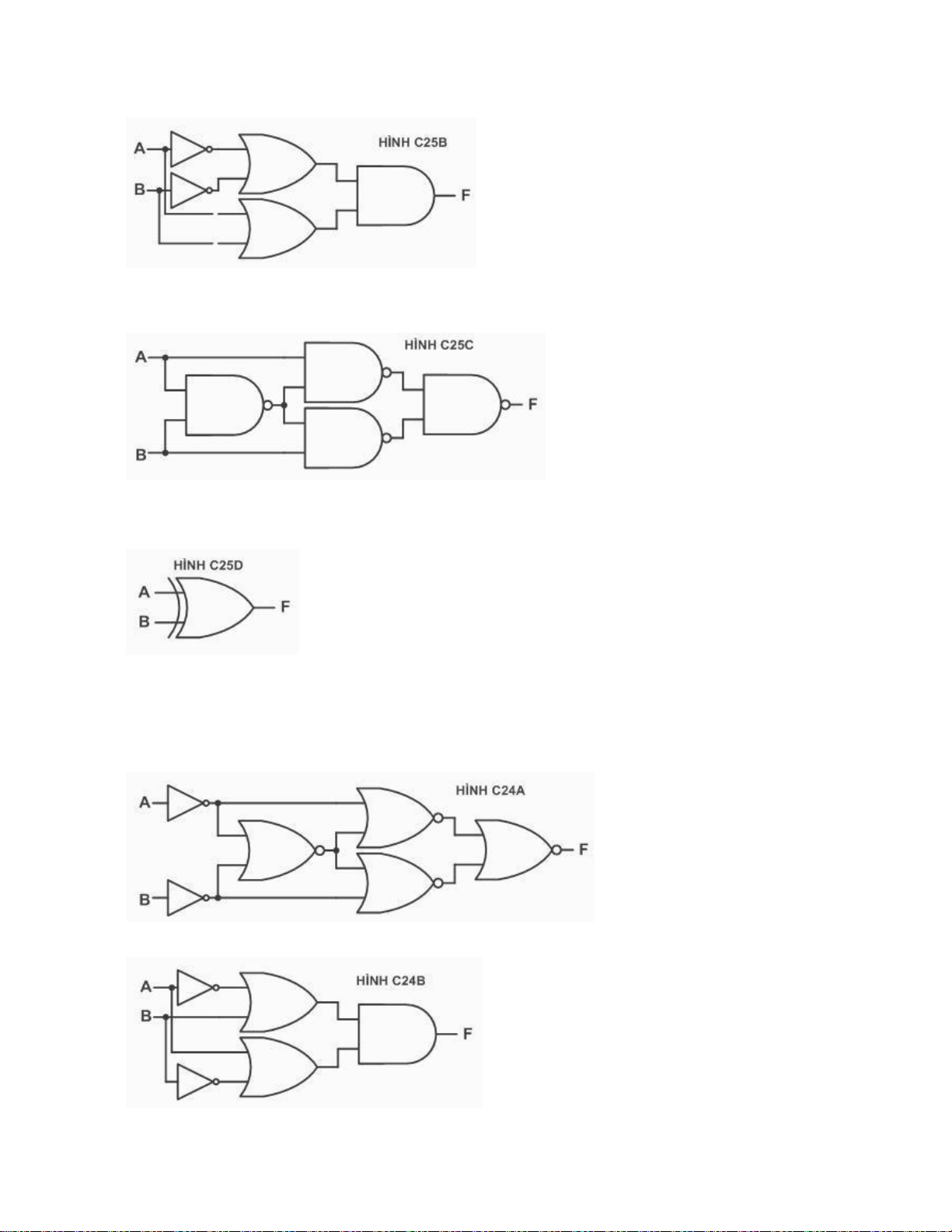
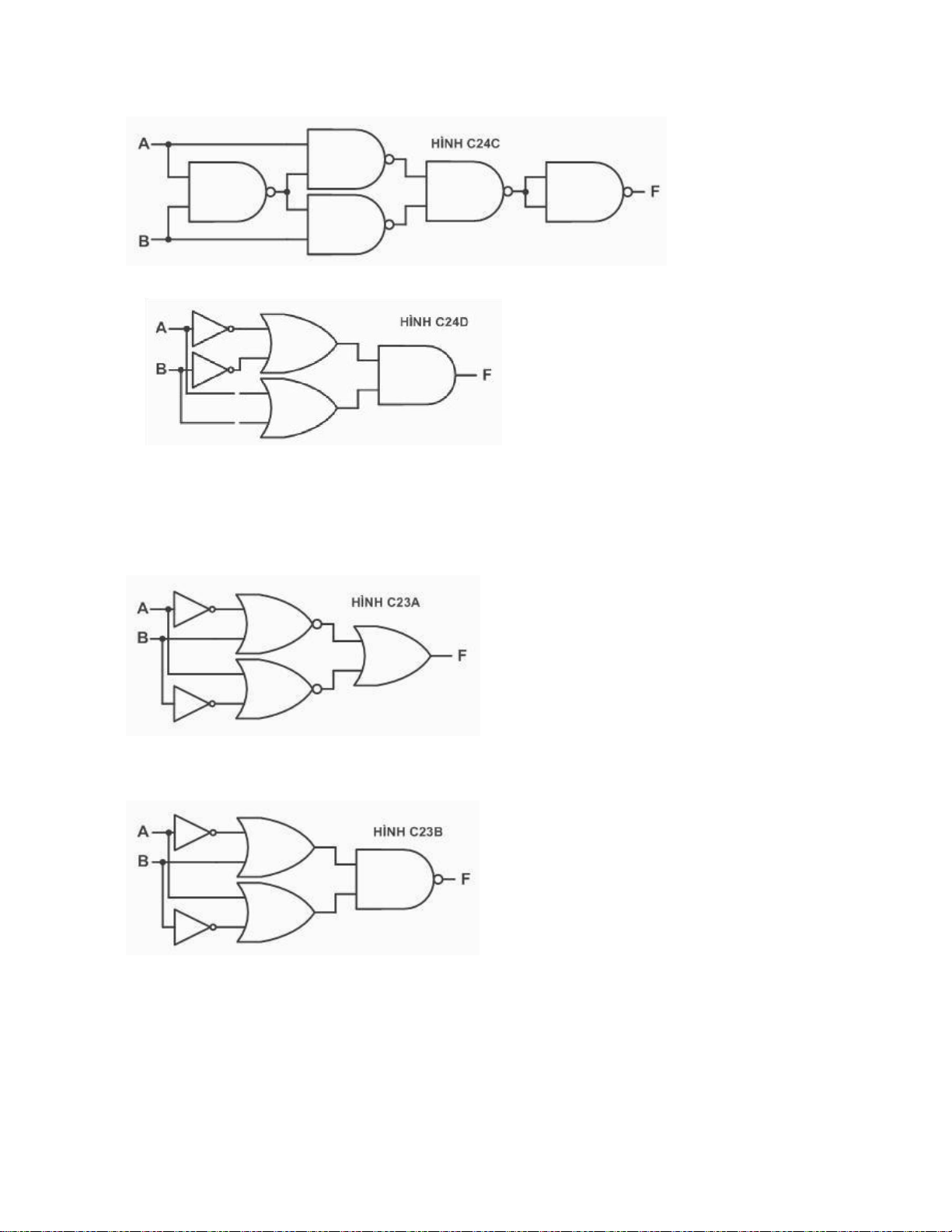
Câu 84: Tìm mạch số không tương đương với các mạch số khác: a. c. (Đ) c. d.
Câu 85: Tìm mạch số không tương đương với các mạch số khác: a. (Đ) lOMoARcPSD| 36067889 b. c. d.
Câu 86: Tìm mạch số không tương đương với các mạch số khác: a. b. lOMoARcPSD| 36067889 c. d. (Đ)
Câu 87: Tìm mạch số không tương đương với các mạch số khác: a. b. lOMoARcPSD| 36067889 d.
Câu 88: Hàm F được biểu diễn bằng bìa Karnaugh như hình trên, biểu diễn
dạng đại số của hàm F là:
a. F (A ,B ,C ,D) = ∑ (0, 2, 3, 4, 8 ,9 ,10 ,14) (Đ)
b. F (A ,B ,C ,D) = ∑ (0, 2, 3, 4, 10, 12, 13, 15)
c. F (A ,B ,C ,D) = ∏ (0, 2, 3, 4, 6, 8, 9, 10, 14, 15)
d. F (A ,B ,C ,D) = ∏ (0, 2, 3, 4, 10, 12, 13, 15, 14)
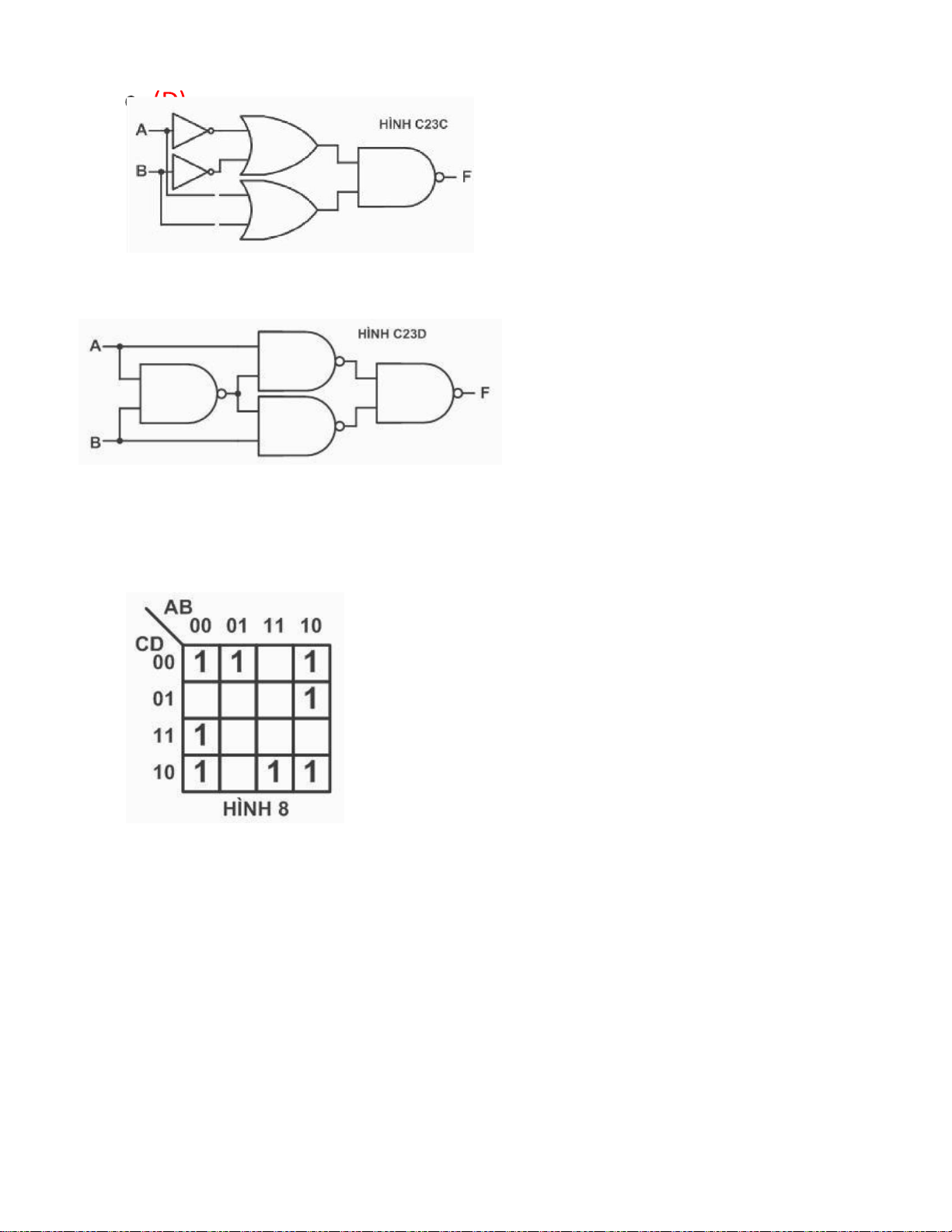
Câu 89: Hàm F được biểu diễn bằng bìa Karnaugh như hình 7, biểu diễn dạng đại số của hàm F là: lOMoARcPSD| 36067889
a. F (A ,B ,C ,D) = ∑ (0 , 2 , 5 , 7 , 8 , 10 , 13 , 15) (Đ)
b. F (A ,B ,C ,D) = ∑ (0 , 2 , 5 , 7 , 8 , 10 , 13)
c. F (A ,B ,C ,D) = ∏ (1 , 3 , 4 , 6 , 9 , 11 , 12 , 13) và d = (14)
d. F (A ,B ,C ,D) = ∏ (1 , 3 , 4 , 6 , 8 , 10 , 13 , 15)
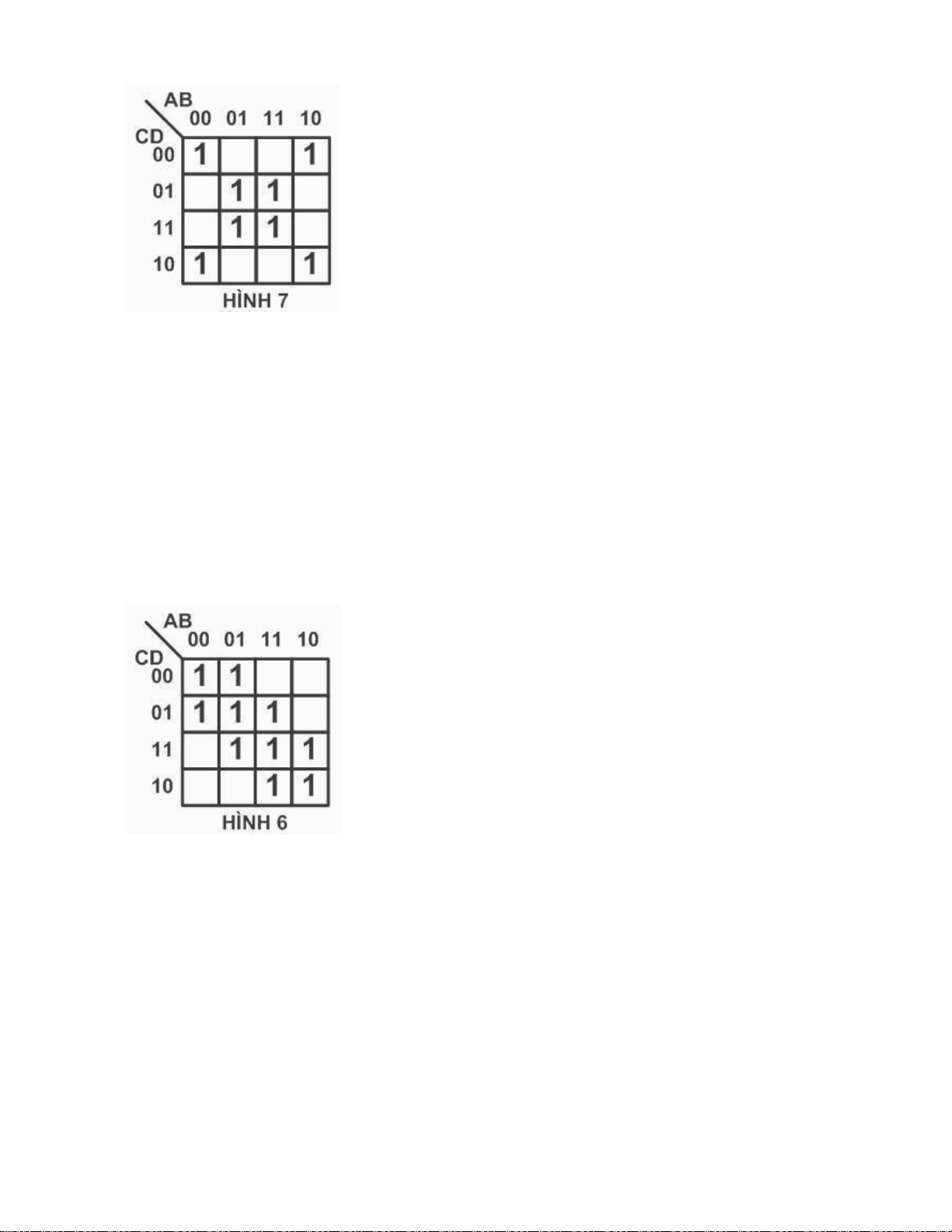
Câu 90: Hàm F được biểu diễn bằng bìa Karnaugh như hình 6, biểu diễn dạng đại số của hàm F là:
a. F (A ,B ,C ,D) = ∑ (0 , 1 , 4 , 5 , 10 , 11 , 12 , 13) d =(7, 15)
b. F (A ,B ,C ,D) = ∑ (0 , 1 , 6 , 7 , 10 , 11 , 12 , 13) d = (5, 15)
c. F (A ,B ,C ,D) = ∏ (2 , 3 , 6 , 7 , 8 , 9 , 12 , 13)
d. F (A ,B ,C ,D) = ∏ (2 , 3 , 6 , 8 , 9 , 12) (Đ)
Câu 91: Hàm F được biểu diễn bằng bìa Karnaugh như hình 5, biểu diễn dạng đại số của hàm F là: lOMoARcPSD| 36067889
a. F (A ,B ,C ,D) = ∑ (0 , 1 , 2 , 3 , 6 , 7 , 10 , 14)
b. F (A ,B ,C ,D) = ∑ (1 , 2 , 3 , 5 , 6 , 7 , 14 , 15)
c. F (A ,B ,C ,D) = ∏ (1 , 2 , 3 , 5 , 6 , 7 , 14 , 15) (Đ)
d. F (A ,B ,C ,D) = ∏ (0 , 1 , 4 , 5 , 8 , 9 , 12 , 13)
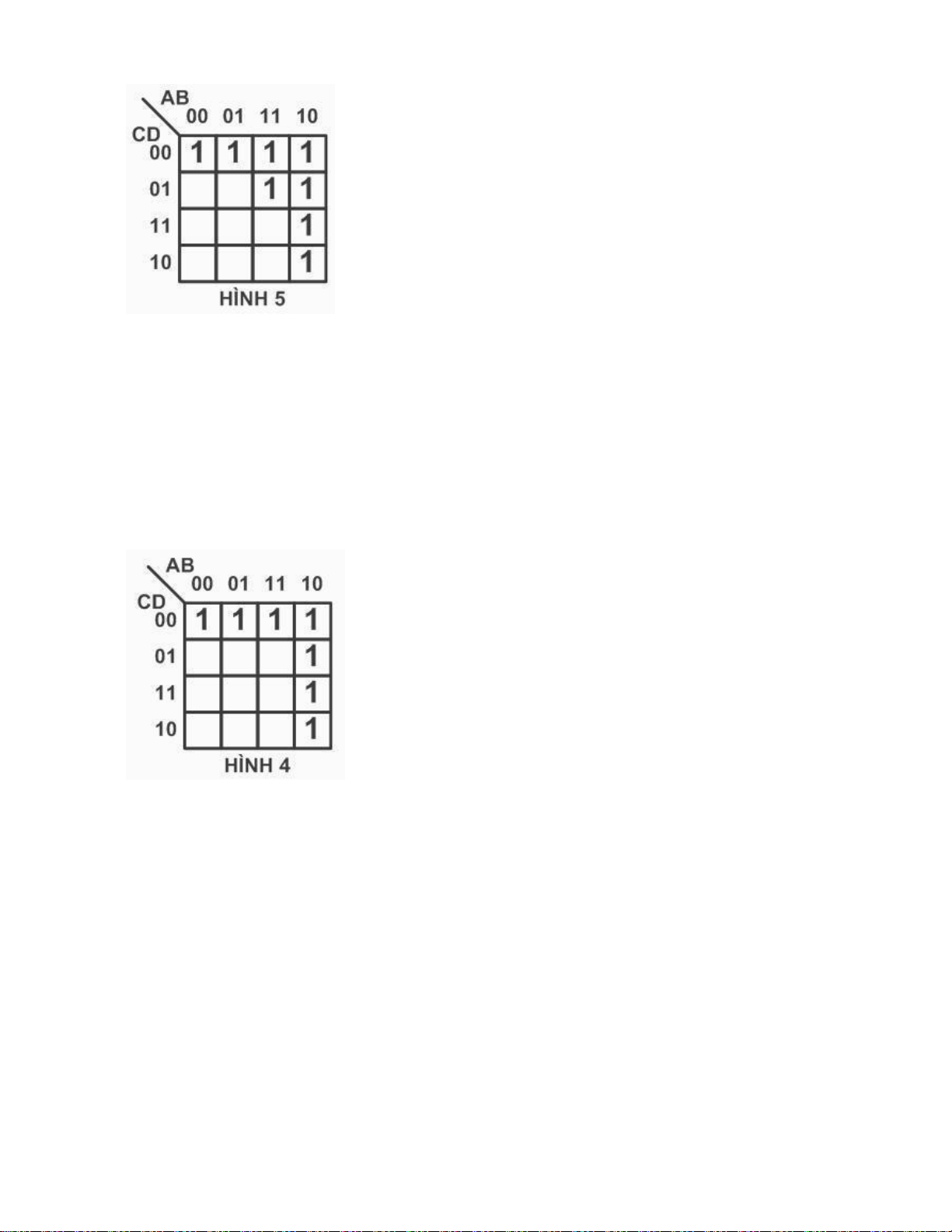
Câu 92 : Hàm F được biểu diễn bằng bìa Karnaugh như hình 4, biểu diễn dạng đại số của hàm F là:
a. F (A ,B ,C ,D) = ∑ (0 , 4 , 8 , 9 , 10 , 11 , 12) (Đ)
b. F (A ,B ,C ,D) = ∑ (0 , 4 , 8 , 12 , 13 , 14 , 15)
c. F (A ,B ,C ,D) = ∏ (0 , 1 , 2 , 3 , 4 , 8 , 12)
d. F (A ,B ,C ,D) = ∏ (0 , 4 , 8 , 9 , 10 , 11 , 12 , 13)
Câu 93: Hàm là dạng rút gọn của hàm:
a. F (A ,B ,C ,D) = ∑ (1 , 3 , 5 , 7 , 8 , 10 , 12 , 14) (Đ)
b. F (A ,B ,C ,D) = ∏ (1 , 3 , 5 , 7 , 8 , 9 , 12 , 13)
c. F (A ,B ,C ,D) = ∑ (0 , 2 , 4 , 6 , 9 , 11 , 13 , 15)
d. F (A ,B ,C ,D) = ∏ (1 , 3 , 5 , 7 , 8 , 10 , 12 , 14) lOMoARcPSD| 36067889
Câu 94: Hàm là dạng rút gọn của hàm:
a. F (A ,B ,C ,D) = ∑ (0 , 1 , 4 , 5 , 8 , 9 , 12 , 13)
b. F (A ,B ,C ,D) = ∑ (0 , 1 , 2 , 3 , 12 , 13 , 14 , 15) (Đ)
c. F (A ,B ,C ,D) = ∑ (0 , 1 , 2 , 3 , 4 , 5 , 6 , 7)
d. F (A ,B ,C ,D) = ∏ (0 , 1 , 2 , 3 , 4 , 5 , 6 , 7)
Câu 95: Hàm là dạng rút gọn của hàm:
a. F (A ,B ,C ,D) = ∏ (0 , 1 , 4 , 5 , 10 , 11 , 14 , 15)
b. F (A ,B ,C ,D) = ∑ (0 , 1 , 4 , 5 , 10 , 11 , 14 , 15) (Đ)
c. F (A ,B ,C ,D) = ∑ (2 , 3 , 6 , 7 , 8 , 9 , 12 , 13)
d. F (A ,B ,C ,D) = ∏ (0 , 1 , 2 , 3 , 4 , 5 , 6 , 7)
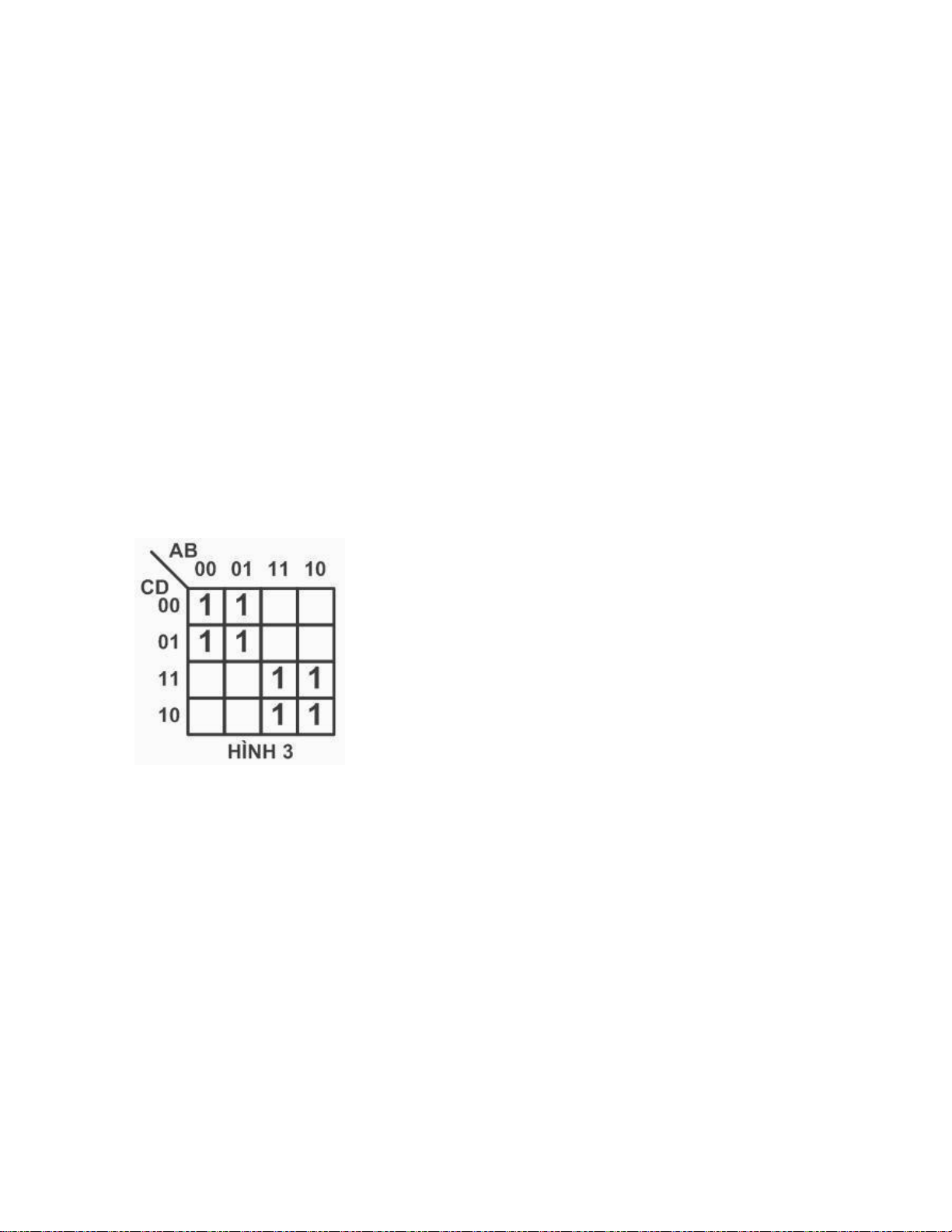
Câu 96 : Hàm F được biểu diễn bằng bìa Karnaugh như hình 3, biểu diễn dạng đại số của hàm F là:
a. F (A ,B ,C ,D) = ∑ (0 , 1 , 4 , 5 , 10 , 11 , 12 , 13)
b. F (A ,B ,C ,D) = ∑ (0 , 1 , 6 , 7 , 10 , 11 , 12 , 13)
c. F (A ,B ,C ,D) = ∏ (2 , 3 , 6 , 7 , 8 , 9 , 12 , 13) (Đ)
d. F (A ,B ,C ,D) = ∏ (0 , 1 , 4 , 5 , 10 , 11 , 14 , 15)
Câu 97: Hàm F được biểu diễn bằng bìa Karnaugh như hình 3, dạng rút gọn của hàm F là: lOMoARcPSD| 36067889 a. b. c. d. (Đ)
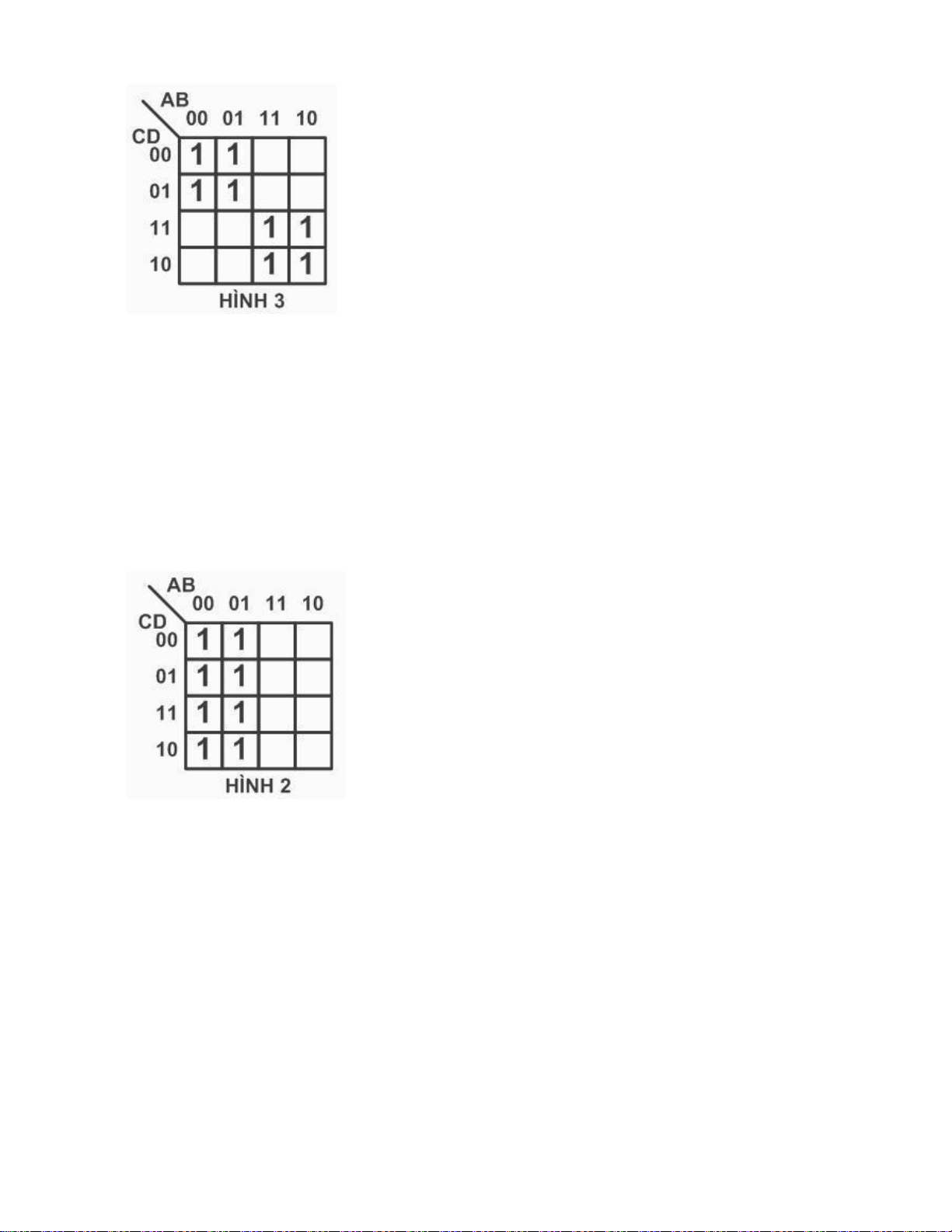
Câu 98: Hàm F được biểu diễn bằng bìa Karnaugh như hình 2, biểu diễn dạng đại số của hàm F là:
a. F (A , B , C , D) = ∑ (0 , 1 , 2 , 3 , 4 , 5 , 6 , 7) (Đ)
b. F (A , B , C , D) = ∑ (0 , 1 , 4 , 5 , 8 , 9 , 12 , 13)
c. F (A , B , C , D) = ∏ (0 , 1 , 2 , 3 , 4 , 5 , 6 , 7)
d. F (A , B , C , D) = ∏ (0 , 1 , 4 , 5 , 8 , 9 , 12 , 13)
Câu 99: Hàm F được biểu diễn bằng bìa Karnaugh như hình 2, dạng rút gọn của hàm F là: lOMoARcPSD| 36067889 a. b. d. (Đ) d.
Câu 100: Hàm F được biểu diễn bằng bìa Karnaugh như hình 1, biểu diễn
dạng đại số của hàm F là:
a. F (A , B , C , D) = ∑ (0 , 1 , 5 , 6 , 8 , 9 , 12 , 13)
b. F (A , B , C , D) = ∑ (0 , 1 , 4 , 5 , 8 , 9 , 12 , 13) (Đ)
c. F (A , B , C , D) = ∏ (0 , 1 , 5 , 6 , 8 , 9 , 12 , 13)
d. F (A , B , C , D) = ∏ (0 , 1 , 4 , 5 , 8 , 9 , 12 , 13)
CHƯƠNG 2: MẠCH LOGIC TỔ HỢP
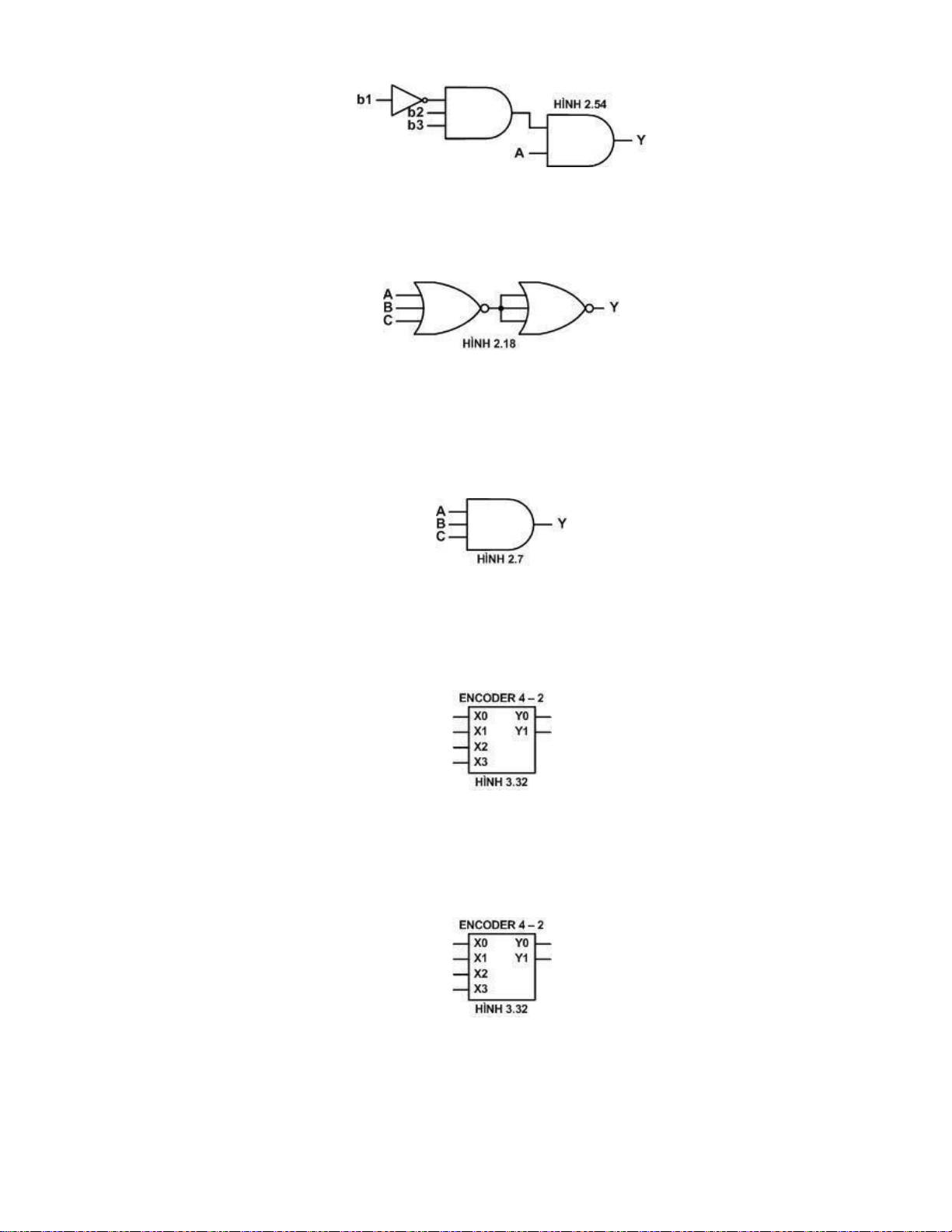
Câu 1: Cho mạch logic như hình 2.54. Đầu ra Y = A khi : lOMoARcPSD| 36067889
A. b1b2b3 = 010 C. b1b2b3 =100 B. b1b2b3= 011 D. b1b2b3 =110
Câu 2: Cho sơ đồ mạch logic như hình 2.18. Biểu thức đại số của Y là: A. Y = A.B.C C. B. Y = A+B+C D.
Câu 3: Cho sơ đồ mạch logic như hình 2.7. Biểu thức đại số của Y là: A. Y = A.B.C C. B. Y = A+B+C D.
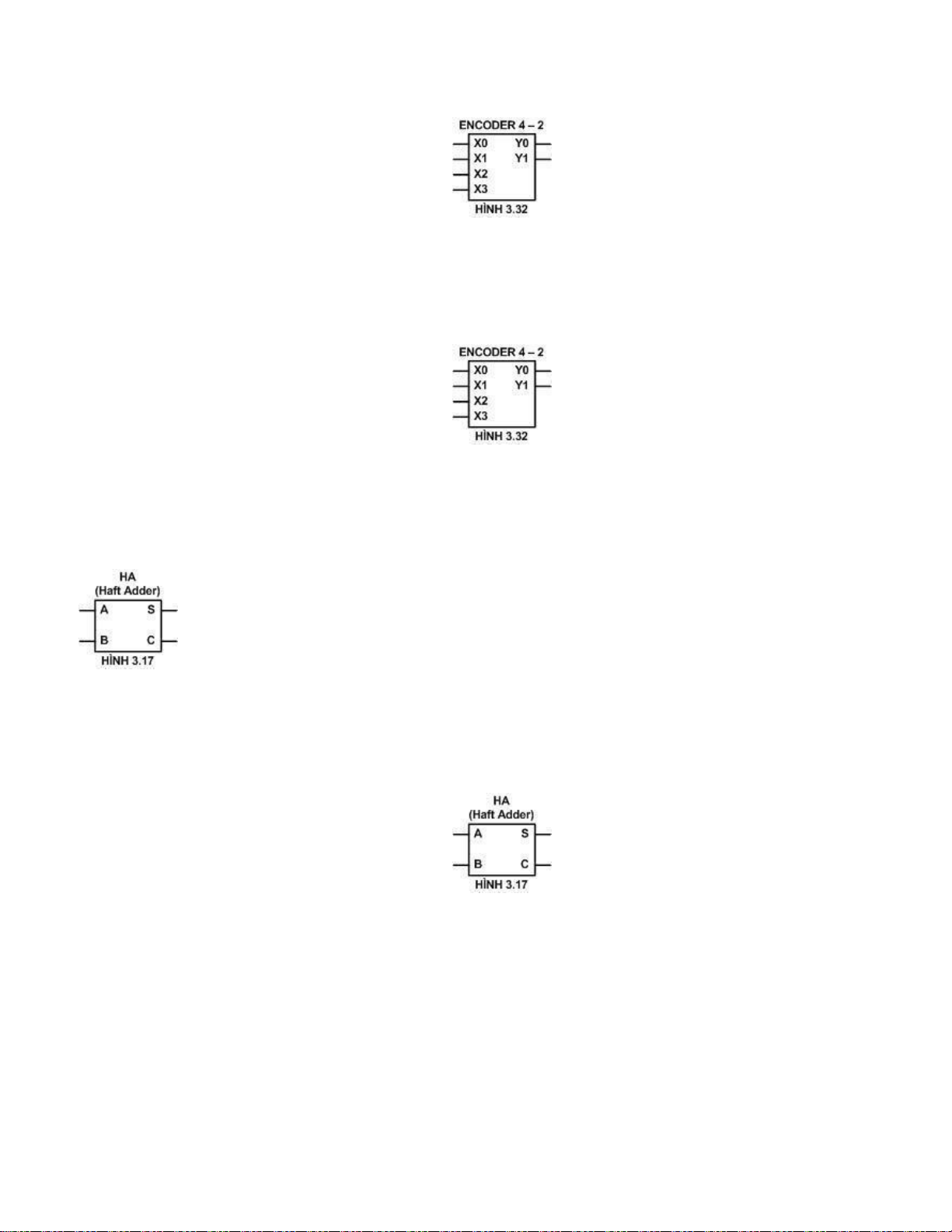
Câu 4: Cho mạch mã hoá nhị phân 4 -2. Khi X0 = 1 (Mã hóa X0) thì:
A. Y0 = 0, Y1 = 1 C. Y0 = 1, Y1 = 1
B. Y0 = 0, Y1 = 0 D. Y0 = 1, Y1 = 0
Câu 5: Cho mạch mã hoá nhị phân 4 -2. Khi X1 = 1 (Mã hóa X1) thì:
A. Y0 = 0, Y1 = 1 C. Y0 = 1, Y1 = 1
B. Y0 = 0, Y1 = 0 D. Y0 = 1, Y1 = 0 lOMoARcPSD| 36067889
Câu 6: Cho mạch mã hoá nhị phân 4 -2. Khi X2 = 1 (Mã hóa X2) thì:
A. Y0 = 0, Y1 = 1 C. Y0 = 1, Y1 = 1
B. Y0 = 0, Y1 = 0 D. Y0 = 1, Y1 = 0
Câu7: Cho mạch mã hoá nhị phân 4 -2. Khi X3 = 1 (Mã hóa X3) thì: A. Y0 = 0, Y1 = 1 C. Y0 = 1, Y1 = 1 B. Y0 = 0, Y1 = 0 D. Y0 = 1, Y1 = 0
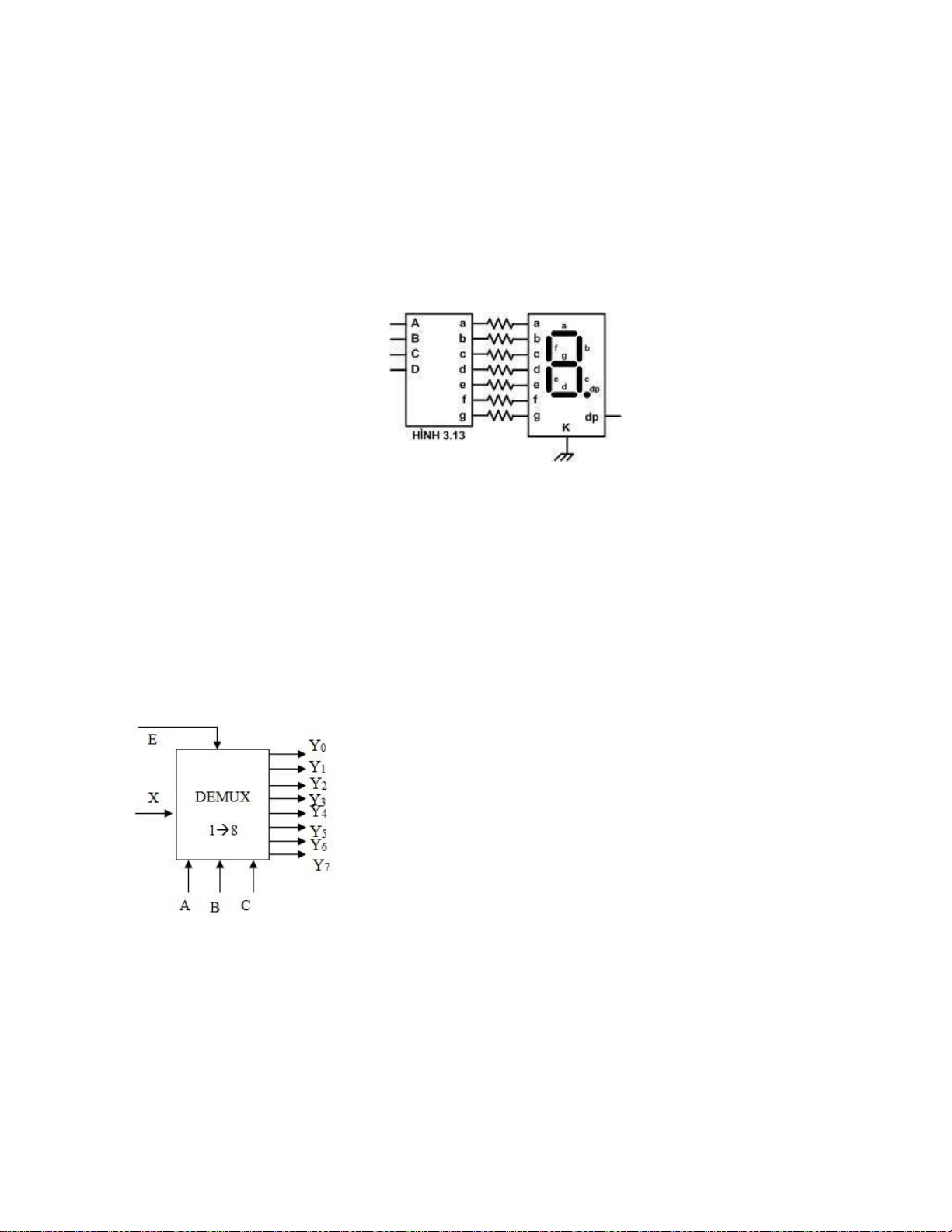
Câu 8: Mạch cộng nửa tổng có biểu thức số nhớ C ở đầu ra: A. C = A + B C. B. D. C = A . B
Câu 9: Mạch cộng nửa tổng có biểu thức số tổng S ở đầu ra: A. S = A + B C. B. D. C = A . B
Câu 10: Phát biểu nào sau đây SAI về MUX A. Số đầu ra luôn là 1
B. Số đầu vào dữ liệu bằng 2n, với n là số đầu vào điều khiển lOMoARcPSD| 36067889
C. Số đầu vào ít hơn số đầu ra.
D. Số đầu vào nhiều hơn số đầu ra
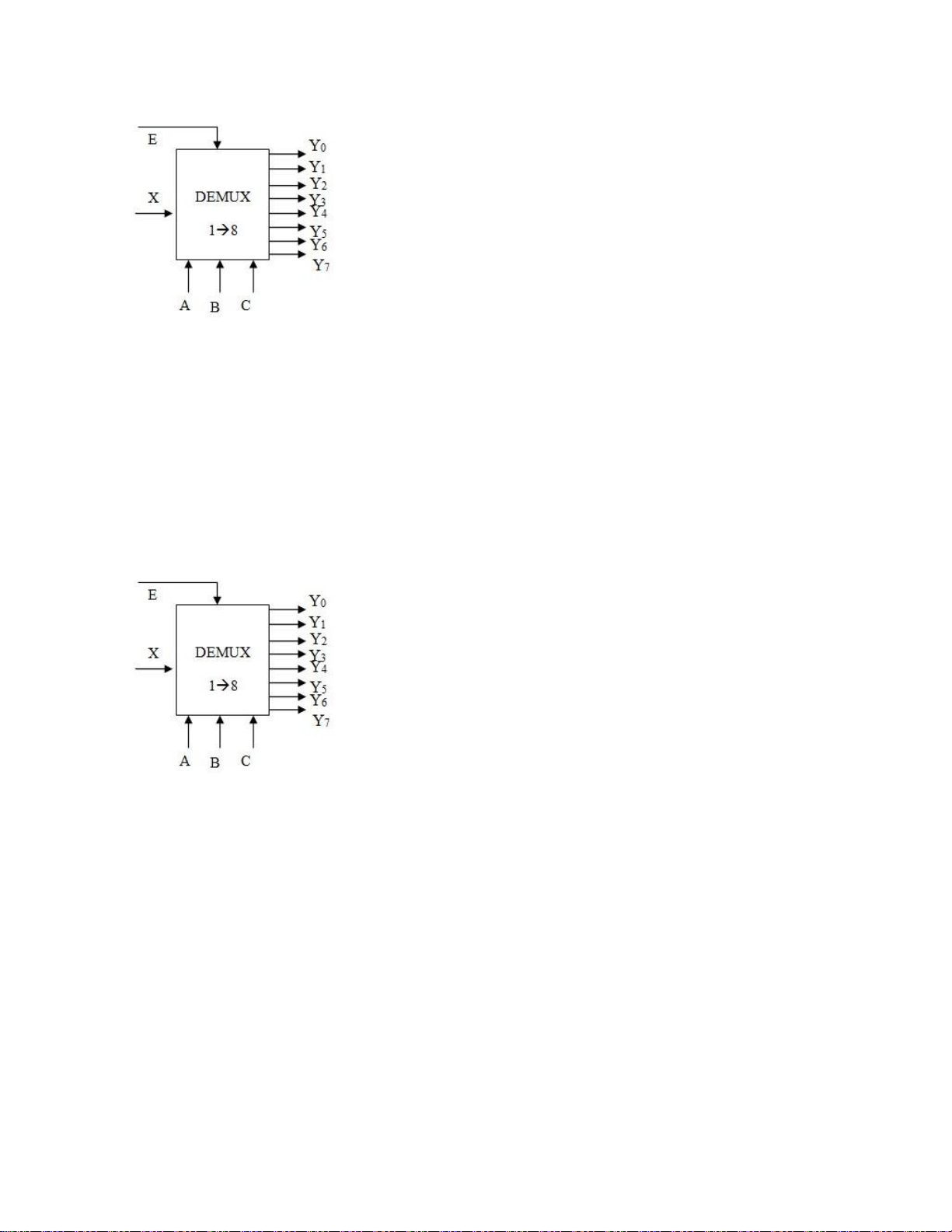
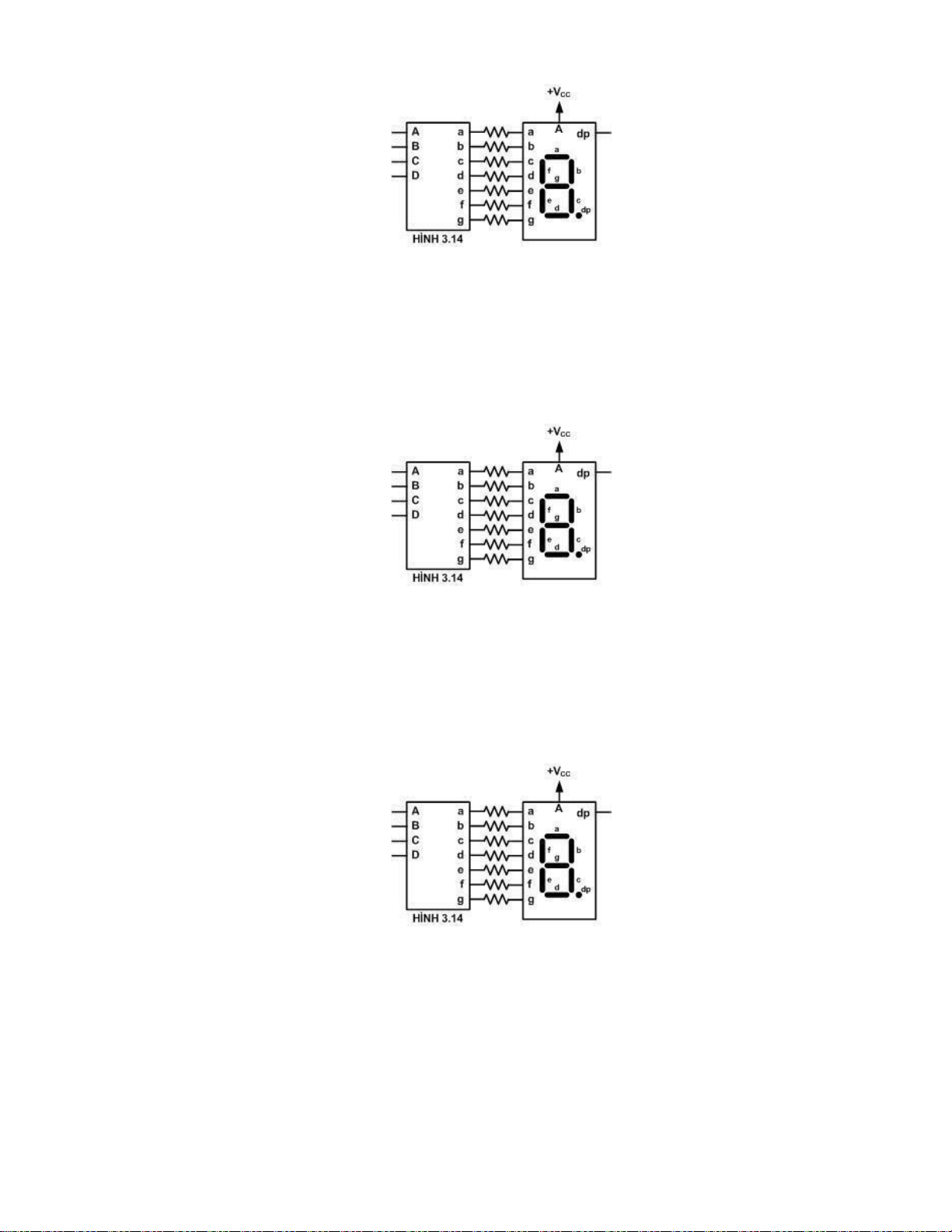
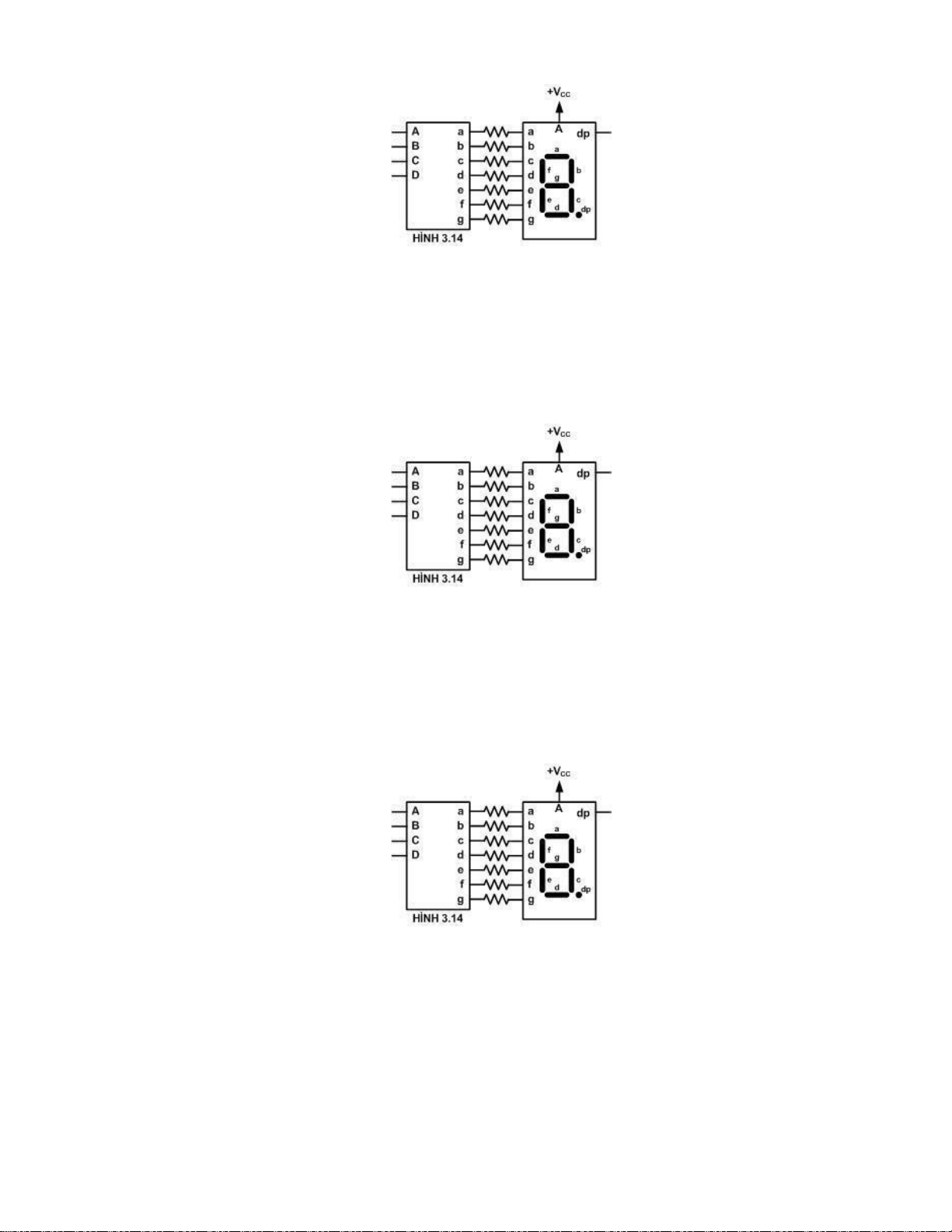
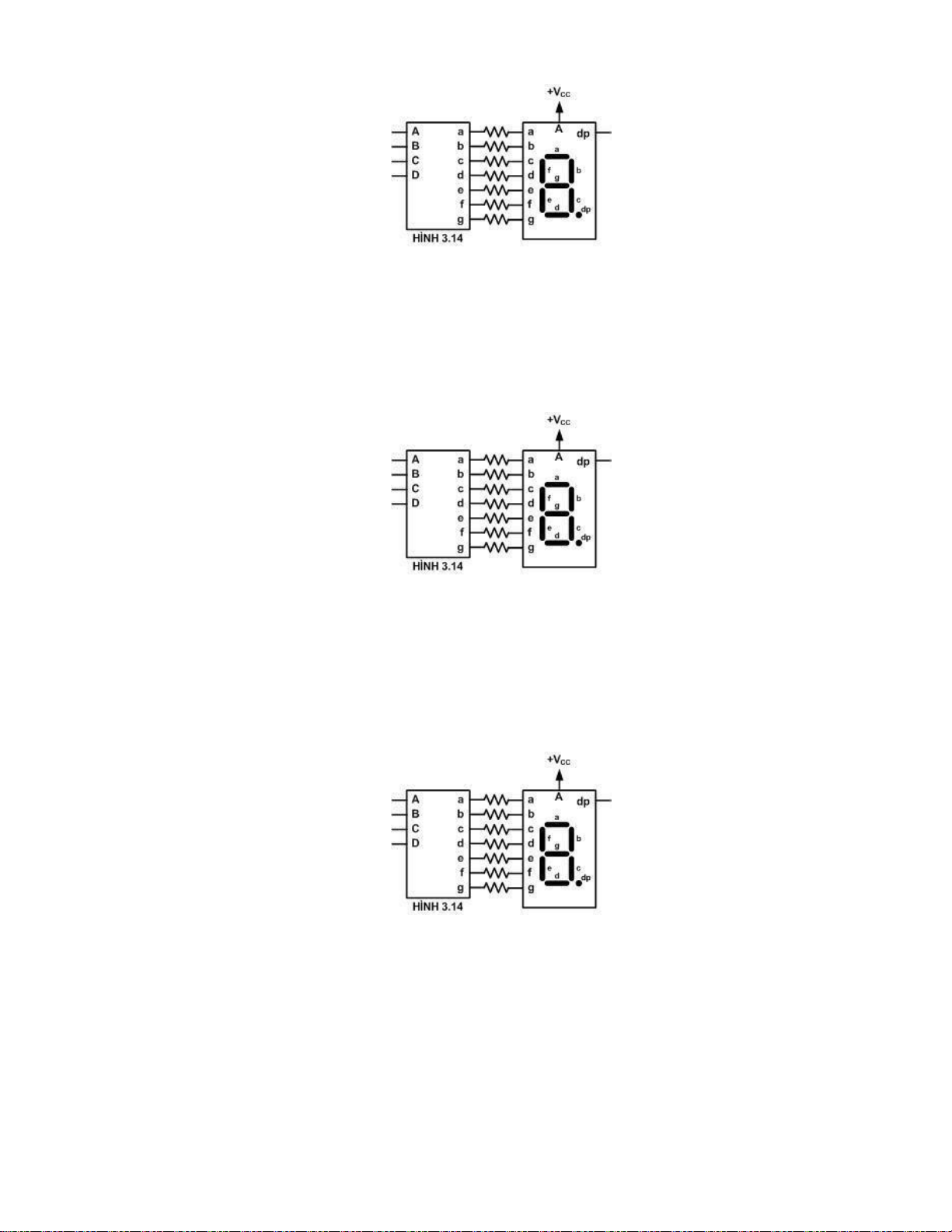
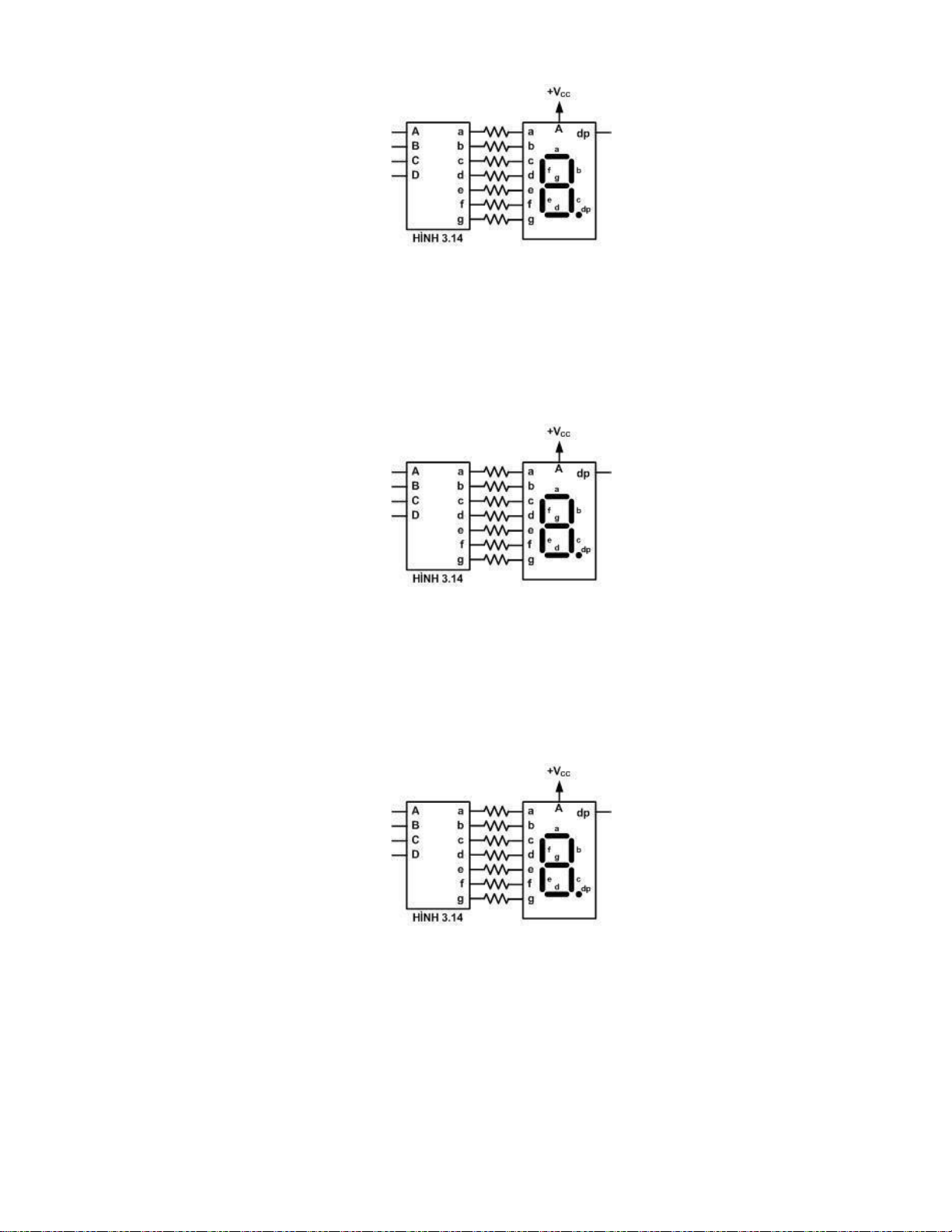
Câu 11: Mạch giải mã BCD sang 7 đoạn loại catod chung như hình 3.13.
Trong đó A – D là 4 đầu vào dữ liệu (A là MSB); a – g là 7 đầu ra.
Khi ABCD = 0010 thì trạng thái đầu ra là:
A. abcdefg=0010010 C. abcdefg=0110011
B. abcdefg=1101101 D. abcdefg=1001100
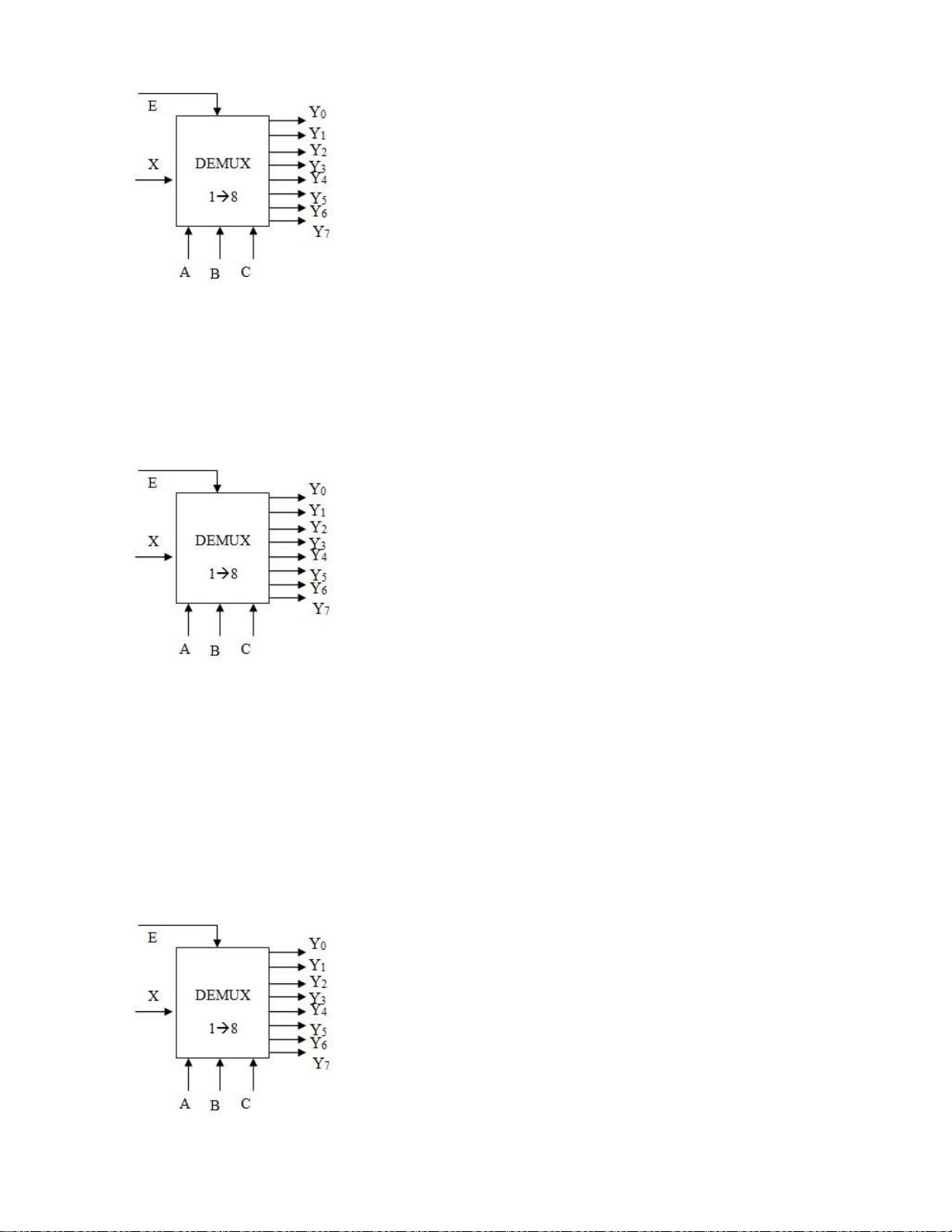
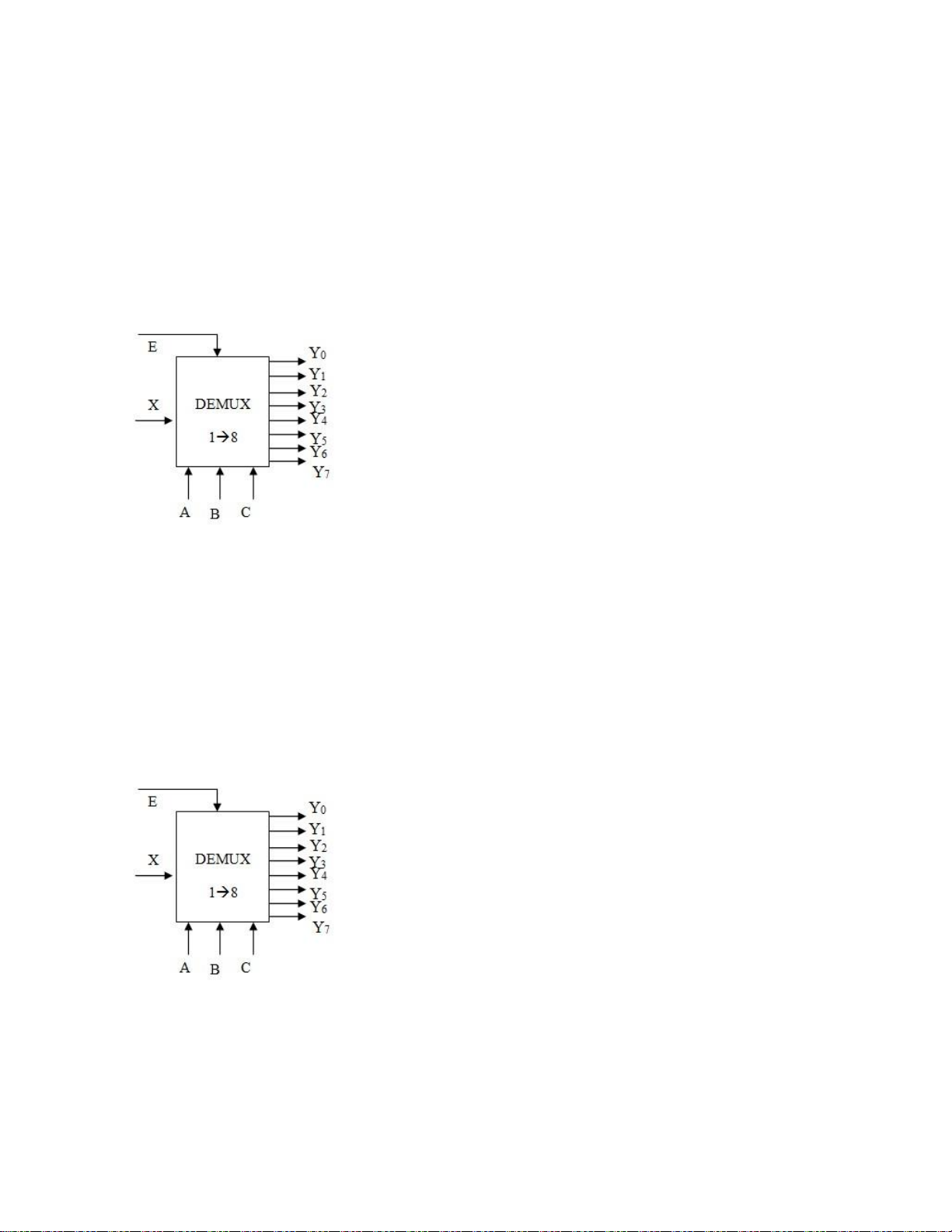
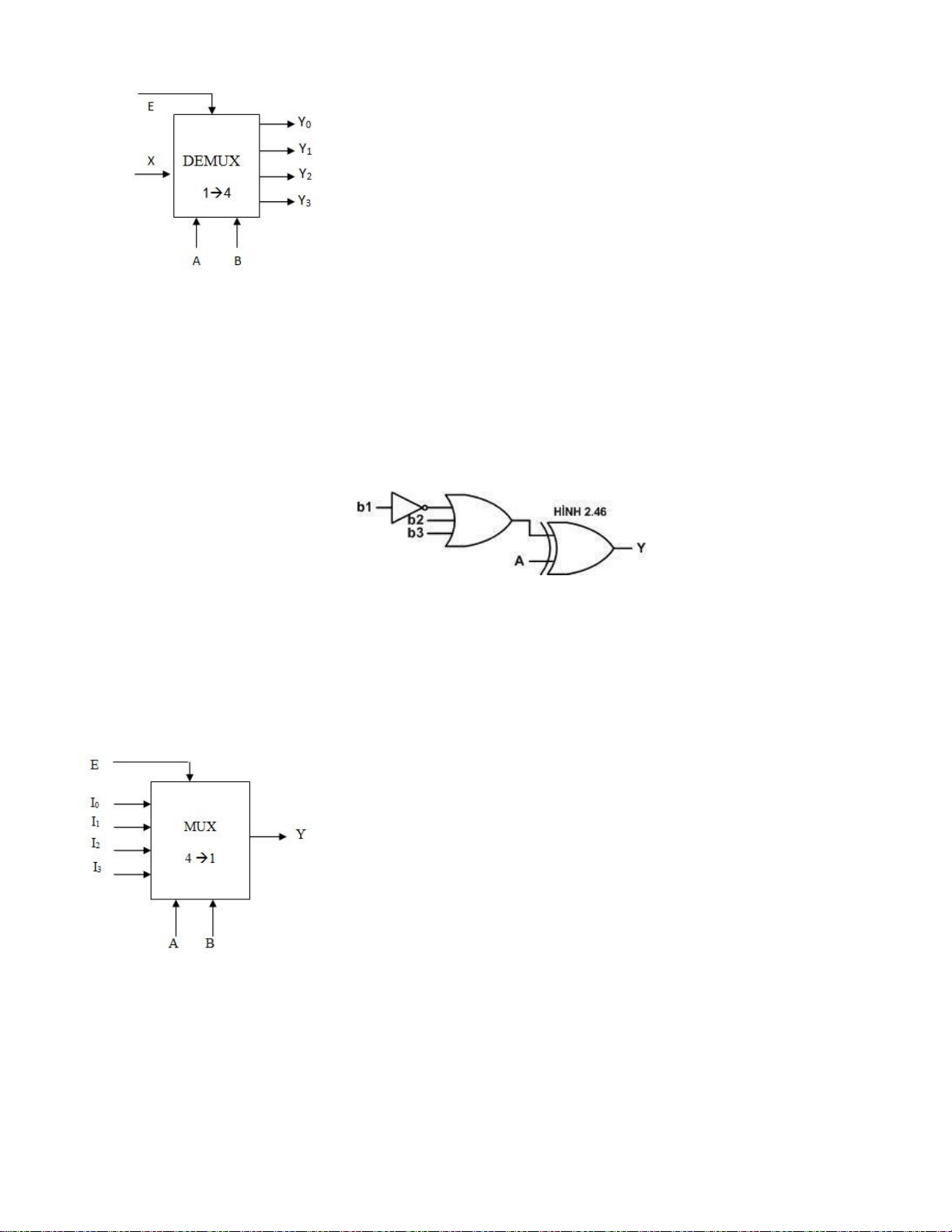
Câu 12: Cho mạch phân kênh 1→ 8. Trong đó X là kênh tín hiệu vào, Y0 – Y7 là
8 kênh tín hiệu ra; A,BC là tín hiệu điều khiển (A là MSB); E là đầu vào cho phép .
Để X kết nối với Y2 phải điều khiển như sau: A. E=0 ; ABC=010 C. E=1 ; ABC=010 B. E=0 ; ABC=101 D. E=1 ; ABC=101
Câu 13: Cho mạch phân kênh 1→ 8. Trong đó X là kênh tín hiệu vào, Y0 – Y7 là
8 kênh tín hiệu ra; A,BC là tín hiệu điều khiển (A là MSB); E là đầu vào cho phép . lOMoARcPSD| 36067889
Để X kết nối với Y0 phải điều khiển như sau: A. E=0 ; ABC=010 C. E=1 ; ABC=000 B. E=0 ; ABC=101 D. E=1 ; ABC=101
Câu 14: Cho mạch phân kênh 1→ 8. Trong đó X là kênh tín hiệu vào, Y0 – Y7 là
8 kênh tín hiệu ra; A,BC là tín hiệu điều khiển (A là MSB); E là đầu vào cho phép .
Để X kết nối với Y1 phải điều khiển như sau: A. E=0 ; ABC=010 C. E=1 ; ABC=001 B. E=0 ; ABC=101 D. E=1 ; ABC=101
Câu 15: Cho mạch phân kênh 1→ 8. Trong đó X là kênh tín hiệu vào, Y0 – Y7 là
8 kênh tín hiệu ra; A,BC là tín hiệu điều khiển (A là MSB); E là đầu vào cho phép .
Để X kết nối với Y3 phải điều khiển như sau: lOMoARcPSD| 36067889 A. E=0 ; ABC=010 B. E=0 ; ABC=101 C. E=1 ; ABC=011 D. E=1 ; ABC=101
Câu 16: Cho mạch phân kênh 1→ 8. Trong đó X là kênh tín hiệu vào, Y0 – Y7 là
8 kênh tín hiệu ra; A,BC là tín hiệu điều khiển (A là MSB); E là đầu vào cho phép .
Để X kết nối với Y4 phải điều khiển như sau: A. E=0 ; ABC=010 C. E=1 ; ABC=001 B. E=0 ; ABC=101 D. E=1 ; ABC=100
Câu 17: Cho mạch phân kênh 1→ 8. Trong đó X là kênh tín hiệu vào, Y0 – Y7 là
8 kênh tín hiệu ra; A,BC là tín hiệu điều khiển (A là MSB); E là đầu vào cho phép .
Để X kết nối với Y5 phải điều khiển như sau: lOMoARcPSD| 36067889 A. E=0 ; ABC=010 C. E=1 ; ABC=101 B. E=0 ; ABC=101 D. E=1 ; ABC=100
Câu 18: Cho mạch phân kênh 1→ 8. Trong đó X là kênh tín hiệu vào, Y0 – Y7 là
8 kênh tín hiệu ra; A,BC là tín hiệu điều khiển (A là MSB); E là đầu vào cho phép .
Để X kết nối với Y6 phải điều khiển như sau: A. E=0 ; ABC=010 C. E=1 ; ABC=110 B. E=0 ; ABC=101 D. E=1 ; ABC=101
Câu 19: Cho mạch phân kênh 1→ 8. Trong đó X là kênh tín hiệu vào, Y0 – Y7 là
8 kênh tín hiệu ra; A,BC là tín hiệu điều khiển (A là MSB); E là đầu vào cho phép .
Để X kết nối với Y7 phải điều khiển như sau: A. E=0 ; ABC=010 C. E=1 ; ABC=111 B. E=0 ; ABC=101 D. E=1 ; ABC=101
Câu 20: Bộ phân kênh 1 sang 2n có: lOMoARcPSD| 36067889 A. 2n đầu vào C. 2n đầu ra B. n đầu vào D. (2n – 1) đầu ra
Câu 21: Mạch tổ hợp có 4 đầu vào là A, B, C, D (với A là MSB và D là LSB) và 1 đầu ra là Y.
Y= 1: Nếu giá trị thập phân tương đương của đầu vào nhỏ hơn 10 Y=0: Ngược lại
Rút gọn biểu thức đầu ra: A. C. B. D.
Câu 22: Bộ cộng 1 bít đầy đủ (FA) là bộ cộng:
A. 2 đầu vào, 2 đầu ra C. 2 đầu vào, 3 đầu ra
B. 2 đầu vào, 1 đầu ra D. 3 đầu vào, 2 đầu ra Câu 23: Cho
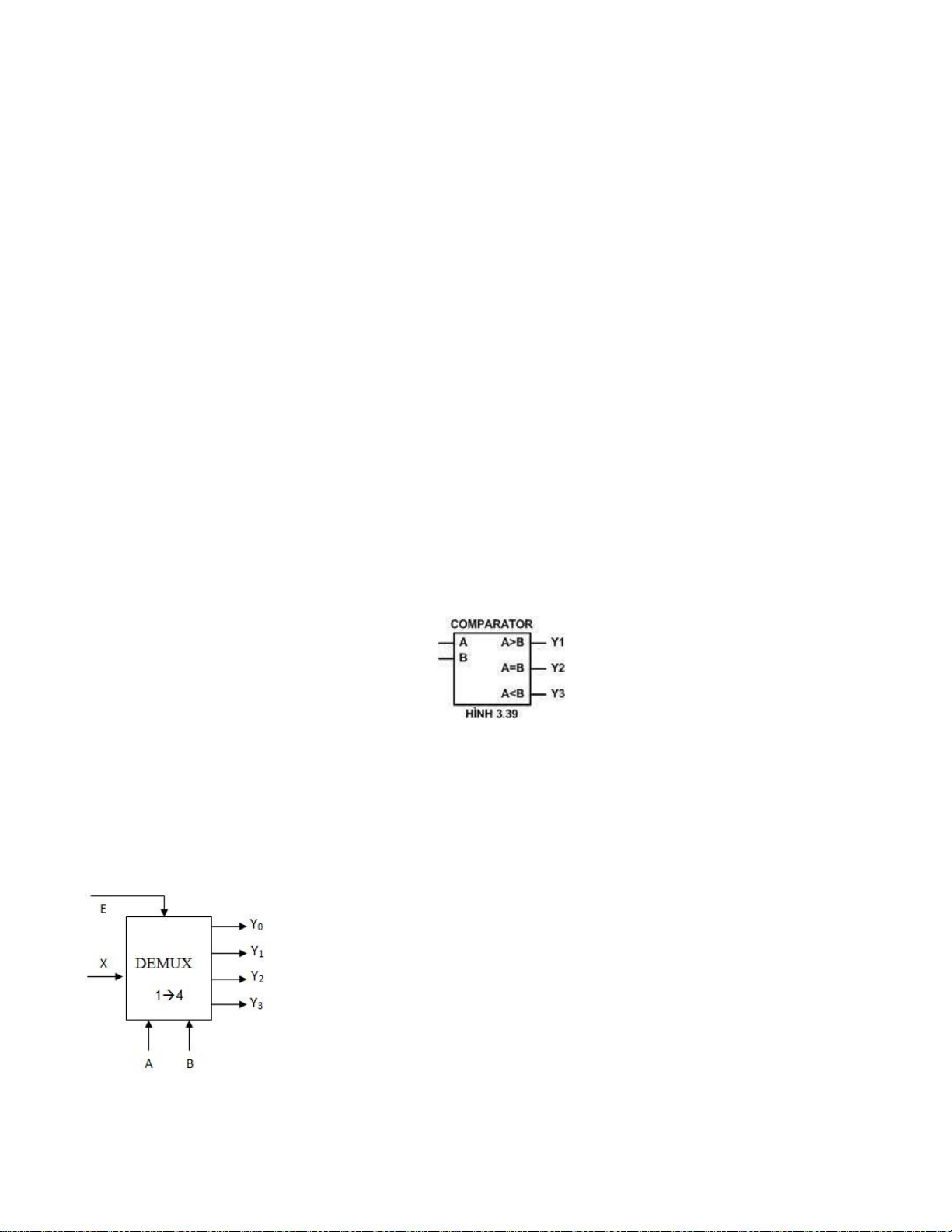
mạch so sánh 1 bít như hình 3.39: A. C. B. D.
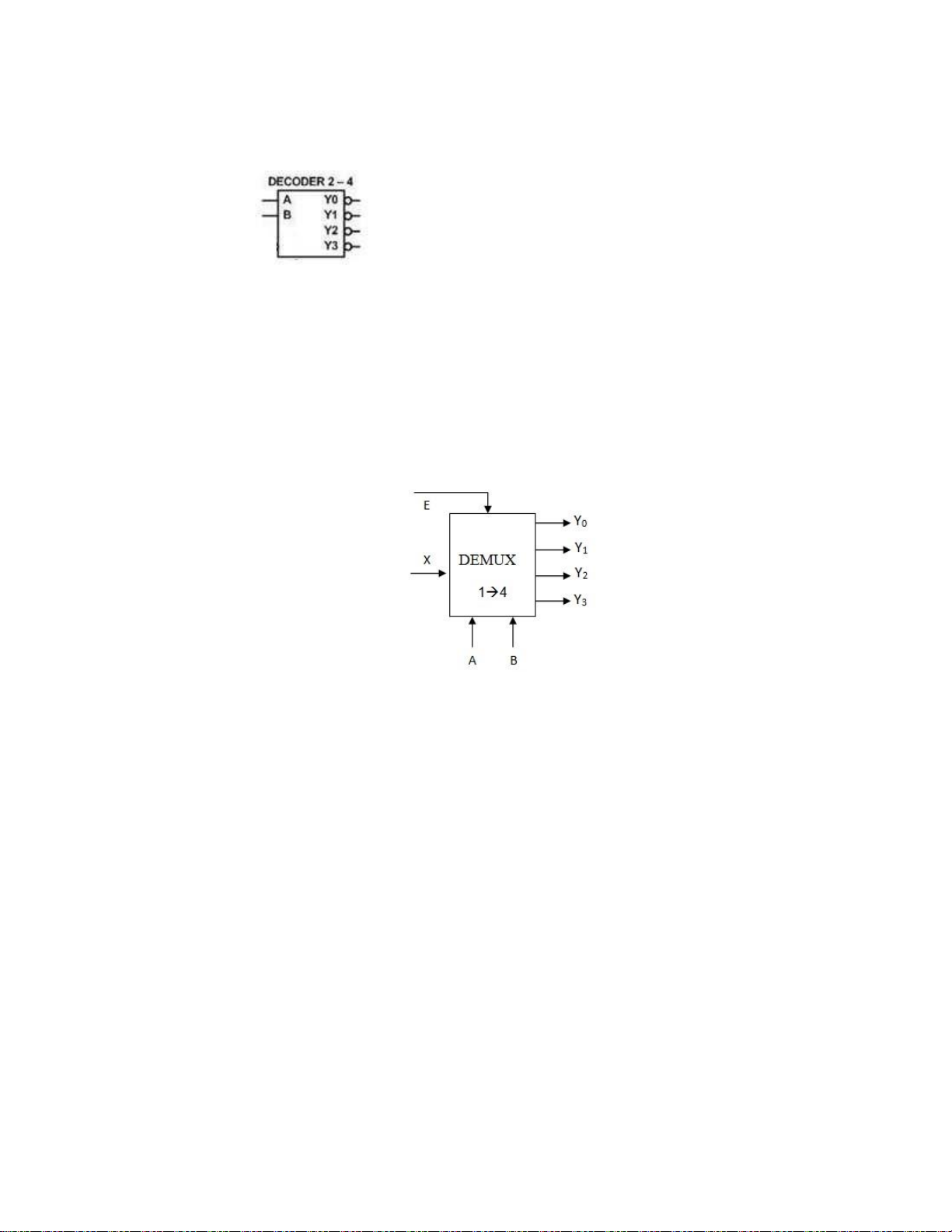
Câu24: Cho mạch phân kênh DeMux: A, B: Tín hiệu điều khiển (A là MSB) Nếu
A=1; B=0, X=1; E = 1 Đầu ra có giá trị là: lOMoARcPSD| 36067889 A. Y0 = 1 C. Y2 = 1 B. Y1 = 1 D. Y3 = 1
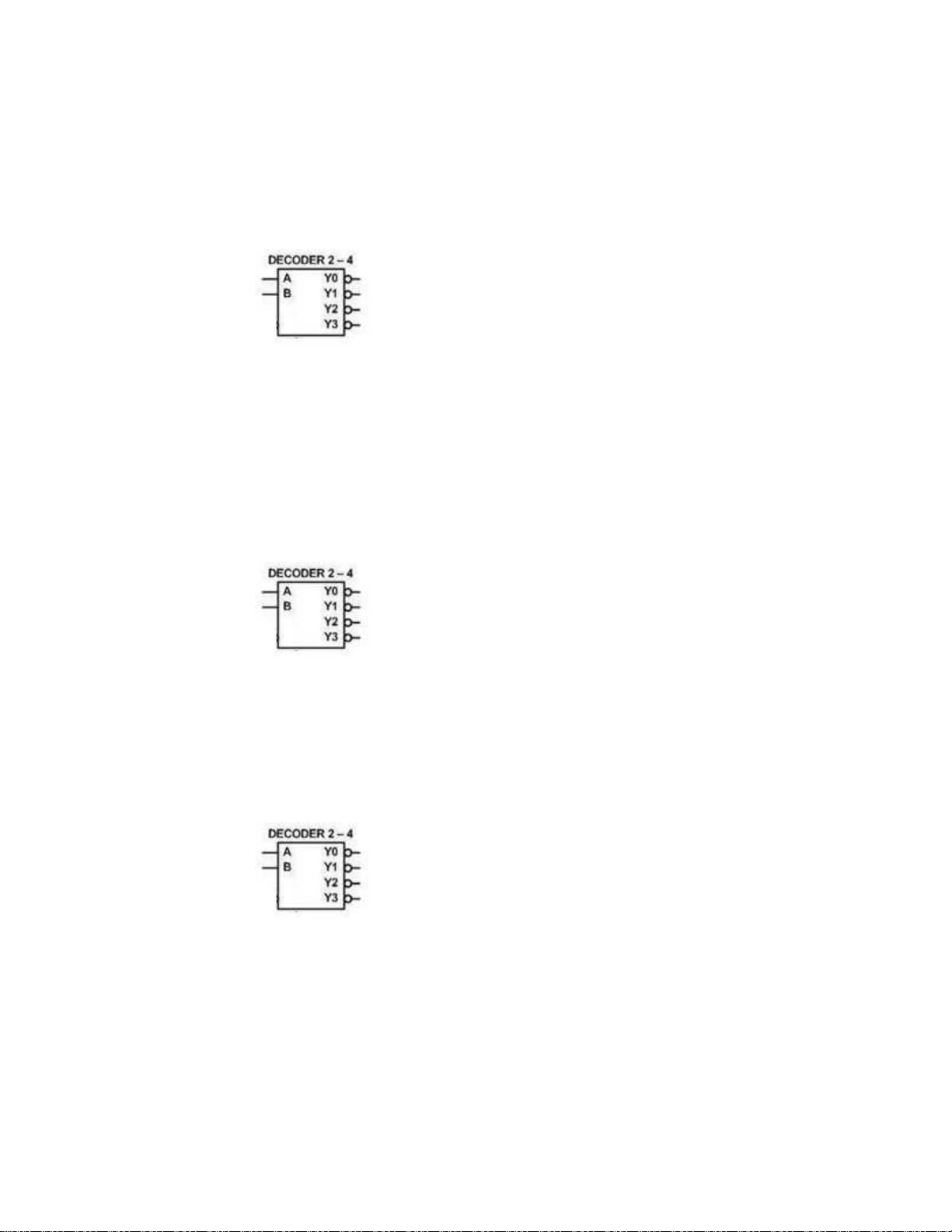
Câu 25: Cho mạch giải mã nhị phân 2 sang 4. A, B là 2 đầu vào (A là MSB); Y0
– Y3 là các đầu ra. Để Y0 ở mức tích cực và Y0, Y1, Y2 ở mức thụ động thì: A. AB =11 C. AB =00 B. AB =00 D. AB =11
Câu 26: Cho mạch giải mã nhị phân 2 sang 4. A, B là 2 đầu vào (A là MSB); Y0
– Y3 là các đầu ra. Để Y1 ở mức tích cực và Y0, Y1, Y2 ở mức thụ động thì: A. AB =11 C. AB =01 B. AB =00 D. AB =10
Câu 27: Cho mạch giải mã nhị phân 2 sang 4. A, B là 2 đầu vào (A là MSB); Y0
– Y3 là các đầu ra. Để Y2 ở mức tích cực và Y0, Y1, Y2 ở mức thụ động thì: A. AB =11 C. AB =10 B. AB =00 D. AB =11 lOMoARcPSD| 36067889
Câu 28: Cho mạch giải mã nhị phân 2 sang 4. A, B là 2 đầu vào (A là MSB); Y0
– Y3 là các đầu ra. Để Y3 ở mức tích cực và Y0, Y1, Y2 ở mức thụ động thì: A. AB =11 C. AB =00 B. AB =00 D. AB =11
Câu 29: Cho mạch phân kênh DeMux. A, B là các tín hiệu điều khiển (A là MSB);
E là tín hiệu chọn. Nếu A = 1, B=1; E = 1 thì: A. Y3 = 1 B. Y3 = 0 C. Y3 = X (Đ)
D. Mạch không hoạt động
Câu 30: Cho mạch phân kênh DeMux. A, B là các tín hiệu điều khiển (A là MSB);
E là tín hiệu chọn. Nếu A = 1, B=1; E = 0 thì: lOMoARcPSD| 36067889 A. Y3 = 1 B. Y3 = 0 C. Y3 = X
D. Mạch không hoạt động (Đ)
Câu 31: Cho mạch logic như hình 2.46. Đầu ra Y = A khi:
A. b1b2b3 = 011 C. b1b2b3 = 100
B. b1b2b3 = 010 D. b1b2b3 = 110
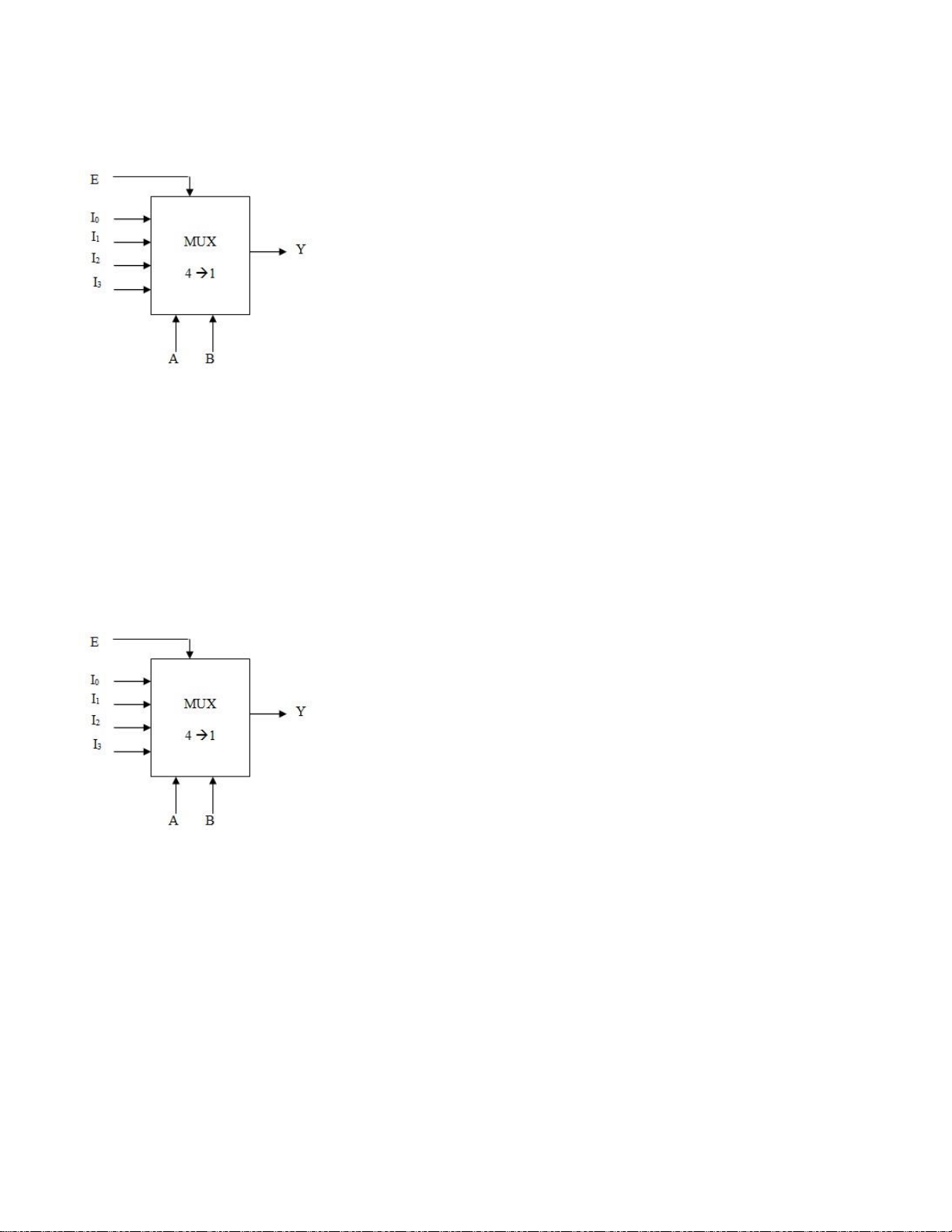
Câu 32: Cho mạch dồn kênh 4 sang 1, trong đó I0 – I3 là 4 tín hiệu vào, A
và B là các tín hiệu điều khiển (với A là MSB), Y là đầu ra . Nếu E = 1 và AB=00 thì : a. Y = I0 (Đ) b. Y = I1 c. Y = I3 d. MUX không hoạt động lOMoARcPSD| 36067889
Câu 33: Cho mạch dồn kênh 4 sang 1, trong đó I0 – I3 là 4 tín hiệu vào, A
và B là các tín hiệu điều khiển (với A là MSB), Y là đầu ra . Nếu E = 1 và AB=01 thì : a. Y = I0 b. Y = I1 (Đ) c. Y = I3 d. MUX không hoạt động
Câu 34: Cho mạch dồn kênh 4 sang 1, trong đó I0 – I3 là 4 tín hiệu vào, A
và B là các tín hiệu điều khiển (với A là MSB), Y là đầu ra . Nếu E = 1 và AB=10 thì : a. Y = I0 b. Y = I1 c. Y = I2 (Đ) d. MUX không hoạt động
Câu 35: Cho mạch dồn kênh 4 sang 1, trong đó I0 – I3 là 4 tín hiệu vào, A
và B là các tín hiệu điều khiển (với A là MSB), Y là đầu ra . Nếu E = 1 và AB=11 thì : lOMoARcPSD| 36067889 a. Y = I0 b. Y = I1 c. Y = I2 d. Y = I3 (Đ)
Câu 36: Cho mạch dồn kênh 4 sang 1, trong đó I0 – I3 là 4 tín hiệu vào, A
và B là các tín hiệu điều khiển (với A là MSB), Y là đầu ra . Nếu E = 0 và AB=11 thì : a. Y = I0 b. Y = I1 c. Y = I3
d. MUX không hoạt động (Đ)
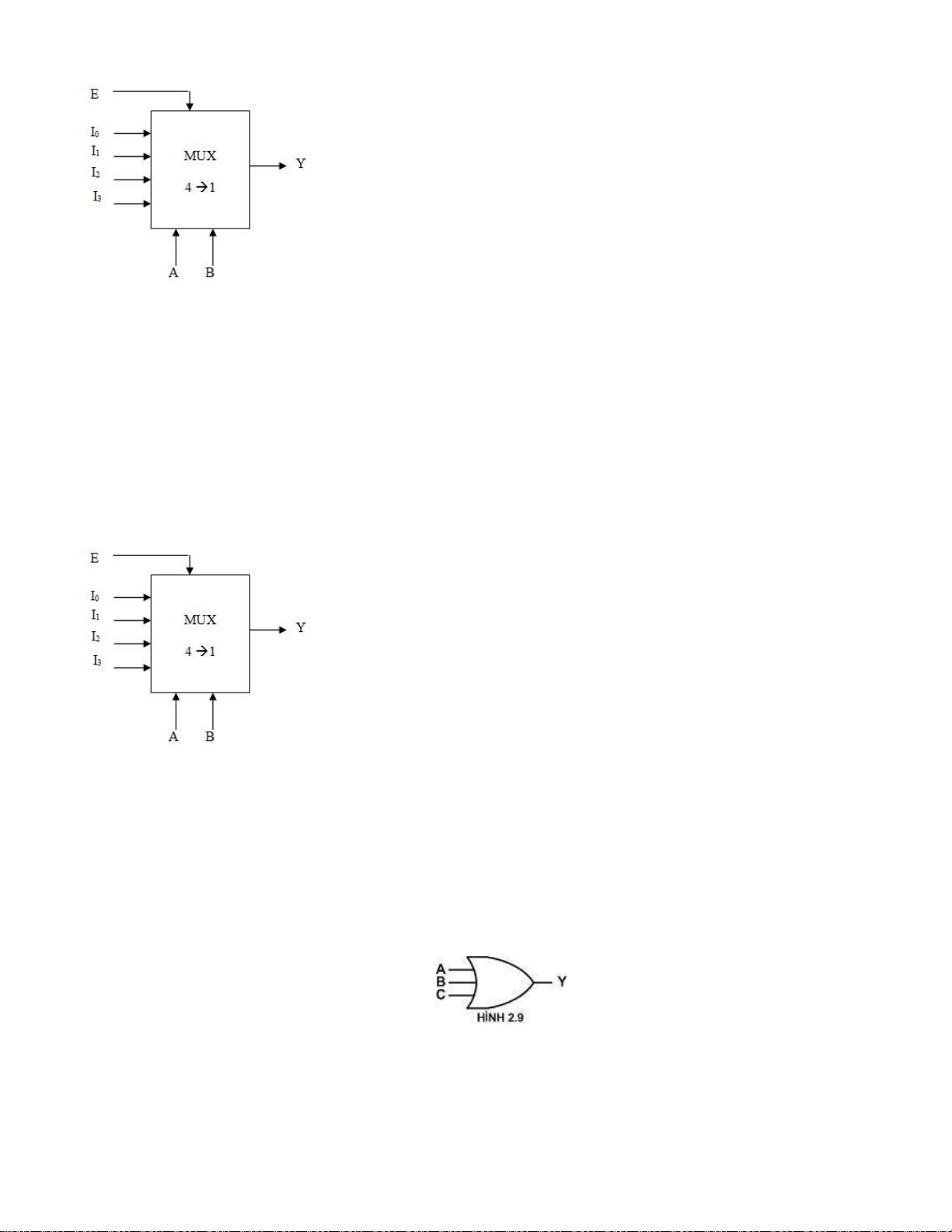
Câu 37: Cho sơ đồ mạch logic như hình 2.9. Biểu thức đại số của Y là: A. C. B. D. lOMoARcPSD| 36067889
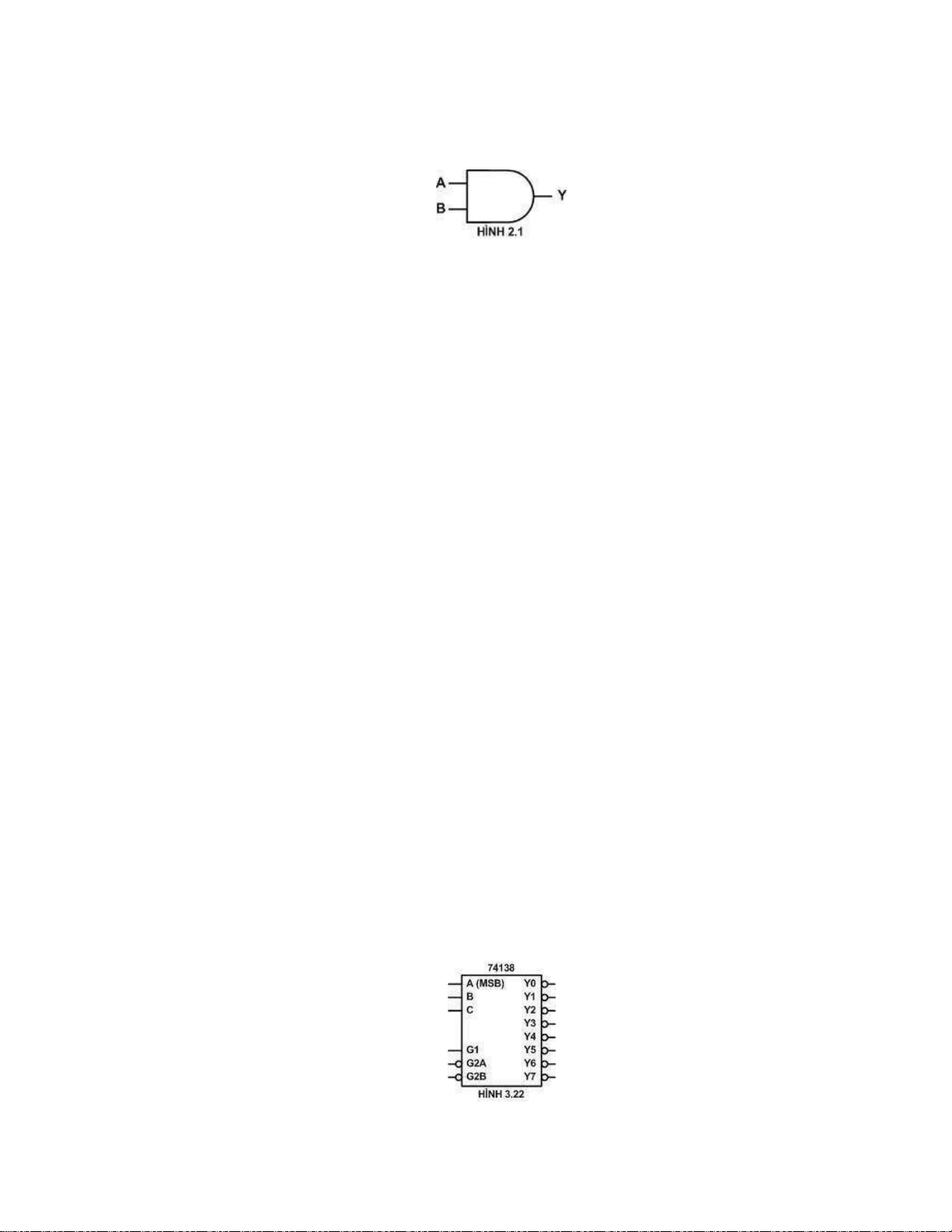
Câu 38: Cho sơ đồ mạch logic như hình 2.1. Biểu thức đại số logic của ngõ ra Y là: A. C. B. D.
Câu 39: Bộ dồn kênh 2n sang 1 có:
A. 2n tín hiệu điều khiển B. 2n đầu vào dữ liệu
C. 2n đầu vào dữ liệu và điều khiển
D. 2n đầu vào dữ liệu, điều khiển và cho phép
Câu 40: Bộ dồn kênh có n đầu vào điều khiển, m đầu vào dữ liệu thì: A. m = n. C. m = 2n m = 2. B. D. m = (2n – 1)
Câu 41: Bộ dồn kênh (MUX) sử dụng n đầu vào điều khiển sẽ có:
a. Có 1 đầu vào dữ liệu và 2n đầu ra
b. Có 2n đầu vào dữ liệu và 1 đầu ra (Đ)
c. Có n đầu vào dữ liệu và 1 đầu ra
d. Có 1 đầu vào dữ liệu và n đầu ra
Câu 42: Cho IC giải mã 74138 như hình 3.22: lOMoARcPSD| 36067889
A. Đây là IC giải mã từ 3 sang 8
B. Đây là IC giải mã từ 6 sang 8
C. Đây là IC giải mã từ 8 sang 6
D. Đây là IC giải mã từ 8 sang 3
Câu 43 : Mạch giải mã BCD sang 7 đoạn loại Cathode chung; A, B, C, D là 4 đầu
vào (A là MSB); a – g là 7 đầu ra. Khi ABCD=0000 thì trạng thái đầu ra là:
A. abcdefg=1111001 C. abcdefg=1011111
B. abcdefg=1111110 D. abcdefg=0100000
Câu 44 : Mạch giải mã BCD sang 7 đoạn loại Cathode chung; A, B, C, D là 4 đầu
vào (A là MSB); a – g là 7 đầu ra. Khi ABCD=0001 thì trạng thái đầu ra là:
A. abcdefg=1111001 C. abcdefg=1011111
B. abcdefg=0110000 D. abcdefg=0100000
Câu 45 : Mạch giải mã BCD sang 7 đoạn loại Cathode chung; A, B, C, D là 4 đầu
vào (A là MSB); a – g là 7 đầu ra. Khi ABCD=0010 thì trạng thái đầu ra là: lOMoARcPSD| 36067889
A. abcdefg=1101101 C. abcdefg=1011111
B. abcdefg=1111110 D. abcdefg=0100000
Câu 46 : Mạch giải mã BCD sang 7 đoạn loại Cathode chung; A, B, C, D là 4 đầu
vào (A là MSB); a – g là 7 đầu ra. Khi ABCD=0011 thì trạng thái đầu ra là:
A. abcdefg=1111001 C. abcdefg=1011111
B. abcdefg=1111110 D. abcdefg=0100000
Câu 47 : Mạch giải mã BCD sang 7 đoạn loại Cathode chung; A, B, C, D là 4 đầu
vào (A là MSB); a – g là 7 đầu ra. Khi ABCD=0100 thì trạng thái đầu ra là:
A. abcdefg=1101101 C. abcdefg=1011111
B. abcdefg=1111110 D. abcdefg=0110011
Câu 48 : Mạch giải mã BCD sang 7 đoạn loại Cathode chung; A, B, C, D là 4 đầu
vào (A là MSB); a – g là 7 đầu ra. Khi ABCD=0101 thì trạng thái đầu ra là: lOMoARcPSD| 36067889
A. abcdefg=1101101 C. abcdefg=1011111
B. abcdefg=1111110 D. abcdefg=1011011
Câu 49 : Mạch giải mã BCD sang 7 đoạn loại Cathode chung; A, B, C, D là 4 đầu
vào (A là MSB); a – g là 7 đầu ra. Khi ABCD=0110 thì trạng thái đầu ra là:
A. abcdefg=1011101 C. abcdefg=1011111
B. abcdefg=1111110 D. abcdefg=0100000
Câu 50 : Mạch giải mã BCD sang 7 đoạn loại Cathode chung; A, B, C, D là 4 đầu
vào (A là MSB); a – g là 7 đầu ra. Khi ABCD=0111 thì trạng thái đầu ra là:
A. abcdefg=1110000 C. abcdefg=1011111
B. abcdefg=1111110 D. abcdefg=0100000
Câu 51 : Mạch giải mã BCD sang 7 đoạn loại Cathode chung; A, B, C, D là 4 đầu
vào (A là MSB); a – g là 7 đầu ra. Khi ABCD=1000 thì trạng thái đầu ra là: lOMoARcPSD| 36067889
A. abcdefg=1111111 C. abcdefg=1011111
B. abcdefg=1111110 D. abcdefg=0100000
Câu 52 : Mạch giải mã BCD sang 7 đoạn loại Cathode chung; A, B, C, D là 4 đầu
vào (A là MSB); a – g là 7 đầu ra. Khi ABCD=1001 thì trạng thái đầu ra là:
A. abcdefg=1101101 C. abcdefg=1011111
B. abcdefg=1111011 D. abcdefg=0100000
Câu 53 : Mạch giải mã BCD sang 7 đoạn loại Anode chung; A, B, C, D là 4 đầu
vào (A là MSB); a – g là 7 đầu ra. Khi ABCD=0000 thì trạng thái đầu ra là:
A. abcdefg=1111001 C. abcdefg=1011111
B. abcdefg=0000001 D. abcdefg=0100000
Câu 54: Mạch giải mã BCD sang 7 đoạn loại Anode chung; A, B, C, D là 4 đầu
vào (A là MSB); a – g là 7 đầu ra. Khi ABCD=0001 thì trạng thái đầu ra là: lOMoARcPSD| 36067889
A. abcdefg=1111001 C. abcdefg=1011111
B. abcdefg=1001111 D. abcdefg=0100000
Câu 55 : Mạch giải mã BCD sang 7 đoạn loại Anode chung; A, B, C, D là 4 đầu
vào (A là MSB); a – g là 7 đầu ra. Khi ABCD=0010 thì trạng thái đầu ra là:
A. abcdefg=1111001 C. abcdefg=0010010
B. abcdefg=1001111 D. abcdefg=0100000
Câu 56 : Mạch giải mã BCD sang 7 đoạn loại Anode chung; A, B, C, D là 4 đầu
vào (A là MSB); a – g là 7 đầu ra. Khi ABCD=0011 thì trạng thái đầu ra là:
A. abcdefg=1111001 C. abcdefg=1011111
B. abcdefg=0000110 D. abcdefg=0100000
Câu 57: Mạch giải mã BCD sang 7 đoạn loại Anode chung; A, B, C, D là 4