Đề cương giữa học kỳ 1 Toán 9 năm 2023 – 2024 trường THCS Cự Khối – Hà Nội

UBND QUẬN LONG BIÊN
TRƯỜNG THCS CỰ KHỐI
ĐỀ CƯƠNG ÔN TẬP KIỂM TRA GIỮA HỌC KÌ I Môn: TOÁN 9
Năm học: 2023 – 2024
I. Nội dung kiến thức ôn tập: A. ĐẠI SỐ 1. Căn bậc hai số học: 2. Hằng đăng thức
3. Liên hệ giữa phép nhân, phép chia với phép khai phương
4. Biến đổi đơn giản biểu thức chứa căn bậc hai B. HÌNH HỌC
1. Hệ thức lượng trong tam giác vuông
2. Tỉ số lượng giác của góc nhọn
3. Hệ thức giữa cạnh và góc trong tam giác vuông
II. Câu hỏi ôn tập
1. Kết quả của phép tính 25+144 là: A. 17 B. 169 C. 13 D. 13 ± 2. Biểu thức 3
− x xác định khi và chỉ khi: 2 x −1
A. x ≥ 3 và x ≠ 1 −
B. x ≤ 0 và x ≠1
C. x ≥ 0 và x ≠1
C. x ≤ 0 và x ≠ 1 − 3. Tính 2 2 5 + ( 5) − có kết quả là: A. 0 B. 10 − C. 50 D. 10 4. Tính: ( − )2 1 2 − 2 có kết quả là: A. 1− 2 2 B. 2 2 −1 C. 1 D. 1 − 5. 2
−x + 2x −1 xác định khi và chỉ khi: A. x∈ R B. x =1 C. x∈∅ D. x ≥1 2 6. Rút gọn biểu thức: x − với x x
> 0 có kết quả là: A. −x B. 1 − C. 1 D. x 2
7. Biểu thức x xác định khi và chỉ khi: x +1 A. x > 1 − B. x ≥ 1 − C. x∈ R D. x ≥ 0
8. Rút gọn 4 − 2 3 ta được kết quả: A. 2 − 3 B. 1− 3 C. 3 −1 D. 3 − 2
9. Tính 17 − 33. 17 + 33 có kết quả là: A. 16 ± B. 256 ± C. 256 D. 16
10. Tính − 0,1. 0,4 kết quả là: A. 0,2 B. 0, − − 2 C. 4 D. 4 100 100 11. Biểu thức 2 − xác định khi : x −1 A. x >1 B. x ≥ 1 C. x < 1 D. x ≠ 0 3
12. Rút gọn biểu thức a với a > 0, kết quả là: a A. 2 a B. ±a C. a D. −a 3
13. Rút gọn biểu thức a với a < 0, ta được kết quả là: a A. a B. a2 C. −|a| D. −a
14. Căn bậc hai của 4 là A. -3. B. 2; -2 C. -4; 4 D. -81.
15. Căn bậc hai số học của 81 là A. -6. B. 5. C. 9. D. -5;5.
16. Biểu thức √121 bằng A. 81. B. -9; 9. C. -9. D. 11.
17: Giá trị biểu thức √2x + 1 khi x = 4: A. 5 B. -5 C. 3 D.24
18 Giá trị biểu thức �6y + 1 khi y = 4: a. 5 b. 20 c. 4 D. -4 19. Biểu thức 1 P =
xác định với mọi giá trị của x thoả mãn: x −1 A. x ≠ 1 B. x ≥ 0
C. x ≥ 0 và x ≠ 1 D. x < 1
20. Điều kiện xác định của biểu thức P(x) = x +10 là: A. x ≥ 10 − B. x ≤ 10 C. x ≤ 10 − D. x > 10 −
21. Điều kiện xác định của biểu thức 1− x là : A.x = 0 B. x ≤ 1 − C. x <1 D. x ≤1
22 Giá trị của biểu thức √x+1 khi x = 4 là √x−1 A. 6 B. 0 C. 3 D. 7
23: Phân tích đa thức x +2√x ta được kết qủa là A.x(√x + 2) B. √x. (x + 2) C. √x. �√x − 2� D. Đáp án khác
24. Trong hình bên, độ dài AH bằng: B A. 5 12 H B. 2, − 4 3 C. 2 D. 2,4 A 4 C
25. Cho ∆ABC có AH là đường cao xuất phát từ A (H ∈ BC) hệ thức
nào dưới đây chứng tỏ ∆ABC vuông tại A. A. BC2 = AB2 + AC2 B. AH2 = HB. HC C. AB2 = BH. BC D. A, B, C đều đúng
26. Cho ∆ABC có AH là đường cao xuất phát từ A (H ∈ BC). Nếu  0
BAC = 90 thì hệ thức nào dưới đây đúng: A. AB2 = AC2 + CB2 B. AH2 = HB. BC C. AB2 = BH. BC D. Không câu nào đúng 27. Cho AB ∆
C vuông tại A, có AB=3cm; AC=4cm. Độ dài đường cao AH là: A. 5cm B. 2cm C. 2,6cm D. 2,4cm 28. AB ∆
C vuông tại A có AB =2cm; AC =4cm. Độ dài đường cao AH là: A. 2 5 cm B. 5 cm C. 4 5 cm D. 3 5 cm 5 5 5
29. Cho tam giác ABC có B� = 450, C� = 300, AB = 6cm. Độ dài cạnh AC bằng A.6 2c . m cm B. 3 2 c . m C.12 2c . m D.12 . 2
30. Cho tam giác ABC vuông tại A ta có: cosC= ? A. AC B. AB BC BC C. AC D. AB AB AC
31. ∆ABC vuông tại A có AB = 3cm và. 𝐵𝐵� = 60° Độ dài cạnh AC là: A. 6cm B. 6 3 cm C. 3 3 D. Một kết quả khác
III. Dạng bài tham khảo 1. ĐẠI SỐ
Bài 1: Thực hiện phép tính:
a) A = ��4 − √5�2 + ��√5 + 10�2
b) A = ��1 − √3�2 − ��√3 + 3�2
c) B = 5 32 − 3 50 + 200 + 7 11− 6 2 d) 2 . √45 + √45 − 20�1 + √10. √2 3 √21 5  3 75  10  14 − 7 15 − 5  1 B = 2 45 − 20 +  :  +  : .   e) 2  15 3  f) 1− 2 1− 3 7 −   5  15 4 12   + − ( 6 + 11); g)  6 + 1 6 − 2 3 − 6 
Bài 2: Cho 2 biểu thức x + 3 x −1 5 x − 2 P = ;Q = + ; x > 0, x ≠ 4 x − 2 x + 2 x − 4
a) Tính giá trị của biểu thức P khi x = 9
b) Rút gọn biểu thức Q c) Tìm x để Q = 2
d) Tìm giá trị của x để biểu thức P đạt giá trị nhỏ nhất. Q
Bài 3: Cho hai biểu thức:
A = x + x + 4 và B = 3x − 4 x + 2 x −1 − + với x > 0; x ≠ 4. x − 2 x − 2 x x 2− x
a) Tính giá trị của biểu thức A khi x = 9.
b) Chứng minh B = x +1 x − 2 c) Tìm x để B = 3
d) Tìm giá trị của x để biểu thức A đạt giá trị nhỏ nhất. B x 1 5 x 2 Bài 4: Cho x 3 P  và Q   với x > 0, x ≠ 4. x 2 x  2 x4
a) Tính giá trị của P khi x  9 b) Rút gọn Q
c) Tìm các giá trị x nguyên để Q nguyên
d) Tìm x để P đạt GTNN Q
Bài 5: Cho biểu thức 1 A = và x −1 x + 2 10 −5 x B = + −
(x ≥ 0; x ≠ 4; x ≠ 9) 1+ x
x − 2 3− x x − 5 x + 6
a) Tính giá trị biểu thức A khi x = 25 . b) Chứng minh rằng 1 B = . x − 2 c) Tìm x đề B > 0
d) Tìm giá trị nhỏ nhất của biểu thức P = A : B.
Bài 6: Cho hai biểu thức: 2 x +1   A = và 2 x −5 x −1 B = − : 0 ≥ ≠ ≠  + − 
(x 0;x 1;x 9) x +3  x 3 x 9  x −3
a) Tính giá trị biểu thức A khi x = 49.
b) Rút gọn biểu thức B. c) Tìm x để A : B > 0
d) Tìm giá trị nhỏ nhất của biểu thức: M = A – 1 x + 3
Bài 7. Cho biểu thức P = � √𝒙𝒙 + 𝟏𝟏 � : 𝟐𝟐 𝒙𝒙−𝟒𝟒 √𝒙𝒙−𝟐𝟐 √𝒙𝒙−𝟐𝟐 1. Rút gọn P.
2. Tìm x để p = 4 5
3. So sánh P với 1
4. Tìm x để P < 2 √𝑥𝑥+1
5. Tìm GTNN của P
6. Tìm x nguyên để P nhận giá trị nguyên
Bài 8. Cho biểu thức P= � 𝟐𝟐 + 𝟏𝟏 � : √𝒙𝒙+𝟏𝟏 √𝒙𝒙−𝟑𝟑 √𝒙𝒙+𝟑𝟑 √𝒙𝒙−𝟑𝟑 1. Rút gọn P.
2. Tìm x để p= √𝑥𝑥 6
3. Tính P khi 2|𝑥𝑥 − 3| − 1 = 7
4. Tìm x để P < 1
5. Tìm GTLN của P
Bài 9: Cho biểu thức E= 𝑥𝑥+√𝑥𝑥 : �√𝑥𝑥+1 − 1 + 2−𝑥𝑥 � với 𝑥𝑥 ≥ 0, 𝑥𝑥 ≠ 1 𝑥𝑥−2√𝑥𝑥+1 √𝑥𝑥 1−√𝑥𝑥 𝑥𝑥−√𝑥𝑥 a) Rút gọn E b) Tìm x để E>1
c) Tìm GTNN của E với x>1
d) Tìm x∈ 𝑍𝑍 để E∈ 𝑍𝑍 e) Tìm x để E=9 2
Bài 10: cho biểu thức P=� 1 + √𝑥𝑥 � : √𝑥𝑥 với x>0 √𝑥𝑥 √𝑥𝑥+1 𝑥𝑥+√𝑥𝑥 a) Rút gọn P b) Tìm x để P=-1 c) Tính P tại x= 8 − 8 √5−1 √5+1
d) Tìm x để P> √𝑥𝑥 + 2 e) So sánh P với 1 f) Tìm GTNN của P 2. HÌNH HỌC
Bài 1: Cho tam giác ABC vuông tại A có cạnh AB =6cm, AC = 8cm, Kẻ đường cao AK.
Kẻ KE vuông góc với AB, KF vuông góc AC
a) Tính độ dài BC, AK, BK.
b) Chứng minh AEKF là hình chữ nhật
c) Chứng minh AE.AB =AF.AC
Bài 2: Cho tam giác ABC vuông tại A có cạnh AB =3cm, AC = 4cm, Kẻ đường cao AH.
Kẻ HE vuông góc với AB.
a) Tính độ dài AH, BH.
b) Chứng minh AE.AB = AC2 – HC2.
c) Chứng minh AE . AB = HB . HC = EH . AC.
Bài 3: Cho tam giác CDE nhọn, đường cao CH . Gọi M,N theo thứ tự là hình chiếu của H lên CD, CE . Chứng minh a) CD.CM=CE.CN;
b) Tam giác CMN đồng dạng với tam giác CED
Bài 4: Cho tam giác ABC có ba góc nhọn và AH là đường cao
a) Chứng minh 𝐴𝐴𝐵𝐵2 + 𝐶𝐶𝐶𝐶2 = 𝐴𝐴𝐶𝐶2 + 𝐵𝐵𝐶𝐶2
b) Gọi M,N theo thứ tự là hình chiếu của H lên AB, AC . Chứng minh AM.AB=AN.AC
Bài 5: Cho hình chữ nhật ABCD có AB=8cm, BC = 15cm .
a)Tính độ dài đoạn thẳng BD
b) Vẽ AH vuông góc với BD tại H. Tính độ dài đoạn thẳng AH
c)Đường thẳng AH cắt BC và DC lần lượt tại I và K . Chứng minh 𝐴𝐴𝐶𝐶2 = 𝐶𝐶𝐻𝐻. 𝐶𝐶𝐻𝐻
Bài 6. Cho tam giác ABC vuông tại A, đường cao AH. Cho biết BH=4cm, CH = 9cm. Gọi
D, E lần lượt là hình chiếu vuông góc của H trên các cạnh AB,AC.
a) Tính độ dài độ dài đoạn thẳng DE.
b) Các đường thẳng vuông góc với DE tại D và E lần lượt cắt BC tại M,N . Chứng minh MN=1 𝐵𝐵𝐶𝐶. 2
c) Tính diện tích tứ giác DENM.
Bài 7. Cho tam giác ABC vuông tại C, đường cao CK.
a) Cho biết AB= 10cm, AC = 8cm. Tính BC, CK, BK, AK.
b) Gọi H, I theo thứ tự là hình chiếu của K trên BC và AC. Chứng minh CB.CH=CA.CI
c) Gọi M là chân đường vuông góc kẻ từ K xuống IH. Chứng minh: 1 = 1 + 1 KM2 CH2 CI2
Bài 8. Cho tam giác ABC vuông tại A, có đường cao là AH ; HB= 9cm, HC = 16cm. a. Tính AB,AC,AH
b. Gọi D, E lần lượt là hình chiếu vuông góc của H trên AB, AC tứ giác ADHE là hình gì?
c. Tính chu vi và diện tích của tứ giác ADHE
Bài 9. Cho tam giác ABC vuông tại A biết AB=3cm, BC =5cm.
a. Giải tam giác vuông ABC (số đo góc làm tròn đến độ)
b. Từ B kẻ đường thẳng vuông góc với BC, đường thẳng này cắt đường thẳng AC tại D. c. Tính độ dài AD,BD.
d. Gọi E,F là hình chiếu của A trên BC, BD. Chứng minh BF.BD=BE.BC
Bài 10. Cho tam giác ABC vuông tại A, có AC>AB . Đường cao AH. Gọi D,E lần lượt là
hình chiếu của H trên AB,AC.
a. Chứng minh AD.AB=AE.AC và tam giác ABC đồng dạng với tam giác AED
b. Cho biết BH = 2cm, HC = 4,5cm. Tính độ dài đoạn thẳng DE.
c. Tính số đo góc ABC làm tròn đến độ.
d. Tính diện tích tam giác ADE.
Bài 11. Tứ giác MNEF vuông tại M, F có EF là đáy lớn, hai đường chéo ME và NF vuông góc với nhau tại O.
a. Cho biết MN = 9cm và MF = 12cm .Hãy i) Giải tam giác MNF ii) Tính MO, FO
iii) Kẻ NH vuông góc với EF tại H . Tính diện tích tam giác FNE . từ đó tính diện tích tam giác FOH
b. Chứng minh 𝑀𝑀𝑀𝑀2 = 𝑀𝑀𝑀𝑀. 𝑀𝑀𝐹𝐹
Bài 12. Cho tam giác DEF biết DE=6cm, DF=8cm, EF=10cm.
a) Chứng minh tam giác DEF là tam giác vuông.
b) Vẽ đường cao DK. Hãy tính DK, FK.
c) Giải tam giác cuông EDK
d) Vẽ phân giác trong DM của tam giác DEF . Tính các độ dài các đoạn thẳng ME, MF
e) Tính sinF trong các tam giác vuông DFK và DEF. từ đó suy ra ED.DF=DK.EF
Bài 13. Tính giá trị các biểu thức sau: a) 2 0 2 0 2 0 2 0 2 0 2 0 2 0
cos 15 + cos 25 + cos 35 + cos 45 + cos 55 + cos 65 + cos 75 . b) 2 0 2 0 2 0 2 0 2 0 2 0 2 0
sin 10 − sin 20 + sin 30 − sin 40 − sin 50 − sin 70 + sin 80 . c) 0 0 0 0 0
sin15 + sin 75 − cos15 − cos75 + sin30 d) 0 0 0 0
sin35 + sin67 − cos23 − cos55 e) 2 0 2 0 2 0 2 0
cos 20 + cos 40 + cos 50 + cos 70 f) 0 0 0 0
sin20 − tan 40 + cot 50 − cos70
Bài 14. Rút gọn các biểu thức sau: a) (1− cosα)(1+ cosα) b) 2 2 1+ sin α + cos α c) 2 sinα − sinα cos α d) 4 4 2 2
sin α + cos α + 2sin α cos α e) 2 2 2
tan α − sin a tan α f) 2 2 2 cos α + tan α cos α
Bài 15. Chứng minh các hệ thức sau: cosα 1+ sinα 2 2
(sinα + cosα) − (sinα − cosα) = b) = 4 a) 1−sinα cosα sinα.cosα
3. Bài toán ứng dụng thực tế)
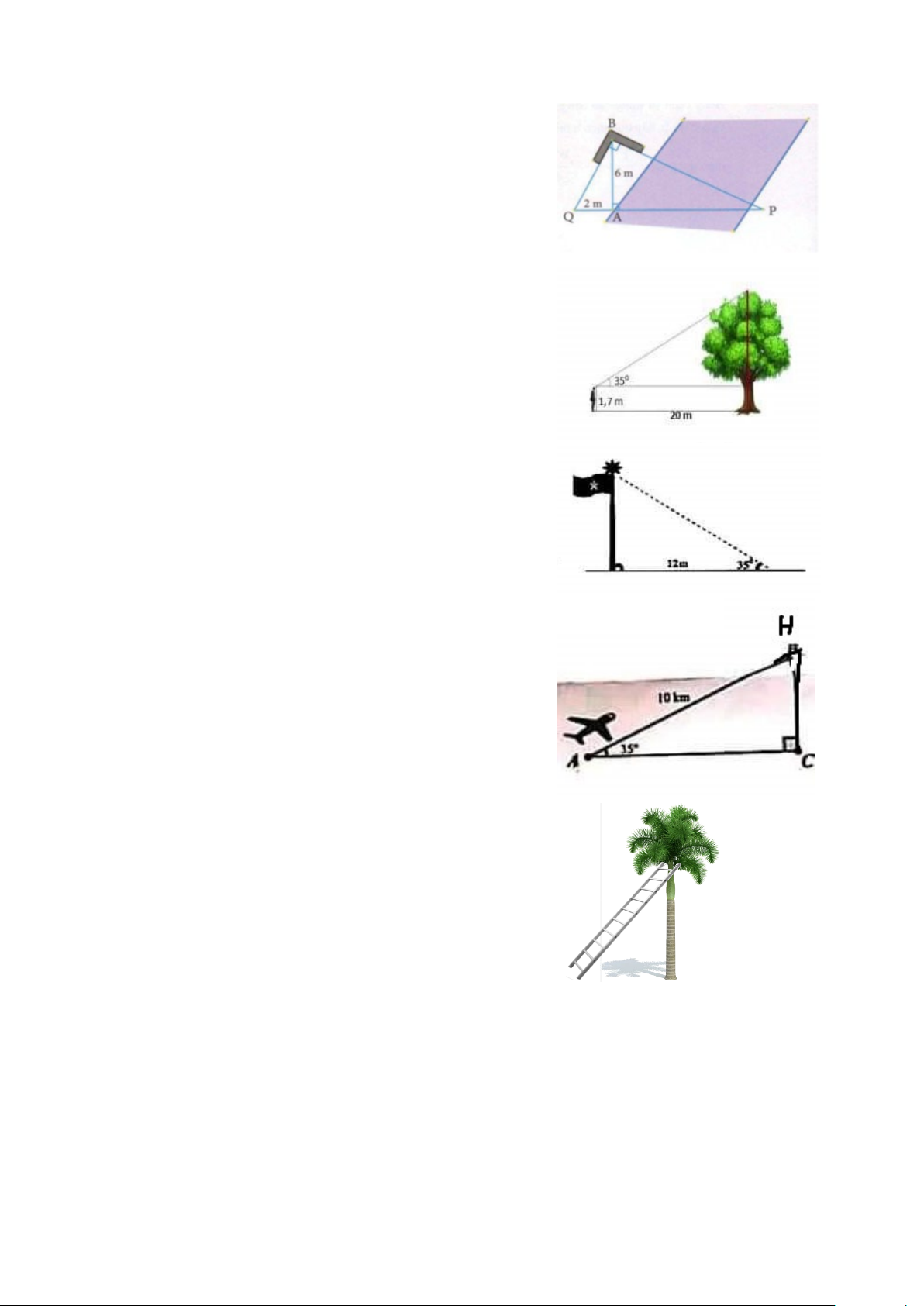
Bài 1. Hùng muốn tính khoảng cách AP nối hai
điểm ở hai bên bờ sông .Bạn ấy đặt đỉnh góc
vuông ê ke vào đầu điểm B của một cái sào BA
dài 6m. Nhìn theo hai cạnh góc vuông của ê ke
thì lần lượt thấy điểm Q và điểm P. Hùng đo thấy
đoạn QA dài 2m.Em hãy tính chiều dài AP .
Bài 2. Để đo chiều cao của một cái cây trong sân
trường một bạn học sinh đã dùng giác kế đứng
cách gốc cây một khoảng 20m thì nhìn thấy ngọn
cây bởi một góc 350. Tinh chiều cao của cây (hình
vẽ bên) biết bạn học sinh cao 1.7m
Bài 3. Một cột cờ vuông góc với mặt đất có bóng
dài 12m, tia nắng của mặt trời tạo với mặt đất một
góc là 350(hình bên).Tính chiều cao của cột cờ?
Bài 4. Hình vẽ bên minh họa một chiếc máy bay
đang cất cánh từ sân bay . Đường bay đang cất
cánh từ sân bay . Đường bay lên tạo với phương
nằm ngang một góc 350 . Hỏi khi bay được 10 km
thì máy bay có độ cao là bao nhiêu so với mặt đất
(làm tròn đến chữ thập phân thứ nhất)
Bài 5. Một cây cau có chiều cao 6m. Để hái một
buồn cau xuống, phải đặt thang tre sao cho đầu
thang tre đạt độ cao đó, khi đó góc của thang tre
với mặt đất là bao nhiêu, biết chiếc thang dài 8m
Ban giám hiệu xác nhận TT/NTCM duyệt Giáo viên lập
Nguyễn Xuân Lộc Nguyễn Đình Tuấn