

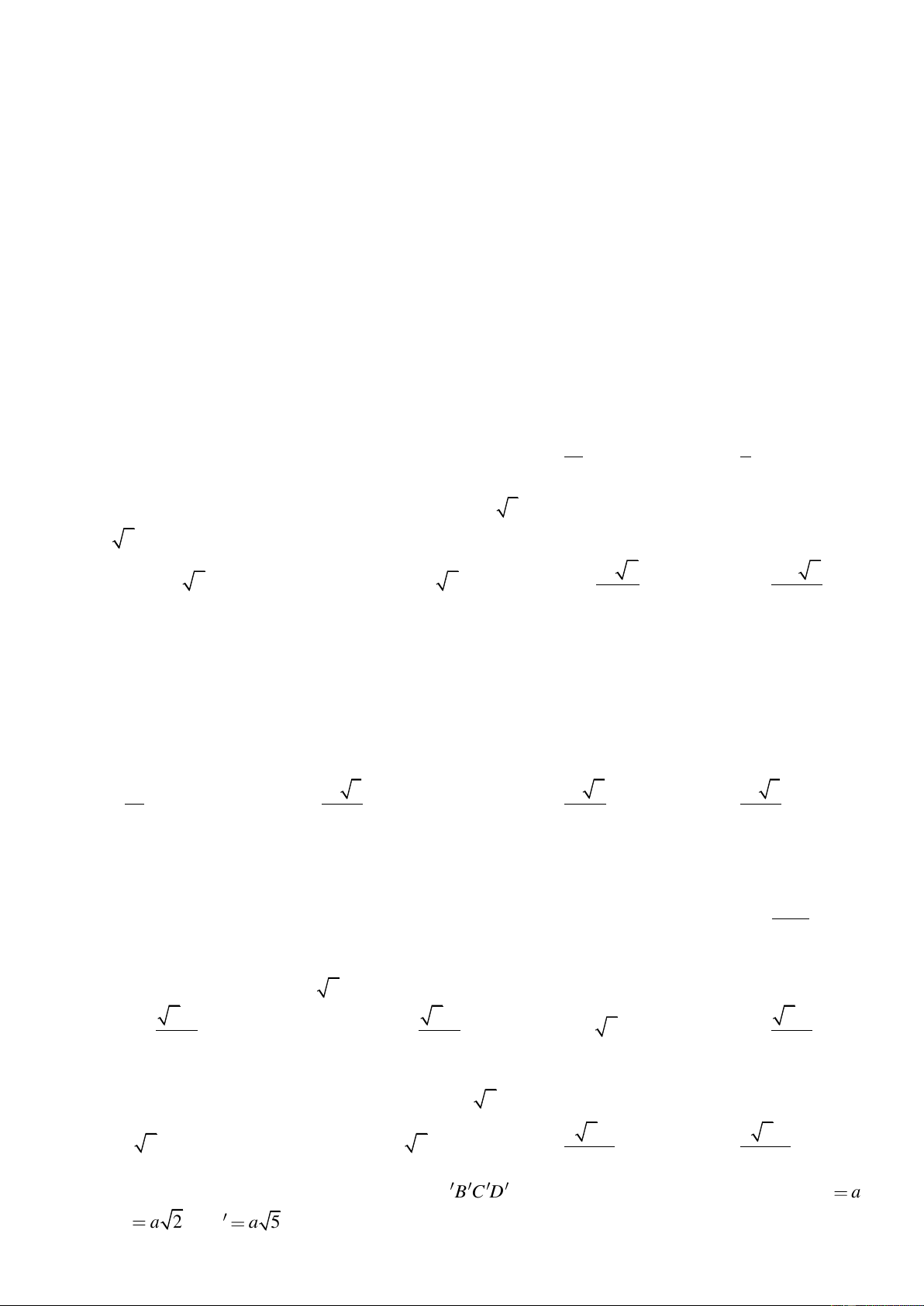

Preview text:
TRƯỜNG THPT HOÀNG VĂN THỤ
ĐỀ CƯƠNG ÔN GIỮA HỌC KỲ I MÔN TOÁN NĂM HỌC 2023- 2024 1. MỤC TIÊU
1.1. Kiến thức. Học sinh ôn tập các kiến thức về: Giải tích :
- Sự đồng biến, nghịch biến của hàm số - Cực trị của hàm số
- Giá trị lớn nhất, giá trị nhỏ nhất của hàm số
- Đường tiệm cận của đồ thị hàm số.
- Khảo sát sự biến thiên và vẽ đồ thị hàm số. Hình học :
- Hình đa diện, khối đa điện
- Khối đa diện lồi, khối đa diện đều.
- Thể tích khối đa diện.
1.2. Kĩ năng: Học sinh rèn luyện các kĩ năng:
- Tìm khoảng đồng biến nghịch biến, điểm cực trị, giá trị cực trị của hàm số, giá trị lớn nhất, giá trị nhỏ
nhất của hàm số, đường tiệm cận của đồ thị hàm số từ đồ thị, bảng biến thiên, hàm số.
- Tìm khoảng đồng biến, nghịch biến, cực trị của hàm số hợp.
- Tìm số nghiệm của phương trình từ đồ thị hoặc bảng biến thiên
- Tìm điều kiện của tham số để hàm số đồng biến trên (a;b) , nghịch biến trên (a;b) , có cực trị….
- Tìm điều kiện để đồ thị hàm số có k đường tiệm cận.
- Nhận biết hình- khối đa diện, hình – khối đa diện lồi, hình – khối đa diện đều.
- Biết cách tính thể tích của khối chóp, khối lăng trụ, khối đa diện. 2. NỘI DUNG
Mức độ nhận biết:
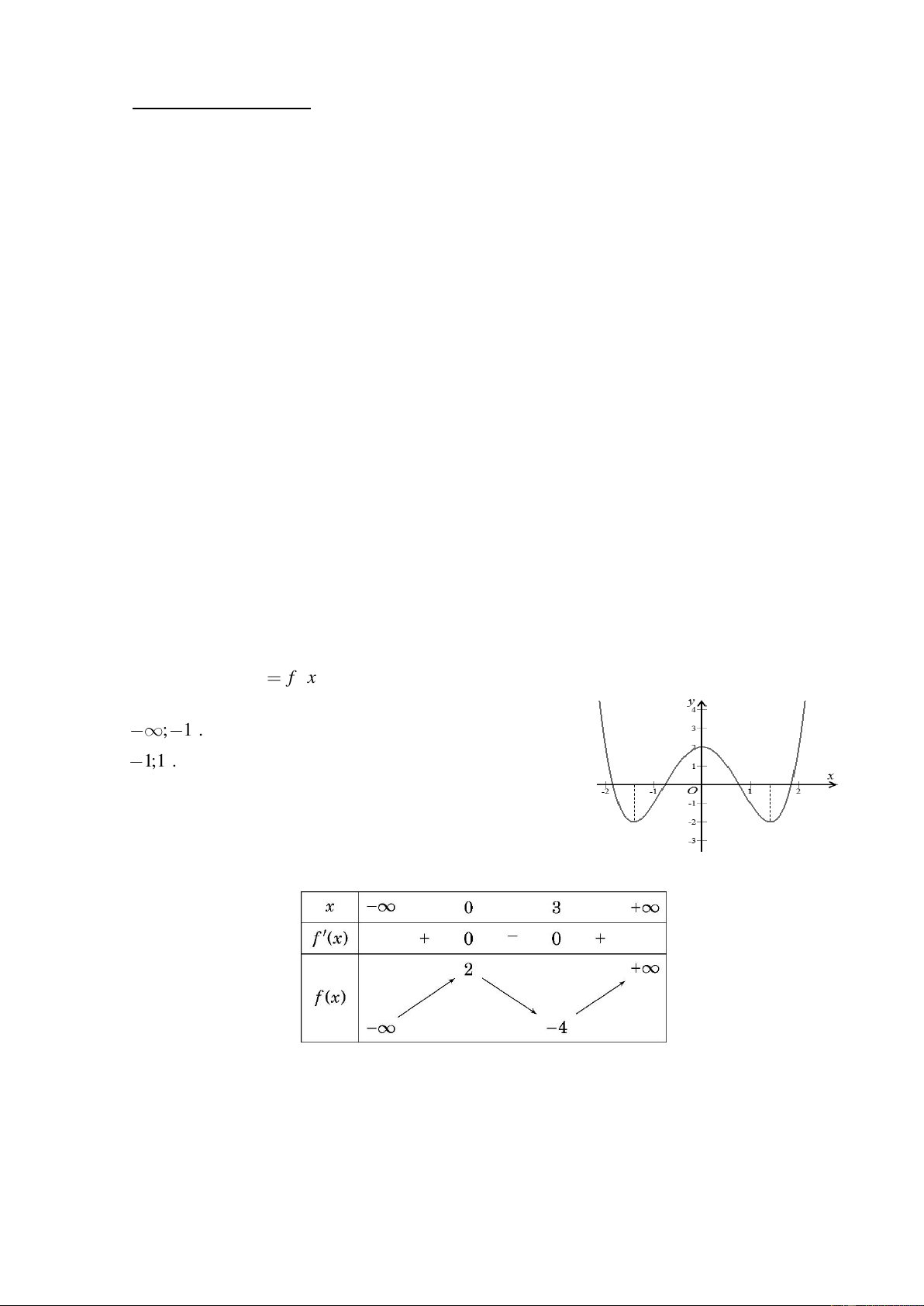
Câu 1: Cho hàm số y
f x có đồ thị như hình vẽ bên. Hàm số đã cho nghịch biến trên khoảng nào dưới đây? A. ; 1 . B. 1;1 . C. 1; 2 . D. 0;1 .
Câu 2: Cho hàm số y = f ( x) có bảng biến thiên như sau:
Giá trị cực tiểu của hàm số đã cho bằng A. 2 . B. 3 . C. 0 . D. 4 − .
Câu 3: Cho hàm số y = f ( x) xác định, liên tục trên đoạn 2
− ;2 và có đồ thị là đường cong trong
hình vẽ dưới đây. Hàm số f ( x) đạt cực đại tại điểm nào ? A. x = 2 − . B. x = 1 − .
C. x = 1 .
D. x = 2
Câu 4.Cho hàm số y = f (x) có bảng biến thiên như sau
Mệnh đề nào dưới đây đúng?
A. Hàm số đạt cực tiểu tại x = −5
B. Hàm số có bốn điểm cực trị
C. Hàm số đạt cực tiểu tại x = 2
D. Hàm số không có cực đại
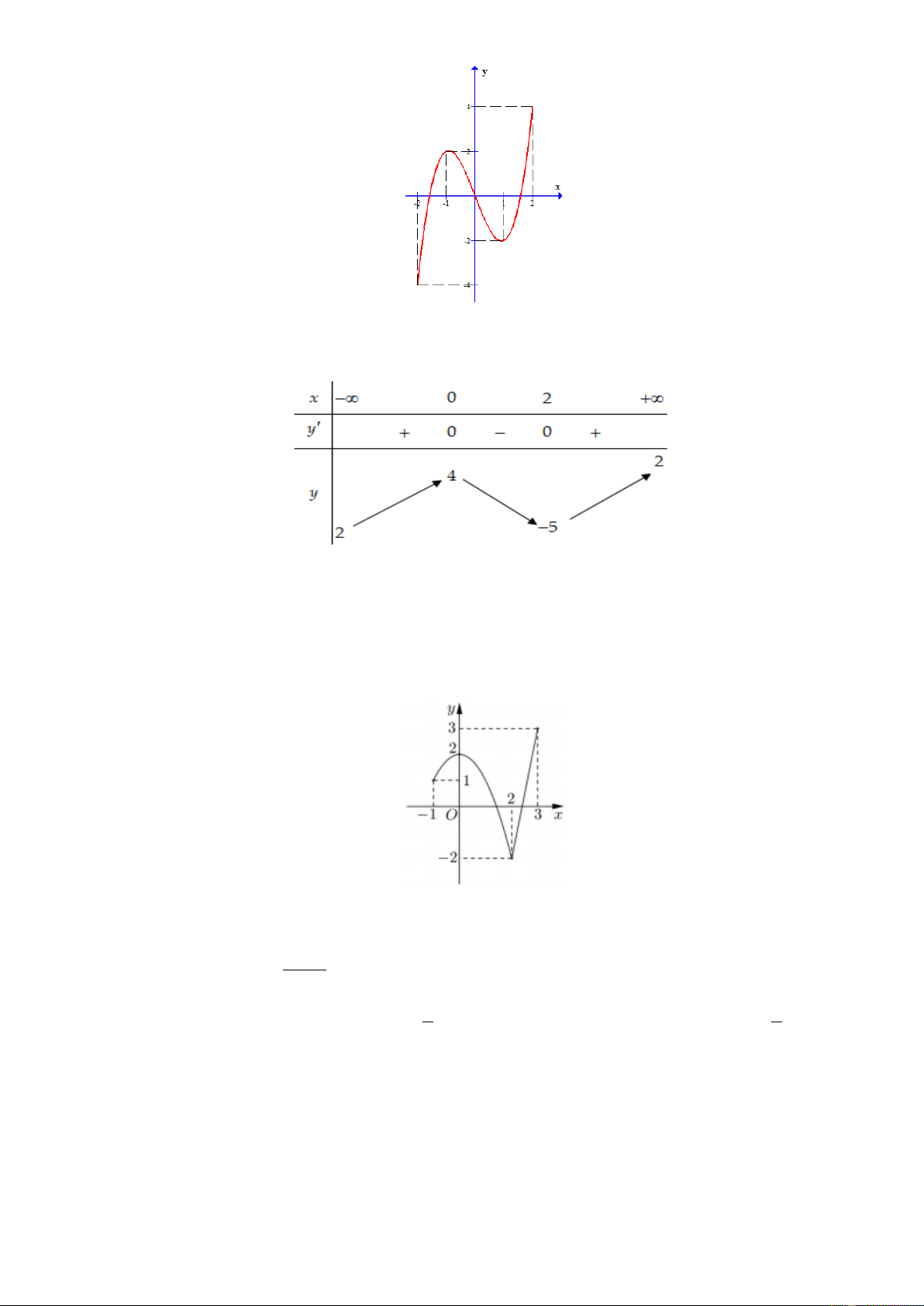
Câu 5: Cho hàm số y = f ( x) liên tục trên đoạn 1 − ;
3 và có đồ thị như hình vẽ dưới dây. Gọi M và
m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn 1 − ;
3 . Giá trị của M − m bằng A. 1 B. 4 C. 5 D. 0 3x +1
Câu 6: Cho hàm số y = 2x − .Khẳng định nào sau đây đúng? 1
A. Đồ thị hàm số có tiệm cận ngang là 3 y =
. B. Đồ thị hàm số có tiệm cận đứng là 3 y = . 2 2
C. Đồ thị hàm số không có tiệm cận. D. Đồ thị hàm số có tiệm cận đứng là x = 1 .
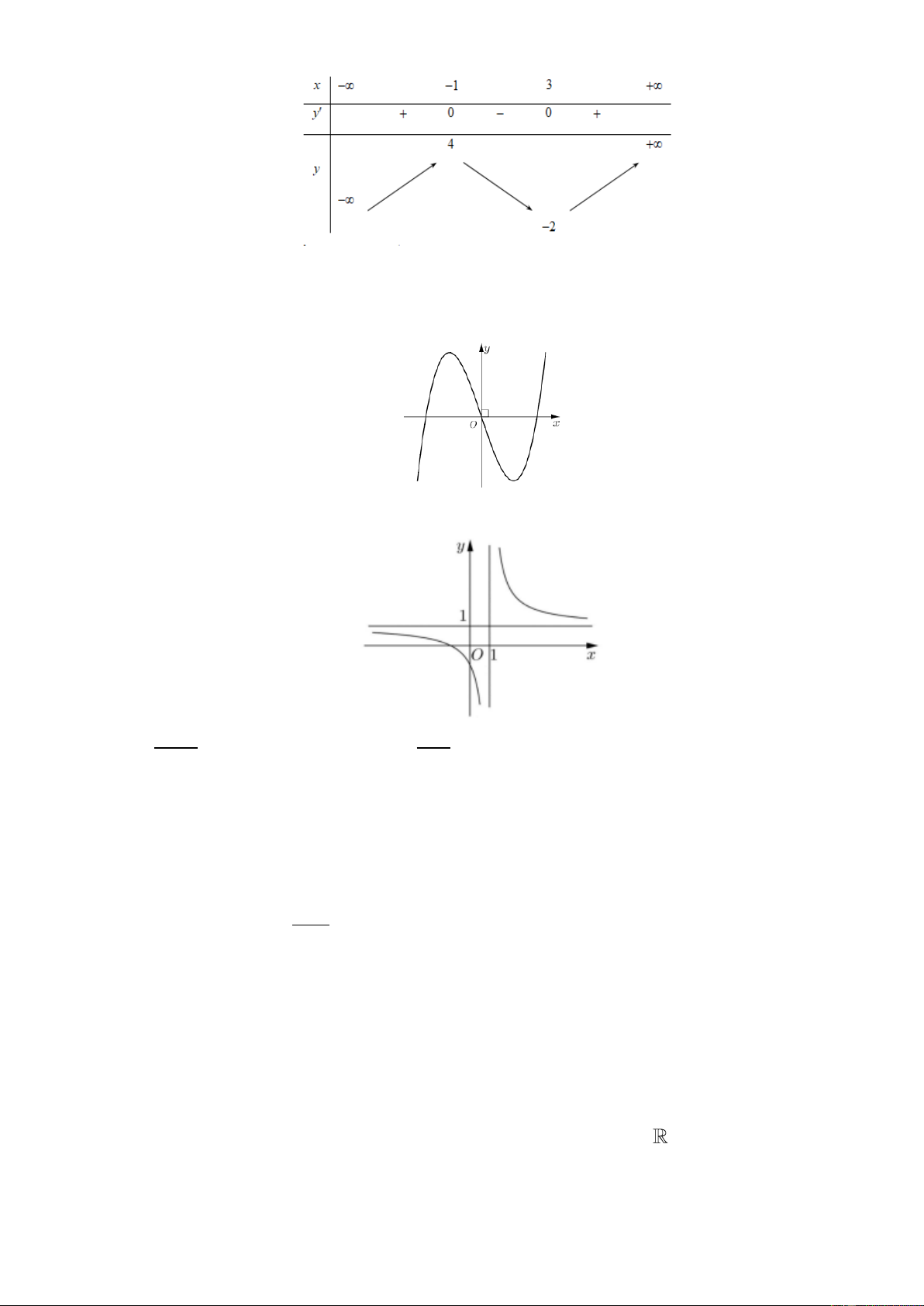
Câu 7: Cho hàm số y = f ( x) có bảng biến thiên như sau:
Số nghiệm của phương trình f ( x) − 2 = 0 là: A. 0 . B. 3 . C. 1. D. 2
Câu 8: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên? A. 3
y = x − 3x . B. 3
y = −x + 3x . C. 4 2
y = x − 2x . D. 4 2
y = −x + 2x .
Câu 9:Đường cong trong hình vẽ dưới đây là đồ thị của hàm số nào? 2x −1 x +1 A. y = y =
y = x + x + D. 3
y = x − 3x −1 x − B. 1 x − C. 4 2 1 1
Câu 10: Biết rằng đường thẳng y = 2
− x + 2 cắt đồ thị hàm số 3
y = x + x + 2 tại điểm duy nhất; kí hiệu
(x ; y là tọa độ của điểm đó. Tìm y 0 0 ) 0
A. y = 4
B. y = 0
C. y = 2 D. y = 1 − 0 0 0 0
Mức độ thông hiểu: x − 2
Câu 11: Cho hàm số y = x + . Mệnh đề nào dưới đây đúng? 1
A. Hàm số đồng biến trên khoảng (− ; +)
B. Hàm số nghịch biến trên khoảng ( 1 − ;+)
C. Hàm số nghịch biến trên khoảng (− ; − ) 1
D. Hàm số đồng biến trên khoảng (− ; − ) 1
Câu 12: Đồ thi hàm số nào sau đây có 3 điểm cực trị: A. 4 2
y = 2x + 4x +1 B. 4 2
y = x + 2x −1 C. 4 2
y = x − 2x −1 D. 4 2
y = −x − 2x −1.
Câu 13: Cho hàm số f ( x) có đạo hàm f ( x) = x( − x)( x + )3 1 4 , x
. Số điểm cực đại của hàm số đã cho là A. 3. B. 4 . C. 2 . D. 1.
Câu 14: Cho hàm số y = f ( x) có báng biến thiên như sau:
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là: A. 2. B. 3. C. 4. D. 1. 4
Câu 15: Tính giá trị nhỏ nhất của hàm số y = 3x +
trên khoảng (0; +) ? 2 x 33 A. 3 min y = 3 9 .
B. min y = 7 . C. min y = . D. 3 min y = 2 9 . (0;+) (0;+) (0;+) 5 (0;+)
Câu 16: Tìm giá trị nhỏ nhất m của hàm số y = 4 x − 2
x + 13 trên đoạn −2;3 .
A. m = 13
B. m = 51
C. m = 51 D. m = 49 4 2 4 2x + 4
Câu 17: Gọi M, N là giao điểm của đường thẳng y = x +1và đường cong y = . Khi đó hoành độ x −1
trung điểm I của đoạn thẳng MN bằng: 5 5 A. B. 2 C. 1 D. − 2 2 3 x
Câu 18: Tiếp tuyến của đồ thi hàm số 2 y =
+3x − 2 có hệ số góc k = 9 − ,có phương trình là: 3 A. y = 9 − x −11 B. y = 9 − x + 43 C. y = 9 − x − 43 D. y = 9 − x − 27 2x −1
Câu 19: Gọi M là giao điểm của đồ thị hàm số y =
với trục Oy. Phương trình tiếp tuyến với đồ x − 2 thị tại M là: 3 1 3 1 3 1 3 1 A. y = − x − . B. y = − x + . C. y = x + . D. y = x − . 4 2 4 2 4 2 4 2
Câu 20: Đạo hàm của hàm số y = ( x + x + )1 2 3 1 là 1 2x +1 2x +1 1 A. y = (x + x+ )8 2 3 1 .B. y = .C. y =
.D. y = ( x + x + )2 2 3 1 . 3 3 2 2 x + x +1 3 3 ( x + x + )2 2 3 1
Mức độ vận dụng:
Câu 21: Cho hàm số y = − 3 x − 2
mx + (4m + 9) x + 5 , với m là tham số. Hỏi có bao nhiêu giá trị
nguyên của m để hàm số nghịch biến trên khoảng (−; +) A. 5 B. 4 C. 6 D. 7 Câu 22: Hàm số 3
y = x − mx +1 có 2 cực trị khi: A. m 0 B. m = 0 C. m 0 D. m 0 1
Câu 23: Tìm giá trị thực của tham số m để hàm số 3 2 y = x − mx + ( 2
m − 4) x + 3 đạt cực đại 3 tại x = 3 . A. m = 1 − B. m = 7 −
C. m = 5 D. m = 1 x + m 16
Câu 24: Cho hàm số y =
( m là tham số thực) thoả mãn min y + max y = . Mệnh đề nào x + 1 1;2 1;2 3 dưới đây đúng?
A. 0 m 2 .
B. 2 m 4 .
C. m 0 .
D. m 4 .
Câu 25: Cho hàm số f ( x) 3 = x + ( 2 m + ) 2
1 x + m − 2 với m là tham số thực. Tìm tất cả các giá trị của
m để hàm số có giá trị nhỏ nhất trên đoạn 0;2 bằng 7. A. m = 1 . B. m = 7 . C. m = 2 . D. m = 3 .
Câu 26: Số tiếp tuyến đi qua điểm A ( 1; - 6) của đồ thi hàm số 3
y = x − 3x +1 là: A. 1 B. 0 C. 2 D. 3
Câu 27: Trong các tiếp tuyến tại các điểm trên đồ thị hàm số 3 2
y = x − 3x + 2 , tiếp tuyến có hệ số góc nhỏ nhất bằng A. - 3 B. 0 C. - 4 D. 3 Câu 28: Cho hàm số 3 2
y = x − 3x +1. Đồ thị hàm số cắt đường thẳng y = m tại 3 điểm phân biệt khi: A. 3 − m 1 B. 3 − m 1 C. m 1 D. m 3 −
Câu 29: Tìm tất cả các giá trị thực của tham số m để đường thẳng y = m
− x cắt đồ thị của hàm số 3 2
y = x − 3x − m + 2 tại ba điểm phân biệt ,
A B,C sao cho AB = BC . A. m (− ; − ) 1
B. m (− : +)
C. m (1: +) D. m (− ;3 )
Câu 30: Một đoàn tàu chuyển động thẳng khởi hành từ một nhà ga. Quãng đường s (mét) đi được của
đoàn tàu là một hàm số của thời gian t (phút), hàm số đó là s = 6t2 – t3. Thời điểm t ( giây) mà tại đó
vận tốc v (m/s) của chuyển động đạt giá trị lớn nhất là: A. t = 4s. B. t = 2s. C. t = 6s D. t = 8s
Mức độ vận dụng cao: Câu 31: Cho hàm số 4 2
y = ax + bx + c ( a 0 ) có đồ thị như hình vẽ dưới đây.
Mệnh đề nào dưới đây đúng?
A. a 0 , b 0 , c 0 .
B. a 0 , b 0 , c 0 . C. a 0 , b 0 , c 0 . D. a 0 , b 0 , c 0 . ax + b
Câu 32: Đường cong ở hình sau là đồ thị của hàm số y =
với a,b,c,d là các số thực. Mệnh đề cx + d nào dưới đây đúng?
A. y 0,x 1
B. y 0, x 1
C. y 0, x 2
D. y 0, 2
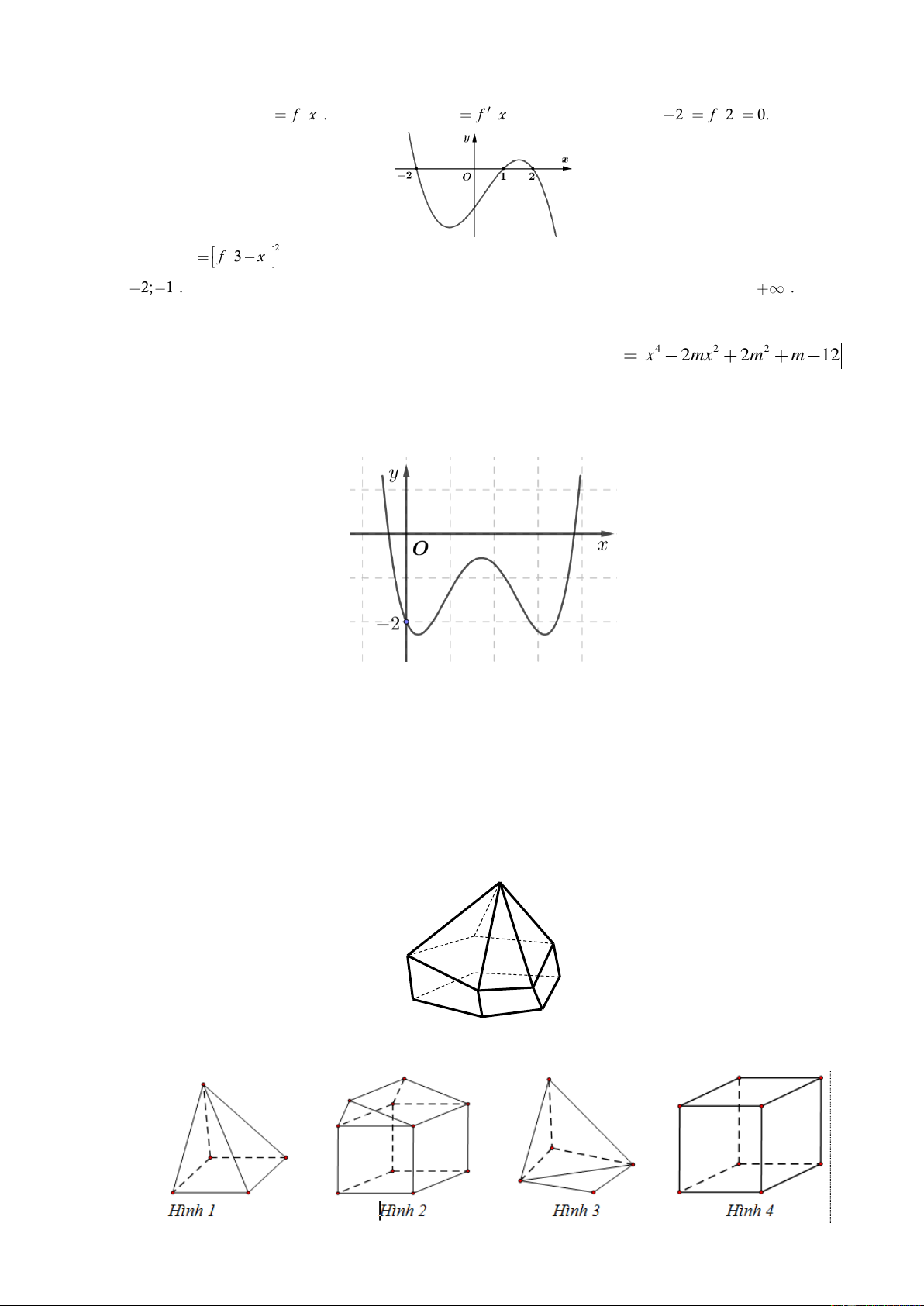
Câu 33: Cho hàm số y
f x . Đồ thị hàm số y
f x như hình sau và f 2 f 2 0. Hàm số 2 g x f 3 x
nghịch biến trên khoảng nào trong các khoảng sau? A. 2; 1 . B. 1;2 . C. 2;5 . D. 5; .
Câu 34. Tìm số các giá trị nguyên của tham số m để đồ thị hàm số 4 2 2 y x 2mx 2m m 12 có bảy điểm cực trị A. 1. B. 4 . C. 0 . D. 2 .
Câu 35. Cho hàm số bậc bốn y = f ( x) có đồ thị là đường cong trong hình vẽ bên.
Số nghiệm thực phân biệt của phương trình f ( 2
x f (x)) + 2 = 0 là A. 8 . B. 12 . C. 6 . D. 9 . HÌNH HỌC.
Mức độ nhận biết:
Câu 1. Cho khối đa diện đều. Khẳng định nào sau đây là sai?
A. Số đỉnh của khối lập phương bằng 8 .
B. Số mặt của khối tứ diện đều bằng 4 .
C. Khối bát diện đều là loại 4; 3 .
D. Số cạnh của khối bát diện đều bằng 12 .
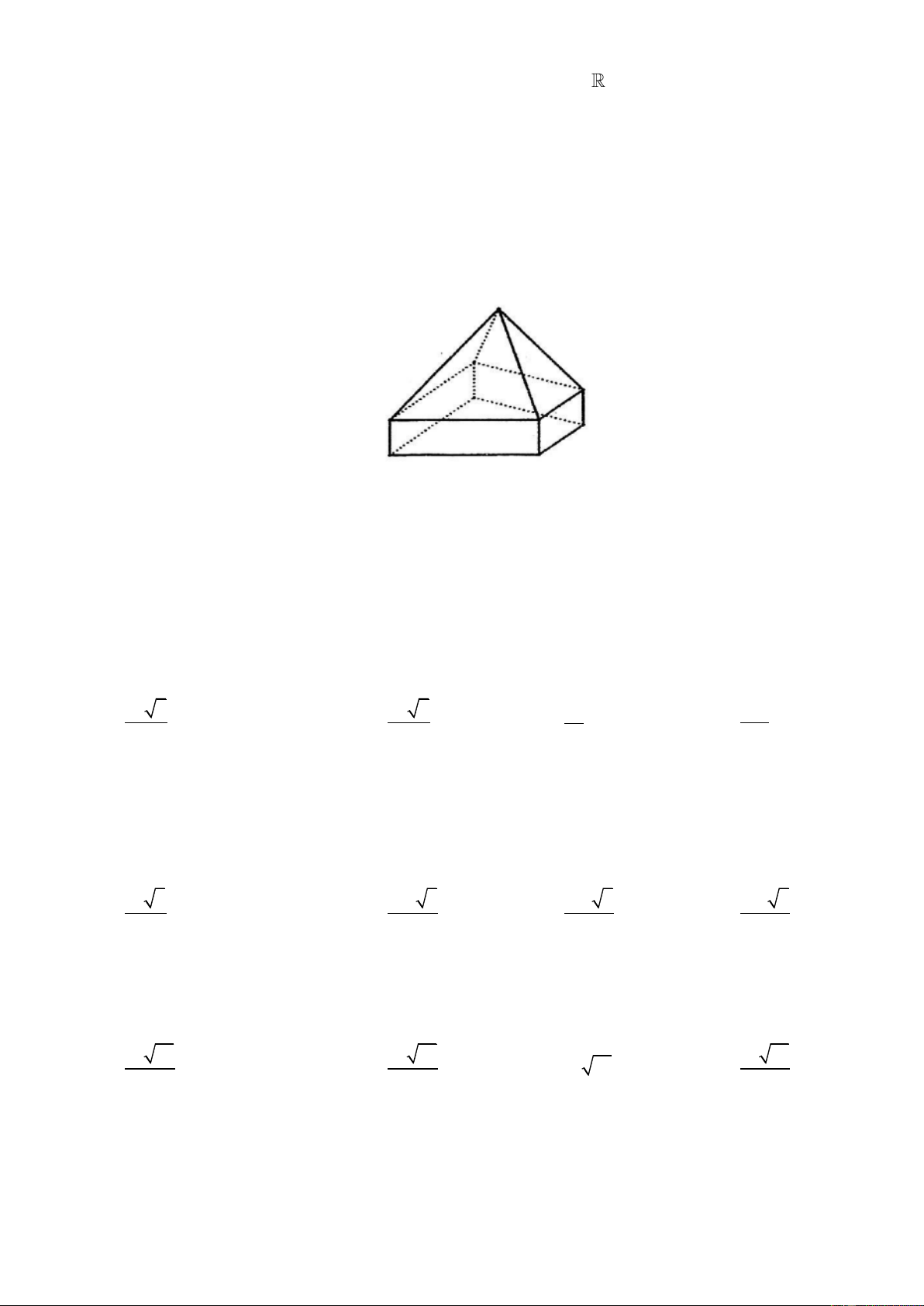
Câu 2. Hình đa diện trong hình vẽ có bao nhiêu mặt?
A. 12 B. 11 C. 6 D. 10
Câu 3. Hình nào dưới đây không phải là hình đa diện? A. Hình 3 . B. Hình 2 . C. Hình 4 . D. Hình 1.
Câu 4. Cho khối chóp có diện tích đáy B = 6 và chiều cao h = 2 . Thể tích của khối chóp đã cho bằng: A. 6 . B. 3 . C. 4 . D. 12 .
Câu 5.Cho khối chóp có diện tích đáy 2
B = 6a và chiều cao h = 2a . Thể tích khối chóp đã cho bằng: A. 3 2a . B. 3 4a . C. 3 6a . D. 3 12a .
Câu 6.Cho khối lập phương có cạnh bằng 6 . Thể tích của khối lập phương đã cho bằng A. 216 . B. 18 . C. 36 . D. 72 .
Câu 7.Thể tích khối lập phương cạnh 2 bằng A. 6 . B. 8 . C. 4 . D. 2 .
Câu 8. Cho khối hộp chữ nhật có 3 kích thước 3; 4;5 . Thể tích của khối hộp đã cho bằng? A. 10 . B. 20 . C. 12 . D. 60 .
Câu 9.Cho khối lăng trụ có đáy là hình vuông cạnh a và chiều cao bằng 4a . Thể tích của khối lăng trụ đã cho bằng 16 4 A. 3 16a B. 3 4a C. 3 a D. 3 a 3 3
Câu 10.Cho khối lăng trụ có diện tích đáy bằng 2 a
3 , khoảng cách giữa hai đáy của lăng trụ bằng
a 6 . Tính thể tích V của khối lăng trụ 3 a 2 3 3a 2 A. 3 V = 3a 2 B. 3 V = a 2 C. V = D. V = 3 4
Mức độ thông hiểu:
Câu 11. Hình hộp chữ nhật có ba kích thước đôi một khác nhau có bao nhiêu mặt phẳng đối xứng? A. 6 mặt phẳng
B. 9 mặt phẳng
C. 3 mặt phẳng
D. 4 mặt phẳng
Câu 12. Hình lăng trụ tam giác đều có tất cả các cạnh bằng nhau có bao nhiêu mặt phẳng đối xứng?
A. 4 . B. 3 . C. 5 . D. 6 .
Câu 13. Cho khối chóp tứ giác đều có tất cả các cạnh đều bằng a thì thể tích của khối chóp đó là: 3 a 3 a 3 3 a 2 3 a 3 A. B. C. D. 2 4 6 2
Câu 14. Cho tứ diện ABCD có AD vuông góc với mặt phẳng ( ABC) biết đáy ABC là tam giác vuông
tại B và AD =10, AB =10, BC = 24 . Tính thể tích của tứ diện ABCD . 1300 A. V =1200 B. V = 960 C. V = 400 D. V = 3
Câu 15. Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông cạnh a , cạnh bên SA vuông góc
với mặt phẳng đáy và SA = a 2 . Tính thể tích V của khối chóp S.ABCD 3 2a 3 2a 3 2a A. V = B. V = C. 3 V = 2a D. V = 6 4 3
Câu 16. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = 3a và AD = 4a . Cạnh bên
SA vuông góc với mặt phẳng ( ABCD) và SA = a 2 . Thể tích của khối chóp S.ABCD bằng 3 4 2a 3 2 2a A. 3 4 2a . B. 3 12 2a . C. . D. . 3 3
Câu 17. Cho hình lăng trụ đứng ABC .
D A B C D có đáy ABCD là hình chữ nhật, AB a , AD a 2 , AB
a 5 (tham khảo hình vẽ). Tính theo a thể tích V của khối lăng trụ đã cho. 3 2a 2 A. 3 V a 2 . B. 3 V 2a 2 . C. 3 V a 10 . D. V . 3
Câu 18. Lăng trụ tam giác đều có độ dài tất cả các cạnh bằng 3. Thể tích khối lăng trụ đã cho bằng: 27 3 9 3 9 3 27 3 A. . B. . C. . D. .. 4 2 4 2
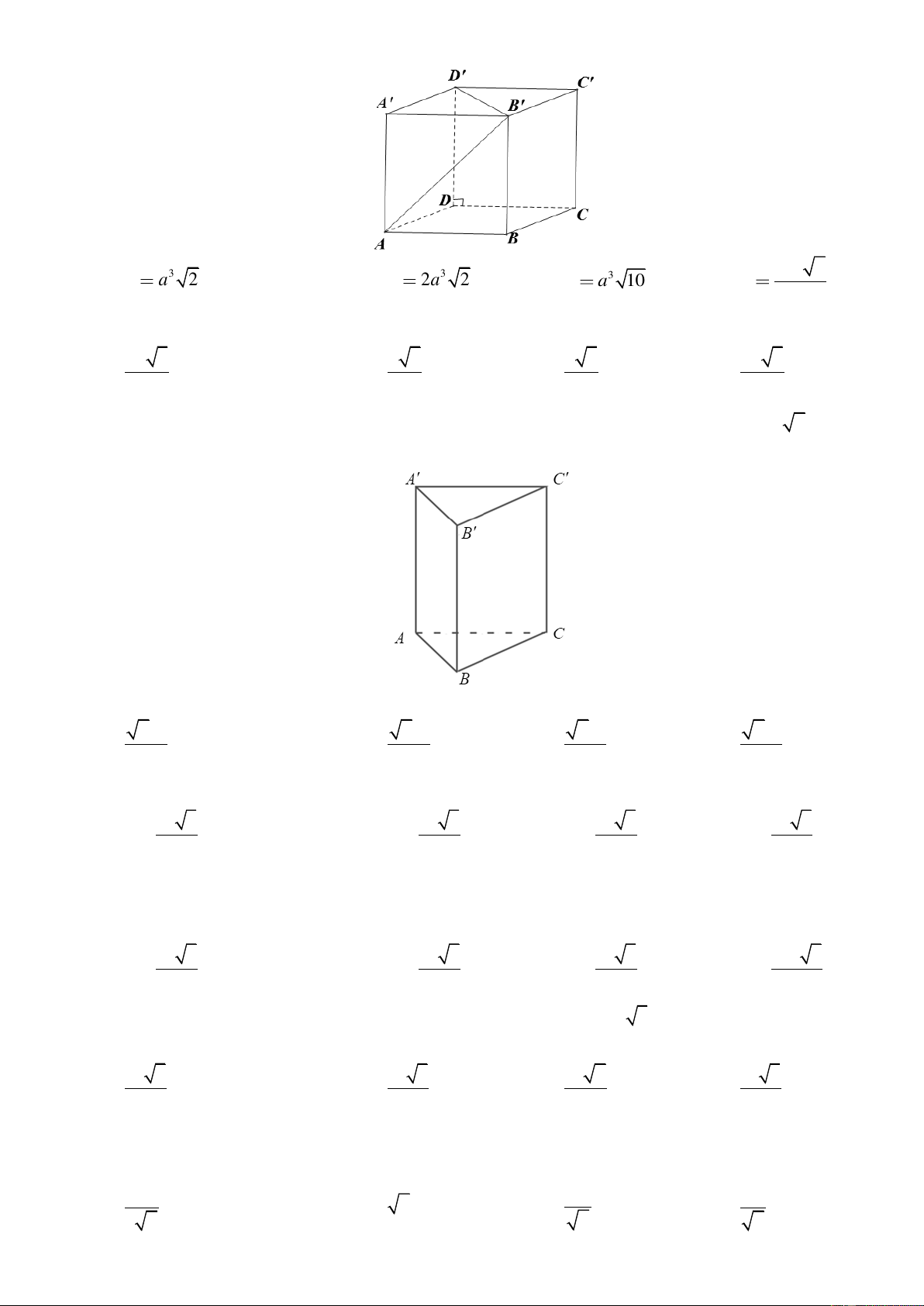
Câu 19. Cho khối lăng trụ đứng AB . C A B C
có đáy là tam giác đều cạnh a và AA' = 2a (minh
họa như hình vẽ bên dưới).
Thể tích của khối lăng trụ đã cho bằng 3 6a 3 6a 3 6a 3 6a A. . B. . C. . D. . 2 4 6 12
Câu 20. Thể tích của khối lăng trụ tam giác đều có tất cả các cạnh bằng a . 3 a 3 3 a 3 3 a 3 3 a 3 A. V = B. V = C. V = D. V = 12 2 4 6
Mức độ vận dụng:
Câu 21. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B và AB = 2a . Tam giác
SAB đều và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích V của khối chóp S.ABC 3 a 3 3 a 3 3 a 3 3 2a 3 A. V = B. V = C. V = D. V = 4 3 12 3
Câu 22. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA = a 3 ⊥ và SA ( ABCD) , H là hình
chiếu của A trên cạnh SB. Thể tích khối chóp S.AHC là: 3 a 3 3 a 3 3 a 2 3 a 3 A. B. C. D. 8 6 8 12
Câu 23. Cho khối chóp có đáy hình thoi cạnh a (a 0) các cạnh bên bằng nhau và cùng tạo với đáy
góc 45 . Thể tích của khối chóp đã cho bằng 1 3 3a 1 A. 3 a . B. 3 2a . C. . D. 3 a . 3 2 2 2
Câu 24. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a 6 , góc giữa cạnh bên và mặt đáy bằng 0
60 . Tính thể tích V của khối chóp S.ABC? A. 3 V = 9a B. 3 V = 2a C. 3 V = 3a D. 3 V = 6a
Câu 25. Khối chóp S.ABC có đáy ABC là tam giác vuông cân tại A, AB = 2a. SA vuông góc với mặt
phẳng (ABC) và SA = 2a. Khoảng cách từ C đến mặt phẳng (SAB) tính theo a bằng: a a A. B. 3a C. 2a D. 2 3
Câu 26.Cho hình chóp S.ABC . Gọi M , N , P lần lượt là trung điểm của S ,
A SB, SC . Tỉ số thể tích VS.ABC bằng VS.MNP A. 12 . B. 2 . C. 8 . D. 3 .
Câu 27.Cho hình hộp ABC . D A B C D
có thể tích bằng V . Thể tích của khối tứ diện ACB D bằng: V V V V A. B. C. D. 2 3 4 6
Câu 28. Cho hình chóp .
S ABCD . Gọi A , B , C , D theo thứ tự là trung điểm của SA , SB , SC , SD .
Tính tỉ số thể tích của hai khối chóp . S A B C D và . S ABCD . 1 1 1 1 A. B. C. D. 16 4 8 2
Câu 29. Kim tự tháp Kê - ốp ở Ai Cập được xây dựng vào khoảng 2500 năm trước Công nguyên. Kim
tự tháp này là một khối chóp tứ giác đều có chiều cao là 147 m , cạnh đáy là 230 m . Thể tích của nó là A. 3 2592100 m . B. 3 2952100 m . C. 3 2529100 m . D. 3 2591200 m .
Câu 30. Cho hình chóp S.ABC . Gọi M , N , P theo thứ tự là trung điểm của SA , SB , SC . Tính tỉ số
thể tích của 2 khối chóp S.MNP và S.ABC bằng 1 1 1 1 A. . B. . C. . D. . 4 8 16 2
Mức độ vận dụng cao:
Câu 31. Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng 2a . Tam giác SAB cân tại S và 3
nằm trong mặt phẳng vuông góc với đáy 4a
. Biết thể tích khối chóp S.ABCD bằng . Gọi là góc 3
giữa SC và mặt đáy, tính tan . 3 2 5 7 5 A. tan = . B. tan = . C. tan = . D. tan = . 3 5 7 5
Câu 32. Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và D , AB = AD = a , CD = 2a .
Hình chiếu của đỉnh S lên mặt ( ABCD) trùng với trung điểm của BD. Biết thể tích tứ diện SBCD 3
bằng a . Khoảng cách từ đỉnh A đến mặt phẳng (SBC) là: 6 a 3 a 2 a 3 a 6 A. B. C. D. 2 6 6 4
Câu 33. Cho hình chóp S.ABC có 0
AB = a, BC = a 3, ABC = 60 . Hình chiếu vuông góc của S lên
mặt phẳng ( ABC) là một điểm thuộc cạnh BC . Góc giữa đường thẳng SA và mặt phẳng ( ABC) là 0
45 . Giá trị nhỏ nhất của thể tích khối chóp S.ABC bằng 3 a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 3 8 12 6 1
Câu 34. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B , BC = AD = a . 2
Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy, góc giữa SC và mặt phẳng ( ABCD) bằng 15 sao cho tan =
. Tính thể tích khối chóp S.ACD theo a . 5 3 a 3 a 3 a 2 3 a 3 A. V = . B. V = . C. V = . D. V = . S . ACD 2 S . ACD 3 S . ACD 6 S . ACD 6
Câu 35. Cho hình khối tứ diện ABCD có cạnh AB = x ; x 0 , các cạnh còn lại đều bằng 2 3 . Tìm
x để khối tứ diên ABCD có thể tích đạt giá trị lớn nhất. 3 a 3 a 3 a 2 3 a 3 A. V = . B. V = . C. V = . D. V = . S . ACD 2 S . ACD 3 S . ACD 6 S . ACD 6
2.3.Ma trận đề minh họa
Mức độ nhận thức Tổng Nội Vận dụng dung Đơn vị kiến
Nhận biết Thông hiểu Vận dụng Số câu Tổng TT kiến thức cao Thờ i % thức
Số Thời Số Thời Số Thời Số Thời gian TN TL
câu gian câu gian câu gian câu gian Đơn điệu 1 2 1 4 10 Cực trị 1 2 1 1 5 12,5 Giải Max, min 1 2 1 1 5 12,5 1 tích Tiệm cận 1 2 1 4 10 Khảo sát sự biến thiên và vẽ đồ 2 3 3 2 10 25 thị hàm số Hình- Khối đa diện 1 1 2,5 Hinh Khối đa diện lồi, 2 học 1 1 2,5 khối đa diện đều Thể tích khối đa diện 3 4 2 1 10 25 2.4. Đề minh họa
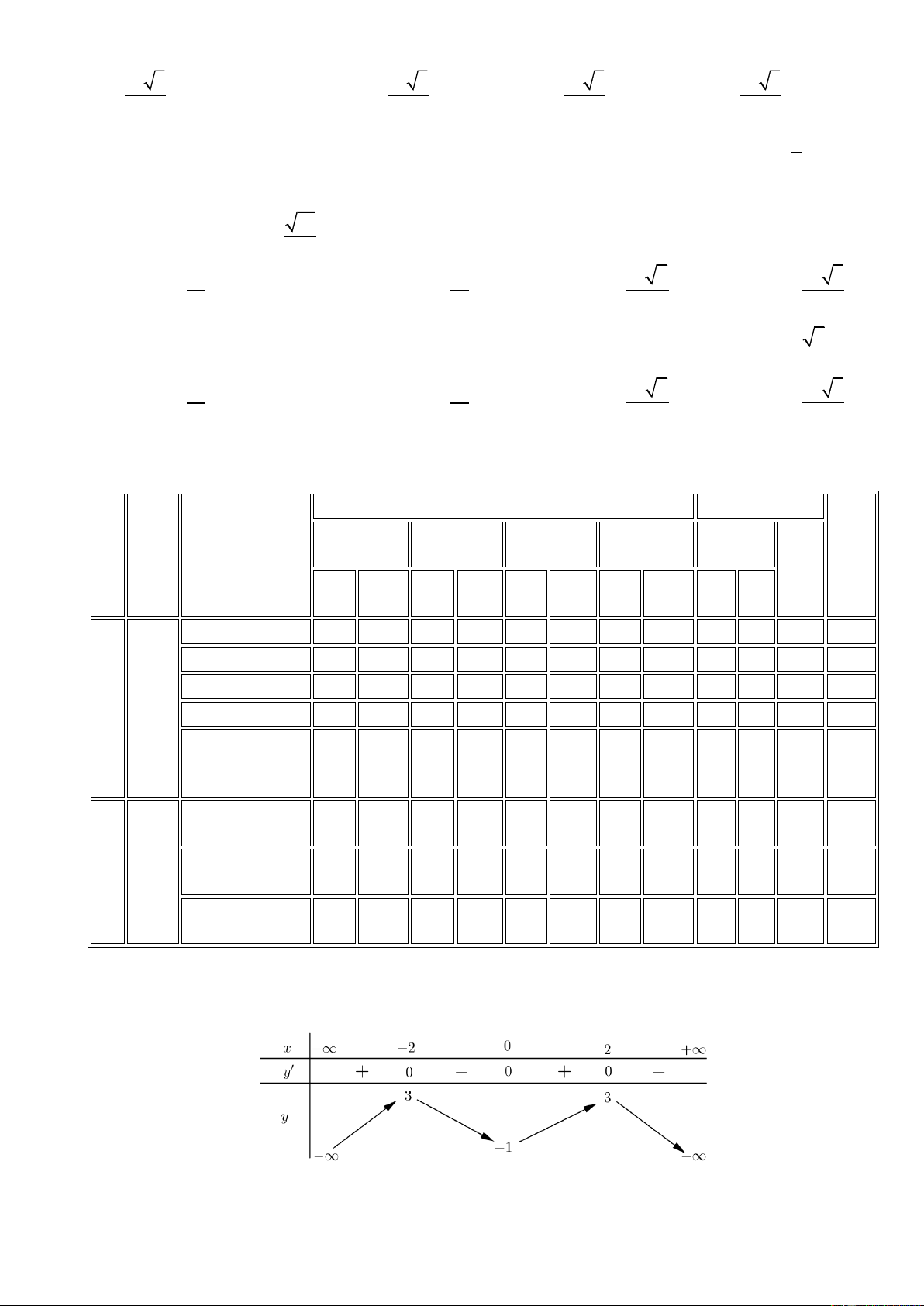
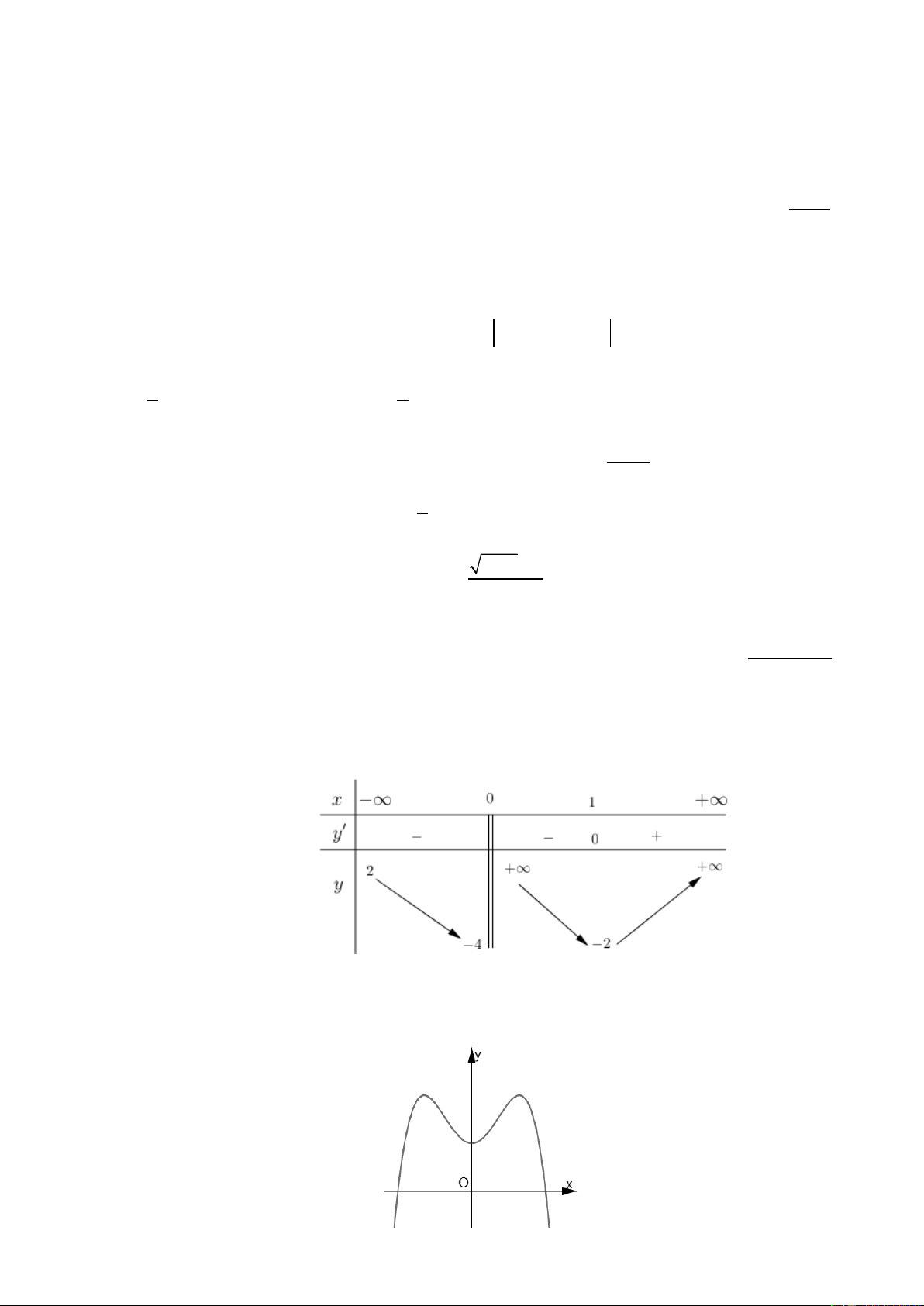
Câu 1.Cho hàm số f (x) có bảng biến thiên như hình vẽ sau
Hàm số f (x) đồng biến trên khoảng nào dưới đây? A. (0; 2). B. ( 2 − ;0). C. ( 2 − ;2). D. ( ; − 3). Câu 2. Cho hàm số 3 2
y = x − 2x + x +1. Mệnh đề nào dưới đây đúng? 1
A. Hàm số nghịch biến trên khoảng (1; +)
B. Hàm số nghịch biến trên khoảng ;1 3 1 1
C. Hàm số nghịch biến trên khoảng ; −
D. Hàm số đồng biến trên khoảng ;1 3 3
Câu 3.Trong các hàm số dưới đây, hàm số nào nghịch biến trên các khoảng xác định của nó? 2x − 3 A. 4
y = −x . B. 3 2
y = −x + 3x − 2021. C. y =
y = −x − x + . x + . D. 3 3 2022 1 1
Câu 4. Tìm tập hợp tất cả các giá trị của tham số thực m để hàm số 3 2 y =
x + mx + 4x − m đồng biến 3 trên khoảng (− ; +) . A. 2 − ;2. B. ( ; − 2) . C. (− ; 2 − .
D. 2; +) .
Câu 5. Cho hàm số y = f ( x) có đạo hàm f ( x) = ( x − )( x + )2 ' 1 2 3 x
. Hàm số y = f (x) có bao nhiêu điểm cực trị? A. 1. B. 3. C. 0. D. 2.
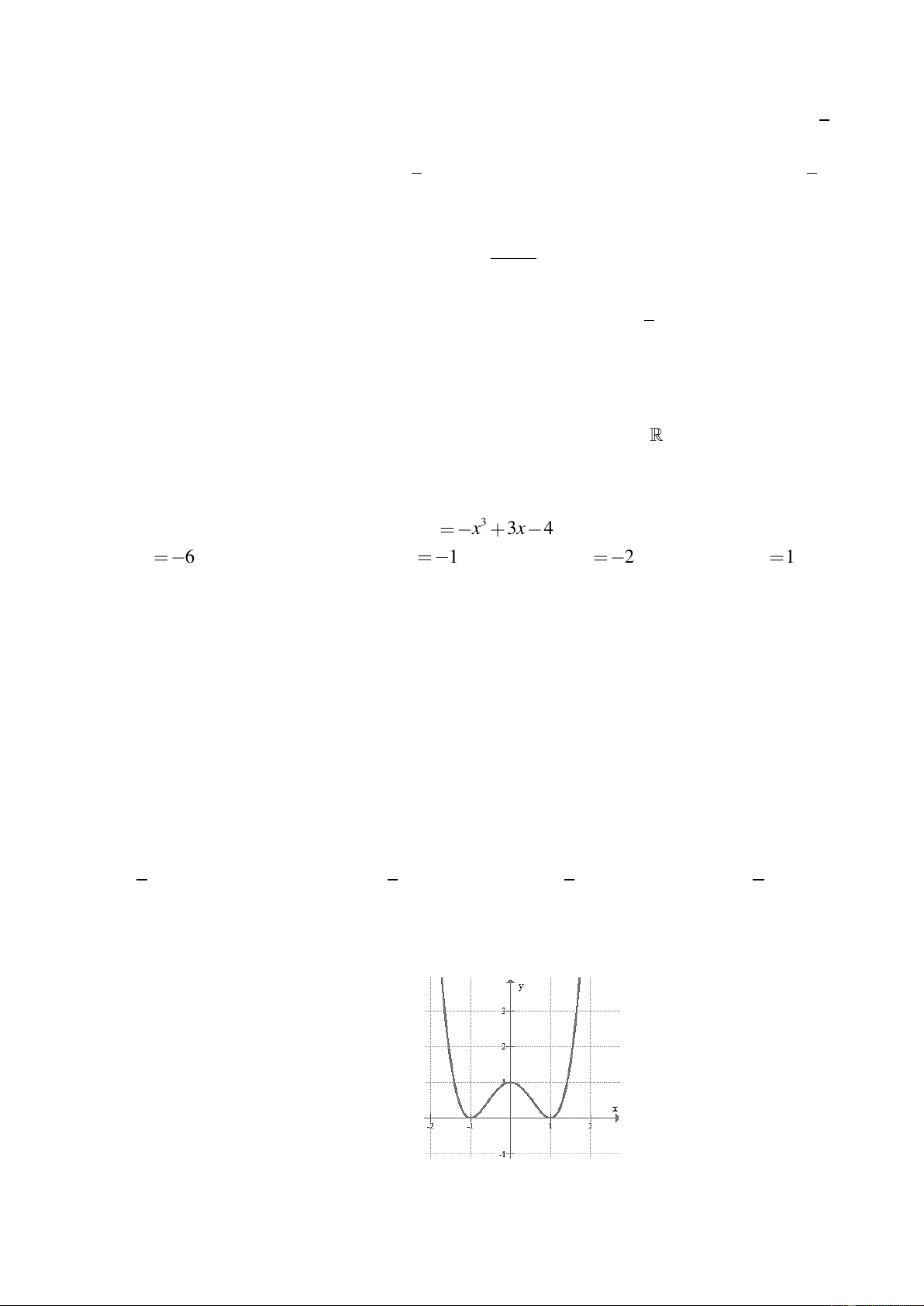
Câu 6. Tìm giá trị cực tiểu y của hàm số 3 y x 3x 4 . CT A. y 6 B. y 1 C. y 2 D. y 1 CT CT CT CT
Câu 7. Có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số y = (m + ) 4 x + ( m − ) 2 1 2 5 x − 3m
có đúng 3 điểm cực trị? A. 3. B. 4. C. 0. D. 5.
Câu 8. Tìm tập hợp tất cả các giá trị của m để hàm số 3
y = x + ( m − ) 2 2 3
1 x + m x − 3 đạt cực tiểu tại x = 1 − . A. 5 ;1 . B. 5 . C. . D. 1 .
Câu 9. Gọi S là tập hợp tất cả các giá trị của tham số m để đồ thị hàm số 3 2
y = x − 3mx + 2m + 5 có hai điểm cực trị ,
A B sao cho diện tích O
AB bằng 7 (với O là gốc tọa độ). Tích các phần tử của S là: 5 7 5 7 A. − . B. . C. . D. − . 2 2 2 2
Câu 10.Cho hàm số y = f ( x) liên tục trên đoạn 1 −
;1 và có đồ thị như hình vẽ.
Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn 1 − ;1 . Giá trị của
M − m bằng A. 0 . B. 1. C. 2 . D. 3 .
Câu 11. Giá trị lớn nhất của hàm số 4 2
f (x) = −x +12x +1 trên đoạn 1 − ;2bằng: A. 1. B. 37 . C. 33 . D. 12 .
Câu 12. Giá trị nhỏ nhất của hàm số f ( x) 3
= x −3x + 2 trên đoạn 3 − ; 3 bằng A. 0 . B. 16 − . C. 20 . D. 4 . x + m
Câu 13. Biết rằng có đúng một giá trị của tham số m để giá trị nhỏ nhất của hàm số y = x −1 trên đoạn 2
− ;0 bằng 10. Giá trị đó của tham số m thuộc tập hợp nào trong các tập hợp sau? A. (10;20) . B. ( 3 − 0; 2 − 0) . C. ( 1 − 0;0). D. (0;10) .
Câu 14. Tìm m để giá trị lớn nhất của hàm số 3
y = x − 3x + 2m −1 trên đoạn 0;2 là nhỏ nhất. Giá
trị của m thuộc khoảng nào? 3 2 A. − ; −1 . B. ; 2 . C. 1 − ;0. D. (0 ) ;1 . 2 3 5x +1
Câu 15. Phương trình đường tiệm cận ngang của đồ thị hàm số y = x − là 1 1 A. y = 1. B. y = . C. y = 1 − . D. y = 5 . 5 x + 9 − 3
Câu 16. Số tiệm cận đứng của đồ thị hàm số y = là 2 x + x A. 1 B. 2 C. 0 D. 3 x −1
Câu 17. Có bao nhiêu giá trị nguyên dương của tham số m để đồ thị hàm số y = có 3 2
x − 8x + m đường tiệm cận? A. 14 . B. 8 . C. 15 . D. 16 .
Câu 18. Cho hàm số y = f ( x) có bảng biến thiên như sau:
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là: A. 4 . B. 1. C. 3 . D. 2 .
Câu 19. Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình sau? A. 3 2
y = x − 3x +1. B. 3 2
y = −x + 3x +1. C. 4 2
y = −x + 2x +1. D. 4 2
y = x − 2x +1.
Câu 20. Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên y O x A. 3
y = −x + 3x +1. B. 3
y = x − 3x +1. C. 4 2
y = x − 2x +1. D. 4 2
y = −x + 2x +1.
Câu 21. Số giao điểm của đồ thị hàm số 3 2
y = x + x và đồ thị hàm số 2
y = x + 5x A. 3. B. 0 . C. 1. D. 2.
Câu 22. Số giao điểm của đồ thị hàm số 3
y = −x + 7x với trục hoành là A. 0 . B. 3 . C. 2 . D. 1.
Câu 23. Cho hàm số f ( x) 4 2
= ax + bx + c(a, ,
b c ) . Đồ thị của hàm số y = f ( x) như hình vẽ sau :
Số nghiệm của phương trình 4 f ( x) − 3 = 0 là A. 2 B. 0 C. 4 D. 3
Câu 24. Cho hàm số y = ( x − )( 2 3
x + 2) có đồ thị (C ) . Mệnh đề nào dưới đây đúng?
A. (C ) cắt trục hoành tại hai điểm. B. (C ) cắt trục hoành tại một điểm.
C. (C ) không cắt trục hoành.
D. (C ) cắt trục hoành tại ba điểm. x −1
Câu 25. Hệ số góc của tiếp tuyến của đồ thị hàm số y =
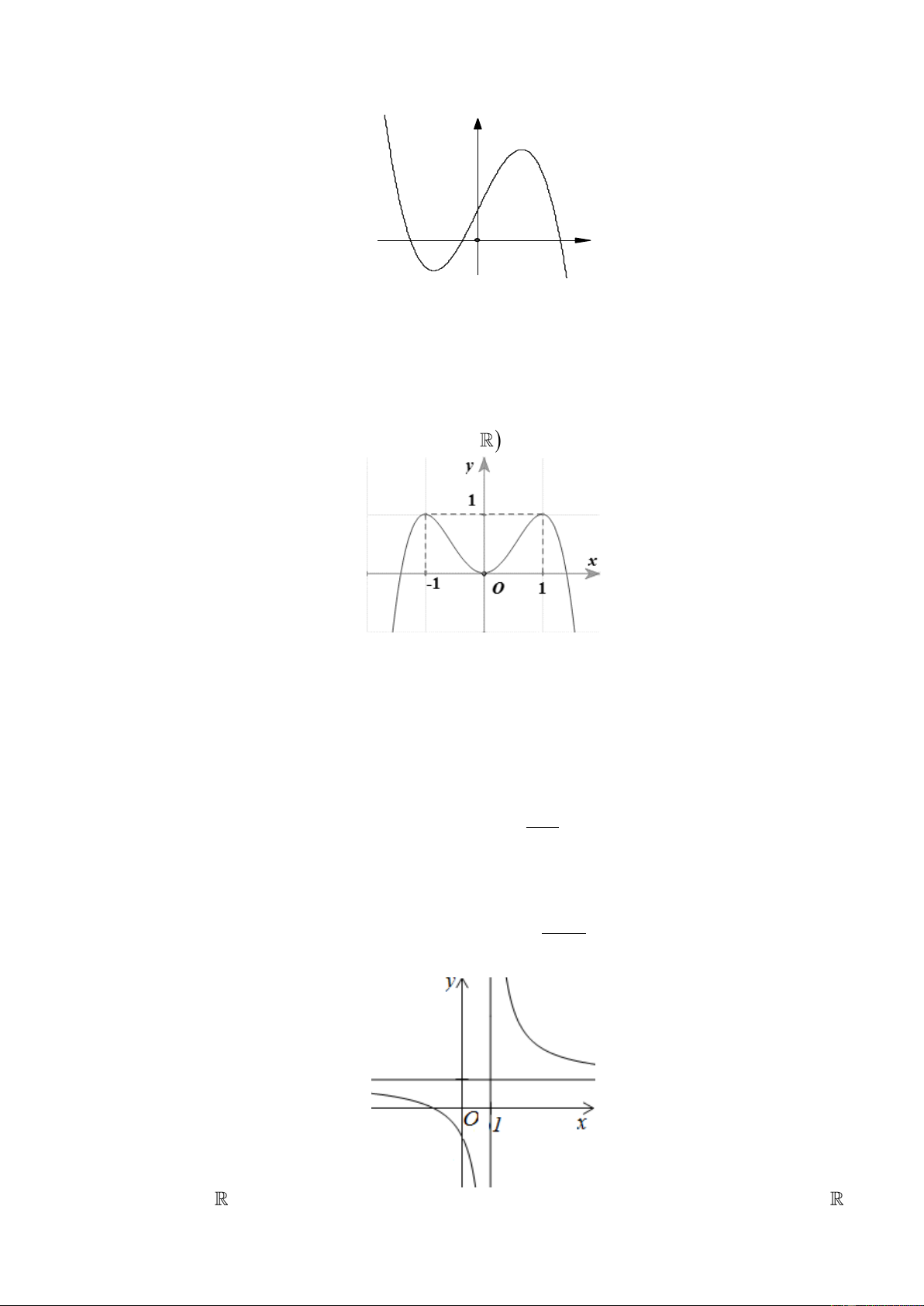
tại giao điểm của đồ thị hàm số với trục x +1 tung bằng: A. - 2 B. 2 C. 1 D. -1 ax + b
Câu 26. Đường cong ở hình bên là đồ thị của hàm số y =
với a,b,c,d là các số thực. Mệnh đề cx + d nào dưới đây đúng?
A. y 0,x
B. y 0,x 1
C. y 0,x 1
D. y 0,x
Câu 27. Cho hàm số y = f ( x) có đạo hàm y ' = f '( x) 0 x
. Tìm tập hợp tất cả các giá trị của
tham số m để bất phương trình f ( 3 2
x − x + m) f ( 2 2
x + 2) nghiệm đúng với mọi x 1 − ;2. A. (6;+) . B. ( ;2 − ). C. 6;+) . D. ( ;2 − .
Câu 28. Cho một tấm nhôm hình vuông cạnh 36 cm. Người ta cắt ở bốn góc bốn hình vuông bằng
nhau rồi gặp tấm nhôm lại để được một cái hộp chữ nhật không nắp. Tính cạnh của các hình vuông
được cắt bỏ sao cho thể tích của khối hộp đó lớn nhất ? A. 9 cm. B. 4 cm. C. 8 cm. D. 6 cm.
Câu 29. Hình đa diện sau có bao nhiêu cạnh? A. 15 B. 12 C. 20 D. 16
Câu 30. Khối lập phương là khối đa diện đều loại A. 5; 3 . B. 4; 3 . C. 3; 3 . D. 3; 4 .
Câu 31. Cho khối chóp có diện tích đáy B = 3 và chiều cao h = 4 . Thể tích của khối chóp đã cho bằng A. 6 . B. 12 . C. 36 . D. 4 .
Câu 32. Cho khối chóp S.ABC có đáy ABC là tam giác vuông tại B , AB = a, AC = 2a, SA ⊥ ( ABC )
và SA = a . Thể tích của khối chóp đã cho bằng 3 a 3 3 a 3 3 a 3 2a A. . B. . C. . D. . 3 6 3 3
Câu 33.Cho khối chóp .
S ABC có SA vuông góc với đáy, SA = 4 , AB = 6 , BC = 10 và CA = 8 .
Tính thể tích V của khối chóp . S ABC .
A. V = 32
B. V = 192
C. V = 40 D. V = 24
Câu 34. Cho hình chóp đều tứ giác S.ABCD có cạnh đáy bằng 3a , mặt bên tạo với mặt phẳng đáy một góc 0
60 . Thể tích khối chóp S.ABCD là 3 a 3 3 2a 3 3 9a 3 3 3a 3 A. . B. . C. . D. . 2 9 2 2
Câu 35. Cho hình chóp S.ABC có cạnh bên SA vuông góc với mặt phẳng ( ABC ) và đáy ABC là
tam giác vuông tại B , AB = a, BC = 3a . Góc giữa SC và mặt phẳng đáy bằng 0 45 . Thể tích của khối
chóp S.ABC là 3 a 10 3 a 10 3 a 10 A. . B. . C. 3 a 10 . D. . 6 2 3
Câu 36. Nếu cạnh đáy của hình chóp tam giác tăng lên 2 lần và chiều cao của hình chóp đó tăng lên 3
lần thì thể tích của nó tăng lên bao nhiêu lần? A. 16 lần. B. 18 lần. C. 12 lần. D. 36 lần.
Câu 37. Cho khối chóp S.ABC . Gọi M , N lần lượt là trung điểm của ,
SA SB . Khi đó tỷ số thể tích
của hai khối chóp S.MNC và S.ABC bằng: 1 1 1 1 A. B. C. D. 8 4 3 2
Câu 38. Cho khối lăng trụ có đáy là hình vuông cạnh a và chiều cao bằng 4a . Thể tích của khối lăng trụ đã cho bằng 16 4 A. 3 16a B. 3 4a C. 3 a D. 3 a 3 3
Câu 39.Tính thể tích V của khối lập phương ABC . D A B C D
, biết AC = a 3 . 3 3 6a 1 A. 3 V = a B. V = C. 3
V = 3 3a D. 3 V = a 4 3
Câu 40. Cho hình lăng trụ đứng AB . C A B C có 0
AB = a, BC = 4a, ABC = 120 và góc giữa đường thẳng A B
và mặt phẳng đáy bằng 0
60 . Thể tích của khối lăng trụ AB . C A B C là A. 3 V = a . B. 3 V = 3a . C. 3 V = 6a . D. 3 V = 2a .
Hoàng Mai, ngày 6 tháng 10 năm 2023 TỔ TRƯỞNG
Nguyễn Thị Thu Phương




