Đề cương GK2 Toán 11 (chuyên) năm 2024 – 2025 trường chuyên Bảo Lộc – Lâm Đồng
Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 11 đề cương ôn tập giữa học kì 2 môn Toán 11 (chuyên) năm học 2024 – 2025 trường THPT chuyên Bảo Lộc, tỉnh Lâm Đồng.
Chủ đề: Đề giữa HK2 Toán 11 259 tài liệu
Môn: Toán 11 3.6 K tài liệu
Tác giả:
Preview text:
TRƯỜNG THPT CHUYÊN BẢO LỘC TỔ: TOÁN
ĐỀ CƯƠNG ÔN TẬP GIỮA HỌC KỲ II
NĂM HỌC: 2024 – 2025 LỚP 11 (CT CHUYÊN) NỘI DUNG KIẾN THỨC: I. Giải tích:
1) Phương trình mũ và phương trình logarit
2) Bất phương trình mũ và logarit.
3) Hệ phương trình mũ và logarit
4) Chuyên đề Giải phương trình, bất phương trình, hệ phương trình đại số
5) Chuyên đề tìm GTLN,GTNN của biểu thức 6) Nguyên hàm II. Hình học: 1) Khối tròn xoay 2) Khối nón. 3) Khối trụ 4) Khối cầu.
5) Hệ trục tọa độ.
MỘT SỐ CHỦ ĐỀ THAM KHẢO: 1) Phương trình mũ: Baøi 1.
Giaûi caùc phöông trình sau (ñöa veà cuøng cô soá hoaëc logarit hoaù): x 1 0 x5 x 1 x 1 a) x 1 0 x 1 5 16 0,125.8 b) x 1 5 2 5 2 Baøi 2.
Giaûi caùc phöông trình sau (ñöa veà cuøng cô soá hoaëc logarit hoaù): x a) x x x x2 3 .8 6 b) 3 2 2 3 c) x x2 3 .2 1 Baøi 3.
Giaûi caùc phöông trình sau (ñaët aån phuï daïng 1): x x
a) 7 4 3 2 3 6 b) 2 cos2x cos 4 4 x 3 Baøi 4.
Giaûi caùc phöông trình sau (ñaët aån phuï daïng 1):
a) 25x 2(3 ).5x x 2x 7 0 b) x2 x2 3.25 (3x 10).5 3 x 0
c) 3.4x (3 10).2x x 3 x 0
d) 9x 2( 2).3x x 2x 5 0 Baøi 5.
Giaûi caùc phöông trình sau (ñaët aån phuï daïng 2):
a) 64.9x 84.12x 27.16x
0 b) 3.16x 2.81x 5.36x c) 2 x x 2 6.3 13.6 6.2 x 0 x x x
d) 7 5 2 2 53 2 2 31 2 1 2 0. Baøi 6.
Giaûi caùc phöông trình sau (ñaët aån phuï daïng 3): x x x x
a) 2 3 2 3 14
b) 2 3 2 3 4 x x c) (2 3)x (7 4 3)(2 3)x 4(2 3) d) x 3 5 21 7 5 21 2 x x x x
e) 7 4 3 32 3 2 0 f) 3 3 3 8 3 8 6. Baøi 7.
Giaûi caùc phöông trình sau (söû duïng tính ñôn ñieäu): x x x x x a) x 2 3 2 3 4
b) 3 2 3 2 5
Năm học : 2024 – 2025 Trang 1 x x c) x x
3 2 2 3 2 2 6x d) x3 3 5 16. 3 5 2 x x x e) 3 7 2 x
f) 2 3 2 3 2x 5 5
g) 2x 3x 5x 10x
h) 2x 3x 5x i) 2 x 1 x x 2 2 2 (x 1)
k) 3x 5 2x
l) 2x 3 x m) x 1
2 4x x 1 x n) x 2 2 3 1
o) 4x 7x 9x 2
p) 52x 1 53x x 1 0 q) x x x x 3 8 4 7 r) x x x x 6 2 5 3 s) x x x x 9 15 10 14 Baøi 8.
Giaûi caùc phöông trình sau (ñöa veà phöông trình tích):
a) 8.3x 3.2x 24 6x b) x x x 1 12.3 3.15 5 20 c) x 3 8 .2 2 x x x 0 d) x x x 2 3 1 6 e) 4 2 2 2 2
x 3x2 4 2x6x5 42. 2x3x7 1 f) x x 1x x 1 4 2 2 1 g) 2 x x x
x x3 x2 .3 3 (12 7 )
8 19x 12 h) 2 x 1 x x x x 1 x .3 x(3 2 ) 2(2 3 ) i) sin x 1sin 4 2
x cos(xy) 2 y 0 k) 2 2 2 2 2(x x) 1x 2(x x) 1 2 2 2 .2 x 1 0 Baøi 9.
Tìm m ñeå caùc phöông trình sau coù nghieäm:
a) 9x 3x m 0 b) 9x 3x m 1 0 c) x x 1 4 2 m d) 2
3 x 2.3x ( 3).2x m 0
e) 2x ( 1).2x m
m 0 f) 25x 2.5x m 2 0 g) x 2 16 ( 1).2 x m
m 1 0 h) 25x .5x m 1 2m 0 i) 2 2 sin x cos 81 81 x m k) 2 2 42x 2 3
2.3 x 2m 3 0
l) x 1 3 x x 1 3 4 14.2 x 8 m m) 2 2 x 1x x 1 9 8.3 x 4 m n) 2 2 1 1 t 1 1 9 ( 2).3 t m 2m 1 0 Baøi 10.
Tìm m ñeå caùc phöông trình sau coù nghieäm duy nhaát: a) .2x 2 x m 5 0
b) .16x 2.81x 5.36x m x x x x 7 3 5 7 3 5 c) 5 1 5 1 2x m d) m 8 2 2 e) x x 3 4 2 3 m f) 9x 3x m 1 0 Baøi 11.
Tìm m ñeå caùc phöông trình sau coù 2 nghieäm traùi daáu: a) x x 1 (m 1).4 (3m 2).2 3m 1 0 b) x x 2
49 (m 1).7 m 2m 0
c) 9x 3( 1).3x m 5m 2 0
d) ( 3).16x (2 1).4x m m m 1 0 e) 4x 2 1 .2x m +3m 8 0
f) 4x 2x 6 m Baøi 12.
Tìm m ñeå caùc phöông trình sau:
a) .16x 2.81x 5.36x m
coù 2 nghieäm döông phaân bieät.
b) 16x .8x (2 1).4x .2x m m m
coù 3 nghieäm phaân bieät. c) 2 2 x x 2 4 2
6 m coù 3 nghieäm phaân bieät. 2 2
d) 9x 4.3x 8 m coù 3 nghieäm phaân bieät.
2) Phương trình logarit Baøi 1.
Giaûi caùc phöông trình sau (ñöa veà cuøng cô soá hoaëc muõ hoaù): a) log x x
2 (9 2 ) 3 x
b) log3(3 8) 2 x c) log x x 7(6 7 ) 1 x d) 1 lo 3 g (4.3 1) 2x 1 e) x log (3 ) 5 log x 2(9 2 ) 5 x
f) log2(3.2 1)2x 1 0
Năm học : 2024– 2025 Trang 2 g) log x x
2(12 2 ) 5 x h) log5(26 3 ) 2 i) x 1 log x x 2(5 25 ) 2 k) 1 log4(3.2 5) x l) x 1 log x x x 1 (5 25 ) 2 m) 1 log 1 (6 36 ) 2 6 5 Baøi 2.
Giaûi caùc phöông trình sau (ñöa veà cuøng cô soá hoaëc muõ hoaù): a) 2
log5 (x 2x 65) 2 b) 2 log
(x 4x 5) 1 x x 1 c) 2
log (5x 8x 3) 2 d) 3 2
log (2x 2x 3x 1) 3 x x 1 e) log f) log (x 2) 2 3(x 1) 2 x x Baøi 3.
Giaûi caùc phöông trình sau (ñaët aån phuï): a) 2 2
log3 x log3 x 1 5 0 b) 2
log x 3log x log x 2 2 2 1/2 7 2 c) log 2 x log x d) 2 log 4x log 8 x 4 0 6 1 2 8 2 9 r) 2 log
5 log 5x log
5 s) log 3 log x 1 x x 4 x 2 x 9 t) 1 2 1 u) 1 3 1
4 lg x 2 lg x
5 lg x 3 lg x v) 2 3 log2 x 14lo 1
g 6 x 40log4 x 0 x x x Baøi 4.
Giaûi caùc phöông trình sau (ñaët aån phuï): a) 2 log log x log 6
x (x 12) log x 11 x 0 b) 2 2 2 6.9 6.x 13. 3 3 x c) 2 . x log d) 2
2 x 2(x 1).log2 x 4 0
log x (x )
1 log x 6 2x 2 2 e) 2
(x 2) log (x 1) 4(x 1) log (x 1) 16 0 f) log (2 x) log x 2 3 3 2 x 2x g) 2
log3(x 1)(x 5)log3(x 1)2x 6 0 h) 4 log3 x 1 log3 x 4 i) 2 2
log2(x 3x 2) log2(x 7x 12) 3 log2 3 Baøi 5.
Giaûi caùc phöông trình sau (ñaët aån phuï): a) log
7 x log3( x 2)
b) log2(x 3) log3(x 2) 2
c) log (x 1) log (2x log x 6 3 5 1) 2 d) log x 3 log x 2 6 e) log 3 7 4 x x f) log 1 x 2 log3 x g) log 9 2 log log 3 2 2 2 .3 x x x x h) 2 2 log3 7(9 12x
4x ) log2 3(6x 23x 21) 4 x x i) log 2
x x 1.log 2
x x 1 log 2 x x 1 2 3 6 Baøi 6.
Giaûi caùc phöông trình sau (söû duïng tính ñôn ñieäu): a) log 3 log 5 2 log x log 2 2 x x x (x 0) b) 2 2 3 5 x x
c) log5(x 3) 3 x
d) log2(3 x) x e) 2 log log x
2 (x x 6) x log2 (x 2) 4 f) 2 x 2.3 3 g) 4(x 2)log
2 (x 3) log3(x 2) 15(x 1) Baøi 7.
Giaûi caùc phöông trình sau (ñöa veà phöông trình tích):
a) log2 x 2.log7 x 2 log2 x.log7 x b) log2 x.lo 3 g x 3 3.lo 3 g x log2 x
Năm học : 2024 – 2025 Trang 3 c) 2 2 log x
9 log x.log 2x 1 3 3 1 Baøi 8.
Giaûi caùc phöông trình sau (phöông phaùp ñoái laäp): a) 2 3
ln(sin x) 1 sin x 0 b) log 2 x x 2 2 1 1 x c) 2x 1 32x 8 2 2 2
log3(4x 4x 4) Baøi 9.
Tìm m ñeå caùc phöông trình sau coù nghieäm duy nhaát: a) 2 log
x 2(m 1)x log
(2x m 2) 0 b) log x 2 log 2 mx 2 3 2 3 2 lgmx c) log 2
x mx m 1 log x 0 d) 2 52 52 lgx 1 e) 2
log3(x 4mx) log3(2x 2m 1) f) 2 log
(x m 1) log
(mx x ) 0 2 2 7 2 2 7 Baøi 10.
Tìm m ñeå caùc phöông trình sau:
a) log 4x m
coù 2 nghieäm phaân bieät. 2 x 1 b) 2 log coù 2 nghieäm x
3 x (m 2).log3 x 3m 1 0
1, x2 thoaû x1.x2 = 27. c) 2 2 2 2
2log (2x x 2m 4m ) log (x mx 2m ) coù 2 nghieäm x
x x 1 . 4 2 1, x2 thoaû 2 2 1 2 d) 2 2
log3 x log3 x 1 2m 1 0 coù ít nhaát moät nghieäm thuoäc ñoaïn 3 1 ;3 . e) 4log x 2 2
log2 x m 0 coù nghieäm thuoäc khoaûng (0; 1).
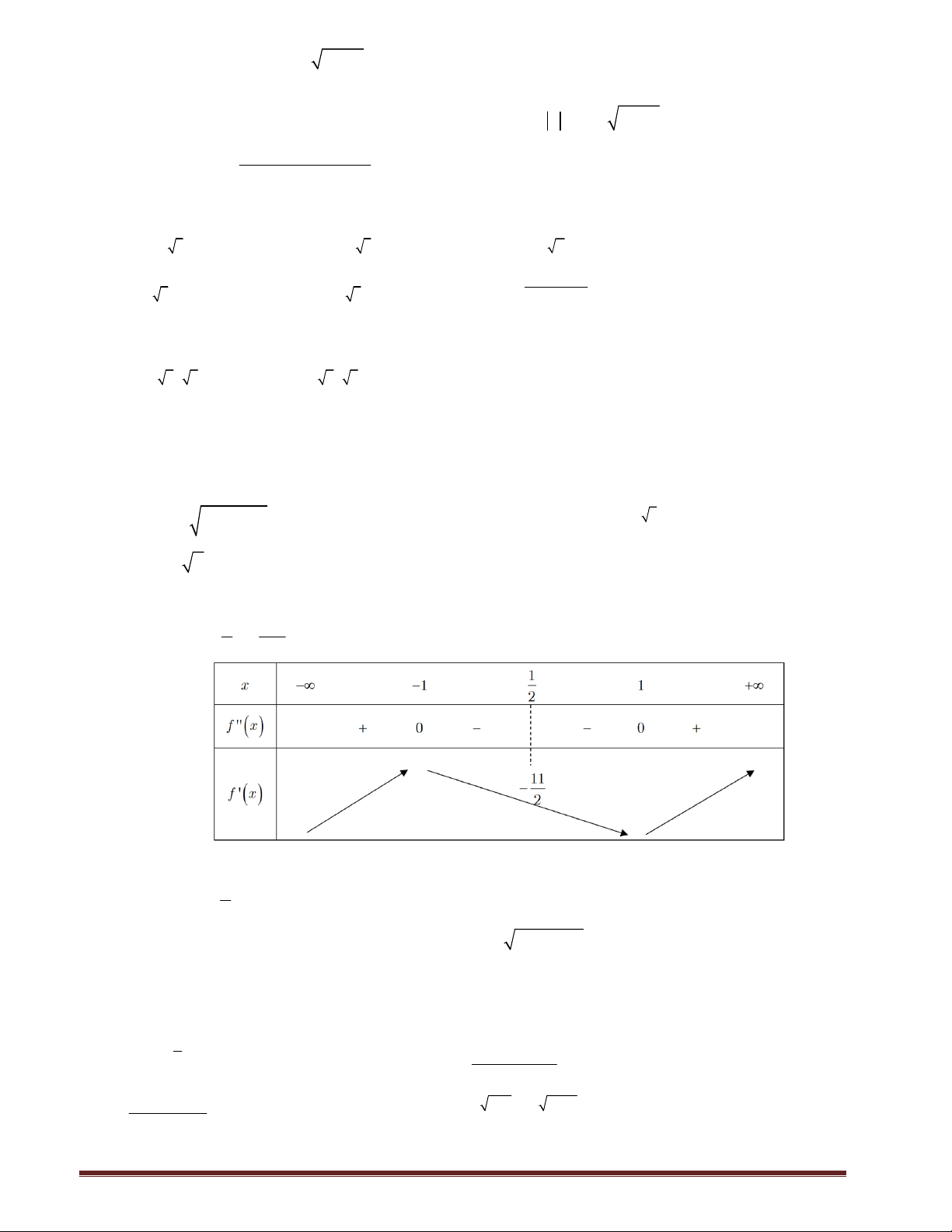
Bài 10.Cho hàm số y f x và f x 0,xℝ . Biết hàm số y f x có bảng biến thiên như hình 1 137 vẽ và f . 2 16 2
Có bao nhiêu giá trị nguyên của 4 5 m 2
020; 2020 để hàm số x mx g x e
. f x đồng biến 1 trên 1 ; . 2
Bài 11. Cho hàm số y f x thỏa mãn f x 2 2020
x x 2020, x .
ℝ Có bao nhiêu số nguyên m
thỏa mãn f log m f log 2020 ? m
3) Bất phương trình mũ và logarit Baøi 1.
Giaûi caùc baát phöông trình sau (söû duïng tính ñôn ñieäu): x x x a) x 2 2 21 2 1 3 1 b) 0 2x 1 x x2 c) 2.3 2 1 d) x4 2x4 3 2 13 3x 2x
Năm học : 2024– 2025 Trang 4 2x x e) 3 3 2x 3 x 4 0 f) 0 4x 2 2 x x 6 g) x x x 2 2 2 x 3x 5 2 2x 3 .2x 3x 5 2 2x 3 Baøi 2.
Tìm m ñeå caùc baát phöông trình sau coù nghieäm: a) 4x .2x m m 3 0 b) 9x .3x m m 3 0 2 2 x x 1
c) 2x 7 2x 2 m d) 2 1 2 1 m 0 Baøi 3.
Tìm m ñeå caùc baát phöông trình sau nghieäm ñuùng vôùi:
a) (3 1).12x (2 ).6x 3x m m 0 , x > 0. b) x x 1 (m 1)4 2
m 1 0 , x.
c) .9x 2 1 6x .4x m m m 0 , x [0; 1]. d) x x2 .
m 9 (m 1).3
m 1 0 , x.
e) cosx m cosx 2 4 2 2 1 2
4m 3 0 , x. f) x x 1 4 3.2 m 0 , x.
g) 4x 2x m 0 , x (0; 1)
h) 3x 3 5 3x m , x.
i) 2.25x (2 1).10x ( 2).4x m m
0 , x 0. k) x 1 4 .(2x m 1) 0 , x. Baøi 4.
Tìm m ñeå moïi nghieäm cuûa (1) ñeàu laø nghieäm cuûa baát phöông trình (2): 2 1 1 1 2 1 x 1 x 1 a) 3 12 (1) 2x 2x 8 (1) 3 3 b) 2 2
4x 2mx (m 1) 0 (2) m 22 2
x 3m 6 x m 1 0 (2) 2 1 2 2x 1 x 1 x 1 x c) 2 9.2 4 0 (1) 9. 12 (1) d) 2 ( 3 3 m
1)x m(x 3) 1 0 (2) 2 2x
m 2x 23m 0 (2) Baøi 5.
Giaûi caùc baát phöông trình sau (söû duïng tính ñôn ñieäu): a) 2 ( x 1)log x x
0,5x (2x 5) log0,5 x 6 0 b) log (2 ) 1 log (4 2) 2 2 3 5 lg x c) 3 2 d) 5 x 0 log x 1 log x 1 x 2 3 2 3x 1 Baøi 6.
Tìm m ñeå caùc baát phöông trình sau coù nghieäm: a) log 2
x 2x m 1/2 3 b) 1 log 100 log 100 0 x 2 m 2 c) 1 2 1 log x 1 d) m 1
5 log x 1 log x 1 log x m m m
e) log2 x m log2 x f) 2 2 log (x 1) log (x x 2) xm xm Baøi 7.
Tìm m ñeå caùc baát phöông trình sau nghieäm ñuùng vôùi: a) log 2 7x 7 log 2
mx 4x m 2 2 , x b) log
x x m
x x m , x [0; 2] 2 2 2 4 log2 2 2 5 c) 2 2
1 log5(x 1) log5(mx 4x m) , x. d) m 2 2 log m m 1 x 2 1 log 1 x 2 1 log 1 0 , x 1 m 1 m 1 m 2 2 2 Baøi 8.
Giaûi baát phöông trình, bieát x = a laø moät nghieäm cuûa baát phöông trình: a) 2
x x 2 log 2
log x 2x 3; a 9 / 4 . m m
Năm học : 2024 – 2025 Trang 5 b). 2 2
log (2x x 3) log (3x x); a 1 m m
Bài 9. Tìm tập S tất cả các giá trị thực của số m để tồn tại duy nhất cặp số ; x y thỏa mãn 2 log
4x 4y 6 m 1 và 2 2
x y 2x 4 y 1 0 . 2 2 x y 2
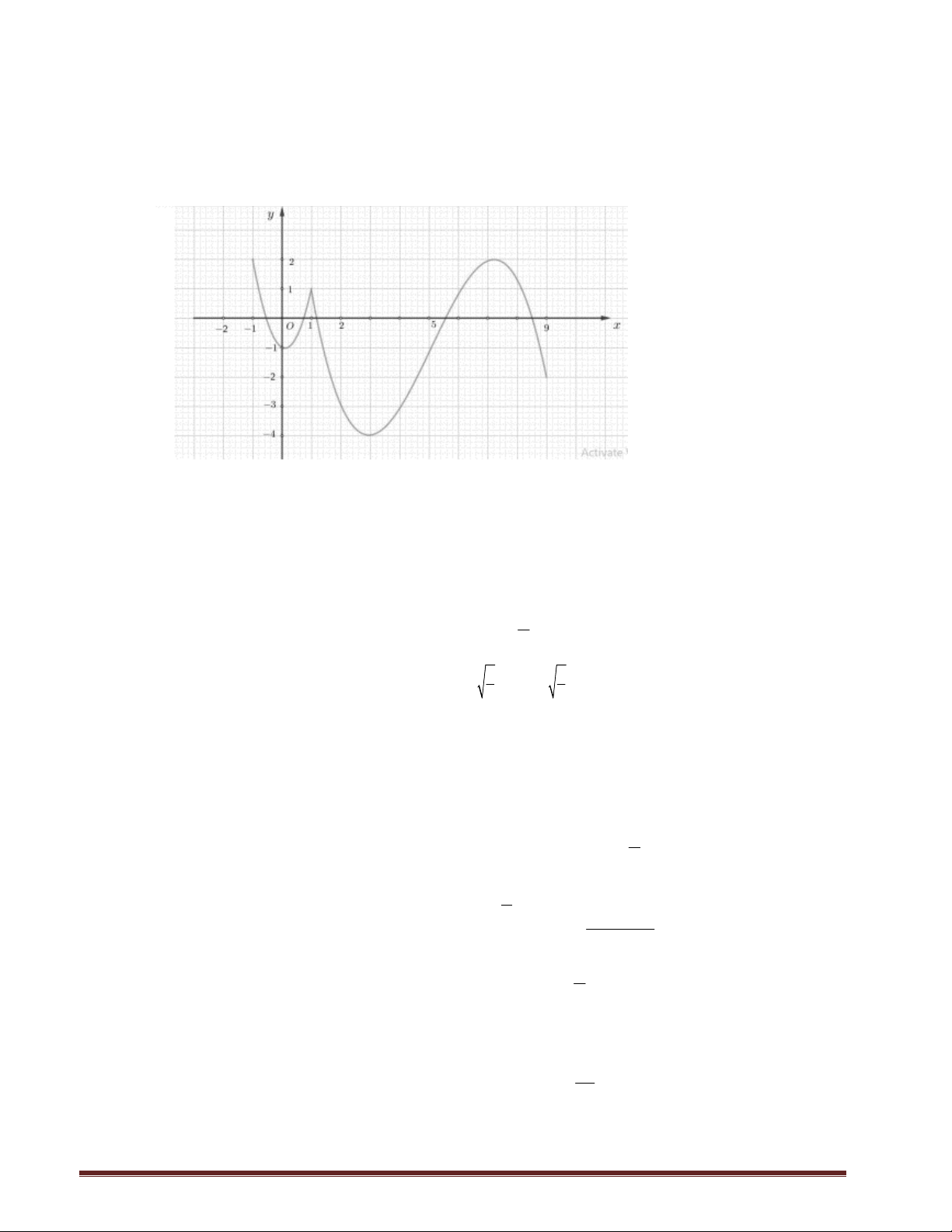
Bài 10. Cho hàm số y f x liên tục trên đoạn 1;9 và có đồ thị là đường cong trong hình vẽ dưới đây
Có bao nhiêu giá trị nguyên của tham số m để bất phương trình f x 2
f x f x f x 2 16.3 2 8 .4
m 3m f x .6
nghiệm đúng với mọi giá trị thuộc 1;9?
4) Hệ phương trình mũ và logarit Baøi 1.
Giaûi caùc heä phöông trình sau: x log 1 2 log y
log 3x 2y 2
log (6x 4y) 2 2 2 2 a)
log x log y 1 x y b) x c) d) y 2 log 2
x 3y 2
log (6y 4x) 2 log x log y 4 y y
log x log y 1 3 3 4 4 2 2 log 2 2 log y log x log y log 3 3 x
2 x y 6 4 e) x y 16 x 2.y 27 f) 2 2 g) log
log x log y 2
log y log x 1
3 x log3 y 1 2 2 3 3 log2 xy log 4 2 y log2 x log x y x 2 2 2 h) 3 .x 2.y 10 i) k) 2 x log log y x log 2 y 2 2 2
4 x log2 y 2 2 y 2 2 2 5
log2 x y 5 log2 x y log x log
l) lg x lg y lg (xy) x m) y y n) 2 2 lg x lg 4
lg (x y) lg x.lg y 0 2 2 log 1
6 (x y ) 1 lg y lg3 y 2 2
lg x y 1 lg8 log y 2 2 log log x 1 o) p) x q) xy y x lg log y x 1 23 3
x y lg x y lg3 log
2 y x 1 Baøi 2.
Giaûi caùc heä phöông trình sau: lg yx 5 x lg y 4 x2y a) x 36 ( x y)3 lg b) c) y 27 x 1000 4
x 2y log6 x 9 3 log
5(x y) x y
Năm học : 2024– 2025 Trang 6 lg
2 log x 2 log y 5 0 x lg y 2 1 x d) 3 4 e) lg4 lg3 y ( 4x) (3y) 2 xy 32 Baøi 3.
Giaûi caùc heä phöông trình sau: log 3x
2 x log4 y log4 z 2 x log
2 3 log2 y y log2 a) log 2
3 y log9 z log9 x 2 b) 2 log y
x log 12 log x y log 4 z lo 1 g 6 x lo 1 g 6 y 2 3 3 3 3 Baøi 4.
Giaûi caùc heä phöông trình sau: x 2y log x 4 x y 3 1 a) 2 2 y b) 3 log
2 x log2 y 1
log x y log x y 2 2 4 log x y y log x 3 .2 18 c) 8 8 x y 4
d) log x y 1 log 1
4 x log4 y 1 3 Bài 5. Bài 6. 5) Nguyên hàm Baøi 1.
Tính caùc nguyeân haøm sau: a) 1 x 1 dx b) 1 dx c) dx 1 x 1 x x 2 3 1 x 1 d) 1 x x dx e) dx dx 4 f) x x 3 x x x(x 1) g) dx 1 h) 1 x dx x dx 3 4 i) 3
x x 2 x 1 x x 1 x x k) dx l) dx m) dx 3 2
(2x 1) 2x 1 2 x 5x 6 2 x 6x 8 Baøi 2.
Tính caùc nguyeân haøm sau:
a) sin 2x sin 5xdx b) cos x sin3xdx c) 2 4
(tan x tan x)dx d) cos2x dx dx dx e) 1 f) sin x cos x 2sin x 1 cos x 1 sin 3 sin g) x x dx dx h) dx cos i) x cos x cos
x cos x 4
Năm học : 2024 – 2025 Trang 7
k) cos x cos2x cos3xdx l) 3 cos xdx m) 4 sin xdx Baøi 3.
Tính caùc nguyeân haøm sau: ln a) x xdx e dx b) c) sin x dx x d) cos x dx e) x.sin x dx f) 3 sin xdx ln(ln x) g) dx h) sin(ln x)dx i) cos(ln x)dx x Baøi 4.
Tính caùc nguyeân haøm sau: a) x e .cos xdx b) x 2
e (1 tan x tan x)dx c) x e .sin 2xdx d) ln(cos x) ln(1 x) x dx e) dx dx 2 f) cos x 2 x 2 cos x 2 x ln 2 x x 1 3 g) x ln x dx h) dx i) dx 2 x 1 2 1 x x
Bài 5. Cho hàm số y f x thỏa mãn f x 0, x
0 và có đạo hàm f x liên tục trên khoảng
0; thỏa mãn f x x 2 2
1 f x, x 0 và f 1
1 . Tính giá trị của biểu thức 2 f
1 f 2 ... f 2020 .
6) Khối cầu – Mặt cầu Baøi 1.
Trong maët phaúng (P), cho ñöôøng thaúng d vaø moät ñieåm A ngoaøi d. Moät goùc xAy di
ñoäng quanh A, caét d taïi B vaø C. Treân ñöôøng thaúng qua A vuoâng goùc vôùi (P) laáy ñieåm S. Goïi
H vaø K laø caùc hình chieáu vuoâng goùc cuûa A treân SB vaø SC.
a) Chöùng minh A, B, C, H, K thuoäc cuøng moät maët caàu.
b) Tính baùn kính maët caàu treân, bieát AB = 2, AC = 3, 0
BAC 60 . Baøi 2.
Cho hình choùp tam giaùc ñeàu S.ABC, coù caïnh ñaùy baèng a vaø goùc hôïp bôûi maët beân
vaø ñaùy baèng 600. Goïi O laø taâm cuûa tam giaùc ABC. Trong tam giaùc SAO döïng ñöôøng trung
tröïc cuûa caïnh SA, caét SO taïi K. a) Tính SO, SA.
b) Chöùng minh SMK ∼ SOA( vôùi M laø trung ñieåm cuûa SA). Suy ra KS.
c) Chöùng minh hình choùp K.ABC laø hình choùp ñeàu. suy ra: KA = KB +KC.
d) Xaùc ñònh taâm vaø baùn kính maët caàu ngoaïi tieáp hình choùp S.ABC. Baøi 3.
Cho hình choùp S.ABC. bieát raèng coù moät maët caàu baùn kính R tieáp xuùc vôùi caùc caïnh
cuûa hình choùp vaø taâm I cuûa maët caàu naèm treân ñöôøng cao SH cuûa hình choùp.
a) Chöùng minh raèng S.ABC laø hình choùp ñeàu.
b) Tính chieàu cao cuûa hình choùp, bieát raèng IS R 3 Baøi 4.
Cho töù dieän ñeàu ABCD coù caïnh laø a.
a) Xaùc ñònh taâm vaø baùn kính maët caàu ngoaïi tieáp töù dieän.
b) Tính dieän tích maët caàu vaø theå tích khoái caàu ñoù. Baøi 5.
Cho moät hình choùp töù giaùc ñeàu coù caïnh ñaùy laø a, caïnh beân hôïp vôùi maët ñaùy moät goùc 600.
Năm học : 2024– 2025 Trang 8
a) Xaùc ñònh taâm vaø baùn kính maët caàu ngoaïi tieáp hình choùp.
b) Tính dieän tích maët caàu vaø theå tích khoái caàu ñoù. Baøi 6.
Cho hình choùp S.ABC coù SA (ABC) vaø tam giaùc ABC vuoâng taïi B. Goïi AH, AK
laàn löôït laø caùc ñöôøng cao cuûa caùc tam giaùc SAB vaø SAC.
a) Chöùng minh raèng naêm ñieåm A, B, C, H, K cuøng ôû treân moät maët caàu.
b) Cho AB = 10, BC = 24. Xaùc ñònh taâm vaø tính baùn kính maët caàu ñoù. Baøi 7.
Cho hình choùp S.ABCD coù ABCD laø hình vuoâng caïnh baèng a, SA = a 7 vaø SA
(ABCD). Moät maët phaúng (P) qua A vaø vuoâng goùc vôùi SC, caét SB, SC, SD laàn löôït taïi H, M, K.
a) Chöùng minh raèng baûy ñieåm A, B, C, D, H, M, K cuøng ôû treân moät maët caàu.
b) Xaùc ñònh taâm vaø tính baùn kính maët caàu ñoù.
Bài 8. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Tam giác SAB nằm trong mặt
phẳng vuông góc với mặt phẳng ABCD . Biết rằng AB a, AD a 3 và ASB 60 . Tính
diện tích khối cầu ngoại tiếp hình chóp S.ABCD .
7) Hình trụ - Khối trụ Baøi 1.
Cho hình truï baùn kính ñaùy R, chieàu cao OO = h, A vaø B laø hai ñieåm thay ñoåi treân
hai ñöôøng troøn ñaùy sao cho ñoä daøi AB = a khoâng ñoåi 2 2
h a h 4R .
a) Chöùng minh goùc giöõa hai ñöôøng thaúng AB vaø OO’ khoâng ñoåi.
b) Chöùng minh khoaûng caùch giöõa hai ñöôøng thaúng AB vaø OO’ khoâng ñoåi. Baøi 2.
Trong khoâng gian cho hình vuoâng ABCD caïnh a. Goïi I vaø H laàn löôït laø trung ñieåm
cuûa caùc caïnh AB vaø CD. Khi quay hình vuoâng ñoù xung quanh truïc IH ta ñöôïc moät hình truï troøn xoay.
a) Tính dieän tích xung quanh cuûa hình truï troøn xoay ñöôïc taïo neân.
b) Tính theå tích cuûa khoái truï troøn xoay ñöôïc taïo neân bôûi hình truï troøn xoay ñoù. Baøi 3.
Moät hình truï coù baùn kính ñaùy R vaø coù thieát dieän qua truïc laø moät hình vuoâng.
a) Tính dieän tích xung quanh vaø dieän tích toaøn phaàn cuûa hình truï.
b) Tính theå tích cuûa khoái laêng truï töù giaùc ñeàu noäi tieáp trong khoái truï ñaõ cho. Baøi 4.
Cho hình truï baùn kính ñaùy R, chieàu cao h. Goïi A vaø B laø hai ñieåm laàn löôït naèm
treân hai ñöôøng troøn ñaùy (O, R) vaø (O, R) sao cho OA vaø OB hôïp vôùi nhau moät goùc baèng x
vaø vaø hai ñöôøng thaúng AB, OO hôïp vôùi nhau moät goùc baèng y.
a) Tính baùn kính R theo h, x, y.
b) Tính Sxq, Stp vaø theå tích V cuûa hình truï theo h, x, y. Baøi 5.
Cho hình truï baùn kính ñaùy baèng a vaø truïc OO’ = 2a. OA vaø OB’ laø hai baùn kính cuûa
hai ñöôøng troøn ñaùy (O), (O’) sao cho goùc cuûa OA vaø OB’ baèng 300.
a) Tính ñoä daøi ñoaïn thaúng AB’.
b) Tính tang cuûa goùc giöõa AB’ vaø OO’.
c) Tính khoaûng caùch giöõa AB’ vaø OO’. Baøi 6.
Moät khoái truï coù caùc ñaùy laø hai hình troøn taâm O vaø O’, baùn kính R vaø coù ñöôøng cao
h R 2 . Goïi A laø moät ñieåm treân ñöôøng troøn taâm O vaø B laø moät ñieåm treân ñöôøng troøn taâm
O’ sao cho OA vuoâng goùc vôùi O’B.
Năm học : 2024 – 2025 Trang 9
a) Chöùng minh raèng caùc maët beân cuûa töù dieän OABO’ laø nhöõng tam giaùc vuoâng. Tính tæ soá
theå tích cuûa khoái töù dieän OABO’ vaø khoái truï.
b) Goïi laø maët phaúng qua AB vaø song song vôùi OO’. Tính khoaûng caùch giöõa truïc OO’ vaø maët phaúng .
c) Chöùng minh raèng laø tieáp dieän cuûa maët truï coù truïc OO’ vaø coù baùn kính ñaùy baèng R 2 . 2
8) Hình nón – Khối nón Baøi 1.
Cho hình choùp töù giaùc ñeàu S.ABCD coù chieàu cao SO = h vaø SAB ( > 450).
Tính dieän tích xung quanh cuûa hình noùn ñænh S vaø coù ñöôøng troøn ñaùy ngoaïi tieáp hình vuoâng ABCD. Baøi 2.
Moät hình noùn coù ñoä daøi ñöôøng sinh baèng 1 vaø goùc giöõa ñöôøng sinh vaø ñaùy laø .
a) Tình dieän tích xung quanh vaø theå tích cuûa khoái noùn.
b) Goïi I laø ñieåm treân ñöôøng cao SO cuûa hình noùn sao cho SI k 0 k 1 . Tính dieän tích SO
cuûa thieát dieän qua I vaø vuoâng goùc vôùi truïc.
Baøi 3. Cho hình noùn coù ñöôøng cao SO = h vaø baùn kính ñaùy R. Goïi M laø ñieåm treân ñoaïn OS, ñaët
OM = x (0 < x < h).
a) Tính dieän tích thieát dieän (C) vuoâng goùc vôùi truïc taïi M.
b) Tính theå tích V cuûa khoái noùn ñænh O vaø ñaùy (C) theo R, h vaø x. Xaùc ñònh x sao cho V ñaït giaù trò lôùn nhaát. TTCM. Đỗ Lê Hải Thụy
Năm học : 2024– 2025 Trang 10