Đề cương học kì 2 Toán 9 năm 2023 – 2024 trường THCS Phan Chu Trinh – Hà Nội

TRƯỜNG THCS PHAN CHU TRINH
ĐỀ CƯƠNG ÔN TẬP HỌC KÌ II Năm học: 2023 – 2024 MÔN: TOÁN KHỐI 9
Dạng 1: Toán tổng hợp về rút gọn x 1 x 1 3 x 1
Bài 1. Cho biểu thức A    với x  0, x  1 x 1 x 1 x 1 a) Rút gọn biểu thức A
b) Tính giá trị của A khi x = 9.
c) Tìm giá trị của x để A  0,5
d) Tìm các giá trị nguyên của x để A nhận giá trị nguyên.
e) Tìm m để phương trình mA  x  2 có hai nghiệm phân biệt.
f) Tính các giá trị của x để A < 1
g) Tính giá trị nhỏ nhất của biểu thức A
Bài 2. Cho A = x  x 1 và B = 2 x x  x  2  với x > 0; x ≠ 1 x  2 x 1 x  x
a) Chứng minh rằng B = x  2 b) Cho P = A.B. So sánh P với 3. x x  1  x 1   1 2  Bài 3. Cho A  và B     :      x  1 x 1 x  x    x 1 x 1
a) Rút gọn biểu thức B với x  0; x  1.
b) Cho biểu thức P  A.B . Tìm x thỏa mãn: P. x 6 x 3 x4 . x  1  
Bài 4. Cho biểu thức A  và  1 x     . x  x B x 1
 x 1 x 1 2 x 1 a) Chứng minh rằng x B  với x  0,x  1 ; x  1 b) Với x  ,
 x  1. Hãy tìm giá trị lớn nhất của P  . AB . x  x 1 x 1 x Bài 5. Cho x A  và B    ( x  0; x  1.) x 1 x  x  2 x  2 x 1 x 1
a) Tính giá trị biểu thức A khi x 16 b) Chứng minh B  x 1
c) Tìm giá trị nhỏ nhất của biểu thức P  . A B khi x  1 4 x   1   x  x  Bài 6. Cho A  và 15 2 1 B     : với x  0; x  25 . 25  x  x 25 x 5    x  5  
a) Rút gọn biểu thức B .
b) Tìm tất cả các giá trị nguyên của x để biểu thức P  .
A B đạt giá trị nguyên lớn nhất.     Bài 7. Cho. 1 x 15 x 2 x 1 A  ; B     : 1 x x  25 x  5 x  5  
với x  0, x  25 tìm x để biểu thức M  B  A nhận giá trị nguyên. 1
Dạng 2: Các bài tập về hệ phương trình bậc nhất hai ẩn
Bài 1: Giải các hệ phương trình sau 3x  y  3 2
 x  y  3x  y  4 2
  x  y  x 1  4  x  2 y 1  5 a)  b)  c)  d)  . 2x  y  7   x  y    2x  y  5   x  y  3 x 1  5  4 x  y 1  2   1 2   2  3   3 15 2 x 1   5 x  y x  y  2 y 1     y  2 e)  f) x  4 2  g) 5 4   2   1 5 3   y 1  2   x 1   x  y x  y x  4  y  2 3    a   1 x  y  3
Bài 2: Cho hệ phương trình  ax  y  a
a) Giải hệ phương trình với a = - 2
b) Xác định giá trị của a để hệ có nghiệm duy nhất thỏa mãn x + y > 0 x  2y  3
Bài 3: Cho hệ phương trình xmy  Tìm giá trị nguyên của m để hệ có nghiệm duy nhất (x, 1
y) sao cho x, y là các số nguyên.
Dạng 3: Các bài toán liên quan đến phương trình bậc hai một ẩn và hệ thức Vi-ét Bài 1: Cho phương trình 2
x  m  2 x  2m  0 (1) với x là ẩn số, m là tham số.
a) Giải phương trình (1) với m = 1
b) Tìm m để phương trình (1) có hai nghiệm phân biệt x ; x thỏa mãn x  x  x x  3. 1 2 2 1 2 1 2
Bài 2. Cho phương trình : 2
x  2mx  2m 1 0 (với m là tham số)
a) Giải phương trình khi m = – 3.
b) Tìm m để phương trình có nghiệm phân biệt x1 và x2 thỏa mãn 2 2 2(x  x )  5x x  27 1 2 1 2 Bài 3: Cho phương trình 2 x  4x  m 1  0
a) Giải phương trình với m = - 11
b) Tìm m để phương trình có hai nghiệm x ; x thỏa mãn 2 2 x  x 10 1 2 1 2
c) Tìm m để phương trình có hai nghiệm dương
d) Tìm hệ thức liên hệ độc lập giữa hai nghiệm của phương trình Bài 4: Cho phương trình 2 x  2m   1 x  m  4  0
a) Tìm m để phương trình có hai nghiệm trái dấu
b) CMR phương trình có nghiệm phân biệt với mọi m
c) Chứng minh biểu thức M  x (1  x )  x (1  x ) không phụ thuộc m 1 2 2 1 Bài 5: Cho phương trình 2 x  4x  m  1  0(1)
a) Giải phương trình (1) khi m = 2
b) Tìm giá trị của m để phương trình (1) có hai nghiệm x ; x thỏa mãn 2 2 x  x  5 x  x 1 2  1 2 1 2
c) Tìm m để phương trình có nghiệm kép
d) Tìm m để nghiệm x ; x của phương trình thỏa mãn 3x  5x  6 1 2 1 2 Bài 6: Cho phương trình 2
x 2mx  2m 1  0  1 (m là tham số) Tìm m để pt  
1 có hai nghiệm phân biệt x ,x thỏa mãn 2x 2mx  1 2x 2mx 4  10. 1 1 2 2  1 2 2
Bài 7: Cho phương trình : x2 – 2mx + m2 – m + 1 = 0 (1) (m là tham số)
a) Giải phương trình (1) với m = 2.
b) Tìm m để phương trình (1) có hai nghiệm x 2 1, x2 thỏa mãn: x + 2mx = 9 1 2 .
Bài 8: Cho phương trình : 2
x  2x  (m  3)  0 (1) ( m là tham số)
Tìm m để phương trình  
1 có hai nghiệm phân biệt x , x thỏa mãn 2     1 2 x 2x x x 12 1 2 1 2 Bài 9. Cho phương trình 2
x  2(m 1)x  6m  4  0 (1) (với m là tham số)
a) Chứng minh rằng phương trình (1) luôn có hai nghiệm phân biệt với mọi m
b) Tìm m để phương trình (1) có hai nghiệm x ;x thỏa mãn 2m  2 2 x  x  4x  4 1 2 1 2 2
Dạng 4: Các bài toán về hàm số bậc nhất (d) và đồ thị hàm số (P) 2 y  ax a  0
Bài 1. Cho đường thẳng d : y  2
 x  3 và parabol   2 P : y  x .
a) Vẽ (d) và (P) trên cùng một hệ trục tọa độ Oxy.
b) Gọi A, B là giao điểm của (d) và (P) sao cho A có hoành độ nhỏ hơn hoành độ của điểm B. Tìm tọa độ điểm A và B.
c) Gọi H, K là hình chiếu của điểm A và B xuống trục tung. Tính diện tích tứ giác ABHK.
Bài 2. Trong cùng hệ trục tọa độ gọi (P) là đồ thị hàm số y = ax2 và (d) là đồ thị hsố y = - x + m.
a) Tìm a biết rằng (P) đi qua A(2; -1) và vẽ (P) với a tìm được.
b)Tìm m sao cho (d) tiếp xúc (P) (ở câu a) và tìm tọa độ tiếp điểm. Bài 3. Cho hàm số 2
y  x có đồ thị (P) và y  3
 x  2 có đồ thị là (d). Gọi (d) cắt (P) tại hai điểm
A, B với A là điểm có hoành độ lớn hơn B. Tính diện tích tam giác OAB. Bài 4. Cho parabol (P): 2
y  x và đường thẳng y  mx  m 1
a) Tìm m để (P) và (d) cắt nhau tại hai điểm phân biệt có hoành độ x , x thỏa mãn x  x  2 1 2 1 2
b) Tìm m để (P) và (d) cắt nhau tại hai điểm nằm cùng bên trái của trục tung. Bài 5. Cho hàm số 2
y  0,5x có đồ thị là parabol (P), đường thẳng y  mx  2. Tìm m để d cắt
(P) tại hai điểm phân biệt có hoành độ x , x mà 2 2
x  x có giá trị nhỏ nhất. 1 2 1 2
Bài 6. Cho đường thẳng d : y  2x  k  3 (k là tham số) và parabol   2 P : y  x
a) Tìm toạ độ giao điểm của (d) và (P) khi k  4.
b) Tìm giá trị của k để (P) và (d) cắt nhau tại 2 điểm phân biệt có tọa độ x ; y , x ; y thỏa mãn 2 2  1 1 
điều kiện x x (y  y )  6  1 2 1 2
Dạng 5: Giải bài toán bằng cách lập phương trình
Bài 1: Đề ủng hộ các bạn học sinh nghèo vùng núi, trong đợt ủng hộ thứ nhất hai lớp 9A và 9B đã
quyên góp được 450 cuốn vở mới, sang đợt ủng hộ thứ hai số vở quên góp được của lớp 9A tăng
15%, số vở quên góp được của lớp 9B tăng 10%. Vì vậy hai lớp đã quyên góp được 550 cuốn vở
mới. Hỏi trong đợt ủng hộ thứ nhất mỗi lớp đã quyên góp được bao nhiêu quyển vở mới.
Bài 2. Hai máy cày cùng cày một thửa ruộng thì sau 2 giờ xong. Nếu cày riêng thì máy thứ nhất hoàn
thành sớm hơn máy thứ hai là 3 giờ. Hỏi mỗi máy cày riêng thì thì sau bao lâu xong thửa ruộng.
Bài 3: Một phòng họp có 100 người được sắp xếp ngồi đều trên các dãy ghế. Nếu có thêm 44
người thì phải kê thêm 2 dãy ghế và mỗi dãy ghế thêm 2 người. Hỏi lúc đầu phòng họp có bao nhiêu dãy ghế?
Bài 4: Tìm số tự nhiên có hai chữ số biết rằng chữ số hàng đơn vị kém chữ số hàng chục 3 đơn vị,
tổng các bình phương hai chữ số của số đó bằng 45. 3
Bài 5: Hai lớp 9A,9B tham gia đợt trồng cây vì môi trường xanh sạch đẹp. Cả hai lớp có 81 bạn
tham gia. Mỗi bạn lớp 9A trồng được 5 cây, mỗi bạn lớp 9B trồng được 4 cây. Cả hai lớp trồng
được 364 cây. Tính số học sinh mỗi lớp.
Bài 6. Cho một hình chữ nhật. Nếu tăng độ dài mỗi cạnh của nó lên 1 cm thì diện tích của hình chữ nhật tăng thêm 2
13cm . Nếu giảm chiều dài đi 2 cm, chiều rộng đi 1 cm thì diện tích hình chữ nhật sẽ giảm đi 2
15cm . Tính chiều dài và chiều rộng của hình chữ nhật đã cho ?
Bài 7: Một hình chữ nhật có chu vi là 100m. Nếu tăng chiều rộng gấp đôi và giảm chiều dài 10m
thì diện tích hình chữ nhật tăng thêm 2
200m . Tính chiểu rộng của hình lúc đầu.
Bài 8: Một tam giác vuông có chu vi 30m, cạnh huyền 13m. Tính độ dài mỗi cạnh góc vuông.
Bài 9: Hai người đi xe đạp cùng khởi hành 1 lúc ở cùng một chỗ trên cùng một tuyến đường.
Người thứ nhất đi về phía bắc, người thứ hai đi về phía đông. Sau 2 giờ, họ cách nhau 60km. Biết
vận tốc người thứ nhất lớn hơn vận tốc người thứ hai là 6km/h. Tính vận tốc của mỗi người.
Bài 10: Một người đi xe đạp khởi hành từ điểm A. Sau đó 2 giờ 30 phút, một ngƣời đi xe máy
cũng khởi hành từ A đuổi theo người đi xe đạp và bắt kịp người đi xe đạp tại 1 điểm cách A là
60km. Tính vận tốc của mỗi ngườ biết vận tốc của người đi xe máy lớn hơn vận tốc của người đi xe đap là 25km/h
Bài 11: Một ca nô xuôi dòng 44km, rồi ngược dòng 27km hết tất cả 3h30. Biết vận tốc thực của ca
nô là 20km/h. Tính vận tốc dòng nước.
Bài 12. Một đội xe theo kế hoạch phải chuyển xong 200 tấn than trong một thời gian quy định, mỗi
ngày chuyển được một khối lượng than như nhau. Nhờ được bổ sung thêm xe, thực tế mỗi ngày đội
chuyển thêm được 5 tấn so với kế hoạch. Vì vậy chẳng những đã hoàn thành công việc sớm hơn 1
ngày so với quy định mà còn chuyển vượt mức kế hoạch 25 tấn. Tính khối lượng than mà đội xe phải
chuyển trong một ngày theo kế hoạch ?
Dạng 6: Các bài toán hình tổng hợp
Bài 1: Cho nửa đường tròn tâm O đường kính AB. Lấy điểm C thuộc nửa đường tròn và điểm D
nằm trên đoạn OA. Vẽ các tiếp tuyến Ax , By của nửa đường tròn. Đường thẳng qua C vuông góc
với CD cắt tiếp tuyến Ax, By lần lượt tại M và N.
a) Chứng minh các tứ giác ADCM và BDCN nội tiếp được đường tròn b) Chứng minh rằng  o MDN  90
c) Gọi P là giao điểm của AC và DM, Q là giao điểm của BC và DN. Chứng minh rằng PQ // AB. Bài 2: Cho A
 BC vuông tại A (AB > AC), trên cạnh AC lấy điểm M. Đường tròn đường kính
MC cắt BC tại E và cắt đường thẳng BM tại D (E khác C; D khác M)
a) Chứng minh tứ giác ABCD nội tiếp b) Chứng minh  ABD   MED
c) Đường thẳng AD cắt đường tròn đường kính MC tại N (N khác D). Đường thẳng MD cắt CN tại
K, MN cắt CD tại H. Chứng minh KH // NE
Bài 3: Từ một điểm A ở ngoài đường tròn (O), vẽ hai tiếp tuyến AB, AC và cát tuyến AMN của
đường tròn đó. (B, C, M, N nằm trên đường tròn và AM < AN). Gọi I là trung điểm của dây MN.
a) Chứng minh năm điểm A, B, I, O, C cùng nằm trên một đường tròn
b) Nếu AB = OB thì tứ giác ABOC là hình gì? Tại sao?
c) Tính diện tích hình tròn và độ dài đường tròn ngoại tiếp tứ giác ABOC theo bán kính R của (O) khi AB = R
Bài 4: Cho đoạn thẳng AB và C là một điểm nằm giữa A và B. Người ta kẻ cùng một nửa mặt
phẳng bờ AB hai tia Ax và By vuôn góc với AB. Trên tia Ax lấy một điểm I. 4
Tia Cz vuông góc với tia CI tại C và cắt By tại K. Đường tròn đường kính IC cắt IK tại P.
Chứng minh: a)Tứ giác CPKB nội tiếp b) AI.BK = AC.CB c) A  BP vuông
d) Giả sử A, B, I cố định. Hãy xác định vị trí điểm C sao cho diện tích hình thang vuông ABKI lớn nhất.
Bài 5: Qua điểm A cho trước nằm ngoài đường tròn (O) vẽ hai tiếp tuyến AB, AC (B, C là các tiếp
điểm), lấy điểm M trên cung nhỏ BC, vẽ MH  BC;MI  AC;MK  AB
a) Chứng minh các tứ giác BHMK, CHMI nội tiếp đường tròn b) Chứng minh 2 MH  MI.MK
c) Qua M vẽ tiếp tuyến với đường tròn (O) cắt AB, AC tại P, Q. Chứng minh chu vi APQ không
phụ thuộc vào vị trí điểm M.
Bài 6: Cho (O) có đường kính BC. Gọi A là một điểm thuộc cung BC  AB    AC. D là điểm
thuộc bán kính OC. Đường vuông góc với BC tại D cắt AC ở E, cắt tia BA ở F.
a) Chứng minh tứ giác ADCF nội tiếp
b) Gọi M là trung điểm của EF. Chứng minh  AME  2 ACB
c) Chứng minh AM là tiếp tuyến của (O)
d) Tính diện tích hình giới hạn bởi các đoạn thẳng BC, BA và cung nhỏ AC của (O) biết BC = 8cm;  o ABC  60 .
Bài 7: Cho đường tròn (O; R) và đường thẳng d không qua O cắt đường tròn tại hai điểm A, B. Lấy
một điểm M trên tia đối của tia BA, kẻ hai tiếp tuyến MC, MD với đường tòn (C, D là các tiếp
điểm). Gọi H là trung điểm của AB
a) Chứng minh rằng các điểm C, D, O, H cùng nằm trên một đường tròn
b) Đoạn OM cắt đường tròn tại I. Chứng minh rằng I là tâm đường tròn nội tiếp M  CD
c) Đường thẳng qua O, vuông góc với OM cắt các tia MC, MD thứ tự tại P và Q. Tìm vị trí của
điểm M trên d sao cho diện tích tam giác MPQ bé nhất.
Bài 8. Cho tam giác ABC nhọn có AB  AC . Đường tròn tâm O đường kính BC cắt các cạnh AB,
AC lần lượt tại các điểm M, N (M khác B, N khác C). Gọi H là giao điểm của BN và CM, P là giao điểm của AH và BC.
a) Chứng minh AMHN là tứ giác nội tiếp. b) Cminh AH.AP  AN.AC .
c) Từ điểm A kẻ các tiếp tuyến AE, AF của đường tròn tâm O đường kính BC (E, F là các tiếp
điểm) (F thuộc cung nhỏ CN).
Chứng minh ΔAEH” ΔAPE và ba điểm E, H, F thẳng hàng.
Bài 9. Cho đường tròn O; R đường kính AB . Dây MN vuông góc với AB tại I sao cho IA  IB .
Trên đoạn MI lấy điểm E E  M , E  I  . Tia AE cắt đường tròn tại điểm thứ hai là K .
a) Chứng minh bốn điểm: B, E, I , K cùng thuộc một đường tròn; b) Chứng minh: 2 AE.AK=AM ; c) Chứng minh: 2 BI.BA+AE.AK=4R ;
d) Xác định vị trí của điểm I sao cho chu vi tam giác MIO đạt giá trị lớn nhất. Tính giá trị đó.
Bài 10. Cho ∆ABC nội tiếp đường tròn tâm O đường kính AB sao cho AC< BC; E là một điểm thuộc
đoạn BC (E khác B và C). Tia AE cắt đường tròn (O) tại điểm thứ hai D. Kẻ EH  AB tại H.
a) Chứng minh 4 điểm A, C, E, H cùng nằm trên một đường tròn.
b) Tia CH cắt (O) tại điểm thứ hai F. Chứng minh rằng EH // DF.
c) Chứng minh rằng đường tròn ngoại tiếp ∆CHO đi qua điểm D.
d) Gọi I và K lần lượt là hình chiếu vuông góc của điểm F trên các đường thẳng CA và CB. Chứng
minh rằng AB, DF, IK cùng đi qua một điểm. 5
Bài 11: Cho điểm A nằm ngoài (O;R). Từ điểm A vẽ các tiếp tuyến AB và AC với B, C là các tiếp
điểm và cát tuyến AMN với đường tròn (O;R). MN không đi qua tâm O và AM  AN
a) Chứng minh tứ giác ABOC là tứ giác nội tiếp b) Chứng minh 2 AM .AN  AB
c) Tiếp tuyến tại điểm N của (O;R) cắt đường thẳng BC tại điểm F. Chứng minh đường thằng FM
là tiếp tuyến của (O;R) (HD cm FMNOH cùng thuộc 1 đt)
d) Gọi P là giao điểm của dây BC và dây MN. E là giao điểm của đường tròn ngoại tiếp tam giác
MON và đường tròn ngoại tiếp tứ giác ABOC với E khác O Chứng minh ba điểm P, E, O thẳng hàng
Bài 12: Một viên than tổ ong có dạng hình trụ, đường kính đáy là 114mm, chiều cao là 100mm.
Viên than này có 19 lỗ “tổ ong” hình trụ có trục song song với trục của viên than, mỗi lỗ có đường
kính 12mm. Tính thể tích nhiên liệu đã được nén của mỗi viên than (làm tròn đến cm3).
Bài 13: Một cửa hàng bán xăng dầu dự định đặt làm một chiếc bồn chứa dầu bằng sắt hình trụ có chiều
cao 1,8 m, bán kính đáy 0,6 m. Hỏi chiếc bồn đó chứa đầy được bao nhiêu lít dầu? (Bỏ qua bề dầy của bồn).
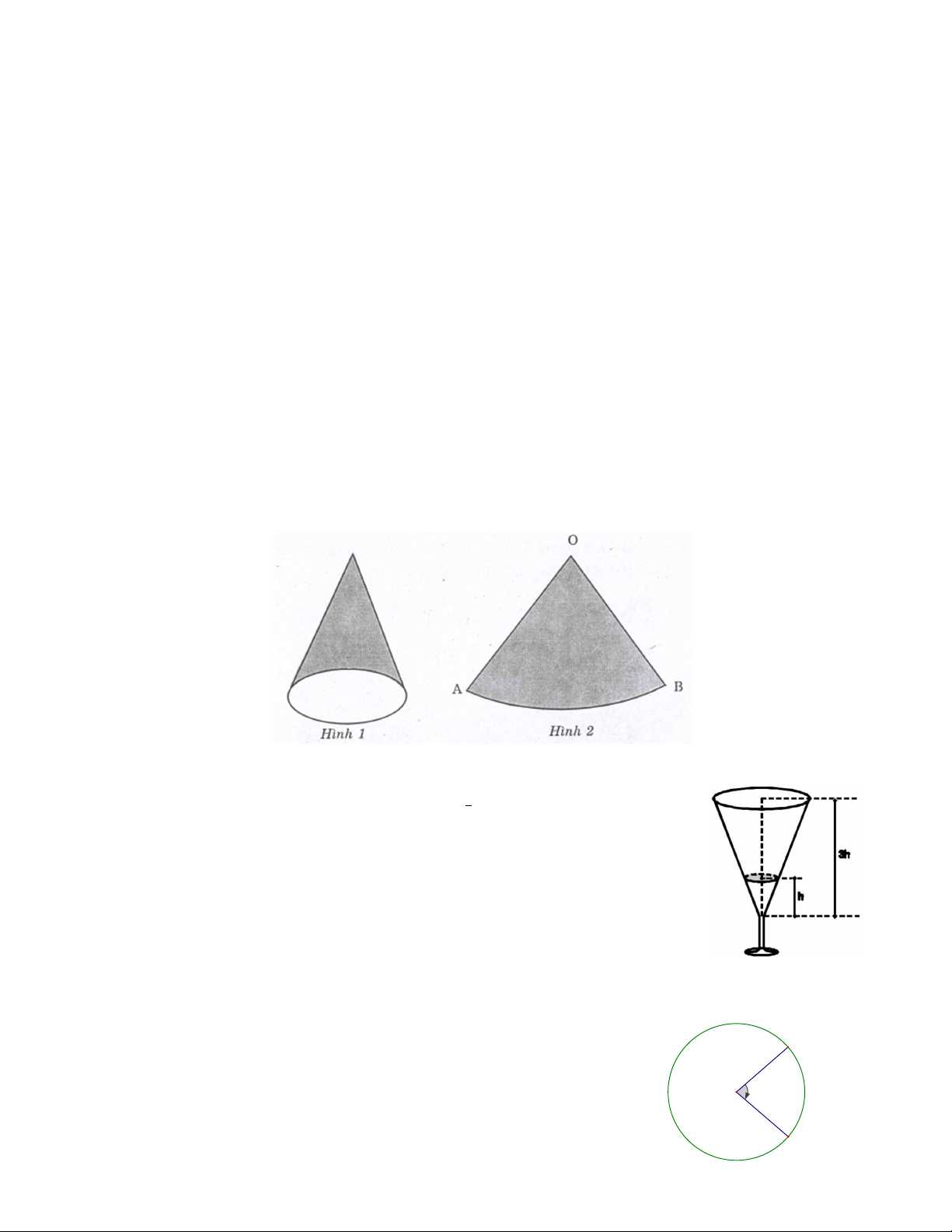
Bài 14: Để làm một cái mũ chú hề như hình 1, mũ là hình nón có đường kính đáy là 160mm, chiều
cao là 400mm. Bạn An cần một tờ giấy thủ công màu và cắt ra thành một hình quạt tròn OAB (hình 2)
(Độ dài làm tròn đến một chữu số thập phân).
Hãy xác định bán kính hình quạt và góc AOB (làm tròn đến độ, lấy 𝜋 ≈ 3,14)
Bài 15: Một chiếc cốc hình nón đựng rượu đến 13 chiều cao của cốc. Biết thể
tích của rượu trong cốc là 2cm3. Tính thể tích của cốc.
Bài 16: Đường tròn lớn của Trái Đất dài khoảng 40000km. Tính bán kính Trái Đất.
Bài 17: Chân một đống cát đổ trên một nền phẳng nằm ngang là một hình tròn có chu vi 10m. Hỏi
chân đống cát đó chiếm một diện tích là bao nhiêu mét vuông? A
Bài 18: Cho đường tròn tâm O có bán kính R = 3cm,  0 AOB  78 . 3cm a) Tính sđ  AqB và sđ  ApB 780 q O p b) Tính độ dài hai  Aq , B  ApB
c) Tính diện tích hình quạt tròn OAqB B 6
Bài 19: Một vệ tinh nhân tạo địa tĩnh chuyển động theo quỹ đạo
tròn cách bề mặt Trái Đất một khoảng 36000km, tâm quỹ đạo vệ
tinh trùng với tâm O của Trái Đất. Vệ tinh phát tính hiệu vô tuyến
theo đường thẳng đến một vị trí trên mặt đất. Hỏi vị trí xa nhất
trên Trái Đất có thể nhận tín hiệu từ vệ tinh này cách vệ tinh một
khoảng là bao nhiêu km? (ghi kết quả gần đúng chính xác đến
hàng đơn vị). Biết rằng Trái Đất được xem như một hình cầu có bán kính 6400km.
Dạng 7: Một số bài toán nâng cao
Bài 1: Giả thiết a  6. Xác định giá trị nhỏ nhất của biểu thức T  a  2 3a  9  a  2 3a  9 1 1 1
Bài 2: Cho a, b, c > 0 và a  b  c  1. Chứng minh rằng    9 2 2 2 a  2bc b  2ca c 1ab
Bài 3: Cho x  0; y  0 thỏa mãn 2 x  y 1. Chứng minh rằng 1 x  y  5
Bài 4: Giải phương trình 4 2 4
x 1  x  x  x  1  1 x 1
Bài 5: Giải phương trình 2
2x  1  7  2x  4x  12x  13 a  b b  c c  a  a b c 
Bài 6: Cho a, b, c > 0, chứng minh:    4     c a b
 b  c c  a a  b  3 9 4
Bài 7: a) Cho a,b, c  0 thỏa mãn a  2b  3c  20. Tìm giá trị nhỏ nhất của A  a  b  c    a 2b c
b) Tìm cặp số (x;y) với y là số nhỏ nhất thỏa mãn điều kiện: x2 + 5y2 + 2y - 4xy - 3 = 0 1 1
c) Cho x, y > 0 và thỏa mãn x2 + y2 = 1.Tìm giá trị nhỏ nhất của biểu thức P  x   y  x y 7