







Preview text:
BÀI TẬP: GIẢI TÍCH II
CHƯƠNG V: TÍCH PHÂN MẶT
TÍCH PHÂN MẶT LOẠI II
Bài 1: Tính các tích phân mặt loại hai:
1. I yzdydz zxdzdx xydxdy S
S là phía ngoài của tứ diện: x y z 0, x y z a(a 0) . x2 y2 z2 2. I
zdxdy ; S là phía ngoài của mặt ellipsoïde: 1 2 a b2 c2 S
3. I x2dydz y2dzdx z2dxdy ; S là phía ngoài của: S
a) Nửa hình cầu: x2 y2 z2 a2 , z 0 .
b) Hình cầu: (x 1)2 ( y 1)2 (z 2)2 a2 ?
4. I y zdydz z xdzdx x ydxdy S
S là phía ngoài của mặt nón: x2 y2 z2 ,0 z h x2 y2
5. F t f x, y, zds ; S : x2 y2 z2 t2 , f S 0 : z
Hướng dẫn giải
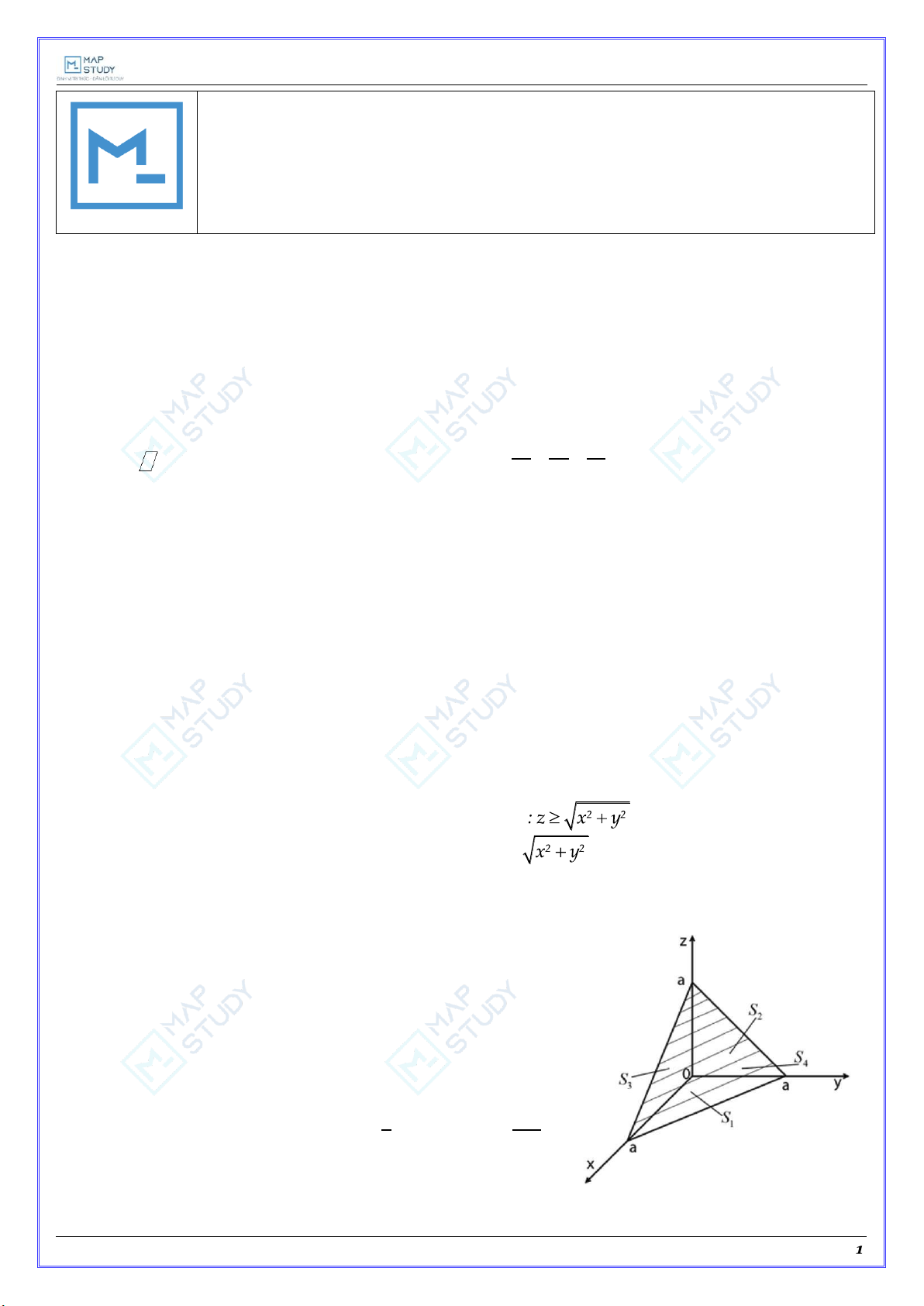
1) Ta có (hình vẽ): I S S1 S2 S3 S4
Trên S : z 0,dz 0 . 1
Phía ngoài của tứ diện ứng với phía dưới của S1 . a ax 1 a a 4
Do đó: I xydxdy dx xydy
x a x2dx 1 2 24 S1 0 0 0
Thầy Phạm Ngọc Lam Trường a 4
Tương tự: I 2 I3 24 S2 S3
Ta cũng được: I 4
xydxdy yzdydz zxdzdx S4 S1 S2 S3
S , S , S là hình chiếu trên các mặt phẳng tọa độ xOy, yOz, zOx của S . 1 2 3 4
Dấu + chỉ phía trên của mặt phẳng x y z a , ứng với phía ngoài của tứ diện đối với các mặt phẳng tọa độ đó. 3a4
Theo trên thì: I . 4 24 a4 a4 a4 3a4
Vậy: I I I I I 0. 1 2 3 4 24 24 24 24
2) Ta có phương trình của nửa trên (dưới) của ellipsoïde đã cho là z c x2
y2 z c x2 y2 1 1 a2 b2 a2 b2 x2 y2
Các nửa này có hình chiếu trên mặt phẳng xOy là miền D : 1 . a2 b2 x2 y2
Do đó: I c c
dxdy 2c dxdy 1 2 2 a b D D
Chuyển sang tọa độ độc cực suy rộng: x arcosφ, y brsinφ , ta có: 2π 1 1 1 4πabc 3/ 2
I 2c dφ 1 r2 abrdr 4πabc
1 r 2 3 3 0 0 0
3) a) Phương trình của nửa mặt cầu đã cho đối với các mặt phẳng tọa dộ xOy, yOz, zOx là:
z a2 x2 y2 , x a2 y2 z2 , y a2 x2 z2 2 Do đó: I 1 x d2 ydz 2 2 2
2 2 2 2
a y z a y z
dydz 0 S
y2 z2 a2 ,z0 Tương tự:
Thầy Phạm Ngọc Lam Trường 2 I 2
y2dzdx 0 S I
a2 x2 y2 2dxdy 3 z2dxdy S
x2 y2 a2 2π a a a2r2 r4 πa4
Chuyển sang tọa độ độc cực ta có: I dφ a2 r2 rdr 2π 3 2 0 0 2 4 0 4
Vậy: I I I I 0 0 πa πa4 1 2 3 2 2 b) Xét I 1 z2dxdy S
Mặt S gồm 2 phần:
S1 (phía trên mặt phẳng z 2 ): z 2 a2 x2 y2
S (phía dưới mặt phẳng z 2 : z 2 a2 x2 y2 2
Hình chiếu của S ,S trên mặt phẳng x Oy là miền D : (x 1)2 (y 1)2 a2 1 2 Ta có: 2 I 2 2 2
2 a 2 (x 1) 2 ( y 1) 2 2 dxdy 8 2 a (x 1) 2 ( y 1) 2dxdy 1
2 a (x 1) ( y 1) D D
Chuyển sang tọa độ độc cực: x 1 rcosφ, y 1 rsinφ,0 φ 2π 2π a 1 3/ 2 16π a thì: I 8
a2 r2rdr 16π
a2 r2 a3 1 dφ 3 0 3 0 0 8π 8π Tương tự: I a3 , I a3 2 3 3 3 32
Vậy: I I I I πa3 1 2 3 3
4) Xét I 1
x ydxdy , hình chiếu của mặt nón trên mặt phẳng xOy là miền D : x2 y2 h2 , phía S
ngoài của mặt nón có pháp tuyến hợp với Oz một góc tù, do đó:
Thầy Phạm Ngọc Lam Trường 2π h 2π h
I x ydxdy dφ rcosφ sinφrdr cosφ sinφdφ r2dr 0 1 S 0 0 0 0 Xét I 2
z xdzdx , đối với mặt phẳng xOy,S gồm 2 phần S : y z2 x2 ,S : y cùng 1 2 S
có hình chiếu trên mặt phẳng xOy là miền D giới hạn bởi: z x, z x, z h và có pháp tuyến
ngược hướng nhau. Do đó I 0 , tương tự I 0 . 2 3
Vậy: I I I I 0. 1 2 3
5) Ở đây: z t2 x2 y2 t
S 1 z'2 z'2dxdy dxdy dxdy. x y
t2 x2 y2
vì f 0 trên mặt cầu S giới hạn bởi mặt nón z x2 y2 nên: 1
x2 y2 dxdy
F t x2 y2 ds t s
t2 x2 y2 1 D t 2
D là hình chiếu của phần mặt cầu S trên mặt phẳng xOy : x2 y2 1 2
(khử z từ: x2 y2 z2 t2 và z x2 y2 ).
Chuyển sang tọa độ độc cực và do đối xứng, ta có: t t / π/ 2 2 3 r dr 2 r2dr2
t / 2 t2 r2 t2 d t2 r2
F t 4 t π t dφ π t 0 0 t2 r2 0 t2 r2 0 t2 r2 t/ 2 1/
d t2 r2 2
π t t2 r2d t2 r2 t2 0 0 t2 r2 t/ 2 2 t/ 2 π
π t t2 r2 3/ 2 t2 2 t4 t2 r 2
8 5 2 . 3 6 0 0
Bài 2: Áp dụng công thức Ostrogradski, tính:
Thầy Phạm Ngọc Lam Trường 4
x2dydz y2dzdx z2dxdy , S: phía ngoài của hình lập phương: 0 x, y, z a 1) I S
xdydz ydzdx zdxdy,S : phía ngoài của tứ diện: x y z a, x 0, y 0, z 0 2) I S
x y zdydz y z xdzdx z x ydxdy 3) I S
S: phía ngoài của mặt: x y z y z x z x y 1.
4) I x2cos y2cos z2cos ds S x2 y2 z2
S: phía ngoài của phần mặt nón:
0 0 z b a2 a2 b2
5) I x, y, z cosn,edS S
S: mặt trơn kín, e const, n là pháp tuyến ngoài của S . cosr,n
dS (tích phân Gauss); S: trơn, kín giới hạn miền V ; n : pháp tuyến
6) I x, y, z r2 S
ngoài của S tại ,, S,r ( x)2 ( y)2 ( z)2 ,x, y, z R3
Hướng dẫn giải
1) Các hàm P x2 ,Q y2 , R z2 là các hàm luỹ thừa nên chúng cùng các đạo hàm riêng của chúng
liên tục trong hình lập phương 0 x , y, z a, đó là một miền compact. Do đó:
I x2dydz y2dzdx z2dxdy 2x y zdV S V a a a a a a z2
2 dx dyx y zdz 2 dx x y z dy 2 0 0 0 0 0 0 a a a a a2 a y2 a2 a a2x2
2 dx ax ay dy 2 axy a y dx 2a2x a3 dx 2
a3x 3a4 . 0 0 2 0 2 2 0 0 2 0 2) Tương tự như 1):
I xdydz ydzdx zdxdy 1 1 1dV 3V S V
Thầy Phạm Ngọc Lam Trường a 3
V là thể tích tứ diện: V . 6 a 3 a3
Do đó: I 3 . 6 2
3) Ở đây: P x y z,Q y z x, R z x y
Do đó: I 1 1 1dV 3V V
V : thể tích của miền giới hạn bởi S .
Dùng phép đổi biến tổng quát: u x y z, v y z x, w z x y.
D x, y, z 1 1 1 Ta có: J
D u, v, w D u,v,w 1 1 1 4 D x, y, z 1 1 1 1 1 1 3 3 1 Do đó: I
dudvdw 8 dudvdw 6 1. 4 4 6
u v w 1
u v w 1 u,v,w0
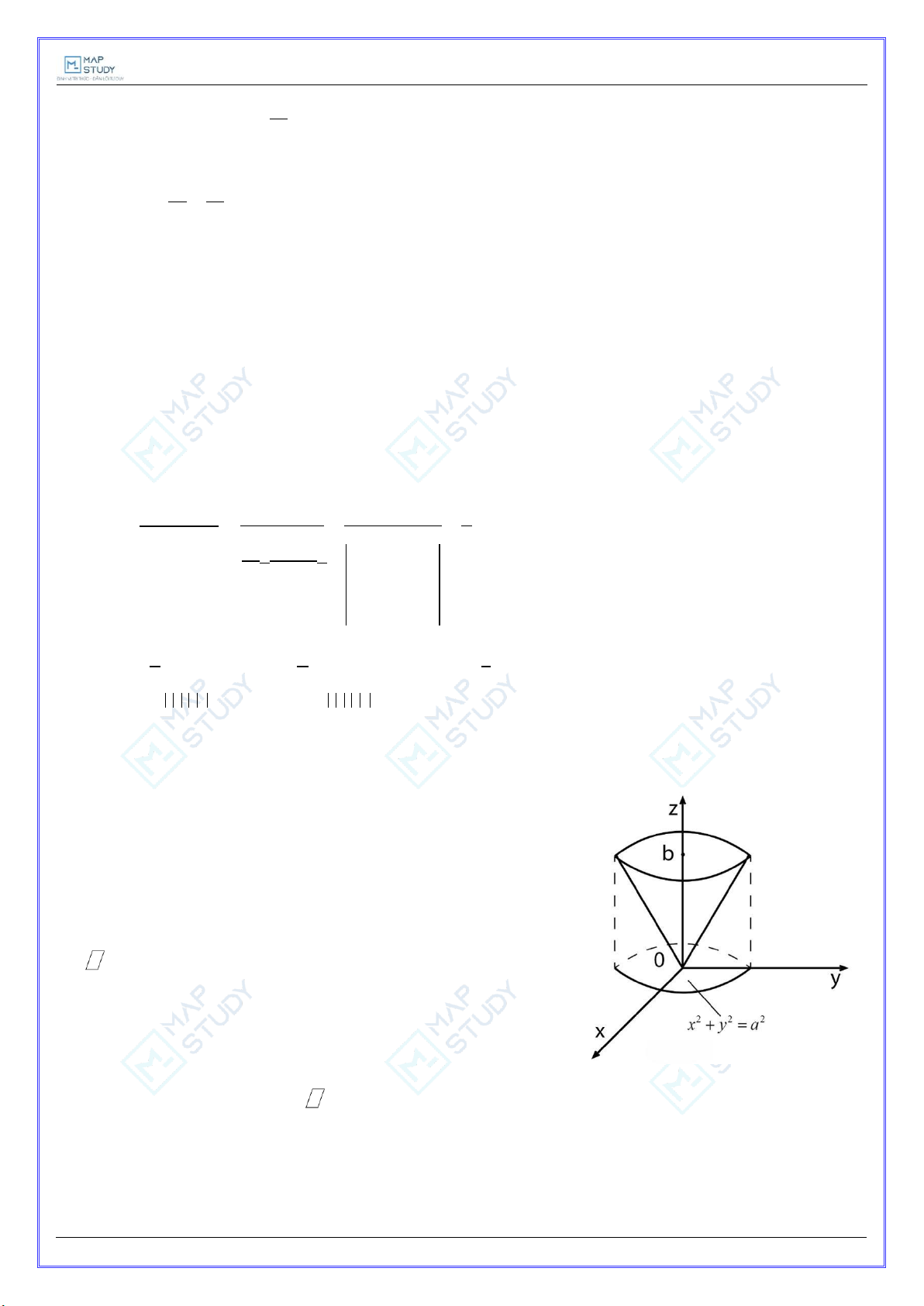
4) S: không kín, ta bổ xung thêm mặt S : z b để được mặt S S kín (hình vẽ). 1 1
Áp dụng công thức Ostrogradski, đối với mặt kín S S ta có: 1
I x2dydz y2dzdx z2dxdy S
x21ydz y2dzdx z2dxdy x2dydz y2dzdx z2dxdy SS1 S1
Trên S : z b,dz 0 1
nên: b2dxdy b2.a2.π, 2x y zdV S1
x2 y2 a2 SS1 V
Chuyển sang toạ độ trụ:
Thầy Phạm Ngọc Lam Trường 6 2π a b 2π
a 2 b 3 b2 b2
2 dφ rdr r cosφ sinφ zdz 2 dφ br r cosφ sinφ r r 3 2 dr SS a 2 2a 1 0 0 b 0 0 r a 2π a3b a2b2 a2b2 a2b2
2 cosφ sinφ
dφ 0 2 2π π 0 12 8 8 2 a 2b 2π a2b2π Vậy: I a2b2π . 2 2
5) Giả sử e a,b,c const,n cosα,cosβ,cosγ.
n e acosα bcosβ ccosγ
cose ,n n e
a2 b2 c2
I x, y, z cos n, e ds acosα bcosβ ccosγ
adydz bdzdx cdxdy ds S S
a2 b2 c2 S
a2 b2 c2 a b b dV
0 dV 0 x
a2 b2 c2 y y D
a2 b2 c2
a2 b2 c2 V 6) Xét:
a) S không bao quanh điểm x, y, z : r n
Ta có: cosr ,n r n ξ x η y ξ z
và: I x, y, z cosα cosβ cosγds 3 3 3 S r r r
Áp dụng công thức Ostrogradski (các hàm thỏa mãn các điều kiện của công thức):
3 3(ξ x)2 3(η y)2 3(ζ z)2 3 3
I x, y, z dV 3 5 3 dV 0. 3 V r r V r r
b) Mặt S bao quanh điểm (x, y ,z) (hình vẽ).
Xét mặt cầu S tâm M bán kính . Khi đó các hàm lại có đủ 1
các điều kiện để áp dụng công thức Ostrogradski trong miền
V1 gồm giữa S và S1 .
cosr n
ds 0.dV 0 (theo a) r2 ss1 V1
Thầy Phạm Ngọc Lam Trường
cosr n
cosr n
Do đó: I x, y, z 2 ds ds 2 r S S r 1
(Pháp tuyến ngoài của S và pháp tuyến trong của S1 là ngược nhau, cùng là pháp tuyến ngoài của S S ). 1 1
Vậy: I x, y, z r n r 1 ds
4πε2 4π . (vì với S : ) ds ds
r / /n và r ε r 3 3 2 2 1 ε S S r S ε 1 1 1
Bài 3: Áp dụng công thức Stockes, tính:
1) I y zdx z xdy x ydz C là đường x2 y2 z2 a2 , x y z 0 theo chiều ngược C
kim đồng hồ nếu nhìn từ phía dương của trục Ox .
2) I y zdx z xdy x ydz C
C là ellipse x2 y2 1, x z 1, theo chiều ngược kim đồng hồ nếu nhìn từ phía dương của Ox .
3) I y2 z2 dx z2 x2 dy x2 y2 dz C
C là đường x2 y2 z2 2Rx,x2 y2 2rx(0 r R,z 0) theo chiều sao cho phần nhỏ nhất của
phía ngoài của phần mặt cầu giới hạn bởi C ở bên trái.
y2z2dx z2x2dy x2y2dz 4) I C
C là đường khép kín: x acost, y acos2t, z acos3t , theo chiều tăng của t.
Hướng dẫn giải
1) Áp dụng công thức Stockes dối với S là mặtt tròn giới hạn bởi đường tròn
x2 y2 z2 a2 , x y z 0
(ở đây P y z,Q z x , R x y thỏa mãn các điều kiện của công thức).
Thầy Phạm Ngọc Lam Trường 8 cosα cosβ cosγ dx
I y zdx z xdy x ydz x y ds C S z x
y z z x x y
1 1cosα 1 1cosβ 1 1cosγds 0. S
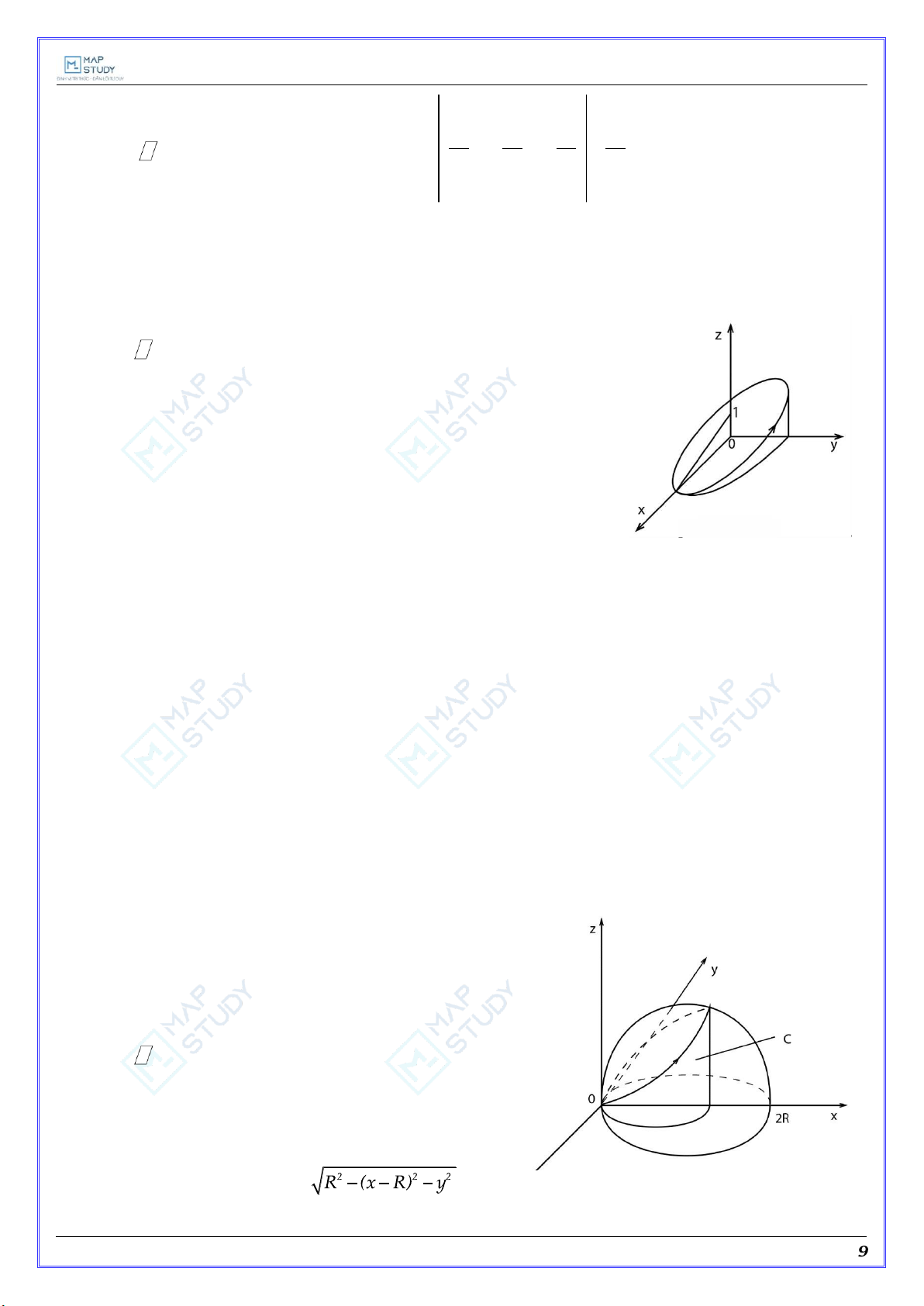
2) Áp dụng công thức Stockes vào S là hình ellipse giới hạn bởi ellipse x2 y2 1, x z 1 (hình vẽ).
Ta có: I y zdx z xdy x ydz C
2dydz dzdx dxdy S 2
dydz dzdx dxdy D 1 D2 D3 3
D : hình chiếu của S trên mặt phẳng x Oy : x2 y2 1, do đó: dxdy π12 π D3
D2 : hình chiếu của S trên mặt phẳng xOz : D 0 , do đó: 2 dzdx 0 D2
D : hình chiếu của S trên mặt phảng yOz : khử x từ x2 y2 1, x z 1, ta có: D : y2 (z 1)2 1 1 3
, do đó: dydz π12 π D3
Vậy: I 2π 0 π 4π
3) Áp dụng công thức Stockes đối với phần mặt cầu
x2 y2 z2 2Rx giới hạn bởi mặt trụ x2 y2 2rx
với z 0 (hình vẽ).
Ta có: I y2 z2 dx z2 x2 dy x2 y2 dz C
2 y zcosα z xcosβ x ycosγds S
ở đây phương trình của S : z
Thầy Phạm Ngọc Lam Trường z x R cosα x
1 z'2 z'2
z 1 z'2 z'2 x y x y ' z y cosβ y ,
1 z'2 z'2
z 1 z'2 z'2 x y x y 11 cosγ
1 z'2 z'2 x y
(lấy cosγ 0 , vì pháp tuyến của phía trên của S làm với Oz một góc tù). x R y Do đó: cosα
cosγ,cosβ cosγ z z
y zx R z x y
và: I 2
x ycosγds z z S 2
y zx R z x y 2R y 2 x z ydxdy
1 dxdy 2πRr z
x2 y2 2rx
x2 y2 2rx y y y (vì
dxdy 0 do hàm trên hai nửa hình tròn lấy các giá trị: như nhau nhưng trái dấu z z z 2 2
x y 2rx nhau).
4) Khi 0 t π thì M x, y, z vẽ đường C tại Aa,a,a đến Ba,a,a và khi π t 2π; M vẫn
vẽ đường C nhưng theo hướng ngược lại từ Ba,a,a đến Aa,a,a, do đó đường C là khép kín
nhưng không giới hạn mặt S nào, do đó theo công thức Stockes: I 0 .
Bài 4: Tìm tọa độ trọng tâm của:
1) Phần mặt đồng chất p 1 : az x2 y2 0 z a
2) Phần mặt đồng chất ρ 1 : z x2 y2 bị cắt bởi mặt trụ x2 y2 ax .
Tìm moment quán tính đối với gốc tọa độ của các mặt dồng chất ρ 1 .
3) Mặt toàn phần: - a x, y,z a
4) Mặt toàn phần: x2 y2 R2 ,0 z H của hình trụ.
Thầy Phạm Ngọc Lam Trường 10
Hướng dẫn giải
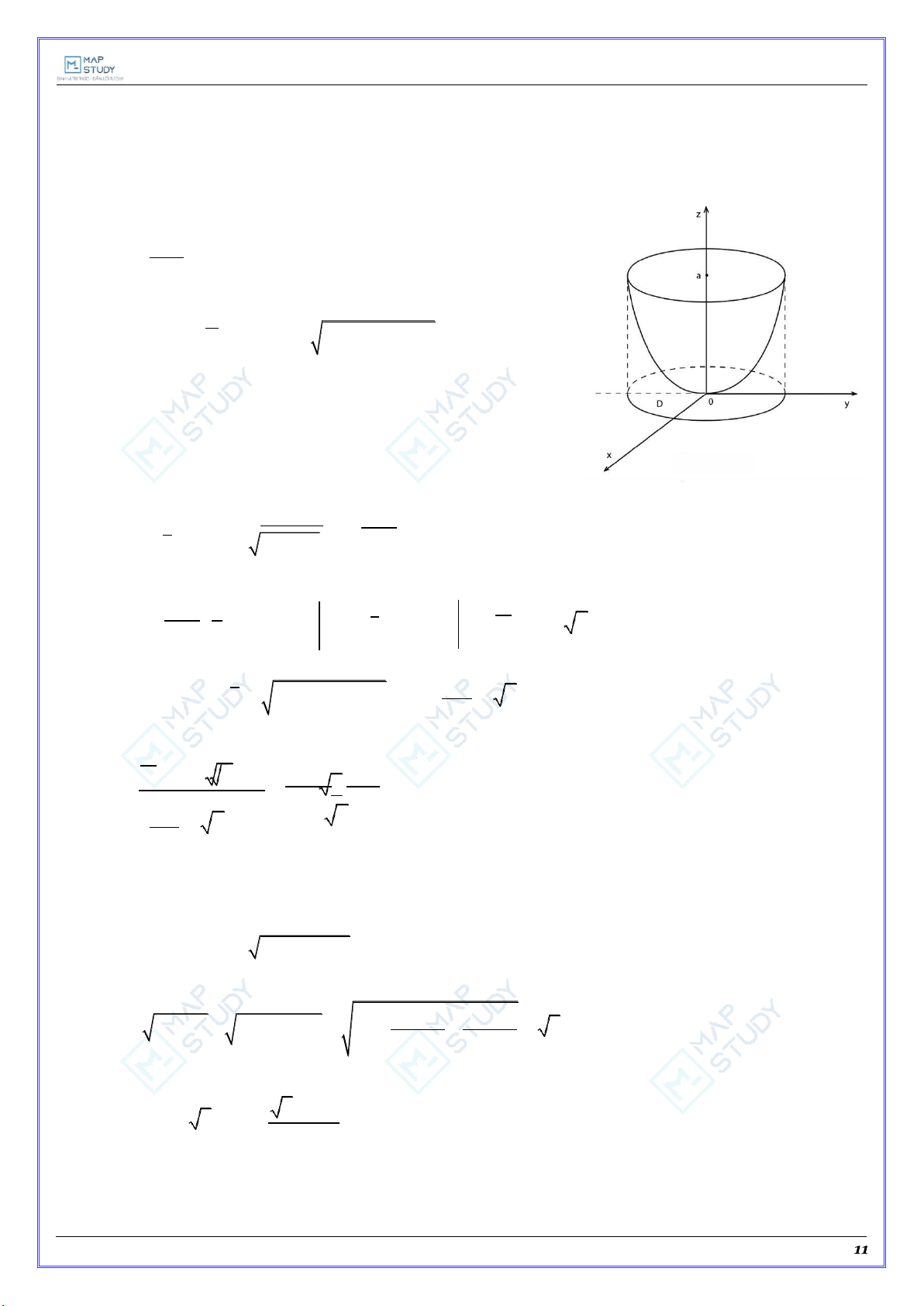
1) Vì là mặt đồng chất và do đối xứng nên trọng tâm của nó phải ở trên trục Oz (hình vẽ) nghĩa là
x y 0 . G G Mxy Ta có: z G M 1
với: M zds x2 y2
a2 4 x2 y2 dxdy xy a2 S D
với D : x2 y2 a2
Chuyển sang tọa độ độc cực ta có: 1 2π a π a 3/ 2 1/ 2 M
dφ r2 a2 4r2rdr
a2 4r2 a2 a2 4r2 d a2 4r2 xy 2 a 16a2 0 0 0 a 2 a π π 2 5/ 2
a2 4r2 a2 a2 4r2 a3 25 5 1 16a2 5 60 0 3 0 1 πa2
Tương tự: M dS a2 4 x2 y2 dxdy 5 5 1. a 6 S D
π a3 25 5 1 Vậy: z
25 1 60 5 .a G
πa2 5 5 1 10 5 5 1 6
2) Tương tự như 1), ta có:
M dS 1 z'2x z'2dxdy S
x2 y2 ax
ở đây: z x2 y2 ; ; 1 z'2 z'2 1 x2 y2 2 x y x2 y2 x2 y2 M
x2 y2 ax
2 π a2 Vậy: 2dxdy 4
Thầy Phạm Ngọc Lam Trường 1 4 x xds x 2dxdy G M S
2 πa2 x2 y2 ax 4 π/ 2 acosφ 4a π/ 2 8a π/ 2 8a 31 π a
cosφdφ r2dr cos4φdφ cos4φdφ
πa2 π/ 2 0 3π 3π 3π 4 2 2 2 π/ 2 0 1 4 π/2 acosφ 4a π/ 2 yds
cos3φsinφdφ 0. (vì cos3φsinφ là hàm lẻ) G y M
πa2 sinφdφ r2dr 3π S π/ 2 0 π/ 2 1 4 π/2 acosφ 4a π/ 2 4a 2 16a zds
cos3φdφ 2 G z M
πa2 dφ r2dr 3π 3π 3 9π S π/ 2 0 π/ 2
3) Moment quán tính của mặt toàn phần của hình lập phương đã cho đối với gốc tọa độ là: 6 I 0
∬ x2 y2 z2 ds. S i1 i
S i 1,6 là các mặt của khối lập phương 1
+) Xét S1 : a x a,a y a,z a,ds dxdy. Do đó: a a a a a 20a4 3
x2 y2 z2 ds dx x2 y2 a2 dy 4dxx2 y2 a2 dy 4 ax2 4 a dx 3 3 S 1 a a 0 0 0 6.20a4
Do đối xứng nên: I 6I 40a4 0 1 3
5) Moment quán tính của mặt toàn phần S của hình trụ đối với gốc tọa độ là:
I x2 y2 z2 ds 0 S Sd St Sb
S ,S , S là đáy dưới, dáy trên và mặt bên của hình trụ. d 1 b
Với S : z 0, S : z H,ds dxdy , hình chiếu của chúng trên mặt phẳng xOy cùng là miền d t
D : x2 y2 R2 , do đó:
2x2 y2 H2 dxdy Sd St D 2π R
πR2H2 2
x2 y2 dxdy πR2H 2 2 dφr3dr πR2H 2 πR4 D 0 0
Thầy Phạm Ngọc Lam Trường 12 với S : y
đối với mặt phẳng xOz,dS Rdxdz và hình chiếu của S trên mặt phẳng b b xOz là D : 1
R x R,0 z H, do đó: R H3 dx H 2 2 2R
R z dz 2πRH R 3 S b R 0 Vậy: I
πR R(R H) H 0 2 2 3 3 HẾT
Thầy Phạm Ngọc Lam Trường
