







Preview text:
Đề cương bài giảng chương II
ĐẠO HÀM - VI PHÂN HÀM MỘT BIẾN Chương II :
ĐẠO HÀM _ VI PHÂN HÀM MỘT BIẾN
. ĐẠO HÀM : (SV tự đọc)
1.1. Đạo hàm của hàm số:
1. Đạo hàm của hàm số tại một điểm
2. Ý nghĩa của đạo hàm
a. Ý nghĩa hình học
b. Ý nghĩa cơ học
3. Đạo hàm một phía
4. Đạo hàm trong một khoảng , đoạn
5. Điều kiện để hàm số có đạo hàm: Điều kiện cần và đủ để hàm số y = f ( x) có đạo hàm
tại x là nó có đạo hàm bên trái và đạo hàm bên phải tại x và f '( x + ) = f '( x – ) . 0 0 0 0
6. Liên hệ giữa tính liên tục và tính có đạo hàm của hàm số.
1.2. Các qui tắc tính đạo hàm :
1. Cho u, v là các hàm theo biến x và có đạo hàm , khi đó:
a. (u v) ' = u ' v '.
b. (uv)' = u 'v + uv ' ( / u
u ' v – uv ' c. , v s 0 v = v2
d. Nếu hàm y = y (u ) có đạo hàm đối với u và u = u ( x) có đạo hàm đối với x .Khi đó:
y ' = u ' .y ' x x u
e. Nếu hàm số y = f ( x) có hàm ngược x = f –1 ( y) có đạo hàm tại y0 là ( f –1 )'( y ) s 0 0
và y = f ( x) liên tục tại x = f –1 ( y ) thì tồn tại đạo hàm f '( x ) với 0 0 0 1
f '( x0 ) = ( f –1 )'( y ) . 0
1.3. Bảng công thức tính đạo hàm:
Cho u ( x) là hàm theo biến x có đạo hàm đối với x là u ' . Khi đó :
1. y = c ( c là hằng số ) y ' = 0 . 2.
y = xα (α ϵ R)
y ' = α xα –1 ;
y = uα (α ϵ R)
y ' = αu 'uα –1 . 3. y = x y ' = 1
( x > 0) ; y = u y ' = u ' (u > 0) 2 x 2 u 4. y = 1 y ' = – 1 ( x s 0) ; y = 1
y ' = – u ' (u s 0) x x2 u u2 5. y = ex y ' = ex ; y = eu
y ' = u 'eu 6. y = ax
y ' = ax.ln a ; y = au
y ' = u ' au .ln a 7. y = ln x y ' = 1 ; y = ln u y ' = u ' x u 8.
y = log x y ' = 1 ( ( x s 0) ; y = log u y ' = u ' u s 0) a a x ln a u ln a 9. y = sin x y ' = cos x ; y = sin u
y ' = u 'cos x
10. y = cos x
y ' = – sin x ; y = cos u
y ' = –u 'sin x GVC.Phan Thị Quản Trang12
Đề cương bài giảng chương II
ĐẠO HÀM - VI PHÂN HÀM MỘT BIẾN
11. y = tan x
y ' = 1 = 1+ tan2 x ; y = tan u y ' = u ' =
u '.(1+ tan2 u ) cos2 x cos2 u u '
12. y = cot x
y ' = – 1 = –(1+ cot2 x) ; y = cot u y ' = –
= –u '.(1+ cot2 u ) sin2 x sin2 u 1 u ' 13. y = arcsin x y ' = ; y = arcsin u y ' = 1– x2 1– u2 – 1 –u '
14. y = arccos x y ' = ; y = arccos u y ' = 1– x2 1– u2 1 u '
15. y = arctan x y ' = ; y = arctan u y ' = 1+ x2 1+ u2 – 1 –u '
16. y = arccot x y ' = ; y = arccot u y ' = 1+ x2 1+ u2 Chú ý :
Nếu hàm số có dạng : y = Lu ( x) v( x) , u ( x) > 0 ( thì :
y ' = u ( x) v( x) . v '( x) ln u ( x) + v ( x) u '( x) L u ( x)
bằng cách : + Lấy ln hai vế : ln y = v ( x).ln u ( x) y '
+ Lấy đạo hàm hai vế :
= v '( x)ln u ( x) + v ( x) u '( x) y ' y u ( x )
1.4. Đạo hàm cấp cao:
1. Định nghĩa : (SV tự đọc) Đạo (
hàm của đạo hàm cấp (n –1) gọi là đạo hàm cấp n , kí hiệu f n) ( x) . Ta có : ( (
f n) ( x) = n–1) L f ( x) '
2. Công thức Leibnitz :
Cho u = u ( x), v = v ( x) là các hàm số của x , có đạo hàm đến cấp n đối với x , khi đó : (n) o (0) (n) 1 (1) (n–1) 2 (2) (n–2) n (n) (0) n
k (k ) (n–k )
(u.v) = C u v + C u v + C u v + + C u v = Σ n n n n C u v n k =0 (0) (0) với u
= u, v = v . .VI PHÂN :
2.1. Định nghĩa vi phân: 1. Định nghĩa 1:
Cho hàm số y = f ( x) liên tục trong lân cận U ( x0 ) của điểm x . Cho x một số gia x : 0 0
x + x ϵ U ( x 0
0 ) ( x còn gọi là vi phân của biến độc lập x ) . Nếu số gia của hàm :
y = f ( x0 + x) – f ( x0 )
được biểu diễn dưới dạng :
y = A. x + α ( x) (1)
Trong đó A là hằng số không phụ thuộc vào x , α ( x) là VCB cấp cao hơn VCB x khi
x → 0 thì ta nói rằng hàm số
y = f ( x) khả vi tại x0 và biểu thức A. x gọi là vi phân của hàm
y = f ( x) tại x0 , kí hiệu : dy ( x0 ) hay df ( x0 ) . Ta có :
df ( x0 ) = A. x 2. Định nghĩa 2 :
Nếu hàm số y = f ( x) khả vi tại mọi x ϵ(a;b) , ta nói y = f ( x) khả vi trong khoảng (a;b).
Khi đó biểu thức vi phân A. x là một hàm theo biến x trong khoảng (a;b) , kí hiệu dy hay df , ta có :
dy = df = A. x (2) GVC.Phan Thị Quản Trang13
Đề cương bài giảng chương II
ĐẠO HÀM - VI PHÂN HÀM MỘT BIẾN
3. Ý nghĩa của vi phân :
+ Biểu thức của vi phân A. x là bậc nhất đối với x , nên thông thường nó đơn giản hơn f
+ Nếu A s 0 thì vi phân df là VCB tương đương với số gia f vì số hạng còn lại ở (1) là
α ( x) là VCB cấp cao hơn x .
2.2. Liên hệ giữa đạo hàm và vi phân:
Định lí : Cho hàm số f ( x) xác định trong khoảng (a;b) . Điều kiện cần và đủ để f ( x)
khả vi trong khoảng (a;b) là nó khả đạo trong khoảng (a;b) . Khi đó : dy = f '( x). x
Đặc biệt: nếu y = x dy = dx = x .Do đó, công thức dùng để tính vi phân của hàm số:
dy = f '( x).dx
2.3. Đạo hàm cho bởi phương trình tham số:
x = x (t ) y
Giả sử hàm số = f ( x ) cho dưới dạng tham số :
( ) với x (t ) là hàm đơn điệu theo t y = y t
và có x '(t ) s 0 thì ta có : y ' = y 't x x 't ( y ' – x ) 't y " .x ' y ' .x " t t
và : y " = ( y ' ) ' = = t 2 t 2 ( x 2 x x x ' x ' )3 t t
2.4. Ứng dụng của vi phân:
Giả sử hàm số y = f ( x) khả vi tại x0 , khi đó ta có : dy = f '( x0 ). x
và số gia của hàm y = f ( x0 + x) – f ( x0 )
Khi x khá bé thì y dy
Nên : f ( x0 + x) – f ( x0 ) f '( x0 ). x
f ( x0 + x) f ( x0 ) + f '( x0 ). x (*)
(*) là công thức dùng để tính gần đúng một biểu thức .
2.5. Vi phân cấp cao:
Giả sử hàm số y = f ( x) khả vi trên khoảng (a;b) . Vi phân dy = f '( x).dx gọi là vi phân cấp
một của hàm số y = f ( x) tại x ϵ(a;b) . dy = f '( x).dx là hàm theo biến x , trong đó dx không đổi .
Nếu hàm số dy khả vi trên khoảng (a;b) thì vi phân của vi phân cấp một dy được gọi là vi
phân cấp hai của y = f ( x) tại x , kí hiệu : d 2 f hay d 2 y . Ta có :
d 2 y = f "( x)(dx)2 ............................. (
d n y = f n) ( x)(dx)n - - - - - - - - - - - - -
. CÁC ĐỊNH LÍ VỀ HÀM KHẢ VI :
3.1. Các định lí về giá trị trung bình:
1. Định lí Fermat : Giả sử hàm f ( x) xác định trong khoảng (a;b) . Nếu f ( x) đạt cực trị
tại điểm c ϵ(a;b) và nếu tồn tại đạo hàm hữu hạn f '(c) thì đạo hàm tại đó phải bằng 0 .
2. Định lí Roll: Nếu f ( x) liên tục trên a;b khả vi trong khoảng (a;b) và f (a ) = f (b)
thì Ec ϵ(a;b) : f '(c)=0. GVC.Phan Thị Quản Trang14
Đề cương bài giảng chương II
ĐẠO HÀM - VI PHÂN HÀM MỘT BIẾN
3. Định lí Lagrange _ Công thức về số gia giới nội:
a. Định lí Lagrange : Nếu f ( x) liên tục trên a;b , khả vi trong khoảng (a;b)
f (b) – f (a)
thì tồn tại điểm c ϵ(a;b) sao cho : f '(c) = b – a
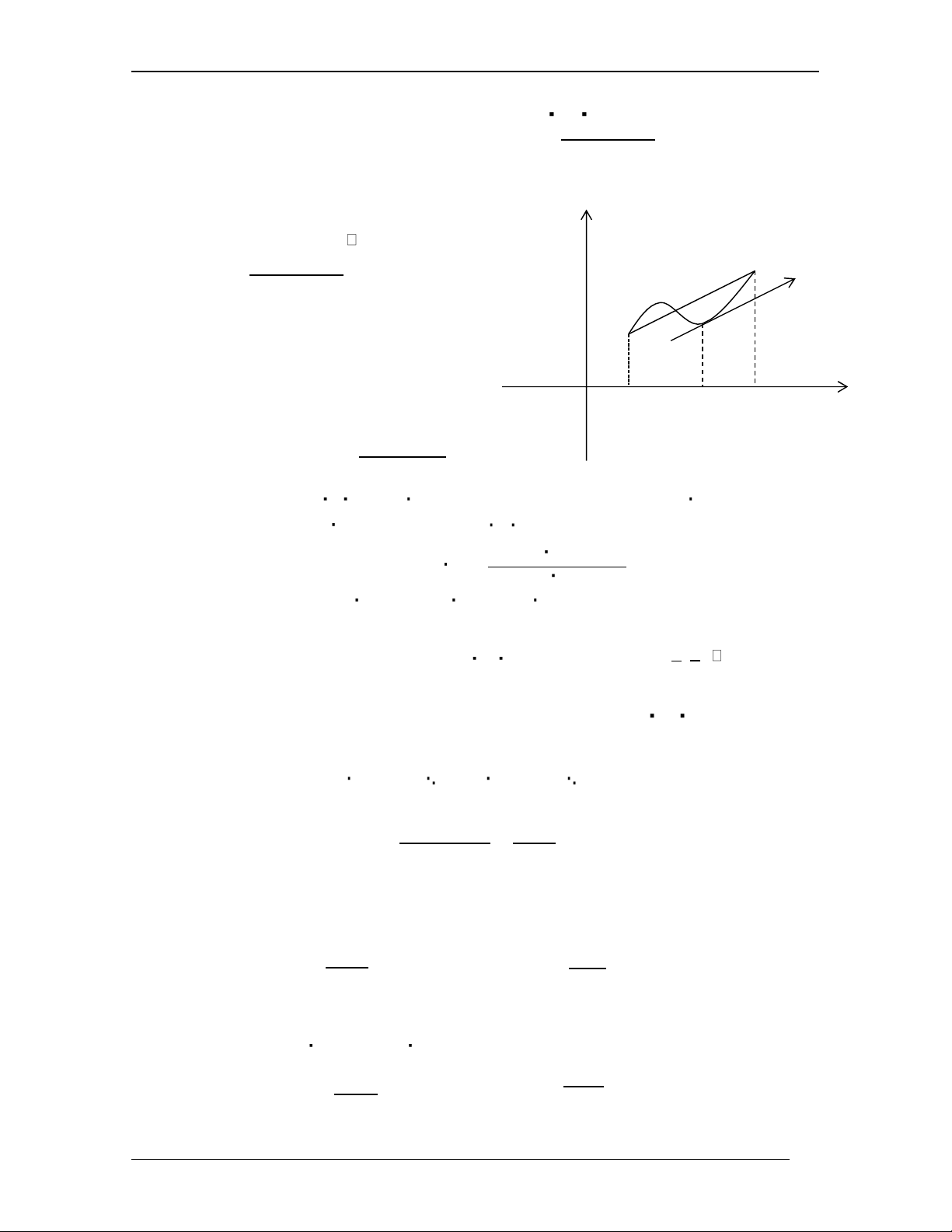
b. Ý nghĩa hình học :
Giả sử đường biểu diễn hàm f ( x) trong y
khoảng (a;b) là cung AB
f (b) – f (a) B Tỉ số : là hệ số góc của b – a
tiếp tuyến tại M (c; f (c)) . A
Định lí Lagrange khẳng định rằng :
Cung AB có ít nhất một điểm mà tại
điểm đó tiếp tuyến với cung AB song O a c b x song dây cung AB .
c. Công thức về số gia giới nội:
f (b) – f (a)
Từ công thức : f '( c) = (*) b – a
Đặt a = x , b = x + x b – a = x
, Ec nằm giữa hai điểm x ; x + x nên c có thể 0 0 0 0 viết :
c = x0 + θ . x ; trong đó : 0 θ 1
Công thức (*) được viết : f '( x0 + θ . x) = f ( x0 + x) – f ( x0 ) x Hay :
f ( x0 + x) – f ( x0 ) = x. f '( x0 + θ. x) (3)
(3) được gọi là công thức số gia hữu hạn
Nếu cho θ một giá trị nào đó thoả mãn 0 θ 1 . Chẳng hạn : θ = 1 1 ; ; thì ta tính 2 3
gần đúng được biểu thức cần tính.
4. Định lí Cauchy : Giả sử f ( x) , g ( x) là hai hàm số liên tục trên a;b , khả vi trong
khoảng (a;b) . Khi đó trong khoảng (a;b) có ít nhất một điểm c tại đó :
L f (b) – f (a ) g '(c) = L g (b) – g (a ) f '(c)
Nếu thêm điều kiện g '( x) s 0 với mọi x ϵ(a;b) thì công thức trên có thể viết :
f (b) – f (a ) = f '(c)
g (b) – g (a) g '(c)
5. Qui tắc L'Hospital:
a. Định lí 1: Giả sử hàm f ( x) , g ( x) khả vi ở lân cận điểm x , f ( x 0
0 ) = g ( x0 ) = 0
và g '( x) s 0 ở lân cận điểm x , x s x . 0 0 f '( x) f ( x) Nếu có : lim =
( ) A thì cũng tồn tại lim = A
x→ x0 g ' x
x→ x0 g ( x )
b. Định lí 2: Giả sử hàm f ( x) , g ( x) khả vi ở lân cận điểm x0 , trừ tại điểm x , 0
lim f ( x) = ; lim g ( x) = và
g '( x) s 0 ở lân cận điểm x . 0 x→ x0 x→x0 f '( x) f ( x) Nếu = có : lim A . lim
= A thì cũng tồn tại
x→ x0 g '( x)
x→ x0 g ( x) GVC.Phan Thị Quản Trang15
Đề cương bài giảng chương II
ĐẠO HÀM - VI PHÂN HÀM MỘT BIẾN Chú ý :
+ Nếu A = hoặc x → định lí trên vẫn đúng . f '( x) 0
+ Khi áp dụng qui tắc L'Hospital , nếu tỉ số lại có dạng hoặc thì ta có thể áp dụng g '( x) 0 f '( x) f ( x)
qui tắc L'Hospital lần nữa , còn nếu E lim lim .
x→ x0 g '( x) thì chưa kết luận được x→ x0 g ( x )
3.2. Công thức Taylor và công thức Maclaurin:
Định lí : Nếu hàm f ( x) xác định trên a;b
có đạo hàm hữu hạn đến cấp (n +1) trong
khoảng (a; b), x0 ϵ(a;b) . Khi đó : 6x ϵ a;b , Ec ở giữa hai điểm x0 và x sao cho hàm
f ( x) được khai triển dưới dạng : (n) 2 ( x ) (n+1) 0 n ( n+1
f ( x) = f ( x ( ( ( c) (
0 ) + f '( x0 ) x – x0 ) + f "( x0 ) x – x0 ) + + f
x – x0 ) + f x – x0 ) 1! 2! n! (n +1)! n ( f k ) ( x ) (n+1) 0 k = ( f ( x ( c) ( 0 ) + Σ
x – x0 ) + f
x – x )n+1 (1) 0 k ! (n +1)! k =1
(1) gọi là công thức Taylor của hàm f ( x) tại x0 .
Nếu x0 = 0 ϵ(a;b) . Công thức Taylor trở thành công thức Maclaurin: n ( f k ) (0) ( n+1) (
f ( x) = f (0) + Σ c) Với xk + f xn+1 (
c nằm giữa 0 và x . 2) k ! (n +1)! k =1 ( n+1) ( ( R c)
n ( x) = f (
x – x0 )n+1 gọi là phần dư bậc n của f ( x) trong công thức Taylor và n +1)! ( f n+1) (c) Rn ( x) = (
xn+1 gọi là phần dư bậc n của f ( x) trong công thức Maclaurin. n +1)!
Ví dụ :Viết công thức Taylor của đa thức P ( x) = x5 – 4x3 + 2x2 + 6x – 24 tại điểm
x0 = –1 (hay còn nói : khai triển đa thức P ( x) theo các luỹ thừa của ( x +1) . Tính gần
đúng giá trị P (–0, 9) .
3.3. Công thức Maclaurin của hàm sơ cấp cơ bản:
1. y = ex
2. y = sin x
3. y = cos x
4. y = (1+ x)α y =
1 (α = –1); y = (α = 1 1+ x x 2 5.
y = (1– x)α y = 1 (α = –1); y = (α = 1 1– x 1– x 2 6.
y = ln (1+ x) ; y = ln (1– x)
Ví dụ 1: Viết khai triển Maclaurin đến số hạng thứ 10 của hàm số y = (1– x2 )ex .
Ví dụ 2: Viết khai triển Maclaurin của y = sin2 x . GVC.Phan Thị Quản Trang16
Đề cương bài giảng chương II
ĐẠO HÀM - VI PHÂN HÀM MỘT BIẾN
. Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số:
4.1. Khảo sát hàm số y = f ( x) : x3
Ví dụ: Khảo sát sự biến thiên và vẽ đồ thị của hàm số : y = x –1
4.2. Khảo sát hàm cho bởi phương trình tham số:
x = x (t ) 1. Định nghĩa :
Trong hệ toạ độ Oxy cho điểm M ( x, y ) với (
( ) t ϵ R ) , trong đó y = y t
x (t ), y (t ) đều là những hàm đơn trị . Khi t biến thiên M di chuyển vạch nên đường cong
(C ) , khi đó hệ phương trình trên gọi là những phương trình tham số của đường cong (C ) . 2. Ví dụ :
a. Đường thẳng (d ) đi qua điểm M 0 ( x0; y0 ) , vectơ chỉ phương u = (a;b) có
x = x + t.cosα phương trình : 0 (t ϵ )
y = y + t.sin α 0
b. Đường tròn tâm I (a;b) và bán kính R có phương trình là :
x = a + R.cos t
(0 t 2π ) với t là góc hợp bởi vectơ IM và trục Ox
y = b + R sin t x 2
c. Phương trình tham số của đường Elip : + y2 = 1 là : a2 b2
x = a.cos t
(0 t 2π ) với t là góc hợp bởi vectơ OM và trục Ox
y = b.sin t
x = x (t )
3. Khảo sát đường cong cho bởi phương trình tham số : (t ϵ )
y = y (t )
B1: Tìm miền xác định suy ra miền biến thiên bởi các tính chất chẵn , lẻ , tuần hoàn cho cả hai
hàm số x (t ), y (t ) .
B2 : Tính các đạo hàm y ' ; y " x x2
B3. Tìm tiệm cận : Khi t → t0 hoặc t → mà :
x (t ) → a •
thì x = a là tiệm cận đứng. y (t ) → x (t ) → •
thì y = b là tiệm cận ngang.
y (t ) → b x (t ) → y (t ) → a •
đồng thời x (t ) y (t ) →
L y (t ) – a.x (t ) → b
thì y = ax + b là tiệm cận xiên.
B4: Lập bảng biến thiên: GVC.Phan Thị Quản Trang17
Đề cương bài giảng chương II
ĐẠO HÀM - VI PHÂN HÀM MỘT BIẾN t B5: vẽ đồ thị .
Ví dụ 1: Khảo sát sự biến thiên và vẽ đồ thị của hàm số cho bởi phương trình tham số
x = R (t – sin t )
( R > 0) . Đường cong này được gọi là đường cyclôit
y = R (1– cos t )
Đó là quĩ đạo của một điểm M nằm trên đường tròn bán kính R lăn không trượt trên trục Ox , xuất phát từ gốc O .
Ví dụ 2: Khảo sát và vẽ đồ thị hàm số cho bởi phương trình tham số :
x = a cos3 t
(a, b > 0) . Đường cong này gọi là đường Astrôit
y = b sin3 t at 2 x = 1+ t2
Ví dụ 3: Đường cyxôit có phương trình tham số : , t ϵ y = at3 1+ t 2 x = 3t 1+ t3
Ví dụ 4: Lá Descartes x3 + y3 – 3xy = 0 có phương trình tham số : , t ϵ . y = 3t 2 1+ t3
4.3. Khảo sát hàm số trong hệ tọa độ cực:
1. Hệ toạ độ cực : M
Trong mặt phẳng toạ độ, cho nửa trục Ox và điểm M . .
Gọi r = OM ,φ = (Ox
;OM ) là một góc định hướng O x
lấy giá trị dương khi OM quay theo chiều ngược với chiều quay kim đồng hồ .
Điểm M hoàn toàn được xác định bởi cặp số (r,φ ) , ngược lại khi cho cặp số (r,φ ) thì ta xác
định được điểm M . Do đó cặp số (r,φ ) gọi là toạ độ cực của điểm M và hệ toạ độ đó gọi là hệ
toạ độ cực . Trong đó :
+ O gọi là gốc cực .
+ Ox gọi là trục cực .
+ OM gọi là vectơ bán kính của M
+ φ = (Ox;OM ) gọi là góc cực .
Chú ý : Theo định nghĩa trên thì r 0, 0 φ 2π . Ta có thể mở rộng sao cho r và φ đều có
thể lấy các giá trị trong khoảng (– ; ) . Khi đó cặp số (r,φ ) của M gọi là toạ độ cực mở rộng của M . GVC.Phan Thị Quản Trang18
Đề cương bài giảng chương II
ĐẠO HÀM - VI PHÂN HÀM MỘT BIẾN
2. Công thức liên hệ giữa toạ độ cực và toạ độ Descartes:
Trong mặt phẳng cho điểm M . Đối với hệ toạ độ cực M y
có toạ độ (r,φ ) , đối với hệ toạ độ Descartes M có toạ độ
( x, y ) . Khi đó :
M ( x; y )
x = r.cosφ r
+ Nếu cho (r,φ ) thì : y
= r.sin φ O r = x2 + y2
+ Nếu cho ( x, y ) thì : tan φ = y
(chọn φ sao cho y và sin φ cùng dấu) x
3. Phương trình của đường trong hệ toạ độ cực :
Cho hàm số r = f (φ ) , đồ thị hàm số này trong hệ toạ độ cực được gọi là đường cong trong hệ
toạ độ cực và phương trình r = f (φ ) được gọi là phương trình đường cong trong hệ toạ độ cực . Các ví dụ :
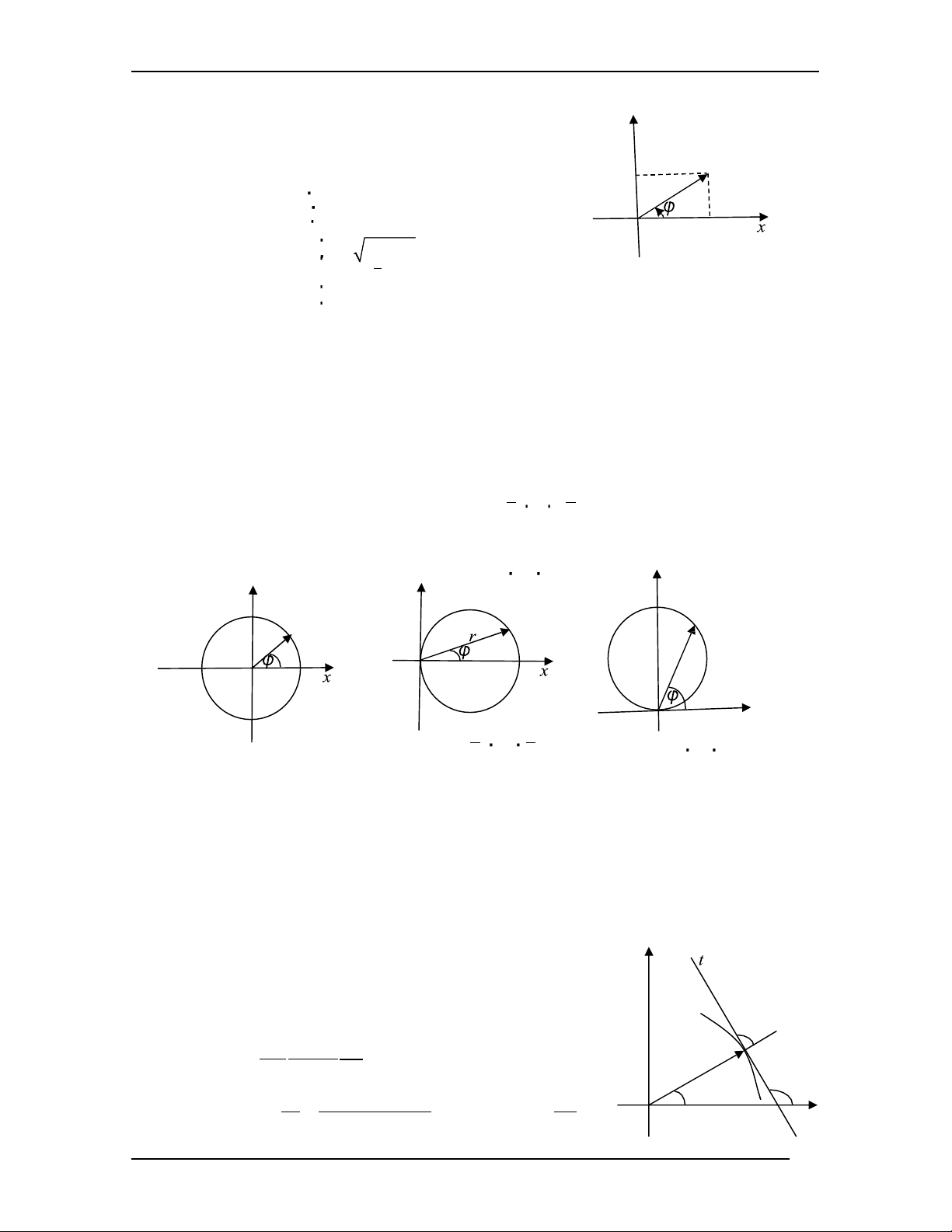
+ Đường tròn tâm O , bán kính R : x2 + y2 = R2 có phương trình trong hệ toạ độ cực : r = R .
+ Đường tròn tâm I ( R; 0) , bán kính R : x2 + y2 = 2Rx có phương trình trong hệ toạ độ cực :
r = 2R cosφ π π , – φ 2 2
+ Đường tròn tâm I (0; R) , bán kính R : x2 + y2 = 2Ry có phương trình trong hệ toạ độ cực
r = 2R sin φ , 0 φ π y y y M M M r r O O O x π π r = R
r = 2R cosφ, – φ
r = 2R sin φ , 0 φ π 2 2
4. Khảo sát đường cong trong hệ toạ độ cực: r = f (φ )
B1: Tìm miền xác định của r = f (φ ) .Xét tính chẵn,lẻ và tuần hoàn(nếu có). Suy ra khoảng cần khảo sát.
B2: Tính r ' = f '(φ ) . Xét dấu r ' = f '(φ )
B3: Lập bảng biến thiên , xét sự biến thiên của r = f (φ ) theo φ .
Để vẽ đồ thị được chính xác hơn , ta thường xác định
tiếp tuyến với đường cong tại mỗi điểm y M của nó .
Gọi V là góc dương giữa vectơ OM và vectơ chỉ phương
của tiếp tuyến với đồ thị tại điểm M ; gọi α là góc dương
giữa trục cực và tiếp tuyến , ta có : V = α – φ . V M
Do đó : tan V = tan α – tan φ
1+ tan α. tan φ dy
r 'sin φ + r cosφ dr O φ α Mặt khác : tan α = = , trong đó : r ' = x dx
r ' cosφ – r sin φ dφ GVC.Phan Thị Quản Trang19
Đề cương bài giảng chương II
ĐẠO HÀM - VI PHÂN HÀM MỘT BIẾN
Suy ra : tanV = r r ' Bảng r ' biến thiên: r V Đồ thị
a. Ví dụ 1:Vẽ đường hoa hồng ba cánh có phương trình : r = a sin 3φ (a > 0) .
b. Ví dụ 2: Đường hoa hồng bốn cánh có phương trình : r = a sin 2φ (a > 0) .
c. Ví dụ 3: Đường Lemniscate de Bernoulli : x2 + y2 = a2 (x2 – y2 ) (a > 0) có phương trình
trong hệ toạ độ cực là r = a cos 2φ .
d. Ví dụ 4 : Đường hình trái tim Carđiôit có phương trình: r = a (1+ cosφ ) (a > 0) . GVC.Phan Thị Quản Trang20
Đề cương bài giảng chương II
ĐẠO HÀM - VI PHÂN HÀM MỘT BIẾN BÀI TẬP :
Bài 1: Tính các đạo hàm sau: 1– x 1– sin x
1. a. y = arctan b. y = ln
c. y = 3 x3 – 3x 1+ x 1+ sin x x
2. a. y = x cos2x , với x > 0
b. y = (sin x ) tan x , với sin x > 0
c. y = x e .ln(sin x) , với x > 0
3. a. ey + xy = e
b. y = tan(x – y)
c. ex + x2 + y3 = 2 tại điểm (0;1) .
Bài 2: Tính các đạo hàm cấp n của các hàm số sau:
1. a. y = eax
b. y = sin (ax + b)
c. y = cos (ax + b)
2. a. y = ( x – a )α ; α ϵ R b. y = (1– x2 )ex
c. y = x.sin2 x x2
3. a. y = 3 x b. y = c. y = 2x x2 –1 x2 + 3x + 2
Bài 3: Tính đạo hàm cấp hai y "( x) của các hàm số cho bởi phương trình tham số: at 2 x =
x = R(t – sin t)
x = Rcos3t 1+ t 2 a. ; R > 0 b. ; R > 0 c.
y = R(1– cos t)
y = R sin3 t y = at3 1+ t 2
Bài 4: Tìm các đường tiệm cận của các hàm số sau: at 2 x = 3t x = 1+ t 2 1+ t3 a. b. y = at3 3t2 y = 1+ t 2 1+ t3 Bài 5:
Cho P(x) = x5 + 3x4 – 2x3 – 5x2 + 4 .
Viết công thức khai triển Taylor của P ( x) tại điểm x = 1 và tính gần đúng P (1, 01) .
Bài 6: chứng minh rằng phương trình: x5 + x4 + x2 +10x – 5 = 0 chỉ có một nghiệm dương và ( nghiệm 1
dương và nghiệm này nằm trong khoảng 0; . 2
Bài 7: Khai triển Maclaurin của các hàm số sau: x
1. a. y = f ( x) =
(với n = 3 ) b.
y = f ( x) = ln (cos x) (với n = 3 ) 2. a. ( sin x
y = e 2 x– x2
(với n = 5 ) b. y = ln
(với n = 6 ) x
3. a. y = sin2 x b.
y = (1– x2 ).ex
Bài 8 Khảo sát và vẽ đồ thị hàm số: 4x x2 – 2x + 2 2 2 1. a. y = b. y =
c. y = x + x2 + 4 x –1 x
2. a. y = 3 x3 – 3x
b. y = e 2 x – x2
c. y = x.ex
3. a. y = ln ( x2 +1) b. y = GVC.Phan Thị Quản Trang21
Đề cương bài giảng chương II
ĐẠO HÀM - VI PHÂN HÀM MỘT BIẾN
Bài 9: Khảo sát và vẽ đồ thị hàm số: t2 x =
x = a cos t
x = 2t – t 2 t –1 9.1. ; a > 0 9.2. 9.3.
y = a sin t
y = 3t – t3 y = t t2 –1
Bài 10: Chứng minh rằng: 1. a.
ex 1+ x , 6x ϵ R
b. 1+ rx (1+ x)r , (r > 1, x > –1) x2 x 2. a. ln (1+ x) x – , 6x 0 b.
< arctan x , 6x > 0 2 x2 +1 2 x2 +1 3.
2 , 6x ϵ R 3 x2 + x + 1
arccos a – arccos b 4.
1 , 6a,b ϵ R : 0 < b < a < 1 a2 – b2
arcsin a – arcsin b 5.
1 , 6a, b ϵ R : 0 < b < a < 1 a2 – b2 Bài 11:
Tính các giới hạn sau: ( 1 1 ( x2 –1 ( 1 – 1. a. lim 2 2 b. lim c. lim cot x – x→0 sin x x x→1 ln x x→0 x
( ex2 – cos 2x ln (1– x2 ) 3 1– x2 –1 2. a. lim x.sin x lim
c. lim arcsin 3x x→0 b. x→1 sin2 x x→0 1 ( π π x x x b. ( 1 ( tan 3. a. lim tan lim tan x c. lim 2 – x 2a x 2x +1 a x→0 x x→a + x 1 (
x x – π 4. a.
lim (tan x) 2 x – π
b. lim (sin x) x – (π 2) c. lim sin π – x→π x→( π x→ 2 2 2 π x 1
5. a. lim(1– x) tan
b. lim ( e – x – ( 2x ) sin x c. lim sin 2x) cos x → ( π – x 1 2 x→0 x→ 2 ln x – x +1 ex –1– x 6. a. lim xx b. lim c. lim x→0+ x→0 x→1 ( x –1)2 x2 1 x2.sin x – sin x
Bài 12: Chứng minh rằng: lim x = 0 và lim
= 1 . Có thể dùng qui tắc x→0 sin x x x + cos x
L'Hospital để tính chúng được không? Vì sao? GVC.Phan Thị Quản Trang22




