Đề cương môn Toán cao cấp - Trường Đại học bách khoa - Đại học đà nẵng.
1. Đường cong cho trong tọa độ cực r = r (φ ), φ1 φ φ2
Đề cương môn Toán cao cấp - Trường Đại học bách khoa - Đại học đà nẵng.
Tài liệu gồm 13 trang , giúp bạn tham khảo, ôn tập và đạt kết quả cao
Môn: Toán cao cấp(TCC10) 10 tài liệu
Trường: Trường Đại học Bách khoa, Đại học Đà Nẵng 642 tài liệu
Tác giả:
Preview text:
Đề cương bài giảngchương III:
PHÉP TÍNH TÍCH PHÂN HÀM MỘT BIẾN . Chương III:
PHÉP TÍNH TÍCH PHÂN HÀM MỘT BIẾN
. TÍCH PHÂN BẤT ĐỊNH :
1.1. Nguyên hàm : (SV tự đọc)
1.2. Định nghĩa tích phân bất định : (SV tự đọc)
1.3. Các tính chất của tích phân bất định : (SV tự đọc)
1.4. Bảng tính tích phân của các hàm :
< 1 > . 0dx = C < dx 2 > . +
xmdx = xm+1 C (m s –1) < 3 > . = ln x + C m +1 x
< 4 > . axdx = ax + C
< 5 > . exdx = ex + C ln a
< 6 > . cos x.dx = sin x + C ;
cos (ax + b).dx = 1 sin (ax + b) + C a
< 7 > . sin x.dx = – cos x + C ;
sin (ax + b).dx = – 1 cos (ax + b) + C a
< 8 > . tan x.dx = – ln cos x + C ;
tan(ax + b).dx = – 1 ln cos(ax + b) + C a
< 9 > . cot x.dx = ln sin x + C ;
cot(ax + b).dx = 1 ln sin(ax + b) + C a < dx dx 1 10 > . = = tan
(ax + b) + C
(1+ tan2 x)dx = tan x + C ; cos2 x cos2 (ax + b) a < dx dx 11 > . = ( 1+ cot2 x)dx
= – cot x + C ; sin2 x
sin2 (ax + b) = – 1 cot (ax + b) + C a x
< 12 > . dx = arcsin x + C = – arccos x + C ; dx
= arcsin + C (a > 0) 1– x2 a2 – x2 a dx < dx x 13 > .
= arctan x + C = – arccot x + C ; = 1 arctan + C (a > 0) 1+ x2 a2 + x2 a a a + x < dx x dx = 1 + 14 > . = 1 ln + C ; ln C 1– x2 2 1– x a2 – x2 2a a – x < 1 1 15 > . dx = ln + C ; dx x –1 =
ln x – a + C x2 –1 2 x2 – a2 x +1 2a x + a < 16 > .
dx = ln (x + x2 +1)+ C ; dx = ln x + + C x2
< 17 > . x2 + b.dx = x + b ln x + + C 2 2 < a2 – x2 18 > . .dx = x a2 x + arcsin + C a2 – x2 2 2 a
GVC.Phan Thị Quản Trang23
Đề cương bài giảngchương III:
PHÉP TÍNH TÍCH PHÂN HÀM MỘT BIẾN .
1.5. Các phương pháp tính tích phân:
1. Phương pháp đổi biến:
Trường hợp 1: Giả sử tính tích phân: I = f (φ( x))φ ' (x).dx
B1: Đặt u = φ ( x) du = φ '( x) dx B2:
I = f (u).du = F (u) + C , với F ( x) là một nguyên hàm của f ( x)
Trường hợp 2: Giả sử tính tích phân:
I = f (x).dx
B1: Đặt x = φ (t ) dx = φ '(t ) dt , trong đó φ (t ) là hàm đơn điệu và khả vi theo biến t B2:
I = f (x).dx = f (φ (t)).φ '(t)dt = g(t)dt = G(t) + C , với G ( x) là một nguyên hàm của g ( x) .
2. Phương pháp từng phần:
Giả sử tính tích phân: I = u.dv , trong đó u = u ( x), v = v ( x)
là hai hàm khả vi . Khi đó :
u.dv = uv – v.du .
1.6. Tích phân các hàm hữu tỉ: 1 1
ln ax + b + C a khi m = 1 * 1. Dạng1: I = = 1
(ax + b) m dx , (m ϵ N ) . Đặt u = ax + b . I1 –1 + C khi m s 1
a (m –1)(ax + b)m–1 2. Dạng2: I = dx , = b2 – 4ac 2
ax2 + bx + c u
Nếu < 0 : Biến đổi đưa I → 1 du
, (k > 0) = 1 arctan + C 2 a u2 + k 2 ak k
Nếu = 0 : Biến đổi đưa I → 1
du = – 1 + C 2 a u 2 au
Nếu > 0 : Tam thức ax2 + bx + c có hai nghiệm α , β . Khi đó
1 : ax2 + bx + c = a(x − α).(x − β) . Ta có : 1 I = dx = 1 ( 1 dx 2 –
a ( x – α )( x – β )
a (α – β ) x – α x – β 1 x – α I = ln + C 2
a (α – β ) x – β 3. Dạng3: I = Ax + B dx 3
ax2 + bx + c
A (2ax + b) + B – Ab
A ln ax2 + bx + c + ( B – Ab I I 3 = 2a 2a dx =
ax2 + bx + c 2a 2a 2 Chú ý:
Nếu tam thức ax2 + bx + c có hai nghiệm α, β. Khi đó: I = Ax + B dx = Ax + B dx = 1 ( E + F dx 3
ax2 + bx + c
a ( x – α )( x – β ) a x – α x – β
I = 1 ( E ln x – α + F ln x – β ) + C 3 a
GVC.Phan Thị Quản Trang24
Đề cương bài giảngchương III: ( x )
PHÉP TÍNH TÍCH PHÂN HÀM MỘT BIẾN . 4. Dạng4: I = Pm
dx , trong đó P ( x) , Q ( x) lần lượt là các đa thức bậc m, n . 4 Q ( x) m n n
a. Nếu m < n :
B1: Phân tích Qn ( x) thành tích các nhân tử . Pm ( x)
B2: Phân tích Qn ( x ) thành tổng các phân thức đơn giản có dạng trên .
B3: Tính tích phân .
b. Nếu m n : P ( x)
B1: Chia tử thức cho mẫu thức : m
= M ( x) + R ( x) , Trong đó M ( x), R ( x) là các đa Q Qn ( x) n ( x)
thức và bậc R ( x) < bậc Qn ( x) .
B2: Tính tích phân của một đa thức và tích phân của hàm hữu tỉ dạng (a).
1.7. Tích phân các hàm lượng giác: 1. Dạng1 :
I1 = R (sin x, cos x) dx , R (sin x, cos x) là hàm theo sin x, cos x .
Phương pháp chung : x B1: Đặt t = tan dx = 2 dt 2 1+ t 2 2t 1– t 2
B2: Biễu diễn sin x, cos x theo t : sin x = , cos x = 1+ t 2 1+ t 2
B3: Đưa tích phân lượng giác về tích phân hữu tỉ . Đặc biệt:
+ Nếu R (sin x, cos x) = –R (– sin x, cos x) ( R là hàm lẻ đối với sin x ). Đặt t = cos x .
+ Nếu R (sin x, cos x) = –R (sin x, – cos x) ( R là hàm lẻ đối với cos x ). Đặt t = sin x .
+ Nếu R (sin x, cos x) = R (– sin x, – cos x) ( R là hàm chẵn đối với sin x, cos x ) . Đặt t = tan x .
Chú ý : Đối với tích phân I = cosm x.sinn x.dx ( m, n là các số tự nhiên chẵn ) , thì hạ
bậc rồi tính tích phân .
2. Dạng2 : I = sin ax.cos bxdx ;
I = sin ax.sin bxdx ;
I = cos ax.cos bxdx 2 2 2
B1: Biến đổi tích thành tổng :
sin ax.cos bx = 1
L sin (a + b) x + sin (a – b) x 2
sin ax.sin bx = 1 L cos (a – b) x – cos (a + b) x 2
cos ax.cos bx = 1 L cos (a + b) x + cos (a – b) x 2 B2: Tính tích phân
1.8. Tích phân các hàm vô tỉ:
Phương pháp 1: Đổi biến bằng cách
Đặt u = φ ( x) du = φ '( x) dx .
I = f (φ(x))φ ' (x).dx
= f (u).du _ f (u ) là một hàm hữu tỉ
GVC.Phan Thị Quản Trang25
Đề cương bài giảngchương III:
PHÉP TÍNH TÍCH PHÂN HÀM MỘT BIẾN .
Phương pháp 2: Đổi biến bằng cách đối với dạng :
. Đặt x = a. tan t
– π < t < π 2 2
. Đặt x = a.sin t
– π t π a2 – x2 2 2
x2 – a2 . Đặt x = a 0 t π ; t s π cos t 2
. TÍCH PHÂN XÁC ĐỊNH :
2.1. Định nghĩa tích phân xác định :
Cho hàm số y = f ( x) xác định trên đoạn [a, b] .
• Chia đoạn [a, b] thành n đoạn nhỏ bởi các điểm a = x < x < < x = b 0 1 n • Trên mỗi đoạn [x
i–1; xi ] , ta lấy điểm i tùy ý . Đặt
x = x – x , 6i = 1 ; n i i i–1 n
• Lập tổng I = f ( n i ). xi i =1
Khi d → 0 , với d = max x , (tức là n → ) mà lim I
tồn tại hữu hạn , không phụ thuộc vào i n
cách chia đoạn [a, b] và không phụ thuộc vào cách chọn điểm i trên mỗi đoạn , thì giới hạn đó
gọi là tích phân xác định của hàm số f ( x) trên đoạn [a, b] , khi đó ta nói rằng hàm số f ( x) khả
tích (có tích phân ) trên đoạn [a, b] . b b n Kí hiệu:
lim f ( ). x i i
f (x)dx . Vậy: f (x)dx = d →0 a a i =1
a;b gọi là các cận của tích phân. a : cận dưới , b : cận trên
f ( x) : hàm dưới dấu tích phân
f ( x).dx biểu thức dưới dấu tích phân
2.2. Ý nghĩa của tích phân xác định: b
Nếu hàm số y = f ( x) 0 , xác định và liên tục trên đoạn [a, b] , thì tích phân: f (x)dx là diện a
tích của hình phẳng giới hạn bởi các đường:đường (C ) : y = f ( x); y = 0 và hai đường thẳng
x = a; x = b .
2.3. Các tính chất của tích phân xác định : (SV tự đọc) Chú ý: b a • f (x)dx =
– f (x)dx a b b b b •
f (x)dx = f (t)dt = f (u)du a a a b a = b • f (x)dx = 0 khi f (x) = 0 a L
GVC.Phan Thị Quản Trang26
Đề cương bài giảngchương III:
PHÉP TÍNH TÍCH PHÂN HÀM MỘT BIẾN .
2.4. Đạo hàm theo cận trên:
1. Định lí về giá trị trung bình: Nếu f ( x) liên tục trên đoạn [a;b] thì tồn tại điểm c ϵ[a;b] b sao cho:
f (x)dx = f (c).(b – a) a
2. Định lí đạo hàm theo cận trên: Nếu f ( x) liên tục trên đoạn [a;b] thì hàm số x
( x) = f (t)dt
với a x b
là một nguyên hàm của hàm số f ( x) trên đoạn [a;b] . a
3. Định lí Newton_ Lepnitz: Nếu f ( x) liên tục trên đoạn [a;b] và F ( x) là một nguyên hàm
của hàm số f ( x) trên đoạn [a;b] thì: b K / h b = f (x)dx F (x)
= F (b) – F (a) a a
2.5. Các phương pháp tính tích phân xác định:
1. Phương pháp 1: (Công thức Newton- Lepnitz)
Nếu F(x) là một nguyên hàm của f(x) b K / h b thì : = f (x)dx F (x)
= F (b) – F (a) a a
2. Phương pháp 2: ( Phương pháp đổi biến ) b
a. Tính : I = f (φ(x))φ ' (x).dx a
B1: Đổi biến : Đặt u = φ ( x) du = φ '( x) dx B2: Đổi cận :
u1 = φ (a ); u2 = φ (b) . u2
B3: Tính tích phân: I = f (u ) du = F (u2 ) – F (u1 ) (F(x) là một nguyên hàm của f(x)) u1 β
b. Tính : I = f ( x) dx . α
B1: Đổi biến : Đặt x = φ (t ) dx = φ '(t ) dt
( φ (t ) là hàm đơn trị)
B2: Đổi cận : a = φ (α ) ; b = φ (β ) . b β β
B3: Tính tích phân : I = f (φ (t ))φ '(t ) dt = = G(t) α g(t)dt a α
( G ( x) là một nguyên hàm của g ( x) )
3. Phương pháp 3: (Phương pháp từng phần) Giả sử u = u ( x), v = v ( x) là các hàm có
đạo hàm theo biến x , khi đó : b b
udv = uv ba – vdv a a
GVC.Phan Thị Quản Trang27
Đề cương bài giảngchương III:
PHÉP TÍNH TÍCH PHÂN HÀM MỘT BIẾN . Chú ý:
a. Ứng dụng phương pháp đổi biến ta chứng minh được: •
Nếu f ( x) liên tục trên đoạn [–a; a] thì: 0
khi f ( x) ham le a f (x)dx = a –a
2 f (x)dx
khi f (x) ham chan 0 a+T T
• Nếu f ( x) là hàm tuần hoàn , chu kì T thì: f (x)dx = f (x)dx , với a là số bất kì. a 0 π π π π 2 •
x. f (sin x)dx = f (sin x)dx = π f (sin x)dx . 2 0 0 0 π π 2 π x.sin x 2
Ứng dụng tính: I = dx ; I =
sinn xdx = cosn xdx 1 2 2 1+ cos x 0 0 0
b. Ứng dụng phương pháp từng phần ta chứng minh được:
(n –1).(n – 3) π π ( π . Khi n chan 2 2 n.(n – 2) 2 sin xdx = cos xdx = n n
(n –1).(n – 3) 0 0 Khi n le n.(n – 2)
. TÍCH PHÂN SUY RỘNG:
3.1. TPSR có cận vô hạn: (loại 1)
1. Định nghĩa 1: Giả sử hàm số f ( x) xác định trên [a;
) và khả tích trên [a;b], 6b > a Khi b đó : = f (x)dx
lim f (x)dx b a a
2. Định nghĩa2: Giả sử hàm số f ( x) xác định trên (– ;b] và khả tích trên [a;b], 6a < b b b Khi đó : = f (x)dx
lim f( ) x dx a→– – a
3. Định nghĩa3: Giả sử hàm số f ( x) xác định trên (– ; + ) và khả tích trên c
[a;b], 6a, b : a < b . Khi đó : f (x)dx = f (x)dx + f (x)dx , với 6cϵ(– ; + ) – – c c Chú ý: Tích phân
f (x)dx hội tụ cả hai tích phân f (x)dx và
f (x)dx cùng hội tụ, – – c ngược lại phân kì.
3.2. TPSR của các hàm không bị chặn trong khoảng lấy tích phân: (Loại 2)
1. Định nghĩa 4: Giả sử hàm số f ( x) xác định và liên tục trên [a;b) và có lim f (x) = . Khi x→b– b–s b
đó : lim f (x)dx = s → f (x)dx 0+ a a
GVC.Phan Thị Quản Trang28
Đề cương bài giảngchương III:
PHÉP TÍNH TÍCH PHÂN HÀM MỘT BIẾN .
2. Định nghĩa 5: Giả sử hàm số f ( x) xác định và liên tục trên (a;b]
và có lim f (x) = x→a+ b b .Khi đó :
lim f (x)dx = f (x)dx
s →0+ a+s a
3. Định nghĩa 6: Giả sử hàm số f ( x) xác định và liên tục trên [a; c) (c;b] và có b c b
lim f (x) = ; lim f (x) = Khi đó :
f (x)dx = f (x)dx
+ f (x)dx x→c– x→c+ a a c
4. Định nghĩa 7: Giả sử hàm số f ( x) xác định và liên tục trên (a;b) và có b c b
lim f (x) = ; lim f (x) = Khi đó :
f (x)dx = f (x)dx + f (x)dx
,Với c ϵ(a;b) . x→a+ x→b– a a c Chú ý: c
Tích phân trong định nghĩa 6 và 7 hội tụ cả hai tích phân
f (x)dx và a b
f (x)dx cùng hội tụ, ngược lại phân kì. c
Các tích phân trong các định nghĩa 1 → 7 , nếu nó tồn tại hữu hạn, ta nói nó hội tụ . Ngược lại gọi là phân kì
3.3. Các tiêu chuẩn xét sự hội tụ hay phân kì của TPSR
1. Đối với TPSR loại 1:
a. Tiêu chuẩn 1: Giả sử các hàm f ( x), g ( x) khả tích trên đoạn [a;b], 6b > a và
6x ϵ[a; ) f ( x) g ( x) 0 . Khi đó:
• Nếu f (x)dx hội tụ thì g(x)dx hội tụ a a
• Nếu g(x)dx phân kì thì f (x)dx phân kì a a
b. Tiêu chuẩn 2: Giả sử các hàm f ( x), g ( x) khả tích trên đoạn [a;b], 6b > a và 6 f (x)
x ϵ[a; ) f ( x) 0, g ( x) 0 . Đồng thời lim
= K (0 < K < ) . Khi đó: hai tích x g(x) phân
f (x)dx ; g(x)dx cùng hội tụ hoặc cùng phân kì. a a c. Hệ quả: • f (x) Nếu lim = 0 và hội tụ thì hội tụ g(x)dx f (x)dx x g(x) a a f (x) • Nếu lim = và phân kì thì phân kì g(x)dx f (x)dx x g(x) a a
2. Đối với TPSR loại 2:
a. Tiêu chuẩn 1: Giả sử các hàm f ( x), g ( x) khả tích trên nửa khoảng (a;b] , đồng thời
lim f (x) = , lim g(x) = và
6x ϵ(a;b], f ( x ) g ( x) 0 . Khi đó: x→a+ x→a+
GVC.Phan Thị Quản Trang29
Đề cương bài giảngchương III:
PHÉP TÍNH TÍCH PHÂN HÀM MỘT BIẾN . b b
• Nếu f (x)dx hội tụ thì g(x)dx hội tụ a a b b
• Nếu g(x)dx phân kì thì f (x)dx phân kì a a
b. Tiêu chuẩn 2: Giả sử các hàm f ( x), g ( x) khả tích trên nửa khoảng (a; ]
b , lim f (x) = , x→a+ f (x)
lim g(x) = và 6x ϵ(a;b]: f ( x) 0, g ( x) 0 . Đồng thời lim
= K (0 < K < ) . + x→a+ x→a g(x) b b
Khi đó: hai tích phân suy rộng:
f (x)dx ; g(x)dx cùng hội tụ hoặc cùng phân kì. a a c. Hệ quả: b b
• Nếu lim f (x) = 0 và TPSR +
g(x)dx hội tụ thì TPSR f (x)dx hội tụ x→a g(x) a a f (x) b b • Nếu lim phân kì +
= vàTPSR g(x)dx
phân kì TPSR f (x)dx x→a g(x) a a
Chú ý: Người ta thường dùng các TPSR sau đây để xét sự hội tụ hay phân kì của TPSR khác 1 b ♦ 1
dx (a > 0) ; dx (b < 0)
Hội tụ nếu α > 1 và phân kì nếu α 1. α α x a – x 0 1 b 1 ♦ ( ( a < 0) ; b > 0)
Hội tụ nếu 0 < α < 1 và phân kì nếu α 1. x α dx x α dx a 0
. ỨNG DỤNG TÍCH PHÂN:
4.1. Tính diện tích của hình phẳng(H):
1. Trường hợp 1: Đường cong cho bởi phương trình y = f ( x)
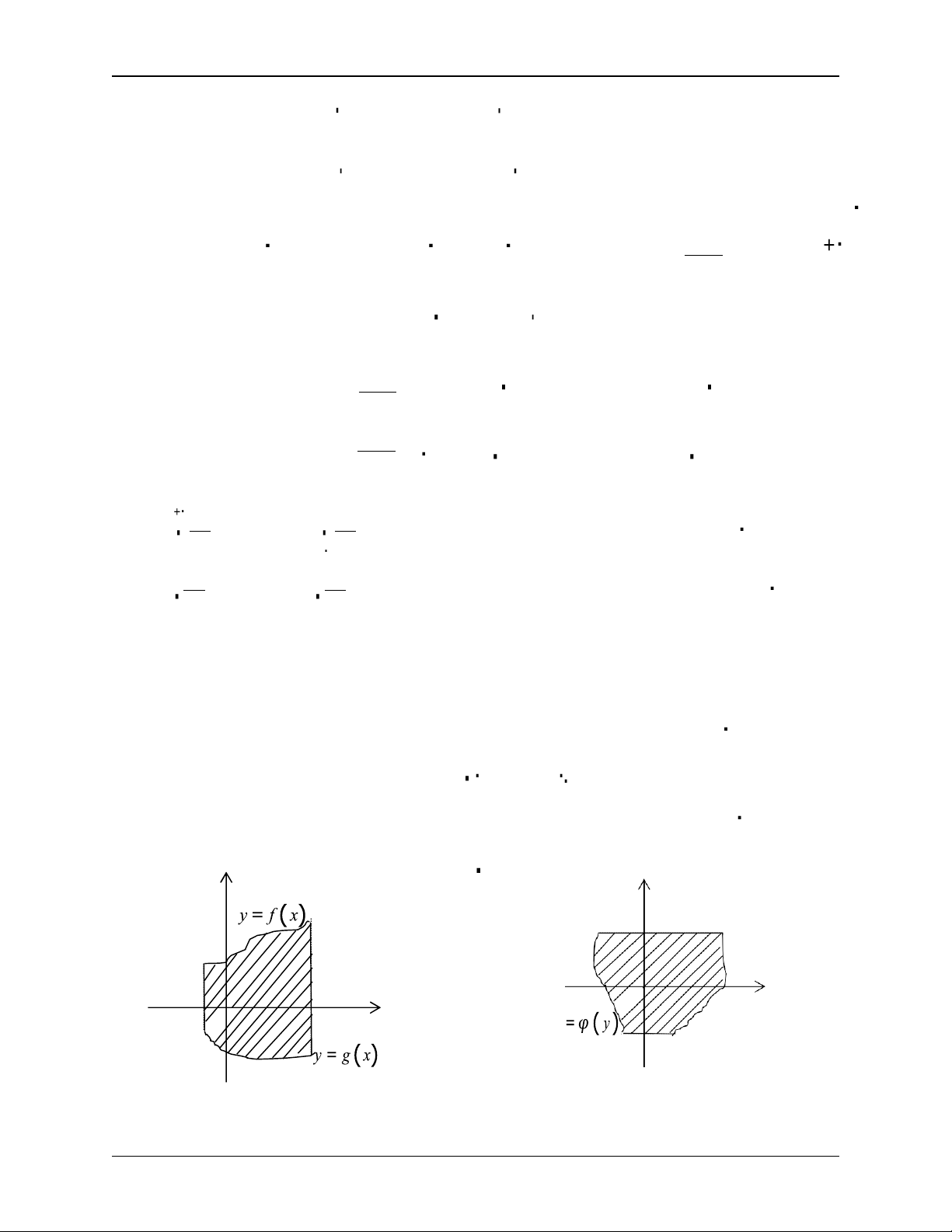
a. (H) giới hạn bởi : x = a; x = b; y = f (x); y = g( x) ; 6x ϵ[a;b]: f ( x) g ( x) . b
Khi đó diện tích hình phẳng (H) :
S = L f ( x) – g ( x) dx (1) ( Hình 1) a
b. (H) giới hạn bởi :
y = c; y = d; x = φ( y); x = ψ ( y) ; 6y ϵ[c; d ]:ψ ( y) φ ( y) . d
Khi đó diện tích hình phẳng (H) :
S = [ψ ( y) – φ( y)].dy (2) (Hình 2) y c y d
x =ψ ( y ) O x a b O x x c (Hình 1) (Hình 2)
GVC.Phan Thị Quản Trang30
Đề cương bài giảngchương III:
PHÉP TÍNH TÍCH PHÂN HÀM MỘT BIẾN . x = x(t)
2. Trường hợp 2: Đường cong cho bởi phương trình tham số :
(α t β )
y = y(t)
Khi đó công thức tính diện tích vẫn là (1) và (2)
3. Trường hợp 3: Đường cong cho trong tọa độ cực φ = φ φ = φ 1 φ = φ 2
(H) giới hạn bởi : 2 ;
6φ ϵ[φ ;φ ]: r (φ ) r (φ ) = r
r = r (φ) 1 2 1 2 r 1 1
r = r (φ) r = r 2 φ = φ 2 1 φ 1 2
Khi đó diện tích hình phẳng (H) : S =
[r 2 (φ) – r 2 (φ)].dφ 2 2 1 φ1
4.2. Tính thể tích :
1. Vật thể bất kì : Khi cắt vật thể (T ) bởi một mặt phẳng vuông góc với trục Ox . Thiết diện
thu được là S ( x), a x b . Khi đó thể tích của vật thể được xác định bởi công thức : b
V = S ( x) dx a
2. Vật thể tròn xoay :
a. Quay quanh trục Ox :
Quay ( H ) giới hạn bởi :
x = a ; x = b ; y = 0; y = f (x); f (x) 0, 6x ϵ[a;b] Quanh trục b
Ox , tạo nên một vật thể tròn xoay có thể tích : V = π f 2 ( x ) dx (1) a
b. Quay quanh trục Oy :
Quay ( H ) giới hạn bởi :
y = c ; y = d ; x = 0; x = g( y); g( y) 0, 6y ϵ[c; d ] Quanh trục d
Oy , tạo nên một vật thể tròn xoay có thể tích :
V = π g 2 ( y ) dy (2) c Chú ý: x = x(t)
Nếu đường cong cho bởi phương trình tham số :
(α t β ) thì các công thức của
y = y(t)
thể tích tròn xoay ở (1) và (2) vẫn sử dụng được.
Nếu đường cong cho trong tọa độ cực: r = r (φ ), φ1 φ φ2 thì chuyển sang tham số bởi
x = r(φ).cosφ công thức:
; (φ1 φ φ2 ) và áp dụng các công thức trên tính V tròn xoay
y = r(φ).sin φ
(xem φ là tham số) với điều kiện y là hàm đơn trị theo x trên đoạn [a;b] , trong đó
a = x (φ1 );b = x (φ2 ) .
GVC.Phan Thị Quản Trang31
Đề cương bài giảngchương III:
PHÉP TÍNH TÍCH PHÂN HÀM MỘT BIẾN .
4.3. Tính độ dài của cung phẳng: y B
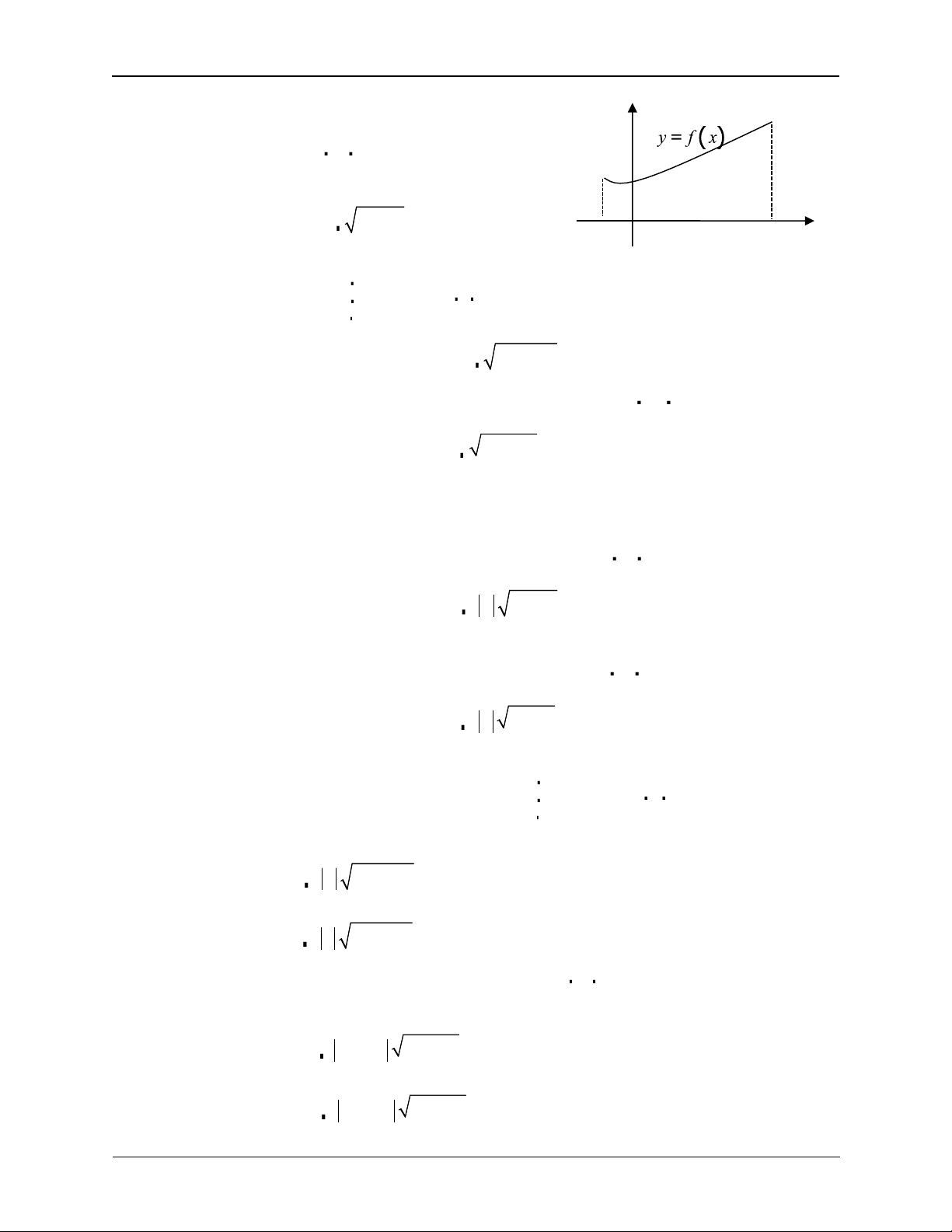
1. Trường hợp 1: Đường cong cho bởi phương
trình y = f ( x) và a x b .Khi đó độ dài đường A
cong AB được xác định bởi công thức: b
L = 1+ y '2 .dx a O b x a
2. Trường hợp 2: Đường cong cho bởi x = x(t) phương trình tham số :
(α t β )
y = y(t) β
L = x '2 + y '2 .dt α
3. Trường hợp 3: Đường cong cho trong tọa độ cực r = r (φ ), φ1 φ φ2 φ2
L = r2 + r '2 .dφ φ1
4.4. Tính diện tích mặt tròn xoay: Quay cung L chạy từ A đến B , có độ dài, quanh một trục tạo nên mặt tròn xoay
1. Quay quanh trục Ox :
Quay đường cong (L) cho bởi phương trình y = f ( x) với a x b , quanh trục Ox , tạo nên b
một mặt tròn xoay có diện tích : S = 2π y 1+ y '2 .dx (1) a
2. Quay quanh trục Oy :
Quay đường cong (L) cho bởi phương trình x = g ( y ) với c x d , quanh trục Oy , tạo nên d
một mặt tròn xoay có diện tích : S = 2π x 1+ x '2 .dy (2) c Chú ý: x = x(t)
a. Nếu đường cong cho bởi phương trình tham số :
(α t β ) thì các công thức của
y = y(t) diện tích tròn xoay là: β •
S = 2π y
x '2 + y '2 .dt Quanh trục Ox . α β •
S = 2π x
x '2 + y '2 .dt Quanh trục Oy . α
b. Nếu đường cong cho trong tọa độ cực: r = r (φ ), φ1 φ φ2
thì các công thức của diện tích tròn xoay là: φ2 •
S = 2π r.sin φ
r 2 + r '2 .dφ Quanh trục Ox . φ1 φ 2 •
S = 2π r.co sφ
r 2 + r '2 .dφ Quanh trục Oy . φ1
GVC.Phan Thị Quản Trang32
Đề cương bài giảngchương III:
PHÉP TÍNH TÍCH PHÂN HÀM MỘT BIẾN . BÀI TẬP:
Bài 1: Tính các tích phân sin x.cos x cos x 1. a. .dx b. dx c. dx
2 cos2 x – sin2 x x x2 +1 2. a. dx dx c. cos x b. dx ex +1 1+ cos2 x 1+ sin2 x dx 3. a. dx
b. x.(2x + 5)10.dx c. x ex –1 x2dx dx x2 4. a. b. dx c. x x2 x 1– x2 x cos x
5. a. arctan x.dx b. ln2 xdx c. dx 2 sin x 6. a.
cos(ln x).dx
b. x arctan x dx c. e x dx x2 ln (ln x) x 7. a.
(x2¬2x + 5)e –x.dx b. dx c. arcsin dx x 1– x x 8. a. arccos .dx dx c.
sin2 x.e –xdx x +1 b. ln2 x x2 ( dx 3x – 2) dx 9. a. b. c. dx x2 + 2x + 5 x2 – 4x + 5 dx dx 10. a. b. c. xdx x ( x +1) 5x2 – 2x ln xdx dx e xdx 11. a. b. x
1– 4 ln x – ln2 x c.
2 cos2 x + sin x cos x + sin2 x ( dx 5x3 + 2)dx
(x3 + x +1)dx 12. a. b. c. x ( x +1)2
x3 – 5x2 + 4x x (x2 +1) 1 x x –1 dx 13. a. dx b. dx c. x2 x 3 x +1 – x –1 x +1 1 x –1 14. a. dx b. x2 dx c. dx x2 x +1 x2 – x x4 x2 +1 1 1 cos5 x 15. a. dx b. dx c. dx sin3x sin4 x sin3x 16.
a. cos63xdx b.
sin5 x.3 cos xdx c. dx
4 sin3xcos5 x cos xdx 17. a. c. cot6 xdx
b. sin x.sin 2x.sin 3xdx 1+ cos x dx dx cos xdx c. 18. a. b. 1+ 3 cos2 x
sin2 x – 6 sin x + 5
cos x + 2 sin x + 3
GVC.Phan Thị Quản Trang33
Đề cương bài giảngchương III:
PHÉP TÍNH TÍCH PHÂN HÀM MỘT BIẾN .
Bài 2: Chứng minh rằng: 1 1 a. dt x Ξ dt + Ξ 1 tan x tdt co t x ( x > 0) b. 1+ t 2 dt 1+ t 2 1+ t 2 t 1+ t2 ( ) x 1 1 1 e e Bài 3: Tính: 1 1– x2 0 dx 1 ln (1+ x) 1 dx dx a. dx d. x2 b. c. 1+ x2 1+ x2 ( ) 2 2 –1 0 –1 2 Bài 4: Tính: 2x dx arctan x 1. a. dx b. c. dx 2 – x2 +1 2 x 1+ x2 x 1 – ln x dx 2. a. e x dx b. dx x 2 c. 1+ ex 0 1 0 1 1 ( 0 x –1) dx 2 e x x 3. a. dx b. c. dx 3 3 x –1 –1 x5 x –1 1
Bài 5; Xét sự hội tụ hay phân kì của tích phân: 1. a. dx ln (1+ x2 )dx b. e–xdx x c. 3 x +1 x 0 1 0 ln x x ln x 2. a. dx dx c.
e–x2 dx 3 b. 2 x5 2 x6 0 arctan xdx dx 1 ln (1+ x2 ) 3. a. b. 3 c. dx 0 x4 +1 e 2 x ln (ln x) 0 1 2 1 1 x xdx sin x 4. a. dx b. c. dx – x 0 0 esin x –1 0 3
3 x4 (ex – e Bài 6:
1. Tinh diện tích hình phẳng giới hạn bởi các đường: 2 x
a. y = x2 ; y = ; y = 2x
b. y2 = 2x +1; x – y –1 = 0 2
c. r = a (1+ cosφ ) ; r = acosφ
d. Một nhịp ycloit: x = R (t – sin t ) : y = R (1– cos t ) và trục Ox
2. Tính diện tích hình giới hạn bởi 2 x y2
x = acos3t
a. Đường elip: + = 1
b. Đường astroit: ; a, b > 0 a2 b2
y = bsin3t
c. Đường hoa hồng 3 lá: r = asin3φ
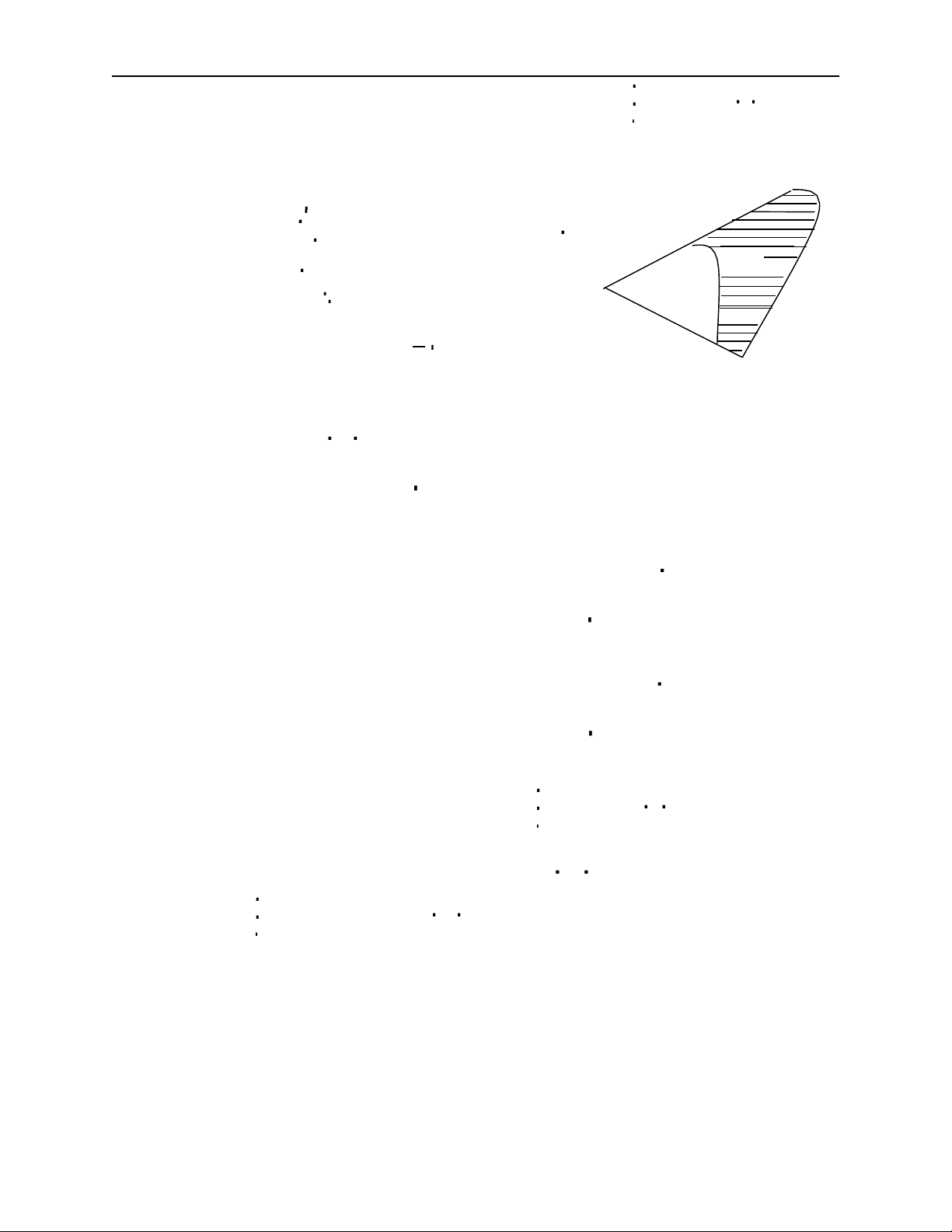
d. Đường Lemniscate Bernoulli: r = a cos2φ ; a > 0 x2 2 2 3. Parabol y =
chia hình tròn x + y
8 ra hai phần .Tính diện tích từng phần 2
4. Tính thể tích của vật thể tròn xoay tạo nên bởi hình phẳng (H) giới hạn bởi các đường :
y = x2 + 4x + 3; y = 3 khi quay quanh trục Ox, Oy .
GVC.Phan Thị Quản Trang34
Đề cương bài giảngchương III:
PHÉP TÍNH TÍCH PHÂN HÀM MỘT BIẾN .
5. Tính thể tích của vật thể tròn xoay tạo nên bởi hình phẳng (H) giới hạn bởi các đường :
y = x2; y = 4 khi quay quanh quanh đường thẳng x = –2 .
6. Tính thể tích của vật thể tròn xoay tạo nên bởi
a. Một nhịp xycloit: x = R (t – sin t ) : y = R (1– cos t )
khi quay quanh quanh trục Ox .
x = acos3t
b. Đường Astroit: ; a, b > 0
khi quay quanh trục Ox .
y = bsin3t
7. Tính độ dài cung của đường cong: 2 y = x2 – 2 gồm giữa 2 giao điểm của nó với trục Ox .
8. Tính độ dài của đường:
x = acos3t a. Astroit: ; a > 0
b. Cacđioit r = a (1+ cosφ )
y = asin3t
9. Tính diện tích mặt tròn xoay tạo bởi
a. Đường elip: 4x2 + y2 = 4 quay quanh quanh trục Oy .
x = acos3t b. Đường Astroit:
; a > 0 quay quanh quanh trục Oy . y = asin3t
c. Đường cacđioit r = 2a (1+ cosφ ) quay quanh quanh trục Ox .
x = R (t – sin t )
d. Một nhịp xycloit: y = R (1– cos t ) , R > 0 quay quanh quanh trục Ox . *****
GVC.Phan Thị Quản Trang35