Đường cong Bezier Thuật toán de Casteljau
Thuật toán de Casteljau dựa trên dãy các điểm điều khiển để xây dựng với giá trị t trong
đoạn [0, 1] tương ứng với một điểm P(t). Do đó, thuật toán sinh ra một dãy các điểm từ
các điểm điều khiển cho trước. Khi các điểm điều khiển thay đổi, đường cong sẽ thay đổi
theo. Cách xây dựng đường cong dựa trên phép nội suy tuyến tính và do đó rất dễ dàng
giao tiếp. Ngoài ra, phương pháp này cũng đưa ra nhiều tính chất quan trọng của đường cong.
Parabol dựa trên ba điểm
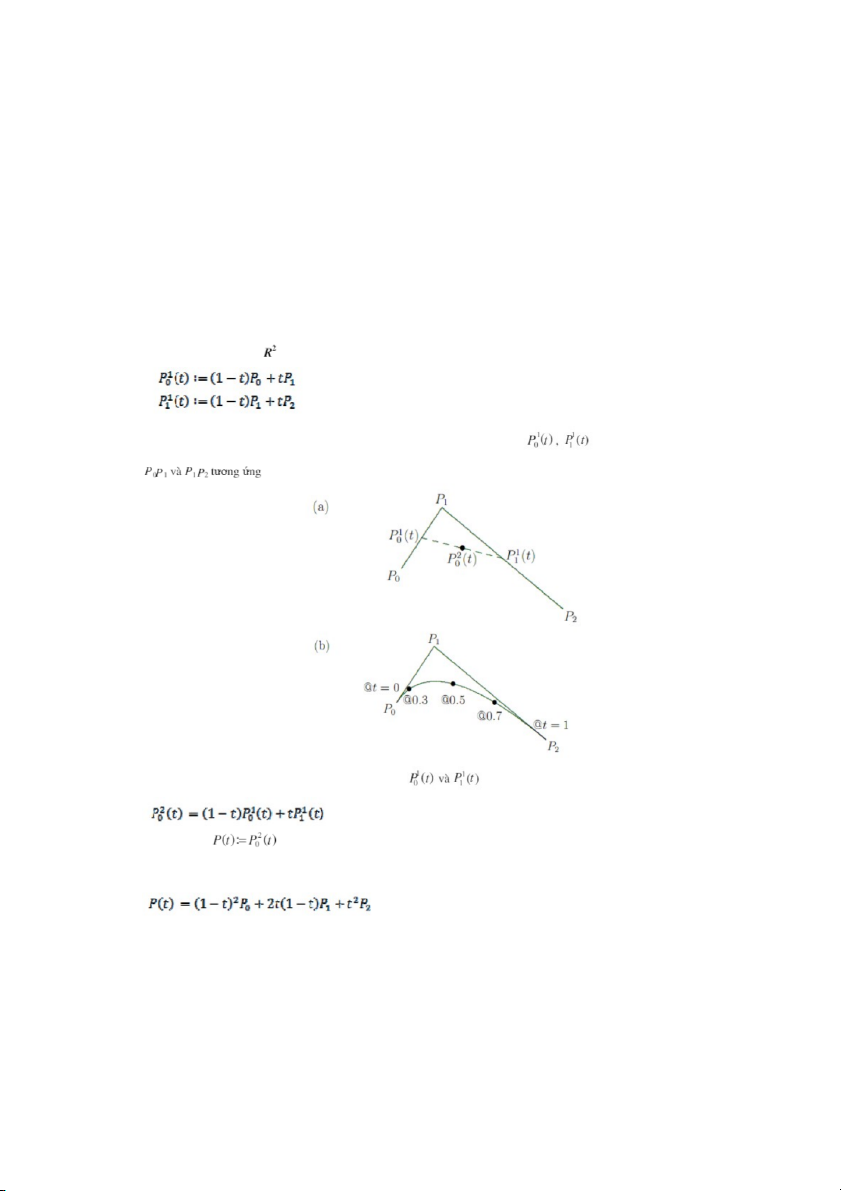
Trong mặt phẳng xét ba điểm P0, P1, P2. Đặt Trong đó, t
∈ [0, 1]. Nói cách khác, với mỗi t ∈ [0, 1], các điểm
nằm trên các đoạn thẳng
Lặp lại phép nội suy tuyến tính trên các điểm mới ta được: Quỹ tích của
khi t thay đổi trong đoạn [0, 1] sẽ cho ta đường cong như trên hình (b) Dễ dàng suy ra 1
Suy ra P(t) là đường cong parabol theo biến t.
Ví dụ: Phương trình đường cong Bezier P(t) tương ứng ba điểm điều khiển P0(1, 0), P1(2, 2), P2(6, 0) là:
Thuật toán de Casteljau cho L + 1 điểm điều khiển
Trong mặt phẳng R2 xét L+1 điểm P0, P1,..., PL. Với mỗi giá trị t cho trươc, ta xây dựng theo quy nạp đường cong như sau:
Cài đặt minh họa thuật toán Casteljau Point Casteljau(float t) { Point Q[Max]; int i, r;
for (i = 0; i <= L; i++) { Q[i].x = P[i].x; Q[i].y = P[i].y; }
for (r = 1 ; r <= L; r++) {
for (i = 0; i <= L - r; i++) {
Q[i].x = (1 - t)*Q[i].x + t*Q[i + 1].x;
Q[i].y = (1 - t)*Q[i].y + t*Q[i + 1].y; } } return(Q[0]); }
Để vẽ đường cong Bezier ta chỉ cần áp dụng gọi hàm Casteljau trong thủ tục DrawCurve sau:
void DrawCurve(float a, float b, int NumPoints) {
float Delta = (b – a)/(float)NumPoints; float t = a; int i;
moveto(Casteljau(t).x, Casteljau(t).y) ;
for (i = 1; i <= NumPoints; i++) { t += Delta ;
lineto(Casteljau(t).x, Casteljau(t).y) ; } } Mặt cong B-Spline 2 Pij là điểm kiểm soát
N và M là đa thức B-spline
Với các mặt cong mở mặt cong phụ thuộc vào các nút vector
Đặc điểm của mặt cong B-Spline
*ƒ Số bậc caonhất của bề mặt theo mỗi hướng thì bằng số điểm kiểm soát -1 theo hướng đó.
ƒ *Đạo hàm riêng của phương trình bề mặt theo mỗi tham biến có bậc bằng số điểm kiểm
soát theo tham biến đó trừ 2.
ƒ* Bề mặt B-spline thì không chịu ảnh hưởng của phép biến đổi anfine. Bề mặt sẽ thay đổi
nếu ta thay đổi đa giác kiểm soát.
ƒ *Ảnh hưởng của một điểm kiểm soát đơn được giới hạn bởi + - k/2 h/2 khoảng đối với mỗi tham số.
ƒ *Nếu số đỉnh của đa giác kiểm soát bằng số bậc theo mỗi tham biến và không có điểm kép
nào thì mặt B-spline sẽ chuyển thành mặt Bezier.
ƒ* Nếu các đa giác kiểm soát có dạng tam giác thì lưới đa giác kiểm soát sẽ có hình dáng gần giống với bề mặt cong. 3
ƒ* Mỗi mặt B-Spline luôn nằm trong bao lồi của đa giác kiểm soát .
ƒ* Mỗi mặt B-Spline có dáng điệu luôn bám theo hình dáng của đa giác kiểm soát. 4