Đề cương ôn tập cung và góc lượng giác, công thức lượng giác – Phùng Hoàng Em
Tài liệu gồm 12 được biên soạn bởi thầy Phùng Hoàng Em bao gồm tóm tắt lý thuyết, phân dạng toán, ví dụ minh họa và tuyển chọn các bài tập trắc nghiệm chủ đề cung và góc lượng giác
Chủ đề: Chương 1: Hàm số lượng giác và phương trình lượng giác (KNTT)
Môn: Toán 11
Thông tin:
Tác giả:
Thông tin :
Chủ đề:
Chương 1: Hàm số lượng giác và phương trình lượng giác (KNTT)
Môn:
Tác giả:
Tài liệu liên quan:
Preview text:
ĐẠI SỐ 10 Chương VI. LƯỢNG GIÁC GV: PHÙNG V. HOÀNG EM
ĐỀ CƯƠNG ÔN TẬP CHƯƠNG VI
Môn: Toán – ĐẠI SỐ 10 ÔN GIỮA KỲ ****************
A. LÝ THUYẾT CẦN NHỚ
1. Công thức cơ bản.
○ sin2 x + cos2 x = 1, suy ra: sin2 x = 1 − cos2 x và cos2 x = 1 − sin2 x ; 1 1 ○ 1 + tan2 x = , suy ra: cos2 x = cos2 x 1 + tan2 x 1 1 ○ 1 + cot2 x = , suy ra: sin2 x = sin2 x 1 + cot2 x sin x cos x ○ tan x = ; cot x = ; tan x. cot x = 1. cos x sin x
2. Công thức cộng. (Dùng để tách góc, hoặc ghép góc)
○ sin(a + b) = sin acos b + sin b cos a.
○ cos(a − b) = cos acos b + sin asin b. tan a + tan b ○ ○ sin(a tan(a .
− b) = sin a cos b − sin b cos a. + b) = 1−tanatanb tan a − tan b
○ cos(a + b) = cos acos b − sin asin b. ○ tan(a − b) = . 1 + tan a tan b
3. Công thức góc nhân đôi. (Dùng để giảm góc)
○ sin2α = 2sinαcosα.
○ cos2α = 2cos2 α − 1 = 1 − 2sin2 α 2 tan α
○ cos2α = cos2 α − sin2 α. ○ tan2α = . 1 − tan2 α
4. Công thức hạ bậc. (Dùng để làm mất bình phương) 1 ○ − cos 2α sin2 α = . 2 1 ○ + cos 2α cos2 α = . 2 1 π ○ − cos 2α tan2 α = , α 6= + kπ, k ∈ Z. 1 + cos2α 2
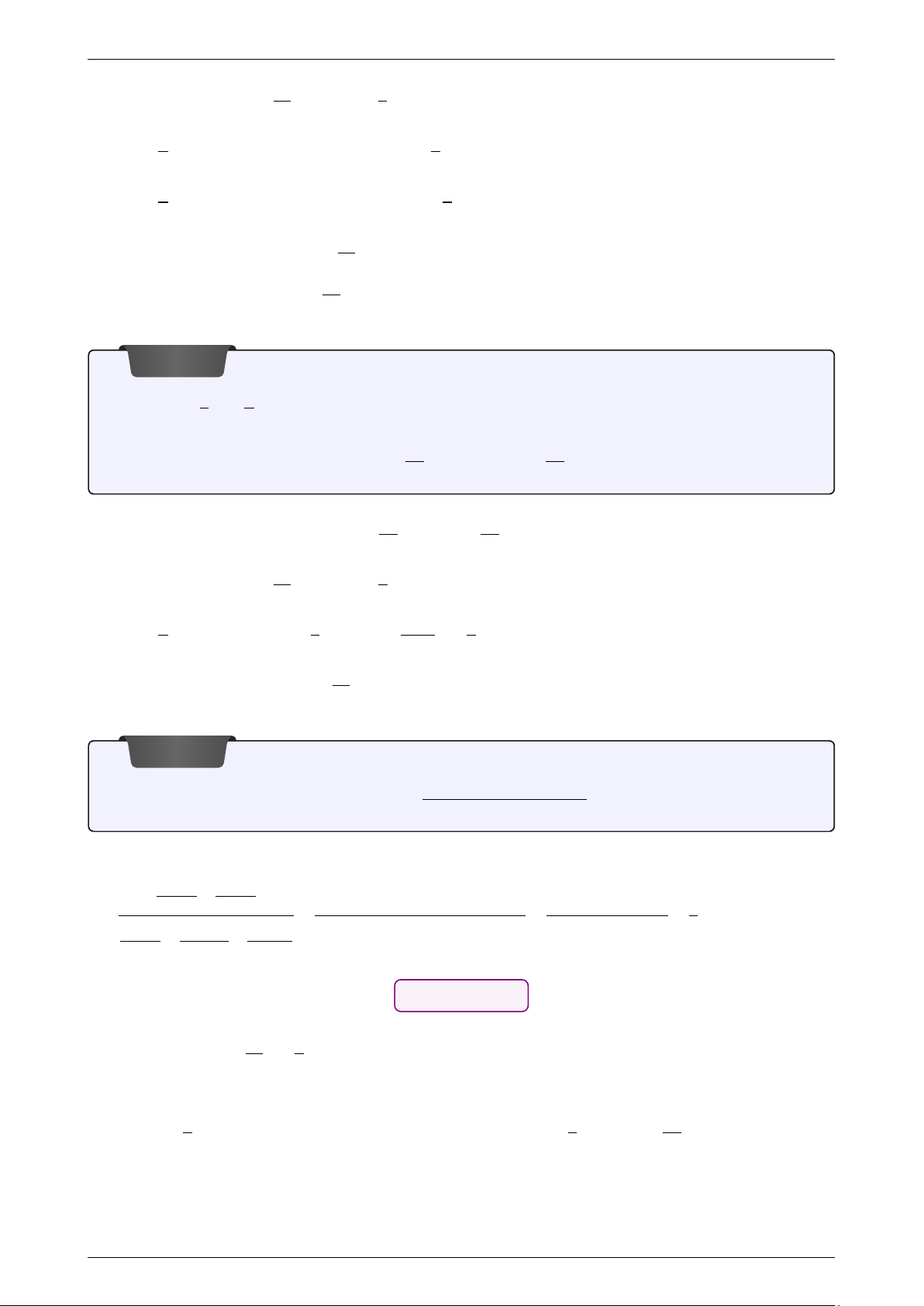
5. Dấu của các tỉ số lương giác tương ứng trên các góc phần tư.
Để xác định dấu của các giá trị lượng giác của một góc α ta y
xác định vị trí điểm cuối của cung AM = α trên đường tròn y B
lượng giác. Điểm M thuộc góc phần tư nào thì ta áp dụng II I
bảng xác định dấu của các giá trị lượng giác. Góc phần tư Giá trị lượng giác I II III IV A0 A x sin α α + + − − cos α + − − + M tan α + − + − III IV cot α + − + − B0 GV: Phùng Hoàng Em – St 1 ĐẠI SỐ 10 Chương VI. LƯỢNG GIÁC
B. CÁC DẠNG TOÁN TỰ LUẬN
d Dạng 1. Cho trước 1 tỉ số lượng giác, tính các tỉ số lượng giác còn lại
1. Ta thực hiện theo các bước:
○ Sử dụng công thức thích hợp để tính tỉ số tiếp theo (chú ý nhóm công thức cơ bản);
○ Ứng với miền của α đề cho, xem Mục 5. để chọn kết quả đúng.
○ Tính toán các tỉ số còn lại.
2. Nếu đề cho trước 1 tỉ số lượng giác, yêu cầu tính giá trị biểu thức. Ta thường biến đổi
biểu thức đó về giá trị đã cho. Sau đó, thay kết quả. VÍ DỤ MINH HỌA Ví dụ 1 1 ³ π ´ Biết sin α = và α ∈
; π . Tính giá trị của cosα; tanα và cotα. 3 2 Lời giải. p 1 8 2 2
Từ sin2 α + cos2 α = 1 nên cos2 α = 1 − sin2 α = 1 − = ⇒ cos α = ± . 9 9 3 p ³ π ´ 2 2 ○ Do α ∈
; π nên cosα < 0. Suy ra cosα = − . 2 3 sin α 1 1 p ○ tanα = p ; cot α = 2. cos α = − 2 2 tan α = −2 Ví dụ 2 3 µ 3π ¶
Cho cos α = , với α ∈
; 2π . Tính giá trị của sin2α và tan2α. 5 2 Lời giải. 16 4
Ta có sin2 α + cos2 α = 1 ⇒ sin2 α = 1 − cos2 α = ⇒ sin α = ± 25 5 µ 3π ¶ 4 ○ Do α ∈
; 2π nên sinα < 0 ⇒ sinα = − 2 5 3 ○ −4 −24
sin 2α = 2sinαcosα = 2 · · = 5 5 25 sin α 3 2 tan α 24 ○ tanα = ⇒ tan 2α = = − cos α = − 4 1 − tan2 α 7 Ví dụ 3 3 π
Cho tan α = − , với
< α < π. Tính giá trị của sin α, sin 2α và cos 2α. 4 2 Lời giải.1 9 25 16 Ta có = 1 + tan2 α = 1 + = ⇒ cos2 α = . cos2 α 16 16 25 GV: Phùng Hoàng Em – St 2 ĐẠI SỐ 10 Chương VI. LƯỢNG GIÁC 9 3
○ sin2 α = 1 − cos2 α = ⇒ sin α = ± . 25 5 π 3 ○ Do
< α < π nên sin α > 0, do đó sin α = . 2 5 π 4 ○ Do
< α < π nên cos α < 0, do đó cos α = − . 2 5 24
• sin 2α = 2 sin α cos α = − 25 7
• cos 2α = 2 cos2 α − 1 = 25 Ví dụ 4 3 π Cho sin α = với
< α < π. Tính giá trị của biểu thức 5 2 µ 9π ¶ µ 3π ¶ P = cos
− α + 2 tan α + . 2 2 Lời giải. 9π 9π
Áp dụng công thức cộng, ta có P = cos . cos α + sin
. sin α = sinα − 2cotα. 2 2 16 4
○ cos2 α = 1 − sin2 α = ⇒ cos α = ± 25 5 π 4 cos α 4 ○ Do
< α < π ⇒ cos α = − và cot α = 2 5 sin α = − 3 49
○ Suy ra, P = sinα − 2cotα = . 15 Ví dụ 5 sin α − cosα
Cho tan α = 3. Tính giá trị biểu thức B = .
sin3α + 3cos3α + 2sinα Lời giải.
Ta biến đổi biểu thức B về tan α như sau: sin α cos α − cos3α cos3α
tan α¡tan2α + 1¢ − ¡tan2α + 1¢ 3(9 + 1) − (9 + 1) 2 B = = = = . sin3α 3cos3α 2 sin α
tan3α + 3 + 2tanα¡tan2α + 1¢ 27 + 3 + 2.3(9 + 1) 9 + + cos3α cos3α cos3α LUYỆN TẬP 1 12 π
Bài 1. Cho cos α = − và
< α < π. Tính sin α và tan α. 13 2
Bài 2. Tính các giá trị lượng giác còn lại của góc α, biết 1 2 3π a) sin α =
và 900 < α < 1800;
b) cos α = − và π < α < . 3 3 2
Bài 3. Tính các giá trị lượng giác còn lại của góc α, biết
a) tan α = 2 và π < α < 2π;
b) cos α = 0,8 và tanα + cotα > 0. GV: Phùng Hoàng Em – St 3 ĐẠI SỐ 10 Chương VI. LƯỢNG GIÁC 12 π
Bài 4. Cho sin α = và
≤ α ≤ π. Tính các giá trị lượng giác còn lại của góc α. 13 2 µ 3π ¶
Bài 5. Cho tan α = 3 và α ∈ π;
. Tính các giá trị lượng giác còn lại của góc α. 2 3 3π µ 19π ¶
Bài 6. Cho sin α = − và
< α < 2π. Tính cos α, tan α; cos 2α và sin α + . 5 2 4 π µ 3π ¶
Bài 7. Cho tan α = −2 và
< α < π. Tính cos α, cos α −
; cot α và tan2α. 2 4 2 3π
Bài 8. Cho cos α = và ≤ α ≤ 2π. 3 2 p
9sin2α + 5.tanα
a) Tính tan α, sin2α, tan2α. b) Tính A = 5 + 6cosα ³ π´ ³ π ´
c) Tính sin 2α,cos2α,tan2α,cot2α. d) Tính sin α + và cos − α . 4 3 π
Bài 9. Cho 0 ≤ α ≤ . Xác định dấu của các giá trị lượng giác sau: 2 ³ π´ ³ π´ a) sin α + b) cos α − c) tan (−α). 4 2
Bài 10. Cho tan α = 2, tính giá trị biểu thức M = cos2 α − sin2 α.
2 sin α − 3cosα
Bài 11. Cho cot α = 3. Tính giá trị biểu thức M = .
5 sin3 α + cos3 α 2 tan α + 3cotα
Bài 12. Cho cos α = . Tính giá trị biểu thức A = . 3 tan α + cotα 1 π π
Bài 13. Cho sin x + cos x = và ≤ x ≤ . Tính sin 2x và cos 2x. 2 4 2 GV: Phùng Hoàng Em – St 4 ĐẠI SỐ 10 Chương VI. LƯỢNG GIÁC
d Dạng 2. Rút gọn biểu thức hoặc chứng minh đẳng thức
1. Các phương pháp thường dùng:
○ Biến đổi vế phức tạp của đẳng thức về vế đơn giản;
○ Biến đổi tương đương để đẳng thức đi đến kết quả hiển nhiên đúng;
○ Phối hợp cả hai cách trên. 2. Chú ý:
○ Nếu trong đẳng thức, các góc đều giống nhau, ta ưu tiên nhóm công thức cơ bản (Nhóm 1);
○ Nếu trong đẳng thức, có xuất hiện góc gấp đôi và bình phương tỉ số lượng giác,
ta ưu tiên nhóm nhân đôi và hạ bậc (Nhóm 3,4);
○ Nếu cần tách góc, ta ưu tiên nhóm công thức cộng (Nhóm 2). VÍ DỤ MINH HỌA Ví dụ 1 Rút gọn biểu thức: 2 sin2 x − 1 a) A = sin2 x + sin2 x tan2 x; b) B = .
c) A = cos2 α¡sin2 α + 1¢ + sin2 x − sin x cos x sin4 α Lời giải. 1
a) A = sin2 x + sin2 x tan2 x = sin2 x ¡1 + tan2 x¢ = sin2 x · = tan2 x. cos2 x 2 sin2 x − 1
2 sin2 x − ¡sin2 x + cos2 x¢ sin x + cos x b) B = = = = 1 + cot x; sin2 x − sin x cos x sin x (sin x − cos x) sin x
c) A = sin2 α¡1 − sin2 α¢ + cos2 α + sin4 α = sin2 α − sin4 α + cos2 α + sin4 α = 1. Ví dụ 2 Rút gọn các biểu thức: p ³ π ´ 2 cos a − 2cos + a 4 a) A = p .
b) B = (tan a − tan b)cot(a − b) − tan a tan b. ³ π ´ − 2 sin a + 2 sin + a 4 Lời giải. p ³ π π ´
2 cos a − 2 cos cos a − sin sin a p2sina a) Ta có 4 4 A = p = p = tan a. ³ π π ´ − 2 sin a + 2 sin cos a + cos sin a 2 cos a 4 4
b) Ta có B = tan(a − b)(1 + tan a tan b)cot(a − b) − tan a tan b = 1. GV: Phùng Hoàng Em – St 5 ĐẠI SỐ 10 Chương VI. LƯỢNG GIÁC Ví dụ 3
Chứng minh các đẳng thức sau trong điều kiện có nghĩa của biểu thức 3 1
1 − cosα + cos2α
a) sin4 α + cos4 α = + cos4α; b) 4 4
sin 2α − sinα = cotα; 2 + sin2 α
sin4 α − cos4 α + cos2 α α c) = 3 tan2 α + 2; d) = cos2 . 1 − sin2 α 2(1 − cosα) 2 Lời giải. 1
a) VT = (sin2 α + cos2 α)2 − 2sin2 αcos2 α = 1 − sin2 2α 2 1 − cos4α 3 1 = 1 − = + cos 4α = VP. 4 4 4
1 − cosα + 2cos2 α − 1
cos α(2cosα − 1) cos α b) VT = =
2 sin αcosα − sinα = sinα(2cosα − 1)
sin α = cotα = VP. 2 + sin2 α 2 + sin2 α 2 c) VT = = =
+ tan2 α = 2 + 2 tan2 α + tan2 α = 3 tan2 α + 2 = VP. 1 − sin2 α cos2 α cos2 α
sin4 α + cos2 α(1 − cos2 α)
sin4 α + cos2 αsin2 α
sin2 α(sin2 α + cos2 α) d) VT = = = 2(1 − cosα) 2(1 − cosα) 2(1 − cosα) α 2 cos2 1 − cos2 α 1 + cosα 2 α = = = = cos2 = VP. 2(1 − cosα) 2 2 2 Ví dụ 4
Chứng minh biểu thức sau không phụ thuộc vào giá trị của biến x 1 − cos2x + sin2x P = · cot x. 1 + cos2x + sin2x Lời giải. 2 sin2 x cos x 2 sin x(sin x cos x ○ + 2 sin x cos x + cos x) P = · = · = 1. 2 cos2 x + 2sin x cos x sin x 2 cos x(sin x + cos x) sin x
○ Vậy giá trị của biểu thức P không phụ thuộc vào giá trị của biến x. LUYỆN TẬP 2
Bài 1. Không sử dụng MTCT, hãy tính giá trị sin 15◦, cos 15◦, sin 75◦ và cos 75◦. 4 cos2 x − 2
Bài 2. Rút gọn biểu thức M = . sin x + cos x q
Bài 3. Rút gọn biểu thức N =
sin2 x (4 + cot x) + cos2 x (1 + 3tan x).
Bài 4. Rút gọn biểu thức C = (tan x − cot x)2 − (tan x + cot x)2.
Bài 5. Đơn giản biểu thức 1 − cosα 1
1 − sin2α.cos2α a) A = − ; b) B = − cos2α. sin2α 1 + cosα cos2α
Bài 6. Chứng minh các đẳng thức sau: GV: Phùng Hoàng Em – St 6 ĐẠI SỐ 10 Chương VI. LƯỢNG GIÁC 2 1
a) cos4α − sin4α = 2cos2α − 1; b) 1 − cot4α = − ; sin2α sin4α 1 + sin2α c) = 1 + 2tan2α;
d) 2(1 − sinα)(1 + cosα) = (1 − sinα + cosα)2. 1 − sin2α
Bài 7. Đơn giản biểu thức 1 − cosα 1
1 − sin2α.cos2α a) A = − ; b) B = − cos2α. sin2α 1 + cosα cos2α
Bài 8. Chứng minh các hệ thức sau
1 + sin4α − cos4α 2
sin2α(1 + cosα) sin α + tanα a) = ; b) = ;
1 − sin6α − cos6α 3cos2α
cos2α(1 + sinα) cos α + cotα tan α − tanβ
cos2α − sin2α c) d) = sin2αcos2α.
cot α − cotβ = tanαtanβ;
cot2α − tan2α
Bài 9. Rút gọn giá trị của biểu thức sau: µ 5π ¶ µ 3π ¶
a) A = cos(4π − α).tan(7π + α) + cos − α + cos
− α + sin (5π + α); 2 2 ³ π ´
b) B = 2sin(π + α) + cos
− α + sin (π − α) + cos (π + α); 2 ³ π ´
c) C = sin(π + α) − cos
− α + tan (π − α) cot (−α); 2 µ ¶ ³ π ´ 3π
d) D = sin(5π + α) − cos − α + tan
− α + cot(4π − α); 2 2 µ 3π ¶ µ ¶ ³ π ´ 3π
e) E = cos(π − α) + sin α − − tan + α cot − α ; 2 2 2 µ 3π ¶
f) F = cot(α − 4π)cos α −
+ cos(α + 6π) − 2 sin(α − π). 2
Bài 10. Chứng minh các đẳng thức sau:
a) (1 − sin2x).tan2x + (1 − cos2x)cot2x = 1;
b) 1 − sin2x − sin2x.cot2x = 0; (sin x + cos x)2 − 1
c) cos4 x + sin2 x cos2 x + sin2 x = 1; d) = tan2x; 2 cot x − sin2x 1 µ 1 + 3cos2 x ¶
e) sin4 x + sin4 x cot2 x + cos4 x + cos4 x.tan2 x = 1; f) tan x − sin x = cos x; 4 sin x µ 2 sin2 x + 1 ¶ g) 2 cot x − cos x = 6 sin x;
h) tan2 x − sin2 x tan2 x + 2cos2 x + sin2 x = 2; cos x
Bài 11. Chứng minh các đẳng thức sau: sin3x + cos3x sin2x − cos2x tan x − 1 a) = 1 − sin x cos x; b) = ; sin x + cos x 1 + 2sin x cos x tan x + 1 (sin x + cos x)2 − 1
c) (1 + cot x)sin3x + (1 + tan x)cos3x = sin x + cos x; d) = 2tan2x; cot x − sin x cos x sin2x + 2cos2x − 1 sin2x − tan2x e) = sin2x; f) = tan6x; cot2x cos2x − cot2x g) cos4x − sin4x = cos2x;
h) cos4x − 2cos2x = sin4x − 1; 1 − sin2xcos2x
i) sin4x + sin2x.cos2x + cos2x = 1; j) − cos2x = tan2x. cos2x GV: Phùng Hoàng Em – St 7 ĐẠI SỐ 10 Chương VI. LƯỢNG GIÁC cot2 α 1 + tan2 α
tan2 α + cot2 α
Bài 12. Chứng minh rằng · = . 1 + cot2 α tan2 α 1 + tan4 α sin2 x − cos2 y
Bài 13. Chứng minh rằng biểu thức B =
+ cot2 x cot2 y độc lập với x; y sin2 x sin2 y
C. CÂU HỎI TRẮC NGHIỆM
Câu 1. Góc có số đo 1080◦ thì có số đo là bao nhiêu rađian? A 6π. B 3π. C 12π. D 4π.
Câu 2. Tính số đo bằng rad của góc 22◦300. π 7π 9π 5π A . B . C . D . 8 12 12 12 π
Câu 3. Tính số đo bằng độ của góc . 36 A 6◦. B 8◦. C 5◦. D 10◦.
Câu 4. Đổi 2 rad ra độ. µ 360 ¶◦ A = 2◦. B . C 360◦. D 180◦. π 47π
Câu 5. Giá trị của sin là 6 p p 3 1 1 2 A . B . C − . D . 2 2 2 2
Câu 6. Tìm số dương T nhỏ nhất thoả sin(x + T) = sin x với mọi x. π A T = π. B T = 2π. C T = . D T = 4π. 2
Câu 7. Cho x là số thực, hãy chọn mệnh đề sai. A −1 ≤ sin x ≤ 1. B cos 2x ≤ 1.
C ¯¯ sin 3x¯¯ ≤ 1. D −1 ≤ tan x ≤ 1.
Câu 8. Chọn mệnh đề sai (với k là số nguyên tuỳ ý)?
A sin(x + k2π) = sin x.
B cos(x + kπ) = cos x.
C tan(x + k2π) = tan x.
D cot(x + kπ) = cot x.
Câu 9. Trong các đẳng thức sau, đẳng thức nào đúng?
A sin (180◦ − a) = −cos a.
B sin (180◦ − a) = −sin a.
C sin (180◦ − a) = sin a.
D sin (180◦ − a) = cos a.
Câu 10. Trong các đẳng thức sau, đẳng thức nào sai? ³ π ´ ³ π ´ ³ π ´ ³ π ´ A sin − x = cos x. B sin + x = cos x. C tan − x = cot x. D tan + x = cot x. 2 2 2 2
Câu 11. Tìm mệnh đề đúng trong các mệnh đề sau. ³ π ´ ³ π ´
A tan (π − a) = tan a. B cos − a = −sin a. C cot + a = −tan a.
D sin (π + a) = sin a. 2 2 ³ π´
Câu 12. Đơn giản biểu thức M = cos a −
+ sin (a − π) ta được kết quả nào sau đây? 2 A M = cos a + sin a. B M = 2sin a. C M = sin a − cos a. D M = 0.
Câu 13. Cho góc lượng giác α = 2017◦. Khẳng định nào sau đây đúng?
A sin α > 0 và cosα < 0.
B sin α > 0 và cosα > 0.
C sin α < 0 và cosα < 0.
D sin α < 0 và cosα > 0. 2017π
Câu 14. Cho góc lượng giác α =
. Khẳng định nào sau đây đúng? 4
A sin α > 0 và cosα < 0.
B sin α > 0 và cosα > 0.
C sin α < 0 và cosα < 0.
D sin α < 0 và cosα > 0. GV: Phùng Hoàng Em – St 8 ĐẠI SỐ 10 Chương VI. LƯỢNG GIÁC
Câu 15. Trong các đẳng thức sau, đẳng thức nào là đúng? p p 3 p 1 3 A cos 150◦ = . B cot 150◦ = 3. C tan 150◦ = − p . D sin 150◦ = − . 2 3 2
Câu 16. Trong các đẳng thức sau, đẳng thức nào là đúng?
A cos2 α − sin2 α = 1.
B sin2 α = 1 − cos2 α.
C sin2 α − cos2 α = 1.
D cos α + sinα = 1.
Câu 17. Giá trị của biểu thức S = 3 − sin2 90◦ + 2cos2 60◦ − 3tan2 45◦ bằng 1 1 A S = . B S = − . C S = 1. D S = 3. 2 2
Câu 18. Đẳng thức nào sau đây là công thức sai?
A cos 2x = 1 − sin2 2x.
B cos 2x = 2cos2 x − 1.
C cos 2x = 1 − 2sin2 x.
D cos 2x = cos2 x − sin2 x.
Câu 19. Đẳng thức nào sau đây là công thức đúng?
A sin 2x = 2sin2 x − 1.
B sin 2x = 1 − 2sin2 x.
C sin 2x = 1 − cos2 x.
D sin 2x = 2sin x.cos x.
Câu 20. Trong các giá trị sau đây, cos α có thể nhận giá trị nào? p 7 A 2. B . C −0,7. D −1,2. 4 ³ π´
Câu 21. Cho góc lượng giác α ∈ 0;
. Khẳng định nào sau đây đúng? 2
A sin α > 0 và sin2α > 0.
B sin α > 0 và cos2α < 0.
C cos α < 0 và cos2α < 0.
D cos α < 0 và sin2α > 0. 3 π
Câu 22. Cho tan α =
với 0 < α < . Tính sinα. 4 2 3 3 4 4 A − . B . C . D − . 5 5 5 5
Câu 23. Cho cos 1350◦ = a; sin675◦ = b. Nhận xét nào sau đây sai? A a = 0. B a > b. C a2 + b2 = 1. D 2b2 − a2 = 1. 1 π
Câu 24. Cho sin α = với
< α < π. Giá trị của cot α là 2 2 p p p p 3 3 A 3. B − 3. C . D − . 3 3 1
Câu 25. Biết sin α =
và cos α < 0. Tính giá trị của tanα. 3 1 1 p p
A tan α = − p .
B tan α = − p . C tan α = 2 2. D tan α = 3. 2 2 3 3 π
Câu 26. Cho tan α = − ở đó
< α < π. Tính giá trị của sin α. 4 2 3 4 3 4 A sin α = − . B sin α = . C sin α = . D sin α = − . 5 5 5 5 3π
Câu 27. Cho cot α = 3 và π < α <
. Tính giá trị của sin α. 2 3 3 1 1 A sin α = p . B sin α = − p . C sin α = p . D sin α = − p . 10 10 10 10 3 ³ π ´
Câu 28. Cho sin α = , ở đó α ∈
; π . Tính giá trị biểu thức M = 2sinαcosα. 5 2 24 24 12 12 A M = . B M = − . C M = − . D M = . 25 25 25 2 ³ π π ´ 4
Câu 29. Cho α ∈ ;
và thỏa mãn điều kiện cos2 α − sin2 α = − . Tính giá trị của sinα. 4 2 5 3 2 3 1 A sin α = p . B sin α = p . C sin α = p . D sin α = p . 2 10 10 10 10 GV: Phùng Hoàng Em – St 9 ĐẠI SỐ 10 Chương VI. LƯỢNG GIÁC 1 ³ π ´
Câu 30. Cho cos α = − , ở đó α ∈
; π . Tính giá trị của tanα. 3 2 p p 1 1
A tan α = −2 2. B tan α = 2 2.
C tan α = − p .
D tan α = − p . 2 2 2 2 12 π
Câu 31. Cho cos α = − và
< α < π. Tính giá trị của tan α. 13 2 2 5 5 5 A tan α = . B tan α = − . C tan α = . D tan α = − . 3 12 12 12 2 3π
Câu 32. Cho sin α = − với π < α <
. Tính giá trị của tan α. 5 2 p p p p 2 21 2 21 2 15 2 15 A tan α = − . B tan α = . C tan α = − . D tan α = . 21 21 15 15 4 π
Câu 33. Cho cos α =
với 0 < α < . Tính giá trị của sinα. 13 2 p p p p 3 13 3 17 3 17 3 13 A sin α = . B sin α = . C sin α = − . D sin α = − . 13 13 13 13 3π
Câu 34. Cho cot α = −3 với
< α < 2π. Tính giá trị của cos α. 2 p p p p 3 10 3 10 10 10 A cos α = . B cos α = − . C cos α = . D cos α = − . 10 10 10 10 p 3π
Câu 35. Cho tan α = 4 + 15 và
< α < 2π. Tính giá trị của cos α. 2 p p p p p p p p 2 − 5 3 − 5 5 − 2 5 − 5 A cos α = . B cos α = . C cos α = . D cos α = . 4 4 4 3 8 π
Câu 36. Cho sin α = và
< α < π. Tính giá trị của tan α. 17 2 8 8 8 8 A tan α = − . B tan α = − . C tan α = − . D tan α = − . 13 15 11 9 3 ³ π´
Câu 37. Cho cos α = với α ∈ 0; . Tính sin α. 5 2 4 4 16 16 A sin α = − . B sin α = . C sin α = − . D sin α = . 5 5 25 25 3 µ 3π ¶
Câu 38. Cho sin α = − với α ∈ π; . Tính cos α. 5 2 4 4 16 16 A cos α = − . B cos α = . C cos α = − . D cos α = . 5 5 25 25 1
Câu 39. Cho cot α = . Tính giá trị của biểu thức P = tanαcot2 α. 3 1 1 1 A P = . B P = . C P = . D P = 3. 27 9 3 2
Câu 40. Cho tan α = . Tính cotα. 3 p 2 3 45 3 A cot α = − . B cot α = − . C cot α = . D cot α = . 3 2 9 2 4 ³ π ´
Câu 41. Cho cos α = − với α ∈
; π . Tính giá trị của biểu thức P = sinα + cosα. 5 2 1 1 7 7 A P = . B P = − . C P = . D P = − . 5 5 5 5
Câu 42. Đẳng thức nào sau đây là đúng?
A cos 45◦ = sin30◦ cos15◦ − cos30◦ sin15◦.
B cos 45◦ = cos30◦ cos15◦ + sin30◦ sin15◦.
C cos 45◦ = cos30◦ cos15◦ − sin30◦ sin15◦.
D cos 45◦ = sin30◦ sin15◦ − cos15◦ cos30◦. 12 3π ³ π ´
Câu 43. Cho sin θ = − và
< θ < 2π. Tính cos − θ . 13 2 4 p p 5 19 7 2 3 2 A − . B − . C − . D − . 13 50 26 13 GV: Phùng Hoàng Em – St 10 ĐẠI SỐ 10 Chương VI. LƯỢNG GIÁC 3 4 π π
Câu 44. Cho sin x = ,sin y = , với 0 < x < và
< y < π. Tính giá trị sin(x − y). 5 5 2 2 7 7 A sin(x − y) = − . B sin(x − y) = −1. C sin(x − y) = 1. D sin(x − y) = . 25 25
Câu 45. Cho tan a + tan b = 2 và tan(a + b) = 4, giá trị của tan a.tan b bằng 1 1 A . B − . C 1. D −1. 2 2 ³ π´
Câu 46. Cho P = sin x +
. Khẳng định nào sau đây đúng? 3 p p p A 2P = sin x + 3cos x. B 2P = sin x + 3cos x. p p 3 1 C P = sin x − 3cos x. D P = sin x + cos x. 2 2 1 π ³ π´
Câu 47. Biết sin a = p , với 0 < a < . Tính giá trị biểu thức P = cos a + . 3 2 3 p p p p 6 − 3 3 − 3 6 − 3 6 + 3 A P = . B P = . C P = . D P = . 6 6 4 4 π µ 7π ¶
Câu 48. Cho cot α = 2 và 0 < α < . Tính sin α + . 2 6 p p p p 3 + 2 3 + 2 2 + 3 2 + 3 A − p . B p . C − p . D p . 2 5 2 5 2 5 2 5 α
Câu 49. Cho cos x = . Tính cos2x. 2 α2 α2 α2 α2 A −1 + . B − 1. C −1 + . D −1 − . 2 4 4 2 1 π
Câu 50. Biết sin α =
với 0 < α < , tính cos2α. 2 2 1 1 1 3 A cos 2α = . B cos 2α = . C cos 2α = . D cos 2α = . 2 3 4 4 1 π
Câu 51. Biết cos 2α =
với − < α < 0, tính cos2 α. 4 4 5 1 3 7 A cos2 α = . B cos2 α = . C cos2 α = . D cos2 α = . 8 8 8 8 3 π
Câu 52. Biết cos 2α =
với 0 < α < , tính sin2 α. 8 4 9 5 3 11 A sin2 α = . B sin2 α = . C sin2 α = . D sin2 α = . 16 16 16 16 11π
Câu 53. Cho góc α =
+ kπ (k ∈ Z), để α ∈ (−18; −12) thì giá trị của k bằng bao nhiêu? 5 A −8. B −7. C −6. D −5.
Câu 54. Trên đường tròn bán kính R = 8 cm, lấy cung có số đo 54◦. Tính độ dài ` của cung tròn. A ` = 7,54 cm. B ` = 5,74 cm. C ` = 4,75 cm. D ` = 7,47 cm. Câu 55. y
Cung lượng giác α được biểu diễn bởi điểm nào trên đường tròn lượng giác thì B sin α = 0?
A Điểm B và điểm B0. B Điểm O. A0 O A x
C Điểm A và điểm A0.
D Các điểm A, A0, B, B0. B0
Câu 56. Trong một ngày, kim giờ và kim phút gặp nhau bao nhiêu lần? A 24 lần. B 23 lần. C 22 lần. D 21 lần.
Câu 57. Bánh xe máy có đường kính (kể cả lốp xe) 55 cm. Nếu xe chạy với vận tốc 50 km/h thì
trong một giây bánh xe quay được bao nhiêu vòng? GV: Phùng Hoàng Em – St 11 ĐẠI SỐ 10 Chương VI. LƯỢNG GIÁC A 8, 04 vòng. B 8, 03 vòng. C 8, 02 vòng. D 8, 01 vòng. sin2 x − 2sin x.cos x
Câu 58. Cho tan x = 2. Tính giá trị biểu thức A = . cos2 x + 3sin2 x A A = 4. B A = 0. C A = 1. D A = 2.
2 sin α − 3cosα
Câu 59. Cho cot α = 3. Tính giá trị biểu thức M = .
5 sin3 α + cos3 α 35 35 3 3 A M = − . B M = − . C M = − . D M = − . 16 32 16 32
Câu 60. Cho sin x + cos x = m. Tính theo m giá trị của A = sin x.cos x. m2 − 1 1 A A = m2 − 1. B A = . C A = . D A = m2 + 1. 2 m2 − 1 —HẾT—
BẢNG ĐÁP ÁN TRẮC NGHIỆM 1. A 2. A 3. C 4. B 5. C 6. B 7. D 8. B 9. C 10. D 11. C 12. D 13. D 14. B 15. C 16. B 17. B 18. A 19. D 20. C 21. A 22. B 23. C 24. B 25. A 26. C 27. D 28. B 29. C 30. A 31. D 32. B 33. B 34. A 35. B 36. B 37. B 38. A 39. C 40. D 41. B 42. C 43. C 44. B 45. A 46. A 47. A 48. A 49. A 50. A 51. A 52. B 53. B 54. A 55. C 56. C 57. A 58. B 59. A 60. B GV: Phùng Hoàng Em – St 12
Document Outline
- Dạng 1. Cho trước 1 tỉ số lượng giác, tính các tỉ số lượng giác còn lại
- Dạng 2. Rút gọn biểu thức hoặc chứng minh đẳng thức