Đề cương ôn tập cuối học kì 1 Toán 8

ĐỀ CƯƠNG ÔN TẬP CUỐI HỌC KÌ 1 TOÁN 8
NĂM HỌC 2023 – 2024 I. PHẦN ĐẠI SỐ 2   Bài 1. 1 4 Cho đơn thức: 2 3 2 3 A = − x y z  xy z    2  3
a) Thu gọn đơn thức A .
b) Chỉ ra phần hệ số và bậc của đơn thức. −
c) Tính giá trị của đơn thức sau khi thu gọn tại 1 x = 2; y = ; z = 1 − . 2 Bài 2. Cho các đa thức sau: 2
A = −x y + − ( 2 − xy ) 2 2 3 5
+ 8xB = xy + 8 + 4x y + xy a) Tinh: A + ; B A − B
b) Tính: A + 2B Bài 3.
Rút gọn các biểu thức sau, rồi tính giá trị biểu thức: a) 2 2
A = x − 8xy +16 y tai x − 4 y = 3 − b) 2 2
B = 9x + 4 y +12xy − 2024 tại 3x + 2 y = 50 c) 2
C = (x − 3y) − (x − 2 y)(2 y + x) tại x = 2; y = 1 − d) 3 2 2 3
D = x + 6x y +12xy + 8 y tại x = 2 − y e) 2 3 2
E = −x(x − y) + (x − y) + y ( y − 2x) tại | 2x −1|= 1; y = 2 − f) 3 2 3
F = −(2x − y) − x(2x − y) − y tại 2 2
(x − 2) + y = 0
g) G = x + y ( 2 2
x − xy + y ) + x − y ( 2 2 ( ) 3(2
) 4x + 2xy + y ) tại x + y = 2; y = 3 −
h) H = x + y ( 2 2
x − xy + y ) + x − y ( 2 2 ( 3 ) 3 9 (3
) 9x + 3xy + y ) tại 3x − y = 5; x = 2 Bài 4.
Rút gọn các biểu thức sau rồi tính giá trị biểu thức: a) 2
A = (2 − x)(x + 2) − (x + 3) tại x = 5 b) 2
B = (2x + 5) − 4(x − 3)(3 + x) tại 1 x = 10 c) 3 2
C = x − 3x + 3x + 2023 tai x = 101 d) 3 2
D = x − 6x +12x −100 tại x = 98 − e) 3 2
E = (x +1) + 6(x +1) +12x + 20 tại x = 5 − f) F = x −
( 2x + x+ )− ( 3 (2 1) 4 2 1 7 x + ) 1 tại 1 x = 2 g) 3 G = −x − + x − ( 2 x + x + ) 2 ( 2) (2 4) 2
4 − x (x − 6) tại x = 2 − h) 3 H = x − − x + ( 2 ( 1) (
2) x − 2x + 4) + 3(x + 4)(x − 4) tại 1 x = 2 − Bài 5.
Chứng minh giá trị của đa thức sau không phụ thuộc vào giá trị của biến:
a) A = x + y ( 2 2
x − xy + y ) + y x + y x − y − x ( 2 ( 3 ) 3 9 3 ( 3 )( 3 )
3xy + x − 5) − 5x +1 b) B = x − y ( 2 2
x + xy + y ) − x x − y
x + y + y ( 2 (2 ) 4 2 2 (2 )(2 )
y − 2xy ) + 2023 Bài 6.
Phân tích đa thức thành nhân tử: a) 2 3
2xy + 5x y − x y b) 2 2
(x + y) − 9x c) 2
2(x − y) + xy − x d) 2 3x + 2x −1 e) 2 −x + 4x − 3 f) 2 x − 7x +12 g) x ( 2 2 5
x − y ) + 2y(x + y) Trang 1 h) 3 2 x − x −1 2 i) 2 2
3x + 3y − x − 2xy − y j) 4 4 x y + 64 k) 3 2 2 3
x + 3x y + 3xy + y − x − y 1) 8 x + x +1 m) 3 3 x + y − ( 2 2 2 x − y ) n) (x + y)2 2 2
− 2x − 2y +1 o) 2 x + 5x + 6 p) ( 2 x + x + )( 2
1 x + x + 2) − 6 Bài 7.
Phân tích đa thức thành nhân tử: a) 3
x y + x − y −1 b) 2
x (x − 2) + 4(2 − x) c) 3 2
x − x − 20x d) (x + )2 2 2 1 − (x +1) e) 2 6x − 7x + 2 f) 4 2 x + 8x +12 g) ( 3 x + x + )( 3 1 x + x) − 2
h) (x +1)(x + 2)(x + 3)(x + 4) +1 i) −(x + )2 2 + x( 2 x + ) 2 2 4 2 − 3x j) 4 4 81x + 4 y Bài 8. Tìm x , biết: a) 2
(x + 2) − x(x + 3) = 2 b) 2
(x + 2)(x − 2) − (x +1) = 7 c) 2
6x − (2x +1)(3x − 2) = 1
d) (x + 2)(x + 3) − (x − 2)(x +1) = 2
e) 6(x −1)(x +1) − (2x −1)(3x + 2) + 3 = 0 f) 2
x(3x +1) + (x −1) − (2x +1)(2x −1) = 0 g) 3 3
(x +1) + (2 − x) − 9(x − 3)(x + 3) = 0 i) 3 x − − x + ( 2 x − x + ) 2 ( 1) ( 3) 3 9 + 3x = 25 k) 3 x + − x + ( 2 x − x + ) 2 ( 2) ( 1) 1 − 6(x −1) = 23 m) x + ( 2 (
3) x − 3x + 9) − x(x − 2)(x + 2) +11 = 0
n) x(x − 3) − x + 3 = 0
o) (x −1)(x + 2) − 2x − 4 = 0 p) 3 2
x − 3x − 4x +12 = 0 q) 3 2
9(x −1) − x + x = 0 r) 3 2
x − 2x + x − 2 = 0 t) ( 2
9 − x )(2x +1) = 0 Bài 9. Tìm x , biết: a) 1 9 2 x + x + = 4 4 b) 2 2
25x −16(x + 2) = 0 c) 2 2
(2x +1) = (x −1) Trang 2 d) 2 9x − 6x = 1 − e) 2 4x − 9 = 0 f) 3 2
x − 9x + 27x − 35 = 0 g) 2
x − 6x − 7 = 0 h) 2 x + 4x + 3 = 0 i) 2
2x − 5x + 3 = 0
k) x(x − 5) = 6 m) 4 2
x − 5x + 4 = 0 2     n) 1 1 x + − 3 x + + 2 = 0      x   x 
o) (x −1)x(x +1)(x + 2) − 24 = 0 p) 4 3 2
x − 4x + 6x − 4x +1 = 0 PHẦN THỐNG KÊ
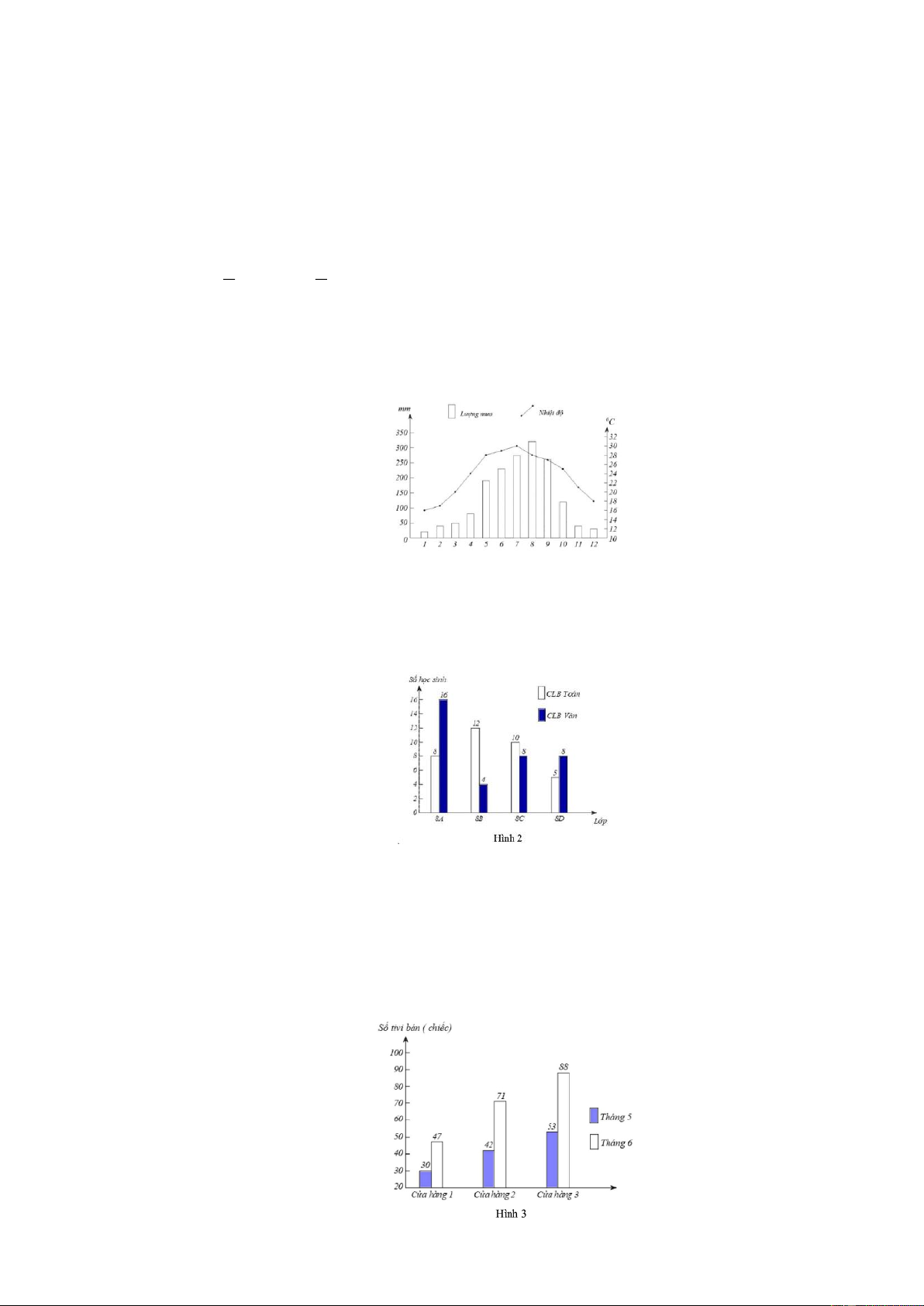
Bài 10. Cho biểu đồ về lượng mưa và nhiệt độ trong năm 2022 của Hà Nội (Hình 1)
a) Tháng nào có nhiệt độ cao nhất, thấp nhất? Vì sao lại có sự khác biệt này?
b) Tháng nào có lượng mưa nhiều nhất, it nhất?
c) Em thích tháng nào nhất trong năm và tháng đó có nhiệt độ và lượng mưa như thế nào?
Bài 11. Biểu đồ ở Hình 2 thể hiện số lượng học sinh khối lớp 8 tham gia hai câu lạc bộ Toán và Văn của trường.
a) Lập bảng thống kê cho biểu đồ trên.
b) Cho biết về sự khác nhau về việc tham gia đăng kí hai câu lạc bộ Toán và Văn của hai lớp 8 A và 8B .
c) Nếu lớp 8 A có số lượng tham gia câu lạc bộ môn Toán chiếm 20% tồng số học sinh cả
lớp. Hãy tính xem lớp 8 A có bao nhiêu học sinh.
d) Hãy so sánh tỉ số học sinh tham gia CLB Toán và CLB Văn của hai lớp 8A và 8B .
Bài 12. Biểu đồ ở Hình 3 thống kê số lượng ti vi bán được của ba cửa hàng trong tháng 5 và tháng 6 của năm 2018.
a) So sánh số lượng ti vi bán được của mỗi cửa hàng trong tháng 5 và tháng 6 . Trang 3
b) Cửa hàng 3 bán được nhiều ti vi nhất trong cả tháng 5 và tháng 6 . Em có thể đưa ra một
lí do phù hợp nhất để giải thích cho kết quả này được không?
Em đồng ý với những nhận xét nào sau đây:
+ Cửa hàng 3 bán ti vi với giá rẻ nhất.
+ Cửa hàng 3 chăm sóc khác hàng tốt nhất.
+ Cửa hàng 3 có nhiều loại ti vi cho người mua hàng lựa chọn.
+ Cửa hàng 3 ở vị trí thuận lợi cho việc đi lại mua bán của người mua hàng?
c) Số lượng ti vi mà cả ba cửa hàng bán được trong tháng 6 nhiều hơn số lượng ti vi mà cả
ba cửa hàng bán được trong tháng 5 là bao nhiêu chiếc? Em có biết giải bóng đá World Cup
2018 diễn ra vào tháng nào không? Sự kiện đó có liên quan đến việc mua bán ti vi trong tháng 6 hay không?
d) Lập bảng thống kê cho biểu đồ trên.
Bài 13. Một cửa hàng bán quần áo đưa ra chương trình khuyến mại giảm giá như biểu đồ ở Hình 4 .
a) Trong các mặt hàng trên, sản phầm nào được giảm giá nhiều nhất, it nhất với mức giåm bao nhiêu phần trăm?
b) Hãy giải thích vì sao trong biểu đồ trên tổng các thành phần lại không phải 100% . Với
Hình 4 các số liệu ở biểu đồ ta có thể biểu diễn bằng biểu đồ nào?
c) Cô Hải đã mua 2 chiếc áo sơ mi với giá mỗi chiếc sau khi giảm giá là 325000 đồng và 4
chiếc quần âu. Khi đó tổng số tiền hóa đơn cô Hải thanh toán tại quầy là 1850000 đồng. Em
hãy tính xem mỗi chiếc áo sơ mi và mỗi chiếc quần âu cô Hải mua trị giá bao nhiêu tiền nếu chưa được giảm giá? II. PHẦN HÌNH HỌC
Bài 14. Cho hình thang ABCD(AB / /CD), M là trung điểm của CD . Gọi E là giao điểm của AC
và BM , F là giao điểm của BD và AM . Đường thẳng EF cắt BC và AD lần lượt tại G và H .
a) Chứng minh rằng EA 2 = AB . EC CD
b) Chứng minh rằng EF ‖ CD .
c) Chứng minh rằng GE = EF = FH .
d) Gọi O là giao điểm của AC và BD . Chứng minh rằng OM , DG,CH đồng quy.
Bài 15. Cho hình bình hành ABC ,
D M là trung điểm của AB . Gọi G là giao điểm của AC và
DM . Lấy điểm E thuộc đoạn thẳng AM . Các đường thẳng GE và CD cắt nhau tại F .
a) Chứng minh rằng G là trọng tâm của tam giác ABD .
b) Chứng minh rằng GC = 2GA.
c) Kẻ đường thẳng qua G cắt các cạnh AD và BC lần lượt tại I và K . Chứng minh rằng EI ‖ KF .
d) Gọi N là trung điểm của AD . Chứng minh rằng BF = 2EN .
Bài 16. Cho hình vuông ABCD có tâm O , gọi E là trung điểm AB  DE cắt AC tại F.BF cắt CD tại I .
a) Chứng minh D là trung điểm IC .
b) Chứng minh ABDI là hình bình hành.
c) Gọi H là trung điểm AI . CH cắt B ,
D AD tại L, G . Chứng minh L là trung điểm OD .
d) GO cắt DF tại J . Chứng minh ,
A J , L thằng hàng.
Bài 17. Cho hình vuông ABCD , trên cạnh BC lấy M (MB  MC) . Từ A kẻ Ax vuông góc AM
cắt đường thẳng CD tại N .
a) Chứng minh AN = AM Trang 4 DK DQ
6b) BD cắt MN tại Q  AQ cắt DC tại K . Chứng minh = . DC QB
c) Lấy điểm P thuộc BD sao cho PM vuông góc BC . Chứng minh tứ giác NDMP là hình bình hành.
d) Đường thẳng MP cắt AC tại S . Từ M kẻ đường thẳng song song với AK cắt đường
thẳng AC tại J.MN giao với AC tại E, MK giao với AC tại H . Chứng minh:
ES.JH = EHJS
Bài 18. Cho tam giác ABC vuông tại (
A AB  AC) , vẽ đường cao AH . Trên tia HC lấy điểm D
sao cho HD = AH . Đường thẳng vuông góc với BC tại D cắt AC tại E . Gọi M là trung
điểm của BE , tia AM cắt BC tại G . Kè EI vuông góc AH .
a) Chứng minh HDEI là hình chữ nhật.
b) Chứng minh AE = AB . c) Chứng minh G .
B AC = GC  AE d) Chứng minh: BG = HD . BC AH + HC III. PHẦN NÂNG CAO Bài 19. a b c Cho abc = 2 . Tính 2 B = + + ab + a + 2 bc + b +1 ac + 2c + 2 2023 2024 2025 Bài 20.
a + b + c =
ab + bc + ca = A = a − + b + c + Cho a, , b c thỏa mãn: 0, 0 . Tính ( 1) ( 1) 1 1 1 Bài 21. xyz =
Cho x, y, z là các số thỏa mãn :
1, và x + y + z = + + . x y z Tính A = ( 68 x − )( 69 y − )( 70 1 1 z − ) 1 2 2 2 Bài 22.
B = x + y + z − xy + xz − x − y − z + Tìm min của 2 3 2 2 2 2 8 2000 .
Bài 23. Tìm giá trị nhỏ nhất của biểu thức: 2 2
B = xy(x − 2)( y + 6) +12x − 24x + 3y +18 y + 2045 − Bài 24. 27 12x
Tìm GTNN hoặc GTLN của: M = . 2 x + 9 2 2 2 ax + ay + az + Bài 25. 1 1 1
Tính giá trị biểu thức sau P = + +
(x − y)(x − z)
( y − x)( y − z)
(z − x)(z − y)
Bài 26. Cho a, ,
b c là các số thực dương. Chứng minh bất đẳng thức: a + b b + c c + a 1 1 1 + +  + + . 2 2 2 bc + a ac + b ab + c a b c
VI. MỘT SỐ ĐỀ THAM KHẢO ĐỀ 1 2 2 Bài 1. A = x − − x − 1) Cho biểu thức: (2 3) (2 5)
a) Thu gọn biểu thức A .
b) Tính giá trị biểu thức A khi x =102 .
2) Phân tích các đa thức sau thành nhân tử
a) 3(x − y) − y( y − x) b) 2 2
x −10x + 25 − y Bài 2. Tìm x , biết: a) 2
4x − 20x + 25 = 49 ; c) x + ( 2x − x+ ) 2 2 ( 2) 2
4 − x(x −1) = 2x ; b) 2
x (x − 3) + 3 − x = 0 ; d) 3 3 2
(x +1) − (x −1) − 6(x −1) = 19 − . Họ và tên Lớp Chiều cao (m) Trang 5 Bài 3. M ột công ty may m
Nguyễn Văn An ặc khảo sát chi 8 ề A u c ao của một s
1,68 ố học sinh khối 8 và thu được một phần bảng số liệu như sau: Nguyễn Văn Bình 8 B 1,6 Trần Văn Dũng 8D 1,58 a) Hãy phân loại Nguyễn Ngọc Diệp 8C 2,66 dữ liệu "Lớp" và "Chiều cao".
b) Bảng dữ liệu trên có hợp lí không? Giải thích. Bài 4.
Cho tam giác ABC(AB  AC) , đường phân giác AD . Qua trung điểm M của BC, k ?
đường thẳng song song với AD , cắt AC, AB theo thứ tự ở E và K . Gọi O là giao điểm
của AM và DK . a) Chứng minh A . O OK = D . O OM
b) ChoAB = 5cm, AC =10cm, BC =12cm . Tính DB . c) Chứng minh AB BD AE = AK và = . CE CM
d) Chứng minh BK = CE . Bài 5. Cho a, ,
b c là các số thực thỏa mãn abc = 1. Chứng minh rằng 1 1 1 + + =1. 1+ a + ab 1+ b + bc 1+ c + ca ĐỀ 2 2 Bài 1.
A = x + y x − y + 1) Cho biểu thức ( )( ) y
a) Thu gọn biểu thức A .
b) Tính giá trị biểu thức A khi x =100 .
2) Phân tích các đa thức sau thành nhân tử: a) 2 2
x − y − 2x + 2 y ; b) 2 2
4x − y + 4x +1 Bài 2. Tìm x , biết: a) 2
(x − 4) − (x − 2)(x + 2) = 6 ; c) 2
2x + 3x − 5 = 0 ;
b) x(x − 3) − 2x + 6 = 0; d) 3 x − − x + ( 2
x − x + ) + ( 2 ( 1) ( 3) 3 9 3 x − 4) = 2 . Bài 3.
Để chuẩn bị cho giải Archimedes Cup, lớp 8C3 đã làm bảng hỏi về các môn thể thao yêu
thích của các bạn trong lớp và thu được kết quả sau: Môn thể thao Số bạn Bóng đá 15 Cầu Lông 9 Cờ vua 6 Bóng bàn 2
a) Vẽ biểu đồ hình cột biểu diễn bảng thống kê.
b) Nhận xét về các môn học yêu thích. Số bạn yêu môn bóng đá chiếm bao nhiêu phần trăm số học sinh cả lớp. Bài 4.
Cho tam giác ABC vuông tại (
A AB  AC) . Kẻ AH vuông góc với BC tại H . Qua B kẻ
đường thẳng vuông góc với AB , cắt đường thẳng AH tại D . Tia AB và tia CD cắt nhau tại E .
a) Chứng minh BE = DE ; BA DC
b) Qua E kẻ đường thẳng song song với AC , đường thẳng này lần lượt cắt các đường thẳng A ,
D BC tại I , K . Chứng minh EI = EK.
c) G?iN là giao điểm của EH và AC ; G ?iQ là giao điểm của DN và BC ; Gọi P là
giao điểm của BN và AD . Chứng minh NA = NC và PQ / /BD . Trang 6
d) Gọi G là giao điểm của đường thẳng AQ và CD . Qua Q kẻ đường thẳng song song với
CE , cắt đường thẳng AC tại T . Chứng minh GH / / AC và PT ⊥ AD . Bài 5. Cho a, ,
b c là các số thực khác 0 và thỏa mãn: 3 3 3
a + b + c = 3abc . Tính giá trị của biểu thức:  a   b   c  A = 1+ 1+ 1+     .  b  c  a  ĐỀ 3 2 Bài 1. A = x − + x − x + + 1) Cho biểu thức ( 2) ( 3)( 3) 4x
a) Thu gọn biểu thức A .
b) Tính giá trị của biểu thức A khi x = 2 .
2) Phân tích các đa thức sau thành nhân tử
a) x(x − 3) − 2x + 6 b) 2 2
4x + 6 y − y − 9 Bài 2. Tìm x , biết: a) 2
x(x +1) − x − 2x = 5 ; c) 3 2 4
− x + x −8x + 2 = 0 ; b) 3
36x − 4x = 0 ; d) (x − x)2 2 + ( 2 4
7 x − 4x) +12 = 0 . Bài 3.
Cho hai biểu đồ doanh thu 6 tháng cuối năm của một công ty (đơn vị: ti đồng)
Doanh thu 6 tháng cuối năm
Doanh thu 6 tháng cuối năm.
a) Dữ liệu trong 2 biểu đồ có như nhau không? Lập bảng thống kê cho dữ liệu đó.
b) Có thể căn thứ vào độ dốc của 2 đường gấp khúc trên hai biểu đồ để đánh giá về tốc độ
tăng doanh thu trong 6 tháng cuối năm của dữ liệu không? Tại sao? Bài 4.
Cho tam giác ABC vuông tại (
A AB  AC) , đường cao AH . Gọi M là trung điểm của AC
. Đường thẳng HM cắt đường thẳng AB tại E . Lấy điểm F sao cho M là trung điểm EF .
a) Chứng minh tứ giác AECF là hình bình hành.
b) Qua F kẻ đường thẳng song song với AH cắt AC kéo dài tại K . Chứng minh AH = AC . FK EF
c) QuaH kẻ đường thẳng song song với AB cắt AF tại Q . G?iP là giao điểm của HC và
FK. Chứng minh PQ / / AC .
d) Gọi N là trung điểm của AF và D là giao điểm của PQ với FC . Chứng minh ba điểm
K , D, N thẳng hàng. Bài 5.
x + y + z xy + yz + zx =
Cho các số thực x, y, z thỏa mãn ( )( )
xyz . Chứng minh rằng: 2023 2023 2023 2023 x + y + z
= (x + y + z) . ĐỀ 4 2 Bài 1.
A = x − y + x x + 1) Cho biểu thức ( ) 2 ( y)
a) Thu gọn biểu thức A .
b) Tính giá trị biểu thức A khi x =1 và y = 3 − .
2) Phân tích các đa thức sau thành nhân tử: a) 2 2
16x − (x +1) ; b) 2
x − 6x − 7 . Bài 2. Tìm x , biết: 1 a) 3 x = x 4 c) 3 2
x − 2x − 4x + 8 = 0 ; Trang 7 b) (x + )2 2 2 9 − 36x = 0 ; d) 3 2
x + 9x −10x = 0 Bài 3.
Cho biểu đồ xuất khẩu gạo của nước ta năm 2020.
a) Lập bảng thống kê cho biểu đồ trên.
b) Biết rằng tổng lượng gạo xuất khẩu là 6,15 triệu khẩu trong năm 2020. Bài 4. A AB 
K HD ⊥ AB D 
Cho ABC vuông tại ( AC) , đường cao AB AH . ? ( ) .
a) Chứng minh rằng BD = BH ; BA BC
b) Gọi O là giao điểm của AH và CD . Qua O kẻ đường thẳng song song với DH cắt BC
tại F . Gọi E là giao điểm của DH và AF . Chứng minh rằng: HD = HE ;
c) G ọi I là giao điểm của AH và CE . Chứng minh rằng: BI / / AC ;
d) G?iK là giao điểm của AB và CI,G là giao điểm của AF và CO . Chứng minh rằng
K , H , G thẳng hàng. Bài 5.
Cho các số hữu tỉ a, ,
b c thỏa mãn điều kiện ab + bc + ca = 3. Chứng minh rằng biểu thức
sau là bình phương của một số hữu ti:
( 2a + )( 2b + )( 2 3 3 c + 3) S = 16 ĐỀ 5 2 Bài 1. M = x +
− x x + − x − x + 1) Cho biểu thức (4 3) 11 ( 6) 5( 2)( 2)
a) Thu gọn biểu thức M .
b) Tính giá trị biểu thức M khi x = 2 − .
2) Phân tích các đa thức sau thành nhân tử: a) 4 3
x + x y − x − y ; b) (x − x)2 2 − ( 2 2
2 x − 2x) − 3. Bài 2. Tìm x , biết: a) (x + )2 2 2 4 −16x = 0 ; c) 2
9(5 − x) + x −10x = 25 − ; b) 3 2
x − 2x − 9x +18 = 0 ; d) (x + )2 2 − ( 2 1 6 x + ) 1 + 9 = 0 . Bài 3.
Cho biểu đồ thống kê số lượng máy điều hòa nhiệt độ và máy sưởi được bán trong 6 tháng
đầu năm của một cứa hàng kinh doanh.
a) Trong tháng 6 , cửa hàng đó bán được loại máy nào nhiều hơn?
b) Phân tích xu thế về số lượng máy mỗi loại mà cửa hàng đó bán được. Giải thích. Bài 4.
Cho hình thang ABCD(AB / /C ; D AB  C )
D . Gọi O là giao điểm của AC và BD .
a) Chúng minh OA = OB . AC BD
b) Qua O kẻ đường thẳng song song với AD cắt DC ở E ; qua O kẻ đường thẳng song
song với BC cắt CD ở F . Chứng minh DE = CF .
c) Gọi I là giao điểm của các đường thẳng AD và OF, J là giao điểm của các đường thẳng
BC và OE . Chứng minh IJ song song với AB .
d) Gọi H là giao điểm của AD và BC, K là trung điểm của EF . Chứng minh H ,O, K thẳng hàng. 2 2 Bài 5.
x + y + xy − x − y + =
Cho x, y thỏa mãn 5 2 6 8 4 4 0 .
Tính giá trị biểu thức 2023 2023 P = x + y . Trang 8