Đề Cương Ôn Tập Cuối Học Kỳ 1 Toán 9 Năm Học 2025-2026

ĐỀ CƯƠNG HỌC KÌ I -NĂM HỌC 2025 - 2026 Môn: Toán 9
RÚT GỌN BIỂU THỨC VÀ BÀI TOÁN SAU RÚT GỌN + − −
Bài 1: Cho hai biểu thức x 2 x x A = và 2 3 3 B = +
với x  0, x  1. x x −1 x −1
1) Tính giá trị của biểu thức A khi x = 9 . 2) Chứng minh 2 x B = . x +1
3) Tìm tất cả các giá trị của x để . A B = 4 . +
Bài 2: Cho hai biểu thức 3 x x A = và 4 2 B = −
với x  0, x  4 . x + 2 x − 4 x − 2
1) Tính giá trị của biểu thức A khi x = 9 . 2) Chứng minh x B = . x + 2 3
3) Tìm số nguyên dương x lớn nhất thỏa mãn A − B  . 2 + +
Bài 3: Cho hai biểu thức x 4 x A = và 3 1 2 B = −
với x  0, x  1. x −1 x + 2 x − 3 x + 3
1) Tính giá trị của biểu thức A khi x = 9 . 2) Chứng minh 1 B = . x −1 A x
3) Tìm tất cả các giá trị của x để  + 5 . B 4 +  −  +
Bài 4: Cho hai biểu thức 4( x 1) x x A = và 15 2 1 B =  +  :
với x  0, x  25 . 25 − x  x 25 x 5  − + x − 5  
1) Tính giá trị của biểu thức A khi x = 9 .
2) Rút gọn biểu thức B .
3) Tìm tất cả các giá trị nguyên của x để biểu thức P = A B đạt giá trị nguyên lớn nhất. − − +
Bài 5: Cho hai biểu thức x 2 x x x A = và 1 1 B = + −
với x  0, x  1 x x +1 x −1 x −1
1) Tính giá trị của biểu thức A khi x = 16 .
2) Rút gọn biểu thức B .
3) Xét biểu thức P = .
A B . Tìm tất cả các giá trị của x sao cho P nhận giá trị nguyên. + +
Bài 6: Cho hai biểu thức x 1 x A = và 3 5 B = −
với x  0, x  1. x + 2 x −1 x −1
1) Tính giá trị của biểu thức A khi x = 4 . 2 2) Chứng minh B = . x +1
3) Tìm tất cả giá trị của x để biểu thức P = 2A B + x đạt giá trị nhỏ nhất. Trang 1
HÀM SỐ BẬC HAI- BÀI TOÁN TƯƠNG GIAO
Bài 7: Trên mặt phẳng tọa độ Oxy , cho đường thẳng (d) : y = −x + 6 và parabol 2
(P) : y = x .
a) Vẽ đồ thị hai hàm số trên cùng một mặt phẳng tọa độ.
b) Tìm tọa độ các giao điểm của (d ) và (P) ;
Bài 8: Cho đường thẳng y = x + 2m +1 ( d ) và parabol 2
y = 2x (P)
a) Với m = 1, hãy vẽ hai đồ thị hàm số trên cùng một mặt phẳng tọa độ. Tìm tọa độ giao
điểm của (d ) và (P) .
b) Tìm m để ( d ) cắt ( P ) tại hai điểm phân biệt;
c) Tìm m để (d ) tiếp xúc với (P) . Bài 9: Cho parabol 2
(P) : y = x và đường thẳng 2
(d) : y = 2x − m + 9 .
a) Với m = 1, vẽ hai đồ thị trên cùng một mặt phẳng tọa độ. Tìm tọa độ giao điểm của (P) và ( d )
b) Tìm m để đường thẳng (d ) cắt parabol (P) tại hai điểm nằm về hai phía của trục tung. Bài 10: Cho parabol 2
(P) : y = x và đường thẳng 2
(d) : y = 2x + m .
a) Với m = 0 , tìm tọa độ giao điểm của ( d ) và (P)
b) Chứng minh (d ) luôn cắt (P) tại hai điểm phân biệt với mọi m;
c) Tìm tất cả các giá trị của m để ( d ) cắt ( P ) tại hai điểm phân biệt có hoành độ x , x 1 2
thỏa mãn (x +1 x +1 = 3 − 1 )( 2 ) Bài 11: Cho parabol 2
(P) : y = x và đường thẳng (d) : y = mx − m +1.
a) Với m = 1, tìm tọa đô giao điểm của (d ) và (P)
b) Tìm các giá trị của tham số m để (d ) cắt (P) tại hai điểm phân biệt , A B có hoành độ x , x
x + x = x + x 1 2 thỏa mãn 2 2 1 2 1 2 Bài 12: Cho parabol 1 2 1 (P) : y =
x và đường thẳng 2
(d ) : y = mx − m + m +1. 2 2
a) Với m = 1, vẽ đồ thị hai hàm số trên cùng một mặt phẳng tọa độ. Tìm tọa độ các giao điểm ,
A B của (d ) và (P) .
b) Tìm các giá trị của m để (d ) cắt (P) tại hai điểm phân biệt có hoành độ x , x 1 2 sao cho: x − x = 2 . 1 2
PHƯƠNG TRÌNH BẬC HAI- ĐỊNH Lí VI-ÉT VÀ ỨNG DỤNG
Bài 13: Cho phương trình 2
x − 5x + m = 0 ( m là tham số).
a) Giải phương trình trên khi m = 6 .
b) Tìm m để phương trình có hai nghiệm phân biệt x , x − = 1 2 thỏa mãn x x 3. 1 2
Bài 14: Giải phương trình 2
x − 2(m −1)x − m − 3 = 0(1) (với m là tham số).
a) Giải phương trình với m = −3 .
b) Với giá trị nào của m thì phương trình (1) có các nghiệm x , x x + x =10 1 2 thỏa mãn 2 2 1 2 Trang 2
Bài 15: Cho phương trình 2
x − (m + 2)x + 3m −3 = 0 (1) , với x là ẩn, m là tham số.
a) Giải phương trình (1) khi m = −1.
b) Tìm các giá trị của m để phương trình (1) có hai nghiệm phân biệt x , x x x 1 2 sao cho 1 , 2
là độ dài hai cạnh góc vuông của một tam giác vuông có độ dài cạnh huyền bằng 5 .
Bài 16: Cho phương trình: 2
x + 5x + m = 0 (*) (m là tham số)
a) Giải phương trình (*) khi m = −3 .
b) Tìm m để phương trình ( * ) có hai nghiệm x , x 9x + 2x =18 1 2 thỏa mãn 1 2 .
Bài 17: Cho phương trình: 2
x − (m −1)x − m = 0(1) (với x là ẩn số, m là tham số). Xác định
các giá trị của m để phương trình (1) có hai nghiệm phân biệt x ; x 1 2 thỏa mãn điều kiện:
x 3 − x + 20  3 3 − x . 1 ( 2 ) ( 2 )
Bài 18: Cho phương trình 2 2
x − 2(m + 2)x + m + 3m − 2 = 0(1) ( m là tham số)
a) Giải phương trình (1) khi m = 3 .
b) Tìm các giá trị của tham số m để phương trình (1) có hai nghiệm phân biệt x x 1 ; 2 sao cho biểu thức 2 2
A = 2018 + 3x x − x − x 1 2 1
2 đạt giá trị nhỏ nhất.
Bài 19: Cho phương trình 2 2
x − 2(m +1)x − m −1 = 0 , với m là tham số.
a) Chứng minh rằng với mọim , phương trình đã cho luôn có hai nghiệm trái dấu.
b) Tìm giá trị lớn nhất của biểu thức 2 2
T = x + x + x x 1 2 1 2
Bài 20: Cho phương trình 2
x − 2(m −1)x − m − 3 = 0
a) Giải phương trình với m = −3 .
b) Tìm hệ thức liên hệ giữa các nghiệm không phụ thuộc vào giá trị của m .
Bài 21: Cho phương trình 2 2
x − 2(m +1) + m − 4m + 3 = 0 (với m là tham số).
a) Tìm m để phương trình đã cho có nghiệm.
b) Tìm m để phương trình đã cho có hai nghiệm cùng dấu.
c) Tìm m để phương trình đã cho có hai nghiệm khác dấu.
d) Tìm m để phương trình đã cho có hai nghiệm dương.
e) Tìm m để phương trình đã cho có hai nghiệm âm.
Bài 22: Cho phương trình 2
x − 2(m + 2)x + m −1 = 0 . Tìm m để phương trình
a) Có hai nghiệm phân biệt.
b) Có hai nghiệm phân biệt cùng dấu.
c) Có hai nghiệm dương phân biệt.
d) Có hai nghiệm âm phân biệt.
GIẢI TOÁN BẰNG CÁCH LẬP PHƯƠNG TRìNH, HỆ PHƯƠNG TRìNH
Bài 23: Hai người làm chung công việc trong 12 giờ thì xong. Nếu mỗi người làm một 5
mình thì thời gian để người thứ nhất hoàn thành công việc ít hơn người thứ hai là 2 giờ. Hỏi
nếu làm một mình thì mỗi người phải làm trong bao nhiêu giờ để xong công việc? Trang 3
Bài 24: Hai đội công nhân làm chung một công việc thì sau 15 ngày làm xong. Nếu đội thứ
nhất làm riêng trong 3 ngày rồi dừng lại và đội thứ hai làm tiếp công việc đó trong 5 ngày
thì cả hai đội hoàn thành được 25% công việc. Hỏi nếu mỗi đội làm riêng thì trong bao
nhiêu ngày làm xong công việc?
Bài 25: Quãng đường từ A đến B dài 90 km . Một người đi xe máy từ A đến B . Khi đến
B , người đó nghỉ 30 phút rồi quay trở về A với vận tốc lớn hơn vận tốc lúc đi là 9 km / h .
Thời gian kể từ lúc bắt đầu đi từ A đến lúc trở về đến A là 5 giờ. Tính vận tốc xe máy lúc
đi từ A đến B .
Bài 26: Một xe ô tô và một xe máy cùng khởi hành từ A để đi đến B với vận tốc mỗi xe
không đổi trên toàn bộ quãng đường AB dài 120 km . Do vận tốc xe ô tô lớn hơn vận tốc
xe máy là 10 km / h nên xe ô tô đến B sớm hơn xe máy 36 phút. Tính vận tốc của mỗi xe.
Bài 27: Một tàu tuần tra chạy ngược dòng 60 km , sau đó chạy xuôi dòng 48 km trên cùng
một dòng sông có vận tốc dòng nước là 2 km / h . Tính vận tốc của tàu tuần tra khi nước yên
lặng, biết thời gian xuôi dòng ít hơn thời gian ngược dòng 1 giờ.
Bài 28: Một phân xưởng theo kế hoạch cần phải sản xuất 1100 sản phẩm trong một số ngày
quy định. Do mỗi ngày phân xưởng đó sản xuất vượt mức 5 sản phẩm nên phân xưởng đã
hoàn thành kế hoạch sớm hơn thời gian quy định 2 ngày. Hỏi theo kế hoạch, mỗi ngày phân
xưởng phải sản xuất bao nhiêu sản phẩm?
Bài 29: Một tổ sản xuất phải làm xong 4800 bộ đồ bảo hộ y tế trong một số ngày quy định.
Thực tế, mỗi ngày tổ đó đã làm được nhiều hơn 100 bộ đồ bảo vệ y tế so với với số bộ đồ
bảo hộ y tế phải làm trong một ngày theo kế hoạch. Vì thế 8 ngày trước khi hết thời hạn, tổ
sản xuất đã làm xong 4800 bộ đồ bảo hộ y tế đó. Hỏi theo kế hoạch, mỗi ngày tổ sản xuất
phải làm bao nhiêu bộ đồ bảo hộ y tế? (Giả định rằng số bộ đồ bảo hộ y tế tổ đó làm xong
trong mỗi ngày là bằng nhau).
Bài 30: Một mảnh vườn hình chữ nhật có diện tích 2
720m . Nếu tăng chiều dài thêm 10 m
và giảm chiều rộng 6 m thì diện tích mảnh vườn không đổi. Tính chiều dài và chiều rộng của mảnh vườn.
Bài 31: Một mảnh đất hình chữ nhật có chu vi bằng 28 m và độ dài đường chéo bằng 10 m .
Tính chiều dài và chiều rộng của mảnh đất đó theo đơn vị mét.
Bài 32: Để chở 15 tấn thiết bị, một đội vận chuyển dự định sử dụng các xe tải loại nhỏ. Do
thay đổi kế hoạch, đội vận chuyển quyết định sử dụng các xe tải loại lớn. Vì vậy, số xe tải
sử dụng giảm đi 2 xe so với dụ định và mỗi xe tải loại lớn chở nhiều hơn mỗi xe tải loại nhỏ
là 2 tấn. Hỏi đội vận chuyển sử dụng bao nhiêu xe tải loại lớn? (Biết mỗi xe tải cùng loại
đều chở số tấn thiết bị bằng nhau). HÌNH HỌC
Bài 33: Cho ABC nội tiếp đường tròn (O) có ABC = 80 và ACB = 40 . Tia phân giác
của góc BAC cắt (O) tại D .
a) Tính số đo các góc của ACD .
b) Chứng minh rằng BC là đường trung trực của đoạn thẳng OD .
c) OD cắt BC tại M . Gọi N, P lần lượt là hình chiếu vuông góc của D lên AB, AC .
Chứng minh rằng BMDN,CDMP là các tứ giác nội tiếp. Trang 4
d) Chứng minh rằng DNB  = DP 
C , từ đó suy ra M , N, P thẳng hàng.
Bài 34: Cho ABC vuông tại A . Từ điểm B kẻ tiếp tuyến BM với đường tròn ( C,CA ) (
M là tiếp điểm, M khác A ).
a) Chứng minh ràng BACM là tứ giác nội tiếp.
b) Trên đoạn thẳng AB lấy điểm N , trên tia đối của tia MB lấy điểm P sao cho AN = MP
. Chứng minh rằng NPC cân.
c) Gọi I là trung điểm NP . Chứng minh rằng ,
A I , M thẳng hàng.
Bài 35: Cho ABC nhọn có đường cao BE . Gọi H , K lần lượt là hình chiếu của E lên B , A BC
a) Chứng minh rằng BHEK là tứ giác nội tiếp, từ đó suy ra EHK = EBC . b) Chứng minh rằng 2
BH  BA = BK  BC = BE .
c) Kẻ đường cao CF của ABC . Gọi I là trung điểm EF . Chứng minh rằng BCEF là tứ
giác nội tiếp, từ đó suy ra H , I, K thẳng hàng.
Bài 36: Cho ABC vuông cân tại đỉnh A . Gọi E là một điểm bất kì trên tia CA sao cho
A nằm giửa hai điểm C và E . Gọi M , H lần lượt là chân các đường vuông góc kẻ từ
điểm A đến BC, BE .
a) Chứng minh rằng AMBH là tứ giác nội tiếp.
b) Chứng minh rằng HM là tia phân giác của góc AHB
c) Lấy điểm N sao cho M là trung điểm của đoạn thẳng AN . Gọi K là giao điểm của
EN , AB . Chứng minh H , K , M thẳng hàng. Bài 37: Cho AB 
C( AB  AC) nội tiếp (O) . Tiếp tuyến của (O) tại A cắt BC tại S . Gọi I
là chân đường vuông góc từ O đến BC
a) Chứng minh rằng SAOI là tứ giác nội tiếp, từ đó suy ra SOA = SIA .
b) Gọi D, H lần lượt là hình chiếu của A lên SO, SB . Chứng minh rằng OAH = AD .
c) Kẻ đường kính AK của (O) . Chứng minh rằng BAD = CAK , từ đó suy ra AB = CAH .
d) Gọi AH , AI lần lượt cắt (O) tại M , N . Chứng minh rằng BCNM là hình thang cân. Bài 38: Cho AB 
C( AB  AC) nhọn, nội tiếp (O) . Kẻ các đường cao BE, CF cắt nhau tại H .
a) Chứng minh rằng tứ giác BCEF nội tiếp đường tròn tâm M . b) Chứng minh rằng 1 AFE =
AOB , từ đó suy ra OA ⊥ EF . 2
c) Gọi EF cắt BC tại K . Chứng minh rằng EKC = ABC − ACB .
d) Gọi AH cắt BC tại D . Chứng minh rằng 2 BC = 4.MD .MK. NÂNG CAO
Bài 39: Một nhà hát có 500 ghế ngồi và hiện tại giá vé vào cửa là 100 nghien đồng một vé.
Với mức giá này, nhà hát luôn bán hết vé mỗi buổi biểu diễn. Nhà hát dự định tăng giá vé,
và mỗi lần tăng giá là bội số của 5 nghìn đồng. Sau khi thử nghiệm, nhà hát nhận thấy rằng
với mỗi lần tăng giá 5 nghìn đồng, sẽ có 10 ghế bị bỏ trống do không bán được vé. Hỏi nhà
hát nên tăng giá vé lên bao nhiêu để tối đa hóa doanh thu mỗi buổi biểu diễn ? Trang 5
Bài 40: Một bãi đỗ xe có 200 chỗ đậu và giá thuê mỗi chỗ là 30 nghìn đồng mỗi giờ. Với
giá này, tất cả các chỗ đều được thuê kín. Ban quản lý muốn tăng giá thuê theo bội số của 2
nghìn đồng và nhận thấy rằng với mỗi lần tăng giá 2 nghìn đồng có 4 chỗ không được thuê.
Hỏi ban quản lý nên tăng giá bao nhiêu để tối đa hóa doanh thu ?
Bài 41: Một sân vận động có 10000 chỗ ngồi, hiện đang bán vé với giá 500 nghìn đồng mỗi
vé, và luôn bán hết trong các sự kiện. Ban quản lý muốn tăng giá vé theo bội số của 50
nghìn đồng. Quan khảo sát, họ nhận thấy rằng cứ mỗi lần tăng giá 50 nghìn đồng, số vé bán
được giảm đi 500 vé. Hỏi ban quản lý nên tăng giá vé bao nhiêu để đạt được doanh thu cao nhất?
Bài 42: Một nhà tài trợ dự kiến tổ chức một buổi đi dã ngoại tập thể nhằm giúp các bạn học
sinh vùng cao trải nghiệm thực tế tại một trang trại trong 1 ngày ( từ 14h00 ngày hôm trước
đến 12h00 ngày hôm sau). Cho biết số tiền dự kiến là 30 triệu đồng và giá thuê các dịch vụ
và phòng nghỉ là 17 triệu đồng 1 ngày, giá mỗi suất ăn trưa, ăn tối là 60000 đồng và mối
suất ăn sáng là 30000 đồng. Hỏi có thể tổ chức cho nhiều nhất bao nhiêu bạn tham gia được ?
Bài 43: Một cửa hàng bán đồng hồ với giá 1 triệu đồng mỗi chiếc và trung bình mỗi tháng
bán được 100 chiếc. Cửa hàng dự định tăng giá mỗi chiếc thêm 50 nghìn đồng để tối ưu lợi
nhuận. Theo khảo sát, mỗi lần tăng giá 50 nghìn đồng thì số lượng đồng hồ bán ra giảm 5
chiếc. Biết chi phí nhập mỗi chiếc đồng hồ là 600 nghìn đồng. Hỏi cửa hàng nên đặt giá bán
mới là bao nhiêu để đạt lợi nhuận cao nhất?
MỘT SỐ ĐỀ THAM KHẢO ĐỀ SỐ 1 + −
Bài 1. (2 điểm ) Cho hai biểu thức x 2 x A = và 3 2 20 B = −
với x  0; x  25 . x − 5 x + 5 x − 25
a) Tính giá trị của biểu thức A khi x = 9 . 1
b) Chứng minh rằng B = . x − 5
c) Tìm tất cả các giá trị của x để A = B | x − 4 | . Bài 2:
1. ( 1.5 điểm ) Trong mặt phẳng tọa độ Oxy cho đường thẳng (d) : y = mx + 2 và parabol 2
(P) : y = x a) Vẽ 2
(P) : y = x
b) Với m = −1, tìm tọa độ giao điểm của (d ) và (P) (bằng 2 cách )
2. (1.5 điểm ) Cho phương trình: 2
x − 2mx + 4 = 0
a) Giải phương trình đã cho khi m = 3 .
b) Tìm giá trị của m để PT (1) có hai nghiệm x , x 2 2 1 2 thỏa mãn: ( x +1 + x +1 = 2 1 ) ( 2 )
Bài 3: (1.5 điểm ) Một người mua hai loại hàng và phải trả tổng cộng là 21, 7 triệu đồng, kể
cả thuế giá trị gia tăng (VAT) với mức 10\% đối với loại hàng thứ nhất và 8% đối với loại
hàng thứ hai. Nếu thuế VAT là 9% đối với cả hai loại hàng thì người đó phải trả tổng cộng Trang 6
21, 8 triệu đồng. Hỏi nếu không kể thuế VAT thì người đó phải trả bao nhiêu tiển cho mỗi loại hàng?
Bài 4.( 3 điểm ) Cho nửa đường tròn (O; R) đường kính AB và dây EF ( E thuộc cung
AF , AE  BF ) . Các đường thẳng AE và BF cắt nhau tại M ; AF cắt BE tại H .
1) Chứng minh MEHF là tứ giác nội tiếp. 2)Chứng minh 2
BF.BM + AE.AM = AB
3)Gọi I là trung điểm của MH . Chứng minh IO vuông góc với EF và OF là tiếp tuyến
của đường tròn ngoại tiếp tam giác MEF .
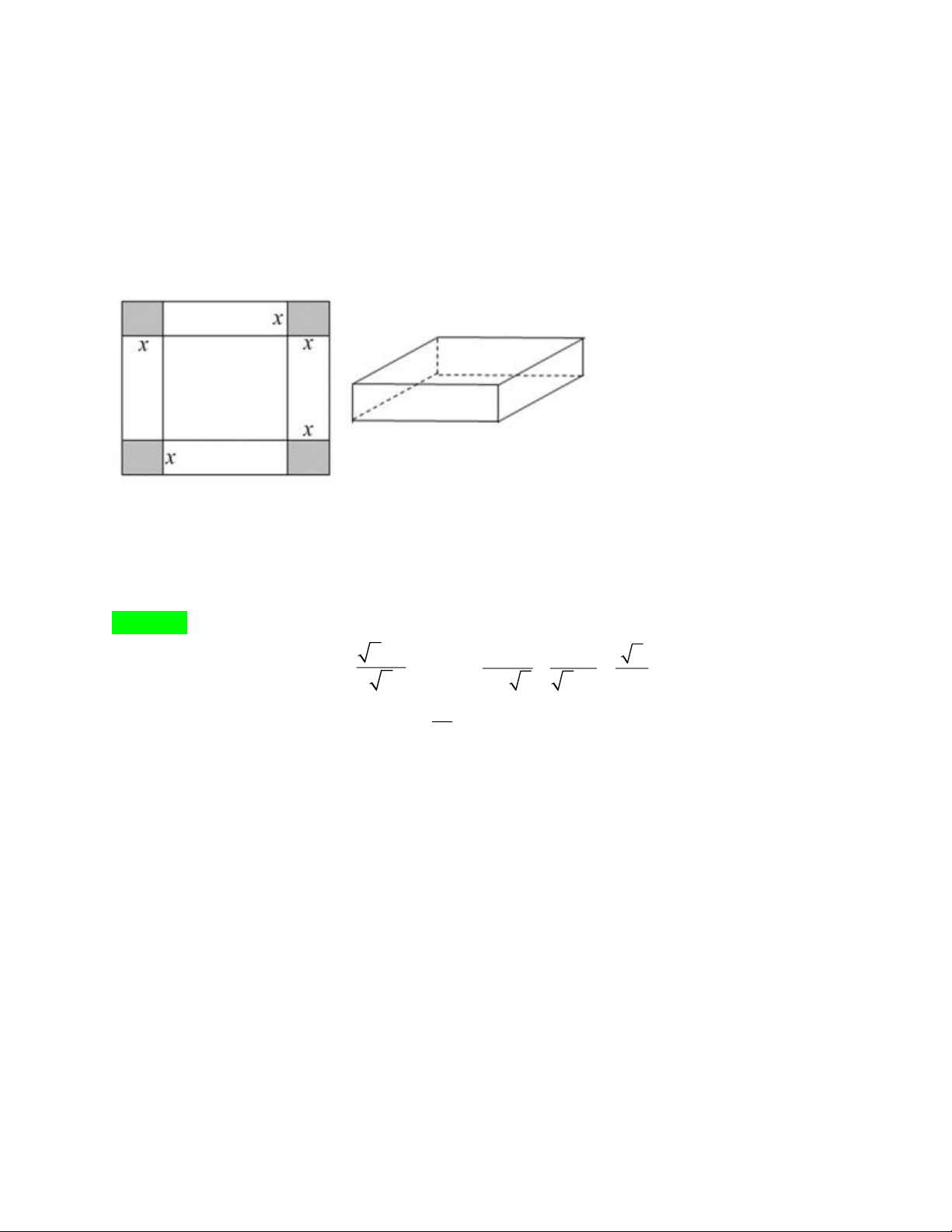
Bài 5. (0, 5 điểm)
Cho một tấm nhôm hình vuông cạnh 18 dm. Người ta cắt ở bốn góc của tấm nhôm đó bốn
hình vuông bằng nhau, mỗi hình vuông có cạnh bằng x(dm) , rồi gập tấm nhôm lại như hình
vẽ dưới đây để được một cái khay có dạnh hình hộp chữ nhật không nắp. Hỏi hình vuông bị
cắt ở mỗi góc có cạnh bao nhiêu dm để được khay có thể tích lớn nhất? ĐỀ SỐ 2 +
Bài 1. Cho hai biểu thức: x 1  x +  x A = và 1 2 B = −   
với x  0, x  1. x  x − x x −1 x −1
a) Tính giá trị của biểu thức A khi 25 x = 4
b) Rút gọn biểu thức B
c) Tìm giá trị x thỏa mãn A + B = 2 Bài 2. 1) Cho 2
(P) : y = x và đường thẳng (d) : y = x + 2 a) Vẽ 2
(P) : y = x
b) Tìm tọa độ giao điểm của đường thẳng (d ) và (P) 2) Cho phương trình 2
x − mx + m −1 = 0
a) Tìm m để phương trình có nghiệm kép. Tìm nghiệm kép đó.
b) Tìm m để phương trình có hai nghiệm x , x 1
2 sao cho tổng bình phương hai nghiệm lớn hơn 2.
Bài 3. Để hoàn thành một công việc theo dự định cần một số công nhân làm trong số ngày
nhất định. Nếu bớt đi hai công nhân thì phải mất thêm ba ngày mới hoàn thành công việc.
Nếu thêm 5 công nhân thì công việc hoàn thành sớm được 4 ngày. Hỏi theo dự định cần bao
nhiêu công nhân và làm trong bao nhiêu ngày? Trang 7
Bài 4. Cho ABC có 3 góc nhọn nội tiếp đường tròn (O); AB  AC và đường cao
AD, BE, CF cắt nhau tại H .
a) Chứng minh tứ giác AEHF nội tiếp được đường tròn. Xác định tâm I của đường tròn này.
b) Chứng minh rằng: DB .DC = DH .DA
c) Gọi K là giao điểm của đường tròn (O) và đường tròn (I)(K khác A ). Chứng minh OI// HK .
Bài 5. Kiểm tra ngẫu nhiên 1000 chiếc điều hòa của nhà máy A sản xuất thì có 10 chiếc
không đạt chất lượng. Trong lô hàng có 2500 chiếc điều hòa. Hãy dự đoán xem có khoảng
bao nhiêu chiếc điều hòa đạt chất lượng ? ĐỀ SỐ 3 − +
Bài 1: Cho hai biểu thức x x x A = và 1 6 24 B = − −
với x  0; x  16 . x − 4 x + 4 4 − x x −16
1) Tính giá trị của biểu thức A khi x = 25 . − 2) Chứng minh rằng: x 1 B = . x − 4
3) Tìm số tự nhiên x để A  B . Bài 2:
1. Trong mặt phẳng tọa độ Oxy cho đường thẳng (d) : y = 3x − 2 và parabol 2
(P) : y = x
a) Vẽ (d ) và ( P ) trên cùng hệ trục tọa độ
b) Tìm tọa độ giao điểm của (d ) và (P) 2. Cho phương trình: 2
x + 3x + m +1 = 0
a) Giải phương trình khi m = 0
b) Tìm m để phương trình có hai nghiệm phân biệt x ; x x = 2x 1 2 sao cho 1 2
Bài 3: Một phòng họp có 360 chỗ ngồi và được chia thành các dãy có số chỗ ngồi bằng
nhau. Nếu thêm cho mỗi dãy 4 chỗ ngồi và bớt đi 3 dãy thì số chỗ ngồi trong phòng không
đổi. Hỏi ban đầu số chỗ ngồi trong phòng họp được chia thành bao nhiêu dãy.
Bài 4: Cho tam giác ABC nhọn ( AB  AC ) nội tiếp đường tròn ( O ) các đường cao
AD, BE, CF cắt nhau tại H . Vẽ CI vuông góc với OA tại I . Gọi M là trung điểm BC .
a) Chứng minh O, M , I,C cùng thuộc một đường tròn.
b) Chứng minh góc BAD bằng góc OAC .
c) Chứng minh M , I, F thẳng hàng.
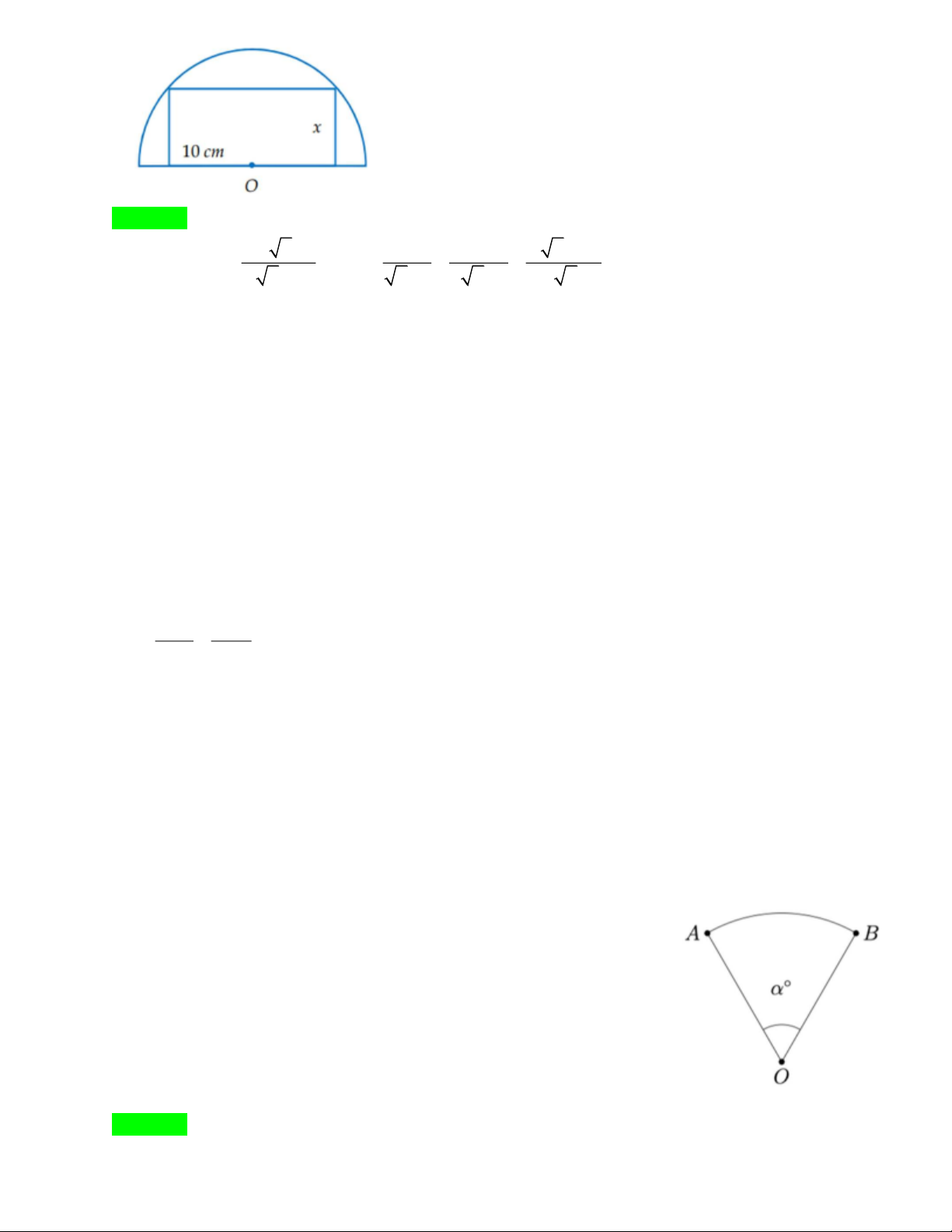
Bài 5: Một tấm bìa dạng nửa hình tròn với bán kính 10 cm . Tìm x để cắt được hình chữ
nhật có diện tích lớn nhất. Trang 8 ĐỀ SỐ 4 + + + + Bài 1: Cho x x 1 x x A = và 1 2 1 B = − −
với x  0, x  1. x +1
x −1 x x −1 x + x +1
1) Tính giá trị của A khi x = 2 .
2) Rút gọn biểu thức B .
3) Tìm x sao cho C = −AB nhận giá trị là số nguyên. Bài 2: 1) Cho parabol 2
(P) : y = x và đường thẳng (d) : y = 2x +1.
a) Vẽ đồ thị của (P) và (d ) trên cùng một hệ trục tọa độ
b) Xác định giao điểm của Parabol (P) và đường thẳng ( d ) . 2) Cho phương trình 2
x + 4x + m +1 = 0 (1) (với m là tham số)
a) Giải phương trình với m = 2 .
b) Tìm điều kiện của m để phương trình (1) có nghiệm.
c) Tìm tất cả các giá trị của m sao cho phương trình có hai nghiệm x ; x 1 2 thỏa mãn điều − − kiện x 1 x 1 1 2 + = 3 − . 2x 2x 2 1
Bài 3: Hai người cùng xây một bức tường. Sau khi làm chung được 4 giờ người thứ nhất
nghỉ, người thứ hai làm thêm 8 giờ nữa thì hoàn thành một bức tường. Hỏi ngay từ đầu nếu
chỉ có một người xây thì sau bao lâu hoàn thành được bức tường? Biết người thứ nhất xây
bức tường đó một mình nhanh hơn người thứ hai làm một mình là 6 giờ.
Bài 4: Cho nửa đường tròn tâm O đường kính AB . Vẽ bán kính OC vuông góc với
AB, M là một điểm bất kỳ trên cung AC ( M khác ,
A C và khác điểm chính giữa cung AC
); BM cắt AC tại H . Gọi K là chân đường vuông góc kẻ từ H đến AB .
1) Chứng minh tứ giác BCHK là tứ giác nội tiếp.
2) Chứng minh CA là phân giác góc MCK .
3) Kẻ CP vuông góc với BM (P  BM ) và trên đoạn BM lấy điểm
E sao cho BE = AM . Chứng minh ME = 2CP .
Bài 5: Một người muốn làm một chiếc quạt có chu vi là 80 cm
(hình minh họa). Tìm số đo của góc AOB(AOB = a) sao cho diện
tích của chiếc quạt là lớn nhất. ĐỀ SỐ 5 Trang 9 + +
Bài 1. Cho hai biểu thức 2 x 3 x x A = và 1 2 6 B = + +
với x  0; x  4 . x +1 x − 2 x + 2 4 − x
a) Tính giá trị của A khi x = 16 ; + b) Chứng minh x 1 B = x + 2 c) Đặt P = .
A B , hãy so sánh P và P . Bài 2.
1. Trong mặt phẳng tọa độ Oxy cho parabol 2
(P) : y = x và đường thẳng (d) : y = −x + 6 a) Vẽ parabol (P)
b) Tìm tọa độ các giao điểm của (d ) và (P) 2. Cho phương trình 2
x + 2(m − 2)x − 2m + 3 = 0 ( m là tham số). 1− 3
a) Biết rằng phương trình có hai nghiệm x = và x , hãy tính 2 2
A = x − x x + x 1 2 2 1 1 2 2
b) Tìm m để phương trình có hai nghiệm khác nhau x , x 4x = x + 3 1 2 mà 2 1 2 .
Bài 3. Để chở hết 120 tấn hàng, một đội xe dự định dùng một số xe cùng loại. Lúc sắp khởi
hành, đội xe được bổ sung thêm 5 xe cùng loại, nhờ vậy so với dự định ban đầu mỗi xe phải
chở ít hơn 2 tấn hàng. Hỏi lúc đầu, đội có bao nhiêu xe ? (biết rằng khối lượng hàng mỗi xe phải chở bằng nhau）
Bài 4. Cho đường tròn (O; R) và một điểm A nằm ngoài đường tròn. Từ A vẽ các tiếp
tuyến AB, AC với đường tròn ( B,C là các tiếp điểm). Gọi H là giao điểm của AO và BC .
a) Chứng minh bốn điểm ,
A B,O,C cùng thuộc một đường tròn và AO vuông góc với BC .
b) Ké đường kính BD của (O) , gọi M là giao điểm thứ hai của AD với đường tròn ( O ).
Chứng minh DC = 2OH và AH.AO = AM .AD
c) Gọi N là giao điểm thứ hai của MH với ( O ) . Chứng minh OHD = OMD và DN / /BC
Bài 5. Một khách sạn có 50 phòng. Hiện tại mỗi phòng cho thuê với giá 400 ngàn đồng một
ngày thì toàn bộ phòng được thuê hết. Biết rằng cứ mỗi lần tăng giá thêm 20 ngàn đồng thì
có thêm 2 phòng trống. Giám đốc phải chọn giáp hòng mới là bao nhiêu để thu nhập của
khách sạn trong ngày là lớn nhất ? Hết Trang 10