Đề Cương Ôn Tập Cuối Kỳ 1 Toán 9 Kết Nối Tri Thức 2025-2026

ĐỀ CƯƠNG ÔN TẬP HỌC KÌ I MÔN TOÁN 9
I. GIỚI HẠN NỘI DUNG ÔN TẬP (Hết tuần 15)
- Đại số: Đến hết Bài 9. Biến đổi đơn giản và rút gọn biểu thức chứa căn thức bậc hai.
- Hình: Đến hết Bài 17. Vị trí tương đối của hai đường tròn.
II. BÀI TẬP THAM KHẢO
DẠNG 1: Hệ phương trình bậc nhất hai ẩn; Phương trình và bất phương trình bậc nhất
một ẩn; Phương trình vô tỉ.
Bài 1. Giải các hệ phương trình x − y = 3 2x + y = 5  5 − x + 2y = 4 1)  2)  3)  3  x − 4y = 2 5  x − 2y = 8 6x − 3y = 7 − 4x − 3y = 6 x + y = 2 ì 3) ï   ï 3x - 2y = 1 ï
0,4x + 0,2y = 0,8 4) 1 5 5) í x + y = 
ïï 2x + 3 3y = 4 6 2 4 ïî 3
 x − y + 4 = 0
2(x + y) + 3(x − y) = 4  x y 6)  7)   − = 1
2x + 3y −1 = 0
(x + y) + 2(x − y) = 5 8) 2 3 5
 x −8y = 3 3x + 2 y −1  5 + = 1 1 1  − = 1 −  2( x + ) 1 − = 9  9)  3 2  y − 3   x y − 2 4x + y y +1 10) 11)    + = 3 − 4 3 2   (x + ) − =   1 5 4 2 + = 5    x y − 2  y − 3
Bài 2. Giải các phương trình sau:  2  2 1) − − = x + 6 x 9 4 x 0  (8 − 2x) = 0 2) ( )( )  3  æ + - ö 3) ( − = x + ) 3x 11 x 7 5 3 ç ÷ - = x x ç ÷ 0 4) 2 5 8 0 çè 4 12 ÷ ø
5) 4x( x − 3) − 3x + 9 = 0 6) ( - )( + ) 2 3 x 5 x 2 = x - 5x
7) (x- )2 = ( x + )2 3 2 7 8) (x + )( - x) 2
2 3 4 = x + 4x + 4
Bài 3. Giải các phương trình sau: x +1 3x +1 1 1) − = 2) 6 1 5 − = 2
x −1 x − x x x + 3 x − 2 2x + 6 2 3 3x + 5 1 2 2x − 3 3) + = 4) + = 2 x − 3 x + 3 x − 9 2 x + 2 2 − x x − 4 x +1 x −1 2 1 2x − 9 2 5) − = 6) − = 2 2x − 2 2x + 2 x −1 3 2 x + 2 x + 8 x − 2x + 4
Bài 4. Giải các bất phương trình sau:
1) 3(2x − 3)  4(2 − x) +13
2) 8x +17 − 3(2x + 3)  10(x + 2) 3) 2
x − 3x +1  2(x −1) − x(3 − x) − + −
4) x 1 4x 3 1 5x −  5 10 25 + + x + x − x + x − 5) 3x 5 x 2 − 2 1 4 3 1 4 x  1+ 6) −  − 2 3 3 4 6 12
Bài 5. Giải các phương trình sau 1)
4( x − 3) + 9x − 27 =10 2)
4x − 8 = 6 − x − 2 1
3) 5 x − 5 + 9x − 45 = 16 4) 4x − 8 + 9x −18 = 15 3 Trang 1 1 2 5) 4x −12 +
9x − 27 = 4 + x − 3 6)
4x − 8 − 5 x − 2 + 9x −18 +1 = 0 3 3 7 1 7) 5 4x −16 −
9x − 36 = 36 − 3 x − 4 8)
x − 3 + 9x − 27 − 4x −12 = 6 3 2 x − 5 3 9)
4x − 20 + x − 5 = 4 + 3
10) 16x + 48 − 7 x + 3 + 4x +12 = 6 − 9 4
Bài 6. Giải các phương trình sau 1) 2x +1 = 3 2) 3 x − 2 − 5 = 4 3) 2 x +1 = 2 4) (x + )2 4 2 = 8 5) 2
9 −12x + 4x = 4
6) 5x + 4 = x + 2 7) x + 5 = 2x
8) 2x −1 = x −1 9) 2
5x − 2x + 2 = x +1 10) 2
x + 2x +1 = 2x −1 11) 2
x − 3 − 2 x − 9 = 0 12) 2
x + 2 − x − 4 = 0
DẠNG 2: Giải bài toán bằng cách lập phương trình, hệ phương trình, bất phương trình.
Bài 1: Một công nhân dự định làm 14 sản phẩm trong thời gian đã định. Nhưng trên thực tế công
ty đã giao 21 sản phẩm nên để hoàn thành đúng thời gian đã định, người đó phải làm mỗi giờ
thêm 3 sản phẩm. Tính năng suất dự định của công nhân đó.
Bài 2: Một ca nô đi xuôi dòng từ địa điểm A đến địa điểm B, rồi lại đi ngược dòng từ địa điểm B
trở về địa điểm A. Thời gian cả đi lẫn về là 3 giờ. Tính tốc độ của dòng nước. Biết tốc độ của ca
nô khi nước lặng yên là 27km/h và độ dài quãng đường AB là 40km.
Bài 3: Trong một khu đất có dạng hình vuông, người ta dành một mảnh đất, có
dạng hình chữ nhật ở góc khu đất để làm bể bơi (hình 1).
Biết diện tích bể bơi bằng 1250 cm2. Tính độ dài cạnh khu đất đó.
Bài 4: Một xe máy đi từ A đến B trong một thời gian dự định. Nếu vận tốc tăng thêm 14km/h thì
đến B sớm hơn dự định 2 giờ. Nếu giảm vận tốc đi 4km/h thì đến B muộn hơn 1 giờ. Tính vận
tốc và thời gian dự định của người đó.
Bài 5: Hai vòi nước cùng chảy vào một cái bể không có nước thì trong 5 giờ sẽ đầy bể. Nếu vòi
thứ nhất chảy trong 3 giờ và vòi thứ 2 chảy trong 4 giờ thì được 2 bể nước. Hỏi nếu mỗi vòi chảy 3
một mình thì trong bao lâu mới đầy bể?
Bài 6: Để hoàn thành một công việc, hai tổ phải làm chung trong 6 giờ. Sau 2 giờ làm chung thì
tổ II được điều đi làm việc khác, tổ I đã hoàn thành công việc còn lại trong 10 giờ. Hỏi nếu mỗi
tổ làm riêng thì sau bao lâu sẽ làm xong công việc đó?
Bài 7: Bạn Bình mua một quyển từ điển và một món đồ chơi với tổng số tiền theo giá niêm yết là
750 nghìn đồng. Vì Bình mua đúng dịp cửa hàng có chương trình khuyến mại nên khi thanh toán
giá quyển từ điển được giảm 20%, giá món đồ chơi được giảm 10%, do đó Bình chỉ phải trả 630
nghìn đồng. Hỏi Bình mua mỗi thứ giá bao nhiêu tiền?
Bài 8: Cô Linh chia số tiền 500 triệu đồng của mình cho hai khoản đầu tư. Sau một năm, tổng số
tiền lãi thu được là 28 triệu đồng. Lãi suất cho khoản đầu tư thứ nhất là 5% /năm và khoản đầu
tư thứ hai là 6% /năm. Tính số tiền cô Linh đầu tư cho mỗi khoản.
Bài 9: Trong một kì thi gồm ba môn Toán, Ngữ Văn và Tiếng Anh, điểm số môm Toán và Ngữ
văn tính theo hệ số 2 , điểm môn Tiếng Anh tính theo hệ số 1. Để trúng tuyến, điểm số trung bình
của ba môn ít nhất bằng 8 . Bạn Nam đã đạt 9,1 điểm môn Toán, và 6,9 môn Ngữ Văn. Hãy lập
và giải bất phương trình để tìm điểm số môn Tiếng Anh tối thiểu mà bạn Nam phải đạt để trúng tuyển.
Bài 10: Một ngân hàng đang áp dụng lãi suất gửi tiết kiệm kì hạn 1 tháng là 0, 4% . Hỏi nếu
muốn có một số tiền lãi hãng tháng ít nhất là 3 triệu đồng thì số tiền gửi tiết kiệm ít nhất là bao
nhiêu (làm tròn đến triệu đồng)?
Dạng 3: Căn bậc hai Trang 2
3.1. Rút gọn biểu thức dạng số
Bài 1: Rút gọn các biểu thức sau 1) 2 75 − 5 27 − 192 + 4 48 2) 2 48 + 4 27 + 75 + 2 3 3) 5 12 + 3 27 − 2 108 − 192 4)
4 12 + 108 − 8 3 + 7 − 4 3 5)
3 45 − 7 125 + 500 +16 9 − 4 5 6) 1 5 18 − 3 32 + 50 5
Bài 2: Rút gọn các biểu thức sau 1 1 1) A = − 5 − 2 5 2) A = − 6 − 2 5 2 − 7 2 + 7 5 − 2 8 2 5 − 5 − 3) A = 5 − + 4) A = − ( − )2 6 3 1 3 5 +1 2 − 5 2 −1 − 5) A = ( − )2 6 1 3 + 12 − 6) A = + ( − )2 15 3 1 3 − 2 3 3 −1 5 −1 21 − 15 2 6 + 2 3 2 7) A = 48 − + 8) A = − + 8 − 2 15 7 − 5 3 +1 3 +1 5 − 3 4 1 6 9) A = + +  15 2 6  10) A = + −  (2 6 + 7) 3 +1 3 − 2 3 − 3  6 +1 6 − 2 3 − 6  2 + 3 2 − 3 11) A = + 3 + 5 3 − 5 12) A = + 2 − 3 2 + 3 3 − 5 3 + 5
3.2. Bài toán rút gọn tổng hợp
Bài 1: Cho hai biểu thức: x +1 x 1 1 A = và B = + −
với x  0, x  4 . x − 2 4 − x x + 2 2 − x
a) Tính giá trị của A khi x = 25.
b) Rút gọn biểu thức B. c) Tìm x để A > 0.
d) Với M = A.B . Tìm các giá trị nguyên của x để M có giá trị nguyên. − −
Bài 2: Cho hai biểu thức 3 x 2 2 x 2 7 x 4 A = ; B = − − (x  0). x + 2 x + 2 x 2 x + x
a) Tính giá trị biểu thức A khi x=16.
b) Rút gọn biểu thức B.
c) Cho M = A – B. Tìm số hữu tỉ x để biểu thức M là số nguyên tố. x - 1
Bài 3: Cho hai biểu thức A = và 4 1 x + 7 B = - - với x ³ 0; x ¹ 1 x + 3 x + 1 x - 1 1 - x
a) Tính giá trị của biểu thức A khi x = 4 . x + 2 b) Chứng minh B = . x - 1
c) Xét P = A.B . Chứng minh rằng không tồn tại giá trị nào của x để biểu thức P nhận giá trị nguyên. x − 2 x 6 x 3
Bài 4: Cho hai biểu thức P = và Q = + −
với x  0; x  9 x − 3 x − 3 9 − x x + 3
a) Tính giá trị của P khi x = 16 b) Rút gọn Q
c) Tìm x để biểu thức A = P.Q có giá trị nhỏ nhất. Trang 3 x − 4 2 3 x − 5 x + 2
Bài 5: Cho các biểu thức: A = và B = + − với x ≥ 0; x ≠ 4 x − 2 x − 2 x + 2 4 − x
a) Tính giá trị của A khi x = 49 b) Rút gọn B
c) Với x > 4, tìm giá trị nhỏ nhất của biểu thức P = A.B + + +
Bài 6: Cho hai biểu thức: x 2 x x A = và 1 2 6 B = − +
với x  0; x  4 2x +1 x + 2 x − 2 x − 4 1
a) Tính giá trị của biểu thức A khi x = 4 b) Chứng minh x B = x + 2
c) Tìm giá trị lớn nhất của biểu thức P = . A B x − 3 x 4 x 2
Bài 7: Cho hai biểu thức A = và B = + − với x  0, x  4 . x − 2 x − 2 4 − x x + 2
a) Tính giá trị biểu thức A khi x = 25 .
b) Rút gọn biểu thức B.
c) Đặt P = A.B . Tìm tất cả các giá trị của x là số nguyên tố để 2 P  P . x − 2 x x 1 3 x − 2
Bài 8: Cho hai biểu thức A = và B = + +
với x  0; x  4 x + 2 x + 2 x − 2 x − 4
a) Tính giá trị của biểu thức A khi x = 9 . x
b) Chứng minh rằng B = . x − 2
c) Cho biểu thức P = .
A B . Tìm x là số chính phương để P  1 . x − 2 x + 2 3 12
Bài 9: Cho hai biểu thức A = và B = − −
với x  0; x  4 x + 2 x − 2 x + 2 x − 4
a) Tính giá trị của biểu thức A khi x = 25. x −1 b) Chứng minh B = . x − 2
c) Với P = A.B. Tìm giá trị của x để P  P . x − 3 + −
Bài 10: Cho hai biểu thức: x x x A = và 2 1 3 11 B = + −
với x  0, x  9, x  10 . x −10 x + 3 x − 3 x − 9
a) Tính giá trị của A khi x = 16 . b) Chứng minh 3 x B = . x − 3 c) Cho C = .
A B . Tìm giá trị của x để 4 C = C + + − +
Bài 11: Cho các biểu thức : x x 1 x x x A = và 2 2 B = −
với x  0; x  1. x + 2 x −1 x − x
a) Tính giá trị của biểu thức A khi x = 9 . x + 2 b) Chứng minh B = . x
c) Cho P = AB . So sánh P với 3.
Bài 12: Cho hai biểu thức x - 2 x A = và 1 1 B = - +
với x ³ 0, x ¹ 4 . x + 1 x - 4 2- x x + 2
a) Tính giá trị của biểu thức A khi x = 16. Trang 4 b) Rút gọn B . c) Với P = .
A B . Hãy so sánh biểu thức P và P  1 x   x  x +1
Bài 13: Cho P =  +  : −1  và Q =
với x  0 , x  1.
x −1 x 1  x −1  −     x −1
a) Tính giá trị của Q khi x = 9 b) Rút gọn P.
c) Cho M = P. Q. Chứng minh: M  M x + 3 2 1 x − 3
Bài 14: Với x  0; x  9 , cho P = ; Q = + − x x − 3 x + 3 9 − x
a) Tính giá trị biểu thức P khi x = 36 x
b) Chứng minh rằng Q = x − 3 P c) Biết M =
, tìm x thỏa mãn: 8 x − 25 − x −16 = . x M Q
Bài 15: Cho hai biểu thức x + 3 x A = và 1 1 B = + − với x  , 0 x  4 . x − 2 x − 2 x + 2 4 − x
a) Tính giá trị của A khi x = 16 b) Rút gọn biểu thức B
c) Tìm x để B( x − 2) + 2 x = x − 7(x − 2) + 7
Dạng 4: Hình thực tế
Bài 1: Một chiếc thang dài 3m . Cần đặt chân thang cách chân
tường một khoảng bằng bao nhiêu mét (làm tròn đến số thập
phân thứ hai) để nó tạo được với mặt đất một góc an toàn 65
(tức là đảm bảo thang chắc chắn khi sử dụng)?
Bài 2: Một khúc sông rộng khoảng 250m . Một con đò chèo qua
sông bị dòng nước chảy đẩy xiên nên phải chèo khoảng 320m
mới sang được bờ bên kia. Hỏi dòng nước chảy đã đẩy con đò đi
lệch một góc  bằng bao nhiêu độ (làm tròn đến phút)?
Bài 3: Một cần cẩu đang nâng một khối gỗ trên sông, Biết tay
cẩu AB có chiều dài bằng 16 m và nghiêng một góc 42 so với
phương nằm ngang. Tính chiều dài BC của đoạn dây cáp (kết
quả làm tròn đến hàng phần mười).
Bài 4: Một mảnh gỗ có dạng hình chữ nhật ABCD với đường
chéo AC = 8dm . Do bảo quản không tốt nên mảnh gỗ bị hỏng
phía hai đỉnh B và D . Biết BAC = 64 . Người ta cần biết độ dài
AB và AD để khôi phục lại mảnh gỗ ban đầu. Độ dài AB, AD
bằng bao nhiêu decimet (làm tròn đến hàng phần mười) Trang 5
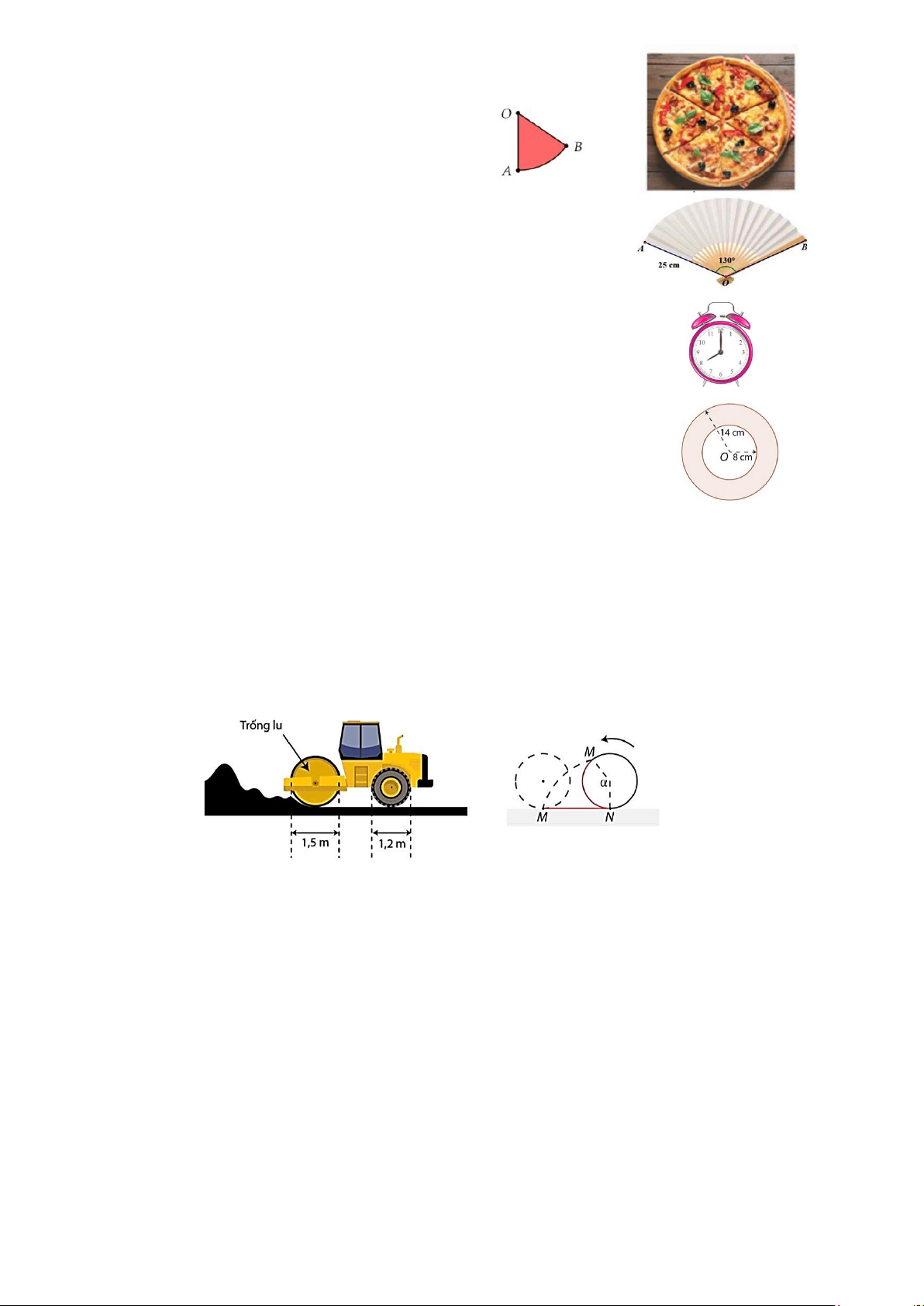
Bài 5: Tính diện tích của miếng bánh pizza có dạng hình
quạt tròn trong hình bên. Biết OA= 15cm và 0 AOB = 55 .
Bài 6: Một cây quạt giấy có bán kính 25cm, biết 0 AOB = 130
Tính diện tích hình quạt AOB được tạo ra.
Bài 7: Kim phút của một đồng hồ treo tường có độ dài 16cm.
Hỏi trong 20 phút thì đầu kim phút chỉ vạch được một cung tròn
có độ dài bằng bao nhiêu cm?
Bài 8: Tính diện tích hình vành khuyên trong hình vẽ sau:
Bài 9: Một máy kéo nông nghiệp có đường kính bánh xe sau là 124 cm và đường kính bánh
xe trước là 80 cm. Hỏi khi bánh xe sau lăn được 20 vòng thì bánh xe trước lăn được bao nhiêu vòng?
Bài 10: Một chiếc xe lu có đường kính trống lu là 1,5 m và đường kính của bánh sau là 1,2m
Khi hoạt động, trống lu quay hết một vòng (360o) trong 5 phút.
a) Mỗi phút, trống lu quay được bao nhiêu độ và xe lu cán được bao nhiêu mét đường ?
b) Để cán được một mét đường thì trống lu phải quay một góc bao nhiêu độ?
c) Để trống lu quay được một vòng thì bánh sau phải quay bao nhiêu vòng?
Dạng 5: Hình tổng hợp
Bài 1. Cho đường tròn (O; R) đường kính AB . Qua điểm A kẻ tiếp tuyến Ax đến đường tròn
(O). Trên tia Ax lấy điểm C sao cho AC  R . Từ điểm C kẻ tiếp tuyến CM với đường tròn
(O;R) ( M là tiếp điểm).
a) Chứng minh rằng bốn điểm ,
A C,O, M cùng thuộc một đường tròn.
b) Chứng minh rằng MB / /OC .
c) Gọi K là giao điểm thứ hai của BC với đường tròn (O; R) . Chứng minh rằng 2
BC.BK = 4R
Bài 2. Cho tam giác ABC có ba góc nhọn (AB < AC), đường tròn tâm D, đường kính BC cắt AB,
AC lần lượt tại E và F (E khác B, F khác C). Các đoạn thẳng BF và CE cắt nhau tại G, tia AG cắt BC tại H.
a) Chứng minh BEC = BFC = 90 ; Từ đó suy ra 4 điểm A, E, G, F cùng thuộc một đường tròn.
b) Gọi I là giao điểm của (D) và AH (I nằm giữa A và G).Chứng minh 2
BI = BH. BC
c) Trong trường hợp BAC = 60 và BC = 6cm . Tính bán kính của đường tròn ngoại tiếp AEF . Trang 6
Bài 3. Cho nửa đường tròn tâm O đường kính AB; AC là một dây cung của nó. Kẻ tiếp tuyến Ax
và kẻ đường phân giác của CAx cắt đường tròn tại E và cắt BC kéo dài tại D.
a) Chứng minh 4 điểm D, E, I, C cùng thuộc một đường tròn.
b) Chứng minh rằng ABD cân và OE // BD.
c) Gọi I là giao điểm của AC và BE. Chứng minh DI vuông góc với AB.
d) Khi C di chuyển trên đường tròn tâm O thì D chạy trên đường nào?
Bài 4. Cho nửa đường tròn tâm O đường kính AB. Kẻ các tiếp tuyến Ax và By cùng phía với nửa
đường tròn đối với AB. Lấy điểm C bất kỳ trên nửa đường tròn đó. Tiếp tuyến của nửa đường
tròn tại C cắt Ax, By lần lượt ở M và N.
a) Chứng minh 4 điểm O, A, M, C cùng thuộc một đường tròn.
b) Chứng minh ∆OMN vuông.
c) Gọi E là giao điểm của OM và AC; F là giao điểm của ON và BC. C/m: OE.OM = OF.ON
d) Gọi giao điểm của MB và AN là K. CK cắt AB tại H. Chứng minh: K là trung điểm của CH.
Bài 5. Cho đường tròn (O; R), d là tiếp tuyến của đường tròn tại điểm B. Điểm A di dộng trên
trên d, vẽ tiếp tuyến AC với đường tròn (C là tiếp điểm). AO cắt BC tại D.
a) Chứng minh: 4 điểm A, B, O, C cùng thuộc 1 đường tròn.
b) Chứng minh: OA . OD = R2.
c) Vẽ đường kính BE của (O). AE cắt đường tròn tại điểm thứ hai là I. Gọi H là trung điểm của
EI. Đường thẳng OH cắt BC tại M. Chứng minh: OH.OM không đổi khi A di chuyển trên d.
d) Chứng minh: ME là tiếp tuyến của (O) và đường thẳng AC đi qua trung điểm ME.
Bài 6. Cho đường tròn (O) đường kính AB . Gọi I là trung điểm của OB . Qua I kẻ dây CD
vuông góc với OB . Tiếp tuyến của (O) tại C cắt AB tại E . a) Chứng minh 2
OI.OE = R .
b) Chứng minh ED là tiếp tuyến của đường tròn (O) .
c) Gọi F là trung điểm của dây AC . Chứng minh D,O, F thẳng hàng.
Bài 7. Cho nửa đường tròn (O) đường kính AB . Lấy điểm C nằm trên đường tròn (O) . Gọi K
là trung điểm của dây cung BC . Qua B dựng tiếp tuyến với (O) cắt OK tại D .
a) Chứng minh rằng DO ⊥ BC và ABC vuông.
b) Chứng minh DC là tiếp tuyến của đường tròn (O) .
c) Vẽ CH ⊥ AB tại H . Gọi I là trung điểm của CH . Tiếp tuyến tại A của đường tròn (O) cắt
BI tại E . Chứng minh E,C, D thẳng hàng.
Bài 8. Cho đường tròn (O) và một điểm M nằm ngoài đường tròn. Từ M kẻ hai tiếp tuyến MA,
MB với đường tròn (O) (A và B là hai tiếp điểm). Gọi I là giao điểm của OM và AB.
a) Chứng minh 4 điểm M, A, O, B cùng thuộc một đường tròn.
b) Chứng minh OM vuông góc với AB tại I
c) Từ B kẻ đường kính BC của (O), đường thẳng MC cắt (O) tại D (D khác C). Chứng minh tam
giác BDC vuông, từ đó suy ra: MD. MC = MI. MO.
d) Qua O vẽ đường thẳng vuông góc với MC tại E và cắt đường thẳng BA tại F. Chứng minh FC là tiếp tuyến của (O) Dạng 6: Nâng cao
Bài 1. Giải phương trình sau: a) 2 2x − 6x −1 = 4x + 5 b) 2
x + 2 + x − 2 + 2 x − 4 = 2(3 − x)
Bài 2. Cho x  1. Tìm GTNN của biểu thức 1 A = 4x + x −1 6 24
Bài 3. Cho x, y là các số dương thỏa mãn x + y  6 . Tính GTNN của P = x + y + + x y Trang 7
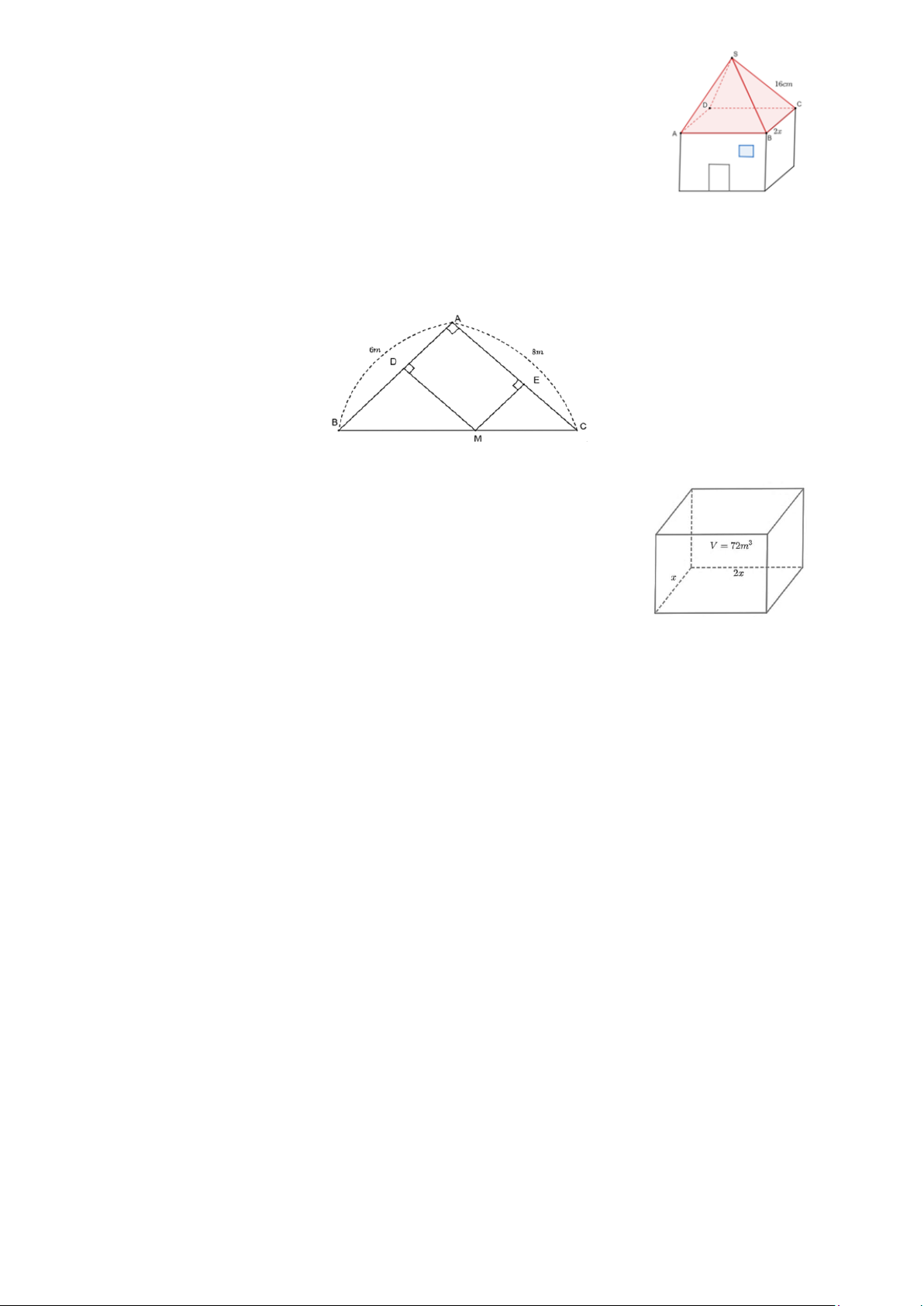
Bài 4. Bạn An làm một căn nhà đồ chơi bằng gỗ có phần mái là một
hình chóp tứ giác đều. Biết các cạnh bên của mái nhà bạn An dùng các
thanh gỗ có chiều dài 16 cm. Bạn An dự định dùng giấy màu để phủ
kín phần mái nhà. Gọi độ dài cạnh đáy của phần mái là 2x (cm). Hỏi
diện tích giấy màu cần sử dụng nhiều nhất là bao nhiêu?
Bài 5. Một người đào ao cá trên thửa ruộng dạng hình tam giác vuông có cạnh AB = 6 cm,
AC = 8. Một chiếc máy xúc ở vị trí M di chuyển trên bờ BC. Gọi D và E là khoảng cách từ M
đến bờ AB, AC. Người đó đào được ao hình chữ nhật ADME. Tính diên tích lớn nhất của ao cá
mà người đó có thể đào.
Bài 6. Bác Nam muốn xây một bể chứa nước dạng hình hộp
chữ nhật không nắp có thể tích bằng 3 72m . Đáy bể có dạng
hình chữ nhật có chiều rộng là x (m), chiều dài gấp đôi chiều
rộng. Bác Nam muốn phần diện tích cần xây (bao gồm diện
tích xung quanh và diện tích đáy bể) là nhỏ nhất để khi tiết
kiệm chi phí thì x bằng bao nhiêu? (kết quả làm tròn với độ chính xác 0,005)
------------------ Chúc các em ôn tập đạt kết quả cao nhất! ---------------------- Trang 8