Đề cương ôn tập cuối kỳ môn Vật lý đại cương 2 | Học viện Công Nghệ Bưu Chính Viễn Thông
Đề cương ôn tập cuối kỳ môn Vật lý đại cương 2 | Học viện CôngNghệ Bưu Chính Viễn Thông. Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời đọc đón xem!
Môn: Vật lý đại cương 2 298 tài liệu
Trường: Học viện Công Nghệ Bưu Chính Viễn Thông 1.7 K tài liệu
Tác giả:
Preview text:
Phương Văn Huy – TĐH 03/K66
ÔN TẬP CUỐI KỲ VẬT LÝ ĐẠI CƯƠNG II
1. Định nghĩa đường cảm ứng điện. Sự khác nhau cơ bản giữa phổ của
đường sức điện trường và phổ cảm ứng điện. Viết công thức xác định
thông lượng cảm ứng điện qua diện tích S. Tính điện thông qua một quả
cầu bao quanh một điện tích điểm.
phương trùng với phương của vecto điện cảm 𝐷 Trả lời:
đường cảm ứng điện là chiều của vecto điện cảm 𝐷
- Đường cảm ứng điện là đường mà tiếp tuyến tại mỗi điểm của nó có
tại điểm đó, chiều của .
- Sự khác nhau giữa phổ của đường sức điện trường và phổ đường cảm ứng điện: K . h 𝑑 i𝑆 đ = i q 𝐷.ua 𝑑 m 𝑆. ặ 𝑐 t 𝑜 p 𝑠 h 𝛼 â
n cách giữa hai môi trường, phổ của đường 𝑑𝜙
4𝜋 .𝑑𝑆 𝑐𝑜𝑠𝛼 cảm 𝑒= 𝐷
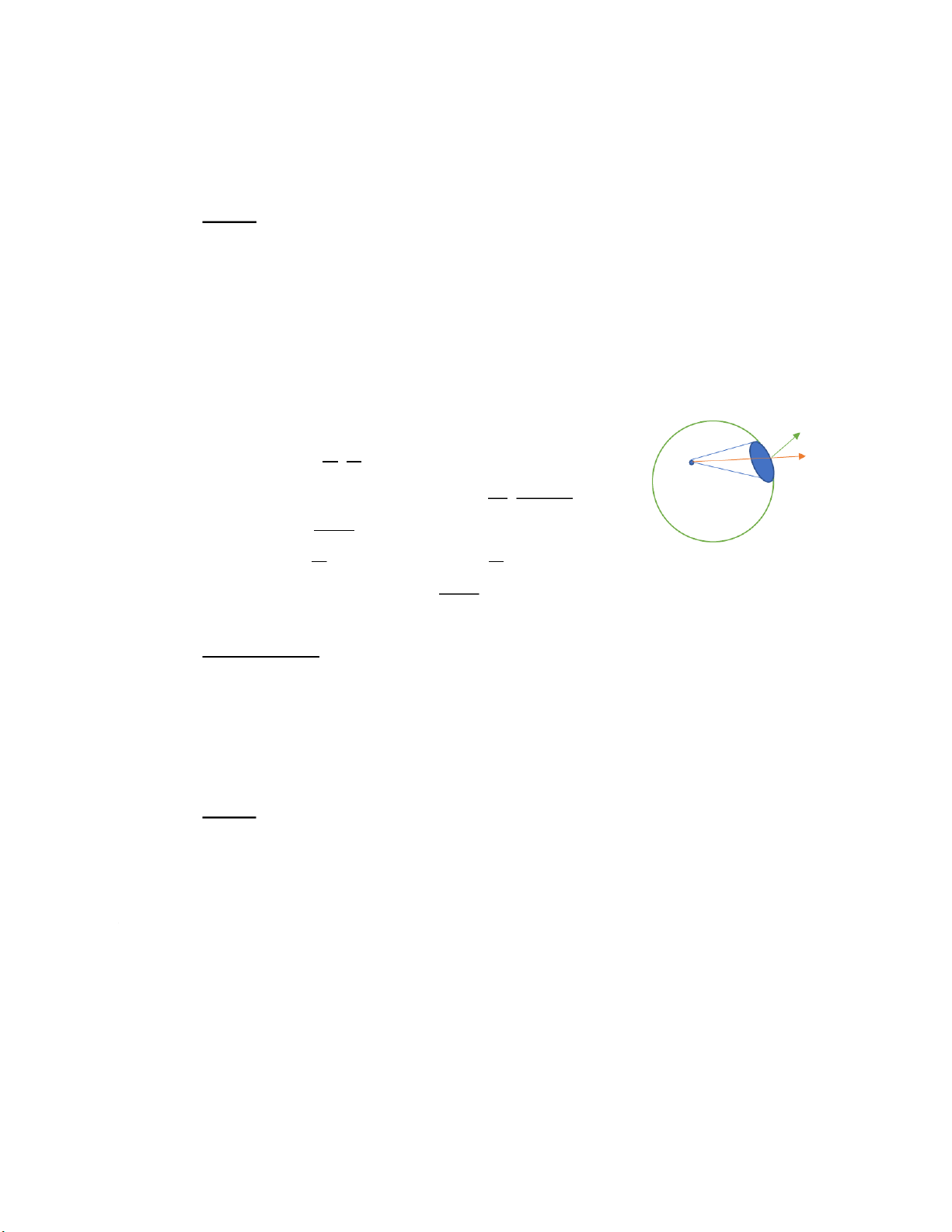
ứng điện là liên tục, còn phổ của đường sức điện trường là không liên +) Xét mặt 𝑑𝑠 𝑛 4𝜋 .|𝑞|𝑟2 , s ề uy ra điện thông q ế ua h 𝑑 ư 𝑆 ớ l n à g : ra ngoài: tục.
𝒅𝑺 có chi u vecto pháp tuy n
𝑑𝜙𝑒= 𝐷. 𝑑𝑆. 𝑐𝑜𝑠𝛼 = |𝑞| 𝑟 𝛼 - T Ta h côón:g
𝐷lư=ợn1g cảm ứng điện (điện thông) qua diện tích S: 𝐷 𝑀 𝑟 2
Đặt 𝑑Ω = 𝑑𝑆𝑐𝑜𝑠𝛼
4𝜋 𝑑Ω → 𝜙𝑒=∫𝑑𝜙𝑒 (𝑆) =𝑞 4𝜋 ∫𝑑Ω q
→ 𝑑𝜙𝑒=|𝑞| 𝑟2 (𝑆) =∫𝑑𝑆𝑐(𝑜𝑆𝑠)𝛼
= 4𝜋 → 𝑑𝜙𝑒= 𝑞 Trong đó: Ω = ∫𝑑Ω (𝑆)
Vậy: Điện thông qua mặt kín S chứa điện tích q bên trong gây ra là: 𝜙𝑒= 𝑞 𝑟2 Bài tập áp dụng:
2. Nêu định nghĩa và ý nghĩa của momen lưỡng cực điện. Xác định vecto
cường độ điện trường gây bởi lưỡng cực điện tại điểm M nằm trên đường
trung trực và cách tâm O của lưỡng cực điện một khoảng r khá lớn so với
khoảng cách giữa hai điện tích. Trả lời:
Phương Văn Huy – TĐH 03/K66
Định nghĩa: Lưỡng cực điện là một hệ 2 điện tích điểm có độ lớn bằng nhau
nhưng trái dấu +𝑞 và – 𝑞 (𝑞 > 0) cách nhau một đoạn l rất nhỏ so với
khoảng cách từ lưỡng cực điện tới những điểm đang xét của trường.
- Để đặc trưng cho tính chất điện của lưỡng cực điện, người ta dùng đại
lượng vector momen lưỡng cực điện hay momen điện của lưỡng cực. Kí hiệu là 𝑃𝑒 : 𝑷𝒆 = 𝒒𝒍
𝑙 : là vector hướng từ -q đến +q
𝑙 : có độ lớn bằng khoảng cách từ -q đến +q. Hình vẽ minh họa: −𝑞 𝑃𝑒 +𝑞
• Ý nghĩa: Biết vector momen lưỡng cực điện 𝑃𝑒 ta có thể xác định được
vector cường độ điện trường do lưỡng cực gây ra. Do đó, ta nói vector
momen điện đặc trưng cho tính chất điện của lưỡng cực điện.
• Xác định 𝑬 tại M thuộc đường trung trực cách O của lưỡng cực một
khoảng r khá lớn so với khoảng cách giữa hai điện tích.
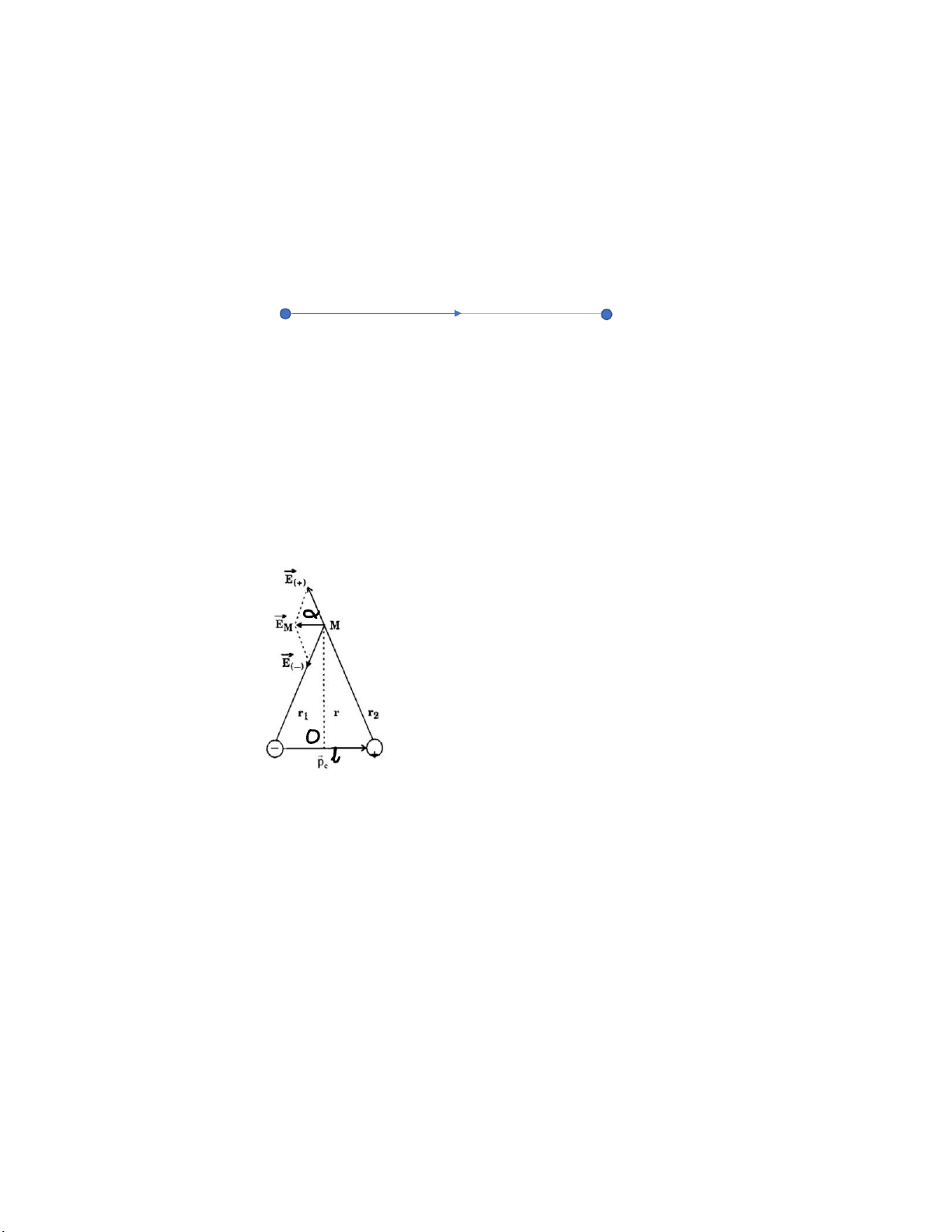
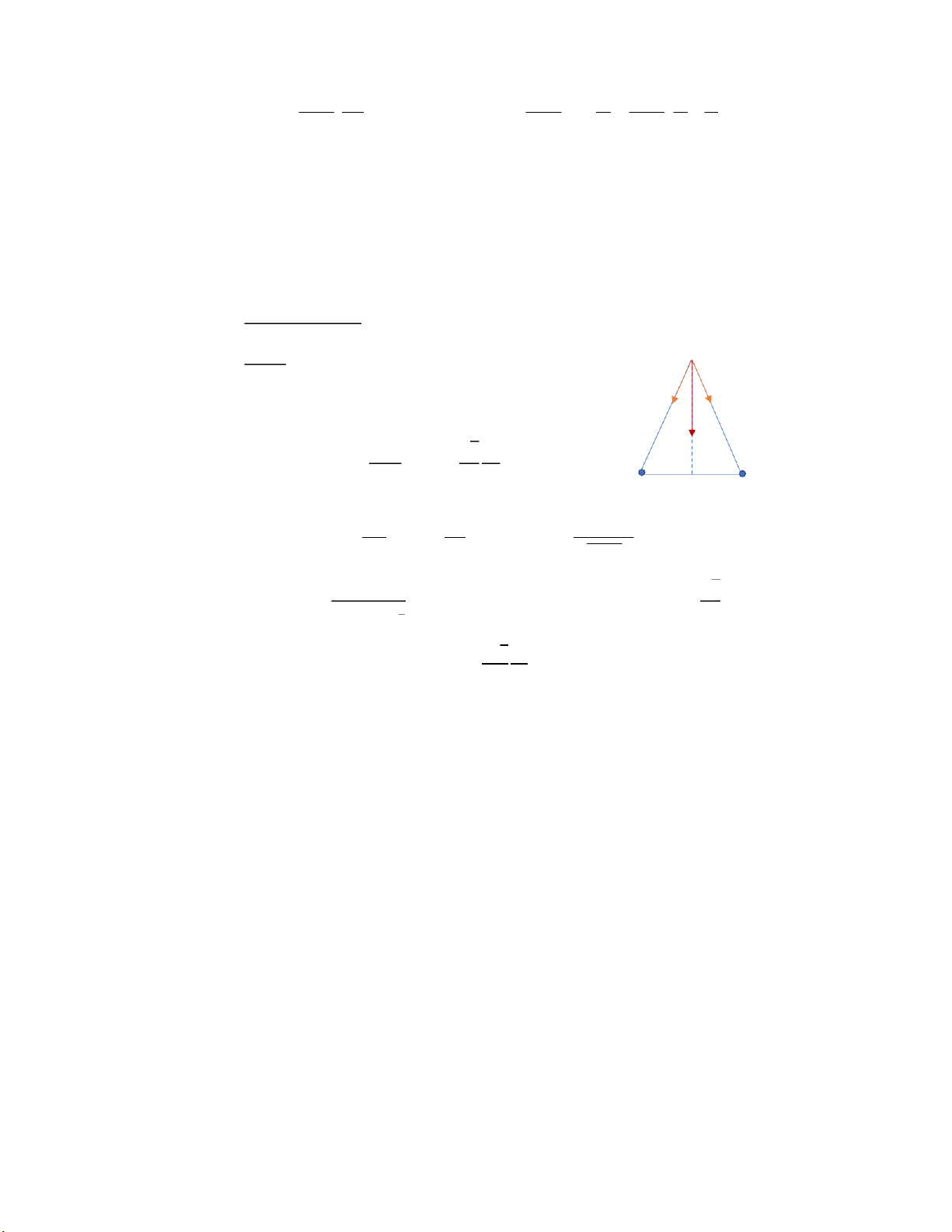
- Xét điểm M nằm trên trung trực của l
Theo nguyên lí chồng chất điện trường, vector cường độ điện trường 𝐸 gây
ra bởi lưỡng cực tại M bằng tổng vector cường độ điện trường gây ra bởi –q và +q của lưỡng cực. 𝐸 = 𝐸1 + 𝐸2
𝐸1 , 𝐸2 hướng như hình vẽ, 𝑟1= 𝑟2
Phương Văn Huy – TĐH 03/K66 𝐸1= 𝐸2= 14𝜋𝜀0.𝑞 𝜀𝑟12
Ta có: E =𝐸1.cos𝛼 + 𝐸2𝑐𝑜𝑠𝛼 = 2𝐸1𝑐𝑜𝑠𝛼 , 𝑣ớ𝑖 𝑐𝑜𝑠𝛼 = 𝑙 2𝑟1
→ 𝐸𝑀=1 4𝜋𝜀0.𝑞𝑙𝜀𝑟13 Vì r ≫ l nên 𝑟1 ~ 𝑟
Mà 𝑞𝑙 = 𝑃𝑒 => 𝐸 = 1 4𝜋𝜀0. 𝑞𝑙𝜀𝑟3=1 4𝜋𝜀0.𝑃𝑒𝜀𝑟3
Do 𝐸 song song, ngược chiều với 𝑙 nên 𝐸 = − 1 4𝜋𝜀0.𝑃𝑒 𝜀𝑟3 Bài tập áp dụng:
3. Phát biểu, viết biểu thức và nêu ý nghĩa của định lý O-G trong điện trường.
Áp dụng định lý O-G xác định cường độ điện trường gây ra bởi mặt phẳng
vô hạn tích điện đều với mật độ điện mặt 𝝈. Từ kết quả trên suy ra cường
độ điện trường trong tụ điện phẳng tích điện. Trả lời:
Phát biểu: Điện thông (thông lượng cảm ứng điện) qua 1 mặt kín bất kỳ
bằng tổng đại số các điện tích chứa trong mặt kín ấy. 𝑛 𝜙𝑒= 𝐷 ∯ . 𝑑𝑆 = ∑𝑞𝑖 𝑖=1
∑𝑞𝑖 Là phép lấy tổng đại số các điện tích chứa trong mặt kín S
*Ý nghĩa: +) Nêu lên mối quan hệ giữa cảm ứng điện D tại những điểm
trên mặt kín S và các điện tích 𝑞𝑖 giới hạn bởi mặt kín đó.
*+) Cho biết cảm ứng điện D, từ đó suy ra cường độ điện trường E
Áp dụng định lý O-G xác định cường độ điện trường gây ra bởi mặt
phẳng vô hạn tích điện đều với mật độ điện mặt 𝝈
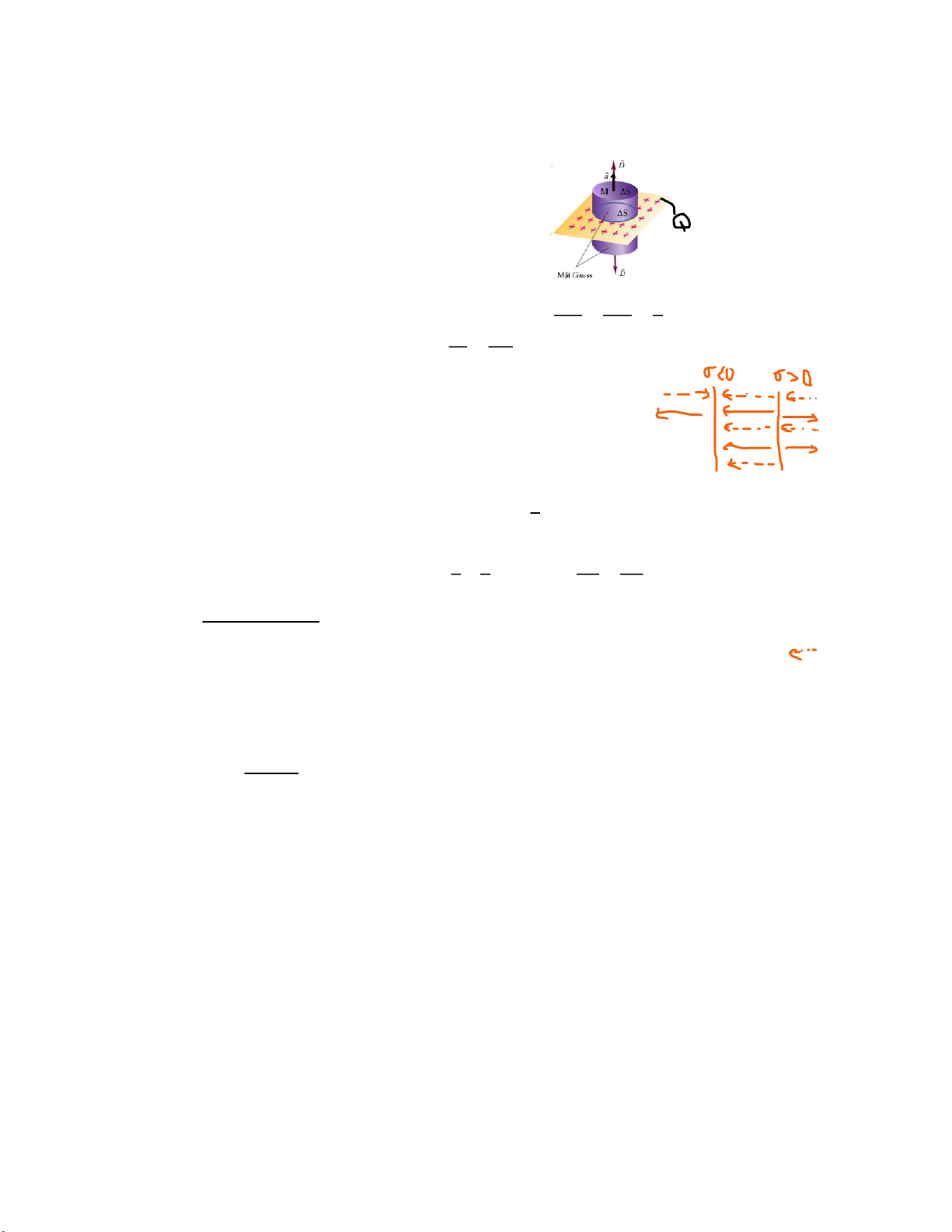
+) Xét điểm M nằm trên mặt phẳng vô hạn.
+) Chọn mặt Gauss là mặt trụ qua điểm M cắt vuông góc mặt phẳng Q, diện tích mặt đáy ∆𝑆.
Phương Văn Huy – TĐH 03/K66
+) Theo định lý O-G ta có: . . . 𝜙 𝑒= 𝐷 ∮ . 𝑑𝑆 =∫𝐷 𝑚ặ𝑡 𝑏ê𝑛
. 𝑑𝑆 + ∫𝐷2 đá𝑦= .∑𝑑𝑆 𝑄𝑖 (𝑆) Có: ∫𝐷. . 𝑑𝑆 𝑚ặ𝑡 𝑏ê𝑛
= 0 ; ∫𝐷.2 đá . 𝑑𝑆 𝑦= 𝐷𝑛2Δ𝑆
→ 𝜙𝑒=𝐷𝑛2Δ𝑆 = 𝑄 → 𝐷𝑛= 𝐷 = 𝑄 2∆𝑆 =𝜎∆ 2 𝑆 ∆𝑆 =𝜎2
⇒ Cường độ điện trường: 𝐸 = 𝐷𝜀0𝜀=𝜎 2𝜀0𝜀
Trường hợp trong khoảng không gian giữa 2 mặt tụ điện
- 𝐷1 , 𝐷2 lần lượt là vector cảm ứng điện do từng mặt gây ra
Vector cảm ứng điện do 2 mặt phẳng mang điện gây ra
𝐷 = 𝐷1 + 𝐷2 ( Theo nguyên lí chồng chất điện trường )
𝐷1 , 𝐷2 có phương vuông góc với mặt phẳng mang điện, có độ lớn 𝐷1= 𝐷2= 𝜎 2
𝐷1 , 𝐷2 cùng chiều => 𝐷 có phương vuông góc với 2 mặt phẳng.
𝐷 = 𝐷1+ 𝐷2=𝜎 2+𝜎 2= 𝜎 → 𝐸 = 𝐷𝜀0𝜀=𝜎 𝜀0𝜀 Bài tập áp dụng:
4. Phát biểu và viết biểu thức đinh lý O-G đối với điện trường (dạng tích
phân và dạng vi phân). Áp dụng định lý tính cường độ điện trường gây ra
bởi mặt trụ dài vô hạn, bán kính tiết diện ngang R, tích điện đều với mật
độ điện mặt 𝝈, đặt tại điểm M cách trục của trụ một khoảng 𝒓 > 𝑹 Trả lời:
Phát biểu: Điện thông cảm ứng điện qua 1 mặt kín bất kỳ bằng tổng đại số
các điện tích chứa trong mặt kín ấy.
Biểu thức định lý O-G:
Phương Văn Huy – TĐH 03/K66 +) Dạng tích phân: ∮𝐷 ( 𝑑𝑆 𝑆) =∑𝑄𝑖
+) Dạng vi phân: 𝑑𝑖𝑣(𝐷 )= 𝜌 - Áp dụng:
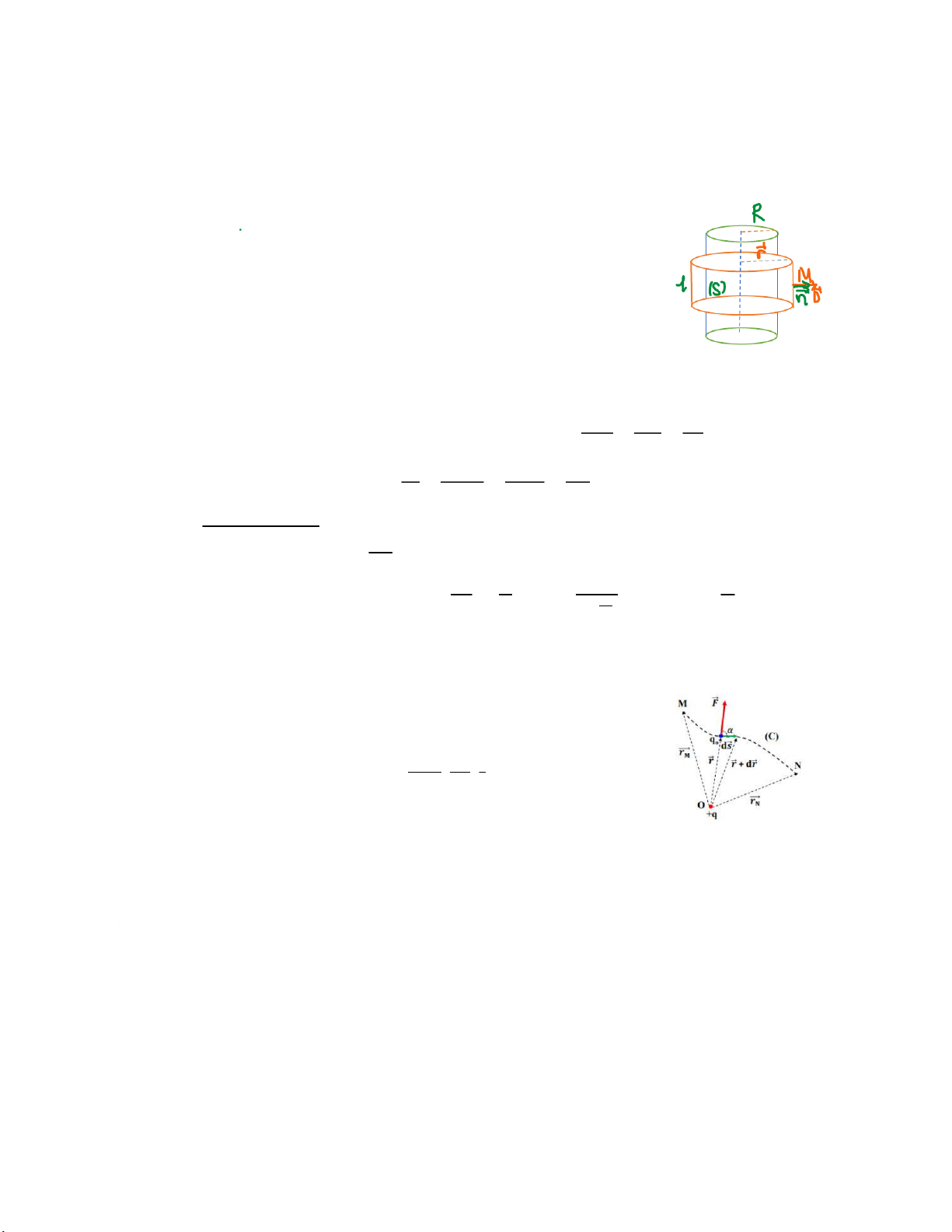
+) Chọn mặt Gauss là mặt trụ đi qua điểm M bán kín r chiều cao l đồng trục
+) Xét điểm M nằm trên mặt Gauss (𝑟, 𝑙) Theo định lý O-G ta có: 𝜙𝑒= 𝐷 ∮ . 𝑑𝑆 =∫𝐷 . 𝑑𝑆 𝑚ặ𝑡 𝑏ê𝑛 + ∫𝐷 . 𝑑𝑆 2 đá𝑦=∑𝑄𝑖 (𝑆)
Trong đó: ∫𝐷2 đá . 𝑑𝑆 𝑦= 0 và ∫𝐷 . 𝑑𝑆 𝑚ặ𝑡 𝑏ê𝑛
= 𝐷. 2𝜋𝑟𝑙 → 𝜙𝑒=𝐷. 2𝜋𝑟𝑙 𝑚ặ𝑡 𝑏ê𝑛
= 𝑄 = 2𝜋𝑅𝑙𝜎 = 𝜆𝑙 → 𝐷 = 𝑄 2𝜋𝑟𝑙 =𝜆2𝜋𝑟 =𝜎𝑅 𝑣à 𝜙𝑒=∫ 𝐷 . 𝑑𝑆 𝑟
→ Cường độ điện trường 𝐸 = 𝐷𝜀0𝜀=𝑄 2𝜋𝜀0𝜀𝑟𝑙 =𝜆 2𝜋𝜀0𝜀𝑟 =𝜎𝑅𝜀0𝜀𝑟 Bài tập áp dụng:
Theo câu trên ta có: 𝐸 = 𝜎𝜀𝑅01𝜀𝑟 là điện trường nằm trong không gian tụ. 𝑅2
Ta lại có: 𝑈 = 𝑉1− 𝑉2=∫𝐸 𝑅1𝑑𝑟 =𝜎𝑅1 𝜀0𝜀ln (𝑅2𝑅1)→ 𝐸 = 𝑈
𝑅1)→ 𝑼 = 𝑬𝒓𝒍𝒏 (𝑹𝟐𝑹𝟏) 𝑟𝑙𝑛(𝑅2
5. Tính công của lực tĩnh điện khi dịch chuyển điện tích điểm 𝒒𝟎 trong điện
trường của điện tích điểm 𝒒. Tại sao nói trường tĩnh điện là trường thế.
- Xét một điện tích điểm 𝑞 đứng yên tại O → gây ra một điện trường tĩnh 𝐸
- Điện tích thử 𝑞0 đặt trong điện trường 𝐸 → chịu tác dụng
của lực điện 𝐹 = 𝑞0𝐸 =1 4𝜋𝜀0𝜀.𝑞0𝑞𝑟2.𝑟
- Vi phân công: 𝑑𝐴 = 𝐹 𝑑𝑠 = 𝐹. 𝑑𝑠. 𝑐𝑜𝑠𝛼 = 𝑞0𝐸. 𝑐𝑜𝑠𝛼. 𝑑𝑠
- Trong dịch chuyển vô cùng nhỏ 𝑑𝑟 ≈𝑑𝑠. 𝑐𝑜𝑠𝛼
Phương Văn Huy – TĐH 03/K66 𝑟𝑁
𝑑𝐴 = 14𝜋𝜀0𝜀.𝑞0𝑞 𝑀𝑁 = ∫ 1 𝑟𝑀 4 = 𝜋 𝑞0 𝜀
𝑞 0𝜀. 𝑞0𝑞. 𝑑𝑟 4𝜋𝜀0𝜀(1𝑟𝑀−1
𝑟2. 𝑑𝑟 → 𝐴𝑀𝑁 = ∫ 𝑑𝐴 𝑟𝑁) 𝑟2
- Nhận xét: Công của lực tĩnh điện trong sự dịch chuyển điện tích 𝑞0 trong
điện trường không phụ thuộc vào dạng đường cong dịch chuyển mà chỉ phụ
thuộc vào điểm đầu và điểm cuối của chuyển dời
- Tính chất thế: Công của lực tĩnh điện trong sự dịch chuyển điện tích 𝑞0
trong điện trường bất kỳ không phụ thuộc vào đường đi chỉ phụ thuộc vào
điểm đầu và điểm cuối của chuyển dời
Trong một đường cong kín: 𝐴 = ∮𝐹 𝑑𝑠 = 𝑞0∮𝐸 𝑑𝑠 = 0 Bài tập áp dụng:
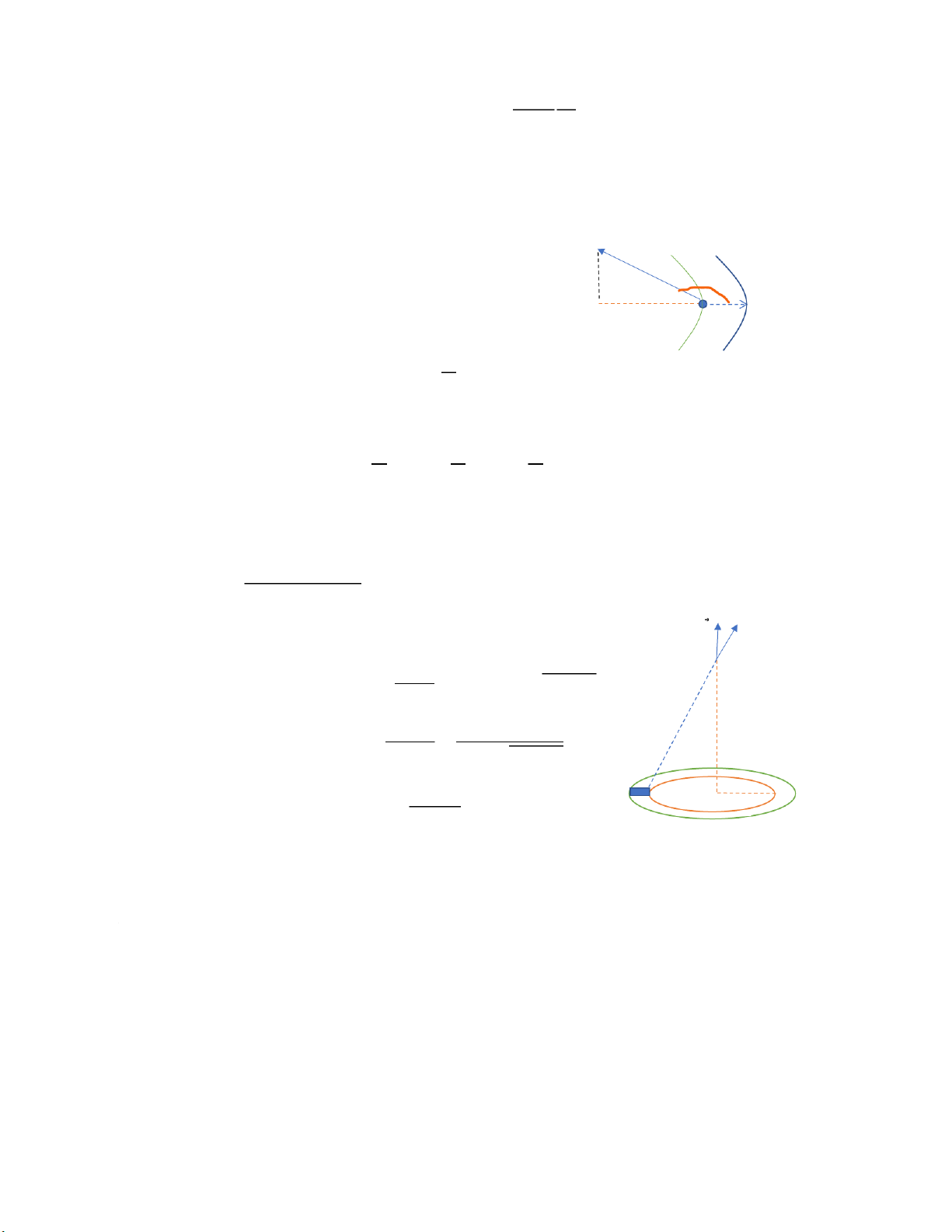
TH1: 𝑥 = 𝑎 → 𝛼 = 45° 𝑀
Theo nguyên lý chồng chất điện trường: 𝐸 𝛼 𝑀 = 𝐸1 + 𝐸2 𝐸 1 𝐸 2 → 𝐸 𝐸 𝑀
𝑀= 𝐸1𝑐𝑜𝑠𝛼 + 𝐸2𝑐𝑜𝑠𝛼 = 2𝐸1𝑐𝑜𝑠𝛼 𝑥 → 𝐸𝑀= 2 𝑘𝑞
𝑀𝐴2𝑐𝑜𝑠𝛼 = √22𝑘𝑞 𝐴 𝐵 𝑎2 𝑞1 𝑎 𝑎 𝑞2
Tìm x để 𝑬𝑴𝒎𝒂𝒙
+) Ta có: 𝐸𝑀= 2 𝑘𝑞𝑀𝐴2𝑐𝑜𝑠𝛼 = 2𝑘𝑞𝑎2sin2𝛼 . 𝑐𝑜𝑠𝛼 = 2𝑘𝑞𝑥(√𝑎2+𝑥2)3
→(𝐸𝑀)′= 2𝑘𝑞 (𝑎2− 2𝑥2
2)→ 𝐸𝑀𝑀𝑎𝑥𝑘ℎ𝑖 (𝐸𝑀)′= 0 𝑎2= 2𝑥2↔ 𝑥 = √2 2𝑎 (𝑎2+ 𝑥2)5
→ 𝑬𝑴𝑴𝒂𝒙 =𝟒√𝟑 𝟗𝒌𝒒𝒂𝟐
6. Định nghĩa hiện tượng điện hưởng. Thế nào là hai phần tử tương ứng?
Phát biểu định lý các phần tử tương ứng. Thế nào là hiện tượng điện
hưởng một phần và điện hưởng toàn phần?
• Hiện tượng điện hưởng là hiện tượng xuất hiện các điện tích cảm ứng
trên bề mặt vật dẫn (lúc đầu không mang điện) khi đặt trong điện trường ngoài.
Phương Văn Huy – TĐH 03/K66
• Hai phần tử tương ứng: là hai phần tử có điện tích cảm ứng bằng nhau và trái dấu.
- Định lí các phần tử tương ứng:
Điện tích cảm ứng trên các phần tử tương ứng có độ lớn bằng nhau và trái dấu.
- Điện hưởng một phần: Độ lớn của điện tích cảm ứng nhỏ hơn độ lớn điện
tích trên vật mang điện
- Điện hưởng toàn phần: Độ lớn của điện tích cảm ứng bằng độ lớn điện
tích trên vật mang điện Bài tập vận dụng:
7. Định nghĩa tụ điện. Thiết lập biểu thức tính điện dung của tụ điện phẳng và tụ điện cầu. Trả lời:
- Định nghĩa: Là hệ gồm hai vật dẫn có tương tác điện hưởng toàn phần. - Thiết lập công thức:
+) Tụ phẳng: Gồm hai mặt phẳng tính điện +𝑄, −𝑄
Cường độ điện trường giữa hai mặt phẳng vô hạn tích điện đều: 𝐸 = 𝜎𝜀0𝜀=𝑄 𝜀0𝜀𝑆 Ta có: 𝑑
𝑑𝑉 = −𝐸𝑑𝑟 → − ∫ 𝑉2 𝑑𝑉 𝑉1=∫𝑄 0 𝜀0 → 𝜀𝑆 𝑉 𝑑 1−𝑟𝑉2= 𝑈 = 𝑄𝑑 𝜀0𝜀𝑆 → 𝐶 = 𝑄 𝑈=𝜀0𝜀𝑆 𝑑
+) Tụ cầu: Gồm hai mặt cầu đồng tâm tích điện +𝑄, −𝑄
Cường độ điện trường gây ra bởi mặt cầu tại điểm cách tâm đoạn r là: 𝐸 = 𝑄4𝜋𝜀0𝜀𝑟2 Ta có: 𝑅2
𝑑𝑉 = −𝐸𝑑𝑟 → − ∫ 𝑉2 𝑑𝑉 𝑉1=∫𝑄 𝑅1 4𝜋𝜀 → 0𝜀𝑟 𝑉1 2 − 𝑑𝑟 𝑉2= 𝑈12 =𝑄
4𝜋𝜀0𝜀(1 𝑅1−1 𝑅2) → 𝐶 = 𝑄 𝑈=4𝜋𝜀𝜀0𝑅1𝑅2 𝑅2− 𝑅1
+) Tụ trụ: Cường độ điện trường gây ra bởi tụ trụ dài vô hạn: 𝐸 = 𝜆 2𝜋𝜀𝜀0𝑟
Phương Văn Huy – TĐH 03/K66 Ta có: 𝑉2 𝑅2
𝑑𝑉 = −𝐸𝑑𝑟 → −∫𝑑𝑉𝑉1=∫𝜆 2𝜋𝜀𝜀0𝑟𝑑𝑟 𝑅1
→ 𝑉1− 𝑉2= 𝑈 = 𝜆 2𝜋𝜀𝜀0ln (𝑅2𝑅1)=𝑄 2𝜋𝜀𝜀0𝑙ln (𝑅2𝑅1)→ 𝐶 = 𝑄𝑈=2𝜋𝜀𝜀0𝑙 ln (𝑅2 𝑅1) Bài tập áp dụng:
+) Ta có 𝑑𝐴 = −𝑞. 𝑑𝑉 = −𝑞(−𝐸𝑑𝑟)= 𝑞𝐸𝑑𝑟 = 𝑞 𝜆 2𝜋𝜀𝜀0𝑟𝑑𝑟
→ 𝐴 = ∫ 𝑑𝐴 = 𝑞 𝜆 2𝜋𝜀𝜀0∫𝑑𝑟𝑟2 𝑟1→ 𝐴 = 𝑞𝜆
2𝜋𝜀𝜀0ln (𝑟2𝑟1)→ 𝜆 = 2𝜋𝜀𝜀0𝐴 𝑟 𝑞𝑙𝑛 (𝑟2 𝑟1) 8. Trình bày
- Điều kiện cân bằng tĩnh điện của một vật dẫn mang điện
- Các tính chất của vật dẫn tích điện cân bằng (có minh chứng)
- Nêu ứng dụng về tính chất của vật dân tĩnh điện cân bằng Trả lời:
- Điều kiện cân bằng tĩnh điện: Mật độ dòng điện trung bình bằng không (𝐽 = 0 )
+) Vecto cường độ điện trường tại mọi điểm bên trong vật dẫn (khối hoặc rỗng) phải bằng
không (𝐸 𝑡𝑟𝑜𝑛𝑔 = 0)
+) Thành phần tiếp tuyến của véc-tơ cường độ điện trường tại mọi điểm trên mặt vật dẫn
phải bằng không 𝐸𝑡 = 0 hay 𝐸𝑛 = 𝐸
- Các tính chất của vật dẫn tích điện cân bằng:
+) Vật dẫn là một khối đẳng thế
Vì vật dẫn là cân bằng tĩnh điện nên 𝐸 𝑡𝑟𝑜𝑛𝑔 = 0
+) Xét hai điểm M, N bất kì trong vật dẫn:
𝑉𝑀− 𝑉𝑁= ∫ 𝐸 𝑀𝑁 𝑑𝑆 = 0 → 𝑉 𝑡𝑟𝑜𝑛𝑔 𝑀≈ 𝑉𝑁
+) Với vật dẫn tích điện, điện tích q chỉ được phân bố trên bề mặt của vật dẫn, bên trong
vật dẫn điện tích bằng không (trung hòa).
Phương Văn Huy – TĐH 03/K66
Chọn mặt khí 𝑆 nằm trong vật dẫn tính điện cân bằng. Áp dụng định lý O-G, ta có: 𝑞 = ∮𝐷 (𝑆) 𝑑𝑆 = 0
vì 𝐷 = 𝜀𝜀0𝐸 𝑡𝑟𝑜𝑛𝑔 = 0
→ Điện tích không tập chung ở bên trong mà chỉ phân bố trên bề mặt vật dẫn
+) Sự phân bố điện tích trên bề mặt vật dẫn chỉ phụ thuộc vào hình dạng của mặt đó.
• Điện tích hầu như bằng không ở những chỗ lõm.
• Điện tích phân bố nhiều hơn ở những chỗ lồi → hiệu ứng mũi nhọn → gió điện
+) Một vật dẫn rỗng hay đặc nếu được giữ ở trạng thái có thế năng luôn không đổi
(chẳng hạn như nối đất) thì có thể coi là trạng thái tĩnh điện cân bằng.
𝐸 𝑡𝑟𝑜𝑛𝑔 = −𝑔𝑟𝑎𝑑 (𝑉)= 0
- Ứng dụng: Máy phát tĩnh điện Vande Graaff Bài tập áp dụng:
Một quả cầu điện môi cô lập có tâm O, bán kính a, hằng số điện môi 𝜀, tích điện 𝑄 (𝑄 > 0)
được phân bố đều theo thể tích. Quả cầu được đặt trong không khí.
a. Dùng định lý O-G dẫn ra các công thức xác định độ lớn của cường độ điện trường tại
điểm A cách O một khoảng 𝑟𝐴 (𝑟𝐴< 𝑎), tại điểm B cách O một khoảng 𝑟𝐵 (𝑟𝐵< 𝑎). Trả lời:
Áp dụng định lý O-G ta có 𝜀0𝜀∮𝐸 𝑑𝑠 = ∑𝑞𝑖
+) Xét tại điểm A (𝑟𝐴> 𝑎) có: ∑𝑞𝑖= 𝑄 3𝜋𝑎3
Suy ra: 𝜀0𝜀. 𝐸. 4𝜋. 𝑟𝐴2= 𝑄 → 𝐸 = 𝑸 𝟐=𝜌.4 2=𝝆𝒂𝟑 𝟒𝝅.𝜺𝟎𝜺.𝒓𝑨 4𝜋.𝜀0𝜀.𝑟𝐴 𝟑𝜺𝟎𝜺𝒓𝑨 𝟐
+) Xét tại điểm B (𝑟𝐵< 𝑎) có: ∑𝑞𝑖= 𝑄 (𝑟𝐵 𝑎)3 3 3𝜋𝑎3.𝑟𝐵
Suy ra: 𝜀0𝜀. 𝐸. 4𝜋. 𝑟𝐵2= 𝑄. 𝑟𝐵𝑎3→ 𝐸 = 𝑸𝒓𝑩
𝟒𝝅𝜺𝟎𝜺𝒂𝟑=𝜌.44𝜋𝜀0𝜀𝑎3=𝝆 𝟑𝜺𝟎𝜺𝒓𝑩
9. - Định nghĩa và nêu ý nghĩa của điện thế.
- Viết công thức tính điện thế tai một điểm trong điện trường gây ra bởi
một hệ các điện tích điểm phân bố rời rạc và tại một điểm trong điện trường bất kỳ.
Phương Văn Huy – TĐH 03/K66
- Thiết lập công thức liên hệ giữa cường độ điện trường và điện thế. Trả lời:
Điện thế: Trong trường hợp tổng quát với một điện trường bất kỳ: ∞ 𝑊𝑀= 𝑞0∫ 𝐸 𝑑𝑆 𝑀 → tỷ số 𝑊 𝑞 𝑀
0 không phụ thuộc vào 𝑞0 mà chỉ phụ thuộc vào vị trí trong điện
trường và điện tích gây ra điện trường. - Tỷ số 𝑉 = 𝑊
𝑞0 được gọi là điện thế của điện trường tại điểm ta đang xét.
Ý nghĩa: 𝐴𝑀𝑁 = 𝑊𝑀− 𝑊𝑁= 𝑞0(𝑉𝑀− 𝑉𝑁)→ 𝑉𝑀− 𝑉𝑁=𝐴𝑀𝑁 𝑞0
Nếu lấy 𝑞0= +1 và 𝑁 ở vô cùng: 𝑉𝑀− 𝑉∞= 𝑉𝑀−𝑊∞ 𝑞0= 𝐴𝑀∞
Vậy: Điện thế tại một điểm trong điện trường là đại lượng có trị số bằng
công của lực tĩnh điện trong sự dịch chuyển một đơn vị điện tích dương từ ∞
điểm đó ra xa vô cùng. 𝑉𝑀=∫𝐸 𝑑𝑆 𝑀
Nếu lấy 𝑞0= +1 thì 𝑉𝑀− 𝑉𝑁= 𝐴𝑀𝑁
Hiệu điện thế giữa 2 điểm M và N trong điên trường là một đại lượng về trị
số bằng công của lực trong sự dịch chuyển một đơn vị điện tích dương từ 𝑀 → 𝑁
• Điện thế của một hệ các điện tích điểm phân bố rời rạc có:
- Điện thế do 𝑞0 gây ra tại điện tích điểm 𝑞 cách nó đoạn 𝑟 là: 𝑉 = 𝑞4𝜋𝜀0𝜀𝑟
+) Với hệ điện tích điểm 𝑞𝑖 gây ra tại điểm nào đó trong điện trường: 𝑛 𝑖=1 =∑𝑞𝑖 𝑉 = ∑𝑉𝑖 𝑖 4𝜋𝜀0𝜀𝑟𝑖
Trong đó 𝑟𝑖 khoảng cách từ điểm đang xét tới 𝑞𝑖
+) Điện thế tại một điểm của điện trường bất kỳ: ∞ ∞ 𝑀=𝑊𝑀 𝑞0=∫𝑞0𝐸 𝑑𝑆 𝑉𝑀= ∫ 𝐸 𝑑𝑆 𝑀𝑞0
BONUS: +) Trong trường hợp, có một hệ điện tích phân bố liên tục thì ta
coi hệ được tạo bởi vô số điện tích điểm 𝑑𝑞 và điện thế được tính bởi:
Phương Văn Huy – TĐH 03/K66 𝑐ả ℎệ = ∫ 1 4𝜋𝜀𝜀0𝑑𝑞 𝑉 = ∫ 𝑑𝑉 𝑐ả ℎệ 𝑟
- Thiết lập công thức liên hệ giữa cường độ điện trường và điện thế:
+) Xét hai điểm 𝑀, 𝑁 có điện thế 𝑉 𝑣à 𝑉 + 𝑑𝑉 (𝑑𝑉 > 0) trong 𝐸
+) Công của lực tĩnh điện dịch chuyển 𝑞0 từ 𝑀 → 𝑁 là: 𝐸
𝑑𝐴 = 𝐹 𝑑𝑠 = 𝑞0𝐸 𝑑𝑠 = 𝑞0𝐸𝑑𝑠. 𝑐𝑜𝑠𝛼, 𝛼 = (𝐸, 𝑑𝑠 ) 𝑉 𝑉 + 𝑑𝑉
Mà 𝑑𝐴 = 𝑞0[𝑉 − (𝑉 + 𝑑𝑉)] = −𝑞0𝑑𝑉 𝑀
→ 𝐸 𝑑𝑠 = −𝑑𝑉 → 𝐸𝑑𝑠. 𝑐𝑜𝑠𝛼 = −𝑑𝑉 < 0 𝛼 𝑁 𝑞0
𝑐𝑜𝑠𝛼 < 0 → 𝛼 > 90° → 𝐸 hướng về theo chiều điện thế giảm 𝑑𝑠
- Chiếu lên Phương dịch chuyển 𝑑𝑠 có: 𝐸𝑑𝑠. 𝑐𝑜𝑠𝛼 = 𝐸𝑠𝑑𝑠 = −𝑑𝑉
→ 𝐸𝑠= − 𝑑𝑉𝑑𝑠
+) Hình chiếu vecto cường độ điện trường trên một phương nào đó có trị số
bằng độ giảm điện thế trên đơn vị dài của phương đó.
- Trong hệ tọa độ 𝑂𝑥𝑦𝑧
+ Hệ thức: 𝐸𝑥= − 𝜕𝑉𝜕𝑥 ; 𝐸𝑦= − 𝜕𝑉𝜕𝑦 ; 𝐸𝑧= − 𝜕𝑉𝜕𝑧 , 𝐸 = 𝑖 𝐸𝑥+ 𝑗 𝐸𝑦+ 𝑘 𝐸𝑧
→ 𝐸 = −𝑔𝑟𝑎𝑑 (𝑉)
+) Vecto cường độ điện trường tại một điểm bằng về giá trị nhưng ngược
chiều với gradien của điện thế tại điểm đó.
Bài tập áp dụng: Một vòng dây bán kính 𝑅, tích điện đều với điện tích 𝑄.
Tính điện thế tại điểm 𝑀 trên trục của vòng dây, cách tâm vòng dây một
đoạn ℎ và điện thế tại tâm vòng dây. Vẽ hình. 𝑑𝑉 𝛼 𝑑𝑉1
+) Chia vòng dây thành các phần tử 𝑑𝑙 điện tích 𝑑𝑄 𝑀
Gây ra điện thế: 𝑑𝑉 =𝑑𝑄4𝜋𝜀0𝜀𝑟 trong đó: 𝑟 = √𝑅2+ ℎ2
+) Điện thế của cả vòng dây gây ra tại M là: 𝑟 ℎ 𝑉𝑀= ∮ 𝑑𝑄 4𝜋𝜀0𝜀𝑟 =𝑄 4𝜋𝜀0𝜀√𝑅2+ ℎ2
+) Điện thế do cả vòng dây gây ra tại tâm O là: 𝑉𝑂=𝑄 𝑑𝑞 𝑅 4𝜋𝜀0𝜀𝑅
Phương Văn Huy – TĐH 03/K66
10. - Thế nào là hiện tượng phân cực điện môi?
- Định nghĩa vecto phân cực điện môi.
- Tìm mối liên hệ giữa vecto phân cực điện môi và mật độ điện tích liên
kết trên bề mặt điện môi. Trả lời:
- Hiện tượng phân cực điện môi: Hiện tượng xuất hiện các điện tích liên
kết trên bề mặt tấm điện môi khi đặt trong điện trường ngoài.
+) Điện tích liên kết sinh ra điện trường phụ 𝐸′
→ Điện trường trong điện môi: 𝐸 = 𝐸 0+ 𝐸 ′
+) 𝐸0 là điện trường ngoài.
- Vectơ phân cực điện môi: Là đại lượng đo bằng tổng mô-men lưỡng cực
điện của các phần tử có trong một đơn vị thể tích của khối điện môi. 𝑛
𝑃 𝑒=∑𝑝 𝑒𝑖𝑖∆𝑉
- Mối liên hệ giữa vecto phân cực điện môi và mật độ điện tích liên kết
trên bề mặt điện môi:
- Xét mội khối điện môi hình trụ xiên có đường sinh dài L và song song với
𝐸0, diện tích đáy ∆𝑆. 𝑛 𝑖=1 𝑒𝑖|
+) 𝑃𝑒=|𝑃 𝑒|=|∑𝑝 ∆𝑉 +) |∑𝑃𝑛
𝑖=1 𝑒𝑖|= 𝜎′∆𝑆𝐿 ; ∆𝑉 = ∆𝑆𝐿𝑐𝑜𝑠𝛼
→ 𝑃𝑒=𝜎′∆𝑆𝐿𝑐𝑜𝑠𝛼 =𝜎′𝑐𝑜𝑠𝛼 → 𝜎′= 𝑃𝑒𝑐𝑜𝑠𝛼 = 𝑃𝑒𝑛
Mật độ điện tích liên kết mặt 𝜎′ trên mặt giới hạn
của khối điện môi có trị số bằng hình chiếu của vecto
phân cực điện môi lên pháp tuyến mặt đó.
Bài tập áp dụng: Hai mặt phẳng song song vô hạn tích điện đều, trái dấu,
có mật độ điện mặt bằng nhau, đặt cách nhau 𝑑 = 2𝑚𝑚. Người ta lấp đầy
khoảng không gian giữa hai mặt phẳng bởi một chất điện môi có hằng số
điện môi 𝜀 = 5. Hiệu điện thế giữa hai mặt phẳng 𝑈 = 100𝑉. Xác định mật
độ điện tích liên kết trên bề mặt của chất điện môi. Trả lời:
+) Mật độ điện tích liên kết trên bề mặt chất điện môi:
𝜎′= 𝑃𝑒𝑛 → 𝜎′= 𝐷𝑛− 𝜀0𝐸𝑛 vì 𝐸𝑛= 𝐸 ; 𝐷𝑛= 𝐷 → 𝜎′= 𝐷 − 𝜀0𝐸
Phương Văn Huy – TĐH 03/K66
+) Thay 𝐷 = 𝜀0𝜀𝐸 ; 𝐸 = 𝑈𝑑→ 𝜎′=𝜀0(𝜀−1)𝑈𝑑
+) Thay số: 𝜎′= 𝜀0(𝜀 − 1)𝑈 𝑑= 8,86.10−12(5 − 1).100 2.10−3 = 1,77.10−6(𝐶 𝑚2)
11. - Trình bày năng lượng tương tác của hệ điện tích điểm, năng lượng của
vật dẫn mang điện và năng lượng của tụ điện. Trả lời:
• Năng lượng tương tác của hệ điện tích điểm:
- Xét điện điện tích 𝑞2 đặt trong điện trường của điện tích điểm 4𝜋𝜀0𝜀𝑞1𝑞2
𝑞1 và cách 𝑞1 một khoảng là 𝑟12 → thế năng: 𝑊12 =1 𝑟12 (1)
- Xét điện tích 𝑞1 đặt trong điện trường của điện tích điểm 𝑞2 và cách 𝑞2 một 4𝜋𝜀0𝜀𝑞1𝑞2
khoảng là 𝑟21 → thế năng: 𝑊21 =1 𝑟21 (2)
- Ta có: 𝑟12 = 𝑟21 = 𝑟
- Từ (1) và (2) suy ra: 𝑊12 = 𝑊21 = 𝑊 = 1 2𝑞1(𝑞24𝜋𝜀0𝜀𝑟)+1 2𝑞2(𝑞14𝜋𝜀0𝜀𝑟) =12(𝑞1𝑉1+ 𝑞2𝑉2)
{𝑉1 𝑙à đ𝑖ệ𝑛 𝑡ℎế 𝑑𝑜 đ𝑖ệ𝑛 𝑡í𝑐ℎ 𝑞1 𝑔â𝑦 𝑟𝑎 𝑡ạ𝑖 𝑞2
𝑉2 𝑙à đ𝑖ệ𝑛 𝑡ℎế 𝑑𝑜 đ𝑖ệ𝑛 𝑡í𝑐ℎ 𝑞2𝑔â𝑦 𝑟𝑎 𝑡ạ𝑖 𝑞1
- Suy ra: Năng lượng tương tác giữa hai điện tích điểm 𝑊 = 12(𝑞1𝑉1+ 𝑞2𝑉2)
+) Năng lượng tương tác của hệ 𝑛 điện tích điểm 𝑞1, 𝑞2, … , 𝑞𝑛: 𝑛
𝑊 = 12(𝑞1𝑉1+ 𝑞2𝑉2+ ⋯ + 𝑞𝑛𝑉𝑛) = 1 2∑𝑞𝑖𝑉𝑖 𝑖=1
• Năng lượng của một vật dẫn mang điện:
+) Chia vật dẫn thành từng phần tử tích điện 𝑑𝑞 → 𝑊 = 12∫ 𝑉𝑑𝑞 (𝑡𝑜à𝑛 𝑣ậ𝑡)
+) Vì là vật dẫn cân bằng tĩnh điện nên: 𝑉 = 𝑐𝑜𝑛𝑠𝑡
→ 𝑊 = 1 (𝑡𝑜à𝑛 𝑣ậ𝑡)=1 (𝑡𝑜à𝑛 𝑣ậ𝑡)=1
2𝑉𝑄 =1 2𝐶𝑉2=1 2𝑄2 2∫𝑉𝑑𝑞 2𝑉∫𝑑𝑞 𝐶
• Năng lượng của tụ điện:
Phương Văn Huy – TĐH 03/K66
- Hệ vật dẫn tích điện cân bằng:
+) Điện tích: 𝑄1, 𝑄2, … , 𝑄𝑛
+) Điện thế tương ứng: 𝑉1, 𝑉2, … , 𝑉𝑛 ⟹ 𝑊 = 𝑛 12∑𝑄𝑖𝑉𝑖 𝑖=1
- Hệ hai vật dẫn tạo thành tụ điện ⟹ 𝑊 = 12(𝑄1𝑉1+ 𝑄2𝑉2)
- Tính chất của tụ điện: 𝑄1= −𝑄2= 𝑄 (điện hưởng toàn phần)
⟹ 𝑊 = 12𝑄(𝑉1− 𝑉2)=1 2𝑄𝑈 ⟹ 𝑊 = 12𝑄2 𝐶=1 2𝐶𝑈2 Bài tập áp dụng:
+) Ta có: 𝐹 = 𝑞𝐸 = 𝑞 𝑈𝑑→ 𝑑 = 𝑞𝑈𝐹
+) Điện dung tụ phẳng: 𝐶 = 𝜀0𝜀𝑆
𝑑→ 𝜀 = 𝐶𝑑𝜀0𝑆 +) Ta có: 𝑄 = 𝐶. 𝑈
12. Tính năng lượng của tụ điện phẳng tích điện từ đó suy ra công thức mật
độ năng lượng điện trường và năng lượng của một điện trường bất kỳ. Trả lời:
- Hệ vật dẫn tích điện cân bằng:
+) Điện tích: 𝑄1, 𝑄2, … , 𝑄𝑛
+) Điện thế tương ứng: 𝑉1, 𝑉2, … , 𝑉𝑛 ⟹ 𝑊 = 𝑛 12∑𝑄𝑖𝑉𝑖 𝑖=1
- Hệ hai vật dẫn tạo thành tụ điện ⟹ 𝑊 = 12(𝑄1𝑉1+ 𝑄2𝑉2)
- Tính chất của tụ điện: 𝑄1= −𝑄2= 𝑄 (điện hưởng toàn phần)
Năng lượng điện trường của tụ điện:
⟹ 𝑊 = 12𝑄(𝑉1− 𝑉2)=1 2𝑄𝑈 ⟹ 𝑊 = 12𝑄2 𝐶=1 2𝐶𝑈2
Phương Văn Huy – TĐH 03/K66
- Xét một tụ điện phẳng, điện dung 𝐶: 𝐶 = 𝜀0𝜀𝑆 𝑑
- Xét năng lượng điện trường tồn tại ở trong lòng một tụ điện phẳng:
𝑊 = 12𝐶𝑈2=1 2(𝜀0𝜀𝑆 𝑑)𝑈2=1
2𝜀0𝜀𝑆𝑑 (𝑈𝑑)2
- Tụ điện phẳng: 𝐸 = 𝑈𝑑 ; ∆𝑉 = 𝑆. 𝑑
→ 𝑊 = 12𝜀0𝜀∆𝑉𝐸2→𝑊∆𝑉 =12𝜀0𝜀𝐸2
⟹ Mật độ năng lượng điện trường:
𝜔𝑒=𝑊∆𝑉 =12𝜀0𝜀𝐸2=1 2𝐸𝐷 → 𝜔 = 12𝐸 𝐷
- Năng lượng điện trường của một điện trường bất kỳ:
𝑊 = ∫ 𝜔𝑒𝑑𝑉 = ∫ 1
2𝜀0𝜀𝐸2𝑑𝑉 = ∫ 1 2𝐸 𝐷 𝑑𝑉 Bài tập áp dụng:
Áp dụng định lý O-G ta có 𝜀0𝜀∮𝐸 𝑑𝑠 = ∑𝑞𝑖
+) Ta có: ∑𝑞𝑖= 𝑄 (𝑟 𝑅)3
Suy ra: 𝜀0𝜀. 𝐸. 4𝜋. 𝑟2= 𝑄. 𝑟3𝑅→ 𝐸 = 𝑸𝒓𝟒𝝅𝜺𝟎𝜺𝑹𝟑
+) Năng lượng điện trường bên trong quả cầu là: 𝑊 = ∫ 𝜔 𝑅 𝑅 𝑒𝑑𝑉 =1 0=1 0(𝑄𝑟 2∫ 4 𝜀
𝜋𝜀0𝜀𝑅3)24𝜋𝑟2𝑑𝑟 0𝜀𝐸2𝑑𝑉 2∫ 𝜀0𝜀 = ∫ 𝑄2 𝑅 𝑟4
8𝜋𝜀0𝜀𝑅6𝑑𝑟 =𝑄2 0 40𝜋𝜀0𝜀𝑅
13. - Thiết lập công thức định luật Ohm dạng vi phân
- Trình bày khái niệm nguồn điện và thiết lập công thức suất điện động của nguồn điện. Trả lời:
- Định luật Ohm dạng vi phân:
Phương Văn Huy – TĐH 03/K66
+) Xét đoạn dây dẫn có độ dài 𝑑𝑙 , diện tích 𝑑𝑆, điện
trở 𝑅 có điện thế ở hai đầu là 𝑉 và 𝑉 + 𝑑𝑉
+) Ta có: 𝑑𝐼 =𝑉−(𝑉+𝑑𝑉 𝑅 ) = − 𝑑𝑉 𝑅
+) 𝑅 = 𝜌 𝑑𝑑𝑙𝑆𝑛→𝑑𝐼 = − 𝑑𝑉 𝑑𝑆𝑛→𝑑𝐼 =1 𝜌(−𝑑𝑉𝑑𝑙 )𝑑𝑆𝑛 𝑉 𝑉 + 𝑑𝑉 𝜌𝑑𝑙 →𝑑𝐼
𝑑𝑆𝑛=1 𝜌𝐸 → j = 1𝜌𝐸
+) Đặt 𝜎 = 1𝜌 : Điện dẫn suất → j = 𝜎𝐸 → 𝐣 = 𝝈𝑬
- Nguồn điện: là nguồn tạo ra trường lạ. Trường lạ tạo ra lực lạ, lực này có
khả năng đưa các điện tích (+) chuyển động để tạo thành dòng điện. (đưa
điện tích (+) từ nơi có điện thế thấp đến nơi có điện thế cao, ngược chiều
điện trường thông thường).
- Công làm dịch chuyển điện tích trong mạch điện: 𝐴 = ∮𝑞(𝐸 + 𝐸 ∗)𝑑𝑙 (𝐶) +) 𝐸
– là vecto cường độ điện trường tĩnh +) 𝐸
∗- là vecto cường độ điện trường lạ 𝜉 = 𝐴𝑞=∮(𝐸( 𝐶)=∮ + 𝐸 𝐸 ∗)𝑑𝑙 ( ∗𝑑𝑙 𝐶) (Do ∮𝐸 ( 𝑑𝑙 𝐶)= 0)
→ 𝜉 = ∮ 𝐸 𝑙𝑑𝑙 (𝐶)
Kết luận: Suất điện động của nguồn điện có giá trị bằng công của lực lạ
trong sự dịch chuyển một đơn vị điện tích dương một vòng quanh mạch kín
của nguồn đó (còn gọi là lưu số của trường lạ)
Bài tập áp dụng: Một thanh dây dẫn dài 𝑙 có thể trượt trên hai cạnh của một
khung dây chữ 𝑈 với vận tốc 𝑣 vuông góc với vecto cảm ứng từ 𝐵 . Cho
𝐵 = 430 𝑚𝑇, 𝑙 = 150 𝑚𝑚 và 𝑣 = 2 𝑚/𝑠, hệ đặt trong không khí. Xác đinh:
+) Suất điện động cảm ứng xuất hiện trong mạch:
+) Độ lớn và chiều dòng điện cảm ứng trong mạch, biết 𝑅 = 45Ω và
giả sử điện trở của thanh trượt và khung không đáng kể. Trả lời:
- Suất điện động cảm ứng xuất hiện trong mạch: 𝐵 𝑅 𝑙 |𝐸 ⨂ 𝑣
𝐶|=|−𝑑𝜙𝑚 𝑑𝑡 |=|−𝐵𝑙𝑑𝑥𝑑𝑡 |= 𝐵𝑙𝑣
Phương Văn Huy – TĐH 03/K66
→|𝐸𝑐|= 0,43.0,15.2 = 0,129 (𝑉) - Dòng điện cảm ứng: 𝐼𝑐=𝐸𝑐𝑅=0,129 45 = 2,9.10−3 (𝐴)
- Từ thông qua khung dây chữ U tang lên khi thanh l chuyển động sang phải
Theo định luật Len-xơ từ trường của dòng cảm ứng sinh ra chống lại sự tăng
của từ thông nên từ trường hướng ra ngoài:
+) Chiều dòng điện cảm ứng: Ngược chiều kim đồng hồ.
14. - Phát biểu và viết biểu thức định luất Biot-Savart-Laplace, minh họa bằng hình ảnh.
- Áp dụng định luật cảm ứng điện từ gây ra bởi một đoạn dòng điện thẳng
tại điểm M, cách dòng điện một khoảng 𝒓; từ đó suy ra biểu thức cho
trường hợp dòng điện thẳng dài vô hạn. Trả lời:
- Định luật Biot-Savart-Laplace:
Vecto từ cảm 𝑑𝐵 do một phần tử dòng điện 𝐼𝑑𝑙 gây ra tại điểm 𝑀, cách
phần tử đó một đoạn 𝑟 là một vecto có: +) Gốc tại điểm 𝑀
+) Phương vuông góc với mặt phẳng chứa phần tử
dòng điện 𝐼𝑑𝑙 và điểm 𝑀
+) Chiều sao cho ba vecto 𝑑𝑙 , 𝑟 , 𝑑𝐵 theo thứ tự
này hợp thành một tam diện thuận.
+) Độ lớn của cảm ứng từ 𝑑𝐵 được xác định bởi
biểu thức: 𝑑𝐵 =𝜇0𝜇
4𝜋 𝐼𝑑𝑙𝑠𝑖𝑛𝜃 𝑟2
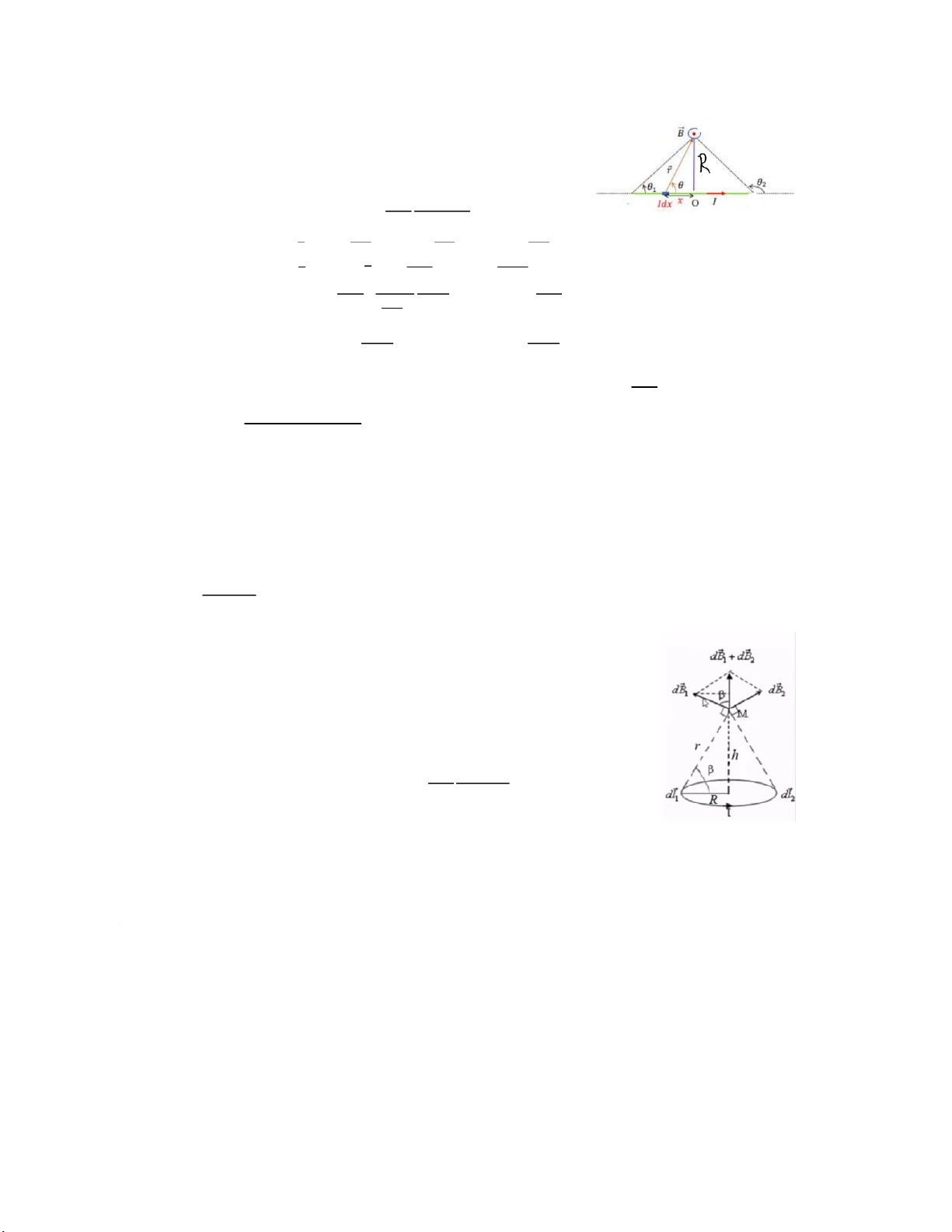
Phương Văn Huy – TĐH 03/K66 - Ứng dụng: 𝑀
+) Xét phần tử dòng điện 𝐼𝑑𝑥 cách điểm O một khoảng 𝑥
+) Phần tử dòng điện này gây ra tại điểm M một
cảm ứng từ 𝑑𝐵 có độ lớn: 𝑑𝐵 =𝜇0𝜇
4𝜋 𝐼𝑑𝑥𝑠𝑖𝑛𝜃 𝑟2
{𝑠𝑖𝑛𝜃 = 𝑅𝑥⟹ {𝑟 = 𝑅 𝑅⟹ { 𝑟 = 𝑅
sin2𝜃𝑑𝜃 =𝑑𝑥 ⟹ { 𝑟 = 𝑅 𝑟 𝑠𝑖𝑛𝜃 𝑠𝑖𝑛𝜃 𝑠𝑖𝑛𝜃 𝑡𝑎𝑛𝜃 = 𝑅 𝑐𝑜𝑡𝜃 = 𝑥 −𝑅 𝑹
𝐬𝐢𝐧𝟐𝜽 = |𝒅𝒙| Suy ra: 𝑠𝑖𝑛𝜃)2𝑅 𝑑𝐵 =𝜇0𝜇𝐼 4𝜋 . 𝑠𝑖𝑛𝜃
sin2𝜃𝑑𝜃 →𝑑𝐵 =𝜇0𝜇𝐼4𝜋𝑅 𝑠𝑖𝑛𝜃𝑑𝜃 (𝑅 → 𝐵 = 𝜇 𝜃2
0𝜇𝐼 𝜃1→ 𝐵 = 𝜇0𝜇𝐼
4𝜋𝑅 ∫ 𝑠𝑖𝑛𝜃𝑑𝜃
4𝜋𝑅 (𝑐𝑜𝑠𝜃1− 𝑐𝑜𝑠𝜃2)
- Trường hợp dòng điện thẳng dài vô hạn: {𝜃1= 0
𝜃2= 𝜋 → 𝐵 = 𝜇0𝜇𝐼 2𝜋𝑅 Bài tập áp dụng:
15. Xác định cảm ứng từ gây ra bởi dòng điện tròn có cường độ 𝑰, bán kính
𝑹, tại điểm 𝑴 nằm trên trục của dòng điện, cách tâm O của dòng điện một
khoảng 𝒉. Từ kết quả trên xét hai trường hợp giới hạn
+) 𝑴 trùng với tâm 𝑶 của dòng điện (𝒉 = 𝟎)
+) 𝑴 ở rất xa dòng điện (𝒉 ≫ 𝑹). Trả lời: - Dòng điện tròn:
+) Do tính chất đối xứng của dòng điện tròn các vecto cảm
ứng từ do hai phần tử 𝐼𝑑𝑙1 và 𝐼𝑑𝑙2 gây ra tại M đối xứng
nhau qua trục của dòng điện, cảm ứng từ do dòng điện dây
ra có phương trùng với trục của vòng dây.
𝐵 = ∫ 𝑑𝐵 → 𝐵 = ∫ 𝑑 𝑐 𝐵
ả 𝑑ò𝑛𝑔 đ𝑖ệ𝑛 𝑐𝑜𝑠𝛽 = ∫ 𝜇0𝜇
4𝜋 𝐼𝑑𝑙𝑠𝑖𝑛𝜃 𝑟2𝑐𝑜𝑠𝛽
𝑐ả 𝑑ò𝑛𝑔 đ𝑖ệ𝑛
Phương Văn Huy – TĐH 03/K66
+) Trong đó: {𝑐𝑜𝑠𝛽 = 𝑅 𝑟
𝑟 = √𝑅2+ ℎ2 và 𝑠𝑖𝑛𝜃 = 1 2𝜋𝑅 Suy ra: 4𝜋 𝐼𝑑𝑙 𝑟2𝑅 4𝜋 𝐼𝑑𝑙𝑅 4𝜋 𝐼𝑑𝑙𝑅
𝐵 = ∫𝜇0𝑐𝜇ả 𝑑ò𝑛𝑔 đ𝑖ệ𝑛
𝑟 =∫𝜇0𝜇𝑐ả 𝑑ò𝑛𝑔 đ𝑖ệ𝑛 =∫ ( 𝜇0𝜇 2 𝑟2+ℎ2)3 0 ( 2 𝑟2+ℎ2)3 → 𝐵 = 𝜇0 4 𝜇 𝜋 𝐼𝑅. 2𝜋𝑅 2=𝜇0𝜇2𝜋 𝐼𝜋𝑅2 2→ 𝐵 = 𝜇0𝜇𝐼𝑅2 (𝑅2+ ℎ2)3 (𝑅2+ ℎ2)3 2(𝑅2+ ℎ2)3 2 =𝝁𝟎𝝁 𝟐𝝅 𝑰𝑺 𝑩 (𝑹𝟐+ 𝒉𝟐)𝟑 𝟐
+) Trường hợp đặc biệt
Nếu 𝑀 ≡ 𝑂 → ℎ = 0 → 𝐵0=𝜇0𝜇𝐼2𝑅
Nếu 𝑀 rất xa vòng dây (ℎ ≫ 𝑅)→ 𝐵 = 𝜇0𝜇𝑅2 2ℎ3
Bài tập áp dụng: Một dây dẫn được uống như hình vẽ, gồm hai cung tròn đồng
tâm có bán kính lần lượt là 𝑎 = 20 𝑚𝑚, 𝑏 = 40 𝑚𝑚 và hai đoạn bán kính vuông
góc với nhau, đặt trong không khí. Dòng điện trong khung có cường độ 𝐼 = 16 𝐴.
Xác định vecto cảm ứng từ do dòng điện gây ra tại tâm O.
- Cảm ứng từ tại O: 𝐵 = 𝐵1 + 𝐵2 + 𝐵3 + 𝐵4 Ta có: 𝐵1= 𝐵3= 0
𝐵2=𝜇0𝐼2𝑏 Thay số: 𝐵1= 6,25.10−5 𝑇
𝐵4=𝜇0𝐼2𝑎 Thay số: 𝐵2=12,56.10−5 𝑇
→ 𝐵 = 𝐵2− 𝐵1= 6,25.10−5 𝑇
- Phương chiều của B: 𝐵 có Phương vuông góc với mặt
phẳng chứa dây dẫn chiều hướng ra ngoài.
16. - Phát biểu viết biểu thức và nêu ý nghĩa của định lý Ampe về lưu số của
vecto cường độ từ trường.
- Áp dụng định lý tìm cảm ứng từ trong lòng cuộn dây điện hình xuyến từ
đó suy ra trường hợp ống dây điện thẳng dài vô hạn. Trả lời:
Phương Văn Huy – TĐH 03/K66
- Phát biểu: Lưu số của vecto cường độ từ trường dọc theo đường cong kín
bất kỳ bằng tổng đại số các dòng điện xuyên qua diện tích giới hạn bởi đường cong đó. - Biểu thức: ∮ ∮ (𝐶) 𝐻 d ạ 𝑑 ng𝑙 = v ∑ i 𝐼𝑖 𝑛 ph 𝑖= â 1n 𝑟𝑜𝑡(𝐻 )= j -) Chú ý:
+) 𝐼𝑖 sẽ mang chiều (+) nếu dòng điện thứ 𝑖 nhận chiều dịch chuyển
trên đường cong (C) làm chiều quay thuận xung quanh nó
+) 𝐼𝑖 sẽ mang dấu (-) nếu dòng điện thứ 𝑖 nhận chiều dịch chuyển trên
đường cong (C) làm chiều quay nghich xung quanh nó.
- Ý nghĩa: Định lý Ampe cho thấy sự khác biệt cơ bản giữa từ trường và
điện trường. Đối với điện trường ∮(∮ 𝐶) 𝐸 = 0 𝑑 c 𝑙
hứng có điện trường là
một trường thế, còn với từ trường thì ∮( ∮ 𝐶) 𝐻 ch ứ 𝑑 n 𝑙 g≠ t 0 ỏ từ trường
không phải là một trường thế mà mà trường xoáy. - Áp dụng:
+) Xét cuộn dây hình xuyến gồm 𝑁 vòng, có dòng điện 𝐼
chạy qua. 𝑅1 và 𝑅2 là bán kính trong và ngoài của cuộn dây
Chọn đường cong C là đường tròn tâm O bán kính R Theo định lý Ampe ta có: ∮( 𝐻 𝐶) = 𝑑𝑙 𝑁𝐼
Cường độ từ trường 𝐻 tại mọi điểm trên đường cong (C) có giá trị như nhau. → ∮(𝐻 𝐶) = 𝑑𝑙
∮𝐻. 𝑑𝑙 (𝐶)= 𝐻 ∮𝑑𝑙
(𝐶)= 𝐻. 2𝜋𝑅 =𝑁𝐼 → 𝐻 = 𝑁𝐼
2𝜋𝑅 =𝑁𝐼𝐿 → 𝐵 = 𝜇0𝜇2𝑁𝐼
𝜋𝑅 với 𝑁 là số vòng dây.
+) Xét ống dây thẳng dài vô hạn: Ống dây thẳng dài vô hạn coi như một
cuộn dây hình xuyến có các bán kính vô cùng lớn (𝑅 → ∞).
→ Cường độ từ trường của ống dây thẳng dài vô hạn: 𝐻 = 𝑁𝐼
𝐿= 𝑛0𝐼 → 𝐵 = 𝜇0𝜇𝑛0𝐼
𝑛0 là số vòng dây trên một đơn vị độ dài của ống dây.
Bài tập áp dụng: Một ống dây hình trụ rỗng có dòng điện 𝐼 = 20 (𝐴) chạy dọc
theo ống dây và phân bố đều trên tiết diện của ống. Coi ống dài vô hạn, cho 𝑎 =
Tài liệu liên quan:
-
Bài tập Vật lý nguyên tử môn Vật lý đại cương 2 | Học viện Công Nghệ Bưu Chính Viễn Thông
11 6 -
Bài tập Vật lý nguyên tử môn Vật lý đại cương 2 | Học viện Công Nghệ Bưu Chính Viễn Thông
12 6 -
Tán xạ ánh sáng và Hiệu ứng Tyndall - Lý thuyết và Ứng dụng môn Vật lý đại cương 2 | Học viện Công Nghệ Bưu Chính Viễn Thông
19 10 -
Chương 23: Quang học lượng tử môn Vật lý đại cương 2 | Học viện Công Nghệ Bưu Chính Viễn Thông
17 9 -
Chương 24: Cơ Học Lượng Tử - Tính Sóng-Hạt và Phương Trình Schrödinger môn Vật lý đại cương 2 | Học viện Công Nghệ Bưu Chính Viễn Thông
18 9