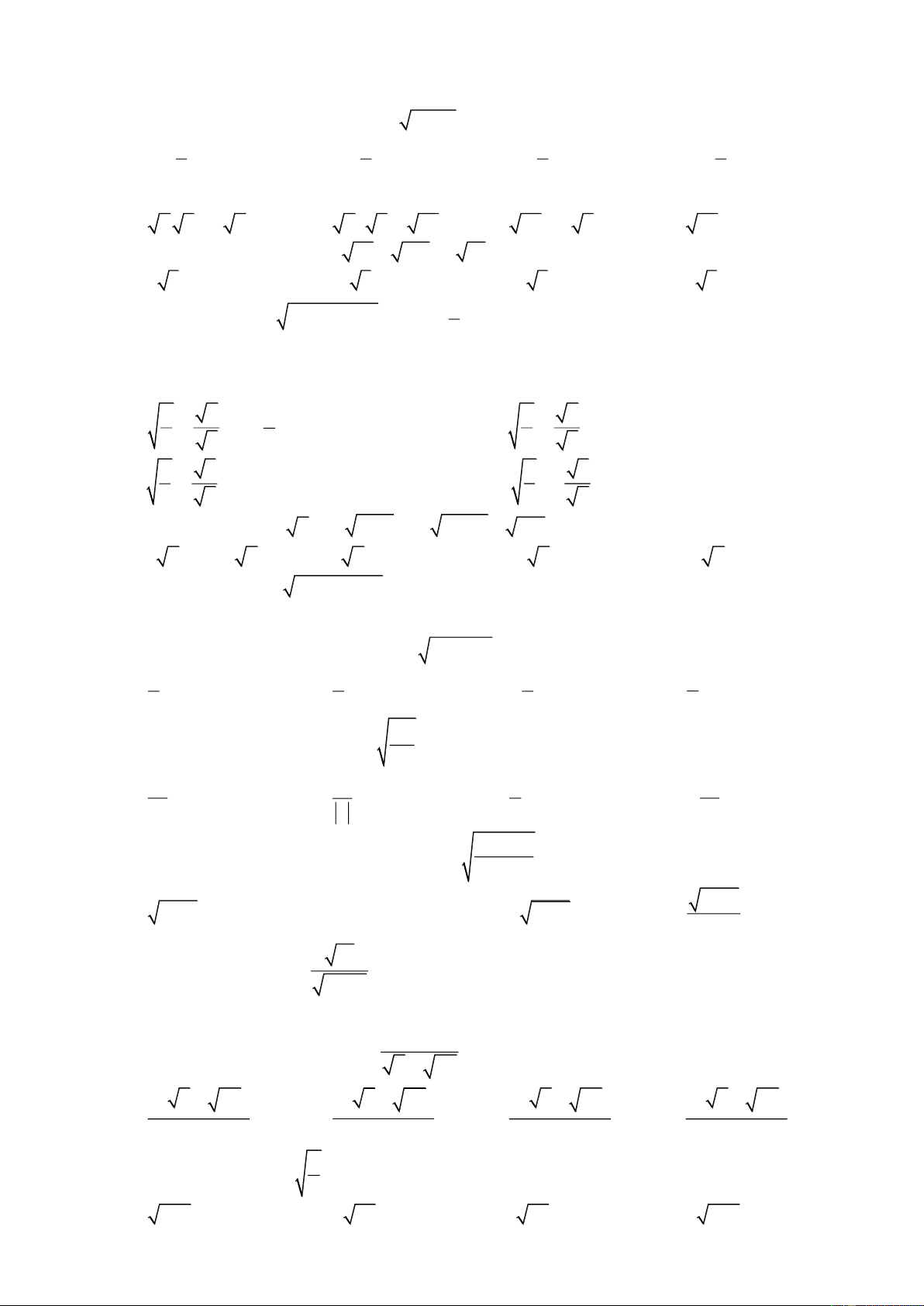

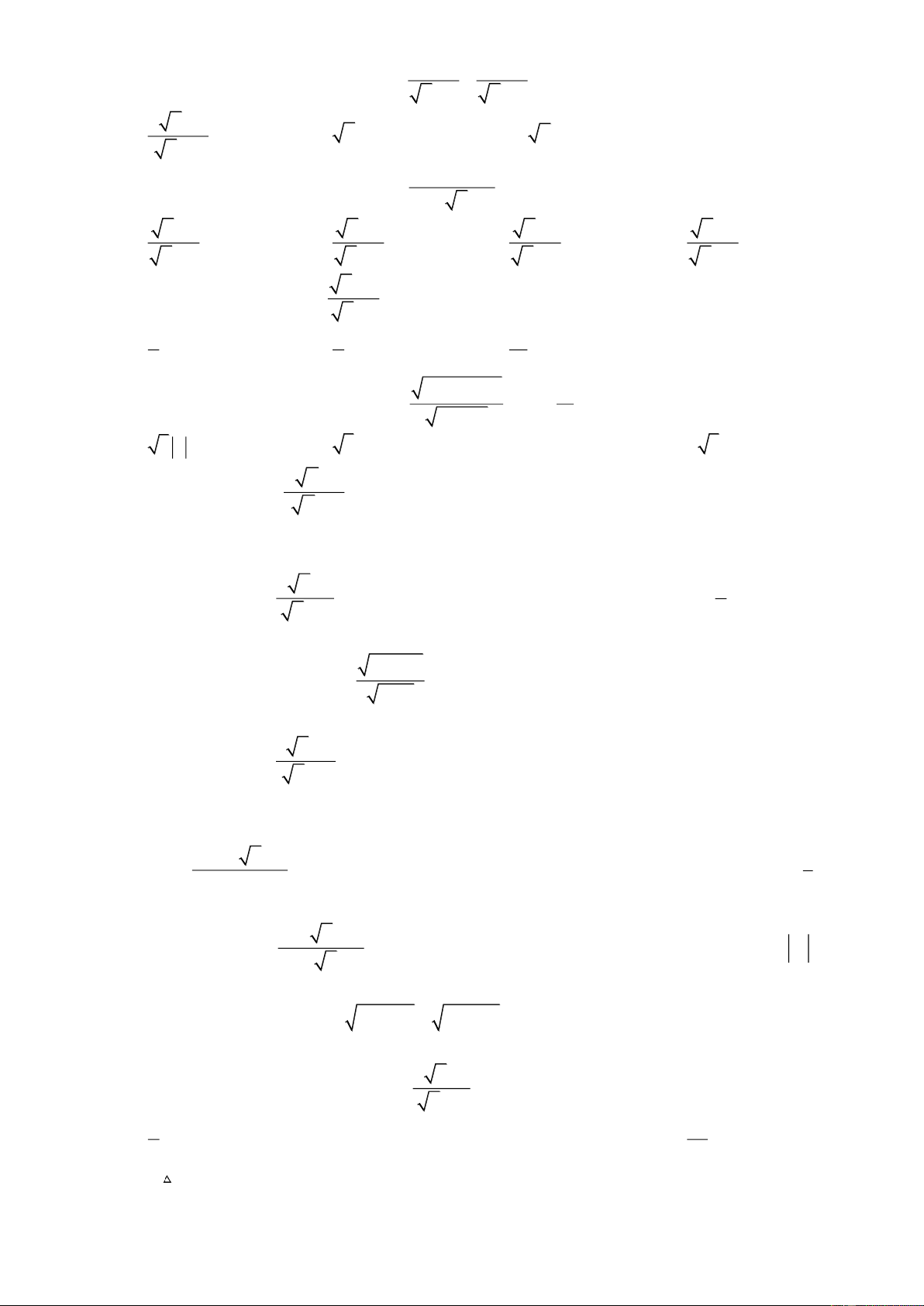

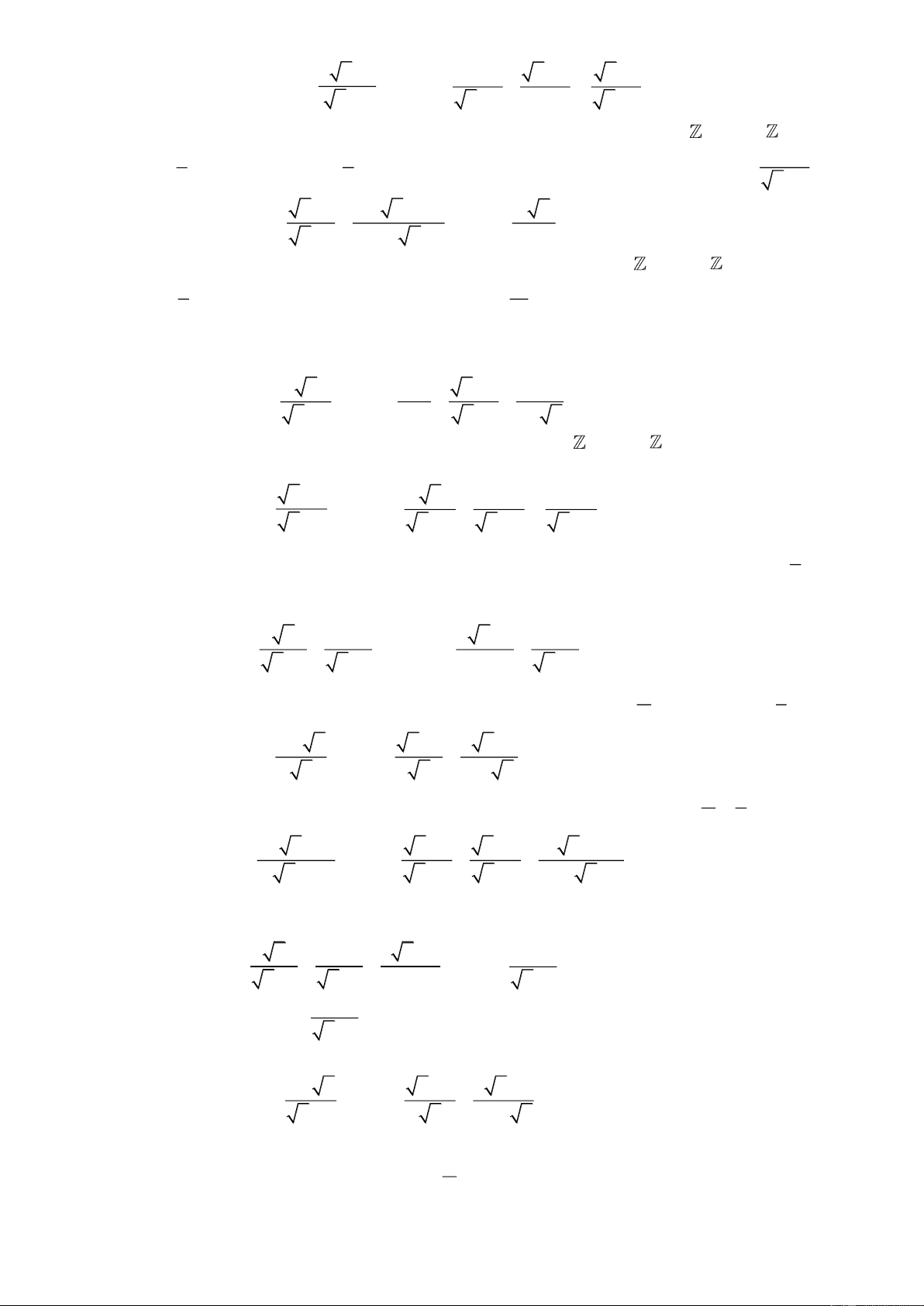








Preview text:
Khi ta cố gắng, vận may sẽ bên ta
Đề cương giữa kỳ 1 toán 9 năm 2023- 2024
ĐỀ CƯƠNG GIỮA HỌC KÌ 1 TOÁN 9 NĂM HỌC 2023 -2024
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN Câu 1:
Điều kiện xác định của biểu thức 2x − 3 là 3 3 3 2 A. x = . B. x . C. x . D. x . 2 2 2 3 Câu 2:
Cho a,b là hai số không âm. Trong các khẳng định sau, khẳng định đúng là:
A. a b = b a .
B. a b = ab .
C. ab = a b .
D. ab = ab . Câu 3:
Kết quả của phép tính A = 48 − 108 + 3 12 là: A. 4 3 . B. 12 3 . C. 16 3 . D. 8 3 . 1 Câu 4: Rút gọn biểu thức 4 2
a (2a −1) với a ta được 2 A. (1− 2a)a . B. ( a − ) 2 2 1 a .
C. a (2a − ) 1 . D. ( − ) 2 1 2a a . Câu 5:
Trong các khẳng định sau đây, khẳng định đúng là: a a a a a A. = với 0 . B. =
với a 0;b 0 . b b b b b a a a a C. = với a, b R . D. b = với a 0; b 0 . b b b Câu 6: Rút gọn biểu thức 3 2
7 a + 6b 25a + 5a 36ab − 16a với a 0,b 0 ta được kết quả là:
A. 3 a + 60ab a . B. 3 a . C. 23 a . D. 11 a . Câu 7: Cho phương trình: 2
4x − 4x +1 = 1 . Khi đó tập nghiệm của phương trình là: A. 1 . B. 0 . C. 0 ;1 . D. 1 . Câu 8:
Tổng các nghiệm của phương trình 2
(3x −1) = x + 2 là: 2 3 1 5 A. . B. . C. − . D. . 3 2 4 4 4 a Câu 9:
Kết quả thu gọn của biểu thức với b 0 là: 2 b 2 a 2 a a 2 a A. . B. . C. . D. − . b b b b x + y
Câu 10: Kết quả thu gọn của biểu thức Q = ( x − y)
( y x 0) là: 2 (x − y) x + y
A. x + y .
B. x + y .
C. − x + y . D. . y − x 5 6
Câu 11: Kết quả của phép tính là: 3 5 2 3 A. 2. B. 4. C. 5 2 . D. 6. 6
Câu 12: Trục căn thức ở mẫu biểu thức
với x 0; y 0 được kết quả là: x + 2 y 6 ( x + 2y ) 6 ( x + 2y ) 6 ( x − 2y ) 6 ( x − 2y ) A. . B. . C. . D. . x + 2 y x − 2 y x − 4 y x − 2 y b
Câu 13: Rút gọn biểu thức a.
(a 0) được kết quả là: a A. −ab . B. − ab . C. ab . D. − −ab .
Câu 14: Trong các khẳng định sau đây, khẳng định đúng là:
Th S: NGUYỄN DUY NINH 1 SĐT: 0961 697 696
Khi ta cố gắng, vận may sẽ bên ta
Đề cương giữa kỳ 1 toán 9 năm 2023- 2024 a a a a a A. = với a, b R . B. = với 0 . b b b b b a a a a C. =
với a 0;b 0 . D. =
với a 0;b 0 . b b b b
Câu 15: Tổng các nghiệm của phương trình 2
(3x −1) = x + 2 là: 1 3 5 2 A. − . B. . C. . D. . 4 2 4 3
Câu 16: Kết quả rút gọn của 2 2( 5 − 6) là: A. 2 3 − 10 . B. 3 2 − 10 . C. 2 5 − 2 6 . D. 4 6 − 4 5 .
Câu 17: Tổng các nghiệm của phương trình ( x + 2)(2 x − 3) = 0 là 1 3 1 9 A. . B. . C. − . D. . 4 2 2 4
Câu 18: Cho A = a − 2 a −1 . Với 1 a 2, ta có thể khẳng định A bằng
A. a −1 −1 .
B. 1− a −1 . C. a −1 +1. D. a +1 −1.
Câu 19: Điều kiện xác định của 2
x + 2x − 3 là:
A. x 1 hoặc x 3 − . B. x 3 − . C. 3 − x 1. D. x 1.
Câu 20: Tronq các khẳng đinh sau, khẳng đinh sai là: A. 4 2 a = a . B. 2
a − 2a +1 = a −1 . C. (a − )
1 (a − 2) = a −1 a − 2 . D. 2 a ( 2 b + ) 2
1 = a b +1 .
Câu 21: Cho phương trình 2
4x − 3 − x = x − 3 . Tổng các nghiệm của phương trình là: A. 3 − . B. 5. C. 2. D. 3. 1
Câu 22: Cho phương trình x +1 −
16x +16 = −1. Khi đó tập nghiệm của phương trình là 3 A. 3 . B. 8 . C. 2 . D. .
Câu 23: Cho phương trình 2
x − 4x + 4 = 2x −1 . Nếu gọi a là nghiệm của phương trình thì giá trị
biểu thức P = a + 2 a là: A. 2. B. 3. C. −1. D. 1.
Câu 24: Rút gọn biểu thức 3 2
7 a + 6b 25a + 5a 36ab − 16a với a 0,b 0 , ta được kết quả là: A. 3 a .
B. 3 a + 60ab a . C. 23 a . D. 11 a . 9
Câu 25: Khử mẫu của biểu thức 2 2 − x y −
x 0; y 0 được kết quả là: 3 2 ( ) x y A. 6 − x . B. 6 −x . C. 6 − −X . D. 6 x .
Câu 26: Nghiệm của phương trình 2 2
(x + 2) − (x − 3) = 1 với 2
− x 3 là: A. x = 0 . B. x = 1 − . C. x =1. D. Vô nghiệm.
Câu 27: Tổng các nghiệm của phương trình 2x + x − 6 = 0 là 1 3 1 9 A. . B. . C. − . D. . 4 2 2 4 x − 3 x − 2
Câu 28: Kết quả thu gọn của biểu thức K = −
( x 0; x 3) là x − 9 x + 3 x − 3 x − 3 A. 1. B. − . C. −1. D. . x + 3 x + 3
Th S: NGUYỄN DUY NINH 2 SĐT: 0961 697 696
Khi ta cố gắng, vận may sẽ bên ta
Đề cương giữa kỳ 1 toán 9 năm 2023- 2024 2x 8
Câu 29: Kết quả thu gọn của biểu thức A = −
(x 0;x 4) x − 2 x − 2 2 x − 4 A. . B. x − 2 . C. 2 ( x + 2). D. 4. x − 2 x −1
Câu 30: Kết quả thu gọn của biểu thức Q = (x 0) là x + 3 x + 2 x +1 x +1 x −1 x −1 A. . B. . C. . D. . x + 2 x − 2 x + 2 x − 2 x + 2
Câu 31: Giá trị của biểu thức P =
tại x = 4 là x +1 6 4 16 A. . B. . C. . D. 2. 5 3 15 3 2 9x + 33x 11
Câu 32: Kết quả thu gọn của biểu thức K = x − là: 3x +11 3 A. 3 x . B. 3x . C. 2 3x . D. − 3x . 2 x − 3
Câu 33: Cho biểu thức P =
với x 0 . Tập hợp các giá trị của x nguyên để P có giá trị x +1
nguyên có số phần tử là: A. 0. B. 3. C. 4. D. 2. 2 x +1 3
Câu 34: Cho biểu thức A =
với x 0 . Số các giá trị nguyên của x để A là: x + 2 2 A. 15. B. 16. C. 4. D. 3. 2 x − 5x
Câu 35: Với x 5, cho biểu thức A =
và B = x . Số giá trị của x để A = B là: x − 5 A. 2. B. 1. C. 0. D. 3. 3 x − 2
Câu 36: Cho biểu thức P =
với x 0; x 4 . Gọi a là giá trị nguyên của x để P đạt giá trị nhó x − 2
nhất. Khi đó giá trị của biểu thức 2
Q = a + 2 là: A. 27. B. 2. C. 11. D. 3. 2x − 5 x + 3 1 Câu 37: Cho P = (x 0;x )
1 Tổng các giá trị nguyên x thỏa mãn điều kiện P là: x −1 3 A. 10. B. 9. C. 7. D. 8. x − x − 2
Câu 38: Cho biểu thức K =
(x 0;x 4; x 9). Các giá trị x thỏa mãn điều kiện K = K là: x − 5 x + 6 A. x .
B. 0 x 9 và x 4 . C. 0 x 4. D. x 9 .
Câu 39: Nghiệm của phương trình 2 2
(x + 2) − (x − 3) = 1 với 2
− x 3 là: A. x =1. B. x = 1 − . C. x = 0 . D. Vô nghiệm. 2 x −1
Câu 40: Tổng tất cả các giá trị của x để A =
nhận giá trị nguyên bằng: x + 2 5 37 A. . B. 9. C. 13. D. . 4 4
Câu 41: Cho ABC vuông tại A , đường cao AH = 4 cm, BH = 2 cm . Khi đó độ dài BC là A. 4 cm . B. 6 cm . C. 10 cm . D. 8 cm .
Th S: NGUYỄN DUY NINH 3 SĐT: 0961 697 696
Khi ta cố gắng, vận may sẽ bên ta
Đề cương giữa kỳ 1 toán 9 năm 2023- 2024 1
Câu 42: Cho ABC vuông tại A , đường cao AH . Biết AH = 6 cm, BH = CH. Khi đó độ dài BH là: 4 A. 12 cm . B. 4 cm . C. 6 cm . D. 3 cm .
Câu 43: Cho tam giác ABC cân tại A có AB = AC = 26 cm, BC = 20 cm . Giá trị sin A bằng: 119 120 60 10 A. sinA = . B. sinA = . C. sinA = . D. sinA = . 169 169 169 13
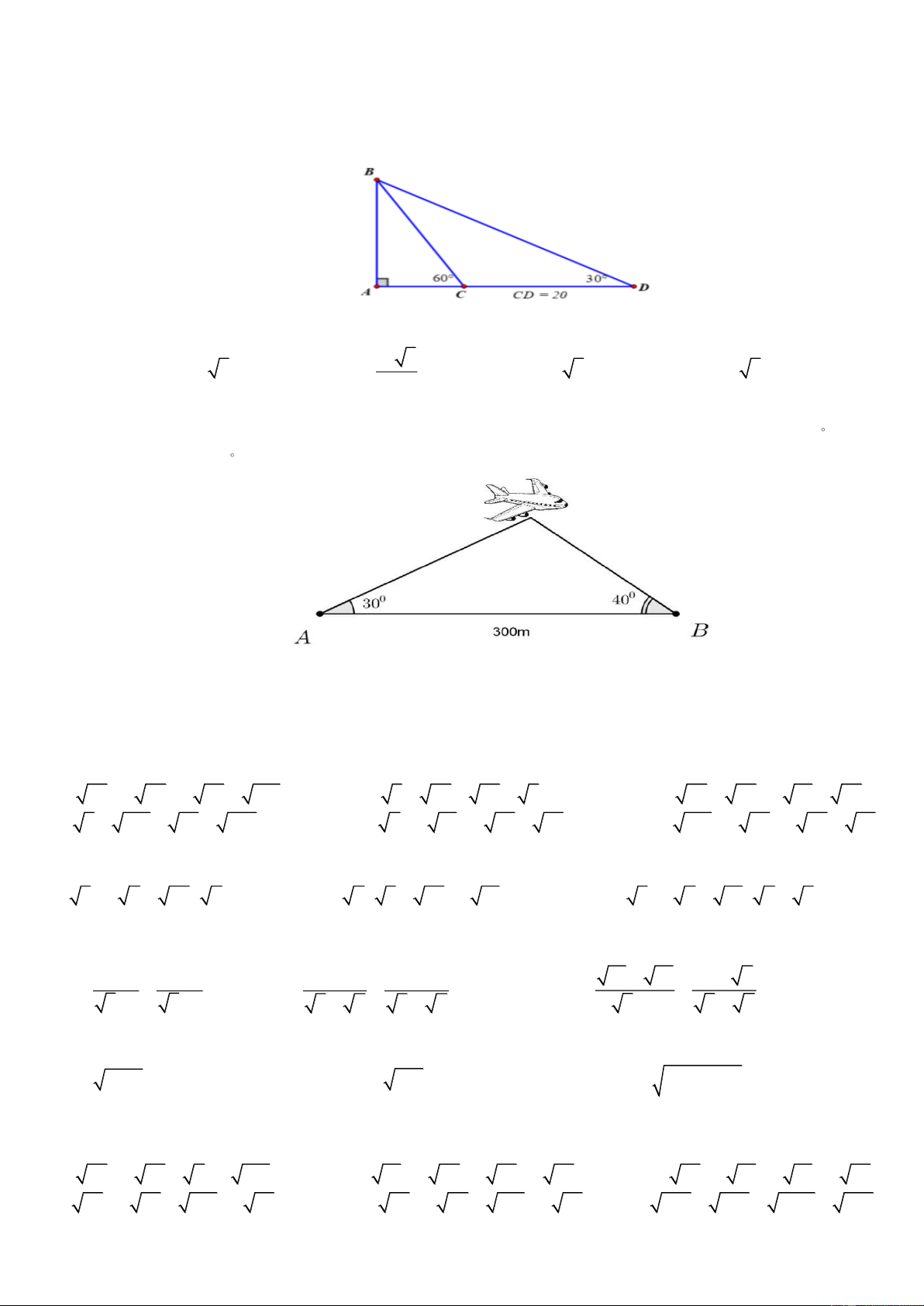
Câu 44: Cho hình vẽ. Biết CD = 3 cm , giá trị của x là: A. 4 cm . B. 3 3 cm . C. 2 3 cm . D. 3 2 cm.
Câu 45: Cho hình thang cân ABCD với AB = 6 cm; BC = 2 2cm . Khi đó độ dài DC là A. 8 cm . B. 10 cm . C. 7 cm . D. 6 2 cm .
Câu 46: Cho Δ MNP vuông tại M với MN = 5c ,
m N = 40 . Độ dài cạnh MP gần nhất với số nào sau đây? A. 6 cm . B. 4,1 cm . C. 5,96 cm. D. 4, 2 cm .
Câu 47: Một cây cột đèn thẳng đứng cao 13 m có bóng trải dài trên mặt đất là 6 m. Gọi a là góc
màtia sáng mặt trời tạo với mặt đất vào thời điểm đó. Giá trị tan a là: 6 205 6 13 13 205 A. . B. . C. . D. . 205 13 6 205
Câu 48: Một người đứng trên mũi tàu quan sát ngọn hải đăng cao 66 m. Người đó dùng giác kế đo
được góc tạo bới đường nhìn lên đỉnh và đường nhìn tới chân hải đăng là 25. Biết đường
nhìn tới chân hải đăng vuông góc với hải đăng, khoảng cách từ vị trí người đó đứng tới
chân hải đăng bằng (làm tròn đến hàng đơn vị): A. 141 m. B. 142 m. C. 31 m. D. 30 m .
Câu 49: Tại hai điểm A, B cách nhau 200 m , người ta nhìn thấy đỉnh núi với góc lần lượt là 34 và 42° (hình vẽ).
Chiều cao của một ngọn núi (làm tròn đến mét) là:
Th S: NGUYỄN DUY NINH 4 SĐT: 0961 697 696
Khi ta cố gắng, vận may sẽ bên ta
Đề cương giữa kỳ 1 toán 9 năm 2023- 2024 A. 538 m. B. 459 m . C. 344 m. D. 885 m .
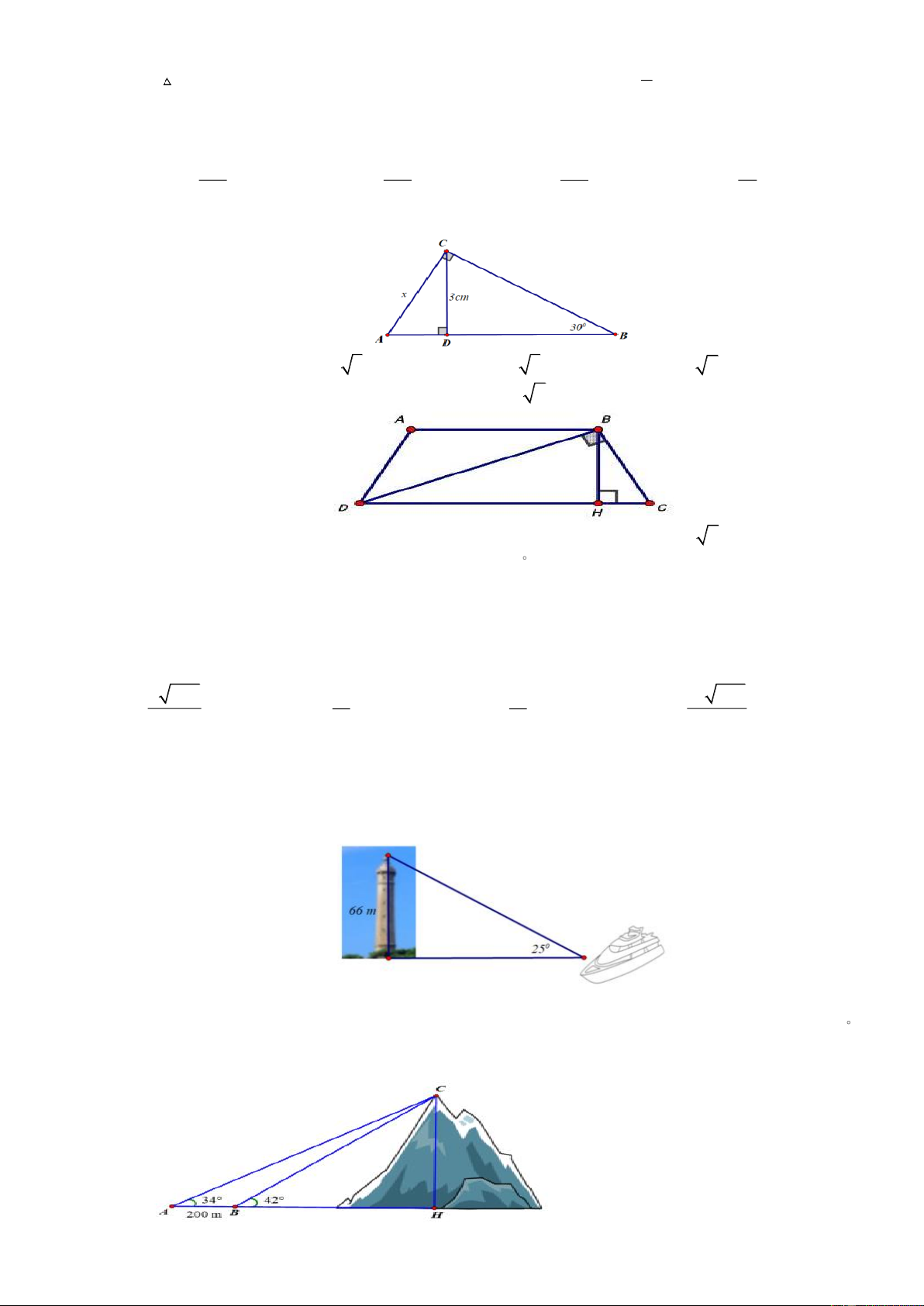
Câu 50: Cho hình vẽ sau:
Khoảng cách AB là: A. 20 m . B. 10 3m . C. 20( 3 − ) 1 m . D. 20 3 m .
Câu 51: Cho tam giác ABC vuông tại A , đường cao AH . Biết AH = x , khẳng định đúng là:
A. x = B . C sin . C cosB .
B. x = BC sinBcosC .
C. x = BC cosB tanC .
D. x = B .
C sinBsinC .
Câu 52: Cho hình bên. Phát biểu SAl là: cos cos A. 2 2
sin B + sin C = 1. B. tan = B B .
C. sinB = cosC . D. tan = B C . sinB sinB
Câu 53: Cho hình vẽ, biểu thức nào sau đây sai? h h b b a c h b A. = . B. = . C. = . D. = . c b a b c c c h
Câu 54: Một chiếc máy bay bay lên với vận tốc 750 km / h . Đường bay lên tạo với phương nằm
ngang một góc 35 (hình bên).
Th S: NGUYỄN DUY NINH 5 SĐT: 0961 697 696
Khi ta cố gắng, vận may sẽ bên ta
Đề cương giữa kỳ 1 toán 9 năm 2023- 2024
Sau 1 phút máy bay lên cao được bao nhiêu km theo phương thẳng đứng? (làm tròn kết quả
đến chữ số thập phân thứ hai) A. 130,76km. B. 21, 79 km . C. 7,17 km . D. 430km.
Câu 55: Cho hình vẽ Độ dài AB là: 10 3 A. AB = 10 3 . B. AB = . C. AB = 7 3 . D. AB = 5 3 . 3
Câu 56: Điểm hạ cánh của một máy bay trực thăng ở giữa hai người quan sát A và B . Biết khoảng
cách giữa hai người này là 300 m, góc "nâng" để nhìn thấy máy bay tại vị trí A là 30 và tại vị trí B là 40
Độ cao của máy bay gần nhất với giá trị nào sau đây? A. 250 m . B. 150 m. C. 200 m . D. 100 m.
PHẦN II. TỰ LUẬN.
DẠNG 1: THỰC HIỆN PHÉP TÍNH
Bài 1: Thực hiện phép tính:
a) 5 48 − 4 27 − 2 75 + 108 b) 4 3 + 27 − 45 + 5 c) 20 − 45 + 3 18 + 72 d) 2 5 − 125 − 80 + 605 e) 3 2 − 4 18 + 2 32 − 50 f) 125 − 4 45 + 3 20 − 80
Bài 2: Thực hiện phép tính: a) ( 8 − 4 2 + 40 ) 2 b) 2 ( 8 − 32 + 3 18) c) ( 8 − 3 2 + 10 ) 2 − 5 Bài 3: Rút gọn 1 1 1 1 15 − 12 6 + 2 6 a) A = − b) B = + c) C = − 3 −1 3 +1 3 − 2 3 + 2 5 − 2 3 + 2 Bài 4: Rút gọn a) 2 A =
64a + 2a với a 0 . b) 6 3
B = 3 9a − 6a với a 0 .
c) C = a ( − a)2 4 3 với a 3. BÀI TẬP VỀ NHÀ
Bài 1: Thực hiện phép tính:
a) 3 24 − 4 54 − 6 + 5 150 b) 12 + 2 27 + 3 75 − 9 48
c) 5 32 − 3 12 − 4 18 + 2 75
d) 3 32 − 2 50 − 162 − 5 98
e) 5 48 − 4 27 + 108 − 2 75 f) 252 − 700 + 1008 − 448
Bài 2: Thực hiện phép tính:
Th S: NGUYỄN DUY NINH 6 SĐT: 0961 697 696
Khi ta cố gắng, vận may sẽ bên ta
Đề cương giữa kỳ 1 toán 9 năm 2023- 2024 a) ( 12 + 3 15 − 4 135) 3 b) 3 3 2 27 − 75 + 12
c) ( 28 − 2 14 + 7 ) 7 + 7 8 2 Bài 3: Rút gọn 4 1 6 2 8 − 12 5 + 27 a) 2 2 5 A = + + b) B = + + C = − 6 − 2 6 + 2 6 3 +1 3 − 2 3 − 3 18 − 48 30 + 162 Bài 3: Rút gọn a) A = ( − a)2 27.48 1 với a 1.
b) A = 3 5a − 20a + 4 45a + a với a 0 .
DẠNG 2: GIẢI PHƯƠNG TRÌNH
Bài 1: Giải phương trình: a) 2
9x −12x + 4 = 3 x −1 = 2 2x − 3 = 13 2x − 3 = 2
Bài 2: Giải phương trình: 2x − 3 = x −1 x −1 = 2x + 3
x + 2 = 2x − 4
1− x − x − 3 = 0
Bài 3: Giải phương trình: 2
4x −12x + 9 = x −1
3 − x = 3x − 5 2
5 − x = x −1 2x + 3x + 7 = 0
Bài 4: Giải phương trình: 1 4x + 20 − x + 5 −
9x + 45 = 4 36x − 36 − 9x − 9 − 4x − 4 = 16 −
x −1 3 2x − 8 8x + 7 18x = 8 3
36x − 72 − 9x −18 + 4x − 8 + x − 2 = 72
9x +18 − x + 2 − 4x + 8 + 2 x + 5 = 0 BÀI TẬP VỀ NHÀ
Bài 1: Giải phương trình: 2
3 x − x − 54 = 0 2
2 3 − 7x − x = 0
2 − x(4 − x) = 0 2
16 − x + 3x = 0
Bài 2: Giải phương trình: 6 − x − 3 − x = 0 x − 2 = x − 2
x −1 − x − 4 = 0 2
x − 5 = 4x − 9
Bài 3: Giải phương trình: 2 x −1 = x −1
x − 4x − 3 = 2 2
x − 2x + 2 = x −1
2x − 4x −1 = 1
Bài 4: Giải phương trình: 7 3
15 x − 7 − 2 9x − 63 − 9 25x −175 = 4x − 24 36x − 216 − x − 6 + 4x − 24 = 49x − 343 2 7
49x − 98 − 9x −18 − 16x − 32 = 4x − 4
7 x + 81x − 81 + x −1 = 100x −100 3 5 1 6 9 −18x 4 + 8x − 9 +18x − 16 + 32x = 1 4 − 8x + 25 − 50x − 49 + 39 = 0 2 3 4 5 49
DẠNG 3: RÚT GỌN VÀ BÀI TOÁN LIÊN QUAN 7 x 2 x − 24
Bài 1. Cho biểu thức A = và B = +
với x 0, x 9 x + 8 x − 3 x − 9
a)Tính giá trị biểu thức A khi x = 25 b) Rút gọn B
c) Tìm các giá trị của x để B 2 ; 1
d) Tìm x để P = .
A B có giá trị nguyên
e) Tìm giá trị lớn nhất của B
f) Tìm x để P = 2 x 10 x 5 Bài 2: Cho A = − −
với x 0; x 25 . x − 5 x − 25 x + 5 1
a. Rút gọn biểu thức A
b. Tính giá trị của A khi x = 9
c. Tìm x để A 2 2 x −1 d. So sánh A với 2
e. Tìm x để A =
f. Tìm các giá trị nguyên của x để A . 3 2
g. Tìm các giá trị nguyên của x để A nhận giá trị nguyên.
h. Tìm giá trị nhỏ nhất của A .
Th S: NGUYỄN DUY NINH 7 SĐT: 0961 697 696
Khi ta cố gắng, vận may sẽ bên ta
Đề cương giữa kỳ 1 toán 9 năm 2023- 2024 2 x +1 2 x − 5 x −1
Bài 3: Cho các biểu thức sau: A = và B = − :
( x 0; x 1; x 9) x + 3 x + 3 x − 9 x − 3
a) Tính giá trị biểu thức A khi x = 49 .
b) Rút gọn biểu thức B .
c) Tìm x để A 2 1 1
d) Tìm x để A e) Tìm x để B =
f) Tính giá trị nhỏ nhất của biểu thức: M = A − . 3 4 x + 3 x +1 3 x −1 2 x
Câu 4. Cho hai biểu thức A = − và B =
( với x 1). x −1 2x − 3 x +1 4x +1
a)Tính giá trị của B khi x = 4 . b)Rút gọn A .
c) Tìm x để A 1 17 d) Tìm x để A e) Tìm x để P =
với P = A: B 2 3
f)Tìm giá trị nhỏ nhất của biểu thức: P = A: B . BÀI TẬP VỀ NHÀ x 4 x + 3 5
Bài 1: Cho hai biểu thức A = và B = + −
(với x 0, x 1). x + 6 x −1 x +1 1− x
a) Tính giá trị của A khi x = 4 . b) Rút gọn B .
c)Tìm x để B d) Tìm x để P = 2 e) Với P = .
A B , tìm các giá trị của x để P 0.
f)Tìm giá trị lớn nhất của biểu thức: P . x + 4 x 4 x +16
Bài 2: Cho hai biểu thức A = và B = + :
với x 0; x 16 x + 2 x + 4 x − 4 x + 2 7
a) Tính giá trị của A khi x = 36.
b) Rút gọn biểu thức B.
c)Tìm x để A = 5
d) Tìm các giá trị của x nguyên để giá trị của biểu thức B ( A − ) 1 là số nguyên. x 1 x x +1 x −1
Bài 3: Cho biểu thức A = − và B = −
với x 0; x 1 x −1 x +1 x −1 x +1 A 5
a Tính giá trị của A tại x = 16. b. Rút gọn biểu thức . B c. Cho P =
Tìm x để P = . B 6 2 + x x −1 2 x +1
Bài 4: cho hai biểu thức A = và B = + x x x + x A 3
a) Tính giá trị của biểu thức A khi x = 64. b) Rút gọn biểu thức B. c) Tìm x để B 2 2.( x − 2) x + 3 x + 2 x + 2
Bài 5: Cho biểu thức: A= và B = − +
với x 0, x 4 ; x 9 x − 3 x − 2 x − 3 x − 5 x + 6
a) Tính giá trị của A khi x = 25.
b) Rút gọn biểu thức B.
c) Tìm các giá trị x nguyên để biểu thức P = A. B có giá trị nguyên. x 3 6 x − 4 3
Bài 6: Cho biểu thức P = + − và Q =
với x 0; x 1. x −1 x +1 x −1 x +1 3
a) Tính giá trị của biểu thức Q = khi x = 25 .
b) Rút gọn biểu thức P. x +1
c) Biết M = P : Q . Tìm giá trị của x để biểu thức M 0 . 9 − x x + 2 2 x + 4
Bài 7: Cho hai biểu thức: A = và B = +
. (Với x 0 và x 4 ). x + 2 x x − 2 x
a) Tính giá trị của biểu thức A khi x = 9. b) Rút gọn biểu thức . B 1
c) Tìm các số thực x để biểu thức P = A +
nhận giá trị là số nguyên. B
Th S: NGUYỄN DUY NINH 8 SĐT: 0961 697 696
Khi ta cố gắng, vận may sẽ bên ta
Đề cương giữa kỳ 1 toán 9 năm 2023- 2024 HÌNH HỌC
Bài 1: Cho tam giác ABC vuông tại A , đường cao AH , có BC =13 cm C = a ( 0 0 a 90 ).
a) Giải tam giác vuông ABC khi a = 50 (Kết quả làm tròn đến chữ số thập phân thứ ba)
b) Chứng minh: BC = ABcosB+ AC . cosC
c) Gọi D , E thứ tự là hình chiếu của H trên các cạnh AB , AC. Trên nửa mặt phẳng bờ AC có chứa
điểm B , vẽ tia Cx vuông góc với AC tại C , tia Cx cắt tia AH tại M . Chứng minh:
AH HM = C . E CA .
d) Hãy xác định độ lớn của góc a để diện tích tứ giác ADHE đạt giá trị lớn nhất. Bài 2:
Cho tam giác ABC vuông tại A , có BC =10 cm , ABC = a
a) Giải tam giác vuông ABC khi 0 a = 60
b) Kẻ đường cao AH . Gọi D và E lần lượt là hình chiếu của H trên AB và AC . Chứng minh AD AB = AE.AC c) Chứng minh 3 AH = BC.BD.CE
d) Tìm a để tứ giác ADHE có diện tích lớn nhất. Bài 3: Cho M
NP vuông tại M , đường cao MH . Biết NP = 8c , m NH = 2cm
a) Tính độ dài các đoạn thẳng MN, MP, MH .
b) Trên cạnh MP lấy điểm K ( K M ; K P ), gọi Q là hình chiếu cuar M trên NK . Chứng minh rằng: .
NQ NK = NH.NP
Bài 4. Cho tam giác ABC vuông tại A, đường cao AH.Biết BC = 8c , m BH = 2cm
a) Tính độ dài các đoạn thẳng AB, AC, AH
b) Trên cạnh AC lấy điểm K (K ,
A K C ) ,gọi D là hình chiếu của A trên BK. Chứng minh rằng B .
D BK = BH.BC 1 c) Chứng minh rằng 2 S = S .cos A BD BHD BKC 4 BÀI TẬP VỀ NHÀ
Bài 1: Cho tam giác ABC vuông tại A có đường cao AH.
a) Cho biết AB = 3c , m AC = 4c .
m Tính độ dài các đoạn BC, HB, HC, AH ;
b) Vẽ HE vuông góc với AB tại E, HF ⊥ AC Tại F. i)Chứng minh 2 A . E EB = EH ii) Chứng minh: 2 A .
E EB + AF.FC = AH c) Chứng minh: 3 BE = B . C cos B
Bài 2: Cho tam giác ABC vuông tại A, đường cao AH.Biết AB = 6c , m AC = 8cm
a) Tính BC, AH , B , C
b) Vẽ AM là trung tuyến của tam giác ABC (M BC).Chứng minh B AH = M AC
c) Vẽ HE vuông góc AB(E AB), HF ⊥ AC (F AC) . Chứng minh EF ⊥ AM tại K và tính độ dài AK
Bài 3. Cho tam giác ABC vuông tại A, đường cao AH
a) Cho biết: AC = 6c , m BC = 10c .
m Tính độ dài AB, AH ,CH và số đo BAH
b) Lấy điểm K bất kỳ thuộc tia đối Ax của tia AB, hạ AI ⊥ CK. Chứng minh tích CI.CK không
thay đổi khi K di chuyển trên Ax
c) Tính giá trị của biểu thức ( C KA C HI )2016 cot .tan
Bài 4. Cho tam giác ABC vuông tại A, đường cao AH (H BC)
a) Biết AB = 12c , m BC = 20c .
m Tính AC, góc B, AH (góc làm tròn đến độ)
b) Kẻ HE vuông góc AB (E AB).Chứng minh 2 2 A .
E AB = AC − HC
c) Kẻ HF vuông góc AC ( F AC).Chứng minh AF = A . E tan C
Th S: NGUYỄN DUY NINH 9 SĐT: 0961 697 696
Khi ta cố gắng, vận may sẽ bên ta
Đề cương giữa kỳ 1 toán 9 năm 2023- 2024 3 AB BE d) Chứng minh rằng = AC CF
MỘT SỐ BÀI TOÁN THỰC TẾ
Bài 1. Bóng của một cột cờ dưới mặt đất dài 8 ,
m khi đó tia nắng mặt trời tại với mặt đất góc 50 . Tính chiều cao cột cờ
Bài 2. Một con mèo ở trên cành cây cao 6,5 .
m Để bắt mèo xuống cần phải đặt một cái thang đạt độ
cao đó, khi đó góc của thang với mặt đất là bao nhiêu,biết chiếc thang dài 6, 7m ? (kết quả làm tròn đến độ)
Bài 3. Một buổi chiều, các tia nắng mặt trời tạo với mặt đất một góc 30 và bóng của tượng đài trên
mặt đất dài 17,32m . Em hãy tính chiều cao của tượng (kết quả làm tròn đến hàng đơn vị)
Bài 4. Một cột đèn cao 7m có bóng trên mặt đất dài 4 .
m Hãy tính góc (làm tròn đến độ) mà tia sáng
mặt trời tạo với mặt đất.
Bài 5. Một máy bay từ mặt đất có đường bay lên tạo với mặt đất một góc 30 . Hỏi sau khi bay được
10km thì khoảng cách của máy bay và mặt đất là bao nhiêu?
Bài 6. Một cây cao 3m. Ở một thời điểm vào ban ngày mặt trời chiếu tạo thành bóng dài 2 . m Hỏi lúc
đó góc tạo bởi tia sáng mặt trời và mặt đất là bao nhiêu? (làm tròn số đo tới độ) BÀI TẬP VỀ NHÀ
Bài 1: Một khúc sông rộng 20m. Một chiếc thuyền qua sông bị dòng nước đẩy xiên nên phải chèo
26m mới sang được bờ bên kia. Hỏi dòng nước đã đẩy chiếc thuyền lệch đi một góc bao nhiêu? (góc làm tròn đến độ)
Bài 2: Một máy bay từ mặt đất có đường bay lên tạo với mặt đất một góc 300. Hỏi sau khi bay được
10km thì khoảng cách của máy bay và mặt đất là bao nhiêu?
Bài 3: Một cột đèn cao 7m có bóng trên mặt đất dài 4m. Hãy tính góc (làm tròn đến độ) mà tia sáng
mặt trời tạo với mặt đất.
Bài 4: Một cây cao 3 m. Ở một thời điểm vào ban ngày mặt trời chiếu tạo thành bóng dài 2 m. Hỏi lúc
đó góc tạo bởi tia sáng mặt trời và mặt đất là bao nhiêu ? (làm tròn số đo góc tới độ).
Bài 5: Một cái thang dài 3m ghi:“ để đảm bảo an toàn khi dùng, phải đặt thang với mặt đất một góc
từ 600 đến 700“. Đo góc thì khó hơn đo độ dài. Vậy hãy cho biết :khi dùng thang đó chân thang phải
đặt cách tường khoảng bao nhiêu mét để đảm bảo an toàn? (làm tròn 2 chữ số thập phân)
MỘT SỐ BÀI TOÁN NÂNG CAO Bài 1: Với các số thực ,
x y thỏa mãn x − x + 6 =
y + 6 − y . Tìm GTLN và GTNN của biểu thức
P = x + y . Bài 2:
Với a,b, c là các số dương thỏa mãn điều kiện a +b + c = 2 . Tìm giá trị lớn nhất của biểu
thức Q = 2a + bc + 2b + ca + 2c + ab . 3x + 6 x + 27
Bi 3:Tìm giá trị nhỏ nhất của các biểu thức sau: M = 1− x + 1+ x P = . x + 2
Bài 4: Cho a, b 0 và 2 2
a + b 2 . Tìm giá trị lớn nhất của biểu thức
P = a 3a (a + 2b) + b 3b (b + 2a)
Bài 5: Cho biểu thức 3 3
P = x + y − 3(x + y) +1996.
Tính giá trị biểu thức P với: 3 3
x = 9 + 4 5 + 9 − 4 5 và 3 3
y = 3 + 2 2 + 3 − 2 2
Bài 6. Cho biểu thức 3 3
P = x + y − 3( x + y) +1993.Tính giá trị biểu thức P với: 3 3
x = 9 + 4 5 + 9 − 4 5 và 3 3
y = 3 + 2 2 + 3 − 2 2
Th S: NGUYỄN DUY NINH 10 SĐT: 0961 697 696
Khi ta cố gắng, vận may sẽ bên ta
Bộ đề thi giữa kỳ 1 toán 9 năm 2023- 2024
LỚP TOÁN THẦY NINH
ĐỀ KIỂM TRA GIỮA HỌC KỲ I ĐỀ SỐ 01 Môn: TOÁN 9
Thời gian làm bài: 90 phút, không kể thời gian phát đề
A. PHẦN TRẮC NGHIỆM (3,0 điểm)
Câu 1. Tìm điều kiện để 2 − 3x có nghĩa, ta có: A. 2 x < . B. 2 x > . C. 2 x ≥ . D. 2 x ≤ . 3 3 3 3 2 2
Câu 2. Giá trị của biểu thức M = ( 2 − )1 + ( 2 + )1 là: A. 2 . B. 0 . C. 2 − . D. 2 2 .
Câu 3. Rút gọn biểu thức 2
3 a b + a b với a < 0 và b ≥ 0 ta được: A. 2 − a b . B. 4 − a b C. 4a b . D. 2 4 a b .
Câu 4. Giá trị của 5 là: 6 −1 A. 6 −1. B. 1− 6 . C. 1 6 x . D. 4 6 9 − x y . 3 Câu 5. Cho A
∆ BC vuông tại A, tỉ số lượng giác nào sau đây là đúng? A. sin AB C = . B. cos AB C = . BC AC C. cot AC C = . D. tan AC C = . BC AB
Câu 6. Nếu sinα = 0,8 thì số đo của góc nhọn α (làm tròn đến độ) là: A. 55° . B. 54° . C. 53° . D. 52° .
Câu 7. Cho tam giác ABC vuông tại A có B
∠ = 30 ,° BC =10cm . Độ dài cạnh AC bằng A. 5 3cm . B. 2 3cm C. 5cm D. 10 3cm . Câu 8. Cho A
∆ BC vuông tại A, đường cao AH, ta có: A. 2 AC = A . B BC . B. 2
AB = AC.HB . C. 2 AH = .
HB HC . D. A .
B AH = AC.BC .
Câu 9. Giá trị của biểu thức ( )2 11 − bằng: A. 11 − . B. 121 . C. 121 − . D. 11.
Câu 10. Các tia nắng mặt trời tạo với mặt đất một góc bằng 40°và bóng của tháp trên mặt đất dài 20 .
m Tính chiều cao của tháp (làm tròn đến mét) A. 24m . B. 20m . C. 17m . D. 13m .
Câu 11. Giá trị của biểu thức ( 8 + 18 − 20). 2 + 2 10 bằng: A. 4 10 B. 2 5 . C. 10. D. 5 2 .
Câu 12. Cho tam giác MNP vuông tại M, đường cao MH. Biết NH = 5c , m HP = 9c .
m Độ dài MH bằng: A. 4 B. 4,5. C. 7 . D. 3 5 .
B. PHẦN TỰ LUẬN (7,0 điểm) + + − + +
Bài 1: Cho hai biểu thức x 2 x 5 A = và 2 x 9 x 3 2 x 1 B = − −
với (x ≥ 0, x ≠ 4, x ≠ 9) x − 3 x − 5 x + 6 x − 2 3− x
a) Tính giá trị của A khi x =16.
b) Rút gọn biểu thức B
c) Biết rằng P = A: B . Tìm giá trị nhỏ nhất của P
Bài 2(1,0 điểm) Giải các phương trình sau: a) 2
x − 6x + 9 = 5
b) 15 x − 7 − 2 9x − 63 − 9 25x −175 = 4x − 24
Th S: NGUYỄN DUY NINH 1 SĐT: 0961 697 696
Khi ta cố gắng, vận may sẽ bên ta
Bộ đề thi giữa kỳ 1 toán 9 năm 2023- 2024 c) 2
4x − 4x +1 = x +1 d) 2 2
x − 4x + 4 = 4x −12x + 9
Bài 3( 3,0 điểm) Cho tam giác ABC vuông tại A ( AB > AC ), đường cao AH ( H ∈ BC ). Vẽ phân giác
AD của góc BAH ( D ∈ BH ). Cho M là trung điểm của BA .
a) Cho AC = 3cm ; AB = 4cm . Hãy giải tam giác ABC ?(Làm tròn đến độ)
b) Tính diện tích tam giác AHC
c) Chứng minh rằng: DH HC = DB AC
d) Gọi E là giao điểm của DM và AH . Chứng minh: S∆ E A C = S DE ∆ C
Bài 4(1,0 điểm)
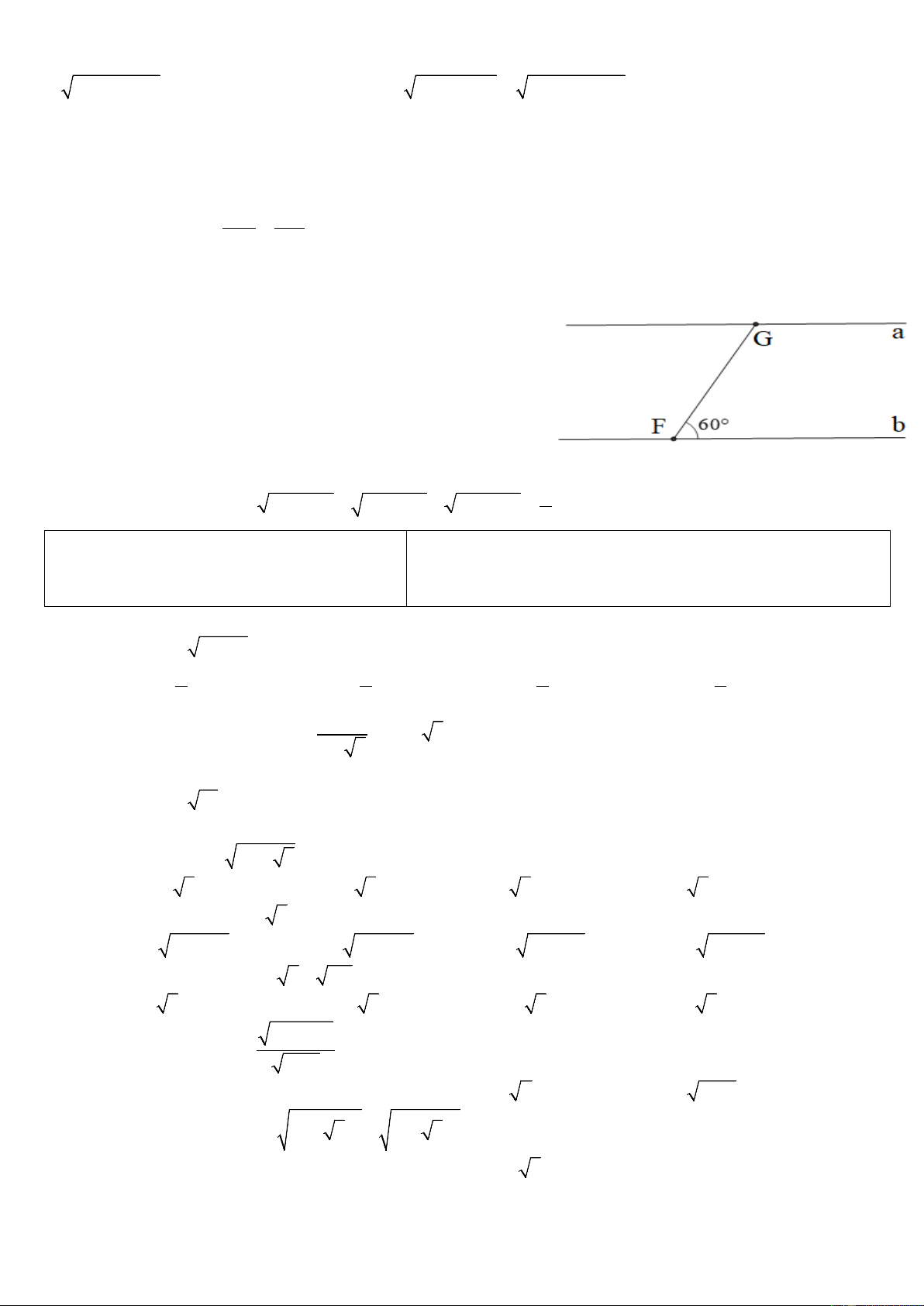
Một con thuyền ở địa điểm F di chuyển từ bờ sông b
sang bờ sông a với vận tốc trung bình là 6 km/h, vượt qua
khúc sông nước chảy mạnh trong 5 phút. Biết đường đi
của con thuyền là FG , tạo với bờ sông một góc 60°. a) Tính FG
b) Tính chiều rộng của khúc sông (làm tròn đến mét)
Bài 5. Giải phương trình: 1
x − 2000 + y − 2001 + z − 2002 = (x + y + z) −3000 2
LỚP TOÁN THẦY NINH
ĐỀ KIỂM TRA GIỮA HỌC KỲ I ĐỀ SỐ 02 Môn: TOÁN 9
Thời gian làm bài: 90 phút, không kể thời gian phát đề
A. PHẦN TRẮC NGHIỆM (3,0 điểm)
Câu 1. Biểu thức 1− 2x xác định khi A. 1 x > . B. 1 x ≥ . C. 1 x < . D. 1 x ≤ . 2 2 2 2
Câu 2. Trục căn thức ở mẫu của 2 = a + b 3 tính tổng a + b là: 2 − 3 A. 1 − . B. 2 . C. 2 − . D. 1.
Câu 3. Biểu thức 16 bằng A. 4.và 4. − B. 4. − C. 4. D. 8.
Câu 4. Biểu thức M = 4 − 2 3 có giá trị rút gọn bằng bao nhiêu? A. 2 − 3 B. 1− 3 C. 3 −1 D. 3 − 2
Câu 5. Với a < 0 thì 2 2 − ab 5 bằng A. 2 4 − 20a b . B. 2 4 − 20a b . C. 2 4 10a b . D. 2 4 − 10a b .
Câu 6: Giá trị của biểu thức 5 + 4.5 bằng A. 5 5. B. 4 5. C. 3 5. D. 2 5. 3 2
Câu 7. Rút gọn biểu thức x + 2x với x > 0 ta được x + 2 A. x B. −x C. x D. x + 2 2 2
Câu 8. Tìm giá trị biểu thức (2− 3) + (1− 3) . A. 3 B. 1 C. 2 3 D. 2
Th S: NGUYỄN DUY NINH 2 SĐT: 0961 697 696
Khi ta cố gắng, vận may sẽ bên ta
Bộ đề thi giữa kỳ 1 toán 9 năm 2023- 2024
Câu 9. Cho tam giác ABC vuông tại A, cạnh BC = 5cm và tỉ số hai hình chiếu của AB, AC trên cạnh
huyền bằng 9 . Chu vi tam giác ABC bằng ? 16 A. 10cm. B.12cm. C.15cm. D.16cm. Câu 10. Cho A
∆ BC có AH là đường cao xuất phát từ A (H ∈ BC) , A
∆ BC vuông tại A khi: A. 2 2 2
AC = AB + BC . B. 2 BC = . HB HC. C. 2 AB = .H HB C. D. 2 AH = . HB HC.
Câu 11. Hãy chọn câu trả lời đúng? A. 0 0 si 37 n = 53 sin . B. 0 0 cos37 = 53 sin . C. 0 0 tan37 = 37 cot . D. 0 0 cot37 = 53 cot . Câu 12. Cho A
∆ BC vuông cân tại A có AB =12cm và 1
tan B = . Độ dài cạnh BC là 3 A. 16c . m B. 18c . m C. 5 3 c . m D. 4 10 c . m
B. PHẦN TỰ LUẬN (7,0 điểm)
Bài 1: Thực hiện phép tính a) 18 − 2 50 + 3 8 b) 7 + 4 3 − 4 + 2 3 c) 5 − 8 − 2 7 + 2 7 + 2 − −
Bài 2: Cho hai biểu thức 4 x A = và x 2 1 5 2 x B = + +
, với x ≥ 0, x ≠ 4. x − 5 x −1
x + 2 x + x − 2
a) Tính giá trị của biểu thức A khi x = 81.
b) Rút gọn biểu thức . B
c) Tìm các giá trị nguyên của x sao cho A < 4. B
Bài 3: Giải các phương trình sau: a) 2
16 − x + 3x = 0
b) 49x − 98 − 9x −18 − 16x − 32 = 4x − 4 c) 2
3x −1− 4x −12x + 9 = 0 d) 2 2
2x −10x +11 = x − 6x + 8
Bài 4: Một buổi chiều, các tia nắng mặt trời tạo với mặt đất một góc 30° và bóng của tượng đài trên
mặt đất dài 17,32m . Em hãy tính chiều cao của tượng (kết quả làm tròn đến hàng đơn vị)
Bài 5: Cho tam giác ABC vuông tại A, đường cao AH (H ∈ BC)
a) Biết AB =12c , m BC = 20c .
m Tính AC, góc B, AH (góc làm tròn đến độ)
b) Kẻ HE vuông góc AB(E ∈ AB).Chứng minh 2 2
AE.AB = AC − HC
c) Kẻ HF vuông góc AC (F ∈ AC).Chứng minh AF = AE.tanC 3
d) Chứng minh rằng AB BE = AC CF
Bài 6. Giải phương trình: 2 2
x − 2x + 3 = 2 2x − 4x + 3
LỚP TOÁN THẦY NINH
ĐỀ KIỂM TRA GIỮA HỌC KỲ I ĐỀ SỐ 03 Môn: TOÁN 9
Thời gian làm bài: 90 phút, không kể thời gian phát đề
A. PHẦN TRẮC NGHIỆM (3,0 điểm)
Câu 1. Tìm điều kiện để x − 2 có nghĩa, ta có: A. x ≥ 2 . B. x ≤ 2 . C. x ≥ 2 − . D. x ≤ 2 − .
Câu 2. Giá trị của biểu thức sin 36° − cos54° bằng: A. 2sin 36°. B. 2cos54° . C. 0 . D. 1.
Câu 3 Căn bậc hai số học của 121là:
Th S: NGUYỄN DUY NINH 3 SĐT: 0961 697 696
Khi ta cố gắng, vận may sẽ bên ta
Bộ đề thi giữa kỳ 1 toán 9 năm 2023- 2024 A. 11. B. 11 − . C. 121. D. 11; 11 − . Câu 4. Biểu thức 2 (3− 2x) là A. 3− 2 .x B. 2x − 3. C. 2x −3 .
D. 3− 2x và 2x − 3. Câu 5. Biểu thức 2 4 9a b bằng A. 2 3ab . B. 2 3 − ab . C. 2 3 a b . D. 2 3a b . −
Câu 6 Giá trị của biểu thức 5 5 là 1− 5 A. − 5. B. 5. C. 5. D. 4 5.
Câu 7. Phương trình 2
(2x −1) = 3 có số nghiệm là: A. 2. B. 1. C. 0. D. Vô số nghiệm − + + Câu 8. Với x x x
x ≥ 0, x ≠ 9, x ≠ 4, rút gọn biểu thức biểu thức 2 9 2 1 3 M = + + x − 5 x + 6 x − 3 2 − x + − + − A. x 1. B. x 1. C. x 1 . D. x 1 . x − 3 x − 3 x − 2 x − 2
Câu 9. Tam giác ABC vuông tại A có AB = 6c ,
m AC = 8cm . Khi đó sin B bằng : A. 4 . B. 5 . C. 4 . D. 3 . 5 4 3 4
Câu 10. Tam giác ABC vuông tại A, đường cao AH, hệ thức nào sau đây đúng? A. 2
AH = CH.BC B. 2
AH = BH.BC C. 2
AH = BH.CH D. 1 1 1 = + 2 2 2 AH AB BC
Câu 11. Hệ thức nào sau đây là đúng? A. 0 0 sin 50 = cos30 . B. 0 0 tan 40 = cot 60 . C. 0 0 cot80 = tan10 . D. 0 0 sin 50 = cos 45 . Câu 12. Cho A
∆ BC vuông tại A có AB = 3cm và BC = 5cm . Giá trị cotB + cotC có bằng A. 12 . B. 25. C. 2.. D. 16 . 25 12 25
B. PHẦN TỰ LUẬN (7,0 điểm)
Bài 1: Thực hiện phép tính − a) 3 32 − 4 8 + 72 b) ( + )2 2 5 − 2; c) 2 3 3 4 − 2 3 − + 3 +1 3 −1
Bài 2: Cho hai biểu thức x + 3 A = và 3 4 1 B = − +
, với x ≥ 0, x ≠ 4. x − 4 x − 2 4 − x x + 2
a) Tính giá trị của biểu thức A khi x = 81.
b) Rút gọn biểu thức . B
c) Tìm các giá trị nguyên của x sao cho B − 3 x ≥ 0. A
Bài 3: Giải các phương trình sau: a) 2 x + 4x + 4 = 4
b) 3 4x +12 − 9x + 27 = 2 + x + 3
c) x − 4x − 3 = 2 d) 2 2
2x + 6x − 3 = x + 4x
Bài 1. Bài 4: Tính chiều cao của một cái tháp, cho biết khi các tia nắng mặt trời tạo với mặt đất một
góc 42° thì bóng của tháp trên mặt đất có chiều dài 150m .
Th S: NGUYỄN DUY NINH 4 SĐT: 0961 697 696
Khi ta cố gắng, vận may sẽ bên ta
Bộ đề thi giữa kỳ 1 toán 9 năm 2023- 2024
Bài 5: Cho tam giác ABC vuông tại . A
a) Giả sử khi AB = 9; AC =12.Tính cạnh BC và các góc còn lại của tam giác ABC (làm tròn đến độ)
b) Gọi H là hình chiếu của A Trên BC, E, F lần lược là hình chiếu của H trên AB, AC.Chứng minh
rằng: AH = EF và AE.AB = AF.AC
c) Gọi K là trung điểm của BC, biết AK cắt EF tại I.Chứng tỏ rằng AK ⊥ EF
Bài 6. Giải phương trình: 2 2
x − 2x + 3 = 2 2x − 4x + 3
LỚP TOÁN THẦY NINH
ĐỀ KIỂM TRA GIỮA HỌC KỲ I ĐỀ SỐ 04 Môn: TOÁN 9
Thời gian làm bài: 90 phút, không kể thời gian phát đề
A. PHẦN TRẮC NGHIỆM (3,0 điểm)
Câu 1: Điều kiện xác định của −x + 3 A. x ≥ 3 B. x ≥ 3 − C. x ≥ 0 D. x ≤ 3
Câu 2: Khử mẫu của biểu thức lấy căn: 7 ta được biểu thức là: 8 A. 7 B. 56 C. 14 D. 56 8 8 4
Câu 3: Căn bậc hai số học của 5 là: A. 25 B. 5 C. 5 D. 5 ±
Câu 4: Đẳng thức nào sau đây là đúng: A. ( − )2 4 15 = 4 − + 15 B. ( − )2 4 15 = 4 + 15 C. ( − )2 4 15 = 4 − − 15 D. ( − )2 4 15 = 4 − 15 + −
Câu 5: Gía trị biểu thức 11 10 11 10 + bằng: 11 − 10 11 + 10 A. 1 B. 22 C. 10 D. 42
Câu 6: Trục căn thức ở mẫu của biểu thức 1 (với a ≥ 0 và a ≠ 1) ta được: a −1 A. a +1 B. a +1 C. a −1 D. a −1 a −1 a −1
Câu 7: Giá trị x thỏa mãn 2
x − 6x + 9 = 4 là: A. a +1 B. a +1 C. a −1 D. x = 0 a −1 a −1
Câu 8: Kết quả phân tích thành nhân tử x y − y x là: A. x = 7 B. x = 1 −
C. x = 7; x = 1 −
D. xy( x − y )
Câu 9: Hệ thức nào sau đây là đúng:
A. sin 60° = cos30°
B. tan 40° = cot 40° C. 2 2 cot 80° + tan 10° =1
D. sin 50° = cos50°
Th S: NGUYỄN DUY NINH 5 SĐT: 0961 697 696
Khi ta cố gắng, vận may sẽ bên ta
Bộ đề thi giữa kỳ 1 toán 9 năm 2023- 2024
Câu 10: Cho tam giác ABC vuông tại ,
A đường cao AH.Hệ thức nào sau đây sai? A. A .
B BC = AC.AH B. 2
BC.BH = AB C. 2
AC = HC.BC D. 2 AH = . HB HC
Câu 11: Tam giác ABC vuông tại A và góc B = 30 ;° BC = 8 Khi đó AC = ? A. 8.cos30° B. 8.sin 30° C. 8.tan 30° D. 8.cot 30°
Câu 12: Tam giác ABC vuông tại A, đường cao AH chia cạnh huyền thành 2 đoạn. BH = 3c , m HC = 9c .
m Độ dài cạnh góc vuông AB là: A. 6cm B. 3 3cm C. 3.9cm D. 2 2 3 + 9 cm
B. PHẦN TỰ LUẬN (7,0 điểm)
Bài 1: Thực hiện phép tính a) 18 − 2 50 + 3 8 b) ( − )2 7 3 + 84 c) 4 4 − 5 −1 5 +1 − + −
Bài 2: Cho biểu thức x 1 x 2 10 5 + = x A x + − và 1 B= x 2 3 x x 5 x 6 − − − +
x(x − 4 x + 4)
a) Tính giá trị của biểu thức B khi 1
x = . b) Rút gọn biểu thức A
P = c) Tìm giá trị của x để P = 2 4 B
Bài 3: Giải các phương trình sau: a) ( x + )2 2 3 = 6 b) 5 1
. 15x − 15x +11 = . 15x 3 3 c) 2 x −1 = x −1 d) 2 2
4x −12x + 9 = 9x − 24x +16
Bài 4: Một người quan sát đứng cách một tòa nhà 25m . Góc nâng từ chỗ anh ta đứng đến nóc tòa nhà là 36° .
1) Tính chiều cao của tòa nhà (làm tròn đến mét).
2) Nếu anh ta dịch chuyển sao cho góc nâng là 32° thì anh ta cách tòa nhà bao nhiêu mét? Khi đó anh
ta tiến lại gần hay cách ra xa tòa nhà (làm tròn đễn chữ số thập phân thứ hai).
Bài 5: Cho tam giác ABC vuông tại A có đường cao AH. a) Cho BH = 4c , m CH = 9c .
m Tính AH và số đo B ∠ (làm tròn đến độ)
b) Gọi E, F lần lượt là hình chiếu của H trên AB và AC. Chứng minh AE.AB = AF.AC
c) Qua A kẻ đường thẳng vuông góc với EF kéo dài cắt BC tại M. Chứng minh M là trung điểm của BC d) Chứng minh 2 2
SAEF = SABC.sin . B sin C
Bài 6. Cho x, y, z dương thỏa mãn x + y + z = 3. Tìm giá trị nhỏ nhất của biểu thức
P = 3x + 4y + 6z
LỚP TOÁN THẦY NINH
ĐỀ KIỂM TRA GIỮA HỌC KỲ I ĐỀ SỐ 05 Môn: TOÁN 9
Thời gian làm bài: 90 phút, không kể thời gian phát đề
A. PHẦN TRẮC NGHIỆM (3,0 điểm)
Câu 1: Căn bậc hai số học của 49 là. A. 7 B. 7 − C. 7 ± D. 256 Câu 2: Tính 4 2
20a b ta được kết quả: A. 2 2a b 5 B. 2 2 5a b C. 2 2 − 5a b D. 2 2 − a b 5
Câu 3: Nếu tam giác ABC vuông tại A thì
A. AC = BC.cos B
B. AB = BC.sin B
C. AC = BC.sin C
D. AC = A . B cot C
Th S: NGUYỄN DUY NINH 6 SĐT: 0961 697 696
Khi ta cố gắng, vận may sẽ bên ta
Bộ đề thi giữa kỳ 1 toán 9 năm 2023- 2024
Câu 4. Khử mẫu của biểu thức lấy căn 4 được kết quả là: 5 A. 2 5 B. 2 5 C. 2 D. 5 5 5 5
Câu 5. Rút gọn các biểu thức 2 12 + 4 3 − 5 27 được: A. 7 − 3 B. 3 C. 14 − 3 D. 7 3
Câu 6. Cho tam giác ABC vuông tại ,
A cạnh huyền a, cạnh góc vuông b, . c Khi đó: A b c a C B A. c = .
a sin B,b = b tan C B. c = .
a sin C,b = . a cot C C. c = .
a tan B,b = . a sin C D. c = .
a cot C,b = a tan B
Câu 7. So sánh 4 với 2 2 ta có kết luận sau: A. 4 < 2 2 B. 4 > 2 2 C. 4 = 2 2 D. 4 ≤ 2 2
Câu 8. Tam giác MPQ vuông tại P. Ta có: A. cos PM M = B. cos PQ M = C. cos MQ M = D. cos MQ M = MQ MQ PM PQ
Câu 9. Cho tam giác ABC vuông tại A, có AC = 5c , m C ∠ = 60 .
° Độ dài cạnh BC là: A. 5cm B. 10cm C. 4 3cm D. 12cm Câu 10. Rút gọn 3 3 M = 64 − − 27 ta được: A. M =1 B. M = 1 − C. M = 7 − D. M = 7
Câu 11. Biểu thức 5x + 2 xác định khi: A. 2 x − ≥ B. 5 x ≥ − C. x ≥ 2 − D. x ≥ 5 − 5 2
Câu 12. Tam giác ABC vuông tại A (hình 2), đường cao AH chia cạnh huyền thành 2 đoạn. BH = 2c , m HC = 6c .
m Độ dài cạnh góc vuông AB là: A. 16cm B. 4cm C. 4 3cm D. 2 2 2 + 6 cm
B. PHẦN TỰ LUẬN (7,0 điểm)
Bài 1: Thực hiện phép tính a) 3 8 − 4 18 + 2 50 b) ( − )2 5 3 + 60 c) 2 2 − 3 −1 3 +1 −
Bài 2: Cho biểu thức x 3 6 x 4 P = + − và 3 Q =
với x ≥ 0; x ≠ 1. x −1 x +1 x −1 x + 2
a) Tính giá trị của biểu thức 3 Q = khi x = 6 − 2 5
b) Rút gọn biểu thức P . x + 2
c) Tìm giá trị nguyên của để biểu thức A = Q x có giá trị nguyên.
Bài 3: Giải các phương trình sau: a) ( x + )2 2 3 = 4
b) 7 x + 81x −81 + x −1 = 100x −100 c) 2
x − 2x = 2 − x d) 2 2
4x − 4x +1 = x − 2x +1
Bài 4: Giông bão thổi mạnh, một cây tre gãy gập xuống làm ngọn cây chạm đất và tạo với mặt đất một
góc 30 độ. Người ta đo được khoảng cách từ chỗ ngọn cây chạm đất đến gốc cây tre là 8,5m. Giả sử
Th S: NGUYỄN DUY NINH 7 SĐT: 0961 697 696
Khi ta cố gắng, vận may sẽ bên ta
Bộ đề thi giữa kỳ 1 toán 9 năm 2023- 2024
cây tre mọc vuông góc với mặt đất, hãy tính chiều cao của cây tre đó? (làm tròn đến chữ số thập phân thứ hai). Bài 5: Cho A ∆ BC vuông tại ,
A có AB = 6c , m AC = 8c . m
a) Tính số đo góc B, gócC (làm tròn đến độ) và đường cao AH.
b) Chứng minh rằng: A .
B cos B + AC.cosC = BC.
c) Trên cạnh AC lấy điểm D sao cho DC = 2 .
DA Vẽ DE vuông góc với BC tại E. Chứng minh rằng: 1 1 4 + = 2 2 2 AB AC 9DE
Bài 6. Cho x > 0 , y 1 1
> 0 và x + y ≤1. Tìm giá trị nhỏ nhất của biểu thức P = + + 4xy . 2 2 x + y xy
LỚP TOÁN THẦY NINH
ĐỀ KIỂM TRA GIỮA HỌC KỲ I ĐỀ SỐ 06 Môn: TOÁN 9
Thời gian làm bài: 90 phút, không kể thời gian phát đề
A. PHẦN TRẮC NGHIỆM (3,0 điểm)
Câu 1. Điều kiện của x để biểu thức 1− 2x có nghĩa. A. 1 x > B. 1 x ≥ C. 1 x < D. 1 x ≤ 2 2 2 2
Câu 2. Kết quả của phép tính 3 3 27 − 125 là: A. 2 B. 2 − C. 3 98 D. 3 − 98
Câu 3. Kết quả của biểu thức 2 7.3 là A. 3 7. B. 2 3 7. C. 21. D. 2 (3 7) .
Câu 4. Trục căn thức ở mẫu của biểu thức 5 , kết quả nào sau đây đúng? 3 A. 5. B. 5 3 . C. 5 3 . D. 25. 3 3 3 9
Câu 5. Kết quả phép tính 50. 2 bằng A. 10 B. 15 C. 20 D. 25.
Câu 6. Cho A
∆ BC vuông tại A ; công thức nào sau đây biểu diễn đúng tỉ sốsin C ? A. sin AB C = . B. sin AB C = . C. sin AC C = . D. sin BC C = . AC BC BC AB Câu 7. Cho MN ∆
P có MH là đường cao xuất phát từ M (H ∈ NP) .Hệ thức nào dưới đây chứng tỏ MN ∆
P vuông tại M A. 2 2 2
NP = MN + MP B. 2
MH = HN.HP C. 2
MN = HN.NP D. ,
A B,C đều đúng
Câu 8. Biểu thức −x xác định khi và chỉ khi: 2 x −1
A. x ≤ 0; x ≠ 1
B. x ≥ 0; x ≠ 1 −
C. x ≤ 0; x ≠ 1 −
D. x ≥ 0; x ≠ 1 Câu 9. Cho A
∆ BC vuông tại A, có AB = 6c ;
m AC = 8cm Độ dài đương cao AH là: A. 10cm B. 48cm C. 4,8cm D. 4cm
Câu 10: Một cái thang dài 4m, đặt dựa vào tường,góc giữa thang và mặt đất là 60°khi đó khoảng
cách giữa chân thang đến tường bằng: A. 2m B. 2 3m C. 4 3m D. 4 m 3 Câu 11: Cho A
∆ BC vuông tại A ; có đường cao AH (H ∈ BC). Hệ thức nào sau đây
Th S: NGUYỄN DUY NINH 8 SĐT: 0961 697 696
Khi ta cố gắng, vận may sẽ bên ta
Bộ đề thi giữa kỳ 1 toán 9 năm 2023- 2024 A. 1 1 1 = + . B. 2
AB = BC.BH. 2 2 2 AH AB AC C. A .
B AC = AH.BC. D. 2
AC = AH.BC.
Câu 12. Cho tam giác ABC vuông tại .
B Công thức tính độ dài cạnh AB là
A. AB = AC.sin . A
B. AB = BC.cosC.
C. AB = AC.cos . A
D. AB = BC.sin C.
B. PHẦN TỰ LUẬN (7,0 điểm)
Bài 1: Thực hiện phép tính 2 2 a) 1 2 45 − 3 72 −
320 + 6 18 b) ( 5 − 10) − 10.( 2 − )1 c) ( + )2 2 3 . 49 − 20 6 2 +
Bài 2: Cho biểu thức x + 4 x x x x A = và 2 9 B = +
.x ≥ 0; x ≠ 9; x ≠ 16. x −16 x − 3 9 − x
a, Tính giá trị của A khi x =18 −8 2.
b, Rút gọn biểu thức B .
c, Tìm giá trị của x để biểu thức B P = < 0. A
Bài 3: Giải các phương trình sau: a) 2
x − 4x + 4 = 5
b) 16x −8 + 36x −18 − 64x − 32 = 10 c) 2
4x −8x +1 = x −1 d) 2
x − x − 6 = x − 3
Bài 4: Hằng ngày hai anh em An và Bình cùng đi bộ từ nhà ở A để đến trường. Trường của An ở vị
trí B , trường của Bình ở vị trí C theo hai hướng vuông góc với nhau. An đi với vận tốc 4
km / h và đến
trường sau 15 phút. Bình đi với vận tốc 3
km / h và đến trường sau 12 phút. Tính khoảng cách BC giữa
hai trường (làm tròn đến mét).
Bài 5: Cho tam giác ABC vuông tại A, có AB = 27c , m AC = 36cm
a) Tính số đo các góc nhọn trong tam giác ABC (làm tròn kết quả tới độ)
b) Vẽ đường thẳng vuông góc với đoạn thẳng BC tại điểm B, đường thẳng này cắt tia CA tại giao
điểm D. Tính chiều dài AD?
c) Vẽ điểm E 'đối xứng với A qua đường thẳng BC.Không tính độ dài đoạn thẳng AE, chứng minh rằng : 1 1 1 = + 2 2 2 AE 4AB 4AC
d) Trên nửa mặt phẳng có bờ BC không chứa điểm A, lấy điểm M sao cho tam giác MBC vuông
cân tại M.Chứng minh AM là tia phân giác của A ∆ BC
Bài 6. Cho các số dương x, y, z thỏa mãn: xy +yz + zx = 1 Tính tổng: ( 2 1+ y )( 2 1+ z ) ( 2 1+ z )( 2 1+ x ) ( 2 1+ x )( 2 1+ y ) S = x + y + z 2 2 2 1+ x 1+ y 1+ z
LỚP TOÁN THẦY NINH
ĐỀ KIỂM TRA GIỮA HỌC KỲ I ĐỀ SỐ 07 Môn: TOÁN 9
Thời gian làm bài: 90 phút, không kể thời gian phát đề
Câu 1. Rút gọn biểu thức ( − − + ) 1 a) 6 5 18 2 50 . 2 −12 5 2 5 b) 6 − − 2 5 2 5 − 2
Câu 2. Giải phương trình
Th S: NGUYỄN DUY NINH 9 SĐT: 0961 697 696
Khi ta cố gắng, vận may sẽ bên ta
Bộ đề thi giữa kỳ 1 toán 9 năm 2023- 2024 a) 5x +1 = 4 b) 18 9 3 2 8 4 4 x x x − − − − + = 14 c) 2
4x − 4x +1 + 2 = 3x 4 + − 4( x + 2)
Câu 3. Cho hai biểu thức: x 2 x 2 4x A = − + và B =
với x ≥ 0 ; x ≠ 4 x − 2 x + 2 x − 4 x − 2
a) Tính giá trị của B tại x x = 9 . b) Chứng minh rằng: 4 A = . x − 2 c) Cho A
P = . Tìm x giá trị nguyên để P thuộc B
Câu 4. Một cột đèn có bóng trên mặt đất dài 6,2 m. Tia nắng mặt trời chiếu qua đỉnh cột đèn tạo với
mặt đất một góc 40° . Tính chiều cao của cột đèn (làm tròn đến đến chữ số thập phân thứ nhất).
Câu 5. Cho tam giác ABC vuông tại A có AB < AC . Kẻ đường cao AH . Gọi D , E lần lượt là hình
chiếu của H lên AB , AC .
a) Cho BH = 3,6 cm, CH = 6,4 cm. Tính AB ,
ACB (góc làm tròn đến độ) 3 3 b) Chứng minh: A .
D AB = AE.AC và AB AC = D B CE
c) Giả sử diện tích của tam giác ABC gấp 2 lần diện tích của tứ giác AEHD . Chứng minh tam giác ABC vuông cân
Câu 6. Cho a , b , c ≥ 0 thỏa mãn a + b + c =1. Tìm giá trị lớn nhất của biểu thức:
P = a a + 2b + b b + 2c + c c + 2a .
LỚP TOÁN THẦY NINH
ĐỀ KIỂM TRA GIỮA HỌC KỲ I ĐỀ SỐ 08 Môn: TOÁN 9
Thời gian làm bài: 90 phút, không kể thời gian phát đề Bài 1. (2,0 điểm)
1. Thực hiện phép tính: a) 1 5 5 3 3 A = 4 8 − 72 + 5 .2 2 b) B + + = + − ( 3 + 5). 2 5 3 +1
2. Giải phương trình sau: 2
x − 4x + 4 +1 = 4x . − − +
Bài 2. (2,0 điểm) Cho các biểu thức x 2 A = và x 3 x 3 B = +
(x > 0, x ≠ ) 1 . x x −1 x −1 a) Tìm x để 1 A = . b) Chứng minh x B = . c) Đặt P = .
A B . Tìm x để 1 P < . 2 x +1 2
Bài 3. (3,5 điểm)
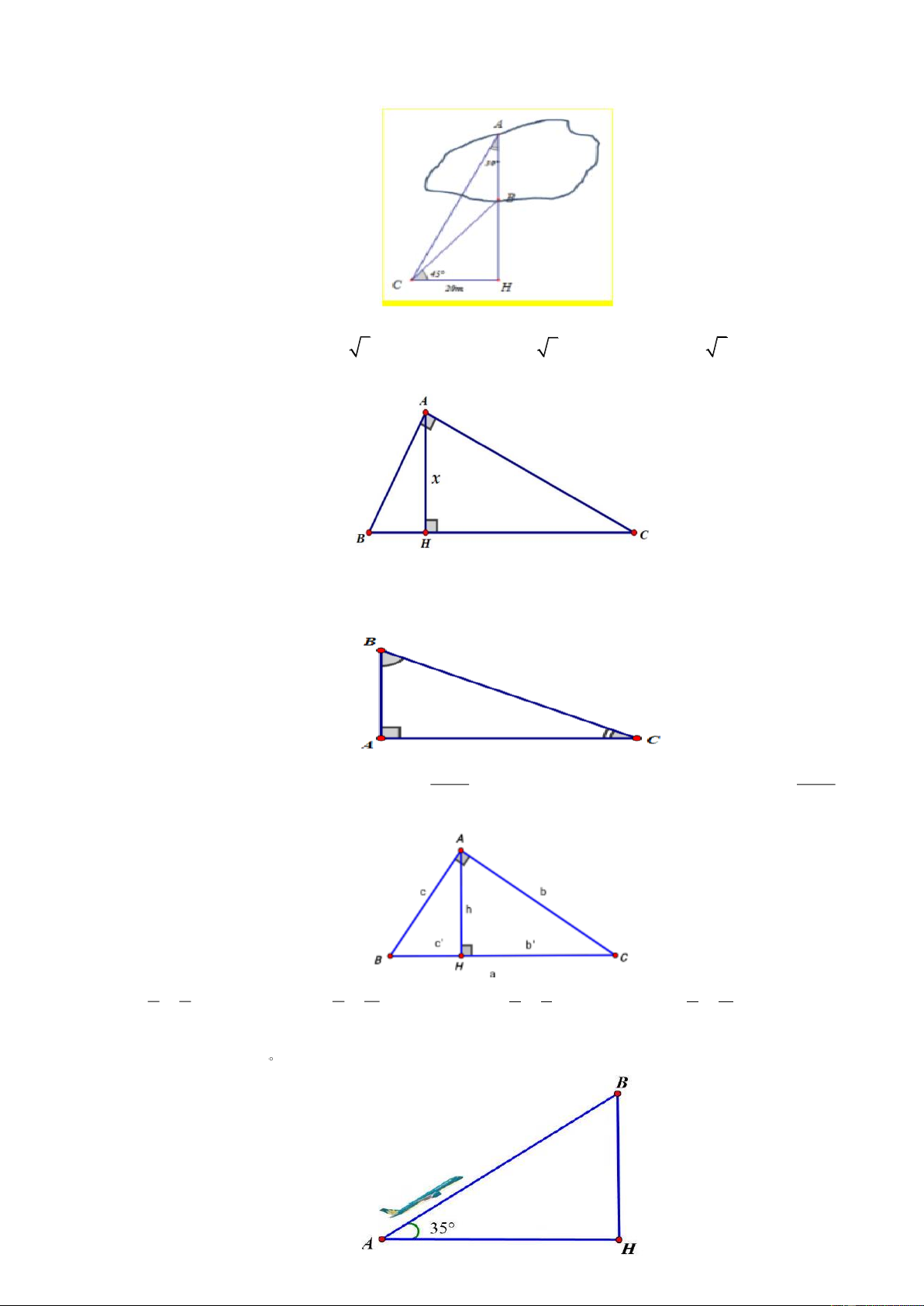
1) Hình vẽ bên minh họa một chiếc máy bay đang cất cánh từ sân bay. Đường bay lên tạo với
phương nằm ngang một góc bằng 32° . Hỏi sau khi bay được quãng đường 15 km thì máy bay đang
ở độ cao bao nhiêu so với mặt đất? (kết quả làm tròn đến số thập phân thứ nhất nhất) 2) Cho A
∆ BC nhọn nội tiếp (O; R) . Gọi H là giao điểm của hai đường cao BF,CE . Gọi I là trung điểm của BC . a) Chứng minh 4 điểm ;
B E; F;C cùng thuộc một đường tròn.
b) Vẽ đường kính AD . Chứng minh BD // CH và H đối xứng với D qua I .
c) Gọi K là trung điểm của AH . Chứng minh EK ⊥ EI .
d) Giả sử B,C cố định, A di chuyển trên đường tròn thì trực tâm H của tam giác ABC di động trên đường nào?
Bài 4: (0,5 điểm) Cho a, b ≥ 0 và 2 2
a + b ≤ 2 . Tìm giá trị lớn nhất của biểu thức
P = a 3a(a + 2b) + b 3b(b + 2a)
Th S: NGUYỄN DUY NINH 10 SĐT: 0961 697 696
Document Outline
- ĐỀ CƯƠNG TOÁN 9 NĂM HỌC 2023 - 2024
- BỘ ĐỀ HS THI GIỮA HỌC KỲ 1 TOÁN 9
- Bài 1: Cho hai biểu thức và với
- Bài 2(1,0 điểm) Giải các phương trình sau:
- Bài 3( 3,0 điểm) Cho tam giác vuông tại (), đường cao (). Vẽ phân giác của góc (). Cho là trung điểm của .
- Bài 4(1,0 điểm)
- Bài 3: Giải các phương trình sau:
- Câu 1. Rút gọn biểu thức
- Câu 2. Giải phương trình
- Câu 3. Cho hai biểu thức: và với ;
- Câu 4. Một cột đèn có bóng trên mặt đất dài m. Tia nắng mặt trời chiếu qua đỉnh cột đèn tạo với mặt đất một góc . Tính chiều cao của cột đèn (làm tròn đến đến chữ số thập phân thứ nhất).
- Câu 5. Cho tam giác vuông tại có . Kẻ đường cao . Gọi , lần lượt là hình chiếu của lên , .
- Câu 6. Cho , , thỏa mãn . Tìm giá trị lớn nhất của biểu thức: .
- Bài 1. (2,0 điểm)
- Bài 3. (3,5 điểm)
- 1) Hình vẽ bên minh họa một chiếc máy bay đang cất cánh từ sân bay. Đường bay lên tạo với phương nằm ngang một góc bằng . Hỏi sau khi bay được quãng đường 15 km thì máy bay đang ở độ cao bao nhiêu so với mặt đất? (kết quả làm tròn đến số thập phân thứ...
- 2) Cho nhọn nội tiếp . Gọi là giao điểm của hai đường cao . Gọi là trung điểm của .
- a) Chứng minh 4 điểm cùng thuộc một đường tròn.
- b) Vẽ đường kính . Chứng minh và đối xứng với qua .
- c) Gọi là trung điểm của . Chứng minh .
- d) Giả sử cố định, di chuyển trên đường tròn thì trực tâm của tam giác di động trên đường nào?




