








Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO ,………
NỘI DUNG ÔN TẬP GIỮA HỌC KỲ II TRƯỜNG THPT …… Môn: TOÁN Khối: 10
Năm học: 2023-2024 A. KIẾN THỨC ÔN TẬP
1. ĐẠI SỐ: Chương VI – Hàm số, đồ thị và ứng dụng Bài 15: Hàm số Bài 16: Hàm số bậc hai
Bài 17: Dấu của tam thức bậc hai
Bài 18: Phương trình qui về phương trình bậc hai
2. HÌNH HỌC VÀ ĐO LƯỜNG: Chương VII – Phương pháp tọa độ trong mặt phẳng
Bài 19: Phương trình đường thẳng
Bài 20: Vị trí tương đối giữa hai đường thẳng. Góc và khoảng cách
Bài 21: Đường tròn trong mặt phẳng tọa độ B. CÁC DẠNG BÀI TẬP I. TRẮC NGHIỆM Bài 15. Hàm số
Câu 1 NB: Xác định quy tắc hàm số.
Câu 1.1. Chọn từ thích hợp để điền vào chỗ (…): Nếu với mỗi giá trị của x thuộc tập hợp số D … giá trị
tương ứng của y thuộc tập hợp số thì ta có một hàm số. A. có. B. có một.
C. có một và chỉ một. D. có một số.
Câu 1.2. Trong các hệ thức sau đây, hệ thức nào cho ta y là hàm số của x ? A. 2 x y . B. 2 y x . C. 2 2 x y 2 . D. x | y |.
Câu 1.3. Biểu thức nào sau đây KHÔNG là hàm số theo biến x ?
A. y 2x 1 . B. 2 y x . C. 2
y x 3x 4 .
D. y 2x 3.
Câu 1.4. Biểu thức nào sau đây là hàm số theo biến x ? A. 2 2 x y 1.
B. | y | 2x 3. C. 4 y 2x 1. D. 3 y 2x 1.
Câu 2 NB : Tìm tập xác định của hàm số.
Câu 2.1. Tập xác định của hàm số 3 y là: x 5 A. D .
B. D \{1;2}.
C. D \{5}.
D. D \{5}.
Câu 2.2. Tập xác định của hàm số 1 y = là: x - 3
A. D = R \ { 3} .
B. D = (1;+ ¥ ) \ {3} . C. D = (3;+ ¥ ) .
D. D = ¡ \ {1;3} . 3x 1
Câu 2.3. Tập xác định của hàm số y là 2 x 2x 3 A. { 3,1} . B. [ 3;1] . C. { x
| x 3,x 1} . D. .
Câu 2.4. Hàm số nào sau đây có tập xác định là ?
A. y x 1 . B. 1 y . C. 2 y x 1 .
D. y x 1. x
Câu 3 NB: Tìm giá trị của hàm số tại điểm
Câu 3.1. Cho hàm số y f (x) 3x 1. Khẳng định nào sau đây là ĐÚNG?
A. f 2 5.
B. f 2 5.
C. f 2 7.
D. f 2 5.
Câu 3.2. Cho hàm số y f (x) 5x . Khẳng định nào sau đây là SAI? A. f 1 5.
B. f 2 10.
C. f 2 10. D. 1 f 1. 5
Câu 3.3. Tìm a biết điểm M(a; -1) thuộc đồ thị của hàm số y f (x) 2x 3. A. a 2. B. a 1. C. a 2 . D. a 6 . Câu 3.4. Cho hàm số 2
f (x) x kx 5 , với k là hằng số. Nếu f (2) 3 thì giá trị của f (2) là bao nhiêu? A. 5 . B. 3 . C. 3. D. -2.
Câu 4 NB: Điểm thuộc đồ thị hàm số
Câu 4.1. Đồ thị hàm số y 3x 2 đi qua điểm: A. 0;2 B. 1;3 C. 2;3 D. 9;0
Câu 4.2. Điểm nào sau đây thuộc đồ thị hàm số y = 1- 2x A. A(2;0). B. 1 B 3 ç ; .÷ ç ÷ ç C. C(1;- ) 1 . D. D(- 1;- ) 3 . 3÷
Câu 4.3. Điểm nào sau đây không thuộc đồ thị hàm số y = x- 2 A. M 2;0 . . B. M 1;1 . C. M - 2;- 4 . D. M 3;1 . 4 ( ) 3 ( ) 2 ( ) 1 ( )
Câu 4.4. Đồ thị hàm số 2
y x 2x 3 đi qua điểm nào sau đây? A. M (1;1) B. N (1;2) C. P(0;2) . D. Q(3;0) .
Câu 5 TH:Tìm tập giá trị hàm số
Câu 5.1. Tập giá trị của hàm số y x 2 là: A. . B. ( ; 2) . C. ( ; 0]. D. [2;) .
Câu 5.2. Tập giá trị của hàm số 2 y 2022x là: A. (0;). B. (;0). C. (;0]. D. [0;) .
Câu 5.3. Tập giá trị của hàm số 2 y 2 x là A. . B. ( ; 0). C. ( ; 0]. D. [0;) .
Câu 5.4. Tập giá trị của hàm số 2
f (x) x 4x 5 là: A. [1;) . B. ( ; 0) . C. ( ; 0]. A. .
Câu 6 TH:Tính đơn điệu của hàm số y = ax+b
Câu 6.1. Hàm số nào nào dưới đây nghịch biến trên khoảng (;) :
A. f x 1 3 .x
B. f x 93 .x
C. f x 9 3x.
D. f x 9 3 . x
Câu 6.2. Hàm số nào nào dưới đây đồng biến trên :
A. f x 6 2x .
B. f x 3 6x .
C. f x x 3
D. f x x 3.
Câu 6.3. Hàm số nào nào dưới đây đồng biến trên khoảng (;) :
A. f x x 2 .
B. f x 2 4x .
C. f x 168x .
D. f x x 2 .
Câu 6.4. Giá trị của m để hàm số f x (m 1)x 2 đồng biến trên khoảng (;) là A. m 1.. B. m 1. . C. m 1.. D. m 2..
Câu 7 TH: Nhận dạng đồ thị hàm số y = ax+b.
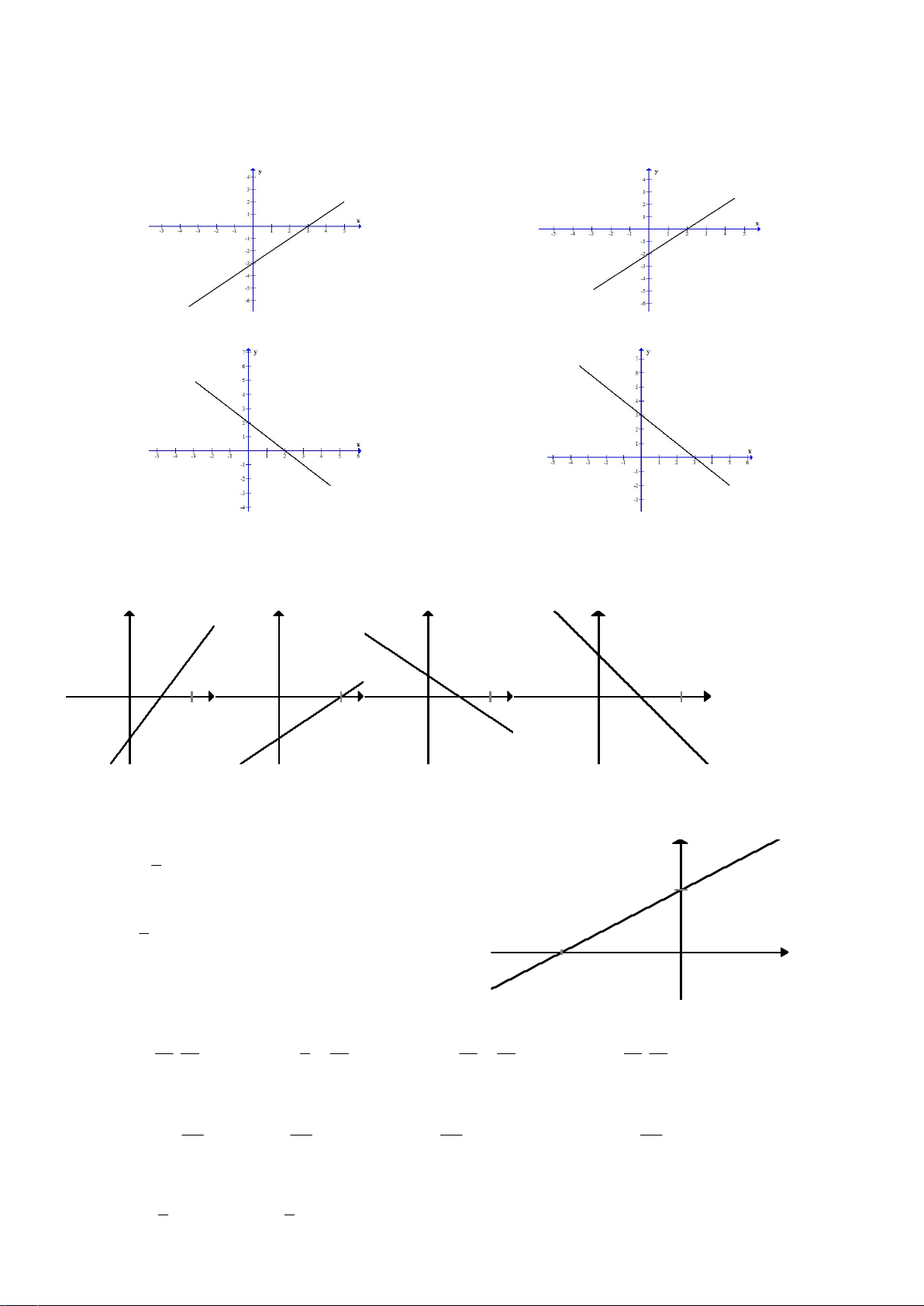
Câu 7.1. Đồ thị hình vẽ là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D
dưới đây. Hỏi hàm số đó là hàm số nào?
A. y = x+1.
B. y = - x + 2. y y = - x+
C. y = 2x + 1. D. 1. x O 1
Câu 7.2. Trong các đồ thị hàm số sau, đồ thị nào là đồ thị của hàm số y x 2? H1 H2 H3 H4 A. H1. B. H3. C. H4. D. H2.
Câu 7.3. Hàm số y = 2x - 1 có đồ thị là hình nào trong bốn hình sau? y y y y x x x x O 1 O 1 O 1 O 1 A. B. C. D.
Câu 7.4. Cho hàm số y = ax + b có đồ thị là hình bên. Tìm a và .b
A. a = - 2 và b = 3 . y B. 3 a = - và b = 2 . 2
C. a = - 3 và b = 3 . D. 3 a = và b = 3 . x 2 -2 O
Bài 16. Hàm số bậc hai
Câu 8 NB: Xác định các yếu tố đỉnh, điểm đặc biệt của hàm số bậc hai Câu 8.1. Cho hàm số 2
y = ax + bx + c (a ¹ 0) có đồ thị (P). Tọa độ đỉnh của (P) là: A. b D b D b D b D I ç- ; . ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç B. I - ; ç - . ÷ I - ç - ÷ I ç ÷ 2a 4a ÷ ç C. ; . a 4a ÷ ç D. ; . 2a 4a ÷ 2 ç a 4a÷ Câu 8.2. Hàm số 2
y ax bx c , (a 0) đồng biến trong khoảng nào sau đậy? A. ; b b . B. ; . C. ; . D. ; . 2a 2a 4a 4a
Câu 8.3. Trục đối xứng của parabol (P) 2
: y = 2x + 6x + 3 là A. 3 x = - . B. 3 y = - . C. x = - 3. D. y = - 3. 2 2
Câu 8.4. Trục đối xứng của parabol (P) 2
: y = - 2x + 5x + 3 là A. 5 x = - . B. 5 x = - . C. 5 x = . D. 5 x = . 2 4 2 4
Câu 9 NB .Đồ thị hàm số bậc hai
Câu 9.1. Chọn từ thích hợp để điền vào chỗ (…): Đồ thị hàm số 2 y 5
x 4x là một đường parabol có bề lõm … A. quay lên. B. quay xuống. C. quay sang trái. D. quay sang phải.
Câu 9.2. Hình nào sau đây là đồ thị của hàm số 2
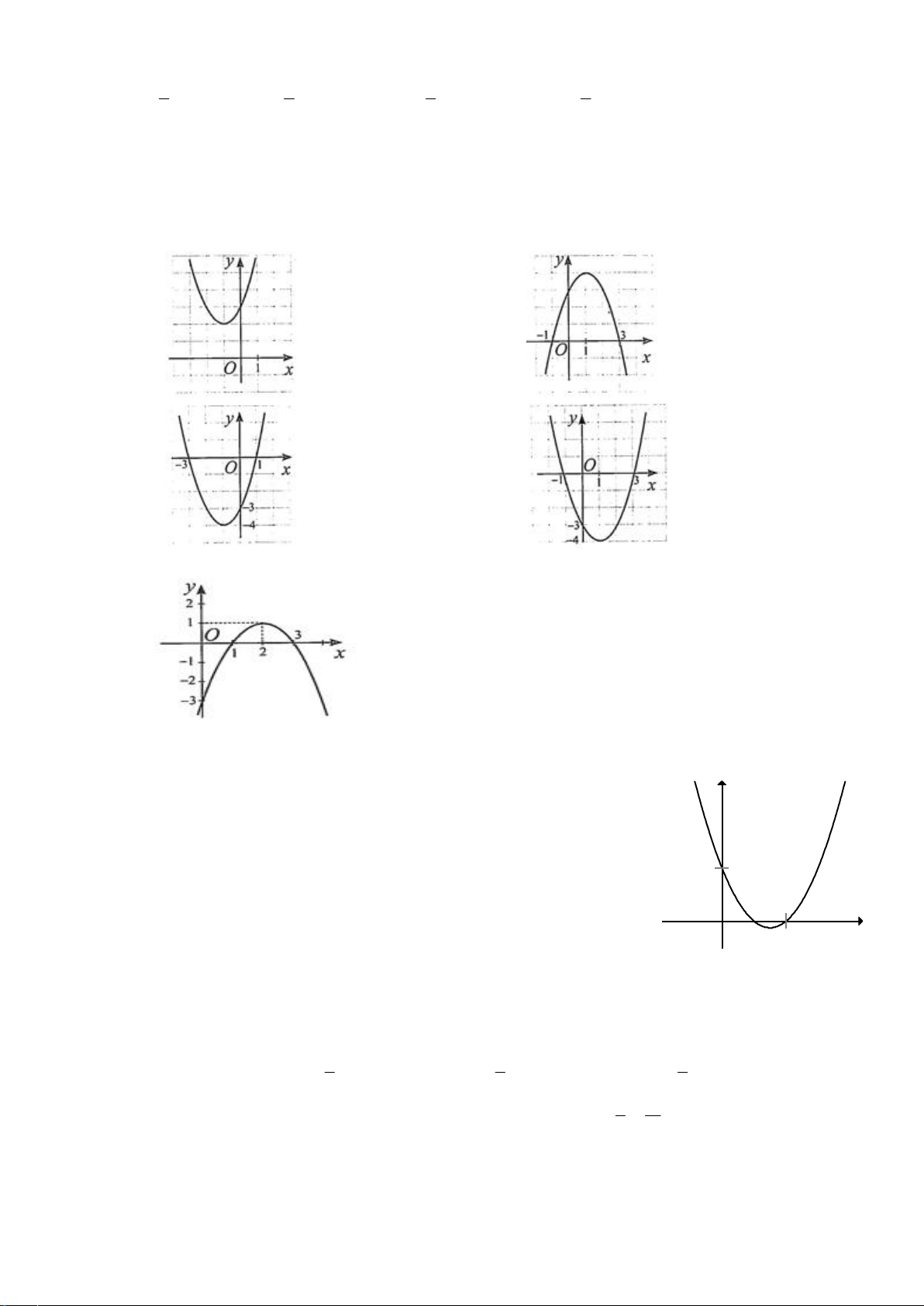
y x 2x 3 ? A. . B. . C. . D. .
Câu 9.3. Hàm số nào sau đây có đồ thị như hình bên dưới? 4 3 A. 2
y x 2x 3. B. 2
y x 4x 3 . C. 2
y x 4x 3. D. 2
y x 2x 3. y
Câu 9.4. Đồ thị hình vẽ là đồ thị của một hàm số trong bốn hàm số được liệt
kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào? A. 2
y = - x + 3x - 1. B. 2
y = - 2x + 3x - 1. C. 2
y = 2x - 3x + 1. 1 x D. 2
y = x - 3x + 1. O
Câu 10 TH Xác định các hệ số trong công thức hàm số bậc hai
Câu 10.1. Tìm parabol (P) 2
: y = ax + 3x - 2, biết rằng parabol cắt trục Ox tại điểm có hoành độ bằng 2. A. 2
y = x + 3x - 2. B. 2
y = - x + x - 2. C. 2
y = - x + 3x - 3. D. 2
y = - x + 3x - 2.
Câu 10.2. Tìm parabol (P) 2
: y = ax + 3x - 2, biết rằng parabol có trục đối xứng x = - 3. A. 1 1 1 2
y = x + 3x - 2. B. 2 y = x + x - 2. C. 2 y = x + 3x - 3. D. 2 y = x + 3x - 2. 2 2 2
Câu 10.3. Tìm parabol (P) 2
: y = ax + 3x - 2, biết rằng parabol có đỉnh 1 11 I ç- ; ç - . ÷÷ ç 2 4 ÷ A. 2
y = x + 3x - 2. B. 2
y = x + x - 4. C. 2
y = 3x + x - 1. D. 2
y = 3x + 3x - 2.
Câu 10.4. Biết parabol (P) 2
: y = ax + 4x + c có hoành độ đỉnh bằng 2 và đi qua điểm M (1; ) 2 . Tính tổng
S = a + c. A. S = - 2. B. S = 3. C. S = 1. D. S = - 3.
Câu 11 TH. Tìm khoảng đồng biến nghịch biến của hàm số bậc hai.
Câu 11.1. Hàm số f x 2
x 2x 3 đồng biến trên khoảng nào dưới đây? A. 1; . B. 2; . C. ; 1 . D. 3 ; . Câu 11.2. Hàm số 2 y 3
x x 2 nghịch biến trên khoảng nào sau đây? A. 1 ; . B. 1 ; . C. 1 ; . D. 1 ; . 6 6 6 6 Câu 11.3. Hàm số 2 y 3
x x 2 nghịch biến trên khoảng nào sau đây? A. 1 ; . B. 1 ; . C. 1 ; . D. 1 ; . 6 6 6 6 Câu 11.4. Hàm số 2
y x 3x đồng biến trên khoảng: A. 3 ; . B. 3 ; . C. 3 ; . D. 3 ; . 2 2 2 2
Bài 17. Dấu của tam thức bậc hai
Câu12 NB. Xét dấu tam thức bậc hai vô nghiệm hoặc có nghiệm kép
Câu 12.1. Cho f x 2
ax bx ca 0 . Điều kiện để f x 0, x là: a 0 a 0 a 0 a 0 A. . B. C. D. . 0 0 0 0
Câu 12.2. Tam thức bậc hai nào sau đây luôn nhận giá trị dương với mọi x ? A. 2 x 3x 2 . B. 2 x 4x 3 . C. 2 x x 1. D. 2 x 3x 3 .
Câu 12.3. Cho f x 2
ax bx c a 0 và 2
b 4ac . Cho biết dấu của khi f x luôn cùng dấu
với hệ số a với mọi x . A. 0. B. 0. C. 0. D. 0.
Câu 12.4. Tam thức bậc hai
nhận giá trị dương khi và chỉ khi:
A. x Î (0;+ ¥ ).
B. x Î (- 2;+ ¥ ). C. x Î ¡ .
D. x Î (- ¥ ;2).
Câu 13NB Xét dấu tam thức bậc hai có hai nghiệm
Câu 13.1. Tam thức bậc hai f x 2
x 5x 6 nhận giá trị dương khi và chỉ khi : A. x ; 2. B. 3;.
C. x2;.
D. x2;3.
Câu 13.2. Tam thức bậc hai f x 2
x 12x 13 nhận giá trị không âm khi và chỉ khi:
A. x \ 1 ;1 3 B. x 1 ;1 3 C. x ; 1 13; D. x 1 ;13
Câu 13.3. Cho tam thức bậc hai 2
f (x) 2x x 1. Giá trị của x để f (x) nhận giá trị dương là A. 1 x 1; B. 1 x 1; . 2 2 C. 1 x ( ; 1) ; . D. 1 x (;1] ; . 2 2 Câu 13.4. Tam thức 2
f (x) x 2x 3 nhận giá trị dương khi và chỉ khi:
A. x (;2) (6;) . B. x ( ; 3) (1;) .
C. x (;1) (3;) .
D. x (1;3) .
Câu 14TH: Giải bất phương trình bậc hai
Câu 14.1. Tập nghiệm của bất phương trình: 2
2x 7x 15 ³ 0 là: A. 3 ç ¥ ; ç úÈ[5;+ ¥ ) - ¥ - È ê ÷ ç B. 3 - C. ( ; 5] 3 + ¥ D. 3 ;5 è 5; ; ÷ 2úû 2 2 ê ÷ ë ø 2
Câu 14.2. Tập nghiệm của bất PT 2
x 4x 3 0 là: A. ; 3 1 ; B. 3 ; 1 C. ; 1 3 ; D. 3 ; 1
Câu 14.3. Tập nghiệm của bất PT 2
x x 6 0 là: A. ; 2 3; B. C. ; 1 6 ; D. 2 ; 3
Câu 14.4. Tam thức bậc hai 2
x 7x 12 nhận giá trị âm khi nào? A. x(3;4) . B. x[3;4]. C. x( ; 3) (4;) D. x( ; 3][4;) .
Câu 15TH: Giải bất phương trình bậc hai trong bài toán tìm tham số để một tam thức bậc hai thỏa mãn điều kiện cho trước
Câu 15.1. Với giá trị nào của m thì phương trình 2 2
x mx m 2m 0 có hai nghiệm trái dấu?
A. m 0;m 2 .
B. 0 m 2.. C. m 2..
D. 0 m 2..
Câu 15.2. Với giá trị nào của m thì phương trình 2
x 2mx m 6 0 có hai nghiệm phân biệt? A. m( ; 2) (3;)
B. m(2;3) . C. m 2..
D. 2 m 3. .
Câu 15.3. Giá trị của tham số m để phương trình 2
x (m 1)x 4 0 có nghiệm là A. (5;3) .
B. (;5][3;) . C. [5;3].
D. (;5) (3;) .
Câu 15.4. Với giá trị nào của m thì 2 2
x (3m 2)x 2m 5m 2 0 với mọi x?
A. m 2;m 6 . B. m 6. C. m 2.
D. 2 m 6.
Bài 18. Phương trình quy về bậc hai
Câu 16NB Giải phương trình quy về phương trình bậc hai 2 2
ax bx c dx ex f
Câu 16.1. Số nghiệm của phương trình 2 2
x 2x 3 2x x 3 là: A. 1. B. 2. C. 0. D. 3.
Câu 16.2. Tập nghiệm của phương trình 2
3x 6x 4 x 8 là A. 3 S ;1 4 . B. S .. C. S {1}. D. S . 4 3
Câu 16.3. Tập nghiệm của phương trình 2
x 3x 1 x 2 là: A. S {3;1}. B. S {3}. C. S {1}. D. S {3;6}.
Câu 16.4. Tập nghiệm của phương trình 2 2
x x 2 2x x 1 là: A. S {3}. B. S { 1 ;2}. C. S {1}. D. S { 1 }.
Câu 17NB Giải phương trình quy về phương trình bậc hai 2
ax bx c dx e
Câu 17.1. Giá trị x 2 là nghiệm của phương trình nào sau đây? A. 2
x x 4 x 4 .
B. x 1 x 3 .
C. x 2 2 3x 2 .
D. x 2 x 1 .
Câu 17.2. Tập nghiệm của phương trình 2
x 3x 1 x 1 là: A. S {1}. B. S {2}. C. S {0}. D. S .
Câu 17.3. Tập nghiệm của phương trình 2
x 4x 3 x 1 là: A. S . B. 1 S . C. S {3}. D. S {1}. 3 Câu 17.4. Phương trình 2
x 2x 2 2x 3 có nghiệm là giá trị nào sau đây? A. x 2 . B. x 1. C. x 1 . D. x 2 .
Câu 18 TH Ứng dụng phương trình quy về phương trình bậc hai để giải bài toán thực tế(Xem ví dụ vận dụng trang 26) Câu 18.1.
Khi một quả bóng được đá lên nó sẽ đạt độ cao nào đó rồi rơi xuống đất. Biết quỹ đạo của
quả bóng là một đường cong parabol trong mặt phẳng toạ độ O th có phương trình 2
h at bt c(a 0) , trong đó t là thời gian (tính bằng giây) kể từ khi quả bóng được đá lên, h
là độ cao (tính bằng mét) của quả bóng. Giả thiết rằng quả bóng được đá lên từ độ cao 1,2 m và
sau 1 giây thì nó đạt độ cao 8,5 m , saut 2 giây thì nó đạt độ cao 6 m . Hỏi quá bóng bay ở độ cao
không thấp hơn 6 m trong thời gian bao lâu? A. 74 giây. B. 3 giây. C. 61 giây. D. 2 giây. 48 49
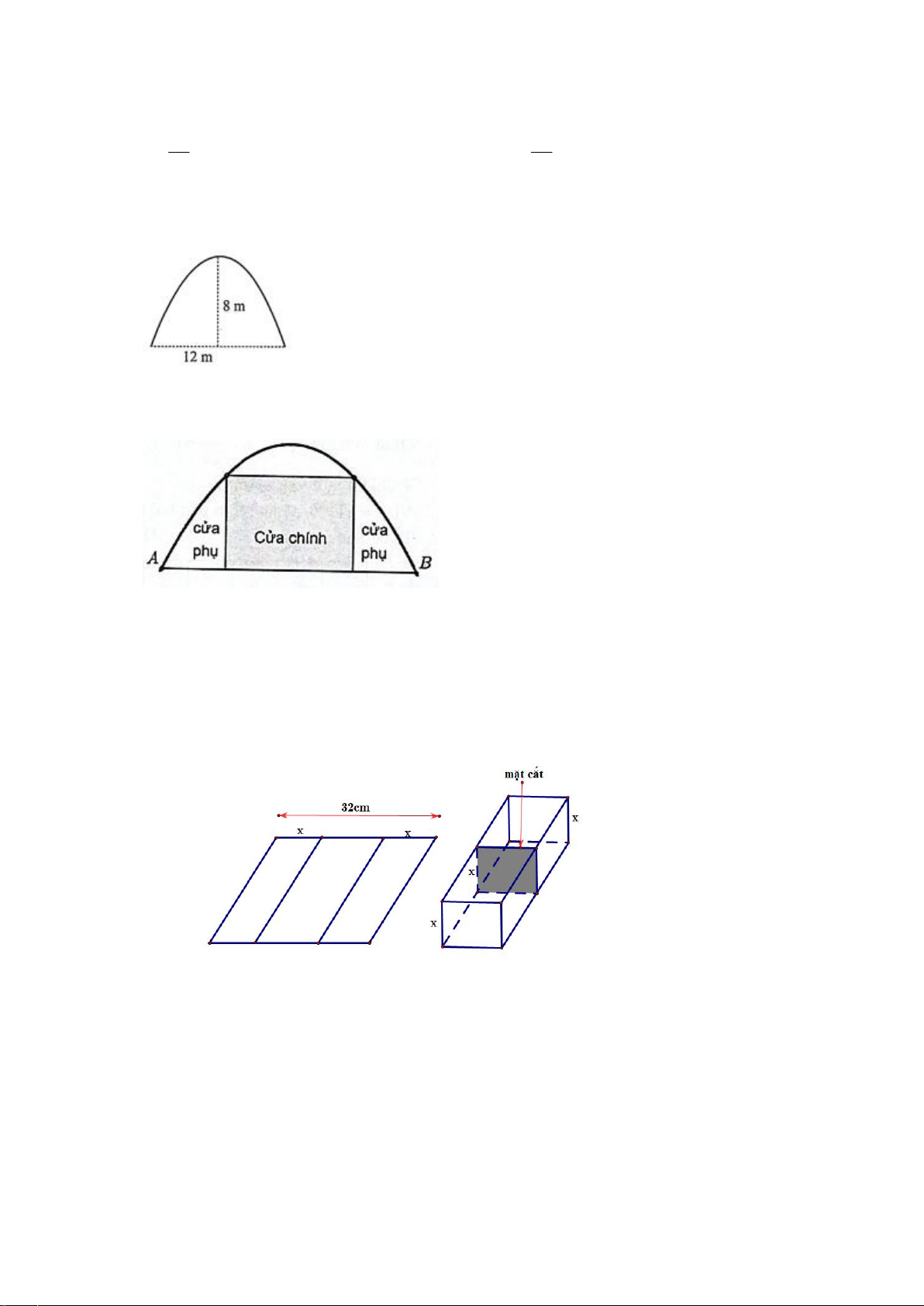
Câu 18.2. Một đường hầm xuyên thẳng qua núi và có mặt cắt là một parabol (thông số như hình bên). Giả
sử một chiếc xe tải có chiều ngang 6 m đi vào vị trí chính giữa miệng hầm. Hỏi chiều cao h của xe tải cần
thoả mãn điều kiện gì để có thể đi vào cửa hầm mà không chạm tường?
A. 0 h 6.
B. 0 h 6.
C. 0 h 7.
D. 0 h 7.
Câu 18.3. Một chiếc cổng hình parabol bao gồm một cửa chính hình chữ nhật ở giữa và hai cánh cửa phụ hai bên như hình vẽ.
Biết chiều cao cổng parabol là 4 m , cửa chính (ở giữa parabol) cao 3 m và rộng 4 m. Tính khoảng
cách giữa hai chân công parabol ây (đoạn AB trên hình vẽ). A. AB = 7m B. AB = 8m. C. AB = 6,5m. D. AB = 9m.
Câu 18.4. Một người muốn uốn tấm tôn phẳng hình chữ nhật có bề ngang 32 cm, thành một rãnh dẫn nước
bằng cách chia tấm tôn đố thành ba phần rồi gấp hai bên lại theo một góc vuông như hình vẽ. Biết rằng diện
tích mặt cắt ngang của rãnh nước phải lớn hơn hoặc bằng tổng 2
120cm . Hỏi độ cao tối thiểu và tối đa của
rãnh dẫn nước là bao nhiêu cm? A. 6cm và 10cm. B. 6cm và 8cm. C. 7cm và 10cm . D. 7cm và 9cm.
Bài 19. Phương trình đường thẳng
Câu 19 NB Viết PT tổng quát của đường thẳng biết điểm đi qua và véc tơ pháp tuyến
Câu 19.1. Phương trình tổng quát của đường thẳng d đi qua M(x0 ;y0) và có vectơ pháp tuyến n (a;b) là :
A. a(x x ) b(y y ) 0
B. a(x x ) b(y y ) 1 0 0 0 0
C. a(x x ) b(y y ) 0
D. a(x x ) b(y y ) 0 0 0 0 0
Câu 19.2. Phương trình của đường thẳng đi qua điểm M (5;4) và có vectơ pháp tuyến n(11;12) là:
A. 5x 4y 7 0 .
B. 5x 4y 7 0 .
C. 11x 12y 7 0 .
D. 11x 12y 7 0 .
Câu 19.3. Phương trình của đường thẳng đi qua điểm M (5;4) và vuông góc với đường thẳng
x 2 y 5 0 là:
A. x 2y 3 0 .
B. 2x y 14 0 .
C. x 2y 13 0.
D. 2x y 0 .
Câu 19.4. Đường thẳng đi qua M 1;
1 và có véc-tơ pháp tuyến n(1;2) thì có phương trình:
A. x 2y 3 0
B. x 2y 5 0
C. x 2y 3 0
D. x 2y 1 0
Câu20 NB Viết phương trình tham số đường thẳng khi biết phương trình tổng quát.
Câu 20.1.Cho đường thẳng có phương trình tổng quát là x 2y 5 0 . Phương trình nào sau đây là
phương trình tham số của ? x 3 2t x t x 3 4t
x 5 2t A. . B. . C. . D. .
y 4 t y 5 2t y 1 2t y t
Câu 20.2.Phương trình tham số của đường thẳng d đi qua M (3; 4
) và vuông góc với đường thẳng
x 2 y 5 0 là:
x 3 2t x 3 t
x 3 2t
x 3 2t A. . B. . C. . D. . y 4 t y 4 2t y 4 t y 4 t
Câu 20.3.Phương trình tham số của đường thẳng d đi qua (
A 0;2) và song song với đường thẳng
3x 2y 1 0 là: x 2t x 2 x 3t x 2 t A. . B. . C. . D. . y 2 3t y 3 2t. y 3 2t y 3 2t
Câu 20.4.Phương trình tham số của đường thẳng : x y d 1 là: 4 3
x 4 3t
x 4 4t
x 4 4t x 4 3t A. . B. . C. . D. . y 4t y 3t. y 3t. y 4t
Câu21 TH Cho tam giác có 3 đỉnh tìm phương trình đường cao hoặc đường trung tuyến.
Câu 21.1.Cho tam giác ABC có (
A 2;1), B(0;3) và C(2; 1
) . Phương trình đường cao AH của tam giác ABC là:
A. x 2y 4 0 .
B. x 2y 4 0 .
C. 2x y 3 0 .
D. 2x y 3 0 .
Câu 21.2. Cho ba điểm A1; 2 , B5; 4 ,C 1
;4. Đường cao AA' của tam giác ABC có phương trình:
A. 3x 4y 8 0
B. 3x 4y 11 0
C. 6x 8y 11 0
D. 8x 6y 13 0
Câu 21.3. Cho tam giác ABC có A 4 ; 1 , B2; 7 ,C 5; 6
và đường thẳng d :3x y 11 0 . Quan hệ
giữa d và tam giác ABC là:
A. Đường cao vẽ từ A
B. Đường cao vẽ từ B
C. Đường trung tuyến vẽ từ A
D. Đường phân giác góc BAC
Câu 21.4. Phương trình tham số đường trung tuyến vẽ từ A của tam giác ABC với (
A 2;1), B(4;5) , C(2; 1 ) là:
x 3 2t
x 2 t A. . B. .
C. x 2y 9 0 .
D. 2x y 3 0.
y 3 t
y 1 t.
Bài 20. Vị trí tương đối hai đường thẳng
Câu 22 NB:Khảo sát vị trí tương đối của hai đường thẳng cho bởi phương trình tổng quát
Câu 22.1. Cho 2 đường thẳng 1: 11x 12y + 1 = 0 và 2: 12x + 11y + 9 = 0. Khẳng định nào sau đây ĐÚNG?
A. Hai đường thẳng song song.
B. Hai đường thẳng cắt nhau nhưng không vuông góc.
C. Hai đường thẳng trùng nhau.
D. Hai đường thẳng vuông góc nhau.
Câu 22.2.Xác định vị trí tương đối của hai đường thẳng sau đây : x 2y 1 0 : 3
x 6y 10 0 1 và 2 . A. Song song.
B. Cắt nhau nhưng không vuông góc. C. Trùng nhau. D. Vuông góc nhau.
Câu 22.3.Trong mặt phẳng toạ độ Oxy , cho hai đường thẳng : x 2y 1 0 , :3x y 7 0 . Nhận 1 2
định nào sau đây là đúng?
A. Hai đường thẳng và vuông góc với nhau.
B. và song song với nhau. 1 2 1 2
C. Hai đường thẳng và trùng nhau.
D. Hai đường thẳng và cắt nhau. 1 2 1 2
Câu 22.4. Cho đường thẳng : x 3y 4 0 . Đường thẳng nào sau đây song song với ? x 1 t x 1 t x 1 3t x 1 3t A. . B. . C. . D. .
y 2 3t
y 2 3t y 2 t y 2 t
Câu 23 NB:Xác định góc giữa hai đường thẳng cho bởi phương trình tham số hoặc tổng quát
Câu 23.1.Số đo góc giữa hai đường thẳng d : 2
x y 1 0 và d :3x y 5 0 bằng: 1 2 A. 30 . B. 60 . C. 90 . D. 45 . x 2 t
Câu 23.2.Góc giữa hai đường thẳng : 2
x y 7 0 và là 1 : 2
y 1 3t. A. 30 . B. 45 . C. 60 . D. 90 .
Câu 23.3. Góc giữa 2 đường thẳng 1 : 2x 2 3y 5 0và 2 : y 6 0 có số đo bằng: A. 600 B. 1250. C. 1450 D. 300
Câu 23.4.Góc giữa hai đường thẳng : 2x 4y 1 0 và : x 3y 1 0 là: 1 2 A. 0 . B. 45 . C. 60 . D. 90 .
Câu 24 NB:Tính khoảng cách từ điểm đến đường thẳng.
Câu 24.1.Trong mặt phẳng toạ độ Oxy , cho điểm A(5;0) và đường thẳng :12x 5y 5 0 . Khoảng cách
từ A đến đường thẳng là: A. 2. B. 8. C. 5. D. 6..
Câu 24.2. Khoảng cách từ O(0;0) đến đường thẳng : 4x 3y 5 0 là: A. 5 . B. 0. C. 1. D. 1 . 5
Câu 24.3. Khoảng cách giữa 2 đường thẳng 1 : 7x y 3 0 và 2 : 7x y 12 0 bằng 9 3 2 A. B. 9 C. . D. 15 50 2 x 1 2t Câu 24.4.
Khoảng cách từ M (4;2) đến đường thẳng d : là y 1 t A. 5. B. 5 . C. 1. D. 3 .
Câu 25 TH: Viết phương trình đường thẳng song song với đường thẳng cho trước Câu 25.1.
Phương trình tổng quát của đường thẳng qua điểm M (1;0) và song song với đường thẳng
: 4x 2 y 1 0 là
A. 4x 2y 3 0 .
B. 2x y 4 0 .
C. 2x y 2 0 .
D. x 2y 3 0 .
Câu 25.2.Cho đường thẳng : 3x y 2 0 . Phương trình nào dưới đây là phương trình của đường thẳng
song song với và đi qua gốc O?
A. x 3y 2 0.
B. 3x y 0 .
C. 3x y 2 0.
D. 3x y 4 0.
Câu 25.3. Trong mặt phẳng Oxy, cho đường thẳng song song với đường thẳng có phương trình:
4x 3y 5 0 và điểm M (2;1) cách một khoảng bằng 2. Phương trình của là:
A. 4x 3y 15 0 .
B. 4x 3y 5 0 .
C. 3x 4y 5 0 .
D. 3x 4y 15 0 .
Câu 25.4. Cho đường thẳng d đi qua hai điểm A(2;2), B(2;1) và đường thẳng đi qua C(1;2) và song
song với đường thẳng d . Phương trình tổng quát của đường thẳng là:
A. 3x 4y 11 0 .
B. 3x 4y 2 0.
C. 4x 3y 2 0.
D. 4x 3y 14 0 .
Câu 26 TH: Tìm đường cao hoặc diện tích tam giác nhờ công thức khoảng cách.
Câu 26.1. Trong mặt phẳng toạ độ, cho tam giác ABC có tọa độ các đỉnh là (
A 1;2), B(3;1),C(5;4). Phương
trình nào sau đây là phương trình đường cao của tam giác vẽ từ A?
A. 2x 3y 8 0..
B. 3x 2y 5 0..
C. 5x 6y 7 0.
D. 3x 2y 5 0..
Câu 25.2. Cho tam giác ABC có các đỉnh A(1;1), B(2;4),C(10;2) . Diện tích S của tam giác ABC là: A. S 3. B. 5 S .. C. 5 S .. D. 3 S .. 4 2 2
Câu 25.3. Cho tam giác ABC có các đỉnh A(0;2), B(2;0),C(2;0) Diện tích S của tam giác ABC là: A. S 4. B. S 6.. C. S 5.. D. S 3.
Câu 25.4. Tính Chiều cao AH của tam giác ABC có các đỉnh (
A 2;0), B(3;0),C(0;4) . A. AH 6. B. AH 5.. C. AH 4.. D. 7 AH .. 2
Bài 21: Đường tròn trong mặt phẳng tọa độ
Câu 27 NB: Tìm phương trình đường tròn khi cho tâm và bán kính.
Câu 27.1 Đường tròn có tâm trùng với gốc tọa độ, bán kính R = 1 có phương trình là:
A. x + (y + )2 2 1 = 1. B. 2 2
x + y = 1. C.
(x - )2 + (y - )2 1
1 = 1. D. (x + )2 + (y + )2 1 1 = 1.
Câu 27.2. Đường tròn có tâm I (1;2), bán kính R = 3 có phương trình là: A. 2 2
x + y + 2x + 4 y - 4 = 0. B. 2 2
x + y + 2x - 4 y - 4 = 0. C. 2 2
x + y - 2x + 4 y - 4 = 0. D. 2 2
x + y - 2x - 4 y - 4 = 0.
Câu 27.3. Đường tròn (C)có tâm I (1;- )
5 và đi qua O (0;0) có phương trình là:
A. (x + )2 + (y- )2 1 5 = 26.
B. (x + )2 + (y- )2 1 5 = 26.
C. (x - )2 + (y + )2 1 5 = 26.
D. (x - )2 + (y + )2 1 5 = 26.
Câu 27.4. Đường tròn đường kính AB với (
A 2;1), B(4;5) có phương trình là:
A. (x- )2 + (y + )2 3 3 = 5.
B. (x+ )2 + (y- )2 3 3 = 20.
C. (x+ )2 + (y- )2 2 1 = 10.
D. (x+ )2 + (y- )2 3 3 = 5.
Câu 28NB Tìm tâm, bán kính của đường tròn cho bởi phương trình:
Câu 28.1.Cho đường tròn 2 2
(C) : (x 1) (y 2) 25 . Đường tròn (C) có:
A. Tâm I(1;2) và bán kính R 25 . B. Tâm I( 1 ; 2
) và bán kính R 25 .
C. Tâm I(1;2) và bán kính R 5. D. Tâm I( 1 ; 2
) và bán kính R 5.
Câu 28.2. Đường tròn
có tâm I và bán kính R lần lượt là: A. I (3;- ) 1 , R = 4. B. I (- 3; ) 1 , R = 4. C. I (3;- ) 1 , R = 2. D. I (- 3; ) 1 , R = 2.
Câu 28.3. Đường tròn
có tâm I và bán kính R lần lượt là: A. I (2;- ) 3 , R = 5. B. I (- 2; ) 3 , R = 5. C.
I (- 4;6), R = 5. D. I (- 2; ) 3 , R = 1.
Câu 28.4. Tọa độ tâm I và bán kính R của đường tròn 2 2
(C) : (x 2) (y 1) 8 là: A. I (2;- )
1 , R = 2 2. B. I (- 2; ) 1 , R = 2 2. C. I (2;- )
1 , R = 8. D. I (- 2; ) 1 , R = 8.
Câu 29TH Viết phương trình tiếp tuyến của đường tròn.
Câu 29.1. Phương trình tiếp tuyến của đường tròn 2 2
(C) : (x 2) (y 3) 25 tại điểm M (5;1) là
A. 3x 4y 9 0 . B. 3x 4y 19 0 . C. 4x 3y 19 0 . D. 3x 4y 9 0 .
Câu 29.2. Phương trình tiếp tuyến của đường tròn 2 2
(C) : (x 2) (y 4) 25 vuông góc với đường thẳng
3x 4y 5 0 là:
A. 4x 3y 21 0;4x 3y 29 0 .
B. 4x 3y 21 0;4x 3y 29 0 .
C. 4x 3y 21 0;4x 3y 29 0 .
D. 3x 4y 21 0;3x 4y 29 0 .
Câu 29.3. Phương trình tiếp tuyến của đường tròn 2 2
x y 2x 4y 4 0 tại điểm ( A 1;5) là
A. x y 5 0 .
B. y 5 0 .
C. y 5 0 .
D. x y 5 0 .
Câu 29.4. Phương trình tiếp tuyến của đường tròn 2 2
x y 2x 4y 3 0 tại điểm M (3;4) là
A. x y 7 0 .
B. x y 7 0 .
C. x y 7 0 .
D. x y 3 0 .
Bài 22: Ba đường conic
Câu 30 NB. Tìm tiêu điểm, tiêu cự của Elip 2 2
Câu 30.1. Cho Elip x y
1 điểm nào sau đây là một tiêu điểm của Elip: 16 7
A. F(3;0). B. F(0;3) .
C. F(0;3). D. F(3;3) . 2 2
Câu 30.2. Đường Elip x y 1 có tiêu cự bằng: A. 6 . B. 8 . C. 9 . D. 3 . 16 7 2 2
Câu 30.3. Cho Elip x y
1 điểm nào sau đây là một tiêu điểm của Elip: 4 1 A. F( 3;0) . B. F(3;0) . C. F(2;0). D. F(0;2). 2 2
Câu 30.4. Đường Elip x y
1 có tiêu cự bằng: A. 2 3 . B. 2 3 . C. 3 . D. 2 . 4 1
Câu 31NB Tìm tiêu điểm, tiêu cự của Hypebol 2 2
Câu 31.1. Cho Hypebol x y
1 điểm nào sau đây là một tiêu điểm của Hypebol: 16 7 A. F( 23;0) . B. F(4;0) . C. F( 7;0). D. F( 7;0) . 2 2
Câu 31.2. Cho Hypebol x y
1 tiêu cự Hypebol bằng: A. 2 23 . B. 23 . C. 4. D. 8. 16 7 2
Câu 31.3. Cho Hypebol x 2
y 1 điểm nào sau đây là một tiêu điểm của Hypebol: 4
A. F( 5;0) . B. F(0;3) .
C. F(0;3). D. F(3;3) . 2
Câu 31.4. Cho Hypebol x 2
y 1 tiêu cự Hypebol bằng: A. 2 5 . B. 5 . C. 3 . D. 2 3 4
Câu 32NB Tìm tiêu điểm, đường chuẩn Parabol
Câu 32.1. Parabol y2 =2 2 x có tiêu điểm là: A. 2 F( ;0). B. 2 F( ;0). C. F( 2;0). D. 2 F(0; ). 2 2 2
Câu 32.2. Đường thẳng nào là đường chuẩn của parabol y 3 2 = x? 2 A. x = 3 . B. x = 3 . C. x = - 3 . D. x = 3 . 8 2 4 4
Câu 32.3. Khoảng cách từ tiêu điểm đến đường chuẩn của parabol 2 y 3x là A. 3 d(F,) .
B. d(F,) 3. C. 3 d(F,) . D. 3 d(F,) . 2 4 8
Câu 32.4. Khoảng cách từ tiêu điểm đến đường chuẩn của parabol 2
y 4x là:
A. d(F,) 2
B. d(F,) 4.
C. d(F,) 1 D. 1 d(F,) . 2
Câu 33 TH Viết phương trình chính tắc của Elip
Câu 33.1. Phương trình chính tắc của Elip đi qua 5 M 2;
và có một tiêu điểm F 2;0 là: 1 3 2 2 2 2 2 2 2 2 A. : x y E
1. B. : x y E
1.C. : x y E
1. D. : x y E 1. 9 5 9 5 5 9 5 3
Câu 33.2. Phương trình chính tắc của Elip (E) nhận F 5;0 là một tiêu điểm và tổng khoảng cách từ một 2
điểm bất kì thuộc Elip đến hai tiêu điểm bằng 14 là: 2 2 2 2 2 2 2 2 A. : x y E
1 . B. : x y E 1 . C. : x y E 1. D. : x y E 1 . 49 24 24 49 25 24 49 25
Câu 33.3. Phương trình chính tắc của Elip đi qua hai điểm M 2; 2 và N 6; 1là : 2 2 2 2 2 2 2 2 A. : x y E x y
1. B. E : 1 . C. : x y E 1. D. : x y E 1. 8 4 2 2 4 4 8 8 4
Câu 33.4. Lập phương trình chính tắc của Elip, biết một trong hai tiêu điểm của Elip là F (4;0) và chu vi 1
của tam giác MF F bằng 18 với M nằm trên (E). 1 2 2 2 2 2 2 2 2 2 A. : x y E 1. B. : x y E 1. C. : x y E 1. D. : x y E 1. 5 3 5 1 4 3 5 3
Câu 34TH: Viết phương trình chính tắc của Hypebol
Câu 34.1. Viết phương trình chính tắc của Hypebol, biết giá trị tuyệt đối hiệu các bán kính qua tiêu của điểm
M bất kỳ trên hypebol là 8, tiêu cự bằng 10. 2 2 2 2 2 2 2 2
A. x y 1
B. x y 1.
C. x y 1.
D. x y 1. 16 9 4 3 4 3 9 16
Câu 34.2. Hypebol có một trong hai tiêu điểm là F(-2;0) và đi qua A(1;0) có phương trình là: 2 2 2 2 2 2 2 2 A. y x 1. B. y x 1. C. x y 1. D. x y 1. 1 3 1 3 3 1 1 3
Câu 34.3 Viết phương trình chính tắc của Hypebol (H) biết (H) đi qua M (3 2;4) và có một trong hai tiêu điểm là F(5;0). 2 2 2 2 2 2 2 2 A. x y 1 B. x y 1. C. x y 1.
D. x y 1. 9 16 16 9 4 3 9 16
Câu 34.4. Lập phương trình chính tắc của Hypebol biết nó đi qua điểm M 1; 0 và tiêu cự bằng 4. 2 2 2 2 2 2 A. x 2 y 1.
B. x y 1.
C. x y 1. D. 2 y x 1. 3 2 4 6 5 3
Câu 35TH: Viết phương trình chính tắc của Parabol (xem bài 7.25 trang 56)
Câu 35.1 Khúc cua của một con đường có dạng hình parabol, điểm đầu vào khúc cua là A điểm cuối là B,
khoảng cách AB 400m Đỉnh parabol (P) của khúc cua cách đường thẳng một khoảng 20 m và cách
đều A, B .Phương trình chính tắc của (P), với 1 đơn vị đo trong mặt phẳng toạ độ tương ứng 1 m trên thực tế là: A. E 2
y 2000x . B. E 2 y 200x . C. E 2
y 100x . D. E 2 y 1000x .
Câu 35.2 Khúc cua của một con đường có dạng hình parabol, điểm đầu vào khúc cua là A điểm cuối là B,
khoảng cách AB 150m Đỉnh parabol (P) của khúc cua cách đường thẳng một khoảng 20 m và cách
đều A, B Phương trình chính tắc của (P), với 1 đơn vị đo trong mặt phẳng toạ độ tương ứng 1 km trên thực tế là: A. E 2 9 y x . B. E 2 9 y x . C. E 2 32 y x . D. E 2 64 y x . 32 64 9 9
Câu 35.3. Một cái Cổng trại có dạng hình Parabol chiều rộng của cổng 4m chiều cao của cổng 3m Phương
trình chính tắc của (P) với 1 đơn vị đo trong mặt phẳng toạ độ tương ứng 1 m trên thực tế là: A. E 2 4 y x. B. E 2 2 y x. C. E 2 3 y x. D. E 2 3 y x. 3 3 4 2
Câu 35.4. Quỹ đạo của một viên đạn được bắn lên từ mặt đất có dạng hình Parabol ngay sau khi đạt độ cao
800 m thì bắt đầu rơi, biết vị trí rơi cách vị trí bắn 600m. Phương trình chính tắc của (P) với 1 đơn vị đo
trong mặt phẳng toạ độ tương ứng 1 km trên thực tế là: A. E 2 9 y x . B. E 2 9 y x. C. E 2 80 y x . D. E 2 160 y x . 80 160 9 9 II. TỰ LUẬN
Câu 1:VDT (1.0 điểm ) Bài toán ứng dụng hàm số bậc hai trong thực tế (tham khảo bài vận dụng 2 trang 15; bài 6.12-6.14 trang 16)
Câu 2:VDT (1.0 điểm ) Ứng dụng dấu tam thức bậc hai (tham khảo bài 6.17-6.19 trang 24)
Câu 3:VDC (1,0 điểm) Viết phương trình đường thẳng tổng hợp.




