-
Thông tin
-
Quiz
Đề cương ôn tập giữa học kì 2 môn Toán 8 bộ sách Cánh Diều
Xin giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 8 tài liệu đề cương hướng dẫn nội dung ôn tập giữa học kì 2 môn Toán 8 bộ sách Cánh Diều, có đáp án và lời giải chi tiết.
PHẦN I. TÓM TẮT NỘI DUNG KIẾN THỨC.
A. Thống kê và xác suất.
Chương VI. Một số yếu tố thống kê và xác suất.
– Thu thập và phân loại dữ liệu.
– Mô tả và biểu diễn dữ liệu trên các bảng, biểu đồ.
– Phân tích và xử lí dữ liệu thu được ở dạng bảng, biểu đồ.
– Xác suất của biến cố ngẫu nhiên trong một số trò chơi đơn giản.
– Xác suất thực nghiệm của một biến cố trong một số trò chơi đơn giản.
B. Hình học.
Chương IX. Tam giác đồng dạng. Hình đồng dạng.
– Định lí Thalès và ứng dụng trong tam giác.
– Đường trung bình của tam giác.
– Tính chất đường phân giác của tam giác.
PHẦN II. MỘT SỐ CÂU HỎI VÀ BÀI TẬP THAM KHẢO.
A. Bài tập trắc nghiệm.
B. Bài tập tự luận.
1. Một số yếu tố thống kê và xác suất.
+ Dạng 1. Các bài toán về thống kê.
+ Dạng 2. Các bài toán về xác suất.
2. Hình học.
3. Một số bài toán thực tế liên quan đến hình học.
4. Một số dạng khác.
PHẦN III. HƯỚNG DẪN GIẢI CHI TIẾT.
Tài liệu chung Toán 8 211 tài liệu
Toán 8 1.8 K tài liệu
Đề cương ôn tập giữa học kì 2 môn Toán 8 bộ sách Cánh Diều
Xin giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 8 tài liệu đề cương hướng dẫn nội dung ôn tập giữa học kì 2 môn Toán 8 bộ sách Cánh Diều, có đáp án và lời giải chi tiết.
PHẦN I. TÓM TẮT NỘI DUNG KIẾN THỨC.
A. Thống kê và xác suất.
Chương VI. Một số yếu tố thống kê và xác suất.
– Thu thập và phân loại dữ liệu.
– Mô tả và biểu diễn dữ liệu trên các bảng, biểu đồ.
– Phân tích và xử lí dữ liệu thu được ở dạng bảng, biểu đồ.
– Xác suất của biến cố ngẫu nhiên trong một số trò chơi đơn giản.
– Xác suất thực nghiệm của một biến cố trong một số trò chơi đơn giản.
B. Hình học.
Chương IX. Tam giác đồng dạng. Hình đồng dạng.
– Định lí Thalès và ứng dụng trong tam giác.
– Đường trung bình của tam giác.
– Tính chất đường phân giác của tam giác.
PHẦN II. MỘT SỐ CÂU HỎI VÀ BÀI TẬP THAM KHẢO.
A. Bài tập trắc nghiệm.
B. Bài tập tự luận.
1. Một số yếu tố thống kê và xác suất.
+ Dạng 1. Các bài toán về thống kê.
+ Dạng 2. Các bài toán về xác suất.
2. Hình học.
3. Một số bài toán thực tế liên quan đến hình học.
4. Một số dạng khác.
PHẦN III. HƯỚNG DẪN GIẢI CHI TIẾT.
Chủ đề: Tài liệu chung Toán 8 211 tài liệu
Môn: Toán 8 1.8 K tài liệu
Thông tin:
Tác giả:
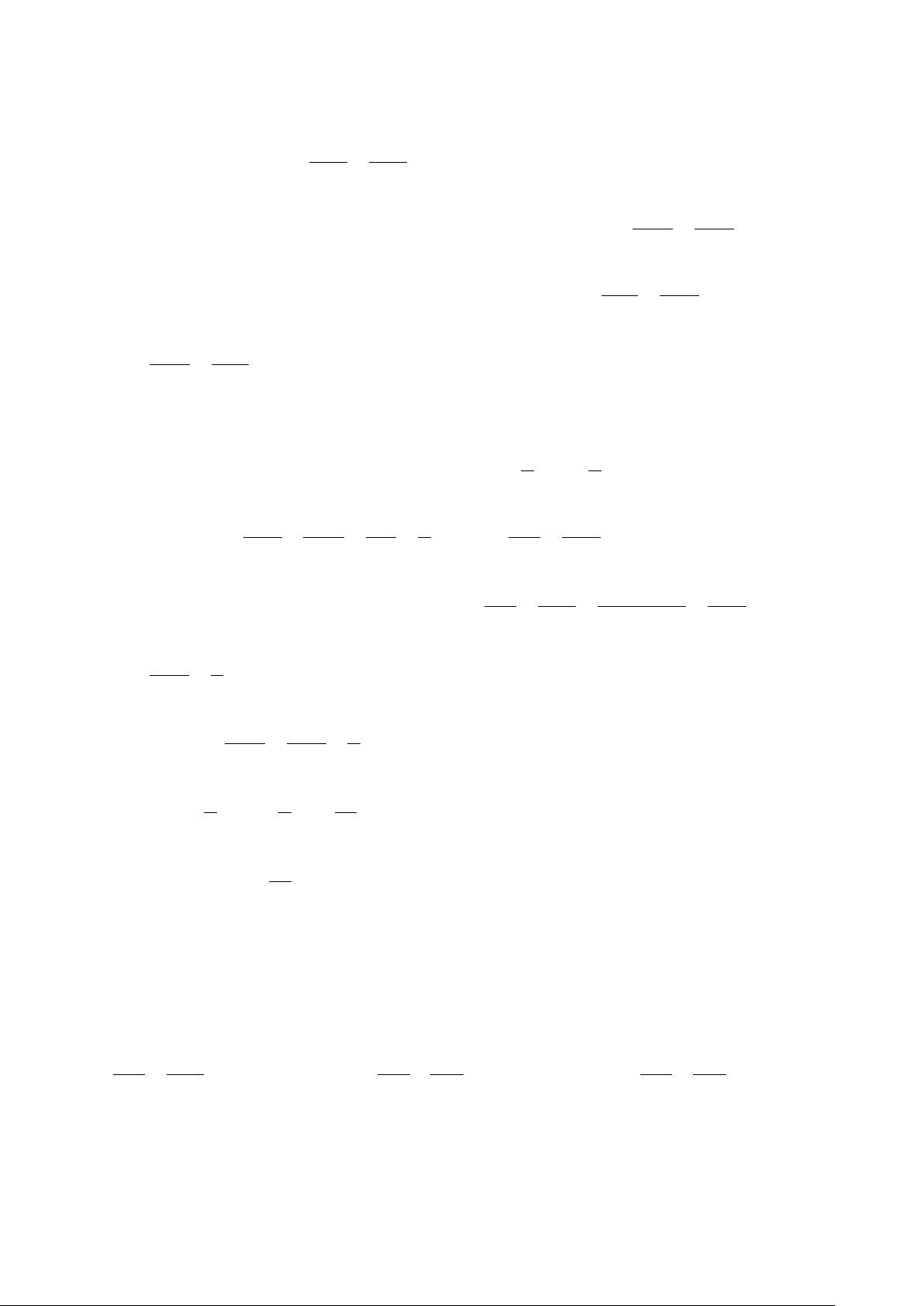
Preview text:
ĐỀ CƯƠNG ÔN TẬP GIỮA HỌC KÌ II
BỘ SÁCH: CÁNH DIỀU MÔN TOÁN – LỚP 8
PHẦN I. TÓM TẮT NỘI DUNG KIẾN THỨC
A. Thống kê và xác suất
Chương VI. Một số yếu tố thống kê và xác suất
– Thu thập và phân loại dữ liệu.
– Mô tả và biểu diễn dữ liệu trên các bảng, biểu đồ.
– Phân tích và xử lí dữ liệu thu được ở dạng bảng, biểu đồ.
– Xác suất của biến cố ngẫu nhiên trong một số trò chơi đơn giản.
– Xác suất thực nghiệm của một biến cố trong một số trò chơi đơn giản. B. Hình học
Chương IX. Tam giác đồng dạng. Hình đồng dạng
– Định lí Thalès và ứng dụng trong tam giác.
– Đường trung bình của tam giác.
– Tính chất đường phân giác của tam giác.
PHẦN II. MỘT SỐ CÂU HỎI, BÀI TẬP THAM KHẢO A. Bài tập trắc nghiệm
Khoanh tròn chữ cái đứng trước câu trả lời đúng.
Câu 1. Hôm nay, lớp bạn Minh trực cổng trường. Bạn Minh ngồi trước cổng trường để
ghi lại các bạn học sinh đi học trễ. Hỏi bạn Minh đã thu thập dữ liệu theo phương pháp nào sau đây? A. Từ nguồn có sẵn. B. Quan sát. C. Lập bảng hỏi. D. Phỏng vấn.
Câu 2. Trong các phương pháp thu thập dữ liệu sau, phương pháp thu thập nào là trực tiếp? A. Xem tin tức trên ti vi.
B. Tìm hiểu thông tin qua sách. C. Tra cứu trên Internet; D. Làm thí nghiệm.
Câu 3. Nhân dịp nghỉ hè, gia đình bạn An muốn đi tắm biển ở Đà Nẵng. Trước khi đi
Đà Nẵng 1 tuần, bạn An đã vào website của Trung tâm dự báo khí tượng thủy văn quốc
gia để tìm hiểu về tình hình thời tiết ở đó. Hỏi bạn An đã dùng phương pháp nào sau
đây để thu thập dữ liệu?
A. Thu thập dữ liệu gián tiếp.
B. Thu thập dữ liệu trực tiếp. C. Phỏng vấn. D. Làm thí nghiệm.
Câu 4. Trong các trường hợp sau, trường hợp nào là thu thập dữ liệu gián tiếp?
A. Phỏng vấn các bạn học sinh về tình hình bạo lực học đường.
B. Lập phiếu hỏi về các món ăn mà các bạn trong lớp yêu thích.
C. Tìm hiểu trên mạng Internet về số ca mắc bệnh COVID-19 ở Việt Nam.
D. Làm thí nghiệm để xác định tính chất hóa học của oxygen.
Câu 5. Trong các dãy dữ liệu sau đây, dữ liệu nào là số liệu liên tục?
A. Số học sinh của mỗi lớp khối 8.
B. Tên các bạn tổ 1 của lớp 8A.
C. Tuổi nghề của các công nhân trong một phân xưởng.
D. Nhiệt độ trung bình (độ C) của các ngày trong năm.
Câu 6. Trong các dãy dữ liệu sau đây, dữ liệu nào là số liệu rời rạc?
A. Số thành viên trong một gia đình.
B. Cân nặng (kg) của các học sinh lớp 8D.
C. Kết quả nhảy xa (mét) của 10 vận động viên.
D. Lượng mưa trung bình (mm) trong một tháng ở Thành phố Hồ Chí Minh.
Câu 7. Kết quả đánh giá mức độ hài lòng của khách hàng về chất lượng dịch vụ của
một khách sạn: Hài lòng, Rất hài lòng, Bình thường, Không hài lòng. Hỏi dữ liệu trên là loại dữ liệu nào?
A. Dữ liệu không là số, có thể sắp thứ tự.
B. Dữ liệu không là số, không thể sắp thứ tự. C. Số liệu rời rạc. D. Số liệu liên tục.
Câu 8. Cho bảng thống kê tỉ lệ các loại mẫu vật trong bảo tàng sinh vật của môi trường
đại học về những lớp động vật có xương sống: Cá, Lưỡng cư, Bò sát, Chim, Thú. Lớp động vật
Tỉ lệ mẫu vật (%) Cá 15% Lưỡng cư 10% Bò sát 20% Chim 25% Thú 30% Tổng 101%
Giá trị chưa hợp lí trong bảng dữ liệu là
A. Dữ liệu về tên các lớp động vật.
B. Dữ liệu về tỉ lệ mẫu vật.
C. Cả A và B đều đúng. D. Cả A và B đều sai.
Câu 9. Khi muốn biểu diễn sự thay đổi của một đại lượng theo thời gian ta nên dùng
loại biểu đồ nào sau đây? A. Biểu đồ tranh.
B. Biểu đồ hình quạt tròn. C. Biểu đồ cột kép.
D. Biểu đồ đoạn thẳng.
Câu 10. Khi muốn so sánh hai tập dữ liệu khác nhau ta nên dùng loại biểu đồ nào sau đây? A. Biểu đồ tranh. B. Biểu đồ cột. C. Biểu đồ cột kép.
D. Biểu đồ đoạn thẳng.
Câu 11. Bạn Minh muốn lập biểu đồ về tỉ lệ số học sinh của lớp 8A xếp loại học lực Tốt,
Khá, Đạt, Chưa đạt ở cuối học kì I. Hỏi bạn Minh nên sử dụng biểu đồ nào sau đây? A. Biểu đồ tranh. B. Biểu đồ cột.
C. Biểu đồ hình quạt tròn.
D. Biểu đồ đoạn thẳng.
Câu 12. Lựa chọn biểu đồ tranh khi muốn
A. so sánh trực quan từng cặp số liệu của hai bộ dữ liệu cùng loại.
B. biểu thị tỉ lệ phần trăm của từng loại số liệu so với tổng thể.
C. biểu diễn sự thay đổi số liệu của một đối tượng theo thời gian.
D. biểu diễn số lượng các loại đối tượng khác nhau, tạo sự lôi cuốn, thu hút bằng hình ảnh.
Câu 13. Dùng loại biểu đồ nào để biểu diễn dữ liệu trong bảng thống kê sau đây là phù hợp nhất?
Xếp loại học lực cuối học kì I của học sinh khối 8
Trường Trung học cơ sở Kim Đồng Loại học lực Số học sinh Tốt 37 Khá 140 Đạt 53 Chưa đạt 10 A. Biểu đồ tranh.
B. Biểu đồ đoạn thẳng.
C. Biểu đồ hình quạt tròn. D. Biểu đồ cột.
Câu 14. Để biểu diễn sự thay đổi sĩ số của các lớp trong một khối ở cuối năm so với
đầu năm học, ta nên chọn loại biểu đồ nào sau đây? A. Biểu đồ tranh. B. Biểu đồ cột. C. Biểu đồ cột kép.
D. Biểu đồ đoạn thẳng.
Câu 15. Quan sát biểu đồ sau:
Tỉ lệ phần trăm sản lượng gạo của Việt Nam
xuất khẩu sang các nước liên minh Châu Âu
trong 6 tháng đầu năm 2022 17% Italy Đức 5% 39% Hà Lan 7% Thụy Điển Ba Lan 13% Khác 19%
Sản lượng gạo xuất khẩu của Việt Nam sang Italy gấp mấy lần sản lượng gạo xuất khẩu của Việt Nam sang Ba Lan? A. 7,8 lần. B. 7 lần. C. 8,7 lần. D. 8 lần.
Câu 16. Quan sát biểu đồ sau:
Số doanh nghiệp thành lập mới và giải thể
của Việt Nam giai đoạn 2017 - 2019 149000 138100 126859 131275 129000 109000 89000 Doanh nghiệp thành lập mới 69000 Doanh nghiệp 49000 giải thể 29000 12113 16314 16800 9000 2017 2018 2019
(Nguồn: Tổng cục thống kê)
Trong giai đoạn 2017 – 2019:
A. Số doanh nghiệp thành lập mới và giải thể đều giảm.
B. Số doanh nghiệp thành lập mới tăng nhanh hơn số doanh nghiệp giải thể.
C. Số doanh nghiệp giải thể tăng nhanh hơn số doanh nghiệp thành lập mới.
D. Số doanh nghiệp thành lập mới giảm, số doanh nghiệp giải thể tăng.
Câu 17. Quan sát biểu đồ sau:
Chênh lệch nhiệt độ tại TP. Hồ Chí Minh Nhiệt độ (°C)
từ 16/01/2023 đến 22/01/2023 35 33 31 32 31 32 32 32 30 25 23 22 22 22 23 22 22 20 Nhiệt độ cao nhất 15 Nhiệt độ 10 thấp nhất 5
0 Thứ Hai Thứ Ba Thứ Tư Thứ Năm Thứ Sáu Thứ Bảy Chủ nhật Ngày trong tuần
(Nguồn : Trung tâm Dự báo khí tượng thủy văn quốc gia)
Ngày nào sau đây chênh lệch giữa nhiệt độ cao nhất và nhiệt độ thấp nhất trong tuần
của TP. Hồ Chí Minh là 9 C? ° A. Thứ Năm. B. Thứ Bảy. C. Chủ nhật. D. Thứ Hai.
Câu 18. Biểu đồ dưới đây thể hiện số sách trong thư viện của một lớp. Môn học Số sách Toán Ngữ văn Tin học Lịch sử và Địa lí Khoa học tự nhiên : 2 quyển sách
Khẳng định nào sau đây là đúng?
A. Số sách Toán trong thư viện là 7 quyển.
B. Số sách Ngữ Văn nhiều hơn số sách Tin học là 2 quyển.
C. Tổng số sách trong thư viện là 21 quyển.
D. Số sách Khoa học tự nhiên nhiều hơn số sách Lịch sử và Địa lí là 8 quyển.
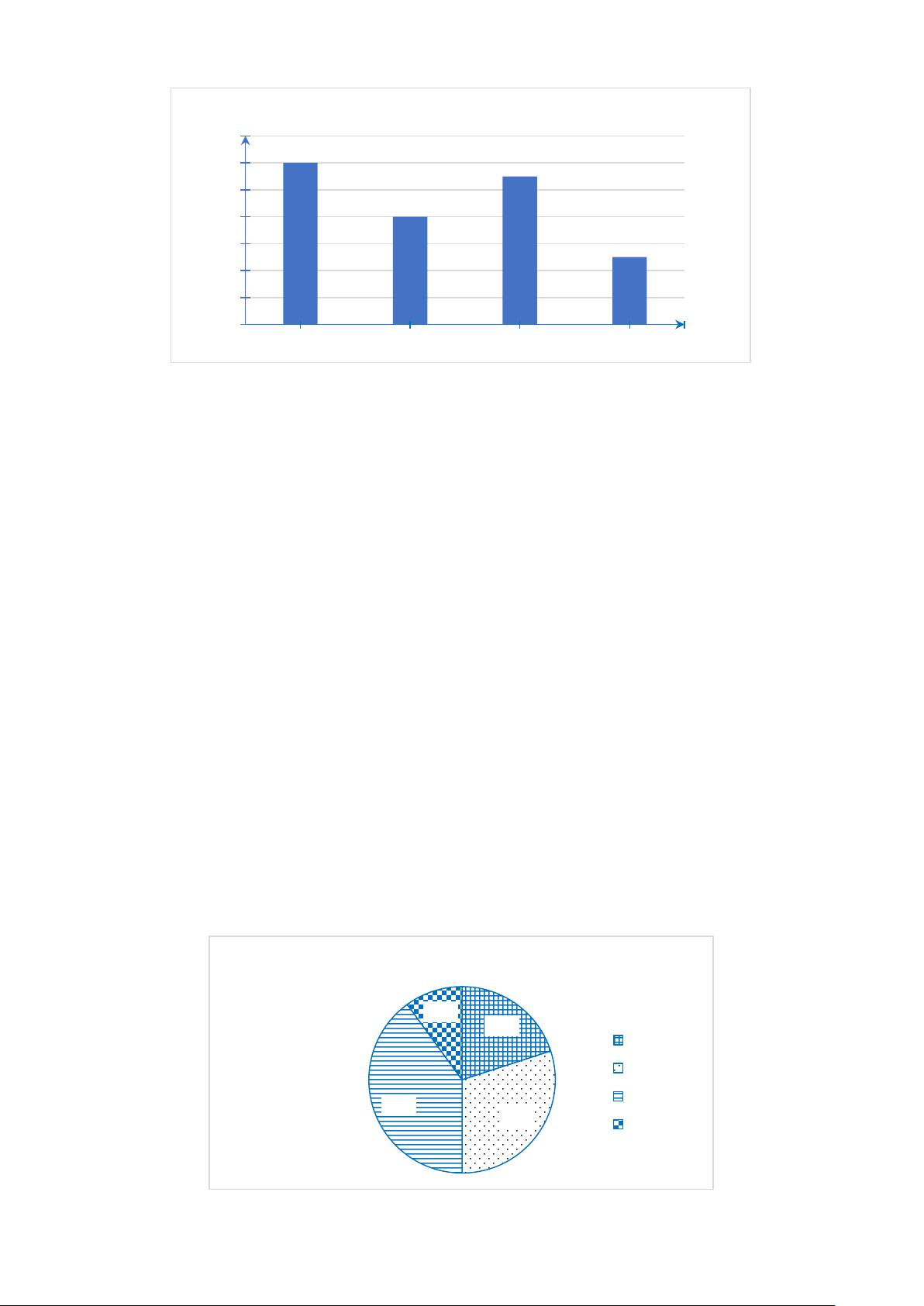
Câu 19. Biểu đồ dưới đây biểu diễn số lượng học sinh của một lớp chọn loại nước
uống trong đợt liên hoan cuối năm. Biết mỗi học sinh chỉ chọn một loại nước uống và
tất cả học sinh của lớp đều tham gia bình chọn. Số người chọn 14 12 12 11 10 8 8 6 5 4 2 0 Nước cam Nước dừa Nước chanh
Nước mía Loại nước
Khẳng định nào sau đây là sai? A. Lớp có 36 học sinh.
B. Loại nước được yêu thích nhất trong lớp là nước cam.
C. Số học sinh chọn nước dừa nhiều hơn số học sinh chọn nước mía.
D. Tổng số học sinh chọn nước dừa và nước mía ít hơn số học sinh chọn nước cam.
Câu 20. Biểu đồ dưới đây biểu diễn tỉ lệ hoa quả bán được trong một ngày của một
cửa hàng. Biết ngày hôm đó cửa hàng bán được 150 kg hoa quả.
Tỉ lệ các loại quả bán được 10% 20% Lê Táo Nhãn 40% 30% Nho
Khẳng định nào sau đây là đúng?
A. Cửa hàng bán được 30 kg táo.
B. Khối lượng nhãn bán được nhiều hơn khối lượng nho bán được là 30 kg.
C. Cửa hàng bán được tổng cộng 45 kg lê và nho.
D. Khối lượng nhãn bán được là 40 kg.
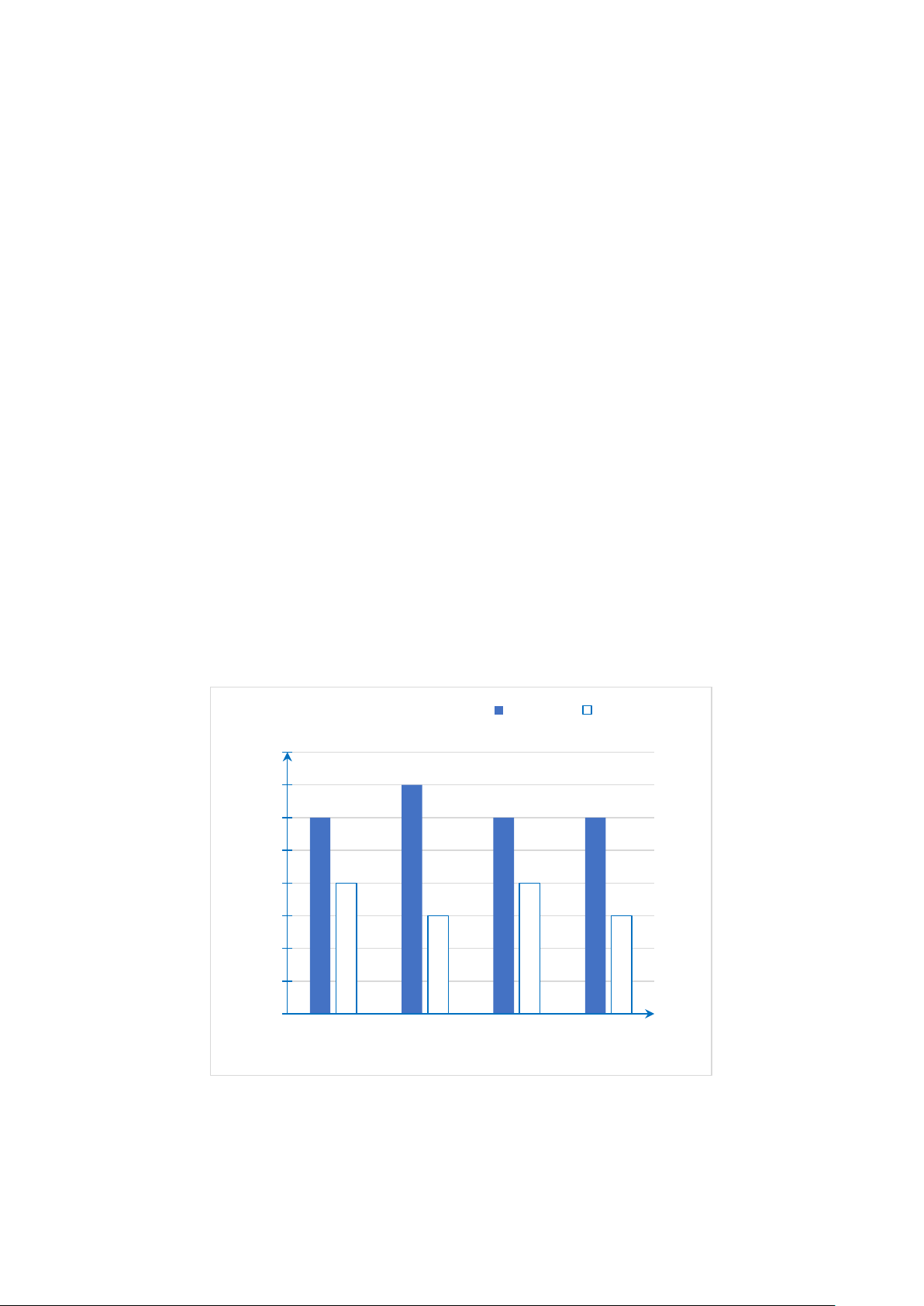
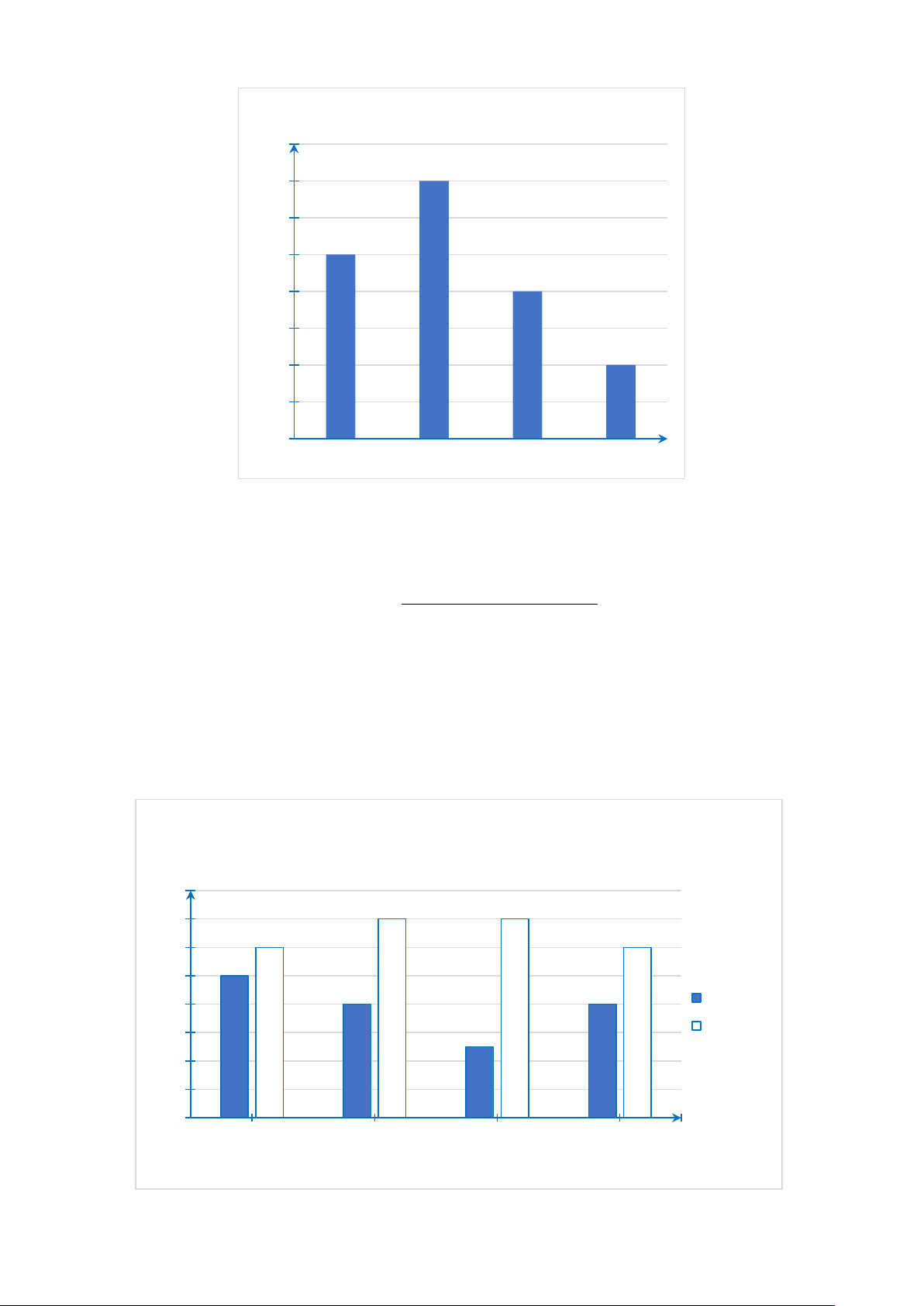
Câu 21. Một công ty kinh doanh vật liệu xây dựng có bốn kho hàng có 50 tấn hàng.
Kế toán của công ty lập biểu đồ cột kép ở hình bên biểu diễn số lượng vật liệu đã xuất
bán và số lượng vật liệu còn tồn lại trong mỗi kho sau tuần lễ kinh doanh đầu tiên. Số lượng Xuất bán Tồn tại vật liệu (tấn) 40 35 35 30 30 30 30 25 20 20 20 15 15 15 10 5 0 Kho 1 Kho 2 Kho 3 Kho 4 Kho
Kế toán đã ghi nhầm số liệu của một kho trong biểu đồ cột kép đó. Theo em, kế toán
đã ghi nhầm số liệu ở kho nào? A. Kho 1. B. Kho 2 và kho 4. C. Kho 1 và kho 3. D. Kho 4.
Sử dụng biểu đồ dưới đây để trả lời các câu hỏi Câu 22, Câu 23.
Biểu đồ dưới đây biểu diễn doanh thu du lịch lữ hành theo giá hiện hành tại Đà Nẵng
qua các năm 2019, 2020, 2021, 2022 (sơ bộ): Tỉ đồng 2500 2267,09 2113,3 1905,6 2000 1500 1000 563,8 635,71 500 0 2018 2019 2020 2021 2022 (sơ bộ) Năm
(Nguồn: Tổng cục thống kê)
Câu 22. Doanh thu du lịch lữ hành theo giá hiện hành tại Đà Nẵng năm 2021 là
A. 1 905,6 tỉ đồng. B. 2 113,3 tỉ đồng. C. 563,8 tỉ đồng. D. 635,71 tỉ đồng.
Câu 23. So với năm 2020, năm 2022 (số liệu sơ bộ) tăng khoảng bao nhiêu phần trăm
(làm tròn kết quả đến hàng đơn vị)? A. 25%. B. 125%. C. 302%. D. 402%.
Sử dụng nội dung sau để trả lời các câu hỏi Câu 24, Câu 25 và Câu 26.
Một hộp chứa 6 tấm thẻ như nhau được đánh số từ 3 đến 8. Rút ngẫu nhiên một tấm thẻ từ hộp.
Câu 24. Có bao nhiêu kết quả có thể? A. 3. B. 5. C. 6. D. 8.
Câu 25. Có bao nhiêu kết quả thuận lợi của biến cố “Rút được tấm thẻ đánh số chẵn”? A. 3. B. 5. C. 6. D. 8.
Câu 26. Có bao nhiêu kết quả thuận lợi của biến cố “Rút được tấm thẻ đánh số chia hết cho 3”? A. 1. B. 2. C. 3. D. 4.
Sử dụng nội dung sau để trả lời các câu hỏi Câu 27, Câu 28 và Câu 29.
Tổ Cường có 13 bạn, gồm có 8 bạn nam và 5 bạn nữ, trong đó có 3 bạn nam và 1 bạn
nữ tham gia vào câu lạc bộ thể thao. Chọn ngẫu nhiên 1 bạn từ tổ.
Câu 27. Xác suất của biến cố “Bạn được chọn có tham gia câu lạc bộ thể thao” là A. 4 . B. 5 . C. 8 . D. 1 . 13 13 13 13
Câu 28. Xác suất của biến cố “Bạn được chọn là bạn nữ tham gia vào câu lạc bộ thể thao” là A. 4 . B. 5 . C. 8 . D. 1 . 13 13 13 13
Câu 29. Xác suất của biến cố “Bạn được chọn là bạn nam không tham gia câu lạc bộ thể thao” là A. 4 . B. 5 . C. 8 . D. 1 . 13 13 13 13
Sử dụng nội dung sau để trả lời các câu hỏi Câu 30 và Câu 31.
Phỏng vấn 200 bạn sinh viên về một quyển sách thì có 40 bạn sinh viên thích quyển sách này.
Câu 30. Xác suất thực nghiệm của biến cố “Một bạn sinh viên thích quyển sách” là A. 20%. B. 30%. C. 15%. D. 40%.
Câu 31. Phỏng vấn ngẫu nhiên thêm 60 bạn sinh viên. Dự đoán trong 60 bạn sinh viên
được phỏng vấn, số sinh viên thích quyển sách là A. 20. B. 12. C. 15. D. 10.
Sử dụng bảng thống kê sau để trả lời các câu hỏi từ Câu 32 đến Câu 25.
Hai bạn Dũng và Nam chơi 1 ván oẳn tù tì gồm 10 lần theo luật chơi: Búa (B) thắng
Kéo (K); Kéo (K) thắng Lá (L), Lá (L) thắng Búa (B) và hòa nhau nếu cùng loại. KÉO – Thắng KÉO LÁ BÚA – Thắng LÁ – Thắng BÚA
Sau đây là kết quả của mỗi ván chơi: Lần thứ 1 2 3 4 5 6 7 8 9 10 Dũng L B B K L B K B K K Nam B K L L K B L K L B
Câu 32. Xác suất thực nghiệm của sự kiện “Dũng ra búa” là A. 3 . B. 1 . C. 2 . D. 1 . 10 2 5 5
Câu 33. Xác suất thực nghiệm của sự kiện “Dũng thắng” là A. 3 . B. 3 . C. 2 . D. 1 . 10 5 5 2
Câu 34. Xác suất thực nghiệm của sự kiện “Dũng và Nam hòa nhau” là A. 4 . B. 1 . C. 1 . D. 2 . 5 2 10 5
Câu 35. Xác suất thực nghiệm của sự kiện “Nam không thua Dũng” là A. 4 . B. 1 . C. 1 . D. 2 . 5 2 10 5
Câu 36. Cho điểm M thuộc đoạn thẳng AB, thỏa mãn AM 3 = . Tỉ số AM là MB 8 AB A. 5. B. 5 . C. 3 . D. 8 . 8 11 11 11
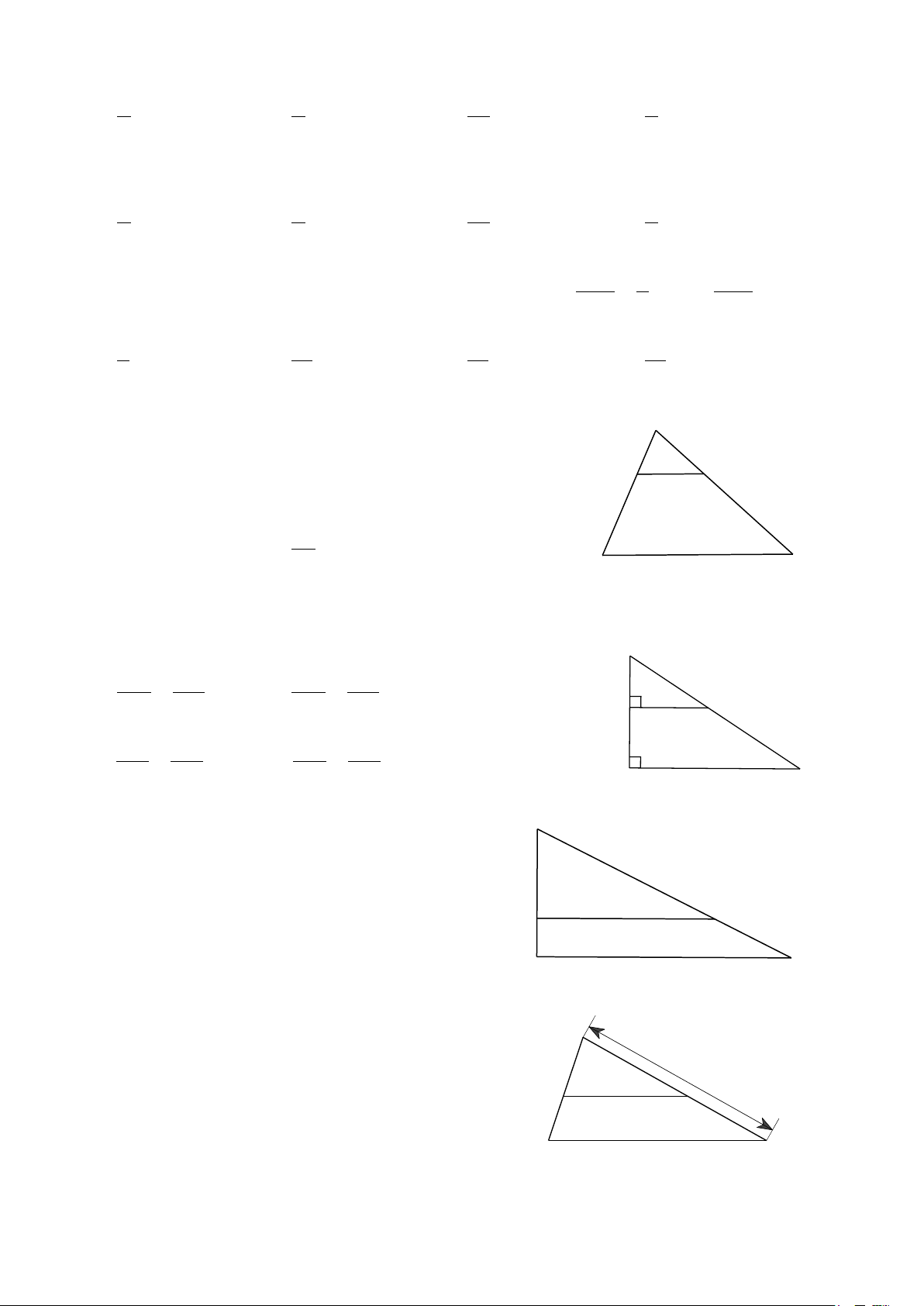
Câu 37. Cho hình bên, trong đó DE // BC, A
AD =12 cm, DB =18 cm và CE = 30 cm. Độ dài D E AC là A. 20 cm. B. 18 cm. 25 B C C. 50 cm. D. 45 cm.
Câu 38. Cho hình bên. Tỉ lệ thức nào sau đây là đúng? B A. BD BE = . B. BD BE = . AD BC AD EC E D C. DE BC = . D. AD BC = . AC BE AB EC A C
Câu 39. Cho hình bên, biết DE // AC. Giá trị B
của x (làm tròn kết quả đến chữ số thập phân 5 cm thứ hai) là D E A. x ≈ 7,15 cm. B. x ≈ 7,10 cm. 2 cm A C C. x ≈ 7,14 cm.
D. x ≈ 7,142 cm. 10 cm
Câu 40. Cho hình bên, biết MN // IK. Giá trị H của x là x 7 cm 12 cm A. x = 4,2 cm. B. x = 2,5 cm. M N 3 cm C. x = 7 cm. D. x = 5,25 cm. I K
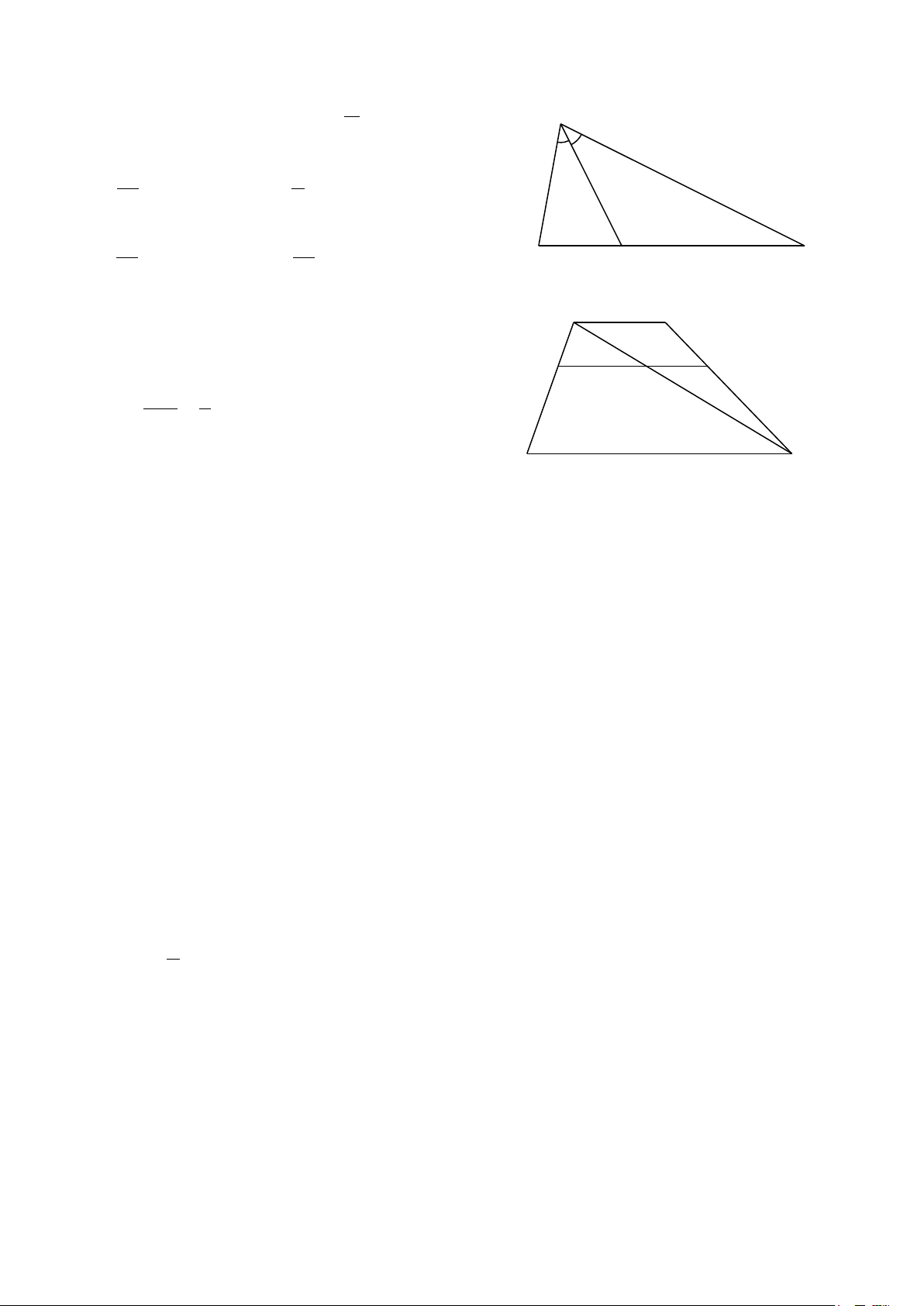
Câu 41. Cho hình bên. Tỉ số x bằng A y A. 7 . B. 1. 7,5 3,5 15 7 x y C. 15. D. 1 . B D 7 15 C
Câu 42. Cho hình thang ABCD ( AB //CD) A B
có BC =15 cm. Điểm E thuộc cạnh AD sao I E F cho AE 1
= . Đường thẳng EF //CD AD 3
(F ∈BC) (hình vẽ). Độ dài BF là D C A. 15 cm. B. 5 cm. C. 10 cm. D. 7 cm. Câu 43. Cho A
∆ BC, I, K lần lượt là trung điểm của AB và AC. Biết BC = 8 cm. Độ dài IK là A. 4 cm. B. 4,5 cm. C. 3,5 cm. D. 14 cm. Câu 44. Cho A
∆ BC đều cạnh 3 cm. Gọi M , N lần lượt là trung điểm của AB và AC.
Chu vi của tứ giác MNCB là A. 8 cm. B. 7,5 cm. C. 6 cm. D. 7 cm.
Câu 45. Cho tam giác ABC. Gọi E, F, P theo thứ tự là trung điểm của các cạnh
AB, BC, C .
A Nhận định nào sau đây đúng?
A. EP là đường trung bình của A ∆ BC. B. 1 EF = BC. 2
C. Chu vi tam giác ABC gấp bốn lần chu vi tam giác EF . P D. PE // EF.
Câu 46. Cho tam giác ABC, các đường trung tuyến BD và CE cắt nhau tại . G Gọi
I, K theo thứ tự là trung điểm của GB, GC. Biết AG = 4 cm. Độ dài các đoạn thẳng
EI và DK lần lượt là A. 3 cm và 3 cm. B. 3 cm và 2 cm. C. 2 cm và 2 cm. D. 1 cm và 2 cm.
Câu 47. Cho tam giác ABC, đường trung tuyến AM. Gọi D là trung điểm của AM , E
là giao điểm của BD và AC, F là trung điểm của EC. Biết AC = 9 cm, độ dài đoạn AE là A. 4,5 cm. B. 3 cm. C. 2 cm. D. 6 cm.
Câu 48. Cho tam giác ABC, AD là đường phân giác của
BAC (D∈ BC). Tỉ lệ thức nào sau đây đúng? A. AB AC = . B. AD BD = . C. DB DC = . D. DB BC = . BD BC AC DC AB AC DC AC
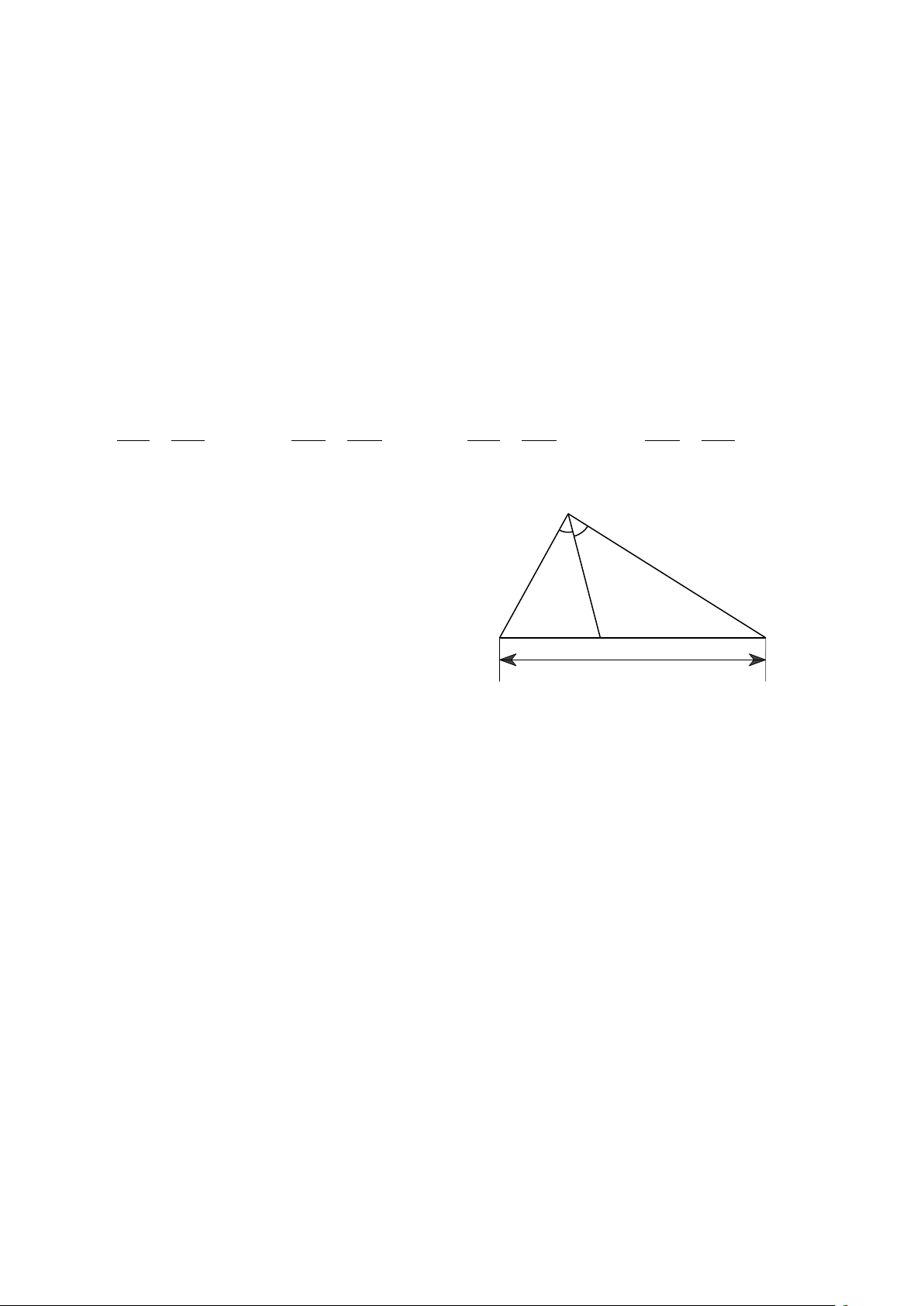
Câu 49. Cho hình bên. Biết rằng các số A
trên hình có cùng đơn vị đo là cm. Giá trị
x và y lần lượt là 15 20 A. 16 cm và 12 cm. x y B. 14 cm và 14 cm. B D C C. 14,3 cm và 10,7 cm. 28 D. 12 cm và 16 cm.
Câu 50. Cho tam giác ABC có D, E lần lượt là trung điểm của các cạnh AB, AC và
DE = 4 cm. Biết đường cao AH = 6 cm, diện tích tam giác ABC là A. 2 24 cm . B. 2 48 cm . C. 2 12 cm . D. 2 32 cm . B. Bài tập tự luận
1. Một số yếu tố thống kê và xác suất
Dạng 1. Các bài toán về thống kê
Bài 1. Em hãy đề xuất phương pháp thu thập dữ liệu cho các vấn đề sau và cho biết
phương pháp thu thập đó là gián tiếp hay trực tiếp:
a) Tên 10 tỉnh/ thành phố có diện tích lớn nhất Việt Nam.
b) Các món ăn được UNESCO công nhận là văn hóa phi vật thể.
c) Loại trái cây yêu thích của học sinh lớp 8A được dùng trong tiệc liên quan cuối năm.
Bài 2. Ghép các dữ liệu với loại dữ liệu thích hợp.
1. Xếp loại mức độ hài lòng của khách hàng: Hài lòng; Khá hài a) Số liệu liên tục. lòng; Chưa hài lòng.
2. Số nhạc cụ mà năm học sinh trong tổ 1 biết chơi: 0; 3; 2; 1; 3. b) Số liệu rời rạc.
3. Chiều cao mực nước thủy văn lớn nhất tại sông Tiền trong 5 c) Dữ liệu không
ngày đầu tháng 8 (đơn vị: mét): 1,68; 1,75; 1,82; 1,66; 1,62. là số, có thể sắp xếp thứ tự.
4. Năm địa điểm du lịch của Việt Nam mà học sinh lớp 8A thích d) Dữ liệu không
nhất: Vinpearl Safari (Phú Quốc), Đà Lạt, Bà Nà Hill (Đà Nẵng), là số, không thể
Đỉnh Fansipan (Sapa – Lào Cai), Vịnh Hạ Long (Quảng Ninh). sắp xếp thứ tự. Bài 3.
1) Bạn An muốn thu thập dữ liệu về số các bạn nữ ở tất cả các lớp trong khối 8 của trường.
a) Bạn An có thể thu thập bằng phương pháp nào?
b) Dữ liệu thu được thuộc loại nào?
2) Sau khi thu thập bạn có được bảng thống kê về số học sinh nữ trong từng lớp của
khối 8 như bảng dưới đây: Lớp
8A1 8A2 8A3 8A4 8A5 8A6 8A7 Số học sinh nữ 15 14 25 22 16 28 30
a) Hãy vẽ biểu đồ đoạn thẳng thể hiện bảng thống kê trên.
b) Hãy vẽ biểu đồ hình quạt tròn thể hiện bảng thống kê trên.
Bài 4. Một cửa hàng quần áo đưa ra chương trình khuyến mãi giảm giá một số mặt
hàng sau: Quần âu giảm giá 25%; Áo sơ mi giảm 35%; Áo khoác giảm 20%; Quần Jean giảm 10%.
a) Trong các mặt hàng trên, sản phẩm nào được giảm giá nhiều nhất, ít nhất và với mức
giảm giá bao nhiêu phần trăm?
b) Bạn An đã biểu diễn tỉ lệ giảm giá của các mặt hàng trên bằng biều đồ hình quạt
tròn. Biểu đồ An sử dụng có phù hợp không?
c) An nên dùng biểu đồ nào để biểu diễn ? Hãy vẽ biểu đồ đó.
d) Mẹ An đã mua 2 chiếc áo sơ mi với giá mỗi chiếc áo sau khi giảm là 325 000 đồng
và 4 chiếc quần âu. Tổng số tiền mẹ An thanh toán tại quầy là 1850 000 đồng. Em hãy
tính xem mỗi chiếc áo sơ mi và quần âu nguyên giá sẽ là bao nhiêu tiền.
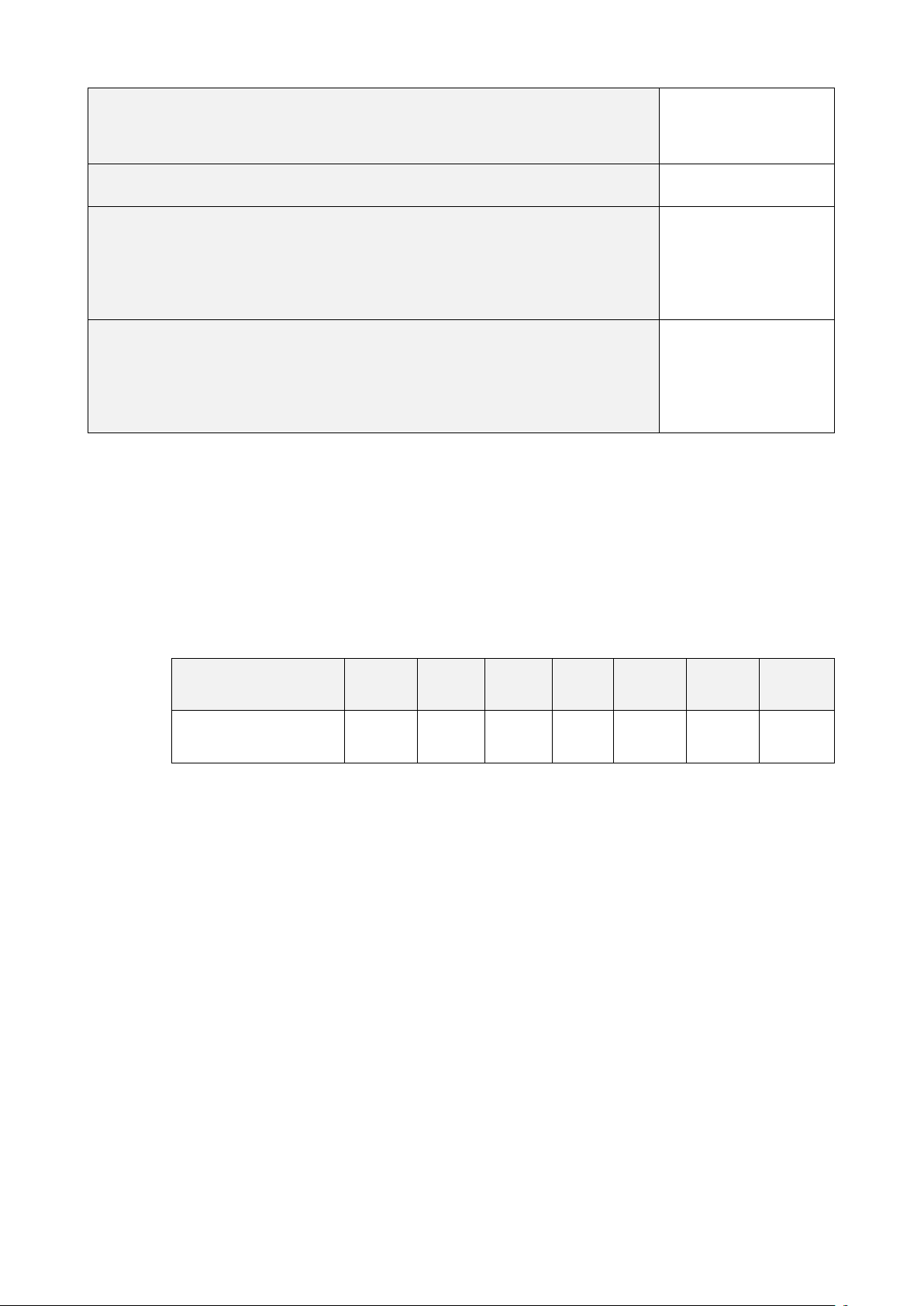
Bài 5. Hình dưới đây thể hiện số lượng học sinh tham gia đăng kí hai Câu lạc bộ cầu
lông và cờ vua của trường:
Học sinh tham gia Câu lạc bộ cầu lông và cờ vua Số học sinh 16 14 14 14 12 12 12 10 10 8 8 8 Cầu lông 6 5 Cờ vua 4 2 0 8A1 8A2 8A3 8A4 Lớp .
a) Lập bảng thống kê cho biểu đồ trên.
b) Cho biết sự khác nhau về việc tham gia đăng kí hai Câu lạc bộ cầu lông và cờ vua của hai lớp 8A3 và 8A4.
c) Nếu lớp 8A1 có số lượng học sinh tham gia Câu lạc bộ cầu lông chiếm 25% tổng
số học sinh cả lớp. Hãy tính xem lớp 8A1 có bao nhiêu học sinh.
d) Hãy so sánh tổng số học sinh tham gia Câu lạc bộ cầu lông và Câu lạc bộ cờ vua.
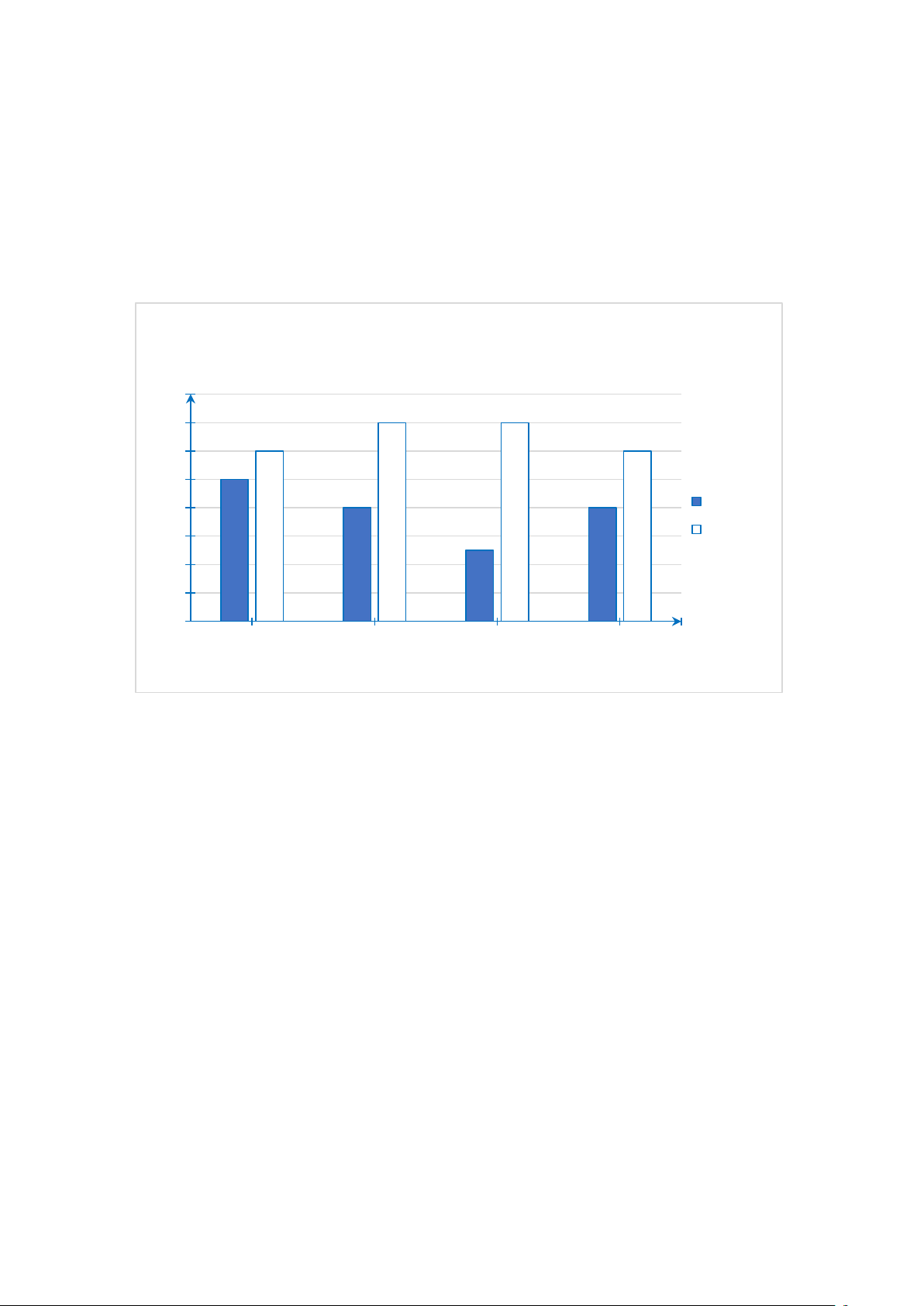
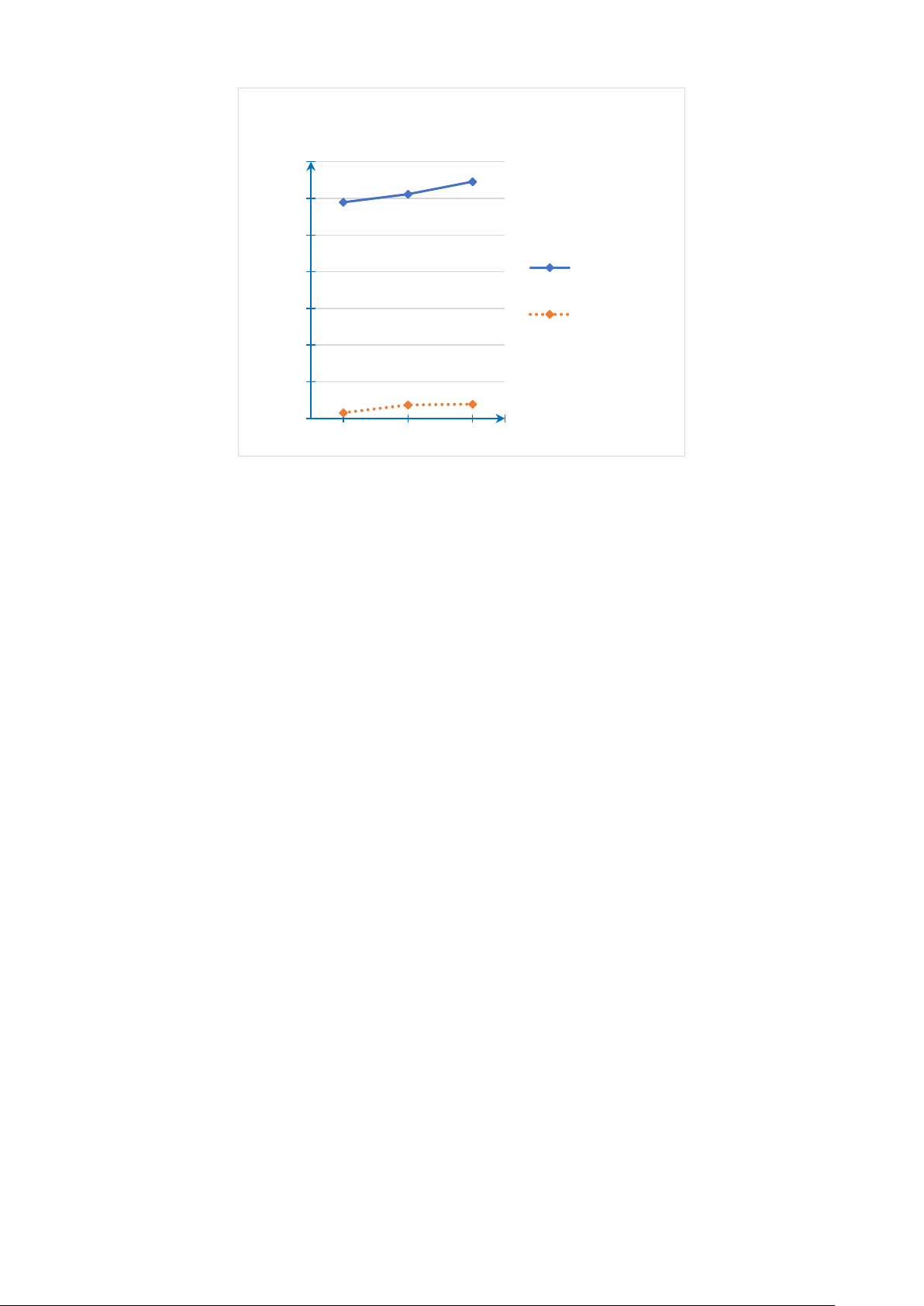
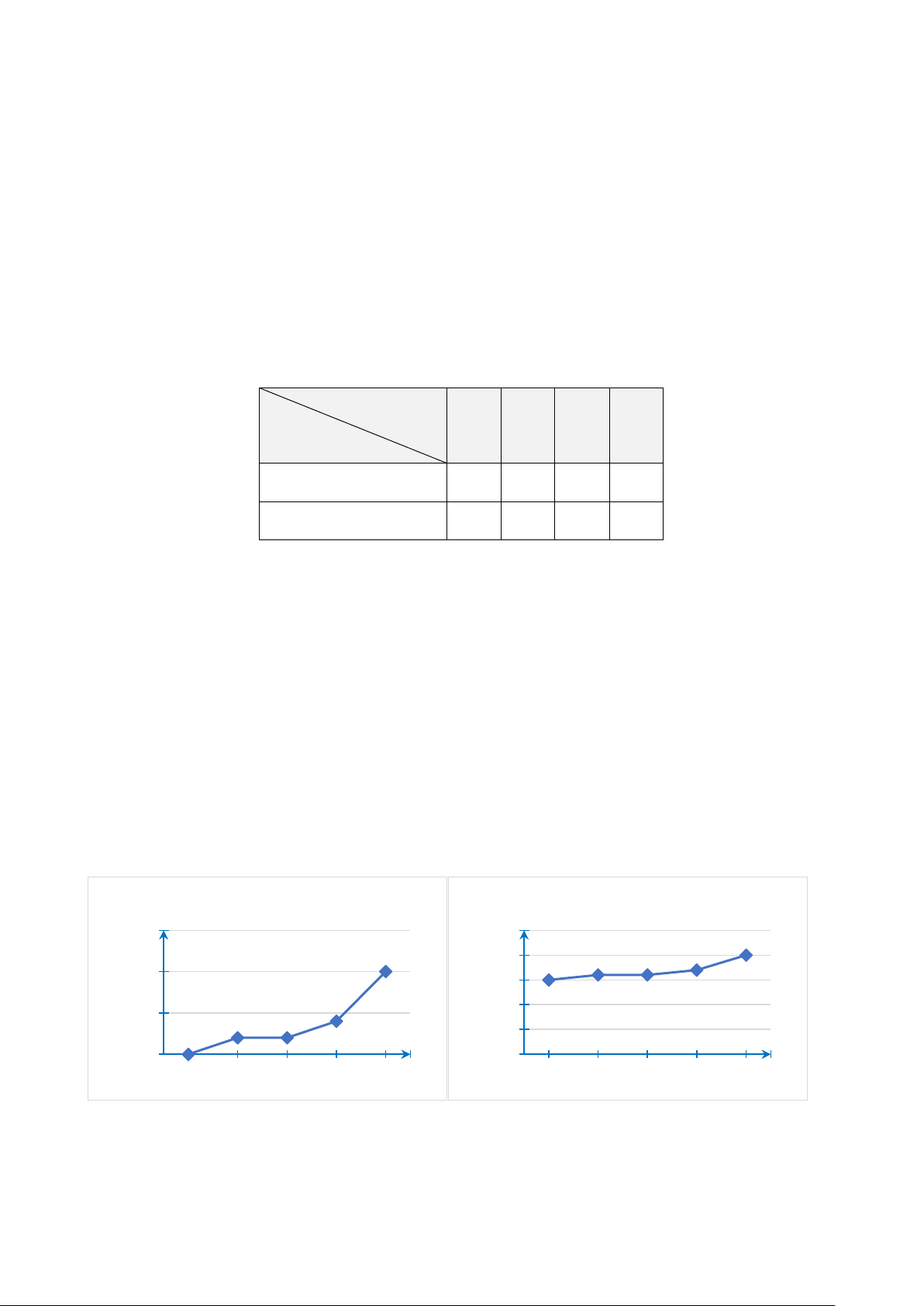
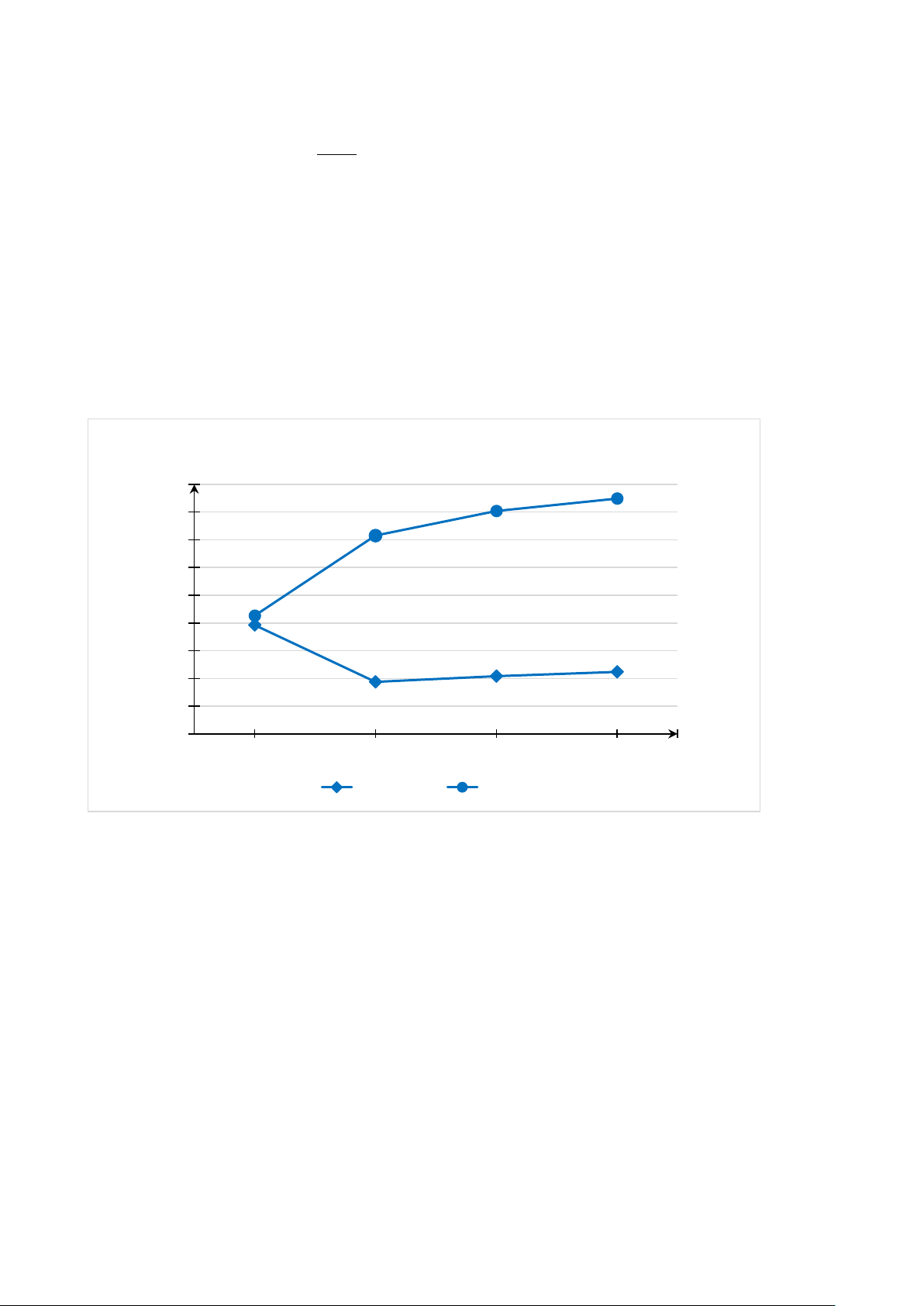
Bài 6. Cho hai biểu đồ dưới đây:
Doanh thu của doanh nghiệp A
Doanh thu của doanh nghiệp A 45 50 40 40 40 30 32 32 34 40 (tỉ đồng) (tỉ đồng) 30 34 thu 35 thu 32 32 20 30 10 oanh oanh D 30 D 0
2018 2019 2020 2021 2022 Năm
2018 2019 2020 2021 2022 Năm
a) Dữ liệu biểu diễn trên hai biểu đồ có như nhau không? Nếu có hãy lập bảng thống kê cho dữ liệu đó.
b) Có thể căn cứ vào độ dốc trên hai đường gấp khúc trên hai biểu đồ để đánh giá về
tốc độ doanh thu trong 5 năm của các dữ liệu được biểu diễn không? Tại sao?
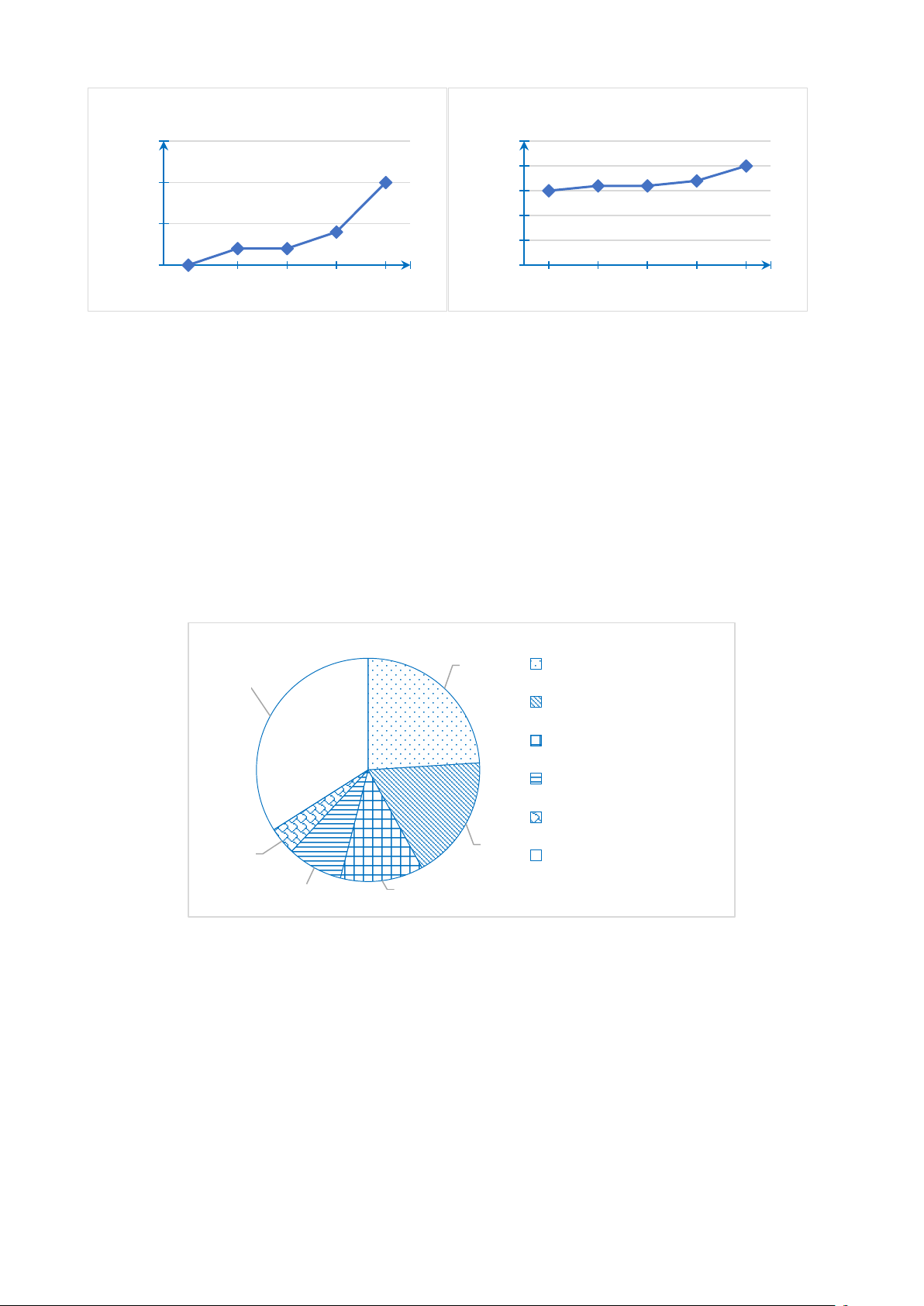
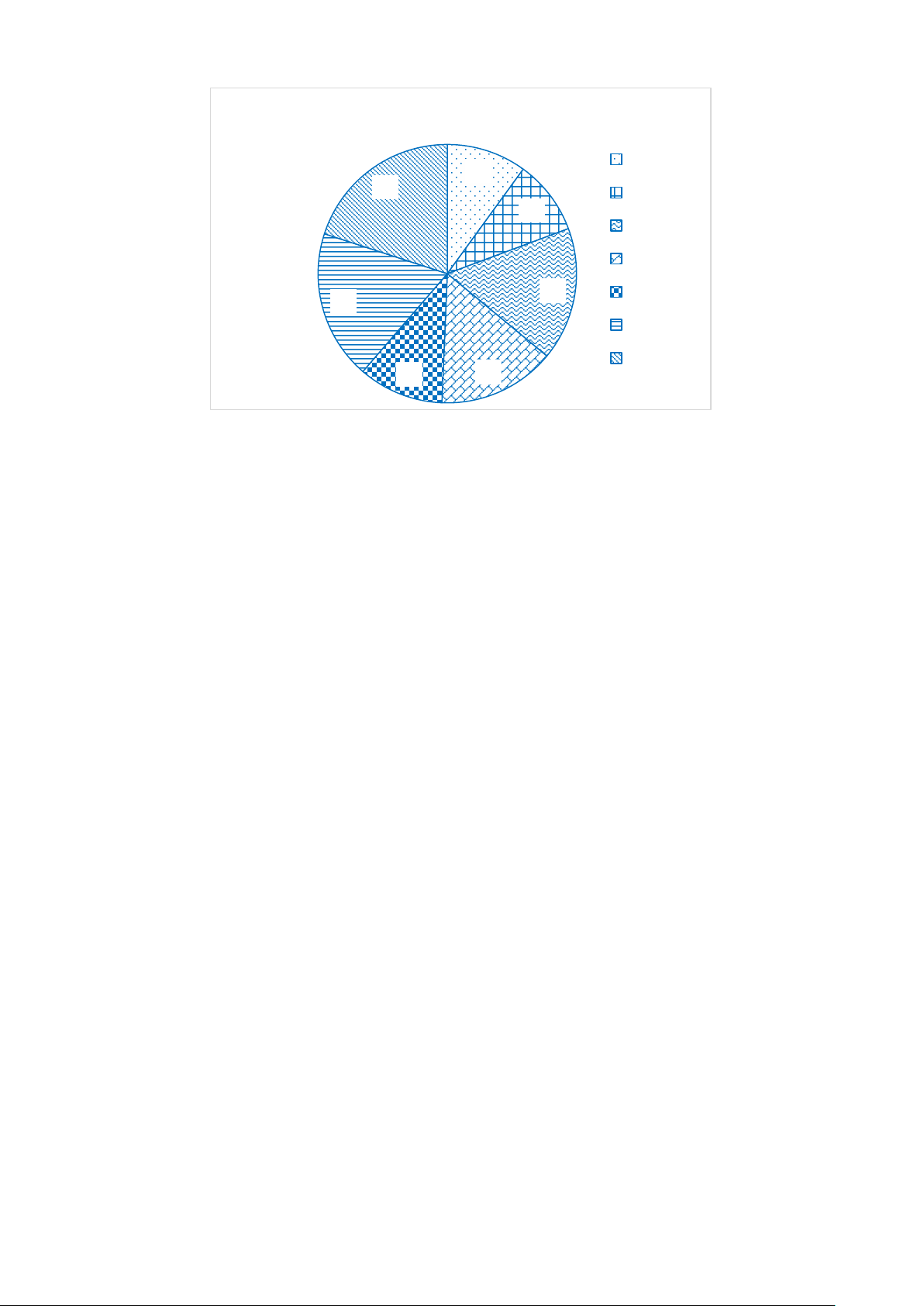
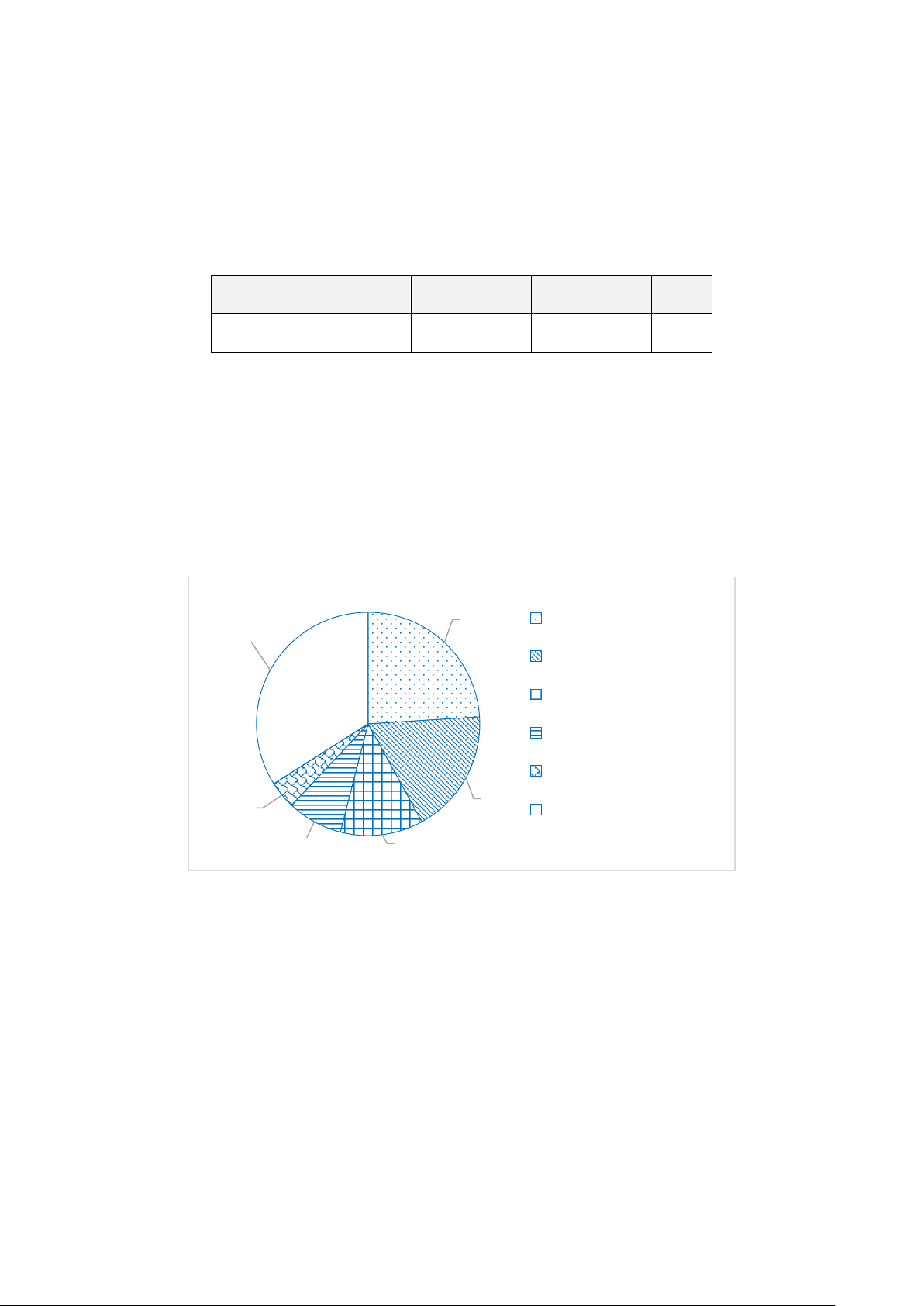
Bài 7. Biểu đồ hình quạt tròn ở hình bên biểu diễn tỉ lệ các yếu tố ảnh hưởng đến sinh
trưởng của cây trồng như: Phân bón, Nước tưới, Giống, Kiểm soát dịch hại, Kiểm soát
cỏ dại, Yếu tố khác. 24% Nước tưới 34% Giống Kiểm soát dịch hại Kiểm soát cỏ dại Yếu tố khác 18% 4% Phân bón 8% 12%
a) Cho biết yếu tố nào ảnh hưởng đến sinh trưởng của cây trồng nhiều nhất?
b) Trong các yếu tố ảnh hưởng đến sinh trưởng của cây thì yếu tố kiểm soát dịch hại
gấp mấy lần yếu tố khác?
c) Vấn đề tưới nước cho cây cũng là một yếu tố quan trọng ảnh hưởng đến sinh trưởng
của cây trồng. Em hãy đề xuất một vài biện pháp khắc phục tình trạng trên để làm giảm
thiệt hại trong việc trồng trọt.
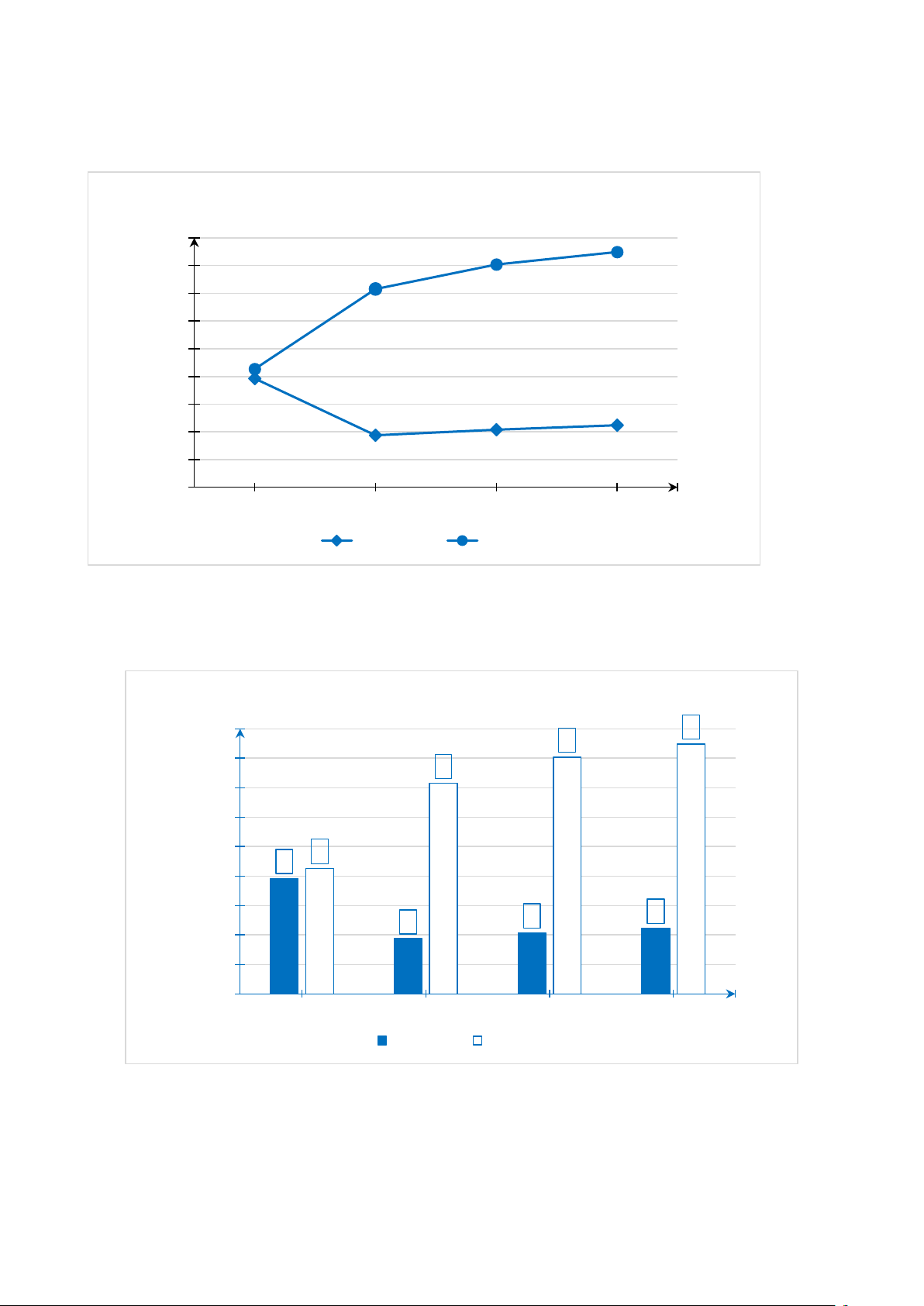
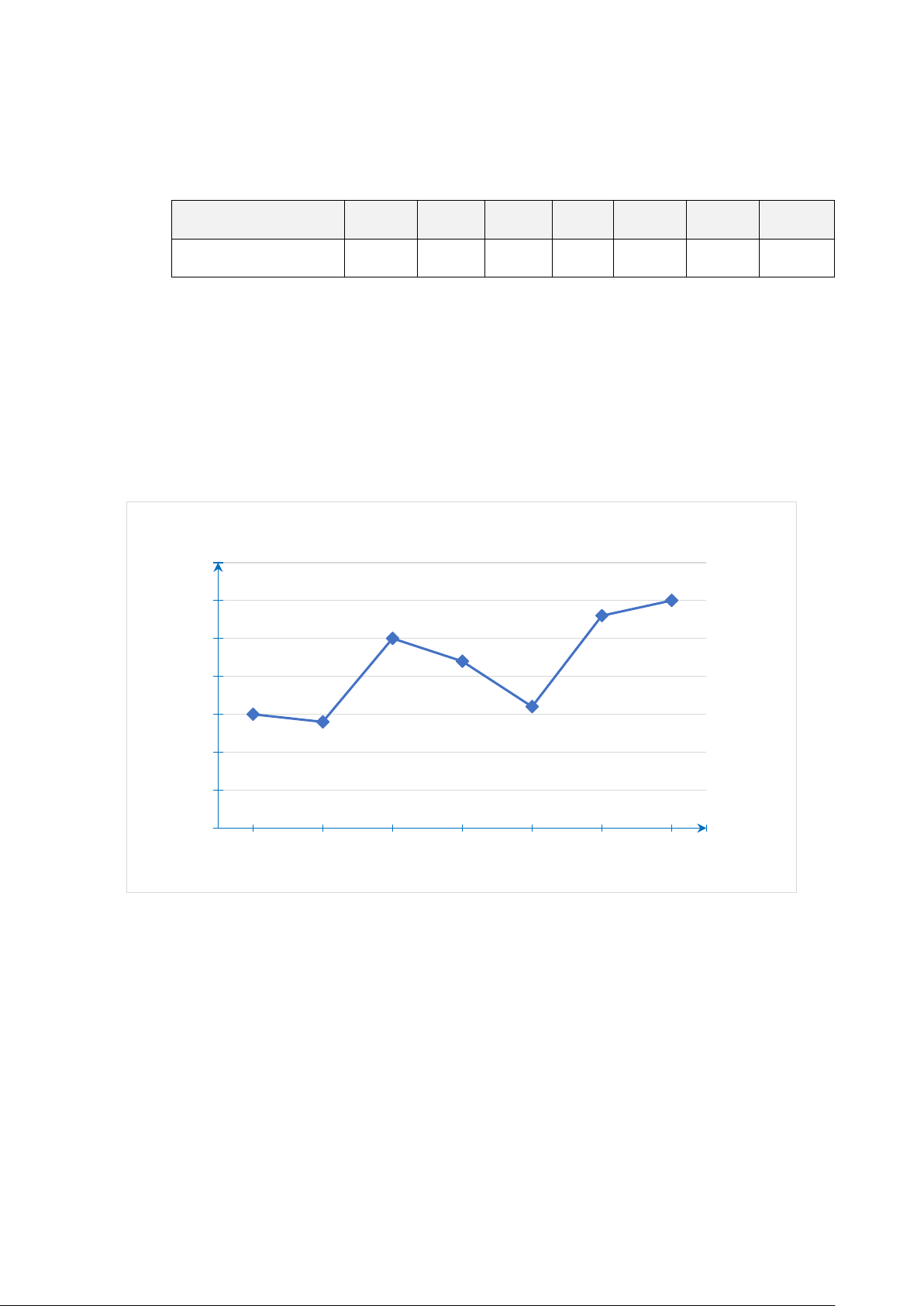
Bài 8. Biểu đồ đoạn thẳng ở hình bên dưới thống kê số lượng gia cầm ở TP. HCM và Kon
Tum qua các năm 2015, 2018, 2019, 2020. (Nguồn: Niêm giám thống kê năm 2021). Số lượng (Nghìn con) 1800 1608 1698 1600 1431 1400 1200 1000 853 800 600 785 400 200 375 416 447 0 2015 2018 2019 2020 Năm TP. HCM Kon Tum
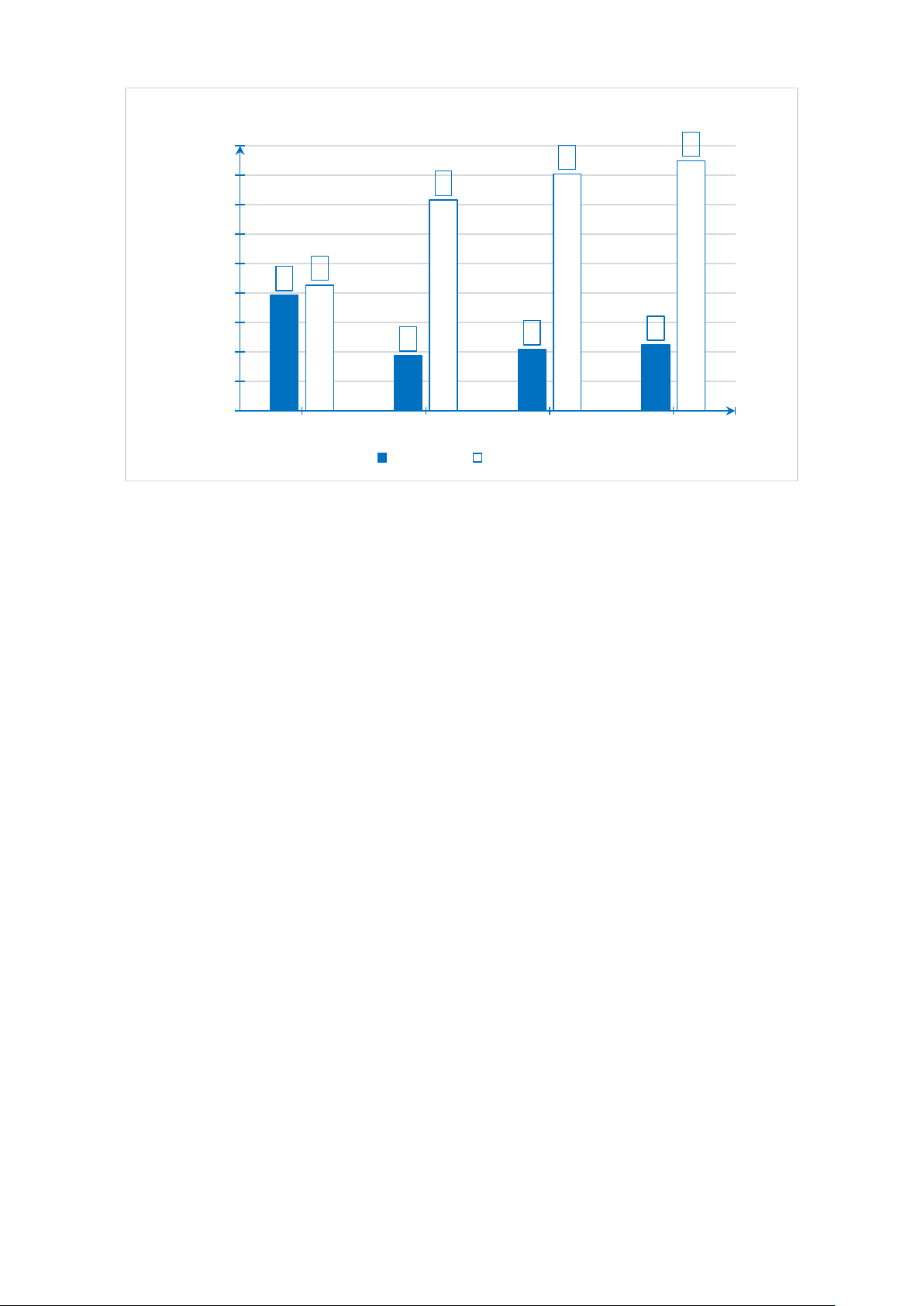
a) Hãy hoàn thành biểu đồ cột kép ở hình bên dưới để nhận được biểu đồ biểu diễn dữ
liệu trong biểu đồ đoạn thẳng ở hình trên. Số lượng (Nghìn con) 1800 ? ? 1600 ? 1400 1200 1000 ? ? 800 600 ? ? ? 400 200 0 2015 2018 2019 2020 Năm TP. HCM Kon Tum
b) TP. HCM và Kon Tum trong năm 2020 lượng gia cầm ở đâu nhiều nhất? Nhiều nhất là bao nhiêu nghìn con?
c) Một bài báo đã nêu ra nhận định “Tổng số lượng gia cầm ở Kon Tum trong năm
2015, 2018, 2019, 2020 là 2023 nghìn con và so với năm 2018 số lượng gia cầm ở
TP. HCM tăng 80% so với số lượng gia cầm ở Kon Tum”. Em hãy cho biết nhận định
trên bài báo có chính xác không?
d) Em hãy đề xuất một vài giải pháp để tăng số lượng gia cầm ở Kon Tum trong những
năm tới để đạt hiệu quả trong chăn nuôi.
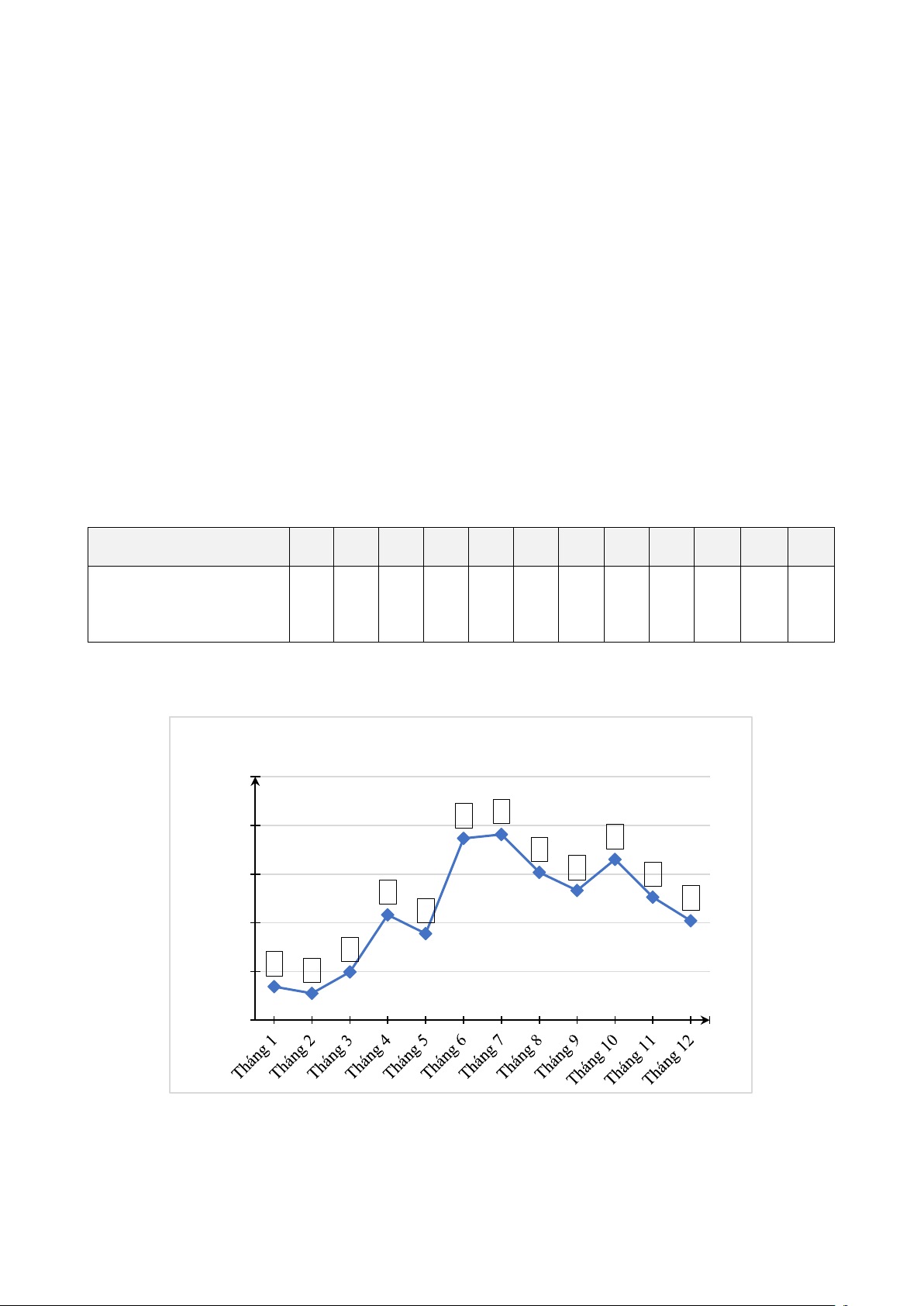
Bài 9. Thống kê tổng số giờ nắng của các tháng trong năm 2022 tại trạm quan trắc Nam
Định từ tháng 1 đến tháng 12 lần lượt là: 34,4; 27,5; 49,4; 108,2; 88,8; 186,6; 190,7;
151,7; 133,2; 165,0; 126,2; 102,1 (đơn vị: giờ) (Nguồn: Tổng cục thống kê).
a) Lập bảng số liệu thống kê số giờ nắng của các tháng trong năm 2022 tại trạm quan
trắc Nam Định theo mẫu sau: Tháng 1 2 3 4 5 6 7 8 9 10 11 12
Tổng số giờ nắng ? ? ? ? ? ? ? ? ? ? ? ? (h)
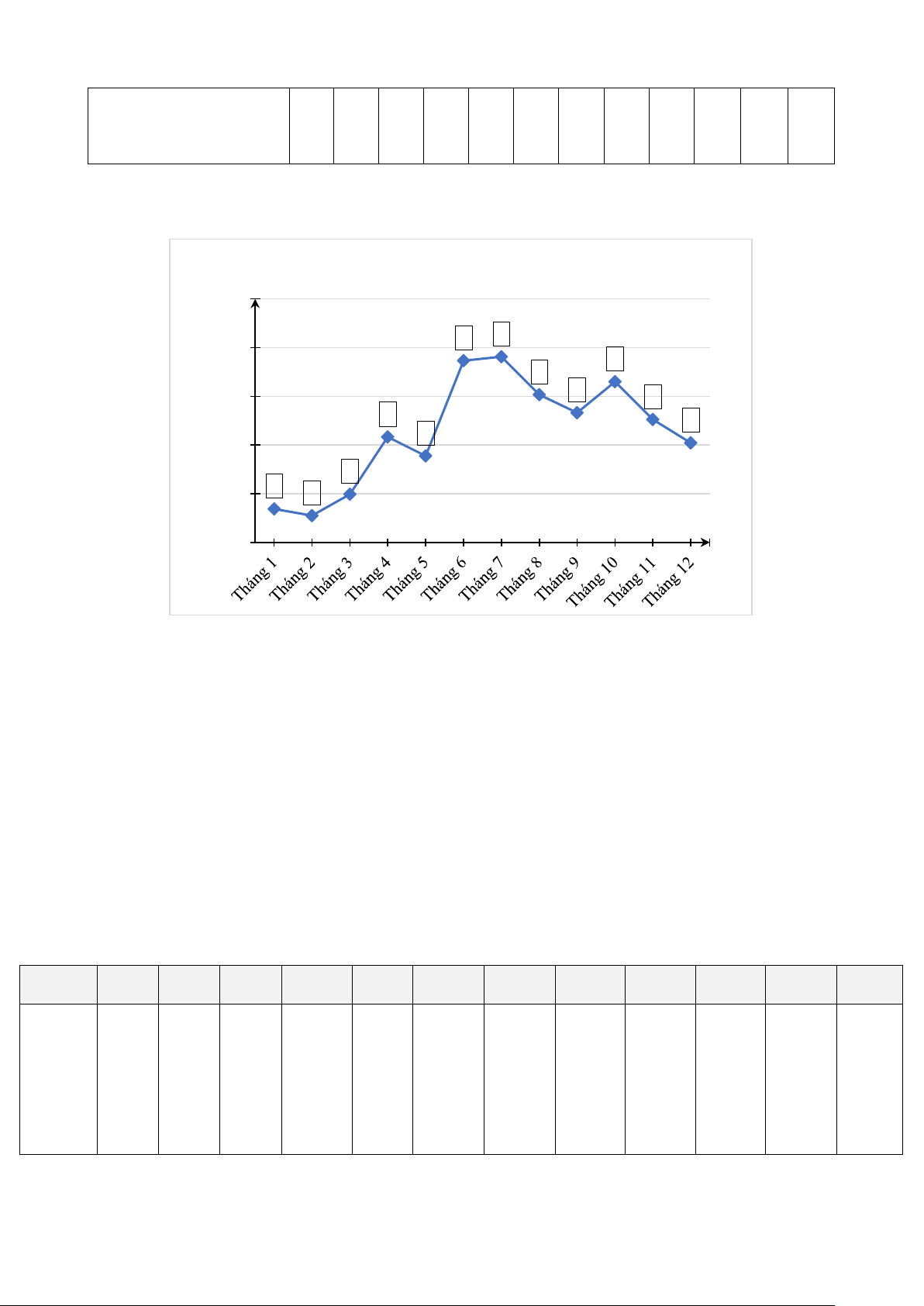
b) Hãy hoàn thành biểu đồ hình bên dưới để nhận được biểu đồ đoạn thẳng biểu diễn
tổng số giờ nắng của các tháng trong năm 2022 tại trạm quan trắc Nam Định. Tổng số giờ nắng (h) 250 ? ? 200 ? ? ? 150 ? ? ? ? 100 ? ? 50 ? 0 Tháng
c) Tổng số giờ nắng tại trạm quan trắc Nam Định trong tháng nào cao nhất? Thấp nhất?
d) Hãy nhận xét về sự thay đổi số giờ nắng của các tháng trong năm 2022 tại trạm quan
trắc Nam Định trong các khoảng thời gian: tháng 1 – tháng 2; tháng 2 – tháng 3; tháng
3 – tháng 4; tháng 4 – tháng 5; tháng 5 – tháng 6; tháng 6 – tháng 7; tháng 7 – tháng 8;
tháng 8 – tháng 9; tháng 9 – tháng 10; tháng 10 – tháng 11; tháng 11 – tháng 12.
e) Một bài báo có nêu thông tin: “So với tháng 9, tổng số giờ nắng tại trạm quan trắc Nam
Định trong tháng 10 tăng lên xấp xỉ 34%”. Thông tin của bài báo đó có chính xác không?
Dạng 2. Các bài toán về xác suất
Bài 10. Một túi đựng 10 tấm thẻ bài có kích thước giống nhau và được ghi số
1; 2; 3; ...; 10. Hoa rút ngẫu nhiên một tấm thẻ từ trong hộp.
a) Liệt kê các kết quả có thể của hành động trên.
b) Liệt kê các kết quả thuận lợi cho các biến cố:
A: “Rút được tấm thẻ có ghi số lẻ”;
B: “Rút được tấm thẻ có ghi số nguyên tố”;
C: “Rút được tấm thẻ có ghi số chia hết cho 3”.
Bài 11. Một túi đựng bút tô màu của bé Mai có 5 chiếc bút màu vàng, 3 chiếc bút màu
cam, 4 chiếc bút màu xanh và 2 chiếc bút màu tím (các chiếc bút có cùng khối lượng
và kích thước). Bé Mai lấy ngẫu nhiên một chiếc bút từ trong túi. Tính xác suất của các biến cố sau:
A: “Lấy được chiếc bút màu tím”;
B: “Lấy được chiếc bút màu cam hoặc màu xanh”;
C: “Không lấy được chiếc bút màu vàng”;
D: “Lấy được chiếc bút màu vàng”.
Bài 12. Bác bảo vệ theo dõi số khách đến cơ quan mỗi ngày trong một tháng. Kết quả thu được như bảng sau: Số khách 0 1 2 3 4 5 6 7 Số ngày 3 6 5 9 3 2 1 1
a) Gọi A là biến cố “Trong một ngày có từ 3 khách trở lên đến cơ quan”. Hỏi có bao
nhiêu ngày biến cố A xảy ra?
b) Tính xác suất thực nghiệm của biến cố A.
c) Hãy ước lượng xác suất của biến cố B: “Trong một ngày có số khách đến cơ quan là số lẻ”.
Bài 13. Một công ty chế biến hạt điều đã thống kê các loại hạt điều thu hoạch được như bảng sau: Loại hạt điều Loại 1 Loại 2 Loại 3
Khối lượng thu hoạch được 1 450 2 230 1860
a) Hãy tính xác suất thực nghiệm của các biến cố sau (làm tròn kết quả đến chữ số thập phân thứ tư):
A: “Hạt điều đạt loại 1”;
B: “Hạt điều đạt loại 2 và loại 3”.
b) Công ty lấy ngẫu nhiêm 100 kg hạt điều chưa phân loại và tiến hành phân loại. Em
hãy dự đoán xem có bao nhiêu kilôgam hạt điều loại 1? 2. Hình học
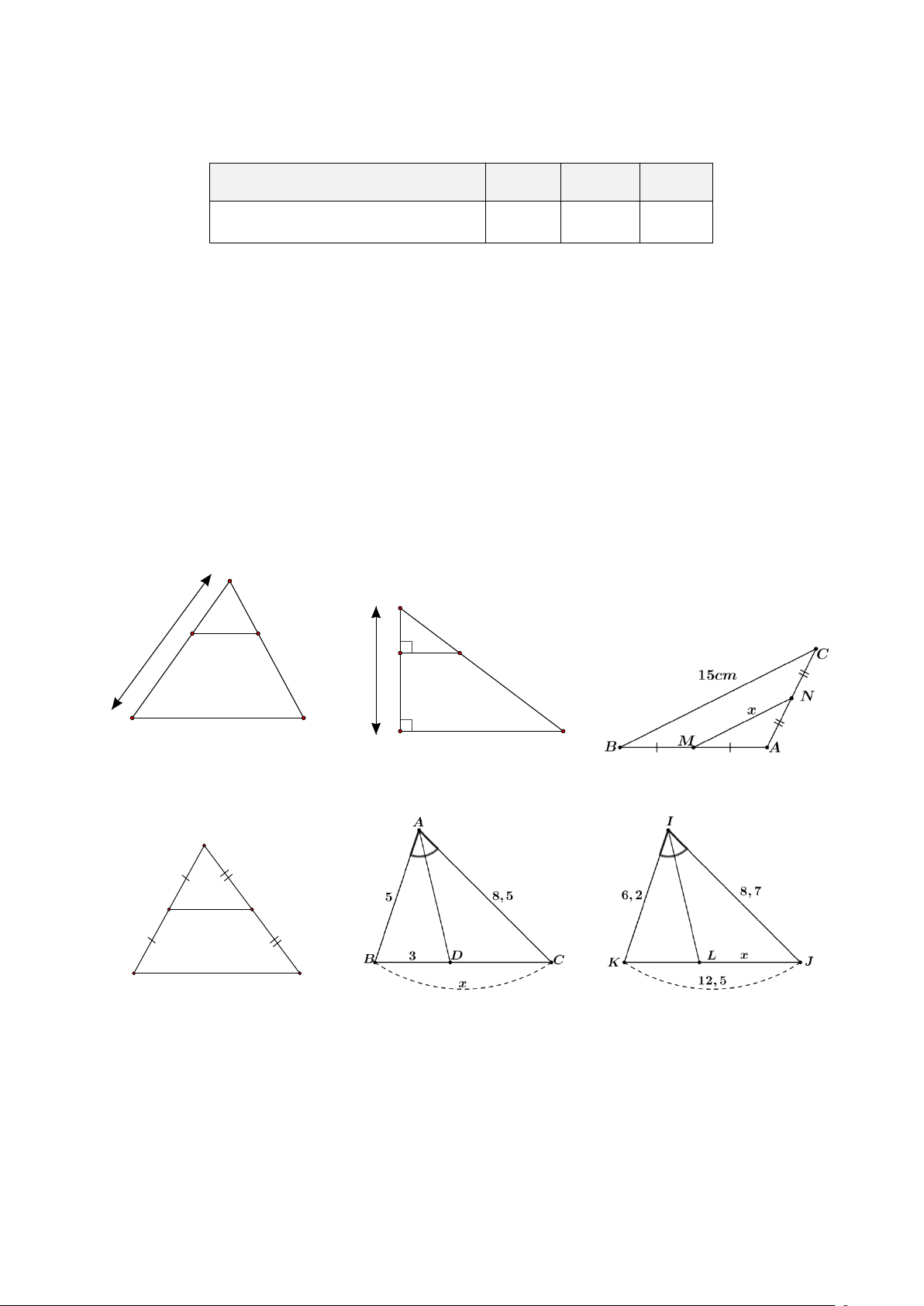
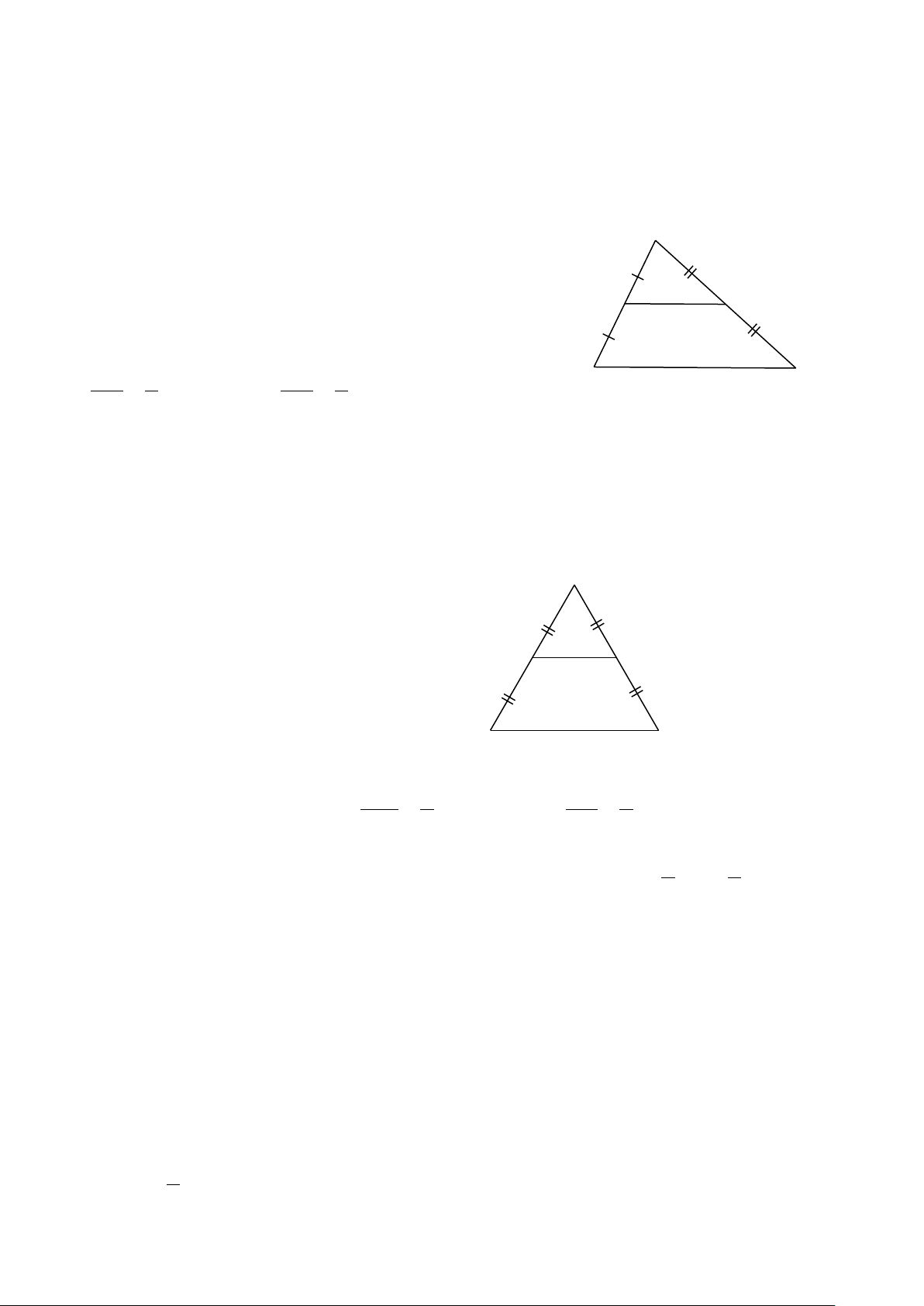
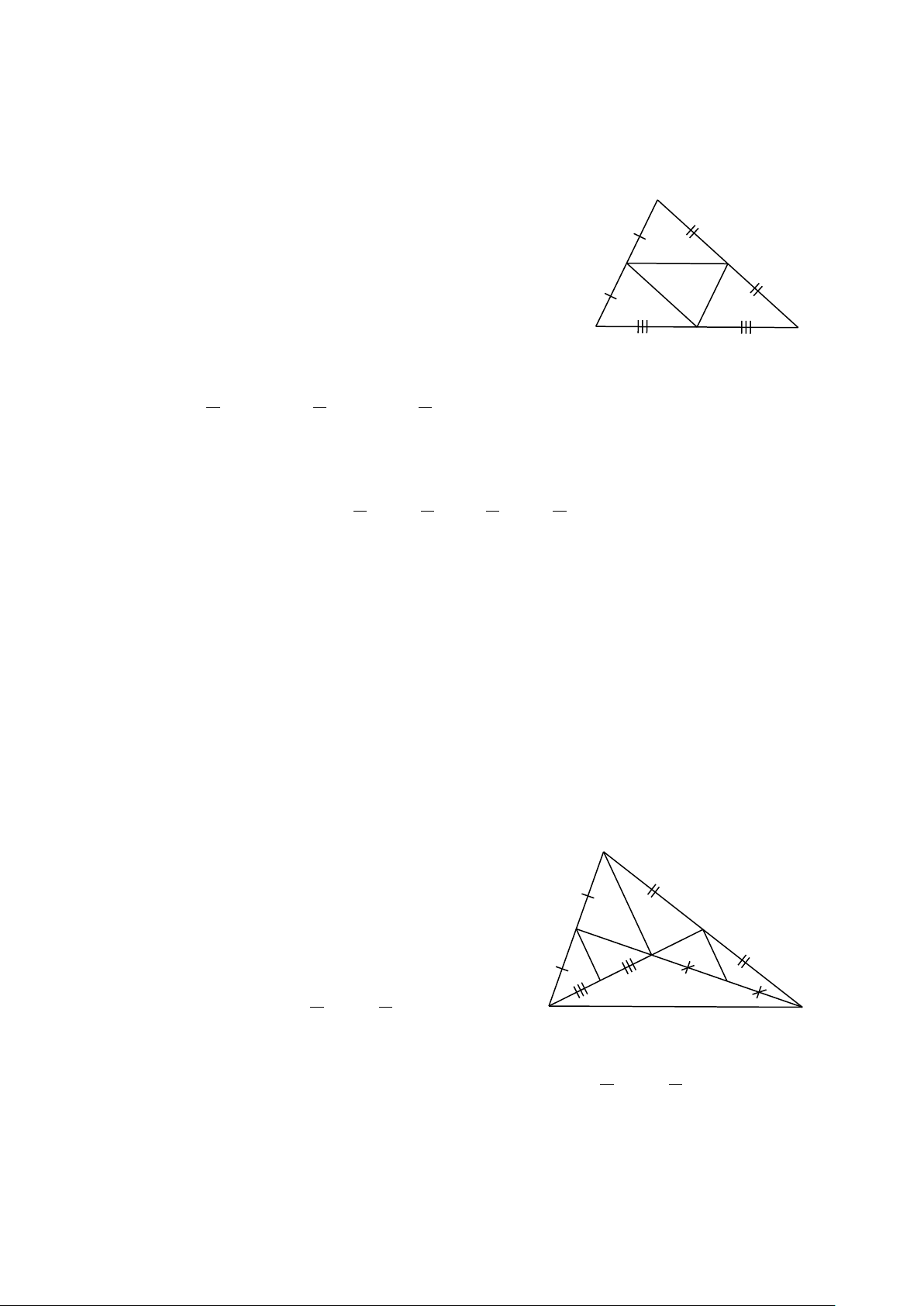
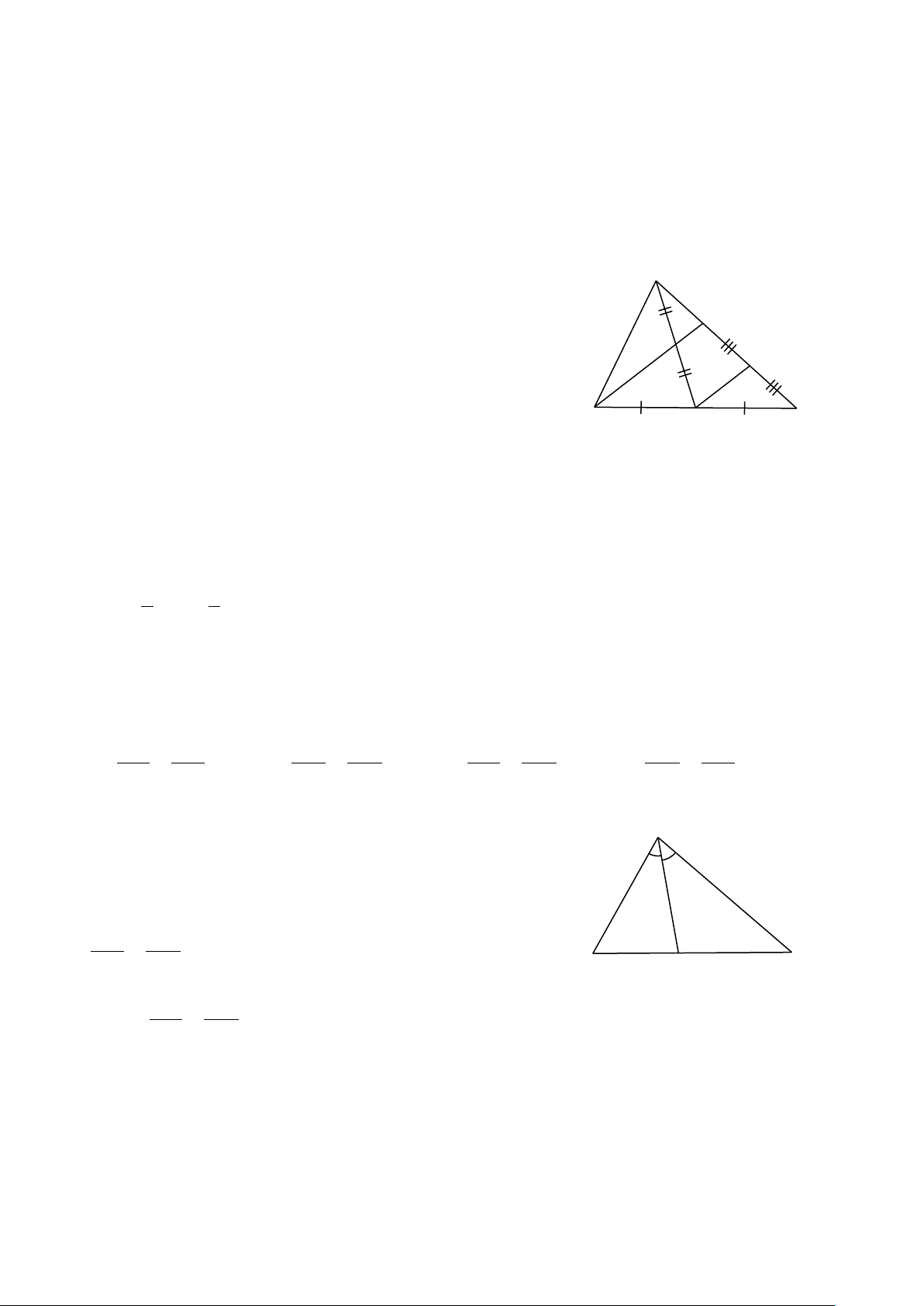
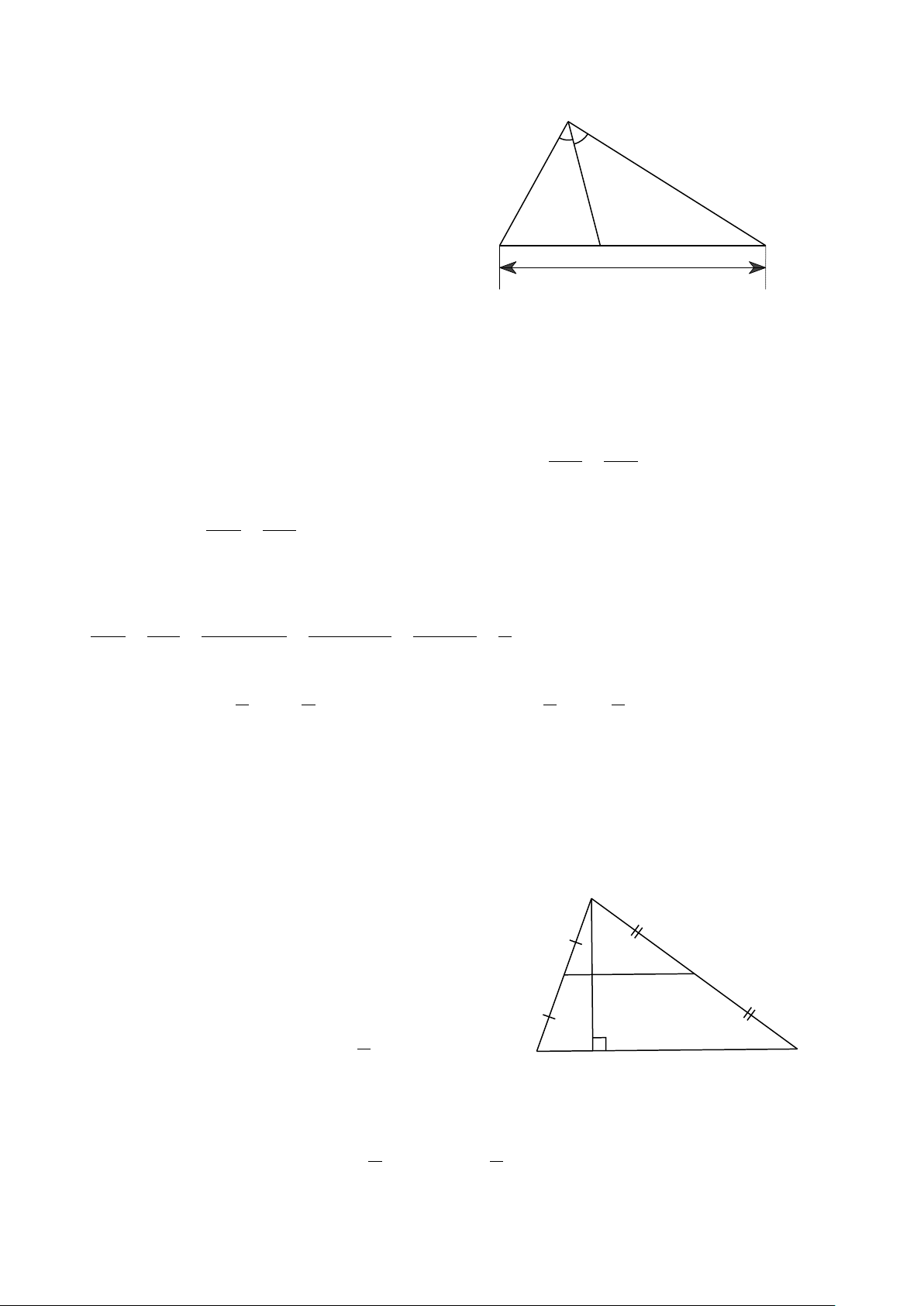
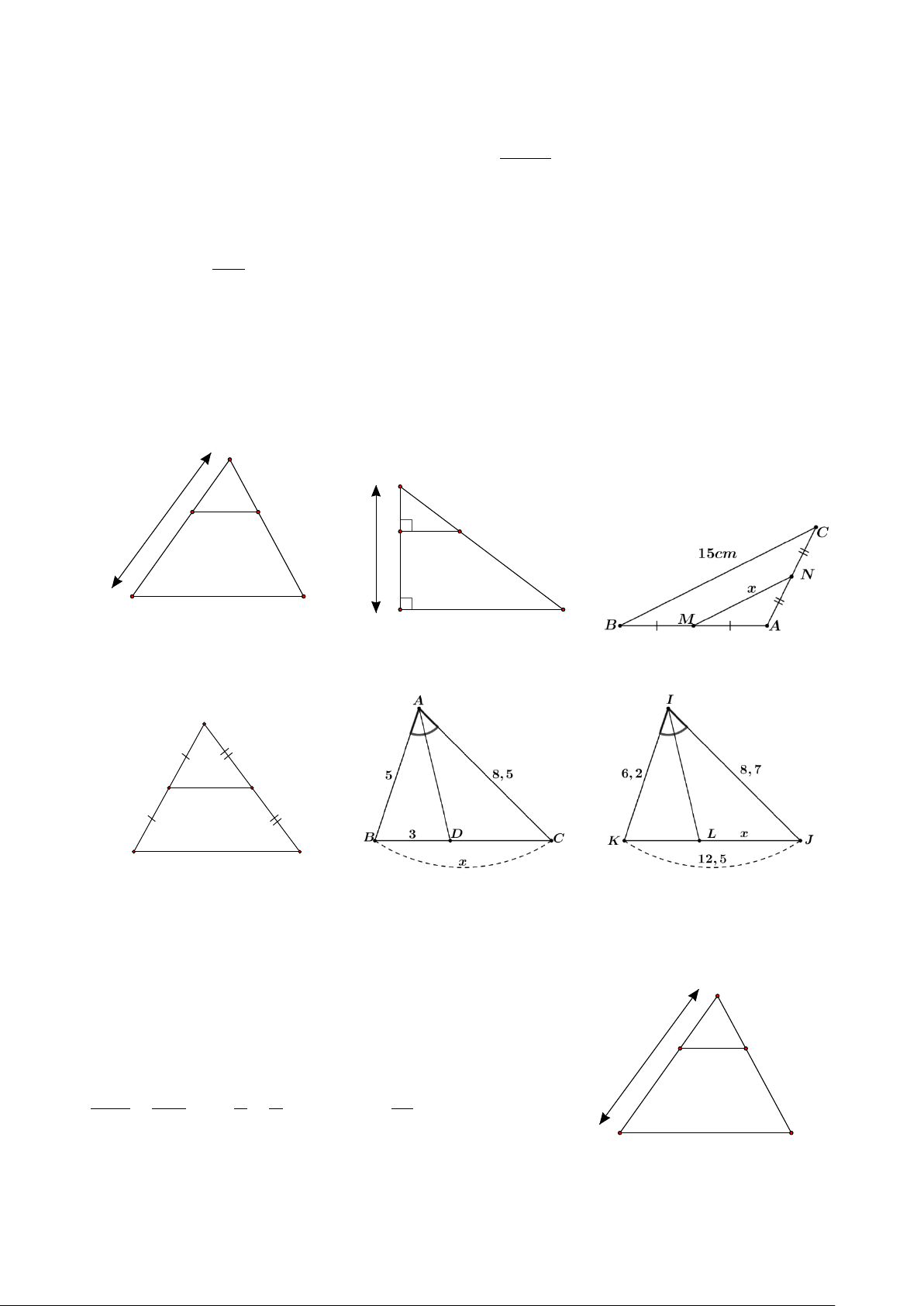
Bài 14. Tìm độ dài x, y trong mỗi trường hợp sau: A M 2 x 7 M N 3 5 F E 6 y 15 B C MN // AB N P Hình 1 Hình 2 Hình 3 A M 3,5cm N x B C Hình 4 Hình 5 Hình 6
Bài 15. Cho tam giác ABC vuông tại A ( AB < AC). Gọi I là trung điểm của cạnh
BC. Qua I vẽ IN vuông góc với AC tại N. Lấy điểm D sao cho N là trung điểm của . ID
a) Chứng minh N là trung điểm của AC và tứ giác ADCI là hình thoi.
c) Đường thẳng BN cắt cạnh DC tại K. Chứng minh DK 1 = . DC 3 Bài 16. Cho A
∆ BC trung tuyến A .
D Vẽ tia phân giác của
ADB cắt AB tại M , tia phân giác của
ADC cắt AC tại N. Chứng minh rằng: a) MB BD = . b) MB NC = . c) MN // BC. MA AD MA NA
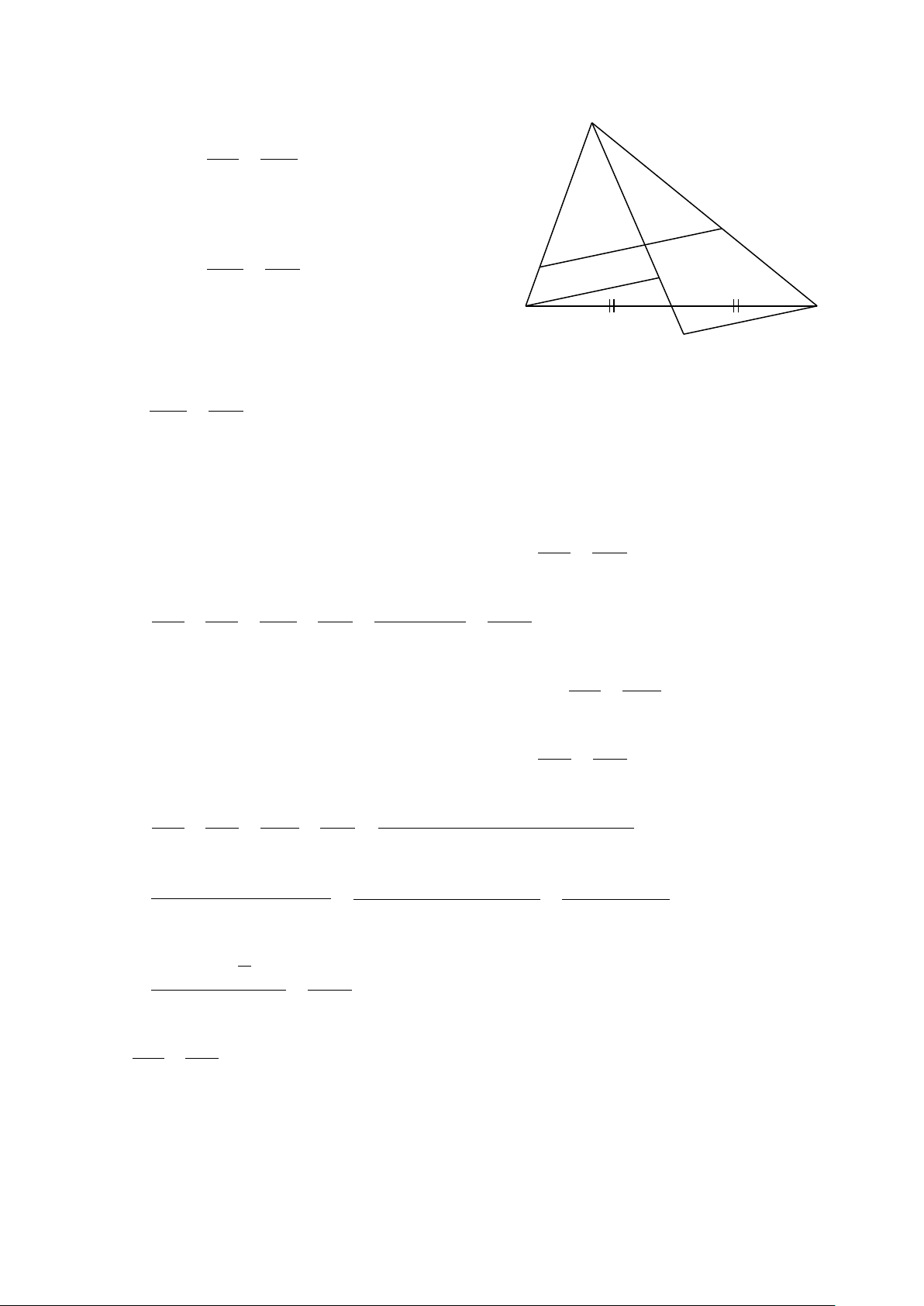
Bài 17. Cho tam giác ABC có AB < AC. Tia phân giác
BAC cắt cạnh BC tại điểm .
D Gọi M là trung điểm của cạnh BC. Qua điểm M kẻ đường thẳng song song với
đường thẳng AD cắt các đường thẳng AC, AB lần lượt tại E và K. Chứng minh rằng:
a) Tam giác AEK cân. b) AK DM = . c) BK = EC. EC MB
Bài 18. Cho tứ giác ABC .
D Gọi E, F, I theo thứ tự là trung điểm của AD, BC, AC. Chứng minh rằng:
a) EI //CD và IF // A . B b) AB CD EF + ≤ . 2
Bài 19. Cho hình thang ABCD có hai đáy AB và .
CD Gọi M là trung điểm của CD,
E là giao điểm của MA và BD, F là giao điểm của MB và AC.
a) Chứng minh rằng EF // A . B
b) Đường thẳng EF cắt AD, BC lần lượt tại H và N. Chứng minh HE = EF = FN.
c) Biết AB = 7,5 cm, CD =12 cm. Tính độ dài HN. Bài 20. Cho A
∆ BC có AD là trung tuyến, trọng tâm G, đường thẳng đi qua G cắt các
cạnh AB, AC lần lượt tại E, F. Từ B, C kẻ các đường song song với EF cắt AD lần
lượt tại M , N. Chứng minh rằng: a) BE MG = . b) BE CF + =1. c) AB AC + = 3. AE AG AE AF AE AF
Bài 21. Cho tam giác ABC có BC =15 cm, CA =18 cm và AB =12 cm. Gọi I và G
lần lượt là tâm đường tròn nội tiếp và trọng tâm A ∆ BC.
a) Chứng minh IG // BC.
b) Tính độ dài đoạn thẳng . IG
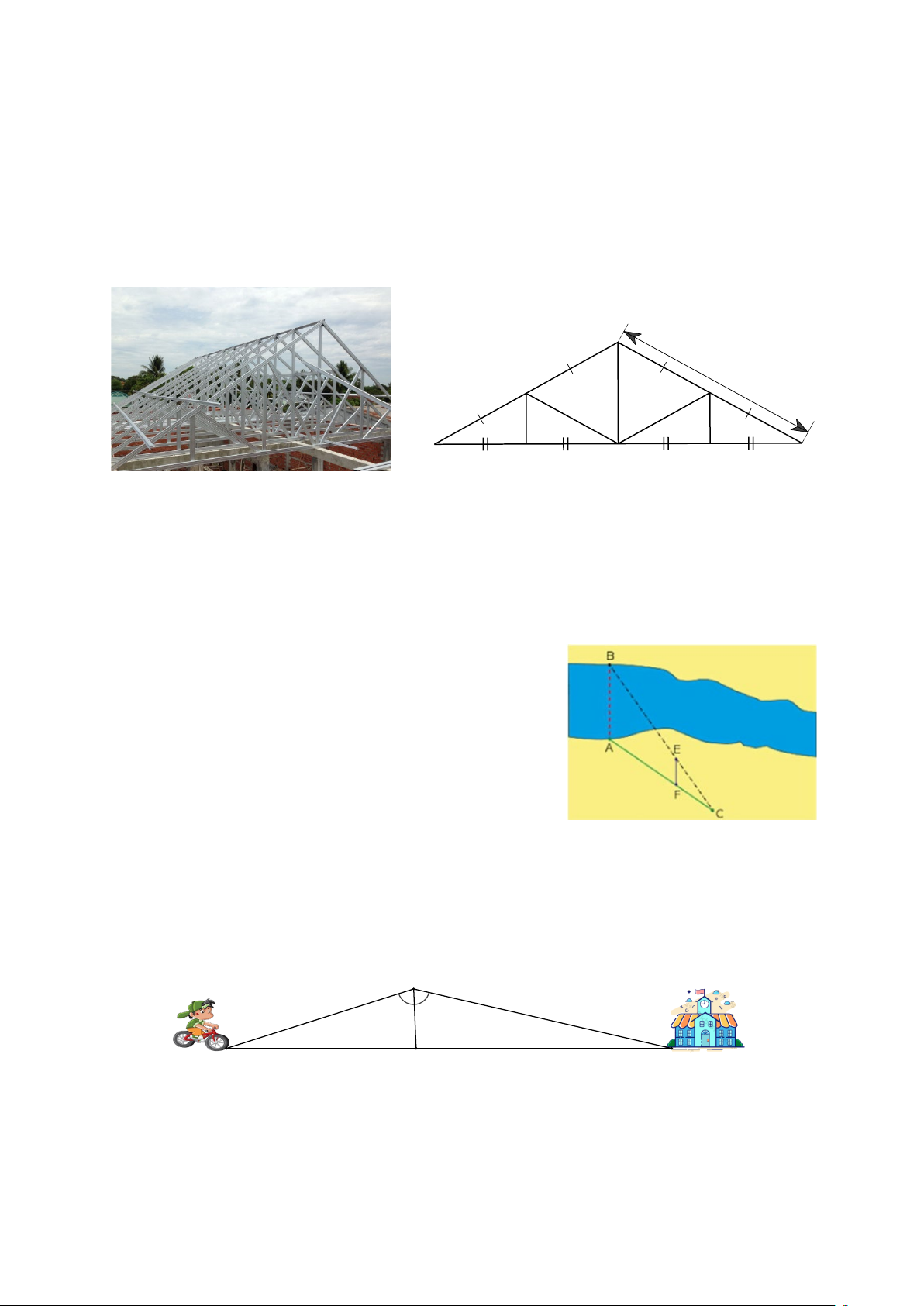
3. Một số bài toán thực tế liên quan đến hình học
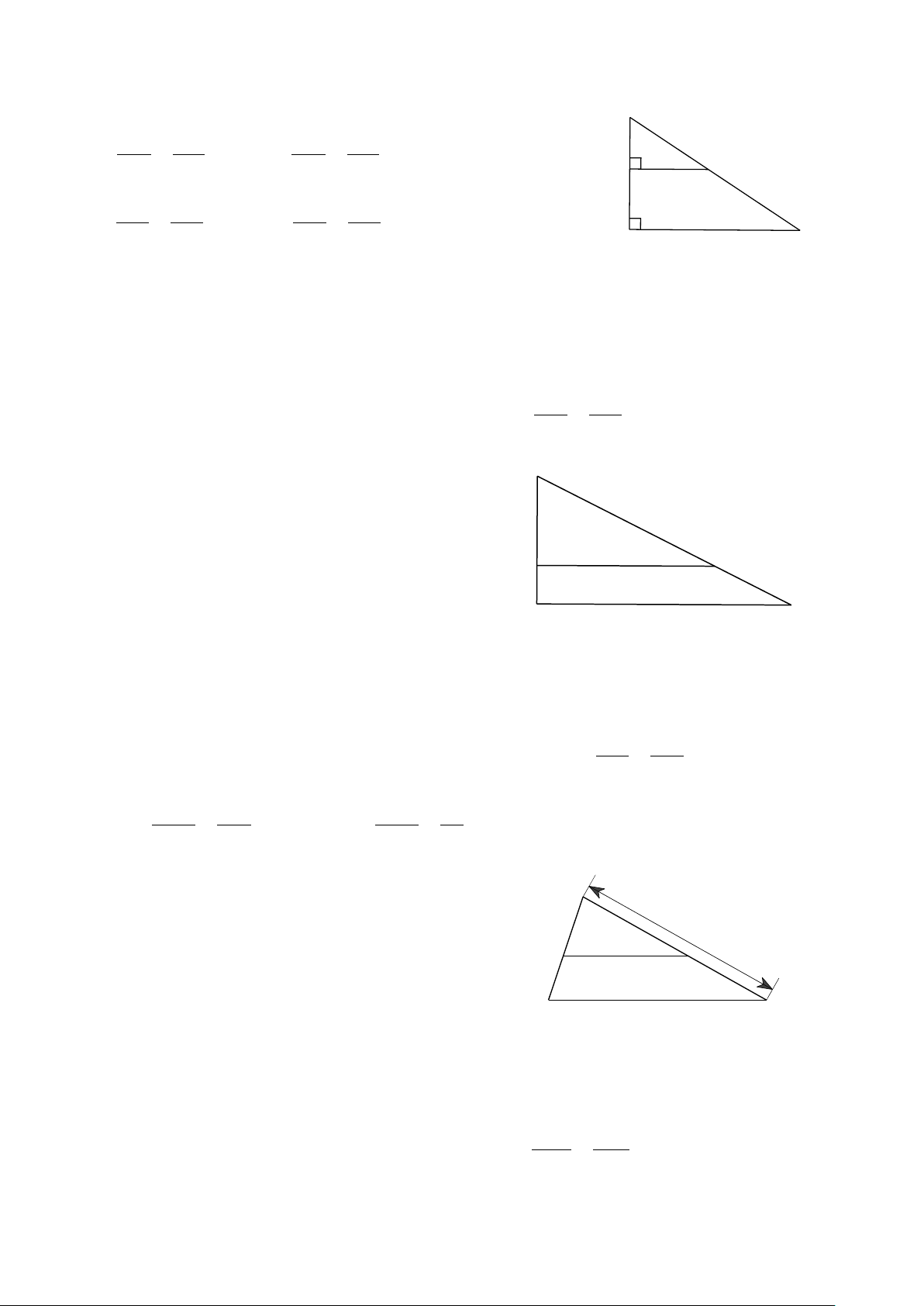
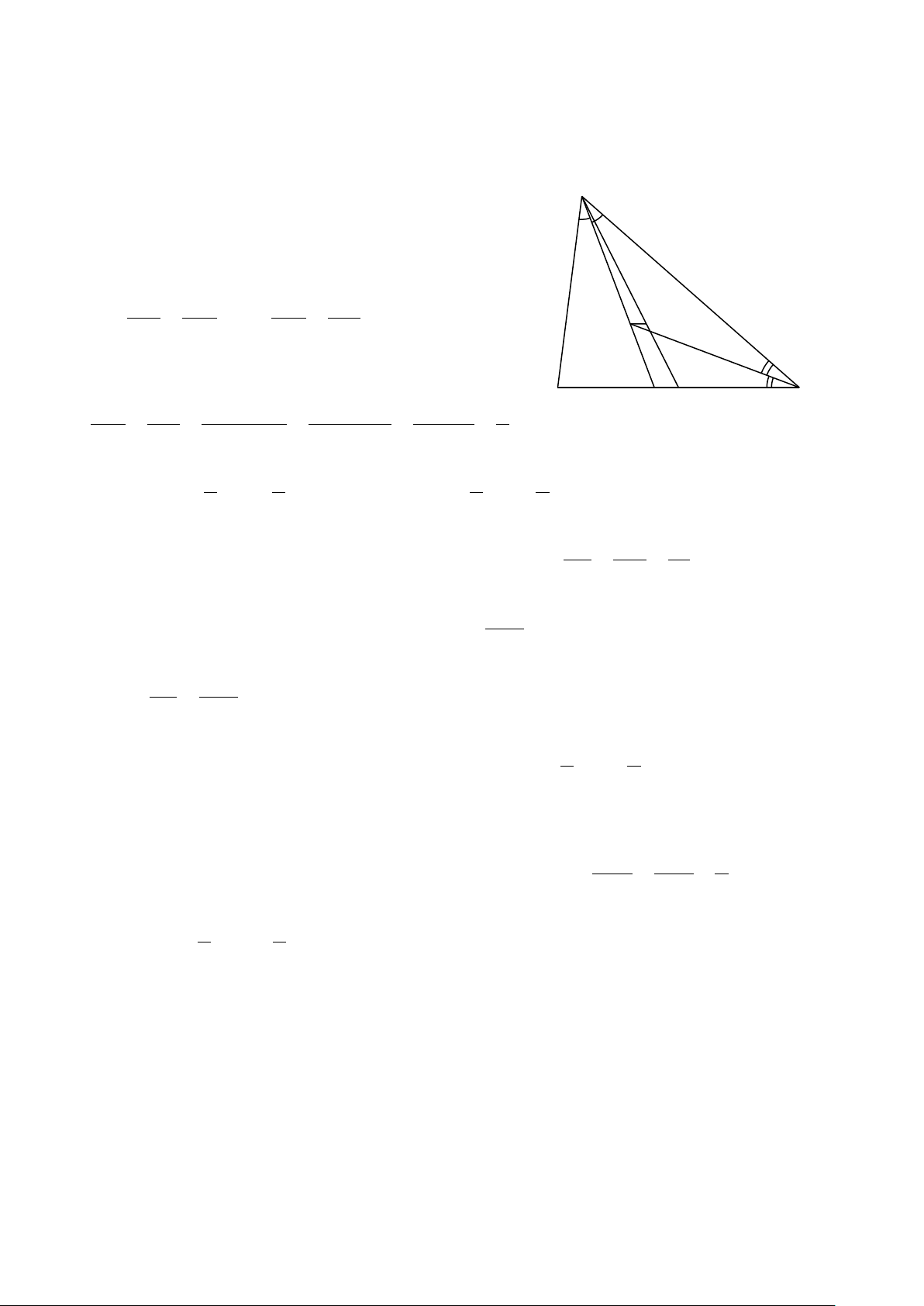
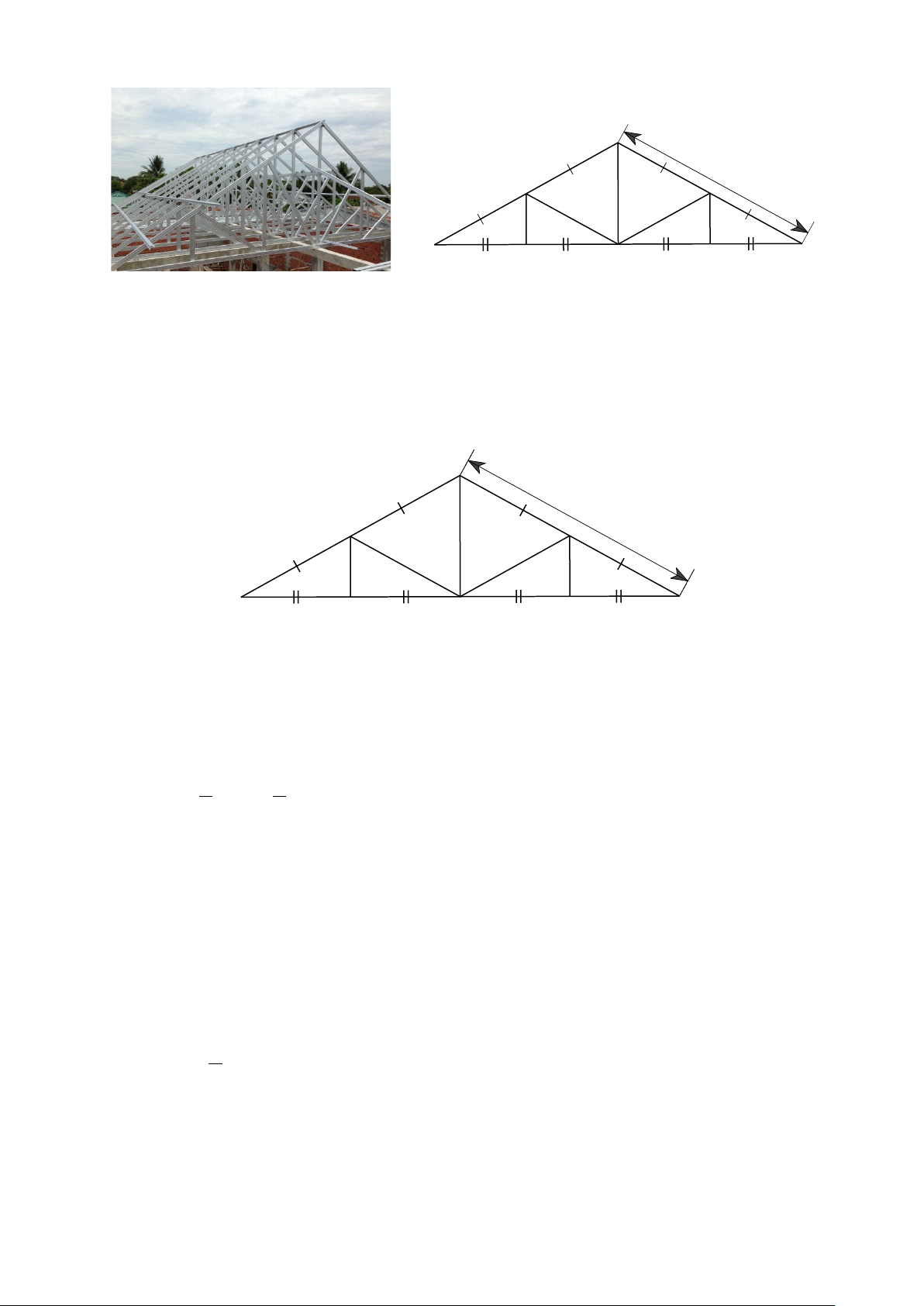
Bài 22. Vì kèo mái tôn là một trong những bộ phận không thể thiếu trong cấu tạo mái
nhà lợp tôn. Nó giúp chống đỡ và giảm trọng lực của những ảnh hưởng từ các yếu tố
bên ngoài tác động vào (Hình a). y 2,7 m 2,8 m x Hình a Hình b
Một vì kèo mái tôn được vẽ lại như Hình b. Tính độ dài x của cây chống đứng bên và
độ dài y của cánh kèo.
Bài 23. Để đo khoảng cách giữa hai vị trí B và E ở
hai bên bờ sông, bác Minh chọn ba vị trí , , A F C
cùng nằm ở bên bờ sông sao cho ba điểm C, , E B
thẳng hàng; ba điểm C, , F A thẳng hàng và
AB // EF. Sau đó bác Minh đo được AF = 50 m,
FC = 35 m và EC = 42 m. Tính khoảng cách giữa
hai vị trí B và E.
Bài 24. Lúc 6 giờ sáng, bạn Hải đi xe đạp từ điểm A đến trường (tại điểm B) phải leo
lên và xuống một con dốc với đỉnh dốc tại điểm C (như hình vẽ). C 0,32 km A 0,4 km H B
Điểm H là một điểm thuộc đoạn thẳng AB sao cho CH đường là phân giác ACB,
AH = 0,32 km và BH = 0,4 km. Biết bạn Hải đi xe đạp đến C lúc 6 giờ 30 phút với
tốc độ trung bình lên dốc là 4 km/h. Hỏi bạn Hải đến trường lúc mấy giờ nếu tốc độ
trung bình xuống dốc là 10 km/h? 4. Một số dạng khác Bài 25.
a) Tìm giá trị lớn nhất của phân thức 14 M = . 2 x − 2x + 4
b) Tìm giá trị nhỏ nhất của phân thức 11 N = . 2 12 − 4x − x
Bài 26. Rút gọn các phân thức sau: 3 3 3 a)
x + y + z − 3xyz A = . 2 2 2
x + y + z − xy − yz − xz 24 20 16 4 b)
x + x + x + ... + x +1 B = . 26 24 22 2
x + x + x + ... + x +1
Bài 27. Cho a ; a; ; a ; + … a ;
a là 2024 số thực thỏa mãn 2k 1 a = với 1 2 3 2023 2024 k (k + k)2 2 k ∈{1; 2; 3; ; … 202 }
4 . Tính tổng S = a + a + a +…+ a . 2024 1 2 3 2024
Bài 28. Cho x, y, z ≠ 0 thoả mãn x + y + z = xyz và 1 1 1 + + = 3. x y z
Tính giá trị của biểu thức 1 1 1 P = + + . 2 2 2 x y z 2 2 2 Bài 29. Cho a b c + +
=1. Chứng minh rằng a b c + + = 0.
b + c c + a a + b
b + c c + a a + b
Bài 30. Biết x ≠ – y; y ≠ –z; z ≠ –x, rút gọn biểu thức sau: 2 2 2 x − yz y − xz z − xy A = ( + +
x + y)(x + z) ( y + x)( y + z) (z + x)(z + y).
Bài 31. Rút gọn biểu thức B (ab bc ca) 1 1 1 1 1 1 abc = + + + + − + + . 2 2 2 a b c a b c
Bài 32. Cho a + b + c = 0, hãy tính giá trị của biểu thức:
a − b b − c c − a c a b C = + + + + . c a
b a − b b − c c − a
HƯỚNG DẪN GIẢI CHI TIẾT
ĐỀ CƯƠNG ÔN TẬP GIỮA HỌC KÌ II
BỘ SÁCH: CÁNH DIỀU MÔN TOÁN – LỚP 8
A. Bài tập trắc nghiệm BẢNG ĐÁP ÁN Câu 1 2 3 4 5 6 7 8 9 10 Đáp án B D A C D A A B D C Câu 11
12 13 14 15 16 17 18 19 20 Đáp án C D D C A B A D D C Câu
21 22 23 24 25 26 27 28 29 30 Đáp án D D C C A B A D B A Câu
31 32 33 34 35 36 37 38 39 40 Đáp án B C B C D C C B C A Câu
41 42 43 44 45 46 47 48 49 50 Đáp án A B A B A C B C D A
Hướng dẫn giải chi tiết
Câu 1. Hôm nay, lớp bạn Minh trực cổng trường. Bạn Minh ngồi trước cổng trường để
ghi lại các bạn học sinh đi học trễ. Hỏi bạn Minh đã thu thập dữ liệu theo phương pháp nào sau đây? A. Từ nguồn có sẵn. B. Quan sát. C. Lập bảng hỏi. D. Phỏng vấn. Hướng dẫn giải Đáp án đúng là: B
Bạn Minh ngồi trước cổng trường để ghi lại các bạn học sinh đi học trễ, do đó bạn
Minh đã thu thập dữ liệu theo phương pháp quan sát.
Câu 2. Trong các phương pháp thu thập dữ liệu sau, phương pháp thu thập nào là trực tiếp? A. Xem tin tức trên ti vi.
B. Tìm hiểu thông tin qua sách. C. Tra cứu trên Internet; D. Làm thí nghiệm. Hướng dẫn giải: Đáp án đúng là: D
Làm thí nghiệm là phương pháp thu thập dữ liệu trực tiếp.
Câu 3. Nhân dịp nghỉ hè, gia đình bạn An muốn đi tắm biển ở Đà Nẵng. Trước khi đi
Đà Nẵng 1 tuần, bạn An đã vào website của Trung tâm dự báo khí tượng thủy văn quốc
gia để tìm hiểu về tình hình thời tiết ở đó. Hỏi bạn An đã dùng phương pháp nào sau
đây để thu thập dữ liệu?
A. Thu thập dữ liệu gián tiếp.
B. Thu thập dữ liệu trực tiếp. C. Phỏng vấn. D. Làm thí nghiệm. Hướng dẫn giải Đáp án đúng là: A
Bạn An đã vào website của Trung tâm dự báo khí tượng thủy văn quốc gia để lấy dữ
liệu, tức là dùng phương pháp thu thập dữ liệu gián tiếp.
Câu 4. Trong các trường hợp sau, trường hợp nào là thu thập dữ liệu gián tiếp?
A. Phỏng vấn các bạn học sinh về tình hình bạo lực học đường.
B. Lập phiếu hỏi về các món ăn mà các bạn trong lớp yêu thích.
C. Tìm hiểu trên mạng Internet về số ca mắc bệnh COVID-19 ở Việt Nam.
D. Làm thí nghiệm để xác định tính chất hóa học của oxygen. Hướng dẫn giải Đáp án đúng là: C
Tìm hiểu trên mạng Internet về số ca mắc bệnh COVID-19 ở Việt Nam là trường hợp
thu thập dữ liệu gián tiếp.
Câu 5. Trong các dãy dữ liệu sau đây, dữ liệu nào là số liệu liên tục?
A. Số học sinh của mỗi lớp khối 8.
B. Tên các bạn tổ 1 của lớp 8A.
C. Tuổi nghề của các công nhân trong một phân xưởng.
D. Nhiệt độ trung bình (độ C) của các ngày trong năm. Hướng dẫn giải Đáp án đúng là: D
Nhiệt độ trung bình (độ C) của các ngày trong năm là số liệu liên tục.
Câu 6. Trong các dãy dữ liệu sau đây, dữ liệu nào là số liệu rời rạc?
A. Số thành viên trong một gia đình.
B. Cân nặng (kg) của các học sinh lớp 8D.
C. Kết quả nhảy xa (mét) của 10 vận động viên.
D. Lượng mưa trung bình (mm) trong một tháng ở Thành phố Hồ Chí Minh. Hướng dẫn giải Đáp án đúng là: A
Số thành viên trong một gia đình là số liệu rời rạc.
Câu 7. Kết quả đánh giá mức độ hài lòng của khách hàng về chất lượng dịch vụ của
một khách sạn: Hài lòng, Rất hài lòng, Bình thường, Không hài lòng. Hỏi dữ liệu trên là loại dữ liệu nào?
A. Dữ liệu không là số, có thể sắp thứ tự.
B. Dữ liệu không là số, không thể sắp thứ tự. C. Số liệu rời rạc. D. Số liệu liên tục. Hướng dẫn giải Đáp án đúng là: A
Dữ liệu thu được: Hài lòng, Rất hài lòng, Bình thường, Không hài lòng là dữ liệu không
là số, có thể sắp thứ tự theo mức độ hài lòng về chất lượng dịch vụ.
Câu 8. Cho bảng thống kê tỉ lệ các loại mẫu vật trong bảo tàng sinh vật của môi trường
đại học về những lớp động vật có xương sống: Cá, Lưỡng cư, Bò sát, Chim, Thú. Lớp động vật
Tỉ lệ mẫu vật (%) Cá 15% Lưỡng cư 10% Bò sát 20% Chim 25% Thú 30% Tổng 101%
Giá trị chưa hợp lí trong bảng dữ liệu là
A. Dữ liệu về tên các lớp động vật.
B. Dữ liệu về tỉ lệ mẫu vật.
C. Cả A và B đều đúng. D. Cả A và B đều sai. Hướng dẫn giải Đáp án đúng là: B
Tổng tỉ lệ luôn bằng 100%, mà theo bảng thống kê đã cho thì tổng tỉ lệ là 101%, do
đó dữ liệu về tỉ lệ mẫu vật là chưa hợp lí.
Câu 9. Khi muốn biểu diễn sự thay đổi của một đại lượng theo thời gian ta nên dùng
loại biểu đồ nào sau đây? A. Biểu đồ tranh.
B. Biểu đồ hình quạt tròn. C. Biểu đồ cột kép.
D. Biểu đồ đoạn thẳng. Hướng dẫn giải Đáp án đúng là: D
Khi muốn biểu diễn sự thay đổi của một đại lượng theo thời gian ta nên dùng biểu đồ đoạn thẳng.
Câu 10. Khi muốn so sánh hai tập dữ liệu khác nhau ta nên dùng loại biểu đồ nào sau đây? A. Biểu đồ tranh. B. Biểu đồ cột. C. Biểu đồ cột kép.
D. Biểu đồ đoạn thẳng. Hướng dẫn giải Đáp án đúng là: C
Khi muốn so sánh hai tập dữ liệu khác nhau ta nên dùng biểu đồ cột kép.
Câu 11. Bạn Minh muốn lập biểu đồ về tỉ lệ số học sinh của lớp 8A xếp loại học lực Tốt,
Khá, Đạt, Chưa đạt ở cuối học kì I. Hỏi bạn Minh nên sử dụng biểu đồ nào sau đây? A. Biểu đồ tranh. B. Biểu đồ cột.
C. Biểu đồ hình quạt tròn.
D. Biểu đồ đoạn thẳng. Hướng dẫn giải Đáp án đúng là: C
Khi muốn lập biểu đồ về tỉ lệ, ta nên dùng biểu đồ hình quạt tròn.
Câu 12. Lựa chọn biểu đồ tranh khi muốn
A. so sánh trực quan từng cặp số liệu của hai bộ dữ liệu cùng loại.
B. biểu thị tỉ lệ phần trăm của từng loại số liệu so với tổng thể.
C. biểu diễn sự thay đổi số liệu của một đối tượng theo thời gian.
D. biểu diễn số lượng các loại đối tượng khác nhau, tạo sự lôi cuốn, thu hút bằng hình ảnh. Hướng dẫn giải Đáp án đúng là: D
Lựa chọn biểu đồ tranh khi muốn biểu diễn số lượng các loại đối tượng khác nhau, tạo
sự lôi cuốn, thu hút bằng hình ảnh.
Câu 13. Dùng loại biểu đồ nào để biểu diễn dữ liệu trong bảng thống kê sau đây là phù hợp nhất?
Xếp loại học lực cuối học kì I của học sinh khối 8
Trường Trung học cơ sở Kim Đồng Loại học lực Số học sinh Tốt 37 Khá 140 Đạt 53 Chưa đạt 10 A. Biểu đồ tranh.
B. Biểu đồ đoạn thẳng.
C. Biểu đồ hình quạt tròn. D. Biểu đồ cột. Hướng dẫn giải Đáp án đúng là: D
Để biểu diễn dữ liệu trong bảng thống kê đã cho, ta nên dùng biểu đồ cột là phù hợp nhất.
Câu 14. Để biểu diễn sự thay đổi sĩ số của các lớp trong một khối ở cuối năm so với
đầu năm học, ta nên chọn loại biểu đồ nào sau đây? A. Biểu đồ tranh. B. Biểu đồ cột. C. Biểu đồ cột kép.
D. Biểu đồ đoạn thẳng. Hướng dẫn giải Đáp án đúng là: C
Để biểu diễn sự thay đổi sĩ số của các lớp trong một khối ở cuối năm so với đầu năm
học, ta nên chọn biểu đồ cột kép.
Câu 15. Quan sát biểu đồ sau:
Tỉ lệ phần trăm sản lượng gạo của Việt Nam
xuất khẩu sang các nước liên minh Châu Âu
trong 6 tháng đầu năm 2022 17% Italy Đức 5% 39% Hà Lan 7% Thụy Điển Ba Lan 13% Khác 19%
Sản lượng gạo xuất khẩu của Việt Nam sang Italy gấp mấy lần sản lượng gạo xuất khẩu của Việt Nam sang Ba Lan? A. 7,8 lần. B. 7 lần. C. 8,7 lần. D. 8 lần. Hướng dẫn giải Đáp án đúng là: A
Sản lượng gạo xuất khẩu của Việt Nam sang Italy chiếm 39%. Sản lượng gạo xuất khẩu
của Việt Nam sang Ba Lan là 5%.
Vậy sản lượng gạo xuất khẩu của Việt Nam sang Italy gấp 39% = 7,8 lần sản lượng 5%
gạo xuất khẩu của Việt Nam sang Ba Lan.
Câu 16. Quan sát biểu đồ sau:
Số doanh nghiệp thành lập mới và giải thể
của Việt Nam giai đoạn 2017 - 2019 149000 138100 126859 131275 129000 109000 89000 Doanh nghiệp thành lập mới 69000 Doanh nghiệp 49000 giải thể 29000 12113 16314 16800 9000 2017 2018 2019
(Nguồn: Tổng cục thống kê)
Trong giai đoạn 2017 – 2019:
A. Số doanh nghiệp thành lập mới và giải thể đều giảm.
B. Số doanh nghiệp thành lập mới tăng nhanh hơn số doanh nghiệp giải thể.
C. Số doanh nghiệp giải thể tăng nhanh hơn số doanh nghiệp thành lập mới.
D. Số doanh nghiệp thành lập mới giảm, số doanh nghiệp giải thể tăng. Hướng dẫn giải Đáp án đúng là: B
Quan sát biểu đồ đoạn thẳng đã cho, ta thấy:
⦁ Số doanh nghiệp thành lập mới và giải thể đều tăng. Do đó cả A, D đều sai.
⦁ Quan sát độ dốc của đường biểu diễn, ta thấy đường biểu diễn số doanh nghiệp thành
lập mới dốc hơn đường biểu diễn số doanh nghiệp giải thể nên số doanh nghiệp thành
lập mới tăng nhanh hơn số doanh nghiệp giải thể.
Vậy ta chọn phương án B.
Câu 17. Quan sát biểu đồ sau:
Chênh lệch nhiệt độ tại TP. Hồ Chí Minh Nhiệt độ (°C)
từ 16/01/2023 đến 22/01/2023 35 33 31 32 31 32 32 32 30 25 23 22 22 22 23 22 22 20 Nhiệt độ cao nhất 15 Nhiệt độ 10 thấp nhất 5
0 Thứ Hai Thứ Ba Thứ Tư Thứ Năm Thứ Sáu Thứ Bảy Chủ nhật Ngày trong tuần
(Nguồn : Trung tâm Dự báo khí tượng thủy văn quốc gia)
Ngày nào sau đây chênh lệch giữa nhiệt độ cao nhất và nhiệt độ thấp nhất trong tuần
của TP. Hồ Chí Minh là 9 C? ° A. Thứ Năm. B. Thứ Bảy. C. Chủ nhật. D. Thứ Hai. Hướng dẫn giải Đáp án đúng là: A
Thứ Hai có chênh lệch giữa nhiệt độ cao nhất và nhiệt độ thấp nhất là 33 C ° − 23 C ° =10 C ° .
Thứ Năm có chênh lệch giữa nhiệt độ cao nhất và nhiệt độ thấp nhất là 32 C ° − 23 C ° = 9 C ° .
Thứ Bảy có chênh lệch giữa nhiệt độ cao nhất và nhiệt độ thấp nhất là 32 C ° − 22 C ° =10 C ° .
Chủ nhật có chênh lệch giữa nhiệt độ cao nhất và nhiệt độ thấp nhất là 32 C ° − 22 C ° =10 C ° .
Vậy ta chọn phương án A.
Câu 18. Biểu đồ dưới đây thể hiện số sách trong thư viện của một lớp. Môn học Số sách Toán Ngữ văn Tin học Lịch sử và Địa lí Khoa học tự nhiên : 2 quyển sách
Khẳng định nào sau đây là đúng?
A. Số sách Toán trong thư viện là 7 quyển.
B. Số sách Ngữ Văn nhiều hơn số sách Tin học là 2 quyển.
C. Tổng số sách trong thư viện là 21 quyển.
D. Số sách Khoa học tự nhiên nhiều hơn số sách Lịch sử và Địa lí là 8 quyển. Hướng dẫn giải Đáp án đúng là: D
Số sách Toán trong thư viện là 7 ⋅ 2 =14 (quyển).
Tương tự, số sách Ngữ văn, Tin học, Lịch sử và Địa lí, Khoa học tự nhiên trong thư
viện lần lượt là 8 quyển, 4 quyển, 4 quyển, 12 quyển.
Sách Ngữ văn nhiều hơn sách Tin học là 8 − 4 = 4 (quyển).
Tổng số sách trong thư viện là 14 + 8 + 4 + 4 +12 = 42 (quyển).
Sách Khoa học tự nhiên nhiều hơn số sách Lịch sử và Địa lí là 12 − 4 = 8 (quyển).
Vậy ta chọn phương án D.
Câu 19. Biểu đồ dưới đây biểu diễn số lượng học sinh của một lớp chọn loại nước
uống trong đợt liên hoan cuối năm. Biết mỗi học sinh chỉ chọn một loại nước uống và
tất cả học sinh của lớp đều tham gia bình chọn. Số người chọn 14 12 12 11 10 8 8 6 5 4 2 0 Nước cam Nước dừa Nước chanh
Nước mía Loại nước
Khẳng định nào sau đây là sai? A. Lớp có 36 học sinh.
B. Loại nước được yêu thích nhất trong lớp là nước cam.
C. Số học sinh chọn nước dừa nhiều hơn số học sinh chọn nước mía.
D. Tổng số học sinh chọn nước dừa và nước mía ít hơn số học sinh chọn nước cam. Hướng dẫn giải Đáp án đúng là: D
Số học sinh của lớp đó là: 12 + 8 +11+ 5 = 36 (học sinh).
Loại nước được yêu thích nhất trong lớp là nước cam, với 12 học sinh lựa chọn.
Số học sinh chọn nước dừa nhiều hơn số học sinh chọn nước mía là 8 − 5 = 3 (học sinh).
Tổng số học sinh chọn nước dừa và nước mía là: 8 + 5 =13 (học sinh), nhiều hơn số
học sinh chọn nước cam. Do đó khẳng định D là sai.
Vậy ta chọn phương án D.
Câu 20. Biểu đồ dưới đây biểu diễn tỉ lệ hoa quả bán được trong một ngày của một
cửa hàng. Biết ngày hôm đó cửa hàng bán được 150 kg hoa quả.
Tỉ lệ các loại quả bán được 10% 20% Lê Táo Nhãn 40% 30% Nho
Khẳng định nào sau đây là đúng?
A. Cửa hàng bán được 30 kg táo.
B. Khối lượng nhãn bán được nhiều hơn khối lượng nho bán được là 30 kg.
C. Cửa hàng bán được tổng cộng 45 kg lê và nho.
D. Khối lượng nhãn bán được là 40 kg. Hướng dẫn giải Đáp án đúng là: C
Cửa hàng bán được số kg táo là: 150⋅30% = 45 (kg).
Tương tự, ta tính được khối lượng lê, nhãn, nho cửa hàng bán được lần lượt là: 30 kg; 60 kg; 15 kg.
Khối lượng nhãn bán được nhiều hơn khối lượng nho là 50 −15 = 45 (kg).
Cửa hàng bán được tổng cộng 30 +15 = 45 kg lê và nho.
Vậy ta chọn phương án C.
Câu 21. Một công ty kinh doanh vật liệu xây dựng có bốn kho hàng có 50 tấn hàng.
Kế toán của công ty lập biểu đồ cột kép ở hình bên biểu diễn số lượng vật liệu đã xuất
bán và số lượng vật liệu còn tồn lại trong mỗi kho sau tuần lễ kinh doanh đầu tiên. Số lượng Xuất bán Tồn tại vật liệu (tấn) 40 35 35 30 30 30 30 25 20 20 20 15 15 15 10 5 0 Kho 1 Kho 2 Kho 3 Kho 4 Kho
Kế toán đã ghi nhầm số liệu của một kho trong biểu đồ cột kép đó. Theo em, kế toán
đã ghi nhầm số liệu ở kho nào? A. Kho 1. B. Kho 2 và kho 4. C. Kho 1 và kho 3. D. Kho 4. Hướng dẫn giải Đáp án đúng là: D
Kế toán đã ghi nhầm số liệu của kho 4 trong biểu đồ cột kép đó. Vì tổng khối lượng ở
kho 4 theo biểu đồ là 30 +15 = 45 (tấn) < 50 tấn.
Sử dụng biểu đồ dưới đây để trả lời các câu hỏi Câu 22, Câu 23.
Biểu đồ dưới đây biểu diễn doanh thu du lịch lữ hành theo giá hiện hành tại Đà Nẵng
qua các năm 2019, 2020, 2021, 2022 (sơ bộ): Tỉ đồng 2500 2267,09 2113,3 1905,6 2000 1500 1000 563,8 635,71 500 0 2018 2019 2020 2021 2022 (sơ bộ) Năm
(Nguồn: Tổng cục thống kê)
Câu 22. Doanh thu du lịch lữ hành theo giá hiện hành tại Đà Nẵng năm 2021 là
A. 1 905,6 tỉ đồng. B. 2 113,3 tỉ đồng. C. 563,8 tỉ đồng. D. 635,71 tỉ đồng. Hướng dẫn giải Đáp án đúng là: D
Doanh thu du lịch lữ hành theo giá hiện hành tại Đà Nẵng năm 2021 là 635,71 tỉ đồng.
Câu 23. So với năm 2020, năm 2022 (số liệu sơ bộ) tăng khoảng bao nhiêu phần trăm
(làm tròn kết quả đến hàng đơn vị)? A. 25%. B. 125%. C. 302%. D. 402%. Hướng dẫn giải Đáp án đúng là: C
So với năm 2020, năm 2022 (số liệu sơ bộ) tăng khoảng
2 267,09 − 563,8 ⋅100% ≈302%. 563,8
Sử dụng nội dung sau để trả lời các câu hỏi Câu 24, Câu 25 và Câu 26.
Một hộp chứa 6 tấm thẻ như nhau được đánh số từ 3 đến 8. Rút ngẫu nhiên một tấm thẻ từ hộp.
Câu 24. Có bao nhiêu kết quả có thể? A. 3. B. 5. C. 6. D. 8. Hướng dẫn giải Đáp án đúng là: C
Trong hộp có 6 tấm thẻ nên khi rút ngẫu nhiên một tấm từ hộp thì có 6 kết quả có thể xảy ra.
Câu 25. Có bao nhiêu kết quả thuận lợi của biến cố “Rút được tấm thẻ đánh số chẵn”? A. 3. B. 5. C. 6. D. 8. Hướng dẫn giải Đáp án đúng là: A
Trong 6 số từ 3 đến 8, có 3 số chẵn là: 4; 6; 8.
Vậy có 3 kết quả thuận lợi của biến cố “Rút được tấm thẻ đánh số chẵn”.
Câu 26. Có bao nhiêu kết quả thuận lợi của biến cố “Rút được tấm thẻ đánh số chia hết cho 3”? A. 1. B. 2. C. 3. D. 4. Hướng dẫn giải Đáp án đúng là: B
Trong 6 số từ 3 đến 8, có 2 số chia hết cho 3 là: 3; 6.
Vậy có 2 kết quả thuận lợi của biến cố “Rút được tấm thẻ đánh số chia hết cho 3”.
Sử dụng nội dung sau để trả lời các câu hỏi Câu 27, Câu 28 và Câu 29.
Tổ Cường có 13 bạn, gồm có 8 bạn nam và 5 bạn nữ, trong đó có 3 bạn nam và 1 bạn
nữ tham gia vào câu lạc bộ thể thao. Chọn ngẫu nhiên 1 bạn từ tổ.
Câu 27. Xác suất của biến cố “Bạn được chọn có tham gia câu lạc bộ thể thao” là A. 4 . B. 5 . C. 8 . D. 1 . 13 13 13 13 Hướng dẫn giải Đáp án đúng là: A
Tổ Cường có 3 bạn nam và 1 bạn nữ tham gia vào câu lạc bộ thể thao, nên xác suất của
biến cố “Bạn được chọn có tham gia câu lạc bộ thể thao” là 3 +1 4 = . 13 13
Câu 28. Xác suất của biến cố “Bạn được chọn là bạn nữ tham gia vào câu lạc bộ thể thao” là A. 4 . B. 5 . C. 8 . D. 1 . 13 13 13 13 Hướng dẫn giải Đáp án đúng là: D
Tổ Cường có 1 bạn nữ tham gia vào câu lạc bộ thể thao, nên xác suất của biến cố “Bạn
được chọn là bạn nữ tham gia vào câu lạc bộ thể thao” là 1 . 13
Câu 29. Xác suất của biến cố “Bạn được chọn là bạn nam không tham gia câu lạc bộ thể thao” là A. 4 . B. 5 . C. 8 . D. 1 . 13 13 13 13 Hướng dẫn giải Đáp án đúng là: B
Tổ Cường có 8 bạn nam, trong đó có 3 bạn nam tham gia vào câu lạc bộ thể thao. Khi
đó có 8 − 3 = 5 bạn nam không tham gia câu lạc bộ thể thao.
Vậy xác suất của biến cố “Bạn được chọn là bạn nam không tham gia câu lạc bộ thể thao” là 5 . 13
Sử dụng nội dung sau để trả lời các câu hỏi Câu 30 và Câu 31.
Phỏng vấn 200 bạn sinh viên về một quyển sách thì có 40 bạn sinh viên thích quyển sách này.
Câu 30. Xác suất thực nghiệm của biến cố “Một bạn sinh viên thích quyển sách” là A. 20%. B. 30%. C. 15%. D. 40%. Hướng dẫn giải Đáp án đúng là: A
Trong 200 bạn, có 40 bạn sinh viên thích quyển sách, do đó xác suất thực nghiệm của
biến cố “Một bạn sinh viên thích quyển sách” là 40 ⋅100% = 20%. 200
Câu 31. Phỏng vấn ngẫu nhiên thêm 60 bạn sinh viên. Dự đoán trong 60 bạn sinh viên
được phỏng vấn, số sinh viên thích quyển sách là A. 20. B. 12. C. 15. D. 10. Hướng dẫn giải Đáp án đúng là: B
Theo kết quả của Câu 30, xác suất thực nghiệm của biến cố “Một bạn sinh viên thích quyển
sách” là 20%. Khi đó, trong 60 bạn, dự đoán có 60⋅ 20% =12 bạn thích quyển sách.
Sử dụng bảng thống kê sau để trả lời các câu hỏi từ Câu 32 đến Câu 25.
Hai bạn Dũng và Nam chơi 1 ván oẳn tù tì gồm 10 lần theo luật chơi: Búa (B) thắng
Kéo (K); Kéo (K) thắng Lá (L), Lá (L) thắng Búa (B) và hòa nhau nếu cùng loại. KÉO – Thắng KÉO LÁ BÚA – Thắng LÁ – Thắng BÚA
Sau đây là kết quả của mỗi ván chơi: Lần thứ 1 2 3 4 5 6 7 8 9 10 Dũng L B B K L B K B K K Nam B K L L K B L K L B
Câu 32. Xác suất thực nghiệm của sự kiện “Dũng ra búa” là A. 3 . B. 1 . C. 2 . D. 1 . 10 2 5 5 Hướng dẫn giải Đáp án đúng là: C
Dũng ra búa tất cả 4 lần trong 10 ván chơi nên xác suất thực nghiệm của sự kiện “Dũng ra búa” là 4 2 = . 10 5
Câu 33. Xác suất thực nghiệm của sự kiện “Dũng thắng” là A. 3 . B. 3 . C. 2 . D. 1 . 10 5 5 2 Hướng dẫn giải Đáp án đúng là: B
Ta có bảng thống kê sau: Lần thứ 1 2 3 4 5 6 7 8 9 10 Dũng L B B K L B K B K K Nam B K L L K B L K L B
Kết quả Dũng Dũng Nam Dũng Nam Dũng Dũng Dũng Nam Hòa
ván chơi thắng thắng thắng thắng thắng
thắng thắng thắng thắng
Trong 10 ván chơi, Dũng thắng 6 lần nên xác suất thực nghiệm của sự kiện “Dũng thắng” là 6 3 = . 10 5
Câu 34. Xác suất thực nghiệm của sự kiện “Dũng và Nam hòa nhau” là A. 4 . B. 1 . C. 1 . D. 2 . 5 2 10 5 Hướng dẫn giải Đáp án đúng là: C
Trong 10 ván chơi, chỉ có 1 lần Dũng và Nam hòa nhau nên xác suất thực nghiệm của
sự kiện “Dũng và Nam hòa nhau” là 1 . 10
Câu 35. Xác suất thực nghiệm của sự kiện “Nam không thua Dũng” là A. 4 . B. 1 . C. 1 . D. 2 . 5 2 10 5 Hướng dẫn giải Đáp án đúng là: D
Nam không thua Dũng tức là Nam thắng Dũng hoặc Nam hòa Dũng.
Trong 10 ván chơi, có 3 lần Nam thắng và 1 lần hòa nhau nên xác suất thực nghiệm
của sự kiện “Nam không thua Dũng” là 3 +1 4 2 = = . 10 10 5
Câu 36. Cho điểm M thuộc đoạn thẳng AB, thỏa mãn AM 3 = . Tỉ số AM là MB 8 AB A. 5. B. 5 . C. 3 . D. 8 . 8 11 11 11 Hướng dẫn giải Đáp án đúng là: C A M B
Theo tính chất tỉ lệ thức ta có từ AM 3 = , suy ra AM 3 = hay AM 3 = . MB 8 AM + MB 3 + 8 AB 11
Câu 37. Cho hình bên, trong đó DE // BC, A
AD =12 cm, DB =18 cm và CE = 30 cm. Độ dài D E AC là A. 20 cm. B. 18 cm. 25 B C C. 50 cm. D. 45 cm. Hướng dẫn giải Đáp án đúng là: C Xét A
∆ BC có DE // BC, theo định lí Thalès ta có: AD AE = . DB EC
Từ đó, theo tính chất tỉ lệ thức ta có AD + DB AE + EC + = hay AD DB AC = DB EC DB EC Suy ra 12 +18 AC = , nên 30 30 AC ⋅ = = 50 cm. 18 30 18
Câu 38. Cho hình bên. Tỉ lệ thức nào sau đây là đúng? B A. BD BE = . B. BD BE = . AD BC AD EC E D C. DE BC = . D. AD BC = . AC BE AB EC A C Hướng dẫn giải Đáp án đúng là: B
Vì DE ⊥ AB và AC ⊥ AB nên DE // AC. Xét A
∆ BC có DE // AC, theo định lí Thalès ta có: BD BE = . AD EC
Câu 39. Cho hình bên, biết DE // AC. Giá trị B
của x (làm tròn kết quả đến chữ số thập phân 5 cm thứ hai) là D E A. x ≈ 7,15 cm. B. x ≈ 7,10 cm. 2 cm A C C. x ≈ 7,14 cm.
D. x ≈ 7,142 cm. 10 cm Hướng dẫn giải Đáp án đúng là: C Xét A
∆ BC có DE // AC, theo hệ quả định lí Thalès ta có: BD DE = . BA AC Suy ra 5 DE = , do đó 5 10 50 DE ⋅ = = ≈ 7,14 cm. 5 + 2 10 7 7
Câu 40. Cho hình bên, biết MN // IK. Giá trị H của x là x 7 cm 12 cm A. x = 4,2 cm. B. x = 2,5 cm. M N 3 cm C. x = 7 cm. D. x = 5,25 cm. I K Hướng dẫn giải Đáp án đúng là: A Xét H
∆ IK có MN // IK, theo định lí Thalès ta có: MH NH = . MI NK Suy ra x 7 = , do đó 3 7 x ⋅ = = 4,2 cm. 3 12 − 7 5
Câu 41. Cho hình bên. Tỉ số x bằng A y A. 7 . B. 1. 7,5 3,5 15 7 x y C. 15. D. 1 . B D 7 15 C Hướng dẫn giải Đáp án đúng là: A Xét A
∆ BC có AD là tia phân giác BAC (do = BAD CAD) nên ta có: DB AB 3,5 7 = = =
(tính chất đường phân giác). DC AC 7,5 15
Câu 42. Cho hình thang ABCD ( AB //CD) A B
có BC =15 cm. Điểm E thuộc cạnh AD sao I E F cho AE 1
= . Đường thẳng EF //CD AD 3
(F ∈BC) (hình vẽ). Độ dài BF là D C A. 15 cm. B. 5 cm. C. 10 cm. D. 7 cm. Hướng dẫn giải Đáp án đúng là: B
Ta có EF //CD, mà AB //CD nên EF // AB //C . D Xét A
∆ DC có EI // DC, theo tính chất tia phân giác của một góc ta có AE AI = . ED IC Xét A
∆ BC có IF // AB, theo tính chất tia phân giác của một góc ta có AI BF = . IC FC Suy ra AE BF =
, theo tính chất tỉ lệ thức ta có: AE BF = . ED FC
AE + ED BF + FC Hay AE BF = , do đó BF AE 1 = = , suy ra BC 15 BF = = = 5 cm. AD BC BC AD 3 3 3 Câu 43. Cho A
∆ BC, I, K lần lượt là trung điểm của AB và AC. Biết BC = 8 cm. Độ dài IK là A. 4 cm. B. 4,5 cm. C. 3,5 cm. D. 14 cm. Hướng dẫn giải A Đáp án đúng là: A Xét A
∆ BC có I, K lần lượt là trung điểm của AB và I K
AC nên IK là đường trung bình của tam giác, do đó IK 1 = , suy ra BC 8 IK = = = 4 cm. B 8 cm C BC 2 2 2 Câu 44. Cho A
∆ BC đều cạnh 3 cm. Gọi M , N lần lượt là trung điểm của AB và AC.
Chu vi của tứ giác MNCB là A. 8 cm. B. 7,5 cm. C. 6 cm. D. 7 cm. Hướng dẫn giải A Đáp án đúng là: B Vì A
∆ BC đều cạnh 3 cm nên M N
AC = BC = CA = 3 cm. Xét A
∆ BC có M , N lần lượt là trung điểm của AB và B 3 cm C
AC nên MN là đường
trung bình của tam giác, do đó MN 1 = , suy ra BC 3 MN = = =1,5 cm. BC 2 2 2
Vì M , N lần lượt là trung điểm của AB và AC nên ta có 1 1
BM = AB = AC = NC, 2 2
do đó BM = NC =1,5 cm.
Vậy chu vi của tứ giác MNCD là:
MN + NC + BC + BM =1,5 +1,5 + 3 +1,5 = 7,5 (cm).
Câu 45. Cho tam giác ABC. Gọi E, F, P theo thứ tự là trung điểm của các cạnh
AB, BC, C .
A Nhận định nào sau đây đúng?
A. EP là đường trung bình của A ∆ BC. B. 1 EF = BC. 2
C. Chu vi tam giác ABC gấp bốn lần chu vi tam giác EF . P D. PE // EF. Hướng dẫn giải A Đáp án đúng là: A Xét A
∆ BC có E, F, P theo thứ tự là trung điểm của E P
các cạnh AB, BC, C ,
A do đó EF, FP, PE đều là các
đường trung bình của tam giác. B F C Khi đó 1 1 1
EF = AC, FP = AB, PE = BC. 2 2 2
Suy ra chu vi tam giác EFP là: 1 1 1 1
EF + FP + PE = AC + AB + BC = ( AB + BC + CA). 2 2 2 2
Do đó chu vi tam giác ABC gấp hai lần chu vi tam giác EF . P
Vậy trong các khẳng định, chỉ có khẳng định A là đúng.
Câu 46. Cho tam giác ABC, các đường trung tuyến BD và CE cắt nhau tại . G Gọi
I, K theo thứ tự là trung điểm của GB, GC. Biết AG = 4 cm. Độ dài các đoạn thẳng
EI và DK lần lượt là A. 3 cm và 3 cm. B. 3 cm và 2 cm. C. 2 cm và 2 cm. D. 1 cm và 2 cm. Hướng dẫn giải A Đáp án đúng là: C Xét A
∆ BG có E, I lần lượt là trung điểm của D E
các cạnh AB, BG nên EI là đường trung bình G của tam giác, do đó 1 1 EI I = AG = ⋅ 4 = 2 cm. K 2 2 B C
Tương tự, DK là đường trung bình của A ∆ CG nên 1 1
DK = AG = ⋅ 4 = 2 cm. 2 2
Câu 47. Cho tam giác ABC, đường trung tuyến AM. Gọi D là trung điểm của AM , E
là giao điểm của BD và AC, F là trung điểm của EC. Biết AC = 9 cm, độ dài đoạn AE là A. 4,5 cm. B. 3 cm. C. 2 cm. D. 6 cm. Hướng dẫn giải A
Đáp án đúng là: B E Xét B
∆ CE có M , F lần lượt là trung điểm của D F
BC, EC nên MF là đường trung bình của tam giác,
do đó MF // BE, hay MF // DE. B M C Xét A
∆ MF có D là trung điểm của AM và DE // MF nên DE là đường trung bình
của tam giác, do đó E là trung điểm của AF. Suy ra AE = EF.
Mà F là trung điểm của EC nên EF = FC, do đó AE = EF = FC hay 1 1
AE = AC = ⋅9 = 3 cm. 3 3
Câu 48. Cho tam giác ABC, AD là đường phân giác của
BAC (D∈ BC). Tỉ lệ thức nào sau đây đúng? A. AB AC = . B. AD BD = . C. DB DC = . D. DB BC = . BD BC AC DC AB AC DC AC Hướng dẫn giải A Đáp án đúng là: C Xét A
∆ BC có AD là đường phân giác của BAC nên AB DB =
(tính chất đường phân giác). AC DC B D C Do đó DB DC =
(tính chất tỉ lệ thức). AB AC
Câu 49. Cho hình bên. Biết rằng các số A
trên hình có cùng đơn vị đo là cm. Giá trị
x và y lần lượt là 15 20 A. 16 cm và 12 cm. x y B. 14 cm và 14 cm. B D C C. 14,3 cm và 10,7 cm. 28 D. 12 cm và 16 cm. Hướng dẫn giải Đáp án đúng là: D Xét A
∆ BC có AD là đường phân giác của BAC nên AB DB =
(tính chất đường phân AC DC giác). Suy ra DC DB =
(tính chất tỉ lệ thức). AC AB
Theo tính chất của dãy tỉ số bằng nhau ta có: DC DB DC + DB BC 28 4 = = = = = .
AC AB AC + AB AC + AB 15 + 20 5 Suy ra 4 4
x = DB = AB = ⋅15 =12 cm và 4 4
y = DC = AC = ⋅ 20 =16 cm. 5 5 5 5
Câu 50. Cho tam giác ABC có D, E lần lượt là trung điểm của các cạnh AB, AC và
DE = 4 cm. Biết đường cao AH = 6 cm, diện tích tam giác ABC là A. 2 24 cm . B. 2 48 cm . C. 2 12 cm . D. 2 32 cm . Hướng dẫn giải A Đáp án đúng là: A Xét A
∆ BC có D, E lần lượt là trung điểm của E D
cạnh AB và AC nên DE là đường trung bình của A ∆ BC, do đó 1 DE = BC. Suy ra 2 B H C
BC = 2⋅ DE = 2⋅ 4 = 8 (cm). Vậy diện tích A ∆ BC là: 1 1 S = ⋅ ⋅ = ⋅ ⋅ = ∆ BC AH ABC 8 6 24 ( 2 cm ). 2 2 B. Bài tập tự luận
1. Một số yếu tố thống kê và xác suất
Dạng 1. Các bài toán về thống kê
Bài 1. Em hãy đề xuất phương pháp thu thập dữ liệu cho các vấn đề sau và cho biết
phương pháp thu thập đó là gián tiếp hay trực tiếp:
a) Tên 10 tỉnh/ thành phố có diện tích lớn nhất Việt Nam.
b) Các món ăn được UNESCO công nhận là văn hóa phi vật thể.
c) Loại trái cây yêu thích của học sinh lớp 8A được dùng trong tiệc liên quan cuối năm. Hướng dẫn giải
a) Phương pháp thu thập dữ liệu đề xuất: thu thập từ nguồn có sẵn như sách, báo, mạng
Internet. Đây là phương pháp thu thập gián tiếp.
b) Phương pháp thu thập dữ liệu đề xuất: thu thập từ nguồn có sẵn như sách, báo, mạng
Internet. Đây là phương pháp thu thập gián tiếp.
c) Phương pháp thu thập dữ liệu đề xuất: lập phiếu hỏi. Đây là phương pháp thu thập trực tiếp.
Bài 2. Ghép các dữ liệu với loại dữ liệu thích hợp.
1. Xếp loại mức độ hài lòng của khách hàng: Hài lòng; Khá hài a) Số liệu liên tục. lòng; Chưa hài lòng.
2. Số nhạc cụ mà năm học sinh trong tổ 1 biết chơi: 0; 3; 2; 1; 3. b) Số liệu rời rạc.
3. Chiều cao mực nước thủy văn lớn nhất tại sông Tiền trong 5 c) Dữ liệu không
ngày đầu tháng 8 (đơn vị: mét): 1,68; 1,75; 1,82; 1,66; 1,62. là số, có thể sắp xếp thứ tự.
4. Năm địa điểm du lịch của Việt Nam mà học sinh lớp 8A thích d) Dữ liệu không
nhất: Vinpearl Safari (Phú Quốc), Đà Lạt, Bà Nà Hill (Đà Nẵng), là số, không thể
Đỉnh Fansipan (Sapa – Lào Cai), Vịnh Hạ Long (Quảng Ninh). sắp xếp thứ tự. Hướng dẫn giải
1 – c; 2 – b; 3 – a; 4 – d. Bài 3.
1) Bạn An muốn thu thập dữ liệu về số các bạn nữ ở tất cả các lớp trong khối 8 của trường.
a) Bạn An có thể thu thập bằng phương pháp nào?
b) Dữ liệu thu được thuộc loại nào?
2) Sau khi thu thập bạn có được bảng thống kê về số học sinh nữ trong từng lớp của
khối 8 như bảng dưới đây: Lớp
8A1 8A2 8A3 8A4 8A5 8A6 8A7 Số học sinh nữ 15 14 25 22 16 28 30
a) Hãy vẽ biểu đồ đoạn thẳng thể hiện bảng thống kê trên.
b) Hãy vẽ biểu đồ hình quạt tròn thể hiện bảng thống kê trên. Hướng dẫn giải
1) a) Bạn An có thể thu thập bằng phương pháp trực tiếp.
b) Dữ liệu thu được thuộc loại dữ liệu số.
2) a) Biểu đồ đoạn thẳng thể hiện bảng thống kê đã cho như sau: Số học sinh nữ 35 30 28 30 25 25 22 20 15 16 14 15 10 5 0 8A1 8A2 8A3 8A4 8A5 8A6 8A7 Lớp
b) Biểu đồ hình quạt tròn thể hiện bảng thống kê đã cho như sau: Sales 8A1 15 30 8A2 14 8A3 8A4 25 28 8A5 8A6 8A7 16 22
Bài 4. Một cửa hàng quần áo đưa ra chương trình khuyến mãi giảm giá một số mặt
hàng sau: Quần âu giảm giá 25%; Áo sơ mi giảm 35%; Áo khoác giảm 20%; Quần Jean giảm 10%.
a) Trong các mặt hàng trên, sản phẩm nào được giảm giá nhiều nhất, ít nhất và với mức
giảm giá bao nhiêu phần trăm?
b) Bạn An đã biểu diễn tỉ lệ giảm giá của các mặt hàng trên bằng biều đồ hình quạt
tròn. Biểu đồ An sử dụng có phù hợp không?
c) An nên dùng biểu đồ nào để biểu diễn ? Hãy vẽ biểu đồ đó.
d) Mẹ An đã mua 2 chiếc áo sơ mi với giá mỗi chiếc áo sau khi giảm là 325 000 đồng
và 4 chiếc quần âu. Tổng số tiền mẹ An thanh toán tại quầy là 1850 000 đồng. Em hãy
tính xem mỗi chiếc áo sơ mi và quần âu nguyên giá sẽ là bao nhiêu tiền. Hướng dẫn giải
a) Trong các mặt hàng trên, sản phẩm được giảm giá nhiều nhất là áo sơ mi giảm 35%,
sản phẩm được giảm giá ít nhất là quần Jean giảm 10%.
b) Bạn An đã biểu diễn tỉ lệ giảm giá của các mặt hàng trên bằng biều đồ hình quạt
tròn. Biểu đồ An sử dụng không phù hợp. Vì tỉ lệ phần trăm được giảm ở đây không
phải tỉ lệ so với tổng thể.
c) An nên dùng biểu đồ cột để biểu diễn. Mặt hàng giảm giá 40% 35% 35% 30% 25% 25% 20% 20% 15% 10% 10% 5% 0% Quần Âu Áo sơ mi Áo Khoác Quần Jean
d) Áo sơ mi giảm 35%, giá sau giảm là 325 000 đồng. Do đó mỗi chiếc áo sơ mi
nguyên giá sẽ là 325 000:65% = 500 000 (đồng).
Giá một chiếc quần Âu sau giảm là 1850 000 − 325 000⋅ 2 = 300 000 (đồng). 4
Quần âu giảm giá 25%, do đó mỗi chiếc quần âu nguyên giá sẽ là
300 000:75% = 400 000 (đồng).
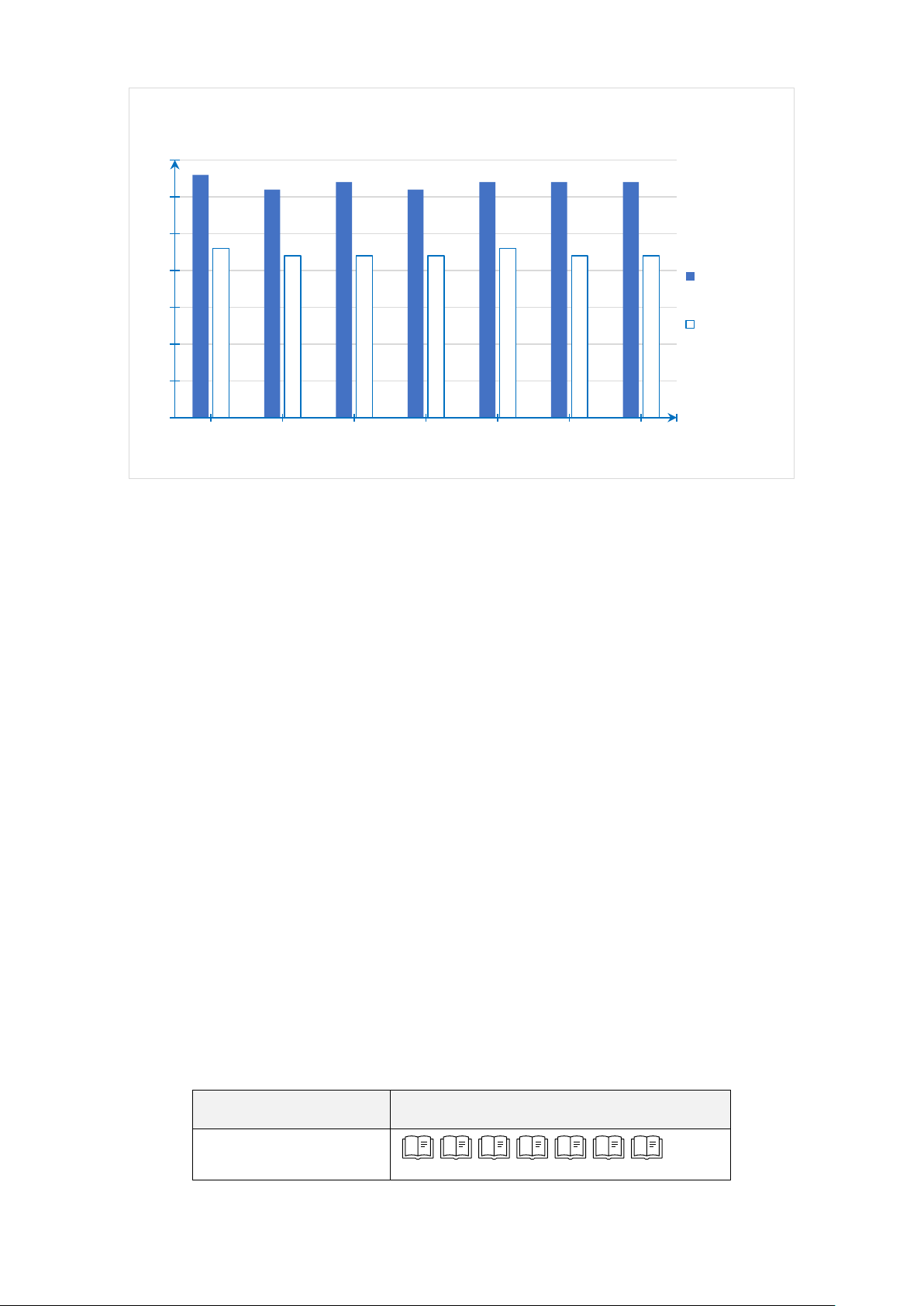
Bài 5. Hình dưới đây thể hiện số lượng học sinh tham gia đăng kí hai Câu lạc bộ cầu
lông và cờ vua của trường:
Học sinh tham gia Câu lạc bộ cầu lông và cờ vua Số học sinh 16 14 14 14 12 12 12 10 10 8 8 8 Cầu lông 6 5 Cờ vua 4 2 0 8A1 8A2 8A3 8A4 Lớp .
a) Lập bảng thống kê cho biểu đồ trên.
b) Cho biết sự khác nhau về việc tham gia đăng kí hai Câu lạc bộ cầu lông và cờ vua của hai lớp 8A3 và 8A4.
c) Nếu lớp 8A1 có số lượng học sinh tham gia Câu lạc bộ cầu lông chiếm 25% tổng
số học sinh cả lớp. Hãy tính xem lớp 8A1 có bao nhiêu học sinh.
d) Hãy so sánh tổng số học sinh tham gia Câu lạc bộ cầu lông và Câu lạc bộ cờ vua. Hướng dẫn giải a) Bảng thống kê: Lớp 8A1 8A2 8A3 8A4 Câu lạc bộ Cầu lông 10 8 5 12 Cờ vua 12 14 14 10
b) Lớp 8A3 đăng kí tham gia cầu lông ít hơn lớp 8A4 (ít hơn 3 bạn) và đăng kí tham
gia cờ vua nhiều hơn lớp lớp 8A4 (nhiều hơn 2 bạn).
c) Vì số lượng tham gia Câu lạc bộ cầu lông của lớp 8A1 chiếm 25% tổng số học sinh
cả lớp nên số học sinh của lớp 8A1 là: 10: 25% = 40 (học sinh).
d) Tổng số học sinh tham gia Câu lạc bộ cầu lông là: 10 + 8 + 5 +12 = 35 (học sinh).
Tổng số học sinh tham gia Câu lạc bộ cờ vua là: 12 +14 +14 +10 = 50 (học sinh).
Vậy tổng số học sinh tham gia Câu lạc bộ cầu lông ít hơn tổng số học sinh tham gia Câu lạc bộ cờ vua.
Bài 6. Cho hai biểu đồ dưới đây:
Doanh thu của doanh nghiệp A
Doanh thu của doanh nghiệp A 45 50 40 40 40 30 32 32 34 40 (tỉ đồng) (tỉ đồng) 30 34 thu 35 thu 32 32 20 30 10 oanh oanh D 30 D 0
2018 2019 2020 2021 2022 Năm
2018 2019 2020 2021 2022 Năm
a) Dữ liệu biểu diễn trên hai biểu đồ có như nhau không? Nếu có hãy lập bảng thống kê cho dữ liệu đó.
b) Có thể căn cứ vào độ dốc trên hai đường gấp khúc trên hai biểu đồ để đánh giá về
tốc độ doanh thu trong 5 năm của các dữ liệu được biểu diễn không? Tại sao? Hướng dẫn giải
a) Dữ liệu biểu diễn trên hai biểu đồ là như nhau. Ta có bảng thông kê sau: Năm 2018 2019 2020 2021 2022
Doanh thu (tỉ đồng) 30 32 32 34 40
b) Không thể căn cứ và độ dốc để đánh giá về tốc độ doanh thu trong trong 5 năm của
các dữ liệu được biểu diễn. Vì độ dốc của biểu đồ phụ thuộc vào việc chọn đơn vị của trục đứng.
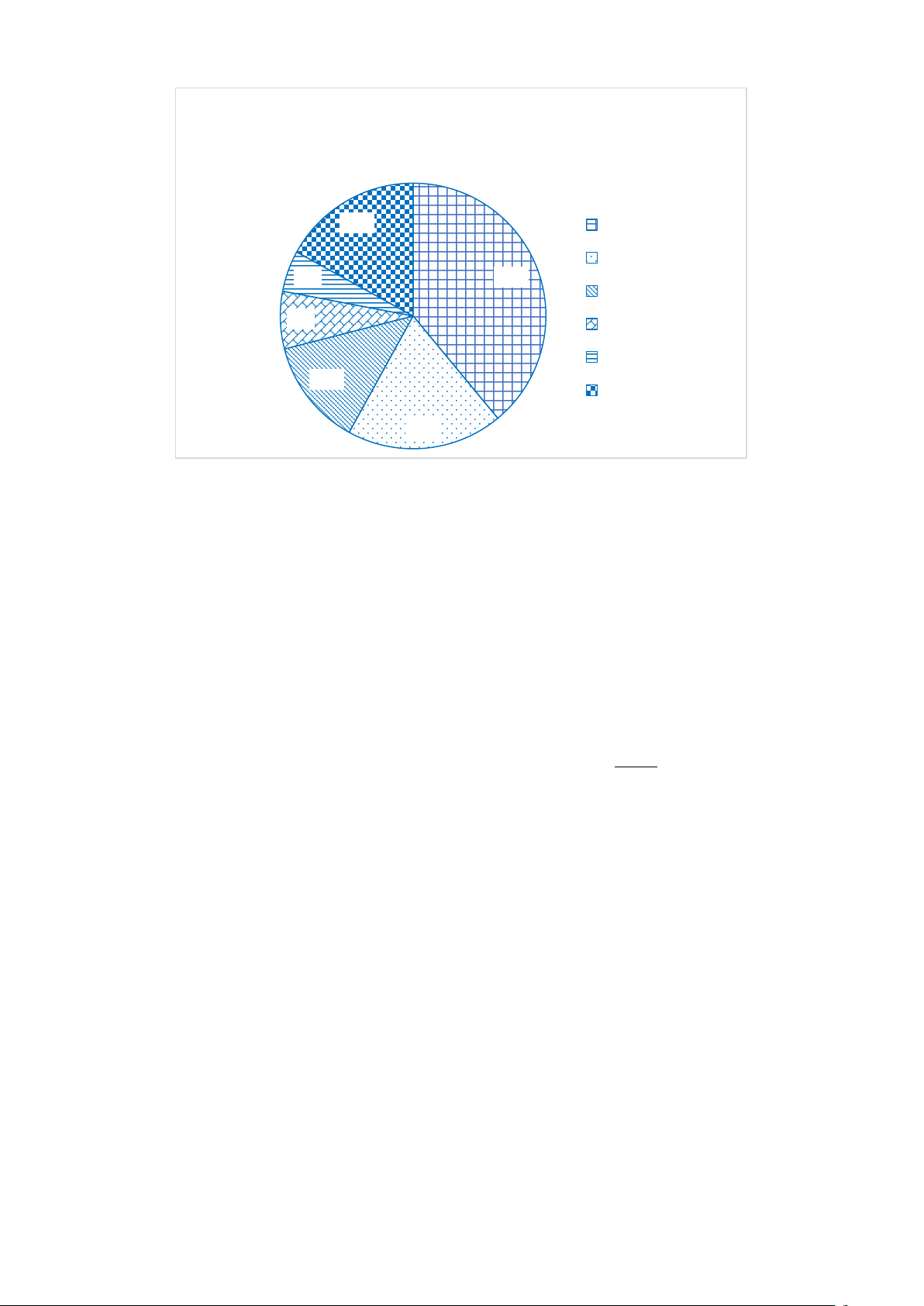
Bài 7. Biểu đồ hình quạt tròn ở hình bên biểu diễn tỉ lệ các yếu tố ảnh hưởng đến sinh
trưởng của cây trồng như: Phân bón, Nước tưới, Giống, Kiểm soát dịch hại, Kiểm soát
cỏ dại, Yếu tố khác. 24% Nước tưới 34% Giống Kiểm soát dịch hại Kiểm soát cỏ dại Yếu tố khác 18% 4% Phân bón 8% 12%
a) Cho biết yếu tố nào ảnh hưởng đến sinh trưởng của cây trồng nhiều nhất?
b) Trong các yếu tố ảnh hưởng đến sinh trưởng của cây thì yếu tố kiểm soát dịch hại
gấp mấy lần yếu tố khác?
c) Vấn đề tưới nước cho cây cũng là một yếu tố quan trọng ảnh hưởng đến sinh trưởng
của cây trồng. Em hãy đề xuất một vài biện pháp khắc phục tình trạng trên để làm giảm
thiệt hại trong việc trồng trọt. Hướng dẫn giải
a) Yếu tố Phân bón (chiếm 34%) ảnh hưởng đến sinh trưởng của cây trồng nhiều nhất.
b) Trong các yếu tố ảnh hưởng đến sinh trưởng của cây thì yếu tố kiểm soát dịch hại
gấp số lần yếu tố khác là: 12% = 3 (lần). 4%
c) Một vài biện pháp khắc phục tình trạng vấn đề tưới nước để làm giảm thiệt hại trong
việc trồng trọt: khoan thêm giếng, lắp đặt thêm ống dẫn nước từ các hồ chứa, xây dựng
phương án tưới cho phù hợp với từng loại cây trồng, áp dụng phương pháp tưới tiết
kiệm nước theo hình thức khô – nước xen kẽ, chỉ vô nước giai đoạn bón phân.
Bài 8. Biểu đồ đoạn thẳng ở hình bên dưới thống kê số lượng gia cầm ở TP. HCM và Kon
Tum qua các năm 2015, 2018, 2019, 2020. (Nguồn: Niêm giám thống kê năm 2021). Số lượng (Nghìn con) 1800 1608 1698 1600 1431 1400 1200 1000 853 800 600 785 400 200 375 416 447 0 2015 2018 2019 2020 Năm TP. HCM Kon Tum
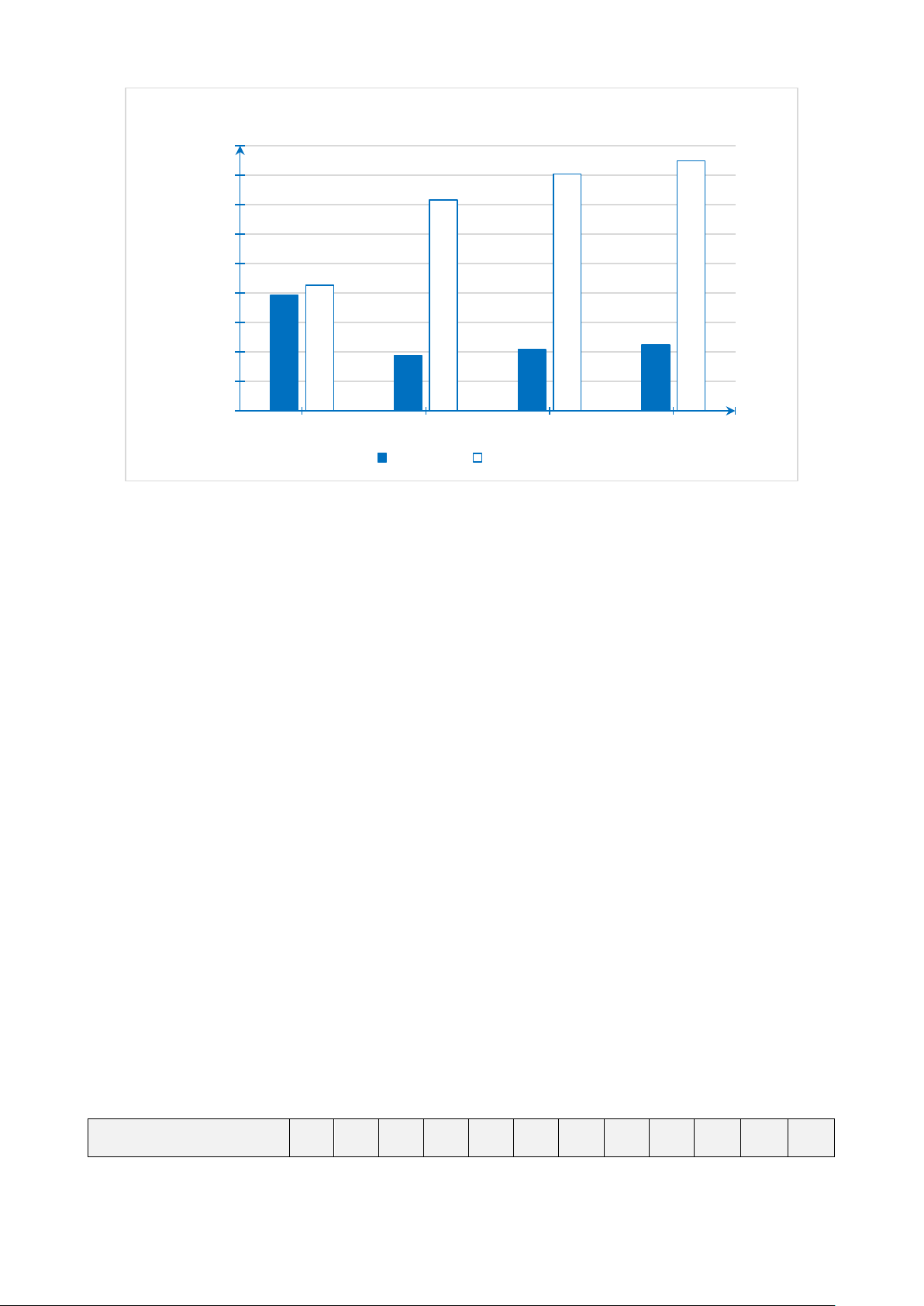
a) Hãy hoàn thành biểu đồ cột kép ở hình bên dưới để nhận được biểu đồ biểu diễn dữ
liệu trong biểu đồ đoạn thẳng ở hình trên. Số lượng (Nghìn con) 1800 ? ? 1600 ? 1400 1200 1000 ? ? 800 600 ? ? ? 400 200 0 2015 2018 2019 2020 Năm TP. HCM Kon Tum
b) TP. HCM và Kon Tum trong năm 2020 lượng gia cầm ở đâu nhiều nhất? Nhiều nhất là bao nhiêu nghìn con?
c) Một bài báo đã nêu ra nhận định “Tổng số lượng gia cầm ở Kon Tum trong năm
2015, 2018, 2019, 2020 là 2023 nghìn con và so với năm 2018 số lượng gia cầm ở
TP. HCM tăng 80% so với số lượng gia cầm ở Kon Tum”. Em hãy cho biết nhận định
trên bài báo có chính xác không?
d) Em hãy đề xuất một vài giải pháp để tăng số lượng gia cầm ở Kon Tum trong những
năm tới để đạt hiệu quả trong chăn nuôi. Hướng dẫn giải
a) Ta hoàn thành được biểu đồ cột kép biểu diễn dữ liệu trong biểu đồ đoạn thẳng như sau: Số lượng (Nghìn con) 1800 1698 1608 1600 1431 1400 1200 1000 785 853 800 600 375 416 447 400 200 0 2015 2018 2019 2020 Năm TP. HCM Kon Tum
b) Trong năm 2020 lượng gia cầm ở Kon Tum nhiều nhất, là 1698 nghìn con.
c) Tổng số lượng gia cầm ở Kon Tum trong năm 2015, 2018, 2019, 2020 là:
853 +1 431+1 608 +1 698 = 5 590 (nghìn con).
Trong năm 2018, số lượng gia cầm ở TP. HCM (375 nghìn con) ít hơn so với số lượng
gia cầm ở Kon Tum (1 431 nghìn con) nên nhận định trên bài báo không chính xác.
d) Một vài giải pháp để tăng số lượng gia cầm ở Kon Tum trong những năm tới để đạt
hiệu quả trong chăn nuôi:
⦁ Đẩy mạnh tuyên truyền, vận động nhân dân chăm sóc tốt đàn gia cầm hiện có;
⦁ Mạnh dạn đầu tư phát triển quy mô chăn nuôi, đa dạng các loại gia cầm;
⦁ Chú trọng việc lai tạo và cải thiện giống gia cầm địa phương;
⦁ Thường xuyên thực hiện vệ sinh tiêu độc khử trùng; …
Bài 9. Thống kê tổng số giờ nắng của các tháng trong năm 2022 tại trạm quan trắc Nam
Định từ tháng 1 đến tháng 12 lần lượt là: 34,4; 27,5; 49,4; 108,2; 88,8; 186,6; 190,7;
151,7; 133,2; 165,0; 126,2; 102,1 (đơn vị: giờ) (Nguồn: Tổng cục thống kê).
a) Lập bảng số liệu thống kê số giờ nắng của các tháng trong năm 2022 tại trạm quan
trắc Nam Định theo mẫu sau: Tháng 1 2 3 4 5 6 7 8 9 10 11 12
Tổng số giờ nắng ? ? ? ? ? ? ? ? ? ? ? ? (h)
b) Hãy hoàn thành biểu đồ hình bên dưới để nhận được biểu đồ đoạn thẳng biểu diễn
tổng số giờ nắng của các tháng trong năm 2022 tại trạm quan trắc Nam Định. Tổng số giờ nắng (h) 250 ? ? 200 ? ? ? 150 ? ? ? ? 100 ? ? 50 ? 0 Tháng
c) Tổng số giờ nắng tại trạm quan trắc Nam Định trong tháng nào cao nhất? Thấp nhất?
d) Hãy nhận xét về sự thay đổi số giờ nắng của các tháng trong năm 2022 tại trạm quan
trắc Nam Định trong các khoảng thời gian: tháng 1 – tháng 2; tháng 2 – tháng 3; tháng
3 – tháng 4; tháng 4 – tháng 5; tháng 5 – tháng 6; tháng 6 – tháng 7; tháng 7 – tháng 8;
tháng 8 – tháng 9; tháng 9 – tháng 10; tháng 10 – tháng 11; tháng 11 – tháng 12.
e) Một bài báo có nêu thông tin: “So với tháng 9, tổng số giờ nắng tại trạm quan trắc Nam
Định trong tháng 10 tăng lên xấp xỉ 34%”. Thông tin của bài báo đó có chính xác không? Hướng dẫn giải
a) Ta lập bảng số liệu thống kê số giờ nắng của các tháng trong năm 2022 như sau: Tháng 1 2 3 4 5 6 7 8 9 10 11 12 Tổng
số giờ 34,4 27,5 49,4 108,2 88,8 186,6 190,7 151,7 133,2 165,0 126,2 102,1 nắng (h)
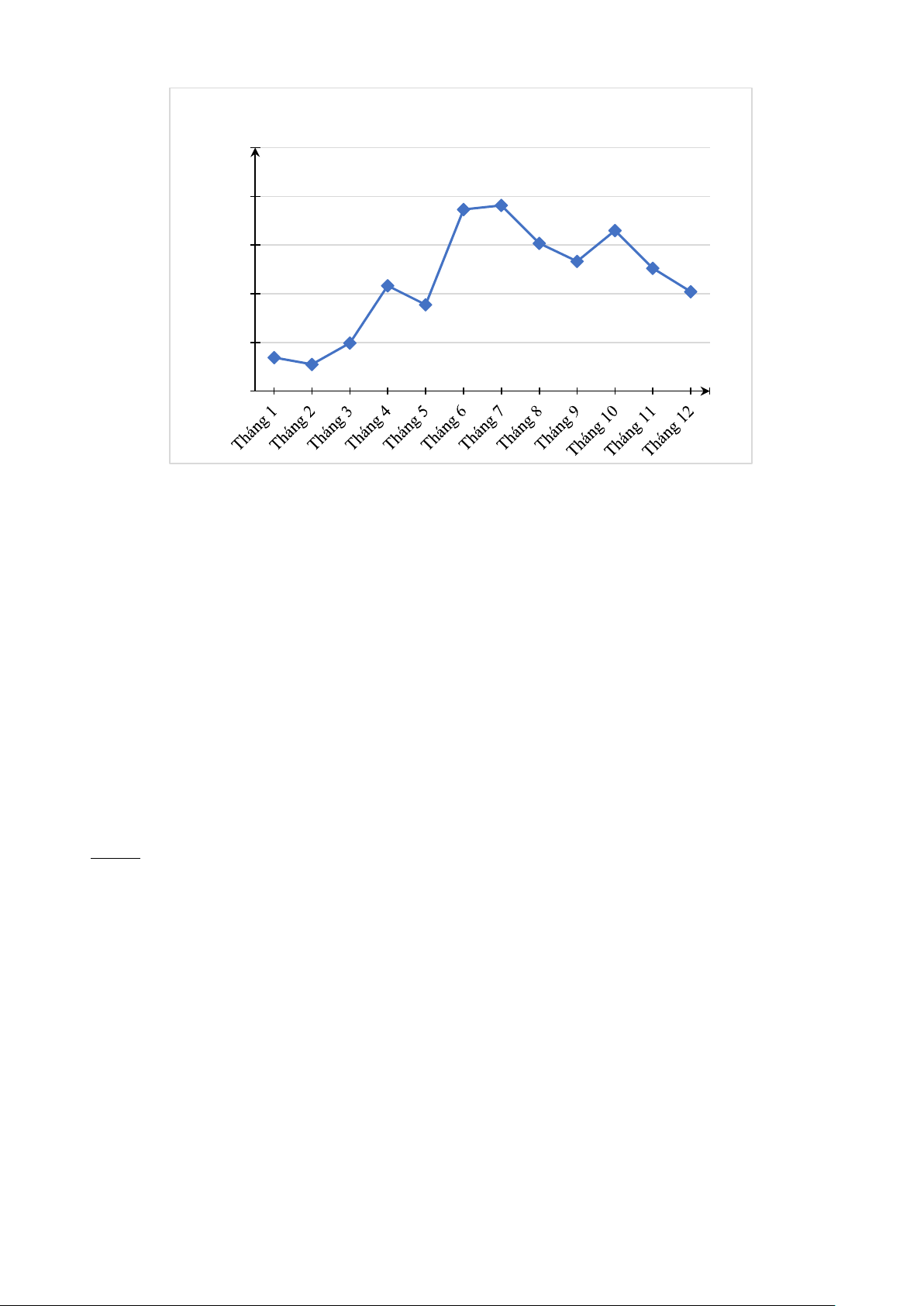
b) Ta hoàn thành được biểu đồ đoạn thẳng biểu diễn số giờ nắng của các tháng trong
năm 2022 tại trạm quan trắc Nam Định như sau: Tổng số giờ nắng (h) 250 186,6190,7 200 165 151,7133,2 150 126,2 108,2 102,1 88,8 100 49,4 34,4 50 27,5 0 Tháng
c) Số giờ nắng tại Nam Định trong tháng 7 là cao nhất (190,7 h) và tháng 2 là thấp nhất (27,5 h).
d) Số giờ nắng của các tháng trong năm 2022 tại Nam Định giảm trong các khoảng
thời gian: tháng 1 – tháng 2; tháng 4 – tháng 5; tháng 7 – tháng 8; tháng 8 – tháng 9;
tháng 10 – tháng 11; tháng 11 – tháng 12.
Số giờ nắng của các tháng trong năm 2022 tại Nam Định tăng trong các khoảng thời
gian: tháng 2 – tháng 3; tháng 3 – tháng 4; tháng 5 – tháng 6; tháng 6 – tháng 7; tháng 9 – tháng 10.
e) So với tháng 9, số giờ nắng tại Nam Định trong tháng 10 bằng 165 ⋅100% ≈123,87%. 133,2
Khi đó tháng 10 tăng khoảng 123,87% −100% = 23,87% so với tháng 9.
Vậy thông tin của bài báo đó không chính xác.
Dạng 2. Các bài toán về xác suất
Bài 10. Một túi đựng 10 tấm thẻ bài có kích thước giống nhau và được ghi số
1; 2; 3; ...; 10. Hoa rút ngẫu nhiên một tấm thẻ từ trong hộp.
a) Liệt kê các kết quả có thể của hành động trên.
b) Liệt kê các kết quả thuận lợi cho các biến cố:
A: “Rút được tấm thẻ có ghi số lẻ”;
B: “Rút được tấm thẻ có ghi số nguyên tố”;
C: “Rút được tấm thẻ có ghi số chia hết cho 3”. Hướng dẫn giải
a) Các kết quả có thể của hoạt động đã cho là các tấm thẻ có ghi số 1; 2; 3; ...; 10. Có 10 kết quả có thể.
b) Các kết quả thuận lợi cho biến cố A là các tấm thẻ ghi số 1; 3; 5; 7; 9.
Các kết quả thuận lợi cho biến cố B là các tấm thẻ ghi số 2; 3; 5; 7.
Các kết quả thuận lợi cho biến cố C là các tấm thẻ ghi số 3; 6; 9.
Bài 11. Một túi đựng bút tô màu của bé Mai có 5 chiếc bút màu vàng, 3 chiếc bút màu
cam, 4 chiếc bút màu xanh và 2 chiếc bút màu tím (các chiếc bút có cùng khối lượng
và kích thước). Bé Mai lấy ngẫu nhiên một chiếc bút từ trong túi. Tính xác suất của các biến cố sau:
A: “Lấy được chiếc bút màu tím”;
B: “Lấy được chiếc bút màu cam hoặc màu xanh”;
C: “Không lấy được chiếc bút màu vàng”;
D: “Lấy được chiếc bút màu vàng”. Hướng dẫn giải
Có 5 + 3 + 4 + 2 =14 kết quả có thể xảy ra và các kết quả là đồng khả năng.
Xác suất của biến cố A là P( A) 2 1 = = . 14 7
Xác suất của biến cố B là P(B) 3 + 4 7 1 = = = . 14 14 2
Xác suất của biến cố C là P(C) 3 + 4 + 2 9 = = . 14 14
Xác suất của biến cố D là P(D) 5 = . 14
Bài 12. Bác bảo vệ theo dõi số khách đến cơ quan mỗi ngày trong một tháng. Kết quả thu được như bảng sau: Số khách 0 1 2 3 4 5 6 7 Số ngày 3 6 5 9 3 2 1 1
a) Gọi A là biến cố “Trong một ngày có từ 3 khách trở lên đến cơ quan”. Hỏi có bao
nhiêu ngày biến cố A xảy ra?
b) Tính xác suất thực nghiệm của biến cố A.
c) Hãy ước lượng xác suất của biến cố B: “Trong một ngày có số khách đến cơ quan là số lẻ”. Hướng dẫn giải
a) Theo bảng thống kê, số ngày có từ 3 khách trở lên đến cơ quan là: 9 + 3 + 2 +1+1=16 (ngày).
b) Số ngày bác bảo vệ theo dõi là: 3 + 6 + 5 + 9 + 3 + 2 +1+1= 30 (ngày).
Xác suất thực nghiệm của biến cố A là: P( A) 16 8 = = . 30 15
c) Theo bảng thống kê, số ngày có khách đến cơ quan là số lẻ là 6 + 9 + 2 +1=18 (ngày)
Xác suất thực nghiệm của biến cố B là P(B) 18 3 = = = 60%. 30 5
Vậy xác suất của biến cố B được ước lượng là 60%.
Bài 13. Một công ty chế biến hạt điều đã thống kê các loại hạt điều thu hoạch được như bảng sau: Loại hạt điều Loại 1 Loại 2 Loại 3
Khối lượng thu hoạch được 1 450 2 230 1860
a) Hãy tính xác suất thực nghiệm của các biến cố sau (làm tròn kết quả đến chữ số thập phân thứ tư):
A: “Hạt điều đạt loại 1”;
B: “Hạt điều đạt loại 2 và loại 3”.
b) Công ty lấy ngẫu nhiêm 100 kg hạt điều chưa phân loại và tiến hành phân loại. Em
hãy dự đoán xem có bao nhiêu kilôgam hạt điều loại 1? Hướng dẫn giải
a) Tổng khối lượng các loại hạt điều thu hoạch được là:
1 450 + 2 230 +1860 = 5 540 (kg).
Xác suất thực nghiệm của biến cố A là P( A) 1 450 = ≈ 0,2617. 5 540
Tổng khối lượng hạt điều loại 2 và loại 3 là: 2 230 +1860 = 4 090 (kg).
Xác suất thực nghiệm của biến cố B là P(B) 4 090 = ≈ 0,7383. 5 540
b) Gọi k là số kilôgam hạt điều loại 1 trong 100 kg hạt điều sau khi phân loại. Ta có ( ) k P A =
≈ 0,2617 suy ra k ≈ 0,2617 ⋅100 = 26,17 ≈ 26 (kg). 100
Vậy có khoảng 26 kg hạt điều loại 1 trong 100 kg hạt điều sau khi phân loại. 2. Hình học
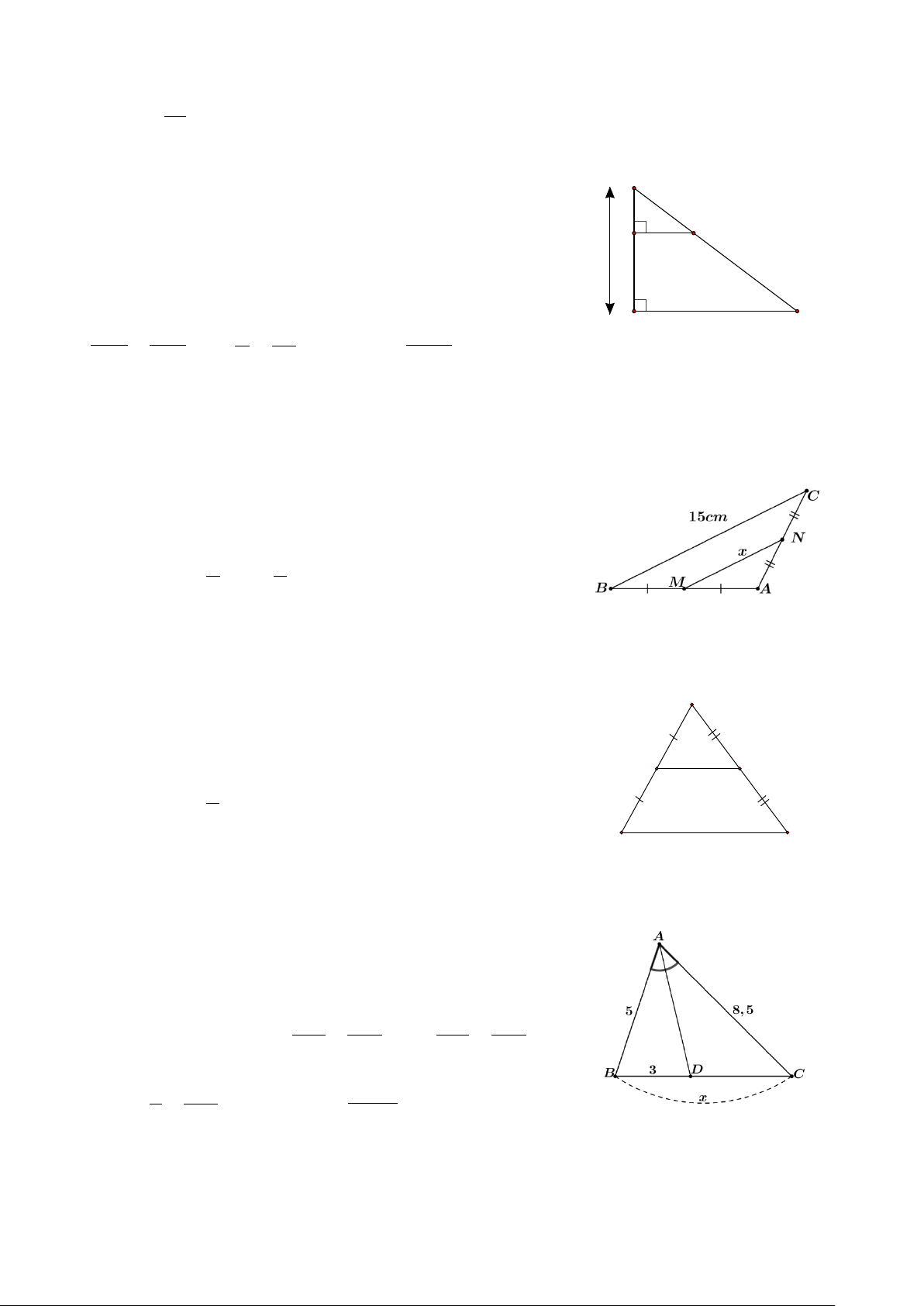
Bài 14. Tìm độ dài x, y trong mỗi trường hợp sau: A M 2 x 7 M N 3 5 F E 6 y 15 B C MN // AB N P Hình 1 Hình 2 Hình 3 A M 3,5cm N x B C Hình 4 Hình 5 Hình 6 Hướng dẫn giải ⦁ Hình 1: A
Ta có MB = AB − AM = 7 − 2 = 5. 2 x
Tam giác ABC có MN // AB, theo định lí Thalès ta có: 7 M N AM AN 6 = hay 2 x = , suy ra 12 x = . MB NC 5 6 5 B C MN // AB Vậy 12 x = . Hình 1 5 ⦁ Hình 2: M
Ta có: EF ⊥ MN, NP ⊥ MN nên EF // N . P 3 5 F E
MP = MF + FP = 5 +15 = 20. y 15
Tam giác MNP có EF // NP, theo định lí Thalès ta có: ME MF N P = hay 3 5 = , suy ra 3 20 y ⋅ = =12. MN MP y 20 5 Hình 2 Vậy y =12. ⦁ Hình 3:
Tam giác ABC có M , N lần lượt là trung điểm của AB
và AC nên MN là đường trung bình của tam giác. Do đó 1 1
MN = BC = ⋅15 = 7,5 (cm). 2 2 Vậy x = 7,5 cm. Hình 3 ⦁ Hình 4: A
Tam giác ABC có M , N lần lượt là trung điểm của AB
và AC nên MN là đường trung bình của tam giác. M 3,5cm N Do đó 1 MN = BC. 2 x B C
Suy ra x = BC = 2MN = 2⋅3,5 = 7(cm). Hình 4 Vậy x = 7 cm. ⦁ Hình 5:
Xét tam giác ABC có AD là phân giác trong góc BAC (do AB DB = BAD CAD), nên = , hay DB DC = AC DC AB AC Do đó 3 DC = , suy ra 8,5 3 DC ⋅ = = 5,1. 5 8,5 5 Hình 5
Khi đó x = BC = DB + DC = 3 + 5,1= 8,1. ⦁ Hình 6:
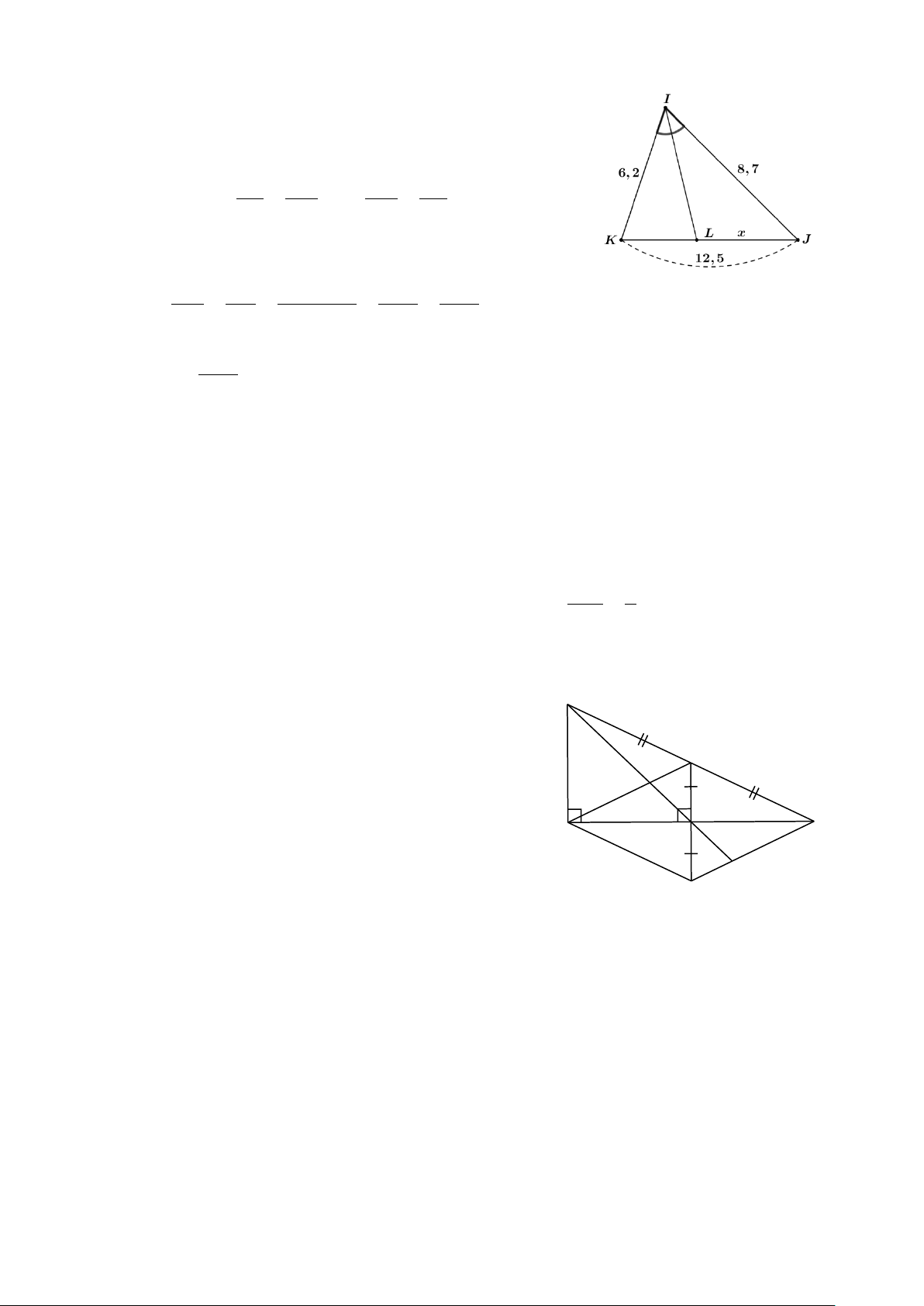
Xét tam giác IKJ có IL là phân giác trong góc KIJ (do =
KIL JIL), nên IK LK = hay LK LJ = IJ LJ IK IJ
Theo tính chất dãy tỉ số bằng nhau ta có: LK LJ LK + LJ KJ 12,5 = = = = . Hình 6 6,2 8,7 6,2 + 8,7 14,9 14,9 Suy ra 12,5 LJ = ⋅8,7 ≈ 7,3. 14,9
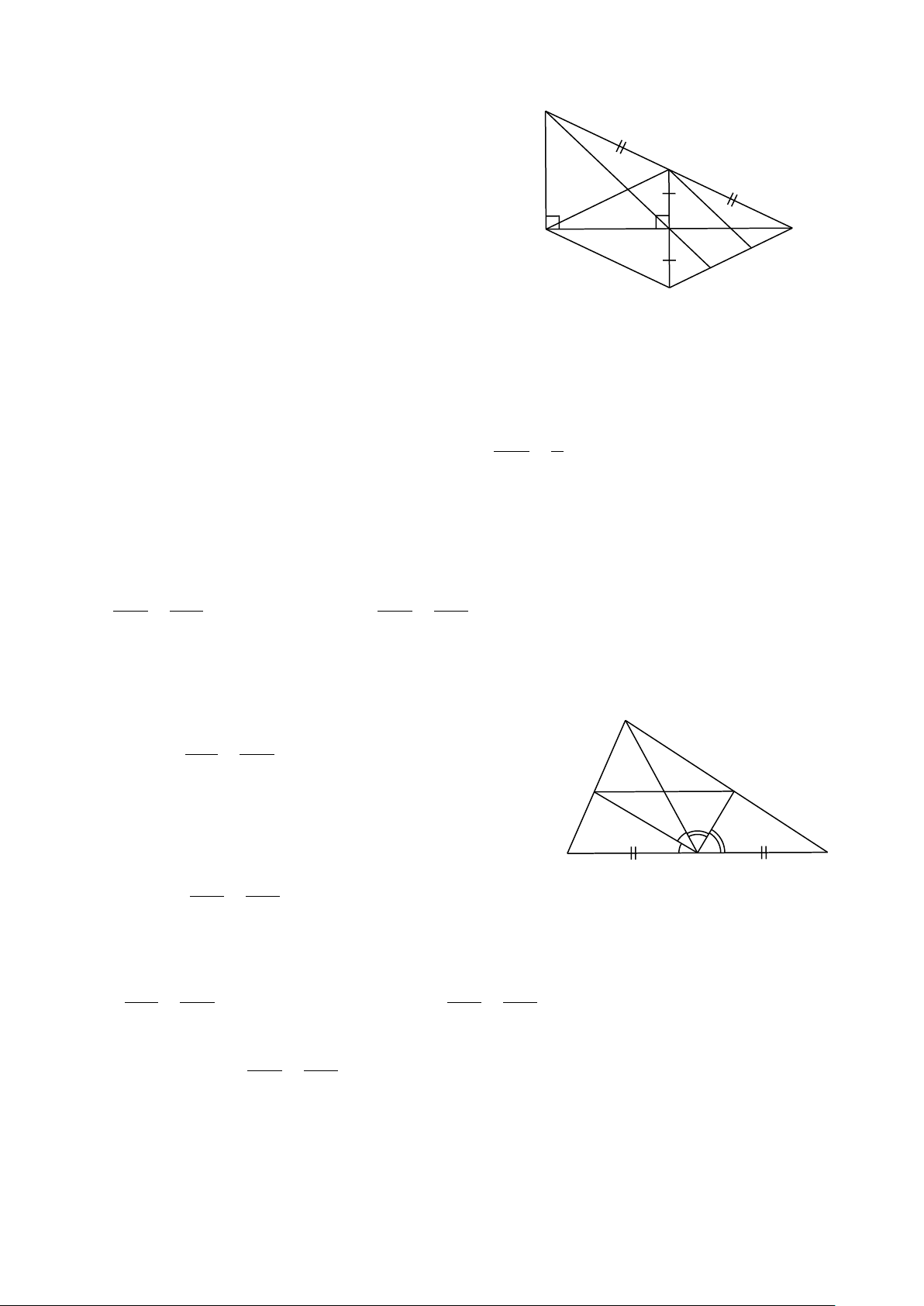
Bài 15. Cho tam giác ABC vuông tại A ( AB < AC). Gọi I là trung điểm của cạnh
BC. Qua I vẽ IN vuông góc với AC tại N. Lấy điểm D sao cho N là trung điểm của . ID
a) Chứng minh N là trung điểm của AC và tứ giác ADCI là hình thoi.
c) Đường thẳng BN cắt cạnh DC tại K. Chứng minh DK 1 = . DC 3 Hướng dẫn giải a) Xét A
∆ BC có AB ⊥ AC; IN ⊥ AC nên B AB // IN. I
Mà I là trung điểm của BC nên IN là đường
trung bình của tam giác, do đó N là trung điểm A C N của AC. K
Xét tứ giác ADCI có: N là trung điểm của D
ID, AC nên ADCI là hình bình hành.
Lại có IN ⊥ AC hay ID ⊥ AC nên hình bình hành ADCI là hình thoi.
b) Kẻ IH // BK (H ∈CD), mà I là trung điểm B
của BC, nên IH là đường trung bình của I B
∆ KC. Do đó H là trung điểm của KC hay KH = HC ( ) 1 A C N Xét D H
∆ IH có N là trung điểm của DI và K
NK // IH (do BK // IH ) nên NK là đường D trung bình của D
∆ IH, suy ra K là trung điểm
của DH hay DK = KH (2) Từ ( )
1 và (2) suy ra DK = KH = HC. Do đó DK 1 = . DC 3 Bài 16. Cho A
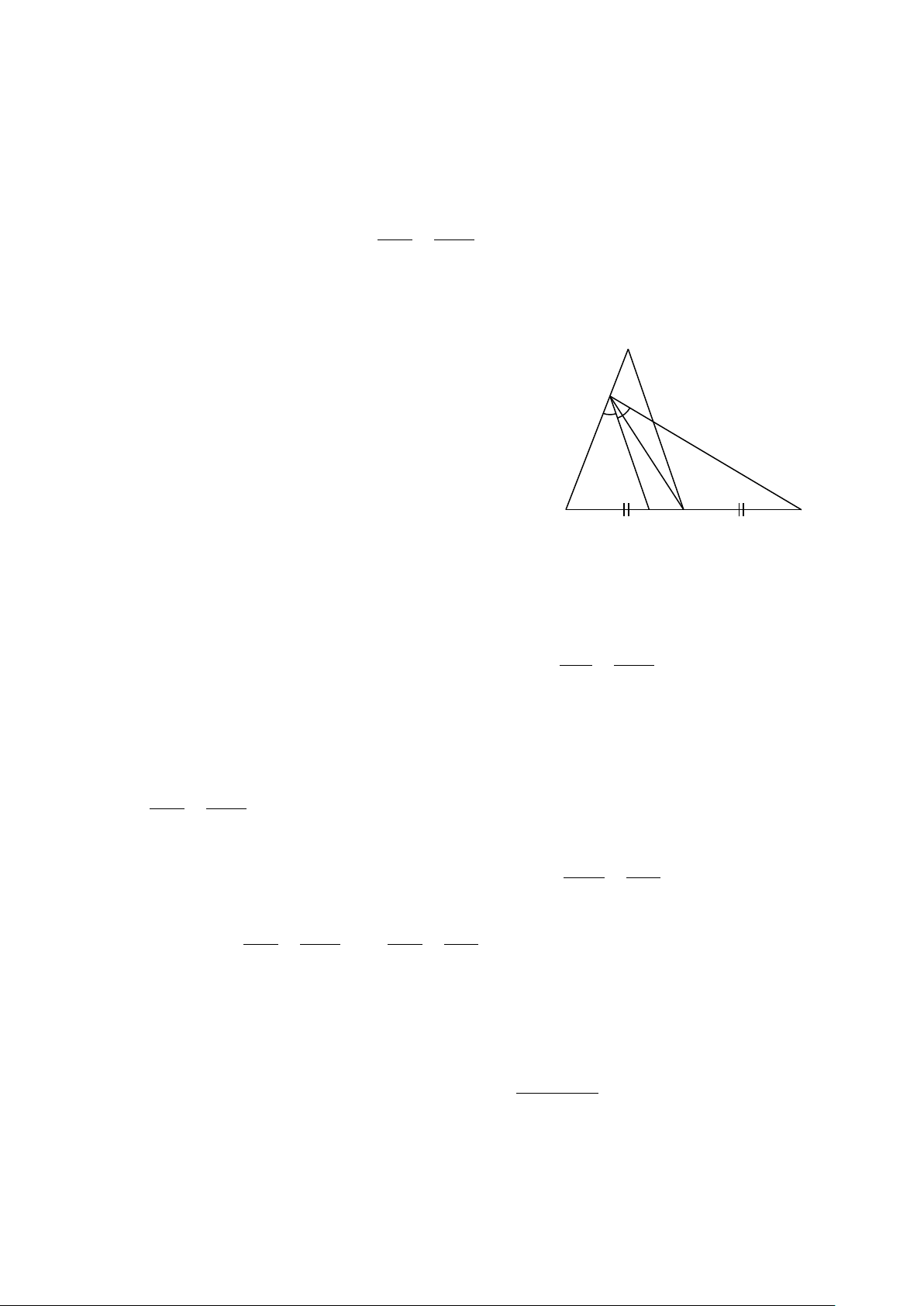
∆ BC trung tuyến A .
D Vẽ tia phân giác của
ADB cắt AB tại M , tia phân giác của
ADC cắt AC tại N. Chứng minh rằng: a) MB BD = . b) MB NC = . c) MN // BC. MA AD MA NA Hướng dẫn giải a) Xét A
∆ BD có DM là đường phân giác của A ADB nên DA MA =
(tính chất đường phân giác DB MB M N trong tam giác). b) Xét A
∆ CD có DN là đường phân giác của B D C ADC nên DA NA =
(tính chất đường phân giác DC NC trong tam giác). Mà DA MA =
(câu a) và DB = DC nên MB NC = . DB MB MA NA c) Xét A
∆ BC có: MB NC =
(câu b) nên MN // BC (định lí Thalès đảo). MA NA
Bài 17. Cho tam giác ABC có AB < AC. Tia phân giác
BAC cắt cạnh BC tại điểm .
D Gọi M là trung điểm của cạnh BC. Qua điểm M kẻ đường thẳng song song với
đường thẳng AD cắt các đường thẳng AC, AB lần lượt tại E và K. Chứng minh rằng:
a) Tam giác AEK cân. b) AK DM = . c) BK = EC. EC MB Hướng dẫn giải
a) Vì AD // KM nên =
BAD BKM (đồng vị). K
Vì AD // EM nên =
CAD CEM (đồng vị). A E
Mà AD là tia phân giác của BAC nên = BAD CA . D Do đó =
BKM CEM , lại có =
CEM AEK nên B D M C = BKM AEK hay = AKE AEK.
Tam giác AEK có =
AKE AEK nên là tam giác cân tại . A b) Xét A
∆ CD có EM // AD, theo định lí Thalès ta có AE DM = . EC MC Mà A
∆ EK cân tại A nên AK = AE.
Lại có điểm M là trung điểm của BC nên MB = MC. Do đó AK DM = . EC MB c) Xét B DM AK
∆ MK có AD // KM , theo định lí Thalès ta có = . BM BK
Theo câu a, ta có AK DM = nên AK AK =
, do đó EC = BK. EC MB EC BK
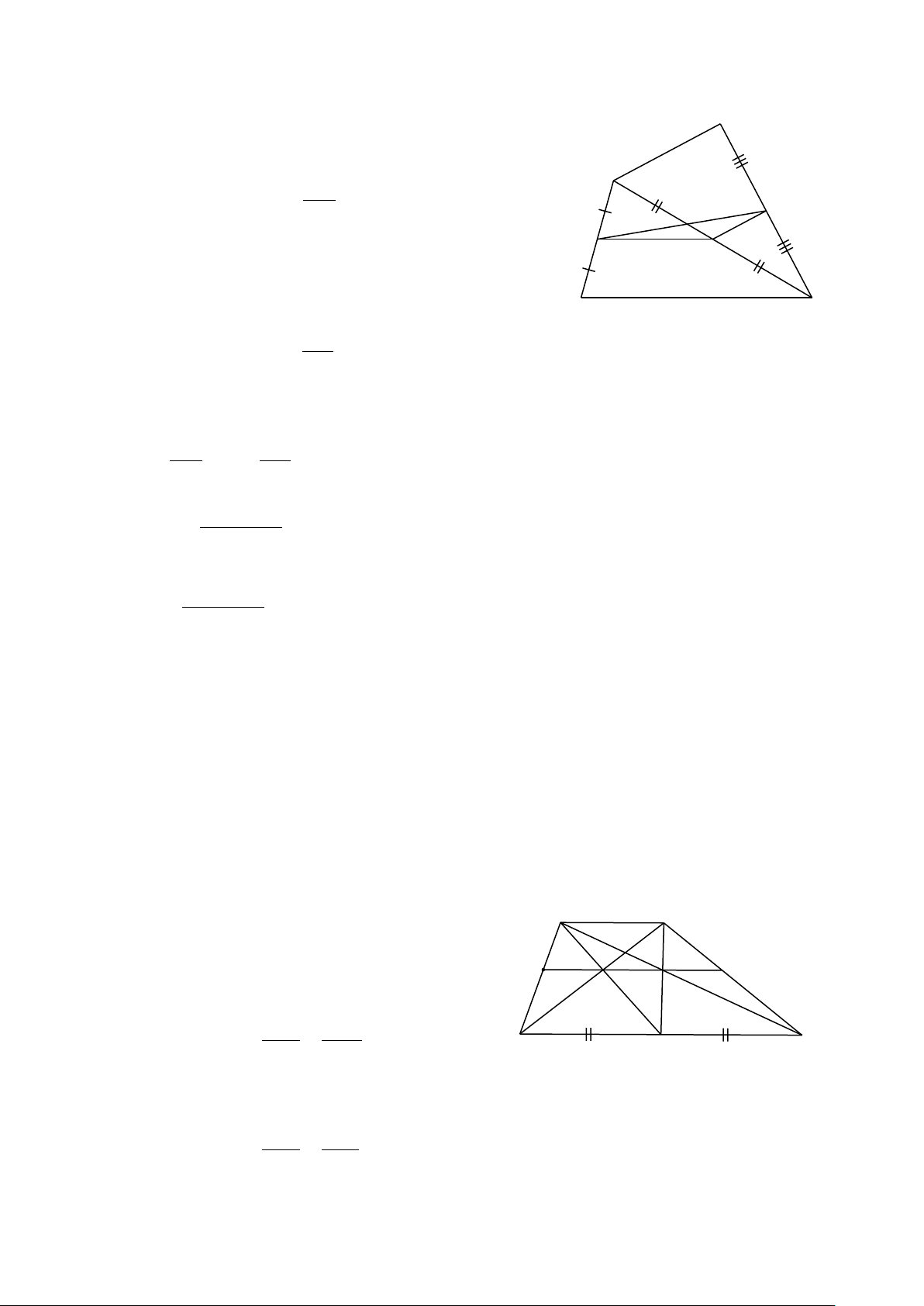
Bài 18. Cho tứ giác ABC .
D Gọi E, F, I theo thứ tự là trung điểm của AD, BC, AC. Chứng minh rằng:
a) EI //CD và IF // A . B b) AB CD EF + ≤ . 2 Hướng dẫn giải a) Xét A
∆ DC có E, I lần lượt là trung điểm của B
AD, AC nên EI là đường trung bình của A ∆ DC. A
Do đó EI //CD và CD EI = . 2 F Xét A
∆ BC có I, F lần lượt là trung điểm của E I
AC, BC nên IF là đường trung bình của A ∆ BC. D C
Do đó IF // AB và AB IF = . 2 b) Trong E
∆ IF ta có: EF ≤ EI + IF (dấu "=" xảy ra khi E, I, F thẳng hàng) Mà CD = ; AB EI IF = (chứng minh ở câu a) 2 2 Do đó AB CD EF + ≤ . 2 Vậy AB CD EF + ≤
(dấu bằng xảy ra khi AB //CD). 2
Bài 19. Cho hình thang ABCD có hai đáy AB và .
CD Gọi M là trung điểm của CD,
E là giao điểm của MA và BD, F là giao điểm của MB và AC.
a) Chứng minh rằng EF // A . B
b) Đường thẳng EF cắt AD, BC lần lượt tại H và N. Chứng minh HE = EF = FN.
c) Biết AB = 7,5 cm, CD =12 cm. Tính độ dài HN. Hướng dẫn giải
a) Vì ABCD là hình thang có hai đáy AB và A B
CD nên AB //C . D
Vì AB // DM (do AB //CD), nên theo hệ quả H N E F
định lí Thalès ta có AE AB = . ( ) 1 EM DM D M C
Vì AB // MC (do AB //CD), nên theo hệ quả
định lí Thalès ta có BF AB = . (2) FM MC
Lại có M là trung điểm của CD nên DM = MC. (3) Từ ( )
1 , (2) và (3) ta có AE BF =
, theo định lí Thalès đảo ta có EF // A . B EM FM b) Xét A HE AE
∆ DM có HE // DM , theo hệ quả định lí Thalès ta có = . DM AM Xét A
∆ MC có EF // MC, theo hệ quả định lí Thalès ta có EF AE = . MC AM Do đó HE EF =
, mà DM = MC nên HE = EF. DM MC
Chứng minh tương tự ta cũng có EF = FN. Suy ra HE = EF = FN.
c) Vì M là trung điểm của CD nên 1 1
DM = MC = CD = ⋅12 = 6 cm. 2 2 Theo câu a, ta có AE AB 7,5 5 = = = . Suy ra AE EM = . EM DM 6 4 5 4
Theo tính chất của dãy tỉ số bằng nhau ta có: AE EM AE + EM AM = = = . 5 4 5 + 4 9 Do đó AE 5 = . AM 9 Mà theo câu b, HE AE 5 = = . DM AM 9 Suy ra 5 5 10 HE = DM = ⋅6 = cm. 9 9 3 Vậy 10 HN = 3HE = 3⋅ =10 cm. 3 Bài 20. Cho A
∆ BC có AD là trung tuyến, trọng tâm G, đường thẳng đi qua G cắt các
cạnh AB, AC lần lượt tại E, F. Từ B, C kẻ các đường song song với EF cắt AD lần
lượt tại M , N. Chứng minh rằng: a) BE MG = . b) BE CF + =1. c) AB AC + = 3. AE AG AE AF AE AF Hướng dẫn giải a) Xét A
∆ BM có EG // BM , theo định lí A Thalès ta có: BE MG = . AE AG b) Xét DC ∆
N có BM //CN, theo định lí F G Thalès ta có: DN DC = . E MD DB M
Mà D là trung điểm của BC (do AD là trung B D C
tuyến của tam giác) nên DC = . DB N Do đó DN DC =
=1, nên DM = DN. MD DB
Suy ra GM + GN = GM + GM + MN = 2GM + 2MD = 2 . GD
Lại có G là trọng tâm A
∆ BC nên AG = 2 . GD Xét A
∆ CN có FG //CN, theo định lí Thalès ta có: CF GN = . AF AG
Suy ra BE CF MG GN GM + GN 2GD + = + = = =1. AE AF AG AG AG 2GD c) Xét A AB AM
∆ BM có EG // BM , theo định lí Thalès ta có: = . AE AG Xét A
∆ CN có FG //CN, theo định lí Thalès ta có: AC AN = . AF AG Suy ra AB AC AM AN + + + + + = + AG GM AG GM MN = AE AF AG AG AG
2AG + 2GM + 2MD 2AG + 2(GM + MD) = 2AG + 2GD = = AG AG AG 1 2AG + 2⋅ AG 2 3AG = = = 3. AG AG Vậy AB AC + = 3. AE AF
Bài 21. Cho tam giác ABC có BC =15 cm, CA =18 cm và AB =12 cm. Gọi I và G
lần lượt là tâm đường tròn nội tiếp và trọng tâm A ∆ BC.
a) Chứng minh IG // BC.
b) Tính độ dài đoạn thẳng . IG Hướng dẫn giải
a) Gọi AD là đường phân giác góc BAC A (D∈BC). Xét A
∆ BC có AD là đường phân giác của BAC nên AB DB = , hay DC DB = . AC DC AC AB I G
Theo tính chất dãy tỉ số bằng nhau ta có: DC DB DC + DB BC 15 1 B D M C = = = = = .
AC AB AC + AB AC + AB 18 +12 2 Suy ra 1 1
CD = AC = ⋅18 = 9 cm và 1 1
BD = AB = ⋅12 = 6 cm. 2 2 2 2 Xét A
∆ CD, có CI là đường phân giác của ACD nên AI AC 18 = = = 2. DI CD 9
Mặt khác, do G là trọng tâm của A
∆ BC nên AG = 2. GM Do đó AI AG =
= 2, theo định lí Thalès đảo ta có IG // BC. ID GM
b) Gọi M là trung điểm của BC. Khi đó 1 1
MB = MC = BC = ⋅15 = 7,5 cm. 2 2
Suy ra DM = BM − BD = 7,5 − 6 =1,5 cm. Xét A IG AG
∆ DM có IG // BC, theo hệ quả định lí Thalès ta có 2 = = . DM AM 3 Suy ra 2 2
IG = DM = ⋅1,5 =1 cm. 3 3
3. Một số bài toán thực tế liên quan đến hình học
Bài 22. Vì kèo mái tôn là một trong những bộ phận không thể thiếu trong cấu tạo mái
nhà lợp tôn. Nó giúp chống đỡ và giảm trọng lực của những ảnh hưởng từ các yếu tố
bên ngoài tác động vào (Hình a). y 2,7 m 2,8 m x Hình a Hình b
Một vì kèo mái tôn được vẽ lại như Hình b. Tính độ dài x của cây chống đứng bên và
độ dài y của cánh kèo. Hướng dẫn giải A y D E 2,7 m 2,8 m x B N M P C Đặt các điểm , ,
A B C, D, E, M , N, P như hình vẽ trên. ⦁ Xét A
∆ MC có E, P lần lượt là trung điểm của AC, MC (do EA = EC,PM = PC)
nên EP là đường trung bình của A ∆ MC. Do đó 1 1
EP = AM = ⋅ 2,7 =1,35 ( m) (tính chất đường trung bình của tam giác). 2 2 Hay x =1,35 ( m).
⦁ Ta có MB = MN + NB và MC = MP + PC
Mà MN = NB = MP = PC nên MB = MC. Xét A
∆ BC có D, M lần lượt là trung điểm của AB, BC (do DB = D , A MB = MC) nên
DM là đường trung bình của A ∆ BC. Do đó 1
DM = AC (tính chất đường trung bình của tam giác). 2
Suy ra AC = 2DM = 2⋅ 2,8 = 5,6 ( m). Hay y = 5,6 ( m).
Vậy độ dài của cây chống đứng bên và độ dài của của cánh kèo lần lượt là x =1,35 ( m); y = 5,6 ( m).
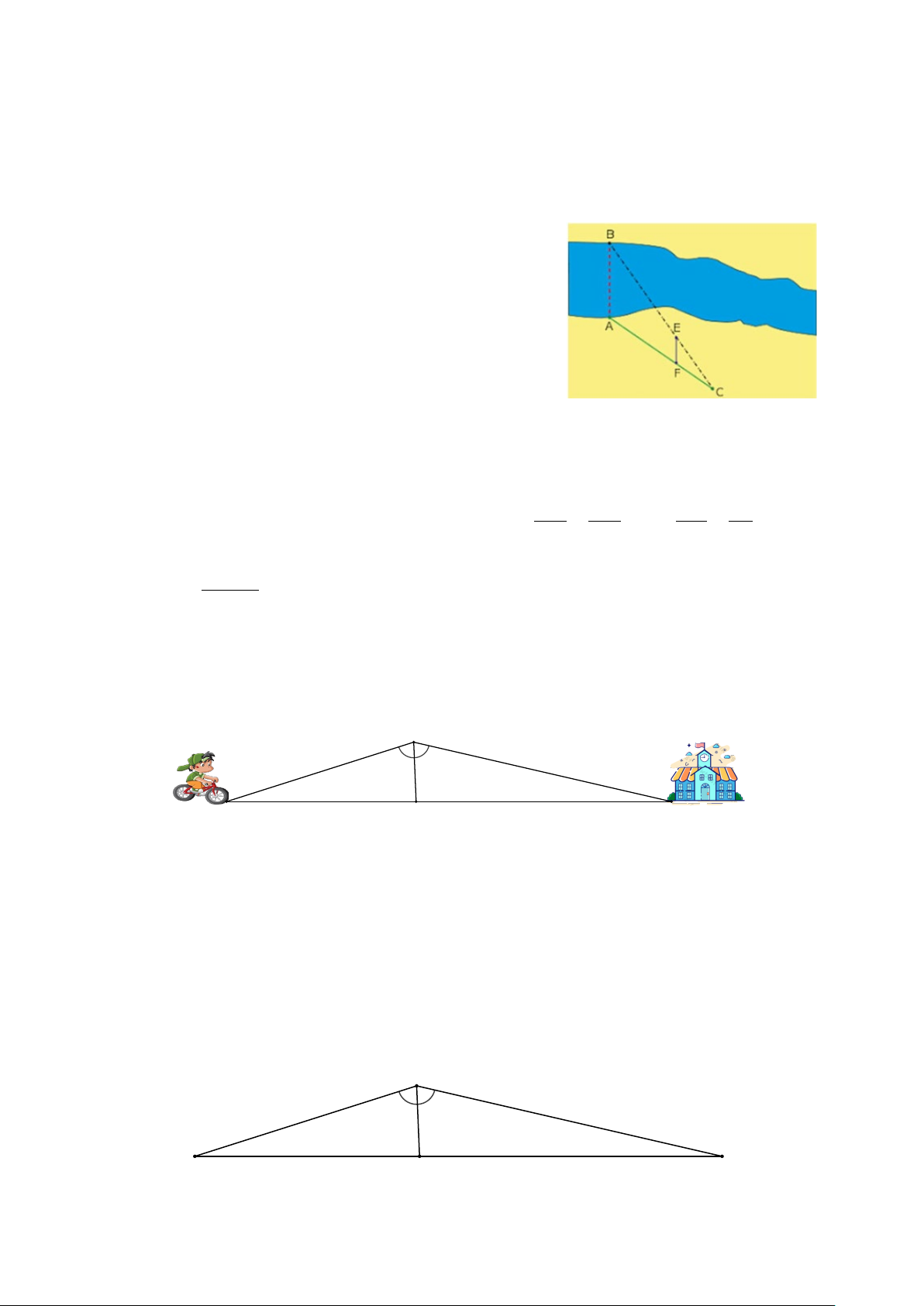
Bài 23. Để đo khoảng cách giữa hai vị trí B và E ở
hai bên bờ sông, bác Minh chọn ba vị trí , , A F C
cùng nằm ở bên bờ sông sao cho ba điểm C, , E B
thẳng hàng; ba điểm C, , F A thẳng hàng và
AB // EF. Sau đó bác Minh đo được AF = 50 m,
FC = 35 m và EC = 42 m. Tính khoảng cách giữa
hai vị trí B và E. Hướng dẫn giải Xét A
∆ BC có AB // EF, theo định lí Thalès ta có EC CF = , hay 42 35 = . EB FA BE 50 Suy ra 42 50 BE ⋅ = = 60 m. 35
Bài 24. Lúc 6 giờ sáng, bạn Hải đi xe đạp từ điểm A đến trường (tại điểm B) phải leo
lên và xuống một con dốc với đỉnh dốc tại điểm C (như hình vẽ). C 0,32 km A 0,4 km H B
Điểm H là một điểm thuộc đoạn thẳng AB sao cho CH đường là phân giác ACB,
AH = 0,32 km và BH = 0,4 km. Biết bạn Hải đi xe đạp đến C lúc 6 giờ 30 phút với
tốc độ trung bình lên dốc là 4 km/h. Hỏi bạn Hải đến trường lúc mấy giờ nếu tốc độ
trung bình xuống dốc là 10 km/h? Hướng dẫn giải C A 0,32 km 0,4 km H B
Thời gian để bạn Hải đi từ A đến C là: 6 giờ 30 phút − 6 giờ = 30 phút = 0,5 giờ.
Quãng đường mà bạn Hải đi từ A đến C trong 0,5 giờ với tốc độ trung bình lên dốc
4 km/h là: AC = S = ⋅ = (km). A→C 4 0,5 2 Xét A
∆ CB có CH là đường phân giác của
ACB, nên ta có: HA CA = hay 0,32 2 = HB CB 0,4 CB Suy ra 0,4 2 CB ⋅ = = 2,5 (km). 0,32
Thời gian để bạn Hải đi hết quãng đường 2,5 km với tốc độ trung bình xuống dốc 10 km/h là: 2,5 = 0,25 (giờ). 10
Như vậy, tổng thời gian bạn Hải đi từ A đến trường B là
0,5 + 0,25 = 0,75 (giờ) = 45 (phút).
Một số dạng khác Bài 25.
a) Tìm giá trị lớn nhất của phân thức 14 M = . 2 x − 2x + 4
b) Tìm giá trị nhỏ nhất của phân thức 11 N = . 2 12 − 4x − x Hướng dẫn giải a) Ta có 14 14 14 M = = = . 2 x − 2x + 4 ( 2 x − 2x + ) 1 + 3 (x − )2 1 + 3
Với mọi x, ta luôn có (x − )2 1 ≥ 0 nên (x − )2 1 + 3 ≥ 0 Suy ra 14 14 ≤ ( hay 14 M ≤ . x − ) , 2 1 + 3 3 3
Dấu “=” xảy ra khi và chỉ khi (x − )2 1 = 0, tức là x =1.
Vậy giá trị lớn nhất của biểu thức M là 14 tại x =1. 3 b) Ta có 11 11 11 N = = = . 2 12 − 4x − x −( 2
x + 4x + 4) +16 −(x + 2)2 +16
Với mọi x, ta luôn có (x + )2 2 ≥ 0 nên −(x + )2 2 +16 ≤16 Suy ra 11 11 ≥ hay 11 N ≥ . −(x + 2) , 2 +16 16 16
Dấu “=” xảy ra khi và chỉ khi (x + )2 2 = 0, tức là x = 2. −
Vậy giá trị nhỏ nhất của biểu thức N là 11 tại x = 2. − 16
Bài 26. Rút gọn các phân thức sau: 3 3 3 a)
x + y + z − 3xyz A = . 2 2 2
x + y + z − xy − yz − xz 24 20 16 4 b)
x + x + x + ...+ x +1 B = . 26 24 22 2
x + x + x + ...+ x +1 Hướng dẫn giải 3 3 3 a) Ta có:
x + y + z − 3xyz A = 2 2 2
x + y + z − xy − yz − xz
(x + y)3 − 3xy(x + y) 3 + z − 3xyz = 2 2 2
x + y + z − xy − yz − xz (x + y)3 3
+ z − 3xy(x + y + z) = 2 2 2
x + y + z − xy − yz − xz
(x + y + z)3 − 3(x + y)z(x + y + z) − 3xy(x + y + z) = 2 2 2
x + y + z − xy − yz − xz
(x + y + z)(x + y + z)2 − 3(x + y)z − 3xy = 2 2 2
x + y + z − xy − yz − xz
(x + y + z)( 2 2 2
x + y + z + 2xy + 2yz + 2zx − 3xz − 3yz − 3xy) = 2 2 2
x + y + z − xy − yz − xz
(x + y + z)( 2 2 2
x + y + z − xy − yz − zx) =
= x + y + z. 2 2 2
x + y + z − xy − yz − xz 24 20 16 4 b) Ta có:
x + x + x + ...+ x +1 B =
, xét phân thức nghịch đảo của phân thức B là: 26 24 22 2
x + x + x + ...+ x +1 26 24 22 2
1 x + x + x + ...+ x +1 = 24 20 16 4
B x + x + x + ...+ x +1 ( 26 22 18 6 2
x + x + x + ... + x + x ) + ( 24 20 4
x + x + ... + x + ) 1 = 24 20 16 4
x + x + x + ... + x +1 2 x ( 24 20 4
x + x + ... + x + ) 1 + ( 24 20 4
x + x + ... + x + ) 1 = 24 20 16 4
x + x + x + ... + x +1 ( 24 20 x + x + ... + ) 1 ( 2 x + ) 1 2 = = x +1. 24 20 16 4
x + x + x + ... + x +1 Vậy 1 B = . 2 x +1
Bài 27. Cho a ; a; ; a ; … a ;
a là 2024 số thực thỏa mãn 2k +1 a = với 1 2 3 2023 2024 k (k + k)2 2 k ∈{1; 2; 3; ; … 202 }
4 . Tính tổng S = a + a + a +…+ a . 2024 1 2 3 2024 Hướng dẫn giải 2k +1 2k +1 (k + )2 2 1 − Ta có k 1 1 a = = = = − k ( . 2
k + k )2 k(k + ) 2 2 1 k ⋅(k + )2 2 1 k (k + )2 1
Do đó S = a + a + a +…+ a 2024 1 2 3 2024 1 1 1 1 1 1 1 1 S ... = − + − + − + + − 2024 2 2 2 2 2 2 2 2 1 2 2 3 3 4 2023 2024 2 1 2024 −1 =1− = . 2 2 2024 2024
Bài 28. Cho x, y, z ≠ 0 thoả mãn x + y + z = xyz và 1 1 1 + + = 3. x y z
Tính giá trị của biểu thức 1 1 1 P = + + . 2 2 2 x y z Hướng dẫn giải
Do x, y, z ≠ 0 nên từ giả thiết x + y + z = xyz ta có: 1 1 1 + + =1. xy yz zx 2 Xét biểu thức: 1 1 1 P = + + 1 1 1 1 1 1 = + + − 2 + + 2 2 2 x y z x y z xy yz zx Khi đó 2
P = 3 − 2⋅1= 9 − 2 = 7. Vậy P = 7. 2 2 2 Bài 29. Cho a b c + +
=1. Chứng minh rằng a b c + + = 0.
b + c c + a a + b
b + c c + a a + b Hướng dẫn giải Với a ≠ − ; b b ≠ − ;
c c ≠ −a ta xét a b c + + =1. ( ) 1
b + c c + a a + b Do a ≠ − ; b b ≠ − ;
c c ≠ −a nên a + b + c ≠ 0.
Khi đó ta nhân hai vế của ( )
1 với a + b + c thì được:
a(a + b + c) b(a + b + c) c(a + b + c) + +
= a + b + c b + c c + a a + b 2 + ( + ) 2 + ( + ) 2 a a b c b b a c
c + c(a + b) Hay + +
= a + b + c b + c c + a a + b 2 2 2 Nên a b c + a + + b +
+ c = a + b + c b + c c + a a + b 2 2 2 Suy ra a b c + + = 0.
b + c c + a a + b 2 2 2 Vậy a b c + + = 0.
b + c c + a a + b
Bài 30. Biết x ≠ – y; y ≠ –z; z ≠ –x, rút gọn biểu thức sau: 2 2 2 x − yz y − xz z − xy A = ( + +
x + y)(x + z) ( y + x)( y + z) (z + x)(z + y). Hướng dẫn giải
Với x ≠ – y; y ≠ –z; z ≠ –x, ta có: 2 2 2 x − yz y − xz z − xy A = ( + +
x + y)(x + z) ( y + x)( y + z) (z + x)(z + y) ( 2 − )( + ) ( 2 − )( + ) ( 2 x yz y z y xz z x
z − xy)(x + y) = ( + +
x + y)( y + z)(z + x) (x + y)( y + z)(z + x) (x + y)( y + z)(z + x) 2 2 2 2 2 2 2 2 2 2 2 2
x y + x z − y z − yz + y z + xy − xz − x z + z x + z y − x y − xy = (
x + y)( y + z)(z + x) 0 = ( + )( + )( + ) = 0. x y y z z x Vậy A = 0.
Bài 31. Rút gọn biểu thức B (ab bc ca) 1 1 1 1 1 1 abc = + + + + − + + . 2 2 2 a b c a b c Hướng dẫn giải
Với a, b, c ≠ 0, ta có ( ) 1 1 1 1 1 1 B ab bc ca abc = + + + + − + + 2 2 2 a b c a b c 1 1 1 1 1 1
1 1 1 abc abc abc ab bc ca = + + + + + + + + − + + 2 2 2 a b c a b c a b c a b c ab bc ca bc ac ab = b + a + +
+ c + b + c + + a − − − c a b a b c
= 2(a + b + c).
Vậy B = 2(a + b + c).
Bài 32. Cho a + b + c = 0, hãy tính giá trị của biểu thức:
a − b b − c c − a c a b C = + + + + . c a
b a − b b − c c − a Hướng dẫn giải
Điều kiện a, b, c ≠ 0.
Với a + b + c = 0, ta có a + b = − ;
c b + c = −a; c + a = − . b Ta có
a − b b − c c − a c a b C = + + + + c a b a b b c c a − − −
a − b b − c c − a c
a − b b − c c − a a
a − b b − c c − a b = + + ⋅ + + + ⋅ + + + ⋅ c a
b a b c a
b b c c a b − − c − a
M N P Xét
a − b b − c c − a c M = + + ⋅ c a
b a − b 2 2 1 c
b − c c − a − + − = + ⋅ + =1 c b bc ac a + ⋅ a b a b − a − b ab c
(b − a)(b + a) − c(b − a) c
(b − a)(b + a − c) =1+ ⋅ =1+ ⋅ a − b ab a − b ab c
−(a − b)(−c − c) 3 ⋅ =1+ ⋅ c 2c 2 =1+ =1 c + . a − b ab ab abc 3 3 Tương tự, 2a 2 =1+ ; =1 b N P + . abc abc 3 3 3 2c 2a 2b 2( 3 3 3
a + b + c )
Khi đó C = M + N + P =1+ +1+ +1+ = 3 + . abc abc abc abc
Mặt khác, do a + b + c = 0 nên ta có (a + b + c)3 = 0 Suy ra (a + b)3 3
+ c + 3(a + b)c(a + b + c) = 0 3 3
a + b + ab(a + b) 3 3
+ c + 3(a + b)c(a + b + c) = 0 3 3 3
a + b + c + (a + b)( 2 3
ab + ac + bc + c ) = 0 3 3 3
a + b + c + 3(a + b)a(b + c) + c(b + c) = 0 3 3 3
a + b + c + 3(a + b)(b + c)(a + c) = 0 3 3 3
a + b + c + 3(−c)(−a)( b − ) = 0 3 3 3
a + b + c − 3abc = 0 3 3 3
a + b + c = 3 . abc 2⋅(3abc) Vậy C = 3 + = 3 + 6 = 9. abc -----HẾT-----