Đề cương ôn tập giữa học kỳ 1 Toán 11 Cánh diều (có đáp án)

Đề cương ôn tập giữa học kỳ 1 Toán 11 Cánh diều có đáp án được soạn dưới dạng file PDF gồm 5 trang giúp các bạn tham khảo, ôn tập và đạt kết quả cao trong kỳ thi sắp tới. Các bạn xem và tải về ở dưới.

63 32 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu chung Toán 11

Môn: Toán 11

Thông tin:

5 trang 9 tháng trước

Tác giả:

Profile Thùy Dương (H)
Trang 1
ĐỀ CƯƠNG ÔN TẬP GIỮA HỌC KỲ I NĂM HỌC 2023-2024
MÔN: TOÁN 11
PHẦN I. TRẮC NGHIỆM
Câu 1: Đổi số đo của góc sang rađian ta được
A. ; B. ; C. ; D. .
Câu 2: Cho góc lượng giác có số đo là . Số đo của các góc lượng giác nào sau đây có cùng
tia đầu là và tia cuối là ?
A. B. ; C. ; D. .
Câu 3: Cho thuộc góc phần tư thứ ba của đường tròn lượng giác. Khẳng định nào sau đây là sai?
A. ; B. ; C. ; D. .
Câu 4: Đơn giản biểu thức ta được
A. ; B. ; C. ; D. .
Câu 5: Đơn giản biểu thức ta được
A. ; B. ; C. ; D. .
Câu 6: Rút gọn biểu thức ta được
A. ; B. ; C. ; D. .
Câu 7: Trong các hàm số sau, hàm số nào có đồ thị đối xứng qua trục tung?
A. ; B. ; C. ; D. .
Câu 8: Mệnh đề nào sau đây là sai?
A. Hàm số tuần hoàn với chu kì ;
B. Hàm số là hàm số không tuần hoàn;
C. Hàm số tuần hoàn với chu kì ;
D. Hàm số tuần hoàn với chu kì .
Câu 9: Cho hàm số có đồ thị như hình vẽ dưới đây:
Hàm số nghịch biến trên khoảng nào?
60
a
=
!
2
p
a
=
4
p
a
=
6
p
a
=
3
p
a
=
( )
,Ou Ov
4
p
Ou
Ov
3
4
p
5
4
p
7
4
p
9
4
p
a
sin 0
a
>
cos 0
a
<
tan 0
a
>
cot 0
a
>
cos sin
aa
=+A
2sin
a
=A
sin cos
aa
=A
0=A
422
sin sin c o s
aaa
=+P
sin
a
=P
sin
a
=P
cos
a
=P
cos
a
=P
( ) ( )
sin cos cos sin=- +-Mxyyxyy
cos=Mx
sin=Mx
sin cos2=Mxy
cos cos2=Mxy
sin=yx
cos=yx
tan=yx
cot=yx
cos=yx
2
p
sin=+yx x
tan=yx
2
p
cot=yx
p
sin=yx
sin=yx
Trang 2
A. B. ; C. D. .
Câu 10: Tập xác định của hàm số là
A. ; B. ;
C. ; D. .
Câu 11: Giá trị lớn nhất của hàm số là
A. ; B. ; C. ; D. .
Câu 12: Phương trình có một nghiệm là
A. B. ; C. ; D. .
Câu 13: Phương trình có tập nghiệm là
A. ; B.
.
C. ; D. .
Câu 14: Các giá trị của tham số để phương trình vô nghiệm là
A. ; B. ; C. ; D. .
Câu 15: Phương trình có số nghiệm thuộc đoạn là
A. 2; B. 3; C. 4 ; D. 5 .
Câu 16: Cho dãy số biết . Dãy số bị chặn trên bởi số nào dưới đây?
A. 0; B. ; C. ; D. 1.
Câu 17: Trong các dãy số cho bởi số hạng tổng quát dưới đây, dãy số nào là dãy số tăng?
A.
.
B. . C. . D.
.
Câu 18: Cho dãy số có các số hạng đầu là . Số hạng tổng quát của dãy số trên là
A. ; B. ; C. ; D.
Câu 19: Cho dãy số là cấp số cộng với
A. số hạng đầu tiên là và công sai là ;
B. số hạng đầu tiên là và công sai là ;
( )
0;
p
3
;
22
pp
æö
--
ç÷
èø
( )
2;
pp
--
53
;
22
pp
æö
--
ç÷
èø
2
3tan 5
1 sin
-
=
-
x
y
x
2,
2
p
p
ìü
=+Î
íý
îþ
DkkRZÇ
,
2
p
p
ìü
=+Î
íý
îþ
DkkRZÇ
{ }
,
pp
=+ÎDkkRZÇ
=D R
M
12cos3=-yx
3=M
2=M
1=M
0=M
sin 1=x
p
=x
2
p
=-x
2
p
=x
3
p
=x
3tan 3 0-=x
2,
3
p
p
ìü
+Î
íý
îþ
kkZ
Æ
,
3
p
p
ìü
+Î
íý
îþ
kkZ
,
6
p
p
ìü
+Î
íý
îþ
kkZ
m
cos =-xm
( ) ( )
;1 1;
¥¥
Î- - È +m
( )
1;
¥
Î+m
[ ]
1; 1Î-m
( )
;1
¥
Î- -m
sin cos=xx
[ ]
;
pp
-
( )
n
u
31
31
-
=
+
n
n
u
n
( )
n
u
1
2
1
3
( )
n
u
n
u
1
2
=
n
n
u
1
=
n
u
n
5
31
+
=
+
n
n
u
n
21
1
-
=
+
n
n
u
n
2; 0; 2; 4; 6;-…
2=-
n
un
2=-
n
un
( )
21=- +
n
un
24=-
n
un
11 3
;0; ; 1; ;
222
-
-- …
1
2
1
2
1
2
1
2
-
Trang 3
C. số hạng đầu tiên là 0 và công sai là ;
D. số hạng đầu tiên là 0 và công sai là .
Câu 20: Cho cấp số cộng có và . Số số hạng thứ 5 của cấp số cộng là
A. 4 ; B. 7 ; C. 10 ; D. 13 .
Câu 21: Một rạp hát có 30 dãy ghế, dãy đầu tiên có 25 ghế. Mỗi dãy sau có hơn dãy trước 3 ghế. Hỏi rạp
hát có tất cả bao nhiêu ghế?
A. 1635 ; B. 1792 ; C. 2055 ; D. 3125 .
Câu 22: Khẳng định nào sau đây là đúng?
A. Qua 2 điểm phân biệt có duy nhất một mặt phẳng;
B. Qua 3 điểm phân biệt bất kì có duy nhất một mặt phẳng;
C. Qua 3 điểm không thẳng hàng có duy nhất một mặt phẳng;
D. Qua 4 điểm phân biệt bất kì có duy nhất một mặt phẳng.
Câu 23: Trong các mệnh đề sau đây, mệnh đề nào sai?
A. Hai mặt phẳng có một điểm chung thì chúng có vô số điểm chung khác nữa;
B. Hai mặt phẳng có một điểm chung thì chúng có một đường thẳng chung duy nhất;
C. Hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường thẳng chung duy nhất;
D. Hai mặt phẳng cùng đi qua 3 điểm không thẳng hàng thì hai mặt phẳng đó trùng nhau.
Câu 24: Cho hình chóp . Khẳng định nào sau đây là sai?
A. Hình chóp có 4 mặt bên đều là các tam giác;
B. Hình chóp có mặt đáy là hình vuông;
C. Đỉnh của hình chóp không nằm trong mặt phẳng ;
D. Hình chóp có tất cả 4 cạnh bên.
Câu 25: Khẳng định nào sau đây là đúng?
A. Hình chóp tứ giác là một hình tứ diện;
B. Hình tứ diện đều có mặt đáy là tam giác đều;
C. Mặt bên của tứ diện đều là hình tam giác cân;
D. Cả A, B, C đều đúng.
Câu 26: Cho hình chóp có là trọng tâm tam giác . Giao tuyến của mặt phẳng và
là
A. với là trung điểm của ;
B. với là trung điểm của ;
C. với là hình chiếu của trên ;
D. với là hình chiếu của trên .
1
2
1
2
-
( )
n
u
1
5=-u
3=d
.S ABCD
ABCD
S
( )
ABCD
ABCD
G
BCD
( )
ACD
( )
GAB
AN
N
CD
AM
M
AB
AH
H
B
CD
AK
K
C
BD
Trang 4
Câu 27: Cho điểm không nằm trên mặt phẳng chứa tam giác . Lấy là các điểm lần
lượt nằm trên các cạnh . Khi cắt nhau tại thì không phải điểm chung của hai mặt
phẳng nào sau đây?
A. và ; B. và ; C. và ; D. và
.
Câu 28: Cho ba mặt phẳng phân biệt có , . Khi
đó ba đường thẳng sẽ
A. đôi một cắt nhau; B. đôi một song song;
C. đồng quy; D. đôi một song song hoặc đồng quy.
Câu 29: Trong không gian, cho ba đường thẳng biết và chéo nhau. Khi đó hai đường
thẳng và sẽ
A. trùng nhau hoặc chéo nhau; B. cắt nhau hoặc chéo nhau;
C. chéo nhau hoặc song song; D. song song hoặc trùng nhau.
Câu 30: Cho hình chóp có đáy là hình bình hành. Gọi lần lượt là trung điểm
của . Trong các đường thẳng sau, đường thẳng nào không song song với ?
A. ; B. ; C. ; D. .
Câu 31: Cho hình chóp có đáy là hình thang với các cạnh đáy và . Gọi lần lượt
là trung điểm của và là trọng tâm của tam giác . Giao tuyến của và là
A. ;
B. đường thẳng qua và song song với ;
C. đường thẳng qua và song song với ;
D. đường thẳng qua và cắt .
Câu 32: Giả sử các đường thẳng và các mặt phẳng là phân biệt. Điều kiện để đường thẳng song song
với mặt phẳng là
A. và ; B. và ; C. và ; D. và
.
Câu 33: Cho đường thẳng . Giả sử đường thẳng không nằm trong . Khẳng định nào sau
đây là đúng?
. Nếu cắt và chứa thì giao tuyến của và là đường thẳng cắt cả và .
A. Nếu thì ; B. Nếu cắt thì cắt ;
C. Nếu thì ;
Câu 34: Cho hình chóp có lần lượt là trung điểm của . Khi đó
A. ; B. ; C. ; D. .
A
( )
a
BCD
,EF
,AB AC
,EF BC
I
I
( )
BCD
( )
DEF
( )
BCD
( )
ABC
( )
BCD
( )
AEF
( )
BCD
( )
ABD
( ) ( ) ( )
,,
abg
( ) ( ) ( ) ( )
,
ab bg
Ç= Ç=ab
( ) ( )
ag
Ç=c
,,abc
,,abc
//ab
,ac
b
c
.S ABCD
ABCD
,,,IJEF
,,,SA SB SC SD
IJ
EF
DC
AD
AB
×S ABCD
AB
CD
,IJ
,AD BC
G
SAB
( )
SAB
( )
IJG
SC
S
AB
G
DC
G
BC
a
( )
P
//ab
( )
ÌbP
//ab
( )
//bP
( )
ÌaQ
( )
ÌbP
( )
//; Ìaba Q
( )
ÌbP
( )
a
Ìa
b
( )
a
D
b
( )
a
( )
b
b
( )
a
( )
b
a
b
( )
//
a
b
//ba
b
( )
a
b
a
//ba
( )
//
a
b
×S ABCD
,MN
,SA SC
( )
///MN ABCD
( )
//MN SAB
( )
//MN SCD
( )
//MN SBC
Trang 5
Câu 35: Cho tứ diện có là trọng tâm của tam giác thuộc cạnh sao cho
là trung điểm của . Khi đó
A. ; B. ;
C. cắt ; D. thuộc mặt phẳng .
PHẦN II. TỰ LUẬN
Bài 1. (1,0 điểm) Giải các phương trình lượng giác:
a) ;
b) và
Bài 2. (1,0 điểm) Cho tứ diện và điểm thuộc cạnh . Gọi là mặt phẳng qua ,
song song với hai đường thẳng và . Gọi lần lượt là giao điểm của mặt phẳng
với các cạnh và .
a) Chứng minh là hình bình hành.
b) Trong trường hợp nào thì là hình thoi?
Bài 3. (1,0 điểm) Cho là góc nhọn và . Tìm để .
-----HẾT-----
ĐÁP ÁN
1
D
6
B
11
C
2
D
7
B
12
C
3
A
8
C
13
C
4
D
9
B
14
A
5
A
10
B
15
A
16
D
21
C
26
A
17
D
22
C
27
D
18
D
23
B
28
D
19
B
24
B
29
B
20
B
25
B
30
C
31
C
32
D
33
C
34
A
35
B
ABCD
G
,ABD Q
AB
2,=AQ QB P
AB
( )
//MN BCD
( )
//GQ BCD
MN
( )
BCD
Q
( )
CDP
22
cos sin2 2 sin-=+xx x
( ) ( )
2
1
31cot 31 0
sin
-- -+=x
x
( )
0;
p
Îx
ABCD
M
AB
( )
a
M
BC
AD
,,NPQ
( )
a
,AC CD
DB
MNPQ
MNPQ
1
sin
22
a
-
=
x
x
1
tan
2
a
= x
| 1/5
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

ĐỀ CƯƠNG ÔN TẬP GIỮA HỌC KỲ I NĂM HỌC 2023-2024 MÔN: TOÁN 11 PHẦN I. TRẮC NGHIỆM
Câu 1: Đổi số đo của góc a = 60! sang rađian ta được p p p p A. a = ; B. a = ; C. a = ; D. a = . 2 4 6 3 p
Câu 2: Cho góc lượng giác (Ou,Ov) có số đo là . Số đo của các góc lượng giác nào sau đây có cùng 4
tia đầu là Ou và tia cuối là Ov ? 3p 5p 7p 9p A. B. ; C. ; D. . 4 4 4 4
Câu 3: Cho a thuộc góc phần tư thứ ba của đường tròn lượng giác. Khẳng định nào sau đây là sai?
A. sina > 0 ;
B. cosa < 0 ;
C. tana > 0 ; D. cota > 0 . æ 9p ö
Câu 4: Đơn giản biểu thức A = cos -a + sin ç ÷ (a -p ) ta được è 2 ø
A. A = cosa + sina ;
B. A = 2sina ;
C. A = sinacosa ; D. A = 0 .
Câu 5: Đơn giản biểu thức 4 2 2
P = sin a + sin acos a ta được
A. P = sina ;
B. P = sina ;
C. P = cosa ; D. P = cosa .
Câu 6: Rút gọn biểu thức M = sin(x - y)cosy + cos(x - y)siny ta được
A. M = cosx ;
B. M = sinx ; C. M = sin c x os2y; D. M = cos co x s2y .
Câu 7: Trong các hàm số sau, hàm số nào có đồ thị đối xứng qua trục tung?
A. y = sinx ;
B. y = cosx ;
C. y = tanx;
D. y = cotx.
Câu 8: Mệnh đề nào sau đây là sai?
A. Hàm số y = cosx tuần hoàn với chu kì 2p ;
B. Hàm số y = x + sinx là hàm số không tuần hoàn;
C. Hàm số y = tanx tuần hoàn với chu kì 2p ;
D. Hàm số y = cotx tuần hoàn với chu kì p .
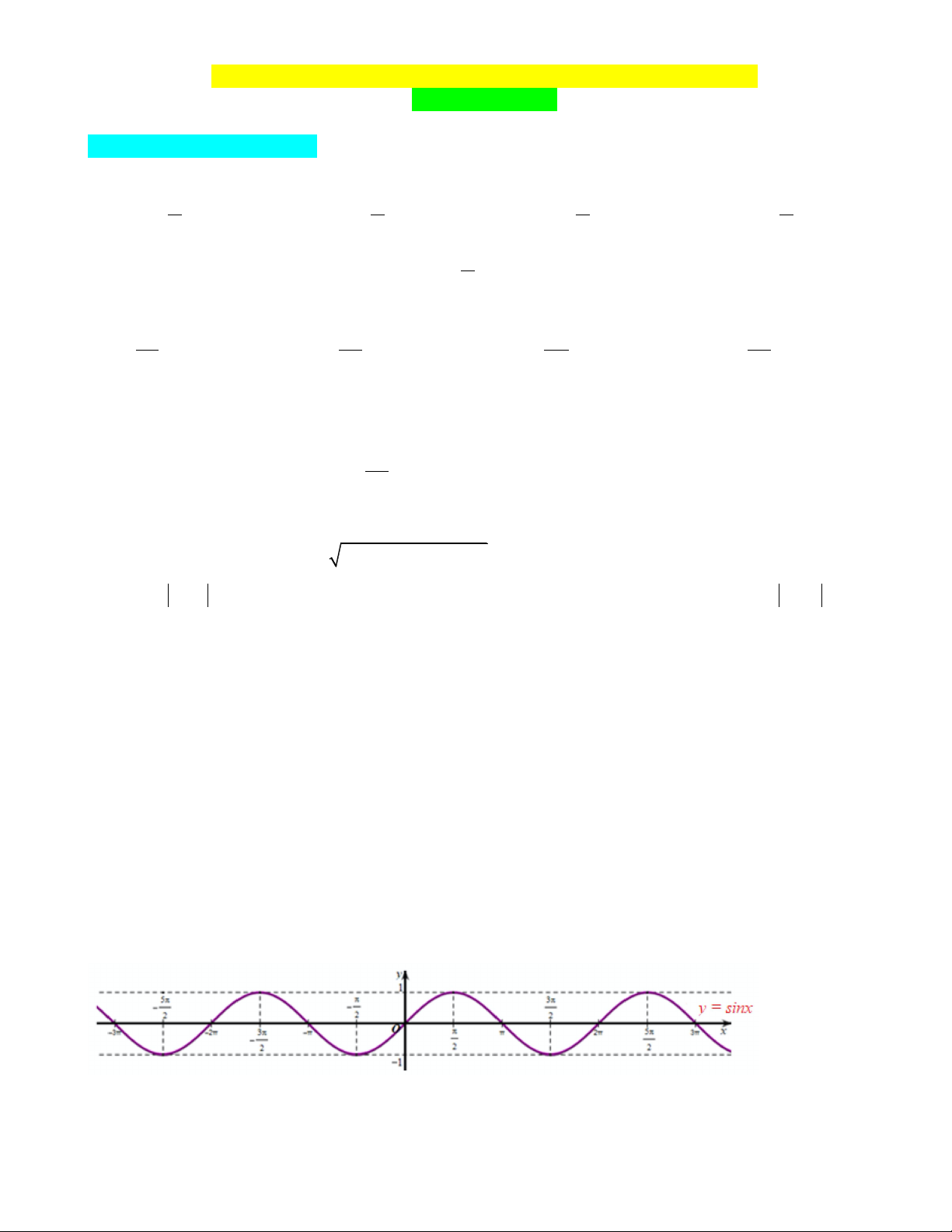
Câu 9: Cho hàm số y = sinx có đồ thị như hình vẽ dưới đây:
Hàm số y = sinx nghịch biến trên khoảng nào? Trang 1 æ 3p p ö æ 5p 3p ö A. (0;p ) B. - ;- ; C. ( 2 - ;- ) p p D. - ;- . ç ÷ ç ÷ è 2 2 ø è 2 2 ø 3tanx - 5
Câu 10: Tập xác định của hàm số y = là 2 1- sin x ìp ü ìp ü
A. D = R Ç í + k2p ,k ÎZý;
B. D = R Ç í + kp ,k ÎZý; î 2 þ î 2 þ
C. D = R Ç {p + p
k ,k ÎZ}; D. D = R .
Câu 11: Giá trị lớn nhất M của hàm số y =1- 2 cos3x là
A. M = 3;
B. M = 2 ;
C. M = 1; D. M = 0 .
Câu 12: Phương trình sinx = 1 có một nghiệm là p p p
A. x = p
B. x = - ; C. x = ; D. x = . 2 2 3
Câu 13: Phương trình 3tanx - 3 = 0 có tập nghiệm là ìp ü ìp ü ìp ü
A. í + k2p ,k ÎZý; B. Æ .
C. í + kp,k ÎZý ;
D. í + kp,k ÎZý . î 3 þ î 3 þ î 6 þ
Câu 14: Các giá trị của tham số m để phương trình cosx = -m vô nghiệm là A. mÎ( ¥ - ;- ) 1 È(1; ¥
+ ); B. mÎ(1; ¥ + ); C. mÎ[ 1 - ; ] 1 ; D. mÎ( ¥ - ;- ) 1 .
Câu 15: Phương trình sinx = cosx có số nghiệm thuộc đoạn [ p - ;p ] là A. 2; B. 3; C. 4 ; D. 5 . 3n -1
Câu 16: Cho dãy số ( u u = ( un ) n ) biết . Dãy số
bị chặn trên bởi số nào dưới đây? n 3n +1 1 1 A. 0; B. ; C. ; D. 1. 2 3
Câu 17: Trong các dãy số (u u
n ) cho bởi số hạng tổng quát
dưới đây, dãy số nào là dãy số tăng? n 1 1 n + 5 2n -1 A. u = B. u = . C. u = . D. u = n 2n . n n n 3n +1 n n +1 .
Câu 18: Cho dãy số có các số hạng đầu là 2; - 0;2;4;6; . S
… ố hạng tổng quát của dãy số trên là A. u = 2 - n;
B. u = n - 2; C. u = 2 - (n + u = 2n - 4 n )1; D. n n n 1 1 3 -
Câu 19: Cho dãy số ;0;- ; 1 - ; ;
… là cấp số cộng với 2 2 2 1 1
A. số hạng đầu tiên là và công sai là ; 2 2 1 1
B. số hạng đầu tiên là và công sai là - ; 2 2 Trang 2 1
C. số hạng đầu tiên là 0 và công sai là ; 2 1
D. số hạng đầu tiên là 0 và công sai là - . 2
Câu 20: Cho cấp số cộng (u u = 5 - d = 3 n ) có và
. Số số hạng thứ 5 của cấp số cộng là 1 A. 4 ; B. 7 ; C. 10 ; D. 13 .
Câu 21: Một rạp hát có 30 dãy ghế, dãy đầu tiên có 25 ghế. Mỗi dãy sau có hơn dãy trước 3 ghế. Hỏi rạp
hát có tất cả bao nhiêu ghế? A. 1635 ; B. 1792 ; C. 2055 ; D. 3125 .
Câu 22: Khẳng định nào sau đây là đúng?
A. Qua 2 điểm phân biệt có duy nhất một mặt phẳng;
B. Qua 3 điểm phân biệt bất kì có duy nhất một mặt phẳng;
C. Qua 3 điểm không thẳng hàng có duy nhất một mặt phẳng;
D. Qua 4 điểm phân biệt bất kì có duy nhất một mặt phẳng.
Câu 23: Trong các mệnh đề sau đây, mệnh đề nào sai?
A. Hai mặt phẳng có một điểm chung thì chúng có vô số điểm chung khác nữa;
B. Hai mặt phẳng có một điểm chung thì chúng có một đường thẳng chung duy nhất;
C. Hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường thẳng chung duy nhất;
D. Hai mặt phẳng cùng đi qua 3 điểm không thẳng hàng thì hai mặt phẳng đó trùng nhau.
Câu 24: Cho hình chóp S.ABCD . Khẳng định nào sau đây là sai?
A. Hình chóp có 4 mặt bên đều là các tam giác;
B. Hình chóp có mặt đáy ABCD là hình vuông;
C. Đỉnh S của hình chóp không nằm trong mặt phẳng ( ABCD);
D. Hình chóp có tất cả 4 cạnh bên.
Câu 25: Khẳng định nào sau đây là đúng?
A. Hình chóp tứ giác là một hình tứ diện;
B. Hình tứ diện đều có mặt đáy là tam giác đều;
C. Mặt bên của tứ diện đều là hình tam giác cân;
D. Cả A, B, C đều đúng.
Câu 26: Cho hình chóp ABCD có G là trọng tâm tam giác BCD . Giao tuyến của mặt phẳng ( ACD) và (GAB) là
A. AN với N là trung điểm của CD ;
B. AM với M là trung điểm của AB ;
C. AH với H là hình chiếu của B trên CD ;
D. AK với K là hình chiếu của C trên BD . Trang 3
Câu 27: Cho điểm A không nằm trên mặt phẳng (a ) chứa tam giác BCD . Lấy E, F là các điểm lần
lượt nằm trên các cạnh AB, AC . Khi EF, BC cắt nhau tại I thì I không phải điểm chung của hai mặt phẳng nào sau đây?
A. (BCD) và (DEF );
B. (BCD) và ( ABC);
C. (BCD) và ( AEF); D. (BCD) và (ABD).
Câu 28: Cho ba mặt phẳng phân biệt (a ),(b ),(g ) có (a )Ç(b ) = ,
a (b )Ç(g ) = b, (a )Ç(g ) = c. Khi
đó ba đường thẳng a,b, c sẽ
A. đôi một cắt nhau;
B. đôi một song song;
C. đồng quy;
D. đôi một song song hoặc đồng quy.
Câu 29: Trong không gian, cho ba đường thẳng a,b, c biết a / /b và a,c chéo nhau. Khi đó hai đường
thẳng b và c sẽ
A. trùng nhau hoặc chéo nhau;
B. cắt nhau hoặc chéo nhau;
C. chéo nhau hoặc song song;
D. song song hoặc trùng nhau.
Câu 30: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I, J, E, F lần lượt là trung điểm của ,
SA SB, SC, SD . Trong các đường thẳng sau, đường thẳng nào không song song với IJ ? A. EF ; B. DC ; C. AD ; D. AB .
Câu 31: Cho hình chóp S × ABCD có đáy là hình thang với các cạnh đáy AB và CD . Gọi I, J lần lượt là trung điểm của ,
AD BC và G là trọng tâm của tam giác SAB . Giao tuyến của (SAB) và (IJG) là A. SC ;
B. đường thẳng qua S và song song với AB ;
C. đường thẳng qua G và song song với DC ;
D. đường thẳng qua G và cắt BC .
Câu 32: Giả sử các đường thẳng và các mặt phẳng là phân biệt. Điều kiện để đường thẳng a song song
với mặt phẳng (P) là
A. a / /b và b Ì (P);
B. a / /b và b / / (P);
C. a Ì (Q) và b Ì (P); D. a / / ; b a Ì (Q) và b Ì (P).
Câu 33: Cho đường thẳng a Ì (a ). Giả sử đường thẳng b không nằm trong (a ). Khẳng định nào sau đây là đúng?
D . Nếu b cắt (a ) và (b ) chứa b thì giao tuyến của (a ) và (b ) là đường thẳng cắt cả a và b .
A. Nếu b / / (a ) thì b / /a ;
B. Nếu b cắt (a ) thì b cắt a ;
C. Nếu b / /a thì b / / (a );
Câu 34: Cho hình chóp S × ABCD có M , N lần lượt là trung điểm của , SA SC . Khi đó
A. MN / / / ( ABCD);
B. MN / / (SAB);
C. MN / / (SCD);
D. MN / / (SBC). Trang 4
Câu 35: Cho tứ diện ABCD có G là trọng tâm của tam giác ABD,Q thuộc cạnh AB sao cho
AQ = 2QB, P là trung điểm của AB . Khi đó
A. MN / / (BCD);
B. GQ / / (BCD);
C. MN cắt (BCD);
D. Q thuộc mặt phẳng (CDP).
PHẦN II. TỰ LUẬN
Bài 1. (1,0 điểm) Giải các phương trình lượng giác: a) 2 2
cos x -sin2x = 2 +sin x;
b) 1 - 3 -1 cotx - 3 +1 = 0 x Î(0;p ) 2 ( ) ( ) và sin x
Bài 2. (1,0 điểm) Cho tứ diện ABCD và điểm M thuộc cạnh AB . Gọi (a ) là mặt phẳng qua M ,
song song với hai đường thẳng BC và AD . Gọi N, P,Q lần lượt là giao điểm của mặt phẳng (a )
với các cạnh AC,CD và DB .
a) Chứng minh MNPQ là hình bình hành.
b) Trong trường hợp nào thì MNPQ là hình thoi? a -
Bài 3. (1,0 điểm) Cho là góc nhọn và 1 1 sin = x . Tìm để tana = x. 2 2x 2 -----HẾT----- ĐÁP ÁN 1 D 6 B 11 C 2 D 7 B 12 C 3 A 8 C 13 C 4 D 9 B 14 A 5 A 10 B 15 A 16 D 21 C 26 A 17 D 22 C 27 D 18 D 23 B 28 D 19 B 24 B 29 B 20 B 25 B 30 C 31 C 32 D 33 C 34 A 35 B Trang 5