
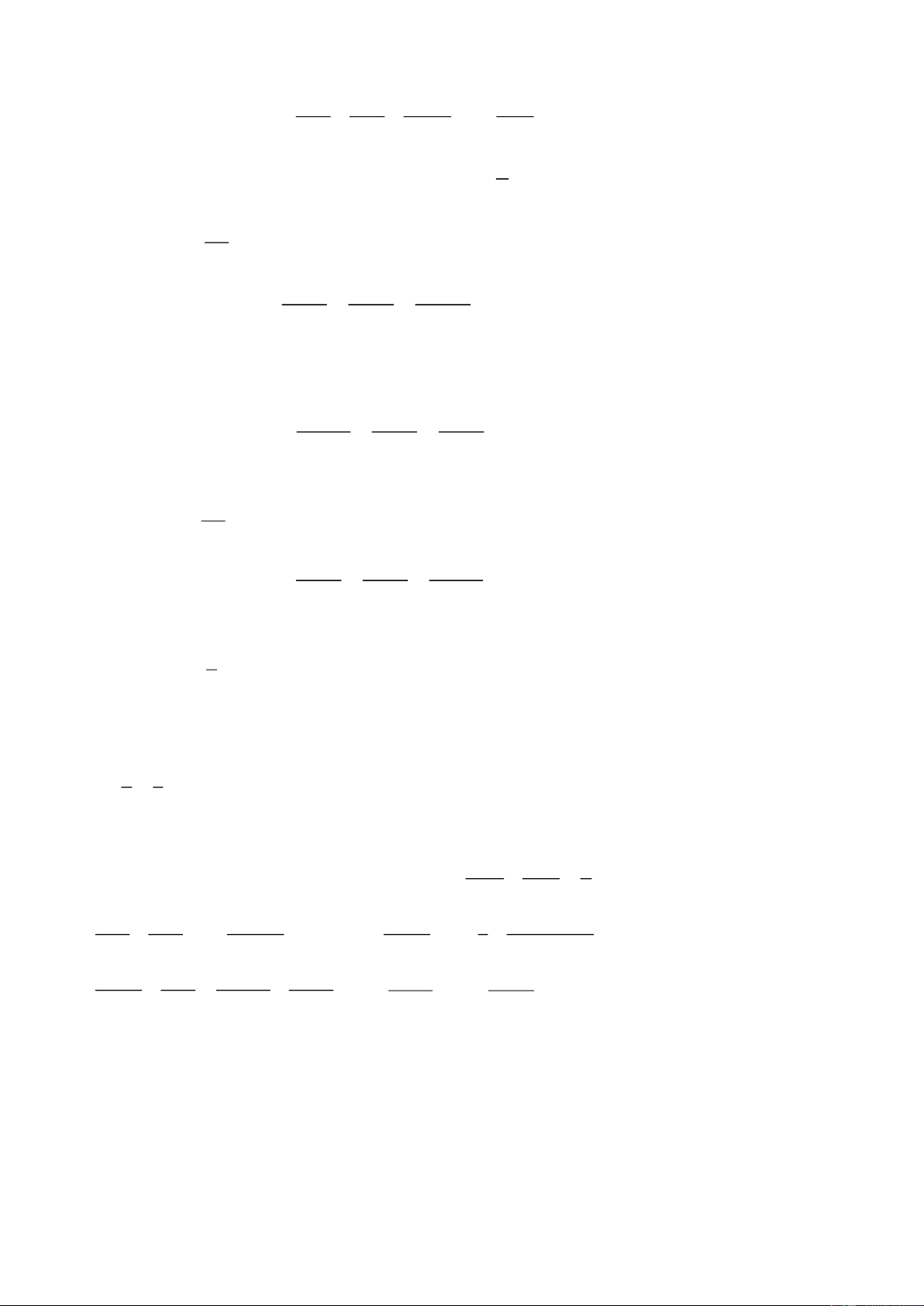



Preview text:
PHÒNG GD – ĐT QUẬN LONG BIÊN
ĐỀ CƯƠNG ÔN TẬP HÈ
TRƯỜNG THCS THANH AM MÔN: TOÁN
Năm học 2023 – 2024 LỚP 8
I. RÚT GỌN BIỂU THỨC 3 − 2x 1 1
Bài 1: Cho biểu thức: A = + + ; − ) 2 x − 4 x − 2 x + (với x 2 x 2 2
a. Rút gọn biểu thức A b. Tính giá trị của biểu thức A khi x = -3 c. Tìm x để 2 A =
d. Tìm giá trị nguyên của x để A nhận giá trị nguyên 5 2 x 3 x + 4
Bài 2: Cho biểu thức P = + − ; − ) 2 x + 3 x − 3 x − (với x 3 x 3 9 a. Rút gọn biểu thức P
b. Tính giá trị của biểu thức P khi x = 5 c. Tìm x để 3 P =
d. Tìm giá trị nguyên của x để P nhận giá trị nguyên 7 x 10x 5
Bài 3: Cho biểu thức M = − −
(với x 5; x − 5 ) x − 5 2 x − 25 x + 5 a. Rút gọn biểu thức M b. Tính M khi x = -2 c. Tìm x để 3 M =
d. Tìm giá trị nguyên của x để M nhận giá trị nguyên 4 x 1 2
Bài 4: Cho biểu thức M = + : 2
x − 4 x − 2 x − 2 a. Rút gọn biểu thức M b. Tính M khi x = 6 c. Tìm x để 1 M =
d. Tìm giá trị nguyên của x để M nhận giá trị nguyên 4 2x x + 1 11x − 3 1
Bài 5: Cho biểu thức P = − + .1+ x + 3 3 − 2 x x − 9 x − 4 1 a. Rút gọn biểu thức P b.Tính P khi x = 2 7 c.Tìm x để P =
d. Tìm giá trị nguyên của x để P nhận giá trị nguyên 4
x −1 x +1 2 2 x − 2x 1
Bài 6: Cho biểu thức A = + + .1− 2
x + 3 x − 3 9 − x x − 2 1 a. Rút gọn biểu thức A b.Tính A khi x = 2 5 − c. Tìm x để A=
d. Tìm giá trị nguyên của x để A nhận giá trị nguyên 6 x 3 6x − 4 2
Bài 7: Cho biểu thức M = + + .1−
x −1 x +1 1− 2 x x + 3 2 a. Rút gọn biểu thức M b.Tính M khi x = 3 3 − c.Tìm x để M =
d. Tìm giá trị nguyên của x để M nhận giá trị nguyên 4 x + 1 2x 2 + 5x
Bài 8: Cho biểu thức P = + + 2 x − 2 x + 2 4 − x a. Rút gọn biểu thức P b. Tính P khi x = 7 c. Tìm x để P = 2
d. Tìm giá trị nguyên của x để P nhận giá trị nguyên 2 x 1 1
Bài 9: Cho biểu thức: A = − + 2 x − 4 2 − x x + 2 a. Rút gọn biểu thức M b.Tính A khi x = 4 − c.Tìm x để 3 A =
d. Tìm giá trị nguyên của x để A nhận giá trị nguyên 4 x 5 x + 10
Bài 10: Cho biểu thức A = − − 2 x + 2 2 − x x − 4 a. Rút gọn biểu thức A b. Tính A khi x = 1 c. Tìm x để 3 A =
d. Tìm giá trị nguyên của x để A nhận giá trị nguyên 2
II. PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN VÀ ỨNG DỤNG
Bài 1. Giải các phương trình sau: 4 1 a) x −
= b) 2x + 5 = 20 − 3x c) (x +1)(2x − 3) = (2x −1)(x + 5) 5 5
d) −2(x − 3) − 4 = 3(x −1) + 8 e) 2
2x + x(x +1)(x −1) = (x +1)(x − x +1) x + 4 x − 3 x f) 3 2
(x −1) − x(x +1) = 5x(2 − x) −11(x + 2) g) − = 4 6 3 x −1 1 − x 2(x −1) 3x − 2 1 2 + 2(x − 6) h) − = 1− i) − 4 = + 2 4 3 3 3 2 3x − 2 x −1 14x − 3 2x + 1 x 7 −1 16 − x k) + = − l) + 2x = 5 9 15 9 6 5
Bài 2. Giải các bài toán sau bằng cách lập phương trình:
a) Lúc 6 giờ, một ô tô xuất phát từ A đến B với vận tốc 40km/h. Lái xe giao hàng tại B trong 30
phút rồi quay lại A với vận tốc 30km/h. Tính quãng đường AB biết ô tô về đến A lúc 10 giờ cùng ngày?
b) Trong dịp Tết nguyên đán 2024, bác An đã chọn Hà Giang là điểm đến cho các thành viên
trong những ngày đầu năm mới. Khi di chuyển từ Hà Nội đến Hà Giang xe du lịch đi với vận tốc
50km/h, lúc về xe đi với vận tốc 60km/h. Biết rằng thời gian lúc về ít hơn thời gian lúc đi là 48
phút. Tính quãng đường từ Hà Nội đến Hà Giang?
c) Một ôtô đi từ A đến B với vận tốc 60km/h. Khi trở về cũng trên tuyến đường đó, ôtô chạy với
vận tốc 40km/h nên thời gian về nhiều hơn thời gian đi là 2 giờ 10 phút. Tính quãng đường AB?
d) Hai người đi xe đạp ngược chiều nhau xuất phát cùng một lúc từ hai địa điểm A và B cách nhau
42km và gặp nhau sau 2 giờ. Tính vận tốc của mỗi người, biết người đi từ A mỗi giờ đi nhanh
hơn người đi từ B là 3km.
e) Hai Ô tô cùng khởi hành từ hai bến cách nhau 175 km để gặp nhau. Xe 1 đi sớm hơn xe 2 là
1giờ 30 phút với vận tốc 30kn/h. Vận tốc của xe 2 là 35km/h. Hỏi sau mấy giờ hai xe gặp nhau?
f) Để hưởng ứng phong trào “ Vì một Việt Nam xanh”, một nhóm thanh niên tình nguyện đã tham
gia trồng cây để phủ xanh một ngọn đồi trọc. Nhóm dự định mỗi ngày trồng 200 cây xanh. Nhưng
khi thực hiện, nhóm huy động được thêm lực lượng tham gia nên mỗi ngày trồng được 250 cây
xanh. Do đó nhóm đã hoàn thành kế hoạch phủ xanh đồi trọc trước 3 ngày. Tính tổng số cây xanh
mà nhóm thanh niên tình nguyện dự định trồng?
g) Để chuẩn bị cho Sea Games 32, một phân xưởng may dự định mỗi ngày phải may xong 90 bộ
quần áo. Khi thực hiện, nhờ cải tiến kĩ thuật, mỗi ngày phân xưởng may được 120 bộ quần áo. Do
đó phân xưởng đã hoàn thành trước kế hoạch 9 ngày và may thêm được 60 b ộ quần áo. Hỏi theo
kế hoạch, phân xưởng phải may bao nhiêu bộ quần áo?
h) Một xưởng mộc nhận một đơn hàng của trường THCS đóng một số bộ bàn ghế. Lúc đầu xưởng
dự định mỗi ngày đóng 60 bộ bàn ghế. Nhưng khi thực hiện, mỗi ngày xưởng chỉ đóng được 50
bộ bàn ghế. Vì vậy để hoàn thành đơn hàng đã nhận thì xưởng phải làm việc thêm 3 ngày nữa so
với số ngày đã định. Tính số bộ bàn ghế xưởng đã nhận đóng theo đơn hàng của trường?
i) Một phân xưởng may đồng phục dự định hoàn thành kế hoạch được giao trong 22 ngày. Nhưng
thực tế, do cải tiến kĩ thuật nên mỗi ngày phân xưởng đã may vượt mức 3 bộ đồng phục nên sau
20 ngày phân xưởng không những đã hoàn thành kế hoạch mà may thêm được 30 bộ đồng phục
nữa. Tính số bộ đồng phục mà phân xưởng phải may theo kế hoạch giao
k) Một lớp học tham gia trồng cây ở một lâm trường trong một thời gian dự định với năng suất
300 cây/ngày. Nhưng thực tế đã trồng thêm được 100 cây/ngày. Do đó đã trồng thêm được tất cả
là 6 cây và hoàn thành trước kế hoạch 01 ngày. Tính số cây dự định trồng.
III. HÀM SỐ VÀ ĐỒ THỊ
Bài 1. Cho hàm số y = f(x) = – 3x + 7 3 − a) Tính f(– 1); f b) Tìm x biết ( ) 8 f x = 4 5
Bài 2. Một ô tô cho thuê xe ô tô tính phí bao gồm 1,5 triệu đồng/ngày và 10 nghìn đồng cho mỗi km di chuyển
a) Viết hàm số bậc nhất biểu thị chi phí thuê xe mỗi ngày y(nghìn đồng) theo x(km) đã di chuyển trong ngày.
b) Chi phí thuê xe trong ngày là bao nhiêu nếu trong ngày xe đó di chuyển quãng đường tổng cộng dài 180km.
Bài 3. Cho hàm số y = f(x) = (6 – 3m)x + m – 6
a) Tìm m để f(2) = 0 b) Biết f(– 1) = – 8. Xác định hệ số a, b của hàm số trên.
Bài 4. Cho hàm số y = (3 – 2m)x – 1
a) Tìm m biết hàm số có hệ số góc là 5 b) Xác định m để đồ thị hàm số đi qua điểm A(– 2; – 3)
c) Vẽ đồ thị hàm số với giá trị m vừa tìm được.
Bài 5. Cho hai hàm số y = 2x – 3 và y = – x có đồ thị lần lượt là (d1) và (d2)
a) Vẽ (d1) và (d2) trên cùng một mặt phẳng toạ độ.
b) Tìm toạ độ giao điểm A của (d1) và (d2) bằng phép tính.
c) Xác định các hệ số a, b của hàm số y = ax + b, biết rằng đồ thị (d3) của hàm số này song song
với (d1) và (d3) đi qua điểm M(– 3; – 4)
Bài 6. Cho hàm số y = (m – 1)x + 4 (m là tham số và m 1) có đồ thị là đường thẳng (d)
a) Tìm m để đường thẳng (d) song song với đường thẳng y = x – 2
b) Gọi giao điểm của (d) với trục hoành là A, trục tung là B. Với giá trị nào của m thì tam giác OAB cân tại O
Bài 7. Cho hàm số y = (1 – m)x + m – 1 (m là tham số và m 1) có đồ thị là đường thẳng (d)
a) Tìm m để (d) cắt đường thẳng y = 2x – 5 tại điểm có hoành độ bằng 2.
b) Tìm m để (d) cùng với các trục toạ độ Ox, Oy tạo thành một tam giác có diện tích bằng 2.
Bài 8. Cho hai đường thẳng (d1): y = – x + 2 và (d2): y = (m – 1)x + 2m – 4
a) Tìm giao điểm A của đường thẳng (d1) với Ox
b) Tìm m để (d2) đi qua gốc toạ độ O. Khi đó tìm toạ độ giao điểm P của (d1) và (d2).
c) Tính diện tích tam giác PAO
Bài 9. Cho hàm số y = (m – 2)x + 3 ( m 2
− ) có đồ thị là đường thẳng (d) trên mặt phẳng toạ độ
a) Tìm giá trị của m để đường thẳng (d) đi qua điểm A(– 2; 1). Vẽ đường thẳng (d) ứng với giá trị m vừa tìm được.
b) Với giá trị nào của m thì đường thẳng (d) song song với đường thẳng (d1): y = 3x + 1.
c) Tìm tất cả các giá trị của m để khoảng cách từ gốc toạ độ đến (d) bằng 1.
Bài 10. Cho hàm số y = x + 4 (d1)
a) Vẽ đồ thị hàm số trên.
b) Xác định toạ độ giao điểm C của (d1) và đồ thị hàm số y = – x – 2 (d2) bằng phép tính.
c) Cho đường thẳng (d3): y = (m2 – 4)x + 7. Tìm m để ba đường thẳng (d1), (d2) và (d3) đồng quy.
IV. HÌNH HỌC KHÔNG GIAN VÀ XÁC SUẤT THỐNG KẾ
Bài 1. Một kho chứa có dạng hình chóp tam giác đều với độ dài cạnh đáy 12m và độ dài trung
đoạn 8m (hình vẽ bên). Người ta muốn sơn phủ bên ngoài cả ba mặt xung quanh của kho chứa đó
và không sơn phủ phần làm cửa có diện tích là 5m2. Biết rằng cứ mỗi mét vuông sơn cần trả 30
000 đồng. Cần phải trả bao nhiêu tiền để hoàn thành việc sơn phủ đó?
Bài 2. Một mái che giếng trời có dạng hình chóp tứ giác đều với độ dài cạnh đáy là 2,5m và độ dài trung đoạn là 2m.
a) Tính diện tích xung quanh của mái che giếng trời đó.
b) Tính số tiền để làm mái che giếng trời đó .Biết rằng
giá để làm mỗi mét vuông mái che là 2 000 000 đồng (bao gồm tiền vật liệu và tiền công)
Bài 3. Bạn Trang cắt miếng bìa hình tam giác đều cạnh dài 20 cm như hình
vẽ và gấp lại theo các dòng kẻ (nét đứt) để được hình chóp tam giác đều.
Tính diện tích xung quanh của hình chóp tam giác đều tạo thành.
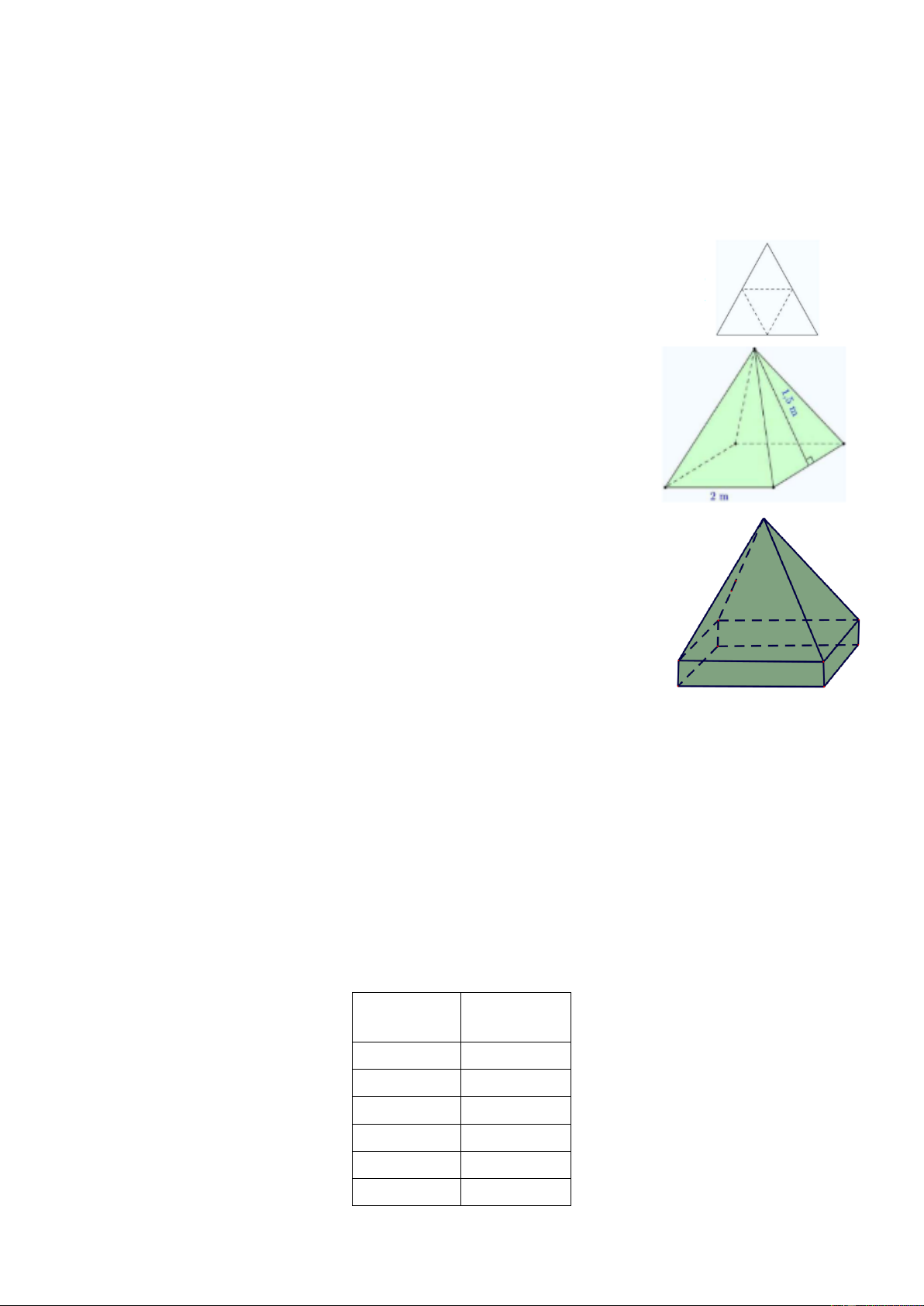
Bài 4. Một công trình trang trí có dạng hình chóp tứ giác đều với độ dài
cạnh đáy 2 m và chiều cao của tam giác mặt bên kẻ từ đỉnh của hình
chóp bằng 1,5 m. Người ta muốn sơn phủ bên ngoài bốn mặt công
trình này. Biết rằng cứ mỗi mét vuông sơn cần trả 40000 đồng. Hỏi
cần trả bao nhiêu tiền để hoàn thành việc sơn phủ đó?
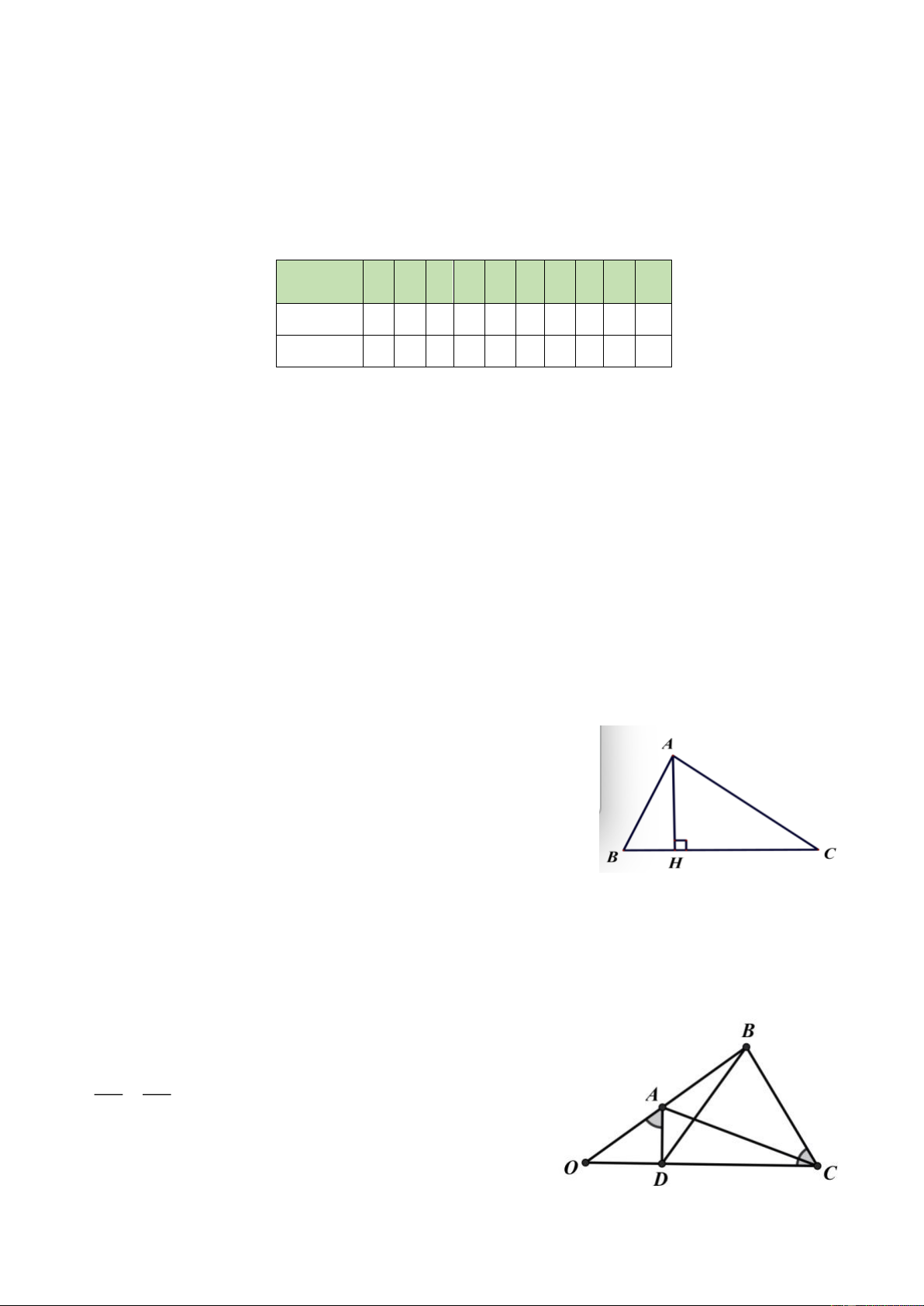
Bài 5. Một khối bê tông có dạng như hình vẽ bên.
Phần dưới của khối bê tông có dạng hình hộp chữ nhật , đáy là hình
vuông cạnh 40cm và chiều cao là 15cm. Phần trên của khối bê tông là
hình chóp tứ giác đều có cạnh đáy bằng 40cm và chiều cao bằng 90cm.
Tính thể tích khối bê tông?
Bài 6. Một hộp chứa 30 thẻ được đánh số từ 1 đến 30. Lấy ngẫu nhiên
một thẻ từ hộp. Tính xác suất của các biến cố:
a) A: “Thẻ lấy ra đánh số chia hết cho 5”
b) B: “Thẻ lấy ra đánh số chia hết cho 2 và 3”
Bài 7. Một hộp có 30 quả bóng được đánh số từ 1 đến 30, đồng thời các quả bóng từ 1 đến 10
được sơn màu cam và các quả bóng còn lại được sơn màu xanh; các quả bóng có kích cỡ và khối
lượng như nhau. Lấy ngẫu nhiện một quả bóng trong hộp.
Tính xác suất của các biến cố sau :
a) “Quả bóng được lấy ra được sơn màu cam”.
b) “Quả bóng được lấy ra được sơn màu xanh”.
c) “Quả bóng được lấy ra ghi số tròn chục”.
d) “Quả bóng được lấy ra được sơn màu xanh và ghi số chia hết cho 3”.
Bài 8. Gieo con xúc xắc cân đối có 6 mặt 100 lần, kết quả thu được ghi ở bảng sau Mặt Số lần xuất hiện 1 chấm 15 2 chấm 17 3 chấm 18 4 chấm 20 5 chấm 16 6 chấm 14
Tính xác suất của thực nghiệm của biến cố:
a) A : “Mặt xuất hiện là mặt 4 chấm”;
b) B : “Mặt xuất hiện có số chấm là số chia hết cho 3”;
c) C : “Mặt xuất hiện có số chấm là số nguyên tố”.
Bài 9. Ngân và Hà cùng chơi trò tung đồng xu, kí hiệu S mặt sấp, N là mặt ngửa; mỗi bạn tung 10
lần và thu được két quả cho trong bảng sau :
Lần thứ 1 2 3 4 5 6 7 8 9 10 Ngân
S N S S N S N S N N Hà
N S S N N S S S N N
a/ Tính xác suất thực nghiệm của biến cố “Tuyết tung đồng xu được mặt ngửa”.
b/ Tính xác suất thực nghiệm của biến cố “Linh tung đồng xu được mặt sấp”.
Bài 10. Một hộp chứa bốn chiếc kẹp nơ tóc có kích thước và mẫu mã giống nhau, trong đó có 1
chiếc màu xanh, 1 chiếc màu hồng, 1 chiếc màu vàng, 1 chiếc màu nâu. Mỗi lần bạn Lan lấy ngẫu
nhiên một chiếc nơ trong hộp, ghi lại màu của chiếc nơ được lấy ra và bỏ lại chiếc nơ đó vào hộp.
Trong 10 lần lấy liên tiếp, có 3 lần xuất hiện màu xanh, 2 lần xuất hiện màu vàng, 4 lần xuất hiện
màu hồng. Tính xác suất thực nghiệm của mỗi biến cố sau:
a) “Chiếc kẹp lấy ra là màu xanh”.
b) “Chiếc kẹp lấy ra là màu hồng”.
c) “Chiếc kẹp lấy ra là màu vàng”.
d) “Chiếc kẹp lấy ra là màu nâu”.
V. HÌNH HỌC TỔNG HỢP
Bài 1: (Vẽ hình vào bài làm) Cho hình vẽ bên, biết 2
AH = BH.CH .
a/ Chứng minh tam giác HAB đồng dạng với tam giác HCA.
b/ Chứng minh tam giác ABC vuông tại A. Bài 2:
Cho tam giác ABC vuông tại A, đường cao AH (H thuộc BC).
a/ Chứng minh tam giác ABC đồng dạng với tam giác HAC, từ đó suy ra 2
AC = BC.HC.
b/ Cho biết HB = 9cm; HC = 16cm. Tính độ dài các cạnh AB, AC của tam giác ABC. Bài 3:
Cho hình vẽ bên với 𝑂𝐴𝐷 ̂ = 𝑂𝐶𝐵 ̂. Chứng minh a/ O AD ∽ O CB ; OA OC b/ = ; OD OB c/ O AC ∽ O DB
Bài 4: Cho tam giác ABC vuông tại A (AB < AC), đường cao AH ( H thuộc BC). a/ Chứng minh A BC ∽ H B ; A
b/ Lấy điểm M thuộc AH. Kẻ đường thẳng đi qua B và vuông góc với CM tại K.
Chứng minh CM .CK = CH.C ; B
c/ Tia BK cắt HA tại D. Chứng minh : 𝐵𝐾𝐻 ̂ = 𝐵𝐶𝐷 ̂ .
Bài 5: Cho tam giác ABC có ba góc nhọn. Kẻ đường cao BE và CF cắt nhau tại H. Gọi K là giao điểm của AH và BC. a/ Chứng minh B AK ∽ B CF và B .
A BF = BK.BC; b/ Chứng minh B KF ∽ B AC ;
c/ Cho đoạn thẳng BC = 4. Tính B . A BF + CE. . CA
Bài 6: Cho tam giác ABC vuông tại A, đường cao AH, biết AB = 6cm, AC = 8cm. a/ Chứng minh A BC ∽ H BA ;
b/ Tính HB, AH; ;
c/ Lấy điểm M trên cạnh AC (M khác A và C), kẻ CI vuông góc với BM tại I. Chứng minh: M . A MC = M . B MI .
Bài 7. Cho ΔABC vuông tại A có AB = 4,5 c ,
m BC = 7,5 c
m . Kẻ đường cao AH . Tia phân
giác góc B cắt AC tại D , cắt AH tại K .
a/ Chứng minh ΔABC ∽ ΔHBA từ đó suy ra A .
B AH = AC. BH
b/ Tính độ dài các đoạn thẳng AH, BH , C H KH DA c/ Chứng minh = . KA DC
Bài 8. Cho ABC vuông tại A, đường cao AH.
a/ Chứng minh: Δ𝐴𝐻𝐶 ∽ Δ𝐵𝐴𝐶. b/ Chứng minh AB2 = BH . BC
c/ Từ H kẻ HE vuông góc với AB tại E. Biết AB = 21cm, AC = 28cm.
Tính độ dài đoạn thẳng BE.
Bài 9. Cho tam giác ABC đường cao AH . Biết AB = 9cm, AC = 12cm.
a/ Chứng minh ∆𝐻𝐵𝐴 ∆𝐴𝐵𝐶.
b/ Chứng minh: 𝐴𝐵2 = 𝐵𝐻. 𝐵𝐶. c/ Tính BC, BH.
d/ Tia phân giác của góc B cắt các cạnh AH, AC lần lượt tại I, D. Chứng minh: 𝐼𝐴. 𝐷𝐴 = 𝐼𝐻. 𝐷𝐶
Bài 10: Cho tam giác ABC vuông tại A, đường cao AH. a/ Chứng minh: A HB đồng dạng với C AB 2 b/ Chứng minh: AH = BH.CH
c/ Từ H kẻ HM, HN lần lượt vuông góc với AB, AC tại M và N. Chứng minh: A MN đồng dạng với A CB.
d/ Kẻ đường thẳng AK vuông góc với MN tại K cắt BC tại I. Chứng minh: I là trung điểm của BC.



