Đề cương ôn tập HK2 Toán 8 năm 2017 – 2018 trường Ngô Sĩ Liên – Hà Nội

Đề cương ôn tập HK2 Toán 8 năm học 2017 – 2018 trường THCS Ngô Sĩ Liên – Hà Nội gồm 43 trang tuyển chọn các bài toán lớp 8 giai đoạn học kỳ 2 điển hình nhằm giúp học sinh tự ôn để chuẩn bị cho kỳ thi HK2 Toán 8, các bài toán có lời giải chi tiết.

50 25 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu chung Toán 8

Môn: Toán 8

Thông tin:

43 trang 4 tháng trước

Tác giả:

Profile Mai Nguyệt
1/
43
Nhóm Toán THCS
Toán h󰉭
Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/
Trường THCS Ngô Sĩ Liên Đề cương ôn tập học kỳ II – Toán 8
Năm học: 2017-2018
Dạng 1: Rút gọn biểu thức
Bài 1. Cho biểu thức
2
2 5 1
3 6 2
x
A
x x x x
+
= − +
+ + − −
a) Rút gọn biểu thức A
b) Tìm x để A > 0
c) Tìm
x
để A nguyên dương.
Bài 2. Cho các biểu thức
2
2
22
1
xx
A
x
+
=
−
và
2
1 2 1
3 2 2
xx
B
x x x
−+
=+
− + −
a) Rút gọn biểu thức A, B;
b) Tính giá trị của A khi
c) Tính C = A – B;
d) Tìm
x
để
.C
Bài 3. Cho biểu thức
2
2 1 3 11
3 3 9
x x x
A
x x x
+−
= + +
+ − −
và
3
1
x
B
x
−
=
+
với
0 9.x
a) Rút gọn A;
b) Với P = A.B, tìm x để
9
.
2
P =
c) Tìm x để B < 1
d) Tìm số nguyên x để P = A.B là số nguyên.
Bài 4. Cho biểu thức
2
3
13
11
xx
A
xx
−+
=−
−−
và
2
2
2
1
x
B
xx
+
=
++
với
0 9.x
a) Rút gọn A;
b) Biết P = A: (1 - B). Tìm x để
1.P
Bài 5. Cho biểu thức
22
1 3 1 2 1
:
1 1 1 1
x x x x
P
x x x x
− + +

= − −

+ − − −

a) Rút gọn P;
b) Tìm các giá trị của x để
3
.
1
P
x
=
−
c) Tìm các giá trị nguyên của x để A > 1
Bài 6. Cho biểu thức
( )
2
2 5 50 5
2 10 2 5
x x x x
P
x x x x
+ − −
= + +
++
a) Tìm điều kiện xác định của P;
b) Rút gọn biểu thức P.
c) Tìm các giá trị của x để
1
0; .
4
PP==
d) Tìm các giá trị của x để P > 0; P < 0.
2/
43
Nhóm Toán THCS
Toán h󰉭
Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/
Bài 7. Cho biểu thức
2
2 5 2
:3
2 5 3 2 3 1
x
P
x x x x
= − +
− + − −
a) Rút gọn P.
b) Tính giá trị của P khi x thỏa mãn
2 1 3x −=
c) Tìm x để P > 1
d) Tìm x nguyên để P nguyên.
Bài 8. Cho biểu thức
2
2 3 2
12
1:
1 1 1
xx
A
x x x x x


= + −


+ − + − −


a) Rút gọn A.
b) Tính giá trị của A tại
1
.
2
x =−
c) Tìm x để A< 1
d) Tìm các giá trị nguyên của x để A có giá trị nguyên.
Dạng 2: Phương trình và bất phương trình
Bài 1. Giải các phương trình sau:
a)
( ) ( )
5 6 4 3 2xx− − = −
d)
3 2 3 1 5
2
2 6 3
xx
x
++
− = +
b)
( )
2
3 4 25 2 8 300x x x x− − = + −
e)
2 2 8 1
7
5 6 3
x x x
x
− + −
− + = +
c)
5 2 8 1 4 2
5
6 3 5
x x x+ − +
− = −
f)
( )
23
13 4
2
7 21
x
x
x
−
+
− + =
Bài 2. Giải các phương trình sau:
a)
( ) ( )
2 3 5 3 0x x x− + − =
d)
2
5 6 0xx− + =
b)
( )
( )( )
2
4 2 3 2 0x x x− − − − =
e)
3 2 2
2 6 3x x x x+ = +
c)
( ) ( )
22
2 5 2xx+ = +
f)
2
11
2 8 0.xx
xx
+ + + − =
Bài 3. Giải các phương trình sau:
a)
( )( )
1 5 15
1 2 1 2x x x x
−=
+ − + −
d)
2
32
1 3 2
1 1 1
xx
x x x x
−=
− − + +
b)
2
1 5 2
2 2 4
x x x
x x x
−−
−=
+ − −
e)
( )
2
7 5 1 1
8 4 8 2 2 8 16
xx
x x x x x x
−−
+ = +
− − −
c)
2 2 2
5 5 25
5 2 10 2 50
x x x
x x x x x
+ − +
−=
− + −
f)
2 2 2
2 1 1
3 2 5 6 4 3x x x x x x
+=
+ + + + + +
Bài 4. Giải các phương trình sau:
a)
53x −=
c)
2 1 1xx+ = −
b)
5 3 16xx− = −
d)
2 1 5 2 3xx+ − − =
3/
43
Nhóm Toán THCS
Toán h󰉭
Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/
Bài 5. Giải các bất phương trình sau rồi biểu diễn tập nghiệm trên trục số:
a)
( )
2
2
3 5 4x x x− − +
f)
2
4 3 0xx− +
b)
( )( ) ( )
2
3 3 2 3x x x− + + +
g)
32
2 3 6 0x x x− + −
c)
4 5 7
35
xx−−
h)
2
0
5
x +
d)
2 1 3 5 4 1
3
2 3 4
x x x+ − +
+ −
i)
2
0
3
x
x
+
−
e)
5 3 2 1 2 3
5
5 4 2
x x x− + −
+ −
k)
1
1
3
x
x
−
−
Dạng 3: Giải bài toán bằng cách lập phương trình
Bài 1. Một người đi xe máy từ A đến B với vận tốc trung bình 40km/h. Khi quay trở về A
người đó tăng vận tốc thêm 5km/h nên thời gian về hết ít hơn thời gian đi 40 phút. Tính
quãng đường AB?
Bài 2. Lúc 6 giờ, một ô tô xuất phát từ A đến B với vận tốc trung bình 40km/h. Khi đến B,
người lái xe làm nhiệm vụ giao nhận hàng trong 30 phút rồi cho xe quay trở về A với vận
tốc trung bình 30km/h. Tính quãng đường AB, biết rằng ô tô về đến A lúc 10 giờ cùng
ngày.
Bài 3. Một người đi xe đạp từ A đến B cách nhau 24km. Một giờ sau, một người đi xe
máy từ A và đến B trước người đi xe đạp 20 phút. Tính vận tốc của mỗi xe, biết vận tốc
của xe máy gấp 3 lần vận tốc xe đạp.
Bài 4. Một ô tô đi từ A đến B cách nhau 90 km trong một thời gian nhất định. Khi đi được
1 giờ người đó dừng lại nghỉ 15 phút. Trên quãng đường còn lại người đó phải tăng vận
tốc them 10 km/h để đến B đúng dự định. Tính vận tốc ban đầu của ô tô?
Bài 5. Một người đi từ A đến B với vận tốc 9km/h. Khi đi từ B trở về A người đó chọn
đường khác dài hơn đường cũ 6km, và đi với vận tốc lớn hơn lúc đi là 3km/h nên thời
gian về ít hơn thời gian đi là 20 phút. Tính chiều dài quãng đường AB.
Bài 6. Lúc 8h30’ một người đi xe máy từ A đến B với vận tốc 40km/h, đến 10h cùng ngày
một người khác đi xe máy từ B đến A với vận tốc 60km/h. Hỏi hai người gặp nhau lúc
mấy giờ, biết rằng họ gặp nhau tại chính giữa quãng đường.
Bài 7. Hai ca nô khởi hành cùng một lúc chạy từ A đến B. Ca nô thứ nhất chạy với vận
tốc 20km/h, ca nô thứ hai chạy với vận tốc 24km/h. Trên đường đi, ca nô thứ hai dừng lại
40 phút để sửa xong vẫn đến B cùng một lúc với ca nô thứ nhất. Tính chiều dài quãng
song AB.
Bài 8. Một ca nô xuôi dòng từ bến A đến bến B hết 1 giờ 10 phút và đi ngược dòng từ B
về A hết 1 giờ 30 phút. Tính khoảng cách giữa hai bến A và B, biết vận tốc của dòng nước
là 2km/h.
4/
43
Nhóm Toán THCS
Toán h󰉭
Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/
Bài 9. Một tổ may áo theo kế hoạch mỗi ngày phải may 30 áo. Tổ đã may mỗi ngày 40 áo
nên đã hoàn thành trước thời hạn 3 ngày, ngoài ra còn may them được 20 chiếc áo nữa.
Tính số áo mà tổ đó phải may theo kế hoạch.
Bài 10. Một đội đánh cá dự định mỗi tuần đánh bắt 20 tấn cá, nhưng mỗi tuần đã vượt
mức 6 tấn nên chẳng những hoàn thành kế hoạch sớm một tuần mà còn vượt mức đánh
bắt 10 tấn. Tính mức cá đánh bắt theo kế hoạch?
Bài 11. Hai tổ sản xuất phải dệt 140 áo len. Trong thực tế tổ 1 đã vượt mức 10% kế hoạc
của mình, tổ 2 vượt mức 5 % kế hoạch của mình nên cả hai tổ đã dệt được 150 áo len. Hỏi
theo kế hoạch mỗi tổ phải dệt được bao nhiêu áo len?
Bài 12. Hai công nhân cùng làm chung một công việc dự định trong 12 giờ sẽ hoàn thành
xong công việc. Họ làm chung với nhau trong 4 giờ thì người thứ nhất chuyển đi làm việc
khác, người thứ hai phải làm nốt công việc trong 10 giờ. Hỏi nếu người thứ hai làm một
mình thì bao lâu sẽ hoàn thành xong công việc.
Bài 13. Hai vòi nước cùng chảy vào một bể thì đầy trong 3 giờ 20 phút. Người ta cho vòi
thứ nhất chảy 3 giờ và vòi thứ hai chảy 2 giờ thì được
4
5
bể. Hỏi nếu mỗi vòi chảy một
mình thì trong bao lâu mới đầy bể?
Bài 14. Hai giá sách có 450 cuốn. Nếu chuyển 50 cuốn từ giá thứ nhất sang giá thứ hai thì
số sách ở giá thứ nhất bằng
5
4
số sách ở giá thứ hai. Tính số sách ban đầu của mỗi giá.
Dạng 4: Bài tập hình học.
Bài 1. Cho góc xAy. Trên tia Ax lấy 2 điểm B và C sao cho AB = 8cm, AC = 15cm. Trên tia
Ay lấy 2 điểm D và E sao cho AD = 10cm, AE = 12cm.
a) CMR:
ABE
và
ADC
đồng dạng;
b) CMR: AB.DC = AD.BE;
c) Tính DC, biết BE = 10cm;
d) Gọi I là giao điểm của BE và CD. CMR: IB.IE =ID.IC.
Bài 2. Cho
ABC
nhọn có hai đường cao BF, CE cắt nhau tại H. Tia AH cắt BC tại D.
a) Chứng minh:
AEC
và
AFB
đồng dạng;
b) Chứng minh AE.AB = AF.AC rồi từ đó suy ra
AEF
đồng dạng với
.ACB
c) Chứng minh:
BDH
đồng dạng
BFC
và BH.BF + CH.CE = BC.
d) Vẽ
DM AB⊥
tại M,
DN AC⊥
tại N. Chứng minh MN //EF.
Bài 3. Cho tam giác ABC vuông tại B, đường cao BH. Cho AB = 15cm, BC = 20cm.
a) Chứng minh:
CHB CBA
b) Chứng minh:
2
.AB AH AC=
c) Tính độ dài AC, BH.
d) Kẻ
HK AB⊥
tại K,
HI BC⊥
tại I. Chứng minh
BKI BCA
e) Kẻ trung tuyến BM của
ABC
cắt KI tại N. Tính diện tích
.BKN
5/
43
Nhóm Toán THCS
Toán h󰉭
Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/
Bài 4. Cho hình bình hành ABCD, AC là đường chéo lớn. kẻ CE vuông góc với AB taị E,
CF vuông góc với AD tại F, BI vuông góc với AC tại I.
a) Chứng minh tam giác AIB đồng dạng với tam giác AEC.
b) Chứng minh tam giác AIE đồng dạng với tam giác ABC.
c) Chứng minh AB.AE + AF.CB =
2
.AC
d) Tia BI cắt đường thẳng CD tại Q và cắt cạnh AD tại K. Chứng minh
2
.BI IK IQ=
Bài 5. Cho hình chữ nhật ABCD có các cạnh AB = 4cm, BC = 3cm. Qua B vẽ đường thẳng
vuông góc với BD cắt DC tại E.
a) Chứng minh tam giác BDC đồng dạng với tam giác EDB, từ đó suy ra
2
.;DB DC DE=
b) Tính DB, CE;
c) Vẽ CF vuông góc với BE tại F. Gọi O là giao điểm của AC và BD. Nối OE cắt CF tại I và
cắt BC tại K. Chứng minh I là trung điểm của đoạn CF.
d) Chứng minh rằng: ba điểm D,K,F thẳng hàng.
Bài 6: Cho tam giác ABC nhọn, các đường cao BD và CE cắt nhau tại H. Đường vuông
góc AB tại B và đường vuông góc với AC tại C cắt nhau tại K. Gọi M là trung điểm của
BC. Chứng minh:
a) Chứng minh
ADB AEC
và
AED ACB
;
b) Chứng minh: HE.HC = HD.HB;
c) Chứng minh H, M, K thẳng hàng và góc AED bằng góc ACB.
d) AH cắt BC tại O. Chứng minh: BE.BA + CD.CA =
2
.BC
e) Chứng minh
1;
HO HD HE
AO BD CE
+ + =
f) Chứng minh H là giao điểm các đường phân giác của tam giác ODE.
g) Cho góc
0
45 ,ACB =
gọi P là trung điểm của DC. Từ D kẻ đường thẳng vuông góc với
BP tại I và cắt CK tại N. Tìm tỉ số diện tích của tứ giác CPIN và diện tích tam giác DCN.
h) Tam giác ABC có điều kiện gì thì tứ giác BHCK là hình thoi? Hình chữ nhật?
Bài 7. Cho tam giác ABC vuông tại A (AB < AC), đường cao AH và trung tuyến AM. Kẻ
MF vuông góc với AC tại F, FD vuông góc MC tại D. Phân giác góc C cắt FD, MF lần lượt
tại I và K. Kẻ ME vuông góc với AB tại E.
a) Chứng minh
CD CI DI
CF CK FI
==
và
IF ;KF=
b) Tứ giác AEMF là hình gì?
c) Chứng minh
AHC MFC
và AH.EB = HB.ME;
d) Chứng minh MF.AB = MF.AC;
e) Chứng minh BH.BC =
2
4.AE
6/
43
Nhóm Toán THCS
Toán h󰉭
Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/
Bài 8. Cho tam giác ABC vuông tại C (CA < CB). Lấy điểm I bất kì trên cạnh AB. Trên nửa
mặt phẳng AB chứa C, kẻ tia Ax, By cùng vuông góc với AB. Đường vuông góc với IC
cắt Ax, By lần lượt tại M và N.
a) Chứng minh tam giác CAI đồng dạng với tam giác CBN.
b) Chứng minh AB.NC = IN.CB.
c) Chứng minh góc MIN là góc vuông.
d) Tìm vị trí của điểm I để diện tích tam giác IMN gấp hai lần diện tích tam giác ABC.
Bài 9. Cho hình thang cân MNPQ (MN//PQ, MN < PQ), NP = 15cm, đường cao NI = 12cm,
QI =16cm.
a) Tính IP;
b) Chứng minh
QN NP⊥
;
c) Tính diện tích hình thang MNPQ;
d) Gọi E là trung điểm của PQ. Đường thẳng vuông góc EN tại N cắt đường thẳng PQ
tại K. Chứng minh rằng:
2
.KN KP KQ=
Bài 10. Cho tam giác nhọn ABC, H là trực tâm, G là trọng tâm, O là giao điểm các đường
trung trực của tam giác. Chứng minh rằng: H, G, O thẳng hàng và HG = 2GO.
Bài 11. Cho hình hộp chữ nhật ABCD.EFGH với AB = 12cm, BC = 9cm, AE = 10cm.
a) Tính diện tích toàn phần và thể tích của hình hộp chữ nhật ABCD.EFGH.
b) Gọi I và O lần lượt là tâm đối xứng của hình chữ nhật EFGH và ABCD. Đường thẳng
OI song song với những mặt phẳng nào?
c) Chứng tỏ rằng hình chóp I.ABCD có các cạnh bên bằng nhau nhưng không phải hình
chóp
d) Tính diện tích xung quanh của hình chóp I.ABCD.
Dạng 5: Một số bài tập nâng cao.
Bài 1. Chứng minh các bất đẳng thức sau:
1)
2 2 2
a b c ab bc ca+ + + +
2)
( )
( ) ( )
2
2 2 2
33a b c a b c ab bc ca+ + + + + +
\\
3)
( ) ( )
2
4a b c a b c+ + −
4) a)
( )
2
22
xy
xy
a b a b
+
+
+
( )
0; 0ab
b)
( )
2
2 2 2
x y z
x y z
a b c a b c
++
+ +
++
( )
0; 0; 0abc
c)
( )
( )( )
2
2 2 2 2
ax+by a b x y + +
5) Với a, b, c là các số thực thỏa mãn
6.a b c ab bc ca+ + + + + =
Chứng minh rằng
2 2 2
3.abc+ +
7/
43
Nhóm Toán THCS
Toán h󰉭
Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/
Bài 2. Cho
25
.
33
a b b a
A
a b a b
−−
=+
−+
Tính giá trị của biểu thức A, biết b > a >0 và
22
10 3 0.a b ab− + =
Bài 3. Cho x, y thỏa mãn
( ) ( )( )
2
2 2 .x y x y+ = − +
Tính giá trị biểu thức
22
.A x y=+
Bài 4. Tìm GTLN, GTNN (nếu có) của các biểu thức sau:
1)
2
6
4 4 3
A
xx
=
++
2)
2
4
64
B
xx
−
=
++
3)
2
2
33
21
xx
C
xx
−+
=
−+
(cho
1x
)
4)
( )
1
4D x x
x
= +
5)
2
12 34
2
x
Q
x
+
=
+
6)
1 2 2 3 4E x x x= − + − + − +
Bài 5. 1) Cho a > 0; b > 0; c > 0 và a + b + c = 6. Tìm GTNN của
3 3 3 3 3 3
a b b c c a
Q
ab bc ca
+ + +
= + +
2) Tìm GTNN của
22
4 600A x y xy x y= + − − + +
Bài 6. Tìm m để hai bất phương trình sau tương đương:
51
2
12 2
mx x+−
+
( )
1;
( )
( )
2
1 22 0xx+ +
(2)
8/
43
Nhóm Toán THCS
Toán h󰉭
Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/
Hướng dẫn giải:
Dạng 1:
Bài 1.
2
2 5 1
3 6 2
x
A
x x x x
+
= − +
+ + − −
Ta có:
22
6 3 2 6 ( 3) 2( 3) ( 2)( 3)x x x x x x x x x x+ − = + − − = + − + = − +
Điều kiện xác định:
2; 3xx −
a) Rút gọn biểu thức
A
Có
2 5 1
3 ( 2)( 3) 2
x
A
x x x x
+
= − −
+ − + −
( )( )
( )( ) ( )( )
( )( )
( )( )
( )( )
22
2
2 2 5 ( 3)
4 5 3 12
( 3)( 2) 3 2 3 2
34
4 3 12 4
3 2 3 2 2
x x x
x x x x
x x x x x x
xx
x x x x
x x x x x
+ − − − +
− − − − − −
= = =
+ − + − + −
+−
− + − −
= = =
+ − + − −
Vậy với
2; 3xx −
thì
4
2
x
A
x
−
=
−
.
b) Tìm
x
để
0A
Với
2; 3xx −
để
0A
=>
4
0
2
x
x
−
−
..
Kết hợp điều kiện
2; 3xx −
4
2
3
x
x
x
−
Vậy với
4
2
3
x
x
x
−
thì
0A
.
c) Tìm
x
để
A
+
.
Với
2; 3xx −
.
Ta có
4 2 2 2
1
2 2 2
xx
A
x x x
− − −
= = = −
− − −
.
Để
A
+
=>
( )
2
2 1; 2
( 2) (2)
2
2
1
2
2
2
2
1
4
4
2
x
xU
x
x
x
x
x
x
x
+
−
−

−
− =
−
−
Ta có bảng:
Vậy với
0;1x
Thì
A
+
.
2x−
2−
1−
1
2
x
0(chọn)
1(chọn)
3(loại)
4(loại)
9/
43
Nhóm Toán THCS
Toán h󰉭
Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/
Bài 2.
2
2
22
1
xx
A
x
+
=
−
2
1 2 1
3 2 2
xx
B
x x x
−+
=+
− + −
Ta có:
( )( )
( )( )
2
2
1 1 1
3 2 1 2
x x x
x x x x
− = − +
− + = − −
nên điều kiện xác định của
;AB
là
1; 2xx
.
a) Rút gọn biểu thức
;AB
.
Với
1; 2xx
, ta có:
( )( )
( )
( )( )
2
21
2 2 2
1 1 1 1 1
xx
x x x
A
x x x x x
+
+
===
− + − + −
( )( ) ( )( )
( )
( )( )
2
2
1 2 1 1 2 1
1 2 2 1 2 1 2 1
xx
x x x x x
B
x x x x x x x x
−
− + − + −
= + = = =
− − − − − − − −
b) Tính giá trị
A
khi
23x −=
.
Với
1; 2xx
, ta có:
2 3 5( )
23
2 3 1( )
x x tm
x
x x loai
− = =

− =

− = − = −

Thay
5x =
vào biểu thức
A
ta được
2.5 5
1 5 2
A
−
==
−
.
c) Tính
C A B=−
.
Với
1; 2xx
, ta có
2 2 3
1 1 1 1
x x x x x
C A B
x x x x
+
= − = − = =
− − − −
d) Tìm
x
để
C
.
Với
1; 2xx
Nếu
3.0
00
10
xC= = =
−
Vậy
0( )x tm=
.
Nếu
0x
( )
3 1 3
3 3 3
3
1 1 1 1
x
xx
C
x x x x
− − −
−
= = = = − −
− − − −
Để
( ) ( )
33
3 1 (3) 1 1; 3
11
C x U x
xx
= − − = = − = −
−−
Ta có bảng:
Vậy
2;0;4x−
thì
C
Bài 3.
a) Với
09x
2
2 1 3 11
3 3 9
x x x
A
x x x
+−
= + +
+ − −
2
2 1 3 11
3 3 9
x x x
x x x
+−
= + −
+ − −
( ) ( )( ) ( )
( )( )
2 3 1 3 3 11
33
x x x x x
xx
− + + + − −
=
+−
( )( )
22
2 6 3 3 11
33
x x x x x x
xx
− + + + − +
=
+−
( )( )
( )
( )( )
2
33
3 9 3
3 3 3 3 3
xx
x x x
x x x x x
+
+
===
+ − + − −
.
1x−
3−
1−
1
3
x
2−
(chọn)
0
(chọn)
2
(loại)
4
(chọn)
10/
43
Nhóm Toán THCS
Toán h󰉭
Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/
b) Với
09x
, ta có:
3 3 3
..
3 1 1
x x x
P A B
x x x
−
= = =
− + +
.
Ta có
( )
9 3 9
6 9. 1 3 9 0 3
2 1 2
x
P x x x x
x
= = = + + = = −
+
(thỏa mãn)
c) Với
09x
thì
3
1 1 3 1 3 1
1
x
B x x
x
−
− + −
+
(vô số nghiệm)
d)
( )
3 1 3
33
3
1 1 1
x
x
P
x x x
+−
= = = −
+ + +
.
Để
P
nguyên thì
( )
1x +
Ư
( )
3
( )
1 1; 3 0; 2;2; 4xx + − −
Bài 4.
a) Với
1x
( )
( )
( )
( )
( )
22
22
3
22
13
1 3 1 3
1 1 1
1 1 1 1
x x x x
x x x x
A
x x x
x x x x x x
+ + − − +
− + − +
= − = − =
− − −
− + + − + +
( )
( )
( )
( )
( )
2
22
21
2 2 2
1
1 1 1 1
x
x
xx
x x x x x x
−
−
===
++
− + + − + +
.
b) Với
1x
thì
( )
( )
22
2
2 2 2 2
12
2 2 2
: 1 : 1 :
1 1 1 1
x x x
x
P A B
x x x x x x x x

+ + − +

+
= − = − =



+ + + + + + + +


2
2 2 2
2 1 2 1 2
:.
1 1 1 1 1
x x x
x x x x x x x x
− + +

= = =

+ + + + + + − −

.
Để
2
1 1 1 2 3
1
P x x
x
−
−
(thỏa mãn).
Bài 5.
22
x 1 x 3x 1 2x 1
P:
x 1 x 1 1 x x 1
− + +

= − −

+ − − −

a) Điều kiện xác định:
1
x 1, x
2
−
.
( )
( )( )
( )
( )( ) ( )( )
( )( )
( )( )
( )( )
( )( )
( )( )
22
2
22
1 3 1 2 1
:
1 1 1 1
1 1 1 1
31
.
1 1 1 1 1 1 2 1
11
2 1 3 1
.
1 1 2 1
11
22
.
1 1 2 1 2 1
x x x x
P
x x x x
x x x x x
x
x x x x x x x
xx
x x x x x
x x x
xx
x x x x
− + +

= − −

+ − − −


− + + −
+
= − +

+ − + − + − +


+−
− + − − + +
=
+ − +
+−
==
+ − + +
b)
3 2 3
P
x 1 2x 1 x 1
= =
− + −
( ) ( ) ( )
5
2 x 1 3 2x 1 2x 2 6x 3 x TM
4
−
− = + − = + =
11/
43
Nhóm Toán THCS
Toán h󰉭
Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/
c)
21
1 1 2 2 1 2 1 2 2 1 <
2 1 2
P x x x x
x
+ − − − −
+
Kết hợp với điều kiện
1
x
2
<
và
1
1,
2
xx
−
−
.
Bài 6.
( )
2
2 5 50 5
2 10 2 5
x x x x
P
x x x x
+ − −
= + +
++
a) ĐKXĐ:
0, 5xx −
.
b)
( )
( )
( )
( )( )
( )
( )
2
2
2
2 5 5
2 5 50 5 50 5
2 10 2 5 2 5 2 5 2 5
x x x
xx
x x x x x
P
x x x x x x x x x x
+
+−
+ − − −
= + + = + +
+ + + + +
( ) ( )
( )( )
( )
3 2 2 3 2
15
2 2 50 50 5 4 5 1
2 5 2 5 2 5 2
x x x
x x x x x x x x
x x x x x x
−+
+ + − + − + − −
= = = =
+ + +
c)
( )
1
0 0 1 0 1
2
x
P x x TM
−
= = − = =
( ) ( )
1 1 1 3
4 1 2 4 4 2 4 6
4 2 4 2
x
P x x x x TM
−
= = − = − = = =
d)
1
0 0 1 0 1
2
x
P x x
−
−
, kết hợp với ĐK
1x
.
1
0 0 1 0 1
2
x
P x x
−
−
, kết hợp với ĐK
1x
và
0, 5xx −
.
Bài 7.
a) Rút gon
P
Với
3
1;
2
xx
, ta có:
2
2 5 2
:3
2 5 3 2 3 1
x
P
x x x x
= − +
− + − −
2 5( 1) 3(1 ) 2
:
(2 3).( 1) (2 3)(x 1) 1 1
2 (5 5) 3 3 2
:
(2 3)( 1) 1
3 5 1 1
(2 3)( 1) 3 5 2 3
x x x
x x x x x
x x x
x x x
xx
x x x x

−−

= − +


− − − − − −


− − − +
=
− − −
− + − −
= =
− − − −
b) Tính giá trị của P khi x thỏa mãn
2 1 3x −=
2 1 3x −=
2 1 3x − =
hoặc
2 1 3x− = −
hoặc
22x =−
2x=
hoặc
1x =−
Với
2x =
thì
1
1
2.2 3
P
−
= = −
−
Với
1x =−
thì
1 1 1
2.( 1) 3 5 5
P
−−
= = =
− − −
12/
43
Nhóm Toán THCS
Toán h󰉭
Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/
c) Tìm
x
để
1P
.
1 1 2 2
1 1 1 0 0
2 3 2 3 2 3
x
P
x x x
− − −
−
− − −
TH1:
2 2 0 1
3
2 3 0
2
xx
x
xx
−
−
TH2:
2 2 0 1
3
1
3
2
2 3 0
2
xx
x
xx
−
−
Vậy để P >1 thì
3
1
2
x
d) Tìm
x
nguyên để
P
nguyên
Để
1
23x
−

−
thì:
2 3 1x −=
hoặc
2 3 1x − = −
hoặc
22x =
2x=
(TMĐK) hoặc
1x =
(KTMĐK)
Vậy để
P
nguyên thì
2x =
Bài 8.
a) Rút gọn
A
2
2 3 2
12
1:
1 1 1
xx
A
x x x x x


= + −


+ − + − −


2
22
2 1 1 2
:
1 1 ( 1)( 1)
xx
x x x x

+
=−

+ − + −

22
2 2 2
2 1 1 2
:
1 ( 1)( 1) ( 1)( 1)
x x x
x x x x x

++
=−

+ + − + −

22
22
2 1 ( 1)
:
1 ( 1)( 1)
xx
x x x
+−
=
+ + −
22
22
2 1 ( 1)( 1)
1 ( 1)
x x x
xx
+ + −
=
+−
2
21
1
x
x
+
=
−
b) Tìm giá trị của
A
tại
1
2
x
−
=
Khi
1
2
x
−
=
thì
2
1
21
2
1
1
1
2
A
−

+


= = −
−

−


c) Tìm
x
để
1A
.
2 2 2
2 1 2 1 2 2
1 1 0 0 1 0 1.
1 1 1
x x x x
xx
x x x
+ + − +
− −
− − −
13/
43
Nhóm Toán THCS
Toán h󰉭
Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/
Dạng 2: Phương trình và bất phương trình
Bài 1.
a)
5 ( 6) 4(3 2 )xx− − = −
5 6 12 8xx − + = −
8 12 5 6
1
71
7
xx
xx
− + = − −
= =
Vậy phương trình có tập nghiệm
1
7
S

=


b)
2
3 4 (25 2 ) 8 300x x x x− − = + −
22
3 100 8 8 300x x x x − + = + −
101 303x − = −
3x=
Vậy phương trình có tập nghiệm S = {3}
c)
5 2 8 1 4 2
5
6 3 5
x x x+ − +
− = −
5(5 2) 10(8 1) 6(4 2) 50x x x + − − = + −
25 10 80 10 24 12 50x x x + − + = + −
58
79 58
79
xx
−
− = =
Vậy phương trình có tập nghiệm
58
79
S
−

=


d)
3 2 3 1 5
2
2 6 3
xx
x
++
− = +
9 6 3 1 12 10
5
65
6
x x x
xx
+ − − = +
−
− = =
Vậy phương trình có tập nghiệm
5
6
S
−

=


e)
2 5 8 1
7
5 6 3
x x x
x
− + −
− + = +
30 6(2 5) 5( 8) 210 10( 1)x x x x − − + + = + −
30 12 30 5 40 210 10 10x x x x − + + + = + −
13 130x=
10x=
Vậy phương trình có tập nghiệm S= {10}
f)
2( 3) 13 4
2
7 21
xx
x
−+
− + =
6 18 21 42 13 4x x x − − + = +
28 20x − = −
5
7
x=
Vậy phương trình có tập nghiệm
5
7
S

=


14/
43
Nhóm Toán THCS
Toán h󰉭
Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/
Bài 2.
a)
2 ( 3) 5( 3) 0x x x− + − =
( 3)(2 5) 0xx − + =
3
30
5
2 5 0
2
x
x
x
x
=
−=

−
+=
=
Vậy phương trình có tập nghiệm
5
3;
2
S
−

=


b)
2
( 4) ( 2)(3 2 ) 0x x x− − − − =
( 2)( 2) ( 2)(3 2 ) 0x x x x − + − − − =
2
( 2)(3 1) 0
1
3
x
xx
x
=
− − =
=
Vậy phương trình có tập nghiệm
1
2;
3
S

=


c)
22
(2 5) ( 2)xx+ = +
22
(2 5) ( 2) 0
( 3)(3 7) 0
3
30
7
3 7 0
3
xx
xx
x
x
x
x
+ − + =
+ + =
=−
+=

−
+=
=
Vậy phương trình có tập nghiệm
7
3;
3
S
−

=−


d)
2
5 6 0xx− + =
2
2 3 6 0x x x − − + =
( 2) 3( 2) 0x x x − − − =
2
( 2)( 3) 0
3
x
xx
x
=
− − =
=
Vậy phương trình có tập nghiệm
2;3 .S =
e)
3 2 2
2 6 3x x x x+ = +
2
2 ( 3) ( 3) 0x x x x + − + =
( 3)(2 1) 0x x x + − =
0
3
1
2
x
x
x
=
= −
=
Vậy phương trình có tập nghiệm
1
0; 3;
2
S

=−


15/
43
Nhóm Toán THCS
Toán h󰉭
Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/
f)
2
11
2 8 0( 0)x x x
xx
+ + + − =
Đặt
1
xa
x
+=
Khi đó phương trình trở thành:
2
2 8 0aa+ − =
2
4 2 8 0
( 4) 2( 4) 0
( 4)( 2) 0
4
2
a a a
a a a
aa
a
a
+ − − =
+ − + =
+ − =
=−
=
+Với a = -4
1
4x
x
+ = −
2
4 1 0xx + + =
2
( 2) 3x + =
3 2( )
3 2( )
x tm
x tm
=+
= − +
+Với a =2
1
2x
x
+ =
2
2 1 0xx − + =
2
( 1) 0x − =
1( )x tm=
Vậy phương trình có tập nghiệm
{ 3 1; 3 1;1}S = − + +
Bài 3. Giải PT
a)
1 5 15
1 2 ( 1)(2 )x x x x
−=
+ − + −
ĐK; x
-1; x
2
=>
2 5( 1) 15xx− − + = −
<=> x - 2 - 5x - 5 = -15
<=> -4x = -15 + 5 + 2
<=> -4x = -8
<=> x = 2 (không thoả mãn ĐK)
Vậy PT đã cho vô nghiệm.
b)
2
1 5 2
2 2 4
x x x
x x x
−−
−=
+ − −
ĐK:
2x
;
2.x −
=> (x - 1). (x - 2) - x(x + 2) = 2 - 5x
<=> x
2
- 3x + 2 - x
2
- 2x = 2 - 5x
<=> 0.x = 0
Vậy PT đã cho vô số nghiệm khác 2; -2
c)
2 2 2
5 5 25
5 2 10 2 50
x x x
x x x x x
+ − +
−=
− + −
ĐK: x
0; x
-5; x
5
16/
43
Nhóm Toán THCS
Toán h󰉭
Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/
=>
5 5 25
( 5) 2 ( 5) 2( 5)( 5)
x x x
x x x x x x
+ − +
−=
− + − +
<=> 2(x + 5)
2
-(x - 5)
2
= x.(x + 25)
<=> 2x
2
+ 20x + 50 - x
2
+ 10x - 25 = x
2
+ 25x
<=> 5x = -25
<=> x = - 5 (không thoả mãn ĐK)
Vậy PT đã cho vô nghiệm.
d)
2
32
1 3 2
1
11
xx
x
x x x
−=
−
− + +
ĐK: x
1
=> x
2
+x + 1 - 3x
2
= 2x(x - 1)
<=> -2x
2
+ x + 1 - 2x
2
+ 2x = 0
<=> 4x
2
- 3x - 1 = 0
<=> (4x + 1)(x - 1) = 0
<=>󰇩

󰇛󰇜
󰇛󰇜
Vậy PT đã cho có tập nghiệm S = {

󰇞
e)
2
7 5 1 1
8 2 ( 2) 8 16
48
xx
x x x x
xx
−−
+ = +
−−
−
ĐK: x
0; x
2
=>7(x - 2) + 2(5 - x) = 4(x - 1) + x
<=> 7x - 14+ 10 - 2x = 4x - 4 + x
<=> 0.x = 0
Vậy PT đã cho vô số nghiệm khác 0; 2
f)
2 2 2
7 1 1
3 2 5 6 4 3x x x x x x
+=
+ + + + + +
<=>
7 1 1
( 1)( 2) ( 2)( 3) ( 1)( 3)x x x x x x
+=
+ + + + + +
ĐK: x
-1; x
-2; x
-3
=> 7(x +3) + x + 1 = x + 2
<=> 7x + 21 + x + 1 - x = 2
<=> 7x = 20
<=> x =
20
7
(TMĐK)
Vậy PT đã cho có tập nghiệm S = {

󰇞
Bài 4.
a)
<=> 󰇣

󰇣
Vậy PT đã cho có tập nghiệm S = {4; 6}
17/
43
Nhóm Toán THCS
Toán h󰉭
Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/
b)

  ĐK: x

<=> 󰇣
 

󰇣


󰇣
(󰇜
Vậy PT đã cho vô nghiệm
c)

<=>󰇣


󰇣

Vậy PT đã cho có tập nghiệm S = {-2;0}
d)


= 3
Khi x

ta có: -2x - 1+ 5x - 2 = 3
<=> 3x = 6 <=> x = 2 (󰇜
Khi

< x <

ta có: 2x + 1 + 5x - 2 = 3
<=> 7x = 4
<=> x =
()
Khi x
ta có: 2x + 1 - 5x + 2 = 3
<=> -3x = 0
<=> x = 0 ()
Vậy PT đã cho vô nghiệm
Bài 5.
a)
( )
2
2
3 5 4x x x− − +
22
6 9 5 4
6 5 4 9
5
5
x x x x
xx
x
x
− + − +
− + −
− −

KL: Vậy nghiệm của bất phương trình là
5x
b)
( )( ) ( )
2
3 3 2 3x x x− + + +
22
9 4 4 3x x x − + + +
4 7 9 4xx +
KL: Vậy nghiệm của bất phương trình đã cho là
4x
c)
4 5 7
35
xx−−
( ) ( )
5. 4 5 3. 7
20 25 21 3
23 46
2
xx
xx
x
x
− −
− −


KL: Vậy nghiệm của bất phương trình đã cho là
2x
18/
43
Nhóm Toán THCS
Toán h󰉭
Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/
d)
2 1 3 5 4 1
3
2 3 4
x x x+ − +
+ −
( ) ( ) ( )
6. 2 1 3.12 4. 3 5 3. 4 1
12 6 36 12 20 12 3
12 20 12 12 3 6 36
44 33
3
4
x x x
x x x
x x x
x
x
+ + − − +
+ + − − −
+ + − − −
−
−

KL: Vậy nghiệm của bất phương trình là
3
4
x
−
e)
5 3 2 1 2 3
5
5 4 2
x x x− + −
+ −
( ) ( ) ( )
4. 5 3 5. 2 1 10. 2 3 100
20 12 10 5 20 30 100
20 10 30 20 100 12 5
60 73
73
60
x x x
x x x
x x x
x
x
− + + − −
− + + − −
+ + − + −
−
−

KL: Vậy nghiệm của bất phương trình là
73
60
x
−
f)
2
4 3 0xx− +
( ) ( )
( )( )
2
3 3 0
. 1 3. 1 0
1 3 0
1 0 1
3 0 3
3
1
1 0 1
3 0 3
x x x
x x x
xx
xx
xx
x
x
xx
xx
− − +
− − −
− −
−



−



−



−



KL: Vậy nghiệm của bất phương trình là
3x
hoặc
1x
g)
32
2 3 6 0x x x− + −
( )
( )
( ) ( )
( )
( )
32
2
2
2 3 6 0
. 2 3. 2 0
2 3 0
x x x
x x x
xx
− + −
− + −
− +
( )
2x −
và
( )
2
3x +
phải cùng dấu, mà
( )
2
30xx+
2 0 2xx −
KL: Vậy nghiệm của bất phương trình là
2x
19/
43
Nhóm Toán THCS
Toán h󰉭
Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/
h)
2
0 2 0 2
5
x
xx
+
+ −
KL: Vây nghiệm của bất phương trình là
2x −
i)
2
0
3
x
x
+
−
2 0 2
23
3 0 3
2 0 2
(KTM)
3 0 3
xx
x
xx
xx
xx
+ −

−


−




+ −



−



KL: Vậy nghiệm của bất phương trình là
23x−
1
)1
3
1 1 3 1 3 2
1 0 0 0 0
3 3 3 3 3
x
k
x
x x x x x
x x x x x
−
−
− − − − − +
− −
− − − − −
2 và
3x−
phải cùng dấu
Mà 2>0 nên
3 0 3xx−
KL: Vậy nghiệm của bất phương trình là
3x
Dạng 3: Giải bài toán bằng cách lập phương trình
Bài 1.
Gọi thời gian người đó đi xe máy từ
A
đến
B
là
x
(giờ)
( 0)x
.
+) Thời gian về ít hơn thời gian đi
40
phút (
40
phút
2
3
=
giờ) nên thời gian về là:
2
x
3
−
(giờ)
+) Lúc đi từ
A
đến
B
xe đi với vận tốc trung bình
40 /km h
nên quãng đường
AB
dài là:
40x
(km)
+) Lúc đi từ
B
về
A
, xe tăng vận tốc thêm
5km/ h
nên quãng đường
AB
dài là:
2
45 (km)
x
3

−


Ta có phương trình:
2
40 45 6
3
xx
x

= =
−


(TMĐK)
Vậy quãng đường AB dài là
40.6 240(km)=
Bài 2. Đổi
30
phút
1
2
=
giờ.
Gọi thời gian ô tô đi từ
A
đến
B
là
x
(giờ)
( 0)x
.
+) Thời gian ô tô đi từ
A
đến
B
rồi trở về A (không kể thời gian giao hàng) là:
10
giờ
6−
giờ
1
2
−
giờ
7
2
=
giờ. => Thời gian ô tô đi từ
B
về
A
là:
7
2
x−
(giờ)
+) Ô tô đi từ
A
đến
B
với vận tốc
40km / h
nên quãng đường AB dài là:
40 ( )x km
20/
43
Nhóm Toán THCS
Toán h󰉭
Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/
+) Ô tô đi từ B về A với vận tốc
30km / h
nên quãng đường AB dài là:
7
30( )( )
2
x km−
Ta có phương trình:
73
40x 30( x) 70x 105 x
22
= − = =
(TMĐK)
Vậy quãng đường AB dài là:
3
40. 60( )
2
km=
.
Bài 3.
Gọi vận tốc của xe đạp là x (km/h), x > 0
Vận tốc của xe máy gấp 3 lần vận tốc của xe đạp
Vận tốc của xe máy là 3x (km/h)
Quãng đường AB dài 24 km
Thời gian xe máy đi từ A đến B là
24 8
3xx
=
(km/h)
Thời gian xe đạp đi từ A đến B là
24
x
(km/h)
Xe máy đi sau xe đạp 1 giờ và đến B trước xe đạp 20 phút =
1
3
giờ, ta có phương trình
24 8 1 16 4
1 12( )
33
x tm
x x x
− = + = =
Vận tốc của xe máy là 12.3 = 36 (km/h)
Vậy vận tôc của xe đạp là 12 km/h, vận tốc của xe máy là 36 km/h
Bài 4.
Gọi vận tốc ban đầu của ô tô là x (km/h), x > 0
Quãng đường AB dài 90km
Thời gian dự định ô tô đi từ A đến B là
90
x
(km/h)
Sau 1 giờ, ô tô đi được 1x = x (km/h)
Quãng đường còn lại của ô tô sau khi đi được 1 giờ là 90 – x (km)
Vận tốc của ô tô tăng thêm 10 km/h
Vận tốc của ô tô đi trên quãng đường còn lại là x + 10 (km/h)
Thời gian ô tô đi trên quãng đường còn lại là
90
10
x
x
−
+
(giờ)
Ô tô nghỉ 15 phút =
1
4
giờ và đến B đúng dự định
Ta có phương trình:
2
90( )
90 1 90 90 5 90 90 410
1 50 3600 0
40( )
4 10 4 10 4( 10)
x ktm
x x x
xx
x tm
x x x x x x
=−
− − +
= + + = + = + − =
=
+ + +
Vậy vận tốc dự định của ô tô là 40 km/h
21/
43
Nhóm Toán THCS
Toán h󰉭
Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/
Bài 5.
Gọi chiều dài quãng đường AB là:
x
( 0, )x km
. Thời gian đi từ A đến B là:
9
x
(giờ).
Quãng đường người đó đi từ B về A dài là:
6x+
(km).
Vận tốc người đó đi từ B về A là:
9 3 12+=
(km/h). Thời gian đi từ B về A là:
6
12
x +
(giờ).
Vì thời gian về ít hơn thời gian đi 20 phút
1
3
h

=


nên ta có phương trình:
61
4x 3x 18 12 30( d )
9 12 3
xx
x tm k
+
− = − − = =
Vậy quãng đường AB dài 30km.
Bài 6.
Từ 8h30’ đến 10h là 1h30’
3
2
=
h.
Quãng đường người đi từ A – B đã đi được trong 1h30’ là:
3
40. 60
2
=
(km)
Gọi thời gian xe đi từ B về A đến chỗ gặp là:
x
( 0)x
(giờ)
Quãng đường xe đi từ B về A đến chỗ gặp là:
60x
(km)
Quãng đưỡng xe đi từ A đến B đến chỗ gặp là:
60 40x+
(km)
Vì hai xe gặp nhau ở chính giữa quãng đường AB nên ta có phương trình:
60x 40x 60 20x 60 3( d )x tm k= + = =
Vậy hai xe gặp nhau lúc:
10 3 13h h h+=
.
Bài 7.
Gọi chiều dài quãng đường AB là
x
(km,
0x
).
Thời gian ca nô thứ nhất đi từ A đến B là:
20
x
(giờ).
Thời gian ca nô thứ hai đi từ A đến B là:
24
x
(giờ).
Do ca nô thứ hai nghỉ 40 phút =
2
3
giờ nên ta có phương trình:
2
24 3 20
xx
+=
40x =
(thỏa)
Vậy quãng đường AB dài 40 km.
Bài 8.
Gọi vận tốc riêng của ca nô là:
x
(km/giờ,
0x
).
Vận tốc của ca nô khi đi xuôi dòng là:
2x+
(km/giờ).
Vận tốc của ca nô khi đi ngược dòng là:
2x−
(km/giờ).
Ta có:
7
1 10'
6
3
1 30'
2
hh
hh
=
=
22/
43
Nhóm Toán THCS
Toán h󰉭
Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/
Theo đề bài ta có phương trình:
73
(x 2). ( 2).
62
x+ = −
16x =
(thỏa mãn ĐK)
Do đó quãng đường AB bằng:
77
( 2). (16 2). 21
66
x + = + =
(km)
Vậy quãng đường AB dài 21 km.
Bài 9.
Gọi số áo mà tổ đó phải may theo kế hoạc là
x
(áo)
*
(x )N
Số áo mà tổ đó đã may trên thực tế là:
20x +
(áo)
Thời gian tổ đó phải may theo kế hoạch là:
30
x
(ngày)
Thời gian thực tế tổ đó đã may là:
2
40
x +
(ngày)
Theo bài ra, ta có phương trình:
20
3
30 40
xx+
−=
4 3( 20) 360
120 120 120
xx+
− =
4 3( 20) 360xx − + =
4 3 60 360xx − − =
420x=
(thỏa mãn)
Vậy số áo mà tổ đó phải may theo kế hoạch là 420 áo.
Bài 10.
Gọi số cá đội đánh cá phải đánh bắt theo kế hoạch là
x
(tấn)
( 0)x
Số cá đội đánh cá đã đánh bắt trên thực tế là
10x+
(tấn)
Thời gian đội đánh cá phải đánh bắt theo kế hoạch là:
20
x
(tuần)
Thời gian thực tế đội đánh cá đã đánh bắt là:
10 10
20 6 26
xx++
=
+
(tuần)
Theo bài ra, ta có phương trình:
10
1
20 26
xx+
−=
13 10( 10) 260
260 260 260
xx+
− =
13 10( 10) 260xx − + =
13 10 100 260xx − − =
3 360x=
120x=
(thỏa mãn)
Vậy số cá đội đánh cá phải đánh bắt theo kế hoạch là 120 (tấn)
23/
43
Nhóm Toán THCS
Toán h󰉭
Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/
Bài 11.
Gọi số áo len tổ 1 phải dệt theo kế hoạch là
x
(áo)
*
(x )N
Số áo len tổ 2 phải dệt theo kế hoạch là
140 x−
(áo)
Thực tế, tổ 1 đã dệt được
10 110
10%
100 100
x x x x x+ = + =
(áo)
Thực tế, tổ 2 đã dệt được
5 105
(140 ) (140 ) (140 )
100 100
x x x− + − = −
(áo)
Theo bài ra, ta có phương trình:
110 105
(140 ) 150
100 100
xx+ − =
110 105(140 ) 15000xx + − =
110 14700 105 15000xx + − =
5 300x=
60x=
(thỏa mãn)
Vậy theo kế hoạch số áo len tổ 1 phải dệt là 60 (áo)
Theo kế hoạch số áo len tổ 2 phải dệt là
140 60 80−=
(áo)
Bài 12.
Gọi thời gian người thứ hai làm một mình hoàn thành xong công việc là
x
(giờ)
(x>12)
1giờ, người thứ hai làm được
1
x
(công việc)
Vì hai công nhân cùng làm chung một công việc dự định trong 12 giờ sẽ hoàn thành xong
công việc nên 1giờ hai người làm chung được
1
12
(công việc)
4 giờ đầu hai người làm chung được
11
4
12 3
=
(công việc)
10 giờ sau người thứ hai làm được
1 10
10
xx
=
(công việc)
Theo bài ra, ta có phương trình:
10 2
3x
=
10.3
15
2
x = =
(thỏa mãn)
Vậy nếu người thứ hai làm một mình thì 15 giờ sẽ hoàn thành xong công việc.
Bài 13. Ta có: 3 giờ 20 phút =
10
3
giờ
Gọi thời gian vòi thứ nhất chảy một mình đầy bể là
x
( giờ) (
0x
).
Trong một giờ vòi thứ nhất chảy được
1
x
(bể).
Trong một giờ cả hai vòi chảy được
10 3
1:
3 10
=
(bể), vậy trong một giờ vòi hai chảy một
mình được:
31
10 x
−
(bể).
24/
43
Nhóm Toán THCS
Toán h󰉭
Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/
Khi vòi thứ nhất chảy 3 giờ và vòi thứ hai chảy 2 giờ thì được
4
5
bể, ta có phương trình
sau:
1 3 1 4 1 3 4
3. 2.
10 5 5 5x x x

+ − = + =


5x=
(TMĐK)
Vậy vòi một chảy một mình trong 5(giờ) thì đầy bể.
Trong một giờ vòi hai chảy một mình được:
3 1 1
10 5 10
−=
(bể).
Vậy vòi hai chảy một mình trong 10 giờ thì đầy bể.
Bài 14.
Gọi số cuốn sách ban đầu ở giá thứ nhất là
x
(cuốn) (
*xN
) thì số cuốn sách ở giá thứ
hai ban đầu là
450 x−
(cuốn).
Số cuốn sách lúc sau ở giá thứ nhất là
50x −
(cuốn).
Số cuốn sách lúc sau ở giá thứ hai là
450 50 500xx− + = −
(cuốn).
Vì nếu chuyển 50 cuốn từ giá thứ nhất sang giá thứ hai thì số sách ở giá thứ nhất bằng
5
4
số sách ở giá thứ hai nên ta có phương trình:
( )
5
50 500
4
xx− = −
5
50 625
4
xx − = −
9
675 300
4
xx = =
(TMĐK).
Vậy số sách ở giá thứ nhất ban đầu là 300 cuốn. Số sách ở giá thứ hai ban đầu là 150 cuốn.
Dạng 4: Các bài tập hình học.
Bài 1.
a) CMR
ABE ADC
Xét
ABE
và
ADC
ADC có:
A
chung
82
12 3
10 2
15 3
AB
AE
AD
AC
==
==
2
3
AB AD
AE AC
= =
Vậy
ABE ADC
(c-g-c)
b) CMR
..AB DC AD BE=
Vì
ABE ADC
(theo câu a)
..
AB BE
AB DC AD BE
AD DC
= =
(đpcm).
c) Tính
DC
biết
10 .BE cm=
Ta có
AB BE
AD DC
=
( )
8 10
12,5
10
DC cm
DC
= =
y
x
12
10
15
8
I
A
C
E
B
D
25/
43
Nhóm Toán THCS
Toán h󰉭
Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/
d) CMR
..IB IE ID IC=
Xét
IBC
và
IDE
Ta có
BIC DIE=
(đối đỉnh)
BCI IED=
(vì
ABE ADC
)
Suy ra
IBC IDE
(g-g)
..
IB IC
IB IE ID IC
ID IE
= =
Vậy
..IB IE ID IC=
(đpcm).
Bài 2.
a) Chứng minh:
AEC AFB
- Xét
AEC
và
AFB
:
+
A
chung
+
( ) 90
90
( ) 90
CE AB gt CEA
CEA BFA
BF AC gt BFA
⊥ =
= =
⊥ =
AEC AFB
(gg)
b) Chứng minh:
..AE AB AF AC=
rồi từ đó suy ra
AEF ACB
- Ta có
AEC AFB
AE AC
AF AB
=
(cạnh tương ứng tỉ lệ)
..AE AB AF AC=
- Xét
AEF
và
ACB
:
+
A
chung
+
..AE AB AF AC=
(cmt)
AE AF
AC AB
=
AEF ACB
(c.g.c)
c) Chứng minh:
BDH BFC
và
2
..BH BF CH CE BC+=
- Xét
ABC
+ BF và CE là đường cao (gt)
+ BF và CE cắt nhau tại H
H là trực tâm của
ABC
(đ/l 3 đường cao trong tam giác)
AH là đương cao
AD là đường cao
AD BC⊥
- Xét
BDH
và
BFC
+
90BDH BFC= =
( )
;BF AC AD BC⊥⊥
+
B
chung
BDH BFC
(gg)
BH BD
BC BF
=
(cạnh tương ứng tỉ lệ)
..BH BF BD BC=
(1)
N
M
D
E
F
H
B
A
C
26/
43
Nhóm Toán THCS
Toán h󰉭
Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/
- Xét
CHD
và
CBE
+
90CEB DHC= =
( )
;CE AB AD BC⊥⊥
+
B
chung
CHD CBE
(gg)
CH CD
CB CE
=
(cạnh tương ứng)
..CH CE CDCB=
(2)
- Từ (1) và (2) ta có:
( )
2
. . . . .BH BF CH CE BD BC CD BC BC BD CD BC BC BC+ = + = + = =
Vậy
2
..BH BF CH CE BC+=
.
d) Vẽ
DM AB⊥
tại
M
,
DN AC⊥
tại
N
. Chứng minh
//MN EF
- Ta có:
( )
( )
)
/ / / /
CE AB gt
CE MD HE MD
MD AB gt
+⊥

⊥
(định lí từ vuông góc đến song song)
( )
( )
)
/ / / /
BF AC gt
BF DN HF DN
ND AC gt
+⊥

⊥
- Xét
AEH
và
AMD
:
//HE MD
(cmt)
AEH AMD
(định lí Talet)
AE AH
AM AD
=
(cạnh tương ứng tỉ lệ)
- Xét
AFH
và
AND
:
//HF DN
(cmt)
AFH AND
(định lí Talet)
AF AH
AN AD
=
(cạnh tương ứng tỉ lệ)
- Vậy
;
AF AH AE AH
AN AD AM AD
==
thì
AF AE
AN AM
=
//EF MN
( định lí Talet đảo)
Bài 3.
a) Chứng minh
CHB CBA
.
+ Ta có
BH AC⊥
(gt) nên
BHC
vuông tại
H
.
+ Xét
CHB
và
CBA
ta có:
0
CHB CBA 90==
Chung
C
CHB CBA(g g) −
.
b) Chứng minh
2
AB AH.AC=
.
Xét
BHA
và
CBA
ta có:
0
AHB ABC 90==
A
chung
BHA CBA(g g) −
AB AH
AC AB
=
(cặp cạnh tương ứng)
2
AB AH.AC=
(đpcm).
O
N
M
I
K
H
A
C
B
27/
43
Nhóm Toán THCS
Toán h󰉭
Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/
c) Tính độ dài
AC,BH
.
- Áp dụng định lý Py-ta-go vào
ABC
vuông tại
B
ta có:
2 2 2 2 2
AC AB BC 15 20 625= + = + =
AC 25cm=
- Ta có:
2
AB AH.AC=
(chứng minh trên)
22
AB 15
AH 9cm
AC 25
= = =
- Theo ý a) và ý b), ta có:
CHB CBA
và
BHA CBA
nên:
CHB BHA
BH BC
AH AB
=
BC.AH 20.9
BH 12cm
AB 15
= = =
.
d) Chứng minh
BKI BCA
.
- Ta có:
CHB BHA
(chứng minh trên)
BCH ABH (1)=
- Tứ giác
BKHI
có:
0
B K I 90= = =
nên là hình chữ nhật.
KI BH=
(tính chất hình chữ nhật)
Gọi
O
là giao điểm của hai đường chéo
BH
và
IK
OB OK=
BOK
cân tại
O
BKI KBH (2)=
Từ
(1),(2) BKI BCH=
- Xét
BKI
và
BCA
có:
BKI BCH=
Chung
B
BKI BCA(g.g)
.
e) Tính diện tích
BKN
.
– Ta có:
BM
là trung tuyến của
ABC
vuông tại
B
nên:
BM AM=
AMB
cân tại
M
BAC ABM=
Mà:
BKI BCH=
(cmt) và:
0
BAC BCH 90+=
0
BKI ABM 90 + =
(cmt)
Suy ra:
BKN
vuông tại
N
.
- Ta có: +
KI BH 12cm==
+
BK KI
BKI BCA
BC CA
=
BC.KI 20.12
BK 9,6cm
CA 25
= = =
28/
43
Nhóm Toán THCS
Toán h󰉭
Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/
- Xét
BKN
và
BCA
có:
0
BNK ABC 90==
BKN BCA=
(cmt)
BKN ACB
(g.g)
22
BKN
ACB
S
BK 9,6 92,16
S AC 25 625
= = =
Mà:
2
ACB
11
S BA.BC .15.20 150cm
22
= = =
2
BKN ACB
92,16 92,16
S .S .150 22,1184cm
625 625
= = =
.
Bài 4.
a) Chứng minh
AIB
∽
AEC
Xét
AIB
và
AEC
có:
A
là góc chung.
0
90AIB AEC==
Do đó:
AIB
AEC
(g.g)
b) Chứng minh
AIE
ABC
Do
AIB
∽
AEC
AI AB
AE AC
=
AI AE
AB AC
=
Xét
AIE
và
ABC
có:
A
là góc chung.
AI AE
AB AC
=
Do đó:
AIE
∽
ABC
(c.g.c)
c) Chứng minh:
2
AB.AE AF.CB AC+=
Ta có:
AI AE
AB.AE AC.AI (1)
AB AC
= =
Xét
AFC
và
CIB
có:
FAC ICB=
(so le trong).
0
AFC CIB 90==
Do đó:
AFC
∽
CIB
(g.g)
AF AC
CI CB
=
AF
AF. . (2)
CI
CB AC CI
AC CB
= =
Từ (1) và (2)
2
. AF. . . .( )AB AE CB AC AI AC CI AC AI CI AC + = + = + =
F
Q
I
E
C
A
K
D
B
29/
43
Nhóm Toán THCS
Toán h󰉭
Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/
d) Chứng minh:
2
.BI IK IQ=
Xét tam giác ABI có:
/ / (3)
IQ IC
AB QC
IB IA
=
(Theo hệ quả định lí Ta-let)
Xét tam giác BIC có:
/ / (4)
IC IB
BC AK
IA IK
=
(Theo hệ quả định lí Ta-let)
Từ (3) và (4)
IQ IB
IB.IB IK.IQ
IB IK
= =
Vậy
2
BI IK.IQ=
(đpcm)
Bài 5.
a) Chứng minh rằng:
BDC
đồng dạng với
EDB
từ đó suy ra
2
BD DC.DE=
.
Xét
BDC
và
EDB
có:
BDC
chung
BCD DBE 90= =
=>
BDC
đồng dạng với
EDB
(g.g)
=>
BD DC
DE BD
=
=>
2
BD DC.DE=
b) Tính
DB,CE
.
Ta có:
DCB
vuông tại
C
=>
222
BD BC DC=+
=>
( )
BD 5 cm=
Ta có
2
BD DC.DE=
=>
( )
2
BD 25
DE cm
DC 4
==
Mà
DE DC CE=+
=>
( )
25 9
CE DE DC 4 cm
44
= − = − =
c) Chứng minh được
CE BD
Xét
EBO
có:
IF BO
=>
IF EI
BO EO
=
(hệ quả định lý Talet)
Xét
EDO
có:
IC DO
=>
IC EI
DO EO
=
(hệ quả định lý Talet)
=>
IF IC
BO DO
=
Mà
BO DO=
(
ABCD
là hình chữ nhật) =>
IF IC=
=>
I
là trung điểm của đoạn
CF
.
d) Chứng minh rằng ba điểm
D,K,F
thẳng hàng.
Xét
BOK
có
CI BO
=>
IK CI
OK OB
=
(hệ quả đl Talet)
K
I
O
F
E
C
D
A
B
30/
43
Nhóm Toán THCS
Toán h󰉭
Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/
Mà
IC IF;OD OB==
=>
OK OD
IK IF
=
Xét
KOD
và
KIF
có:
( )
OK OD
DOK FIK BD CF ;
IK IF
==
=>
KOD
đồng dạng
KIF
(c.g.c)
=>
OKD IKF=
=>
OKD DKE IKF DKE+ = +
=>
DKF 180=
=>
D,K,F
thẳng hàng.
Bài 6.
a) Chứng minh
ADB AEC
và
AED ACB
- Xét
ADB
và
AEC
, có:
BAD
chung
0
90BDA CEA==
ADB AEC
(g-g)
-Vì
ADB AEC
(chứng minh trên)
AD AB AD AE
AE AC AB AC
= =
- Xét
AED
và
ACB
, có
BAD
chung
AD AE
AB AC
=
(chứng minh trên)
AED ACB
(c-g-c)
b) Chứng minh:
..HE HC HD HB=
- Xét
BHE
và
CHD
, có
BHE CHD=
(đối đỉnh)
0
90BEH CDH==
( )
BHE CHD g g −
HB HE
HC HD
=
(tính chất)
..HE HC HD HB=
c) Chứng minh:
,,H M K
thẳng hàng và
AED ACB=
- Ta có
( )
( )
//
BD AC gt
BD CK
CK AC gt
⊥
⊥
hay
( )
/ / 1BH CK
(từ
⊥
đến //)
- Ta có
( )
( )
/ / B
CE AB gt
CE K
BK AB gt
⊥
⊥
hay
( )
/ / B 2CH K
(từ đến //)
31/
43
Nhóm Toán THCS
Toán h󰉭
Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/
- Từ
( )
1
và
( )
2
BHCK
là hình bình hanh
BC
và
HK
cắt nhau tại trung điểm mỗi đường
Mà M là trung điểm của BC
M cũng là trung điểm của HK
Hay H, M, K thẳng hàng
d) AH cắt BC tại O. Chứng minh
2
..BE BA CDCA BC+=
- Xét
BAO
và
BCE
, có
ABC
chung
0
90BEC AOB==
( ) ( ) ( )
. / . . 3
BA BO
BAO BCE g g t c BA BE BO BC
BC BE
= =
Chứng minh tương tự ta có:
( ) ( )
. . 4
CD CB
CDB COA g g CD CA BC CO
CO CA
− = =
Từ
( )
3
và
( )
4
( )
. . . . . .BE BA CD CA BC BO BC CO BC BO CO BC BC + = + = + =
2
..BE BA CDCA BC + =
(đpcm).
e) Chứng minh:
1
HO HD HE
AO BD CE
+ + =
- Ta có:
1
1
.
.
2
2
1
1
.
.
2
2
BHC
BHC
ABC
ABC
S HO BC
HO BC
S
HO
S AO
AO BC
S AO BC
=
= =
=
- CMTT:
1
.AC
2
1
BD.AC
2
AHC
ABC
HD
S
HD
S BD
==
Suy ra
1
.AB
2
1
CE.AB
2
AHB
ABC
HE
S
HE
S CE
==
( )
1
BHC AHC BHC AHC AHB ABC
AHB
ABC ABC ABC ABC ABC
S S S S S S
S
HO HD HE
AO BD CE S S S S S
HO HD HE
dpcm
AO BD CE
++
+ + = + + = =
+ + =
f) Chứng minh H là giao điểm của đường phân giác của tam giác
ODE
- Ta có
( )
AED ACB cmt AED ACB =
(2 góc tương ứng)..
- Do
( )
..
BE BO
BA BE BO BC cmt
BC BA
= =
32/
43
Nhóm Toán THCS
Toán h󰉭
Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/
-Xét
BEO
và
BCA
, có:
ABC
chung
( )
BE BO
cmt
BC BA
=
( ) ( )
.6BEO BCA g g BEO ACB =
Từ
( )
5
và
( )
6 AED BEO=
Ta có:
0
0
90
90
AED DEC
DEC OEC
BEO OEC
+=
=
+=
EH
là phân giác của
DOE
CMTT:
OH
là phân giác của
EOD
Vậy H là giao điểm của đường phân giác của tam giác
ODE
g) Cho góc
0
45ACB =
, Gọi P là trung điểm của DC. Từ D kẻ đường thẳng vuông góc với
BP tại I và cắt CK tại N. Tìm tỉ số diện tích của tứ giác CPIN và diện tích tam giác DCN
- Xét
vDIP
và
vDCN
, có:
Có
PDI
chung
( )
vDIP vDCN g g −
22
11
.
24
DIP
DCN
S
DP
S DC
= = =
Ta có:
13
1 1 .
44
CPIN DCN DIP
DIP
DCN DCN DCN
S S S
S
S S S

−
= = − = − =
Vậy tỉ số diện tích của tứ giác CPIN và diện tích tam giác DCN bằng
3
4
.
h) Tam giác ABC có điều kiện gì thì tứ giác BHCK là hình thoi? Hình chữ nhật?
- Giả sử BHCK là hình thoi
HBC HCB=
mà
ADB AEC ABD ACE =
HBC ABD HCB ACE + = +
ABC ACB=
ABC
cân tại A
Vậy
ABC
cân tại A thì BHCK là hình thoi
- Giả sử BHCK là hình chữ nhật
00
90 90BHC EHD = =
Xét tứ giác:
AEHD
, có
0 0 0
90 , 90 , 90EHD AEH ADH= = =
AEHD
là hình chữ nhật
0
90BAC=
ABC
vuông tại A
Vậy
ABC
vuông tại A thì BHCK là hình thoi.
33/
43
Nhóm Toán THCS
Toán h󰉭
Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/
Bài 7.
a) Xét  và  có:





(vì CK là tia phân giác góc
FCM)
Do đó   (g.g)




󰇛󰇜
Xét có CI là đường phân giác của góc
ACB nên theo tính chất đường phân giác
trong tam giác ta có:




󰇛󰇜
Từ (1) và (2) suy ra






Vì   nên 

, mà 

. Do đó 

 cân tại F FI = FK.
b) Tứ giác AEMF có 

(Vì 󰥚)


(Vì  vuông tại A); 

(Vì 󰥚)
Do đó tứ giác AEMF là hình chữ nhật.
c) Xét  và  có:

chung; 


Do đó   (g.g)
Xét  và  có:
chung; 


Do đó   (g.g)





d) Vì   nên




  (3)
Vì   nên




  (4)
Vì AM là đường trung tuyến của  nên M là trung điểm của BC
 (5)
Từ (3), (4), (5)  
e) Xét  có M là trung điểm của BC;   (Vì cùng vuông góc với AB).
M là trung điểm của AB.
  (6).
Xét  có:
chung; 


Do đó 󰇛󰇜





 (7)
Từ (6), (7) 
󰇛

󰇜
hay 
34/
43
Nhóm Toán THCS
Toán h󰉭
Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/
Bài 8.
a) Chứng minh
NCAI CB
Ta có
0
ACI ICB 90 (do ABC+ =
vuông tại
C
)
0
90 (doCI MN)ICB BCN+ = ⊥
Nên
(1)ACI BCN=
Ta lại có
0
90 (doCAB CBA ABC+ =
vuông tại
C
)
0
90 (do )CBA CBN By AB+ = ⊥
Nên
(2)CAB CBN=
Từ (1) và (2) suy ra
N (g.g)CBCAI
b) Chứng minh
..AB NC NI CB=
.
Xét
CAB
và
CIN
, ta có:
0
90
(do N)
ACB ICN
CA CI
CAI
CB CN
CB
==
=
Suy ra
N (c.g.c)CAB CI
AB CB
IN CN
=
Vậy
..AB NC NI CB=
c) Chứng minh góc
MIN
là góc vuông.
Ta có
N (cmt)CICAB
N CAB CI
CIM MAC
Mà
0
=90MACCAB+
0
=90CIMCIN+
Hay góc
MIN
là góc vuông
d) Tìm vị trí của điểm
I
để diện tích
IMN
gấp hai lần diện tích tam giác
ABC
.
1
.
2
ABC
S CACB
=
11
..
22
IMN
S IM IN IC MN
==
..
..
IMN
ABC
S
IM IN IC MN
S CACB CACB
= =
2.
IMN ABC
SS

=
. 2 .IM IN CACB=
Suy ra I là trung điểm AB.
y
x
N
M
C
B
A
I
35/
43
Nhóm Toán THCS
Toán h󰉭
Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/
Bài 9.
a) Tính
IP
.
Xt
NIP
có
0
90NIP =
(NI là đường cao):
2 2 2
NP NI IP=+
(Định l Py – ta – go)
222
2
15 12
225 144 81
9( )
IP
IP
IP cm
= +
= − =
=
b) Chứng minh
QN NP⊥
Có
16 9 25( )QP QI IP cm= + = + =
Xt
QNI
có
0
90QIN =
(NI là đường cao):
2 2 2
NQ NI IQ=+
(Định l Py – ta – go)
2 2 2
2
12 16
144 256 400
20( )
QN
QN
QN cm
= +
= + =
=
Xt
QNP
có:
2 2 2 2 2 2
(25 20 15 )QP QN NP= + = +
QNP
vuông tại N
QN NP⊥
c) Tính diện tích hình thang
MNPQ
Kẻ
MH QP⊥
Có
25 9 9 7( )IH QP QH IP cm= − − = − − =
Xt
QMH
và
PNI
có:
MQ NP=
(
MNPQ
là hình thang cân)
0
( 90 )MHQ NIP==
MQH NPI=
(
MNPQ
là hình thang cân)
(ch gn)QMH PNI = −
9QH IP cm = =
(2 cạnh tương ứng)
Xt tứ giác
MNIH
có
/ / ; / / ( )MN IH MH NI QP⊥
tứ giác
MNIH
là hình bình hành
7( )MN IH cm = =
2
( ). (7 25).12
192( )
22
MNPQ
MN QP NI
S cm
++
= = =
d) Gọi
E
là trung điểm của
PQ
. Đường thẳng vuông góc với
EN
tại
N
cắt
PQ
tại
K
.
Chứng minh rằng
2
.KN KP KQ=
.
Xt
QNP
vuông tại
N
(cmt) có
E
là trung điểm của
QP
2
1
H
E
I
M
Q
N
P
K
36/
43
Nhóm Toán THCS
Toán h󰉭
Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/
1
2
NE QE PE QP = = =
(tính chất đường trung tuyến trong tam giác vuông)
QNE
cân tại
E
1
EQN N=
(tính chất tam giác cân)
( )
1
Mặt khác,
0
1
12
0
2
90
90
N ENP
NN
N ENP
+=
=
+=
( )
2
Từ
( )
1
và
( )
2
2
EQN N=
Xt
KNQ
và
KPN
có:
K
chung
2
EQN N=
( . )KNQ KPN g g 
KN KQ
KP KN
=
2
.KN KP KQ=
(đpcm).
Bài 10:
* Ta có AH // OM (cùng vuông góc với BC)
MN // AB (chứng minh được MN là đường
trung bình của
ABC
)
BAH OMN=
(góc có cạnh tương ứng song song)
* Chứng minh tương tự ta được
ABH ONM=
* Xét
ABH
và
MNO
có
BAH OMN=
;
ABH ONM=
nên
ABH
đồng dạng với
MNO
AH AB
OM MN
=
, mà
2
AB
MN
=
( tc đường trung bình MN)
2
AH
OM
=
* Gọi giao điểm của HO với AM là G’, ta sẽ chứng minh G’ trùng với G.
- Thật vậy ta có
''HAG G MO=
(AH //OM);
'H 'AG MG O=
( đối đỉnh) nên
'AHG
đồng
dạng với
'MOG
=>
''
2
''
AG AH HG
G M OM G O
= = =
=> G’ là trọng tâm
ABC
, hay
'GG
G’. Khi đó có H, G, O thẳng hàng và HG = 2 GO
Bài 11.
a) Tính diện tích toàn phần và thể tích của hình hộp chữ
nhật.
Diện tích toàn phần của hình hộp chữ nhật là:
( )
( )
2
2. 12 9 .2.10 2.12.9 636 .
tp xq d
S S S cm= + = + + =
Thể tích hình hộp chữ nhật là:
( )
3
. . 12.9.10 1080 .V AB AD AE cm= = =
G'
O
H
N
M
B'
A'
A
B
C
12
9
10
AB cm
BC cm
AE cm
=
=
=
37/
43
Nhóm Toán THCS
Toán h󰉭
Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/
b) Gọi I và O lần lượt là tâm đối xứng của hình chữ nhật EFGH và ABCD. Đường thẳng
OI song song với những mặt phẳng nào?
Ta có:
-
ABFE
là hình chữ nhật suy ra
//AE BF
và
AE BF=
(1)
-
BCFG
là hình chữ nhật suy ra
//BF CG
và
BF CG=
(2)
Từ (1) và (2) suy ra:
//AE CG
và
.AE CG=
Do đó
ABGC
là hình bình hành.
Ta có:
OA OC=
và
EI IG=
OI
là đường trung bình của hình bình hành
AEGC
.
Nên
/ / / / .OI AE CG
Mà
( )
AE mp AEHD
Do đó
( )
//IO mp AEHD
Tương tự:
( )
//IO mp BCGF
,
( )
//IO mp AEFB
,
( )
//IO mp DCGH
c) Chứng tỏ hình chóp I.ABCD có các cạnh bên bằng nhau nhưng không phải hình chóp
đều.
Ta có:
/ / ; .IO AE AE AC IO AC⊥ ⊥
Tương tự ta có:
.IO OB⊥
Xét
IOC
và
IOB
có:
IO
chung
90
o
IOC IOB==
OC OB=
(Do
ABCD
là hình chữ nhật)
Suy ra
IOC IOB =
.IC IB=
Tương tự:
IA IB IC ID= = =
Suy ra hình chóp
.I ABCD
có các mặt bên là tam giác cân.
Mà
ABCD
là hình chữ nhật có
AB BC
Nên hình chóp
.I ABCD
không là hình chóp đều.
d) Tính diện tích xung quanh của hình chóp I.ABCD.
Xét
ABC
vuông tại
B
:
2 2 2
AC AB BC=+
Suy ra
( )
2 2 2 2
12 9 15AC AB BC cm= + = + =
( )
7,5
2
AC
OC OA cm = = =
.
Xét
OIC
vuông tại
O
:
2 2 2
IC OC OI=+
Suy ra
( )
2 2 2 2
7,5 10 12,5IC OC OI cm= + = + =
.
Kẻ
IK CB⊥
.
Xét
ICB
cân tại
I
có
IK
là đường cao suy ra
IK
là đường trung tuyến.
38/
43
Nhóm Toán THCS
Toán h󰉭
Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/
Nên
( )
9
4,5
22
CB
CH HB cm= = = =
.
Xét
ICK
vuông tại
I
:
2 2 2
IK CI CH=−
( )
22
12,5 4,5 11,66 .IK cm = −
Diện tích xung quanh của hình chóp
.I ABCD
là:
( )
2
1
4. 4. . 2.11,66.9 209,88 .
2
xq IBC
S S IH BC cm
= = = =
Dạng 5. Một số bài tập nâng cao.
Bài 1.
( ) ( ) ( )
2 2 2
2 2 2
2 2 2 2 2 2
1)
2 2 2 2 2 2
2 2 2 0
a b c ab bc ca
a b c ab bc ca
a ab b b bc c c ca a
+ + + +
+ + + +
− + + − + + − +
( ) ( ) ( )
2 2 2
0a b b c c a − + − + −
(luôn đúng)
Dấu “=” xảy ra
abc = =
( )
( ) ( )
2
2 2 2
2) 3 3a b c a b c ab bc ca+ + + + + +
Ta chứng minh:
( )
( )
2
2 2 2
3 a b c a b c+ + + +
2 2 2 2 2 2
3 3 3 2 2 2a b c a b c ab bc ca + + + + + + +
2 2 2
2 2 2 2 2 2a b c ab bc ca + + + +
( ) ( ) ( )
2 2 2
0a b b c c a − + − + −
(luôn đúng)
Ta chứng minh:
( ) ( )
2
3a b c ab bc ca+ + + +
Theo trên ta có
2 2 2
a b c ab bc ca+ + + +
2 2 2
2 2 2 3 3 3a b c ab bc ca ab bc ca + + + + + + +
( ) ( )
2
3a b c ab bc ca + + + +
Dấu “=” xảy ra
abc = =
( ) ( )
2
3) 4a b c a b c+ − −
( ) ( ) ( )
( ) ( )
2
2
2
2
24
20
a a b c b c a b c
a a b c b c
+ − + − −
− − + −
( )
2
0a b c − +
(luôn đúng)
4a)
( )
( )
2
22
,0
xy
xy
ab
a b a b
+
+
+
Dùng phép biến đổi tương đương và
,0ab
ta có:
39/
43
Nhóm Toán THCS
Toán h󰉭
Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/
( )
( ) ( ) ( )
2
22
2
22
2 2 2 2 2 2 2 2
2 2 2 2
2
20
xy
xy
x b a b y a a b x y ab
a b a b
x ab x b y a y ab x ab xyab y ab
x b xyab y a
+
+ + + + +
+
+ + + + +
− +
( )
2
0bx ay −
(luôn đúng)
Dấu “=” xảy ra
xy
bx ay
ab
= =
4b)
( )
( )
2
2 2 2
, , 0
x y z
x y z
abc
a b c a b c
++
+ +
++
Ta có
( ) ( )
( )
22
2 2 2 2
, , 0
x y x y z
x y z z
abc
a b c a b c a b c
+ + +

+ + +

+ + +

Dấu “=” xảy ra
x y z
a b c
= =
4c)
( )
( )( )
2
2 2 2 2
ax by a b x y+ + +
2 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2
2 2 2 2
2
2
20
a x abxy b y a x a y b x b y
abxy a y b x
a y b x abxy
+ + + + +
+
+ −
( )
2
0ay bx −
(luôn đúng)
5) Với a,b,c là các số thực thỏa mãn
6.a b c ab bc ca+ + + + + =
Chứng minh
2 2 2
3abc+ +
Từ
( ) ( )
( )
2
2
3
3
abc
a b c ab bc ca ab bc ca
++
+ + + + + +
( )
( )
( ) ( )
( )( )
2
2
6
3
3 18 0
6 3 0
3
6
abc
ab bc ca a b c
a b c a b c
a b c a b c
abc
abc
++
+ + = − + +
+ + + + + −
+ + + + + −
+ +
+ + −
( )
2
2
2 2 2
3
3
33
abc
abc
++
+ + =
Dấu “=” xảy ra
1abc = = =
Bài 2.
Ta có:
2 2 2 2
10 3 0 10 6 5 3 0a b ab a ab ab b− + = + − − =
( ) ( )
2 5 3 5 3 0a a b b a b + − + =
( )( )
2 5 3 0a b a b − + =
20ab − =
hoặc
5 3 0ab+=
40/
43
Nhóm Toán THCS
Toán h󰉭
Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/
2ab=
hoặc
53ab=−
(không thỏa mãn do b > a > 0)
Thay
2ba=
vào biểu thức A, ta được:
2 2 5.2 0 9 9 9
0
3 2 3 2 5 5 5
a a a a a
A
a a a a a a
−−
= + = + = + =
−+
Vậy
9
5
A =
Bài 3.
Từ đề bài: (x + y)
2
= (x - 2).(y + 2)
x
2
+ 2xy + y
2
= xy + 2x – 2y – 4
x
2
+ xy + y
2
– 2x + 2y + 4 = 0
2x
2
+ 2xy + 2y
2
– 4x + 4y + 8 = 0
(x
2
+ 2xy + y
2
) + (x
2
– 4x + 4) + (y
2
+ 4y + 4) = 0
(x + y)
2
+ (x - 2)
2
+ (y + 2)
2
= 0 (*)
Vì
( )
2
2
2
0
( 2) 0
( 2) 0
x y xy
xx
yy
+
−
+
nên (*)
0
20
20
xy
x
y
+=
−=
+=
2
2
x
y
=
=−
Do dó: A = 2
2
+ (-2)
2
= 8
Bài 4. Tìm GTLN, GTNN (nếu có) của các biểu thức
1)
2
2
22
6 6 3 3
3 1 1 1
4 4 3
1
4 2 2.
21
4 2 4 2
2
A
xx
x x x x
x
= = = =
++

+ + + + +
++


Ta có:
22
2
1 1 3
2 0, 2 1 1, 3, 3
22
1
21
2
x x x x x A
x
+ + +

++


Dấu “=” xảy ra
11
0
22
xx + = = −
Vậy GTNN của A là 3 tại
1
2
x =−
2)
( )
2
22
4 4 4
6 4 4 4 2
22
B
x x x x
x
− − −
= = =
+ + + + +
++
Ta có:
( )
2
2 0,xx+
( ) ( )
( )
22
2
4
2 2 2 , 2 2 2, 2, 2
22
x x x x x B
x
−
+ + + + − −
++
Dấu “=” xảy ra
2 0 2xx + = = −
Vậy GTNN của B là -2 tại
2x =−
41/
43
Nhóm Toán THCS
Toán h󰉭
Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/
3)
( )
2
2
33
1
21
xx
Cx
xx
−+
=
−+
( )
( )
( ) ( )
( )
( )
2
2
2 2 2
2 1 1 1
1 1 1
11
1
1
1 1 1
x x x
xx
x
x x x
− + − + +
− − − +
= = = − +
−
− − +
Đặt
1
1
y
x
=
−
2
22
1 1 3 1 3
1 2.
2 4 4 2 4
C y y y y y
= − + = − + + = − +
Ta có:
22
1 1 3 3
0
2 2 4 4
y y y y
− − +
Dấu “=” xảy ra
( )
1 1 1 1
0 1 2 3
2 2 1 2
y y x x TM
x
− = = = − = =
−
Vậy GTNN của C là
3
4
tại
3x =
4)
1 1 15
16 16
xx
Dx
xx
= + = + +
Áp dụng bất đẳng thức cô – si cho hai số dương
16
x
và
1
x
ta có:
1 1 15 1 15 1 15 1 15
2 . 2
16 16 16 16 16 16 2 16
x x x x x x
Dx
x x x
= + = + + + = + = +
Do
4x
nên
15 15.4 15
16 16 4
x
=
Suy ra
1 15 17
2 4 4
D + =
Dấu “=” xảy ra
( )
( )
2
4
1
16
16
4
x TM
x
x
x
x KTM
=
= =
=−
Vậy GTNN của D là
17
4
tại
4x =
5)
( ) ( )
22
2 2 2
2 2 2 2 2
66
12 34 12 36 2 2
1
2 2 2 2 2
xx
x x x x x
Q
x x x x x
++
+ + + − − +
= = = − = −
+ + + + +
Ta có:
( ) ( )
22
22
66
0 1 1
22
xx
xx
xx
++
− −
++
Dấu “=” xảy ra
6 0 6xx + = = −
Vậy GTNN của Q là
1−
tại
6x =−
6)
1 2 2 3 4E x x x= − + − + − +
1 3 2 2 4 2 2 6 6E x x x x − + − + − + = − +
Dấu “=” xảy ra
( )( )
1 3 0
13
2
2
20
xx
x
x
x
x
− −

=

=
−=
Vậy GTNN của E là 6 tại
2x =
42/
43
Nhóm Toán THCS
Toán h󰉭
Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/
Bài 5.
1) Cho a > 0; b > 0; c > 0 và a + b + c = 6. Tìm GTNN của
3 3 3 3 3 3
a b b c c a
Q
ab bc ca
+ + +
= + +
3 3 3 3 3 3 2 2 2 2 2 2
a b b c c a a b b c c a
Q
ab bc ca b a c b a c
+ + +
= + + = + + + + +
( )
2 2 2 2 2 2
2
a b b c c a
b a c b a c a b c
b a c b a c
= + + + + + + + + + + + − + +
Vì
2 2 2 2 2 2
0, 0, 0 0, 0, 0, 0, 0, 0.
a b b c c a
abc
b a c b a c
Áp dụng bất đẳng thức Cô-si cho 2 số dương
2
a
b
và
b
có:
22
2
2 . 2 2 .
aa
b b a a
bb
+ = =
Hoàn toàn tương tự ta có:
2 2 2 2 2
2 ; 2 ; 2 ; 2 ; 2 .
b b c c a
a b c b b c a c c a
a c b a c
+ + + + +
Suy ra
( ) ( ) ( )
4 2 2 2.6 12.Q a b c a b c a b c + + − + + = + + = =
Dấu
""=
xảy ra
2
2
...
2.
6
a
b a b
b
abc
a
c a c
c
abc
= =
= = =
= =
+ + =
Khi đó
Q
đạt GTNN bằng 12.
2)
22
4 600A x y xy x y= + − − + +
( )
( )
( )
( ) ( )
( )
22
2 2 2
2
2
2
2
4 4 4 4 4 16 2400
4 4 4 4 2 3 14 2400
7 49 49
4 2 2 2 1 3 2. 2400 1
3 9 3
7 7148 7148
4 2 1 3
3 3 3
A x y xy x y
A x xy y x y y y
A x y x y y y
A x y y
= + − − + +
= − + − − + + +

= − − − + + + + + − −


= − − + + +


Khi đó
7148 1787
:4
33
AA
Dấu bằng xảy ra
2
2 1 0
3
7
7
0
3
3
xy
x
y
y
−
− − =
=



−
+=

=
Vậy giá trị nhỏ nhất của A bằng
1787
3
khi và chỉ khi
27
;
33
xy
−−
==
43/
43
Nhóm Toán THCS
Toán h󰉭
Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/
Bài 6.
51
2
12 2
mx x+−
+
(1)
và
2
(x 1)(x 22) 0+ +
(2)
Ta có:
2
x 1 1, x+
2
x 1 0, x +
(2) x 22 0 +
22x −
5 6(x 1) 24
(1)
12 12 12
mx +−
+
5 6 6 24mx x + + −
6 24 5 6mx x + − +
(m 6)x 25 +
- Trường hợp 1:
25
6 0 6
6
m m x
m
+ −
+
- Trường hợp 2:
25
6 0 6
6
m m x
m
+ −
+
(1) (2)
6
6
6
157
25
157
22(m 6) 25
22
22
6
22
m
m
m
m
m
m
−
−
−
−

=
−
− + =
=−
=

+
Vậy với
157
22
m
−
=
thì hai bất phương trình đã cho tương đương.
| 1/43
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

1/ 43 Nhóm Toán THCS Toán học là đam mê
Trường THCS Ngô Sĩ Liên
Đề cương ôn tập học kỳ II – Toán 8 Năm học: 2017-2018
Dạng 1: Rút gọn biểu thức x + 2 5 1
Bài 1. Cho biểu thức A = − + 2 x + 3 x + x − 6 2 − x a) Rút gọn biểu thức A b) Tìm x để A > 0
c) Tìm x  để A nguyên dương. 2 2x + 2x 1− 2x x +1
Bài 2. Cho các biểu thức A = B = + 2 1− và x 2 x − 3x + 2 x − 2
a) Rút gọn biểu thức A, B;
b) Tính giá trị của A khi x − 2 = 3; c) Tính C = A – B;
d) Tìm x  để C  . 2x x +1 3 −11x x − 3
Bài 3. Cho biểu thức A = + + và B = với 0  x  9. 2 x + 3 x − 3 9 − x x +1 a) Rút gọn A; 9
b) Với P = A.B, tìm x để P = . 2 c) Tìm x để B < 1
d) Tìm số nguyên x để P = A.B là số nguyên. 2 1 x − x + 3 2 x + 2
Bài 4. Cho biểu thức A = − B =  x  3 x −1 x − và 1 2 x + x + với 0 9. 1 a) Rút gọn A;
b) Biết P = A: (1 - B). Tìm x để P 1.  x −1 x 3x +1  2x +1
Bài 5. Cho biểu thức P = − − :   2 2
x +1 x −1 1− x x −1 a) Rút gọn P; 3
b) Tìm các giá trị của x để P = . x −1
c) Tìm các giá trị nguyên của x để A > 1 2 x + 2x x − 5 50 − 5x
Bài 6. Cho biểu thức P = + + 2x +10 x 2x ( x + 5)
a) Tìm điều kiện xác định của P; b) Rút gọn biểu thức P. 1
c) Tìm các giá trị của x để P = 0; P = . 4
d) Tìm các giá trị của x để P > 0; P < 0. Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 2/ 43 Nhóm Toán THCS Toán học là đam mê  2x 5   2 
Bài 7. Cho biểu thức P = − : 3 +     2
 2x − 5x + 3 2x − 3   1− x  a) Rút gọn P.
b) Tính giá trị của P khi x thỏa mãn 2x −1 = 3 c) Tìm x để P > 1
d) Tìm x nguyên để P nguyên. 2  x   1 2x
Bài 8. Cho biểu thức A = 1+  : −   2 3 2 
x +1   x −1 x + x − x −1 a) Rút gọn A. 1
b) Tính giá trị của A tại x = − . 2 c) Tìm x để A< 1
d) Tìm các giá trị nguyên của x để A có giá trị nguyên.
Dạng 2: Phương trình và bất phương trình
Bài 1. Giải các phương trình sau: 3x + 2 3x +1 5
a) 5 − ( x − 6) = 4(3 − 2x) d) − = 2x + 2 6 3 2x − 2 x + 8 x −1 b) − x ( − x) 2 3 4 25 2 = 8x + x −300 e) x − + = 7 + 5 6 3 5x + 2 8x −1 4x + 2 2 ( x − 3) 13x + 4 c) − = − 5 f) − x + 2 = 6 3 5 7 21
Bài 2. Giải các phương trình sau:
a) 2x ( x − 3) + 5( x − 3) = 0 d) 2 x − 5x + 6 = 0 b) ( 2
x − 4) − ( x − 2)(3− 2x) = 0 e) 3 2 2
2x + 6x = x + 3x 2  1   1 
c) ( x + )2 = ( x + )2 2 5 2 f) x + + 2 x + −8 = 0.      x   x
Bài 3. Giải các phương trình sau: 1 5 15 2 1 3x 2x a) − = − = x +1 x − 2 (x + ) 1 (2 − d) x) 3 2 x −1 x −1 x + x +1 x −1 x 5x − 2 7 5 − x x −1 1 b) − = e) + = + 2 x + 2 x − 2 4 − x 2 8x 4x − 8x
2x ( x − 2) 8x −16 x + 5 x − 5 x + 25 2 1 1 c) − = f) + = 2 2 2 x − 5x 2x +10x 2x − 50 2 2 2 x + 3x + 2 x + 5x + 6 x + 4x + 3
Bài 4. Giải các phương trình sau: a) x − 5 = 3
c) 2x +1 = x −1 b) 5 − x = 3x −16
d) 2x +1 − 5x − 2 = 3 Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 3/ 43 Nhóm Toán THCS Toán học là đam mê
Bài 5. Giải các bất phương trình sau rồi biểu diễn tập nghiệm trên trục số: a) ( x − )2 2 3  x − 5x + 4 f) 2
x − 4x + 3  0
b) ( x − )( x + )  ( x + )2 3 3 2 + 3 g) 3 2
x − 2x + 3x − 6  0 4x − 5 7 − x x + 2 c)  h)  0 3 5 5 2x +1 3 − 5x 4x +1 x + 2 d) + 3  − i)  0 2 3 4 x − 3 5x − 3 2x +1 2 − 3x x −1 e) +  − 5 k)  1 5 4 2 x − 3
Dạng 3: Giải bài toán bằng cách lập phương trình
Bài 1. Một người đi xe máy từ A đến B với vận tốc trung bình 40km/h. Khi quay trở về A
người đó tăng vận tốc thêm 5km/h nên thời gian về hết ít hơn thời gian đi 40 phút. Tính quãng đường AB?
Bài 2. Lúc 6 giờ, một ô tô xuất phát từ A đến B với vận tốc trung bình 40km/h. Khi đến B,
người lái xe làm nhiệm vụ giao nhận hàng trong 30 phút rồi cho xe quay trở về A với vận
tốc trung bình 30km/h. Tính quãng đường AB, biết rằng ô tô về đến A lúc 10 giờ cùng ngày.
Bài 3. Một người đi xe đạp từ A đến B cách nhau 24km. Một giờ sau, một người đi xe
máy từ A và đến B trước người đi xe đạp 20 phút. Tính vận tốc của mỗi xe, biết vận tốc
của xe máy gấp 3 lần vận tốc xe đạp.
Bài 4. Một ô tô đi từ A đến B cách nhau 90 km trong một thời gian nhất định. Khi đi được
1 giờ người đó dừng lại nghỉ 15 phút. Trên quãng đường còn lại người đó phải tăng vận
tốc them 10 km/h để đến B đúng dự định. Tính vận tốc ban đầu của ô tô?
Bài 5. Một người đi từ A đến B với vận tốc 9km/h. Khi đi từ B trở về A người đó chọn
đường khác dài hơn đường cũ 6km, và đi với vận tốc lớn hơn lúc đi là 3km/h nên thời
gian về ít hơn thời gian đi là 20 phút. Tính chiều dài quãng đường AB.
Bài 6. Lúc 8h30’ một người đi xe máy từ A đến B với vận tốc 40km/h, đến 10h cùng ngày
một người khác đi xe máy từ B đến A với vận tốc 60km/h. Hỏi hai người gặp nhau lúc
mấy giờ, biết rằng họ gặp nhau tại chính giữa quãng đường.
Bài 7. Hai ca nô khởi hành cùng một lúc chạy từ A đến B. Ca nô thứ nhất chạy với vận
tốc 20km/h, ca nô thứ hai chạy với vận tốc 24km/h. Trên đường đi, ca nô thứ hai dừng lại
40 phút để sửa xong vẫn đến B cùng một lúc với ca nô thứ nhất. Tính chiều dài quãng song AB.
Bài 8. Một ca nô xuôi dòng từ bến A đến bến B hết 1 giờ 10 phút và đi ngược dòng từ B
về A hết 1 giờ 30 phút. Tính khoảng cách giữa hai bến A và B, biết vận tốc của dòng nước là 2km/h. Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 4/ 43 Nhóm Toán THCS Toán học là đam mê
Bài 9. Một tổ may áo theo kế hoạch mỗi ngày phải may 30 áo. Tổ đã may mỗi ngày 40 áo
nên đã hoàn thành trước thời hạn 3 ngày, ngoài ra còn may them được 20 chiếc áo nữa.
Tính số áo mà tổ đó phải may theo kế hoạch.
Bài 10. Một đội đánh cá dự định mỗi tuần đánh bắt 20 tấn cá, nhưng mỗi tuần đã vượt
mức 6 tấn nên chẳng những hoàn thành kế hoạch sớm một tuần mà còn vượt mức đánh
bắt 10 tấn. Tính mức cá đánh bắt theo kế hoạch?
Bài 11. Hai tổ sản xuất phải dệt 140 áo len. Trong thực tế tổ 1 đã vượt mức 10% kế hoạc
của mình, tổ 2 vượt mức 5 % kế hoạch của mình nên cả hai tổ đã dệt được 150 áo len. Hỏi
theo kế hoạch mỗi tổ phải dệt được bao nhiêu áo len?
Bài 12. Hai công nhân cùng làm chung một công việc dự định trong 12 giờ sẽ hoàn thành
xong công việc. Họ làm chung với nhau trong 4 giờ thì người thứ nhất chuyển đi làm việc
khác, người thứ hai phải làm nốt công việc trong 10 giờ. Hỏi nếu người thứ hai làm một
mình thì bao lâu sẽ hoàn thành xong công việc.
Bài 13. Hai vòi nước cùng chảy vào một bể thì đầy trong 3 giờ 20 phút. Người ta cho vòi 4
thứ nhất chảy 3 giờ và vòi thứ hai chảy 2 giờ thì được
bể. Hỏi nếu mỗi vòi chảy một 5
mình thì trong bao lâu mới đầy bể?
Bài 14. Hai giá sách có 450 cuốn. Nếu chuyển 50 cuốn từ giá thứ nhất sang giá thứ hai thì 5
số sách ở giá thứ nhất bằng số sách ở giá thứ hai. Tính số sách ban đầu của mỗi giá. 4
Dạng 4: Bài tập hình học.
Bài 1. Cho góc xAy. Trên tia Ax lấy 2 điểm B và C sao cho AB = 8cm, AC = 15cm. Trên tia
Ay lấy 2 điểm D và E sao cho AD = 10cm, AE = 12cm. a) CMR: ABE  và ADC đồng dạng; b) CMR: AB.DC = AD.BE; c) Tính DC, biết BE = 10cm;
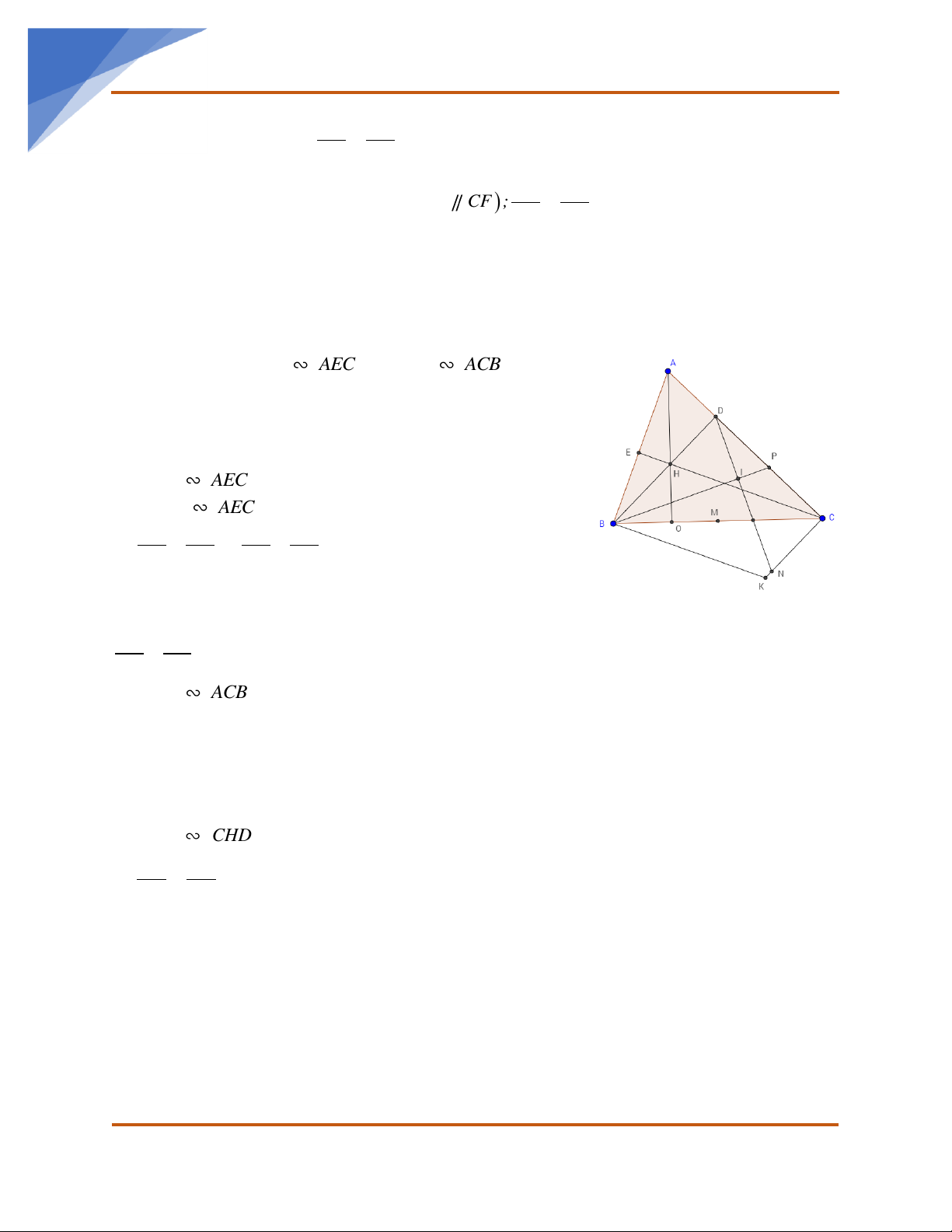
d) Gọi I là giao điểm của BE và CD. CMR: IB.IE =ID.IC. Bài 2. Cho ABC
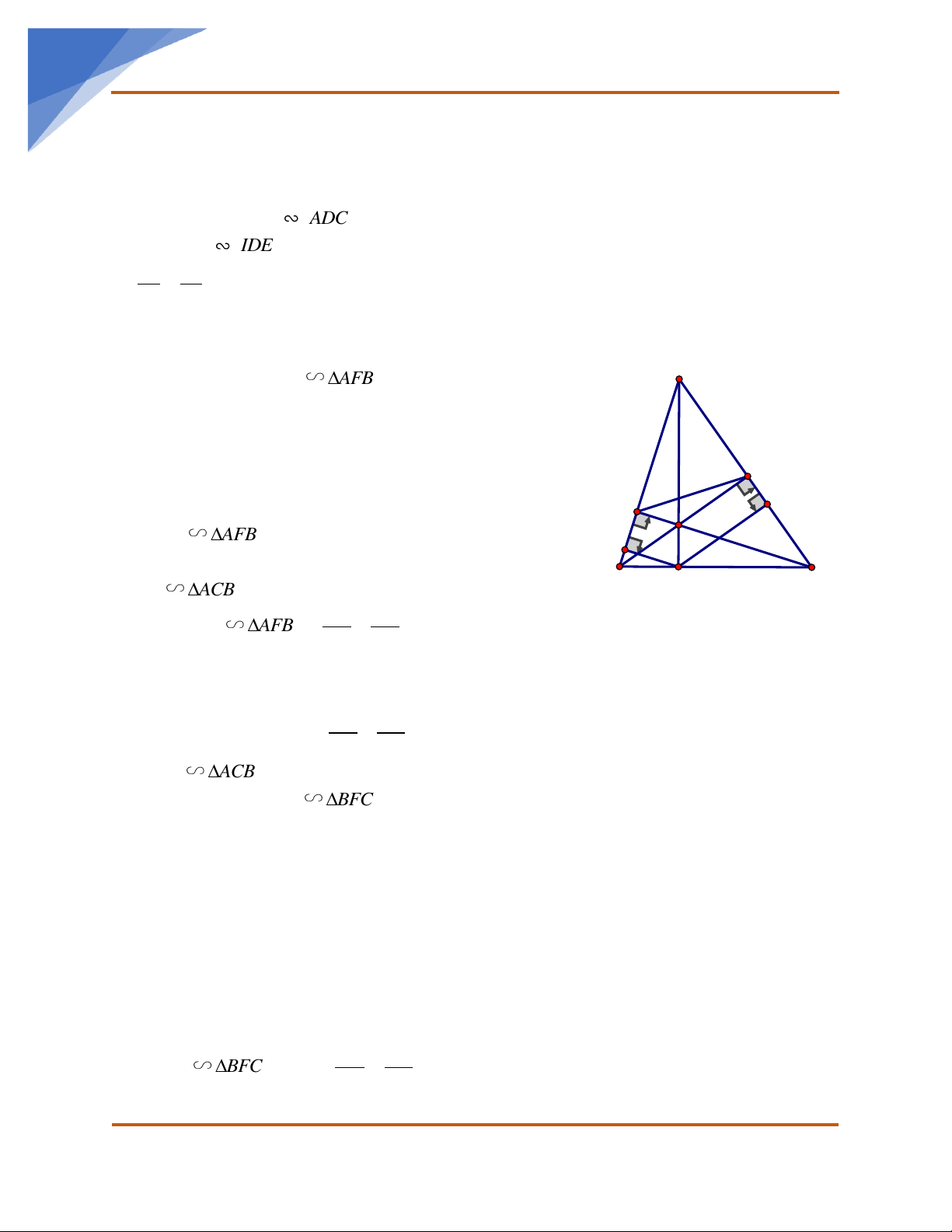
nhọn có hai đường cao BF, CE cắt nhau tại H. Tia AH cắt BC tại D. a) Chứng minh: AEC  và AFB  đồng dạng;
b) Chứng minh AE.AB = AF.AC rồi từ đó suy ra AEF  đồng dạng với AC . B c) Chứng minh: BDH  đồng dạng BFC  và BH.BF + CH.CE = BC.
d) Vẽ DM ⊥ AB tại M, DN ⊥ AC tại N. Chứng minh MN //EF.
Bài 3. Cho tam giác ABC vuông tại B, đường cao BH. Cho AB = 15cm, BC = 20cm. a) Chứng minh: CHB CBA b) Chứng minh: 2
AB = AH.AC c) Tính độ dài AC, BH.
d) Kẻ HK ⊥ AB tại K, HI ⊥ BC tại I. Chứng minh BKI BCA
e) Kẻ trung tuyến BM của ABC
cắt KI tại N. Tính diện tích BKN. Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 5/ 43 Nhóm Toán THCS Toán học là đam mê
Bài 4. Cho hình bình hành ABCD, AC là đường chéo lớn. kẻ CE vuông góc với AB taị E,
CF vuông góc với AD tại F, BI vuông góc với AC tại I.
a) Chứng minh tam giác AIB đồng dạng với tam giác AEC.
b) Chứng minh tam giác AIE đồng dạng với tam giác ABC.
c) Chứng minh AB.AE + AF.CB = 2 AC .
d) Tia BI cắt đường thẳng CD tại Q và cắt cạnh AD tại K. Chứng minh 2
BI = IK.IQ
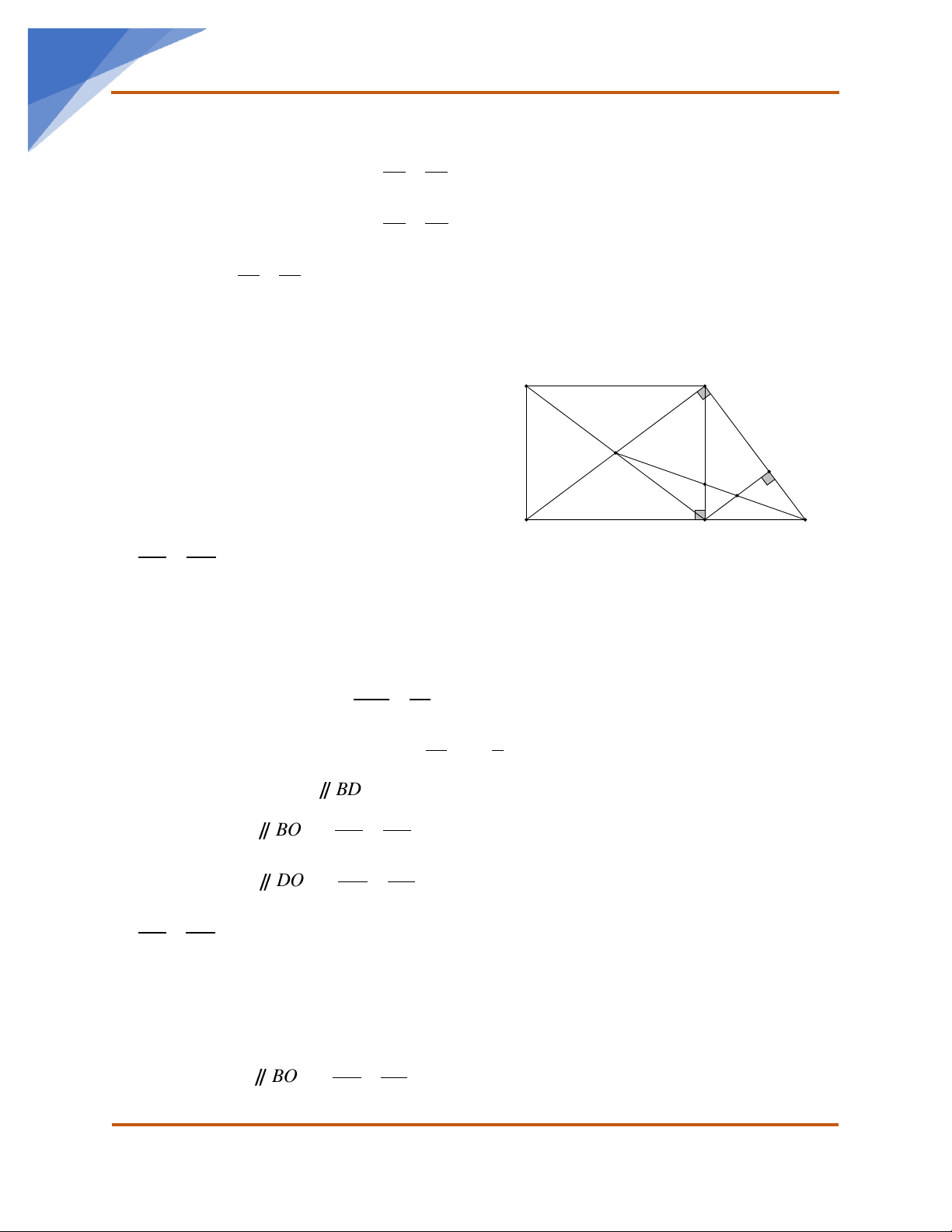
Bài 5. Cho hình chữ nhật ABCD có các cạnh AB = 4cm, BC = 3cm. Qua B vẽ đường thẳng
vuông góc với BD cắt DC tại E.
a) Chứng minh tam giác BDC đồng dạng với tam giác EDB, từ đó suy ra 2
DB = DC.DE; b) Tính DB, CE;
c) Vẽ CF vuông góc với BE tại F. Gọi O là giao điểm của AC và BD. Nối OE cắt CF tại I và
cắt BC tại K. Chứng minh I là trung điểm của đoạn CF.
d) Chứng minh rằng: ba điểm D,K,F thẳng hàng.
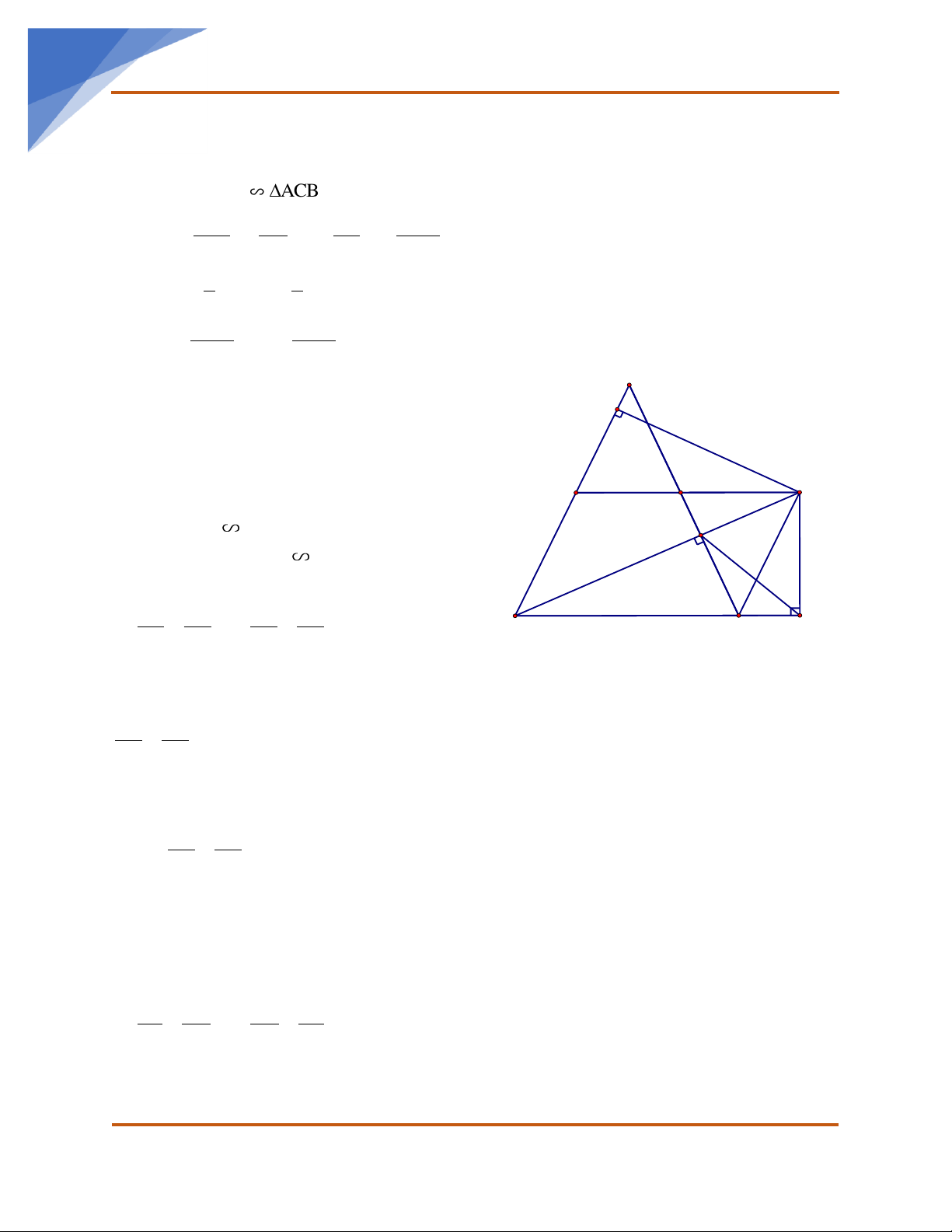
Bài 6: Cho tam giác ABC nhọn, các đường cao BD và CE cắt nhau tại H. Đường vuông
góc AB tại B và đường vuông góc với AC tại C cắt nhau tại K. Gọi M là trung điểm của BC. Chứng minh: a) Chứng minh ADB AEC và AED ACB ;
b) Chứng minh: HE.HC = HD.HB;
c) Chứng minh H, M, K thẳng hàng và góc AED bằng góc ACB.
d) AH cắt BC tại O. Chứng minh: BE.BA + CD.CA = 2 BC . HO HD HE e) Chứng minh + + = 1; AO BD CE
f) Chứng minh H là giao điểm các đường phân giác của tam giác ODE. g) Cho góc 0
ACB = 45 , gọi P là trung điểm của DC. Từ D kẻ đường thẳng vuông góc với
BP tại I và cắt CK tại N. Tìm tỉ số diện tích của tứ giác CPIN và diện tích tam giác DCN.
h) Tam giác ABC có điều kiện gì thì tứ giác BHCK là hình thoi? Hình chữ nhật?
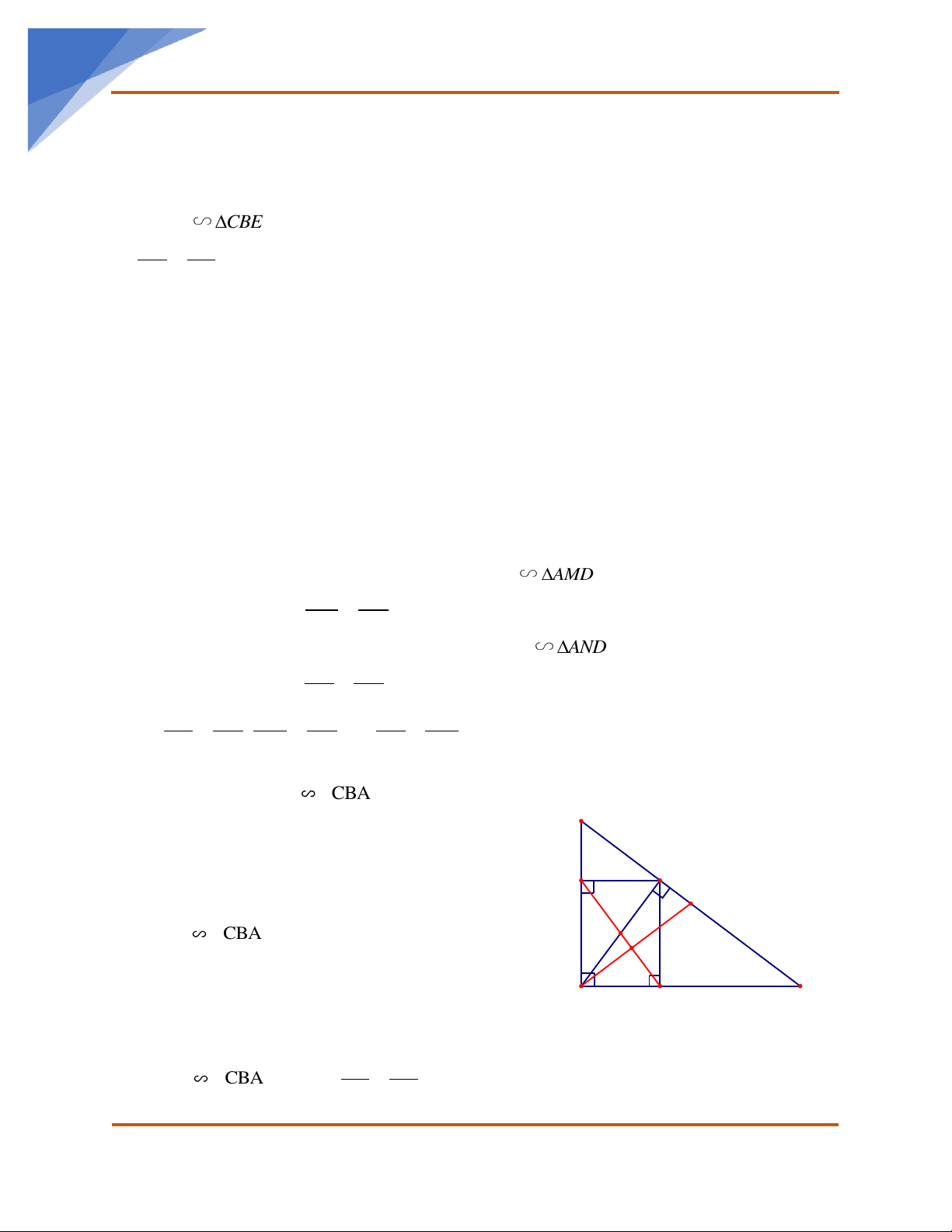
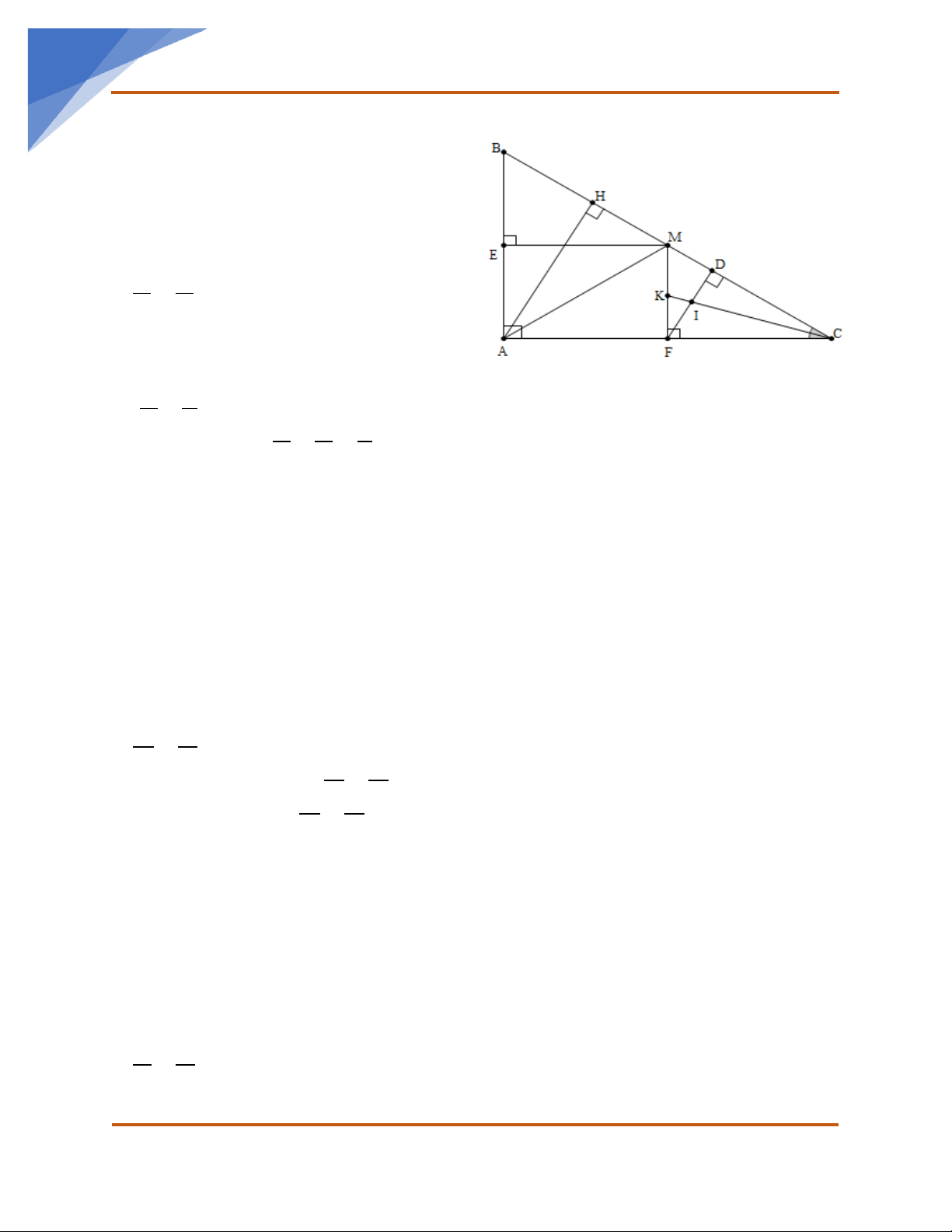
Bài 7. Cho tam giác ABC vuông tại A (AB < AC), đường cao AH và trung tuyến AM. Kẻ
MF vuông góc với AC tại F, FD vuông góc MC tại D. Phân giác góc C cắt FD, MF lần lượt
tại I và K. Kẻ ME vuông góc với AB tại E. CD CI DI a) Chứng minh = = và IF = KF; CF CK FI
b) Tứ giác AEMF là hình gì? c) Chứng minh AHC M
FC và AH.EB = HB.ME; d) Chứng minh MF.AB = MF.AC; e) Chứng minh BH.BC = 2 4AE . Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 6/ 43 Nhóm Toán THCS Toán học là đam mê
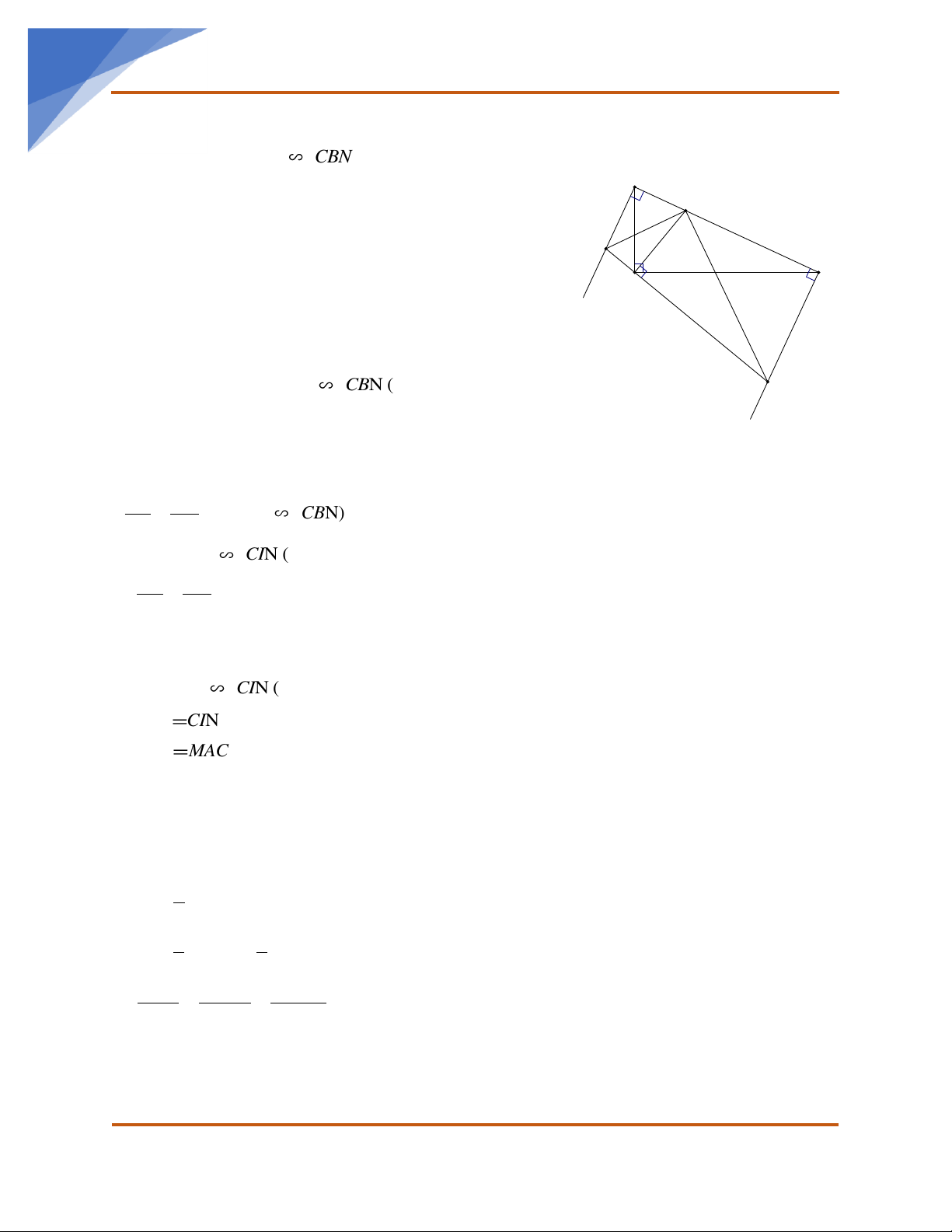
Bài 8. Cho tam giác ABC vuông tại C (CA < CB). Lấy điểm I bất kì trên cạnh AB. Trên nửa
mặt phẳng AB chứa C, kẻ tia Ax, By cùng vuông góc với AB. Đường vuông góc với IC
cắt Ax, By lần lượt tại M và N.
a) Chứng minh tam giác CAI đồng dạng với tam giác CBN. b) Chứng minh AB.NC = IN.CB.
c) Chứng minh góc MIN là góc vuông.
d) Tìm vị trí của điểm I để diện tích tam giác IMN gấp hai lần diện tích tam giác ABC.
Bài 9. Cho hình thang cân MNPQ (MN//PQ, MN < PQ), NP = 15cm, đường cao NI = 12cm, QI =16cm. a) Tính IP;
b) Chứng minh QN ⊥ NP ;
c) Tính diện tích hình thang MNPQ;
d) Gọi E là trung điểm của PQ. Đường thẳng vuông góc EN tại N cắt đường thẳng PQ tại K. Chứng minh rằng: 2 KN = K . P KQ
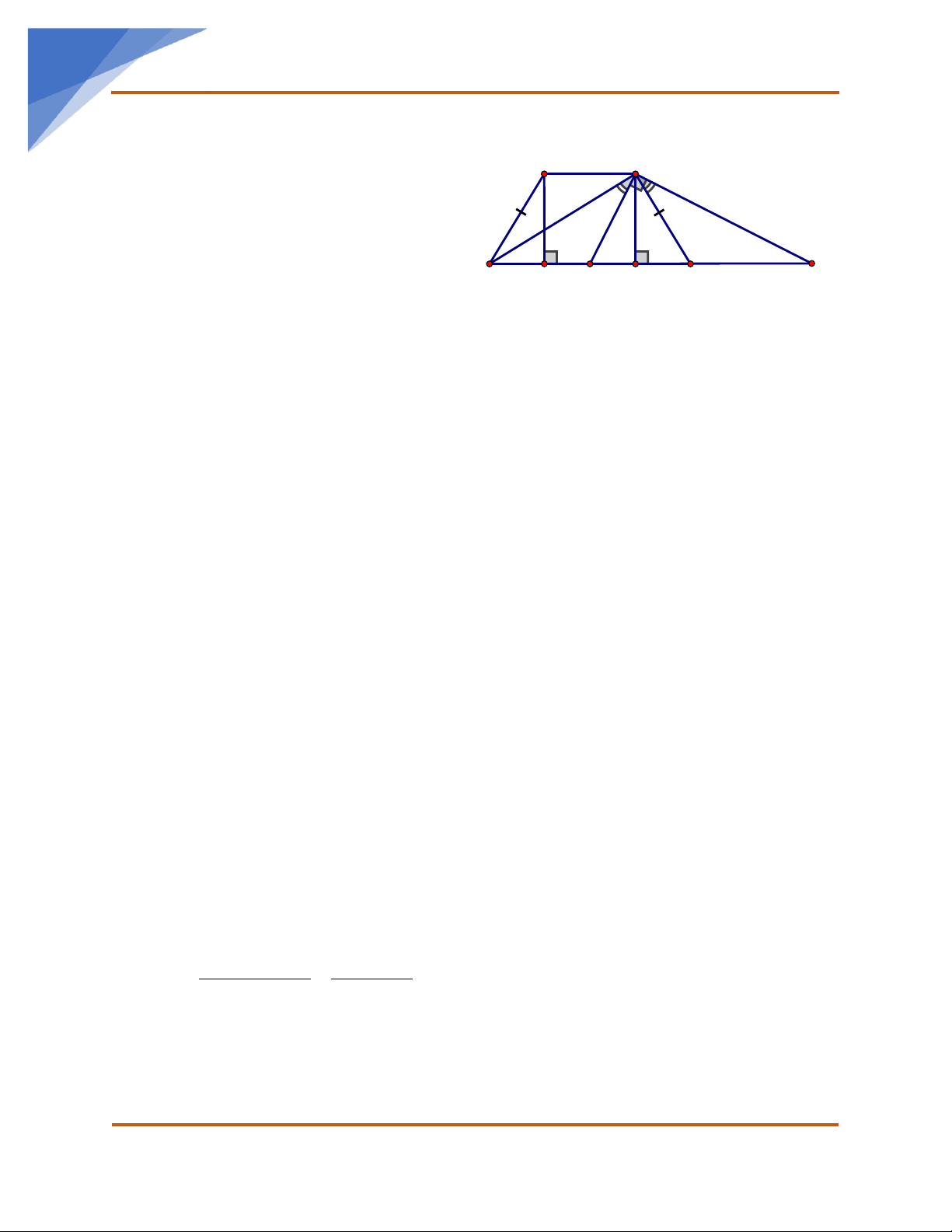
Bài 10. Cho tam giác nhọn ABC, H là trực tâm, G là trọng tâm, O là giao điểm các đường
trung trực của tam giác. Chứng minh rằng: H, G, O thẳng hàng và HG = 2GO.
Bài 11. Cho hình hộp chữ nhật ABCD.EFGH với AB = 12cm, BC = 9cm, AE = 10cm.
a) Tính diện tích toàn phần và thể tích của hình hộp chữ nhật ABCD.EFGH.
b) Gọi I và O lần lượt là tâm đối xứng của hình chữ nhật EFGH và ABCD. Đường thẳng
OI song song với những mặt phẳng nào?
c) Chứng tỏ rằng hình chóp I.ABCD có các cạnh bên bằng nhau nhưng không phải hình chóp
d) Tính diện tích xung quanh của hình chóp I.ABCD.
Dạng 5: Một số bài tập nâng cao.
Bài 1. Chứng minh các bất đẳng thức sau: 1) 2 2 2
a + b + c ab + bc + ca 2 2) ( 2 2 2
3 a + b + c )  (a + b + c)  3(ab + bc + ca) \\
3) (a + b + c)2  4a (b − c) x y ( + )2 2 2 x y 4) a) +  a  0;b  0 a b a + ( ) b x y z ( + + )2 2 2 2 x y z b) + + 
a  0;b  0; c  0 a b c a + b + ( ) c 2 c) ( )  ( 2 2 + )( 2 2 ax+by a b x + y )
5) Với a, b, c là các số thực thỏa mãn a + b + c + ab + bc + ca = 6.Chứng minh rằng 2 2 2
a + b + c  3. Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 7/ 43 Nhóm Toán THCS Toán học là đam mê 2a − b 5b − a Bài 2. Cho A = +
. Tính giá trị của biểu thức A, biết b > a >0 và 3a − b 3a + b 2 2
10a − 3b + ab = 0.
Bài 3. Cho x, y thỏa mãn ( x + y)2 = ( x − 2)( y + 2).Tính giá trị biểu thức 2 2
A = x + y .
Bài 4. Tìm GTLN, GTNN (nếu có) của các biểu thức sau: 6 4 − 2 x − 3x + 3 1) A = 2) B = 3) C = x  ) 2 4x + 4x + 3 2 6 + 4x + x 2 x − 2x + (cho 1 1 1 12x + 34
4) D = x + ( x  4) 5) Q =
6) E = x −1 + 2 x − 2 + x − 3 + 4 x 2 x + 2 3 3 3 3 3 3 a + b b + c c + a
Bài 5. 1) Cho a > 0; b > 0; c > 0 và a + b + c = 6. Tìm GTNN của Q = + + ab bc ca 2) Tìm GTNN của 2 2
A = x + y − xy − x + 4y + 600
Bài 6. Tìm m để hai bất phương trình sau tương đương: mx + 5 x −1 +  2 ( ) 1 ;
( 2x + )1(x+22)  0 (2) 12 2 Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 8/ 43 Nhóm Toán THCS Toán học là đam mê
Hướng dẫn giải: Dạng 1: x + 2 5 1 Bài 1. A = − + 2 x + 3 x + x − 6 2 − x Ta có: 2 2
x + x − 6 = x + 3x − 2x − 6 = x(x + 3) − 2(x + 3) = (x − 2)(x + 3)
Điều kiện xác định: x  2; x  3 −
a) Rút gọn biểu thức A x + 2 5 1 Có A = − − x + 3 (x − 2)(x + 3) x − 2 (x + 2)(x − 2) 2 2 − 5 − (x + 3)
x − 4 − 5 − x − 3 x − x −12 = = = (x + 3)(x − 2) (x +3)(x − 2) (x +3)(x − 2) 2
x − 4x + 3x −12
(x +3)(x − 4) x − 4 = ( = = x + 3)( x − 2)
(x +3)(x − 2) x − 2 x − 4
Vậy với x  2; x  3 − thì A = . x − 2
b) Tìm x để A  0 x − 4
Với x  2; x  3
− để A  0 =>  0 .. x − 2 x  4 
Kết hợp điều kiện x  2; x  3 −  x  2  x  3 − x  4  Vậy với x  2  thì A  0 .  x  −3
c) Tìm x  để A +  .
Với x  2; x  3 − . x − 4 x − 2 − 2 2 Ta có A = = = 1− . x − 2 x − 2 x − 2  2 
(x − 2)U (2) (  x − 2) 1  ;  2 2  +  x − 2   Để A +  => 1−  =   x  2  x  2 x − 2 2   1    x  4 x  4  x − 2 Ta có bảng: x − 2 −2 1 − 1 2 x 0(chọn) 1(chọn) 3(loại) 4(loại)
Vậy với x 0  ;1 Thì A +  . Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 9/ 43 Nhóm Toán THCS Toán học là đam mê 2 2x + 2x 1− 2x x +1 Bài 2. A = B = + 2 1− x 2 x − 3x + 2 x − 2 2 1  − x =  (1− x)(1+ x) Ta có: 
nên điều kiện xác định của ; A B là x  1  ; x  2. 2
x − 3x + 2 =  (x − ) 1 ( x − 2) a) Rút gọn biểu thức ; A B . Với x  1  ; x  2, ta có: 2 2x + 2x 2x ( x + ) 1 2x A = ( = = 1− x)(1+ x)
(1− x)(1+ x) 1− x 2 1− 2x x +1 1− 2x + x −1 x ( x − 2) x B = ( + = = = x − ) 1 ( x − 2) x − 2 (x − ) 1 ( x − 2) (x − ) 1 ( x − 2) x −1
b) Tính giá trị A khi x − 2 = 3 . x − 2 = 3 x = 5(tm) Với x  1
 ; x  2, ta có: x − 2 = 3     x − 2 = 3 − x = 1 − (loai) 2.5 5 −
Thay x = 5 vào biểu thức A ta được A = = . 1− 5 2
c) Tính C = A− B . 2x x 2x + x 3x Với x  1
 ; x  2, ta có C = A − B = − = = 1− x x −1 1− x 1− x
d) Tìm x  để C  . Với x  1  ; x  2 3.0
Nếu x = 0  C =
= 0 Vậy x = 0(t ) m . 1− 0 3x 3 − x 3 − (x − ) 1 − 3 3
Nếu x  0  C = = = = −3− 1− x x −1 x −1 x −1 3 3 Để C  = 3 − −  =  = (x − )
1 U (3) = ( x − ) 1 1;  3 x −1 x −1 Ta có bảng: x −1 3 − 1 − 1 3 x −2 (chọn) 0 (chọn) 2 (loại) 4 (chọn) Vậy x  2 − ;0;  4 thì C Bài 3.
a) Với 0  x  9 2x x +1 3 −11x 2x x +1 3 −11x
2x ( x − 3) + ( x + )
1 ( x + 3) − (3 −11x) A = + + = + − = 2 x + 3 x − 3 9 − x 2 x + 3 x − 3 x − 9 (x +3)(x −3) 2 2
2x − 6x + x + 3x + x − 3 +11x 2 3x + 9x 3x ( x + 3) = 3x ( = = = . x + 3)( x − 3)
(x +3)(x −3) (x +3)(x −3) x −3 Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 10/ 43 Nhóm Toán THCS Toán học là đam mê 3x x − 3 3x
b) Với 0  x  9 , ta có: P = . A B = . = . x − 3 x +1 x +1 9 3x 9 Ta có P = 
=  6x = 9.(x + )
1  3x + 9 = 0  x = −3 (thỏa mãn) 2 x +1 2 x − 3
c) Với 0  x  9 thì B  1 
 1  x − 3  x +1  −3  1 (vô số nghiệm) x +1 3x 3( x + ) 1 − 3 3 d) P = = = 3 − x +1 x +1 x + . 1
Để P nguyên thì ( x + )
1  Ư (3)  ( x + ) 1  1  ;  3  x 0; 2 − ;2;−  4 Bài 4. a) Với x  1 2 − + − + x + x + 1 x x x x − ( 2 2 2 x − x + 3 1 3 1 3 ) A = − = − = 3 x − 1 x − 1 x − 1 (x − ) 1 ( 2 x + x + ) 1 (x − ) 1 ( 2 x + x + ) 1 2x − 2 2( x − ) 1 2 = ( = = . x − ) 1 ( 2 x + x + ) 1 (x − ) 1 ( 2 x + x + ) 2 1 x + x +1 2   +  x + x + 1 − +  x ( 2 2 x 2 2 2 2 )
b) Với x  1 thì P = A : (1− B) = : 1 − = :     2 2 2 2 x + x + 1  x + x + 1 x + x + 1  x + x + 1    2 2  x −1  2 x + x +1 2 = : = . =   . 2 2 2
x + x +1  x + x +1  x + x +1 x −1 x −1 2 Để P  1 
 1  x −1  2  x  3 x − (thỏa mãn). 1  x −1 x 3x +1  2x +1 Bài 5. P = − − :   2 2
 x +1 x −1 1− x  x −1 1 −
a) Điều kiện xác định: x  1  , x  . 2  x −1 x 3x +1  2x +1 P = − − :   2 2
x +1 x −1 1− x x −1  (x − )2 1 x ( x + ) 1 3x +1  (x + ) 1 ( x − ) 1 = ( − + 
x + )( x − ) ( x + )( x − ) ( x + )( x − ) . 1 1 1 1 1 1  2x +1   2 2
x − 2x +1− x − x + 3x +1 ( x + ) 1 ( x − ) 1 = (x + )(x − ) . 1 1 2x +1 2 (x + ) 1 ( x − ) 1 2 = ( = x + )( x − ) . 1 1 2x +1 2x +1 3 2 3 5 − b) P =  =  2(x − ) 1 = 3(2x + )
1  2x − 2 = 6x + 3  x = (TM) x −1 2x +1 x −1 4 Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 11/ 43 Nhóm Toán THCS Toán học là đam mê 2 1 c) P  1 
 1 2  2x +1  2 − x  1− 2  2 − x  1 −  x < 2x +1 2 1 −1
Kết hợp với điều kiện  x <
và x  −1, x  . 2 2 2 x + 2x x − 5 50 − 5x Bài 6. P = + + 2x +10 x 2x ( x + 5)
a) ĐKXĐ: x  0, x  5 − . x + 2x x − 5 50 − 5 x x ( 2 2
x + 2x) 2( x + 5)( x − 5) 50 − 5x b) P = + + = + + 2x +10 x 2x ( x + 5) 2x ( x + 5) 2x ( x + 5) 2x ( x + 5) 3 2 2 3 2
x + 2x + 2x − 50 + 50 − 5x
x + 4x − 5x x ( x − ) 1 ( x + 5) x −1 = = = = 2x ( x + 5) 2x ( x + 5) 2x ( x + 5) 2 x −1 c) P = 0 
= 0  x −1 = 0  x = 1(TM ) 2 1 x −1 1 P =  =  (x − ) 3 4
1 = 2  4x − 4 = 2  4x = 6  x = (TM ) 4 2 4 2 x −1 d) P  0 
 0  x −1  0  x  1, kết hợp với ĐK  x 1. 2 x −1 P  0 
 0  x −1 0  x  1, kết hợp với ĐK  x 1 và x  0, x  5 − . 2 Bài 7. a) Rút gon P 3  2x 5   2 
Với x  1; x  , ta có: P = − : 3 +     2 2
 2x − 5x + 3 2x − 3   1− x   2x 5(x −1)   3(1− x) 2  = − : +    
 (2x − 3).(x −1) (2x − 3)(x−1)   1− x 1− x
2x − (5x − 5) 3 − 3x + 2 = :
(2x − 3)(x −1) 1− x 3 − x + 5 x −1 1 − =  =
(2x − 3)(x −1) 3x − 5 2x − 3
b) Tính giá trị của P khi x thỏa mãn 2x −1 = 3
2x −1 = 3  2x −1 = 3 hoặc 2x −1 = 3 −
 2x = 4 hoặc 2x = 2 −
x = 2hoặc x = 1 − −1
Với x = 2 thì P = = −1 2.2 − 3 −1 1 − 1 Với x = 1 − thì P = = = 2.( 1 − ) − 3 5 − 5 Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 12/ 43 Nhóm Toán THCS Toán học là đam mê
c) Tìm x để P  1 . 1 − 1 − 2 − 2x P  1  1  −1  0   0 2x − 3 2x − 3 2x − 3
2 − 2x  0  x 1  TH1:  3  x  
2x − 3  0  x   2
2 − 2x  0  x 1  3 TH2:  3  1  x
2x − 3  0  x  2  2 3
Vậy để P >1 thì 1  x  2
d) Tìm x nguyên để P nguyên −1 Để
  thì: 2x −3 =1 hoặc 2x −3 = 1
−  2x = 4 hoặc 2x = 2 2x − 3
x = 2(TMĐK) hoặc x =1(KTMĐK)
Vậy để P nguyên thì x = 2 Bài 8. a) Rút gọn A 2  x   1 2xA = 1+  : −   2 3 2 
x +1   x −1 x + x − x −1 2 2x +1  1 2x  = : −   2 2
x +1  x −1 (x +1)(x −1)  2 2 2x +1  x +1 2x  = : −   2 2 2
x +1 (x +1)(x −1) (x +1)(x −1)  2 2 2x +1 (x −1) = : 2 2
x +1 (x +1)(x −1) 2 2
2x +1 (x +1)(x −1) 2 + =  2x 1 = 2 2 x +1 (x −1) x −1 −1
b) Tìm giá trị của A tại x = 2 2  1 −   + − 2 1   1  2  Khi x = thì A = = 1 − 2  1 −  −1    2 
c) Tìm x để A  1. 2 2 2 2x +1 2x +1 2x − x + 2  1  −1 0 
 0  x −1 0  x  1. x −1 x −1 x −1 Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 13/ 43 Nhóm Toán THCS Toán học là đam mê
Dạng 2: Phương trình và bất phương trình Bài 1.
a) 5 − (x − 6) = 4(3 − 2x)
 5− x + 6 =12 −8x
 −x + 8x =12 − 5 − 6 1
 7x =1  x = 7 1 
Vậy phương trình có tập nghiệm S =   7  b) 2
3 − 4x(25 − 2x) = 8x + x − 300 2 2
 3−100x +8x = 8x + x −300  1 − 01x = 3 − 03  x = 3
Vậy phương trình có tập nghiệm S = {3} 5x + 2 8x −1 4x + 2 c) − = − 5 6 3 5
 5(5x + 2) −10(8x −1) = 6(4x + 2) −50
 25x +10 −80x +10 = 24x +12 −50 58 −  7
− 9x = 58  x = 79  58 − 
Vậy phương trình có tập nghiệm S =    79  3x + 2 3x +1 5 d) − = 2x + 2 6 3
 9x + 6 − 3x −1 =12x +10 5 −  6
− x = 5  x = 6  5 − 
Vậy phương trình có tập nghiệm S =    6  2x − 5 x + 8 x −1 e) x − + = 7 + 5 6 3
 30x − 6(2x −5) + 5(x +8) = 210 +10(x −1)
 30x −12x +30 +5x + 40 = 210 +10x −10
13x =130  x =10
Vậy phương trình có tập nghiệm S= {10} 2(x − 3) 13x + 4 5 f) − x + 2 =
 6x −18− 21x + 42 =13x + 4  2 − 8x = 2 − 0  x = 7 21 7 5 
Vậy phương trình có tập nghiệm S =   7  Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 14/ 43 Nhóm Toán THCS Toán học là đam mê Bài 2. x = 3 x − 3 = 0 a) 
2x(x − 3) + 5(x − 3) = 0  (x − 3)(2x + 5) = 0    5 − 2x + 5 = 0 x =  2  5 − 
Vậy phương trình có tập nghiệm S = 3;    2  b) 2
(x − 4) − (x − 2)(3 − 2x) = 0
 (x − 2)(x + 2) − (x − 2)(3− 2 ) x = 0 x = 2 
 (x − 2)(3x −1) = 0  1 x =  3  1
Vậy phương trình có tập nghiệm S = 2;   3 c) 2 2
(2x + 5) = (x + 2) 2 2
 (2x + 5) − (x + 2) = 0
 (x + 3)(3x + 7) = 0 x = 3 − x + 3 = 0     7 − 3x + 7 = 0 x =  3  7 − 
Vậy phương trình có tập nghiệm S =  3; −   3  d) 2 x − 5x + 6 = 0 2
x − 2x −3x + 6 = 0
x(x − 2) −3(x − 2) = 0 x = 2
 (x − 2)(x − 3) = 0  x =3
Vậy phương trình có tập nghiệm S = 2;  3 . e) 3 2 2
2x + 6x = x + 3x 2
 2x (x + 3) − x(x + 3) = 0
x(x + 3)(2x −1) = 0  x = 0   x = −3   1 x =  2  1 
Vậy phương trình có tập nghiệm S = 0; 3 − ;   2  Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 15/ 43 Nhóm Toán THCS Toán học là đam mê 2  1   1  f) x + + 2 x + −8 = 0(x  0)      x   x  1 Đặt x + = a x
Khi đó phương trình trở thành: 2 a + 2a − 8 = 0 2
a + 4a − 2a − 8 = 0
a(a + 4) − 2(a + 4) = 0
 (a + 4)(a − 2) = 0 a = −4  a = 2 1 +Với a = -4  x + = 4 − x 2
x + 4x +1 = 0 2  (x + 2) = 3 x = 3 + 2(tm)
 x =− 3+2(tm) 1 +Với a =2  x + = 2 2
x − 2x +1= 0 2
 (x −1) = 0  x =1(t ) m x
Vậy phương trình có tập nghiệm S = {− 3 +1; 3 +1;1} Bài 3. Giải PT 1 5 15 a) − = x +1 x − 2 (x +1)(2 − ĐK; x  -1; x  2 x)
=> x − 2 − 5(x +1) = 1 − 5
<=> x - 2 - 5x - 5 = -15
<=> -4x = -15 + 5 + 2 <=> -4x = -8
<=> x = 2 (không thoả mãn ĐK)
Vậy PT đã cho vô nghiệm. x −1 x 5x − 2 b) − =
ĐK: x  2 ; x  2. − 2 x + 2 x − 2 4 − x
=> (x - 1). (x - 2) - x(x + 2) = 2 - 5x
<=> x2 - 3x + 2 - x2 - 2x = 2 - 5x <=> 0.x = 0
Vậy PT đã cho vô số nghiệm khác 2; -2 x + 5 x − 5 x + 25 c) − =
ĐK: x  0; x  -5; x  5 2 2 2 x − 5x 2x +10x 2x − 50 Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 16/ 43 Nhóm Toán THCS Toán học là đam mê x+5 x−5 x+25 => − = x(x−5) 2x(x+5) 2(x−5)(x+5)
<=> 2(x + 5)2 -(x - 5)2 = x.(x + 25)
<=> 2x2 + 20x + 50 - x2 + 10x - 25 = x2 + 25x <=> 5x = -25
<=> x = - 5 (không thoả mãn ĐK)
Vậy PT đã cho vô nghiệm. 2 1 3x 2x d) − = ĐK: x  1 x 1 − 3 2 x 1 − x + x 1 +
=> x2 +x + 1 - 3x2 = 2x(x - 1)
<=> -2x2 + x + 1 - 2x2 + 2x = 0
<=> 4x2 - 3x - 1 = 0
<=> (4x + 1)(x - 1) = 0 −1 𝑥 = (𝑇𝑀Đ𝐾) <=>[ 4
𝑥 = 1(𝑘ℎô𝑛𝑔 𝑇𝑀Đ𝐾) −1
Vậy PT đã cho có tập nghiệm S = { } 4 7 5− x x −1 1 e) + = + ĐK: x  0; x  2 2 8x 2x(x − 2) 8x −16 4x −8x
=>7(x - 2) + 2(5 - x) = 4(x - 1) + x
<=> 7x - 14+ 10 - 2x = 4x - 4 + x <=> 0.x = 0
Vậy PT đã cho vô số nghiệm khác 0; 2 7 1 1 f) + = 2 2 2 x + 3x + 2 x + 5x + 6 x + 4x + 3 7 1 1 <=> + = (x +1)(x + 2) (x + 2)(x + 3) (x +1)(x +
ĐK: x  -1; x  -2; x  -3 3)
=> 7(x +3) + x + 1 = x + 2
<=> 7x + 21 + x + 1 - x = 2 <=> 7x = 20 20 <=> x = (TMĐK) 7 20
Vậy PT đã cho có tập nghiệm S = { } 7 Bài 4. 𝑥 − 5 = 1 𝑥 = 6 a)|𝑥 − 5| = 3 <=> [ <=> [ 𝑥 − 5 = −1 𝑥 = 4
Vậy PT đã cho có tập nghiệm S = {4; 6} Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 17/ 43 Nhóm Toán THCS Toán học là đam mê 16
b) |−5𝑥| = 3𝑥 − 16 ĐK: x ≥ 3 −5𝑥 = 3𝑥 − 16 −8𝑥 = −16 𝑥 = 2 <=> [ <=> [ <=> [
(𝑘ℎô𝑛𝑔 𝑇𝑀Đ𝐾) 5𝑥 = 3𝑥 − 16 2𝑥 = −16 𝑥 = −8
Vậy PT đã cho vô nghiệm c) |2𝑥 + 1| = |𝑥 − 1| 2𝑥 + 1 = 𝑥 − 1 𝑥 = −2 <=>[ <=> [ 2𝑥 + 1 = 1 − 𝑥 𝑥 = 0
Vậy PT đã cho có tập nghiệm S = {-2;0}
d) |2𝑥 + 1| − |5𝑥 − 2| = 3 −1 Khi x ≤ ta có: -2x - 1+ 5x - 2 = 3 2
<=> 3x = 6 <=> x = 2 (𝑘ℎô𝑛𝑔 𝑇𝑀Đ𝐾) −1 2
Khi < x < ta có: 2x + 1 + 5x - 2 = 3 2 5 <=> 7x = 4 4
<=> x = (𝑘ℎô𝑛𝑔 𝑇𝑀Đ𝐾) 7 2
Khi x ≥ ta có: 2x + 1 - 5x + 2 = 3 5 <=> -3x = 0
<=> x = 0 (𝑘ℎô𝑛𝑔 𝑇𝑀Đ𝐾)
Vậy PT đã cho vô nghiệm Bài 5. a) ( x − )2 2 3  x − 5x + 4 2 2
x − 6x + 9  x − 5x + 4  6
− x + 5x  4 − 9  −x  5 −  x  5
KL: Vậy nghiệm của bất phương trình là x  5
b) ( x − )( x + )  ( x + )2 3 3 2 + 3 2 2
x −9  x + 4x + 4 + 3
 4x  7 +9  x  4
KL: Vậy nghiệm của bất phương trình đã cho là x  4 4x − 5 7 − x c)  3 5
 5.(4x −5)  3.(7 − x)
 20x − 25  21− 3x  23x  46  x  2
KL: Vậy nghiệm của bất phương trình đã cho là x  2 Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 18/ 43 Nhóm Toán THCS Toán học là đam mê 2x +1 3 − 5x 4x +1 d) + 3  − 2 3 4  6.(2x + )
1 + 3.12  4.(3 − 5x) − 3.(4x + ) 1
 12x + 6 + 36  12 − 20x −12x − 3
 12x + 20x +12x  12 − 3 − 6 − 36  44x  33 − −3  x  4 3 −
KL: Vậy nghiệm của bất phương trình là x  4 5x − 3 2x +1 2 − 3x e) +  − 5 5 4 2
 4.(5x −3) + 5.(2x + )
1  10.(2 − 3x) −100
 20x −12 +10x + 5  20 − 30x −100
 20x +10x + 30x  20 −100 +12 − 5  60x  73 − 73 −  x  60 73 −
KL: Vậy nghiệm của bất phương trình là x  60 f) 2
x − 4x + 3  0 2
x − x − 3x + 3  0  . x ( x − ) 1 − 3.( x − ) 1  0  (x − ) 1 ( x − 3)  0 x −1 0 x 1   x − 3  0 x  3 x  3     x −1 0 x 1 x 1   x −3  0 x  3
KL: Vậy nghiệm của bất phương trình là x  3 hoặc x  1 g) 3 2
x − 2x + 3x − 6  0  ( 3 2
x − 2x ) + (3x − 6)  0 2
x .(x − 2) + 3.(x − 2)  0  (x − 2)( 2 x + 3)  0  (x − 2) và ( 2
x + 3) phải cùng dấu, mà ( 2 x + 3)  0 x
  x − 2  0  x  2
KL: Vậy nghiệm của bất phương trình là x  2 Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 19/ 43 Nhóm Toán THCS Toán học là đam mê x + 2 h)
 0  x + 2  0  x  2 − 5
KL: Vây nghiệm của bất phương trình là x  2 − x + 2 i)  0 x − 3 x + 2  0 x  −2    2 −  x  3 x − 3  0 x  3   x 2 0  +  x  2 −   (KTM) x − 3  0 x  3
KL: Vậy nghiệm của bất phương trình là 2 −  x  3 x −1 k) 1 x − 3 x −1 x −1 x − 3 x −1− x + 3 2  −1  0  −  0   0   0 x − 3 x − 3 x − 3 x − 3 x − 3
 2 và x −3 phải cùng dấu
Mà 2>0 nên x − 3  0  x  3
KL: Vậy nghiệm của bất phương trình là x  3
Dạng 3: Giải bài toán bằng cách lập phương trình Bài 1.
Gọi thời gian người đó đi xe máy từ A đến B là x (giờ) (x  0) . 2 2
+) Thời gian về ít hơn thời gian đi 40 phút ( 40 phút =
giờ) nên thời gian về là: x − (giờ) 3 3
+) Lúc đi từ A đến B xe đi với vận tốc trung bình 40km / h nên quãng đường AB dài là: 40x (km)
+) Lúc đi từ B về A , xe tăng vận tốc thêm 5km / h nên quãng đường AB dài là:  2  45 x − (km)  3   2 
Ta có phương trình: 40x = 45 x −   x = 6 (TMĐK)  3 
Vậy quãng đường AB dài là 40.6 = 240(km) 1
Bài 2. Đổi 30 phút = giờ. 2
Gọi thời gian ô tô đi từ A đến B là x (giờ) (x  0) .
+) Thời gian ô tô đi từ A đến B rồi trở về A (không kể thời gian giao hàng) là: 1 7 7
10 giờ − 6 giờ − giờ =
giờ. => Thời gian ô tô đi từ B về A là: − x (giờ) 2 2 2
+) Ô tô đi từ A đến B với vận tốc 40km / h nên quãng đường AB dài là: 40x(k ) m Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 20/ 43 Nhóm Toán THCS Toán học là đam mê 7
+) Ô tô đi từ B về A với vận tốc 30km / h nên quãng đường AB dài là: 30( − x)(km) 2 7 3
Ta có phương trình: 40x = 30( − x)  70x = 105  x = (TMĐK) 2 2 3
Vậy quãng đường AB dài là: 40. = 60(km) . 2 Bài 3.
Gọi vận tốc của xe đạp là x (km/h), x > 0
Vận tốc của xe máy gấp 3 lần vận tốc của xe đạp
Vận tốc của xe máy là 3x (km/h)
Quãng đường AB dài 24 km 24 8
Thời gian xe máy đi từ A đến B là = (km/h) 3x x 24
Thời gian xe đạp đi từ A đến B là (km/h) x 1
Xe máy đi sau xe đạp 1 giờ và đến B trước xe đạp 20 phút = giờ, ta có phương trình 3 24 8 1 16 4 − =1+  =  x = 12(tm) x x 3 x 3
Vận tốc của xe máy là 12.3 = 36 (km/h)
Vậy vận tôc của xe đạp là 12 km/h, vận tốc của xe máy là 36 km/h Bài 4.
Gọi vận tốc ban đầu của ô tô là x (km/h), x > 0
Quãng đường AB dài 90km 90
Thời gian dự định ô tô đi từ A đến B là (km/h) x
Sau 1 giờ, ô tô đi được 1x = x (km/h)
Quãng đường còn lại của ô tô sau khi đi được 1 giờ là 90 – x (km)
Vận tốc của ô tô tăng thêm 10 km/h
Vận tốc của ô tô đi trên quãng đường còn lại là x + 10 (km/h) 90 − x
Thời gian ô tô đi trên quãng đường còn lại là x + (giờ) 10 1 Ô tô nghỉ 15 phút =
giờ và đến B đúng dự định 4 Ta có phương trình: 90 1 90 − x 90 5 90 − x 90 x + 410 x = 9 − 0(ktm) 2 =1+ +  = +  =
x + 50x − 3600 = 0   x 4 x +10 x 4 x +10 x 4(x +10) x = 40(tm)
Vậy vận tốc dự định của ô tô là 40 km/h Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 21/ 43 Nhóm Toán THCS Toán học là đam mê Bài 5. x
Gọi chiều dài quãng đường AB là: x (x  0, k )
m . Thời gian đi từ A đến B là: (giờ). 9
Quãng đường người đó đi từ B về A dài là: x + 6 (km). x + 6
Vận tốc người đó đi từ B về A là: 9 + 3 =12 (km/h). Thời gian đi từ B về A là: (giờ). 12  1 
Vì thời gian về ít hơn thời gian đi 20 phút = h
 nên ta có phương trình:  3  x x + 6 1 −
=  4x − 3x −18 =12  x = 30( d tm k) 9 12 3
Vậy quãng đường AB dài 30km. Bài 6. 3
Từ 8h30’ đến 10h là 1h30’ = h. 2 3
Quãng đường người đi từ A – B đã đi được trong 1h30’ là: 40. = 60 (km) 2
Gọi thời gian xe đi từ B về A đến chỗ gặp là: x (x  0) (giờ)
Quãng đường xe đi từ B về A đến chỗ gặp là: 60x (km)
Quãng đưỡng xe đi từ A đến B đến chỗ gặp là: 60 + 40x (km)
Vì hai xe gặp nhau ở chính giữa quãng đường AB nên ta có phương trình:
60x = 40x + 60  20x = 60  x = 3(t d m k)
Vậy hai xe gặp nhau lúc: 10h + 3h =13h . Bài 7.
Gọi chiều dài quãng đường AB là x (km, x  0 ). x
Thời gian ca nô thứ nhất đi từ A đến B là: (giờ). 20 x
Thời gian ca nô thứ hai đi từ A đến B là: (giờ). 24 2 x 2 x
Do ca nô thứ hai nghỉ 40 phút = giờ nên ta có phương trình: + =  x = 40 (thỏa) 3 24 3 20
Vậy quãng đường AB dài 40 km. Bài 8.
Gọi vận tốc riêng của ca nô là: x (km/giờ, x  0 ).
Vận tốc của ca nô khi đi xuôi dòng là: x + 2 (km/giờ).
Vận tốc của ca nô khi đi ngược dòng là: x − 2 (km/giờ).  7 1 1 h 0 ' = h  6 Ta có:  3 1  3 h 0 ' = h  2 Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 22/ 43 Nhóm Toán THCS Toán học là đam mê 7 3
Theo đề bài ta có phương trình: (x+ 2). = (x − 2).
x =16 (thỏa mãn ĐK) 6 2 7 7
Do đó quãng đường AB bằng: (x + 2). = (16 + 2). = 21 (km) 6 6
Vậy quãng đường AB dài 21 km. Bài 9.
Gọi số áo mà tổ đó phải may theo kế hoạc là x (áo) * (x  N )
Số áo mà tổ đó đã may trên thực tế là: x + 20 (áo) x
Thời gian tổ đó phải may theo kế hoạch là: (ngày) 30 x + 2
Thời gian thực tế tổ đó đã may là: (ngày) 40
Theo bài ra, ta có phương trình: x x + 20 − = 3 30 40 4x 3(x + 20) 360  − = 120 120 120
 4x −3(x + 20) = 360
 4x −3x −60 = 360
x = 420(thỏa mãn)
Vậy số áo mà tổ đó phải may theo kế hoạch là 420 áo. Bài 10.
Gọi số cá đội đánh cá phải đánh bắt theo kế hoạch là x (tấn) (x  0)
Số cá đội đánh cá đã đánh bắt trên thực tế là x +10 (tấn) x
Thời gian đội đánh cá phải đánh bắt theo kế hoạch là: (tuần) 20 x +10 x +10
Thời gian thực tế đội đánh cá đã đánh bắt là: = (tuần) 20 + 6 26
Theo bài ra, ta có phương trình: x x +10 − = 1 20 26 13x 10(x +10) 260  − = 260 260 260
13x −10(x +10) = 260
13x −10x −100 = 260  3x = 360  x =120(thỏa mãn)
Vậy số cá đội đánh cá phải đánh bắt theo kế hoạch là 120 (tấn) Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 23/ 43 Nhóm Toán THCS Toán học là đam mê Bài 11.
Gọi số áo len tổ 1 phải dệt theo kế hoạch là x (áo) * (x  N )
Số áo len tổ 2 phải dệt theo kế hoạch là 140 − x (áo) 10 110
Thực tế, tổ 1 đã dệt được x +10%x = x + x = x (áo) 100 100 5 105
Thực tế, tổ 2 đã dệt được (140 − x) + (140 − x) = (140 − x) (áo) 100 100
Theo bài ra, ta có phương trình: 110 105 x + (140 − x) = 150 100 100 110x +105(140 − ) x = 15000
110x +14700−105x =15000  5x = 300  x = 60(thỏa mãn)
Vậy theo kế hoạch số áo len tổ 1 phải dệt là 60 (áo)
Theo kế hoạch số áo len tổ 2 phải dệt là 140 − 60 = 80 (áo) Bài 12.
Gọi thời gian người thứ hai làm một mình hoàn thành xong công việc là x (giờ) (x>12) 1
1giờ, người thứ hai làm được (công việc) x
Vì hai công nhân cùng làm chung một công việc dự định trong 12 giờ sẽ hoàn thành xong 1
công việc nên 1giờ hai người làm chung được (công việc) 12 1 1
4 giờ đầu hai người làm chung được 4  = (công việc) 12 3 1 10
10 giờ sau người thứ hai làm được 10  = (công việc) x x 1 10
Theo bài ra, ta có phương trình: + = 10 2 1  = 10.3  x = = 15 (thỏa mãn) 3 x x 3 2
Vậy nếu người thứ hai làm một mình thì 15 giờ sẽ hoàn thành xong công việc. 10
Bài 13. Ta có: 3 giờ 20 phút = giờ 3
Gọi thời gian vòi thứ nhất chảy một mình đầy bể là x ( giờ) ( x  0 ). 1
Trong một giờ vòi thứ nhất chảy được (bể). x 10 3
Trong một giờ cả hai vòi chảy được 1: =
(bể), vậy trong một giờ vòi hai chảy một 3 10 3 1 mình được: − (bể). 10 x Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 24/ 43 Nhóm Toán THCS Toán học là đam mê 4
Khi vòi thứ nhất chảy 3 giờ và vòi thứ hai chảy 2 giờ thì được bể, ta có phương trình 5 1  3 1  4 1 3 4 sau: 3. + 2. − =  + =    x = 5(TMĐK) x 10 x  5 x 5 5
Vậy vòi một chảy một mình trong 5(giờ) thì đầy bể. 3 1 1
Trong một giờ vòi hai chảy một mình được: − = (bể). 10 5 10
Vậy vòi hai chảy một mình trong 10 giờ thì đầy bể. Bài 14.
Gọi số cuốn sách ban đầu ở giá thứ nhất là x (cuốn) ( x N * ) thì số cuốn sách ở giá thứ
hai ban đầu là 450 − x (cuốn).
Số cuốn sách lúc sau ở giá thứ nhất là x − 50 (cuốn).
Số cuốn sách lúc sau ở giá thứ hai là 450 − x + 50 = 500 − x (cuốn). 5
Vì nếu chuyển 50 cuốn từ giá thứ nhất sang giá thứ hai thì số sách ở giá thứ nhất bằng 4 5
số sách ở giá thứ hai nên ta có phương trình: x − 50 = (500 − 5
x)  x − 50 = 625 − x 4 4 9 
x = 675  x = 300 (TMĐK). 4
Vậy số sách ở giá thứ nhất ban đầu là 300 cuốn. Số sách ở giá thứ hai ban đầu là 150 cuốn.
Dạng 4: Các bài tập hình học. Bài 1. x C a) CMR ABE ADC 15 Xét ABE  và ADC ADC có: B A chung 8  AB 8 2 = =  AI AE 12 3  AD 10 2  10 = =  D AC 15 3 12 E y AB AD 2  = = AE AC 3 Vậy ABE ADC (c-g-c) b) CMR A . B DC = A . D BE AB BE Vì ABE A
DC (theo câu a) =  A . B DC = A . D BE (đpcm). AD DC
c) Tính DC biết BE =10c . m AB BE 8 10 Ta có =  =
DC = 12,5(cm) AD DC 10 DC Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 25/ 43 Nhóm Toán THCS Toán học là đam mê d) CMR I . B IE = I . D IC Xét IBC và IDE
Ta có BIC = DIE (đối đỉnh)
BCI = IED (vì ABE ADC ) Suy ra IBC IDE (g-g) IB IC  =  I . B IE = I . D IC ID IE Vậy I . B IE = I . D IC (đpcm). Bài 2. a) Chứng minh: AEC AFB A - Xét AEC  và AFB  : + A chung
CE ⊥ AB(gt)  CEA = 90   F +
  CEA = BFA = 90
BF ⊥ AC(gt)  BFA = 90  E NAEC AFB (gg) M H b) Chứng minh: A .
E AB = AF.AC rồi từ đó suy ra D C AEF ACB B - Ta có AEC AAE AC FB  =
(cạnh tương ứng tỉ lệ)  A .
E AB = AF.AC AF AB - Xét AEF  và ACB : + A chung AE AF + A .
E AB = AF.AC (cmt)  = AC ABAEF ACB (c.g.c) c) Chứng minh: BDH BFC và 2
BH.BF + CH.CE = BC - Xét ABC
+ BF và CE là đường cao (gt) + BF và CE cắt nhau tại H
H là trực tâm của ABC
(đ/l 3 đường cao trong tam giác)
AH là đương cao AD là đường cao  AD ⊥ BC - Xét BDH  và BFC
+ BDH = 90 = BFC ( BF ⊥ AC; AD ⊥ BC ) + B chung  BH BD BDH BFC (gg)  =
(cạnh tương ứng tỉ lệ) BC BF
BH.BF = B . D BC (1) Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 26/ 43 Nhóm Toán THCS Toán học là đam mê - Xét CHD và CBE
+ CEB = DHC = 90 (CE ⊥ A ; B AD ⊥ BC ) + B chung  CHD CBE (gg) CH CD  = (cạnh tương ứng) CB CE
CH.CE = C . D CB (2)
- Từ (1) và (2) ta có: BH BF + CH CE = BD BC + CD BC = BC (BD + CD) 2 . . . .
= BC.BC = BC Vậy 2
BH.BF + CH.CE = BC .
d) Vẽ DM ⊥ AB tại M , DN ⊥ AC tại N . Chứng minh MN / /EF - Ta có:
+) CE ⊥ AB (gt) 
(định lí từ vuông góc đến song song) ⊥
( )  CE / /MD HE / /MD MD AB gt 
+) BF ⊥ AC (gt) ⊥
( )  BF / /DN HF / /DN ND AC gt  - Xét AEH  và AMD
: HE / /MD (cmt)  AEH A
MD (định lí Talet) AE AH  =
(cạnh tương ứng tỉ lệ) AM AD - Xét AFH  và A
ND: HF / /DN (cmt)   AFH A
ND (định lí Talet) AF AH  =
(cạnh tương ứng tỉ lệ) AN AD AF AH AE AH AF AE - Vậy = ; = thì =
EF / /MN ( định lí Talet đảo) AN AD AM AD AN AM Bài 3. a) Chứng minh C  HB C  BA. A + Ta có BH ⊥ AC(gt) nên B  HC vuông tại H . + Xét C  HB và C  BA ta có: 0 H CHB = CBA = 90 K M Chung C  C  HB C  BA(g − g) . O b) Chứng minh 2 AB = AH.AC . N Xét B  HA và C  BA ta có: B C I 0 AHB = ABC = 90 A chung  B  HA C  BA(g − AB AH g)  = (cặp cạnh tương ứng) 2  AB = AH.AC(đpcm). AC AB Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 27/ 43 Nhóm Toán THCS Toán học là đam mê c) Tính độ dài AC, BH .
- Áp dụng định lý Py-ta-go vào A  BC vuông tại B ta có: 2 2 2 2 2 AC = AB + BC = 15 + 20 = 625  AC = 25cm - Ta có: 2
AB = AH.AC (chứng minh trên) 2 2 AB 15  AH = = = 9cm AC 25
- Theo ý a) và ý b), ta có: C  HB C  BA và B  HA C  BA nên: C  HB B  HA BH BC  = BC.AH 20.9  BH = = = 12cm . AH AB AB 15 d) Chứng minh B  KI B  CA. - Ta có: C  HB B
 HA (chứng minh trên)  BCH = ABH (1) - Tứ giác BKHI có: 0
B = K = I = 90 nên là hình chữ nhật.
 KI = BH (tính chất hình chữ nhật)
Gọi O là giao điểm của hai đường chéo BH và IK  OB = OK  B
 OK cân tại O  BKI = KBH (2) Từ (1), (2)  BKI = BCH - Xét B  KI và B  CA có: BKI = BCH Chung B  B  KI B  CA(g.g) . e) Tính diện tích B  KN .
– Ta có: BM là trung tuyến của A
 BC vuông tại B nên: BM = AM  A  MB cân tại M  BAC = ABM Mà: BKI = BCH (cmt) và: 0 BAC + BCH = 90 0  BKI + ABM = 90 (cmt) Suy ra: B  KN vuông tại N . - Ta có: + KI = BH =12cm BK KI + B  KI B  CA  = BC CA BC.KI 20.12  BK = = = 9,6cm CA 25 Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 28/ 43 Nhóm Toán THCS Toán học là đam mê - Xét B  KN và B  CA có: 0 BNK = ABC = 90 BKN = BCA (cmt)  B  KN A  CB(g.g) 2 2 S  BK   9,6  92,16 BKN  = = =     S  AC   25  625 ACB 1 1 Mà: 2 S = BA.BC = .15.20 =150cm ACB 2 2 92,16 92,16 2  S = .S = .150 = 22,1184cm . BKN ACB 625 625 Bài 4. K a) Chứng minh A  IB ∽ A  EC F Xét A  IB và AEC  có: A là góc chung. 0 AIB = AEC = 90 D Q C Do đó: A  IB A  EC (g.g) I b) Chứng minh AIE ABC  Do A  IB ∽ AEC  AI AB  =  AI AE = A B E AE AC AB AC Xét AIE và A  BCcó: A là góc chung. AI AE = AB AC Do đó: A  IE ∽ ABC  (c.g.c) c) Chứng minh: 2 AB.AE + AF.CB = AC AI AE Ta có: =  AB.AE = AC.AI (1) AB AC Xét A  FC và CIB có:
FAC = ICB (so le trong). 0 AFC = CIB = 90 Do đó: AFC  ∽ C  IB (g.g) AF AC  = AF CI  =
 AF.CB = AC.CI (2) CI CB AC CB Từ (1) và (2) 2  A .
B AE + AF.CB = A . C AI + A . C CI = A .
C ( AI + CI ) = AC Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 29/ 43 Nhóm Toán THCS Toán học là đam mê d) Chứng minh: 2
BI = IK.IQ IQ IC
Xét tam giác ABI có: AB / /QC  =
(3) (Theo hệ quả định lí Ta-let) IB IA IC IB
Xét tam giác BIC có: BC / / AK  =
(4) (Theo hệ quả định lí Ta-let) IA IK IQ IB Từ (3) và (4)  =  IB.IB = IK.IQ IB IK Vậy 2 BI = IK.IQ (đpcm) Bài 5.
a) Chứng minh rằng: B
DC đồng dạng với A B
EDB từ đó suy ra 2 BD = DC.DE . Xét B
DC và EDB có: BDC chung O F K
BCD = DBE = 90I => B
DC đồng dạng với EDB (g.g) D C E BD DC => = => 2 BD = DC.DE DE BD b) Tính DB,CE . Ta có: D
CB vuông tại C => 2 2 2
BD = BC + DC => BD = 5 (cm) 2 BD 25 Ta có 2
BD = DC.DE => DE = = (cm) DC 4 25 9
Mà DE = DC + CE => CE = DE − DC = − 4 = (cm) 4 4
c) Chứng minh được CE BD IF EI Xét EBO  có: IF BO => =
(hệ quả định lý Talet) BO EO IC EI Xét E
DO có: IC DO => =
(hệ quả định lý Talet) DO EO IF IC => = BO DO
Mà BO = DO ( ABCD là hình chữ nhật) => IF = IC
=> I là trung điểm của đoạn CF .
d) Chứng minh rằng ba điểm D,K ,F thẳng hàng. IK CI Xét B
OK có CI BO => = (hệ quả đl Talet) OK OB Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 30/ 43 Nhóm Toán THCS Toán học là đam mê OK OD
Mà IC = IF;OD = OB => = IK IF Xét KOD và KIF có: = ( ) OK OD DOK FIK BD CF ; = IK IF => K
OD đồng dạng KIF (c.g.c)
=> OKD = IKF => OKD + DKE = IKF + DKE => DKF = 180 => D,K ,F thẳng hàng. Bài 6. a) Chứng minh ADB AEC và AED ACB
- Xét ADB và AEC  , có: BAD chung 0 BDA = CEA = 90  ADB AEC (g-g) -Vì ADB A
EC (chứng minh trên) AD AB AD AE  =  = AE AC AB AC
- Xét AED và ACB , có BAD chung AD AE = (chứng minh trên) AB ACAED ACB (c-g-c) b) Chứng minh: H . E HC = H . D HB
- Xét BHE và CHD , có
BHE = CHD (đối đỉnh) 0 BEH = CDH = 90  BHE C
HD(g − g) HB HE  = (tính chất) HC HDH . E HC = H . D HB
c) Chứng minh: H , M , K thẳng hàng và AED = ACB
BD ⊥ AC ( gt ) - Ta có
hay BH / /CK ( ) 1 (từ ⊥ đến //) ⊥
( )  BD / /CK CK AC gt 
CE ⊥ AB ( gt )  - Ta có
hay CH / / B K (2) (từ đến //) ⊥
( )  CE / / BK BK AB gt  Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 31/ 43 Nhóm Toán THCS Toán học là đam mê - Từ ( )
1 và (2)  BHCK là hình bình hanh
BC và HK cắt nhau tại trung điểm mỗi đường
Mà M là trung điểm của BC
M cũng là trung điểm của HK
Hay H, M, K thẳng hàng
d) AH cắt BC tại O. Chứng minh 2 B . E BA + C . D CA = BC - Xét BAO  và BCE , có ABC chung 0 BEC = AOB = 90    ( BA BO BAO BCE g.g )  =
(t / c)  B . A BE = B . O BC (3) BC BE CD CB
Chứng minh tương tự ta có: CDB CO
A( g − g )  =  .
CD CA = BC.CO (4) CO CA
Từ (3) và (4)  BE.BA + C .
D CA = BC.BO + BC.CO = BC.( BO + CO) = BC.BC 2  B . E BA + C .
D CA = BC (đpcm). HO HD HE e) Chứng minh: + + = 1 AO BD CE 1  1 S = H . O BC BHC H . O BC  S HO - Ta có: 2 BHC 2   = = 1 S 1 AO S = A .  ABC O BC A . O BC ABC 2  2 1 . HD AC S HD - CMTT: AHC 2 = = S 1 BD ABC BD.AC 2 1 HE.AB S HE Suy ra AHB 2 = = S 1 CE ABC CE .AB 2 HO HD HE S S S S + S + S S BHC AHC AHB BHC AHC AHB ABC  + + = + + = = AO BD CE S S S S S ABC ABC ABC ABC ABC HO HD HE  + + =1(dpcm) AO BD CE
f) Chứng minh H là giao điểm của đường phân giác của tam giác ODE - Ta có AED A
CB (cmt)  AED = ACB (2 góc tương ứng).. BE BO - Do B . A BE = B . O BC (cmt )  = BC BA Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 32/ 43 Nhóm Toán THCS Toán học là đam mê -Xét BEO  và BCA , có: ABC chung BE BO = (cmt) BC BABEO B
CA(g.g)  BEO = ACB(6)
Từ (5) và (6)  AED = BEO 0
AED + DEC = 90   Ta có:
  DEC = OEC EH là phân giác của DOE 0
BEO + OEC = 90  
CMTT: OH là phân giác của EOD
Vậy H là giao điểm của đường phân giác của tam giác ODE g) Cho góc 0
ACB = 45 , Gọi P là trung điểm của DC. Từ D kẻ đường thẳng vuông góc với
BP tại I và cắt CK tại N. Tìm tỉ số diện tích của tứ giác CPIN và diện tích tam giác DCN - Xét vDIP và vDCN , có: Có PDI chung  vDIP v
DCN (g − g) 2 2 SDP   1  1 DIP  = = = .     SDC   2  4 DCN S S − S S 1 3 Ta có: CPIN DCN DIP = =1 DIP − =1− = . S S S 4 4 DCN DCN DCN 3
Vậy tỉ số diện tích của tứ giác CPIN và diện tích tam giác DCN bằng . 4
h) Tam giác ABC có điều kiện gì thì tứ giác BHCK là hình thoi? Hình chữ nhật?
- Giả sử BHCK là hình thoi
HBC = HCB mà ADB A
EC ABD = ACE
HBC + ABD = HCB + ACE
ABC = ACB ABC  cân tại A Vậy ABC
cân tại A thì BHCK là hình thoi
- Giả sử BHCK là hình chữ nhật 0 0
BHC = 90  EHD = 90
Xét tứ giác: AEHD , có 0 0 0
EHD = 90 , AEH = 90 , ADH = 90
AEHD là hình chữ nhật 0  BAC = 90  ABC  vuông tại A Vậy ABC
vuông tại A thì BHCK là hình thoi. Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 33/ 43 Nhóm Toán THCS Toán học là đam mê Bài 7.
a) Xét ∆𝐶𝐷𝐼 và ∆𝐶𝐹𝐾 có: 𝐶𝐷𝐼 ̂ = 𝐶𝐹𝐾 ̂ = 900 𝐶𝐷𝐼 ̂ = 𝐾𝐶𝐹
̂ (vì CK là tia phân giác góc FCM)
Do đó ∆𝐶𝐷𝐼 ~ ∆𝐶𝐹𝐾 (g.g) 𝐶𝐷 𝐶𝐼 ⇒ = (1) 𝐶𝐹 𝐶𝐾
Xét ∆𝐶𝐷𝐹 có CI là đường phân giác của góc
ACB nên theo tính chất đường phân giác trong tam giác ta có: 𝐶𝐷 𝐷𝐼 = (2) 𝐶𝐹 𝐹𝐼 𝐶𝐷 𝐶𝐼 𝐷𝐼 Từ (1) và (2) suy ra = = 𝐶𝐹 𝐶𝐾 𝐹𝐼
Vì ∆𝐶𝐷𝐼 ~ ∆𝐶𝐹𝐾 nên 𝐶𝐼𝐷 ̂ = 𝐶𝐾𝐹 ̂ , mà 𝐶𝐼𝐷 ̂ = 𝐾𝐼𝐹 ̂ . Do đó 𝐶𝐾𝐹 ̂ = 𝐾𝐼𝐹 ̂
⇒∆𝐹𝐾𝐼 cân tại F ⇒ FI = FK.
b) Tứ giác AEMF có 𝐴𝐸𝑀
̂ = 900 (Vì 𝑀𝐸˔𝐴𝐵) 𝐸𝐴𝐹
̂ = 900(Vì ∆𝐴𝐵𝐶 vuông tại A); 𝐴𝐹𝑀
̂ = 900 (Vì 𝑀𝐹˔𝐴𝐶)
Do đó tứ giác AEMF là hình chữ nhật.
c) Xét ∆𝐴𝐻𝐶 và ∆𝑀𝐹𝐶 có: 𝑀𝐹𝐶 ̂ chung; 𝐴𝐻𝐶 ̂ = 𝑀𝐹𝐶 ̂ = 900
Do đó ∆𝐴𝐻𝐶 ~ ∆𝑀𝐹𝐶 (g.g)
Xét ∆𝐴𝐵𝐻 và ∆𝑀𝐵𝐸 có: 𝐵̂ chung; 𝐴𝐻𝐵 ̂ = 𝑀𝐸𝐵 ̂ = 900
Do đó ∆𝐴𝐵𝐻 ~ ∆𝑀𝐵𝐸 (g.g) 𝐴𝐻 𝐵𝐻 ⇒ =
⇒ 𝐴𝐻. 𝐵𝐸 = 𝐵𝐻. 𝑀𝐸 𝑀𝐸 𝐵𝐸 𝐴𝐻 𝐴𝐶
d) Vì ∆𝐴𝐻𝐶 ~ ∆𝑀𝐹𝐶 nên =
⇒ 𝑀𝐹. 𝐴𝐶 = 𝐴𝐻. 𝑀𝐶 (3) 𝑀𝐹 𝑀𝐶 𝐴𝐵 𝐴𝐻
Vì ∆𝐴𝐵𝐻 ~ ∆𝑀𝐵𝐸 nên =
⇒ 𝑀𝐸. 𝐴𝐵 = 𝐴𝐻. 𝑀𝐵 (4) 𝑀𝐵 𝑀𝐸
Vì AM là đường trung tuyến của ∆𝐴𝐵𝐶 nên M là trung điểm của BC ⇒ 𝐵𝑀 = 𝑀𝐶 (5)
Từ (3), (4), (5) ⇒ 𝑀𝐸. 𝐴𝐵 = 𝐴𝐻. 𝑀𝐵
e) Xét ∆𝐴𝐵𝐶 có M là trung điểm của BC; 𝑀𝐸 ∕∕ 𝐴𝐶 (Vì cùng vuông góc với AB).
⇒M là trung điểm của AB. ⇒ 𝐴𝐵 = 2𝐴𝐸 (6).
Xét ∆𝐴𝐵𝐻 𝑣à ∆𝐶𝐵𝐴 có: 𝐵̂ chung; 𝐴𝐻𝐵 ̂ = 𝐵𝐴𝐶 ̂ = 900
Do đó ∆𝐴𝐵𝐻 ~ ∆𝐶𝐵𝐴 (𝑔. 𝑔) 𝐴𝐵 𝐵𝐻 ⇒ =
⇒ 𝐴𝐵2 = 𝐵𝐻. 𝐵𝐶 (7) 𝐵𝐶 𝐴𝐵
Từ (6), (7) ⇒ 𝐵𝐻. 𝐵𝐶 = (2𝐴𝐸)2 hay 𝐵𝐻. 𝐵𝐶 = 4𝐴𝐸2 Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 34/ 43 Nhóm Toán THCS Toán học là đam mê Bài 8.
a) Chứng minh CAI N CB A Ta có 0 ACI + ICB = 90 (do A
 BC vuông tại C ) I 0
ICB + BCN = 90 (do CI ⊥ MN) M
Nên ACI = BCN (1) Ta lại có 0
CAB + CBA = 90 (do A
BC vuông tại C ) C B x 0
CBA + CBN = 90 (do By ⊥ AB)
Nên CAB = CBN (2)
Từ (1) và (2) suy ra CAI  N CB (g.g) N b) Chứng minh A .
B NC = NI.CB . y Xét CAB và CIN , ta có: 0
ACB = ICN = 90  CA CI  = (do CAI  N) CBCB CN Suy ra CAB  N CI (c.g.c) AB CB  = IN CN Vậy A .
B NC = NI.CB
c) Chứng minh góc MIN là góc vuông. Ta có CAB  N CI (cmt)  CAB N CICIM MAC Mà 0 CAB + MAC =90 0
CIN + CIM =90
Hay góc MIN là góc vuông
d) Tìm vị trí của điểm I để diện tích IMN gấp hai lần diện tích tam giác ABC . 1 S = . CA CB ABC  2 1 1 S
= IM.IN = IC.MN IMN 2 2 S IM .IN IC.MN IMN  = = S C . A CB C . A CB ABCS = 2.S IMN ABC
IM.IN = 2C . ACB
Suy ra I là trung điểm AB. Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 35/ 43 Nhóm Toán THCS Toán học là đam mê Bài 9. a) Tính IP . M N Xét NIP có 0
NIP = 90 (NI là đường cao): 1 2 2 2 2
NP = NI + IP (Định lý Py – ta – go) 2 2 2  15 =12 + IP K 2
IP = 225 −144 = 81 Q H E I PIP = 9(cm)
b) Chứng minh QN ⊥ NP
Có QP = QI + IP = 16 + 9 = 25(c ) m Xét QNI có 0
QIN = 90 (NI là đường cao): 2 2 2
NQ = NI + IQ (Định lý Py – ta – go) 2 2 2  QN = 12 +16 2
QN = 144 + 256 = 400  QN = 20(cm) Xét QNP có: 2 2 2 2 2 2
QP = QN + NP (25 = 20 +15 )  Q
NP vuông tại N  QN ⊥ NP
c) Tính diện tích hình thang MNPQ Kẻ MH ⊥ QP
Có IH = QP − QH − IP = 25 − 9 − 9 = 7(c ) m Xét QMH và PNI có:
MQ = NP ( MNPQ là hình thang cân) 0 MHQ = NIP(= 90 )
MQH = NPI ( MNPQ là hình thang cân)  QMH = PNI (ch− gn)
QH = IP = 9cm (2 cạnh tương ứng)
Xét tứ giác MNIH có MN / /IH; MH / / NI (⊥ QP)  tứ giác MNIH là hình bình hành
MN = IH = 7(c ) m
(MN + QP).NI (7 + 25).12 2  S = = = 192(cm ) MNPQ 2 2
d) Gọi E là trung điểm của PQ . Đường thẳng vuông góc với EN tại N cắt PQ tại K . Chứng minh rằng 2 KN = K . P KQ . Xét Q
NP vuông tại N (cmt) có E là trung điểm của QP Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 36/ 43 Nhóm Toán THCS Toán học là đam mê 1
NE = QE = PE = QP (tính chất đường trung tuyến trong tam giác vuông) 2  Q
NE cân tại E
EQN = N (tính chất tam giác cân) ( ) 1 1 0 N + ENP = 90   Mặt khác, 1
  N = N (2) 1 2 0 N + ENP = 90  2  Từ ( )
1 và (2)  EQN = N2 Xét KNQ  và KPN có: K chung EQN = N2  KNQ KKN KQ
PN (g.g)  = 2  KN = K . P KQ (đpcm). KP KN Bài 10: A
* Ta có AH // OM (cùng vuông góc với BC) B'
MN // AB (chứng minh được MN là đường trung bình của ABC  ) H N
 BAH = OMN (góc có cạnh tương ứng song song) G' O
* Chứng minh tương tự ta được ABH = ONM * Xét B C ABH  và M
NO có BAH = OMN ; ABH = ONM A' M nên ABH  đồng dạng với MNO AH AB  = AB AH , mà
= 2 ( tc đường trung bình MN)  = 2 OM MN MN OM
* Gọi giao điểm của HO với AM là G’, ta sẽ chứng minh G’ trùng với G.
- Thật vậy ta có HAG ' = G ' MO (AH //OM); AG 'H = MG 'O ( đối đỉnh) nên AHG' đồng AG ' AH HG ' dạng với MOG' => = = = 2 G ' M OM G 'O
=> G’ là trọng tâm ABC
, hay G '  G G’. Khi đó có H, G, O thẳng hàng và HG = 2 GO Bài 11.
a) Tính diện tích toàn phần và thể tích của hình hộp chữ AB = 12cm BC = 9cm nhật. AE = 10cm
Diện tích toàn phần của hình hộp chữ nhật là: S = S + S = ( + ) + = ( 2 2. 12 9 .2.10 2.12.9 636 cm ). tp xq d
Thể tích hình hộp chữ nhật là: V = AB AD AE = = ( 3 . . 12.9.10 1080 cm ). Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 37/ 43 Nhóm Toán THCS Toán học là đam mê
b) Gọi I và O lần lượt là tâm đối xứng của hình chữ nhật EFGH và ABCD. Đường thẳng
OI song song với những mặt phẳng nào? Ta có:
- ABFE là hình chữ nhật suy ra AE / /BF và AE = BF (1)
- BCFG là hình chữ nhật suy ra BF / /CG và BF = CG (2)
Từ (1) và (2) suy ra: AE / /CG và AE = C . G
Do đó ABGC là hình bình hành.
Ta có: OA = OC và EI = IG
OI là đường trung bình của hình bình hành AEGC .
Nên OI / / AE / /C . G
Mà AE mp ( AEHD)
Do đó IO / /mp ( AEHD)
Tương tự: IO / /mp (BCGF ) , IO / /mp ( AEFB) , IO / /mp ( DCGH )
c) Chứng tỏ hình chóp I.ABCD có các cạnh bên bằng nhau nhưng không phải hình chóp đều.
Ta có: IO / / AE; AE ⊥ AC IO ⊥ A . C
Tương tự ta có: IO ⊥ O . B Xét IOC và IOB có: IO chung = = 90o IOC IOB
OC = OB (Do ABCD là hình chữ nhật) Suy ra IOC = I
OB IC = I . B
Tương tự: IA = IB = IC = ID
Suy ra hình chóp I.ABCD có các mặt bên là tam giác cân.
Mà ABCD là hình chữ nhật có AB BC
Nên hình chóp I.ABCD không là hình chóp đều.
d) Tính diện tích xung quanh của hình chóp I.ABCD. Xét ABC  vuông tại B : 2 2 2
AC = AB + BC Suy ra 2 2 2 2 AC =
AB + BC = 12 + 9 = 15(cm) ACOC = OA = = 7,5(cm) . 2 Xét O
IC vuông tại O : 2 2 2
IC = OC + OI Suy ra 2 2 2 2
IC = OC + OI = 7,5 +10 = 12,5(cm) .
Kẻ IK ⊥ CB . Xét I
CB cân tại I có IK là đường cao suy ra IK là đường trung tuyến. Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 38/ 43 Nhóm Toán THCS Toán học là đam mê CB 9 Nên CH = HB = = = 4,5(cm) . 2 2 Xét I
CK vuông tại I : 2 2 2
IK = CI − CH 2 2  IK = 12,5 − 4,5 11, 66(cm).
Diện tích xung quanh của hình chóp I.ABCD là: 1 S = 4.S
= 4. IH.BC = 2.11,66.9 = 209,88 cm xq IBC ( 2). 2
Dạng 5. Một số bài tập nâng cao. Bài 1. 2 2 2
1) a + b + c ab + bc + ca 2 2 2
 2a + 2b + 2c  2ab + 2bc + 2ca  ( 2 2
a − 2ab + b ) + ( 2 2
b − 2bc + c ) + ( 2 2
c − 2ca + a )  0
 (a − b)2 + (b − c)2 + (c − a)2  0 (luôn đúng)
Dấu “=” xảy ra  a = b = c
(a +b +c )(a+b+c)2 2 2 2 2) 3
 3(ab +bc + ca) Ta chứng minh: ( + + )  ( + + )2 2 2 2 3 a b c a b c 2 2 2 2 2 2
 3a + 3b + 3c a + b + c + 2ab + 2bc + 2ca 2 2 2
 2a + 2b + 2c  2ab + 2bc + 2ca
 (a − b)2 + (b − c)2 + (c − a)2  0 (luôn đúng)
Ta chứng minh: (a + b + c)2  3(ab + bc + ca) Theo trên ta có 2 2 2
a + b + c ab + bc + ca 2 2 2
a + b + c + 2ab + 2bc + 2ca  3ab + 3bc + 3ca
 (a + b + c)2  3(ab + bc + ca)
Dấu “=” xảy ra  a = b = c
(a +b −c)2 3)
 4a (b − c)
a + 2a(b −c) + (b −c)2 2
 4a(b − c)
a − 2a(b −c) + (b −c)2 2  0
 (a −b + c)2  0 (luôn đúng) x y (x + y)2 2 2 4a) +  (a,b  0) a b a + b
Dùng phép biến đổi tương đương và , a b  0 ta có: Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 39/ 43 Nhóm Toán THCS Toán học là đam mê x y (x + y)2 2 2 + 
x b(a + b) + y a(a + b)  (x + y)2 2 2 ab a b a + b 2 2 2 2 2 2 2 2
x ab + x b + y a + y ab x ab + 2xyab + y ab 2 2 2 2
x b − 2xyab + y a  0
 (bx − ay)2  0 (luôn đúng) x y
Dấu “=” xảy ra  bx = ay  = a b x y z
(x + y + z)2 2 2 2 4b) + +  (a, ,bc  0) a b c a + b + cx y z
(x + y)2 z (x + y + z)2 2 2 2 2 Ta có  +  +  + 
(a,b,c  0)  a b c a + b c a + b + c x y z Dấu “=” xảy ra  = = a b c 2 4c) ( + )  ( 2 2 + )( 2 2 ax by a b x + y ) 2 2 2 2 2 2 2 2 2 2 2 2
a x + 2abxy + b y a x + a y + b x + b y 2 2 2 2
 2abxy a y + b x 2 2 2 2
a y + b x − 2abxy  0
 (ay − bx)2  0 (luôn đúng)
5) Với a,b,c là các số thực thỏa mãn a + b + c + ab + bc + ca = 6.Chứng minh 2 2 2
a + b + c  3 a + b + c
Từ (a + b + c)  (ab + bc + ca) ( )2 2 3
ab + bc + ca  3 2 a + b + c
ab + bc + ca = 6 − (a + b + c) ( )  3
 (a + b + c)2 + 3(a + b + c) −18  0
 (a + b + c + 6)(a + b + c − 3)  0
a + b + c  3
 a+b+c 6−
(a +b + c)2 2 3 2 2 2
a + b + c   = 3 3 3
Dấu “=” xảy ra  a = b = c =1 Bài 2. Ta có: 2 2 2 2
10a − 3b + ab = 0  10a + 6ab − 5ab − 3b = 0  2a (5a + 3b) − b (5a + 3b) = 0
 (2a −b)(5a + 3b) = 0  2a −b = 0 hoặc 5a +3b = 0 Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 40/ 43 Nhóm Toán THCS Toán học là đam mê
 2a = b hoặc 5a = 3
− b (không thỏa mãn do b > a > 0)
Thay b = 2a vào biểu thức A, ta được: 2a − 2a 5.2a − a 0 9a 9 9 A = + = + = 0 + = 3a − 2a 3a + 2a a 5a 5 5 9 Vậy A = 5 Bài 3.
Từ đề bài: (x + y)2 = (x - 2).(y + 2)
x2 + 2xy + y2 = xy + 2x – 2y – 4
 x2 + xy + y2 – 2x + 2y + 4 = 0
 2x2 + 2xy + 2y2 – 4x + 4y + 8 = 0
 (x2 + 2xy + y2) + (x2 – 4x + 4) + (y2 + 4y + 4) = 0
 (x + y)2 + (x - 2)2 + (y + 2)2 = 0 (*) (
x + y)2  0 xy  x + y = 0   x = 2 Vì 2
(x − 2)  0 x
nên (*)  x − 2 = 0      y = 2 − 2 ( y + 2)  0 y   y + 2 = 0   Do dó: A = 22 + (-2)2 = 8
Bài 4. Tìm GTLN, GTNN (nếu có) của các biểu thức 6 6 3 3 1) A = = = = 2 2 4x + 4x + 3  3   1 1 1  2 2  1  4 x + x + 2 x + 2. x + +     2 x + +1    4   2 4 2   2  2 2  1   1  3 Ta có: 2 x +  0, x   2 x + +11, x    3, x   A  3     2  2   2   1  2 x + +1    2  1 1
Dấu “=” xảy ra  x + = 0  x = − 2 2 1
Vậy GTNN của A là 3 tại x = − 2 4 − 4 − 4 − 2) B = = = 2 2 6 + 4x + x x + 4x + 4 + 2 (x + 2)2 + 2 Ta có: ( x + )2 2  0, x  ( −  x + )2 +  x   (x + )2 4 2 2 2 , 2 + 2  2, x    −    − ( x B x + 2) 2, 2 2 + 2
Dấu “=” xảy ra  x + 2 = 0  x = 2 −
Vậy GTNN của B là -2 tại x = 2 − Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 41/ 43 Nhóm Toán THCS Toán học là đam mê 2 x − 3x + 3 3) C = x  1 2 ( ) x − 2x +1
( 2x −2x+ )1− x+1+1 (x− )2 1 − ( x − ) 1 +1 1 1 = = = − + (x − ) 1 2 1 (x − )2 1 x −1 (x + )2 1 2 1  1 1  3  1  3 Đặt = y 2 2
C =1− y + y = y − 2. y + + = y − +     x −1  2 4  4  2  4 2 2  1   1  3 3 Ta có: y −  0 y   y − +  y       2   2  4 4 1 1 1 1
Dấu “=” xảy ra  y − = 0  y = 
=  x −1 = 2  x = 3(TM ) 2 2 x −1 2 3
Vậy GTNN của C là tại x = 3 4 1 x 1 15x 4) D = x + = + + x 16 x 16 x 1
Áp dụng bất đẳng thức cô – si cho hai số dương và ta có: 16 x 1 x 1 15x x 1 15x 1 15x 1 15x D = x + = + +  2 . + = 2 + = + x 16 x 16 16 x 16 16 16 2 16 15x 15.4 15 1 15 17 Do x  4 nên  = Suy ra D  + = 16 16 4 2 4 4 x = 4 1 (TM x ) Dấu “=” xảy ra 2  =  x = 16   16 xx = −4  (KTM ) 17 Vậy GTNN của D là tại x = 4 4 12x + 34
x +12x + 36 − x − 2
(x + 6)2 x + 2 (x + 6)2 2 2 2 5) Q = = = − = −1 2 2 2 2 2 x + 2 x + 2 x + 2 x + 2 x + 2 (x + 6)2 (x + 6)2 Ta có:  0 x   −1 1 − x  2 2 x + 2 x + 2
Dấu “=” xảy ra  x + 6 = 0  x = 6 − Vậy GTNN của Q là 1 − tại x = 6 −
6) E = x −1 + 2 x − 2 + x − 3 + 4
E x −1+ 3 − x + 2 x − 2 + 4 = 2 x − 2 + 6  6 (  x − ) 1 (3 − x)  0 1   x  3 Dấu “=” xảy ra     x = 2 x − 2 = 0 x = 2
Vậy GTNN của E là 6 tại x = 2 Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 42/ 43 Nhóm Toán THCS Toán học là đam mê Bài 5. 3 3 3 3 3 3 a + b b + c c + a
1) Cho a > 0; b > 0; c > 0 và a + b + c = 6. Tìm GTNN của Q = + + ab bc ca 3 3 3 3 3 3 2 2 2 2 2 2 a + b b + c c + a a b b c c a Q = + + = + + + + + ab bc ca b a c b a c 2 2 2 2 2 2  a   b   b   c   c   a
=  + b +  + a +  + c +  + b +  + a +  + c − 2(a + b + c)  b   a   c   b   a   c  2 2 2 2 2 2 a b b c c a
Vì a  0,b  0, c  0   0,  0,  0,  0,  0,  0. b a c b a c 2 a 2 2 a a
Áp dụng bất đẳng thức Cô-si cho 2 số dương và b có: 2 + b  2 .b = 2 a = 2 . a b b b 2 2 2 2 2 b b c c a
Hoàn toàn tương tự ta có: + a  2 ; b + c  2 ; b + b  2 ; c + a  2 ; c + c  2 . a a c b a c
Suy ra Q  4(a + b + c) − 2(a + b + c) = 2(a + b + c) = 2.6 = 12. 2
a = b a = bb ...  Dấu " = " xảy ra  
a = b = c = 2. Khi đó Q đạt GTNN bằng 12. 2
a = c a = cc
a + b + c = 6 2) 2 2
A = x + y − xy − x + 4 y + 600 2 2
 4A = 4x + 4y − 4xy − 4x +16y + 2400  4A = ( 2 2
4x − 4xy + y ) − (4x − 2y) + ( 2
3y +14 y ) + 2400    
 4A = (2x − y)2 − 2(2x − y) 7 49 49 2
+1 + 3 y + 2. y + + 2400 −1−        3 9   3  2  
A = ( x − y − )2 7 7148 7148 4 2 1 + 3 y + +     3  3 3 7148 1787 Khi đó A  : 4  A  3 3  2 −
2x − y −1 = 0 x =    3 Dấu bằng xảy ra   7   y + = 0 7 −    3 y =  3 1787 −2 −7
Vậy giá trị nhỏ nhất của A bằng khi và chỉ khi x = ; y = 3 3 3 Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 43/ 43 Nhóm Toán THCS Toán học là đam mê mx + 5 x −1 Bài 6. +  2 (1) và 2 (x +1)(x+ 22)  0 (2) 12 2 Ta có: 2 x +1  1, x  2  x +1  0, x
(2)  x+ 22  0  x  22 − mx + 5 6(x−1) 24 (1)  +  12 12 12
mx + 5+ 6x − 6  24
mx + 6x  24 −5+ 6  (m+ 6) x  25 25
- Trường hợp 1: m + 6  0  m  6
−  x m+6 25
- Trường hợp 2: m + 6  0  m  6
−  x m+6 m  6 − m  6 −  m  6 −  157 − (1)  (2)   25     157 −  m = = 22 −   2 − 2(m+ 6) = 25 m = 22  m + 6  22 157 − Vậy với m =
thì hai bất phương trình đã cho tương đương. 22 Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/