Đề cương ôn tập Lý thuyết điều khiển tự động EMA 2024-2025. Môn Lý thuyết điều khiển tự động (UET) | Trường Đại học Công nghệ, Đại học Quốc gia Hà Nội.

lOMoAR cPSD| 59735516
Đ Ạ I H Ọ C QU Ố C GIA HÀ N Ộ I TRƯ
Ờ NG Đ Ạ I H Ọ C CÔNG NGH Ệ Đ P
Ề CƯƠNG ÔN T Ậ Lý thuy ế u khi n t ng EMA 20213_ t đi ề
ể ự đ ộ – xxx
H ọ và tên
Mã s ố sinh viên
Năm h ọ c
2024 - 2025 1 lOMoAR cPSD| 59735516
ĐỀ CƯƠNG ÔN TẬP PHẦN LÝ THUYẾT
A. Nội dung cần đạt được:
1. Khái niệm về hệ thống điều khiển vòng hở và vòng kín.
2. Xây dựng hàm truyền và phương trình trạng thái mô tả hệ thống điều khiển liên tục.
3. Tính hàm truyền tương đương của hệ thống dùng phương pháp đại số sơ đồ khối và sơ đồ dòng tín hiệu.
4. Phân tích đặc tính động học của hệ thống điều khiển trong miền thời gian và miền tần số.
5. Đánh giá tính ổn định của hệ thống điều khiển.
6. Đánh giá chất lượng quá độ và xác lập của hệ thống điều khiển.
7. Thiết kế bộ điều khiển PID dùng phương pháp Zeigler-Nichols.
B. Câu hỏi lý thuyết Chương 1
Câu 1. Điều khiển là gì? Thế nào là quá trình điều khiển tự động? Ví dụ.
Câu 2. Nêu ý nghĩa của điều khiển tự động ?
Câu 3. Nêu các nguyên tắc điều khiển cơ bản.
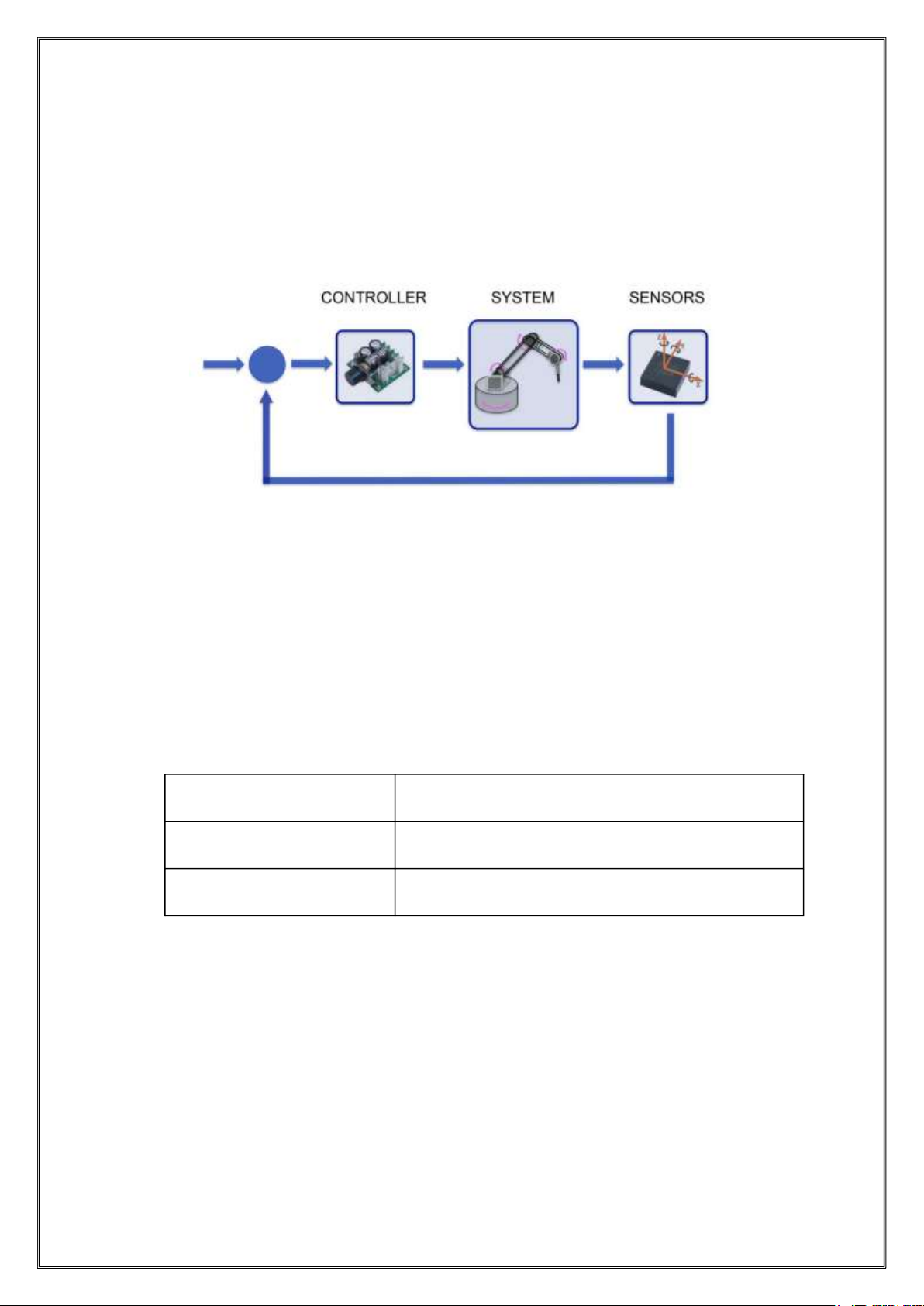
Câu 4. Trình bày cấu trúc cơ bản của một hệ thống điều khiển. Mô tả các phần tử trong hệ
thống. Cho 03 ví dụ minh họa.
Câu 5. Phân loại các hệ thống điều khiển.
Câu 6. Trình bày ưu điểm và nhược điểm của bộ điều khiển vòng hở (open-loop) (không
phản hồi) và bộ điều khiển vòng kín (hệ thống điều khiển hồi tiếp) (closed-loop). Nêu 03 ví dụ.
Câu 7. Trình bày các bước thiết kế một hệ thống điều khiển tự động .
Câu 8. Nêu các bước thiết kế hệ thống điều khiển. Chương 2
Câu 9. Khái niệm hàm truyền. Nêu các đặc tính cơ bản của hàm truyền.
Câu 10. Nêu ưu điểm và nhược điểm của phương pháp hàm truyền đạt.
Câu 11. Trình bày các bước tìm hàm truyền của đối tượng.
Câu 12. Thế nào là sơ đồ khối mô tả hệ thống. Mô tả các thành phần cơ bản trong sơ đồ khối.
Câu 13. Trình bày về các phép ghép nối sơ đồ khối cơ bản.
Câu 14. Trình bày về các phép chuyển đổi nút trong đại số sơ đồ khối.
Câu 15. Thế nào là graph tín hiệu. Mô tả các thành phần cơ bản trong graph tín hiệu. Phát biểu công thức Mason.
Câu 16. Tóm tắt nội dung chương 2 trong 1 trang A4 theo Sơ đồ tư duy Mindmap 2 lOMoAR cPSD| 59735516 Chương 3
Câu 17. Nêu các tín hiệu tác động thử thường xuyên được sử dụng trong điều khiển tự động.
Biểu diễn chúng dưới miền thời gian và miền phức.
Câu 18. Trình bày các khái niệm trạng thái, vectơ trạng thái. Biểu diễn hệ phương trình trạng thái.
Câu 19. Thế nào là đặc tính động học của hệ thống? Các tín hiệu thử cơ bản? Trình bày về
đặc tính thời gian của hệ thống.
Câu 20. Thế nào là đặc tính động học của hệ thống? Các tín hiệu thử cơ bản?
Câu 21. Nêu các khâu động học điển hình và khảo sát đặc tính thời gian của chúng Câu
22. Khái niệm điểm không – điểm cực. Nêu ảnh hưởng của điểm không và điểm cực lên
đáp ứng của hệ thống.
Câu 23. Tóm tắt nội dung chương 3 trong 1 trang A4 theo Sơ đồ tư duy Mindmap Chương 4
Câu 24. Thế nào là ổn định BIBO. Nêu ví dụ minh họa về hệ thống ổn định, biên giới ổn định và không ổn định.
Câu 25. Nêu định nghĩa phương trình đặc tính của hệ thống. Điều kiện cần và đủ để hệ ổn
định dựa vào các nghiệm của phương trình đặc tính như thế nào ?
Câu 26. Tiêu chuẩn ổn định đại số. Phát biểu tiêu chuẩn ổn định Routh
Câu 27. Tiêu chuẩn ổn định đại số. Phát biểu tiêu chuẩn ổn định Hurwitz.
Câu 28. Trình bày khái niệm quỹ đạo nghiệm số. Nêu các nguyên tắc xây dựng quỹ đạo nghiệm số.
Câu 29. Trình bày các tiêu chuẩn chất lượng đánh giá hệ thống điều khiển tự động. Phân tích
sai số xác lập của hệ thống hồi tiếp âm.
Câu 30. Trình bày các thông số đặc trưng của quá trình quá độ.
Câu 31. Phân tích đáp ứng quá độ của hệ thống quán tính bậc nhất và hệ dao động tắt dần.
Câu 32. Tóm tắt nội dung chương 4 trong 1 trang A4 theo Sơ đồ tư duy Mindmap Chương 5
Câu 33. Các yêu cầu thiết kế hệ thống điều khiển tự động. Trình bày ảnh hưởng của các khâu
hiệu chỉnh cơ bản (P, PI, PID) lên chất lượng hệ thống.
Câu 34. Trình bày 2 phương pháp của Ziegler – Nichols để xác định thông số bộ điều khiển PID.
Câu 35. Tóm tắt nội dung chương 5 trong 1 trang A4 theo Sơ đồ tư duy Mindmap
ĐỀ CƯƠNG ÔN TẬP PHẦN THỰC HÀNH 3 lOMoAR cPSD| 59735516 Chương 1 Câu
1. Ứng dụng Laplace giải phương trình vi phân:
1. Giải phương trình vi phân: y t''( ) + 4y t( ) = 9t
với điều kiện ban đầu y(0)=0; y’(0)=7
2. Giải hệ phương trình vi phân sau đây  x t'( ) − 2 ( )x t + 3y t( ) = 0 
 y t'( ) + 2 ( )x t − y t( ) = 0
với điều kiện ban đầu x(0)=8, và y(0)=3
Câu 2. Cho biến đổi Laplace của hàm f(t) như sau: 1. F s( )=
2(s++15)e−7s s s 2. 1 F s( ) = s s( + 2)2 Tìm f(t) Đáp án: 1. 7) 4 1 4 − −5(t ] (u t −7) f t( ) [= + (t − −7)e 25 5 25 2. 1 −2t 1 e−2t + 1
f t( )=− te − 2 4 4 Chương 2
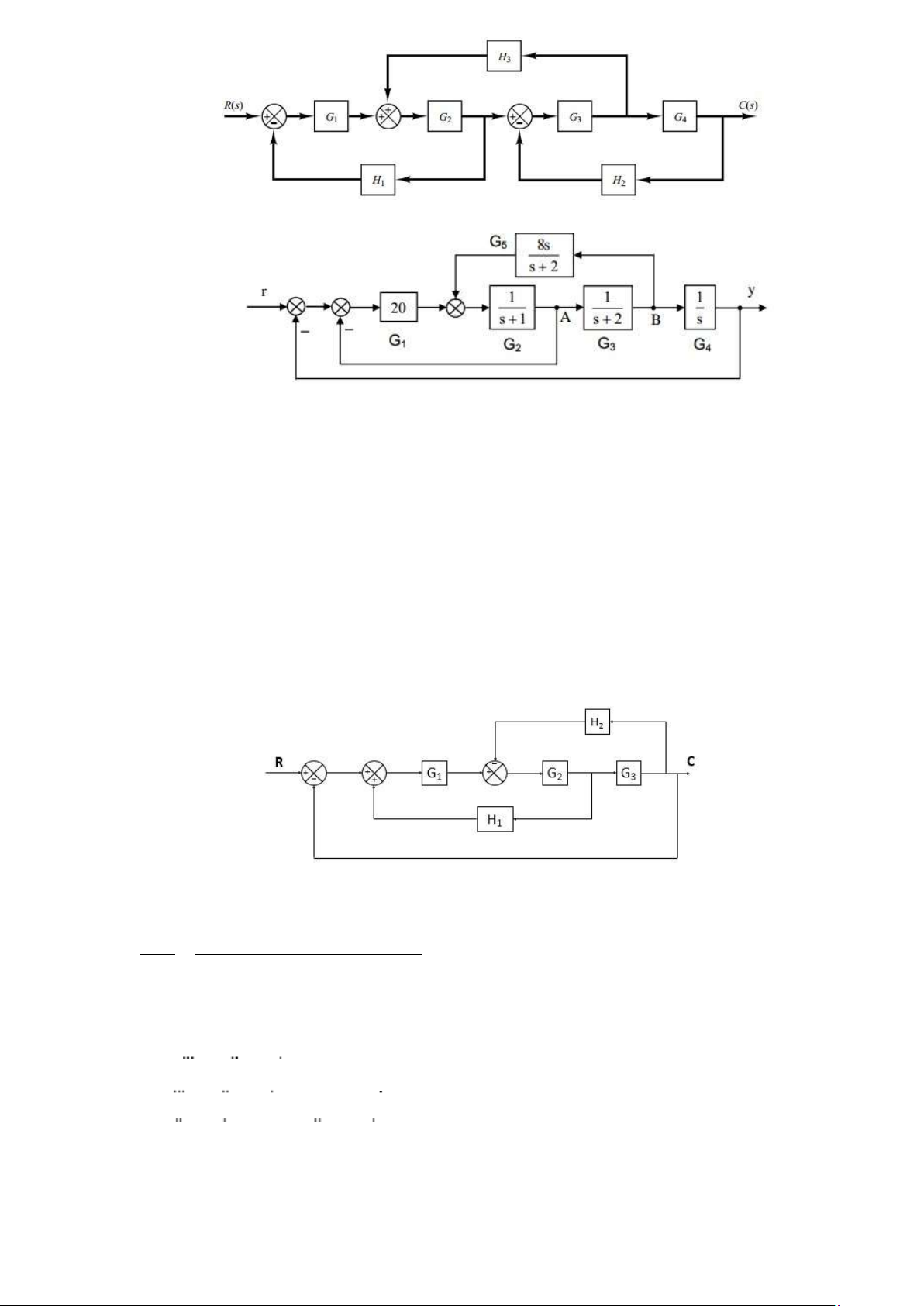
Câu 3. Rút gọn các sơ đồ khối sau đây sử dụng các phép biến đổi sơ đồ. 4 lOMoAR cPSD| 59735516 1. 2.
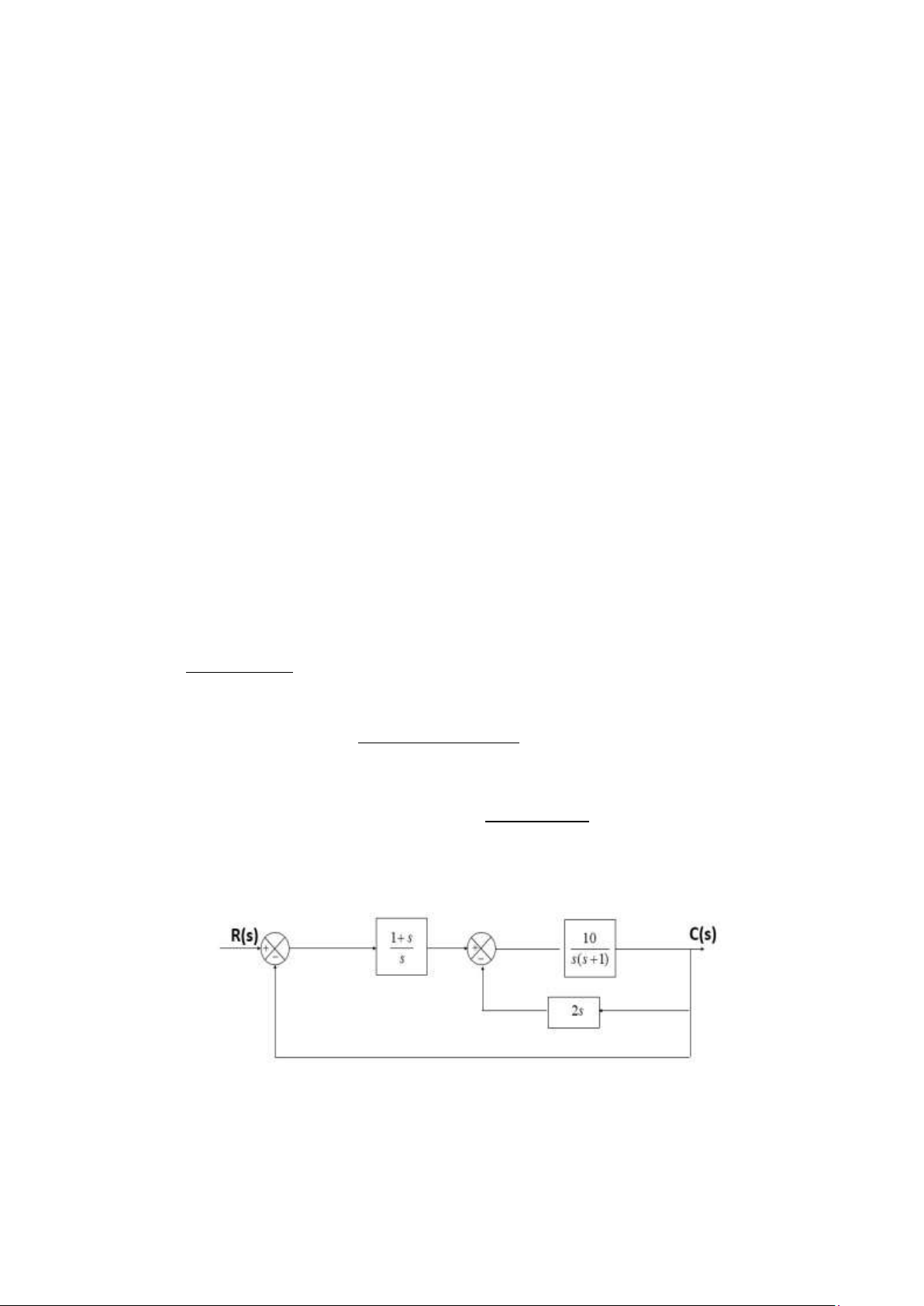
Câu 4. Cho hệ thống và sơ đồ vòng tín hiệu của nó như hình vẽ dưới đây. Tìm hàm truyền của hệ
thống theo 2 cách (sơ đồ khối và sơ đồ tín hiệu). Đáp án: C s( ) GG G1 2 3 =
R s( ) 1−GG H1 2 1 +G G H2 3 2 +GG G1 2 3
Câu 5. Viết phương trình trạng thái của hệ có phương trình vi phân
1. 2y(t)+5y(t)+6y(t)+10y(t)=r(t)
2. y(t)+5y(t)+6y(t)+10y(t)=10r(t)+20r(t)
3. y(t)+8y(t)+4y(t)=2u(t)+10u(t)+3u(t)
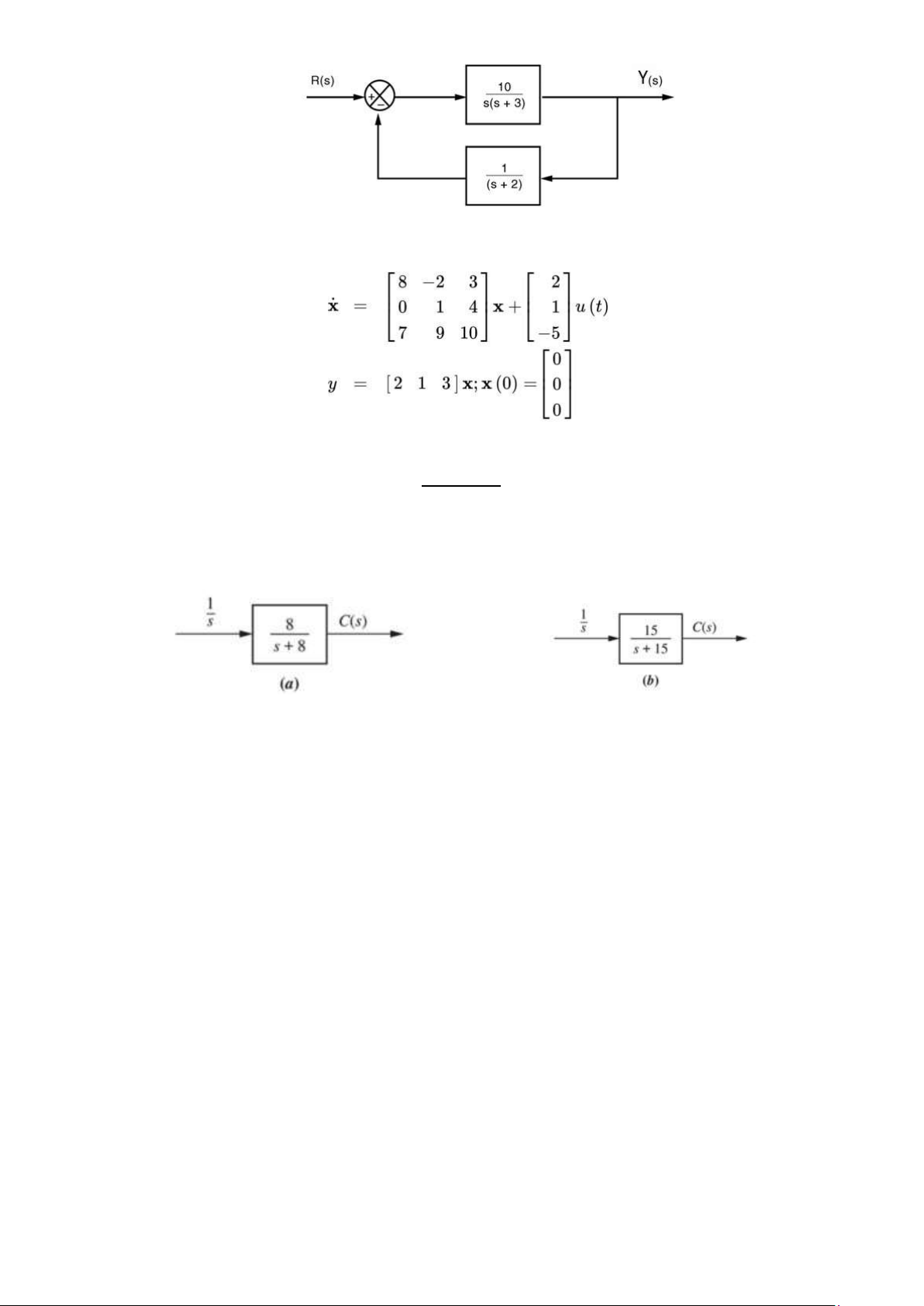
Câu 6. Tìm mô hình không gian trạng thái của hệ thống được mổ tả bởi sơ đồ khối sau: 5 lOMoAR cPSD| 59735516
Câu 7. Hãy tìm hàm truyền và các cực tương ứng của hệ thống không gian trạng thái sau: Chương 3
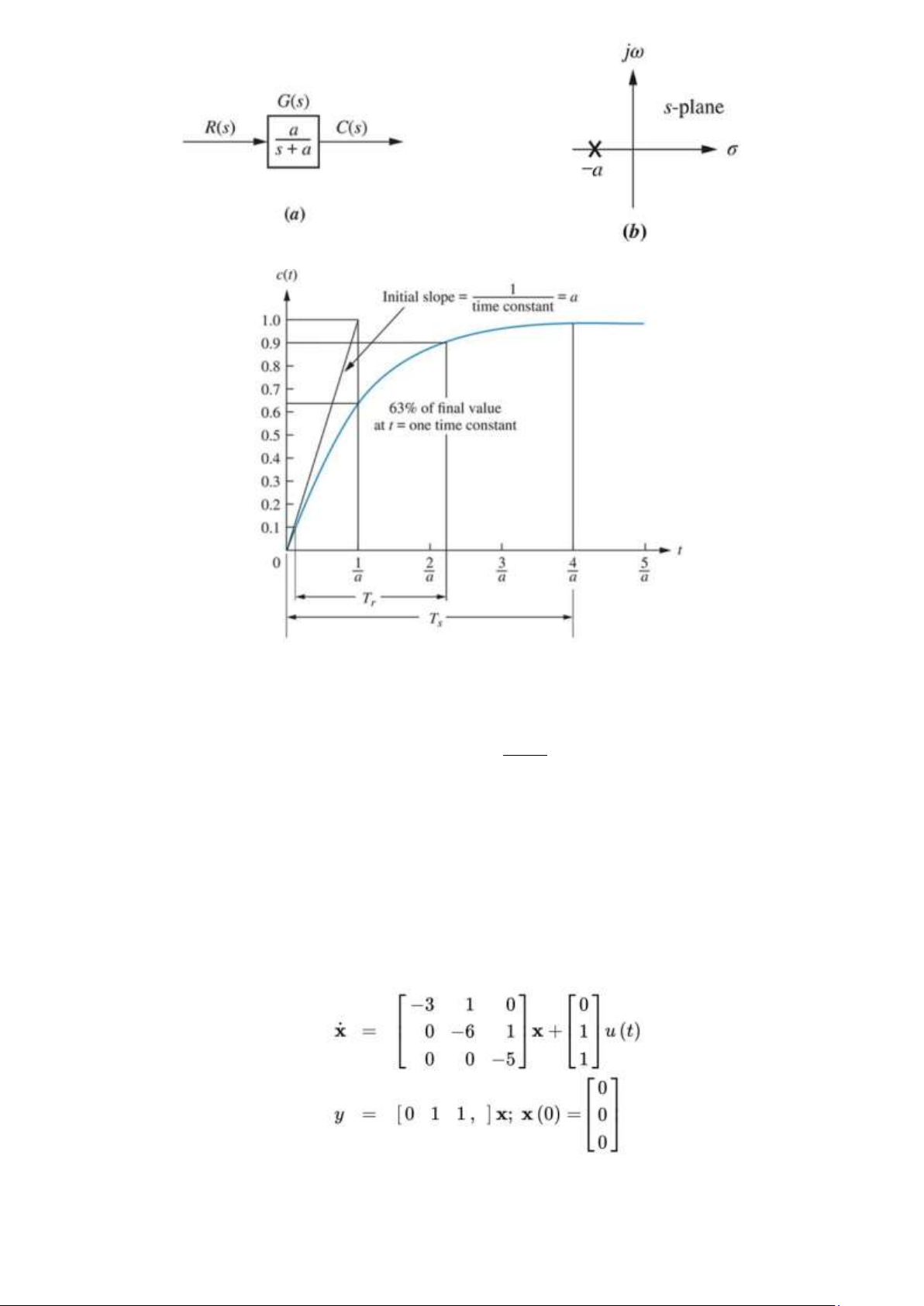
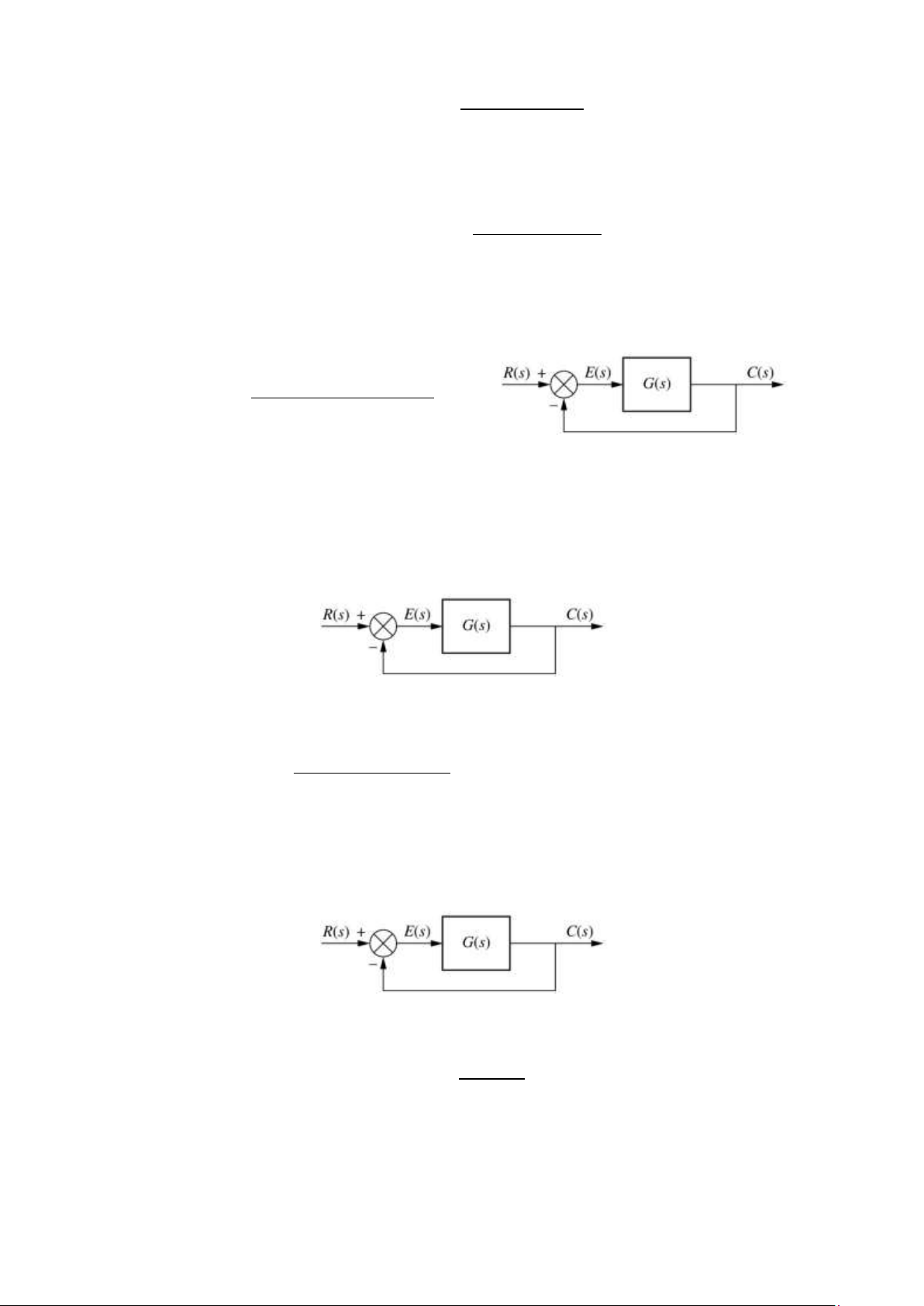
Câu 8. Đối với mỗi hệ thống trong hình dưới đây, hãy tìm biểu thức cho đầu ra (đáp ứng hệ thống).
Đồng thời, hãy chỉ ra hằng số thời gian, thời gian tăng (rise time), và thời gian xác lập (settling time). Câu 9. 6 lOMoAR cPSD| 59735516
First – order system response to a unit step 50
Biết rằng hệ thống bậc 1 có hàm truyền G s( )= s+50 Hãy xác định
- Hằng số thời gian (time constant) Tc
- Thời gian tăng (rise time) Tr
- Thời gian xác lập (settling time) Ts
Câu 10. Sử dụng biến đổi Laplace để tìm y(t), với tín hiệu đầu vào u(t) là hàm bậc thang đơn vị (unit step). 7 lOMoAR cPSD| 59735516
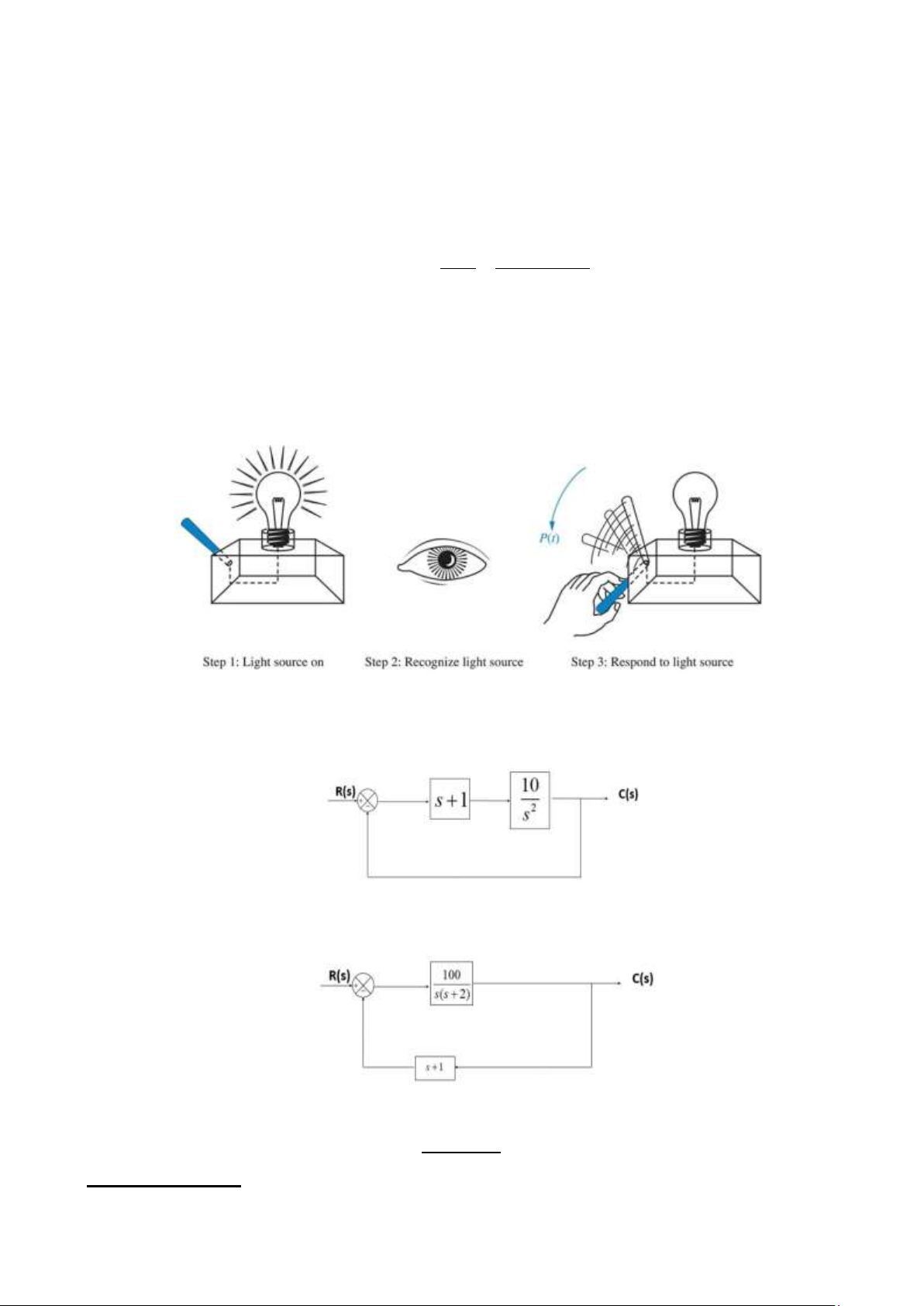
Câu 11. Hình vẽ dưới đây mô tả một mô hình phản ứng của con người đối với tín hiệu thị giác,
thường dùng trong lĩnh vực điều khiển sinh học (bio-control systems).
- Bước 1: Nguồn sáng được bật: Đây là tín hiệu vào cho hệ thống v(t).
- Bước 2: Mắt phát hiện nguồn sáng: Con người dùng thị giác để nhận biết ánh sáng.
- Bước 3: Phản ứng vật lý: Con người thực hiện hành động hướng tay về phía ánh sáng
để tắt hoặc điều chỉnh nguồn sáng, đây là đầu ra vật lý của hệ thống p(t). Hàm truyền
liên hệ giữa đáp ứng vật lý đầu ra P(s) và tín hiệu thị giác đầu vào V(s) được cho bởi:
G s( ) = P s( ) = s+0,5
V s( ) (s+ 2)(s+5) Hãy:
a. Tính đáp ứng đầu ra đối với tín hiệu vào là hàm bậc thang đơn vị bằng phương pháp biến đổi Laplace.
b. Biểu diễn hàm truyền dưới dạng không gian trạng thái.
Câu 12.Cho hệ thống như hình vẽ. Tín hiệu vào r(t) là hàm bậc thang đơn vị. Tìm đáp ứng quá độ c(t). 1. 2. Chương 4
Tiêu chuẩn ổn định 8 lOMoAR cPSD| 59735516
Câu 13. Cho phương trình đặc tính của hệ thống kín: 0
1. s4 + + + + =3s3 s2 9s 12 0
2. s5 + 2s4 + +2s3 4s2 + + =6s 8 0
3. s4 + +4s3 7s2 + + =16s 12
Hãy xét ổn định của hệ thống và cho biết có bao nhiêu nghiệm nằm bên phải mặt phẳng phức.
Câu 14. Ứng dụng tiêu chuẩn ổn định Routh, xác định tính ổn định của hệ điều khiển kín được mô tả
bởi các phương trình đặc trưng sau:
1. s3 + 20s2 +10s+ 400 = 0
2. s3 + 20s2 + +10s 100 = 0 0
3. 2s4 +10s3 + + + =5s2 5s 10
Câu 15. Đối với từng phương trình đặc trưng của hệ điều khiển có hồi tiếp, hãy xác định K sao cho
hệ ổn định. Xác định giá trị K để hệ ở biên giới ổn định và tần số dao động của hệ: 0
1. s4 + 20s3 +15s2 + + =2s K 0
2. s3 + Ks2 + + =5s 10
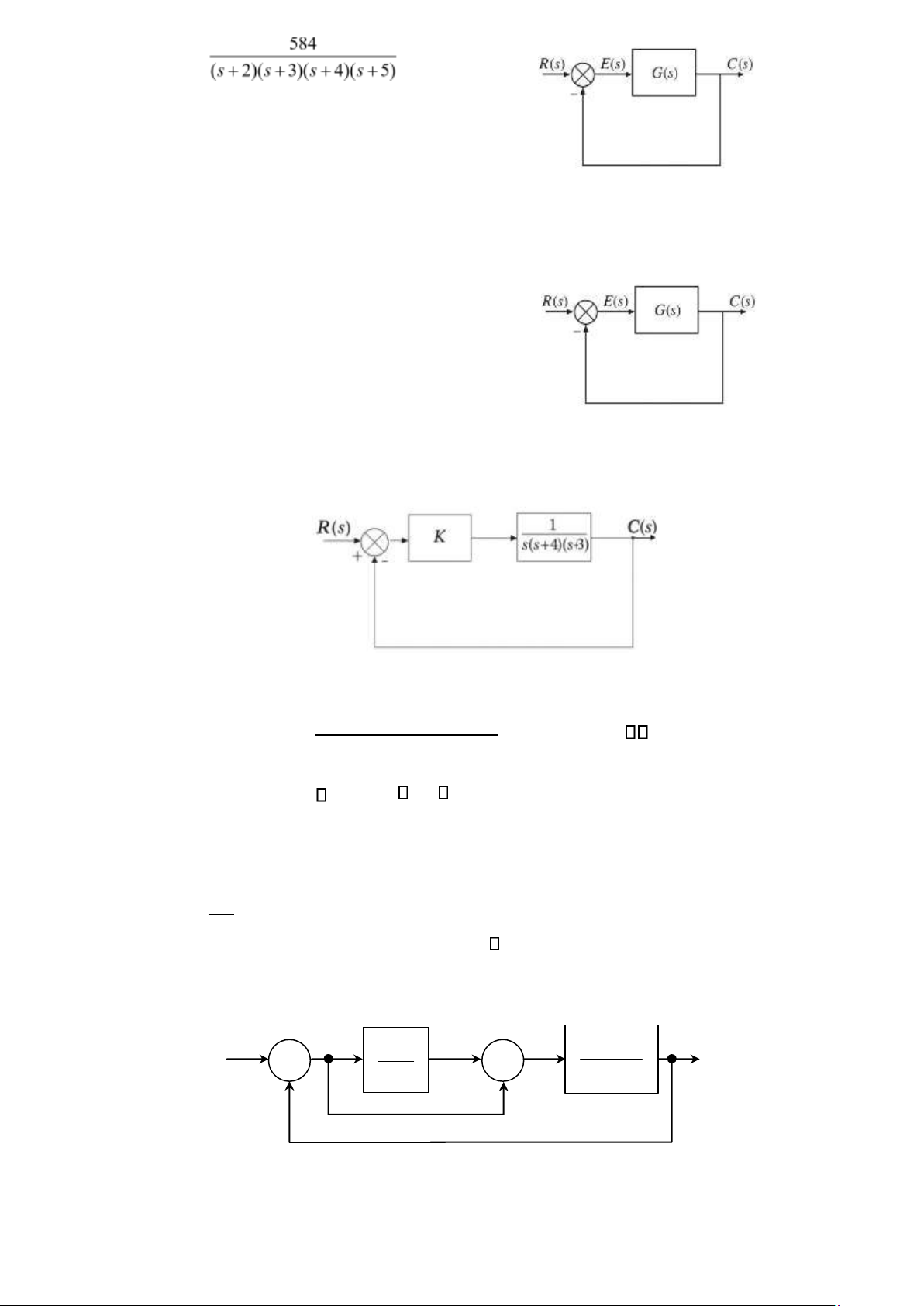
Câu 16. Dùng tiêu chuẩn ổn định Routh, xét xem hệ thống phản hồi trên hình có ổn định không đối với các hàm truyền: 1. 100 G s( )=
s s( 2 + +8s 24) 2. G s( )=
s2(300s23s++6001 s+50) 3. 24 G s( )= s s( +2)(s+4)
Câu 17. Sử dụng tiêu chuẩn ổn định Routh. Xét xem hệ thống điều khiển phản hồi ở hình dưới đây có ổn định hay không
Câu 18. Hãy xác định xem hệ thống hồi tiếp đơn vị (unity-feedback) trong hình dưới đây có ổn định không nếu: 9 lOMoAR cPSD| 59735516 G s( )=
Câu 19. Tìm khoảng giá trị của K để hệ thống vòng kín ổn định nếu: K s( −1) G s( )= s s( +2)(s+3)
Câu 20. Xét hệ thống như hình vẽ. Tìm K để hệ thống ổn định.
Câu 21. Cho hàm truyền hở của hệ như sau: G s( ) = +
s s b s( K s a2( 2  )
 n + n2) (a 0,b 0) − )( + dK =0 ds Biết rằng
tại 0,46 và -2,22 với a=b=1;  =0,5 và ωn=4. Tìm miền của K để hệ ổn định
Câu 22. Một hệ thống điều khiển có sơ đồ khối được thể hiện trong hình vẽ dưới. Hãy xác
định giá trị của K mà tại đó hệ thống bắt đầu không ổn định. R ( s ) + 2 K C ( s ) s 1 + + s( s 2) + − − 10 lOMoAR cPSD| 59735516
Câu 23. Xác định K để hệ thống sau ổn định: G s( )=
K s( (+s24)(+3)s−4) K s( + 2) G s( ) = s s( −1)(s+3)
Quỹ đạo nghiệm số:
Câu 24. Hãy vẽ quĩ đạo nghiệm số của các hệ thống sau: K s( +6) 1.
G s( )= (s+2)(s2 + +8s 25) 400 G s( )= 2. s s( +6)(s K+ ) K G s( )= 3. s s( +2)(s+3)
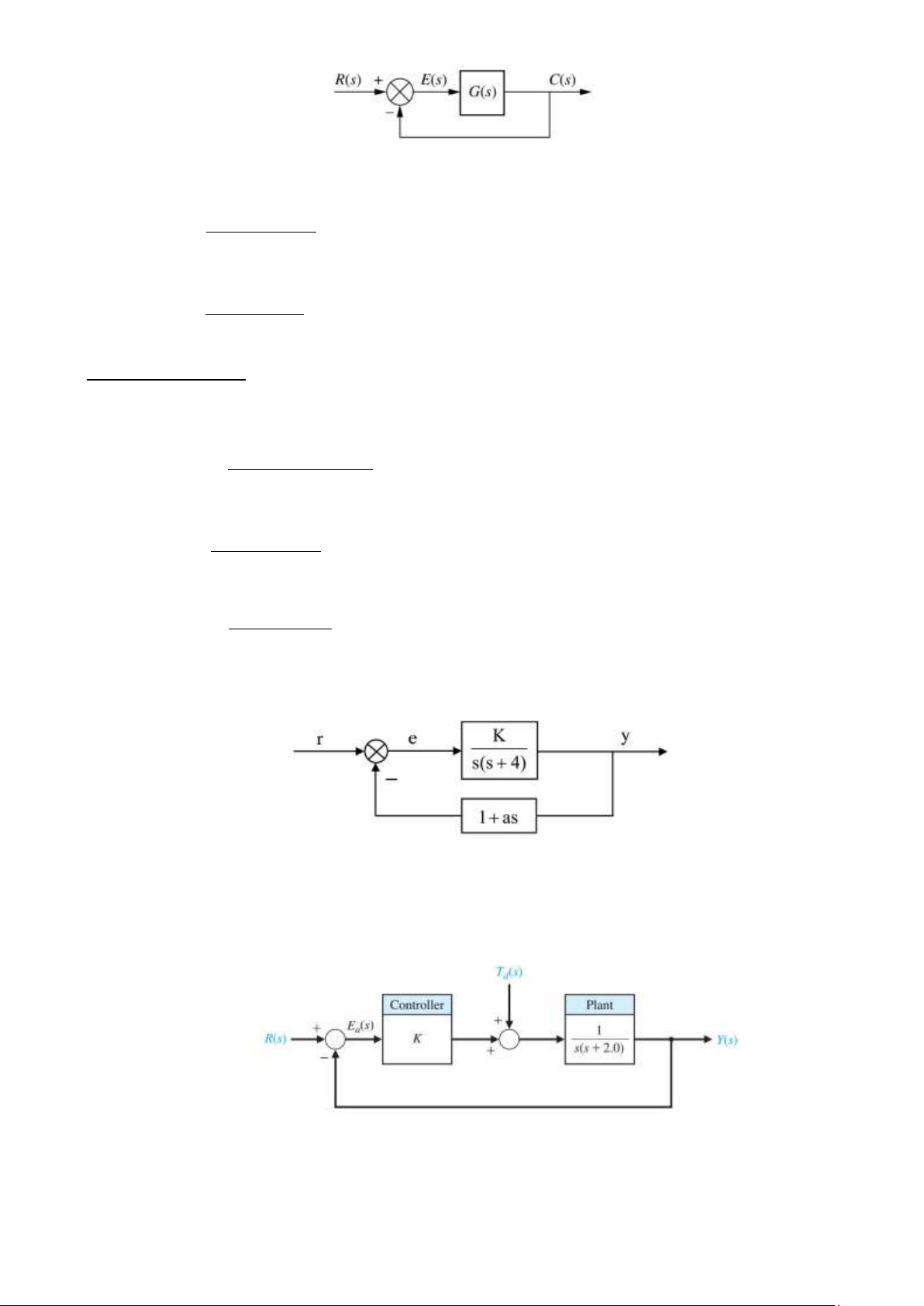
Câu 25. Cho hệ thống có sơ đồ như hình vẽ:
Xác định giá trị hệ số K và a để hệ có:
ω =5n rad/s ξ=0.7 Câu
26. Cho hệ thống hồi tiếp như hình vẽ: Giả sử K=10 11 lOMoAR cPSD| 59735516
1. Viết m-file tính hàm truyền tín hiệu vào của hệ thống T(s)=Y(s)/R(s) và vẽ đáp ứng
bậc thang đơn vị. (Trong trường hợp này để tính hàm truyền tín hiệu vào ta coi tín nhiệu nhiễu td(t)=0).
2. Viết m-file tính hàm truyền từ nhiễu H(s)=Y(s)/ Td(s) và vẽ đáp ứng bậc thang đơn
vị. Ở đây td(t) là tín hiệu nhiễu. (Trong trường hợp này để tính hàm truyền từ nhiễu
ta sẽ coi tín hiều vào r(t)=0)
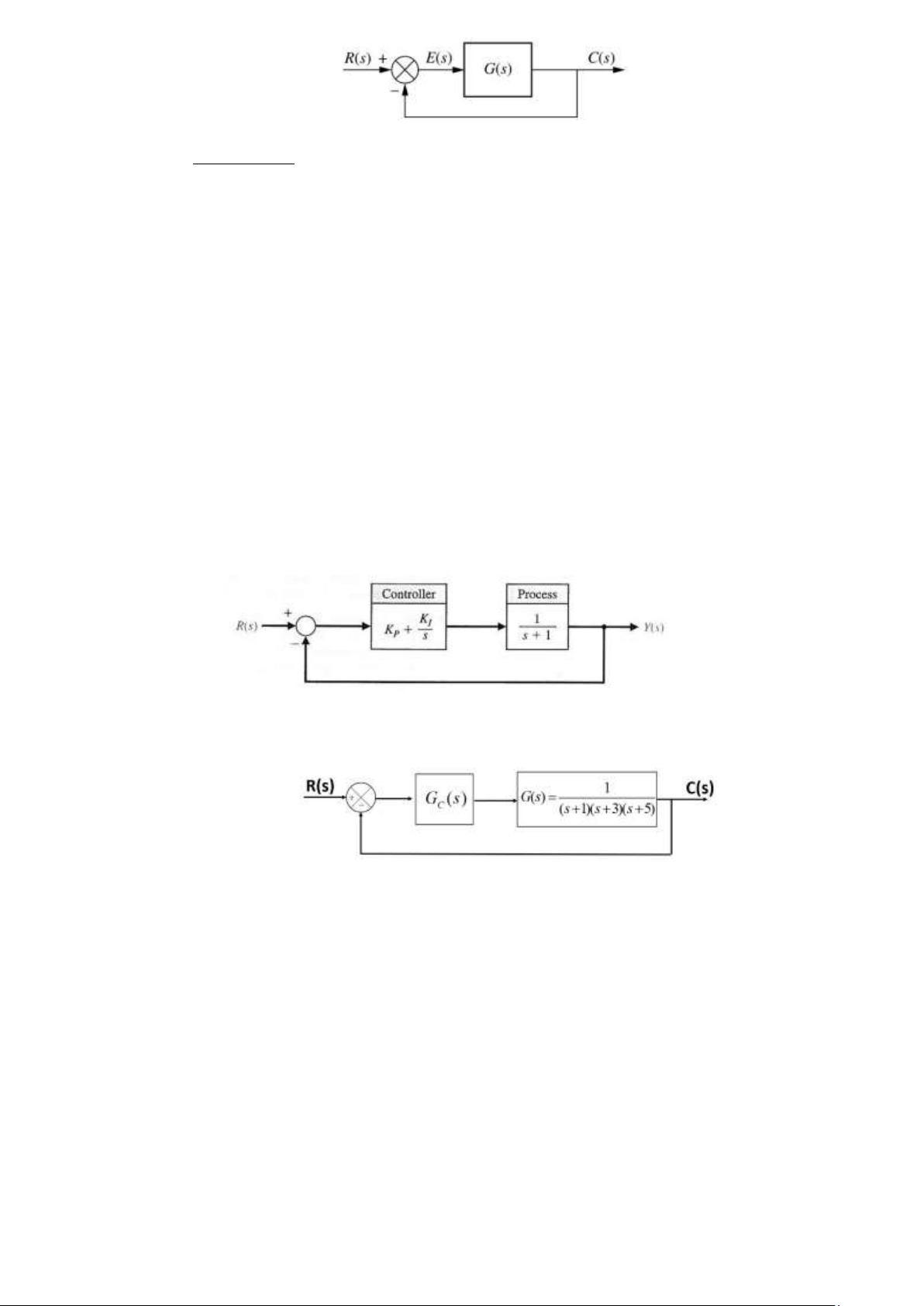
Câu 27. Cho hệ thống hồi tiếp như hình vẽ:
Giả sử rằng mục tiêu của bài toán thiết kế là tìm bộ điều khiển Gc(s) để hệ thống điều
khiển vòng kín có thể theo dõi tín hiệu vào là hàm bậc thang đơn vị với sai số xác lập (t→∞) nhỏ nhất. 1.
Lần thử đầu tiên, hãy xem xét bộ điều khiển tỉ lệ: G (s)=Kc với K là độ lợi tỉ lệ (thông
số điều chỉnh). Giả sử K=2, hãy vẽ đáp ứng bậc thang đơn vị và xác định sai số xác lập (h(∞)
− 1) dựa trên hình vẽ . Ks G (s)=K +c p 2.
Bây giờ chúng ta xét một bộ điều khiển phức tạp hơn: s
với Kp=2 và Ks=20. Bộ điều khiển này còn có tên gọi là bộ đk PI. hãy vẽ đáp ứng bậc thang
đơn vị và xác định sai số xác lập dựa trên hình vẽ . 3.
So sánh và nhận xét kết quả phần 1 và 2.
Câu 28.Cho hệ thống như hình vẽ :
1. Xác định giá trị của K sao cho hệ số tắt  =0.5 và vẽ QĐNS 0 K <∞
2. Xác định c(t) với K tính ở phần 1 và tín hiệu đầu vào là hàm bậc thang đơn vị. Sai số hệ thống
Câu 29. Xác định sai số hàm bậc thang đơn vị, ramp đơn vị, parabolic đơn vị của hệ điều khiển
phản hồi âm đơn vị, với hàm truyền hở đã cho : 1. G s( ) = 12 lOMoAR cPSD| 59735516 2. 100 G s( )= s s( 2 +10s+100) 3. 1000 G s( )=
s s( +10)(s+100)
Các tiêu chuẩn chất lượng
Câu 30. Hệ thống phản hồi đơn vị có G(s) như sau. G s( )= 450(s
s( s++38)(8)(ss2++ +12)(2ss+28)15)
Xác định e(∞) với tín hiệu vào hệ thống là 25u(t), 37tu(t). 47t2u(t).
Câu 31. Hệ thống phản hồi đơn vị: có G(s) như sau: G s( ) =
K s(s s2+(2)(+s5)(+s4)(+s7)+6)
Xác định giá trị của K để e(∞) = 10,000.
Câu 32.Hệ thống phản hồi đơn vị: có G(s) như sau: 5000 G s( )= s s( +75)
a. Xác định %OS, Ts với tín hiệu vào là hàm bậc thang đơn vị.
b. Xác định e(∞) với lối vào 5u(t), 5tu(t), 5t2u(t). 13 lOMoAR cPSD| 59735516
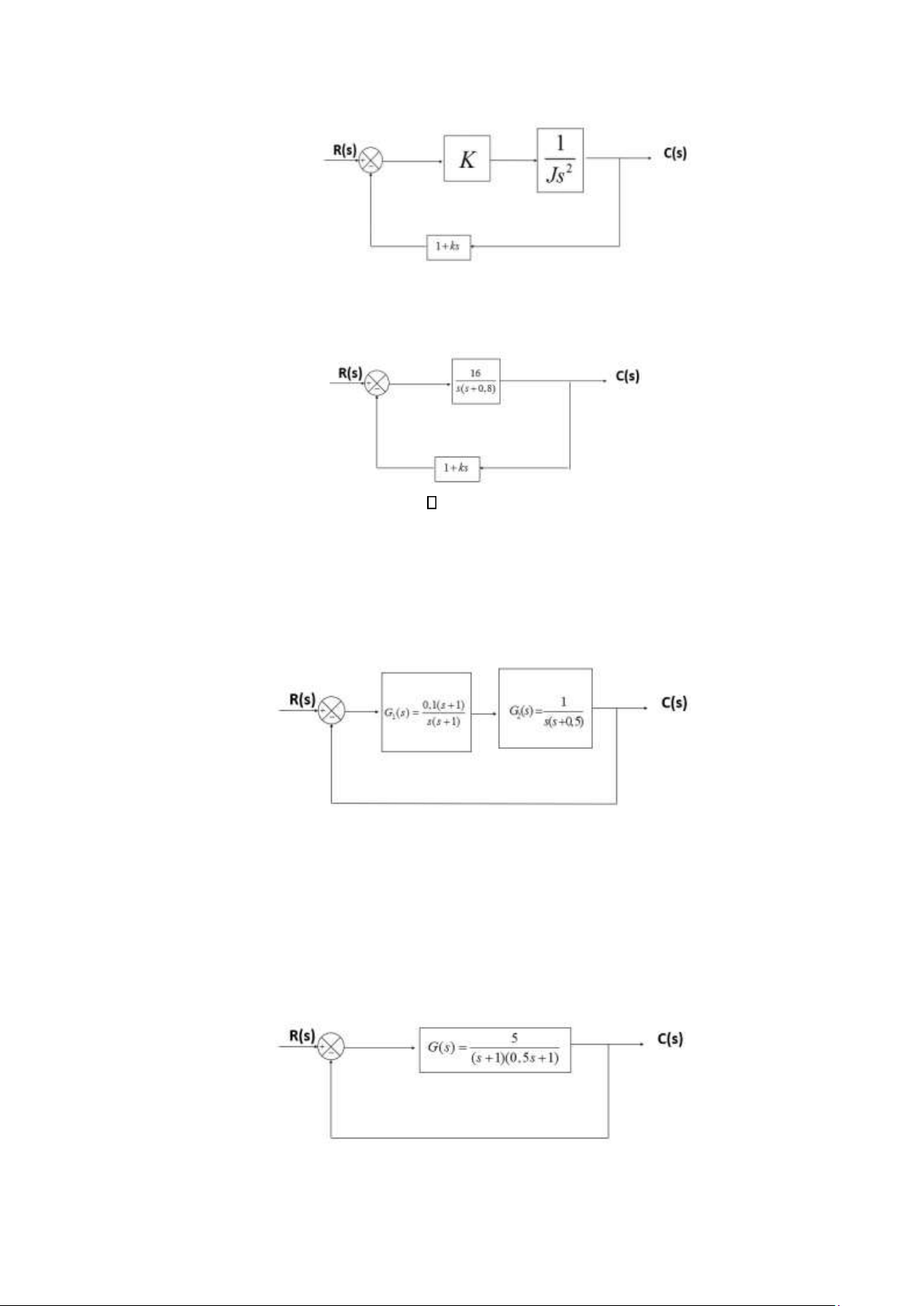
Câu 33. Cho hệ thống kín như hình vẽ. Cho J=1 Kg.m2; tín hiệu vào là hàm bậc thang đơn vị. Tìm
K và k của hệ sao cho độ vọt lố của đáp ứng quá độ bậc hai đạt 25% tại thời điểm t=2 sec.
Câu 34. Cho sơ đồ khối như hình vẽ:
1. Xác định giá trị của k để hệ số tắt  =0,5
2. Tìm độ vọt lố và thời gian xác lập khi tín hiệu vào là hàm bậc thang đơn vị r(t)=1(t), tính
theo hai tiêu chuẩn 2% và 5%.
Câu 35. Một ra đa mặt đất dùng để phát hiện các mục tiêu máy bay rất chính xác. Sơ đồ khối của trục
góc phương vị của ra đa như hình vẽ. Xác định sai số xác lập của hệ thống khi: 1. r(t)=10t 2. r(t)=10t+6t2
Câu 36. Cho hệ thống dùng để định vị một tải trọng được mô tả như hình vẽ.
1. Xác định sai số xác lập khi tín hiệu vào là hàm nấc có biên độ bằng 10
2. Nên sửa đổi G(s) như thế nào để giảm sai số xác lập xuống bằng không ?
Câu 37. Sơ đồ khối của một hệ điều khiển với bộ điều khiển như hình vẽ. Tìm hàm truyền của bộ
điều khiển GC(s) sao cho KV=9. Hàm truyền kín của hệ thống có dạng : 14 lOMoAR cPSD| 59735516 C s( ) K với a và K là số thực M s( ) = =
R s( ) (s2 + 20s + 200)(s + a)
Câu 38. Một ổ đĩa từ có một động cơ và đầu đọc/ghi. Hàm chuyển của hệ thống bao gồm động cơ và đầu đọc/ghi này là: 10 G(s) = s( s+1)
ở đó  = 0,001s. Bộ phận điều khiển sẽ tính sai số giữa vị trí thực sự và vị trí mong muốn của
đầu đọc/ghi và khuyếch đại sai số đó với hệ số khuyếch đại K.
(a) Xác định sai số vị trí ở trạng thái xác lập (ess) nếu tín hiệu vào (vị trí mong muốn) là một hàm bậc thang đơn vị.
(b) Xác định K để sai số ở trạng thái thường trực là 1mm nếu tín hiệu vào là hàm r(t) = 0.1t (m/s).
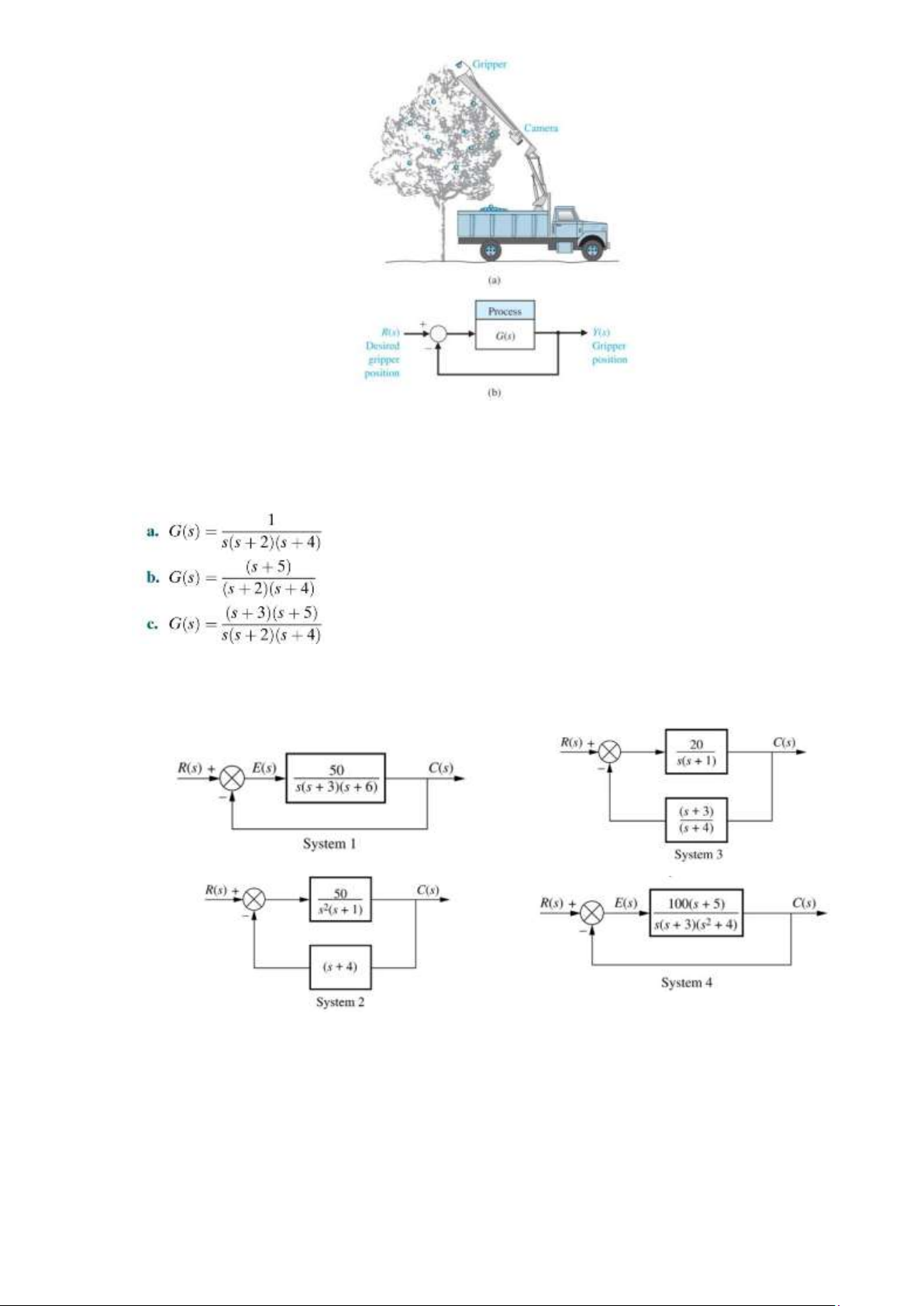
Câu 39. Một cánh tay robot và camera có thể được sử dụng để hái trái cây, như minh họa trong hình
dưới đây. Camera được dùng để đóng vòng phản hồi về máy vi tính, thiết bị này điều khiển
hoạt động của cánh tay. Hàm truyền của quá trình được cho bởi: K G s( )= (s+ 2 5)
1. Hãy tính sai số trạng thái xác lập (steady-state error) của kẹp gắp đối với tín hiệu vào dạng
bậc một (step) có biên độ A (r(t)=A.1(t)) theo giá trị của K.
2. Hãy nêu một tín hiệu nhiễu (disturbance) có thể xảy ra trong hệ thống này. 15 lOMoAR cPSD| 59735516
Câu 40. Xác định biểu thức độ lớn và pha của mỗi G(s) sau:
Câu 41. Vẽ đồ thị độ lớn và đồ thị pha của mỗi G(s) trong câu 40.
Câu 42. Vẽ đồ thị cực của mỗi G(s) trong câu 40. Câu
43. Vẽ đồ thị Nyquist của mỗi hệ thống sau:
Câu 44. Sử dụng tiêu chuẩn Nyquist để xác định tính ổn định của mỗi hệ thống ở câu 43. Chương 5
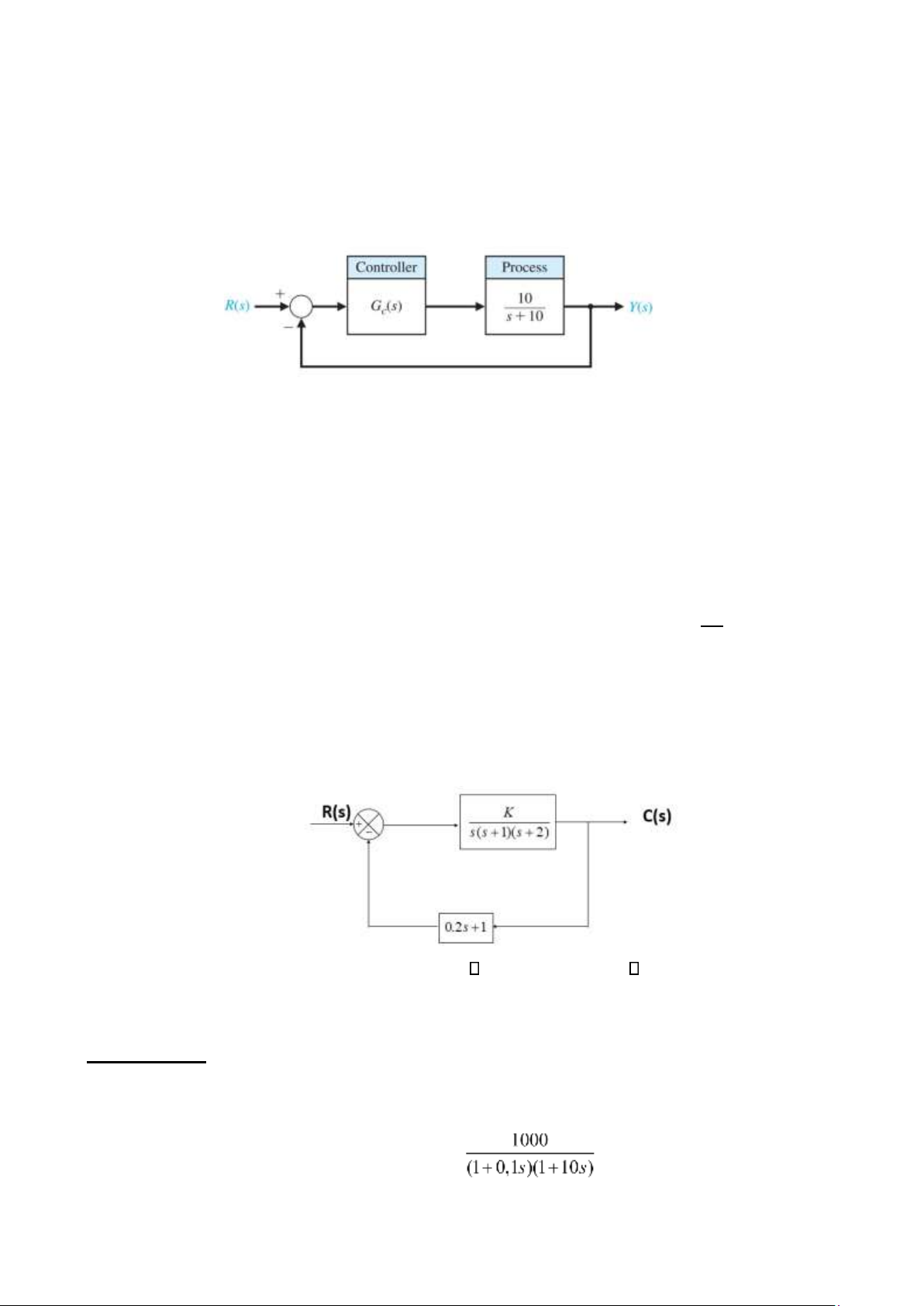
Câu 45. Xét hệ thống phản hồi đơn vị như trong hình dưới đây: 16 lOMoAR cPSD| 59735516 K G s( ) = s s( +3)(s+6)
- Hãy thiết kế một bộ điều khiển PI để làm cho sai số trạng thái xác lập của hệ thống khi tín
hiệu vào là hàm dốc bằng 0 với mọi giá trị của K mà hệ ổn định.
- Sử dụng MATLAB để mô phỏng thiết kế của bạn với K=1. Hiển thị cả tín hiệu vào dạng
ramp và đáp ứng đầu ra trên cùng một đồ thị.
Câu 46. Một hệ thống điều khiển với một bộ điều khiển được cho trong hình dưới đây. Hãy chọn các giá trị KP và KI sao cho:
- Độ vọt lố (overshoot) đối với tín hiệu vào dạng bước (hàm bậc thang đơn vị) (step input) là 5%
- Hằng số vận tốc Kv =5
Hãy kiểm tra lại kết quả của thiết kế của bạn bằng MATLAB.
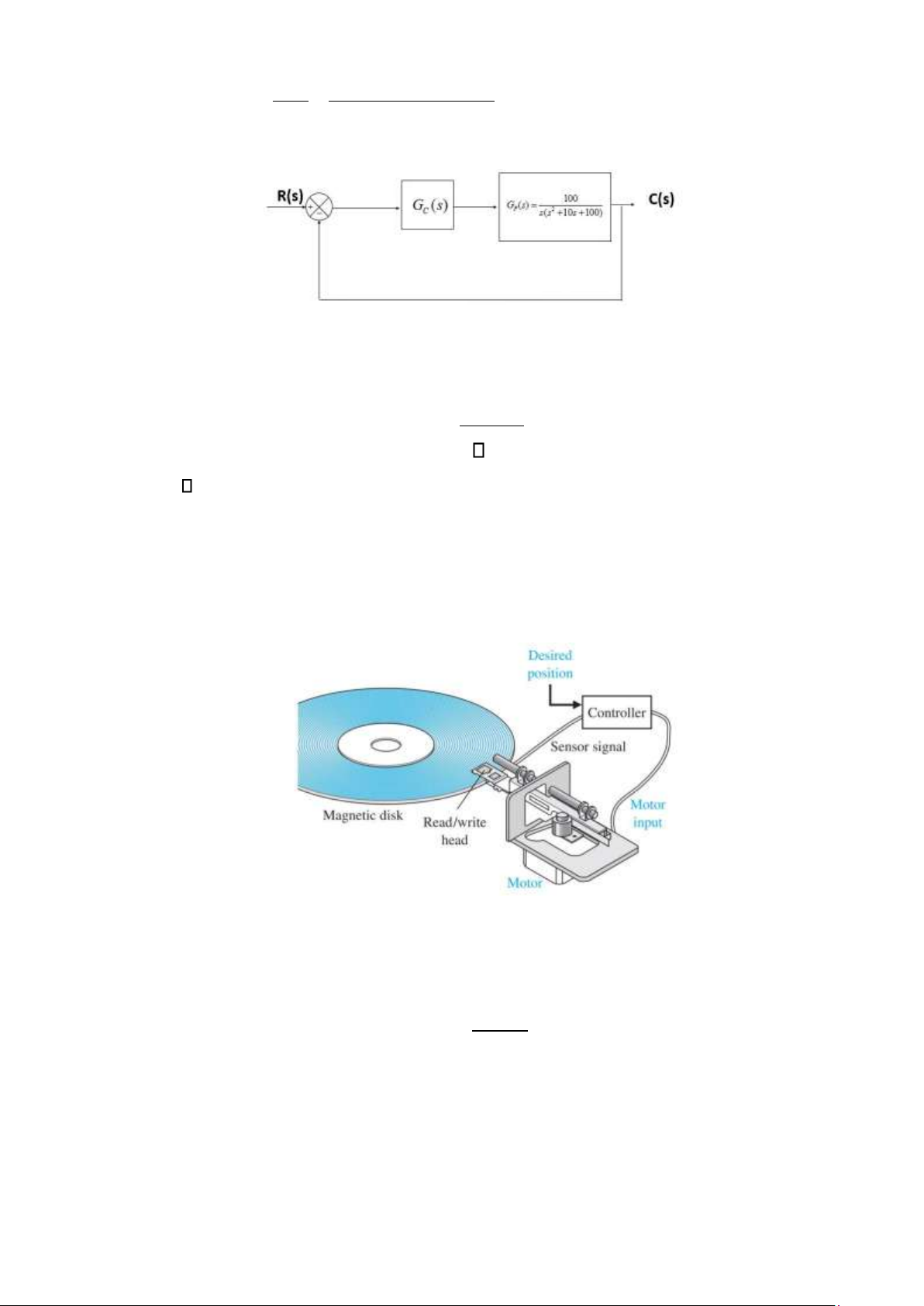
Câu 47. Sử dụng phương pháp Zeigler-Nichols 2 để thiết kế bộ điều khiển PID cho hệ thống
được miêu tả như hình bên dưới. 1
Với Gc(s) là hàm truyền của bộ điều khiển PID có dạngG sC ( )=K p (1+ +T sd ) Tsi
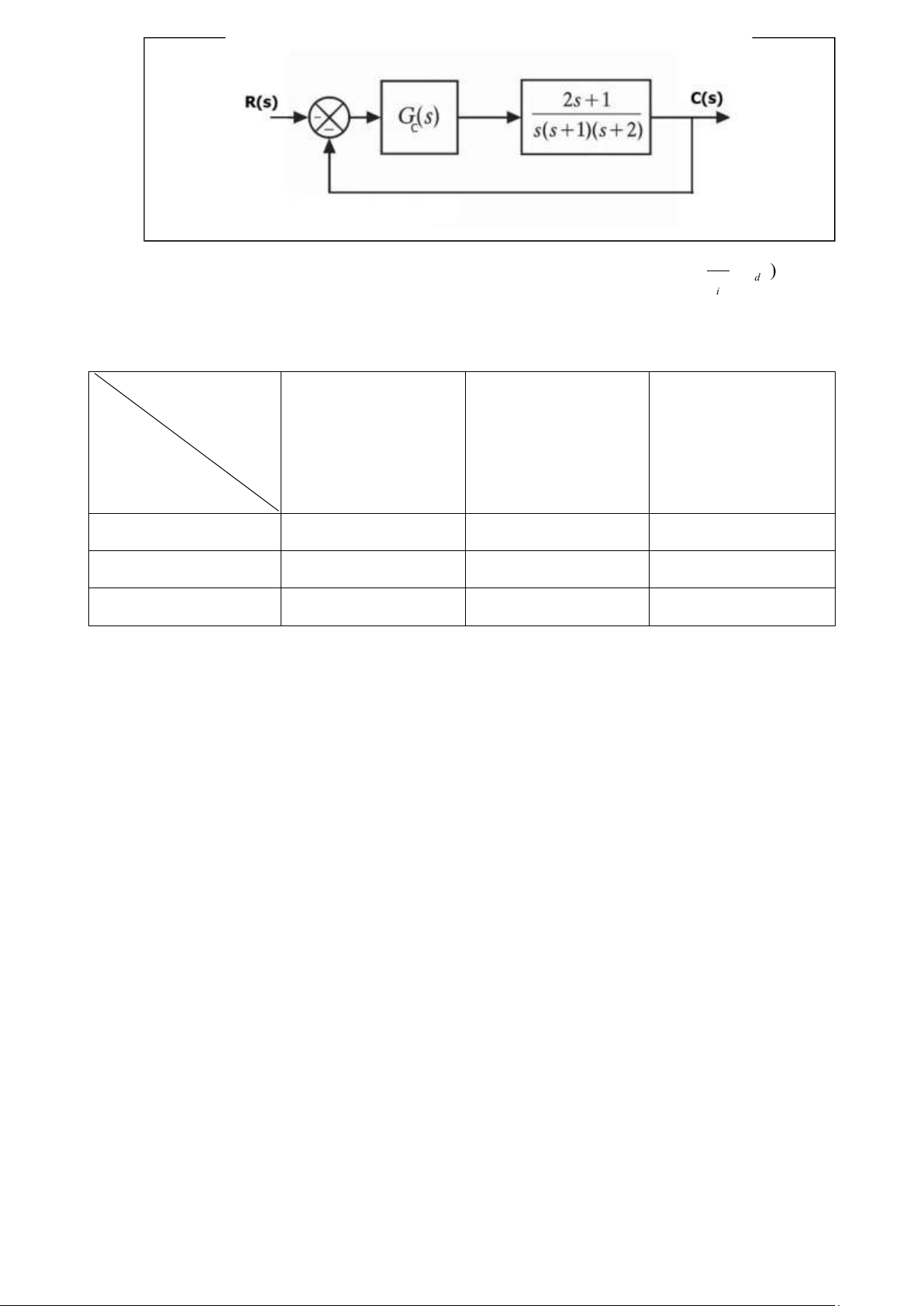
Câu 48. Sử dụng phương pháp Zeigler-Nichols 2 để thiết kế bộ điều khiển PID cho hệ thống
được miêu tả như hình bên dưới. 17 lOMoAR cPSD| 59735516 1
V ớ i G c ( s) là hàm truy ề n c ủ a b ộ đi ề u khi ể n PID có d ạ ng G () s K (1 Ts ) C = p + + d Ts i
Bảng tính các thông số cho bộ điều khiển PID: Thông s ố Kp Ti Td B ộ ĐK P 0,5.Kgh ∞ 0 PI 0,45.Kgh 0,83.Tgh 0 PID 0,6.Kgh 0,5.Tgh 0,125.Tgh 18