Đề cương ôn tập thi olympic 2021 môn Vật lý đại cương 2 | Học viện Công Nghệ Bưu Chính Viễn Thông

ÔN TÂP THI OLYMPIC 2021 - 2 PHẦN 3. QUANG HÌNH Bài 1. HSG QG 2001
Một sợi cáp quang hình trụ rất dài, hai đáy phẳng và vuông góc với trục của sợi cáp, bằng thủy tinh chiết suất n ,
1 được bao xung quanh bằng một hình trụ đồng trục, bán kính lớn hơn nhiều bán kính a
của sợi cáp, bằng thủy tinh chiết suất n 2với n 2< n .1 Một tia sáng SI tới một đáy của sợi cáp quang
dưới góc tới i, khúc xạ trong sợi cáp, và sau nhiều lần phản xạ toàn phần ở mặt tiếp xúc giữa 2 lớp
thủy tinh, có thể ló ra khỏi đáy kia
1. Tìm giá trị lớn nhất im mà I không thể vượt quá để tia sáng không truyền sang lớp vỏ ngoài.
2. Sợi cáp ( cùng với lớp vỏ bọc) được uốn cong cho trục của nó làm thành cung tròn, bán kính
R. Góc I bây giờ là bao nhiêu ?
Cho biết: n1 = 1,50 ; n = 1,48 ; a = 0 2 ,2 mm ; R = 5 cm.
Chú ý : – Chỉ cần xét tia sáng nằm trong mặt phẳng chứa trục của sợi cáp.
– Chỉ cần cho biết giá trị chính xác của sin, cos hoặc tan của im.
Bài 2. Một tia sáng đi tới một môi trường trong suốt có chiết suất n phụ thuộc vào biến y dưới một
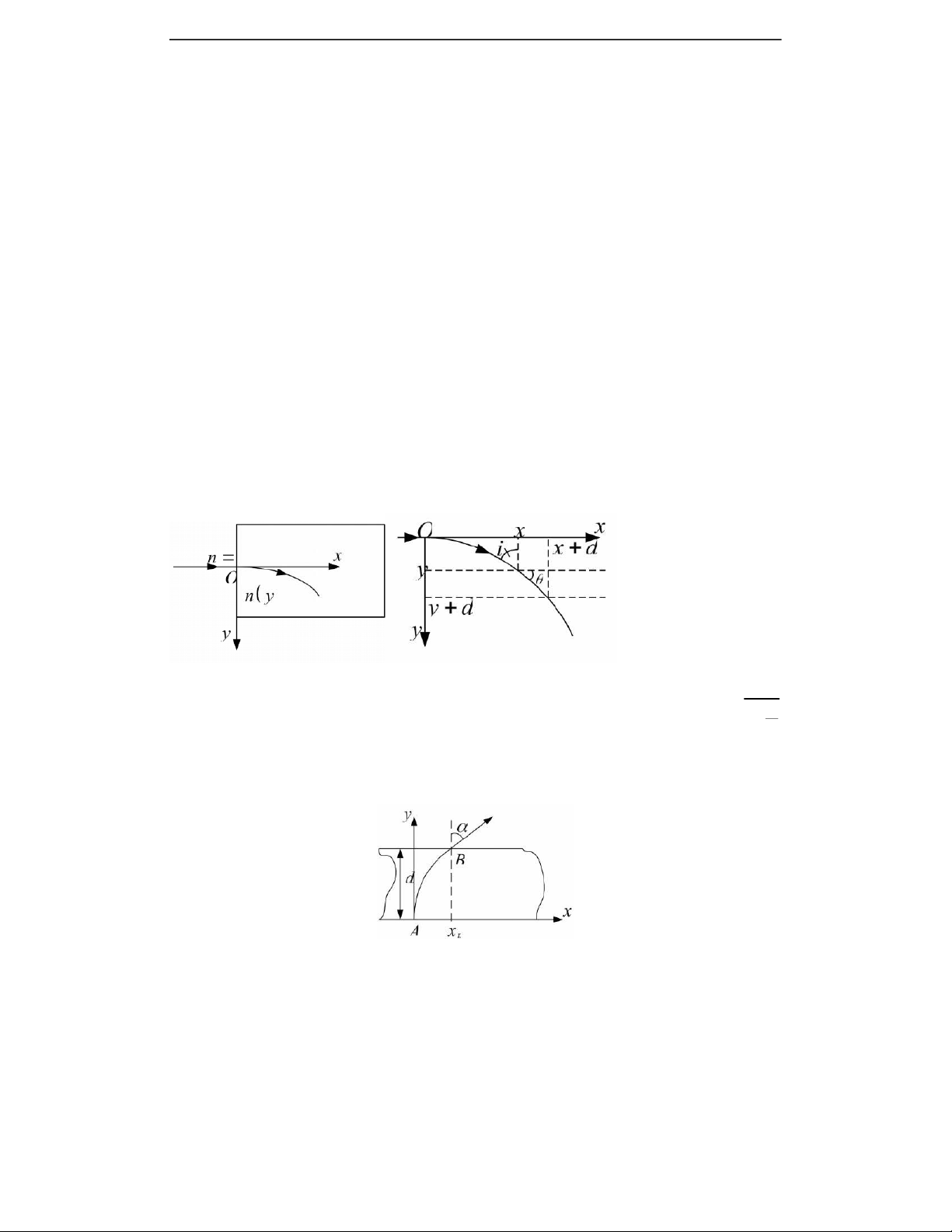
góc vuông tại điểm y = 0 ( như hình vẽ ) Tìm dạng của hàm chiết suất n phụ thuộc vào biến y. Cho
 và tia sáng truyền trong môi trường này có dạng đường Parabol với phương trình y = a.x2  n  n y 0  0 x O x x  dx i n 1 x   y O y   dy n y y y  n
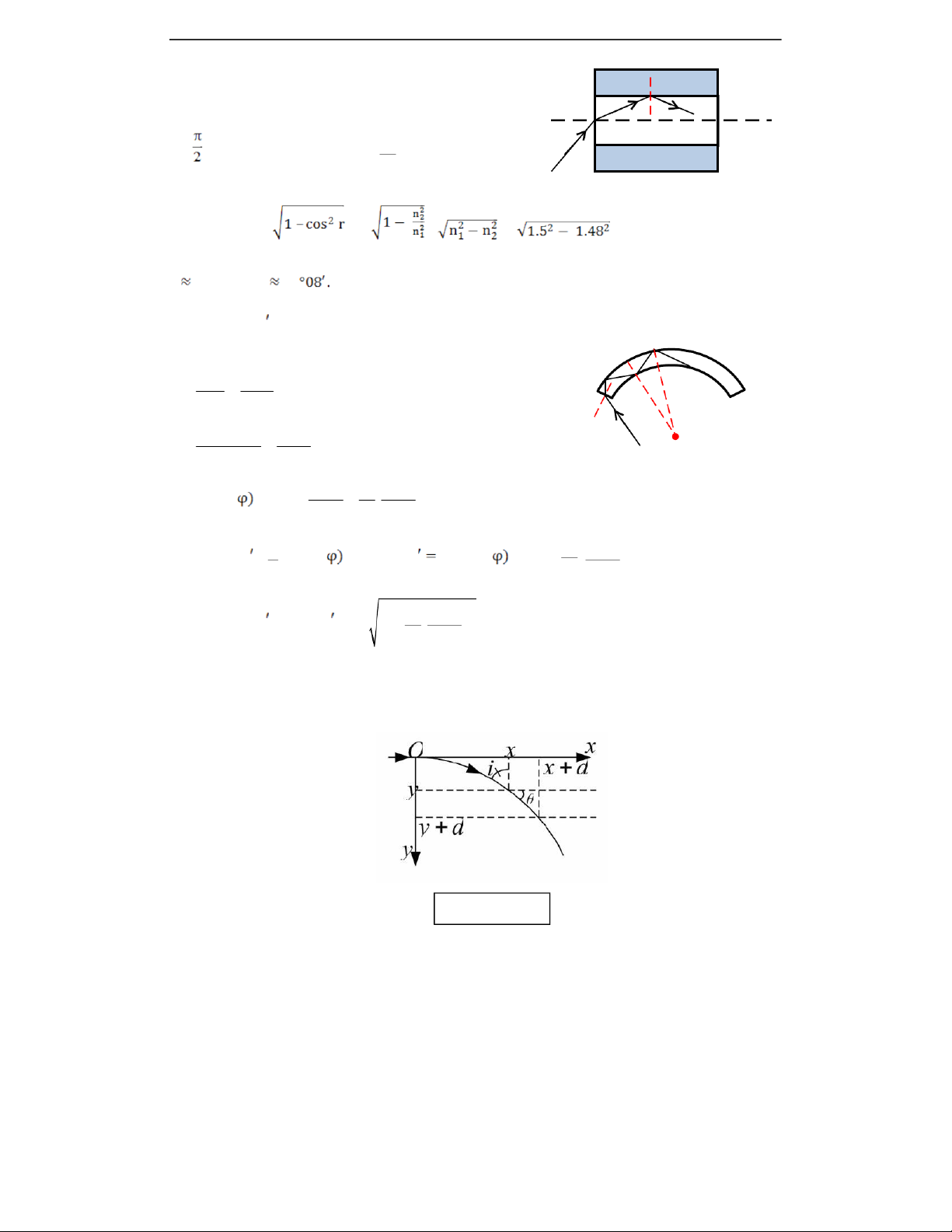
Bài 3. Xét một bản trong suốt, song song, có bề dày d và có giá trị chiết suất cho bởi nx 0 1  R
(Xem hình vẽ ). Một tia sáng đi vào từ không khí tới điểm A, vuông góc với mặt bản ( x 0 ) và  A
ló ra ở điểm B với góc ló là y  B d x A x B Created by Lê Minh Sơn Email : Lesontb@gmail.com
a) Tính chiết suất tại điểm B ( n ) B b) Tính xB
c) Lập phương trình quỹ đạo của tia sáng truyền trong bản
Áp dụng bằng số: n 1,2 0 ; R = 13cm; 0  3  0 y
Bài 4. Giữa hai môi trường trong suốt chiết suất n 0 và
n (n  n 1) có một bản hai mặt song song bề dày e. Bản 1 0 1 n1
mặt được đặt dọc theo trục Ox của hệ toạ độ Oxy như hình
vẽ. Chiết suất của bản mặt chỉ thay đổi theo phương vuông e O
góc với bản mặt theo quy luật n  , với 0 n 1 ky x n0 2 2 n n 0 1 ken 
. Từ môi trường chiết suất n 0 có một tia sáng 2 0
đơn sắc chiếu tới điểm O trên bản mặt, theo phương hợp với Oy một góc  . Lập phương trình xác
định đường truyền của tia sáng trong bản mặt.
Bài 5. CHỌN ĐT OLYMPIC CHÂU Á 2004 O
Một hình trụ bằng thuỷ tinh chiết suất n = 1,53 đặt trong không khí, có P Q
đáy dưới phẳng MN vuông góc với trục O’O của hình trụ (Hình vẽ). Đáy
kia của hình trụ là chỏm cầu PQ có đỉnh O, bán kính cong R = 4mm. Trên
đáy MN có một vết xước thẳng AB dài 1mm. Đặt mắt ở O ta nhìn thấy
một ảnh ảo A’B’ của AB ở cách mắt một khoảng bằng 40cm. O’ M B A N
1. Tính độ cao O’O của hình trụ và kích thước của ảnh A’B’.
2. Thực tế vết xước có độ sâu dọc theo trục O’O bằng 0,01mm. Tính kích thước dọc theo trục O’O của ảnh vết xước.
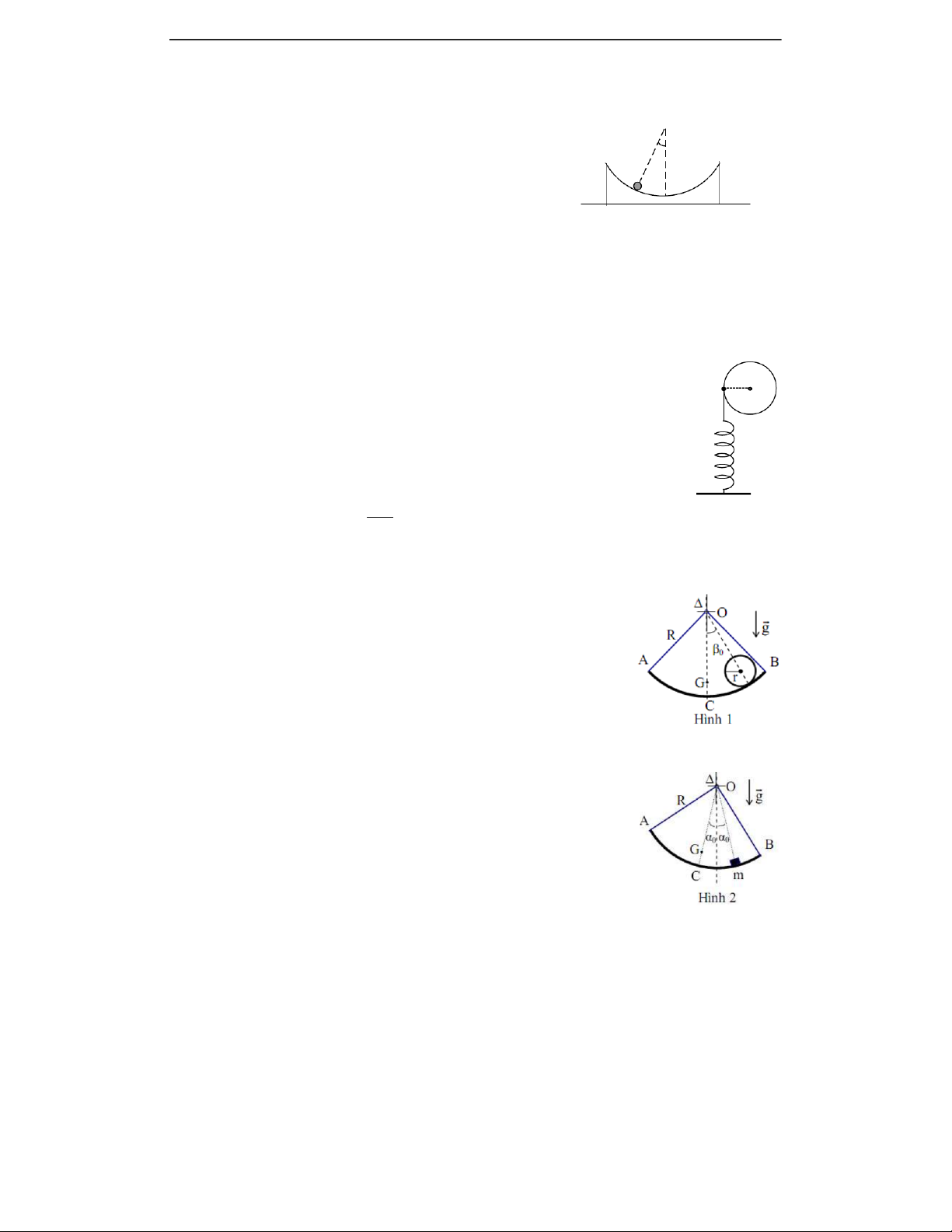
Bài 6. HSG QG 2005 Một vật sáng có khối lượng m, coi như
một chất điểm, được gắn dưới một lò xo có độ cứng k và có
khối lượng không đáng kể. Khi dao động, vật có vị trí cân bằng O1 RCO
nằm trên đường thẳng kéo dài của đường kính O .2 1O 2 của một
quả cầu bằng thủy tinh. Quả cầu có bán kính R, chiết suất n = R
1,5. Khoảng cách từ vị trí cân bằng của vật sáng tới O 1 là R.
Mặt sau quả cầu được tráng bạc (hình vẽ). Ta chỉ xét ảnh của vật sáng tạo bởi các tia đi từ vật đến
quả cầu với góc tới nhỏ. Coi chiết suất của không khí bằng 1.
1. Xác định vị trí ảnh của vật sáng khi vật ở vị trí cân bằng.
2. Khi vật sáng dao động với biên độ A (A có giá trị nhỏ) thì ảnh của vật dao động với vận tốc
cực đại bằng bao nhiêu? Created by Lê Minh Sơn Email : Lesontb@gmail.com PHẦN 4. DAO ĐỘNG Bài 7. HSG QG 2005
Cho vật nhỏ A có khối lượng m và vật B khối lượng M. Mặt
trên của B là một phần mặt cầu bán kính R (xem hình vẽ). Lúc .
đầu B đứng yên trên mặt sàn S, bán kính của mặt cầu đi qua A C
hợp với phương thẳng đứng một góc 0(0 có giá trị nhỏ). Thả  R
cho A chuyển động với vận tốc ban đầu bằng không. Ma sát giữa A 0
A và B không đáng kể. Cho gia tốc trọng trường là g. Giả sử khi mM B
A dao động, B đứng yên (do có ma sát giữa B và sàn S). S
a) Tìm chu kì dao động của vật A.
b) Tính cường độ của lực mà A tác dụng lên B khi bán kính qua vật A hợp với phương thẳng đứng một góc    (  ). 0
c) Hệ số ma sát giữa B và mặt sàn S phải thoả mãn điều kiện nào để B đứng yên khi A dao động? Bài 8. HSG QG 2007
Một đĩa tròn đồng chất, khối lượng m, bán kính R, có thể quay quanh một trục
cố định nằm ngang đi qua tâm O của đĩa (hình vẽ). Lò xo có độ cứng k, một đầu cố O AR
định, một đầu gắn với điểm A của vành đĩa. Khi OA nằm ngang thì lò xo có chiều
dài tự nhiên. Xoay đĩa một góc nhỏ 0 rồi thả nhẹ. Coi lò xo luôn có phương thẳng
đứng và khối lượng lò xo không đáng kể. k
a. Bỏ qua mọi sức cản và ma sát. Tính chu kì dao động của đĩa.
b. Thực tế luôn tồn tại sức cản của không khí và ma sát ở trục quay. Coi mômen 2 kR
cản MC có biểu thức là M200 
. Tính số dao động của đĩa trong trường hợp C  0  0,1rad .
Biết biểu thức tính công của mô men lực M làm vật quay 1 góc  là : A = M.
Bài 9 – HSG QG 2011.
Cho vật 1 là một bản mỏng đều, đồng chất, được uốn theo dạng lòng
máng thành một phần tư hình trụ AB cứng, ngắn, có trục ∆, bán kính R
và được gắn với điểm O bằng các thanh cứng, mảnh, nhẹ. Vật 1 có thể
quay không ma sát quanh một trục cố định (trùng với trục ∆) đi qua điểm
O. Trên Hình 1, OA và OB là các thanh cứng cùng độ dài R, OAB nằm
trong mặt phẳng vuông góc với trục ∆, chứa khối tâm G của vật 1, C là
giao điểm của OG và lòng máng.
1. Giữ cho vật 1 luôn cố định rồi đặt trên nó vật 2 là một hình trụ
rỗng, mỏng, đồng chất, cùng chiều dài với vật 1, bán kính r (r < R), nằm dọc theo đường sinh của
vật 1. Kéo vật 2 lệch ra khỏi vị trí cân bằng một góc nhỏ β rồi thả nhẹ. 0
a) Tìm chu kì dao động nhỏ của vật 2. Biết rằng trong quá trình dao
động, vật 2 luôn lăn không trượt trên vật 1.
b) Biết µ là hệ số ma sát nghỉ giữa vật 1 và vật 2. Tìm giá trị lớn nhất
của góc để trong quá trình dao động điều hoà, vật 2 không bị trượt trên vật 1.
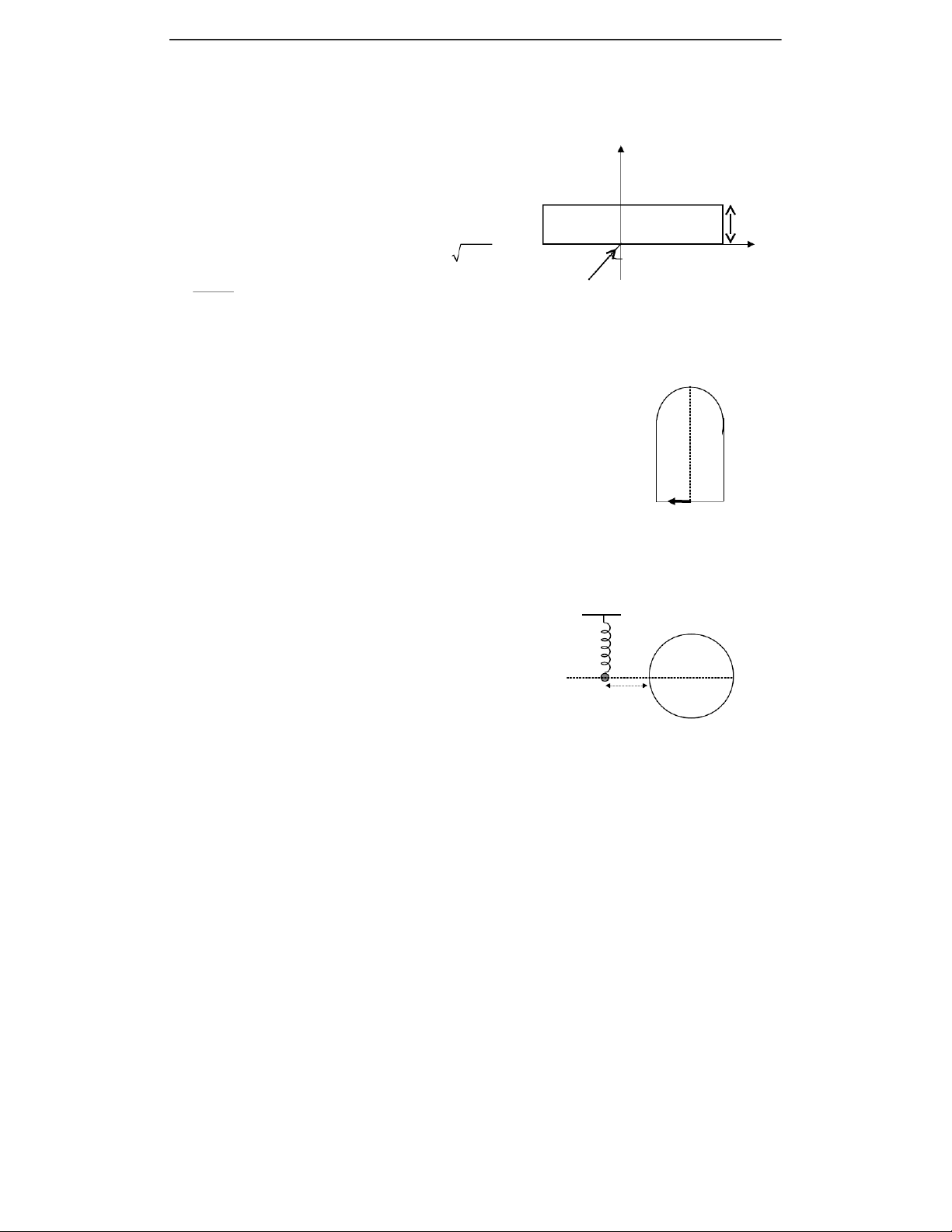
2. Thay vật 2 bằng một vật nhỏ 3. Vật 3 nằm trong mặt phẳng OAB.
Kéo cho vật 1 và vật 3 lệch khỏi vị trí cân bằng sao cho G và vật 3 nằm về
hai phía mặt phẳng thẳng đứng chứa ∆, với các góc lệch đều là α0 như
Hình 2, rồi thả nhẹ. Bỏ qua ma sát. Tìm khoảng thời gian nhỏ nhất để vật 3 đi tới C. Created by Lê Minh Sơn Email : Lesontb@gmail.com
ĐÁP ÁN ĐỀ ÔN TẬP THI OLYMPIC 2021 – 2 BÀI 1 :
1. Góc tới im lớn nhất ứng với tia IJ tới mặt tiếp xúc của hai J n2
lớp thủy tinh dưới góc giới hạn igh tức là ứng với ri I im n n1 2 r = – igh. Do đó: cosr = sini = gh n1 sinim = nsinr = n = n 1 1 = = n 0,224 => im 14
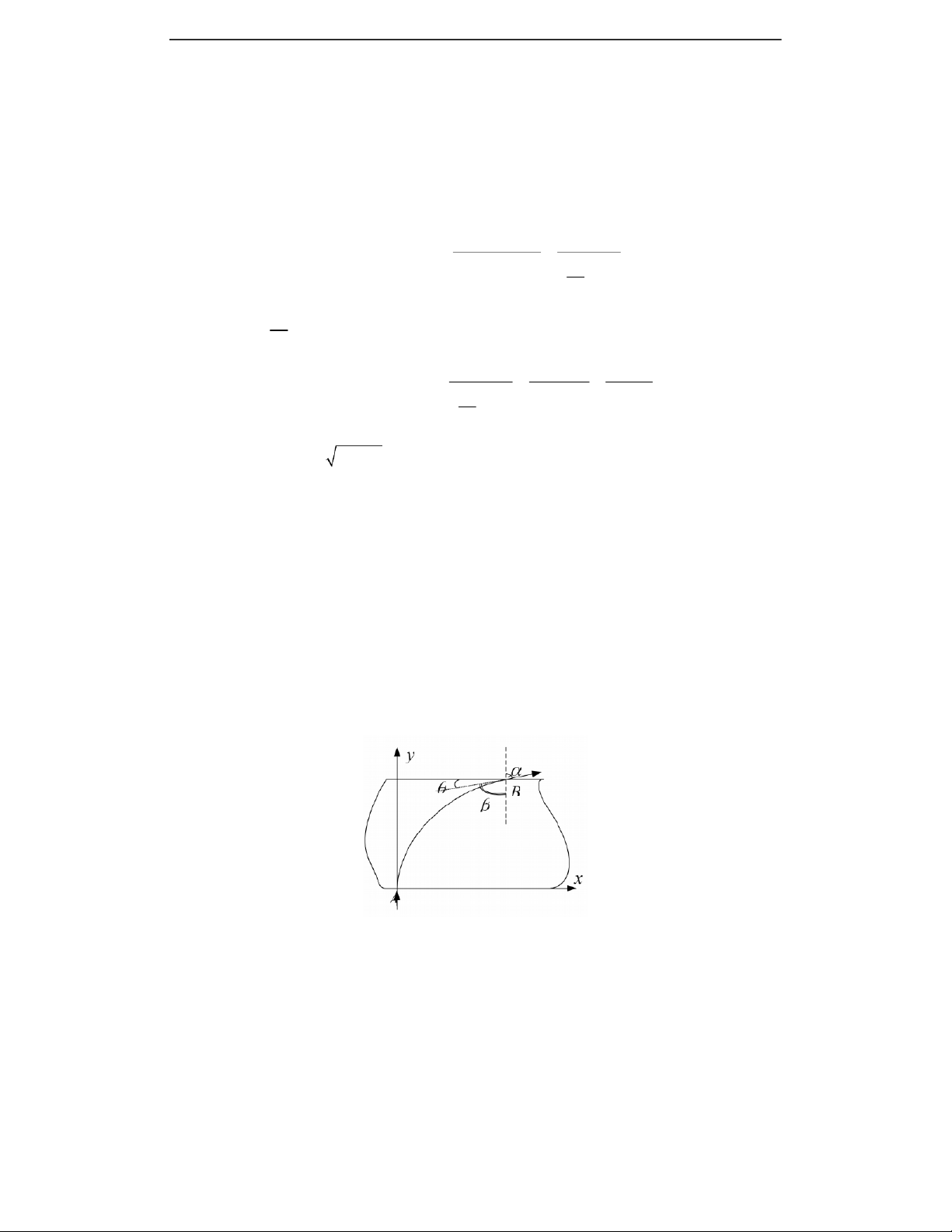
2. Góc tới i m lớn nhất ứng với tia JH tới mép ngoài của hình
vành khăn dưới góc tới i . Trong tam giác OJH, t H gh a có : igh 1 sin J sin H  . Với sinJ = sin J = sin( i IJ 1 + gh ) R OH OJ i  m sin(i  )  sin i gh gh O R a  R a R a n R a sin(i + 2 gh = sin i .  gh R a  n R a 1  n R a Do đó r = - (i + 2 gh nên cosr sin(i + gh = sinigh . 2 n R a 1 2  n R a  sini 2 m = n sin r 1 = n1 1 .  = 0,1588 ; i = 90 n R a  1
BÀI 2 : Vì chiết suất của môi trường chỉ biến thiên theo phương của trục Oy, nên ta chia môi
trường thành các lớp mỏng theo phương của trục Ox (tức là vuông góc với Oy) như hình 4 x O x i x  dx y  y  dy y HÌNH VẼ 4 Created by Lê Minh Sơn Email : Lesontb@gmail.com
Định luật khúc xạ ánh sáng viết liên tiếp cho từng lớp có dạng n siin  n siin  i sin   ... n .. .sin 0 0 1 1 2 2
Áp dụng cho gốc tọa độ O và điểm khảo sát có tọa độ (x;y) ta được: 0 n 0sin  90 . n sin i
CHÚ Ý: Khi viết định luật khúc xạ ánh sáng tại vị trí biên ( Tại O trong trường hợp
này ) ta phải hiểu rằng điểm đang xét là điểm rất gần O thuộc phần chứa môi trường khảo sát
Bình phương hai vế phương trình trên ta được: 2 2 2 n n  0sin i (1) d  2 2 2 x 1 sin co i s dy dx   dy  Từ hình vẽ trên ta có:  22   2   (2)   1  dx dy ax Mặt khác dx 2  (3) 2 1 1 1 sin 4ia x  1 4 ay 1  
Thay (3) vào (2) ta được: 22 2  dy     Thay vào phương   1  dx 
trình (1) ta được: n n   1 4 ay 0 BÀI 3 :
a) Trong bài toán này dữ kiện đề bài cho biết hàm chiết suất của môi trường phụ thuộc
tọa độ. Yêu cầu tìm phương trình quỹ đạo của đường truyền ánh sáng.
Chiết suất của môi trường biến thiên theo trục Ox nên ta chia môi trường thành nhiều
lớp mỏng theo phương song song với Oy.
Chiết suất của bản tại điểm A là n n 
, góc tới tại điểm A là 0
i 90 (như hình vẽ ) A 0 0 y   B  x A
Tại điểm B, chiết suất của môi trường là nB, góc tới là  . Ta có:   0 n n .sin B Created by Lê Minh Sơn Email : Lesontb@gmail.com n n .cos 0 (1) B
CHÚ Ý: Đến đây hay nhầm lẫn rằng góc  
 . Thực tế điều này không đúng vì tại
điểm B chiết suất ở phía trên bằng 1 (trong môi trường không khí), còn chiết suất ở phía
dưới bằng nB (trong môi trường bản mỏng) nên tia sáng khúc xạ ra không khí từ trong
bản đã bị lệch.
Để tìm mối quan hệ giữa hai góc  và  ta xét sự khúc xạ ánh sáng tại điểm B từ trong
bản mỏng ra không khí, pháp tuyến là đường thẳng đứng qua B sin sin   nB Ta có: n sin 1 .sin    B 2 2 n  sin  2 cos  1 sin B    nB
Thay biểu thức trên vào phương trình (1) ta được kết quả: 2 2 0 n sin n    B 2 2 n n  sin  B 0 0 n nx
b) Thay biểu thức chiết suất nB vào phương trình tổng quát của chiết suất 1  R   0   1 n x R n B
Ta sẽ tìm được tọa độ của điểm B:   B
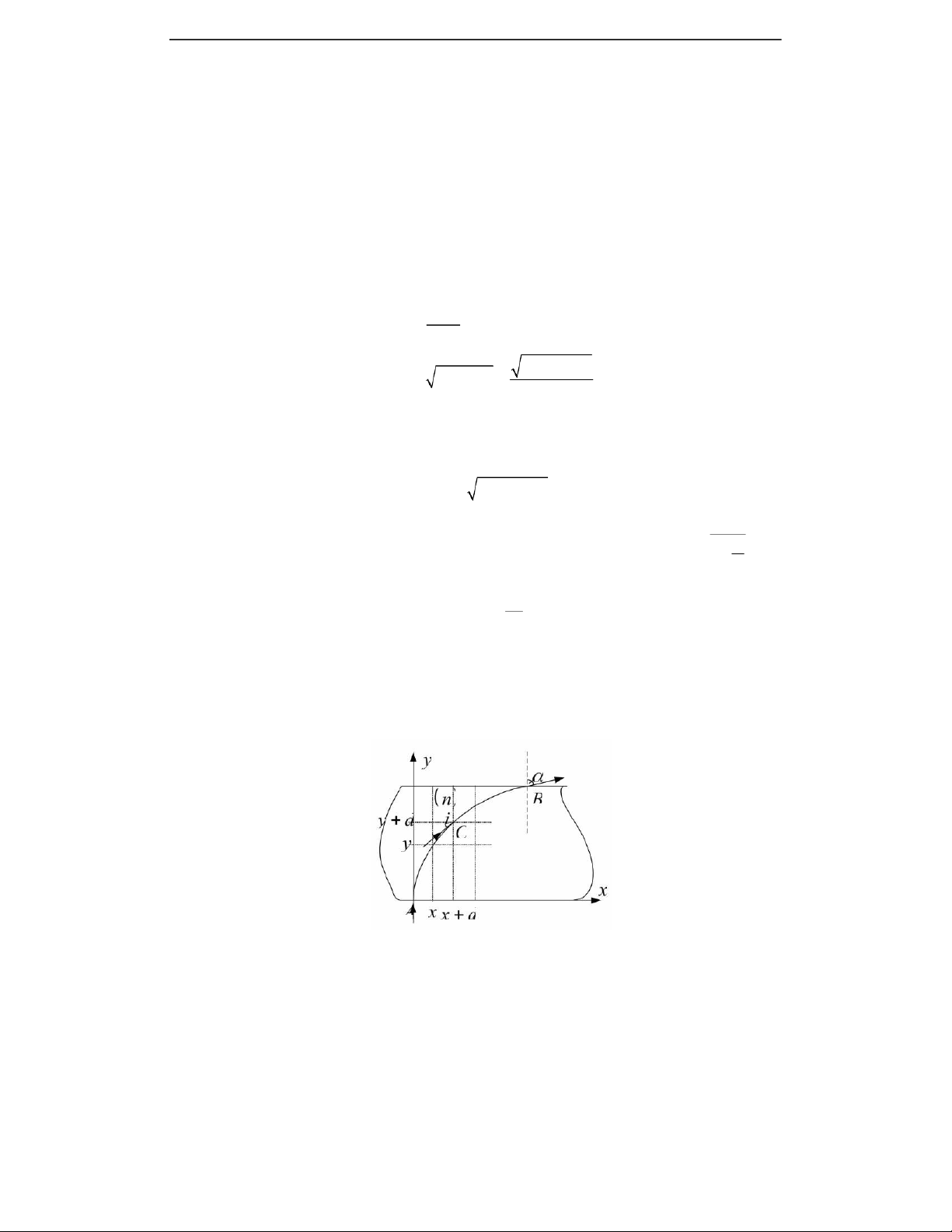
c) Lập phương trình quỹ đạo của đường đi của tia sáng.
Xét tại một điểm tới C bất kì trong bản như hình vẽ . y  n B y  dy i C y x A x x dx  0  sin i = R x Ta có 0.sini  sin n R n n   i R x R Created by Lê Minh Sơn Email : Lesontb@gmail.com 2  cos 2 Rx x  iR
. Từ đó ta có hệ số góc của tiếp tuyến tại điểm đang xét là: sin  tan cos  2 i R x dy ii dx 2 Rx x  R x  Rút ra: dy dx  2 2Rx x yx R x 
Lấy tích phân hai vế ta được: dy dx    2 0 0 2Rx x
Thực hiện phép tích phân bằng cách đặt 2 u  2  Rx x
du 2R x dx Kết quả thu được: x  y 2 Rx  2 2 0
Kết luận phương trình đường đi của tia sáng là một cung tròn tâm I có tọa độ R;0 bán kính R BÀI 4 :
Chia môi trường thành nhiều lớp mỏng bề dày dy bằng y
các mặt phẳng  Oy. Giả sử tia sáng tới điểm M(x,y) M’(x+dx,y+dy)
dưới góc tới i và tới điểm M’(x+dx,y+dy) trên lớp tiếp M(x,y) dy dx i
theo. Coi tia sáng truyền từ M đến M’ theo đường thẳng: x n sin  n 0
0sin =...= n sin i => sin i = n dx sin i n sin  y 0  t  gi   n sin dy  0 xn ( y  ) n sin  2 2 2 2 dy 1 sin i  n n sin   2 2 2 0 00 y y n0sin dx aa sin dy xn(y = ) = n sin cos ky òò 2 2 2 2 0 0 - a a- 0 sin si a na 2 y 2 x =- 2 cos a - ky ) 2 = (cos a - c a os k - y Þ ) 0 k k kx 2 =- k cos cos + a- ky co = s a 2 - sin a  2 y x x a 2 4sin sin a a
Đó là phương trình cần tìm. Đường đi của tia sáng là 1 parabon quay bề lõm về phía dưới. y y x x O O x1 x2 Created by Lê Minh Sơn Email : Lesontb@gmail.com BÀI 5:
1) Kí hiệu d, d’ lần lượt là các khoảng cách AO, OA’ và bán kính OC của chỏm cầu. Áp dụng công
thức lưỡng chất cầu cho chỏm cầu POQ ta được: n 1 1 n  nRd '   (n   2 = 1 , n = n) 1  dd '(1 n) R d d ' R Với d '  40cm ; R  0,4cm ta được d 1,147...  1,15cm  O'O 1  ,15cm
Độ phóng đại của ảnh: n d ' k  . 5  2, 87 53 1 d Độ cao của ảnh: A 'B' 5  3 . 1mm 5  ,3cm 2) d = d- 0,01 mm = 1,146cm 1 Ta có: n 1 1 n   Rd d 37,  95c  m '  '1 d d R 1 d (1  n) nR 1 1 1
Kích thước dọc theo trục OO’ của ảnh vết xước BÀI 6 :
1. Xác định vị trí ảnh của vật sáng khi vật ở vị trí cân bằng.
- Áp dụng công thức lưỡng chất cầu : n n n n n1n2 1 2 2 1   (1) ir d d ' R SS' C '' ' AB nd  1 (2) AB nd 2
- Xác định ảnh của vật khi ở VTCB. Ta có sơ đồ tạo ảnh : MN   1 O  2 O MN  1 O M N   M N d  11 2 2 3 3 ' '' R d d d d d 1 1 2 23 3 O1 RC . O2 1 1,5 1,51 1 d 3R;d 2R d 5R ''         ' 1 21 Rd R 2R R 1 R
O2 là gương cầu tiêu cự f2 : 1 11 1 1 2 5 '       dR  '' 2 d d f 5Rd R 9 22 2 d   2Rd  513 '  2R  R R 32 99 Created by Lê Minh Sơn Email : Lesontb@gmail.com 1,5 1    11,  5 1  13R ' 13R d 0  . Ảnh ảo, cách O2 là . ' dd R  3 2R 7 7 33
2. Khi vật sáng dao động với biên độ A (A có giá trị nhỏ) thì ảnh của vật dao động với vận tốc
cực đại bằng bao nhiêu?
Khi vật sáng dịch chuyển từ MN thì ảnh dịch chuyển từ M3N3 M N ' 1d M N ' d M N ' 1,5d 1 1 MN  1 ; 2 2 M N  2 ; 3 3 M N  3  1,5d d d 1 1 1 2 2 2 3 ' ' ' M N d d d 3 3 3 3 1 2 3  .  => M3N = MN. MN d d d 7 3 7 1 2 3 3
Gọi v' là vận tốc của vật, v' là vận tốc của ảnh. Đạo hàm hai vế theo t ta có v' = v  7 3 3 3k ' v  v   AA  . maxmax 7 7 7m BÀI 7.
a) Tìm chu kì dao động của m
+ Chọn trục tọa độ Ox trùng với quỹ đạo chuyển động C
+ Khi đường bán kính nối vật và tâm mặt cầu(AC) lệch góc  so với    x 0
phương thẳng đứng thì : N mg  m.a N tp (1) m Q AB    Với: a  a a tp tt ht ; đặt att = a Mg N'
+ Chiếu (1) trên trục tọa độ Ox ( Phương tiếp tuyến với đường mg
cong tại điểm xét) : -mgsin = matt = ma
+ Với góc  nhỏ thì sin   => -mg = ma x g g
=> -mg = m.a = m.x” => x” = a = - x = -  x ; với 2  = R R R R
=> m dao động điều hoà với T   2 . g
b) Tìm lực đè của m vào M   + Có : N mg  m.a tp (1) mv mv
+ Chiếu (1) trên phương bán kính AC: N - mgcos = 2 => N = mgcos + 2 R R mv + Lại có :
2 = mgR(cos - cos0) => Lực mà m tác dụng vào M: N = 3mgcos - 2mg cos 2
c) Tìm hệ số ma sát để M đứng yên Created by Lê Minh Sơn Email : Lesontb@gmail.com
+ Lực đẩy M theo phương ngang là do N’=N tạo thành : N = Nsin x
 = 1,5mgsin2 - 2mg cos sin 0 .
+ Áp lực của M lên sàn là : Q = Mg + Ncos = Mg + 3mgcos2 - 2mg cos0 cos.
+ Điều kiện để B đứng yên là: Nx  Q với mọi    .0 Với  nhỏ: N x  (3mg - 2mg cos )
0  tỉ lệ với  nên có giá trị cực đại khi  =  . 0 Nxmax = (3mg cos - 2mg 0 cos )sin 0  = m 0 gcos si 0 n0
+ Bổ đề toán học Dy =dy Khi : y’ =
< 0 thì khi x tăng ( dx > 0) => dy < 0 => y giảm : x, y nghịch biến Dx dx Dy =dy  Khi : y’ =
> 0 thì khi x tăng ( dx > 0) => dy > 0 => y tăng : x, y đồng biến Dx dx
+ Có : Q = Mg + Ncos = Mg + 3mgcos2 - 2mg cos0 cos. dQ => Q’ =
= - 6mgcos.sin + 2mgcos0.sin = 2mgsin(cos – 3cos 0 ) < 0 da
=> Q nghịch biến với . Vậy khi ở vị trí  =  thì Q nhỏ nhất : Q 0 min = Mg + mgcos20
+ Để M không bị trượt với mọi giá trị của  thì : Nxmax < .Qmin N mcos sin aa =>   x max = 0 0 Q 2 M m + cos a min 0 BÀI 8 :
a) Tìm chu kì dao động của đĩa
+ Quay đĩa một góc nhỏ , Điểm A dịch chuyển đoạn R. Do độ dịch chuyển rất nhỏ nên có thể coi
cung tròn là đường thẳng đứng => Lực đàn hồi có phương thẳng đứng : F = k.R đh 
+ Đĩa chịu tác dụng của mômen lực M = -kR  O
2 (dấu – vì M ngược chiều ) AR 2 mR Fđh
+ Đĩa tròn đồng chất, bán kính R có mômen quán tính I2 . k
+ Phương trình chuyển động của vật rắn quay quanh một trục: là gia tốc góc. Vậy: - kR2 =  => 2k m
Vậy đĩa tròn dao động điều hòa với tần số góc:   , Chu kì: T 2   2k m
b) Tính số dao động của đĩa Created by Lê Minh Sơn Email : Lesontb@gmail.com
+ Xét một lần đoạn OA đi qua vị trí nằm ngang. Gọi  , 1  là biên độ 2 M
góc về hai phía so với đường nằm ngang. Biến thiên cơ năng của hệ là A01 A’ 2 1 N 2 2 2 W   kR (    ) 2 1 2 2 kR
+ Công của mômen cản : A  M ( )    ( )     C C 1 2 1 2 200 1
+ Theo định lý biến thiên cơ năng: W  A      100   C 1 2
+ Như vậy, cứ sau mỗi nửa chu kì, biên độ góc giảm rad 
=> Số dao động mà vật thực hiện được cho đến khi dừng lại là: 0 n 5  2( )    1 2 BÀI 9 :
1. Xét vật 2 ở vị trí ứng với góc lệch β Gọi φ là góc mà vật 2 tự quay
quanh mình nó. Chọn chiều dương tất cả các chuyển động ngược chiều kim
đồng hồ. Lực tác dụng lên vật 2 gồm: trọng lực, phản lực, lực ma sát nghỉ.
Phương trình chuyển động của khối tâm vật 2 xét theo phương tiếp tuyến với quỹ đạo: m2a = Fms – m gsinβ (1) 2
Vì β nhỏ => sinβ  β (rad) => m (R – r)β” = F 2 ms – m gβ (2) 2
Phương trình chuyển độngquay của khối trụ nhỏ quanh khối tâm: m2r φ” = F 2 msr
Điều kiện lăn không trượt: (R – r).β’ = -rφ’ => (R – r).β” = -rφ” (3)
Thay (2) và (3) vào (1) ta được: β” + β = 0 (4)
Phương trình (4) biểu diễn dao động điều hòa với chu kì : T = 2π
Từ (2) ⇒ Fms = m rφ” = -m 2 (R-r)β” = m 2 (R – r)ω 2 β = 2 m gβ (5) 2 Phản lực N = m gcosβ 2 = m g(1 - 2
) (6) Điều kiện lăn không trượt: ≤ µ với mọi β (7)
Thay (5) và (6) vào (7) ta có : = f(β) = ≤ µ với 0 ≤ β ≤ β0
Bất phương trình trên cho nghiệm : β0 ≤
Cần chú ý : để có kết quả này cần có thêm điều kiện giới hạn về β 0để sinβ0  β (rad) 0
2. Xét tại thời điểm khối tâm vật 1 và vật 3 có li độ góc tương ứng là α, θ
Phương trình chuyển động của vật 3 theo phương tiếp tuyến với hình trụ: m3R” = - m3g (1) Created by Lê Minh Sơn Email : Lesontb@gmail.com Nghiê ”
m của phương trình là :  = 0cosω t = α 0 cosω 0 t ; với ω 0 = 0
Phương trình quay của G quanh O: m1R2α” = -m1g α
Nghiệm phương trình này: α = α0cosω t ; với ω 1 = 1
Góc lệch của vật 3 so với phương OG là: γ = α -  = 2α cos 0 cos . Khi vật 3
tới C thì γ = 0 => tmin =