Đề cương ôn thi logic học | Trường Đại học Luật, Đại học Quốc gia Hà Nội

ĐỀ CƯƠNG ÔN THI LOGIC HỌC Lưu ý:
- Tài liệu chỉ dành cho người đã có kiến thức nền, không dành cho người mất gốc
- Tài liệu chỉ tóm tắt những kiến thức chính sẽ thi, không bao gồm phần giải thích
- Nhìn tài liệu khá dài nhưng chủ yếu là bài tập
- Phần tô đỏ là phần bắt buộc phải học
CHƯƠNG 1: ĐỐI TƯỢNG NGHIÊN CỨU CỦA LOGIC HỌC
- Logic học đại cương là khoa học nghiên về các hình thức và quy luật của tư duy
phản ánh đúng đối tượng ở trạng thái đứng im tương đối của đối tượng (Mặt hình thức của đối tượng)
CHƯƠNG 2: KHÁI NIỆM
1. Cấu trúc của khái niệm
- Khái niệm nội hàm: Là toàn bộ những dấu hiệu đặc trưng, bản chất của đối tượng
được phản ánh trong khái niệm (dấu hiệu bản chất nhận biết đối tượng)
- Khái niệm ngoại diên: là tập hợp gồm tất cả các đối tượng có chung những dấu
hiệu bản chất đặc trưng được phản ánh trong nội hàm của khái niệm (phạm vi)
- Quan hệ nghịch biến: Nội hàm càng phong phú, càng nhiều dấu hiệu bản chất
(rộng) thì ngoại diên càng hẹp, càng ít đối tượng được phản nahs và ngược lại.
(Mở rộng nội hàm bằng cách thêm các đặc trưng)
2. Quan hệ giữa các khái niệm
a. Quan hệ điều hòa (tương thích)
Là quan hệ giữa những khái niệm mà ngoại diên của chúng ít nhất có 1 bộ phận trùng nhau
- Quan hệ đồng nhất: Là khái niệm giữa những khái niệm ngoại diên của chúng
hoàn toàn trùng nhau, nhưng nội hàm của chúng vẫn có sự phân biệt (thủ đô của VN - Hà Nội)
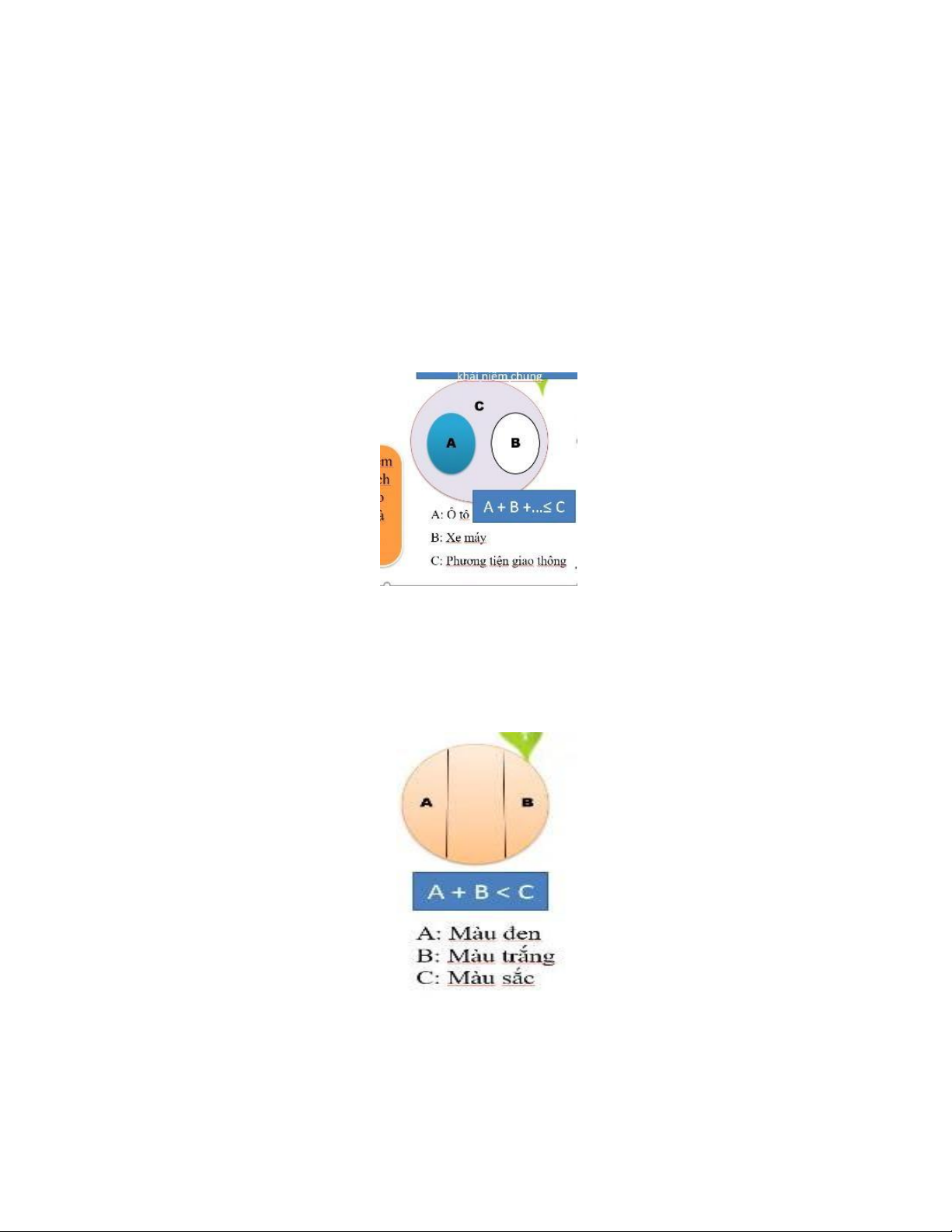
- Quan hệ bao hàm: Là quan hệ giữa những khái niệm mà ngoại diên của khái
niệm này là toàn bộ ngoại diên của khái niệm kia nhưng không ngược lại. Khái
niệm thứ nhất gọi là khái niệm bị bao hàm còn khái niệm thứ 2 gọi là khái niệm
bao hàm (giảng viên - giảng viên trẻ)
- Quan hệ giao nhau: Là quan hệ giữa các khái niệm mà ngoại diên của chúng chỉ
có 1 phần trùng nhau (Ca sĩ - diễn viên: những người vừa là ca sĩ vừa là diễn viên) (sinh viên - thanh niên)
b. Quan hệ không điều hòa
Là quan hệ giữa các khái niệm mà ngoại diên của chúng tách rời nhau, nhưng chúng
cùng lệ thuộc vào ngoại diên của khái niệm chung
- Quan hệ ngang hàng: Là quan hệ giữa các khái niệm mà ngoại diên của chúng
tách rời nhau nhưng nội hàm không có dấu hiệu loại trừ nhau và chúng cùng lệ
thuộc ngoại diên của khái niệm chung (giỏi và khá)
- Quan hệ đối lập: Là quan hệ giữa những khái niệm mà ngoại diên của chúng tách
rời nhau, nội hàm của chúng có những dấu hiệu loại trừ nhau, nhưng tổng ngoại
diên của chúng cộng lại luôn nhỏ hơn ngoại diên của khái niệm chung. (giỏi và kém)
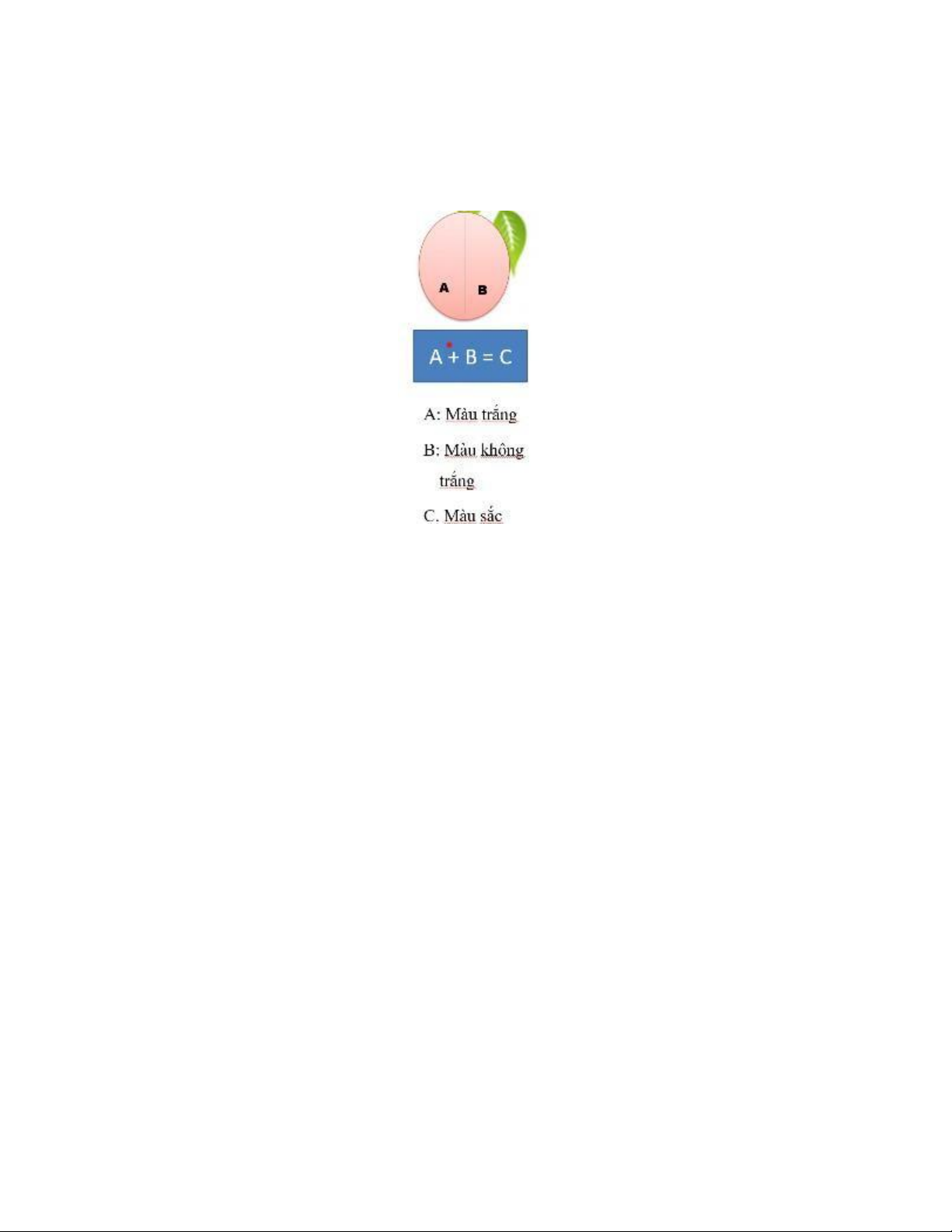
- Quan hệ mâu thuẫn: Là quan hệ giữa những ví dụ mà ngoại diên tách rời nhau,
nội hàm loại trừ nhau và tổng ngoại diên của chúng cộng lại luôn đúng bằng ngoại
diên của 1 khái niệm chung
3. Phép định nghĩa khái niệm 3.1
Bản chất của định nghĩa khái niệm
- Là thao tác logic nhằm vạch ra những dấu hiệu cơ bản nhất trong nội hàm của khái niệm
- Dfd: Đối tượng được định nghĩa (Là khái niệm mà ta phải vạch rõ nội hàm cơ bản của nó ra)
- Dfn: Thứ được dùng để định nghĩa (Là khái niệm có những dấu hiệu chung và cơ
bản cấu thành nội hàm của khái niệm được định nghĩa 3.2
Các quy tắc định nghĩa
a. Định nghĩa phải cân đối
- Ngoại diên Dfn = Dfd (chỉ tính theo chiều Dfn → Dfd) - Vi phạm quy tắc nếu: 
Định nghĩa quá rộng: (ngoại diên Dfn > Dfd) 
Định nghĩa quá hẹp (ngoại diên Dfn < Dfd) 
Định nghĩa vừa quá rộng, vừa quá hẹp (ngoại diên Dfn khác Dfd)
b. Định nghĩa không được vòng quanh:
- Phạm lỗi trong trường hợp định nghĩa vòng quanh
- VD: Tư duy logic là tư duy 1 cách logic
c. Không nên dùng mệnh đề phủ định trong định nghĩa
- Vi phạm nếu định nghĩa dưới dang: Dfd không là Dfn hoặc Dfd không phải Dfn
- Có thể sử dụng nếu như Dfn và Dfd nằm trong quan hệ mâu thuẫn
d. Định nghĩa phải tường minh:
- Rõ ràng, chính xác, ngắn gọn, sáng tỏ
- Quy tắc bị vi phạm trong trường hợp định nghĩa không tường minh, dùng từ hoặc hình ảnh ví von, so sánh
- VD: Trẻ em là mầm non của đất nước 3.3 Bài tập
Câu 1: Phạm lỗi vì Dfn > dfd nên định nghĩa quá hẹp
Câu 2: Phạm lỗi vì định nghĩa vừa quá rộng vừa quá hẹp Dfn khác Dfd
Câu 1: Sai do sử dụng phủ định: Khái niệm tam giác đều và tam giác vuông không nằm trong quan hệ mâu thuẫn
Câu 2: Sai do định nghĩa vòng vo, dùng lại từ lao động, ngoài ra còn có lỗi quá hẹp
Câu 3: Sai do định nghĩa vừa rộng vừa hẹp dfn khác dfd
Câu 4: Sai do định nghĩa không tường minh, dùng từ ví von
Câu 5: Sai do định nghĩa quá rộng dfn > dfd
4. Phép phân chia khái niệm
Phân chia khái niệm lại là thao tác nhằm vào ngoại diên của khái niệm để vạch ra
ngoại diên của các khái niệm thành phần bao chứa trong nó (VD: Khái niệm học lực
được phân chia thành học lực xuất sắc, học lực giỏi, học lực khá, học lực trung bìnhm học lực kém) 4.1
Cấu tạo của phép phân chia: 3 bộ phận
- Khái niệm bị phân chia: Là khái niệm loại mà từ đó ta chỉ vạch ra các khái niệm
cùng chứa nó (Ký hiệu là A)
- Cơ sở phân chia: Là căn cứ, dấu hiệu, mà dựa vào đó ta chia khái niệm loại ra
thành các khái niệm chúng trong đó VD: Khái niệm Người (màu da, vùng địa lý,. .)
- Các khái niệm chúng thành phần: là các khái niệm thu được sau khi phân chia (ký hiệu A1, A2, An) 4.2
Quy tắc phân chia khái niệm
a. Quy tắc 1: Phân chia phải cân đối
- Tổng ngoại diên của các khái niệm thành phần thu được phải đúng bằng ngoại
diên của khái niệm bị chia
- Trường hợp phạm lỗi: 
Chia nhiều thành phần: Tổng ngoại diên của các khái niệm thu được sau phân chia
nhỏ hơn ngoại diên của khái niệm bị phân chia: A1+A2+. . An < A 
Chia thừa thành phần: Khi các khái niệm chúng thành phần được thừa ra so với
ngoại diên của khái niệm loại bị phân chia: A1+A2+. . An > A 
Phân chia vừa thừa vừa thiếu thành phần: Khi ngoại diên của các khái niệm thành
phần thu được không đúng bằng ngoại diên của khái niệm bị chia: A1+A2+. . +An khác A
b. Quy tắc 2: Phân chia phải cùng một cơ sở
- Phải giữ nguyên căn cứ phân chia trong suốt quá trình phân chia
 Quy tắc bị vi phạm khi thay đổi cơ sở trong quá trình đang chia khái niệm
c. Quy tắc 3: Các khái niệm thành phần thu được phải nằm trong quan hệ ngang hàng
- Ngoại diên của chúng phải tách rời nhau.
 Ngược lại sẽ là vi phạm quy tắc này (đồng nhất, bao hàm, giao nhau)
- Ví dụ: Sinh viên giỏi là sinh viên nữ (Quan hệ bao hàm)
d. Quy tắc 4: Phân chia phải liên tục cùng cấp độ
- Khi phân chia thì phải từ khái niệm loại vạch ra các khái niệm chung gần nhất.
- Nếu quy tắc này bị vi phạm, thì sẽ mắc lỗi phân chia nhảy vọt, không cùng cấp độ 4.3 Bài tập Bài 1:
- Phép phân chia này là sai: 
Nó vi phạm quy tắc 1: Định nghĩa không cân đối, định nghĩa thừa 
Nó vi phạm quy tắc 2 do sơ sở phân chia của nó bị thay đổi trong quá trình phân
chia, cơ sở ban đầu của nó là phân chia theo lĩnh khoa học (khoa học tự nhiên và
khoa học xã hội) vì vậy khoa học thời cổ đại và toán học là 2 thành phần bị phân chia sai. 
Nó vi phạm quy tắc 3 vì thành phần toán học và thành phần khoa học tự nhiên có
quan hệ bao hàm nhau, khái niệm khoa học tự nhiên và khoa học thời cổ đại nằm
trong quan hệ giao nhau, khái niệm khoa học xã hội và khái niệm khoa học ngoại
diên của nó không tách rời. 
Nó vi phạm quy tắc 4 do phân loại nhảy vọt, không cùng cấp độ, do KHXH,
KHTN và toán học không cùng cấp độ. Bài 2: Câu 1: 
Vi phạm quy tắc 1: Phân chia không cân đối, vừa thiếu vừa thừa 
Vi phạm quy tắc 2: Thay đổi cơ sở phân chia, động từ phân chia theo nguồn gốc
các nước chuyển sang phân chia theo độ tuổi 
Vi phạm quy tắc 3: Các vắc - xin ngừa Covid-19 của Nga, Mỹ và vắc - xin dành
cho người trên 18 tuổi nằm trong quan hệ giao nhau
Câu 2: Định nghĩa mắc lỗi vì định nghĩa vừa rộng vừa hẹp, dfn khác dfd
CHƯƠNG 3: PHÁN ĐOÁN 1. Phán đoán đơn
a. Các kiểu phán đoán đơn
- Phán đoán toàn thể khẳng định (A)
- Phán đoán toàn thể phủ định (E)
- Phán đoán bộ phận khẳng định (I)
- Phán đoán bộ phận phủ định (O) Bài tập:
Câu 1: Có S không là P => Phán đoán O
Câu 2: Mọi S là P => Phán đoán A
Câu 3: Có S không là P => Phán đoán E
Câu 4: Có S là P => Phán đoán I
Câu 5: Có S là P => Phán đoán I
Câu 6: Mọi S là P => Phán đoán A
Câu 7: Mọi S là P => Phán đoán A
b. Tính chu diên của các thuật ngữ logic trong phán đoán đơn
Mẹo xác định chu diên: Đặt câu hỏi cho S và P, muốn xác định S có chu diên hay
không đặt câu hỏi có phải S nào cũng là P hay không, nếu có thì S+ , nếu không thì S-
và làm điều tương tự với P.
VD: Có sinh viên là thanh niên
Bước 1: Xác định S và P (S là sinh viên, P là thanh niên) Bước 2: Đặt câu hỏi
- Đối với S: Có phải sinh viên nào cũng là thanh niên hay không? Câu trả lời là
không vì có sinh viên là người cao tuổi vẫn đi học => S-
- Đối với P: Có phải thanh niên nào cũng là sinh viên hay không? Câu trả lời là
không vì có thanh niên không là sinh viên, đó là những người trong tuổi thanh
niên nhưng không học đại học => P- - Phán đoán A: - Phán đoán E: - Phán đoán I:
- Phán đoán O: Luôn luôn S-;P+ Bài tập:
1. Một số S là P, phán đoán I (S-, P-): quan hệ giao nhau
2. Mọi S là P, phán đoán A (S+, P+): Quan hệ đồng nhất
3. Một số S là P, phán đoán I (S- P+): Quan hệ bao hàm
4. Mọi S không là P, phán đoán E (S+, P+): Quan hệ ngang hàng
5. Mọi S là P, phán đoán A (S+, P-): Quan hệ bao hàm
6. Một số S là P, phán đoán I ( S-, P-): Quan hệ giao nhau
7. Một số S không là P, phán đoán O ( S-, P+): Quan hệ giao nhau
8. Có S là P, phán đoán I (S-, P-) Quan hệ giao nhau c. Hình vuông Logic
Quan hệ mâu thuẫn: Đó là quan hệ giữa hai cặp phán đoán: A & O, E & I
Quan hệ lệ thuộc (thứ bậc): A & I, E & O. Trong đó, A là bậc trên, I là bậc dưới. Trong
quan hệ lệ thuộc, nếu phán đoán bậc trên đúng thì phán đoán bậc dưới tất yếu đúng, nếu
bậc dưới sai thì bậc trên tất yếu sai. Các trường hợp còn lại thì chưa xác định
Quan hệ đối lập: Đó là hai cặp phán đoán (A & E) gọi là đối lập trên, (I & O ) gọi là đối
lập dưới. Trong quan hệ đối lập trên, các phán đoán không thể cùng đúng, nhưng có thể
cùng sai. Ngược lại, trong quan hệ đối lập dưới, các phán đoán không thể cùng sai nhưng có thể cùng đúng Bài tập:  Chữa 2. Phán đoán phức:
Phán đoán phức là phán đoán được tạo bởi sự liên kết của các thành phần và liên từ logic
VD: Lan học giỏi và hát hay
2.1 Phán đoán phức cơ bản:
a. Phán đoán liên kết (Phép hội) -
Phản ánh mối quan hệ cùng tồn tại giữa các thành phần trong phán đoán - Công thức tổng quát: - Liên từ:  Và; vừa. . ., vừa  Tuy. . , nhưng 
Chẳng những. ., mà còn,. .
- VD: Lan học giỏi và hát hay
b. Phán đoán điều kiện (phép kéo theo)
- Phép kéo theo phản ánh mối quan hệ kéo theo tồn tại của các phán đoán bất kì
được coi là điều kiện với 1 phán đoán bất kì được coi là hệ quả, sự tồn tại của
phán đoán điều kiện kéo theo sự tồn tại của phán đoán hệ quả
- Công thức tổng quát: a → b - Liên từ: 
Nếu, muốn, hễ, dễ,. . .thì  Vì, do. . nên;. . .suy ra 
Nếu trời mưa thì đường ướt
- VD: Nếu trời mưa thì đường ướt
c. Phán đoán phân liệt (phép tuyển)
- Phép tuyển phản ánh mối quan hệ lựa chọn tồn tại giữa các thành phần trong phán
đoán, trong đó nhất thiết phải có 1 thành phần tồn tại
- Phán đoán phân liệt tuyệt đối (tuyển mạnh) 
Phản ánh mối quan hệ lựa chọn tồn tại giữa các thành phần trong phán đoán, trong
đó sự tồn tại của thành phần này loại trừ sự tồn tại của thành phần kia  Công thức tổng quát:  Liên từ: hoặc, hoặc. . 
VD: Trong tam giác vuông ABC hoặc góc A vuông hoặc góc B vuông
- Phán đoán phân liệt tương đối (tuyển yếu) 
Phản ánh mối quan hệ lựa chọn tồn tại giữa các thành phần trong phán đoán, trong
đó sự tồn tại của thành phần này không loại trừ sự tồn tại của thành phần kia  Công thức tổng quát: 
Liên từ logic: hoặc; hay là; 
VD: Trong tam giác ABC hoặc góc A nhọn hoặc góc B nhọn
d. Phán đoán tương đương (Phép tương đương)
- Phép tương đương phản ánh mqh điều kiện hệ quả giữa các thành phần trong phán
đoán, trong đó thành phần này vừa là điều kiện vừa là hệ quả của thành phần kia
- Công thức tổng quát: a ↔ b - Liên từ:  Nếu và chỉ nếu  Khi và chỉ khi. .
- VD: Một số chia hết cho 2 khi và chỉ khi nó là số chẵn
e. Phán đoán phủ định (Phép phủ định: 7)
- Phản ánh sự không tồn tại của các phán đoán thành phần hoặc của phán đoán phức - Công thức tổng quát: - Liên từ:  Không  Không có chuyện là  Làm gì có chuyện
- Nếu phủ định của từng phán đoán phức thì dùng “không” 
7a → b: Nếu không a thì b 
7(a → b): Không có chuyện là nếu a thì b Bài tập: 1. Phép hội:  a: có tri thức  b: có văn hóa 
Liên từ: Không chỉ có. . mà còn 2. Phép kéo theo 
a: Sánh vai với các cường quốc năm châu  b: Học tập thật giỏi: 3. Phép tuyển mạnh:  a: Đỗ  b: Trượt 4. Phép tương đương  a: Số chia hết cho 3 
b: Tổng các chữ số của chúng chia hết cho 3 5. Phép tuyển yếu  a: Bổ ích  b: Thú vị
6. Phép tuyển mạnh, phép kéo theo 
a: Không thể thấy trước 
b: Không buộc phải thấy trước hậu quả 
c: Không phải chịu trách nhiệm hình sự Bài 2:  Chữa bài
2.2 Tính đẳng trị của các phán đoán phức
a. Công thức đẳng trị của phép kéo theo
b. Phép tuyển: (không phân biệt tuyển mạnh hay tuyển yếu) c. Phép hội: d. Phép phủ định: Bài tập mẫu: Câu 1:
- Cấu trúc logic: a ^ b, a là xoay xung quanh mặt trời. b là xoay xung quanh trục của nó
- Các phán đoán đẳng trị: a^b
= 7(a → 7b): Không có chuyện nếu trái đất xoay xung quanh mặt trời thì không xoay xung quanh trục của nó
= 7(b → 7a): Không có chuyện nếu trái đất xoay xung quanh trục của nó thì không xoay xung quanh mặt trời
= 7(7a v 7b): Không có chuyện trái đất không xoay quanh mặt trời hoặc không xoay quanh trục của nó
Câu 2: Hoặc là pháp luật phải nghiêm minh hoặc là chúng ta không có dân chủ
- Cấu trúc logic: a v b, a là pháp luật phải nghiêm minh, b là chúng ta không có dân chủ
- các phán đoán đẳng trị: a v b
= 7a → b: Nếu pháp luật không nghiêm minh thì chúng ta không có dân chủ
= 7b → a: Nếu chúng ta có dân chủ thì pháp luật phải nghiêm minh
= 7 (7a v 7b): Không có chuyện pháp luật không nghiêm minh mà chúng ta lại có dân chủ
CHƯƠNG 4: QUY LUẬT LOGIC, HÌNH THỨC CỦA TƯ DUY
1. Quy luật đồng nhất
a. Cơ sở khách quan: Là tính đồng nhất, tính ổn định tương đối về chất của đối
tượng về chất của các sự vật hiện tượng trong quá trình tồn tại
b. Công thức: a = a (a là a) c. Nội dung:
- Trong quá trình suy nghĩ, lập luận thì tư tưởng phải là xác định, một nghĩa luôn
đồng nhất với chính nó
- Một tư tưởng được coi là chân thực, trước hết phải có nội dung xác định và giữ
nguyên (đồng nhất) nội dung đó trong suốt quá trình tư duy d. Các yêu cầu:
- Yêu cầu 1: Phải có sự đồng nhất của tư duy với đối tượng về mặt phản ánh
- Yêu cầu 2: Tư duy phải đồng nhất với ngôn ngữ về mặt diễn đạt, tức là phải dùng
ngôn ngữ tường minh, đơn nghĩa để diễn đạt chính xác tư tưởng  Hiểu 2 nghĩa
- Yêu cầu 3: Tư duy tái tạo phải đồng nhất với tuy duy nguyên mẫu 
Tư duy nguyên mẫu là tư duy có trước 
Tư suy tái tạo là tư suy có sau, tư duy nhắc lại hoặc hiểu lạit ừ tư duy nguyên mẫu 
Vi phạm nếu tư duy không nhất quán (TDTT khác TDNM) e. Ý nghĩa
- Đảm bảo tính nhất quán trong tư duy
- Đảm bảo yêu cầu phản ánh đúng đối tượng của tính nhất quán
2. Quy luật cấm mâu thuẫn (mâu thuẫn)
a. Cơ sở khách quan: Một đặc điểm, một thuộc tính nào đó của sự vật, hiện
tượng không thể vừa thuộc, vừa không thuộc về một sự vật, hiện tượng ấy ở
trong cùng 1 thời gian, không gian, một mối quan hệ cụ thể
 Tính xác định về chất của các đối tượng được bảo toàn trong một thời gian xác địnhb. Nộidung
- Hai phán đoán đối lập trên hoặc mâu thuẫn nhau về một đối tượng, được xét trong
cùng 1 thời gian, cùng 1 quan hệ, không thể cùng chân thực, ít nhất 1 trong chúng giả dối
- Nói cách khác: Hai tư tưởng mâu thuẫn nhau phản ánh về cùng 1 đối tượng ở 1 phẩm chất xác định
- VD: Bạn này học giỏi toàn diện kém mỗi môn logic c. Yêu cầu:
- Yêu cầu 1: Không được mâu thuẫn trực tiếp trong tư duy khi khẳng định đối
tượng, hay thuộc tính của đối tượng, đồng thời lại phủ định chính nó
- Yêu cầu 2: Không được mâu thuẫn gián tiếp trong tư duy khi khẳng định sự tồn
tại của đối tượng hay thuộc tính của nó nhưng những hệ quả được suy ra từ đối
tượng lại là phủ định chính nó d. Ý nghĩa:
- Tránh những mâu thuẫn trong tư duy lập luận, phát hiện ra mâu thuẫn của người khác
- Hình thành tư duy hệ thống rõ ràng hơn, không mâu thuẫn, tăng thuyết phục, tin cậy
VD1: Trong giờ học sử, cô giáo hỏi học sinh: Ai đã lấy cắp nó thần của ADV. Một
học sinh được gọi và đúng lên trả lời: “Thưa cô, em không biết nhưng em không lấy”
Vi phạm quy luật đông nhất: Tư duy tái tạo không đồng nhất với tư duy nguyên
mẫu ( Tư duy tái tạo là cô giáo muốn hỏi trong lịch sử ai đã lấy nỏ thần của ADV, tư
duy tái tạo: Học sinh tưởng rằng cô giáo hỏi ở hiện tại ai lấy nỏ thần của ADV)
VD2: Một người rất thành công trong công việc khi được hỏi bí kíp thành công là gì,
người này đã đưa ra lời khuyên: Tôi khuyên các bạn là trên đời này nếu muốn thành
công thì không nên nghe lời khuyên của ai cả
Vi phạm quy luật cấm mâu thuẫn: Mâu thuẫn trực tiếp
3. Quy luật bài trung
a. Nội dung, công thức:
- Hai phán đoán mâu thuẫn nhau về cùng một đối tượng, được khảo cứu trong cùng
một thời gian và trong cùng một quan hệ, không thể đồng giả dối: một trong chúng
nhất định phải chân thực, cái còn lại phải giả dối, không có trường hợp thứ 3 - Công thức: a v b 7a b. Yêu cầu:
- Yêu cầu 1: Luật bài trung yêu cầu phải được xác định giá trị logic của những tư
tưởng mâu thuẫn hoặc đối lập nhau và chỉ có 2 khả năng đúng hoăc sai, không có khả năng thứ 3
- Yêu cầu 2: Phải xác định được nội hàm của khái niệm được coi là chuẩn, trên cơ
sở đó ta xác định giá trị logic c. Ý nghĩa
- Chỉ ra cơ sở, cách thức chắc chắn để lựa chọn 1 trong 2 tư tưởng mâu thuẫn nhau
là đúng và loại bỏ sai làm
- Là cơ sở, nguyên tắc trong bác bỏ, chứng minh, phản biện
- Giúp chúng ta có cơ sở chắc chắn để vững tin thể hiện quan điểm của mình
4. Luật lý do đầy đủ:
a. Cơ sở khách quan:
- Mối quan hệ nhân quả chính là cơ ở khách quan, mối quan hệ này được phản ánh
vào tư duy chính là cơ sở để hình thành quy luật này
- Không một lập luận nào có thể được công nhận là chân thực nếu thiếu những cơ
sở đầy đủ cần thiết
b. Nội dung và công thức
- Mỗi luận điểm được rút ra trong quá trình lập luận chỉ được thừa nhận là đúng khi
có đầy đủ lý do chân thực
- Mọi tư tưởng đã định trong tư duy chỉ được công nhận là chân thực nếu như có
đầy đủ các cơ sở cho phép xác minh hay chứng minh tính chân thực ấy
- Công thức: a chân thực vì có b là cơ sở đầy đủ