Đề cương Toán 9 HK2 năm học 2017 – 2018 trường THCS Ngô Sĩ Liên – Hà Nội

Đề cương Toán 9 HK2 năm học 2017 – 2018 trường THCS Ngô Sĩ Liên – Hà Nội gồm 85 trang tuyển chọn các bài toán tiêu biểu trong chương trình học kỳ 2 Toán 9 nhằm hỗ trợ các em học sinh ôn tập, chuẩn bị cho kỳ thi HKII Toán 9, các bài toán đều được phân tích và giải chi tiết. Mời bạn đọc đón xem.

109 55 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

ĐỀ C

ƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 1

TRƯỜNG THCS NGÔ SĨ LIÊN

Năm học: 2017 – 2018

ĐỀ CƯƠNG ÔN TẬP LỚP 9 HKII

MÔN TOÁN

DẠNG 1: Biến đổi các biểu thức chứa căn

Bài 1: Cho biểu thức:

 

2 1

1 1

 

 

 

 

 



 

 

x x

x x x x

1) Rú

t gọn A

2) Tìm x để A < 0

3) Tìm x nguyên để A có giá trị nguyên

Bài 2: Cho biểu thức:

3 2 4

2 2 2

   

  

  

   

  

   

x x x x

x x x x x

1) Rút gọn P

2) Tìm các giá trị của x để P > 0

3) Tính giá trị nhỏ nhất củ

Bài 3: Cho biểu thức:

2 1 1

1 1

 

 

  

 

  



 

x x x

C x

x x x

1) Rút gọn C

2) Tính giá trị của biểu thức C khi

8 2 7 x

3) Tìm

giá trị của x để giá trị biểu thức C bằng –

4) Tìm

giá trị của x để giá trị biểu thức C lớn hơn



5) Tìm

giá trị của x để giá trị biểu thức C nhỏ hơn

2 3x

ài 4: Cho biểu thức







ĐỀ C

ƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 2

1) K

6 2 5, x

tí

nh giá trị biểu thức A

2) Rút gọn biểu thứ

2 1

5 5

 

 

 

 



 

 

x x

3) Tìm

x để biểu thức



M B A

nhận gi

á trị nguy

ên.

ài 5: Tính giá trị của biểu thức







với

7 4 3 x

1) Cho biểu thức

1 4

1 2 2

 

  

   

x x x

x x x x

Chứng minh rằng





2) Tìm

x để

1

 

ài 6: Cho hai biểu thức

2 2



 

  

x x

x x x

và

3 3



 



1) Tìm

ĐKXĐ rồi rút gọn biểu thứ

c A

2) Tìm các giá trị của x để B = 1

3) Tìm m để



có ng

hiệm.

Bài 7: Cho biểu thức

3 3



 

 

 



 

 

x x

với

, 9 x x

1) Rú

t gọn B

2) Tính giá trị của B khi

27 10 2 18 8 2   x

3) Chứng minh

B

ài 8: Cho biểu thức

2 1 3 11

;

3 3

 

  



 

x x x

x x







a) Tí

nh giá trị B tại x = 36

ĐỀ C

ƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 3

b) Rút gọn A

c) Tìm số nguyên P để P = A.B là số nguyên.

Bài 9: Cho biểu thức





với

, 4. x x

Tìm x để B = 2

1) Cho biểu thứ

 



với

0, 4. x x

2) Tí



3) Tìm

x thỏa mãn

 

1 2 1 2 2 2 4      P x x x x x

ài 10: Cho biểu thức

2 2

 





và





x x

a) Tí

nh giá trị Q tại x = 121

b) Rút gọn P

c) Tìm giá trị của x để



 

Q x

d) So sánh A và

DẠNG 2

: Giải bài toán bằng cách lập phương trình hoặc hệ phương trình

Bài 1: Một người đi xe máy từ A đến B cách nhau 120km với vận tốc dự định trước.

Sau khi đi được

uãng đường AB người đó tăng vận tốc lên 10km/h trên quãng

đường còn lại. Tính vận tốc dự định và thời gian lăn bánh trên đường biết rằng

người đó đến B sớm hơn dự định 24 phút.

Bài 2: Quãng đường AB dài 220km. Hai ô tô khởi hành từ A và B đi ngược chiều

nhau. Nếu cùng khởi hành thì sau 2 giờ chúng sẽ gặp nhau. Nếu xe đi từ A khởi

ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 4

hành trước xe kia 1 giờ 6 phút thì hai xe gặp nhau sau khi xe đi từ A đi được 2 giờ

30 phút. Tính vận tốc mỗi xe.

Bài 3: Một ca nô xuôi từ A đến B với vận tốc 30km/h, sau đó lại ngược từ B về A.

Thời gian xuôi ít hơn thời gian ngược 1h 20p. Tính khoảng cách giữa hai bến A và B

biết rằng vận tốc dòng nước là 5km/h và vận tốc riêng của ca nô khi xuôi và ngược

là bằng nhau.

Bài 4: Một ca nô chạy trên sông trong 8 giờ, xuôi dòng 81km và ngược dòng 105km.

Một lần khác cũng chạy trên khúc sông đó, ca nô này chạy trong 4h, xuôi dòng

54km và ngược dòng 42km. Hãy tính vận tốc khi xuôi dòng và ngược dòng của ca

nô, biết vận tốc dòng nước và vận tốc riêng của ca nô không đổi.

Bài 5: Một công nhân dự định làm 150 sản phẩm trong một thời gian nhất định. Sau

khi làm được 2h với năng suất dự kiến người đó đã cải tiến các thao tác nên đã tăng

năng suất được 2 sản phẩm mỗi giờ và vì vậy đã hoàn thành 150 sản phẩm sớm hơn

dự kiến 30 phút. Hãy tính năng suất dự kiến ban đầu.

Bài 6: Một đội sản xuất làm 1000 sản phẩm trong một thời gian quy định. Nhờ tăng

năng suất lao động, mỗi ngày đội làm thêm được 10 sản phẩm so với kế hoạch. Vì

vậy, chẳng những đã làm vượt mức kế hoạch 80 sản phẩm mà còn hoàn thành sớm

hơn 2 ngày so với quy định. Tính số sản phẩm đội sản xuất phải làm trong một

ngày theo kế hoạch.

Bài 7: Để hoàn thành một công việc hai tổ phải làm chung trong 6h. Sau 2h làm

chung thì tổ hai bị điều đi làm việc khác, tổ một đã hoàn thành nốt công việc còn lại

trong 10h. Hỏi nếu mỗi tổ làm riêng thì sau bao lâu sẽ hoàn thành công việc.

ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 5

ài 8: Một đội xe dự định dùng một số xe cùng loại để chở 120 tấn hàng. Lúc sắp

khởi hành đội được bổ sung thêm 5 xe nữa cùng loại. Nhờ vậy, so với ban đầu, mỗi

xe phải chở ít hơn 2 tấn. Hỏi lúc đầu đội có bao nhiêu xe. Biết khối lượng mỗi xe

phải chở như nhau.

Bài 9: Một mảnh đất hình chữ nhật có độ dài đường chéo là 13m và chiều dài hơn

chiều rộng là 7m. Tính chiều dài và chiều rộng của mảnh đất đó.

Bài 10: Cho một số có hai chữ số. Tổng hai chữ số của chúng bằng 10. Tích hai chữ

số ấy nhỏ hơn số đã cho là 12. Tìm số đã cho.

DẠNG 3: Hệ phương trình

Bài 1: Cho hệ phương trình

2 3 6

 





 



mx y

x y

1) G

iải phương trình với m = 1

2) Tìm m để hệ vô nghiệm

Bài 2: Cho hệ phương trình

2 5

3 1

  





 



mx y

1) G

iải hệ phương trình m = 1

2) Tìm m để hệ có nghiệm (x; y) thỏa mãn x – y = 2

3) Chứng minh rằng hệ phương trình có nghiệm duy nhất (x; y) thì điểm M(x

; y)

luôn nằm trên một đường thẳng cố định khi m thay đổi.

ài 3: Cho hệ phương trình

( 1) 3 1

2 5

   





  



m x my m

x y m

. T

ìm m để hệ có nghiệm duy nhất

mà

 S x y

đạt giá t

rị nhỏ nhất.

ĐỀ C

ƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 6

ài 4: Cho hệ phương trình

2 





  



x my

mx y m

1) G

iải hệ khi m = 2

2) Tìm các số nguyên m để cho hệ có nghiệm duy nhất (x; y) với x > 0, y <

3) Tìm các số nguyên m để cho hệ có nghiệm duuy nhất (x; y) với x, y là các số

ngu

yên.

ài 5: Cho hệ phương trình

1 





  



x my

mx y m

1) CMR hệ có nghiệm duy nhất với mọi m

2) Tìm m để hệ có nghiệm duy nhất sao cho x < 1, y < 1

DẠNG 4: Quan hệ giữa (P) và (d)

Bài 1: Cho hàm số

 

  y f x x

ó đồ thị (P) và hàm số

 y x

có đồ thị (d).

1) Vẽ (P)

và (d) trên cùng hệ trục tọa độ

2) Tìm tọa độ giao điểm của (P) và (d)

3) Không tính, hãy so sánh

 

2f

và

 

3f

 

1 2f

và

 

3 2f

ài 2: Cho hàm số



y x

ó đồ thị (P)

1) Tìm các điểm A, B thuộc (P) có hoành độ lần lượt bằng – 1 và 2.

2) Viết phương trình đường thẳng AB

3) Viết phương trình đường thẳng song song với AB và tiếp xúc với (P). Tìm tọ

độ tiếp

điểm

ĐỀ C

ƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 7

ài 3: Cho parabol

 

: P y ax

1) Tìm

a biết (P) đi qua điểm A thuộc đường thẳng (d):

4 2

 y x

có hoà

nh độ

bằng 2.

2) Tìm giao điểm B còn lại của (d) và (P)

3) Tính diện tích tam giác OAB

Bài 4: Cho hàm số

y ax

ó đồ thị (P) và hàm số

2 1  y mx m

có đồ thị (d)

1) Chứng minh (d

) luôn đi qua một điểm M cố định

2) Tìm a để (P) đi qua điểm cố định đó

3) Viết phương trình đường thẳng qua M và tiếp xúc với parabol (P) tại M.

Bài 5: Cho hàm số

y x

có đồ thị (P) và đường thẳng (d):

 y x

1) Vẽ (d) v

à (P) trên cùng hệ trục tọa độ Oxy

2) Tìm tọa độ giao điểm A và B của (d) và (P). Tính chu vi

AOB

3) Tìm

tọa độ giao điểm C thuộc Ox để chu vi

ABC

đạt giá t

rị nhỏ nhấ

ài 6: Cho parabol

 

P

y x

1) Viết ph

ương trình đường thẳng (d) có hệ số góc là k là đi qua M(1,5; - 1

)

2) Tìm

k để đường thẳng (d) và parabol (P) tiếp xúc nhau

3) Tìm k để đường thẳng (d) và parabol (P) cắt nhau tại hai điểm phân biệ

Bài 7: Cho hàm số

 



P y

và

 

 d y x n

1) Cho n = 1

a) Vẽ (P)

và (d) trên cùng một mặt phẳng tọa độ

ĐỀ C

ƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 8

b) Tìm tọa độ giao điểm A và B của (P) và (d)

c) Tính diện tích

AOB

2) Tìm

n để (P) tiếp xúc với (d)

3) Tìm n để (P) và (d) cắt nhau tại hai điểm

4) Tìm n để (P) và (d) cắt nhau tại hai điểm nằm ở hai phía trục tung

Bài 8: Cho parabol (P):

y x

và đường thẳng

1

 y mx m

1) Tìm m để (P) và (d) cắt nhau tại hai điểm phân biệt A và B

2) Gọi

và

à hoành độ của A và B. Tìm m để

2 x x

3) Tìm

m để (P) và (d) cắt nhau tại hai điểm nằm cùng bên trái của trục tung

ài 9: Cho hàm số

y

ó đồ thị là parabol (P), đường thẳng

2.

y mx

Tì

m m để

d cắt (P) tại hai điểm phân biệt có hoành độ

1 2

x x

2 2

1 2

x

có g

iá trị nhỏ nhất.

Bài 10: Cho hàm số

y x

có đồ thị l

à parabol (P), đường thẳng d:

1.

  y mx m

Tìm

m để d cắt parabol (P) tại A và phân biệt với

 

x y

 

x y

 

y

nhỏ

nhất.

DẠNG 5

: Phương trình bậc hai

Bài 1: Cho phương trình

 

3 3 2 0,     x m x m m

là tham số

1) Giải phương trình trên khi m = 1

2) Xác định m để phương trình có một nghiệm là 2. Khi đó phương trình cò

một n

ghiệm nữa, tìm nghiệm đó?

3) CMR phương trình luôn có hai nghiệm phân biệt với mọi m

4) Gọi

là hai

nghiệm của pt. Tìm m để

1 2

1

x x

ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 9

5) Định m

để phương trình có nghiệm này bằng 3 nghiệm ki

ài 2: Cho phương trình

 

2 1 0   

x m x m

, m

là tham số

1) CMR phương trình luôn có hai nghiệm phân biệt

với mọi

2) Với

0

. Hãy

lập phương trình ẩn y có hai nghiệm l

 

y x

và





3) Xác

định m để phương trình có hai nghiệm

thảo mãn

2 3 

x x

4) Tìm

m để phương trình có hai nghiệm cùng âm

Bài 3: Cho phương trình

 

3 2 1 0,



   

k x k

k l

à tham số

1) Giải phương trình khi



2) Tìm

k để phương trình có một nghiệm là 3, khi đó phương trình còn mộ

nghiệm nữa,

tìm nghiệm ấ

3) CMR

phương trình luôn có hai nghiệm

với

mọi k

4) CMR giữa tổng và tích các nghiệm có một sự liên hệ không phụ thuộc k?

5) Tìm k để phương trình

thỏa

mãn

2 1 2

1 3

2

 

x x x

6) Tìm k để tổng bình phương các nghiệm có giá trị nhỏ nhất.

ài 4: Cho phương trình

 

1 4 0,



   

m x m

là tham số

1) Giải phương trình khi x = -

2) CMR

phương trình luôn có nghiệm

với

mọi m

3) Tìm m để phương trình có hai nghiệm trái dấu

4) Tìm m để phương trình có hai nghiệm dương

ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 10

5) CMR

biểu thức

   

2 2 1

1   

x x x x

khô

ng phụ thuộc m

6) Tính giá trị của biểu thức

x

ài 5: Cho phương trình

3( 1) 3 0,    

x m x m

là tham số

1) CMR phương trình luôn có nghiệm với mọi m

2) Tìm hệ thức liên hệ giữa hai nghiệm không phụ thuộc m

3) Xác định m để phương trình có hai nghiệm bằng nhau về giá trị tuyệt đối

và

trái dấu nhau.

ài 6: Cho phương trình

 

2 2 2 5 0,    

x m x m

là tham số

1) CM phương trình luôn có nghiệm với mọi m

2) Gọi

là hai nghiệm của phương trình. Tìm m để

 

2 2 2

(

1 ) 1 4



   

x x x x

3) Tìm hệ thức liên hệ giữa hai nghiệm không phụ thuộc vào m

ài 7: Cho phương trình

   

1 2 4 0



   

m x m

là tham số

1) Tìm m để phương trình có hai nghiệm

thỏa m

ãn điều kiện

17 

x x

2) Tìm

m để biểu thức

 

 

A x x

có g

iá trị nhỏ nhất

3) Tìm hệ thức liên hệ giữa hai nghiệm không phụ thuộc vào x.

ài 8: Cho phương trình

 

1 2 1 0,



   

m x m

là tham số. Tìm m để phương

trình có hai nghiệm

à độ dài hai cạnh góc vuông của một tam giác vuông có

cạnh huyền bằng

Bài 9: Cho phương trình

2 2 0   

x x m

, m

là tham số

1) Giải phương trình khi m = -

2) Tìm

m để phương trình có 4 nghiệm phân biệ

ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 11

ài 10: Cho phương trình

 

1 1 0,



   

m x m

là tham số. Tìm m là phươn

trình có nghiệm duy nhất.

DẠNG 6: Hình học

Bài 1: Cho đường tròn (O) và điểm M nằm ngoài (O). Từ M kẻ hai tiếp tuyến MA,

MB đến (O) (A, B là tiếp điểm). Qua M kẻ cát tuyến MNP (MN < MP) đến (O) sao

cho tia MP nằm giữa hai tia MA và MO. Gọi K là trung điểm của NP

1) Chứng minh rằng các điểm M, A, K, O, B cùng thuộc một đường tròn

2) Chứng minh tia KM là phân giác của



AKB

3) Gọi

Q là giao điểm thứ hai của đường thẳng BK với đường tròn (O). Chứ

inh rằng AQ // NP.

4) Gọi H là giao điểm của AB và MO. Chứng minh rằng

. .

 

MA MH MO MN MP

5) Chứng minh

rằng 4 điểm N, H, O, P cùng thuộc một đường tròn

6) Gọi E là giao điểm của AB và KO. Chứng minh rằng



HE HF

(F l

à giao

điểm của AB và NP).

7) Chứng minh rằng KEMH là tứ giác nội tiếp. Từ đó chứng tỏ rằng OK.

không đổi.

8) Gọi I là giao điểm của đoạn thẳng MO với đường tròn (O). Chứng mỉnh ằng

là tâm đường tròn nội tiếp

MAB

9) Chứng minh





NHA PHA

10) Chứng minh

rằng KE là phân giác góc ngoài của



.AKB

Từ đó su

y ra AE.BF =

AF.BE

11) Chứng minh khi cát tuyến MNP thay đổi thì trọng tâm G của

NA

luôn

chạy t

rên một đường tròn cố đị

nh.

ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 12

12) Nếu M

O = 2R. Tính diện tích hình quạt giới hạn bởi hai bán kính OA, OB v

cung

nhỏ A

ài 2: Cho đường tròn (O) bán kính R có hai đường kính AB và CD vuông góc với

nhau. Trên đoạn thẳng MA lấy điểm M (M khác O). CM cắt (O) tại N. Đường thẳng

vuông góc với AB tại M cắt tiếp tuyến tại N của đường tròn ở P. Chứng minh:

1) Tứ giác OMNP nội tiếp

2) Tứ giác CMPO là hình bình hành

3) CM.CN không phụ thuộc vào vị trí của điểm M

4) Khi M di chuyển trên đoạn thẳng AB thì tâm đường tròn nội tiếp

CND

chuyển trên

một cung tròn cố đị

nh nào.

Bài 3: Cho ba điểm A, B, C trên một đường thẳng theo thứ tự ấy và đường thẳng (d)

vuông góc với AC tại A. Vẽ đường tròn đường kính BC, trên đó lấy điểm M bất kì.

Tia CM cắt đường thẳng d tại D; tia AM cắt đường tròn tại điểm thứ hai N; tia DB

cắt đường tròn tại điểm thứ hai P

1) Chứng minh rằng tứ giác ABMD nội tiếp được

2) Tứ giác APND là hình gì? Tại sao?

3) Chứng minh rằng CM.CD không phụ thuộc vị trí của M

4) Chứng minh trọng tâm G của

MAC

chạy t

rên một đường tròn cố định khi

động

ài 4: Cho đường tròn (O; R) với dây BC cố định (BC không qua O). Gọi A là điểm

chính giữa cung nhỏ BC. Điểm E thuộc cung lớn BC. Nối AE cắt BC tại D. Hạ

CH

tại H; CH cắt BE tại M. Gọi I là trung điểm của BC

1) Chứng minh bốn điểm A, I, H, C thuộc một đường tròn

ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 13

2) Chứng minh

khi E chuyển động trên cung lớn BC thì tích AD.AE không đổi

3) Chứng minh đường tròn ngoại tiếp

BED

tiếp

xúc với AB

4) Tìm vị trí của E để diện tích

MAC

lớn nhất

ài 5: Cho hai đường tròn (O; R) và (O’; R’) cắt nhau tại A và H (O và O’ ở hai phía

của AH). Vẽ các đường kính AOB và AO’C của hai đường tròn. Một đường thẳng d

đi qua A cắt đường tròn (O) tại M, cắt đường tròn (O’) tại N.

1) Chứng minh ba điểm B, H, C thẳng hàng

2) Chứng minh rằng khi đường thẳng d thay đổi thì tỉ số

không

đổi

3) Gọi I, K lần lượt là trung điểm của MN và BC. Chứng minh bốn điểm A, H, I,

K thuộc một đường tròn

4) Xác định vị trí của đường thẳng d để diện tích

HMN

lớn n

hấ

ài 6: Cho hai đường tròn (O; R) và (O’; R’) tiếp xúc ngoài tại A (R = 2R’). Điểm B

thuộc đường tròn (O; R) sao cho AB = R. Điểm M thuộc cung lớn AB của đường

tròn (O; R) sao cho

.M

A MB

Nối

MA cắt đường tròn (O’; R’) tại N. Từ N kẻ đường

thẳng song song với AB cắt đường tròn (O’; R’) tại E, cắt MB tại F.

1) Chứng minh

AOM

đồng dạng với

'AO

2) Chứng minh

rằng độ dài đoạn NF không đổi khi M chuyển động t

rên cung

lớn A

B của đường tròn (O; R).

3) Chứng minh ABFE là hình thang cân

4) Tìm vị trí của M để diện tích tứ giác ABFN lớn nhấ

ài 7: Cho đường tròn (O; R), đường kính AB cố định. Gọi M là trung điểm của

đoạn OB. Dây CD vuông góc với AB tại M. Điểm E chuyển động trên cung lớn CD

(E khác A). Nối AE cắt CD tại K. Nối BE cắt CD tại H.

ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 14

1) Chứng minh

bốn điểm B, M, E, K thuộc một đường tròn

2) Chứng minh AE.AK không đổi

3) Tính theo R diện tích hình quạt tròn giới hạn bởi OB, OC và cung nhỏ BC

4) Chứng minh tâm I của đường tròn ngoại tiếp

BHK

uôn thuộc một đườ

thẳng cố định k

hi điểm E chuyển động trên cung lớn CD.

Bài 8: Cho nửa đường tròn (O; R) đường kính AB. Điểm M thuộc nửa đường tròn.

Gọi H là điểm chính giữa cung AM. Tia BH cắt AM tại I. Tiếp tuyến của nửa đường

tròn tại A cắt BH tại K. Nối AH cắt BM tại E.

1) Chứng minh

BAE

à tam giác cân. Chứng minh

. 

KH KB KE

2) Đường t

ròn tâm B, bán kính BA cắt AM tại N. Chứng minh tứ giác BIEN nội

tiếp

3) Tìm vị trí của M để





MKA

ài 9: Cho đường tròn (O; R) đường kính AB. Điểm H thuộc đoạn OB, H khác O và

B. Dây

CD vuông góc với AB tại H. Đường thẳng d tiếp xúc với đường tròn tạ

i A.

Nối

CO và DO cắt đường thẳng d tại M và N. Các đường thẳng CM và DN cắt

đường tròn (O) tại E và F.

 

, 

E C F D

1) Chứng minh MNFE là tứ giác nội tiếp

2) Chứng minh ME.MC = NF.ND

3) Tìm vị trí của H để AEOF là hình thoi

4) Lấy K đối xứng với C qua A. Gọi G là trọng tâm

.KAB

Chứng minh rằng k

H chuyển động trên đoạn OB thì G thuộc một đường tròn cố đị

nh.

ài 10: Cho

ABC

có hai

đường cao BE, CF cắt nhau tại H. Gọi E’ là điểm đối xứng

với H qua AC, F’ là điểm đối xứng với H qua AB. Chứng minh

ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 15

1) Tứ g

iác BCE’F’ nội tiếp đường tròn (O)

2) Năm điểm A, F’, B, C, E’ cùng thuộc một đường tròn

3) AO và EF vuông góc với nhau

4) Khi A chạy tên (O) thì bán kính đường tròn ngoại tiếp

AEF

không

đổi

DẠNG 7

: Một số bài nâng cao

Bài 1: Giải các phương trình sau

Bài 2: Giải các hệ phương trình sau

Bài 3: Cho đường thẳng

 

1 2.  

y m x

Tì

m m để khoảng cách từ gốc tọa độ O tới

đường thẳng đó lớn nhất.

Bài 4: Cho parabol

 

P

y x

à đường thẳng

 





y x

. Gọi

A và B là hai giao

điểm của (d) và (P). Tìm tọa độ điểm C thuộc cung AB của (P) để diện tích

ABC

đạt giá t

rị lớn nhất.

Bài 5: Cho 4 số a, b, c, d bất kỳ. Chứng minh rằng

   

2 2 2



     

c b d a b c d

ài 6: Cho a, b, c > 0. Chứng minh



   

ca ab

b c

Bài 7: Cho c > 0 và

a

b c

Chứng minh

   



  

a c c b c ab

ài 8: Cho



và

2 2

2.



Tìm

giá trị lớn nhất của biểu thức

   

2 3 2



  

a a a b b b b a

Bài 9: Cho

, 0

a b

. Tìm giá trị nhỏ nhất của biểu thức

   







 

a b

a b b b a

ĐỀ C

ƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 16

ài 10: Giả sử n là một số tự nhiên khác không, chứng minh

1 1 1 1

... 2

3 2 4 3 ( 1)

    

n n

ĐỀ C

ƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 17

ƯỚNG DẪN GIẢI

DẠNG 1

ài 1: ĐKXĐ:

; 1 x x

1) Rú

t gọn A:

 

2 1

1 1

( 1).( 1) ( 1).( 1) 2.( 1)

.( 1) .( 1) ( 1).( 1)

1 1 2( 1)

2 1

2.( 1)

 

 

 

 

 



 

 

 

      

 

 

   

 

 

    

 

 



 













x x

x x x x

x x x x x x x

x x x x x x

x x x x x

x x x

x x

2) Tìm

x để

0A

Để

0A

thì







1 0  x

(vì

1 0 x

)

1 x

Kết hợp điều k

iện

; 1 x x

ta có: Với

1 x

thì A < 0.

3) Tìm x nguyên để A có giá trị nguyên.

Ta có:

1 1 2 2

1 1 1

  

   

  

x x

x x x

Với

x nguyên để A nhận giá trị nguyên thì

-

1 (2)x U

ĐỀ C

ƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 18

1x

1

2

x 4 (TM) 0(KTM) 9 (TM) Vô

nghiệm

Vậy

 

,9x

thì

A nhận giá trị nguyên.

Bài 2: ĐKXĐ:

; 4; 1  x x x

1) Rứt

gọn P:

3 2 4

2 2 2

   

  

  

   

  

   

x x x x

x x x x x

4 3 ( 2)( 2) 4

.( 2) .( 2)

( 1).( 3) 4 4

.( 2) .( 2)

( 1).( 3)

.( 2) .( 2)

   

     



   

 

   

   

    



   

 

   

  



 





x x x x x

x x x x

2) Tìm

các giá trị của x để P > 0.

0P

thì





3 0

  

 

ĐỀ C

ƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 19

Kết hợp điều k

iện ta có:

Với x > 9 thì P > 0

c) Tìm giá trị nhỏ nhất của

có

có ng

hĩa khi

0 3 0 9



      

x x

Với

9x

thì

0P

. Dấu “

=” xảy ra khi x = 9.

có g

iá trị nhỏ nhất bằng 0

Bài 3: ĐKXĐ:

; 1 x x

1) Rú

t gọn C:

 

2 1 1

1 1

2 1 (1 ).( 1)

1 1

( 1). 1

2 1 ( 1)

. 1

( 1). 1

. 1

( 1). 1

. 1

 

 

  

 

  



 

 

   

 

  

 

  

  

 

 

  

 

   

 

  

 

 

 

 

 

 

  

 

 



 

x x x

C x

x x x

x x x x x

C x

x x x

C x x x

x x x

x x

C x

x x x

C x

2) Tí

nh giá trị của biểu thức C khi

8 2 7 x

 

8 2 7 7 2 7 1 7 1 7 1 7 1           x x

ĐỀ C

ƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 20

Vậy

1 7 1 1 7 2      C x

3) Tìm

giá trị của x để giá trị biểu thức C bằng

3

3 1 3     C x

3  x

(vô ng

hiệm)

Vậy không có giá trị nào của x để giá trị biểu thức

3

C

4) Tìm giá trị của x để giá trị biểu thức C lớn hơn



C



  x

 x

Kết hợp điều k

iện ta có

; 1

 x x

thì



C

5) Tìm

giá trị của x để C nhỏ hơn

2 3x

có

2 3 C x 1 2 3   x x

4 2   x

(nghiệm

đúng với

; 1 x x

)

Vậy với

mọi

0; 1 x x

thì

C nhỏ hơn

2 3x

ài 4: 1) ĐKXĐ:

0x

 

6 2 5 5 1 5 1      x x

(t/m

)

Thay vào biểu thức A ta được

 

1 5 1 5 2 5

1 5 1

  

 

 

Vậy…

2) ĐK

XĐ:

; 25 x x

Rú

t gọn B

ĐỀ C

ƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 21

15 2 1

5 5

15 2( 5) 5

 

 

 

 



 

 

 

   



 





 





x x

x x x

3) Với

; 25 x x

có

   –  

 



B A

Chứng minh

0 1

0 ( / )

 



 

M Z

x t m

Vậy x = 0

thì M nhận giá trị nguyên

Bài 5:

1) T

ính giá trị biểu thứ







khi

7 4 3 x

ĐKX

Đ:

; 4 x x

 

7 4 3 3 2 3 2      x x

(t/m

)

Thay vào biểu thức A ta được

 

1 3

2 3 1

3 1

2 3 1 3



 

   

 

Vậy…

2) ĐKXĐ:

; 4 x x

ĐỀ C

ƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 22

Rút gọn B

1 2 2

( 2) (1 )( 1) ( 4)

( 1)( 2)

 

  

   

     



 





x x x

x x x x

x x x x x

x x

3) Với

; 1; 4  x x x

có :

3 1

: 1

2 1

3 1 (2 )(1 )

. 0

2 1 (2 )(1 )

(2 )(1 )

  



  

 

  

  

   



 

 

x x

x x x

x x x x

x x

Vì

; 1; 4  x x x

 x + 5 > 0



(

2 )(1 ) x x

< 0

Kết hợp điều k

iện : x > 4 hoặc

1 x

ài 6: 1) ĐKXĐ:

; 1 x x

Rú

t gọn A:

ĐỀ C

ƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 23

2 ( 1)

( 2)( 1) ( 2)( 1)



 

  

 

 

   





x x

x x x

x x x x

2) Với

; 1 x x

 

3 3

1 1 3( 1) ( 3) 1 2 7 0 1 8

1 2 2

1 2 2)(TM)

1 2 2( )



                



  



 





 





B x x x x x x

x KTM

Vậy…

Bài 7.

1) Ta có

 

  

3 1 3 3 3

9 9

3 3

3 1

3 3

 

    

 

  

 

 

 

 



 

 



 

x x x x x

x x

x x x

x x

2) T

a có

   

2 2

27 10 2 18 8 2 5 2.5 2 2 4 2.4 2 2

5 2 4 2 1

          

    

x x

Vậy

 

B

ĐỀ C

ƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 24

3) X

ét hiệ

1 1 1 3 2

3 3

 

    

 

x x

vậy

B

ài 8.

1) T

a có

 

36 3 3

36 1



 



2) T

a có với

9 x

    

3 3 1 11 3

2 1 3 11

9 9

3 3

     

 

   

 

 

x x x x x

x x x

x x

     

6 4 3 11 3 3 9 3

3 3 3 3

      

  



   

x x x x x x x x

x x x x

3) Xét

3 3 3

. .

3 1 1



  

  

x x x

P A B

x x x

(với

0 9 x

)

  



để

ngu

yên thì

   

1 1;3 0; 4   x x

ài 9.

1) Với

0, 4 x x

để

2 2 2 2 4 9

       



B x x

2) Ta có

  

 

  

2 1

1 2

2 2 2 2



 

   



   

x x x

x x x x

  

 

2 2

2 1

 



  

 



x x

B x

x x

3) X

ét phương trình:

   

 

1 2 1 2 4, DK: 0       P x x x x x x

ĐỀ C

ƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 25

   

1 2 1 2 2 4



       



x x x x x

2 2 2 2 4       x x x x x

4 4 0   x x

 

2 0 2 4      x x x

(thỏa mãn).

Bài 10:





x x

(ĐK

XĐ:

; 9) x x

Tha

121x

vào

Q ta được:

6 6 3

88 44

121 3 121

  



2 2

 





. ĐK

XĐ:

0; 9 x x

  

 

        

2 3

2 2 2 6 6

3 3 3 3 3 3 3 3



 

   

       

x x x

x x x x x x x x

3. Ta có:

  

3 3

 



 

x x

ĐKX

Đ:

; 9 x x

 

  

3 3

6 3

 



 



x x

Lại

có:

 

2 1 3 2 1 2 6 2

2 2

2 6 2 0 2 6 0 1

    

     

        

x x x x x x

x x x

x x x x x

Đặt

t x

 

0t

. K

hi đó phương trình (1) trở thành:

ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 26

  

 

2 6 0 2 2 3 0





       











t TM

t t t t

t K TM

Với

2 2 4    

t x x

(TM

ĐKXĐ)

Vậy tập nghiệm của phương trình (1) là:

 

S

4. Xét h

iệu:

3 3 6 9 3 6 9 3 3 9

 

         

      

 

 

x x x x x x x x x x

A A

x x x

Vì

0 3 9 0 0, 0 0





           

x x A A A A

Vậy

.A A

DẠNG 2

Bài 1:

Gọi vận tốc dự định là

(km

/h) (điều kiện:

0

)

Thời

gian dự định đi hết quãng đường AB là:

120

(giờ)

Thời

gian đi hết

uãng đường AB là:

(giờ)

Vận tốc đ

i trên

uãng đường là:

10

(km

/h)

Thời gian đi hết

uãng đường còn lại là:

10x

(giờ)

Vì

người đó đến B sớm hơn dự đinh 24 phút =

giờ nên

ta có phương trình:

ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 27

 

   

 

  

 

5.120. 10 5.40. 10 2 10

120 40 80 2 5.80

10 5 5 10 5 10 5 10 5 10

600 6000 200 2000 400 2 20 2 20 4000 0

10 2000 0 40 50 0

  

      

    

          





        



 





x x x x

x x x x x x x x x x x

x x x x x x x

x TM

x x x x

x KTM

Vậy vận

tốc dự định đi hết quãng đường AB là 40km/h.

Thời gian lăn bánh trên quãng đường AB là:

120 2 13

5 5





(giờ)

ài 2:

Đổi: 1 giờ 6 phút



(giờ); 2 giờ 3

0 phút



(giờ)

Gọi

vận tốc ô tô đi từ A đến B là

(km

/h), (ĐK:

0)

Gọi

vận tốc ô tô đi từ B đến A là

(km

/h), (ĐK:

0)

Quã

ng đường ô tô đi từ A đến lúc hai xe gặp nhau là:

(km

)

Quãng đường ô tô đi từ B đến lúc hai xe gặp nhau là:

(km)

Vì hai xe đi ngược chiều và gặp nhau sau 2 giờ nên ta có phương trình:

 

2 220 110 1



   x y x y

2 giờ 30 phút ô tô đi từ A đ

i được quãng đường là:

(km)

Thời gian ô tô đi tư B đến lúc gặp nhau sau khi ô tô đi từ A đi được 2 giờ 30

phút là:

5 11 7

2 10 5





(giờ)

giờ ô t

ô đi từ B đi được quãng đường là:

(km

)

ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 28

Vì

hai ô tô đi ngược chiều và gặp nhau sau khi ô tô đi từ A đi được 2 giờ 30

phút nên ta có phương trình:

 

220 2

 x y

Từ (1) và (2) ta có hệ phương trình:

 

5 5

110 110

275

110 60

2 2

5 7 11

5 7

50 50

220 55

220

2 5 10

2 5



   

 

 



  

 

  

   

    

 

  

 

  

 

 





x y x y

x y

x y x

y y

x y y

x y

Vậy vận

tốc ô tô đi từ A là 60 km/h

Vận tốc ô tô đi từ B là 50 km/h

Bài 3:

Gọi khoảng cách giữa hai bến A, B là

 

,

x km

có vận tốc xuôi dòng là 30

 

/km h

, vận tốc dòn

g nước là 5

 

/km h

nên vận

tốc thực của c

a nô là 25

 

m h

và vận tốc ngược dòng là 20

 

m h

Thời gian ca nô chạy xuôi dòng là:

(h)

Thời

gian ca nô chạy ngược dòng là:

(h)

Vì

thời gian xuôi ít hơn thời gian ngược 1h20p =

h nên ta

có phương trình:

2 80 80( )

30 3



     

x x

x x km

 

Vậy k

hoảng cách giữa hai bến A, B là 80 (km).

ĐỀ C

ƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 29

ài 4:

Gọi vận tốc thực của ca nô là

 

, /x x km h

, vận tốc dòn

g nước là

 

, y x, / y y km h

có vận tốc xuôi dòng là:

 

/x y km h

, vận tốc ngược

dòng là:

 

/x y km h

Lần thứ nhất ca

nô chạy xuôi dòng 81 km và ngược dòng 105 km hết 8 giờ

nên ta có phương trình:

81 105

8 

 x y x y

(1)

Lần thứ h

ai ca nô chạy xuôi dòng 54 km và ngược dòng 42 km hết 4 giờ nên

ta có phương trình:

54 42

4 

 x y x y

(2)

Từ (1)

và (2) ta có hệ phương trình:

105

54 42



 



 







 



 



x y x y

Đặt























x y

, ta

được hệ phương trình mới:

81 105 8 81 105 8 42 2

54 42 4 81 63 6 27 21 2 1

27 21. 2







    

  



  

   

     

  



 





a b a b b

a b a b a b

ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 30

1 27 1

27 1 2





 





  

  

  



  

 



 





Trả lại biến cũ ta được:

1 1

27 2 48 24

1 1 21 21 3







   



  



  

   

    

  











x y x x

x y

x y y x y

x y

 

Vậy vận tốc xuôi dòng là 27

 

/km h

và vận tốc ngược dòng là 21

 

/km h

Bài 5:

Gọi số sản phẩm người công nhân đó dự định làm được trong 1 giờ là x (





, sản phẩm).

Sau khi tăng năng suất, số sản phẩm người đó làm đc trong 1 giờ là x+2 (sản

phẩm).

Thời gian dự kiến hoàn thành công việc là:

150

(h).

Số sản phẩm làm trong 2 giờ đầu là:

(sản phẩm).

Số sản phẩm còn lại làm sau khi tăng năng suất là:

150 2 x

(sản phẩm).

Thời gian làm số sản phẩm còn lại đó là:

150 2





(giờ).

Vì người đó hoàn thành sớm hơn dự định 30 phút =

giờ nên ta có phương

trình:

ĐỀ C

ƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 31

     

 

150 150 2 1

2 2

150 150 2 5

2 2

300 2 2 150 2 5 2

300 600 300 4 5 10

10 600 0



 

  

 



 



  



     

     

   







 



x x

x x x x x

x x

x TM

x L

Vậy năng

suất dự kiến ban đầu là 20 sản phẩm.

ài 6:

Gọi

số sản phẩm mà đội phải làm trong một ngày theo kế hoạch là x(sản

phẩm

)

đk:

x > 2,

*x

Số ngày cần hoàn thành công việc theo dự đinh là:

1000

(ngày)

Trong

thực tế mỗi ngày làm thêm được 10 sản phẩm nên số sản phẩm làm

trong

một ngày thực tế là: x+10 (sản phẩm)

Só ngày làm việc trong thực tế là:

1000

2x

(ngày)

Vì vậy đội vượt mức kế hoạch 80 sản phẩm nên số sản phẩm thực tế đội làm

được

là 1000 + 80 = 1080 (sản phẩm) nên ta có phưong trình:

ĐỀ C

ƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 32

1000

(

10). 1080

 

 

 



 



-2x² - 100x +

10000=0

Tìm

được x= -100 (loại) hoặc x = 50 (thỏa mãn điều kiện)

Vậy số sản phẩm

mà đội phải làm trong một ngày theo kế hoạch là 50 sản

phẩm

Bài 7:

Gọi thời gian tổ một làm riêng và hoàn thành công việc là

(giờ,

6x

Gọi thời gian tổ hai làm riêng và hoàn thành công việc là

(giờ,

6y

)

Mỗi

giờ tổ một làm được

(công

việc)

Mỗi giờ tổ hai làm được

(công

việc)

Biết hai tổ làm chung trong 6 giờ thì hoàn thành được công việc nên ta có

phương trình:

6 6

1 

x y

. (1

)

Thực tế để hoàn thành công việc này thì tổ hai làm trong 2 giờ và tổ một làm

trong

10 12 

(giờ),

ta có phương trình:

12 2

1 

x y

(2)

ĐỀ C

ƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 33

Từ (1)

và (2) ta có hệ phương trình:

12 2



 







 





x y

iải hệ ta được:











(thỏa m

ãn điều kiện)

Vậy nếu làm riêng thì tổ một hoàn thành công việc trong 15 giờ và tổ hai

hoàn thành công việc trong 10 giờ.

Bài 8:

Gọi số xe lúc đầu

đội có là x (xe); x > 0,

*x

hối lượng hàng mỗi xe phải chở lúc đầu là

120

(xe)

Số xe lú

c sau của đội có là x + 5 (xe)

Khối lượng hàng mỗi xe phải chở lúc sau là

120

5x

(tấn)

Vì

sau khi được bổ sung thêm 5 xe cùng loại thì mỗi xe phải chở ít hơn 2 tấn

nên ta có phương trình:

120 120

 

x x



+ 10x – 600 = 0

⇔ (x 15)(x+

20) = 0

⇔ x = 15 (thỏa mãn điều kiện) hoặc x = 20(không thỏa mãn điều kiện)

Vậy số xe lúc đầu của đội là 15 xe

ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 34

ài 9:

Gọi chiều dài của mảnh đất là: x (m) (Đk: x > 7).

Chiều rộng mảnh đất là: x – 7 (m)

Vì độ dài đường chéo của mảnh đất hình chữ nhật là 13m, nên ta có phương

trình:

2 2

( 7) 13

  x x

2 2

49 169



   x x x

2 14 120 0

60 0

5( )

   



  













x x

x l

 Chiều rộng : 12 – 7 =

5 (m

)

Vậy mảnh đất

hình chữ nhật có chiều dài 12m; chiều rộng 5m.

Bài 10:

Gọi số có hai chữ số cần tìm là

( Đk:

a

b N

;





;



)

Theo đề bài ra ta có:

a + b = 10 => b = 10 – a

Vì tích của hai chữ số nhỏ hơn số đã cho là 12 nên ta có:

a.b =

- 12

10 ) (10 ) 12



  

a a a

10 10 12



   

a a a

ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 35

2 0  

a a

1( )

 









a l

Suy ra: b = 10 -2 = 8

Vậy số cần tìm là 28.

DẠNG 3: Hệ phương trình

Bài 1:

1) Với m = 1 ta có hệ phương trình:

2 3 6

 





 



x y

3 3 30

2 3 6

 







 



x y

5 36

 











x y



















Vậy nghiệm của hệ phương trình khi m = 1 là

36 14

( ; ) ;

5 5

 



 

 

x y

2) Hệ phương trình

2 3 6

 





 



mx y

x y

vô nghiệm 

1 10

2 3 6

 



m

Bài 2.

1) Thay m = 1 vào hệ phương trình có:

2 5 1

3 1 2

   

 



 

   

 

x y y

x y x

Vậy với m = 1 thì hệ phương trình đã cho có nghiệm (x; y) = (- 2; 1)

2 5 (1)

3 1 (2)

  





 



mx y

(1) <=> y = 2mx + 5

Thế vào (2) có: mx + 3(2mx + 5) = 1 <=> mx = - 2 (*)

ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 36

Hệ phư

ơng trình đã cho có nghiệm duy nhất

<=> phương trình (*) có nghiệm duy nhất

<=> m ≠ 0

Với m ≠ 0 có: (*) <=> x =

2

Tha

y x =

2

vào

(1) có: (1) <=> y = 2m.

2

+ 5 =

Vậy với m ≠ 0 hệ có nghiệm duy nhất (x; y) = (

2

; 1)

Có x – y = 2

2 2 2

2 3 2 3 ( )

  



        

m TM

m m

Vậy m



thì

hệ có nghiệm (x; y) thỏa mãn: x – y = 2.

3) Với

m ≠ 0 hệ có nghiệm duy nhất (x; y) = (

2

; 1) =

> M(

2

; 1) =

> M thuôn thuộc

đường thẳng y = 1 với mọi m ≠ 0.

Bài 3.

 

1 3 1 (1)

5 (2)

    





  





m x my m

x y m

(2) <=

> y = 2x – m –

Thế (2) v

ào (1) có:

(1) <=

> (m – 1)x – m(2x – m – 5) = 3m – 1

<=> (m + 1)x = (m + 1)

(*)

ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 37

Hệ đã cho

có nghiệm duy nhất

<=> phương trình (*) có nghiệm duy nhất

<=> m + 1 ≠ 0

<=> m ≠ - 1

Với m ≠ - 1 có: (*) <=> x = m + 1

Thay x = m + 1 vào (2) có: (2) <=> y = 2(m + 1) – m – 5 = m – 3

Vậy với m ≠ - 1 thì hệ có nghiệm duy nhất (x; y) = (m + 1; m – 3)

S = x

+ y

= (m

+ 1)

(m – 3)

– 4m

+ 10 = (m – 2)

+ 6 ≥ 6 ∀m

≠ - 1.

Dấu “=” xảy ra <=> m = 2 (TM)

Vậy với m = 2 thì hệ có nghiệm duy nhất mà S = x

+ y

đạt giá

trị nhỏ nhất.

Bài 4. 1) Thay m = 2 vào hệ phương trình có:

2 1















 

 









x y

Vậy với

m = 2 thì hệ đã cho có nghiệm (x; y) = (1;

)

(1)

2 1 (2)









 



x my

mx y

(1) <=

> x = 2 –

Thế (1) v

ào (2) có:

(2) <=

> m(2 – my) – 2y = 1

ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 38

<=>

+ 2)

y = 2m – 1

<=> y =

2 1





(vì

+ 2 ≠ 0

∀ m)

Thay y =





vào

(1) có: x = 2 – m.





Vậy hệ phương

trình luôn có nghiệm duy nhất (x; y) = (



;





) với

mọi

0 4 0

0 2 1 2 1 0





 







  

 

 



      

   

   



 

 











x m

y m m

Mà

m ∈ Z

=> m ∈ {- 3; - 2; - 1; 0}

Vậy m ∈ {- 3; - 2; - 1; 0} thì hệ có nghiệm duy nhất (x; y) với x > 0 và y < 0.

3) Vậy hệ ph

ương trình luôn có nghiệm duy nhất (x; y) = (



;





) với

mọi giá

trị m.

x =



có m ∈ Z thì m – 4 ∈ Z.

TH1: m – 4 = 0 <=> m = 4 =>

















=> m

= 4 không thỏa mãn.

TH2: m – 4 ≠ 0 <=> m ≠ 4

ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 39

x ∈ Z

mà m – 4 ∈ Z => (m – 4)x ∈ Z <=>

16 18

2 2



   

 

Z Z

m m

<=>

+ 2 ∈ Ư

(18)

Mà m

+ 2 ≥

2 ∀m

=> m

+ 2 ∈ {2; 3

; 6; 9; 18}

Ta có bảng:

+ 2 2 3 6 9 18

0 1 4 7 16

m 0 1 -1 2 -2



4 -4

x =



1 1

y =

2 1







-1



KL KTM

KTM TM KTM KTM KTM KTM KTM

Vậy m

= - 1thì hệ có nghiệm duy nhất (x; y) với x; y là các số nguyên.

Bài 5:

 

1 1 2

 



 



 



 

  

   

     

  

   









x my

m my y m m y m

mx y m

m m y y m

)

Để hệ phương trình có nghiệm duy nhất thì

 





y m

có ng

hiệm

duy

nhất

1 0  

ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 40

Có

1 0



  

với

mọi

Vậy hệ phương

trình có nghiệm duy nhất với mọi

b. Phư

ơng trình có nghiệm duy nhất với mọi m ( theo câu a).

(I)

2 2

1 . 1

2 2



   



 















m m

x m

m m

Theo đề bài:

 

2 2

1 1 0

2 2

2 1

2 2

1 1 0

2 2

 









   

 





   

 

     

    

  

 





   

  









 

 

 

m m

DẠNG 4

Bài 1:

2. X

ét phương trình hoành độ giao điểm của (P) và (d):

)

ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 41

2 2

3 1 3 1

. 2 . 2 0

2 2 2 2





 





         



 



 







x x x x

Vậy (d

) và (P) cắt nhau tại

   

1 2 3 2  

f f

hai

điểm

;















và

;















   



 

   

1 2 3 2  

f f

ài 2:

1. T

hay

1



vào

hàm số ta được

 

1 1 1

1 1;

2 2







      









Tha

2

vào

hàm số ta được:

   

2 2; 2



    

2. Gọi

pt đường thẳng AB có dạng:

 

, 0  

y ax b a

Vì

A, B thuộc đường thẳng nên ta có

2 2

2 1





    





 

 



   



a b a

a b b

AB:



 

3. Gọi

(d) là đường thẳng cần tìm

/ :



  

AB d y x b

, 1 

ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 42

Xét p

t hoành độ giao điểm của (P) và (d)

1 1 1 1

2 2 2



      

b x x x b

Để (P)

và (d) tiếp xúc thì pt trên có 1 nghiệm

1 1 1

4. . 0

2 8







       

 

 

b b

đường thẳng cần tìm là:

2 8

  

y x

ài 3.

1) Ta có :

 



và

2

;



 

. Tọa độ

 

đi

qua

 

2;1

nên :



 

 



y x

2) Phư

ơng tình hoành độ giao điểm của

 

và

 

1 1 1

4 4 2





  



 



x x

Vậy giao điểm

còn lại là

;











 

3) Gọi

; '

lần

lượt là hình chiếu của

ên trục

hi đó tọa độ

   

2; 0 , 1;0

A

Diện tích tam giác

OAB

là :

  

' ' '

1 1 5

2 2 2 8



       

AB A B BA A AO OBB A B A B A A B B

S S S x x y Y x y x y

ài 4.

ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 43

1) Gọi

 

à điểm cố định mà đồ thị hàm số đi qua

Khi đó :

 

0 0 0 0

0 0

0 2

1 2 1 0

1 0 1



  



         

 

   



x x

y mx m x m y

y y

Vậy đường thẳng

luôn đi qua điểm cố định

 

M

2) Đồ thị

 

đi

qua

 

M

nên :

 

1 . 2

   

a a

Vậy

 



P y x

3) Phư

ơng trình đường thẳng có dạng :

x+b



Đường thẳng đi qua

 

2;1

M

nên :

 

1 2 1

  a b

Phư

ơng tình hoành độ giao điểm của

 

và

 

ax 4 4 0 2

     b x x ax b

có :

 

2 4 4 4



    

b a b

Đường t

hẳng

 

tiếp xú

c parabol

 

khi

 

có ng

hiệm kép hay

 

0 3



   a b

Từ

   

& 3

có :



















Vậy đường thẳng cần tìm

là :



 

ài 5.

1) HS tự vẽ hình

2) Phương tình hoành độ giao điểm của

 

và

 

1 3

2 2





  







x x

ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 44

Tọa độ

; , 3;



  

   



  

có :

 

0 0





    

 

 

 

3 13

0 0

2 2





    

 

 

 

1 3 2 5

 

    

 

 

Vậy chu

3 13

2 5

2 2



 ABC

(đvc

3) Gọi

 

;

0 Ox

C

Chu vi

ABC

 AB AC BC

không

đổi nên chu vi

ABC

nhỏ nhất

khi

AC CB

nhỏ nhất

Gọi















à điểm đối xứng của A qua Ox

Khi đó

' '



      

CA CA CB CA CB A B CA CB

nhỏ nhất k

', ,A C B

thẳng hàng

Hay

C là giao điểm của A’B với Ox

Phương trình đường thẳng

: 3





B y x

Vậy giao điểm

A’B và Ox là

;













4) Phư

ơng tình hoành độ giao điểm của

 

và

 

2 2

1 2 2 0 1

     nx x x nx

ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 45

Để

 

cắt

 

tại

2 điểm nằm cùng 1 phía với trục Ox thì pt

 

có 2

nghiệm

phân biệt cùng dấu nên :

 











 

nên không

có giá trị n thỏa mãn

Bài 6: 1) Viết phương trình đường thẳng (d) có hệ số góc k và đi qua điểm M(1,5;-1)

Đường thẳng (d) có hệ số góc k có dạng

 y kx b

Vì

đường thẳng (d) đi qua điểm M(1,5;1) nên:

,5 1

1,5



 



 

k b

=> Vậy đ

ường thẳng (d):

,5 1



 

kx k

2) Tìm k để đường thẳng (d) và Parabol (P) tiếp xúc nhau

Xét phương trình hoành độ giao điểm của đường thẳng (d) và Parabol (P):

,5 1





4 6 4 0    

x kx k

( 1, 4 , 6 4)    

a b k c k

(1)

(

2 ) 1.(6 4)

6 4



 



  



 

k k

Để thẳng (d

) và Parabol (P) tiếp xúc nhau thì phương trình (1) có nghiệm kép

4 6 4 0

2 3 2 0



 

   

k k

25



ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 46

Phư

ơng trình ẩn k có 2 nghiệm phân biệt: k

= 2,



Vậy, để thẳng (d

) và Parabol (P) tiếp xúc nhau thì: k

= 2; k



3) T

ìm k để đường thẳng (d) và Parabol (P) cắt nhau tại 2 điểm phân biệt

Để đường thẳng (d) và Parabol (P) cắt nhau tại 2 điểm phân biệt thì phương

trình (1) có 2 nghiệm phân biệt.

0 4 6 4 0 2 3 2 0 ( 2)( ) 0

              

















k k k k k k

Vậy, để đ

ường thẳng (d) và Parabol (P) cắt nhau tại 2 điểm phân biệt thì



k

hoặc

2

ài 7.

1) Cho n = 1:

a) Vẽ (P) và (d) trên cùng một mặt phẳng tọa độ

b) Tìm tọa độ giao điểm A và B của (P) và (d)

c) Tính diện tích tam giác AOB

Với n = 1 thì (d):





a) Vẽ (P)

và (d)

b) Xét phương trình hoành độ giao điểm của (P) và (d):

ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 47

2 0

(

1, 1, 2)

 

   



   

a b c

Vì

1 ( 1) 2 0      

a b c

nên phư

ơng trình có 2 nghiệm:

1 

2

+ Với

1 

thì



+ Với

2

thì

2

Vậy tọa

độ giao điểm của (P) và (d) là: A(-1;

) và

B(2;2)

2) Tìm n để (P) tiếp xúc với (d)

Xét phương trình hoành độ giao điểm của (P) và (d):

2 2

 

x n



  

x n

(1)

(

1, 1, 2 )



   

b c n

(

1) 4.1.( 2 )



   

 

Để (P)

tiếp xúc với (d) thì phương trình (1) có nghiệm kép

8 0



 



 







Vậy, để (P) tiếp xúc với (d) thì



n

3) Tìm n để (P) và (d) cắt nhau tại hai điểm

ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 48

Để (P)

và (d) cắt nhau tại hai điểm thì phương trình (1) có 2 nghiệm

8 0



 



 







Vậy, để (

P) và (d) cắt nhau tại hai điểm thì



n

4) Tìm

n để (P) và (d) cắt nhau tại hai điểm nằm ở hai phía trục tung

Để (P) và (d) cắt nhau tại hai điểm nằm ở hai phía trục tung thì phương trì

(1) có

2 nghiệm trái dấ

1.(

2 ) 0

 



 

 

Vậy, để (

P) và (d) cắt nhau tại hai điểm nằm ở hai phía trục tung thì n > 0

Bài 8. Tìm m để (P) và (d) cắt nhau tại hai điểm phân biệt A và B

Xét phương trình hoành độ giao điểm của (P) và (d):

1

 

mx m



   

mx m

(1)

(

1, , 1)



    

b m c m

( ) 4.1( 1)

4 4

     

  

m m

( 2) 0  

với

mọi m

ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 49

Để (P) và (d) cắt nhau tại hai điểm phân biệt A và B thì phương trình (1) có

hai nghiệm phân biệt

0 ( 2) 0 2 0 2           

m m m

Vậy, để (P) và (d) cắt nhau tại hai điểm phân biệt A và B thì

2 

1) Gọi x

và x

là hoành độ của A và B. Tìm m để

1 2

2 

x x

Theo hệ thức Vi – et:

1 2

. 1



   

    

S x x m

P x x m

Theo đề bài:

2 2 2 2

1 2 1 2 1 1 2 2 1 2 1 2

2 2

2 ( ) 4 2 4 ( ) 4 4

( ) 4( 1) 4 4 0 ( 4) 0

            

           

x x x x x x x x x x x x

m m m m m m

0 

(TMĐK) hoặc m = 4 (TMĐK)

Vậy để

1 2

2 

x x

thì m = 0 hoặc m = 4

2) Tìm m để (P) và (d) cắt nhau tại hai điểm nằm cùng bên trái trục tung

Theo hệ thức Vi – et:

1 2

. 1



   

    

S x x m

P x x m

ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 50

Để (P)

và (d) cắt nhau tại hai điểm nằm cùng bên trái trục tung thì phương

trình (1) có 2 nghiệm cùng âm

( 2) 0

1 0 1



   



 







        



 





 

 



P m m

S m

Vậy, (P) và (d) cắt nhau tại hai điểm nằm cùng bên trái trục tung thì m < -1

Bài 9:

Phương trình hoành độ giao điểm của parabol (P) : y =

và đường thẳng

d : y = mx + 2 là:

 x mx



2 4 

x mx



2 4 0  

x mx

(1)

Để đường

thẳng d cắt parabol (P) tại 2 điểm phân biệt thì PT (1) phải có 2

nghiệm phân biệt





có

'

= (-m

)

– 1.(-4)

= m

+ 4 > 0

m

Với

m

(1) luôn có 2 nghiệm phân biệt .Gọi x

à 2 nghiệm phân biệt của

PT(1). Thì x

à hoành độ giao điểm của parabol (P) và đường thẳng d.

Theo Vi ét ta có

1 2





  







  





x x m

x x

(*)

ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 51

Đặt A = x

+ x

= x

+ 2x

+ x

-2x

= (x

)

-2 x

Thay hệ (*) vào A ta được A = (2m)

– 2.(-4)

= 4m

+ 8.

Vì m



m

 4m



0  4m

+ 8

 

 A



Dấu “=” xảy ra  m

= 0  m = 0.

Vậy với m = 0 thì đường thẳng d cắt parabol (P) tại 2 điểm phân biệt có hoành

độ x

mà x

có giá trị nhỏ nhất.

Bài 10

Phương trình hoành độ giao điểm của parabol (P) : y =

và đường thẳng d:

y = - mx – m + 1 là:

1   

x mx m



1 0   

x mx m

(1).

Để đường thẳng d cắt parabol (P) tại 2 điểm phân biệt thì PT (1) phải có 2

nghiệm phân biệt.

Từ pt (1) Ta thấy a - b + c = 1 – m + m – 1 = 0

Nên pt (1) luôn có nghiệm : x

= - 1 và x





= - (m – 1) = 1- m.

Để pt (1) có 2 nghiệm phân biệt thì : x



ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 52

 -1



1 – m

 m



Với



2. T

a có x

= -1

=> y

= (-1)

= 1

=> A(-1;1)

= 1 – m =>

= (1- m

)

=> B

(1 – m ;(1-m)

)

có : y

+ y

= 1+

(1-m)

Mà

(1 - m )



m

 (1 - m )

+ 1



 y

+ y



Dấu “

=” xảy ra  (1 - m )

 1 – m = 0

 m = 1

Vậy với m = 1 thì đường thẳng d cắt parabol (P) tại điểm A và B phân biệt với

A(x

);B(x

) mà(y

+ y

) nhỏ nhất .

DẠNG 5:

Bài 1: Cho pt : x

– (2

m + 3)x +m

+ 3

m + 2 = 0 (1) m là tham số.

1. Giải pt khi m = 1.

Với m = 1 pt (1)có dạng : x

– 5x + 6

= 0

Ta có

(

5) 4.1.6 25 24 1 0



      



  



ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 53

Phương trình có 2 nghiệm phân biệt

5 1



 



 

Vậy với m = 1 pt có tập nghiệm S ={ 2;3}

2. Xác định m để pt có 1 nghiệm là 2.Khi đó pt còn 1 nghiệm nữa, tìm nghiệm đó?

Để pt (1) có 1 nghiệm x = 2=> f(2) = 0

Hay

2 2

2 (2 3).2 3 2 0     

m m m



4 4 6 3 2 0     

m m m



0 

m m



( 1) 0 

m m



0 0

1 0 1

 



  

 

 

 

m m

+.Nếu m = 1.nghiệm còn lại là 3(phần 1).

+.Nếu m = 0 pt (1) có dạng :

3 2 0  

x x

Theo Vi_ét

1 2 2

2 2. 2  

x x x

1 

.=> Nghiệm còn lại là 1.

3. CMR pt luôn có 2 nghiệm phân biệt với

m

Ta có :

 

(2 3) 4.1.( 3 2)      

m m m

2 2

4 12 9 4 12 8     

m m m m

1 0

  m

Vậy

m

pt (1) luôn có 2 nghiệm phân biệt.

4. Gọi

1 2

;x x

là 2 nghiệm của pt.Tìm m để

2 2

1 2

1 

x x

m

gọi

1 2

;x x

là 2 nghiệm của pt(1) .

ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 54

Theo V

i-ét ta có

1 2



 







 



x m

x x m m

)

Để :

2 2 2

1 2 1 1 2 2 1 2

2 2 1



     

x x x x x x x

2 1 2

( ) 2 1   

x x x x

(*)

Thế hệ (I

) vào biểu thức (*) Ta được :

(2m 3) 2.( 3 2) 1    

m m

12 9 2 6 4 1 0

6 4 0

3 2 0(2)



      



  

   

m m m m

m m

Ta thấy

3 2 0



    

b c

=> pt (2) có nghiệm

1; 2   

m m

Vậy với

1; 2   

m m

thì pt có nghiệm

;x x

thoả mãn

1 2

1



5. Xác định m để phương trình có nghiệm này gấp 3 lần nghiệm kia.

Giả sử pt (1) có 2 nghiệm

;x x

Theo Vi-ét t

a có

1 2

2 3(3)

3 2(4)

  





  



x x m

x x m m

.Để



x x

2 2 2

   x x x x

(5).

Thế pt(3) vào pt(5) =>

2 1

3 3(2 3)

3 4



    

m m

m x x x

Tha

3 3(2 3)



  

m m

x x

vào

pt(4)

3 3.(2 m 3)

3 2

4 4





 

ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 55

2 2

3(2 3) 16( 3 2)

3(4 m 12 9) 16 48 32

12 36 27 16 48 32 0

4 12 5 0

    

     

      

    

   

m m m

m m m m

m m

Ta có:

' 6 4.5 36 20 16 0

' 16 4

      

   

Pt có 2 nghiệm

1 2

6 4 1 6 4 5

;

4 2 4 2

     

   m m

Vậy với

1 5

;

2 2

 

 m m

thì phương trình có nghiệm này bằng 3 lần nghiệm kia.

Bài 4

 

2 1 4 0    

x m x m

1. Với

5 

phương trình

8 9 0   

x x

Phương trình có

0  

a b c

nên có 2 nghiệm

1 2

1; 9  

x x

   

1 19

1 1. 4 5 0

2 4

 

 

            

 

 

 





m m m m m m



phương trình luôn có 2 nghiệm phân biệt với mọi m

2. Phương trình có 2 nghiệm trái dấu

. 0 4 0 4      

a c m m

3. Với mọi m ta có





gọi

1 2

,x x

là 2 nghiệm của phương trình. Theo hệ thức vi-

et ta có:

 

1 2

2 1

. 4



  



 



x x m

Để phương trình có 2 nghiệm cùng dương

 

1 2

2 1 0

   4

. 0

4 0

  

 

 



    

  



 



x x

ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 56

     

2 2 1 1 1 2 2 2 1 1 2 1 2

1 1 2          

A x x x x x x x x x x x x x x

   



2 1 2 4 2 2 2 8 10



       m m m m

4. Đặt

1 2

 B x x

có

   

2 2 2

2 1 1 2 2 1 2 1 2

2 4       

B x x x x x x x x x x

   

 

4 1 4 4 4 5      

m m m m



   

m m

ài 5

   

3 7

3 3 4 0

 

 



           





 

 





m m m m m

Phư

ơng trình luôn có 2 nghiệm phân biệt với mọi m

1. Gọi

1 2

,x x

à 2 nghiệm của phương trình. Áp dụng hệ thức vi-ét ta có:

 

1 2

21

3 





 



  





 

 

 





x x m

m x x

x x m

Thay (2) vào (1) ta có

 

2 1 2 1 2 1 2

3 2 2 4



      

x x x x x x x

2. Phư

ơng trình có 2 nghiệm bằng nhau về giá trị tuyệt đối và trái dấ

 

2 1 2



 0 2 1 0 1



         

x x x m m

Thay m=1 vào lai phương trình tìm được

; 2



 x x

vậy

m=1 thỏa mãn

yêu cầu bài toán

Bài 6: x

– 2(

m – 2)x + 2m – 5 = 0

1/ Chứng minh phương trình luôn có nghiệm với mọi m

ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 57



= (m – 2)

– 1(2m – 5)

= m

– 4m + 4 – 2m + 5

= m

– 6m + 9

= (m – 3)

 m

 Phương trình có nghiệm với mọi m

  m

=> phương trình luôn có nghiệm với mọi m

Theo Viet ta có

1 2

2( 2)

2 5

. 2 5





     









   





b m

x x m

c m

x x m

Theo đề bài ta có: B = x

(1 - x

) + x

(1 – x

) < 4

B = x

– x

+ x

– x

< 4

 x

+ x

– 2x

< 4

 2(m – 2) – 2(2m – 5) < 4

 2m – 4 – 4m + 10 – 4 < 0

 -2m + 2 < 0  2m > 2  m > 1

Vậy m > 1 thì phương trình có nghiệm sao cho B < 4

3/ Tìm hệ thức liên hệ giữa 2 nghiệm không phụ thuộc vào m

Ta có

1 2

2 4(1)

2( 2)

. 5

. 2 5

  



  







 



 









x x m

x x

x x m

thay vào (1) ta được

ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 58

1 2

2 4



  

x x

 x

+ x

= x

+ 5 – 4  x

+ x

– x

– 1 = 0

ài 7.

1/ x

+ (4m + 1)x + 2(m- 4) = 0 (*)



= (4m

+ 1)

– 4.1.2

(m – 4)

= 16m

+ 2.4m.1 + 1 – 8m

+ 32

=16m

+ 33

> 0 Với mọi m

 Phương trình (*) có 2 nghiệm phân biệt với mọi m

Theo Viet ta có

1 2

(4 1)

. 2( 4)

  



     







  





b m

x x m

Kết hợp điều k

iện ta được

1 2

2 1

(

4 1)(1)

. 2( 4)(2)

(3)

   





 





 



x x m

x x

Từ (3) =

> x

= 17

+ x

(3’) t

hế vào (1) ta được

+ 17

+ x

= -(4m

+ 1)

 2x

= - 4m – 1 – 17

= - 4m

– 18

= -2m

– 9 thay vào (3’) ta được.

= 17 + (-2m – 9)

= 17

– 2m – 9 = 8 – 2m

ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 59

Thay x

, x

vào (2) ta được:

(-2m – 9) (8 – 2m) = 2(m – 4)

 -16m + 4m

– 72 + 18m – 2m + 8 = 0

 4m

– 64 = 0  4m

= 64  m

= 16 => m =

4

(TM)

Vậy m =

4

thì phương trình có 2 nghiệm x

, x

t/m x

– x

= 17

2/ A = (x

– x

)

2 2 2

1 2 1 2 1 2 1 2

2 ( ) 4    

x x x x x x x x

A =

 

(4 1) 4.2( 4)   

m m

=16m

+ 8m +1 – 8m + 32

=16m

+ 33

Ta có m



0 với mọi m

 16m



0 với mọi m => 16m

+ 33



33 mọi m

Vậy GTNN của A = 33  m = 0

1 2

(4 1)(1)

. 2( 4)(2)

   





 



x x m

Ta có x

+ x

= -4m – 1 => x

+ x

+ 1 = -4m =>

1 2

 





x x

Thay vào (2) ta được

1 2 1 2

1 1

. 2 4 . 8

4 2

   

 

    

 

 

 

x x x x

 -2x

+ x

+ 1 + 16

 x

+ x

+ 2x

+ 17 = 0

ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 60

Vây

hệ thức liên hệ giữa x

, x

không

phụ thuộc m là: x

+ x

+ 2x

+ 17

= 0

Bài 8.

 

2 1 2 1 0    

x m x m

   

1 2 1



    





 

 

Để phư

ơng trình có hai nghiệm phân biệt thì







  

Áp dụng định lí Vi-et, ta có:

 

1 2

   



 









 





x x m x x m

x x m

Theo đề ta

có

 

1 2 1 2 1 2

2 2

2 5

2 1 2 1 5 4 6 3 0



    



        

x x x x x

m m m m m

Suy ra

3 21

 

m

hoặc

3 21

 

m

Vậy





m

hoặc



m

thì

phương trình đã cho có hai nghiệm

phân biệt

1 2

,x x

à độ dài hai cạnh của một tam giác vuông có cạnh huyền

bằng

ài 9. Cho phương trình

4 2

2 0



  

x m

a) Giải phương trình khi

1



Tha

1 

vào

phương trình, ta có:

2 3 0  

x x

ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 61

Đặt

 

0 

t x t

, phương trình trở thành

2 3 0  

t t

Ta có

1 2 3 0     

a b c

Do đó, phương trình có nghiệm

1 

( loại ) và

3

3 3 3     

t x x

Vậy tập nghiệm của phương trình

 

 S

b) Tìm m để phương trình có 4 nghiệm phân biệt

Đặt

 

0 

t x t

, phương trình trở thành

2 2 0   

t t m

 

Để phương trình đã cho có 4 nghiệm phân biệt thì phương trình

 

có 2 nghiệm

dương phân biệt.

1 2 0

' 0 3

2 0 2 3

0 2

2 0





  





  



 

     

  

 



 

 









S m

Vậy

2 3 

thì phương trình đã cho có 4 nghiệm phân biệt.

Bài 10. Cho phương trình

 

2 2

2 1 1 0    

x m x m

Đặt

 

0 

t x t

, phương trình đã cho trở thành

 

2 2

2 1 1 0    

t m t m

 

Ứng với một nghiệm

dương của phương trình

 

thì phương trình đã cho

có 2 nghiệm phân biệt. Do đó để phương trình đã cho có nghiệm duy nhất thì

phương trình

 

phải có một nghiệm

0t

ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 62

Suy ra

1 0





  



 



1

, phương t

rình

 

trở thàn

4 0 

t t

 

4 0

  

 

 

 

 



 



t t

t x

( l

oại vì có 3 nghiệm )

Khi

1



, phương trình

 

trở thành:

0

0 

( nhận )

Vậy

1 

thì

phương trình đã cho có nghiệm duy nhất.

DẠNG 6:

Bài 1:

1. Chứ

ng minh



 

  OKM OAM OBM

2. Dùng

kết quả câu 1, tứ giác MAKB nội tiếp chú ý MA = MB



 

AKM BKM

3. Chứ

ng minh được:





 

B MAB MKB

ĐPCM

4. Chứ

ng minh được:

OM

, dùng hệ thức lượng cho tam giác vuông MAO

.



MO MA

ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 63

Chú ý:

5. Từ kết quả câu 4 :

Tổng quát: Trên tia Mx lấy hai điểm A, B sao cho MA < MB. Trên tia MY lấy hai

điểm N, P sao cho MN < MP. Khi đó ABPN là tứ giác nội tiếp

6. Vì AB = 2AH nên:

. Dùng hệ thức lượng cho tam giác MAO

. AH HM HO

. Chứng minh được:

7. Chứng minh được MEKH là tứ giác nội tiếp, dùng kết quả tổng quát ở câu 5 ta

có:

ĐỀ C

ƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 64

không đối. Từ

8. Vì MO là trung trực của AB nên IA = IB.



IAM IAB

suy ra AI là phân giác



MAB

chú ý MI là phân giác => ĐPCM.

9. Từ câu 2 KF là phân giác góc



AKB

, chú ý nên KE là phân giác góc

ngoài tại đỉnh K. Dùng tính chất đường phân giác

với .

10. Nhậ

n xét: P, Q thay đổi nên có độ dài cả ba cạnh đều thay đổi gây khó

khăn do đó cần đưa về tam giác chứa yếu tố cố định hơn.

Từ kết quả câu 3

Kẻ ta có

Do AM không đối

(P' đối xứng với A qua O)

11. G

ọi S là trung điểm OM, từ G kẻ GL//KS. Vì AS cố đị

nh và:





L cố định

Lại

có:

3 3

 LG SK OM

hông đổi)

ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 65

Bởi vậy G luôn chạy trên đường tròn

;

 

 

 

L OM

cố định.

Do OK.OE không đổi nên E thuộc đường OK cố định trên đó E cách O cố định một

đoạn



không đổi. Vậy E là điểm cố định mà AB luôn đi qua.

12. Từ MO = 2R tính được .

Diện tích hình quạt cần tính là





Bài 2

a. C/m: tứ giác OMNP nội tiếp

Ta có:



90   MP AB OMP

Ta có:



90   ON CP ONP



 OMP ONP



Tứ giác OMNP nội tiếp (DHNB)

b. C/m: Tứ giác CMPO là hình bình

hành

Ta có:

/ /













CO AB

CO MP

MP AB

(1)

Ta có:

 

( CN OCM ONM O

cân tại O)

ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 66







OPM ONM

( cù

ng chắn cung OM)



(

OD//PM)

O

PM DOP



 

OCM DOP

Mà chúng là hai góc đồng vị

 CM

(2)

Từ (1), (

2) suy ra tứ giác CMPO là hình bình hành.

c. C/m : CM . CN không phụ thuộc vào vị trí của điểm M

+) Xét

CO

và

CN

có:



( . )

(=90 )





  



 





OCM chung

COM

CND g g

COM CND

. 3



   

CO CM

CN OC CD R



CM . CN k

hông đổi



CM . CN k

hông phụ thuộc vào vị trí của điểm M

d. K

hi M di chuyển trên đoạn thẳng AB thì tâm đường tròn nội tiếp tam g

iác

CND d

i chuyển trên một cung tròn cố định nào?

+) Goi I là tâm đường tròn nội tiếp

CN



CI l

à tia phân giác của



 

OCN DCI DCN

DI là t

ia phân giác của







CDN

CDI CDN

ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 67



( ) 45

     

DCI CDI DCN CDN

(vì



90 

CND

)



135  

CID



I nằm trên cung tròn chứa góc

135

dựng trên CD.

Bài 3.

a. C/m: tứ giác ABMD nội tiếp

Ta có:



90   

DA AB DAB

Ta có:



( ; ) 90 90

      

M O BMC BMD



 

DAB DMB



Tứ giác ABMD nội tiếp (DHNB)

b. Tứ giác APND là hình gì? Tại sao?

Ta có:



DMA DBA

( cùng chắn cung DA)



DMA DBA

( 2 góc đồi đỉnh)







DBA PBC

( 2 góc đồi đỉnh)





   

NMC PBC NC CP



NC = CP

 C

đường trung trực của NP

Ta có: ON = OP = R

 O

đường trung trực của NP

 CO

là đường trung trực của NP

ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 68





hay





Mà

AC







Tứ g

iác APND là hình thang.

c. C/m : C

M . CD không phụ thuộc vào vị trí của điểm M

+) Xét

CMB

và

CA

có:





( . )

(

=90 )





  



 





ACD chung

B CAD g g

B CAD



  

CM CB

CD CA CB

Mà

A, B, C cố định



CA . CB kh

ông đổi



CM . CD khô

ng đổi



CM . CD khô

ng phụ thuộc vào vị trí của điểm M

d. C

/m: Trọng tâm G của tam giác MAC chạy trên một đường tròn cố định khi

di động.

Gọi

I là trung điểm của AC



Điểm

I cố định và



Kẻ G

J // MB





IG IJ

IM IB

( định lý Tal

et)



Điểm

J cố định

Kẻ GK // MC





( định

lý Talet)



Điểm

K cố định

ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 69



    



 

IJ IK IJ IK JK

IB IC IB IC BC

JK BC

Ta có:



/ /

/ / 90





    









GJ MB

GK MC GJ GK JGK

MB MC

Vậy khi M di động trọng tâm G của tam giác MAC chạy trên đường tròn đường

kính JK cố định.

Bài 4:

a. A là điểm chính giữa



I là trung điểm BC

 OA BC

tại I



90 AIC

ĐỀ C

ƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 70

Suy ra tứ gi

ác AIHC nội tiếp



A, I

, H, C cùng thuộc một đường tròn

Xét và có chung

(góc

nội tiếp chắn hai cung bằng nhau)

c. Có (cùng chắn



)

(góc nội tiếp chắn hai cung bằng nhau)

Suy ra AB tiếp xúc đường tròn ngoại tiếp

d. Có (góc nội tiếp chắn hai cung bằng nhau)



EA l

à phân giác



CEM

, m



cân t

ại E



EA l

à trung trực MC



=AC

=> (cạnh huyền – cạnh góc vuông)

Dấu "=" xảy ra khi HA = HC



vuô

ng cân tại H



hay

ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 71



=> E nằm trên (O) sao cho số đo



90CE

Bài 5.

CHỨNG MINH

1) Ta có



90 AHB AHC

(góc nội tiếp chắn nửa đường tròn)



0 0 0

90 90 180    HBC BHA AHC

. Vậy

, ,B H C

thẳng hàng.

2) Nếu

MN AH

thì

,HM HN

lần lượt là các đường kính nên hiển nhiên ta có

đpcm.

Ngược lại, không mất tính tổng quát, giả sử



HAN

nhọn, ta có



MBH HAN

(cùng bù với



HAM

)



MOH

là góc ở tâm chắn





MBH

là góc nhọn chắn cung



nên



MBH MOH

Chứng minh tương tự ta được



HAN HO N

Suy ra hai tam giác cân

MOH

và

'HO N

đồng dạng (c-g-c)

' '

   

MH MO R

const

HN NO R

3) Ta có



90 BMA CNA

(góc nội tiếp chắn nửa đường tròn)

ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 72



 tg

MNCB

à hình thang vuông.

à đường trung bình của hình thang

MNC



/ / 180

   KI NC KIA KNC

(hai

góc trong cùng phía)

Mặt khác





AHK ANC

(cùng

bù với



AHC

)

Suy ra



180

 AIK AHK

, m

à hai góc ở vị trí đối nhau nên tứ giác

AIKH

nội

tiếp. Vậy 4

điểm

, ,

H K I

cùn

g thuộc một đường tròn.

4) Xét

HMN

và

ABC





NMH ABC

(cùng

chắn cung



của

 

)





MNH ACB

(cùng

chắn cung



của

 

)

Suy ra

HMN

∽

ABC

(g-g)



 





 

HMN

HMN ABC

ABC

AB AB

Mà

B C

cố định nên



HMN

 HM

à đường kính của

 

hi đó



MAH

, đường

thẳng

à đường thẳng cần tìm.

Bài 6.

CHỨNG

MINH

ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 73

1) Ta có





OAM O AN

(đối

đỉnh)

OAM

cân tại

 

 

OA OM R





 

OAM OMA

Chứng minh tương tự



' '



O AN O NA

Xét

AOM

và

'AO N

có



' '

  

OMA OAM O AN O NA

(1)

 

' 

   AOM AO N g g

∽

2) Do

/ /AB FN

nên theo định

lí Talets ta có:



BA MA

FN MN

(2)

Từ (1) ta cũng có





OMA O NA

mà

hai góc ở vị trí so le trong nên

/ / 'OM O N

Lại theo hệ quả định lí Talets ta có

2 ' 2

' ' 2 ' ' 3

   

 

MA OA R R

MN OO R R R R

(3)

Từ (2)(3) suy ra

2 3 3

3 2 2

   

FN BA R

= const.

ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 74

(gt

)



ABFE

à hình thang (4)



BFE MBA

(đồng vị) (5)





AOM

(tí

nh chất góc nội tiếp) (6)



 

AEF AEN



'AO N

(tí

nh chất góc nội tiếp) (7)





AOM AO N

(do

' AOM AO N

∽

) (8)

Từ (5)(6

)(7)(8) suy ra



BFE AEF

(9)

Từ (4)

và (9) suy ra tứ giác

ABFE

à hình thang cân.

4) Kẻ đường cao

của hình thang

, ta

có

 

2 2 4

 



 



 

  

R R AH

AB FN AH

S R AH

(10)

Kẻ

 MK AB K





MAK ANH

(đồng vị)

Suy ra



M NHA

∽

(g-g)

   

MA R

NA R

(11)

Từ (10)(

11) suy ra

BFN

R MK



Vậy

BFN



Gọi

à trung điểm của

và

à điểm thỏa mãn

I AB



 



C

à trung điểm của cung lớn



nên cố định.

ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 75

Ta có

MK MI MO OI CO OI CI     

Suy ra Max

CI

, dấu

'' "

M C  

Bài 7.

CHỨNG MINH

1) Ta có :



AEB



(góc nội tiếp chắn nửa đường tròn

đường kính

)



KEB

 

(1)



CD AB M KMB

   

(2)

Từ (1)(2) suy ra hai đỉnh

và

cùng nhìn cạnh

dưới các góc bằng nhau nên tứ giác

EKBM

nội

tiếp.

2) Xét

AKM

và

ABE





 

chung;

AKM ABE g g

AMK AEB





   





 





∽

. . .2 3

AK AM

AK AE AM AB R R R

AB AE

     

3) Theo giả thiết ta có

là trung trực của

nên

CO CB

OCB 

đều vì

 

CO CB OB R  



COB



ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 76

Vậy diện

tích quạt dưới hạn bởi



, ,OB OC BC

nhỏ :

 

2 2

360 6

R R

S dvdt

 

 

4) Gọi

là điểm đối xứng của

qua

F

cố định do

cố định.



cân tại

à trung trực của

(theo c

ách dựng

 

KAM KFM 

(3)

Tứ g

iác

AEHM

nội

tiếp do hai góc đối diện

và

vuô



KAM MHB 

(4)



180

MHB KHB

 

(5)

Từ

   



4 5 180

FM KHB  

HBF



nội

tiếp

F

thuộc đ

ường tròn ngoại tiếp tam giác



Tâ

của đ

ường tròn ngoại tiếp tam giác

thuộc đ

ường trung

trực của

cố địn

Bài 8.

CHỨNG

MINH

ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 77

8) Ta có



AHB



(góc nội tiếp chắn nửa

đường tròn)

HB AE 

Mặt khác ta lại có

là điểm chính giữa cung

nên



ABH HBM

Xét tam giác

ABE

có

vừa là đường cao

vừa là đường phân giác nên

BAE

cân tại

9) Do

 

N B BA BA BN ABN    

cân tại



(1)

INB MAB

 

AM AH

lần lượt là hai đường cao

trong tam giác

FAB

và cắt nhau tại

nên

là trực tâm của tam giác

FAB

KI AB 



IEB MAB 

(2)(cùng phụ

với



MBA

)

Từ (1)(2) suy ra



INB IEB

mà hai góc cùng

nhìn cạnh

nên tứ giác

NEIB

nội tiếp.

ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 78

10) K





0 / /

so le trong

AK MK AB MKB KBA   



 

cmt

MBK

KBA

nên



MBK MKB MKB  

cân tại

(

K MB





Kẻ

J AB J KMJA



 

hì

nh chữ nhật

 

M JA





Từ (3)(4) suy ra

B JA



Áp dụng hệ thức

lượng trong tam giác vuông

MAB

đường c

 

2 2

4 2 .

B JB AB AB JA AB R R MB



   

 



2 2

2 . 4 0 5 5 1MB R MB R MB R R MB R         

Vậy điểm

cần tìm

là giao của

 

và

 

;

5 1



ÀI 9.

ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 79

a. C/m: tứ giác MNEF nội tiếp

Ta có:



/ /

(2gocs )













 

CD AB

CD MN

MN AB

MND CDN lt

Mà:





CDN CFE

( cùng chắn



)



 

MND CFE



Tứ giác MNEF nội tiếp

(DHNB)

b. C/m: ME.MC = NF.ND

+) Xét

MAE

và

MCA

có:





( . )

(cungchan )





   









AME chung

MAE MCA g g

MAE MCA AE

 

MA ME

MC MA

. (1)

 MA MC ME

+) Xét

NAF

và

NDA

có:





AF ( . )

(cungchan )





   









ANF chung

N NDA g g

NAF NDA AF

 

NA NF

ND NA

ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 80

. (2)

 NA ND NF

+) T

a có: MN // CD (cmt)



















CDN MND

CD NMC

Mà





CDN MCD

( vì

OC

cân tại



 

MND CMN





OMN

cân tại O

Mà

OA NM

Suy ra: A là trung điểm của MN





M AN

(3)

+) Từ (1

), (2), (3) suy ra: ME.MC = NF.ND

c. Tì

m vị trí của điểm H để tứ giác AEOF là hình thoi.

+) Ta có:



//MN





















FEC

MNF

FEC

NME

MNF

NME

Mà

OA





tại





Tứ g

iác AEOF có

OA

tại

I và

IE

(cm

Để tứ giác AEOF là hình thoi thì I là trung điểm của OA

ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 81

+) c/m:

(ch-gn)  

OIE OHC

OI=OH



Khi I là trung điểm của OA thì H là trung điểm của OB

Vậy để tứ giác AEOF là hình thoi thì H là trung điểm của OB.

d. C/m: Khi H chuyển động trên đoạn OB thì G thuộc một đường trong cố định.

+) Từ G kẻ đường thẳng song song với AC và cắt AB tại P

Xét

OKA

có GP // AK ( theo cách vẽ)





 



 











OG OP

OK OA

Suy ra điểm P cố định

+) Ta có:



/ /



    







GP AK

GP GA AGP

GA GK



G thuộc đường tròn đường kính AP khi H chuyển động trên đoạn OB.

Bài 10.

ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 82

a. C/m: tứ giác BF’E’C nội tiếp

+) Ta có: F’ đối xứng với H qua AB



AB l

à đường trung trực của F’H



BF’

= BH

' BHF

cân tại



' '

 

BF H BHF

(1)

+) T

a có: E’ đối xứng với H qua AC



AC l

à đường trung trực của E’H



CE’ = CH

' CHE

cân tại



' '

 

CE H CHE

(2)

+) Ta có :



' '



BHF CHE

(2 góc đối đỉnh)

(3)

Từ (1), (2), (3) suy ra



' '



BF H CE H

Mà E’, F’ là 2 đỉnh liền kề của tứ giác

BCE’F’



Tứ g

iác BCE’F’ nội tiếp (dhnb)

b. C

/m: A, F’, B, C, E’ cùng thuộc một đường tròn

Ta có:



   

AFH AEF

Tứ g

iác AEHF nội tiếp (dhnb)

ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 83



180

 ' 180



   



 



  





FAE FHE

FAE BHF

Ma BHF FHE

Lại có:



'BFH BHF



 

FAE BF H

Mà A, F’ là 2 đỉnh liền kề của tứ giác ABCF’



Tứ giác ABCF’ nội tiếp (dhnb)



A, C, B, F’ thuộc đường tròn ngoại tiếp

'BCF

(4)

+) Ta có: Tứ giác BCE’F’ nội tiếp



B, C, E’, F’ thuộc đường tròn ngoại tiếp

'BCF

(5)

Từ (4), (5) suy ra A, F’, B, C, E’ cùng thuộc một đường tròn

c. C/m:

OA EF

+) Ta có: F’ đối xứng với H qua AB



AB là đường trung trực của F’H



AF’ = AH (6)

+) Ta có: E’ đối xứng với H qua AC



AC là đường trung trực của E’H



AE’ = AH (7)

Từ (6), (7) suy ra AE’ = AF’

 A

đường trung trực của E’F’ (8)

ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 84

+) T

a có: OE’ = OF’ = R





đường trung trực của E’F’ (9)

Từ (8), (9) suy ra OA là đường trung trực của E’F’





E F

+) C/M: Tứ gi

ác BCEF nội tiếp

 

 

EBC EFC

Mà



' '



EBC CF E

( 2 góc nội tiếp cùng chắn cung CE’)



' '

/ / ' '

OA ' '

 





 

CF E EFC

EF E F

Ma E F

OA EF

d. C

/m: Khi A chạy trên (O) thì bán kính đường tròn ngoại tiếp tam

giác AEF

không đổi

Xét

;













có:



90 

ACD

/ /

BH A

 











DC AC

DC BH

Ma C

(10)





' '



 



 









CDH F HB

CDH

BF H

a F HB BF H









' ' '     

F D CB F B CD F B CD

(11)

Từ (10),

(11) suy ra tứ giác BHCD là hình bình hành

Gọi I là trung điểm của BC



là trung điểm của HD

+) Ta có: O là trung điểm của AD

ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI

Tài liệu được thực hiện bởi nhóm : Toán THCS Page 85

 

OI AH

(t/c đườn

g trung bình của

AHD

)



AH =

2OI

Do BC cố định



OI không đổi



AH không đổi

+) Ta có: tứ giác AEHF nội tiếp đường tròn đường kính OH (cmt)



Bán k

ính đường tròn ngoại tiếp tam giác AEF không đổi

Vậy khi A chạy trên (O) thì bán kính đường tròn ngoại tiếp tam giác AEF không

đổi.

Bấm Tải xuống để xem toàn bộ.

| 1/85

| | Tải xuống

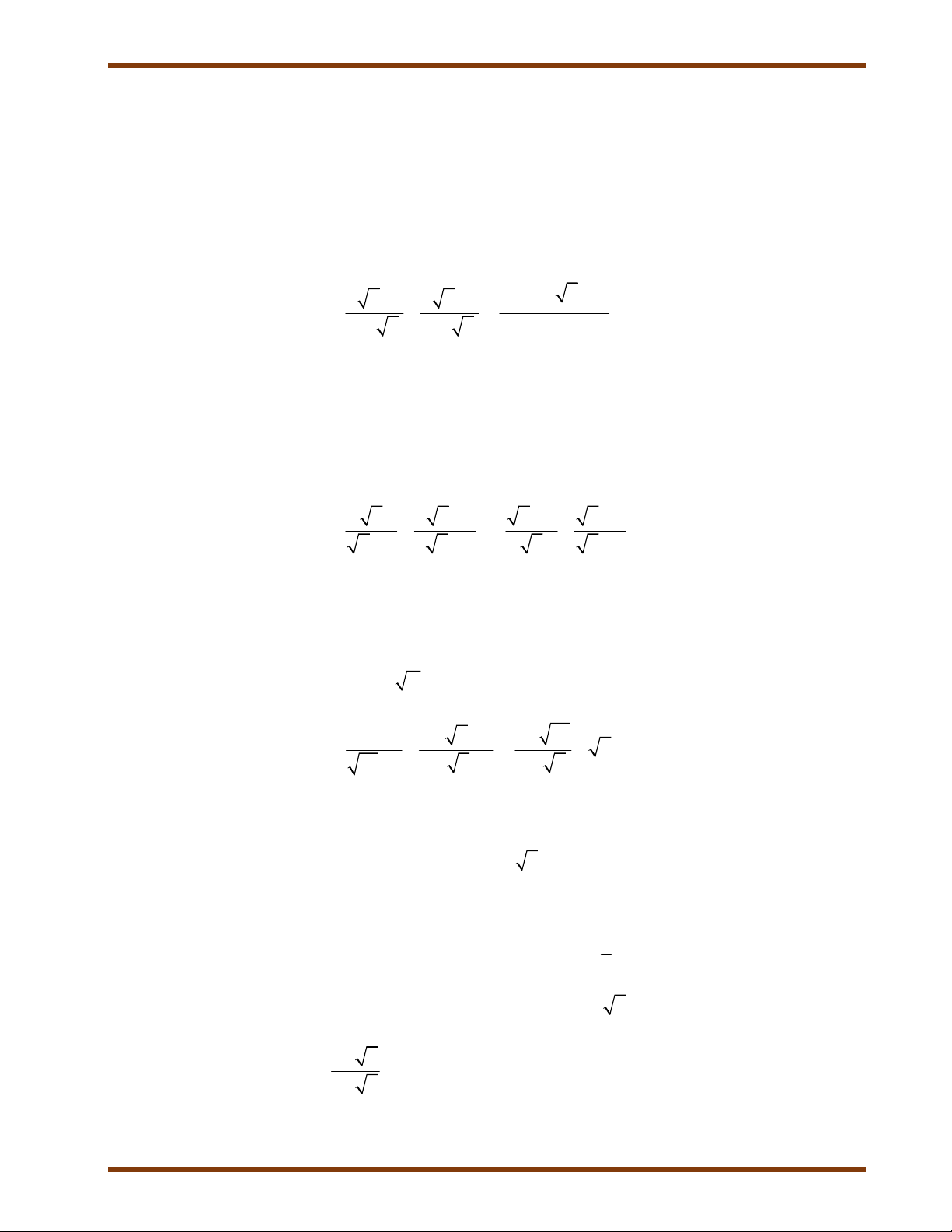
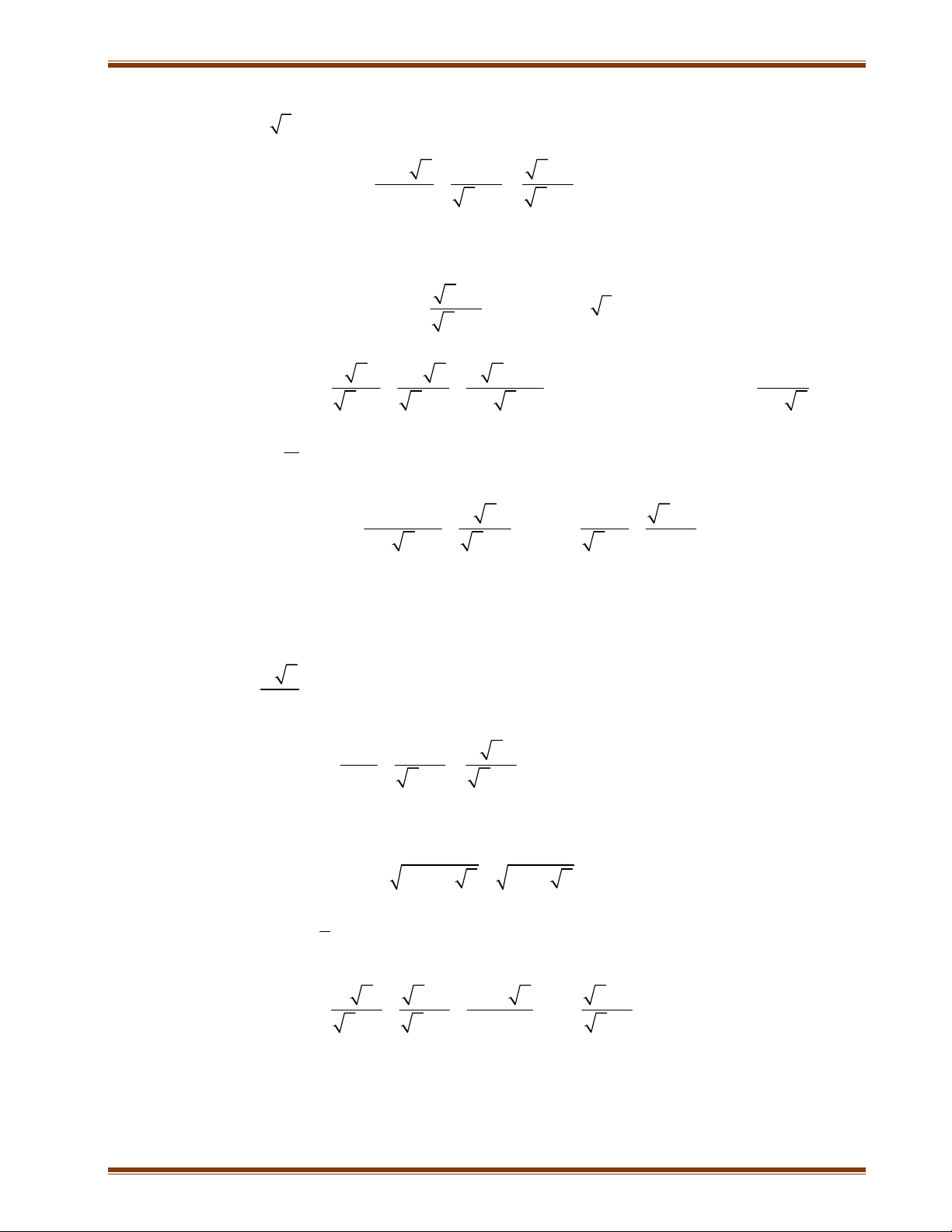
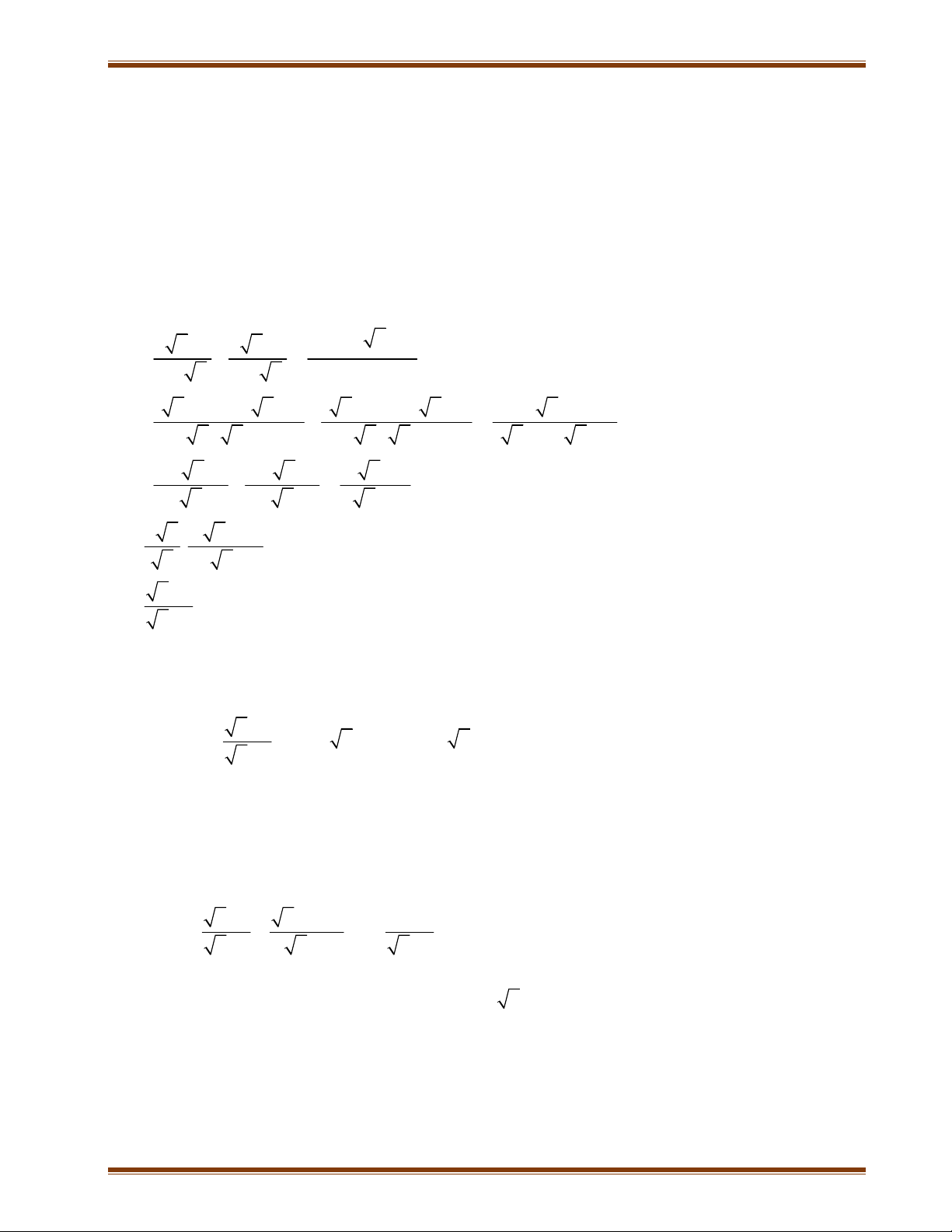
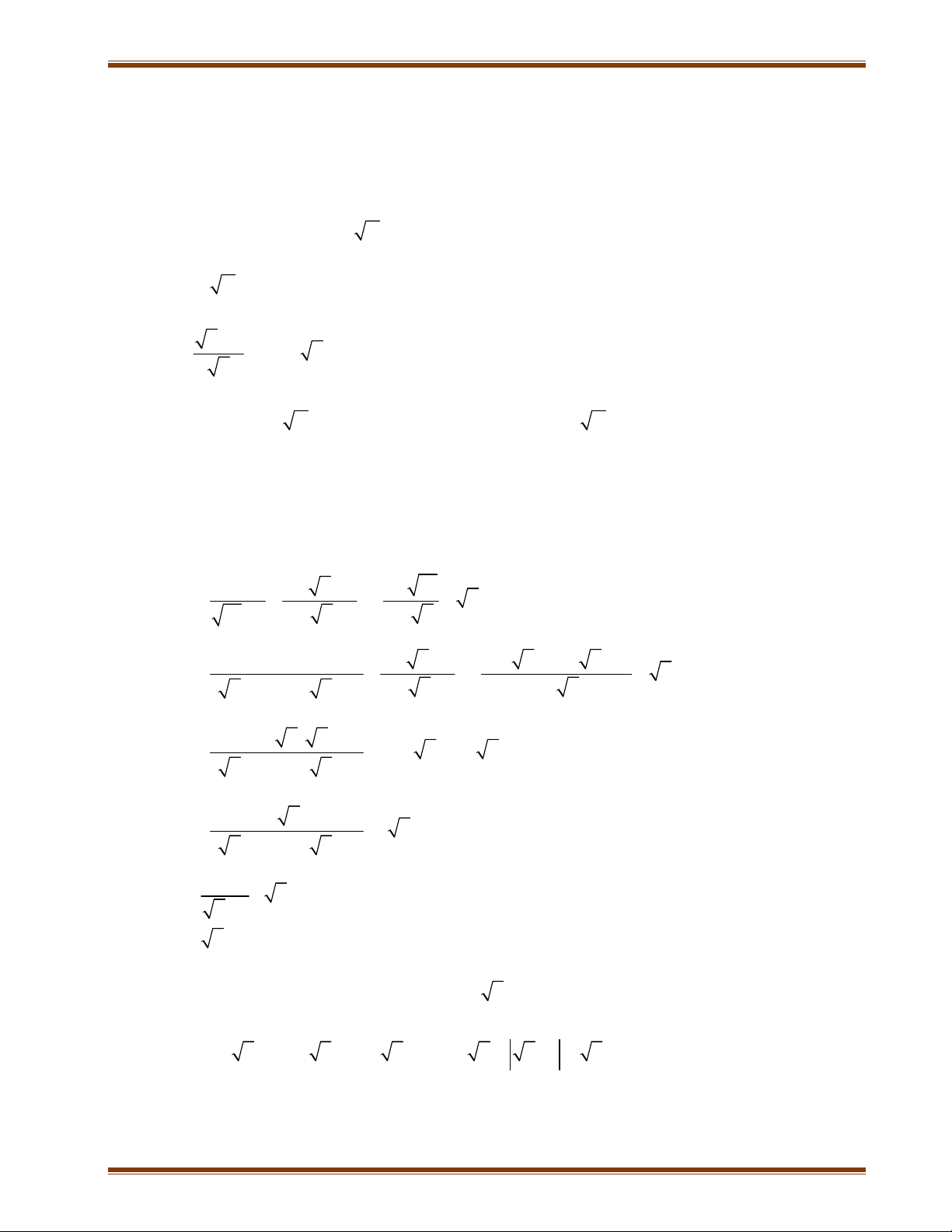
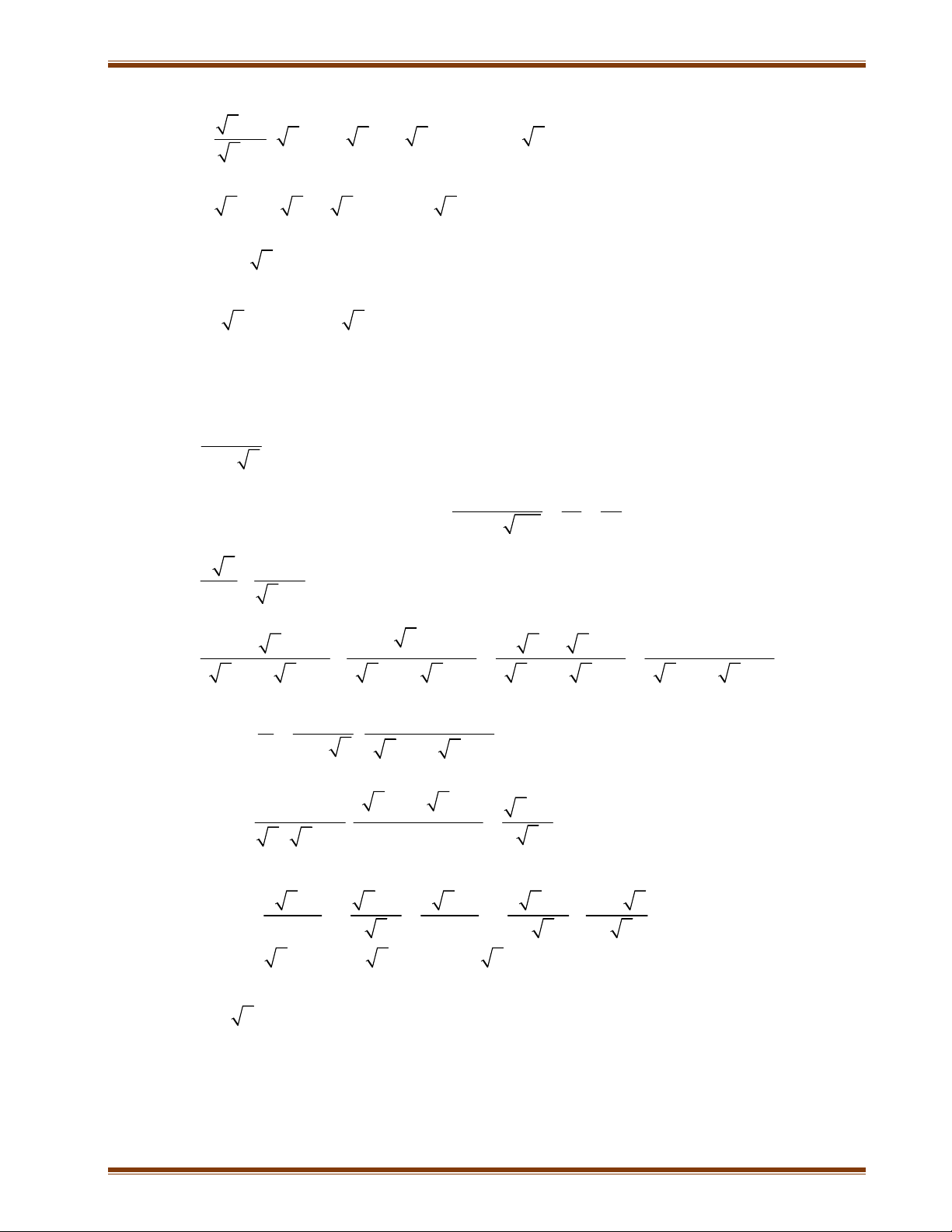
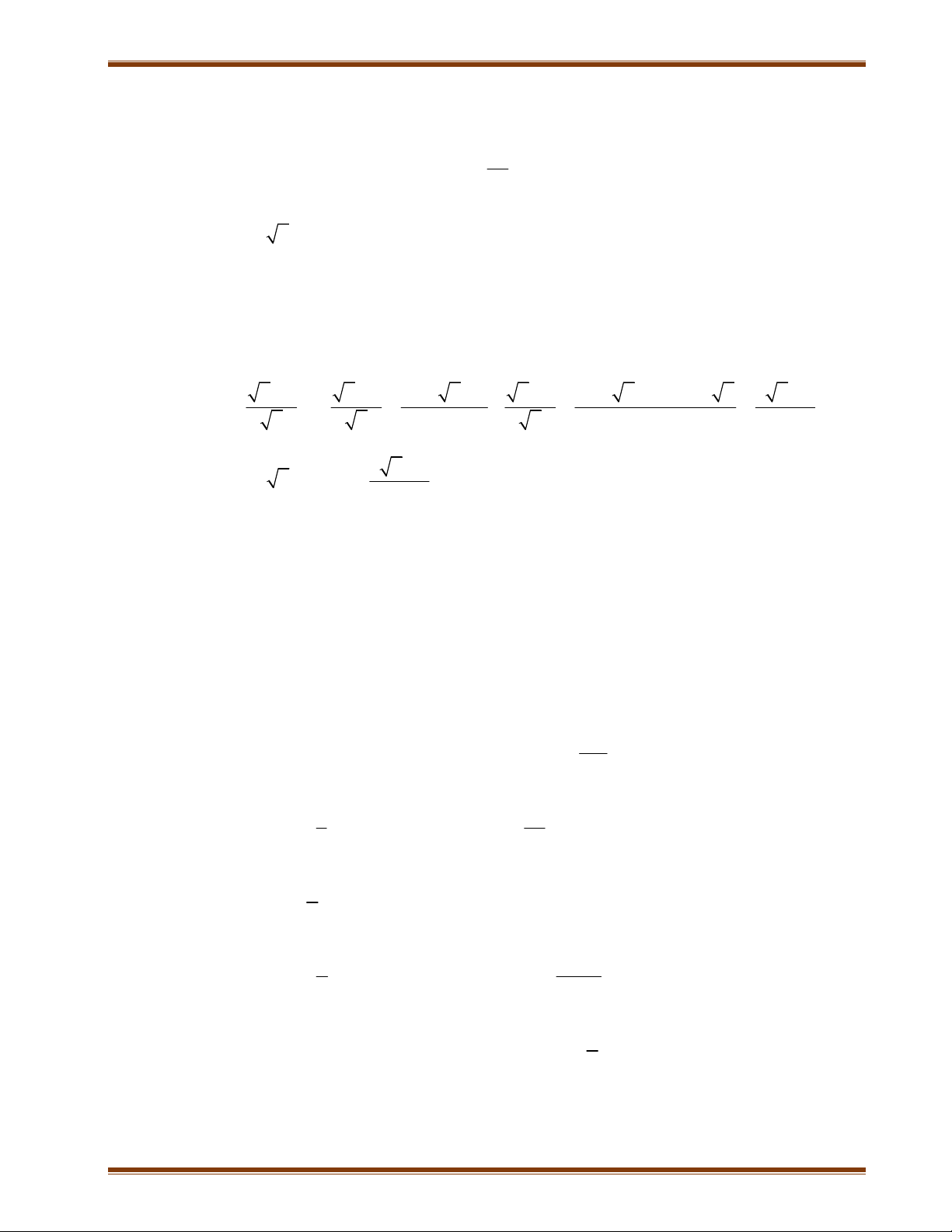
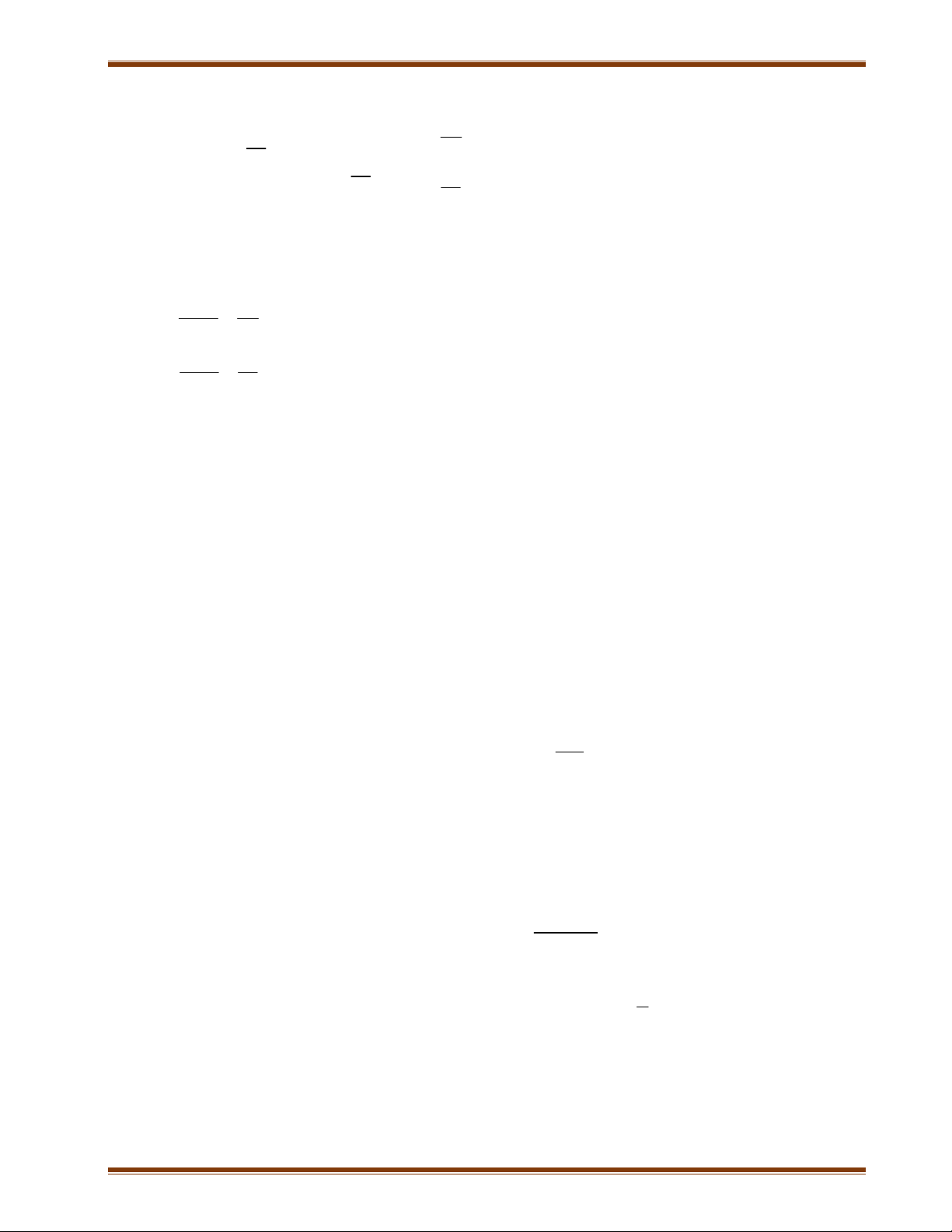
Preview text:

ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI
TRƯỜNG THCS NGÔ SĨ LIÊN
ĐỀ CƯƠNG ÔN TẬP LỚP 9 HKII
Năm học: 2017 – 2018 MÔN TOÁN
DẠNG 1: Biến đổi các biểu thức chứa căn  x x 
x x   2  x  2 x   1 1 1
Bài 1: Cho biểu thức: A     :   x  x x  x x 1   1) Rút gọn A 2) Tìm x để A < 0
3) Tìm x nguyên để A có giá trị nguyên  x 4 x  3   x  2 x  4 
Bài 2: Cho biểu thức: P     :     x 2 2   x x x x 2         1) Rút gọn P
2) Tìm các giá trị của x để P > 0
3) Tính giá trị nhỏ nhất của P 2  2x 1 x   1   x
Bài 3: Cho biểu thức: C       x   2   x 1 x x 1  1       x  1) Rút gọn C
2) Tính giá trị của biểu thức C khi x  8  2 7
3) Tìm giá trị của x để giá trị biểu thức C bằng – 3 1
4) Tìm giá trị của x để giá trị biểu thức C lớn hơn  3
5) Tìm giá trị của x để giá trị biểu thức C nhỏ hơn 2 x  3 1 x
Bài 4: Cho biểu thức A  1 x
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 1
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI
1) Khi x  6  2 5, tính giá trị biểu thức A  15  x 2  x 1
2) Rút gọn biểu thức B     :  x 25 x 5    x  5  
3) Tìm x để biểu thức M  B  A nhận giá trị nguyên. x 1
Bài 5: Tính giá trị của biểu thức A  với x  7  4 3 x  2 x 1 x x  4 3
1) Cho biểu thức B   
. Chứng minh rằng B  x 1 x  2 x  x  2 2  x B 2) Tìm x để P   1 A x  2 x 3 x  3
Bài 6: Cho hai biểu thức A   và B   x  x  2 x  2 x 1 x 1
1) Tìm ĐKXĐ rồi rút gọn biểu thức A
2) Tìm các giá trị của x để B = 1 B x 3) Tìm m để  m có nghiệm. A  x  3 1  x
Bài 7: Cho biểu thức B   :  
với x  0, x  9  x  9 x  3  x  3 1) Rút gọn B
2) Tính giá trị của B khi x  27 10 2  18  8 2 1 3) Chứng minh B  3 2 x x 1 3 11 x x  3
Bài 8: Cho biểu thức A    ; B  x  3 x  3 9  x x 1
a) Tính giá trị B tại x = 36
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 2
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI b) Rút gọn A
c) Tìm số nguyên P để P = A.B là số nguyên. 2
Bài 9: Cho biểu thức B 
với x  0, x  4. Tìm x để B = 2 x  2 x 1
1) Cho biểu thức A  
với x  0, x  4. x  4 x  2 B 2) Tính P  A
3) Tìm x thỏa mãn P  x  
1  x  2 x 1  2x  2 2x  4 2 x 2 6
Bài 10: Cho biểu thức P   và Q  x  9 x  3 x  3 x
a) Tính giá trị Q tại x = 121 b) Rút gọn P Q 2 x 1
c) Tìm giá trị của x để A   P 2 d) So sánh A và 2 A
DẠNG 2: Giải bài toán bằng cách lập phương trình hoặc hệ phương trình
Bài 1: Một người đi xe máy từ A đến B cách nhau 120km với vận tốc dự định trước. 1
Sau khi đi được quãng đường AB người đó tăng vận tốc lên 10km/h trên quãng 3
đường còn lại. Tính vận tốc dự định và thời gian lăn bánh trên đường biết rằng
người đó đến B sớm hơn dự định 24 phút.
Bài 2: Quãng đường AB dài 220km. Hai ô tô khởi hành từ A và B đi ngược chiều
nhau. Nếu cùng khởi hành thì sau 2 giờ chúng sẽ gặp nhau. Nếu xe đi từ A khởi
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 3
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI
hành trước xe kia 1 giờ 6 phút thì hai xe gặp nhau sau khi xe đi từ A đi được 2 giờ
30 phút. Tính vận tốc mỗi xe.
Bài 3: Một ca nô xuôi từ A đến B với vận tốc 30km/h, sau đó lại ngược từ B về A.
Thời gian xuôi ít hơn thời gian ngược 1h 20p. Tính khoảng cách giữa hai bến A và B
biết rằng vận tốc dòng nước là 5km/h và vận tốc riêng của ca nô khi xuôi và ngược là bằng nhau.
Bài 4: Một ca nô chạy trên sông trong 8 giờ, xuôi dòng 81km và ngược dòng 105km.
Một lần khác cũng chạy trên khúc sông đó, ca nô này chạy trong 4h, xuôi dòng
54km và ngược dòng 42km. Hãy tính vận tốc khi xuôi dòng và ngược dòng của ca
nô, biết vận tốc dòng nước và vận tốc riêng của ca nô không đổi.
Bài 5: Một công nhân dự định làm 150 sản phẩm trong một thời gian nhất định. Sau
khi làm được 2h với năng suất dự kiến người đó đã cải tiến các thao tác nên đã tăng
năng suất được 2 sản phẩm mỗi giờ và vì vậy đã hoàn thành 150 sản phẩm sớm hơn
dự kiến 30 phút. Hãy tính năng suất dự kiến ban đầu.
Bài 6: Một đội sản xuất làm 1000 sản phẩm trong một thời gian quy định. Nhờ tăng
năng suất lao động, mỗi ngày đội làm thêm được 10 sản phẩm so với kế hoạch. Vì
vậy, chẳng những đã làm vượt mức kế hoạch 80 sản phẩm mà còn hoàn thành sớm
hơn 2 ngày so với quy định. Tính số sản phẩm đội sản xuất phải làm trong một ngày theo kế hoạch.
Bài 7: Để hoàn thành một công việc hai tổ phải làm chung trong 6h. Sau 2h làm
chung thì tổ hai bị điều đi làm việc khác, tổ một đã hoàn thành nốt công việc còn lại
trong 10h. Hỏi nếu mỗi tổ làm riêng thì sau bao lâu sẽ hoàn thành công việc.
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 4
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI
Bài 8: Một đội xe dự định dùng một số xe cùng loại để chở 120 tấn hàng. Lúc sắp
khởi hành đội được bổ sung thêm 5 xe nữa cùng loại. Nhờ vậy, so với ban đầu, mỗi
xe phải chở ít hơn 2 tấn. Hỏi lúc đầu đội có bao nhiêu xe. Biết khối lượng mỗi xe phải chở như nhau.
Bài 9: Một mảnh đất hình chữ nhật có độ dài đường chéo là 13m và chiều dài hơn
chiều rộng là 7m. Tính chiều dài và chiều rộng của mảnh đất đó.
Bài 10: Cho một số có hai chữ số. Tổng hai chữ số của chúng bằng 10. Tích hai chữ
số ấy nhỏ hơn số đã cho là 12. Tìm số đã cho.
DẠNG 3: Hệ phương trình
mx  y  10
Bài 1: Cho hệ phương trình 2x3y  6 
1) Giải phương trình với m = 1
2) Tìm m để hệ vô nghiệm  2
 mx  y  5
Bài 2: Cho hệ phương trình mx 3y 1 
1) Giải hệ phương trình m = 1
2) Tìm m để hệ có nghiệm (x; y) thỏa mãn x – y = 2
3) Chứng minh rằng hệ phương trình có nghiệm duy nhất (x; y) thì điểm M(x; y)
luôn nằm trên một đường thẳng cố định khi m thay đổi.
(m 1)x  my  3m 1
Bài 3: Cho hệ phương trình 
. Tìm m để hệ có nghiệm duy nhất
2x  y  m  5  mà 2 2
S  x  y đạt giá trị nhỏ nhất.
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 5
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI
x  my  2
Bài 4: Cho hệ phương trình mx y   m 1) Giải hệ khi m = 2
2) Tìm các số nguyên m để cho hệ có nghiệm duy nhất (x; y) với x > 0, y < 0
3) Tìm các số nguyên m để cho hệ có nghiệm duuy nhất (x; y) với x, y là các số nguyên.
x  my  1
Bài 5: Cho hệ phương trình mx y   m
1) CMR hệ có nghiệm duy nhất với mọi m
2) Tìm m để hệ có nghiệm duy nhất sao cho x < 1, y < 1
DẠNG 4: Quan hệ giữa (P) và (d) 3 1
Bài 1: Cho hàm số y  f  x 2  
x có đồ thị (P) và hàm số y 
x  2 có đồ thị (d). 2 2
1) Vẽ (P) và (d) trên cùng hệ trục tọa độ
2) Tìm tọa độ giao điểm của (P) và (d) 3) Không tính, hãy so sánh a) f  2   và f  3  
b) f 1 2 và f  3  2 1 Bài 2: Cho hàm số 2 y   x có đồ thị (P) 2
1) Tìm các điểm A, B thuộc (P) có hoành độ lần lượt bằng – 1 và 2.
2) Viết phương trình đường thẳng AB
3) Viết phương trình đường thẳng song song với AB và tiếp xúc với (P). Tìm tọa độ tiếp điểm.
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 6
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI
Bài 3: Cho parabol P 2 : y  ax 1 1
1) Tìm a biết (P) đi qua điểm A thuộc đường thẳng (d): y  x  có hoành độ 4 2 bằng 2.
2) Tìm giao điểm B còn lại của (d) và (P)
3) Tính diện tích tam giác OAB Bài 4: Cho hàm số 2
y  ax có đồ thị (P) và hàm số y  mx  2m 1 có đồ thị (d)
1) Chứng minh (d) luôn đi qua một điểm M cố định
2) Tìm a để (P) đi qua điểm cố định đó
3) Viết phương trình đường thẳng qua M và tiếp xúc với parabol (P) tại M. 1 3 Bài 5: Cho hàm số 2 y 
x có đồ thị (P) và đường thẳng (d): y  2x  2 2
1) Vẽ (d) và (P) trên cùng hệ trục tọa độ Oxy
2) Tìm tọa độ giao điểm A và B của (d) và (P). Tính chu vi AOB
3) Tìm tọa độ giao điểm C thuộc Ox để chu vi ABC đạt giá trị nhỏ nhất. 1
Bài 6: Cho parabol P 2 : y  x 4
1) Viết phương trình đường thẳng (d) có hệ số góc là k là đi qua M(1,5; - 1)
2) Tìm k để đường thẳng (d) và parabol (P) tiếp xúc nhau
3) Tìm k để đường thẳng (d) và parabol (P) cắt nhau tại hai điểm phân biệt. 2 x 1
Bài 7: Cho hàm số P : y 
và d  : y  x  n 2 2 1) Cho n = 1
a) Vẽ (P) và (d) trên cùng một mặt phẳng tọa độ
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 7
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI
b) Tìm tọa độ giao điểm A và B của (P) và (d)
c) Tính diện tích AOB
2) Tìm n để (P) tiếp xúc với (d)
3) Tìm n để (P) và (d) cắt nhau tại hai điểm
4) Tìm n để (P) và (d) cắt nhau tại hai điểm nằm ở hai phía trục tung.
Bài 8: Cho parabol (P): 2
y  x và đường thẳng y  mx  m 1
1) Tìm m để (P) và (d) cắt nhau tại hai điểm phân biệt A và B
2) Gọi x và x là hoành độ của A và B. Tìm m để x  x  2 1 2 1 2
3) Tìm m để (P) và (d) cắt nhau tại hai điểm nằm cùng bên trái của trục tung. 1 Bài 9: Cho hàm số 2 y 
x có đồ thị là parabol (P), đường thẳng y  mx  2. Tìm m để 2
d cắt (P) tại hai điểm phân biệt có hoành độ x  x mà 2 2
x  x có giá trị nhỏ nhất. 1 2 1 2 Bài 10: Cho hàm số 2
y  x có đồ thị là parabol (P), đường thẳng d: y  mx  m 1.
Tìm m để d cắt parabol (P) tại A và phân biệt với A x ; y , B  x , y mà  y  y nhỏ 1 2  2 2  1 1  nhất.
DẠNG 5: Phương trình bậc hai
Bài 1: Cho phương trình 2
x   m   2 2
3 x  m  3m  2  0, m là tham số
1) Giải phương trình trên khi m = 1
2) Xác định m để phương trình có một nghiệm là 2. Khi đó phương trình còn
một nghiệm nữa, tìm nghiệm đó?
3) CMR phương trình luôn có hai nghiệm phân biệt với mọi m
4) Gọi x , x là hai nghiệm của pt. Tìm m để 2 2 x  x  1 1 2 1 2
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 8
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI
5) Định m để phương trình có nghiệm này bằng 3 nghiệm kia.
Bài 2: Cho phương trình 2
x  2m  
1 x  m  0 , m là tham số
1) CMR phương trình luôn có hai nghiệm phân biệt x , x với mọi m 1 2 1
2) Với m  0 . Hãy lập phương trình ẩn y có hai nghiệm là y  x  và 1 1 x2 1 y  x  2 2 x1
3) Xác định m để phương trình có hai nghiệm x , x thảo mãn x  2x  3 1 2 1 2
4) Tìm m để phương trình có hai nghiệm cùng âm
Bài 3: Cho phương trình 2
x  2k  3 x  2k 1  0, k là tham số 1
1) Giải phương trình khi k  2
2) Tìm k để phương trình có một nghiệm là 3, khi đó phương trình còn một
nghiệm nữa, tìm nghiệm ấy.
3) CMR phương trình luôn có hai nghiệm x , x với mọi k 1 2
4) CMR giữa tổng và tích các nghiệm có một sự liên hệ không phụ thuộc k? 1 1 3
5) Tìm k để phương trình x , x thỏa mãn    2 1 2 x x x x 1 2 1 2
6) Tìm k để tổng bình phương các nghiệm có giá trị nhỏ nhất.
Bài 4: Cho phương trình 2
x  2m  
1 x  m  4  0, m là tham số
1) Giải phương trình khi x = - 5
2) CMR phương trình luôn có nghiệm x , x với mọi m 1 2
3) Tìm m để phương trình có hai nghiệm trái dấu
4) Tìm m để phương trình có hai nghiệm dương
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 9
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI
5) CMR biểu thức A  x 1 x  x 1 x không phụ thuộc m 1  2  2  1 
6) Tính giá trị của biểu thức x  x 1 2
Bài 5: Cho phương trình 2
x  3(m 1)x  m  3  0, m là tham số
1) CMR phương trình luôn có nghiệm với mọi m
2) Tìm hệ thức liên hệ giữa hai nghiệm không phụ thuộc m
3) Xác định m để phương trình có hai nghiệm bằng nhau về giá trị tuyệt đối và trái dấu nhau.
Bài 6: Cho phương trình 2
x  2m  2 x  2m  5  0, m là tham số
1) CM phương trình luôn có nghiệm với mọi m
2) Gọi x , x là hai nghiệm của phương trình. Tìm m để B  x (1 x )  x 1 x  4 1 2 2  2  1 2
3) Tìm hệ thức liên hệ giữa hai nghiệm không phụ thuộc vào m.
Bài 7: Cho phương trình 2
x  4m  
1 x  2 m  4  0 m là tham số
1) Tìm m để phương trình có hai nghiệm x , x thỏa mãn điều kiện x  x  17 1 2 2 1
2) Tìm m để biểu thức A   x  x 2 có giá trị nhỏ nhất 1 2
3) Tìm hệ thức liên hệ giữa hai nghiệm không phụ thuộc vào x.
Bài 8: Cho phương trình 2
x  2m  
1 x  2m 1  0, m là tham số. Tìm m để phương
trình có hai nghiệm x , x là độ dài hai cạnh góc vuông của một tam giác vuông có 1 2 cạnh huyền bằng 5.
Bài 9: Cho phương trình 4 2
x  2x  m  2  0 , m là tham số
1) Giải phương trình khi m = - 1
2) Tìm m để phương trình có 4 nghiệm phân biệt
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 10
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI
Bài 10: Cho phương trình 2
x  m   2 2
1 x  m 1  0, m là tham số. Tìm m là phương
trình có nghiệm duy nhất. DẠNG 6: Hình học
Bài 1: Cho đường tròn (O) và điểm M nằm ngoài (O). Từ M kẻ hai tiếp tuyến MA,
MB đến (O) (A, B là tiếp điểm). Qua M kẻ cát tuyến MNP (MN < MP) đến (O) sao
cho tia MP nằm giữa hai tia MA và MO. Gọi K là trung điểm của NP
1) Chứng minh rằng các điểm M, A, K, O, B cùng thuộc một đường tròn
2) Chứng minh tia KM là phân giác của  AKB
3) Gọi Q là giao điểm thứ hai của đường thẳng BK với đường tròn (O). Chứng minh rằng AQ // NP.
4) Gọi H là giao điểm của AB và MO. Chứng minh rằng 2
MA  MH.MO  MN.MP
5) Chứng minh rằng 4 điểm N, H, O, P cùng thuộc một đường tròn
6) Gọi E là giao điểm của AB và KO. Chứng minh rằng 2
AB  4HE.HF (F là giao điểm của AB và NP).
7) Chứng minh rằng KEMH là tứ giác nội tiếp. Từ đó chứng tỏ rằng OK.OE không đổi.
8) Gọi I là giao điểm của đoạn thẳng MO với đường tròn (O). Chứng mỉnh ằng I
là tâm đường tròn nội tiếp MAB 9) Chứng minh   NHA  PHA
10) Chứng minh rằng KE là phân giác góc ngoài của .
AKB Từ đó suy ra AE.BF = AF.BE
11) Chứng minh khi cát tuyến MNP thay đổi thì trọng tâm G của NAP luôn
chạy trên một đường tròn cố định.
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 11
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI
12) Nếu MO = 2R. Tính diện tích hình quạt giới hạn bởi hai bán kính OA, OB và cung nhỏ AB.
Bài 2: Cho đường tròn (O) bán kính R có hai đường kính AB và CD vuông góc với
nhau. Trên đoạn thẳng MA lấy điểm M (M khác O). CM cắt (O) tại N. Đường thẳng
vuông góc với AB tại M cắt tiếp tuyến tại N của đường tròn ở P. Chứng minh:
1) Tứ giác OMNP nội tiếp
2) Tứ giác CMPO là hình bình hành
3) CM.CN không phụ thuộc vào vị trí của điểm M
4) Khi M di chuyển trên đoạn thẳng AB thì tâm đường tròn nội tiếp CND di
chuyển trên một cung tròn cố định nào.
Bài 3: Cho ba điểm A, B, C trên một đường thẳng theo thứ tự ấy và đường thẳng (d)
vuông góc với AC tại A. Vẽ đường tròn đường kính BC, trên đó lấy điểm M bất kì.
Tia CM cắt đường thẳng d tại D; tia AM cắt đường tròn tại điểm thứ hai N; tia DB
cắt đường tròn tại điểm thứ hai P
1) Chứng minh rằng tứ giác ABMD nội tiếp được
2) Tứ giác APND là hình gì? Tại sao?
3) Chứng minh rằng CM.CD không phụ thuộc vị trí của M
4) Chứng minh trọng tâm G của MAC chạy trên một đường tròn cố định khi M di động.
Bài 4: Cho đường tròn (O; R) với dây BC cố định (BC không qua O). Gọi A là điểm
chính giữa cung nhỏ BC. Điểm E thuộc cung lớn BC. Nối AE cắt BC tại D. Hạ
CH  AE tại H; CH cắt BE tại M. Gọi I là trung điểm của BC
1) Chứng minh bốn điểm A, I, H, C thuộc một đường tròn
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 12
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI
2) Chứng minh khi E chuyển động trên cung lớn BC thì tích AD.AE không đổi
3) Chứng minh đường tròn ngoại tiếp BED tiếp xúc với AB
4) Tìm vị trí của E để diện tích MAC lớn nhất
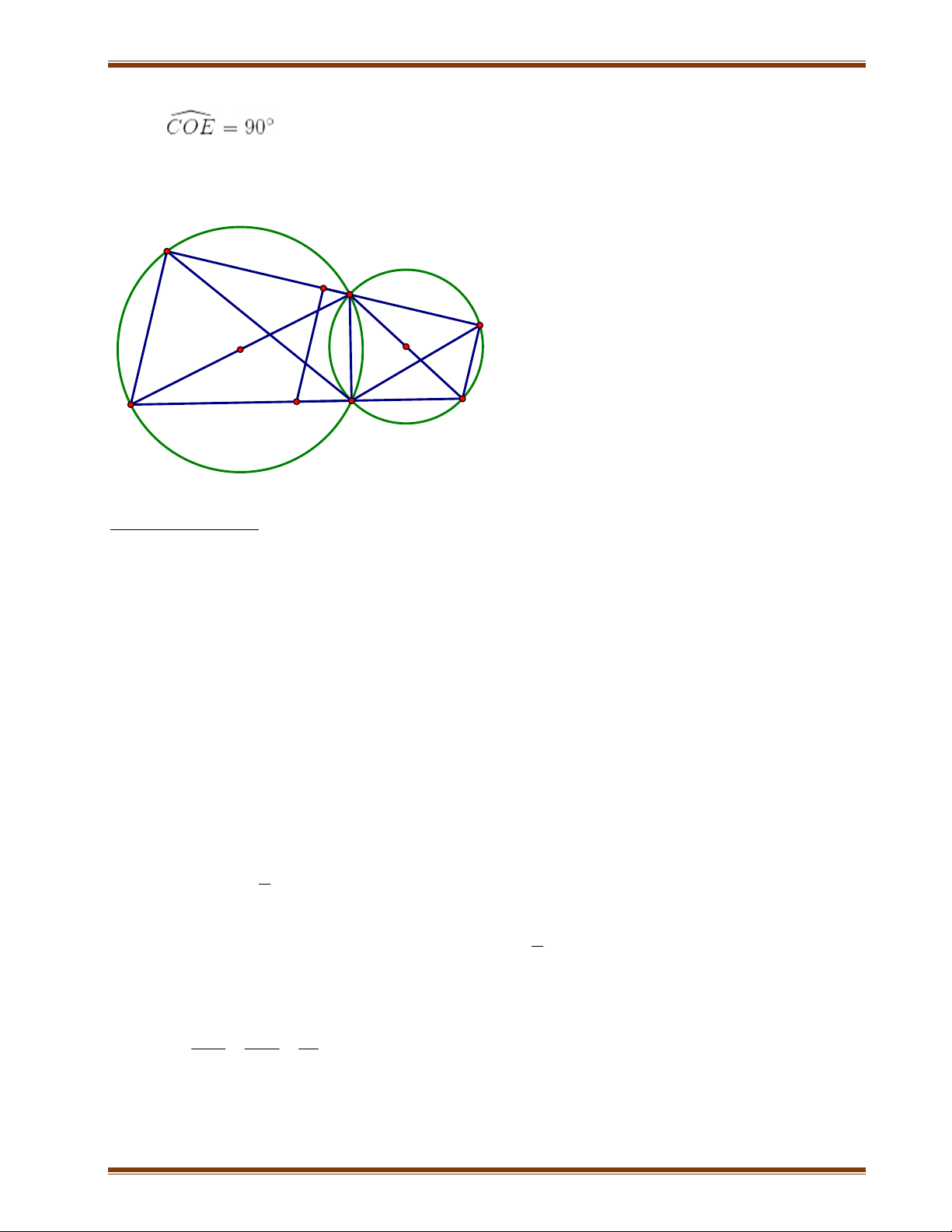
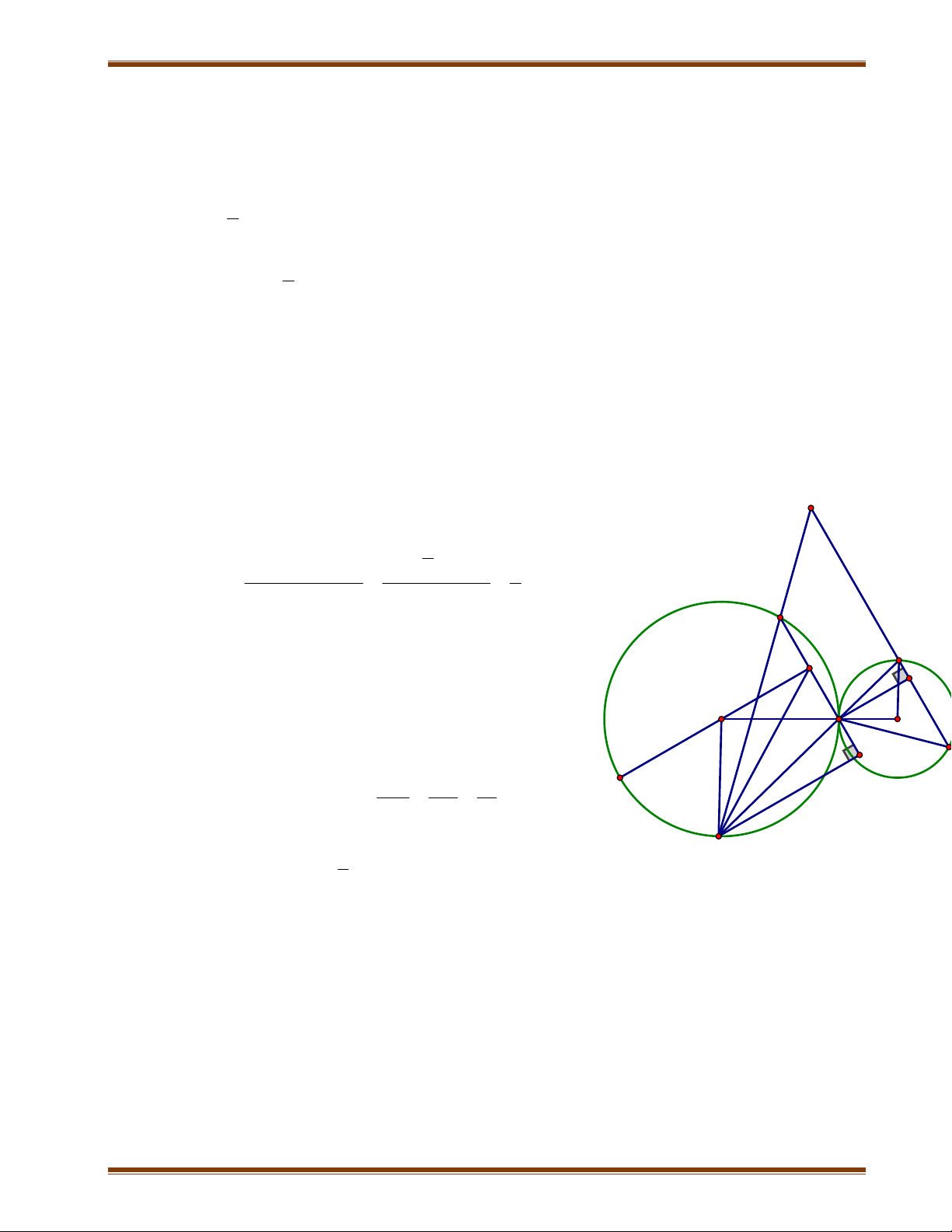
Bài 5: Cho hai đường tròn (O; R) và (O’; R’) cắt nhau tại A và H (O và O’ ở hai phía
của AH). Vẽ các đường kính AOB và AO’C của hai đường tròn. Một đường thẳng d
đi qua A cắt đường tròn (O) tại M, cắt đường tròn (O’) tại N.
1) Chứng minh ba điểm B, H, C thẳng hàng HM
2) Chứng minh rằng khi đường thẳng d thay đổi thì tỉ số không đổi HN
3) Gọi I, K lần lượt là trung điểm của MN và BC. Chứng minh bốn điểm A, H, I,
K thuộc một đường tròn
4) Xác định vị trí của đường thẳng d để diện tích HMN lớn nhất.
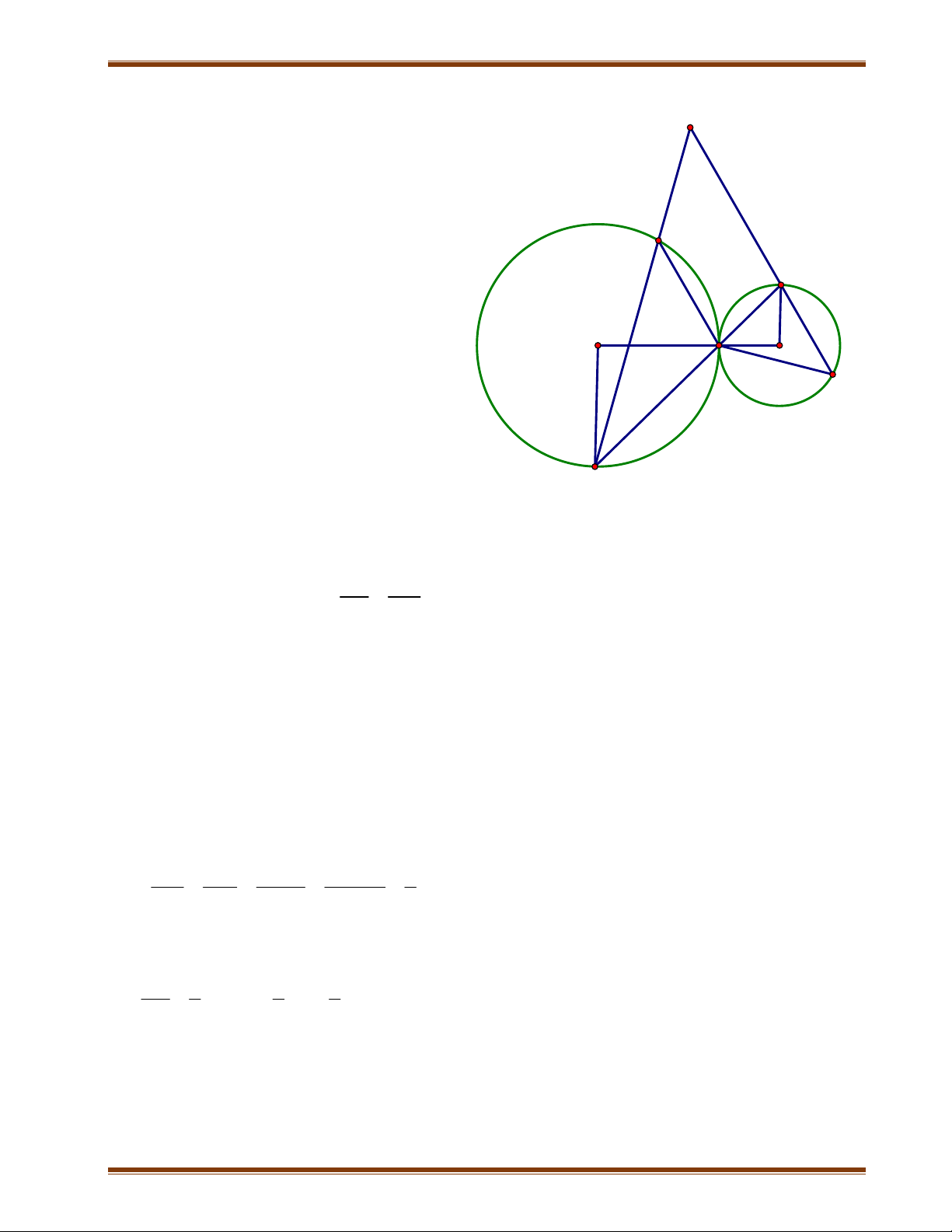
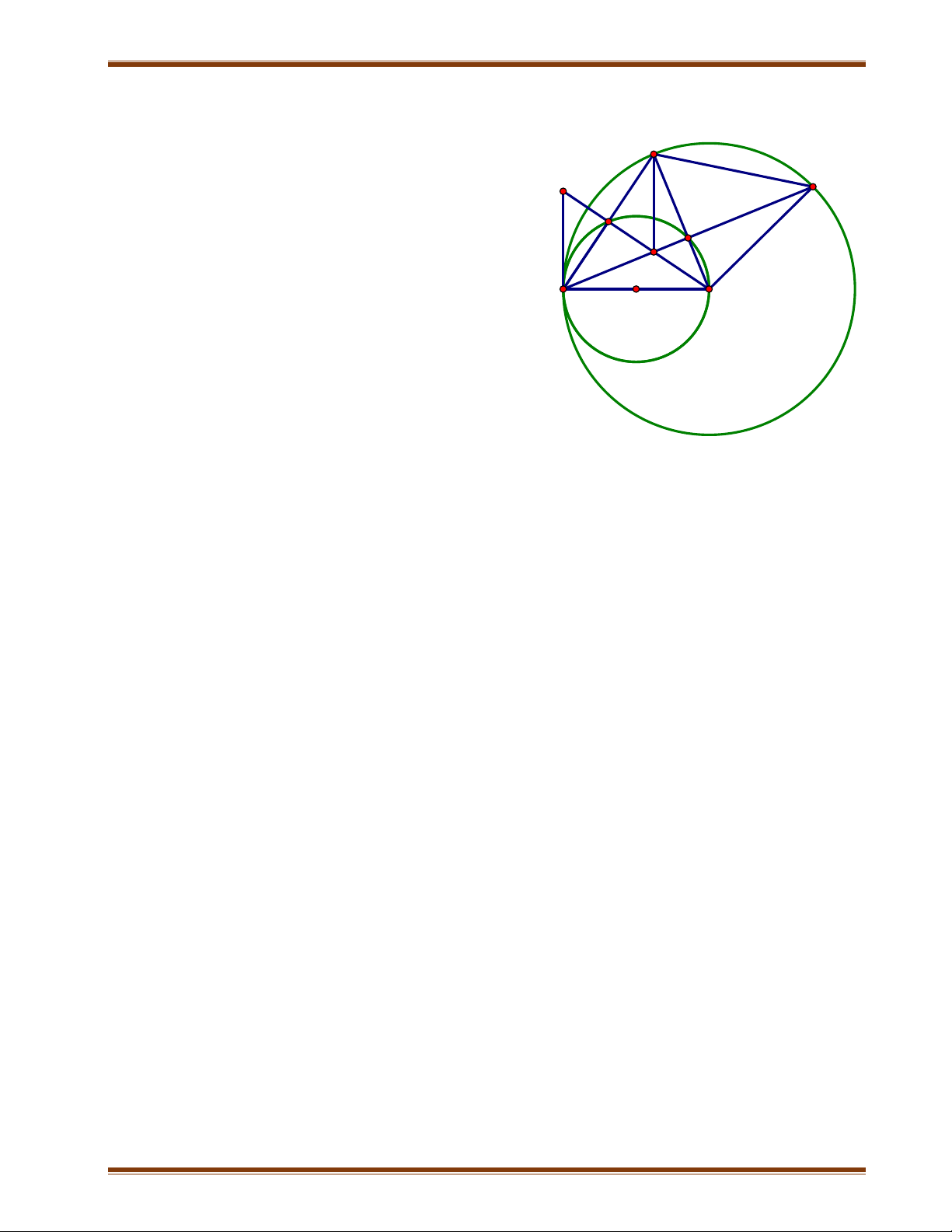
Bài 6: Cho hai đường tròn (O; R) và (O’; R’) tiếp xúc ngoài tại A (R = 2R’). Điểm B
thuộc đường tròn (O; R) sao cho AB = R. Điểm M thuộc cung lớn AB của đường
tròn (O; R) sao cho MA  M .
B Nối MA cắt đường tròn (O’; R’) tại N. Từ N kẻ đường
thẳng song song với AB cắt đường tròn (O’; R’) tại E, cắt MB tại F.
1) Chứng minh AOM đồng dạng với AO ' N
2) Chứng minh rằng độ dài đoạn NF không đổi khi M chuyển động trên cung
lớn AB của đường tròn (O; R).
3) Chứng minh ABFE là hình thang cân
4) Tìm vị trí của M để diện tích tứ giác ABFN lớn nhất.
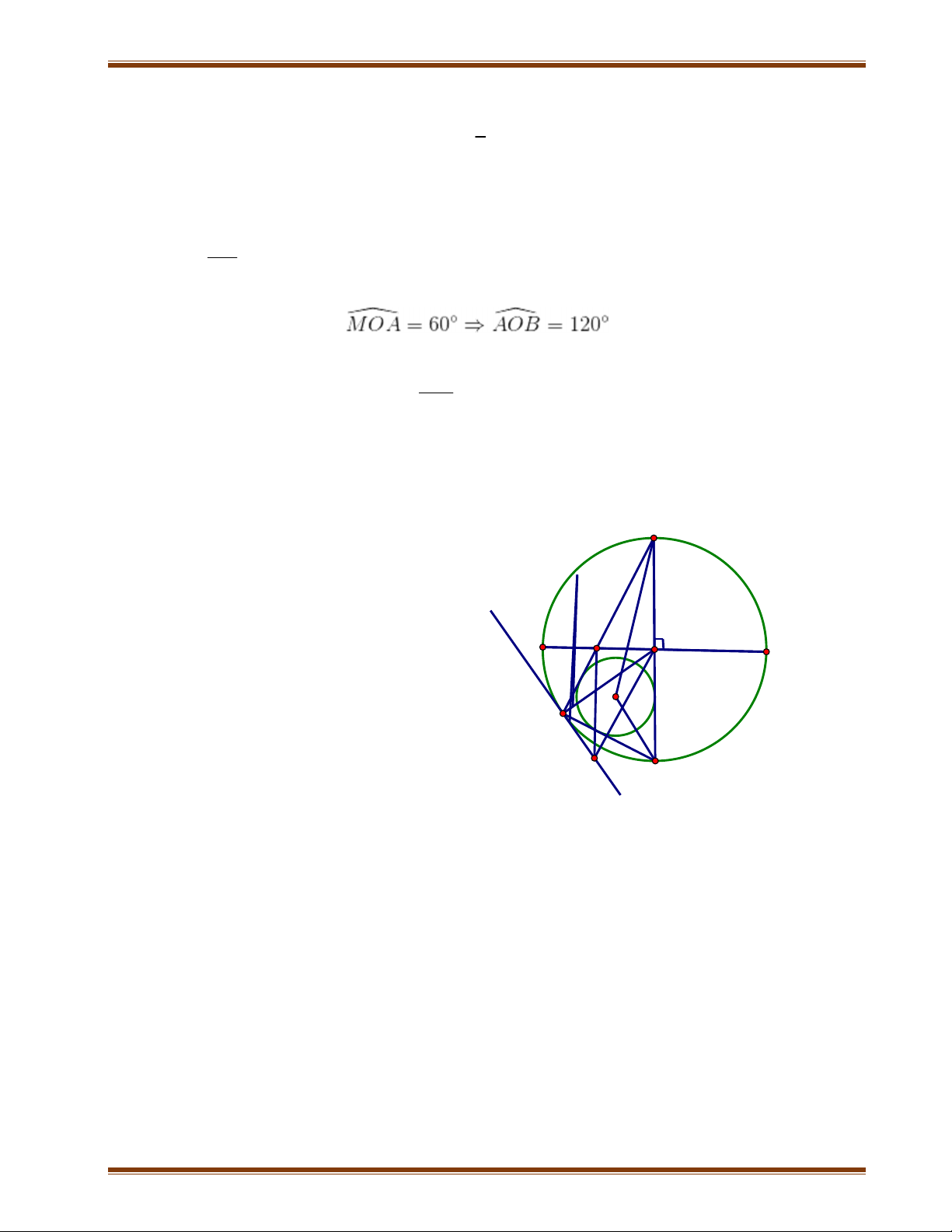
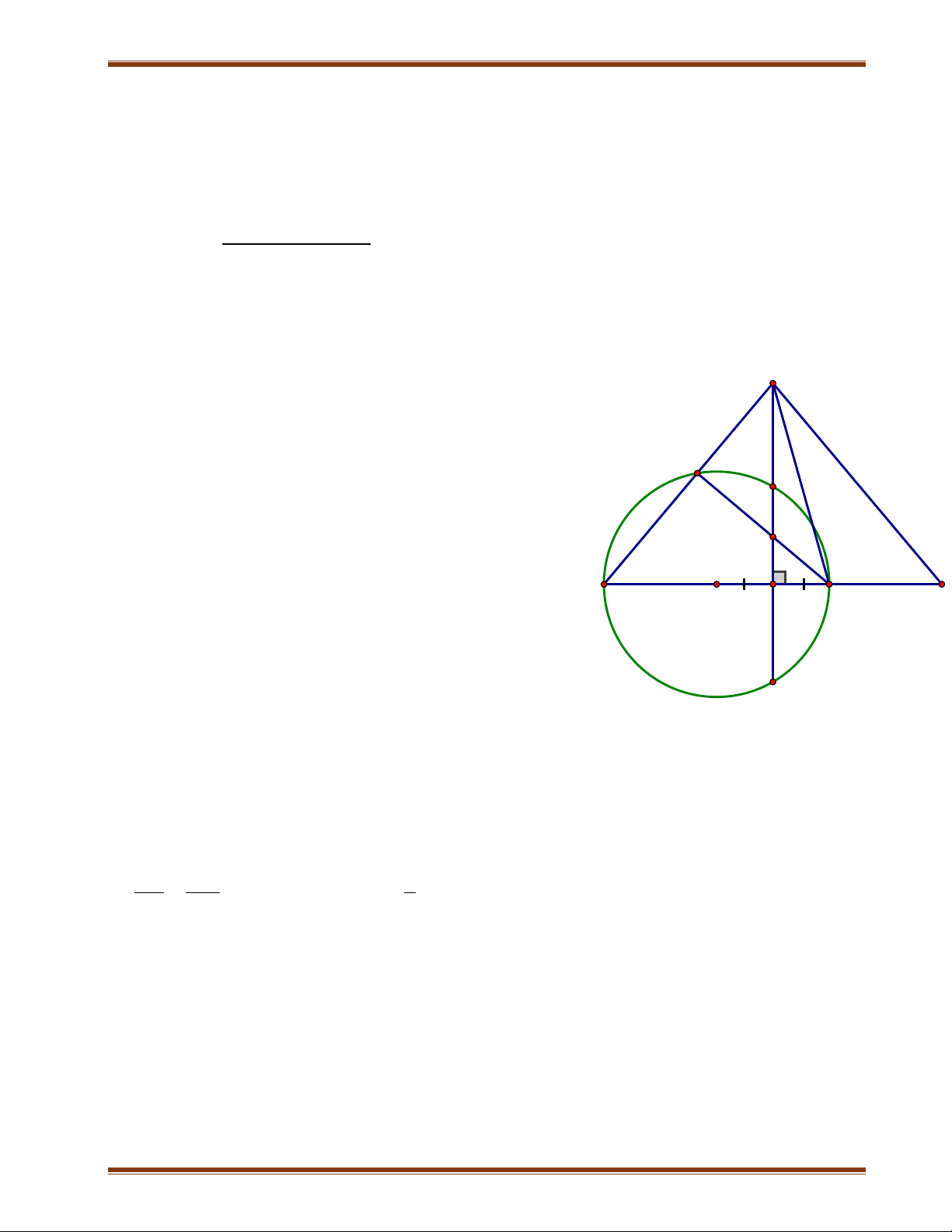
Bài 7: Cho đường tròn (O; R), đường kính AB cố định. Gọi M là trung điểm của
đoạn OB. Dây CD vuông góc với AB tại M. Điểm E chuyển động trên cung lớn CD
(E khác A). Nối AE cắt CD tại K. Nối BE cắt CD tại H.
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 13
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI
1) Chứng minh bốn điểm B, M, E, K thuộc một đường tròn
2) Chứng minh AE.AK không đổi
3) Tính theo R diện tích hình quạt tròn giới hạn bởi OB, OC và cung nhỏ BC
4) Chứng minh tâm I của đường tròn ngoại tiếp BHK luôn thuộc một đường
thẳng cố định khi điểm E chuyển động trên cung lớn CD.
Bài 8: Cho nửa đường tròn (O; R) đường kính AB. Điểm M thuộc nửa đường tròn.
Gọi H là điểm chính giữa cung AM. Tia BH cắt AM tại I. Tiếp tuyến của nửa đường
tròn tại A cắt BH tại K. Nối AH cắt BM tại E.
1) Chứng minh BAE là tam giác cân. Chứng minh 2
KH .KB  KE
2) Đường tròn tâm B, bán kính BA cắt AM tại N. Chứng minh tứ giác BIEN nội tiếp
3) Tìm vị trí của M để   90o MKA
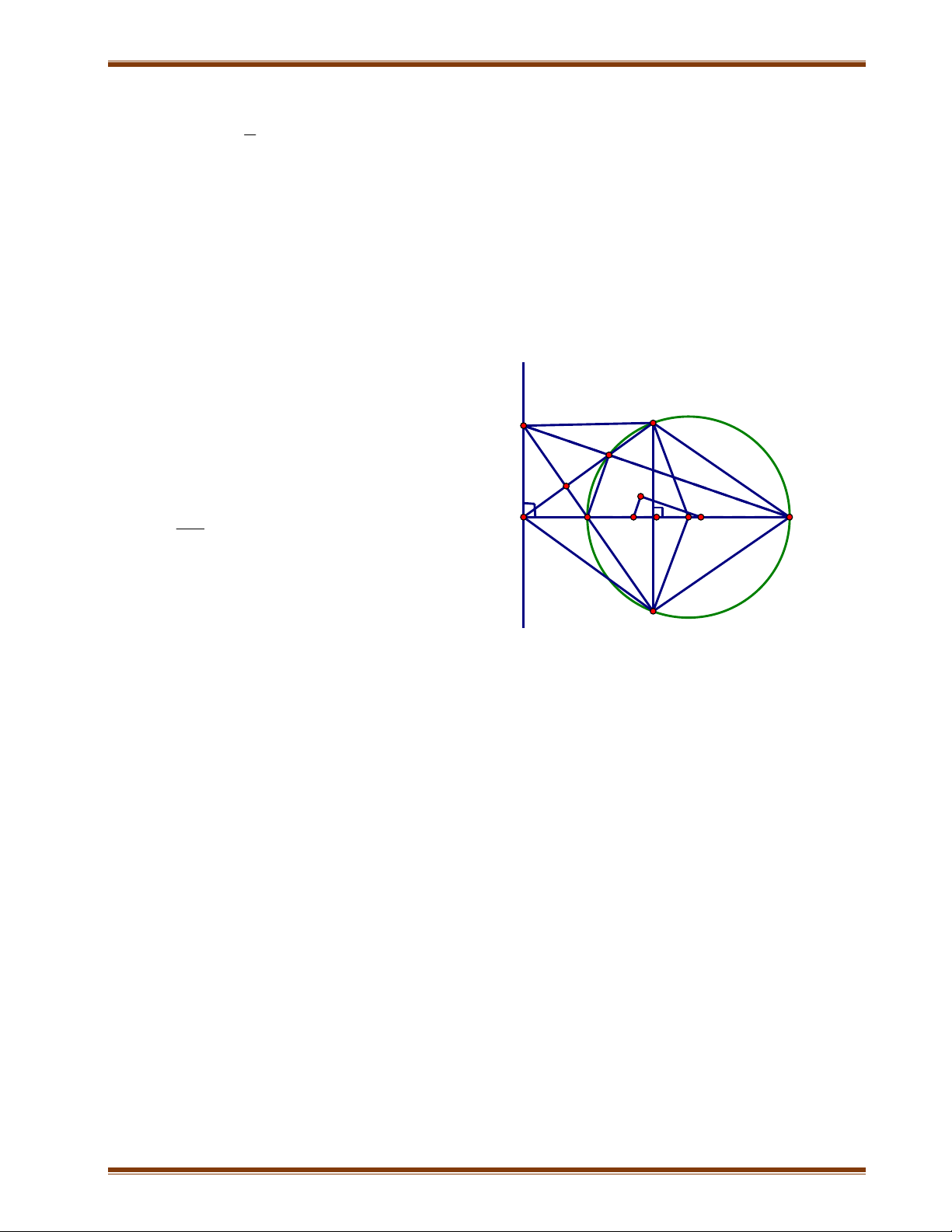
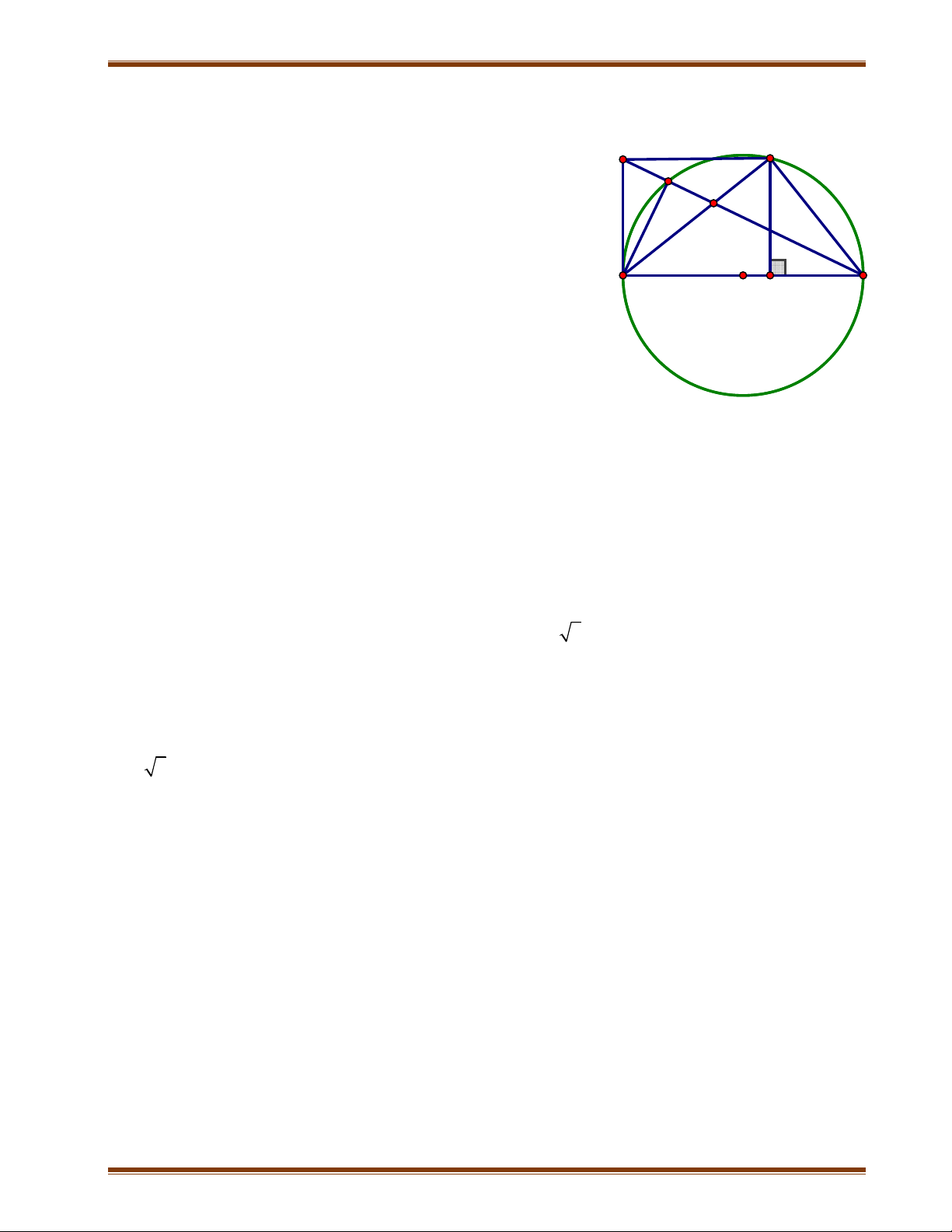
Bài 9: Cho đường tròn (O; R) đường kính AB. Điểm H thuộc đoạn OB, H khác O và
B. Dây CD vuông góc với AB tại H. Đường thẳng d tiếp xúc với đường tròn tại A.
Nối CO và DO cắt đường thẳng d tại M và N. Các đường thẳng CM và DN cắt
đường tròn (O) tại E và F.  E  C, F  D
1) Chứng minh MNFE là tứ giác nội tiếp 2) Chứng minh ME.MC = NF.ND
3) Tìm vị trí của H để AEOF là hình thoi
4) Lấy K đối xứng với C qua A. Gọi G là trọng tâm KA .
B Chứng minh rằng khi
H chuyển động trên đoạn OB thì G thuộc một đường tròn cố định.
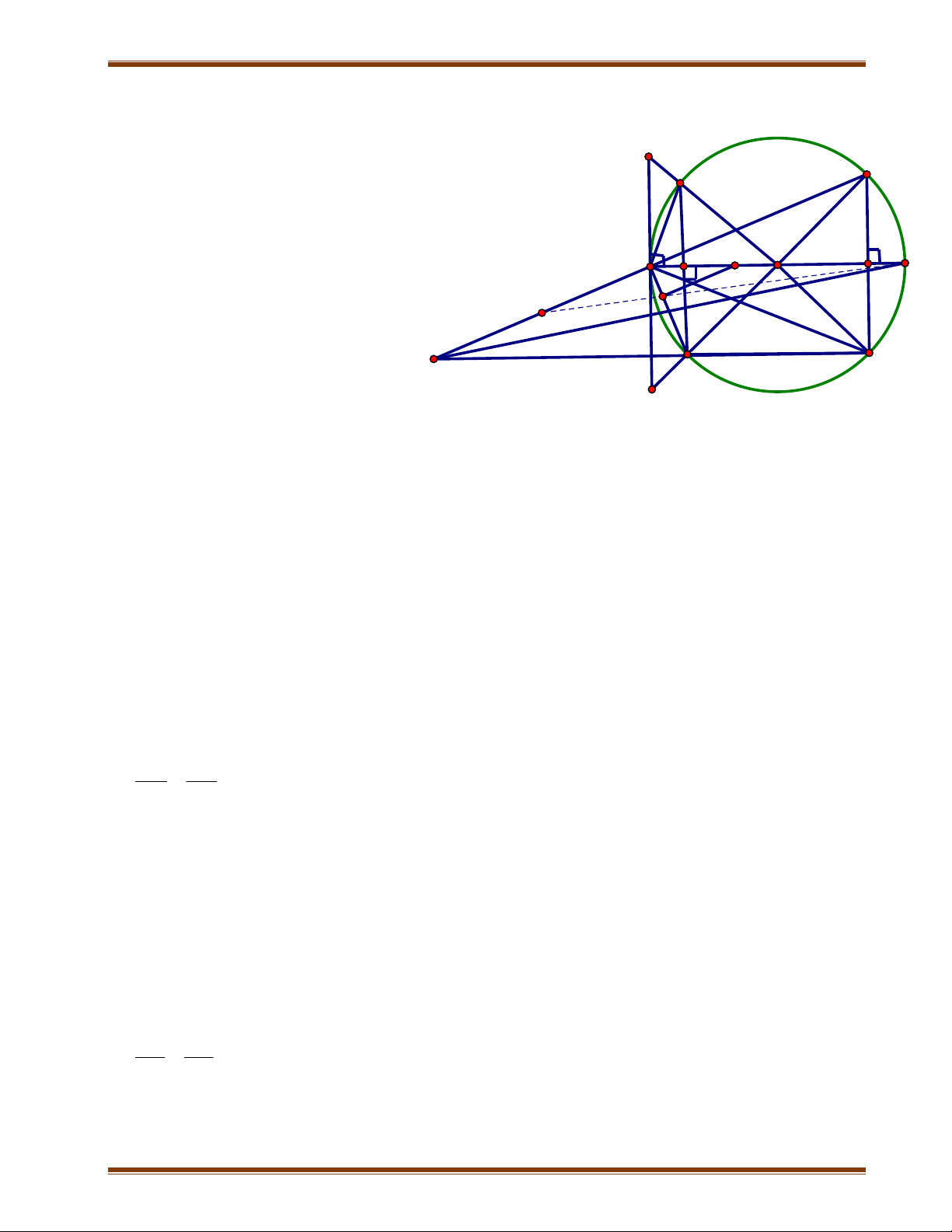
Bài 10: Cho ABC có hai đường cao BE, CF cắt nhau tại H. Gọi E’ là điểm đối xứng
với H qua AC, F’ là điểm đối xứng với H qua AB. Chứng minh
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 14
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI
1) Tứ giác BCE’F’ nội tiếp đường tròn (O)
2) Năm điểm A, F’, B, C, E’ cùng thuộc một đường tròn
3) AO và EF vuông góc với nhau
4) Khi A chạy tên (O) thì bán kính đường tròn ngoại tiếp AEF không đổi.
DẠNG 7: Một số bài nâng cao
Bài 1: Giải các phương trình sau
Bài 2: Giải các hệ phương trình sau
Bài 3: Cho đường thẳng y  m  
1 x  2. Tìm m để khoảng cách từ gốc tọa độ O tới
đường thẳng đó lớn nhất.
Bài 4: Cho parabol  P 2
: y  x và đường thẳng d  : y  x  2 . Gọi A và B là hai giao
điểm của (d) và (P). Tìm tọa độ điểm C thuộc cung AB của (P) để diện tích ABC
đạt giá trị lớn nhất.
Bài 5: Cho 4 số a, b, c, d bất kỳ. Chứng minh rằng
a c2 b d 2 2 2 2 2   
 a  b  c  d bc ca ab
Bài 6: Cho a, b, c > 0. Chứng minh  
 a  b  c a b c
Bài 7: Cho c > 0 và a,b  .
c Chứng minh c a  c  c b  c  ab
Bài 8: Cho a,b  0 và 2 2
a  b  2. Tìm giá trị lớn nhất của biểu thức
P  a 3a a  2b  b 3b b  2a a  b
Bài 9: Cho a,b  0 . Tìm giá trị nhỏ nhất của biểu thức P  a3ab  b3ba
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 15
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI
Bài 10: Giả sử n là một số tự nhiên khác không, chứng minh 1 1 1 1    ...   2 2 3 2 4 3 (n 1) n
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 16
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI HƯỚNG DẪN GIẢI DẠNG 1
Bài 1: ĐKXĐ: x  0; x  1 1) Rút gọn A:  x x 
x x   2 x  2 x   1 1 1 A     :   x  x x  x x 1   2
 ( x 1).(x  x 1) ( x 1).(x  x 1)  2.( x 1) A     :  x.( x 1) x.( x 1)   
( x 1).( x 1)  
 x  x 1 x  x 1 2( x 1) A     :   x x x 1   2 x x 1 A  . x 2.( x 1) x 1 A  x 1 2) Tìm x để A  0 x 1 Để A  0 thì  0 
x 1  0 (vì x 1  0 )  x  1 x 1
Kết hợp điều kiện x  0; x  1 ta có: Với 0  x  1 thì A < 0.
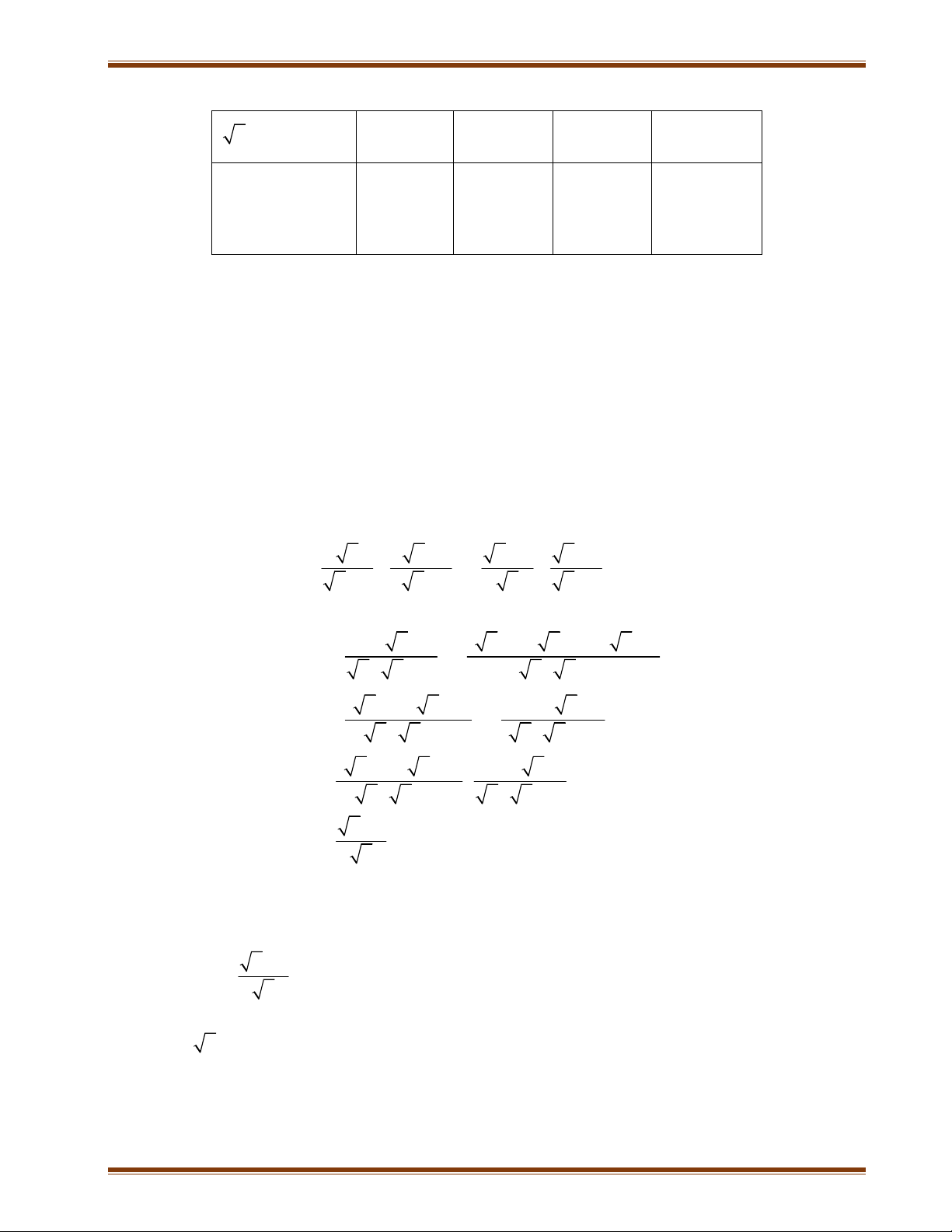
3) Tìm x nguyên để A có giá trị nguyên. x 1 x 1 2 2 Ta có: A    1 x 1 x 1 x 1
Với x nguyên để A nhận giá trị nguyên thì x - 1U (2)
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 17
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI x 1 1 1 2 2 x 4 (TM) 0(KTM) 9 (TM) Vô nghiệm Vậy x 4, 
9 thì A nhận giá trị nguyên.
Bài 2: ĐKXĐ: x  0; x  4; x  1 1) Rứt gọn P:  x 4 x  3   x  2 x  4  P     :     x 2 2   x x x x 2        
 x  4 x  3   ( x  2)( x  2)  x  4  P    :    x.( x 2)   x.( x 2)       
 ( x 1).( x  3)   x  4  x  4  P    :    x.( x 2)   x.( x 2)       
( x 1).( x  3) x  x P  : x.( x  2) x.( x  2) x  3 P  x
2) Tìm các giá trị của x để P > 0. x  3 P  0 thì  0 x  x  3  0  x  9
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 18
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI
Kết hợp điều kiện ta có: Với x > 9 thì P > 0
c) Tìm giá trị nhỏ nhất của P
Ta có P có nghĩa khi x  3   0 
x  3  0  x  9 x
Với x  9 thì P  0 . Dấu “=” xảy ra khi x = 9. P có giá trị nhỏ nhất bằng 0
Bài 3: ĐKXĐ: x  0; x  1 1) Rút gọn C: 3  2x 1 x   1   x C    .  x   3   x 1 x x 1  1       x    2x 1 x
 (1 x).(x  x 1)    C   .  x   
 ( x 1).x  x   1 x  x 1  1  x     
2x 1 x ( x 1)   C 
.x  x 1 x   ( x 1).x x 1         x  x 1   C  . x  2 1  ( x 1).x x 1       1 C  . x  2 1 x 1 C  x 1
2) Tính giá trị của biểu thức C khi x  8  2 7 x         2 8 2 7 7 2 7 1 7 1  x  7 1  7 1
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 19
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI
Vậy C  x 1  7 11  7  2
3) Tìm giá trị của x để giá trị biểu thức C bằng 3 C  3   x 1  3  
x  3 (vô nghiệm)
Vậy không có giá trị nào của x để giá trị biểu thức C  3 1 
4) Tìm giá trị của x để giá trị biểu thức C lớn hơn 3 1  1  2 4 C   x 1   x   x  3 3 3 9 4 1 
Kết hợp điều kiện ta có x  ; x  1 thì C  9 3
5) Tìm giá trị của x để C nhỏ hơn 2 x  3
Ta có C  2 x  3  x 1  2 x  3  4
  2 x (nghiệm đúng với x  0; x  1)
Vậy với mọi x  0; x  1 thì C nhỏ hơn 2 x  3
Bài 4: 1) ĐKXĐ: x  0 Khi x      2 6 2 5 5 1  x  5 1 (t/m) 1  5   1 5 2  5
Thay vào biểu thức A ta được A   1  5   1 5 Vậy…..
2) ĐKXĐ: x  0; x  25 Rút gọn B
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 20
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI  15  x 2  x 1 B     :  x 25 x 5    x  5  
15  x  2( x  5)  x  5 B  .   x  25 x 1   1 B  x 1
3) Với x  0; x  25 . x
Ta có M  B – A  1 x Chứng minh 0  M  1 M  Z  M  0
 x  0 (t / m)
Vậy x = 0 thì M nhận giá trị nguyên Bài 5: x 1
1) Tính giá trị biểu thức A  khi x  7  4 3 x  2
ĐKXĐ: x  0; x  4 Khi x      2 7 4 3 3 2  x  3  2 (t/m) 3   1 3 2 3 1 
Thay vào biểu thức A ta được A    3 1 2  3 1 3 Vậy…..
2) ĐKXĐ: x  0; x  4
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 21
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI Rút gọn B x 1 x x  4 B    x 1 x  2 x  x  2
x ( x  2)  (1 x )( x 1)  ( x  4) B 
( x 1)( x  2) 3 B  2 x
3) Với x  0; x  1; x  4 . Ta có : B P   1 A 3 1 x P  :  1  2  x 1 x 3 1 x
(2  x )(1 x ) P  .   0 2  x 1 x
(2  x )(1 x ) x  5 P   0
(2  x )(1 x )
Vì x  0; x  1; x  4  x + 5 > 0
 (2  x)(1 x) < 0
Kết hợp điều kiện : x > 4 hoặc 0  x  1
Bài 6: 1) ĐKXĐ: x  0; x  1 Rút gọn A:
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 22
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI x  2 x A   x  x  2 x  2 x  2 x ( x 1) A  
( x  2)( x 1)
( x  2)( x 1) 1 A  x 1
2) Với x  0; x  1 3 x  3 B  1  
 1  3( x 1)  ( x  3)  x 1  x  2 x  7  0   x  2 1  8 x 1 x 1  x 1  2 2  x  1 2 2)(TM) 1  
 x  1 2 2(KTM )  2 Vậy….. Bài 7. 1) Ta có  x  3 1  x
 x  3  x  3  x  3 B   :       x 9 x  3  x  3  x 9      x x  x   1 x  3 x 1  . 
 x 3 x 3 x x  3 2) Ta có 2 2 x 
27 10 2  18  8 2  x  5  2.5 2  2  4  2.4 2  2
 5  2 2  4  2 2 1 1 Vậy B   1  2
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 23
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI 1 x 1 1 3 x  2 1
3) Xét hiệu B      0 vậy B  . 3 x  3 3 x  3 3 Bài 8. 36  3 3
1) Ta có B 36   36 1 7
2) Ta có với 0  x  9 2 x x   x x
 x 3 x 3 x  1 11 x 3 2 1 3 11 A     x  3 x  3 9  x x  9
2x  6 x  x  4 x  3 11 x  3 3x  9 x 3 x   
 x 3 x 3
 x 3 x 3 x  3 3 x x  3 3 x 3) Xét P  . A B  . 
(với 0  x  9 ) x  3 x 1 x 1 3  P  3 
để P nguyên thì x 1  1;  3  x  0;  4 . x 1 Bài 9. 2
1) Với x  0, x  4 để B  2 
 2  2  2 x  4  x  9 x  2 2 x x x  x    1 1 2 2) Ta có A     x  4 x  2
 x  2 x 2  x  2 x  2 B
 x  2 x  2 2  x  2 P   .  A x  2 2 x   1 x 1
3) Xét phương trình: P  x  
1  x  2 x  
1  x  2 x  4,DK: x  0
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 24
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI x  2 
 x  1 x  2 x  1  2x  2 x  4 x 1 
x  2  x  2 x  2  x  2 x  4
 x  4 x  4  0   x  2 2  0 
x  2  x  4 (thỏa mãn). Bài 10: 6 1. Q 
(ĐKXĐ: x  0; x  9) x  3 x 6 6 3
Thay x  121 vào Q ta được: Q    121 3 121 88 44 2 x 2 2. P  
. ĐKXĐ: x  0; x  9 x  9 x  3 2 x  x 3 2 
2 x  2 x  6 6 P    
 x 3 x 3  x 3 x 3  x 3 x 3  x 3 x 3 Q 6 6 3. Ta có: A   :
ĐKXĐ: x  0; x  9 P
x  3 x  x 3 x  3
 x 3 x 3 6  x  3  .  x  x  3 6 x 2 x 1 x  3 2 x 1 2 x  6 2x  x A       0 Lại có: 2 x 2 2 x 2 x
 2 x  6  2x  x  0  2x  x  6  0   1
Đặt t  x t  0 . Khi đó phương trình (1) trở thành:
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 25
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI t  2 TM  2 2t t 6 0
t 22t 3 0          3 t  K TM   2
Với t  2  x  2  x  4 (TM ĐKXĐ)
Vậy tập nghiệm của phương trình (1) là: S    4 4. Xét hiệu: 2  x  3  x  3 x  6 x  9 x  3
x  6 x  9  x  3 x 3 x  9 2 A  A            x  x x x x x 3 x  9 Vì 2 2
x  0  3 x  9  0 
 0, x  0  A  A  0  A  A x Vậy 2 A  . A DẠNG 2: Bài 1:
Gọi vận tốc dự định là x (km/h) (điều kiện: x  0 ) 120
Thời gian dự định đi hết quãng đường AB là: (giờ) x 1 40 Thời gian đi hết quãng đường AB là: (giờ) 3 x 2
Vận tốc đi trên quãng đường là: x 10 (km/h) 3 2 80 Thời gian đi hết
quãng đường còn lại là: (giờ) 3 x 10 2
Vì người đó đến B sớm hơn dự đinh 24 phút = giờ nên ta có phương trình: 5
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 26
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI 120 40 80 2
5.120. x 10 5.40. x 10 5.80x
2x  x 10        x x x 10 5
5x  x 10
5x  x 10
5x  x 10
5x  x 10 2 2
 600x  6000  200x  2000  400x  2x  20x  2x  20x  4000  0  x  40 TM  2
 x 10x  2000  0   x  40 x  50  0  x  50   KTM  
Vậy vận tốc dự định đi hết quãng đường AB là 40km/h. 120 2 13
Thời gian lăn bánh trên quãng đường AB là:   (giờ) 40 5 5 Bài 2: 11 5 Đổi: 1 giờ 6 phút  (giờ); 2 giờ 30 phút  (giờ) 10 2
Gọi vận tốc ô tô đi từ A đến B là x (km/h), (ĐK: x  0)
Gọi vận tốc ô tô đi từ B đến A là y (km/h), (ĐK: y  0)
Quãng đường ô tô đi từ A đến lúc hai xe gặp nhau là: 2x (km)
Quãng đường ô tô đi từ B đến lúc hai xe gặp nhau là: 2y (km)
Vì hai xe đi ngược chiều và gặp nhau sau 2 giờ nên ta có phương trình:
2x  2 y  220  x  y  110   1 5
2 giờ 30 phút ô tô đi từ A đi được quãng đường là: x (km) 2
Thời gian ô tô đi tư B đến lúc gặp nhau sau khi ô tô đi từ A đi được 2 giờ 30 5 11 7 phút là:   (giờ) 2 10 5 7 7
giờ ô tô đi từ B đi được quãng đường là: y (km) 5 5
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 27
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI
Vì hai ô tô đi ngược chiều và gặp nhau sau khi ô tô đi từ A đi được 2 giờ 30 5 7
phút nên ta có phương trình: x  y  220 2 2 5
Từ (1) và (2) ta có hệ phương trình:  5 5
x  y  110 x  y  275
x  y  110    
x  y  110 x  60 2 2  5 7    11     TM  x  y  220 5 7 y  55 y  50 y  50 
 x  y  220     2 5 10    2 5
Vậy vận tốc ô tô đi từ A là 60 km/h
Vận tốc ô tô đi từ B là 50 km/h Bài 3:
Gọi khoảng cách giữa hai bến A, B là x  x  0, km
Ta có vận tốc xuôi dòng là 30 km / h , vận tốc dòng nước là 5 km / h nên vận
tốc thực của ca nô là 25 km / h và vận tốc ngược dòng là 20 km / h . x
Thời gian ca nô chạy xuôi dòng là: (h) 30 x
Thời gian ca nô chạy ngược dòng là: (h) 20 4
Vì thời gian xuôi ít hơn thời gian ngược 1h20p = h nên ta có phương trình: 3 x x 4  
 3x  2x  80  x  80(km) TM  20 30 3
Vậy khoảng cách giữa hai bến A, B là 80 (km).
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 28
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI Bài 4:
Gọi vận tốc thực của ca nô là x  x  0, km / h , vận tốc dòng nước là
y  y  0, y  x, km / h .
Ta có vận tốc xuôi dòng là: x  y km / h , vận tốc ngược dòng là: x  y km / h .
Lần thứ nhất ca nô chạy xuôi dòng 81 km và ngược dòng 105 km hết 8 giờ nên ta có phương trình: 81 105   8 (1) x  y x  y
Lần thứ hai ca nô chạy xuôi dòng 54 km và ngược dòng 42 km hết 4 giờ nên ta có phương trình: 54 42   4 (2) x  y x  y
Từ (1) và (2) ta có hệ phương trình:  81 105   8   x  y x  y  54 42    4  x  y x   y  1 a    x  y Đặt 
, ta được hệ phương trình mới: 1 b   x   y  1 b  81  a 105b  8 81  a 105b  8  42b  2   21       
54a  42b  4
81a  63b  6
27a  21b  2 1    27a  21.  2   21
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 29
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI  1  1 27a  1 a    b    27   21   1   b  1 27a 1 2     21 b      21
Trả lại biến cũ ta được:  1 1    x  y 27
x  y  27  2x  48 x  24        TM  1 1 x  y  21 y  x  21 y  3       x  y 21 
Vậy vận tốc xuôi dòng là 27 km / h và vận tốc ngược dòng là 21 km / h . Bài 5:
Gọi số sản phẩm người công nhân đó dự định làm được trong 1 giờ là x ( *
x   , sản phẩm).
Sau khi tăng năng suất, số sản phẩm người đó làm đc trong 1 giờ là x+2 (sản phẩm). 150
Thời gian dự kiến hoàn thành công việc là: (h). x
Số sản phẩm làm trong 2 giờ đầu là: 2x (sản phẩm).
Số sản phẩm còn lại làm sau khi tăng năng suất là: 150  2x (sản phẩm). 150  2x
Thời gian làm số sản phẩm còn lại đó là: (giờ). x  2 1
Vì người đó hoàn thành sớm hơn dự định 30 phút = giờ nên ta có phương 2 trình:
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 30
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI 150  150  2x  1  2     x  x  2  2 150 150  2x 5    x x  2 2
 300 x  2  2x 150  2x  5x  x  2 2 2
 300x  600  300x  4x  5x 10x 2
 x 10x  600  0
 x  20TM    x  30  L 
Vậy năng suất dự kiến ban đầu là 20 sản phẩm. Bài 6:
Gọi số sản phẩm mà đội phải làm trong một ngày theo kế hoạch là x(sản phẩm)
đk: x > 2, x   * 1000
Số ngày cần hoàn thành công việc theo dự đinh là: (ngày) x
Trong thực tế mỗi ngày làm thêm được 10 sản phẩm nên số sản phẩm làm
trong một ngày thực tế là: x+10 (sản phẩm) 1000
Só ngày làm việc trong thực tế là: (ngày) x  2
Vì vậy đội vượt mức kế hoạch 80 sản phẩm nên số sản phẩm thực tế đội làm
được là 1000 + 80 = 1080 (sản phẩm) nên ta có phưong trình:
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 31
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI  1000  (x 10).  1080    x  2   -2x² - 100x + 10000=0
Tìm được x= -100 (loại) hoặc x = 50 (thỏa mãn điều kiện)
Vậy số sản phẩm mà đội phải làm trong một ngày theo kế hoạch là 50 sản phẩm. Bài 7:
Gọi thời gian tổ một làm riêng và hoàn thành công việc là x (giờ, x  6 ).
Gọi thời gian tổ hai làm riêng và hoàn thành công việc là y (giờ, y  6 ) 1
Mỗi giờ tổ một làm được (công việc) x 1
Mỗi giờ tổ hai làm được (công việc) y
Biết hai tổ làm chung trong 6 giờ thì hoàn thành được công việc nên ta có phương trình: 6 6   1. (1) x y
Thực tế để hoàn thành công việc này thì tổ hai làm trong 2 giờ và tổ một làm 12 2
trong 2 10  12 (giờ), ta có phương trình:   1 (2) x y
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 32
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI  6 6   1   x y
Từ (1) và (2) ta có hệ phương trình: 12 2    1   x y x  15 Giải hệ ta được:  (thỏa mãn điều kiện) y  10 
Vậy nếu làm riêng thì tổ một hoàn thành công việc trong 15 giờ và tổ hai
hoàn thành công việc trong 10 giờ. Bài 8:
Gọi số xe lúc đầu đội có là x (xe); x > 0, x   * 120
Khối lượng hàng mỗi xe phải chở lúc đầu là (xe) x
Số xe lúc sau của đội có là x + 5 (xe) 120
Khối lượng hàng mỗi xe phải chở lúc sau là (tấn) x  5
Vì sau khi được bổ sung thêm 5 xe cùng loại thì mỗi xe phải chở ít hơn 2 tấn nên ta có phương trình: 120 120  2  x x  5
 2x2 + 10x – 600 = 0
⇔ (x 15)(x+20) = 0
⇔ x = 15 (thỏa mãn điều kiện) hoặc x = 20(không thỏa mãn điều kiện)
Vậy số xe lúc đầu của đội là 15 xe
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 33
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI Bài 9:
Gọi chiều dài của mảnh đất là: x (m) (Đk: x > 7).
Chiều rộng mảnh đất là: x – 7 (m)
Vì độ dài đường chéo của mảnh đất hình chữ nhật là 13m, nên ta có phương trình: 2 2 2
(x  7)  x  13 2 2
 x 14x  49  x  169 2
 2x 14x 120  0 2
 x  7x  60  0  x  5(l)  x 12  
Chiều rộng : 12 – 7 = 5 (m)
Vậy mảnh đất hình chữ nhật có chiều dài 12m; chiều rộng 5m. Bài 10:
Gọi số có hai chữ số cần tìm là ab ( Đk: a,b  N ; 0  a  9 ; 0  b  9 ) Theo đề bài ra ta có:
a + b = 10 => b = 10 – a
Vì tích của hai chữ số nhỏ hơn số đã cho là 12 nên ta có: a.b = ab - 12 => .(
a 10  a)  a(10  a) 12 => 2
10a  a  10a 10  a 12
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 34
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI a  1  (l) => 2
a  a  2  0 =>  a  2  Suy ra: b = 10 -2 = 8 Vậy số cần tìm là 28.
DẠNG 3: Hệ phương trình Bài 1:
1) Với m = 1 ta có hệ phương trình:  36 x 
x  y  10 3
 x  3y  30
x  y  10   5        2x  3y  6  2x  3y  6  5x  36  14  y    5  36 14
Vậy nghiệm của hệ phương trình khi m = 1 là  ( ; x y)  ;    5 5 
mx  y  10 m 1 10 2 2) Hệ phương trình  vô nghiệm    => m  2x  3y  6  2 3 6 3 Bài 2.
1) Thay m = 1 vào hệ phương trình có:  2
 x  y  5  y  1    x  3y  1 x  2   
Vậy với m = 1 thì hệ phương trình đã cho có nghiệm (x; y) = (- 2; 1)  2
 mx  y  5 (1) 2)  mx  3y  1 (2)  (1) <=> y = 2mx + 5
Thế vào (2) có: mx + 3(2mx + 5) = 1 <=> mx = - 2 (*)
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 35
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI
Hệ phương trình đã cho có nghiệm duy nhất
<=> phương trình (*) có nghiệm duy nhất <=> m ≠ 0 2
Với m ≠ 0 có: (*) <=> x = m 2 2 Thay x =
vào (1) có: (1) <=> y = 2m. + 5 = 1 m m 2 
Vậy với m ≠ 0 hệ có nghiệm duy nhất (x; y) = ( ; 1) m Có x – y = 2 2  2 2  1  2 
 3  2  3m  m  (TM ) m m 3 2 Vậy m =
thì hệ có nghiệm (x; y) thỏa mãn: x – y = 2. 3 2 2 
3) Với m ≠ 0 hệ có nghiệm duy nhất (x; y) = ( ; 1) => M( ; 1) => M thuôn thuộc m m
đường thẳng y = 1 với mọi m ≠ 0.    m  
1 x  my  3m 1 (1)
Bài 3. 2x y  m5 (2) 
(2) <=> y = 2x – m – 5 Thế (2) vào (1) có:
(1) <=> (m – 1)x – m(2x – m – 5) = 3m – 1
<=> (m + 1)x = (m + 1)2 (*)
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 36
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI
Hệ đã cho có nghiệm duy nhất
<=> phương trình (*) có nghiệm duy nhất <=> m + 1 ≠ 0 <=> m ≠ - 1
Với m ≠ - 1 có: (*) <=> x = m + 1
Thay x = m + 1 vào (2) có: (2) <=> y = 2(m + 1) – m – 5 = m – 3
Vậy với m ≠ - 1 thì hệ có nghiệm duy nhất (x; y) = (m + 1; m – 3)
S = x2 + y2 = (m + 1)2 + (m – 3)2 = m2 – 4m + 10 = (m – 2)2 + 6 ≥ 6 ∀m ≠ - 1.
Dấu “=” xảy ra <=> m = 2 (TM)
Vậy với m = 2 thì hệ có nghiệm duy nhất mà S = x2 + y2 đạt giá trị nhỏ nhất.
Bài 4. 1) Thay m = 2 vào hệ phương trình có: x  1
x  2 y  2     1 2x  2 y  1 y     2 1
Vậy với m = 2 thì hệ đã cho có nghiệm (x; y) = (1; ) 2
x  my  2 (1)
2) mx2y 1 (2)  (1) <=> x = 2 – my Thế (1) vào (2) có:
(2) <=> m(2 – my) – 2y = 1
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 37
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI
<=> (m2 + 2)y = 2m – 1 2m 1 <=> y = (vì m2 + 2 ≠ 0 ∀ m) 2 m  2 2m 1 2m 1 m  4 Thay y = vào (1) có: x = 2 – m. = 2 m  2 2 m  2 2 m  2 m  4 2m 1
Vậy hệ phương trình luôn có nghiệm duy nhất (x; y) = ( ; ) với mọi 2 m  2 2 m  2 m.  m  4  0 m  4  x   2 0  m  m  4  0 2  1        1  4   m  y  0 2m 1 2m 1  0 m  2   0    2  2   m  2 Mà m ∈ Z
=> m ∈ {- 3; - 2; - 1; 0}
Vậy m ∈ {- 3; - 2; - 1; 0} thì hệ có nghiệm duy nhất (x; y) với x > 0 và y < 0. m  4 2m 1
3) Vậy hệ phương trình luôn có nghiệm duy nhất (x; y) = ( ; ) với mọi giá 2 m  2 2 m  2 trị m. m  4 x = 2 m  2
có m ∈ Z thì m – 4 ∈ Z.  4 x   
TH1: m – 4 = 0 <=> m = 4 => 9 
=> m = 4 không thỏa mãn. 7  y    18
TH2: m – 4 ≠ 0 <=> m ≠ 4
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 38
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI 2 m 16 18
x ∈ Z mà m – 4 ∈ Z => (m – 4)x ∈ Z <=>  Z  1  Z 2 2 m  2 m  2 <=> m2 + 2 ∈ Ư(18) Mà m2 + 2 ≥ 2 ∀m
=> m2 + 2 ∈ {2; 3; 6; 9; 18} Ta có bảng: m2 + 2 2 3 6 9 18 m2 0 1 4 7 16 m 0 1 -1 2 -2  7 4 -4 m  4 5 1 x = 2 1 1 0 2 m  2 3 3 2m 1 1 1 1 y =  -1  2 m  2 2 2 2 KL KTM KTM TM KTM KTM KTM KTM KTM
Vậy m = - 1thì hệ có nghiệm duy nhất (x; y) với x; y là các số nguyên. Bài 5:
x  my  1 x  1  my x  1 my x  1  my a.       (I) mx  y   m  m    1 my  2  y  m
m  m y  y    m  2 m    1 y  2m 
Để hệ phương trình có nghiệm duy nhất thì  2 m  
1 y  2m có nghiệm duy nhất 2  m 1  0
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 39
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI Có 2 2
m  0  m 1  0 với mọi m .
Vậy hệ phương trình có nghiệm duy nhất với mọi m
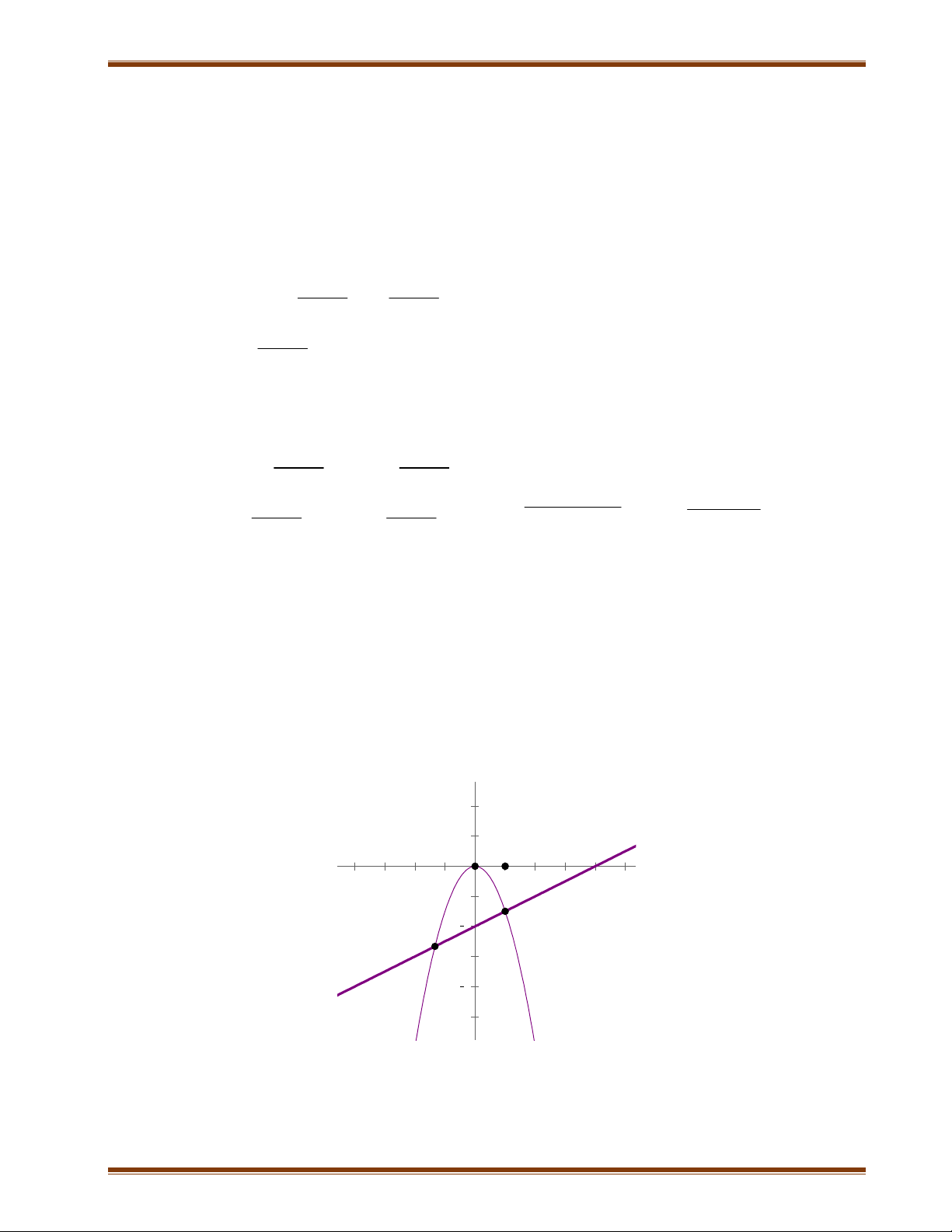
b. Phương trình có nghiệm duy nhất với mọi m ( theo câu a). 2  2m 2m x  1 . m  1  2 2  (I) m  2 m  2   2  m y  2   m  2 Theo đề bài: 2 2  2m  2m 1  1   0 m    m  2  2 x  1  m  2  m  2           2 1    2 2 1  m m m m y  1  2m 2m  0      0 2 2  1 1  0 2 2  m  2  m  2   m  2   m  2 DẠNG 4: Bài 1: 1. 2 5 B 2 A (P) 4 (d)
2. Xét phương trình hoành độ giao điểm của (P) và (d):
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 40
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI  3 x  1 y   3 1 3 1  2 2 2 x .x 2 x .x 2 0           4   2 2 2 2 x   8  3 y     3
Vậy (d) và (P) cắt nhau tại f 1 2  f  3  2 hai điểm  4 8   3  A  ;    và B 1;     3 3   2  3. a. f  2    f  3  
b. f 1 2  f  3  2 Bài 2: 1 1  1 1. Thay  x  1
 vào hàm số ta được : y   . 2 1    A 1  ;    2 2  2  1 Thay 2
x  2 vào hàm số ta được: y   2  2  B 2; 2 . 2
2. Gọi pt đường thẳng AB có dạng: y  ax  , b a  0  1  1   a  b a  
Vì A, B thuộc đường thẳng nên ta có  2   2  2 2    a  b b  1    1
PT AB: y   x 1 2
3. Gọi (d) là đường thẳng cần tìm 1
d / / AB  d : y  
x  b ,b  1 2
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 41
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI
Xét pt hoành độ giao điểm của (P) và (d) 1 1 1 1 2 2  x  b   x  x  x  b  0 2 2 2 2
Để (P) và (d) tiếp xúc thì pt trên có 1 nghiệm 2  1  1 1    0  
 4. .b  0  b     2  2 8 1 1
PT đường thẳng cần tìm là: y   x  2 8 Bài 3. 1 1 1)
Ta có : Ad  và x  2 ; y  .2   1 . Tọa độ A2  ;1 A A 4 2 1 1
 P đi qua A2  ;1 nên : 2 1  .2 a  a   P 2 : y  x 4 4 2)
Phương tình hoành độ giao điểm của d  và  P : 1 1 1 x  2 2 x  x    4 4 2 x  1    1
Vậy giao điểm còn lại là  B 1  ;    4  3)
Gọi A'; B ' lần lượt là hình chiếu của ; A B lên trục Ox .
Khi đó tọa độ A'2;0, B  1  ;0
Diện tích tam giác OAB là : 1 1 1 5 S  S  S  S  x  x y  Y  x . y  x . y  OAB A' B ' BA A' AO OBB '  A B   A B  2 2 A A 2 B B 8 Bài 4.
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 42
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI 1)
Gọi  x ; y là điểm cố định mà đồ thị hàm số đi qua 0 0  x  2  0 x  2 
Khi đó : y  mx  2m 1   x  2 0 0
m  y 1  0    0 0 0 0   y 1  0 y  1  0  0
Vậy đường thẳng luôn đi qua điểm cố định M  2   ;1 2)
Đồ thị  P đi qua M  2  
;1 nên :  a  2 1 1 . 2  a  4 1 Vậy  P 2 : y  x 4 3)
Phương trình đường thẳng có dạng : y  ax+b
Đường thẳng đi qua M  2   ;1 nên : 1  2  a  b   1
Phương tình hoành độ giao điểm của d  và  P : 1 2 2 ax  b 
x  x  4ax  4b  0 2 4
Ta có :    a2 ' 2
 4b  4a  4b
Đường thẳng d  tiếp xúc parabol  P khi pt 2 có nghiệm kép hay
 '  0  a  b 3  1  a    Từ  3
2 & 3 ta có :  1 b    3 1 1
Vậy đường thẳng cần tìm là : y   x  3 3 Bài 5. 1) HS tự vẽ hình 1 3 x  1 2)
Phương tình hoành độ giao điểm của d  và  P : 2 x  2x    2 2 x  3 
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 43
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI  1   9 Tọa độ  A 1; , B 3;      2   2  2
Ta có : AO    2  1  5 1 0   0     2  2 2
BO    2  9  3 13 3 0   0     2  2 2 AB   2  1 9   1 3    2 5    2 2  5 3 13 Vậy chu vi ABC :   2 5 (đvcv) 2 2 3) Gọi C  ; x 0  Ox
Chu vi ABC : AB  AC  BC
Do AB không đổi nên chu vi ABC nhỏ nhất khi AC  CB nhỏ nhất  1 Gọi  A' 1;  
 là điểm đối xứng của A qua Ox  2 
Khi đó CA  CA'  CA  CB  CA' CB  A' B  CA  CB nhỏ nhất khi A',C, B thẳng hàng
Hay C là giao điểm của A’B với Ox 5
Phương trình đường thẳng A' B : y  x  3 2  6
Vậy giao điểm A’B và Ox là  C ; 0    5  4)
Phương tình hoành độ giao điểm của d và  P : 1  1 2 2 nx 1 
x  x  2nx  2  0   1 2
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 44
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI
Để d cắt  P tại 2 điểm nằm cùng 1 phía với trục Ox thì pt   1 có 2 nghiệm 1    0
phân biệt cùng dấu nên : 
mà P  2  0 nên không có giá trị n thỏa mãn  0 P
Bài 6: 1) Viết phương trình đường thẳng (d) có hệ số góc k và đi qua điểm M(1,5;-1)
Đường thẳng (d) có hệ số góc k có dạng y  kx  b
Vì đường thẳng (d) đi qua điểm M(1,5;1) nên:
k.1,5  b  1 
b  11, 5k
=> Vậy đường thẳng (d): y  kx 1,5k 1
2) Tìm k để đường thẳng (d) và Parabol (P) tiếp xúc nhau
Xét phương trình hoành độ giao điểm của đường thẳng (d) và Parabol (P): 1 2
x  kx 1, 5k 1 4 2
 x  4kx  6k  4  0 (a  1,b  4k, c  6k  4) (1) 2
  b '  ac 2  ( 2
 k) 1.(6k  4) 2
 4k  6k  4
Để thẳng (d) và Parabol (P) tiếp xúc nhau thì phương trình (1) có nghiệm kép    0 2
 4k  6k  4  0 2
 2k  3k  2  0   25
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 45
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI 1
Phương trình ẩn k có 2 nghiệm phân biệt: k1 = 2, k2 = 2 1
Vậy, để thẳng (d) và Parabol (P) tiếp xúc nhau thì: k = 2; k = 2
3) Tìm k để đường thẳng (d) và Parabol (P) cắt nhau tại 2 điểm phân biệt
Để đường thẳng (d) và Parabol (P) cắt nhau tại 2 điểm phân biệt thì phương
trình (1) có 2 nghiệm phân biệt. 1 2 2
   0  4k  6k  4  0  2k  3k  2  0  (k  2)(k  )  0 2  1  k    2 k  2 
Vậy, để đường thẳng (d) và Parabol (P) cắt nhau tại 2 điểm phân biệt thì 1  k  hoặc k  2 2 Bài 7. 1) Cho n = 1: a)
Vẽ (P) và (d) trên cùng một mặt phẳng tọa độ b)
Tìm tọa độ giao điểm A và B của (P) và (d) c)
Tính diện tích tam giác AOB 1
Với n = 1 thì (d): y  x 1 2 a) Vẽ (P) và (d) b)
Xét phương trình hoành độ giao điểm của (P) và (d):
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 46
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI 2 x 1  x 1 2 2 2
 x  x  2  0
(a  1, b  1  , c  2) 
Vì a  b  c  1 (1)  2  0 nên phương trình có 2 nghiệm: x  1  , x  2 1 2 1 + Với x  1  thì y  1 1 2
+ Với x  2 thì y  2 2 2 1
Vậy tọa độ giao điểm của (P) và (d) là: A(-1; ) và B(2;2) 2 2)
Tìm n để (P) tiếp xúc với (d)
Xét phương trình hoành độ giao điểm của (P) và (d): 2 x 1  x  n 2 2 2
 x  x  2n  0 (1)
(a  1, b  1, c  2n) 2   ( 1  )  4.1.( 2  n)  1 8n
Để (P) tiếp xúc với (d) thì phương trình (1) có nghiệm kép    0  1 8n  0 1  n  8 1 
Vậy, để (P) tiếp xúc với (d) thì n  8 3)
Tìm n để (P) và (d) cắt nhau tại hai điểm
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 47
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI
Để (P) và (d) cắt nhau tại hai điểm thì phương trình (1) có 2 nghiệm    0  1 8n  0 1   n  8 1 
Vậy, để (P) và (d) cắt nhau tại hai điểm thì n  8 4)
Tìm n để (P) và (d) cắt nhau tại hai điểm nằm ở hai phía trục tung
Để (P) và (d) cắt nhau tại hai điểm nằm ở hai phía trục tung thì phương trình (1) có 2 nghiệm trái dấu  ac  0  1.( 2  n)  0  n  0
Vậy, để (P) và (d) cắt nhau tại hai điểm nằm ở hai phía trục tung thì n > 0
Bài 8. Tìm m để (P) và (d) cắt nhau tại hai điểm phân biệt A và B
Xét phương trình hoành độ giao điểm của (P) và (d): 2
x  mx  m 1 2
 x  mx  m 1  0 (1)
(a  1, b   ,
m c  m 1) 2
  (m)  4.1(m 1) 2
 m  4m  4 2
 (m  2)  0 với mọi m
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 48
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI
Để (P) và (d) cắt nhau tại hai điểm phân biệt A và B thì phương trình (1) có hai nghiệm phân biệt 2
   0  (m  2)  0  m  2  0  m  2 
Vậy, để (P) và (d) cắt nhau tại hai điểm phân biệt A và B thì m  2
1) Gọi x1 và x2 là hoành độ của A và B. Tìm m để x  x  2 1 2 Theo hệ thức Vi – et: b
S  x  x   m 1 2 a c
P  x .x   m 1 1 2 a Theo đề bài: 2 2 2 2
x  x  2  (x  x )  4  x  2x x  x
 4  (x  x )  4x x  4 1 2 1 2 1 1 2 2 1 2 1 2 2 2
 (m)  4(m 1)  4  m  4m  0  m(m  4)  0
 m  0 (TMĐK) hoặc m = 4 (TMĐK)
Vậy để x  x  2 thì m = 0 hoặc m = 4 1 2
2) Tìm m để (P) và (d) cắt nhau tại hai điểm nằm cùng bên trái trục tung Theo hệ thức Vi – et: b
S  x  x   m 1 2 a c
P  x .x   m 1 1 2 a
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 49
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI
Để (P) và (d) cắt nhau tại hai điểm nằm cùng bên trái trục tung thì phương
trình (1) có 2 nghiệm cùng âm 2   0 (m  2)  0   m  1 
 P  0  m 1  0    m  1 m  0    S  0 m  0  
Vậy, (P) và (d) cắt nhau tại hai điểm nằm cùng bên trái trục tung thì m < -1 Bài 9: 1
Phương trình hoành độ giao điểm của parabol (P) : y = 2
x và đường thẳng 2 d : y = mx + 2 là: 1 2 x  mx  2 2  2 x  2mx  4  2
x  2mx  4  0 (1)
Để đường thẳng d cắt parabol (P) tại 2 điểm phân biệt thì PT (1) phải có 2
nghiệm phân biệt  '  0
Ta có  ' = (-m)2 – 1.(-4)
= m2 + 4 > 0 m .
Với m PT(1) luôn có 2 nghiệm phân biệt .Gọi x1,x2 là 2 nghiệm phân biệt của
PT(1). Thì x1,x2 là hoành độ giao điểm của parabol (P) và đường thẳng d.  b x  x   2m 1 2   Theo Vi ét ta có a  (*)  c x x   4  1 2   a
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 50
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI Đặt A = x12 + x22 = x12 + 2x1x2+ x22 -2x1x2 = (x1+x2)2 -2 x1x2
Thay hệ (*) vào A ta được A = (2m)2 – 2.(-4) = 4m2 + 8.
Vì m2  0 m  4m2  0  4m2 + 8  8  A  8
Dấu “=” xảy ra  m2 = 0  m = 0.
Vậy với m = 0 thì đường thẳng d cắt parabol (P) tại 2 điểm phân biệt có hoành
độ x1,x2 mà x1+x2 có giá trị nhỏ nhất. Bài 10
Phương trình hoành độ giao điểm của parabol (P) : y = 2
x và đường thẳng d: y = - mx – m + 1 là: 2
x  mx  m 1  2
x  mx  m 1  0 (1).
Để đường thẳng d cắt parabol (P) tại 2 điểm phân biệt thì PT (1) phải có 2 nghiệm phân biệt.
Từ pt (1) Ta thấy a - b + c = 1 – m + m – 1 = 0 c
Nên pt (1) luôn có nghiệm : x1 = - 1 và x2  = - (m – 1) = 1- m. a
Để pt (1) có 2 nghiệm phân biệt thì : x1  x2
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 51
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI  -1  1 – m  m  2.
Với m  2. Ta có x1 = -1 => y1 = (-1)2 = 1 => A(-1;1)
x2 = 1 – m => y2 = (1- m)2 => B (1 – m ;(1-m)2) Ta có : y1 + y2 = 1+ (1-m)2 Mà (1 - m )2  0 m  (1 - m )2 + 1  1  y1 + y2  1  Dấu “=” xảy ra  (1 - m )2 = 0  1 – m = 0  m = 1
Vậy với m = 1 thì đường thẳng d cắt parabol (P) tại điểm A và B phân biệt với
A(x1;y1);B(x2;y2) mà(y1 + y2) nhỏ nhất . DẠNG 5:
Bài 1: Cho pt : x2 – (2m + 3)x +m2 + 3m + 2 = 0 (1) m là tham số. 1. Giải pt khi m = 1. Với m = 1 pt (1)có dạng : x2 – 5x + 6 = 0 2   ( 5
 )  4.1.6  25  24  1  0 Ta có    1  1
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 52
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI 5 1 x   2 1
Phương trình có 2 nghiệm phân biệt 2 5 1 x   3 2 2
Vậy với m = 1 pt có tập nghiệm S ={ 2;3}
2. Xác định m để pt có 1 nghiệm là 2.Khi đó pt còn 1 nghiệm nữa, tìm nghiệm đó?
Để pt (1) có 1 nghiệm x = 2=> f(2) = 0 Hay 2 2
2  (2m  3).2  m  3m  2  0  2
4  4m  6  m  3m  2  0  2 m  m  0 m  0 m  0
 m(m 1)  0       m 1  0 m 1
+.Nếu m = 1.nghiệm còn lại là 3(phần 1).
+.Nếu m = 0 pt (1) có dạng : 2
x  3x  2  0
Theo Vi_ét x x  2  2.x  2  x  1.=> Nghiệm còn lại là 1. 1 2 2 2
3. CMR pt luôn có 2 nghiệm phân biệt với m .
Ta có :    m  2 2 (2 3)
 4.1.(m  3m  2) 2 2
 4m 12m  9  4m 12m  8  1  0m
Vậy m pt (1) luôn có 2 nghiệm phân biệt.
4. Gọi x ; x là 2 nghiệm của pt.Tìm m để 2 2 x  x  1 . 1 2 1 2
m gọi x ; x là 2 nghiệm của pt(1) . 1 2
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 53
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI
x  x  2m  3 Theo Vi-ét ta có 1 2  (I) 2
x x  m  3m  2  1 2 Để : 2 2 2 2 x  x
 1  x  2x x  x  2x x  1 1 2 1 1 2 2 1 2 2
 (x  x )  2x x  1 (*) 1 2 1 2
Thế hệ (I) vào biểu thức (*) Ta được : 2 2
(2 m 3)  2.(m  3m  2)  1 2 2
 4m 12m  9  2m  6m  4 1  0 2
 2m  6m  4  0 2
 m  3m  2  0(2)
Ta thấy a  b  c  1 3  2  0 => pt (2) có nghiệm m  1  ; m  2  . 1 2 Vậy với m  1  ; m  2
 thì pt có nghiệm x ; x thoả mãn 2 2 x  x  1 . 1 2 1 2
5. Xác định m để phương trình có nghiệm này gấp 3 lần nghiệm kia.
x  x  2m  3(3)
Giả sử pt (1) có 2 nghiệm x ; x Theo Vi-ét ta có 1 2 1 2  2
x x  m  3m  2(4)  1 2
.Để x  3x  x  x  3x  x (5). 1 2 1 2 2 2 2m  3 3(2m  3)
Thế pt(3) vào pt(5) => 2m  3  4x  x   x  2 2 1 4 4 2m  3 3(2m  3) Thay x   x  vào pt(4) 2 1 4 4 2m  3 3.(2 m 3) => 2 .
 m  3m  2 4 4
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 54
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI 2 2
 3(2m  3)  16(m  3m  2) 2 2
 3(4 m 12m  9)  16m  48m  32 2 2
 12m  36m  27 16m  48m  32  0 2  4
 m 12m  5  0 2
 4m 12m  5  0 2
 '  6  4.5  36  20  16  0 Ta có:   '  16  4 6   4 1  6   4 5  Pt có 2 nghiệm m   ; m   1 2 4 2 4 2 1 5 Vậy với m  ; m 
thì phương trình có nghiệm này bằng 3 lần nghiệm kia. 2 2 Bài 4 2
x  2m  
1 x  m  4  0
1. Với m  5 phương trình 2
 x  8x  9  0
Phương trình có a  b  c  0 nên có 2 nghiệm x  1; x  9  1 2 2 2  1  19 1) 
  m  
1  1.m  4 2
 m  m  5  m    0      m  2  4
 phương trình luôn có 2 nghiệm phân biệt với mọi m
2. Phương trình có 2 nghiệm trái dấu  .
a c  0  m  4  0  m  4 3. Với mọi m ta có 
  0 gọi x , x là 2 nghiệm của phương trình. Theo hệ thức vi- 1 2
x  x  2 m 1 1 2   et ta có: 
x .x  m  4  1 2
Để phương trình có 2 nghiệm cùng dương x  x  0 2 m 1  0 m  1  1 2          m  4 x .x  0 m  4  0 m  4  1 2  
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 55
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI 2)
A  x 1 x
 x 1 x  x  x x  x  x x  x  x  2x x 1  2  2  1  1 1 2 2 2 1  1 2  1 2 3)  2m  
1  2m  4  2m  2  2m  8  10
4. Đặt B  x  x 1 2
Ta có B   x  x 2  x  2x x  x   x  x 2 2 2 2  4x x 1 2 1 1 2 2 1 2 1 2
 m  2  m     2 4 1 4 4
4 m  m  5 4) 2  B  2  m  m  5 Bài 5 2 2  3  7 5) 
  m   1   m  3 2
 m  3m  4  m    0      m  2  4
Phương trình luôn có 2 nghiệm phân biệt với mọi m
1. Gọi x , x là 2 nghiệm của phương trình. Áp dụng hệ thức vi-ét ta có: 1 2
x  x  2 m 1 
 x  x  2m  2 1 1 2   1 2      x x  m  3
m  x x  3 2  1 2  1 2    Thay (2) vào (1) ta có 6)
x  x  2 x x  3  2  x  x  2x x  4 1 2  1 2  1 2 1 2
2. Phương trình có 2 nghiệm bằng nhau về giá trị tuyệt đối và trái dấu 7)
 x  x  x  x  0  2 m 1  0  m  1 1 2 1 2  
Thay m=1 vào lai phương trình tìm được x  2 ; x   2 vậy m=1 thỏa mãn 1 2 yêu cầu bài toán
Bài 6: x2 – 2(m – 2)x + 2m – 5 = 0
1/ Chứng minh phương trình luôn có nghiệm với mọi m
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 56
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI '
 = (m – 2)2 – 1(2m – 5) = m2 – 4m + 4 – 2m + 5 = m2 – 6m + 9 = (m – 3)2  m
 Phương trình có nghiệm với mọi m 2/ '
  m => phương trình luôn có nghiệm với mọi m  b 2(m  2) x  x     2(m  2) 1 2   Theo Viet ta có a 1  c 2m  5 x .x    2m  5 1 2   a 1
Theo đề bài ta có: B = x1(1 - x2) + x2(1 – x1) < 4
B = x1 – x1x2 + x2 – x1x2 < 4  x1 + x2 – 2x1x2 < 4
 2(m – 2) – 2(2m – 5) < 4
 2m – 4 – 4m + 10 – 4 < 0
 -2m + 2 < 0  2m > 2  m > 1
Vậy m > 1 thì phương trình có nghiệm sao cho B < 4
3/ Tìm hệ thức liên hệ giữa 2 nghiệm không phụ thuộc vào m
x  x  2m  4(1) 1 2
x  x  2(m  2)  Ta có 1 2    x .x  5 thay vào (1) ta được 1 2
x .x  2m  5 m   1 2   2
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 57
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI x .x  5 1 2 x  x  2
 4  x1 + x2 = x1.x2 + 5 – 4  x1 + x2 – x1.x2 – 1 = 0 1 2 2 Bài 7.
1/ x2 + (4m + 1)x + 2(m- 4) = 0 (*)
 = (4m + 1)2 – 4.1.2(m – 4)
= 16m2 + 2.4m.1 + 1 – 8m + 32
=16m2 + 33 > 0 Với mọi m
 Phương trình (*) có 2 nghiệm phân biệt với mọi m  b (4m 1) x  x    (4m 1) 1 2   Theo Viet ta có a 1   c x .x   2(m  4) 1 2   a
x  x  (4m 1)(1) 1 2 
Kết hợp điều kiện ta được x .x  2(m  4)(2) 1 2
x  x 17(3)  2 1
Từ (3) => x2 = 17 + x1 (3’) thế vào (1) ta được X1 + 17 + x1 = -(4m + 1)  2x1 = - 4m – 1 – 17 2x1 = - 4m – 18
X1 = -2m – 9 thay vào (3’) ta được. X2 = 17 + (-2m – 9)
X2 = 17 – 2m – 9 = 8 – 2m
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 58
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI
Thay x1, x2 vào (2) ta được:
(-2m – 9) (8 – 2m) = 2(m – 4)
 -16m + 4m2 – 72 + 18m – 2m + 8 = 0
 4m2 – 64 = 0  4m2 = 64  m2 = 16 => m = 4 (TM)
Vậy m = 4 thì phương trình có 2 nghiệm x1, x2 t/m x2 – x1 = 17 2/ A = (x1 – x2)2 = 2 2 2
x  x  2x x  (x  x )  4x x 1 2 1 2 1 2 1 2 A =  m  2 (4 1)  4.2(m  4) =16m2 + 8m +1 – 8m + 32 =16m2 + 33 Ta có m2  0 với mọi m
 16m2  0 với mọi m => 16m2 + 33  33 mọi m
Vậy GTNN của A = 33  m = 0
x  x  (4m 1)(1) 3/ 1 2 
x .x  2(m  4)(2)  1 2 x  x 1
Ta có x1 + x2 = -4m – 1 => x1 + x2 + 1 = -4m => 1 2 m  Thay vào (2) ta được 4   x  x 1  x  x 1 1 2 1 2 x .x  2
 4  x .x   8 1 2   1 2  4   2  -2x1x2 + x1 + x2 + 1 + 16  x1 + x2 + 2x1x2 + 17 = 0
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 59
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI
Vây hệ thức liên hệ giữa x1, x2 không phụ thuộc m là: x1 + x2 + 2x1.x2 + 17 = 0 Bài 8. 2
x  2m  
1 x  2m 1  0
 '   m   2 1   2m   1   2  '  m
Để phương trình có hai nghiệm phân biệt thì  '  0 2
 m  0  m  0
Áp dụng định lí Vi-et, ta có: 
x  x  2 m 1
x  x  2m  2 1 2   1 2   
x x  2m 1 x x  2m 1  1 2  1 2 Theo đề ta có 2
x  x  5   x  x 2 2 2  2x x  5 1 2 1 2 1 2  4 2 m  2m   1  2m   2
1  5  4m  6m  3  0 3   21 3  21 Suy ra m  hoặc m  4 4 3  21 3   21 Vậy m  hoặc m 
thì phương trình đã cho có hai nghiệm 4 4
phân biệt x , x là độ dài hai cạnh của một tam giác vuông có cạnh huyền 1 2 bằng 5
Bài 9. Cho phương trình 4 2
x  2x  m  2  0
a) Giải phương trình khi m  1  Thay m  1
 vào phương trình, ta có: 4 2
x  2x  3  0
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 60
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI Đặt 2
t  x t  0 , phương trình trở thành 2
t  2t  3  0 .
Ta có a  b  c  1 2  3  0
Do đó, phương trình có nghiệm t  1
 ( loại ) và t  3 . 1 2 2
t  3  x  3  x   3 .
Vậy tập nghiệm của phương trình S    3
b) Tìm m để phương trình có 4 nghiệm phân biệt Đặt 2
t  x t  0 , phương trình trở thành 2
t  2t  m  2  0 .   1
Để phương trình đã cho có 4 nghiệm phân biệt thì phương trình   1 có 2 nghiệm dương phân biệt. a  0 1   m  2  0   '  0  m  3   2  0    2  m  3 S  0 m  2    m  2  0  P  0 
Vậy 2  m  3 thì phương trình đã cho có 4 nghiệm phân biệt.
Bài 10. Cho phương trình 2
x  m   2 2
1 x  m 1  0
Đặt t  x t  0 , phương trình đã cho trở thành 2
t  m   2 2
1 t  m 1  0   1
Ứng với một nghiệm t dương của phương trình  
1 thì phương trình đã cho
có 2 nghiệm phân biệt. Do đó để phương trình đã cho có nghiệm duy nhất thì phương trình  
1 phải có một nghiệm t  0 .
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 61
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI m  1 Suy ra 2
m 1  0  m  1  
Khi m  1 , phương trình   1 trở thành: 2 t  4t  0
 t t  4  0 t  0
x  0 ( loại vì có 3 nghiệm )     t  4 x  2    Khi m  1  , phương trình   1 trở thành: 2 t  0  x  0 ( nhận ) Vậy m  1
 thì phương trình đã cho có nghiệm duy nhất. DẠNG 6: Bài 1: 1. Chứng minh    0
OKM  OAM  OBM  90
2. Dùng kết quả câu 1, tứ giác MAKB nội tiếp chú ý MA = MB  
 AKM  BKM . E 3. Chứng minh được:   
AQB  MAB  MKB  ĐPCM 4. Chứng minh được:
OM  AB , dùng hệ thức lượng cho tam giác vuông MAO 2
 MH .MO  MA . Q A K P N M F I H O B
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 62
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI Chú ý: 5. Từ kết quả câu 4 : .
Tổng quát: Trên tia Mx lấy hai điểm A, B sao cho MA < MB. Trên tia MY lấy hai
điểm N, P sao cho MN < MP. Khi đó ABPN là tứ giác nội tiếp . 6. Vì AB = 2AH nên:
. Dùng hệ thức lượng cho tam giác MAO 2
 AH  HM .HO . Chứng minh được:
7. Chứng minh được MEKH là tứ giác nội tiếp, dùng kết quả tổng quát ở câu 5 ta có:
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 63
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI không đối. Từ .
8. Vì MO là trung trực của AB nên IA = IB.  
IAM  IAB suy ra AI là phân giác  MAB , chú ý MI là phân giác => ĐPCM.
9. Từ câu 2 KF là phân giác góc  AKB , chú ý nên KE là phân giác góc
ngoài tại đỉnh K. Dùng tính chất đường phân giác với .
10. Nhận xét: P, Q thay đổi nên
có độ dài cả ba cạnh đều thay đổi gây khó
khăn do đó cần đưa về tam giác chứa yếu tố cố định hơn. Từ kết quả câu 3 . Kẻ ta có Do AM không đối
(P' đối xứng với A qua O) AL 2
11. Gọi S là trung điểm OM, từ G kẻ GL//KS. Vì AS cố định và:   L cố định AS 3 2 1
Lại có: LG  SK  OM (Không đổi) 3 3
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 64
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI  1
Bởi vậy G luôn chạy trên đường tròn  ;  L OM  cố định.  3 
Do OK.OE không đổi nên E thuộc đường OK cố định trên đó E cách O cố định một 2 R đoạn OE 
không đổi. Vậy E là điểm cố định mà AB luôn đi qua. OK
12. Từ MO = 2R tính được . 2  R
Diện tích hình quạt cần tính là S  . 3 Bài 2
a. C/m: tứ giác OMNP nội tiếp C Ta có: 
MP  AB  OMP  90 d Ta có: 
ON  CP  ONP  90 M A B O  
 OMP  ONP I N
 Tứ giác OMNP nội tiếp (DHNB) P D
b. C/m: Tứ giác CMPO là hình bình hành CO  AB  Ta có:
  CO / /MP (1) MP  AB Ta có:  
OCM  ONM ( CN O cân tại O)
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 65
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI  
OPM  ONM ( cùng chắn cung OM)  
OPM  DOP (OD//PM)    OCM  DOP
Mà chúng là hai góc đồng vị
 CM / /OP (2)
Từ (1), (2) suy ra tứ giác CMPO là hình bình hành.
c. C/m : CM . CN không phụ thuộc vào vị trí của điểm M
+) Xét COM và CND có:  OCM :  chung    COM
CND (g.g)  
COM  CND (=90 )    CO CM 2  
 CM .CN  OC.CD  3R CN CD  CM . CN không đổi
 CM . CN không phụ thuộc vào vị trí của điểm M
d. Khi M di chuyển trên đoạn thẳng AB thì tâm đường tròn nội tiếp tam giác
CND di chuyển trên một cung tròn cố định nào?
+) Goi I là tâm đường tròn nội tiếp CND 1
 CI là tia phân giác của    OCN  DCI  DCN 2 1
DI là tia phân giác của    CDN  CDI  CDN 2
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 66
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI 1    
 DCI  CDI 
(DCN  CDN )  45 (vì  CND  90 ) 2   CID  135
 I nằm trên cung tròn chứa góc 135 dựng trên CD. Bài 3.
a. C/m: tứ giác ABMD nội tiếp N Ta có: 
DA  AB  DAB  90 D M Ta có: G K BC   M  ( ; O
)  BMC  90  BMD  90 B J I O C A 2  
 DAB  DMB d P
 Tứ giác ABMD nội tiếp (DHNB)
b. Tứ giác APND là hình gì? Tại sao? Ta có:  
DMA  DBA ( cùng chắn cung DA)  
DMA  DBA ( 2 góc đồi đỉnh)  
DBA  PBC ( 2 góc đồi đỉnh)    
 NMC  PBC  NC  CP
 NC = CP  C  đường trung trực của NP
Ta có: ON = OP = R  O  đường trung trực của NP
 CO là đường trung trực của NP
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 67
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI
 CO  NP hay  AC  NP Mà AC  AD  OA  NP
 Tứ giác APND là hình thang.
c. C/m : CM . CD không phụ thuộc vào vị trí của điểm M
+) Xét CMB và CAD có:  ACD :  chung 
  CMB CAD (g.g)  
CMB  CAD (=90 )    CM CB  
 CM .CD  C . A CB CA CD Mà A, B, C cố định  CA . CB không đổi  CM . CD không đổi
 CM . CD không phụ thuộc vào vị trí của điểm M
d. C/m: Trọng tâm G của tam giác MAC chạy trên một đường tròn cố định khi M di động. IG 1
Gọi I là trung điểm của AC  Điểm I cố định và  IM 3 IG IJ 1 Kẻ GJ // MB   
( định lý Talet)  Điểm J cố định IM IB 3 IG IK 1 Kẻ GK // MC   
( định lý Talet)  Điểm K cố định IM IC 3
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 68
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI IJ IK IJ  IK JK 1      IB IC IB  IC BC 3 1  JK  BC 3 GJ / /MB   Ta có: 
GK / /MC   GJ  GK  JGK  90  MB  MC 
Vậy khi M di động trọng tâm G của tam giác MAC chạy trên đường tròn đường kính JK cố định. Bài 4: E O I C B D H A M
a. A là điểm chính giữa  BC
I là trung điểm BC  OA  BC tại I  0  AIC  90
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 69
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI
Suy ra tứ giác AIHC nội tiếp
 A, I, H, C cùng thuộc một đường tròn b. Xét và có chung
(góc nội tiếp chắn hai cung bằng nhau) c. Có (cùng chắn  AB )
(góc nội tiếp chắn hai cung bằng nhau)
Suy ra AB tiếp xúc đường tròn ngoại tiếp d. Có
(góc nội tiếp chắn hai cung bằng nhau)  EA là phân giác  CEM , mà  cân tại E
 EA là trung trực MC  AM =AC =>
(cạnh huyền – cạnh góc vuông)
Dấu "=" xảy ra khi HA = HC  vuông cân tại H  hay
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 70
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI 
=> E nằm trên (O) sao cho số đo  0 CE  90 Bài 5. M I A N O O' K C B H CHỨNG MINH 1) Ta có   0
AHB  AHC  90 (góc nội tiếp chắn nửa đường tròn)    0 0 0
HBC  BHA  AHC  90  90  180 . Vậy B, H ,C thẳng hàng.
2) Nếu MN  AH thì HM , HN lần lượt là các đường kính nên hiển nhiên ta có đpcm.
Ngược lại, không mất tính tổng quát, giả sử  HAN nhọn, ta có   MBH  HAN (cùng bù với  HAM ) 
MOH là góc ở tâm chắn  HM , 
MBH là góc nhọn chắn cung  HM nên  1  MBH  MOH . 2 1
Chứng minh tương tự ta được   HAN  HO ' N 2
Suy ra hai tam giác cân MOH và HO ' N đồng dạng (c-g-c) MH MO R     const HN NO ' R ' 3) Ta có   0
BMA  CNA  90 (góc nội tiếp chắn nửa đường tròn)
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 71
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI
 tg MNCB là hình thang vuông.
KI là đường trung bình của hình thang MNCB   0
 KI / / NC  KIA  KNC  180 (hai góc trong cùng phía) Mặt khác  
AHK  ANC (cùng bù với  AHC ) Suy ra   0
AIK  AHK  180 , mà hai góc ở vị trí đối nhau nên tứ giác AIKH nội tiếp. Vậy 4 điểm ,
A H , K , I cùng thuộc một đường tròn.
4) Xét HMN và ABC  
NMH  ABC (cùng chắn cung 
AH của O )  
MNH  ACB (cùng chắn cung 
AH của O ' )
Suy ra HMN ∽ ABC (g-g) S HM HM HMN   S  S . HMN ABC S AB AB ABC Mà ,
A B,C cố định nên S
max  HM max  HM là đường kính của HMN O Khi đó  0
MAH  90 , đường thẳng d / / BC là đường thẳng cần tìm. Bài 6. CHỨNG MINH
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 72
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI 1) Ta có  
OAM  O ' AN (đối F đỉnh)
OAM cân tại O OA  OM  R B  
 OAM  OMA . N Chứng minh tương tự O   O'
O ' AN  O ' NA A E
Xét AOM và AO ' N có    
OMA  OAM  O ' AN  O ' NA (1) M
 AOM ∽ AO ' N  g  g 
2) Do AB / /FN nên theo định BA MA lí Talets ta có:  FN MN (2) Từ (1) ta cũng có  
OMA  O ' NA mà
hai góc ở vị trí so le trong nên
OM / /O ' N
Lại theo hệ quả định lí Talets ta có MA OA R 2R ' 2 :     (3) MN OO ' R  R ' 2R ' R ' 3 Từ (2)(3) suy ra BA 2 3 3   FN  BA  R = const. FN 3 2 2
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 73
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI
3) AB / /EF (gt)  tg ABFE là hình thang (4)  
BFE  MBA (đồng vị) (5)  1 MBA  
AOM (tính chất góc nội tiếp) (6) 2   1 AEF  AEN  
AO ' N (tính chất góc nội tiếp) (7) 2  
AOM  AO ' N (do AOM ∽ AO ' N ) (8) Từ (5)(6)(7)(8) suy ra  
BFE  AEF (9)
Từ (4) và (9) suy ra tứ giác ABFE là hình thang cân.
4) Kẻ đường cao AH của hình thang, ta có F  3  R  R AH  AB FN .    AH  2  5 S    . R AH ABFN 2 2 4 B (10) N I
Kẻ MK  AB  K . H O O'  
MAK  ANH (đồng vị) A K MK MA R C
Suy ra AKM ∽ NHA (g-g)     2 (11) AH NA R ' 5 M Từ (10)(11) suy ra S  . R MK ABFN 8 Vậy S max  MK max ABFN
Gọi I là trung điểm của AB và C là điểm thỏa mãn
CI  AB , C O  C là trung điểm của cung lớn  AB nên cố định.
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 74
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI
Ta có MK  MI  MO  OI  CO  OI  CI
Suy ra Max MK  CI , dấu '  "  M  C . Bài 7. CHỨNG MINH 1) Ta có : K  0
AEB  90 (góc nội tiếp chắn nửa đường tròn đường kính AB ) E C  0  KEB  90 (1) H  0
CD  AB  M  KMB  90 (2) A F
Từ (1)(2) suy ra hai đỉnh O M B
E và M cùng nhìn cạnh
KB dưới các góc bằng nhau nên tứ giác EKBM nội tiếp. D 2) Xét A  KM và A  BE :   A chung;  AK  M ∽ ABE  g  g   AMK AEB 0 90      AK AM 3 2  
 AK.AE  AM.AB  .
R 2R  3R . AB AE 2
3) Theo giả thiết ta có CD là trung trực của OB nên CO  CB   
OCB đều vì CO  CB  OB R 0 COB  60
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 75
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI 2 2 R 60 R
Vậy diện tích quạt dưới hạn bởi 
OB, OC, BC nhỏ : S   dvdt 360 6
4) Gọi F là điểm đối xứng của A qua CD  F cố định do , A CD cố định.
 KAF cân tại K do KM là trung trực của AF (theo cách dựng F)  
 KAM  KFM (3)
Tứ giác AEHM nội tiếp do hai góc đối diện E và M vuông  
 KAM  MHB (4)   0
MHB  KHB 180 (5) Từ       0
3 4 5  KFM  KHB  180  KHBF nội tiếp
 F thuộc đường tròn ngoại tiếp tam giác BHK
 Tâm I của đường tròn ngoại tiếp tam giác BHK thuộc đường trung
trực của BF cố định. Bài 8. CHỨNG MINH
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 76
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI 8) Ta có  0
AHB  90 (góc nội tiếp chắn nửa E
đường tròn) HB  AE K N H
Mặt khác ta lại có H là điểm chính giữa cung M AM nên   ABH  HBM I B A
Xét tam giác ABE có BH vừa là đường cao O
vừa là đường phân giác nên B  AE cân tại . B 9) Do N  , B B 
A  BA  BN  A  BN cân tại B  
 INB  MAB (1)
AM , AH lần lượt là hai đường cao
trong tam giác FAB và cắt nhau tại I
nên I là trực tâm của tam giác FAB  KI  AB  
 IEB  MAB (2)(cùng phụ với  MBA ) Từ (1)(2) suy ra  
INB  IEB mà hai góc cùng
nhìn cạnh IB nên tứ giác NEIB nội tiếp.
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 77
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI 10) Khi K M  0  
MAK  90  MK / / AB  MKB  KBA so le trong H mà  
MBK  KBA cmt nên I   MBK  MKB  M
 KB cân tại M B A
 MK  MB (3) O J
Kẻ MJ  AB  J  KMJA hình chữ nhật
 KM  JA 4
Từ (3)(4) suy ra MB  JA
Áp dụng hệ thức lượng trong tam giác vuông MAB đường cao MJ : 2
MB  JB AB   AB  J  2 .
A AB  4R  2 . R MB
 MB  R MB  R   MB  R2 2 2 2 2 . 4 0
 5R  MB   5 1  R
Vậy điểm M cần tìm là giao của  ; O R và
 ;B 5 1R. BÀI 9.
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 78
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI
a. C/m: tứ giác MNEF nội tiếp N F C Ta có: CD  AB  O   CD / /MN P I MN  AB B  A H  
 MND  CDN (2 goc slt) G K Mà:  
CDN  CFE ( cùng chắn  CE ) E D   M
 MND  CFE
 Tứ giác MNEF nội tiếp (DHNB) b. C/m: ME.MC = NF.ND
+) Xét MAE và MCA có:  AME : chung  
  MAE  M ( CA g.g)   
MAE  MCA (cung chan AE)  MA ME   MC MA 2
 MA  MC . ME (1)
+) Xét NAF và NDA có:  ANF : chung      A N F   ( NDA g.g)   
NAF  NDA (cung chan AF )  NA NF   ND NA
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 79
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI 2  NA  . ND NF (2)   CDN  MND
+) Ta có: MN // CD (cmt)    MCD   NMC Mà  
CDN  MCD ( vì OCD cân tại O)    MND  CMN  OMN cân tại O Mà OA  NM
Suy ra: A là trung điểm của MN
 AM  AN (3)
+) Từ (1), (2), (3) suy ra: ME.MC = NF.ND
c. Tìm vị trí của điểm H để tứ giác AEOF là hình thoi. +) Ta có:    FEC  MNF   
  FEC  NME   MNF  NME    EF//MN Mà OA  NM
 OA  EF tại I  IE  IF
Tứ giác AEOF có OA  EF tại I và IE  IF (cmt)
Để tứ giác AEOF là hình thoi thì I là trung điểm của OA
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 80
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI
+) c/m: OIE  OHC (ch-gn)  OI=OH
 Khi I là trung điểm của OA thì H là trung điểm của OB
Vậy để tứ giác AEOF là hình thoi thì H là trung điểm của OB.
d. C/m: Khi H chuyển động trên đoạn OB thì G thuộc một đường trong cố định.
+) Từ G kẻ đường thẳng song song với AC và cắt AB tại P
Xét OKA có GP // AK ( theo cách vẽ) OG OP     OK OA  OP 1    OG 1 OA 3 Ma   OK 3   Suy ra điểm P cố định GP / / AK  +) Ta có: 
  GP  GA  AGP  90 GA  GK 
 G thuộc đường tròn đường kính AP khi H chuyển động trên đoạn OB. Bài 10.
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 81
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI
a. C/m: tứ giác BF’E’C nội tiếp A
+) Ta có: F’ đối xứng với H qua AB
 AB là đường trung trực của F’H E' O  BF’ = BH E
 BHF ' cân tại B F' F H I   C
 BF ' H  BHF ' (1) B D
+) Ta có: E’ đối xứng với H qua AC
 AC là đường trung trực của E’H  CE’ = CH
 CHE ' cân tại C  
 CE ' H  CHE ' (2) +) Ta có :  
BHF '  CHE ' (2 góc đối đỉnh) (3) Từ (1), (2), (3) suy ra  
BF ' H  CE ' H
Mà E’, F’ là 2 đỉnh liền kề của tứ giác BCE’F’
 Tứ giác BCE’F’ nội tiếp (dhnb)
b. C/m: A, F’, B, C, E’ cùng thuộc một đường tròn Ta có:  
AFH  AEF  90  Tứ giác AEHF nội tiếp (dhnb)
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 82
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI   FAE FHE 180        
  FAE  BHF '  
Ma BHF '  FHE  180  Lại có:   BFH  BHF '  
 FAE  BF ' H
Mà A, F’ là 2 đỉnh liền kề của tứ giác ABCF’
 Tứ giác ABCF’ nội tiếp (dhnb)
 A, C, B, F’ thuộc đường tròn ngoại tiếp BCF ' (4)
+) Ta có: Tứ giác BCE’F’ nội tiếp
 B, C, E’, F’ thuộc đường tròn ngoại tiếp BCF ' (5)
Từ (4), (5) suy ra A, F’, B, C, E’ cùng thuộc một đường tròn
c. C/m: OA  EF
+) Ta có: F’ đối xứng với H qua AB
 AB là đường trung trực của F’H  AF’ = AH (6)
+) Ta có: E’ đối xứng với H qua AC
 AC là đường trung trực của E’H  AE’ = AH (7)
Từ (6), (7) suy ra AE’ = AF’
 A  đường trung trực của E’F’ (8)
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 83
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI +) Ta có: OE’ = OF’ = R
 O  đường trung trực của E’F’ (9)
Từ (8), (9) suy ra OA là đường trung trực của E’F’
 OA  E ' F '
+) C/M: Tứ giác BCEF nội tiếp  
 EBC  EFC Mà  
EBC  CF ' E ' ( 2 góc nội tiếp cùng chắn cung CE’)  
 CF ' E '  EFC
 EF / / E ' F '
Ma OA  E ' F '  OA  EF
d. C/m: Khi A chạy trên (O) thì bán kính đường tròn ngoại tiếp tam giác AEF không đổi AD
 DC  AC  Xét   ;  O  có:  ACD  90
  DC / / BH (10)  2  Ma BH  AC    CDH F '    HB   
  CDH  BF ' H  
Ma F ' HB  BF ' H      
 F ' D  CB  F ' B  CD  F ' B  CD (11)
Từ (10), (11) suy ra tứ giác BHCD là hình bình hành
Gọi I là trung điểm của BC
 I là trung điểm của HD
+) Ta có: O là trung điểm của AD
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 84
ĐỀ CƯƠNG TOÁN 9 – THCS NGÔ SĨ LIÊN – HÀ NỘI 1  OI 
AH (t/c đường trung bình của AHD ) 2  AH = 2OI
Do BC cố định  OI không đổi  AH không đổi
+) Ta có: tứ giác AEHF nội tiếp đường tròn đường kính OH (cmt)
 Bán kính đường tròn ngoại tiếp tam giác AEF không đổi
Vậy khi A chạy trên (O) thì bán kính đường tròn ngoại tiếp tam giác AEF không đổi.
Tài liệu được thực hiện bởi nhóm : Toán THCS Page 85

Đề cương Toán 9 HK2 năm học 2017 – 2018 trường THCS Ngô Sĩ Liên – Hà Nội

Thông tin :

Tài liệu liên quan:

Đề cương giữa kì 1 Toán 9 năm 2024 – 2025 trường THCS Cự Khối – Hà Nội

Đề cương giữa kì 1 Toán 9 năm 2024 – 2025 trường THCS Văn Quán – Hà Nội

Ôn tập giữa kỳ 1 Toán 9 năm 2024 – 2025 trường THCS Đô Thị Việt Hưng – Hà Nội

Đề cương giữa học kì 1 Toán 9 năm 2024 – 2025 trường THCS Độc Lập – Thái Nguyên

Đề cương giữa học kì 1 Toán 9 năm 2024 – 2025 trường THCS Trần Đại Nghĩa – BR VT