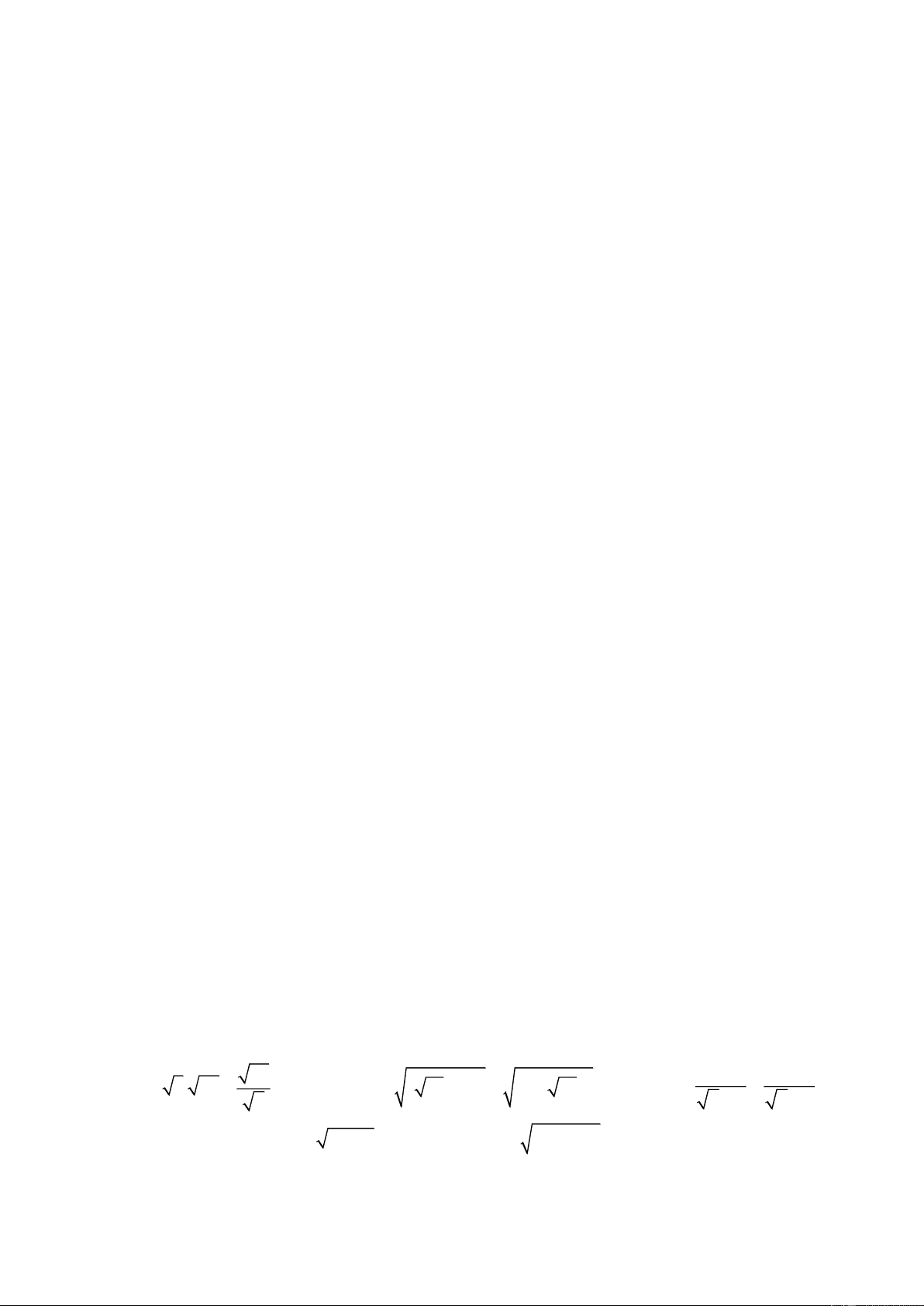
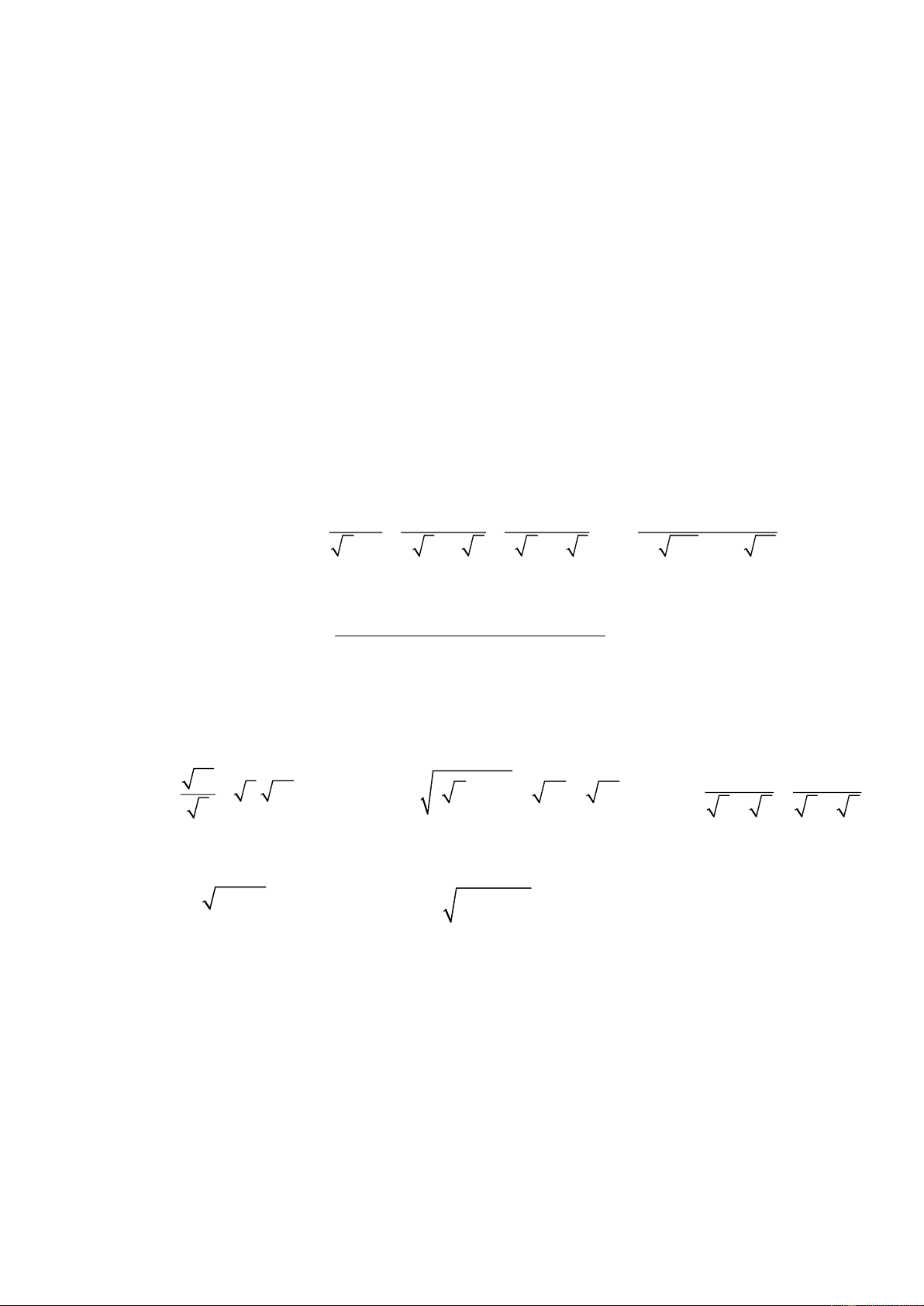
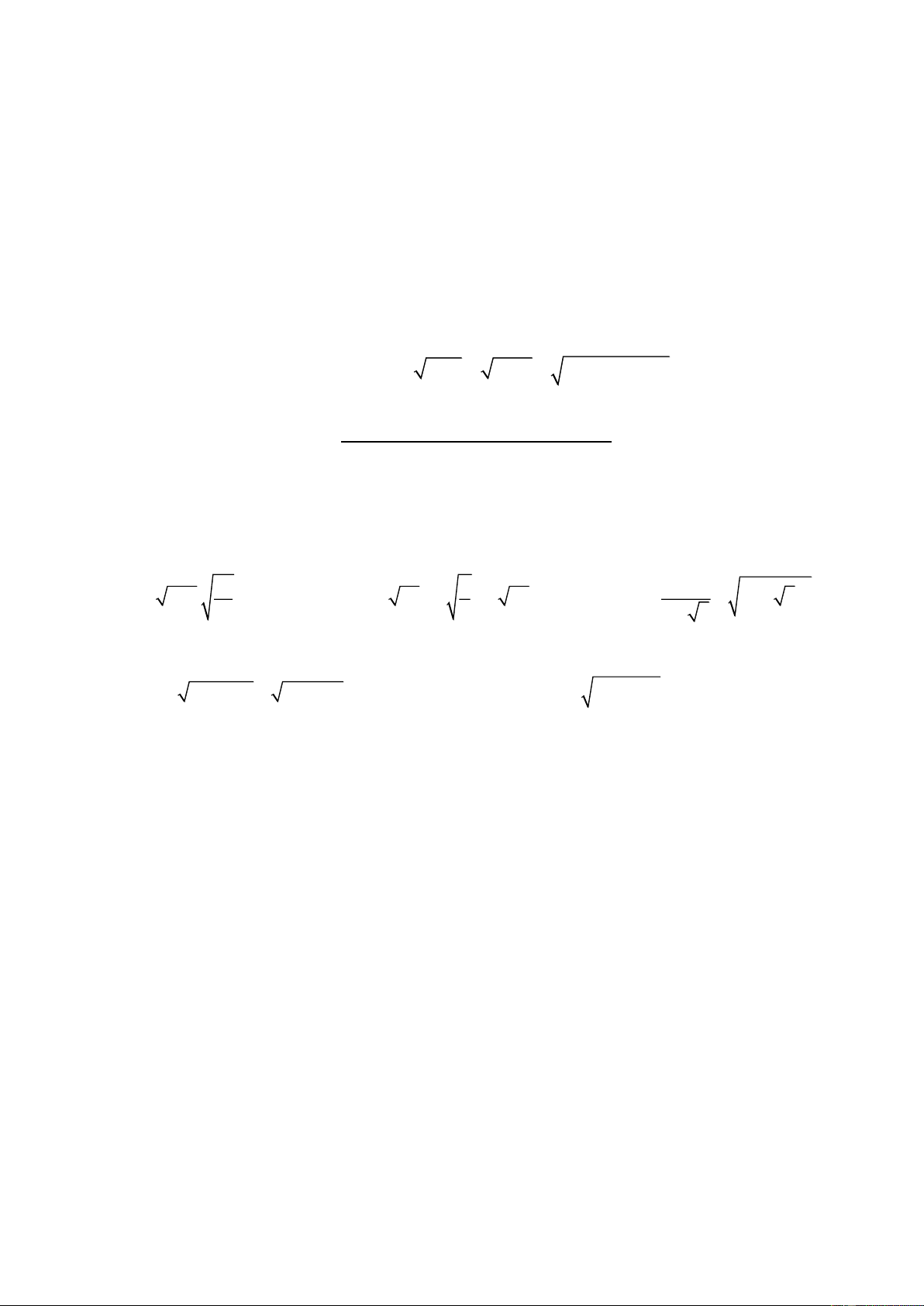

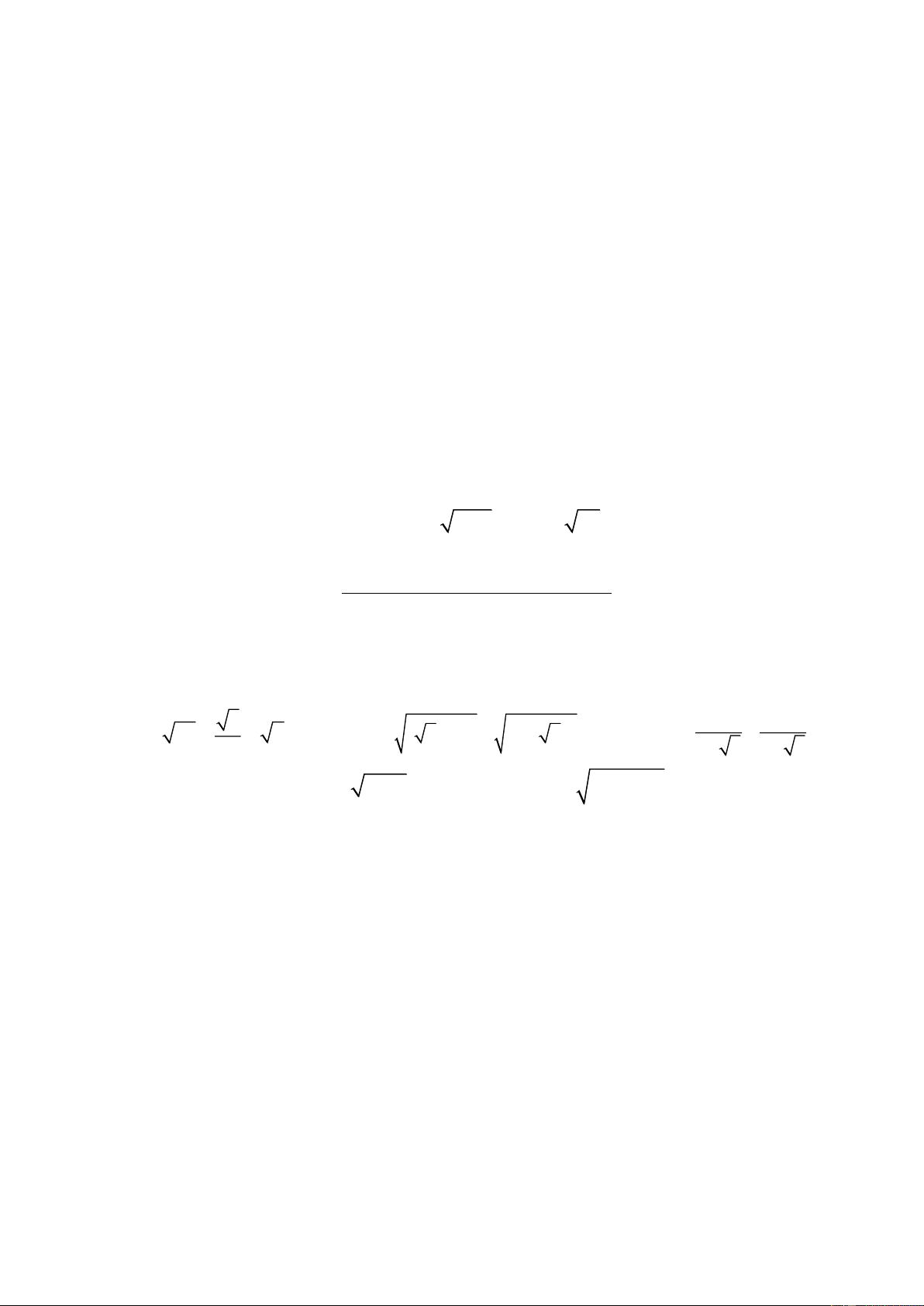
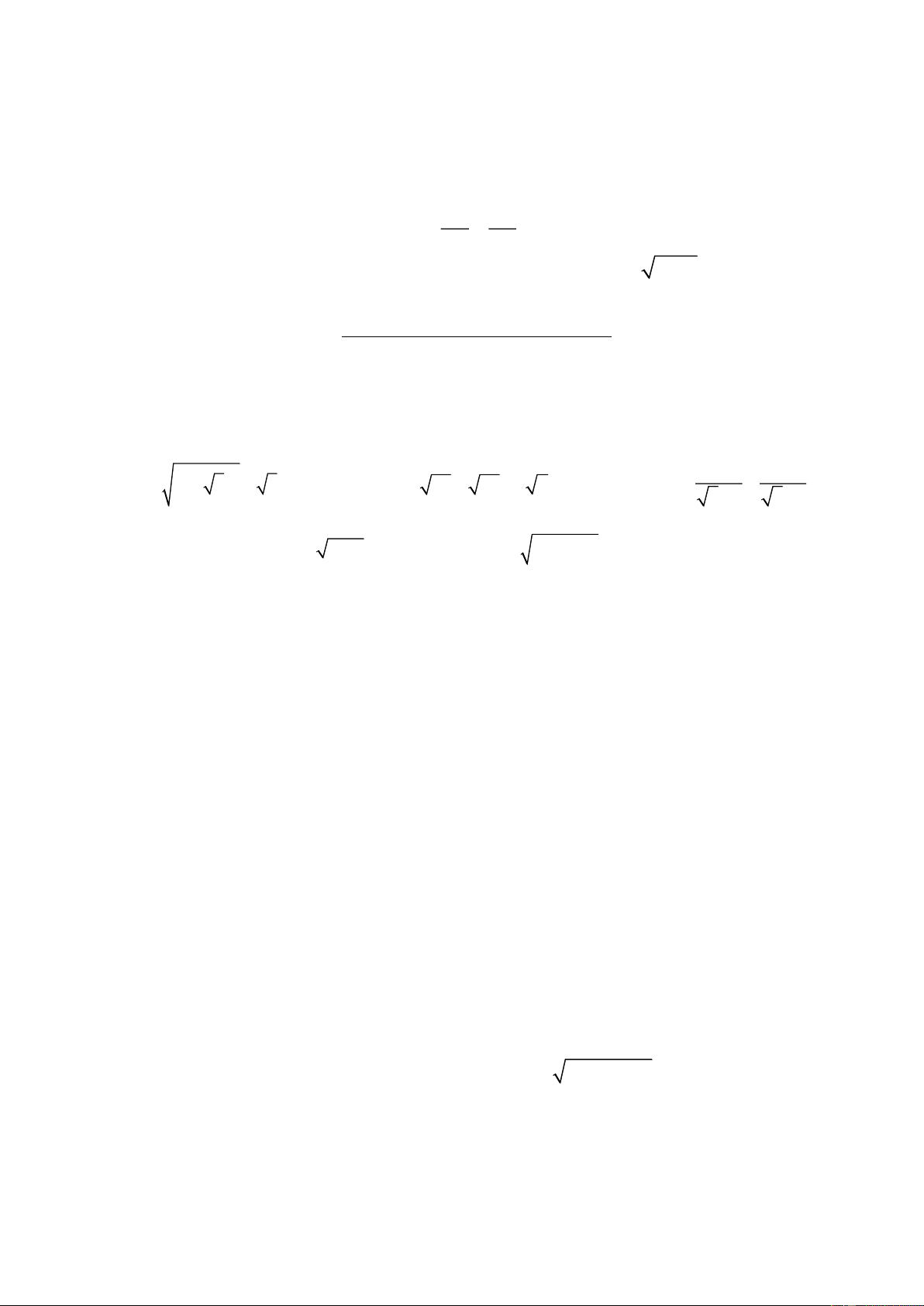
Preview text:
Trường THCS Long Toàn
ĐỀ CƯƠNG ÔN TẬP TOÁN 9 - HỌC KỲ I
NĂM HỌC: 2023 - 2024
I. CÁC KIẾN THỨC TRỌNG TÂM
1. Chủ đề 1: CĂN BẬC HAI, CĂN BẬC BA.
- Thực hiện được các phép tính, các phép biến đổi đơn giản liên quan đến căn bậc hai
- Vận dụng thành thạo các kiến thức về căn bậc hai để thực hiện được các dạng bài
tập tính toán, rút gọn biểu thức (chứng minh đẳng thức), tìm x, giải phương trình, bất
phương trình, so sánh các số... có chứa căn thức bậc hai.
2. Chủ đề 2: HÀM SỐ BẬC NHẤT.
- Biết cách xác định các hệ số a, b của hàm số bậc nhất (hay xác định hàm số, lập
phương trình đường thẳng) trong từng trường hợp cụ thể.
- Vẽ được đồ thị, nắm được tính chất của hàm số bậc nhất y = ax + b (a 0). Nắm
được điều kiện để hai đường thẳng cắt nhau, song song, trùng nhau.
- Biết cách chứng minh các điểm thẳng hàng; chứng minh đường thẳng luôn đi qua 1
điểm, … (vận dụng cao)
- Tính được chu vi, diện tích các hình trên mặt phẳng tọa độ, …
3. Chủ đề 3: HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG.
- Vận dụng được các hệ thức lượng trong tam giác vuông vào việc chứng minh, tính
toán độ dài các cạnh, độ lớn các góc nhọn trong tam giác vuông.
- Giải thành thạo dạng toán “giải tam giác vuông”.
- Biết sử dụng máy tính cầm tay để hỗ trợ cho việc tính kết quả cạnh, góc.
- Có kỹ năng vẽ hình theo nội dung (gt) của bài toán.
4. Chủ đề 4: ĐƯỜNG TRÒN.
Vận dụng tốt mối quan hệ đường kính và dây của đường tròn, liên hệ giữa dây và
khoảng cách từ tâm đến dây, dấu hiệu nhận biết tiếp tuyến, tính chất hai tiếp tuyến cắt
nhau, vị trí tương đối của đường thẳng và đường tròn, của hai đường tròn để chứng minh
tiếp tuyến của đường tròn, chứng minh đẳng thức, chứng minh hai đường thẳng song
song, hai đoạn thẳng bằng nhau, hai góc bằng nhau, ba điểm thẳng hàng, …
II. CÁC ĐỀ THAM KHẢO (Đề minh họa kiểm tra HKI năm học 2023-2024) ĐỀ 1 Bài 1 (3,0 điểm). 1. Thực hiện phép tính: 50 2 2 3 3 a) 3. 27
b) 15 4 3 15 c) 2 7 2 7 2
2. Tìm x, biết: a) 4x 7 3 b) x2 7 2 5
Bài 2 (1,0 điểm) Cho hàm số bậc nhất y = (m –1) x + 2 (m≠1) (1).
1) Tìm điều kiện của m để hàm số (1) đồng biến trên R. 1
2) Tìm giá trị của m và k để đồ thị hàm số (1) và đường thẳng y = x + k – 1 trùng nhau.
Bài 3 (1,5 điểm) Cho hàm số y = -x + 4
1) Vẽ đồ thị (d) của hàm số đã cho.
2) Đường thẳng (d) cắt trục tung tại điểm A và cắt tục hoành tại điểm B. Gọi M là
trung điểm của AB. Tính diện tích tam giác OMB. (đơn vị trên trục số tương ứng cm) Bài 4 (1,5 điểm).
Cho tam giác ABC vuông tại A đường cao AH=6cn. Tính AB, AC, BC? biết CH =
8cm. (làm tròn lấy một chữ số thập phân) Bài 5 (2,5 điểm).
Cho đường tròn tâm O và một điểm A nằm ngoài đường tròn này. Từ A vẽ hai tiếp
tuyến AB, AC của đường tròn (O) (B và C là tiếp điểm). Gọi H là giao điểm của OA và BC.
1) Chứng minh OA vuông góc với BC tại H.
2) Từ B vẽ đường kính BD của (O), đường thẳng AD cắt đường tròn (O) tại E (E
khác D). Chứng minh: AE.AD = AC2.
3) Qua O vẽ đường thẳng vuông góc với cạnh AD tại K và cắt đường BC tại F.
Chứng minh rằng FD là tiếp tuyến của đường tròn (O). 1 1 1 1
Bài 6 (0,5 điểm). Cho A ... . 2 2 2 3 3 2 3 4 4 3 99 100 100 99
Chứng minh rằng A là một số hữu tỉ. ĐỀ 2 Bài 1 (3,0 điểm). 1. Thực hiện phép tính: 80 3 3 a) 5. 20 7 42 b) 28 63 c) 5 3 5 3 5 2. Tìm x, biết:
a) 5x 6 3 0 b x2 ) 3 5 2
Bài 2 (1,0 điểm). Cho hàm số y m
1 x m 2 (1)
1) Tìm điều kiện của m để hàm số luôn nghịch biến.
2) Tìm giá trị của m để đồ thị của hàm số (1) song song với đồ thị hàm số y 3 x 1.
Bài 3 (1,5 điểm). Cho hàm số y 2x 4.
a) Vẽ đồ thị (d) của hàm số y 2x 4 .
b) Xác định các hệ số a và b của hàm số y ax b , biết rằng đồ thị (d’) của hàm số
này song song với (d) và đi qua điểm A0; 3 . 2
Bài 4 (1,5 điểm). Cho tam giác ABC vuông tại A, có đường cao AH = 6 cm. Hãy tính
ACB và độ dài các cạnh của ABC, biết CH = 8 cm (độ dài làm tròn 0,01; góc làm tròn đến độ).
Bài 5 (2,5 điểm). Cho đường tròn (O; R) có đường kính AB. Từ điểm D thuộc (O; R) (D
khác A, B), vẽ tiếp tuyến cắt tiếp tuyến tại A của đường tròn ở E và cắt tiếp tuyến tại B
của đường tròn ở F. Tia AD cắt tia BF ở C. Chứng minh: a) ADE DAE b) FB = FC c) AE. BC = 2R2
Bài 6 (0,5 điểm). Giải phương trình: x 1 4 x x 1 4 x 1 ĐỀ 3 Bài 1 (3,0 điểm).
1. Thực hiện phép tính: 16 1 a) 250. b) 50 2 5 72 c) 2 4 2 5 10 2 3 5 2. Tìm x, biết:
a) 25x 25 16x 16 3 b) x2 5 2 7
Bài 2 (1,0 điểm). Cho hàm số bậc nhất y = (m – 3)x + m + 1 (m ≠ 3) (1).
a) Tìm điều kiện của m để hàm số (1) đồng biến, nghịch biến trên R.
b) Tìm giá trị của m để đồ thị hàm số (1) đi qua gốc tọa độ.
Bài 3 (1,5 điểm). Cho hàm số y = x + 3.
a) Vẽ đồ thị của hàm số đã cho.
b) Xác định hệ số a và b của đường thẳng (d): y = ax + b, biết (d) song song với
đường thẳng y = x + 3 và cắt trục hoành tại điểm có hoành độ bằng 3.
Bài 4 (1,5 điểm). Cho tam giác ABC vuông tại A, đường cao AH. Biết BH = 9cm, HC =
16cm. Tính AH, AC và HAC (góc làm tròn đến độ).
Bài 5 (2,5 điểm). Cho đường tròn (O) và một điểm M nằm ngoài đường tròn. Từ M kẻ
tiếp tuyến MA với đường tròn (O) (A là tiếp điểm). Qua A vẽ đường thẳng vuông góc với
OM tại H, cắt đường tròn (O) tại B (B ≠ A). Kẻ đường kính AC của (O).
a) Chứng minh BC song song OM.
b) Chứng minh MB là tiếp tuyến của đường tròn (O). 3
c) Đường thẳng MC cắt đường tròn (O) tại điểm thứ hai là D. Chứng minh
MHD OCD .
Bài 6 (0,5 điểm). Tìm giá trị nhỏ nhất của biểu thức A 2023 x 2024 1 x . ĐỀ 4 Bài 1 (3,0 điểm): 1. Thực hiện phép tính: a) ; b) ; c) . 2. Tìm x, biết: a) ; b) .
Bài 2 (1,0 điểm): Cho hàm số bậc nhất (1).
1. Tìm điều kiện của m để hàm số (1) đồng biến trên .
2. Tìm giá trị của m để đồ thị hàm số (1) và đường thẳng song song nhau.
Bài 3 (1,5 điểm): Cho hàm số .
1. Vẽ đồ thị (d) của hàm số đã cho.
2. Đường thẳng (d) cắt trục tung tại điểm A và cắt tục hoành tại điểm B. Tính diện
tích tam giác ABO (đơn vị trên trục số tương ứng là cm).
Bài 4 (1,75 điểm): Cho tam giác ABC vuông tại A, AB = 6cm, BC = 10cm, đường cao AH. 1. Tính độ dài BH.
2. Giải tam giác vuông ABC.
Bài 5 (2,25 điểm): Cho đường tròn (O). Qua điểm M ở ngoài đường tròn, vẽ hai tiếp
tuyến MA, MB đến đường tròn (A, B là tiếp điểm). Kẻ đường kính AC của đường tròn. 1. Chứng minh . 2. Chứng minh .
3. Gọi K là giao điểm thứ hai của MC với đường tròn (O). Chứng minh .
Bài 6 (0,5 điểm): Cho biểu thức
. Tìm các số thực để A là số nguyên. ĐỀ 5 Bài 1 (3,0 điểm). 1. Thực hiện phép tính: 4 1 1 3 a) 3 50 2 b) 2 3 2 3 c) 12 2 2 3 3
2. Tìm x, biết: a) 3x 7 5 b) x2 1 2 6 0
Bài 2 (1,0 điểm) Cho hàm số bậc nhất y m
1 x m 2m 1 (1)
1) Tìm điều kiện của m để hàm số luôn nghịch biến.
2) Tìm giá trị của m để đồ thị của hàm số (1) song song với đồ thị hàm số y 3 x 1.
Bài 3 (1,5 điểm) Cho hàm số 1 y
x 2 có đồ thị là đường thẳng (D) 2
1) Vẽ (D) trên hệ trục tọa độ Oxy.
2) Đường thẳng (D) cắt Ox, Oy lần lượt tại A, B.
a) Xác định tọa độ A, B.
b) Tính diện tích tam giác OAB.
Bài 4 (1,5 điểm). Cho ABC vuông tại A, đường cao AH. Biết AB = 15cm, BH = 9cm.
Tính BC, AH và ABC . (Số đo góc làm tròn đến độ)
Bài 5 (2,5 điểm). Cho (O) đường kính BC. Trên tiếp tuyến Bx của (O) lấy điểm A (A
khác B). Qua A vẽ tiếp tuyến AD với đường tròn (D là tiếp điểm).
1) Chứng minh BDC vuông.
2) BD cắt OA tại H. Chứng minh BD OA và OH.OA = R2.
3) Đường thẳng vuông góc với BC tại O cắt AC tại I và cắt đường thẳng CD tại N. Chứng minh IN = IO.
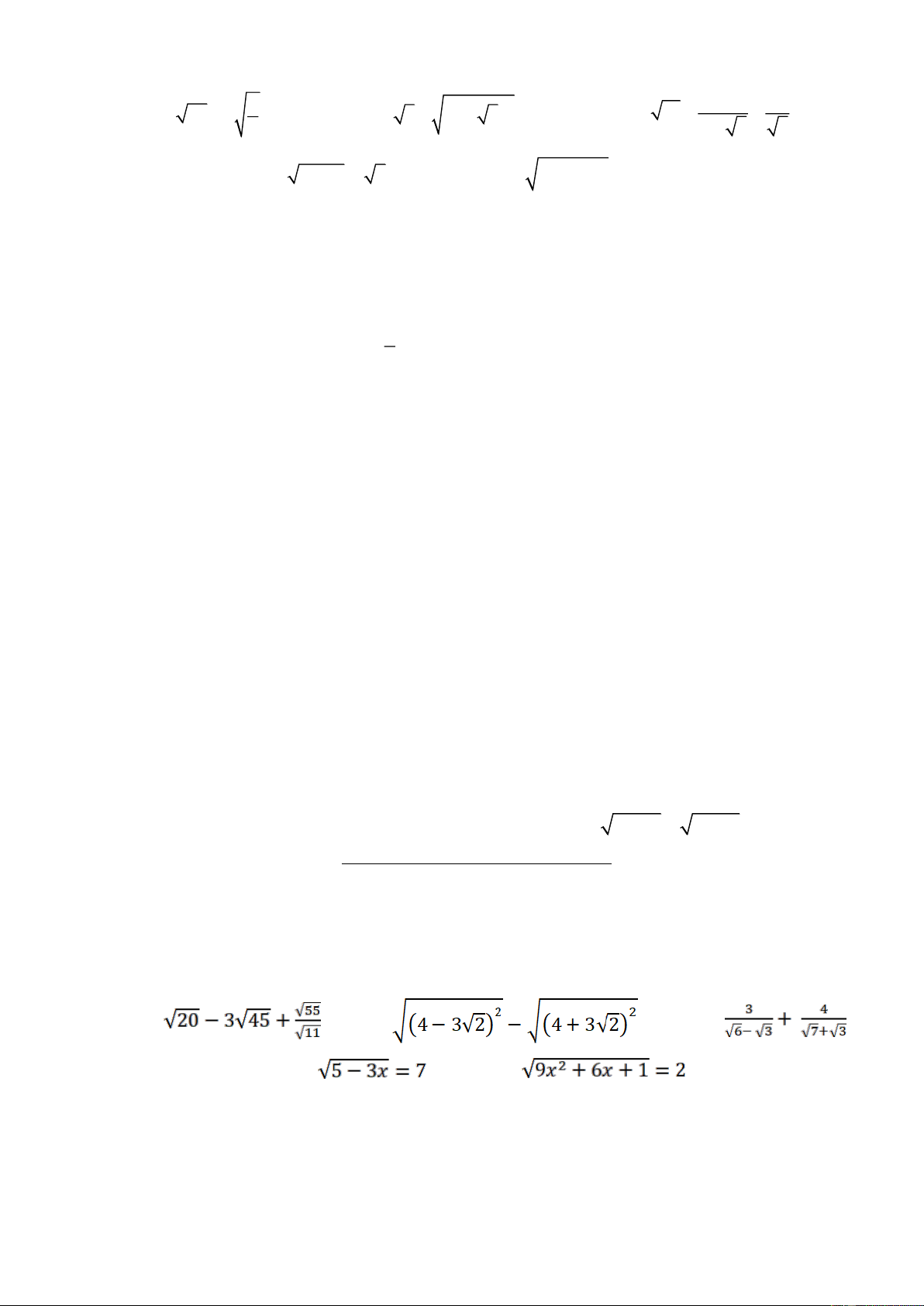
Bài 6 (0,5 điểm). Tìm giá trị lớn nhất của biểu thức: A 3x 6 8 3x ĐỀ 6 Bài 1 (3,0 điểm). 1. Thực hiện phép tính: a) b) c) 2. Tìm x, biết: a) b)
Bài 2 (1,0 điểm) Cho hàm số bậc nhất y = (m + 6) x – 7 (m ≠ - 6) (1).
1) Tìm điều kiện của m để hàm số (1) đồng biến trên R.
2) Tìm giá trị của m và k để đồ thị hàm số (1) và đường thẳng y = x + k – 1 cắt nhau
tại 1 điểm trên trục tung. 5
Bài 3 (1,5 điểm) Cho hàm số y = x – 4
1) Vẽ đồ thị (d) của hàm số đã cho.
2) Đường thẳng (d) cắt trục tung tại điểm A và cắt tục hoành tại điểm B. Tính
khoảng cách từ O đến đường thẳng (d). (đơn vị trên trục số tương ứng cm)
Bài 4 (1,5 điểm). Giải tam giác ABC vuông tại A. Biết AB = 4cm; BC = 8cm. Bài 5 (2,5 điểm).
Cho đường tròn (O; R) đường kính AB. Lấy điểm C trên cung AB sao cho AC < BC. a) Chứng minh A BC vuông.
b) Qua A vẽ tiếp tuyến (d) với đường tròn (O), BC cắt (d) tại F. Qua C vẽ tiếp tuyến
(d/) với đường tròn (O) cắt (d) tại D. Chứng minh DA = DF.
c) Vẽ CH vuông góc với AB (H thuộc AB), BD cắt CH tại K. Chứng minh K là trung điểm của CH?
Bài 6 (0,5 điểm). Giải phương trình: 2
1 x 1 4x 3x ĐỀ 7
Bài 1. (1,5 điểm)
1. Thực hiện phép tính: 8 2 2 2 2 a) 32 2
b) 6 3 5 6 c) 2 1 5 1 5
2. Tìm x , biết: a) 2 x 3 8 0 b) x 2 3 1 8
Bài 2. (1,0 điểm). Cho hàm số bậc nhất y (m 2)x 3 (1).
1) Tìm điều kiện của m để hàm số (1) là hàm số bậc nhất.
2) Tìm giá trị của m và k để đồ thị hàm số (1) và đường thẳng y 3x k 1 song song với nhau.
Bài 3. (1,5 điểm). Cho hàm số y x 2
1) Vẽ đồ thị (d) của hàm số đã cho.
2) Gọi giao điểm của (d) với trục Ox là A, với trục Oy là B
a) Xác định tọa độ các điểm A, B
b) Tính chu vi tam giác OAB (đơn vị đo trên mỗi trục tọa độ là cm)
Bài 4. (1,0 điểm). Cho tam giác ABC vuông tại A đường cao AH, biết AC = 6 cm, HC =
3 cm. Tính AB, AH, BC (làm tròn lấy một chữ số thập phân)
Bài 5. (2,5 điểm). Cho đường tròn (O; R) và điểm A nằm ngoài (O). Từ A kẻ hai tiếp
tuyến AB, AC với (O) (B, C là các tiếp điểm). Gọi H là giao điểm của OA và BC. 6
a) Tính OH. OA theo R.
b) Chứng minh bốn điểm A, B, O, C cùng thuộc một đường tròn.
c) Chứng minh OA là đường trung trực của BC.
d) Lấy D đối xứng với B qua O. Gọi E là giao điểm của đoạn thẳng AD với (O) (E
không trùng với D). Chứng minh DE BD BE BA
Bài 6. (0,5 điểm). Tìm giá trị nhỏ nhất của biểu thức B x 7 x 5 ĐỀ 8 Bài 1 (3,0 điểm).
1. Thực hiện từng bước các phép tính: 2 1 1 a) 1 3 3 b) 50 72 3 2 c) 5 1 5 1
2. Tìm x, biết: a) x 5 4 b) x2 5 3 7
Bài 2 (2,5 điểm) Cho đường thẳng (d): y m 4 x m 6 (m 4 ; m là tham số).
1) Tìm điều kiện của m để hàm số (d) đồng biến trên R.
2) Tìm m để đường thẳng (d) đi qua điểm A(-1;2).
3) Vẽ đường thẳng (d) với giá trị vừa tìm được của m ở câu 2).
4) Tìm giá trị của m để đường thẳng (d) song song với đường thẳng y = -2x + 3 (d1).
5) Vẽ đường thẳng (d1) trên cùng một mặt phẳng tọa độ với đường thẳng (d). Gọi B
là giao điểm của 2 đường thẳng trên. Tìm tọa độ điểm B.
Bài 3 (1,5 điểm) Cho tam giác ABC vuông tại A, có đường cao AH. Hãy tính các cạnh
của tam giác ABC, biết CH = 9cm, BH = 4cm.
Bài 4 (2,5 điểm) Cho đường tròn (O; R), dây BC khác đường kính. Hai tiếp tuyến với
đường tròn tại B và C cắt nhau ở A. Kẻ đường kinh CD, kẻ BH vuông góc với CD tại H.
Gọi K là giao điểm của OA và BC.
a) Chứng minh: K là trung điểm của BC
b) Chứng minh ABC CBH
c) Gọi I là giao điểm của AD và BH. Chứng minh I là trung điểm BH.
Bài 5 (0,5 điểm). Giải phương trình: 2 2
3x 21x 18 2 x 7x 7 2 -------HẾT-------
Chúc các em ôn tập tốt! 7




