Đề + Đáp án các năm - Xác suất thống kê | Trường Đại học CNTT Thành Phố Hồ Chí Minh

lOMoAR cPSD| 40551442
ĐẠI HỌC QUỐC GIA TP. HỒ CHÍ MINH ĐỀ THI GIỮA KỲ MÔN XSTK
TRƯỜNG ĐẠI HỌC CÔNG NGHỆ THÔNG TIN Học kỳ 2, năm học 2020-2021. BỘMÔNTOÁN–LÝ Ngày thi: .../ .../2021
Thời gian làm bài: 60 phút. Được
sử dụng tài liệu giấy.
Câu 1.(2.5 điểm) Trong một cửa hiệu kinh doanh điện thoại di động, tỉ lệ điện thoại
di động của hãng Nokia, Samsung và Iphone lần lượt là 20%, 50% và 30%. Tỉ lệ bị trục
trặc (về cài đặt) trong thời gian bảo hành của các loại diện thoại di động của hãng Nokia,
Samsung và Iphone tương ứng là 6%, 8%, 7%. Giả sử một khách hàng mua ngẫu nhiên
một điện thoại di động và điện thoại đó không bị trục trặc trong suốt thời gian bảo
hành. Tính xác suất để điện thoại đó của hãng Samsung.
Câu 2.(2 điểm) Một nhà máy dệt có 1000 ống sợi. Xác suất để trong 1 giờ máy hoạt
động có 1 ống sợi bị đứt là 0.002. Tính xác suất để trong 1 giờ máy hoạt động có không
quá 4 ống sợi bị đứt.
Câu 3.(3 điểm) Thời gian tải một tập tin có dung lượng dưới 20MB từ một website
được mô hình hóa bởi biến ngẫu nhiên X (tính theo phút) có hàm mật độ như sau: C(5x
x ) nếu x [0,5],
f(x) = ( 3 − 4 ∈∈ 0
nếu x / [0,5]. a) Xác định C. b)
Tính thời gian trung bình để tải một tập tin có dung lượng dưới 20MB từ website đó. c)
Giả sử bạn thấy tập tin đó vẫn chưa tải xong sau khi bắt đầu tải được 2
phút. Tính xác suất phải mất hơn 2 phút nữa mới tải xong tập tin.
Câu 4.(2.5 điểm) Giả sử nồng độ chloride trong máu (mmol/L) có phân phối chuẩn
với trung bình là 104 và độ lệch chuẩn là 5. a.
Tính tỉ lệ người có nồng độ chloride trong máu nhiều hơn 105. b.
Chọn ngẫu nhiên 1000 người. Tính xác suất có từ 200 đến 300 người có
nồngđộ chloride trong máu nhiều hơn 105. Hết
Cán bộ coi thi không giải thích gì thêm. Trưởng Bộ môn Toán-Lý CAO THANH TÌNH 1 lOMoAR cPSD| 40551442 lOMoAR cPSD| 40551442 lOMoAR cPSD| 40551442
ĐẠI HỌC QUỐC GIA TP. HỒ CHÍ MINH
ĐỀ THI GIỮA KỲ MÔN XSTK
TRƯỜNG ĐẠI HỌC CÔNG NGHỆ THÔNG TIN
Học kỳ 2, năm học 2021-2022. BỘMÔNTOÁN–LÝ
Ngày thi: .../ .../2022 Thời gian làm bài: 60 phút.
Được sử dụng tài liệu giấy.
Câu 1.(2 điểm) Cho A, B, C là các biến cố. Giả sử
P(A) = 0.5, P(B) = 0.6, P(C) = 0.7, P(A|B) = 0.2, P(B ∪ C) = 0.85.
a) Hỏi hai biến cố A và B có độc lập nhau không?
b) Hỏi hai biến cố B và C có độc lập nhau không? Đáp án:
a) P(A|B) 6= P(A) suy ra A,B không độc lập. (1đ)
b) P(B ∩ C) = P(B) + P(C) − P(B ∪ C) = 0.45 (0.5 đ)
P(B ∩ C) 6= P(B).P(C) suy ra B,C không độc lập. (0.5đ)
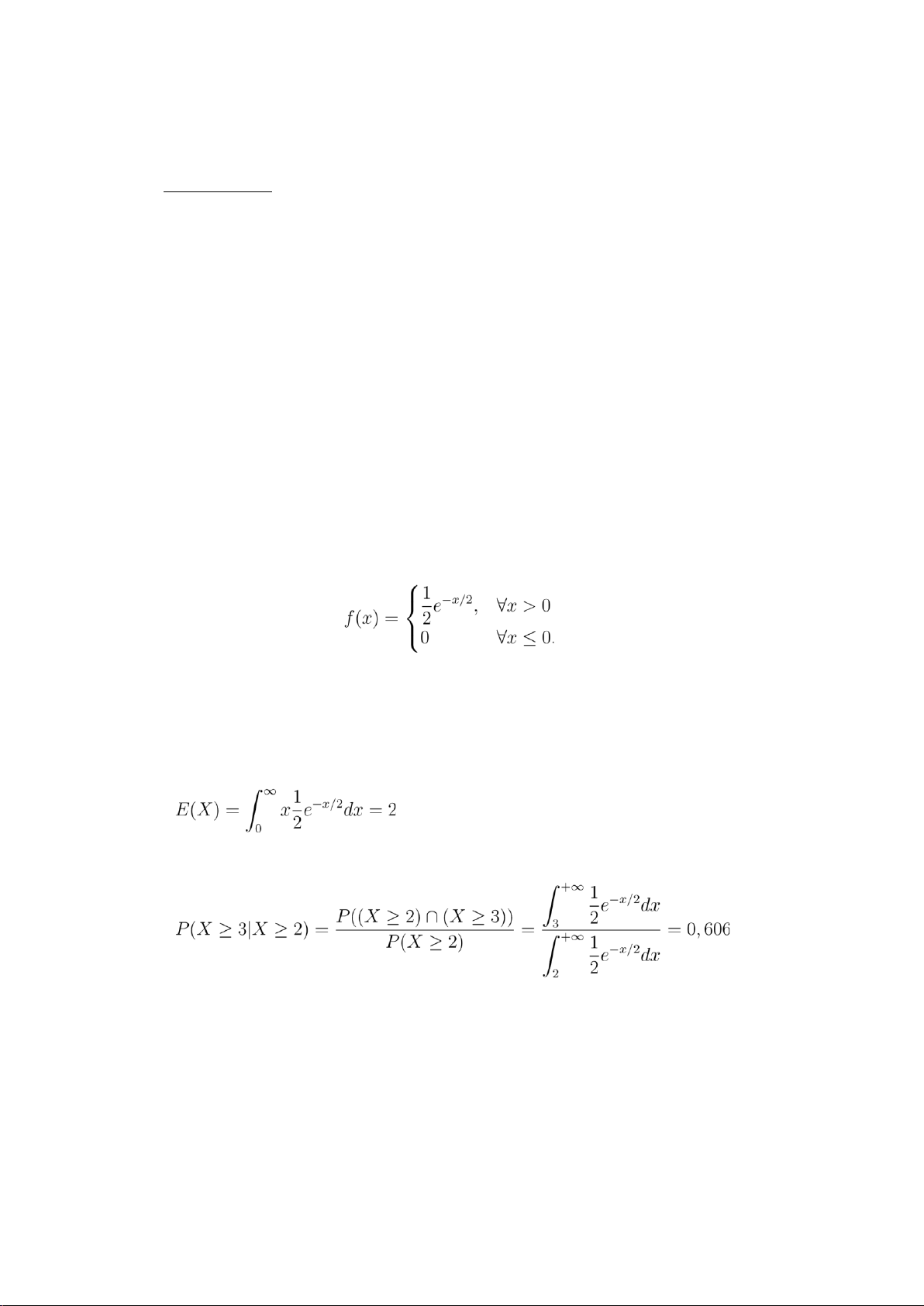
Câu 2.(3 điểm) Cho X là thời gian sử dụng của một loại pin (tính bằng năm). Giả sử
hàm mật độ xác suất của X được cho bởi ,
a. Tính thời gian sử dụng trung bình của loại pin đó.
b. Giả sử có một viên pin loại này đã được sử dụng 2 năm. Tính xác suất để
pin này sử dụng được ít nhất 3 năm. Đáp án: a) .
Đúng công thức 1đ, ra đúng kết quả tích phân 0.5đ, tổng cộng 1.5đ (phần tính tích
phân sinh viên có thể dùng máy tính rồi ghi kết quả) b) .
Đúng công thức 1đ, ra đúng kết quả tích phân 0.5đ, tổng cộng 1.5đ (phần tính tích
phân sinh viên có thể dùng máy tính rồi ghi kết quả)
Câu 3.(3 điểm) Một loại virus máy tính mới tấn công một thư mục bao gồm 1350
tệp. Mỗi tệp bị hỏng với xác suất 0.75 độc lập với các tệp khác.
a. Xác suất có 1000 tệp bị hỏng là bao nhiêu?
b. Xác suất có từ 1000 đến 1020 tệp bị hỏng là bao nhiêu? 1 lOMoAR cPSD| 40551442 Đáp án
Gọi X là số tệp bị hỏng trong 1350 tệp. Ta có X ∼ B(n;p) với n = 1350 và p = 0,75.
Vì np = 1350.0,75 = 1012,5 và n(1 − p) = 1350.0,25 = 337,5 nên có thể dùng xấp xỉ
phân phối chuẩn X ≈ N(µ,σ2) với µ = np = 1012,5 và
σ = pnp(1 − p) = p1350.0,75.0,25 = 15,91. (1đ)
a. Dùng hiệu chỉnh liên tục và xấp xỉ phân phối chuẩn để tính
b. Dùng hiệu chỉnh liên tục và xấp xỉ phân phối chuẩn
Nếu sinh viên không biết dùng xấp xỉ và không tính ra được kết quả nhưng biết đưa
về công thức tính theo phân phối Nhị thức thì cho nửa số điểm cho mỗi phần, tức là
tổng điểm tối đa 1.5đ.
Câu 4.(2 điểm) Giả sử kit xét nghiệm nhanh covid của công ty A sản xuất có hiệu
quả như sau: chỉ có 60% người bị nhiễm covid khi xét nghiệm nhanh bằng loại kit đó
nhận kết quả dương tính; chỉ có 70% người không bị nhiễm covid khi xét nghiệm nhanh
bằng loại kit đó nhận kết quả âm tính.
Giả sử tỉ lệ nhiễm covid ở thành phố H là 30%.
a) Một người ở thành phố H xét nghiệm covid bằng kit xét nghiệm của công
ty A lần thứ nhất cho kết quả âm tính. Tính xác suất người đó bị nhiễm covid ?
b) Một người ở thành phố H xét nghiệm covid bằng kit loại đó lần thứ nhấtra kết
quả âm tính nên liền xét nghiệm thêm lần nữa và cũng ra kết quả âm tính. Hỏi xác
suất người đó bị nhiễm covid là bao nhiêu ? Đáp án:
Gọi Ai là biến cố xét nghiệm cho ra kết quả là âm tính ở lần thứ i. Ta có A1,A2 độc lập
nhau và P(A1) = P(A2).
Gọi B là biến cố bị nhiễm covid.
P(B) = 0.3,P(A¯i|B) = 0.6,P(Ai|B¯) = 0.7. (0.5đ) 2 lOMoAR cPSD| 40551442
a) P(A1) = P(A1|B)P(B) + P(A1|B¯)P(B¯) = 0.61 (0.5đ) P A |B P B b) 3 lOMoAR cPSD| 40551442 lOMoAR cPSD| 40551442 lOMoAR cPSD| 40551442
ĐẠI HỌC QUỐC GIA TP. HỒ CHÍ MINH
ĐỀ THI GIỮA KỲ MÔN XSTK
TRƯỜNG ĐẠI HỌC CÔNG NGHỆ THÔNG TIN
Học kỳ 1, năm học 2022-2023. BỘMÔNTOÁN–LÝ Ngày thi: .../ .../2022
Thời gian làm bài: 60 phút. Được
sử dụng tài liệu giấy.
Câu 1.(2 điểm) Một người đầu tư độc lập vào ba dự án A, B, C. Xác suất các dự án này
có lợi nhuận tương ứng là 0.4, 0.7, 0.8.
a) Tính xác suất có dự án mà người đó đầu tư có lợi nhuận.
b) Tính xác suất có ít nhất hai dự án mà người đó đầu tư có lợi nhuận.
Câu 2.(3 điểm) Mức tiêu thụ xăng (đơn vị: 10 nghìn lít) một ngày tại một trạm xăng là
biến ngẫu nhiên X liên tục có hàm mật độ xác suất , a. Tìm k;
b. Tính xác suất mức tiêu thụ xăng trong một ngày của trạm hơn 8000 lít.
c. Tính lượng xăng được tiêu thụ trung bình mỗi ngày.
Câu 3.(3 điểm) Khối lượng của một sản phẩm (đơn vị tính là “gram”) do một máy sản
xuất ra là biến ngẫu nhiên liên tục X, thỏa X ∼ N(100,4). Sản phẩm được xem là đạt kỹ
thuật nếu có khối lượng từ 94 đến 106 gram.
a) Tìm tỷ lệ sản phẩm đạt yêu cầu kỹ thuật của nhà máy.
b) Hỏi trung bình trong 400 sản phẩm bất kì, có bao nhiêu sản phẩm không
đạt yêu cầu kỹ thuật?
c) Hãy tính xác suất có không quá 10 sản phẩm không đạt yêu cầu kỹ thuật
trong 400 sản phẩm bất kì.
Câu 4.(2 điểm) Một nhà máy sản xuất có 4 phân xưởng. Phân xưởng I,II, III, IV có tỷ lệ
sản phẩm bị lỗi lần lượt là 1%;4%;2%;5%. Biết rằng tỷ lệ tham gia chế tạo sản phẩm
của các phân xưởng I, II, III, IV lần lượt là 30%;10%;40%;20%. Từ kho của nhà máy,
ta lấy ra ngẫu nhiên 1 sản phẩm để kiểm tra.
a) Tính xác suất sản phẩm lấy ra đó bị lỗi.
b) Giả sử sản phẩm được lấy ra đó bị lỗi; hãy tìm xác suất sản phẩm đó là do phân xưởng II sản xuất. Hết
Cán bộ coi thi không giải thích gì thêm. Trưởng Bộ môn Toán-Lý CAO THANH TÌNH lOMoAR cPSD| 40551442 lOMoAR cPSD| 40551442 lOMoAR cPSD| 40551442 lOMoAR cPSD| 40551442
ĐẠI HỌC QUỐC GIA TP. HỒ CHÍ MINH
TRƯỜNG ĐẠI HỌC CÔNG NGHỆ THÔNG TIN BỘMÔNTOÁN–LÝ
ĐỀ THI GIỮA KỲ MÔN XÁC SUẤT THỐNG KÊ
Học kỳ 1, năm học 2019 -2020.
Ngày thi: .../ .../2019 Thời gian làm bài:
60 phút Được sử dụng tài liệu giấy.
Câu 1.(2 điểm) Trung bình cứ 800 máy vi tính thì có 1 máy bị hỏng khi có bão kèm sấm
to. Một công ty có 4000 máy tính đang hoạt động ở trong vùng bị cơn bão kèm sấm to quét qua.
a) Tính xác suất công ty đó có ít hơn 10 máy tính bị hỏng.
b) Hỏi trung bình sau một cơn bão có sấm to, công ty đó bị hỏng bao nhiêu máy ?
Câu 2.(3 điểm) Một nhà máy sản xuất một chi tiết của điện thoại di động có tỷ lệ sản
phẩm đạt tiêu chuẩn chất lượng là 90%. Trước khi xuất xưởng, người ta dùng một thiết bị
kiểm tra để kết luận sản phẩm có đạt yêu cầu chất lượng hay không. Thiết bị có khả năng
phát hiện đúng chất lượng sản phẩm với xác suất là 0.95. Chọn ngẫu nhiên một sản phẩm để kiểm tra.
a) Tính xác suất sản phẩm đó đạt tiêu chuẩn và được thiết bị kiểm tra kết luận đạt tiêu chuẩn.
b) Tính xác suất sản phẩm đó được thiết bị kiểm tra kết luận đạt chuẩn.
c) Giả sử thiết bị kiểm tra kết luận là sản phẩm đó đạt tiêu chuẩn, xác suất thiết
bị đó không đạt tiêu chuẩn là bao nhiêu ?
Câu 3.(3 điểm) Cho X là biến ngẫu nhiên liên tục với hàm mật độ như sau:
nếu 0 < x < 1,
nếu x /∈ (0,1).
a) Tìm K và hàm phân phối xác suất của X.
b) Tính giá trị trung bình của X. c) Tính .
Câu 4.(2 điểm) Giả sử số máy vi tính được bán ra trong ngày của một cửa hàng là biến
ngẫu nhiên rời rạc X có phân phối xác suất như sau:
P(0) = 0.1, P(1) = 0.3, P(2) = 0.2, P(3) = 0.2, P(4) = 0.1, P(5) = 0.1
a) Tính xác suất P(0 < X < 3).
b) Giả sử mỗi máy tính được bán với giá 10 triệu đồng. Tính doanh thu trung bìnhmỗi
ngày từ việc bán máy vi tính của cửa hàng. Hết Trưởng Bộ môn Toán-Lý lOMoAR cPSD| 40551442
ĐẠI HỌC QUỐC GIA TP. HỒ CHÍ MINH
TRƯỜNG ĐẠI HỌC CÔNG NGHỆ THÔNG TIN BỘMÔNTOÁN–LÝ CAO THANH TÌNH lOMoAR cPSD| 40551442
ĐẠI HỌC QUỐC GIA TP. HỒ CHÍ MINH
TRƯỜNG ĐẠI HỌC CÔNG NGHỆ THÔNG TIN BỘMÔNTOÁN–LÝ
ĐỀ THI GIỮA KỲ MÔN XÁC SUẤT THỐNG KÊ
Học kỳ 1, năm học 2018 - 2019.
Ngày thi: .../ .../2018 Thời gian làm bài: 60
phút Được sử dụng tài liệu giấy.
Câu 1.(2 điểm) Một chương trình gồm có 2 mô đun. Xác suất mô đun 1 bị lỗi là 10%. Xác
suất mô đun 2 bị lỗi là 15%. Xác suất chương trình bị lỗi là 20%. Biết rằng chương trình bị
lỗi nếu ít nhất một mô đun bị lỗi. Hỏi việc mô đun 1 bị lỗi và mô đun 2 bị lỗi có liên quan nhau không ?
Câu 2.(3 điểm) Thời gian sống X (tính bằng năm) của một loại máy tính là một đại lương
ngẫu nhiên liên tục với mật độ xác suất
nếu 0 < x ≤ 10,
nếu x /∈ (0,10].
a) Tìm K. Tìm hàm phân phối F(x) của X.
b) Hỏi thời gian sống trung bình của loại máy tính đó là bao nhiêu năm.
c) Nếu thời gian bảo hành là một năm thì xác suất để một máy tính phải đưa đi
bảo hành trong vòng một năm bằng bao nhiêu ?
Câu 3.(3 điểm) Một bài thi trắc nghiệm có 10 câu. Mỗi câu có 4 phương án trả lời, trong
đó chỉ có 1 phương án đúng. Tất cả sinh viên đều trả lời hết các câu hỏi. Sinh viên thi đạt
nếu trả lời đúng ít nhất 4 câu.
a) Nếu sinh viên không ôn bài, sinh viên sẽ chọn câu trả lời một cách ngẫu nhiên.Hỏi
nếu sinh viên không ôn bài, thì xác suất thi đạt là bao nhiêu ?
b) Nếu sinh viên có ôn bài, thì xác suất thi đạt là 95%. Giả sử 60% sinh viên có ôn bài.
Nếu sinh viên A thi đạt, thì xác suất sinh viên không chuẩn bị bài là bao nhiêu ?
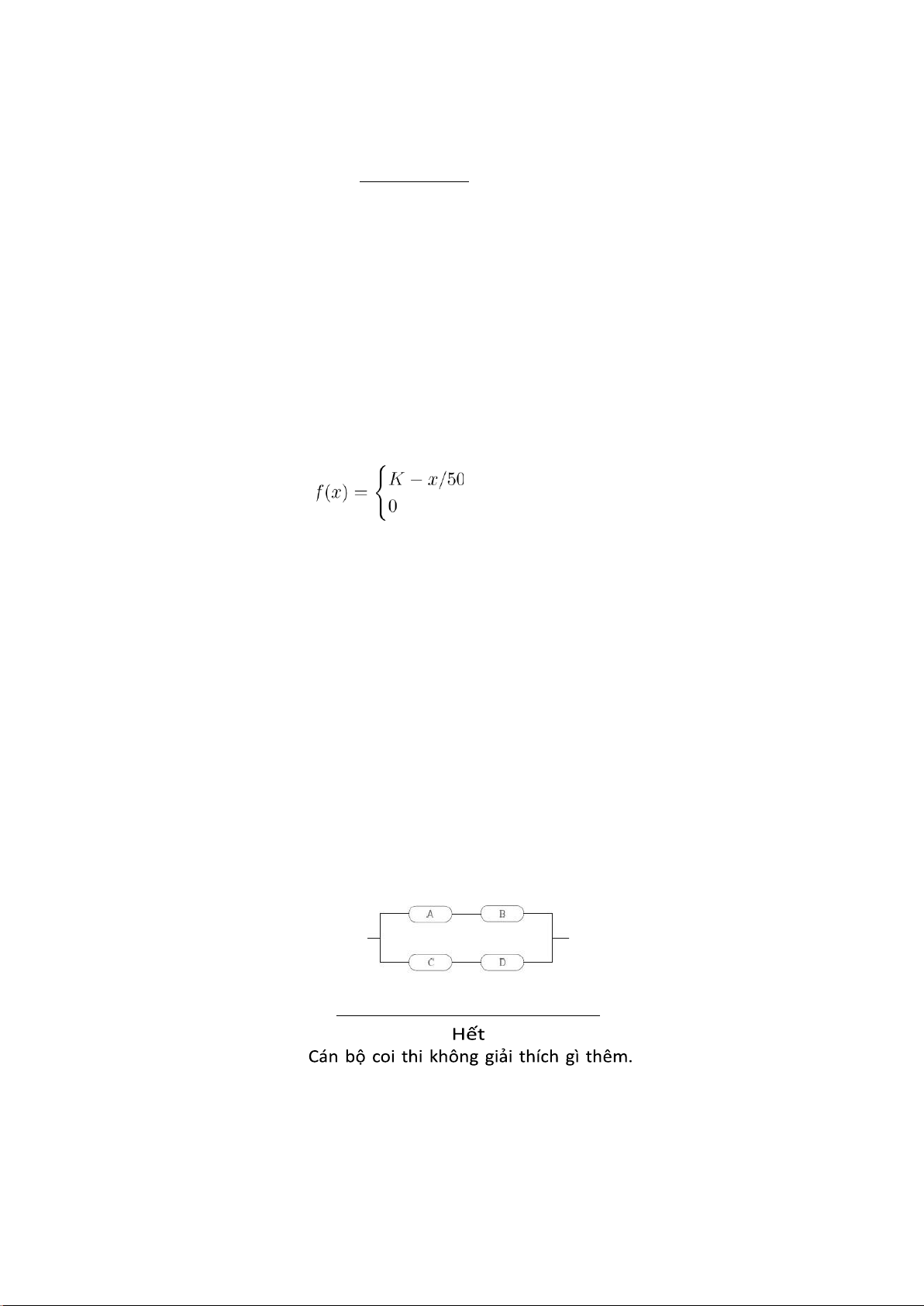
Câu 4.(2 điểm) Cho các thiết bị A,B,C,D làm việc một cách độc lập với nhau và độ tin cậy
của mỗi thiết bị (xác suất mỗi thiết bị hoạt động tốt) lần lượt là 90%, 85%, 95%, 93%. Một
hệ thống gồm các thiết bị mắc nối tiếp chỉ hoạt động tốt nếu tất cả các thiết bị đều hoạt
động tốt. Một hệ thống gồm các thiết bị mắc song song hoạt động tốt nếu có ít nhất một
trong các thiết bị đó hoạt động tốt. Xác định độ tin cậy của hệ thống sau:
Q.Trưởng Bộ môn Toán-Lý CAO THANH TÌNH lOMoAR cPSD| 40551442 lOMoAR cPSD| 40551442
ĐỀ THI GIỮA KỲ MÔN XSTK
Học kỳ 2, năm học 2018-2019.
Ngày thi: .../ .../2019 Thời
gian làm bài: 60 phút. Được
sử dụng tài liệu giấy.
Phần 1: (7 điểm) Trả lời tất cả các câu 1.1 - 1.3:
Câu 1.1.(2 điểm) Giả sử xác suất ổ cứng của một máy tính bị hỏng đột ngột là 2%.
Để đảm bảo dữ liệu lưu trên máy tính đó, người ta sao lưu dữ liệu của máy tính lên hai
thiết bị lưu trữ dự phòng với xác suất bị hỏng của mỗi thiết bị lần lượt là 3% và 4%. Ổ
cứng của máy tính và hai thiết bị lưu dự phòng hoạt động độc lập với nhau. Thông tin
được lưu trữ chỉ bị mất trong tình huống không may khi cả ba thiết bị gặp sự cố (bị
hỏng). Hãy tính xác suất thông tin lưu trữ được an toàn ?
Câu 1.2.(2 điểm) Một công ty có 70% nhân viên biết C++, 60% nhân viên biết Fortran
và 50% biết cả hai ngôn ngữ này. Tỷ lệ nhân viên biết ít nhất một trong hai ngôn ngữ
này là bao nhiêu ? Giả sử một nhân viên biết C++, hỏi xác suất nhân viên đó cũng biết Fortran là bao nhiêu ?
Câu 1.3.(3 điểm) Từ một hãng sản xuất linh kiện điện tử, các nhà thống kê nhận thấy
tuổi thọ của linh kiện điện tử đó là một đại lượng ngẫu nhiên liên tục (đơn vị: năm) có hàm mật độ như sau
nếu x ≥ 1, 0 nếu x < 1.
a) Xác định C và hàm phân phối của X.
b) Tìm tuổi thọ trung bình của linh kiện điện tử đó do hãng này sản xuất.
c) Tính tỷ lệ linh kiện điện tử do hãng này sản xuất có tuổi thọ không quá 2 năm.
Phần 2: (3 điểm) Chọn một trong ba câu sau:
Câu 2.1. Trong một vùng dân cư, cứ 1000 người thì có 250 người có hút thuốc lá.
Biết tỉ lệ người bị viêm họng trong số người hút thuốc lá là 75%, và trong số người
không hút thuốc lá là 25%. Khám ngẫu nhiên một người và thấy người đó bị viêm họng.
Tính xác suất người đó hút thuốc lá ? lOMoAR cPSD| 40551442
ĐẠI HỌC QUỐC GIA TP. HỒ CHÍ MINH
TRƯỜNG ĐẠI HỌC CÔNG NGHỆ THÔNG TIN BỘMÔNTOÁN–LÝ 1
Câu 2.2. Một công cụ tìm kiếm internet tìm một từ khóa trên các trang web độc lập
nhau. Có khoảng 20 % trang web chứa từ khóa cần tìm.
a) Tính xác suất có ít nhất 5 trong 10 trang web chứa từ khóa cần tìm.
b) Tính xác suất công cụ tìm kiếm phải duyệt ít nhất 5 trang web mới phát
hiện được từ khóa cần tìm.
Câu 2.3. Giả sử số yêu cầu được gởi đến một hệ thống tương tác có phân phối
Poisson với trung bình 12 yêu cầu trong 1 phút.
a) Tính xác suất có 10 yêu cầu trong 1 phút.
b) Tính xác suất có 10 yêu cầu trong 3 phút. Hết
Cán bộ coi thi không giải thích gì thêm.
Q.Trưởng Bộ môn Toán-Lý lOMoAR cPSD| 40551442 CAO THANH TÌNH 2 lOMoAR cPSD| 40551442
Ôn tập bài kiểm tra số 1 Nguyễn Minh Trí Ngày 5 tháng 4 năm 2023
Câu 1. Top 10 loại phần mềm máy tính bán chạy nhất trong năm gần đây bao gồm 3
phần mềm dành cho việc kê khai thuế, 5 phần mềm chống vi-rút hoặc chương
trình bảo mật và 2 phần mềm “khác”. Chọn ngẫu nhiên một phần mềm trong danh sách top 10.
a. Xác suất phần mềm đó không dành cho việc kê khai thuế là bao nhiêu?
b. Xác suất mà nó được sử dụng cho thuế hoặc là chương trình “khác” là baonhiêu?
Câu 2. Năm quốc gia có số lượng phát hành phim hàng đầu trong một năm cụ thể là
Hoa Kỳ với 471 bản phát hành, Vương quốc Anh với 386 bản phát hành, Nhật
Bản với 79 bản, Đức với 316 bản và Pháp với 132 bản. Chọn ngẫu nhiên 1 bản
phát hành mới. Tìm xác suất
a. Bản phát hành đó đến từ Châu Âu
b. Bản phát hành đó đến từ Châu Á
Câu 3. Hai mươi hai phần trăm sinh viên tại một trường UIT là nữ. Năm phần trăm
sinh viên trong trường UIT đang học chuyên ngành khoa học máy tính. Hai
phần trăm sinh viên nữ học chuyên ngành khoa học máy tính. Nếu một sinh
viên được chọn ngẫu nhiên, hãy tìm xác suất
a. sinh viên này là nữ biết sinh viên này học chuyên ngành khoa học máy tính;
b. sinh viên này đang học chuyên ngành khoa học máy tính biết sinh viên nàylà nữ.
Câu 4. Trong một nhà máy sản xuất giấy, các máy A, B, C sản xuất lần lượt 20%, 30%
và 50% tổng số giấy. Tỉ lệ sản phẩm lỗi của các máy A, B, C lần lượt là 3%, 2%
và 1%. Một tờ giấy được chọn ngẫu nhiên. a. Tìm xác suất mà nó bị lỗi.
b. Giả sử tờ giấy đó bị lỗi. Xác suất nó được sản xuất bởi máy A là bao nhiêu?
Câu 5. Khi bắt đầu một nghiên cứu về một nhóm người, 15% được phân loại là người
hút thuốc nặng, 30% là người hút thuốc nhẹ và 55% là người không hút thuốc.
Trong nghiên cứu kéo dài 5 năm, người ta xác định rằng tỷ lệ tử vong của
những người hút thuốc nặng và nhẹ lần lượt cao gấp 5 và 3 lần so với những 1 lOMoAR cPSD| 40551442
người không hút thuốc. Một người tham gia được chọn ngẫu nhiên đã chết
trong khoảng thời gian 5 năm.
a. Tính xác suất mà người tham gia là một người không hút thuốc.
b. Tính xác suất mà người tham gia là một người nghiện hút thuốc.
Câu 6. Giả sử X là một biến ngẫu nhiên liên tục có hàm mật độ xác suất được cho bởi a. Tìm C
b. Tính P(X > 1)
Câu 7. Giả sử X là một biến ngẫu nhiên liên tục có hàm mật độ xác suất được cho bởi a. Tìm C
b. Tính P(1 < X ≤ 2)
Câu 8. Lượng thời gian, tính bằng giờ, mà một máy hoạt động trước khi hỏng hóc là
một biến ngẫu nhiên liên tục với hàm mật độ xác suất là Ce−x/ , x ≥ 0 f(x) = ( 120 0, x < 0 a. Tính C
b. Tính xác suất máy này hoạt động được từ 98 đến 145 giờ.
Câu 9. Trung bình có 15 vụ tai nạn máy bay xảy ra mỗi năm.
a. Tính xác suất không xảy ra tai nạn trong tháng.
b. Tính xác suất xảy ra nhiều nhất 2 tai nạn trong tháng.
Câu 10. Axline Computers sản xuất máy tính cá nhân tại hai nhà máy, một ở Texas và
một ở Hawaii. Nhà máy ở Texas có 40 nhân viên; nhà máy Hawaii có 20. Chọn
ngẫu nhiên 10 nhân viên để tham gia một khóa học nâng cao tay nghề.
a. Xác suất mà không có nhân viên nào trong mẫu làm việc tại nhà máy ởHawaii là bao nhiêu? 2 lOMoAR cPSD| 40551442
b. Xác suất một trong những nhân viên trong mẫu làm việc tại nhà máy ởHawaii là bao nhiêu?
Câu 11. Thời gian cần thiết để hoàn thành bài kiểm tra cuối kỳ trong một khóa học đại
học có phân phối chuẩn với trung bình là 80 phút và độ lệch chuẩn là 10 phút.
a. Xác suất hoàn thành bài kiểm tra trong một giờ hoặc ít hơn là bao nhiêu?
b. Xác suất một học sinh hoàn thành bài thi trong hơn 60 phút nhưng dưới 75phút là bao nhiêu?
Câu 12. Thời gian sử dụng (tính bằng giờ) của một pin cho laptop là một biến ngẫu
nhiên có phân phối chuẩn với giá trị trung bình 3,5 giờ và độ lệch chuẩn 0,4 giờ.
a. Tính xác suất các laptop được sử dụng nhiều hơn 4 giờ.
b. Sau khi sử dụng liên tục trong bao lâu thì có 10% laptop còn pin? 3