Đề giao lưu học sinh giỏi Toán 12 năm 2022 – 2023 cụm trường THPT – Bắc Ninh

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề thi giao lưu học sinh giỏi THPT môn Toán 12 năm học 2022 – 2023 cụm trường THPT Gia Bình, Thuận Thành, Lương Tài, trực thuộc sở Giáo dục và Đào tạo tỉnh Bắc Ninh;

28 14 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 12

Môn: Toán 12

Thông tin:

59 trang 8 tháng trước

Tác giả:

Profile Nguyễn Vân
Trang 1/7 - Mã đề 101
SỞ GD VÀ ĐT BẮC NINH
CỤM TRƯỜNG THPT GIA BÌNH,
THUẬN THÀNH, LƯƠNG TÀI
ĐỀ THI GIAO LƯU HỌC SINH GIỎI THPT
NĂM HỌC 2022 - 2023
Môn: Toán - Lớp 12
Ngày thi: 8 tháng 01 năm 2023
( Đề thi gồm 7 trang) Thời gian: 90 phút (không kể thời gian phát đề)
Họ và tên thí sinh:.............................................................................. SBD:.....................
Mã đề thi
101
Câu 1. Cho
2 5
log 3; log 2;a b
và
12
9 .
log
125 . .
m ab n
p ab q b
(
,m n
là các số nguyên tố). Giá trị của
m n p q
bằng
A.
4
B.
8
C.
2
D.
6
Câu 2. Tìm họ tất cả các nguyên hàm của hàm số
2
1
( )
1
x x
f x
x
.
A.
2
1
1 .
( 1)
C
x
B.
2
ln( 1) .x x C
C.
2
ln 1 .x x C
D.
2
ln 1 .
2
x
x C
Câu 3. Cho hình chóp S. ABC có
3, 4, 5AB AC BC
và góc giữa các cạnh bên với đáy bằng
60
.
Thể tích của khối chóp đã cho bằng
A.
15 3
B.
5 3
C.
5 3
6
D.
5
3
Câu 4. Tổng các nghiệm của phương trình
2 2
log 1 .log 2 7 0
x
x
là
A.
2
1 log 7
B.
3
C.
4
D.
5
Câu 5. Cho hàm số
y f x
là hàm đa thức bậc 4, có bảng biến thiên như sau
Số nghiệm của phương trình
1 1f x
là
A.
4
B.
5
C.
3
D.
6
Câu 6. Gọi
,m n
lần lượt là số đường tiệm cận đứng và số đường tiệm cận ngang của đồ thị hàm số
3
1x x
y
x x
. Giá trị của
m n
bằng
A.
2
B.
4
C.
3
D.
5
Câu 7. Cho hàm
y f x
có
2 3
' 1 ;
m
f x x x x x x
. Có bao nhiêu giá trị nguyên của
1;99m
để hàm số
y f x
nghịch biến trên
 ; 2
?
A.
44
B.
50
C.
99
D.
49
Câu 8. Cho hình lăng trụ đứng
.ABC A B C
có đáy là tam giác vuông và
AB BC a
,
2AA a
,
M
là trung điểm của
BC
. Tính khoảng cách
d
của hai đường thẳng
AM
và
B C
.
Trang 2/7 - Mã đề 101
A.
7
7
a
d
. B.
2
2
a
d
. C.
3
3
a
d
. D.
2
2
a
d
.
Câu 9. Cho dãy số
n
a
thỏa mãn
1
1a
và
1
10 1
n n
a a
,
2n
. Tìm giá trị nhỏ nhất của
n
để
log 100
n
a
A.
102
. B.
103
. C.
100
. D.
101
.
Câu 10. Có bao nhiêu giá trị nguyên của
m
để tập nghiệm của bất phương trình
3 2 0
x x
x m
chứa
không quá
8
giá trị nguyên?
A.
15
B.
16
C.
8
D.
17
Câu 11. Cho hai khối trụ có cùng thể tích; bán kính đáy và chiều cao của hai khối trụ lần lượt là
1 1
,
R h
và
2 2
,R h
. Biết rằng
1
2
3
2
R
R
. Tỉ số
1
2
h
h
bằng
A.
9
4
. B.
2
3
. C.
4
9
. D.
3
2
.
Câu 12. Cho phương trình
2
2 cos 3 3 2 cos 3 2 0.x m x m
Số giá trị nguyên của tham số
m
để
phương trình đã cho có đúng 3 nghiệm thuộc khoảng
; .
6 3
là
A.
1
B.
4
C.
3.
D.
2
Câu 13. Cho hàm số
1
( )
2
x
y C
x
và
: 2 1d y x m
(
m
là tham số thực). Gọi
1
k
,
2
k
là hệ số góc
của tiếp tuyến của
C
tại giao điểm của
d
và
C
. Tính
1 2
.k k
.
A.
1 2
. 4k k
. B.
1 2
. 2k k
. C.
1 2
. 3k k
. D.
1 2
1
.
4
k k
.
Câu 14. Xét các số thực dương
, , ,a b x y
thỏa mãn
1, 1a b
và
x y
a b ab . Giá trị nhỏ nhất của biểu
thức
2P x y
bằng
A.
3 2 2
. B.
2 2
. C.
3
3 6
2
. D.
3 2 2
2
.
Câu 15. Cho khối chóp
.S ABC
có
SA SB SC a
và
20 , 30 , 40ASB BSC CSA
. Mặt
phẳng
bất kì qua
A
cắt
SB
,
SC
tại
B
,
C
. Tìm giá trị nhỏ nhất của chu vi
AB C
.
A.
3a
. B.
2a
. C.
a
. D.
2a
.
Câu 16. Trong không gian, cho hình chóp
.S ABC
có
SA
,
AB
,
BC
đôi một vuông góc với nhau và
SA a
,
AB b
,
BC c
. Mặt cầu đi qua
S
,
A
,
B
,
C
có bán kính bằng
A.
2 2 2
1
2
a b c
. B.
2 2 2
a b c
. C.
2 2 2
2 a b c
. D.
2
3
a b c
.
Câu 17. Cho đồ thị hàm số
2y f x
có đồ thị như hình vẽ
Hàm số
2
3g x f x
nghịch biến trên khoảng nào dưới đây?
A.
 ; 1
B.
1; 0
C.
0;1
D.
1; 3
Trang 3/7 - Mã đề 101
Câu 18. Gọi
,M m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2
3y x x
trên
0;2
. Giá trị
của
M m
bằng
A.
3
B.
2
C.
0
D.
4
Câu 19. Cho hình chóp tứ giác
.S ABCD
có đáy
ABCD
là hình thang vuông tại
A
và
B
,
AB BC a
,
2AD a
,
SA ABCD
và
2SA a
. Gọi
E
là trung điểm của
AD
. Kẻ
EK SD
tại
K
. Tính thể
tích của khối cầu đi qua sáu điểm
S
,
A
,
B
,
C
,
E
,
K
?
A.
3
6
a
V
. B.
3
6V a
. C.
3
3
2
a
V
. D.
3
4
3
a
V
.
Câu 20. Trong không gian với hệ trục tọa độ Oxyz, gọi
là góc hợp bởi đường thẳng
và mặt phẳng . Khi đó, giá trị
cos
bằng bao nhiêu
A. . B. . C. . D. .
Câu 21. Trong không gian
Oxyz
, cho mặt cầu
2 2 2
: 2 4 4 5 0
S x y z x y z
và mặt phẳng
: 2 1 0P x y z
. Gọi
M
là một điểm bất kì trên mặt cầu
S
. Khoảng cách từ
M
đến
P
có giá trị
nhỏ nhất bằng
A.
6 2
. B.
0
. C.
4 6
2
3
. D.
2 6 2
.
Câu 22. Trong không gian
Oxyz
, cho hình hộp
.ABCD A B C D
biết
1;0;1A
,
2;1;2B
,
1; 1;1D
,
4;5; 5C
. Tọa độ của điểm
A
là:
A.
4;6; 5A
. B.
3; 4; 1A
. C.
3;5; 6A
. D.
3;5;6A
.
Câu 23. Cho hình nón có bán kính đáy bằng
3
và chiều cao bằng
6
, một khối trụ có bán kính đáy thay đổi
nội tiếp khối nón đã cho (như hình vẽ). Thể tích lớn nhất của khối trụ bằng
A.
6
. B.
8
. C.
4
. D.
10
.
Câu 24. Tập xác định của hàm số
1
3 2
3
1y x x
là
A.
; 1 1;D
B.
1;1 \ 0D
C.
0;1D
D.
1;1D
Câu 25. Biến cố
A
liên quan đến một phép thử ngẫu nhiên
T
có hữu hạn kết quả đồng khả năng xuất hiện.
Khẳng định nào sau đây là đúng?
A.
n A
P A
n
. B.
1
P A
P A
.
C.
n
P A
n A
. D.
\n A
P A
n
.
3 4 3
:
x y z
d
: 2 1 0
P x y z
3
2
3
2
1
2
1
2
Trang 4/7 - Mã đề 101
Câu 26. Cho hàm số
2
3 khi 1
( )
4 khi 1
x x
f x
x x
. Tính tích phân
3
1
1 df x x
.
A.
3
.
2
B.
5
.
2
C.
1.
D.
7
.
2
Câu 27. Tính thể tích của một hình hộp chữ nhật biết rằng ba mặt của hình này có diện tích là
2
20 cm
,
2
10 cm
,
2
8 cm
.
A.
3
1600cm
B.
3
80 cm
C.
3
40cm
D.
3
38 cm
Câu 28. Cho hàm số
( )f x
liên tục trên
[ ; ]
a b
và số thực k tùy ý. Trong các khẳng định sau, khẳng định nào
sai?
A.
( ) 0
a
a
kf t dt
B.
( ) ( )
b a
a b
f x dx f x dx
C.
2
2
(2 ) 2 ( )
b b
a a
f x dx f x dx
D.
( ) ( )
b b
a a
kf x dx k f t dt
Câu 29. Quay xung quanh trục
Ox
hình phẳng giới hạn bởi đồ thị của hàm số
0,5
( 3) log 1y x x
, trục
Ox
, và đường thẳng
1x
ta thu được khối tròn xoay có thể tích bằng
A.
3
2
0,5
2
( 3) (log +1)dxx x
. B.
3
2
0,5
1
( 3) (log +1)dxx x
.
C.
2
2
0,5
1
( 3) (log +1)dxx x
. D.
2
2
0,5
1
( 3) (log +1)dxx x
.
Câu 30. Cho hàm số
y f x
có đồ thị hàm số
'y f x
như hình vẽ
Hàm số
1 2g x f x
đạt cực đại tại điểm nào?
A.
1;x
B.
0x
C.
1; 2x x
D.
1
; 1
2
x x
Câu 31. Tổng các nghiệm của phương trình
2
1
2
2
2
1
log 2
x
x
x
x
là
A.
4
B.
1
C.
5
D.
3
Câu 32. Cho hàm số bậc ba
f x
có đồ thị hàm số như hình vẽ bên. Biết hàm số
f x
đạt cực trị tại hai điểm
1 2
,x x
thỏa mãn
2 1
4x x
và
1 2
2f x f x
. Gọi
1 2
,S S
là diện tích của hai hình phẳng được cho
trong hình vẽ bên. Tính tỉ số
1
2
S
S
.
Trang 5/7 - Mã đề 101
A.
3
5
. B.
3
8
. C.
5
.
3
D.
8
5
.
Câu 33. Gọi
S
là tập tất cả các giá trị nguyên của
m
để bất phương trình
2 2
2 2 2 0
x
m m e mx m m
nghiệm đúng với mọi
x
thuộc
. Tổng giá trị tất cả các phần tử của
S
bằng
A.
2
B.
0
C.
5
D.
4
Câu 34. Cho hàm số
3 2
3y f x x bx cx
thỏa mãn
0;2
min 1 1f x f
. Giá trị lớn nhất của
hàm số
1 1g x f x x
là
A.
17
B.
55
C.
3 2
D.
5
Câu 35. Cho hàm số
y f x
có
3 2
' 3 10 ;f x x x x x
. Có bao nhiêu giá trị nguyên dương của
m
để hàm số
2
2 2 3g x f x mx m
có
13
điểm cực trị?
A.
5
B.
2
C.
3
D.
4
Câu 36. Cho tích phân
2
3
2
0
e 5 cos cos sin
d .e
cos
x
b
x x x
I x a c
x
, với
a
,
b
,
c
là các số thực. Tính
giá trị của biểu thức
P a b c
?.
A. 10. B. 2. C. 4. D. 16.
Câu 37. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật,
1AB
,
10AD
,
SA SB
,
SC SD
. Biết mặt phẳng
SAB
và
SCD
vuông góc nhau đồng thời tổng diện tích của hai tam giác
SAB
và
SCD
bằng
2
. Thể tích khối chóp
.S ABCD
bằng
A.
2
. B.
1
. C.
3
2
. D.
1
2
.
Câu 38. Cho hình trụ có đáy là hai đường tròn tâm
O
và
O
, bán kính đáy bằng chiều cao và bằng
R
. Trên
đường tròn đáy có tâm
O
lấy điểm
A
, trên đường tròn tâm
O
lấy điểm
B
. Đặt
là góc giữa
AB
và đáy.
Biết rằng thể tích khối tứ diện
OO AB
đạt giá trị lớn nhất. Khẳng định nào sau đây đúng?
A.
1
tan
2
. B.
1
tan
2
. C.
tan 1
. D.
tan 2
.
Câu 39. Cho hàm số
( )f x
xác định, có đạo hàm, liên tục và đồng biến trên
[1; 4]
thỏa mãn
2
3
2 ( ) [ ( )] , [1; 4], (1)
2
x xf x f x x f
. Giá trị
(4)f
bằng
A.
391
18
. B.
361
18
. C.
381
18
. D.
371
18
.
Câu 40. Cho hình chóp
.S ABC
có
0
; 2 2, 3 , 45SA ABC AB a BC a ABC
. Gọi
I
là trực tâm
của tam giác
SBC
. Giá trị lớn nhất của thể tích khối chóp
.I ABC
bằng
A.
3
2
a
. B.
3
4
a
. C.
3
a
. D.
3
2
2
a
.
Trang 6/7 - Mã đề 101
Câu 41. Có bao nhiêu giá trị nguyên của
m
để hàm số
4 2
64y x mx x
có đúng
5
điểm cực trị?
A.
5
B.
19
C.
6
D.
24
Câu 42. Cho hình tứ diện đều
ABCD
. Trên mỗi cạnh của tứ diện, ta đánh dấu
3
điểm chia đều cạnh tương
ứng thành các phần bằng nhau. Gọi
S
là tập hợp các tam giác có ba đỉnh lấy từ
18
điểm đã đánh dấu. Lấy ra
từ
S
một tam giác, xác suất để mặt phẳng chứa tam giác đó song song với đúng một cạnh của tứ diện đã cho
bằng
A.
2
45
. B.
9
34
. C.
2
5
. D.
4
15
Câu 43. Cho các hàm số
;y f x y g x
liên tục và có đạo hàm trên
, trong đó hàm số
2 'g x f x
là hàm số bậc ba có đồ thị như hình vẽ.
Hàm số
2 3 2
2 2 2023y f x x x x
nghịch biến trên khoảng nào dưới đây?
A.
1
;1
3
B.
1;2
C.

1
;
3
D.
2; 0
Câu 44. Cho các hàm số
5 3
4
; 0; 0
4 2
x
x
f x g x ax bx cx a b
và
7
3 ; 9 81
3
g g
.
Số giá trị nguyên của
m
để phương trình
2
1 2 1 2 4 1f g x f m g x
có 3 nghiệm phân biệt
là
A.
15
B.
17
C.
19
D.
0
Câu 45. Cho hàm số
2
2
ln 4 5
x
y f x e x x
. Có bao nhiêu cặp số
;x y
với
;x y
thỏa
mãn
2 2
2 4f x y f x y
?
A.
12
B.
11
C.
8
D.
4
Câu 46. Cho hàm số
f x
liên tục trên
, có bảng biến thiên như sau
Có tất cả bao nhiêu giá trị nguyên của tham số
m
để giá trị lớn nhất của hàm số
2
4 12
32
16
x x
y f m
x
f
x
nhỏ hơn
16
3
?
A.
8
. B.
10
. C.
11
. D.
9
.
Trang 7/7 - Mã đề 101
Câu 47. Cho mặt cầu
S
có bán kính
R
không đổi, hình trụ
T
bất kì nội tiếp mặt cầu
S
. Thể tích khối
trụ
T
là
1
V
; và thể tích phần còn lại của khối cầu là
2
V
. Giá trị lớn nhất của
1
2
V
V
bằng bao nhiêu?
A.
1 2 3
2
. B.
2 3 1
2
. C.
1 3
2
. D.
3 1
2
.
Câu 48. Cho phương trình
2
2 4 3
2
3 2 .
x mx m
m
x m
Có bao nhiêu số nguyên
m
để phương trình có đúng
hai nghiệm phân biệt thuộc đoạn
6; 0
?
A.
3.
B.
1.
C.
2.
D.
0.
Câu 49. Cho hàm số
y f x
có đạo hàm liên tục trên
0;1
, thỏa mãn
2
2
4. 2 1f x x f x
với mọi
x
thuộc đoạn
0;1
và
1 2f
. Giá trị
1
0
dI xf x x
bằng
A.
11
4
. B.
4
3
. C.
3
4
. D.
5
3
.
Câu 50. Cho hai hàm số
3 2
3 1 2f x ax x bx d
và
2
2g x cx x d
có bảng biến thiên như
hình vẽ. Biết rằng đồ thị của hai hàm số đã cho cắt nhau tại ba điểm phân biệt có hoành độ
1 2 3
, ,x x x
thỏa mãn
2 2 2
1 2 3
30x x x
. Diện tích hình phẳng giới hạn bởi các đường
, , 3, 6y f x y g x x x
bằng
A.
1123
12
. B.
1231
12
. C.
1321
12
. D.
2113
12
.
------------- HẾT -------------
Thí sinh không được sử dụng bất cứ tài liệu gì.
Cán bộ coi thi không giải thích gì thêm.
Trang 1/7 - Mã đề 102
SỞ GD VÀ ĐT BẮC NINH
CỤM TRƯỜNG THPT GIA BÌNH,
THUẬN THÀNH, LƯƠNG TÀI
ĐỀ THI GIAO LƯU HỌC SINH GIỎI THPT
NĂM HỌC 2022 - 2023
Môn: Toán - Lớp 12
Ngày thi: 8 tháng 01 năm 2023
( Đề thi gồm 7 trang) Thời gian: 90 phút (không kể thời gian phát đề)
Họ và tên thí sinh:.............................................................................. SBD:.....................
Mã đề thi
102
Câu 1. Cho hai khối trụ có cùng thể tích; bán kính đáy và chiều cao của hai khối trụ lần lượt là
1 1
,R h
và
2 2
,R h
. Biết rằng
1
2
3
2
R
R
. Tỉ số
1
2
h
h
bằng
A.
3
2
. B.
9
4
. C.
2
3
. D.
4
9
.
Câu 2. Cho khối chóp
.S ABC
có
SA SB SC a
và
20 , 30 , 40ASB BSC CSA
. Mặt
phẳng
bất kì qua
A
cắt
SB
,
SC
tại
B
,
C
. Tìm giá trị nhỏ nhất của chu vi
AB C
.
A.
2a
. B.
3a
. C.
2a
. D.
a
.
Câu 3. Cho đồ thị hàm số
2y f x
có đồ thị như hình vẽ
Hàm số
2
3g x f x
nghịch biến trên khoảng nào dưới đây?
A.
1; 0
B.
0;1
C.
1; 3
D.
 ; 1
Câu 4. Gọi
,m n
lần lượt là số đường tiệm cận đứng và số đường tiệm cận ngang của đồ thị hàm số
3
1x x
y
x x
. Giá trị của
m n
bằng
A.
3
B.
5
C.
2
D.
4
Câu 5. Cho dãy số
n
a
thỏa mãn
1
1a
và
1
10 1
n n
a a
,
2n
. Tìm giá trị nhỏ nhất của
n
để
log 100
n
a
A.
102
. B.
103
. C.
100
. D.
101
.
Câu 6. Cho hàm số
y f x
có đồ thị hàm số
'y f x
như hình vẽ
Hàm số
1 2g x f x
đạt cực đại tại điểm nào?
Trang 2/7 - Mã đề 102
A.
1;x
B.
0x
C.
1; 2x x
D.
1
; 1
2
x x
Câu 7. Tìm họ tất cả các nguyên hàm của hàm số
2
1
( )
1
x x
f x
x
.
A.
2
1
1 .
( 1)
C
x
B.
2
ln( 1) .x x C
C.
2
ln 1 .x x C
D.
2
ln 1 .
2
x
x C
Câu 8. Trong không gian
Oxyz
, cho hình hộp
.ABCD A B C D
biết
1; 0;1A
,
2;1;2B
,
1; 1;1D
,
4;5; 5C
. Tọa độ của điểm
A
là:
A.
3;5; 6A
. B.
3;5;6A
. C.
4;6; 5A
. D.
3; 4; 1A
.
Câu 9. Cho hàm số
( )f x
liên tục trên
[ ; ]
a b
và số thực k tùy ý. Trong các khẳng định sau, khẳng định nào sai?
A.
( ) 0
a
a
kf t dt
B.
( ) ( )
b a
a b
f x dx f x dx
C.
2
2
(2 ) 2 ( )
b b
a a
f x dx f x dx
D.
( ) ( )
b b
a a
kf x dx k f t dt
Câu 10. Cho hình lăng trụ đứng
.ABC A B C
có đáy là tam giác vuông và
AB BC a
,
2AA a
,
M
là trung điểm của
BC
. Tính khoảng cách
d
của hai đường thẳng
AM
và
B C
.
A.
7
7
a
d
. B.
2
2
a
d
. C.
3
3
a
d
. D.
2
2
a
d
.
Câu 11. Trong không gian, cho hình chóp
.S ABC
có
SA
,
AB
,
BC
đôi một vuông góc với nhau và
SA a
,
AB b
,
BC c
. Mặt cầu đi qua
S
,
A
,
B
,
C
có bán kính bằng
A.
2 2 2
a b c
. B.
2 2 2
2 a b c
. C.
2 2 2
1
2
a b c
. D.
2
3
a b c
.
Câu 12. Cho hàm số
1
( )
2
x
y C
x
và
: 2 1d y x m
(
m
là tham số thực). Gọi
1
k
,
2
k
là hệ số góc
của tiếp tuyến của
C
tại giao điểm của
d
và
C
. Tính
1 2
.k k
.
A.
1 2
. 3k k
. B.
1 2
. 4k k
. C.
1 2
1
.
4
k k
. D.
1 2
. 2k k
.
Câu 13. Cho hàm
y f x
có
2 3
' 1 ;
m
f x x x x x x
. Có bao nhiêu giá trị nguyên của
1;99m
để hàm số
y f x
nghịch biến trên
 ; 2
?
A.
44
B.
50
C.
99
D.
49
Câu 14. Cho hàm số
y f x
là hàm đa thức bậc 4, có bảng biến thiên như sau
Số nghiệm của phương trình
1 1f x
là
A.
6
B.
5
C.
3
D.
4
Trang 3/7 - Mã đề 102
Câu 15. Cho hình nón có bán kính đáy bằng
3
và chiều cao bằng
6
, một khối trụ có bán kính đáy thay đổi
nội tiếp khối nón đã cho (như hình vẽ). Thể tích lớn nhất của khối trụ bằng
A.
6
. B.
8
. C.
4
. D.
10
.
Câu 16. Xét các số thực dương
, , ,a b x y
thỏa mãn
1, 1a b
và
x y
a b ab
. Giá trị nhỏ nhất của biểu
thức
2P x y
bằng
A.
3
3 6
2
. B.
3 2 2
2
. C.
3 2 2
. D.
2 2
.
Câu 17. Tính thể tích của một hình hộp chữ nhật biết rằng ba mặt của hình này có diện tích là
2
20 cm
,
2
10 cm
,
2
8 cm
.
A.
3
1600cm
B.
3
80 cm
C.
3
40cm
D.
3
38 cm
Câu 18. Quay xung quanh trục
Ox
hình phẳng giới hạn bởi đồ thị của hàm số
0,5
( 3) log 1y x x
, trục
Ox
, và đường thẳng
1x
ta thu được khối tròn xoay có thể tích bằng
A.
2
2
0,5
1
( 3) (log +1)dxx x
. B.
3
2
0,5
2
( 3) (log +1)dxx x
.
C.
3
2
0,5
1
( 3) (log +1)dxx x
. D.
2
2
0,5
1
( 3) (log +1)dxx x
.
Câu 19. Cho hình chóp S. ABC có
3, 4, 5AB AC BC
và góc giữa các cạnh bên với đáy bằng
60
.
Thể tích của khối chóp đã cho bằng
A.
15 3
B.
5 3
C.
5 3
6
D.
5
3
Câu 20. Trong không gian
Oxyz
, cho mặt cầu
2 2 2
: 2 4 4 5 0S x y z x y z
và mặt phẳng
: 2 1 0
P x y z
. Gọi
M
là một điểm bất kì trên mặt cầu
S
. Khoảng cách từ
M
đến
P
có giá trị
nhỏ nhất bằng
A.
2 6 2
. B.
6 2
. C.
0
. D.
4 6
2
3
.
Câu 21. Trong không gian với hệ trục tọa độ Oxyz, gọi
là góc hợp bởi đường thẳng
và mặt phẳng . Khi đó, giá trị
cos
bằng bao nhiêu
A. . B. . C. . D. .
Câu 22. Cho phương trình
2
2 cos 3 3 2 cos 3 2 0.x m x m
Số giá trị nguyên của tham số
m
để
phương trình đã cho có đúng 3 nghiệm thuộc khoảng
; .
6 3
là
A.
1
B.
4
C.
3.
D.
2
3 4 3
:
x y z
d
: 2 1 0
P x y z
1
2
1
2
3
2
3
2
Trang 4/7 - Mã đề 102
Câu 23. Cho hình chóp tứ giác
.
S ABCD
có đáy
ABCD
là hình thang vuông tại
A
và
B
,
AB BC a
,
2
AD a
,
SA ABCD
và
2
SA a
. Gọi
E
là trung điểm của
AD
. Kẻ
EK SD
tại
K
. Tính thể
tích của khối cầu đi qua sáu điểm
S
,
A
,
B
,
C
,
E
,
K
?
A.
3
4
3
a
V
. B.
3
6
V a
. C.
3
3
2
a
V
. D.
3
6
a
V
.
Câu 24. Cho hàm số
2
3 khi 1
( )
4 khi 1
x x
f x
x x
. Tính tích phân
3
1
1 d
f x x
.
A.
1.
B.
7
.
2
C.
3
.
2
D.
5
.
2
Câu 25. Có bao nhiêu giá trị nguyên của
m
để tập nghiệm của bất phương trình
3 2 0
x x
x m
chứa
không quá
8
giá trị nguyên?
A.
8
B.
17
C.
15
D.
16
Câu 26. Gọi
,
M m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2
3
y x x
trên
0;2
. Giá trị
của
M m
bằng
A.
0
B.
3
C.
4
D.
2
Câu 27. Tập xác định của hàm số
1
3 2
3
1
y x x
là
A.
 
; 1 1;D
B.
0;1
D
C.
1;1
D
D.
1;1 \ 0
D
Câu 28. Biến cố
A
liên quan đến một phép thử ngẫu nhiên
T
có hữu hạn kết quả đồng khả năng xuất hiện.
Khẳng định nào sau đây là đúng?
A.
\
n A
P A
n
. B.
1
P A
P A
.
C.
n
P A
n A
. D.
n A
P A
n
.
Câu 29. Cho
2 5
log 3; log 2;
a b
và
12
9 .
log
125 . .
m ab n
p ab q b
(
,
m n
là các số nguyên tố). Giá trị của
m n p q
bằng
A.
6
B.
4
C.
8
D.
2
Câu 30. Tổng các nghiệm của phương trình
2 2
log 1 .log 2 7 0
x
x
là
A.
2
1 log 7
B.
3
C.
4
D.
5
Câu 31. Cho hình trụ có đáy là hai đường tròn tâm
O
và
O
, bán kính đáy bằng chiều cao và bằng
R
. Trên
đường tròn đáy có tâm
O
lấy điểm
A
, trên đường tròn tâm
O
lấy điểm
B
. Đặt
là góc giữa
AB
và đáy.
Biết rằng thể tích khối tứ diện
OO AB
đạt giá trị lớn nhất. Khẳng định nào sau đây đúng?
A.
1
tan
2
. B.
tan 1
. C.
tan 2
. D.
1
tan
2
.
Câu 32. Cho hàm số
( )
f x
xác định, có đạo hàm, liên tục và đồng biến trên
[1; 4]
thỏa mãn
2
3
2 ( ) [ ( )] , [1; 4], (1)
2
x xf x f x x f
. Giá trị
(4)
f
bằng
A.
371
18
. B.
391
18
. C.
361
18
. D.
381
18
.
Trang 5/7 - Mã đề 102
Câu 33. Cho hàm số
3 2
3y f x x bx cx
thỏa mãn
0;2
min 1 1f x f
. Giá trị lớn nhất của
hàm số
1 1g x f x x
là
A.
5
B.
55
C.
3 2
D.
17
Câu 34. Cho tích phân
2
3
2
0
e 5 cos cos sin
d .e
cos
x
b
x x x
I x a c
x
, với
a
,
b
,
c
là các số thực. Tính
giá trị của biểu thức
P a b c
?.
A. 4. B. 16. C. 10. D. 2.
Câu 35. Cho hàm số bậc ba
f x
có đồ thị hàm số như hình vẽ bên. Biết hàm số
f x
đạt cực trị tại hai điểm
1 2
,x x
thỏa mãn
2 1
4x x
và
1 2
2f x f x
. Gọi
1 2
,S S
là diện tích của hai hình phẳng được cho
trong hình vẽ bên. Tính tỉ số
1
2
S
S
.
A.
3
5
. B.
3
8
. C.
5
.
3
D.
8
5
.
Câu 36. Cho hình chóp
.S ABC
có
0
; 2 2, 3 , 45SA ABC AB a BC a ABC
. Gọi
I
là trực tâm
của tam giác
SBC
. Giá trị lớn nhất của thể tích khối chóp
.I ABC
bằng
A.
3
2
2
a
. B.
3
4
a
. C.
3
a
. D.
3
2
a
.
Câu 37. Cho hàm số
y f x
có
3 2
' 3 10 ;f x x x x x
. Có bao nhiêu giá trị nguyên dương của
m
để hàm số
2
2 2 3g x f x mx m
có
13
điểm cực trị?
A.
4
B.
5
C.
2
D.
3
Câu 38. Tổng các nghiệm của phương trình
2
1
2
2
2
1
log 2
x
x
x
x
là
A.
1
B.
3
C.
4
D.
5
Câu 39. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật,
1AB
,
10AD
,
SA SB
,
SC SD
. Biết mặt phẳng
SAB
và
SCD
vuông góc nhau đồng thời tổng diện tích của hai tam giác
SAB
và
SCD
bằng
2
. Thể tích khối chóp
.S ABCD
bằng
A.
3
2
. B.
1
2
. C.
2
. D.
1
.
Câu 40. Gọi
S
là tập tất cả các giá trị nguyên của
m
để bất phương trình
2 2
2 2 2 0
x
m m e mx m m
nghiệm đúng với mọi
x
thuộc
. Tổng giá trị tất cả các phần tử của
S
bằng
A.
4
B.
0
C.
5
D.
2
Câu 41. Cho hàm số
f x
liên tục trên
, có bảng biến thiên như sau
Trang 6/7 - Mã đề 102
Có tất cả bao nhiêu giá trị nguyên của tham số
m
để giá trị lớn nhất của hàm số
2
4 12
32
16
x x
y f m
x
f
x
nhỏ hơn
16
3
?
A.
11
. B.
9
. C.
8
. D.
10
.
Câu 42. Cho hàm số
y f x
có đạo hàm liên tục trên
0;1
, thỏa mãn
2
2
4. 2 1f x x f x
với mọi
x
thuộc đoạn
0;1
và
1 2f
. Giá trị
1
0
dI xf x x
bằng
A.
4
3
. B.
3
4
. C.
5
3
. D.
11
4
.
Câu 43. Cho phương trình
2
2 4 3
2
3 2 .
x mx m
m
x m
Có bao nhiêu số nguyên
m
để phương trình có đúng
hai nghiệm phân biệt thuộc đoạn
6; 0
?
A.
3.
B.
1.
C.
2.
D.
0.
Câu 44. Cho hàm số
2
2
ln 4 5
x
y f x e x x
. Có bao nhiêu cặp số
;x y
với
;x y
thỏa
mãn
2 2
2 4f x y f x y
?
A.
11
B.
8
C.
4
D.
12
Câu 45. Cho hai hàm số
3 2
3 1 2f x ax x bx d
và
2
2g x cx x d
có bảng biến thiên như
hình vẽ. Biết rằng đồ thị của hai hàm số đã cho cắt nhau tại ba điểm phân biệt có hoành độ
1 2 3
, ,x x x
thỏa mãn
2 2 2
1 2 3
30x x x
. Diện tích hình phẳng giới hạn bởi các đường
, , 3, 6y f x y g x x x
bằng
A.
1231
12
. B.
1321
12
. C.
2113
12
. D.
1123
12
.
Câu 46. Cho các hàm số
;y f x y g x
liên tục và có đạo hàm trên
, trong đó hàm số
2 'g x f x
là hàm số bậc ba có đồ thị như hình vẽ.
Trang 7/7 - Mã đề 102
Hàm số
2 3 2
2 2 2023y f x x x x
nghịch biến trên khoảng nào dưới đây?
A.
2; 0
B.
1
;1
3
C.
1;2
D.

1
;
3
Câu 47. Cho mặt cầu
S
có bán kính
R
không đổi, hình trụ
T
bất kì nội tiếp mặt cầu
S
. Thể tích khối
trụ
T
là
1
V
; và thể tích phần còn lại của khối cầu là
2
V
. Giá trị lớn nhất của
1
2
V
V
bằng bao nhiêu?
A.
1 2 3
2
. B.
2 3 1
2
. C.
1 3
2
. D.
3 1
2
.
Câu 48. Cho các hàm số
5 3
4
; 0; 0
4 2
x
x
f x g x ax bx cx a b
và
7
3 ; 9 81
3
g g
.
Số giá trị nguyên của
m
để phương trình
2
1 2 1 2 4 1f g x f m g x
có 3 nghiệm phân biệt
là
A.
17
B.
19
C.
0
D.
15
Câu 49. Cho hình tứ diện đều
ABCD
. Trên mỗi cạnh của tứ diện, ta đánh dấu
3
điểm chia đều cạnh tương
ứng thành các phần bằng nhau. Gọi
S
là tập hợp các tam giác có ba đỉnh lấy từ
18
điểm đã đánh dấu. Lấy ra
từ
S
một tam giác, xác suất để mặt phẳng chứa tam giác đó song song với đúng một cạnh của tứ diện đã cho
bằng
A.
2
45
. B.
9
34
. C.
2
5
. D.
4
15
Câu 50. Có bao nhiêu giá trị nguyên của
m
để hàm số
4 2
64y x mx x
có đúng
5
điểm cực trị?
A.
19
B.
6
C.
24
D.
5
------------- HẾT -------------
Thí sinh không được sử dụng bất cứ tài liệu gì.
Cán bộ coi thi không giải thích gì thêm.
Trang 1/7 - Mã đề 103
SỞ GD VÀ ĐT BẮC NINH
CỤM TRƯỜNG THPT GIA BÌNH,
THUẬN THÀNH, LƯƠNG TÀI
ĐỀ THI GIAO LƯU HỌC SINH GIỎI THPT
NĂM HỌC 2022 - 2023
Môn: Toán - Lớp 12
Ngày thi: 8 tháng 01 năm 2023
( Đề thi gồm 7 trang) Thời gian: 90 phút (không kể thời gian phát đề)
Họ và tên thí sinh:.............................................................................. SBD:.....................
Mã đề thi
103
Câu 1. Cho phương trình
2
2 cos 3 3 2 cos 3 2 0.
x m x m
Số giá trị nguyên của tham số
m
để
phương trình đã cho có đúng 3 nghiệm thuộc khoảng
; .
6 3
là
A.
2
B.
1
C.
4
D.
3.
Câu 2. Quay xung quanh trục
Ox
hình phẳng giới hạn bởi đồ thị của hàm số
0,5
( 3) log 1
y x x
, trục
Ox
, và đường thẳng
1
x
ta thu được khối tròn xoay có thể tích bằng
A.
3
2
0,5
2
( 3) (log +1)dx
x x . B.
3
2
0,5
1
( 3) (log +1)dx
x x .
C.
2
2
0,5
1
( 3) (log +1)dx
x x . D.
2
2
0,5
1
( 3) (log +1)dx
x x .
Câu 3. Cho hình chóp S. ABC có
3, 4, 5
AB AC BC
và góc giữa các cạnh bên với đáy bằng
60
.
Thể tích của khối chóp đã cho bằng
A.
5 3
B.
5 3
6
C.
5
3
D.
15 3
Câu 4. Gọi
,
m n
lần lượt là số đường tiệm cận đứng và số đường tiệm cận ngang của đồ thị hàm số
3
1
x x
y
x x
. Giá trị của
m n
bằng
A.
5
B.
4
C.
3
D.
2
Câu 5. Có bao nhiêu giá trị nguyên của
m
để tập nghiệm của bất phương trình
3 2 0
x x
x m
chứa
không quá
8
giá trị nguyên?
A.
8
B.
17
C.
15
D.
16
Câu 6. Cho hàm số
2
3 khi 1
( )
4 khi 1
x x
f x
x x
. Tính tích phân
3
1
1 d
f x x
.
A.
7
.
2
B.
3
.
2
C.
5
.
2
D.
1.
Câu 7. Trong không gian với hệ trục tọa độ Oxyz, gọi
là góc hợp bởi đường thẳng
và mặt phẳng . Khi đó, giá trị
cos
bằng bao nhiêu
A. . B. . C. . D. .
Câu 8. Trong không gian, cho hình chóp
.
S ABC
có
SA
,
AB
,
BC
đôi một vuông góc với nhau và
SA a
,
AB b
,
BC c
. Mặt cầu đi qua
S
,
A
,
B
,
C
có bán kính bằng
A.
2 2 2
a b c
. B.
2 2 2
2
a b c
. C.
2 2 2
1
2
a b c
. D.
2
3
a b c
.
3 4 3
:
x y z
d
: 2 1 0
P x y z
3
2
3
2
1
2
1
2
Trang 2/7 - Mã đề 103
Câu 9. Tính thể tích của một hình hộp chữ nhật biết rằng ba mặt của hình này có diện tích là
2
20 cm
,
2
10 cm
,
2
8 cm
.
A.
3
80cm
B.
3
40 cm
C.
3
38 cm
D.
3
1600cm
Câu 10. Tìm họ tất cả các nguyên hàm của hàm số
2
1
( )
1
x x
f x
x
.
A.
2
1
1 .
( 1)
C
x
B.
2
ln( 1) .x x C
C.
2
ln 1 .x x C
D.
2
ln 1 .
2
x
x C
Câu 11. Cho khối chóp
.S ABC
có
SA SB SC a
và
20 , 30 , 40ASB BSC CSA
. Mặt
phẳng
bất kì qua
A
cắt
SB
,
SC
tại
B
,
C
. Tìm giá trị nhỏ nhất của chu vi
AB C
.
A.
2a
. B.
a
. C.
2a
. D.
3a
.
Câu 12. Cho hàm số
y f x
có đồ thị hàm số
'y f x
như hình vẽ
Hàm số
1 2g x f x
đạt cực đại tại điểm nào?
A.
1;x
B.
0x
C.
1; 2x x
D.
1
; 1
2
x x
Câu 13. Cho dãy số
n
a
thỏa mãn
1
1a
và
1
10 1
n n
a a
,
2n
. Tìm giá trị nhỏ nhất của
n
để
log 100
n
a
A.
103
. B.
100
. C.
101
. D.
102
.
Câu 14. Cho hai khối trụ có cùng thể tích; bán kính đáy và chiều cao của hai khối trụ lần lượt là
1 1
,
R h
và
2 2
,R h
. Biết rằng
1
2
3
2
R
R
. Tỉ số
1
2
h
h
bằng
A.
3
2
. B.
9
4
. C.
2
3
. D.
4
9
.
Câu 15. Cho hàm số
1
( )
2
x
y C
x
và
: 2 1d y x m
(
m
là tham số thực). Gọi
1
k
,
2
k
là hệ số góc
của tiếp tuyến của
C
tại giao điểm của
d
và
C
. Tính
1 2
.k k
.
A.
1 2
. 3k k
. B.
1 2
. 4k k
. C.
1 2
1
.
4
k k
. D.
1 2
. 2k k
.
Câu 16. Gọi
,M m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2
3y x x
trên
0;2
. Giá trị
của
M m
bằng
A.
3
B.
4
C.
2
D.
0
Trang 3/7 - Mã đề 103
Câu 17. Xét các số thực dương
, , ,a b x y
thỏa mãn
1, 1a b
và
x y
a b ab . Giá trị nhỏ nhất của biểu
thức
2P x y
bằng
A.
3
3 6
2
. B.
3 2 2
2
. C.
3 2 2
. D.
2 2
.
Câu 18. Cho hàm số
y f x
là hàm đa thức bậc 4, có bảng biến thiên như sau
Số nghiệm của phương trình
1 1f x
là
A.
4
B.
5
C.
3
D.
6
Câu 19. Cho
2 5
log 3; log 2;a b
và
12
9 .
log
125 . .
m ab n
p ab q b
(
,m n
là các số nguyên tố). Giá trị của
m n p q
bằng
A.
6
B.
4
C.
8
D.
2
Câu 20. Cho hình nón có bán kính đáy bằng
3
và chiều cao bằng
6
, một khối trụ có bán kính đáy thay đổi
nội tiếp khối nón đã cho (như hình vẽ). Thể tích lớn nhất của khối trụ bằng
A.
4
. B.
10
. C.
6
. D.
8
.
Câu 21. Cho đồ thị hàm số
2y f x
có đồ thị như hình vẽ
Hàm số
2
3g x f x
nghịch biến trên khoảng nào dưới đây?
A.
 ; 1
B.
1; 0
C.
0;1
D.
1; 3
Câu 22. Tập xác định của hàm số
1
3 2
3
1
y x x
là
A.
1;1 \ 0D
B.
0;1D
C.
1;1D
D.
 ; 1 1;D
Câu 23. Cho hình lăng trụ đứng
.ABC A B C
có đáy là tam giác vuông và
AB BC a
,
2AA a
,
M
là trung điểm của
BC
. Tính khoảng cách
d
của hai đường thẳng
AM
và
B C
.
Trang 4/7 - Mã đề 103
A.
3
3
a
d
. B.
7
7
a
d
. C.
2
2
a
d
. D.
2
2
a
d
.
Câu 24. Trong không gian
Oxyz
, cho mặt cầu
2 2 2
: 2 4 4 5 0
S x y z x y z
và mặt phẳng
: 2 1 0
P x y z
. Gọi
M
là một điểm bất kì trên mặt cầu
S
. Khoảng cách từ
M
đến
P
có giá trị
nhỏ nhất bằng
A.
2 6 2
. B.
0
. C.
4 6
2
3
. D.
6 2
.
Câu 25. Cho hàm số
( )
f x
liên tục trên
[ ; ]
a b
và số thực k tùy ý. Trong các khẳng định sau, khẳng định nào
sai?
A.
( ) ( )
b b
a a
kf x dx k f t dt
B.
( ) 0
a
a
kf t dt
C.
( ) ( )
b a
a b
f x dx f x dx
D.
2
2
(2 ) 2 ( )
b b
a a
f x dx f x dx
Câu 26. Cho hình chóp tứ giác
.
S ABCD
có đáy
ABCD
là hình thang vuông tại
A
và
B
,
AB BC a
,
2
AD a
,
SA ABCD
và
2
SA a
. Gọi
E
là trung điểm của
AD
. Kẻ
EK SD
tại
K
. Tính thể
tích của khối cầu đi qua sáu điểm
S
,
A
,
B
,
C
,
E
,
K
?
A.
3
4
3
a
V
. B.
3
6
V a
. C.
3
3
2
a
V
. D.
3
6
a
V
.
Câu 27. Biến cố
A
liên quan đến một phép thử ngẫu nhiên
T
có hữu hạn kết quả đồng khả năng xuất hiện.
Khẳng định nào sau đây là đúng?
A.
\
n A
P A
n
. B.
1
P A
P A
.
C.
n
P A
n A
. D.
n A
P A
n
.
Câu 28. Tổng các nghiệm của phương trình
2 2
log 1 .log 2 7 0
x
x
là
A.
2
1 log 7
B.
3
C.
4
D.
5
Câu 29. Cho hàm
y f x
có
2 3
' 1 ;
m
f x x x x x x
. Có bao nhiêu giá trị nguyên của
1;99
m
để hàm số
y f x
nghịch biến trên

; 2
?
A.
49
B.
50
C.
99
D.
44
Câu 30. Trong không gian
Oxyz
, cho hình hộp
.
ABCD A B C D
biết
1;0;1
A
,
2;1;2
B
,
1; 1;1
D
,
4;5; 5
C
. Tọa độ của điểm
A
là:
A.
3; 4; 1
A
. B.
3;5; 6
A
. C.
3;5;6
A
. D.
4;6; 5
A
.
Câu 31. Cho hàm số
y f x
có
3 2
' 3 10 ;f x x x x x
. Có bao nhiêu giá trị nguyên dương của
m
để hàm số
2
2 2 3
g x f x mx m có
13
điểm cực trị?
A.
5
B.
2
C.
3
D.
4
Câu 32. Cho hàm số bậc ba
f x
có đồ thị hàm số như hình vẽ bên. Biết hàm số
f x
đạt cực trị tại hai điểm
1 2
,
x x
thỏa mãn
2 1
4
x x
và
1 2
2
f x f x
. Gọi
1 2
,
S S
là diện tích của hai hình phẳng được cho
trong hình vẽ bên. Tính tỉ số
1
2
S
S
.
Trang 5/7 - Mã đề 103
A.
3
5
. B.
3
8
. C.
5
.
3
D.
8
5
.
Câu 33. Cho hình chóp
.S ABC
có
0
; 2 2, 3 , 45SA ABC AB a BC a ABC
. Gọi
I
là trực tâm
của tam giác
SBC
. Giá trị lớn nhất của thể tích khối chóp
.I ABC
bằng
A.
3
a
. B.
3
2
2
a
. C.
3
2
a
. D.
3
4
a
.
Câu 34. Cho hàm số
( )f x
xác định, có đạo hàm, liên tục và đồng biến trên
[1; 4]
thỏa mãn
2
3
2 ( ) [ ( )] , [1; 4], (1)
2
x xf x f x x f
. Giá trị
(4)f
bằng
A.
371
18
. B.
361
18
. C.
381
18
. D.
391
18
.
Câu 35. Cho hàm số
3 2
3y f x x bx cx
thỏa mãn
0;2
min 1 1f x f
. Giá trị lớn nhất của
hàm số
1 1g x f x x
là
A.
17
B.
5
C.
55
D.
3 2
Câu 36. Cho tích phân
2
3
2
0
e 5 cos cos sin
d .e
cos
x
b
x x x
I x a c
x
, với
a
,
b
,
c
là các số thực. Tính
giá trị của biểu thức
P a b c
?.
A. 2. B. 4. C. 16. D. 10.
Câu 37. Tổng các nghiệm của phương trình
2
1
2
2
2
1
log 2
x
x
x
x
là
A.
1
B.
3
C.
4
D.
5
Câu 38. Gọi
S
là tập tất cả các giá trị nguyên của
m
để bất phương trình
2 2
2 2 2 0
x
m m e mx m m
nghiệm đúng với mọi
x
thuộc
. Tổng giá trị tất cả các phần tử của
S
bằng
A.
2
B.
4
C.
0
D.
5
Câu 39. Cho hình trụ có đáy là hai đường tròn tâm
O
và
O
, bán kính đáy bằng chiều cao và bằng
R
. Trên
đường tròn đáy có tâm
O
lấy điểm
A
, trên đường tròn tâm
O
lấy điểm
B
. Đặt
là góc giữa
AB
và đáy.
Biết rằng thể tích khối tứ diện
OO AB
đạt giá trị lớn nhất. Khẳng định nào sau đây đúng?
A.
tan 1
. B.
tan 2
. C.
1
tan
2
. D.
1
tan
2
.
Câu 40. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật,
1AB
,
10AD
,
SA SB
,
SC SD
. Biết mặt phẳng
SAB
và
SCD
vuông góc nhau đồng thời tổng diện tích của hai tam giác
SAB
và
SCD
bằng
2
. Thể tích khối chóp
.S ABCD
bằng
A.
3
2
. B.
1
2
. C.
2
. D.
1
.
Trang 6/7 - Mã đề 103
Câu 41. Cho phương trình
2
2 4 3
2
3 2 .
x mx m
m
x m
Có bao nhiêu số nguyên
m
để phương trình có đúng
hai nghiệm phân biệt thuộc đoạn
6; 0
?
A.
3.
B.
1.
C.
2.
D.
0.
Câu 42. Cho hàm số
f x
liên tục trên
, có bảng biến thiên như sau
Có tất cả bao nhiêu giá trị nguyên của tham số
m
để giá trị lớn nhất của hàm số
2
4 12
32
16
x x
y f m
x
f
x
nhỏ hơn
16
3
?
A.
10
. B.
11
. C.
9
. D.
8
.
Câu 43. Cho các hàm số
5 3
4
; 0; 0
4 2
x
x
f x g x ax bx cx a b
và
7
3 ; 9 81
3
g g
.
Số giá trị nguyên của
m
để phương trình
2
1 2 1 2 4 1f g x f m g x
có 3 nghiệm phân biệt
là
A.
0
B.
15
C.
17
D.
19
Câu 44. Cho các hàm số
;y f x y g x
liên tục và có đạo hàm trên
, trong đó hàm số
2 'g x f x
là hàm số bậc ba có đồ thị như hình vẽ.
Hàm số
2 3 2
2 2 2023y f x x x x
nghịch biến trên khoảng nào dưới đây?
A.
1;2
B.

1
;
3
C.
2; 0
D.
1
;1
3
Câu 45. Cho hình tứ diện đều
ABCD
. Trên mỗi cạnh của tứ diện, ta đánh dấu
3
điểm chia đều cạnh tương
ứng thành các phần bằng nhau. Gọi
S
là tập hợp các tam giác có ba đỉnh lấy từ
18
điểm đã đánh dấu. Lấy ra
từ
S
một tam giác, xác suất để mặt phẳng chứa tam giác đó song song với đúng một cạnh của tứ diện đã cho
bằng
A.
9
34
. B.
2
5
. C.
4
15
D.
2
45
.
Trang 7/7 - Mã đề 103
Câu 46. Cho hai hàm số
3 2
3 1 2f x ax x bx d
và
2
2g x cx x d
có bảng biến thiên như
hình vẽ. Biết rằng đồ thị của hai hàm số đã cho cắt nhau tại ba điểm phân biệt có hoành độ
1 2 3
, ,x x x
thỏa mãn
2 2 2
1 2 3
30x x x
. Diện tích hình phẳng giới hạn bởi các đường
, , 3, 6
y f x y g x x x
bằng
A.
1321
12
. B.
1123
12
. C.
1231
12
. D.
2113
12
.
Câu 47. Cho mặt cầu
S
có bán kính
R
không đổi, hình trụ
T
bất kì nội tiếp mặt cầu
S
. Thể tích khối
trụ
T
là
1
V
; và thể tích phần còn lại của khối cầu là
2
V
. Giá trị lớn nhất của
1
2
V
V
bằng bao nhiêu?
A.
1 3
2
. B.
1 2 3
2
. C.
2 3 1
2
. D.
3 1
2
.
Câu 48. Cho hàm số
2
2
ln 4 5
x
y f x e x x
. Có bao nhiêu cặp số
;x y
với
;x y
thỏa
mãn
2 2
2 4f x y f x y
?
A.
4
B.
12
C.
11
D.
8
Câu 49. Có bao nhiêu giá trị nguyên của
m
để hàm số
4 2
64y x mx x
có đúng
5
điểm cực trị?
A.
5
B.
19
C.
6
D.
24
Câu 50. Cho hàm số
y f x
có đạo hàm liên tục trên
0;1
, thỏa mãn
2
2
4. 2 1f x x f x
với mọi
x
thuộc đoạn
0;1
và
1 2f
. Giá trị
1
0
d
I xf x x
bằng
A.
11
4
. B.
4
3
. C.
3
4
. D.
5
3
.
------------- HẾT -------------
Thí sinh không được sử dụng bất cứ tài liệu gì.
Cán bộ coi thi không giải thích gì thêm.
Trang 1/7 - Mã đề 104
SỞ GD VÀ ĐT BẮC NINH
CỤM TRƯỜNG THPT GIA BÌNH,
THUẬN THÀNH, LƯƠNG TÀI
ĐỀ THI GIAO LƯU HỌC SINH GIỎI THPT
NĂM HỌC 2022 - 2023
Môn: Toán - Lớp 12
Ngày thi: 8 tháng 01 năm 2023
( Đề thi gồm 7 trang) Thời gian: 90 phút (không kể thời gian phát đề)
Họ và tên thí sinh:.............................................................................. SBD:.....................
Mã đề thi
104
Câu 1. Cho hình nón có bán kính đáy bằng
3
và chiều cao bằng
6
, một khối trụ có bán kính đáy thay đổi nội
tiếp khối nón đã cho (như hình vẽ). Thể tích lớn nhất của khối trụ bằng
A.
6
. B.
8
. C.
4
. D.
10
.
Câu 2. Trong không gian, cho hình chóp
.S ABC
có
SA
,
AB
,
BC
đôi một vuông góc với nhau và
SA a
,
AB b
,
BC c
. Mặt cầu đi qua
S
,
A
,
B
,
C
có bán kính bằng
A.
2 2 2
1
2
a b c
. B.
2 2 2
a b c
. C.
2 2 2
2 a b c
. D.
2
3
a b c
.
Câu 3. Cho hàm số
y f x
có đồ thị hàm số
'y f x
như hình vẽ
Hàm số
1 2g x f x
đạt cực đại tại điểm nào?
A.
0x
B.
1; 2x x
C.
1
; 1
2
x x
D.
1;x
Câu 4. Cho đồ thị hàm số
2y f x
có đồ thị như hình vẽ
Hàm số
2
3g x f x
nghịch biến trên khoảng nào dưới đây?
A.
1; 0
B.
0;1
C.
1; 3
D.
 ; 1
Trang 2/7 - Mã đề 104
Câu 5. Trong không gian
Oxyz
, cho mặt cầu
2 2 2
: 2 4 4 5 0
S x y z x y z
và mặt phẳng
: 2 1 0
P x y z
. Gọi
M
là một điểm bất kì trên mặt cầu
S
. Khoảng cách từ
M
đến
P
có giá trị
nhỏ nhất bằng
A.
2 6 2
. B.
6 2
. C.
0
. D.
4 6
2
3
.
Câu 6. Tìm họ tất cả các nguyên hàm của hàm số
2
1
( )
1
x x
f x
x
.
A.
2
1
1 .
( 1)
C
x
B.
2
ln( 1) .
x x C
C.
2
ln 1 .
x x C
D.
2
ln 1 .
2
x
x C
Câu 7. Cho hình lăng trụ đứng
.
ABC A B C
có đáy là tam giác vuông và
AB BC a
,
2
AA a
,
M
là trung điểm của
BC
. Tính khoảng cách
d
của hai đường thẳng
AM
và
B C
.
A.
2
2
a
d
. B.
2
2
a
d
. C.
3
3
a
d
. D.
7
7
a
d
.
Câu 8. Cho hàm số
( )
f x
liên tục trên
[ ; ]
a b
và số thực k tùy ý. Trong các khẳng định sau, khẳng định nào sai?
A.
( ) ( )
b a
a b
f x dx f x dx
B.
2
2
(2 ) 2 ( )
b b
a a
f x dx f x dx
C.
( ) ( )
b b
a a
kf x dx k f t dt
D.
( ) 0
a
a
kf t dt
Câu 9. Quay xung quanh trục
Ox
hình phẳng giới hạn bởi đồ thị của hàm số
0,5
( 3) log 1
y x x
, trục
Ox
, và đường thẳng
1
x
ta thu được khối tròn xoay có thể tích bằng
A.
3
2
0,5
2
( 3) (log +1)dx
x x . B.
3
2
0,5
1
( 3) (log +1)dx
x x .
C.
2
2
0,5
1
( 3) (log +1)dx
x x . D.
2
2
0,5
1
( 3) (log +1)dx
x x .
Câu 10. Cho hình chóp S. ABC có
3, 4, 5
AB AC BC
và góc giữa các cạnh bên với đáy bằng
60
.
Thể tích của khối chóp đã cho bằng
A.
5
3
B.
15 3
C.
5 3
D.
5 3
6
Câu 11. Cho hàm
y f x
có
2 3
' 1 ;
m
f x x x x x x
. Có bao nhiêu giá trị nguyên của
1;99
m
để hàm số
y f x
nghịch biến trên

; 2
?
A.
44
B.
49
C.
50
D.
99
Câu 12. Xét các số thực dương
, , ,
a b x y
thỏa mãn
1, 1
a b
và
x y
a b ab
. Giá trị nhỏ nhất của biểu
thức
2
P x y
bằng
A.
3 2 2
. B.
2 2
. C.
3
3 6
2
. D.
3 2 2
2
.
Câu 13. Trong không gian
Oxyz
, cho hình hộp
.
ABCD A B C D
biết
1;0;1
A
,
2;1;2
B
,
1; 1;1
D
,
4;5; 5
C
. Tọa độ của điểm
A
là:
A.
3; 4; 1
A
. B.
3;5; 6
A
. C.
3;5;6
A
. D.
4;6; 5
A
.
Trang 3/7 - Mã đề 104
Câu 14. Cho phương trình
2
2 cos 3 3 2 cos 3 2 0.x m x m
Số giá trị nguyên của tham số
m
để
phương trình đã cho có đúng 3 nghiệm thuộc khoảng
; .
6 3
là
A.
4
B.
3.
C.
2
D.
1
Câu 15. Trong không gian với hệ trục tọa độ Oxyz, gọi
là góc hợp bởi đường thẳng
và mặt phẳng . Khi đó, giá trị
cos
bằng bao nhiêu
A. . B. . C. . D. .
Câu 16. Tập xác định của hàm số
1
3 2
3
1y x x
là
A.
1;1 \ 0D
B.
0;1D
C.
1;1D
D.
 ; 1 1;D
Câu 17. Cho hàm số
y f x
là hàm đa thức bậc 4, có bảng biến thiên như sau
Số nghiệm của phương trình
1 1f x
là
A.
6
B.
5
C.
3
D.
4
Câu 18. Cho hình chóp tứ giác
.S ABCD
có đáy
ABCD
là hình thang vuông tại
A
và
B
,
AB BC a
,
2AD a
,
SA ABCD
và
2SA a
. Gọi
E
là trung điểm của
AD
. Kẻ
EK SD
tại
K
. Tính thể
tích của khối cầu đi qua sáu điểm
S
,
A
,
B
,
C
,
E
,
K
?
A.
3
6V a
. B.
3
3
2
a
V
. C.
3
4
3
a
V
. D.
3
6
a
V
.
Câu 19. Tính thể tích của một hình hộp chữ nhật biết rằng ba mặt của hình này có diện tích là
2
20 cm
,
2
10 cm
,
2
8 cm
.
A.
3
80cm
B.
3
40 cm
C.
3
38 cm
D.
3
1600cm
Câu 20. Gọi
,M m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2
3y x x
trên
0;2
. Giá trị
của
M m
bằng
A.
0
B.
3
C.
4
D.
2
Câu 21. Tổng các nghiệm của phương trình
2 2
log 1 .log 2 7 0
x
x
là
A.
3
B.
4
C.
5
D.
2
1 log 7
Câu 22. Cho hàm số
1
( )
2
x
y C
x
và
: 2 1d y x m
(
m
là tham số thực). Gọi
1
k
,
2
k
là hệ số góc
của tiếp tuyến của
C
tại giao điểm của
d
và
C
. Tính
1 2
.k k
.
A.
1 2
. 3k k
. B.
1 2
. 4k k
. C.
1 2
1
.
4
k k
. D.
1 2
. 2k k
.
3 4 3
:
x y z
d
: 2 1 0
P x y z
1
2
3
2
3
2
1
2
Trang 4/7 - Mã đề 104
Câu 23. Cho hàm số
2
3 khi 1
( )
4 khi 1
x x
f x
x x
. Tính tích phân
3
1
1 d
f x x
.
A.
7
.
2
B.
3
.
2
C.
5
.
2
D.
1.
Câu 24. Gọi
,
m n
lần lượt là số đường tiệm cận đứng và số đường tiệm cận ngang của đồ thị hàm số
3
1
x x
y
x x
. Giá trị của
m n
bằng
A.
2
B.
4
C.
3
D.
5
Câu 25. Cho dãy số
n
a
thỏa mãn
1
1
a
và
1
10 1
n n
a a
,
2
n
. Tìm giá trị nhỏ nhất của
n
để
log 100
n
a
A.
103
. B.
100
. C.
101
. D.
102
.
Câu 26. Cho hai khối trụ có cùng thể tích; bán kính đáy và chiều cao của hai khối trụ lần lượt là
1 1
,
R h
và
2 2
,
R h
. Biết rằng
1
2
3
2
R
R
. Tỉ số
1
2
h
h
bằng
A.
9
4
. B.
2
3
. C.
4
9
. D.
3
2
.
Câu 27. Biến cố
A
liên quan đến một phép thử ngẫu nhiên
T
có hữu hạn kết quả đồng khả năng xuất hiện.
Khẳng định nào sau đây là đúng?
A.
n
P A
n A
. B.
\
n A
P A
n
.
C.
n A
P A
n
. D.
1
P A
P A
.
Câu 28. Có bao nhiêu giá trị nguyên của
m
để tập nghiệm của bất phương trình
3 2 0
x x
x m
chứa
không quá
8
giá trị nguyên?
A.
17
B.
16
C.
8
D.
15
Câu 29. Cho khối chóp
.
S ABC
có
SA SB SC a
và
20 , 30 , 40
ASB BSC CSA . Mặt
phẳng
bất kì qua
A
cắt
SB
,
SC
tại
B
,
C
. Tìm giá trị nhỏ nhất của chu vi
AB C
.
A.
3
a
. B.
2
a
. C.
a
. D.
2
a
.
Câu 30. Cho
2 5
log 3; log 2;
a b
và
12
9 .
log
125 . .
m ab n
p ab q b
(
,
m n
là các số nguyên tố). Giá trị của
m n p q
bằng
A.
4
B.
8
C.
2
D.
6
Câu 31. Cho hàm số
y f x
có
3 2
' 3 10 ;f x x x x x
. Có bao nhiêu giá trị nguyên dương của
m
để hàm số
2
2 2 3
g x f x mx m có
13
điểm cực trị?
A.
5
B.
3
C.
4
D.
2
Câu 32. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình chữ nhật,
1
AB
,
10
AD
,
SA SB
,
SC SD
. Biết mặt phẳng
SAB
và
SCD
vuông góc nhau đồng thời tổng diện tích của hai tam giác
SAB
và
SCD
bằng
2
. Thể tích khối chóp
.
S ABCD
bằng
A.
3
2
. B.
1
2
. C.
2
. D.
1
.
Trang 5/7 - Mã đề 104
Câu 33. Cho hình chóp
.S ABC
có
0
; 2 2, 3 , 45SA ABC AB a BC a ABC
. Gọi
I
là trực tâm
của tam giác
SBC
. Giá trị lớn nhất của thể tích khối chóp
.I ABC
bằng
A.
3
a
. B.
3
2
2
a
. C.
3
2
a
. D.
3
4
a
.
Câu 34. Cho hàm số
3 2
3y f x x bx cx
thỏa mãn
0;2
min 1 1f x f
. Giá trị lớn nhất của
hàm số
1 1g x f x x
là
A.
5
B.
55
C.
3 2
D.
17
Câu 35. Tổng các nghiệm của phương trình
2
1
2
2
2
1
log 2
x
x
x
x
là
A.
1
B.
5
C.
3
D.
4
Câu 36. Cho hình trụ có đáy là hai đường tròn tâm
O
và
O
, bán kính đáy bằng chiều cao và bằng
R
. Trên
đường tròn đáy có tâm
O
lấy điểm
A
, trên đường tròn tâm
O
lấy điểm
B
. Đặt
là góc giữa
AB
và đáy.
Biết rằng thể tích khối tứ diện
OO AB
đạt giá trị lớn nhất. Khẳng định nào sau đây đúng?
A.
1
tan
2
. B.
tan 1
. C.
tan 2
. D.
1
tan
2
.
Câu 37. Cho hàm số bậc ba
f x
có đồ thị hàm số như hình vẽ bên. Biết hàm số
f x
đạt cực trị tại hai điểm
1 2
,x x
thỏa mãn
2 1
4x x
và
1 2
2f x f x
. Gọi
1 2
,S S
là diện tích của hai hình phẳng được cho
trong hình vẽ bên. Tính tỉ số
1
2
S
S
.
A.
3
5
. B.
3
8
. C.
5
.
3
D.
8
5
.
Câu 38. Cho hàm số
( )f x
xác định, có đạo hàm, liên tục và đồng biến trên
[1; 4]
thỏa mãn
2
3
2 ( ) [ ( )] , [1; 4], (1)
2
x xf x f x x f
. Giá trị
(4)f
bằng
A.
391
18
. B.
361
18
. C.
381
18
. D.
371
18
.
Câu 39. Cho tích phân
2
3
2
0
e 5 cos cos sin
d .e
cos
x
b
x x x
I x a c
x
, với
a
,
b
,
c
là các số thực. Tính
giá trị của biểu thức
P a b c
?.
A. 2. B. 16. C. 10. D. 4.
Câu 40. Gọi
S
là tập tất cả các giá trị nguyên của
m
để bất phương trình
2 2
2 2 2 0
x
m m e mx m m
nghiệm đúng với mọi
x
thuộc
. Tổng giá trị tất cả các phần tử của
S
bằng
A.
5
B.
2
C.
4
D.
0
Trang 6/7 - Mã đề 104
Câu 41. Cho các hàm số
5 3
4
; 0; 0
4 2
x
x
f x g x ax bx cx a b
và
7
3 ; 9 81
3
g g
.
Số giá trị nguyên của
m
để phương trình
2
1 2 1 2 4 1f g x f m g x
có 3 nghiệm phân biệt
là
A.
15
B.
19
C.
0
D.
17
Câu 42. Cho hàm số
f x
liên tục trên
, có bảng biến thiên như sau
Có tất cả bao nhiêu giá trị nguyên của tham số
m
để giá trị lớn nhất của hàm số
2
4 12
32
16
x x
y f m
x
f
x
nhỏ hơn
16
3
?
A.
8
. B.
10
. C.
11
. D.
9
.
Câu 43. Cho hàm số
y f x
có đạo hàm liên tục trên
0;1
, thỏa mãn
2
2
4. 2 1f x x f x
với mọi
x
thuộc đoạn
0;1
và
1 2f
. Giá trị
1
0
dI xf x x
bằng
A.
4
3
. B.
5
3
. C.
11
4
. D.
3
4
.
Câu 44. Cho hàm số
2
2
ln 4 5
x
y f x e x x
. Có bao nhiêu cặp số
;x y
với
;x y
thỏa
mãn
2 2
2 4f x y f x y
?
A.
4
B.
12
C.
11
D.
8
Câu 45. Cho mặt cầu
S
có bán kính
R
không đổi, hình trụ
T
bất kì nội tiếp mặt cầu
S
. Thể tích khối
trụ
T
là
1
V
; và thể tích phần còn lại của khối cầu là
2
V
. Giá trị lớn nhất của
1
2
V
V
bằng bao nhiêu?
A.
1 2 3
2
. B.
2 3 1
2
. C.
1 3
2
. D.
3 1
2
.
Câu 46. Cho hình tứ diện đều
ABCD
. Trên mỗi cạnh của tứ diện, ta đánh dấu
3
điểm chia đều cạnh tương
ứng thành các phần bằng nhau. Gọi
S
là tập hợp các tam giác có ba đỉnh lấy từ
18
điểm đã đánh dấu. Lấy ra
từ
S
một tam giác, xác suất để mặt phẳng chứa tam giác đó song song với đúng một cạnh của tứ diện đã cho
bằng
A.
4
15
B.
9
34
. C.
2
5
. D.
2
45
.
Câu 47. Cho hai hàm số
3 2
3 1 2f x ax x bx d
và
2
2g x cx x d
có bảng biến thiên như
hình vẽ. Biết rằng đồ thị của hai hàm số đã cho cắt nhau tại ba điểm phân biệt có hoành độ
1 2 3
, ,x x x
thỏa mãn
2 2 2
1 2 3
30x x x
. Diện tích hình phẳng giới hạn bởi các đường
, , 3, 6y f x y g x x x
bằng
Trang 7/7 - Mã đề 104
A.
2113
12
. B.
1123
12
. C.
1231
12
. D.
1321
12
.
Câu 48. Có bao nhiêu giá trị nguyên của
m
để hàm số
4 2
64y x mx x
có đúng
5
điểm cực trị?
A.
19
B.
6
C.
24
D.
5
Câu 49. Cho phương trình
2
2 4 3
2
3 2 .
x mx m
m
x m
Có bao nhiêu số nguyên
m
để phương trình có đúng
hai nghiệm phân biệt thuộc đoạn
6; 0
?
A.
1.
B.
2.
C.
3.
D.
0.
Câu 50. Cho các hàm số
;y f x y g x
liên tục và có đạo hàm trên
, trong đó hàm số
2 'g x f x
là hàm số bậc ba có đồ thị như hình vẽ.
Hàm số
2 3 2
2 2 2023y f x x x x
nghịch biến trên khoảng nào dưới đây?
A.
1;2
B.

1
;
3
C.
2; 0
D.
1
;1
3
------------- HẾT -------------
Thí sinh không được sử dụng bất cứ tài liệu gì.
Cán bộ coi thi không giải thích gì thêm.
ĐÁP ÁN CÁC MÃ ĐỀ
------------------------
Mã đề [101]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
B
D
B
B
D
A
D
A
A
A
C
D
A
D
B
A
C
D
D
B
A
C
B
B
D
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
D
C
C
C
B
C
A
D
D
B
C
B
A
A
A
C
D
B
B
B
A
C
A
C
C
Mã đề [102]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
D
C
B
C
A
B
D
A
C
A
C
B
D
A
B
B
C
D
B
B
D
D
A
B
C
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
C
D
A
C
B
D
B
A
A
A
D
C
D
D
A
C
B
A
A
B
C
C
A
D
B
Mã đề [103]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
A
C
A
D
C
A
B
C
B
D
A
B
D
D
B
B
B
D
C
D
C
A
B
D
D
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
A
A
B
A
B
B
A
C
D
B
B
D
B
C
D
A
D
C
A
C
A
A
C
C
C
Mã đề [104]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
B
A
A
B
B
D
D
B
C
C
B
D
B
C
C
A
A
C
B
C
A
B
A
A
D
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
C
B
D
B
B
D
D
C
A
B
D
A
A
D
C
D
A
D
C
C
A
D
B
C
A
1
CÂU HỎI ĐỀ HSG CỤM 12 NĂM 2022
Mức 2
Câu 1: Cho hàm số
y f x
có đồ thị hàm số
'y f x
như hình vẽ
Hàm số
1 2g x f x
đạt cực đại tại điểm nào?
A.
0x
B.
1; 2x x
C.
1
; 1
2
x x
D.
1;x
Câu 2: Cho hàm
y f x
có
2 3
' 1 ;
m
f x x x x x x
. Có bao nhiêu giá trị nguyên của
1;99m
để hàm số
y f x
nghịch biến trên
; 2
?
A.
49
B.
50
C.
99
D. 44
Câu 3: Gọi
,M m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2
3y x x
trên
0;2
. Giá trị của
M m
bằng
A.
4
B.
2
C.
0
D.
3
Câu 4: Gọi
,m n
lần lượt là số đường tiệm cận đứng và số đường tiệm cận ngang của đồ thị hàm số
3
1x x
y
x x
. Giá trị của m n bằng
A.
2
B.
4
C.
3
D.
5
Câu 5: Cho hàm số
y f x
là hàm đa thức bậc 4, có bảng biến thiên như sau
2
Số nghiệm của phương trình
1 1f x
là
A.
6
B.
5
C.
3
D.
4
Câu 6: Tập xác định của hàm số
1
3 2
3
1y x x
là
A.
1;1 \ 0D
B.
0;1D
C.
1;1D
D.
; 1 1;D  
Câu 7: Cho
2 5
log 3; log 2;a b và
12
9 .
log
125 . .
m ab n
p ab q b
(
,m n
là các số nguyên tố). Giá trị của
m n p q
bằng
A.
8
B.
2
C.
6
D.
4
Câu 8: Xét các số thực dương
, , ,a b x y
thỏa mãn
1, 1a b
và
x y
a b ab . Giá trị nhỏ nhất của biểu thức
2P x y
bằng
A.
3 2 2
. B.
2 2
. C.
3
3 6
2
. D.
3 2 2
2
.
Câu 9: Tổng các nghiệm của phương trình
2 2
log 1 .log 2 7 0
x
x
là
A.
3
B.
4
C.
5
D.
2
1 log 7
Câu 10: Có bao nhiêu giá trị nguyên của
m
để tập nghiệm của bất phương trình
3 2 0
x x
x m
chứa không
quá
8
giá trị nguyên?
A.
15
B.
16
C.
8
D.
17
Mức 3
Câu 1; Cho đồ thị hàm số
2y f x
có đồ thị như hình vẽ
Hàm số
2
3g x f x
nghịch biến trên khoảng nào dưới đây?
A.
0;1
B.
1;3
C.
; 1
D.
1;0
Hướng dẫn
3
Gọi là đồ thị hàm số .
Tịnh tiến sang trái 2 đơn vị ta được đồ thị hàm số .
Lấy đối xứng đồ thị hàm số qua Oy ta được đồ thị hàm số .
Ta có ; .
Bảng xét dấu
Vậy hàm số nghịch biến trên khoảng .
Câu 2: Cho hàm số
y f x
có
3 2
' 3 10 ;f x x x x x
. Có bao nhiêu giá trị nguyên dương của
m
để
hàm số
2
2 2 3g x f x mx m có
13
điểm cực trị?
A.
2
B.
3
C.
4
D.
5
Hướng dẫn
+
3 2
' 0 3 10 0 0; 5; 2f x x x x x x x
+ đặt
2
( ) 2 2u x x mx m . Ta có
( ). '( )
'( ) ( ) 3 ' . ' ( ) 3
( )
u x u x
g x f u x f u x
u x
C
2
y g x f x
C
2
y g x f x
y f x
y f x
2 2
3 2 . 3
y f x y x f x
2
2
2
0
0
0
0 3 0 3
3 0
3 3
6
x
x
x
y x x
f x
x
x
y
2
3
y f x
0;1
4
( ) 3 0
( ) 3
' ( ) 3 ( ) 3 2 ( ) 1(1)
( ) 8
( ) 3 5
u x
u x
f u x u x u x
u x
u x
;
( ) 0
( ). '( ) 0
'( ) 0
u x
u x u x
u x
+Do vậy số điểm cực trị của hàm
2
2 2 3g x f x mx m bằng số nghiệm bội lẻ của
( ) 0; 1; 3; 8u x
+số điểm cực trị của
( )u x
Ta có bảng biến thiên của hàm
( )u x
:
Dựa vào bảng biến thiên, ta có:
2
2
2
2;3
1 5
6 0
8 2 3
2
1 0
1 5
2
m
m m
m
ycbt m m
m m
m
1 5 1 5
2; ;3 ; 2;3
2 2
m m m
Câu 3: Cho hàm số
3 2
3y f x x bx cx
thỏa mãn
0;2
min 1 1f x f
. Giá trị lớn nhất của hàm số
1 1g x f x x
là
A. 5 B. 55 C. 3 2 D.
17
Hướng dẫn:
+
0;2
min 1 1f x f
nên suy ra hàm đạt cực tiểu tại x=1
3
'(1) 0 3 2 0 0
( ) 3 3
(1) 1 4 1 3
f b c b
f x x x
f b c c
Dễ dàng lập được bảng biến thiên của
3
( ) 3 3f x x x
+ Xét hàm
1 1g x f x x ;
Nhận xét:
2 2
1 1 2 2 1 2 2t x x t x t
min 2, 1;max 2, 0t khi x t khi x
Dựa vào bbt của f(x), suy ra
max ( ) (2) 5g x f
5
Câu 4: Tổng các nghiệm của phương trình
2
1
2
2
2
1
log 2
x
x
x
x
là
A.
5
B.
3
C.
4
D.
1
Hướng dẫn:
Điều kiện: x>0
Đặt
2
1
x
t
x
, phương trình có dạng
1 1
1 1
2 2
2 2
log 2 log 2 0
t t
t t
Xét
1 1 1
1 1 1
2
2 2 2
2
2
1 1 1 1
( ) log 2 '( ) .2 .ln 2 ''( ) .2 . ln 2 0; 0
.ln 2 2 .ln 2 4
t t t
f t t f t f t t
t t
Suy ra f’(t) có không quá 1 nghiệm, suy ra f(t) có không quá 2 nghiệm.
Nhận xét
2
2
2 2
1
2
1
2 2 1 0
( ) 0
4
2 3
1 4 1 0
4
x
x
t x x
x
f t
t
x
x x x
x
. Vậy tổng tất cả các nghiệm của
phương trình là 5.
Câu 5: Gọi
S
là tập tất cả các giá trị nguyên của
m
để bất phương trình
2 2
2 2 2 0
x
m m e mx m m
nghiệm đúng với mọi
x
thuộc
. Tổng giá trị tất cả các phần tử của
S
bằng
A.
4
B.
0
C.
5
D.
2
Hướng dẫn:
+ Đặt
2 2
( ) 2 2 2
x
f x m m e mx m m
, nhận xét
0 0
f
nên yêu cầu tương đương
( ) (0);f x f x
,
suy ra x=0 là điểm cực tiểu của hàm số
'(0) 0
f
+
2 2
'( ) 2 2 '(0) 4 0 0, 4
x
f x m m e m f m m m m
+ Với
0 ( ) 0;m f x x
( thỏa mãn)
+ Với
4 ( ) 8 8 8 8 1 0;
x x
m f x e x e x x
( do đường thẳng y=x+1 là tiếp tuyến của đồ thị
hàm số
x
y e
tại x=0 ) hoặc có thể vẽ bbt của f(x) để suy ra
0;f x x
, suy ra m=4 thỏa mãn
Vậy m=0 hoặc m=4.
Câu 6: Cho hàm số
( )
f x
xác định, có đạo hàm, liên tục và đồng biến trên
[1; 4]
thỏa mãn
2
3
2 ( ) [ ( )] , [1; 4], (1)
2
x xf x f x x f
. Giá trị
(4)
f
bằng
6
A.
391
18
. B.
361
18
. C.
381
18
. D.
371
18
.
Hướng dẫn:
Ta có:
2 2
2 ( ) [ ( )] (1 2 ( )) [ ( )]
x xf x f x x f x f x
4 4
2
1 1
4
1
[ ( )] ( ) ( )
1 2 ( )
1 2 ( ) 1 2 ( )
14 14 391
1 2 ( ) 1 2 (4) 2 (4)
3 3 18
f x f x f x
x x dx xdx
f x
f x f x
f x f f
Câu 7: Cho tích phân
2
3
2
0
e 5cos cos sin
d .e
cos
x
b
x x x
I x a c
x
, với
a
,
b
,
c
là các số thực. Tính giá trị của
biểu thức
P a b c
.
A. 4. B. 16. C. 10. D. 2.
Lời giải
Chọn A
3 3
2
0 0
cos sin
5 e d e . d
cos
x x
x x
I x x
x
3
3
2
0
0
e .cos e .sin
5e d
cos
x x
x
x x
x
x
3
3
2
0
0
e .cos e . cos
5e d
cos
x x
x
x x
x
x
3
3
0
0
e
5e d
cos
x
x
x
x
3
3
3
0
0
e
5e 7e 6
cos
x
x
x
.
Do đó
7
a
,
3
b
,
6
c
. Vậy
4
P a b c
.
Câu 8: Cho hàm số bậc ba
f x
có đồ thị hàm số như hình vẽ bên. Biết hàm số
f x
đạt cực trị tại hai điểm
1 2
,
x x
thỏa
mãn
2 1
4
x x
và
1 2
2
f x f x
. Gọi
1 2
,
S S
là diện tích của hai hình phẳng được cho trong hình vẽ
bên. Tính tỉ số
1
2
S
S
.
7
A.
8
5
. B.
3
5
. C.
3
8
. D.
5
.
3
.
Lời giải
Không mất tính tổng quát, tịnh tiến đồ thị hàm bậc ba
y f x
sao cho điểm uốn của đồ thị thuộc
trục tung
1 2
0 x x
. Lại có
2 1
4x x nên
1 2
2, 2x x .
Theo giả thiết, ta có
2
' 2 2 4f x k x x k x
với
0k
.
Suy ra
3
4
3
x
f x k x C
.
Do
16 16
2 2 2 2 1
3 3
k k
f f C C C
Suy ra
3
4 1
3
x
f x k x
và
2
16
2 1
3
k
f x f
.
8
Ta có
0 0
3
2
2 2
20
1 4
3 3
x k
S f x dx k x dx
.
Xét
21
2 2 2 2
32
2.1 2
. 3
3
1 1 1
20
5
3
IABC
k
f
S S
S BC IC
k
S S S S
.
Câu 9: Cho hình chóp
.S ABC
có
0
; 2 2, 3 , 45SA ABC AB a BC a ABC . Gọi
I
là trực tâm của tam giác
SBC
. Giá trị lớn nhất của thể tích khối chóp
.I ABC
bằng
A.
3
2
a
. B.
3
4
a
. C.
3
a . D.
3
2
2
a
.
Hướng dẫn
+ Gọi
H
là trực tâm của tam giác ,
K AH BC
, ta chứng minh được
HI SBC
, suy ra trong
mặt phẳng
SAK
có
0
90KIH I thuộc đường tròn đường kính
HK
.
+ Gọi
E
là hình chiếu vuông góc của I lên
AK
IE ABC
.
1
.
3
I ABC ABC
V IE S
+
0 2
1 1 2
. .sin 45 3 .2 2. 3
2 2 2
ABC
S AB BC a a a
2
.
.
I ABC
V IE a
, suy ra thể tích
.I ABC
lớn nhất khi
và chỉ khi
IE
lớn nhất. Do
I
thuộc nửa đường tròn đường kính
HK
nên
2
HK
IE
, suy ra
IE
lớn
nhất bằng
2
HK
khi
I
là điểm chính giữa của cung
HK
.
+ Chọn hệ trục như hình vẽ với tam giác
ABC
, ta có
0
2 2; 45 2
AB a ABC AO BO a OC a
0;2 ; 2 ;0 ; ;0 : 0; ; 2 ; 2 ;A a B a C a H x AC a a BH a x
.
9
Ta có
2
max
. 0 2 2 . 0
2
a
AC BH a a x x a HK a IE
3
2
.
max
2 2
I ABC
a a
V a
Câu 10: Cho hình trụ có đáy là hai đường tròn tâm
O
và
O
, bán kính đáy bằng chiều cao và bằng
R
. Trên
đường tròn đáy có tâm
O
lấy điểm
A
, trên đường tròn tâm
O
lấy điểm
B
. Đặt
là góc giữa
AB
và đáy. Biết
rằng thể tích khối tứ diện
OO AB
đạt giá trị lớn nhất. Khẳng định nào sau đây đúng?
A.
tan 2
. B.
1
tan
2
. C.
1
tan
2
. D.
tan 1
.
Lời giải
+ Gọi
A
là hình chiếu của
A
lên mặt phẳng chứa đường tròn tâm
O
.
+ Gọi
B
là hình chiếu của
B
lên mặt phẳng chứa đường tròn tâm
O
.
+ Gọi
R
là bán kính của đường tròn tâm
O
, Ta có:
BAB
.
Suy ra:
tan
R
AB
. Gọi
I
là trung điểm của
AB
OI AB
.
+ Ta có:
2 2
2
1
4
2 tan
R
OI OB IB
.
Và:
2
2
1 1
. 4
2 4tan tan
OAB
R
S OI AB
.
I
A'
B'
O'
O
B
A
10
Suy ra:
3
.
2
1 1 1 1
. . . 4
3 3 36 tan tan
OO AB OAB O A B OAB
R
V V OO S
.
+ Ta có:
OO AB
V
đạt giá trị lớn nhất khi và chỉ khi
2
1 1
. 4
tan tan
đạt giá trị lớn nhất.
Xét hàm số
2
. 4
f t t t
với
0;2
t
Qua bảng biến thiên, ta có
max
V
khi
2
t hay
1
tan
2
.
Cách 2:
3
1
. '. ( , ').sin( . ') sin( . ')
6 6
OO AB
R
V OA OA d OA OA OAOA OAOA
Vậy thể tích max khi
0
' 1
( . ') 90 ' 2 tan
'
2
AA
OA OA AB R
AB
Mức 4
Câu 1: Cho hàm số
2
2
ln 4 5
x
y f x e x x
. Có bao nhiêu cặp số
;
x y
với
;x y
thỏa mãn
2 2
2 4
f x y f x y
?
A.
12
B.
11
C.
8
D.
4
Hướng dẫn:
Ta nhận thấy:
+
2
2 2
2
ln 4 5 ln 2 1
x x
y f x e x x e x
nên hàm số có đồ thị đối xứng nhau qua đường thẳng
2
x
.
+
2
2
2 2 4
'
2 4 5
x
x x
y e
x x x
nên hàm số đồng biến trên
2;

, nghịch biến trên
;2

Từ đó suy ra
4
2
2
m n
m n
f m f n
m n
m n
Suy ra
2 2
2 2
2 2
2 4 0(1)
2 4
2 4 4 0(2)
x y x y
f x y f x y
x y x y
+ (1)
2 2
2 2
2 4 0 1 2 5 1 5 1;0;1;2;3
x y x y x y x x
11
Với
1
1 3
3
x
y y
x
; Với
0
0 4
2
x
y y
x
; Với
2
0 2 5( )
x y l
+(2)
2 2
2 2
2 4 4 0 1 2 9 1 3 4; 3; 2; 1;0;1;2
x y x y x y x x
Với
4
2
2
x
y
x
; Với
2
3
2 5( )
1
x
y l
x
; Với
2
2
2 8( )
0
x
y l
x
Với
1 1; 5
x y y
Vậy có 11 cặp thỏa mãn
Câu 2: Có bao nhiêu giá trị nguyên của
m
để hàm số
4 2
64
y x mx x
có đúng
5
điểm cực trị?
A.
19
B.
6
C.
24
D.
5
Hướng dẫn
+ xét
4 2 3
( ) 64 64
f x x mx x x x mx
3 2
32
'( ) 4. 2 64; '( ) 0 2 ( )
f x x mx f x m x g x
x
;
2
32
'( ) 4 ; '( ) 0 2
g x x g x x
x
x
2
0

'( )
g x
0
( )
g x



TH1: Nếu
24
m
thì
'( ) 0
f x
có 1 nghiệm bội lẻ, suy ra f(x) có một điểm cực trị dương , suy ra f(x) có tối đa 2
nghiệm nên
( )
y f x
có tối đa 3 điểm cực trị (loại)
TH2: Nếu
24
m
, khi đó f’(x) có 3 nghiệm bội lẻ, suy ra f(x) có 3 điểm cực trị.
Khi đó, để
( )
y f x
có 5 điểm cực trị
0
f x
có 2 nghiệm bội lẻ
3
64 0
x mx
có đúng 1 nghiệm
bội lẻ khác 0
3 2
64
64 0 ( )
x mx m x h x
x
Ta có bbt
x
3
32
0

'( )
h x
0
24
12
( )
h x



Suy ra,
30
m
. Vậy
25 30
m
, có 6 giá trị nguyên của m
Câu 3: Cho các hàm số
5 3
4
; 0; 0
4 2
x
x
f x g x ax bx cx a b
và
7
3 ; 9 81
3
g g
. Số giá trị
nguyên của
m
để phương trình
2
1 2 1 2 4 1
f g x f m g x
có 3 nghiệm phân biệt là
A.
17
B.
19
C.
0
D.
15
Hướng dẫn
Nhận xét, f(x) đồng biến trên R và thỏa mãn
( ) (1 ) 1 1 ( ) (1 )
f x f x f x f x
Pt
2 2 2
( (1 2 )) 1 (1 2 ( 4)) ( (1 2 )) ( 2 ( 4)) 1 2 2 4
f g x f m g x f g x f m g x g x g x m
Đặt
( ) 1 2 2 ( 4) ( ) 2. 1 2 2 ( 4)
h x g x g x h x g x g x
Do g’(x) là hàm bậc 4 trùng phương có 1 điểm cực trị nên đồ thị hàm số đối xứng nhau qua Oy và đồng biến khi
x>0. Suy ra
1 2 4
'( ) 0 ' 1 2 '( 4) 1; 5
1 2 4
x x
h x g x g x x x
x x
( 1) (3) 2. (3) 3 (3) 7; (5) ( 9) 2 (9) (9) 81
h g g g h g g g
( do hàm g(x) là hàm lẻ nên g(-9)=-g(9))
Ta có bbt
x
1
5

'( )
h x
0
-
( )
h x

81
Dựa vào bbt, để phương trình có 3 nghiệm phân biệt
2
7 81 8; 7;....;8
m m
. Có 17 giá trị nguyên
thỏa mãn
Câu 4: Cho các hàm số
;
y f x y g x
liên tục và có đạo hàm trên
, trong đó hàm số
2 '
g x f x
là hàm số bậc ba có đồ thị như hình vẽ.
30,2
-
7
13
Hàm số
2 3 2
2 2 2023y f x x x x
nghịch biến trên khoảng nào dưới đây?
A.
1;2
B.
1
;
3

C.
2;0
D.
1
;1
3
Hướng dẫn
Hàm số
g x
là hàm số bậc 3 nên có dạng:
2 ' 4 1 4 , 0 ' 2 4 1 4g x f x a x x x a f x a x x x
Đặt
2 ' 6 2 1t x f t a t t t
Đạo hàm của hàm số
2 3 2
2 2 2021y f x x x x
là
2 2 2 2 2
1
' 2 ' 2 3 4 1 2 4 4 1 3 1
3
y xf x x x ax x x x x x
Lập bảng xét dấu
Dựa vào bảng xét dấu trên ta có hàm số đã cho nghịch biến trên
1; 2 .
Câu 5: Cho hàm số
f x
liên tục trên
, có bảng biến thiên như sau
14
Có tất cả bao nhiêu giá trị nguyên của tham số
m
để giá trị lớn nhất của hàm số
2
4 12
32
16
x x
y f m
x
f
x
nhỏ hơn
16
3
?
A.
11
. B.
9
. C.
8
. D.
10
.
Lời giải
Chọn C
+ Ta có
2 2 2
32
32 32 32
4 4;4 1 6
16 8 16 16
x
x x x
f
x x x x
.
Dấu = xảy ra tương ứng khi x=-4 và x=4
+
2
2
4 12 16 2 64 4 4 4 12 32x x x x x
Dấu bằng xảy ra tương ứng khi x=4 và x=-4
Vậy suy ra
2
2 4 4 12 32
32
32
3 6 1
16
x x
x
f
x
.
Dấu bằng xảy ra tương ứng khi x=4 và x=-4.
Từ đó ta có:
2
4 12 2
max max ; 32
32
3
16
x x
f m f m f m
x
f
x
15
Yêu cầu bài toán
2 16
3 3
16
32
3
f m
f m
16
32 6
3
f m
.
Dựa và bảng biến thiên của hàm số f(x) ta có
5; 4; 3; 1;0;1;2;3
m
.
CÁC CÂU HỎI THI CỤM
Câu 1. Tìm họ tất cả các nguyên hàm của hàm số
2
1
( )
1
x x
f x
x
.
A.
2
1
1 .
( 1)
C
x
B.
2
ln( 1) .
x x C
C.
2
ln 1 .
x x C
D.
2
ln 1 .
2
x
x C
Câu 2. Cho hàm số
2
3
( )
4
x
f x
x
khi
khi
1
1
x
x
. Tính tích phân
3
1
1 d
f x x
.
A.
1.
B.
7
.
2
C.
3
.
2
D.
5
.
2
Lời giải
3 3 2
1 1 0
1 d 1 d 1 d
f x x f x x f t t
1 2
3 2
2
0 1
1 2 2
0 1 1
3 7
3 d 4 d 3. 4 1 4
3 2 2 2
t t
t t t t t
.
Câu 3. Cho hàm số
( )
f x
liên tục trên
[ ; ]
a b
và số thực k tùy ý. Trong các khẳng định sau, khẳng định nào sai
?
A.
( ) ( )
b a
a b
f x dx f x dx
B.
2
2
(2 ) 2 ( )
b b
a a
f x dx f x dx
C.
( ) ( )
b b
a a
kf x dx k f t dt
D.
( ) 0
a
a
kf t dt
Câu 4. Quay xung quanh trục
Ox
hình phẳng giới hạn bởi đồ thị của hàm số
0,5
( 3) log 1
y x x
, trục
Ox
, và đường thẳng
1
x
ta thu được khối tròn xoay có thể tích bằng
16
A.
3
2
0,5
2
(x 3) (log x+1)dx
. B.
3
2
0,5
1
(x 3) (log x+1)dx
.
C.
2
2
0,5
1
(x 3) (log x+1)dx
. D.
2
2
0,5
1
(x 3) (log x+1)dx
.
Câu 5. Tính thể tích của một hình hộp chữ nhật biết rằng ba mặt của hình này có diện tích là
2
20cm
,
2
10cm
,
2
8cm
.
A.
3
40cm
B.
3
38cm
C.
3
1600cm
D.
3
80cm
Lời giải
Giả sử hình chữ nhật có ba kích thước là
a
,
b
,
c
. Ta có
. 20
. 10
. 8
a b
a c
b c
2 2 2
. . 1600
a b c
. . 40
a b c
.
Vậy thể tích khối hộp chữ nhật là
3
40cm
.
Câu 6. Cho hai khối trụ có cùng thể tích; bán kính đáy và chiều cao của hai khối trụ lần lượt là
1 1
,
R h
và
2 2
,
R h
. Biết rằng
1
2
3
2
R
R
. Tỉ số
1
2
h
h
bằng
A.
9
4
. B.
2
3
. C.
4
9
. D.
3
2
.
Lời giải
Gọi
1 2
,
V V
lần lượt là thể tích của khối trụ thứ nhất và thứ hai.
Ta có:
2
2 2
1 2
1 2 1 1 2 2
2 1
4
9
h R
V V R h R h
h R
.
Câu 7. Trong không gian, cho hình chóp
.
S ABC
có
SA
,
AB
,
BC
đôi một vuông góc với nhau và
SA a
,
AB b
,
BC c
. Mặt cầu đi qua
S
,
A
,
B
,
C
có bán kính bằng
A.
2
3
a b c
. B.
2 2 2
a b c
. C.
2 2 2
2
a b c
. D.
2 2 2
1
2
a b c
.
Câu 8. Cho hình chóp S. ABC có
3, 4, 5
AB AC BC
và góc giữa các cạnh bên với đáy bằng
60
. Thể
tích của khối chóp đã cho bằng
A.
5 3
B.
5 3
6
C.
5
3
D.
15 3
17
Câu 9. Cho hình chóp tứ giác
.S ABCD
có đáy
ABCD
là hình thang vuông tại A và B ,
AB BC a
,
2AD a
,
SA ABCD
và
2SA a
. Gọi E là trung điểm của AD . Kẻ
EK SD
tại K . Tính thể
tích của khối cầu đi qua sáu điểm
S
, A, B ,
C
, E , K ?
A.
3
6
a
V
. B.
3
6V a
. C.
3
3
2
a
V
. D.
3
4
3
a
V
.
Lời giải
Vì E là trung điểm AD nên
ABCE
là hình vuông cạnh
a
, nên
CE AD
.
Mặt khác
SA ABCD CE SA
.
Từ đó chứng minh được
SK KC
.
Dễ thấy có
90SEC SKC SAC SBC . Suy ra A , B , E , K luôn nhìn
SC
dưới 1 góc vuông
nên
S
, A, B ,
C
, E , K nằm trên mặt cầu đường kính
SC
.
Gọi I là trung điểm
SC
thì mặt cầu đi qua qua sáu điểm
S
, A, B ,
C
, E , K có bán kính
2
SC
R
.
Ta có
ABCE
là hình vuông cạnh
a
, nên
2AC a
.
Tam giác
SAC
vuông cân tại A, cạnh
2AC SA a
nên
2SC a
, suy ra
2
SC
R a
.
Vậy thể tích mặt cầu đi qua sáu điểm
S
, A, B ,
C
, E , K là:
3
4
3
a
V
Câu 10. Cho hình nón có bán kính đáy bằng
3
và chiều cao bằng
6
, một khối trụ có bán kính đáy thay đổi nội
tiếp khối nón đã cho (như hình vẽ). Thể tích lớn nhất của khối trụ bằng
18
A.
10
. B.
6
. C.
8
. D.
4
.
Lời giải
Đặt
OO l
,
B O x
,
6SO h
và
SO y
.
Áp dụng định lý Talet vào tam giác
SOB
ta được
2
3 6
O B SO x y
y x
OB SO
.
Ta có
6 6 2l y x
. Suy ra
2
. . 6 2 . . . 6 2V x x x x x
.
Áp dụng bất đẳng thức Cô-si cho 3 số
x
,
x
và
6 2x
ta được
3
6 2
. . . 6 2 8
3
x x x
V x x x
.
Vậy
max
8V
khi
2x
.
Câu 11. Trong không gian
Oxyz
, cho hình hộp
.ABCD A B C D
biết
1;0;1A
,
2;1;2B
,
1; 1;1D
,
4;5; 5C
. Tọa độ của điểm
A
là:
A.
4;6; 5A
. B.
3;4; 1A
. C.
3;5; 6A
. D.
3;5;6A
.
19
Lời giải
Gọi
; ;
A a b c
. ' ' ' '
ABCD A B C D
là hình hộp
(2;5; 7)
AC AB AD AA AA AC AB AD

1; ; 1
AA a b c

1 2 3
5 5
1 7 6
a a
b b
c c
Vậy:
3;5; 6
A
.
Câu 12. Trong không gian
Oxyz
, cho mặt cầu
2 2 2
: 2 4 4 5 0
S x y z x y z
và mặt phẳng
: 2 1 0
P x y z
. Gọi
M
là một điểm bất kì trên mặt cầu
S
. Khoảng cách từ
M
đến
P
có
giá trị nhỏ nhất bằng
A.
6 2
. B.
0
. C.
4 6
2
3
. D.
2 6 2
.
Giải
Mặt cầu
S
có tâm
1; 2;2
I
và bán kính
2
R
.
, 6
d I P R
suy ra mặt phẳng
P
không cắt mặt cầu
S
.
Điểm
M S
thỏa mãn
,
d M P
nhỏ nhất bằng
, 6 2
d I P R
.
Câu 24. Trong không gian với hệ trục tọa độ Oxyz, gọi
là góc hợp bởi đường thẳng
và mặt phẳng . Khi đó, giá trị
cos
bằng bao nhiêu
A. . B. . C. . D. .
Giải
có VTCP là và có VTPT là .
Vì là góc không tù nên từ
Câu 14. Biến cố
A
liên quan đến một phép thử ngẫu nhiên
T
có hữu hạn kết quả đồng khả năng xuất hiện.
Khẳng định nào sau đây là đúng ?
A.
n A
P A
n
. B.
1
P A
P A
. C.
n
P A
n A
. D.
\
n A
P A
n
.
3 4 3
:
1 2 1
x y z
d
: 2 1 0
P x y z
1
2
3
2
3
2
1
2
d
1;2; 1
u
P
2;1;1
n
.
1.2 2.1 1.1
1 3
sin cos .
2 2
6. 6
.
u n
u n
20
Câu 15. Cho hình tứ diện đều
ABCD
. Trên mỗi cạnh của tứ diện, ta đánh dấu
3
điểm chia đều cạnh tương ứng
thành các phần bằng nhau. Gọi
S
là tập hợp các tam giác có ba đỉnh lấy từ
18
điểm đã đánh dấu. Lấy
ra từ
S
một tam giác, xác suất để mặt phẳng chứa tam giác đó song song với đúng một cạnh của tứ
diện đã cho bằng
A.
2
45
. B.
9
34
. C.
2
5
. D.
4
15
Lời giải
Cách 1:
Gọi các điểm được đánh dấu để chia đều các cạnh của tứ diện đều
ABCD
như hình vẽ.
+ Gọi
S
là tập hợp các tam giác có ba đỉnh lấy từ
18
điểm đã đánh dấu.
Số phần tử của
S
là số cách chọn ra 3 điểm không thẳng hàng trong số 18 điểm đã cho.
Chọn ra 3 điểm trong 18 điểm trên: có
3
18
C
cách.
Chọn ra 3 điểm thẳng hàng trong 18 điểm trên có
3
3
6. 6
C
cách.
Suy ra số tam giác thỏa mãn là
3
18
6 810
C
+ Gọi
T
là tập hợp các tam giác lấy từ
S
sao cho mặt phẳng chứa tam giác đó song song với đúng một
cạnh của tứ diện
ABCD
.
- Chọn 1 cạnh của tứ diện để mặt phẳng chứa tam giác chỉ song song với đúng cạnh đó: có
1
6
6
C
cách.
Xét các tam giác mà mặt phẳng chứa nó chỉ song song với cạnh
BD
, suy ra tam giác đó phải có một
cạnh song song với
BD
.
- Có 6 cách chọn cạnh song song với
BD
là
1 1 2 2 3 3 1 1 2 2 3 3
, , , , ,
M N M N M N E F E F E F
.
N3
Q3Q1
P3
P1
N1
F1
F3E3
E1
M3
M1
F2E2
Q2
N2
M2
P2
B
D
C
A
21
- Giả sử ta chọn cạnh
2 2
M N là cạnh của tam giác. Cần chọn đỉnh thứ 3 của tam giác trong 16 điểm còn
lại.
Do
2 2
M N ABD
mà mặt phẳng chứa tam giác song song với BD nên đỉnh thứ 3 không thể là 7
điểm còn lại nằm trong
mp ABD
.
Do mặt phẳng chứa tam giác chỉ song song với BD nên đỉnh thứ 3 không được trùng với một trong ba
điểm
2 2 2
, ,E F P . Vậy đỉnh thứ 3 chỉ được chọn trong
16 7 3 6
điểm còn lại.
Suy ra có 6 tam giác có 1 cạnh là
2 2
M N và mặt phẳng chứa nó chỉ song song với BD .
Vậy số tam giác mà mặt phẳng chứa nó chỉ song song với cạnh BD là:
6.6 36
.
Tương tự cho các trường hợp khác, ta có số tam giác mà mặt phẳng chứa nó chỉ song song với đúng
một cạnh của tứ diện
ABCD
là:
36.6 216
.
Vậy xác suất cần tìm là
216 4
810 15
n T
n S
.
Cách 2
+) Gọi
S
là tập hợp các tam giác có ba đỉnh lấy từ
18
điểm đã đánh dấu.
Chọn ra 3 điểm trong 18 điểm trên: có
3
18
C
cách.
Trong số
3
18
C
đó, có 6 cách chọn ra 3 điểm thẳng hàng trên các cạnh.
Suy ra
3
18
6 810n S C
+) Xét phép thử: “Lấy ngẫu nhiên một phần thử thuộc
S
”. Ta có
810n
.
22
+) Gọi
T
là biến cố: “Mặt phẳng chứa tam giác được chọn song song với đúng một cạnh của tứ diện
đã cho”.
Chọn một cạnh của tứ diện: 6 cách, (giả sử chọn
AB
).
Chọn đường thẳng song song với
AB
: 6 cách, (giả sử chọn
PQ
).
Chọn đỉnh thứ 3: 6 cách,
, , , , ,
M N E K F I
.
Suy ra
6.6.6 216.
n T
Vậy
216 4
810 15
n T
n
.
Câu 16. Cho dãy số
n
a
thỏa mãn
1
1
a
và
1
10 1
n n
a a
,
2
n
. Tìm giá trị nhỏ nhất của
n
để
log 100
n
a
A.
100
. B.
101
. C.
102
. D.
103
.
Lời giải.
1 1
1 1
10 1 10 (1)
9 9
n n n n
a a a a
.
Đặt
1 1
1 1 8
9 9 9
n n
b a b a
. Từ
1
(1) 10 , 2
n n
b b n
Dãy
n
b
là cấp số nhân với công bội là
10
q
. Nên
1 1
1
8
. .10
9
n n
n
b b q
.
Do đó
1
1 8 1
10 , 1,2,...
9 9 9
n
n n
a b n
.
Ta có
100 1 100
8 1
log 100 10 10 10
9 9
n n
n
a a
.
Vậy giá trị nhỏ nhất của
n
để
log 100
n
a là
102
n
.
Câu 17. Cho phương trình
2
2cos 3 3 2 cos3 2 0.
x m x m
Số giá trị nguyên của tham số
m
để phương
trình đã cho có đúng 3 nghiệm thuộc khoảng
; .
6 3
là
A.
3.
B.
2
C.
1
D.
4
Lời giải.
Với
; 3 ; .
6 3 2
x x
Đặt
cos3 1 1
t x t
. Phương trình trở thành
2
2 3 2 2 0.
t m t m
23
Ta có

2
2 5m phương trình có hai nghiệm
1
2
1
.
2
2
t
t m
Ta thấy ứng với một nghiệm
1
1
2
t
thì cho ta hai nghiệm
x
thuộc khoảng
; .
6 3
Do đó yêu cầu bài toán
2
2
1 0
1
t
t
(tham khảo hình vẽ)
1 2 0 1 2
2 1 3
m m
m m
Câu 18. Cho hình lăng trụ đứng .
ABC A B C
có đáy là tam giác vuông và
AB BC a
,
2
AA a
,
M
là
trung điểm của
BC
. Tính khoảng cách
d
của hai đường thẳng
AM
và
B C
.
A.
2
2
a
d
. B.
2
2
a
d
. C.
3
3
a
d
. D.
7
7
a
d
.
Lời giải
O
24
Tam giác
ABC
vuông và
AB BC a
nên
ABC
chỉ có thể vuông tại
B
.
Ta có
'
AB BC
AB BCB
AB BB
.
Kẻ
// //
MN B C B C AMN
, , , ,
d d B C MN d B C AMN d C AMN d B AMN
.
Vì tứ diện
BAMN
là tứ diện vuông nên
2 2
2 2 2 2 2 2
1 1 1 1 1 1 1 7 7
.
7
2
2
2
a
d
d BA BM BN a a
a
a
Câu 19. Cho hàm số
1
( )
2
x
y C
x
và
: 2 1
d y x m
(
m
là tham số thực). Gọi
1
k
,
2
k
là hệ số góc của tiếp
tuyến của
C
tại giao điểm của
d
và
C
. Tính
1 2
.
k k
.
A.
1 2
1
.
4
k k
. B.
1 2
. 2
k k
. C.
1 2
. 3
k k
. D.
1 2
. 4
k k
.
Lời giải
Xét phương trình hoành độ giao điểm
1
2 1 (1)
2
x
x m
x
.
Phương trình
(1)
có hai nghiệm phân biệt
2
( ) 2 ( 6) 2 3 0
2
f x x m x m
x
có hai nghiệm phân
biệt
2
( 2) 0
4 12 0
f
m R
m m
.
C
B
A
C'
B'
A'
M
A
B
B'
C
N
M
25
Gọi
1 2
,x x là hai nghiệm của phương trình
(1)
, khi đó
1 2
1 2
6
2
3 2
.
2
m
x x
m
x x
.
Hệ số góc của tiếp tuyến của
C
tại giao điểm của
d
và
C
là
1
2
1
2
2
2
1
2
1
2
k
x
k
x
.
Ta có
1 2
2 2 2 2
1 2 1 2 1 2
1 1 1 1
. . 4
3 2 62 2 . 2( ) 4
2. 4
2 2
k k
m mx x x x x x
.
Câu 20. Cho khối chóp
.S ABC
có
SA SB SC a
và
20 , 30 , 40ASB BSC CSA . Mặt phẳng
bất kì qua
A
cắt
SB
,
SC
tại
B
,
C
. Tìm giá trị nhỏ nhất của chu vi
AB C
.
A. 3a . B.
2a
. C.
a
. D.
2a
.
Trải các tam giác
SAB
,
SBC
,
SCA
trên một mặt phẳng như hình trên. Tam giác
SAC
trở thành tam giác
SA C
.
Khi đó
2C AB B C C A AA a
. Dấu “=” xảy ra khi
A
,
B
,
C
,
A
thẳng hàng.
Vậy chu vi tam giác
AB C
nhỏ nhất bằng
2a
.
MỨC 4
26
Câu 21. Cho phương trình
2
2 4 3
2
3 2 .
x mx m
m
x m
Có bao nhiêu số nguyên
m
để phương trình có đúng hai
nghiệm phân biệt thuộc đoạn
6;0
?
A.
0.
B.
1.
C.
2.
D.
3.
Lời giải
Với điều kiện trên
2
2 4 3
2
3 2
x mx m
m
x m
2 2
2 1
2
3 2
x m m
m
x m
.
Đặt
, 0
t x m t
ta được:
2
2
2 1
2
3 2
t m
m
t
*
.
Nhận thấy: Hàm số
2
2
2 1
3 2
t m
f t
đồng biến trên khoảng
0;
.
Hàm số
2
m
g t
t
nghịch biến trên khoảng
0;
.
Và
2 2
f m g m
. Vậy
*
có nghiệm duy nhất
2
t m
.
Khi đó
2
2
2 2
x
x m m
x m
.
Để phương trình có đúng hai nghiệm phân biệt thuộc đoạn
6;0
6 2 2 0 1 4
2 2 2 2
m m
m m
.
Do
m
nguyên nên
1;3;4
m
.
Câu 22. Cho hàm số
y f x
có đạo hàm liên tục trên
0;1
, thỏa mãn
2
2
4. 2 1
f x x f x
với mọi
x
thuộc đoạn
0;1
và
1 2
f
. Giá trị
1
0
d
I xf x x
bằng
A.
3
4
. B.
5
3
. C.
11
4
. D.
4
3
.
Hướng dẫn
Ta có
2 2
2 2
4. 2 1 4 4. 2 1 .
f x x f x f x f x x
27
Lấy tích phân hai vế từ
0
đến 1 ta được
1 1
2
2
0 0
4 d 4. 2 1 df x f x x x x
1 1
2
0 0
20
d 4 d .
3
f x x f x x
(*)
Xét
1
0
dI f x x
. Đặt
( ) d '( )d
d d
u f x u f x x
v x v x
1
1
0
0
( ) ' d .I xf x xf x x
Khi đó (*)
1 1
2
1
0
0 0
20
d 4 ( ) 4 ' d
3
f x x xf x xf x x
1 1
2
0 0
4
d 4 ' d 0
3
f x x xf x x
2
1 1 1 1
2
2
0 0 0 0
d 4 ' d 4 d 0 2 d 0 2f x x xf x x x x f x x x f x x
2
( )f x x C . Vì
(1) 2f
nên
2
1 ( ) 1.C f x x
Vậy
1
0
3
d .
4
xf x x
Câu 23. Cho hai hàm số
3 2
3 1 2f x ax x bx d
và
2
2g x cx x d
có bảng biến thiên như hình vẽ.
Biết rằng đồ thị của hai hàm số đã cho cắt nhau tại ba điểm phân biệt có hoành độ
1 2 3
, ,x x x thỏa mãn
2 2 2
1 2 3
30x x x
. Diện tích hình phẳng giới hạn bởi các đường
, , 3, 6y f x y g x x x
bằng
A.
2113
12
. B.
1123
12
. C.
1231
12
. D.
1321
12
.
Lời giải
Ta có
2
3 6f x ax x b
Từ BBT suy ra
f x
và có chung hai nghiệm là
và
g x
28
2 6
3
3
.
3
a c
c a
d b b d
c a
Từ BBT suy ra đồ thị hàm số
g x
có đỉnh
1
; 4
I
c
và
0
c
2
1 2 1 3 12
. 4 4
c
c d d b
c c c c
Xét
3 2
0 3 2 1 3 0 *
f x g x ax c x b x d
Từ giả thiết suy ra phương trình (*) có 3 nghiệm phân biệt
1 2 3
, ,
x x x
thỏa mãn
2
2 2 2
1 2 3 1 2 3 1 2 2 3 3 1
2 2
2
2 2
30 2 30
3 12
2
3 2 3
2. 30 2. 30
3 2 3 10 30 0 29 26 3 0
1
3
29
x x x x x x x x x x x x
c
c b c
c
a a c c
c c c c c
c tm
c loai
1; 1; 9; 3
c a b d
3 2
4 7 10
f x g x x x x
6 6
3 2
3 3
1321
d 4 7 10d
12
S f x g x x x x x x
Câu 24. Cho hình chóp .
S ABCD
có đáy
ABCD
là hình chữ nhật,
1
AB
,
10
AD ,
SA SB
,
SC SD
. Biết
mặt phẳng
SAB
và
SCD
vuông góc nhau đồng thời tổng diện tích của hai tam giác
SAB
và
SCD
bằng
2
. Thể tích khối chóp .
S ABCD
bằng
A.
2
. B.
1
. C.
3
2
. D.
1
2
.
Lời giải
29
Ta có
. .
2
S ABCD A SCD
V V
2
, .
3
SCD
d A SCD S
Ta có
SAB SCD Sx
//
AB
. Gọi
M
là trung điểm của
CD
,
N
là trung điểm của
AB
.
SM CD
,
SN AB
SM Sx
,
SN Sx
.
Mặt khác
SAB SCD
SN SCD
tại
S
,
90
NSM
, ,
d A SCD d N SCD SN
.
2 1
. . . .
3 2
S ABCD
V SN SM CD
.
2 2 2 2
10
SN SM MN AD
.
1 1 1
2 . .
2 2 2
SAB SCD
S S SN AB SM CD AB SN SM
4
SN SM
2 2
2 . 16
SN SM SN SM
. 3
SN SM
. Vậy
.
2 1
. .3.1 1
3 2
S ABCD
V
.
Câu 25. Cho mặt cầu
S
có bán kính
R
không đổi, hình trụ
T
bất kì nội tiếp mặt cầu
S
. Thể tích khối trụ
T
là
1
V
; và thể tích phần còn lại của khối cầu là
2
V
. Giá trị lớn nhất của
1
2
V
V
bằng bao nhiêu?
A.
3 1
2
. B.
1 2 3
2
. C.
2 3 1
2
. D.
1 3
2
.
Lời giải
S
A
N
B
C
D
M
O
x
30
Gọi I là tâm mặt cầu. Gọi H là tâm đường tròn đáy của hình trụ.
Ta có
1
2 1
1
V V
V V V
. Do đó để
1
2
V
V
đạt GTLN thì
1
V đạt GTLN.
Đặt
0IH x x R
. Ta có
2
1
.2V HA IH
2 2
.2R x x
3 2
2 2x xR
Đặt
3 2
2 2g x x xR
.
Ta có
2 2
6 2g x x R
2 2
3
0 6 2 0
3
R
g x x R x
Bảng biến thiên
Suy ra
1
V có GTLN là
3
4 3
9
R
. Thể tích khối cầu là
3
4
3
V R
Khi đó
1
2 1
1
V V
V V V
3
3 3
4
1 3
3
1
2
4 4 3
3 9
R
R R
.
| 1/59
| | Tải xuống

Có thể bạn quan tâm:

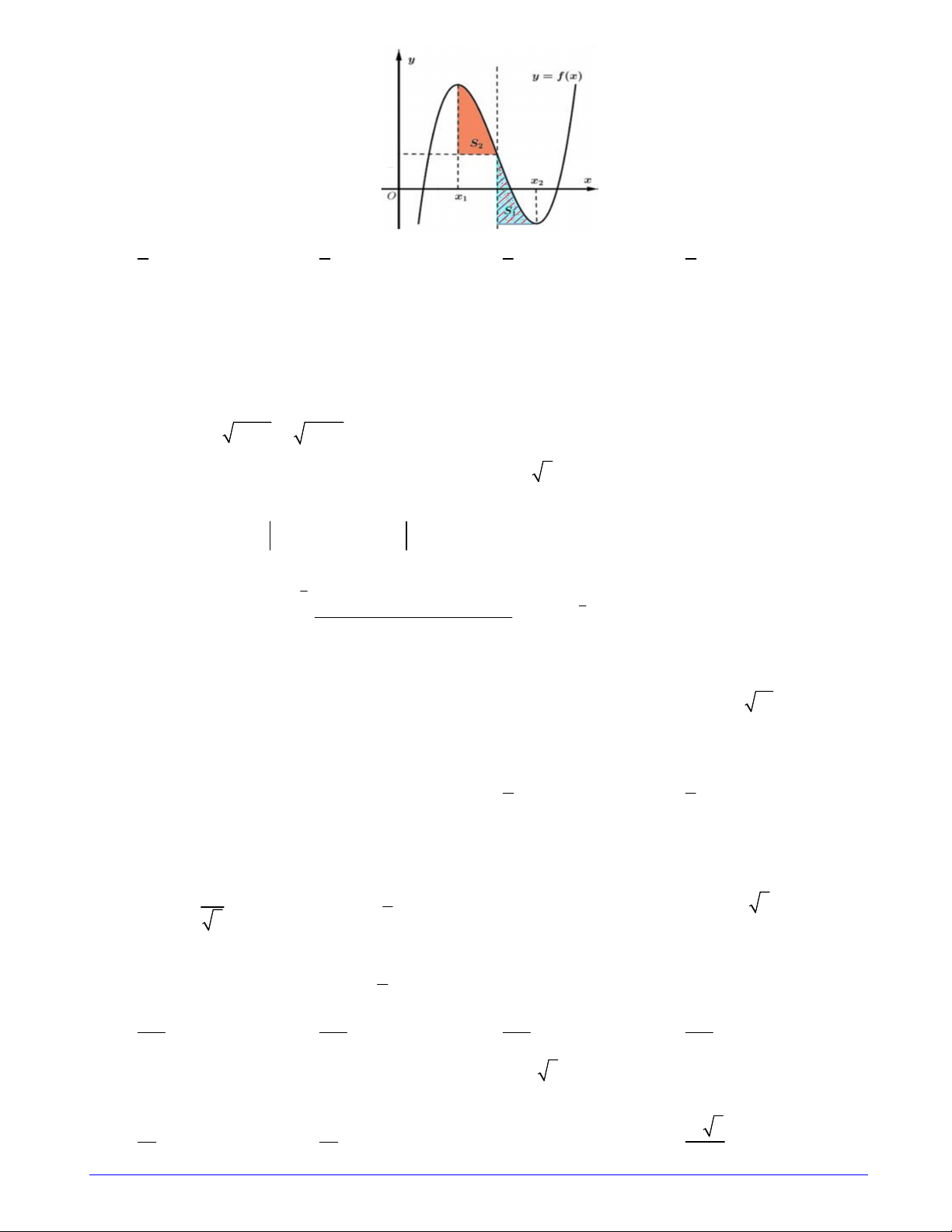
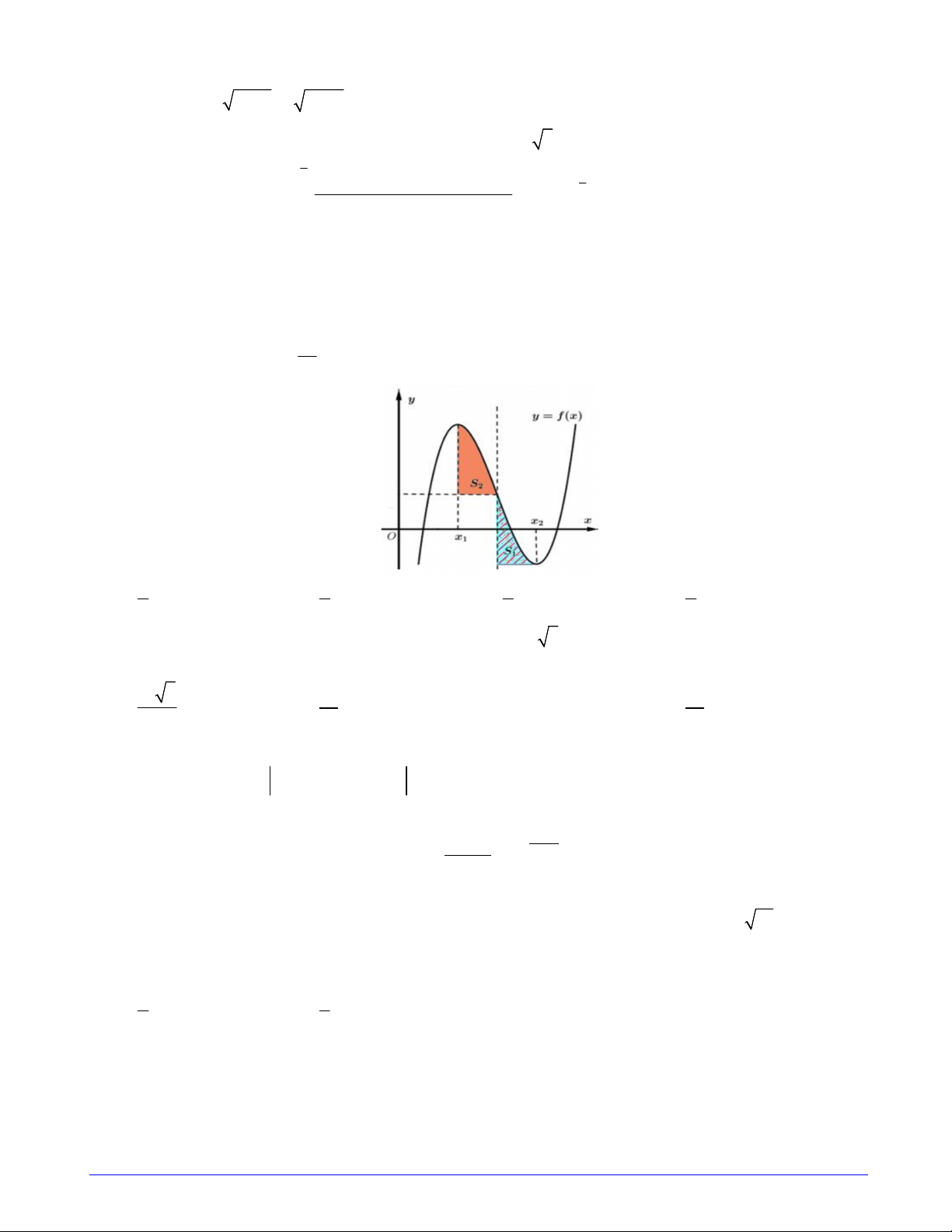
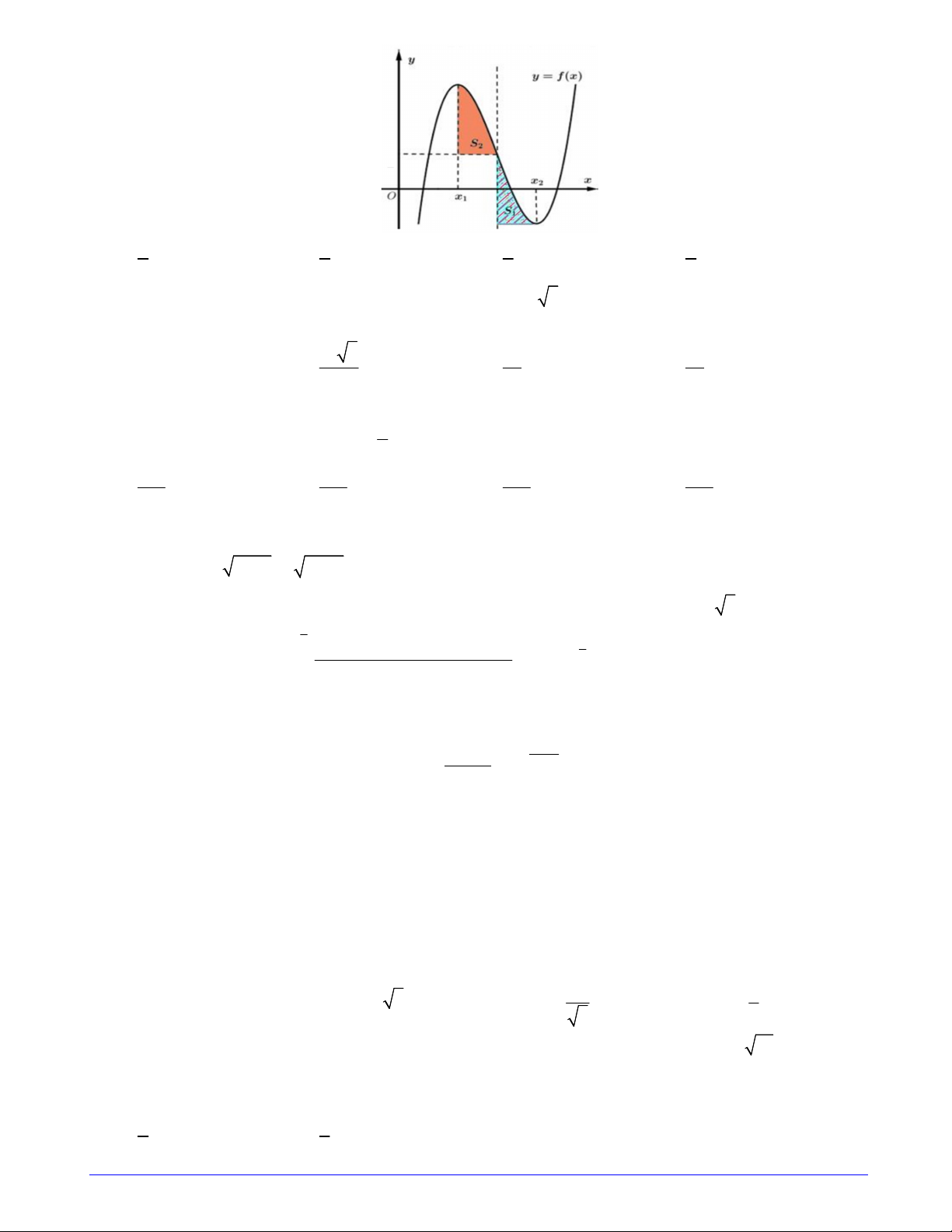
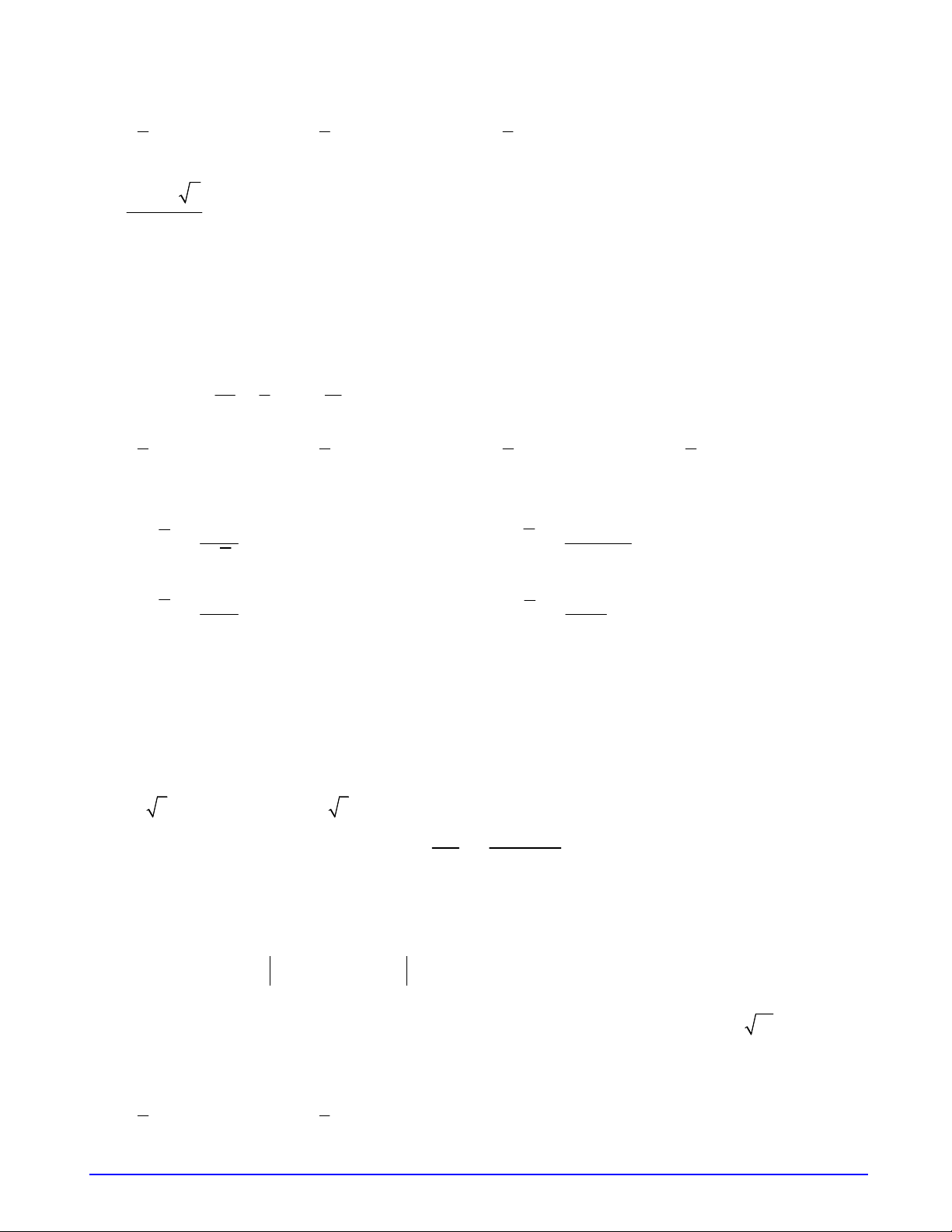
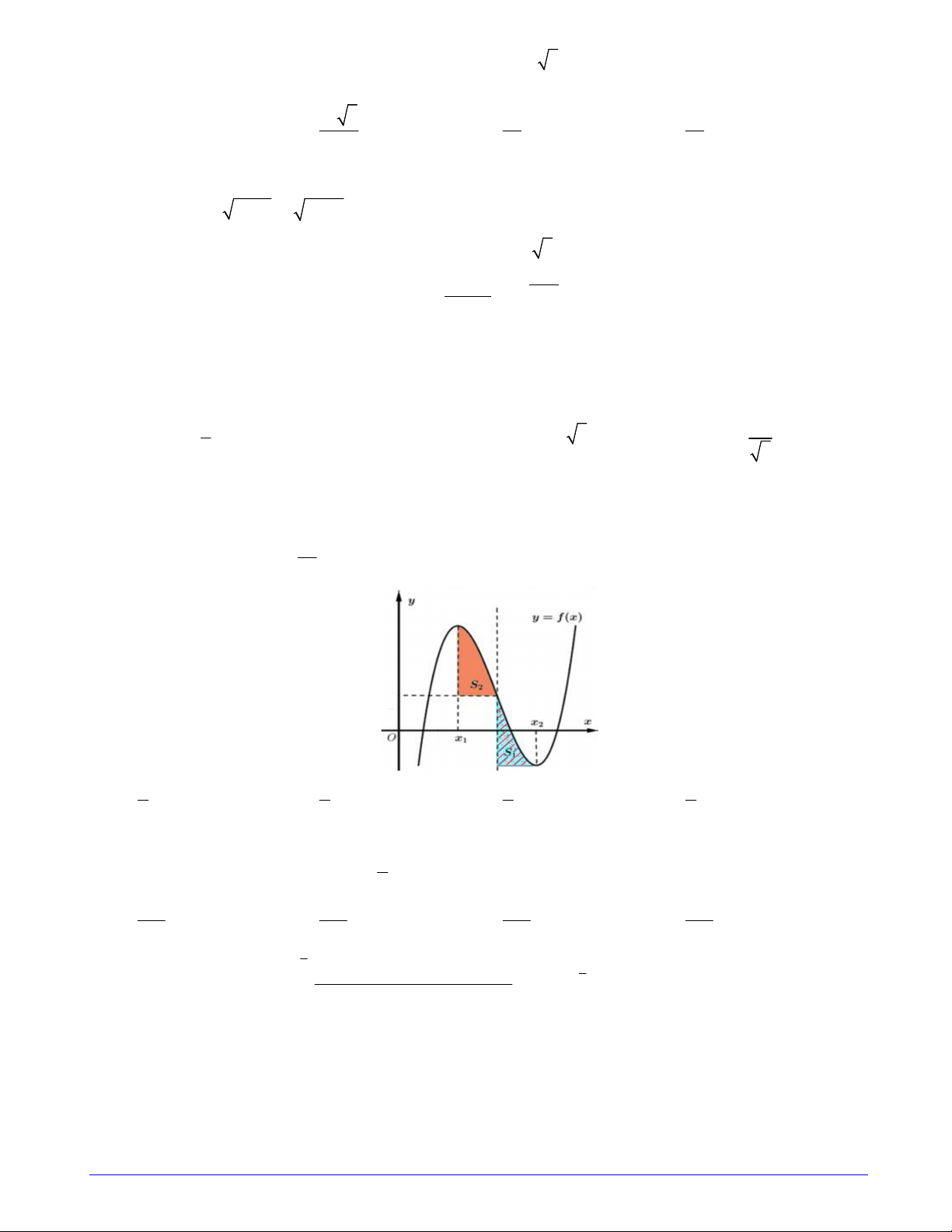
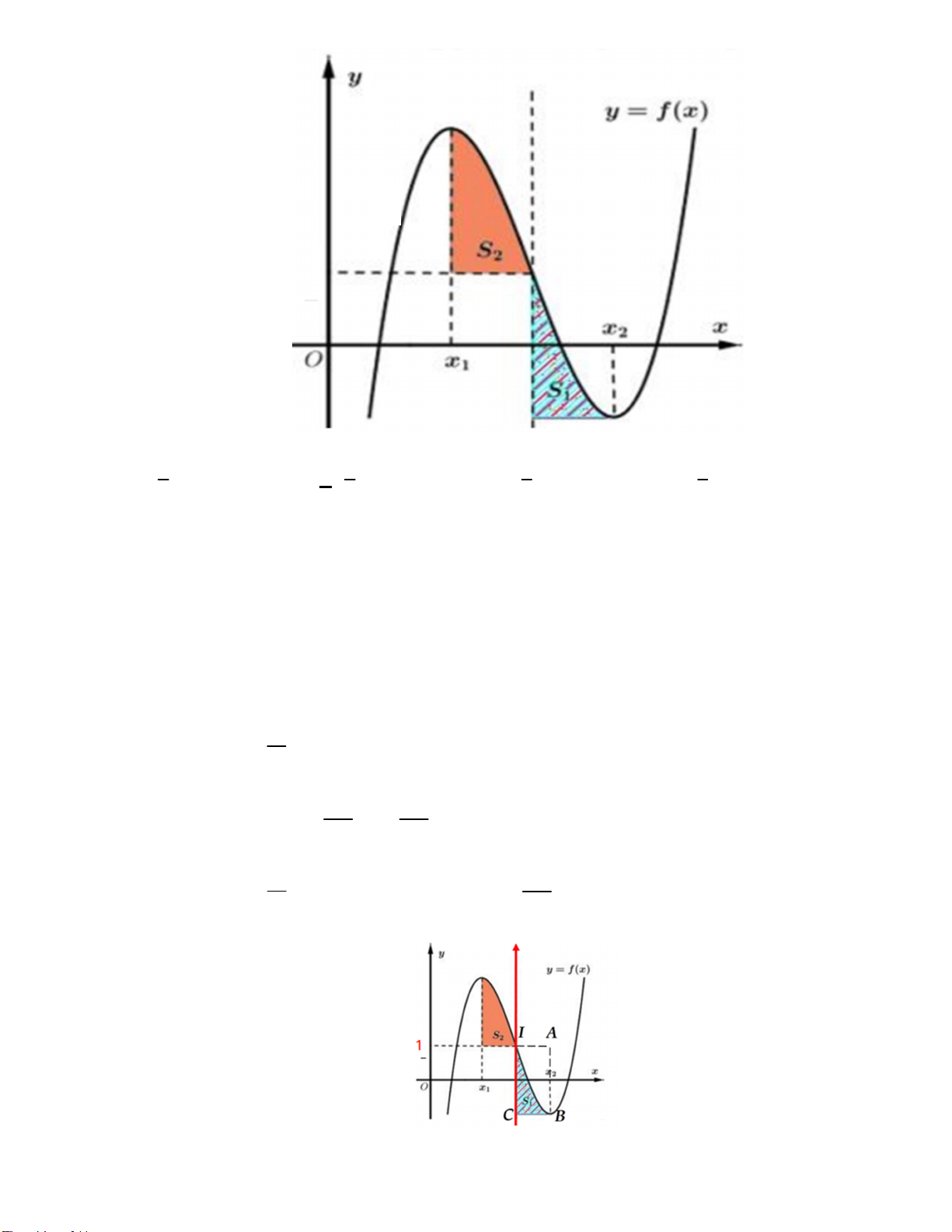
Preview text:

SỞ GD VÀ ĐT BẮC NINH
ĐỀ THI GIAO LƯU HỌC SINH GIỎI THPT
CỤM TRƯỜNG THPT GIA BÌNH, NĂM HỌC 2022 - 2023 THUẬN THÀNH, LƯƠNG TÀI Môn: Toán - Lớp 12
Ngày thi: 8 tháng 01 năm 2023 ( Đề thi gồm 7 trang)
Thời gian: 90 phút (không kể thời gian phát đề) Mã đề thi
Họ và tên thí sinh:.............................................................................. SBD:..................... 101  9    m.ab n
Câu 1. Cho a  log 3;b  log 2; và log ( ,
m n là các số nguyên tố). Giá trị của 12    2 5   125 . p ab  q.b m  n  p  q bằng A. 4 B. 8 C. 2 D. 6 2 x  x  1
Câu 2. Tìm họ tất cả các nguyên hàm của hàm số f (x)  . x 1 1 A. 1  C. B. 2 x  ln(x  1) C. (x  2 1) 2 x C. 2 x  ln x  1 C. D.  ln x  1 C. 2
Câu 3. Cho hình chóp S. ABC có AB  3, AC  4,BC  5 và góc giữa các cạnh bên với đáy bằng  60 .
Thể tích của khối chóp đã cho bằng 5 3 5 A. 15 3 B. 5 3 C. D. 6 3
Câu 4. Tổng các nghiệm của phương trình log    1 .log 2x x  7  0 là 2 2 A. 1  log 7 B. 3 C. 4 D. 5 2
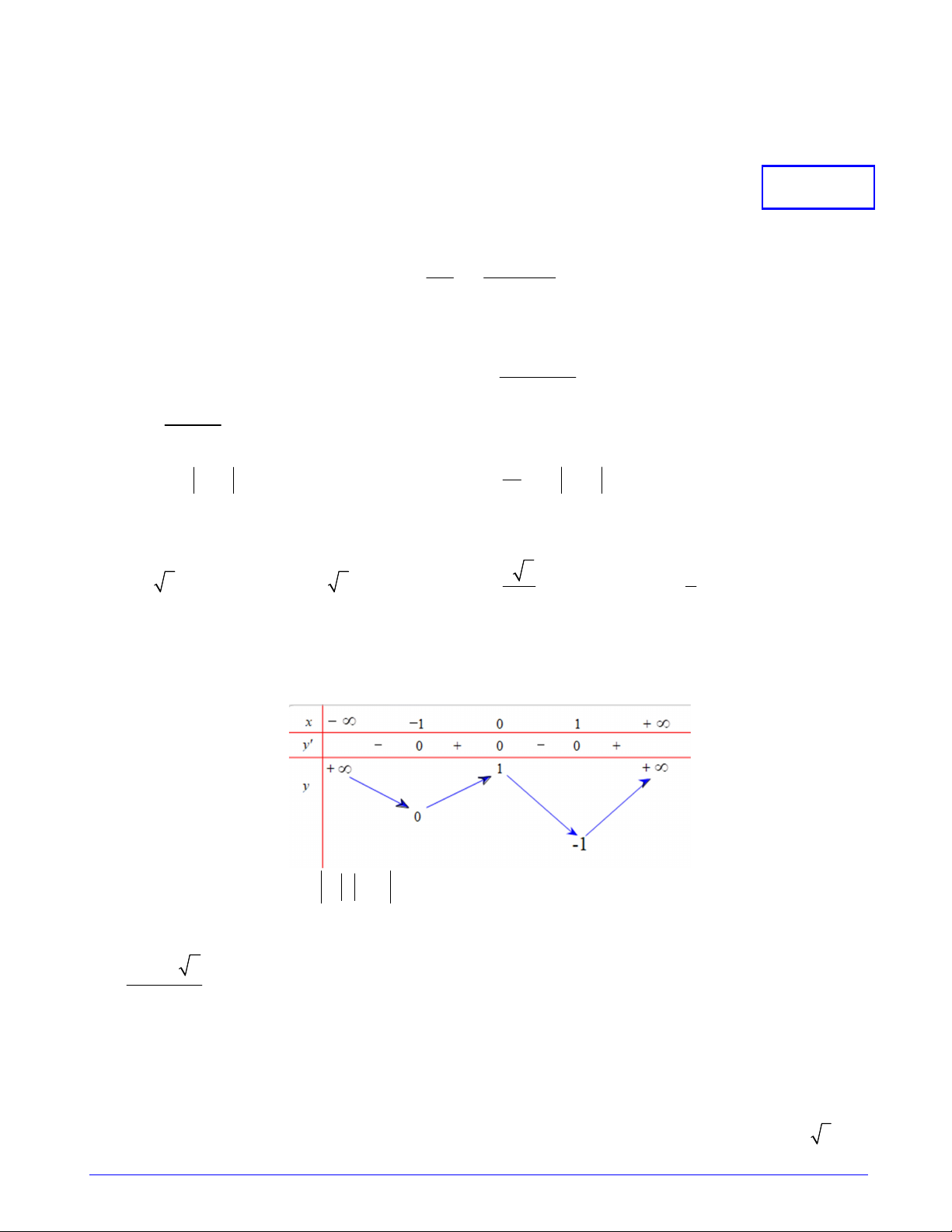
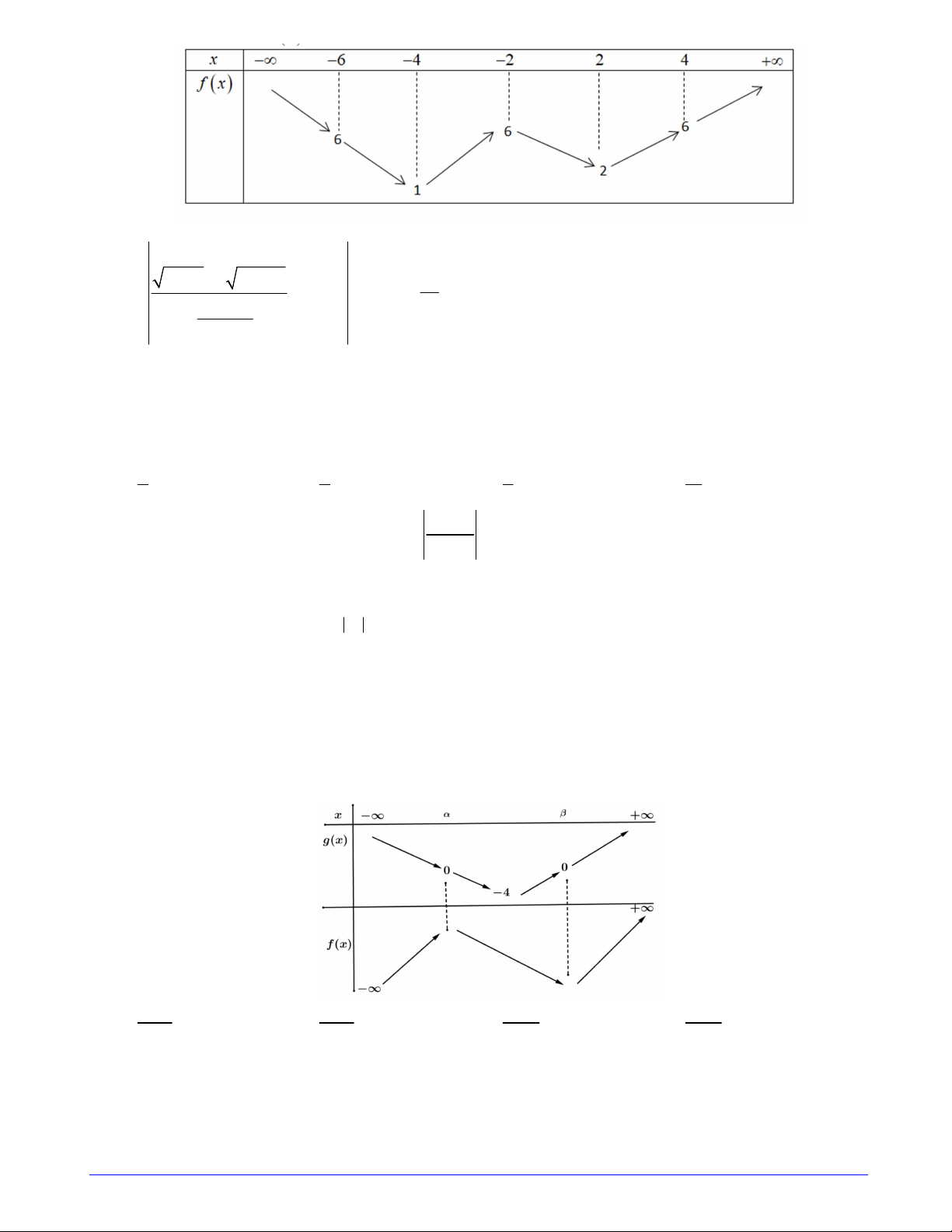
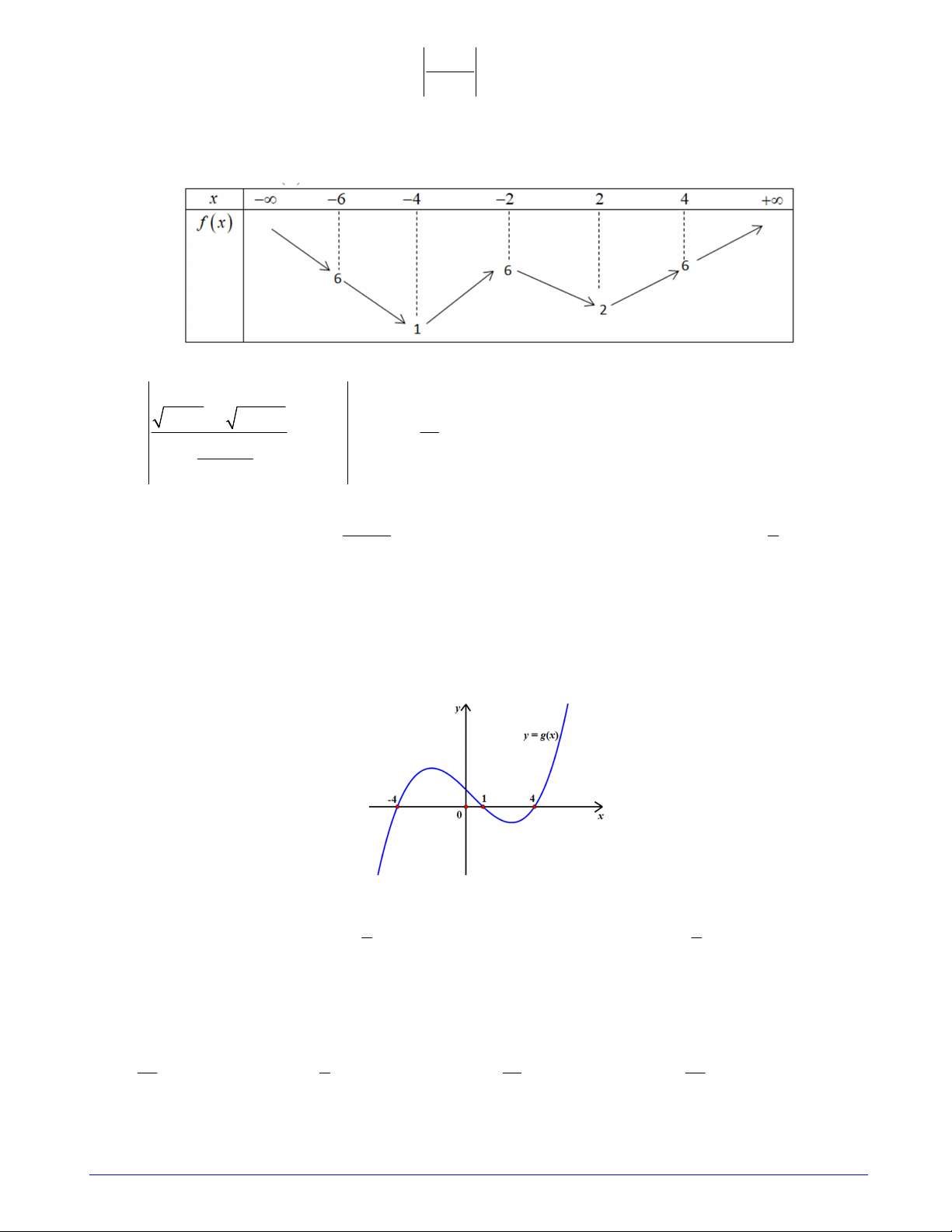
Câu 5. Cho hàm số y  f xlà hàm đa thức bậc 4, có bảng biến thiên như sau
Số nghiệm của phương trình f x 1  1 là A. 4 B. 5 C. 3 D. 6 Câu 6. Gọi ,
m n lần lượt là số đường tiệm cận đứng và số đường tiệm cận ngang của đồ thị hàm số x  1 x y 
. Giá trị của m  n bằng 3 x  x A. 2 B. 4 C. 3 D. 5 m
Câu 7. Cho hàm y  f x có f x  2 x x    3 '
1 x  x;x   . Có bao nhiêu giá trị nguyên của m  1;9  
9 để hàm sốy  f xnghịch biến trên ;2? A. 44 B. 50 C. 99 D. 49
Câu 8. Cho hình lăng trụ đứng ABC. 
A BC  có đáy là tam giác vuông và AB  BC  a , A  A  a 2 , M
là trung điểm của BC . Tính khoảng cách d của hai đường thẳng AM và BC . Trang 1/7 - Mã đề 101 a a a a A. d  7 . B. d  2 . C. d  3 . D. d  2 . 7 2 3 2
Câu 9. Cho dãy số a thỏa mãn a  1 và a  10a 1, n  2. Tìm giá trị nhỏ nhất của n để n  1 n n1 loga  100 n A. 102 . B. 103 . C. 100 . D. 101.
Câu 10. Có bao nhiêu giá trị nguyên của m để tập nghiệm của bất phương trình   3x 2x x m  0 chứa
không quá 8 giá trị nguyên? A. 15 B. 16 C. 8 D. 17
Câu 11. Cho hai khối trụ có cùng thể tích; bán kính đáy và chiều cao của hai khối trụ lần lượt là R ,h và 1 1 R ,h R 3 h
. Biết rằng 1  . Tỉ số 1 bằng 2 2 R 2 h 2 2 9 2 4 3 A. . B. . C. . D. . 4 3 9 2 Câu 12. Cho phương trình 2
2 cos 3x  3 2mcos3x  m  2  0. Số giá trị nguyên của tham số m để   
phương trình đã cho có đúng 3 nghiệm thuộc khoảng     ;     . là  6 3 A. 1 B. 4 C. 3. D. 2 x  1 Câu 13. Cho hàm số y 
(C) và d : y  2x  m 1 (m là tham số thực). Gọi k , k là hệ số góc x  2 1 2
của tiếp tuyến của C  tại giao điểm của d và C . Tính k .k . 1 2 1 A. k .k  4 . B. k .k  2 . C. k .k  3 . D. k .k  . 1 2 1 2 1 2 1 2 4
Câu 14. Xét các số thực dương a, b, x, y thỏa mãn a  1, b  1 và x y
a  b  ab . Giá trị nhỏ nhất của biểu thức P  x  2 y bằng 3 3 6 3  2 2 A. 3  2 2 . B. 2 2 . C. . D. . 2 2
Câu 15. Cho khối chóp S.ABC có SA  SB  SC  a và    ASB  2  0 , BSC  3  0 , CSA  4  0 . Mặt
phẳng  bất kì qua A cắt SB , SC tại B , C . Tìm giá trị nhỏ nhất của chu vi ABC  . A. a 3 . B. a 2 . C. a . D. 2a .
Câu 16. Trong không gian, cho hình chóp S.ABC cóSA, AB , BC đôi một vuông góc với nhau và
SA  a , AB  b , BC  c . Mặt cầu đi qua S , A , B , C có bán kính bằng 1 2a b c A. 2 a  2 b  2 c . B. 2  2  2 a b c . C. 2  2  2 2 a b c . D. . 2 3
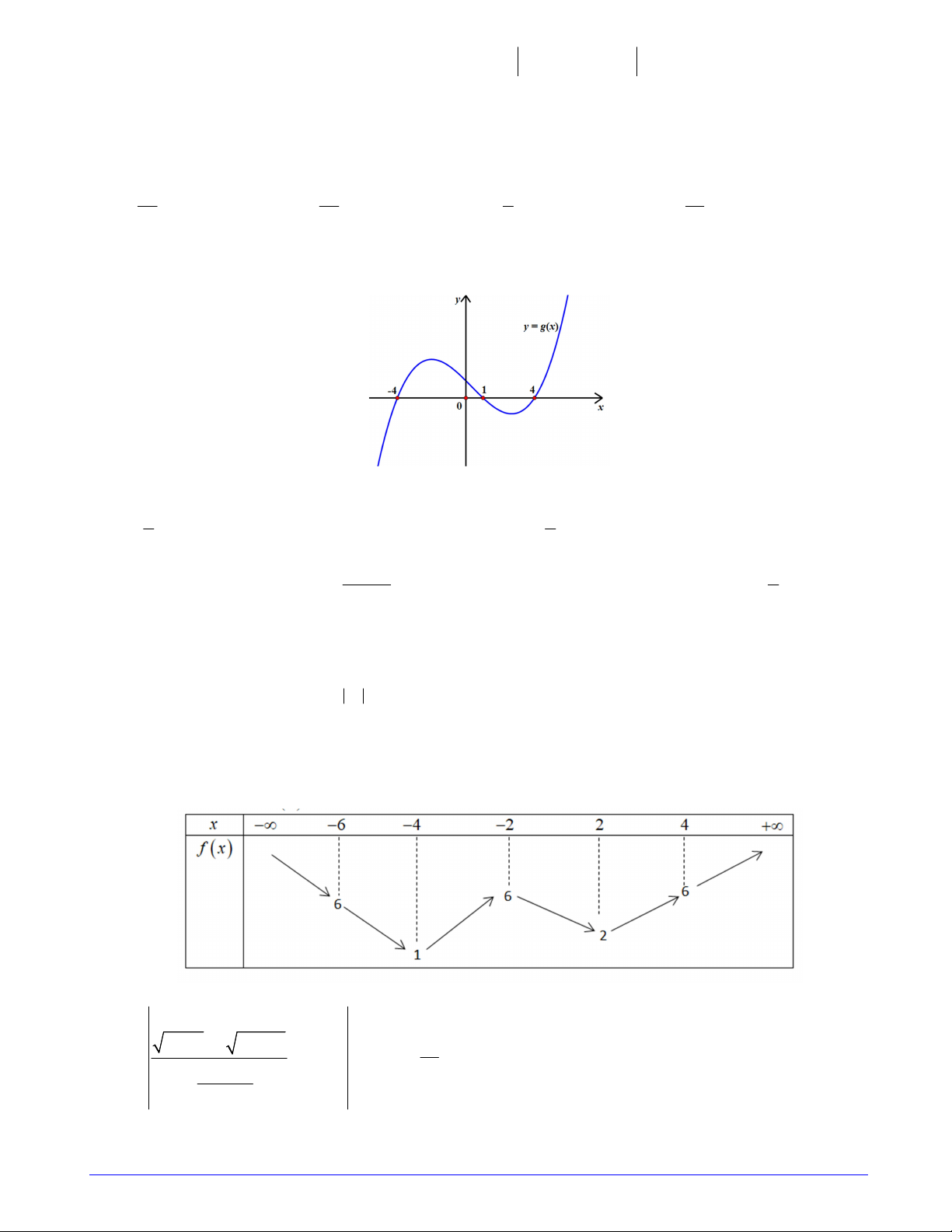
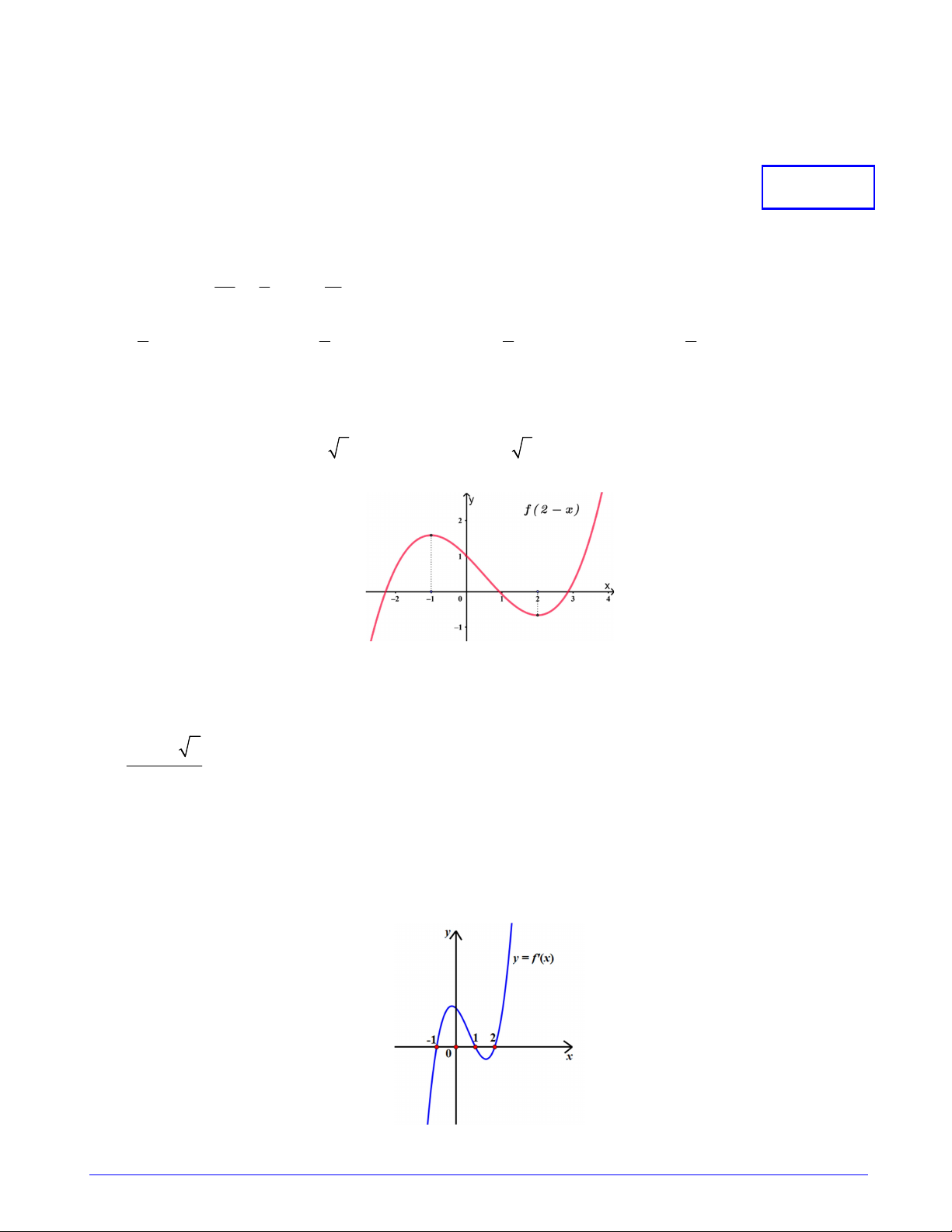
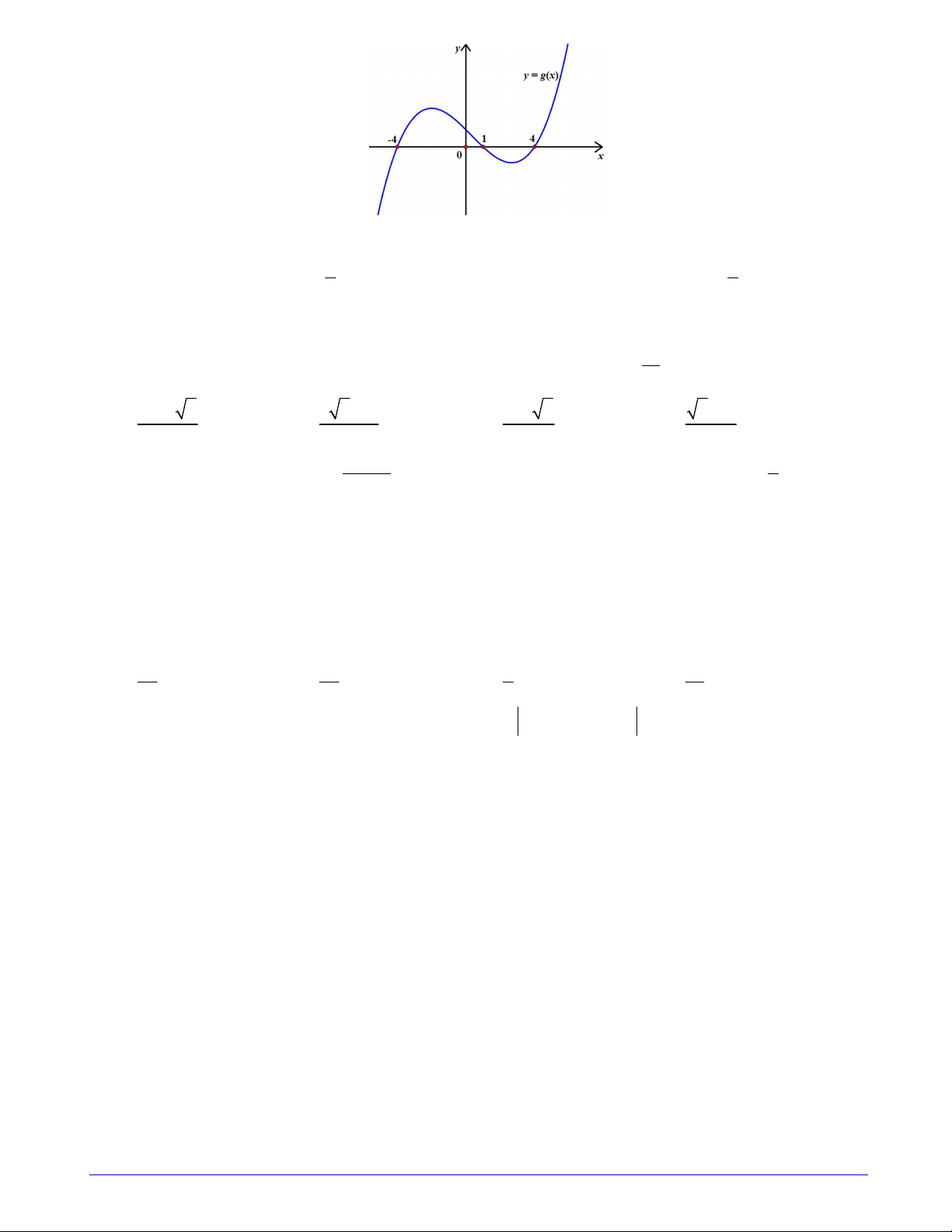
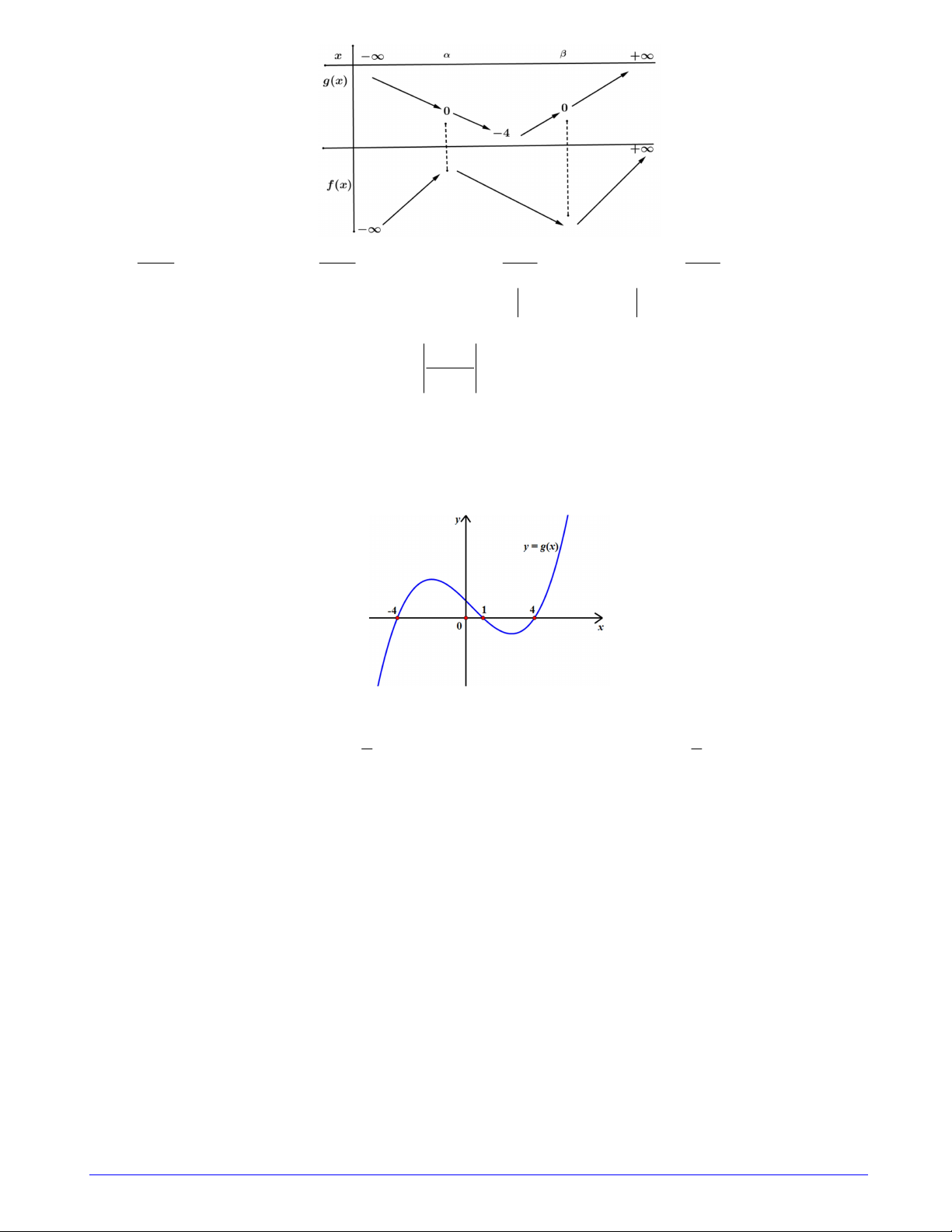
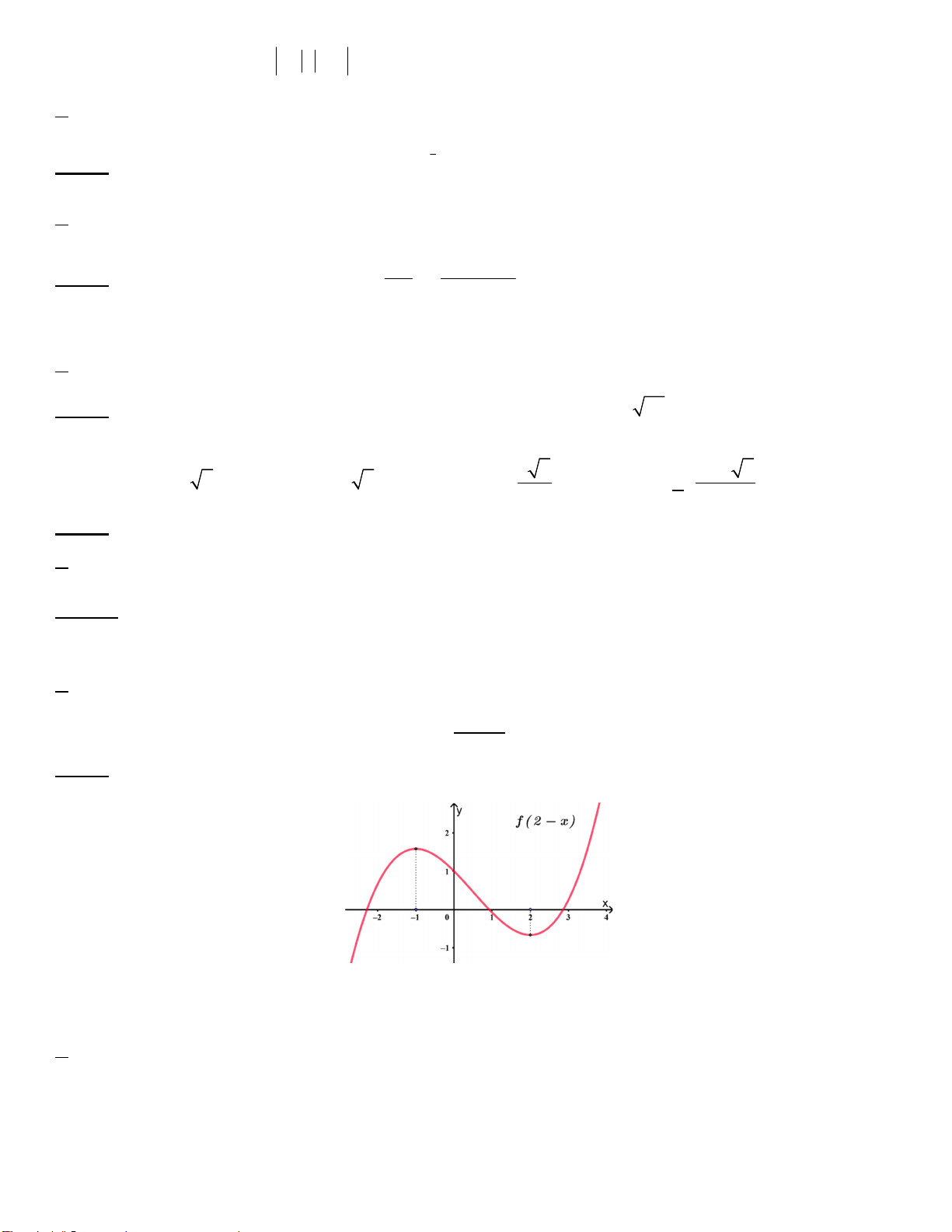
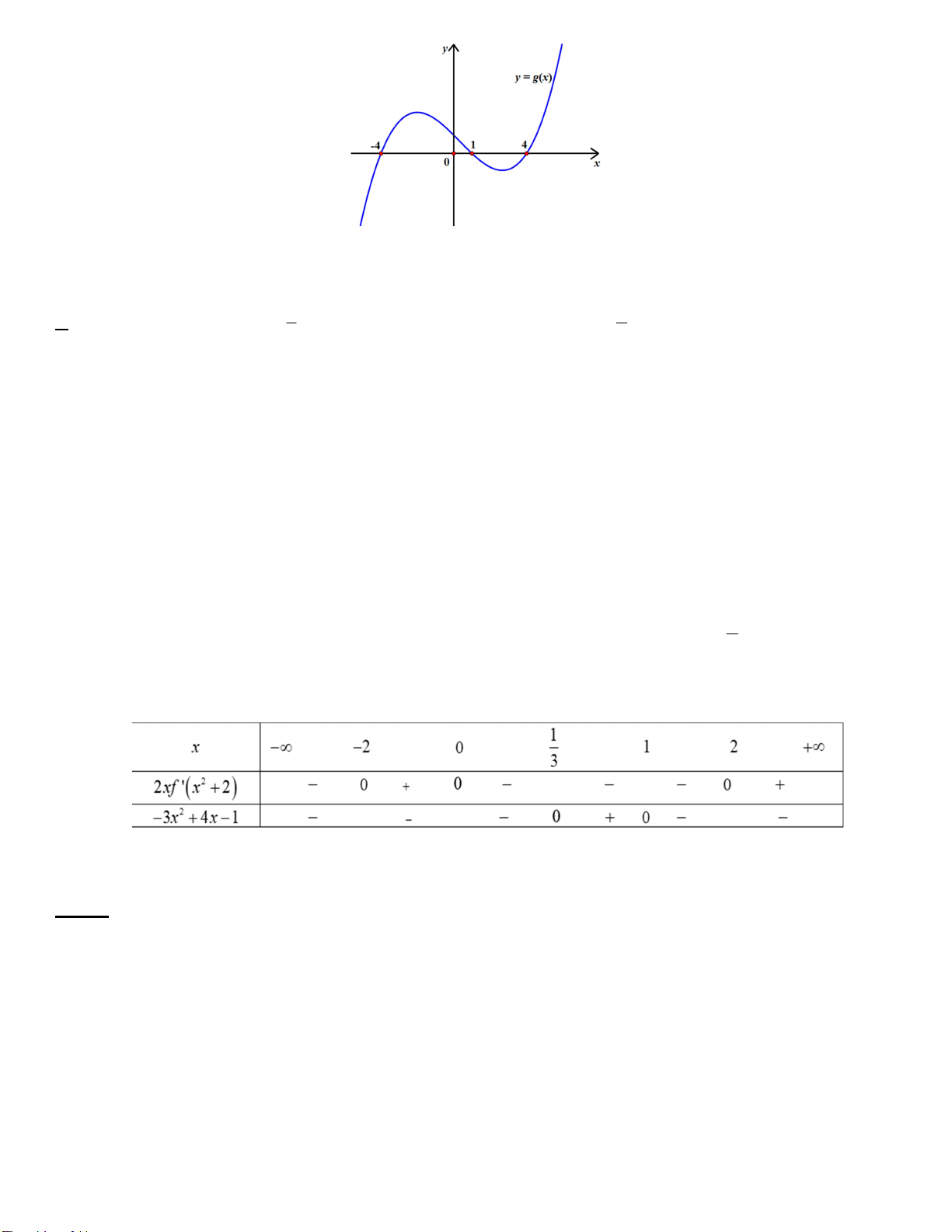
Câu 17. Cho đồ thị hàm số y  f 2  x có đồ thị như hình vẽ
Hàm số g x  f  2
x  3 nghịch biến trên khoảng nào dưới đây? A. ;  1 B. 1;0 C. 0;  1 D. 1;3 Trang 2/7 - Mã đề 101
Câu 18. Gọi M,m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  x  2 x  3 trên 0;2   . Giá trị của M  m bằng A. 3 B. 2 C. 0 D. 4
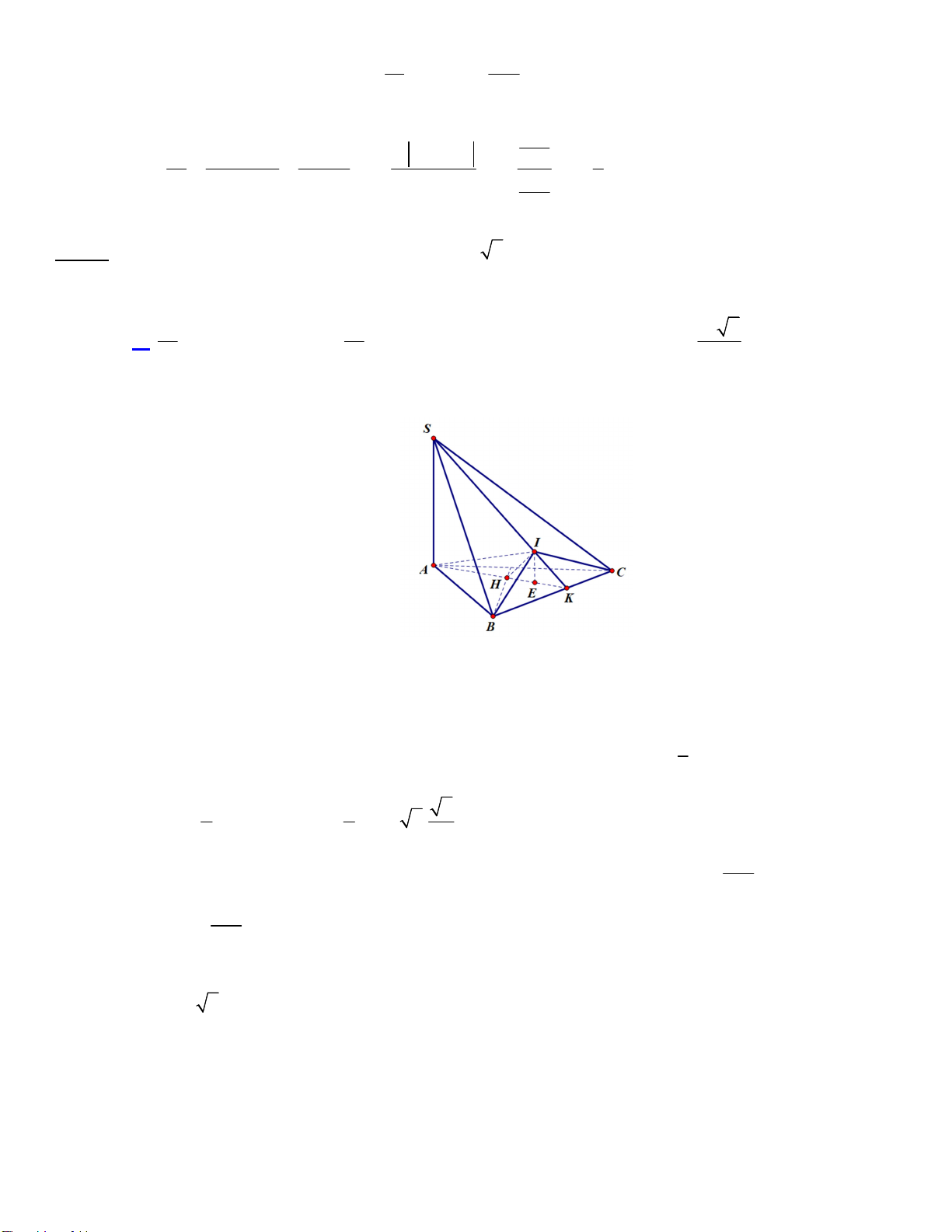
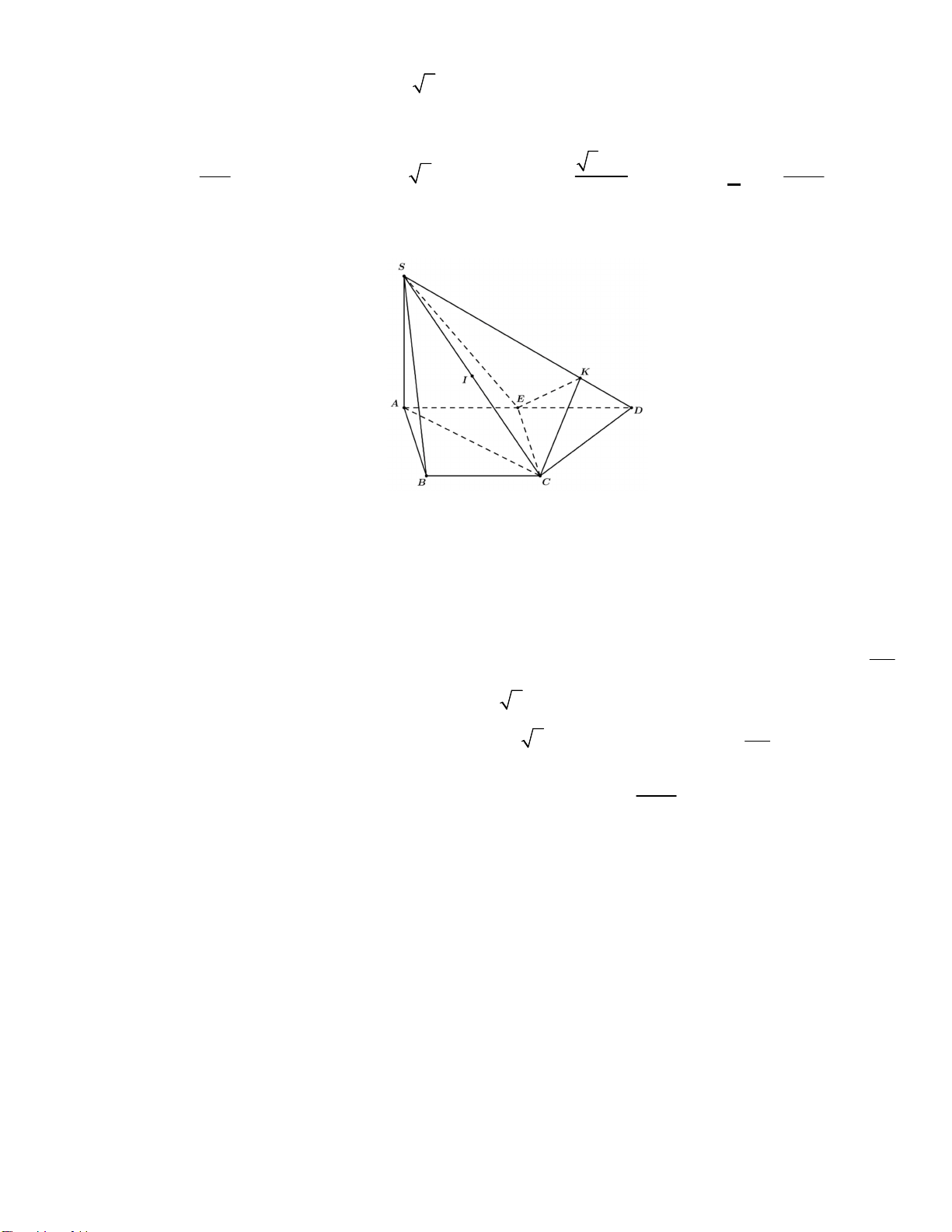
Câu 19. Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình thang vuông tại A và B , AB  BC  a ,
AD  2a , SA  ABCD và SA  a 2 . Gọi E là trung điểm củaAD . Kẻ EK  SD tại K . Tính thể
tích của khối cầu đi qua sáu điểm S , A , B , C , E , K ?  3 a  3 3 a  3 4 a A. V  . B. V   3 6 a . C. V  . D. V  . 6 2 3
Câu 20. Trong không gian với hệ trục tọa độ Oxyz, gọi  là góc hợp bởi đường thẳng x  3 y  4 z  3 d :  
và mặt phẳng P : 2x  y  z 1  0 . Khi đó, giá trị cos bằng bao nhiêu 1 2 1 3 1 1 A.  3 . B. . C. . D.  . 2 2 2 2
Câu 21. Trong không gian Oxyz , cho mặt cầu S  2 2 2
: x  y  z  2x  4 y  4z  5  0 và mặt phẳng
P:x  y  2z 1 0. Gọi M là một điểm bất kì trên mặt cầu S. Khoảng cách từ M đến P có giá trị nhỏ nhất bằng 4 6 A. 6  2 . B. 0 . C.  2 . D. 2 6 2. 3
Câu 22. Trong không gian Oxyz , cho hình hộp ABC . D 
A BC D biết A1;0; 1, B2;1;2, D1;1; 1,
C 4;5;5. Tọa độ của điểm  A là: A. A4;6;5. B. A3;4;  1 . C. A3;5;6. D. A3;5;6.
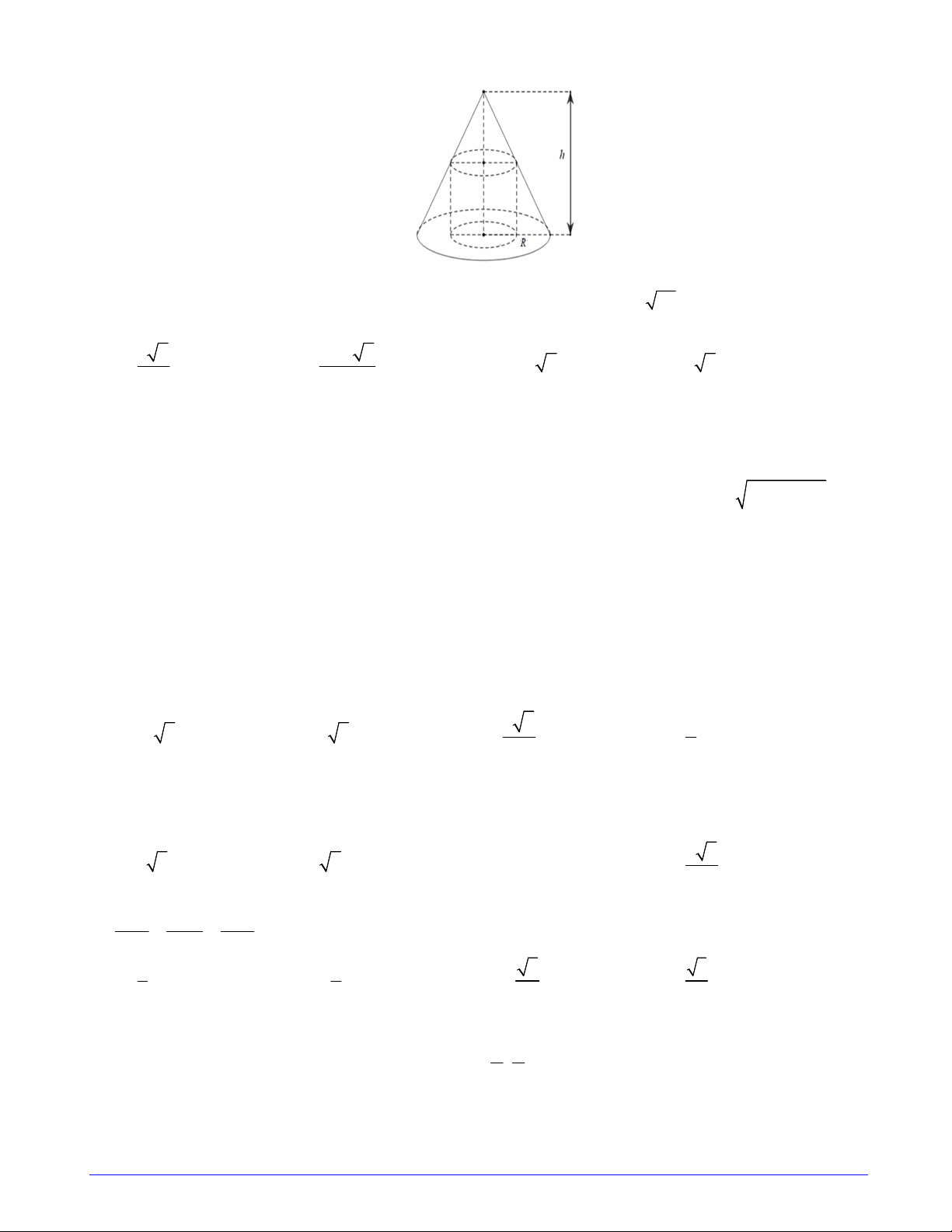
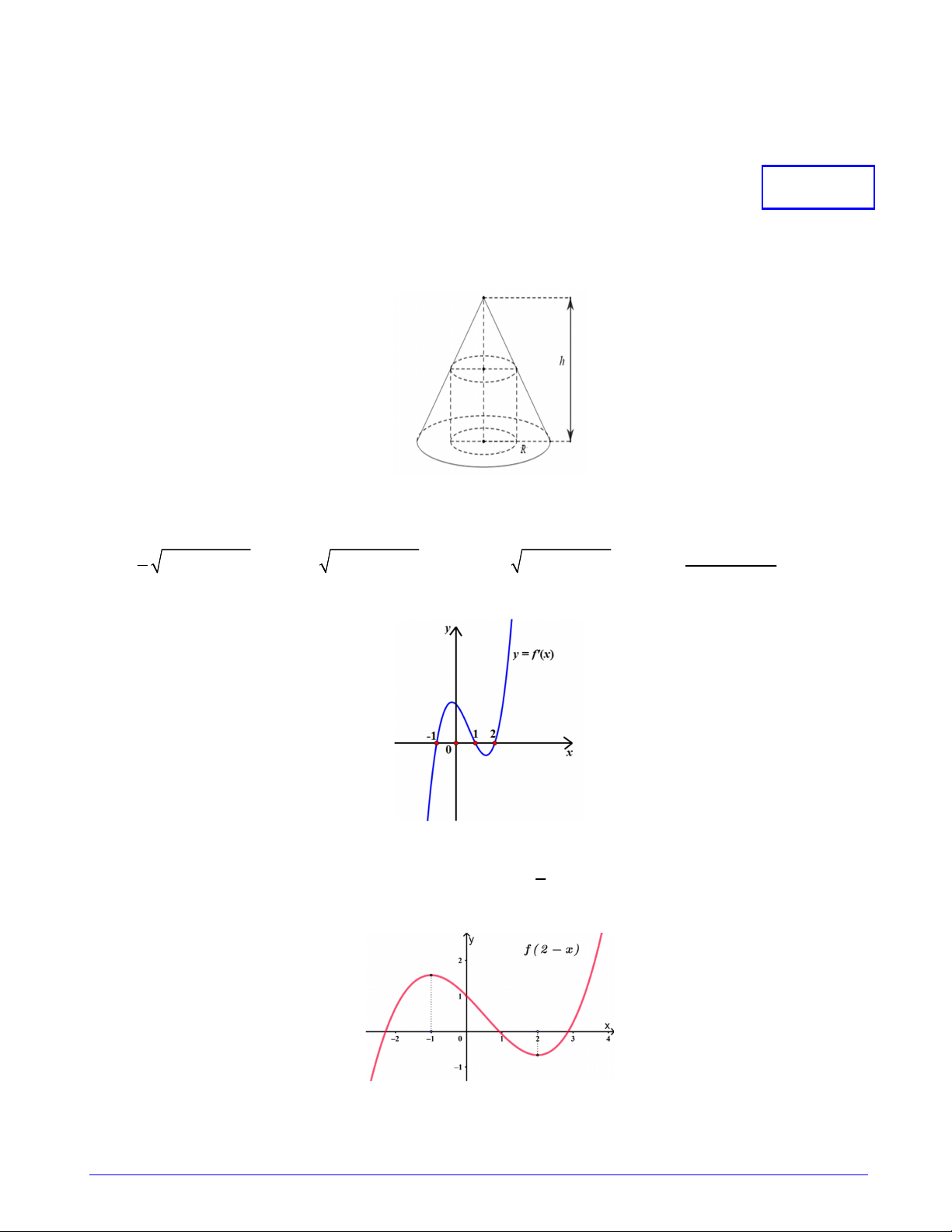
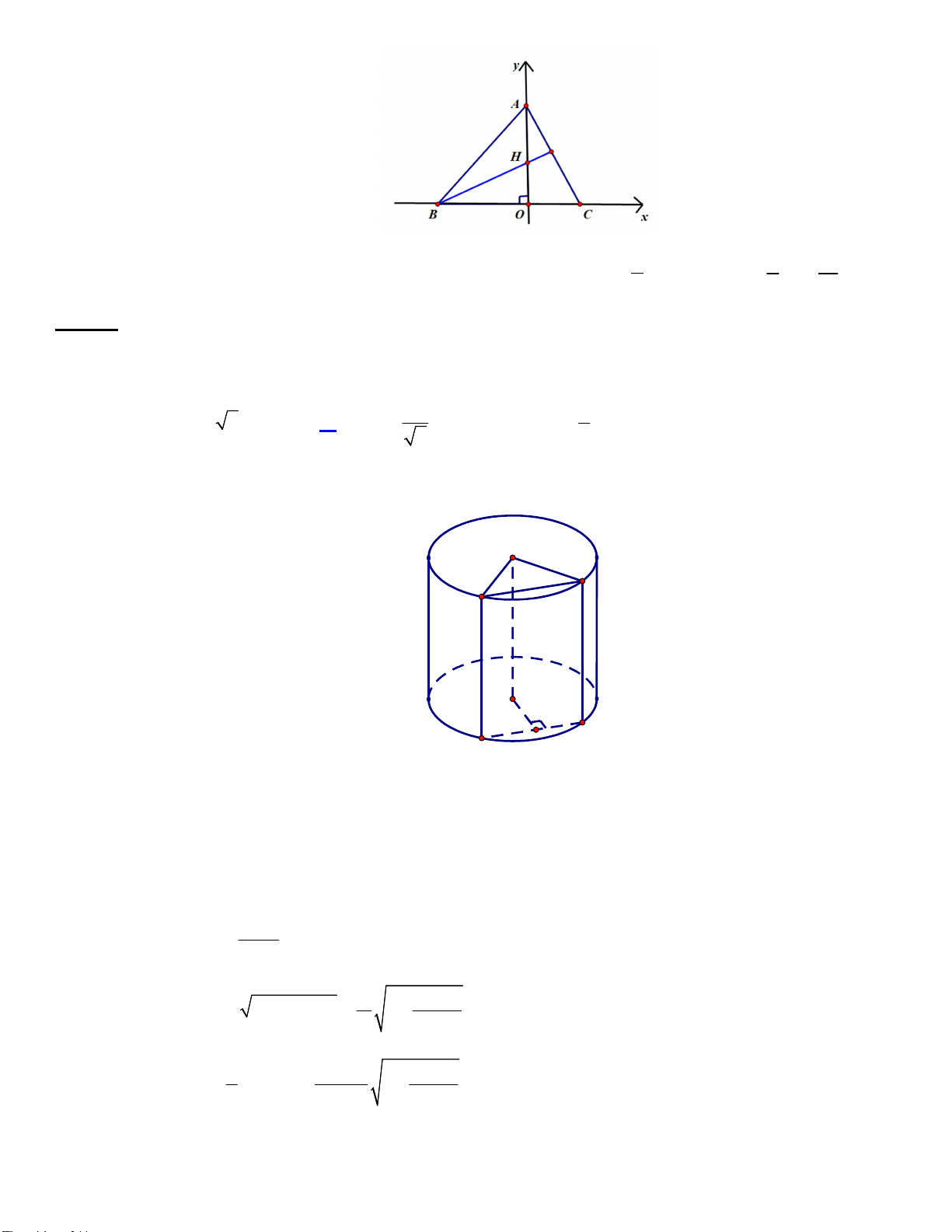
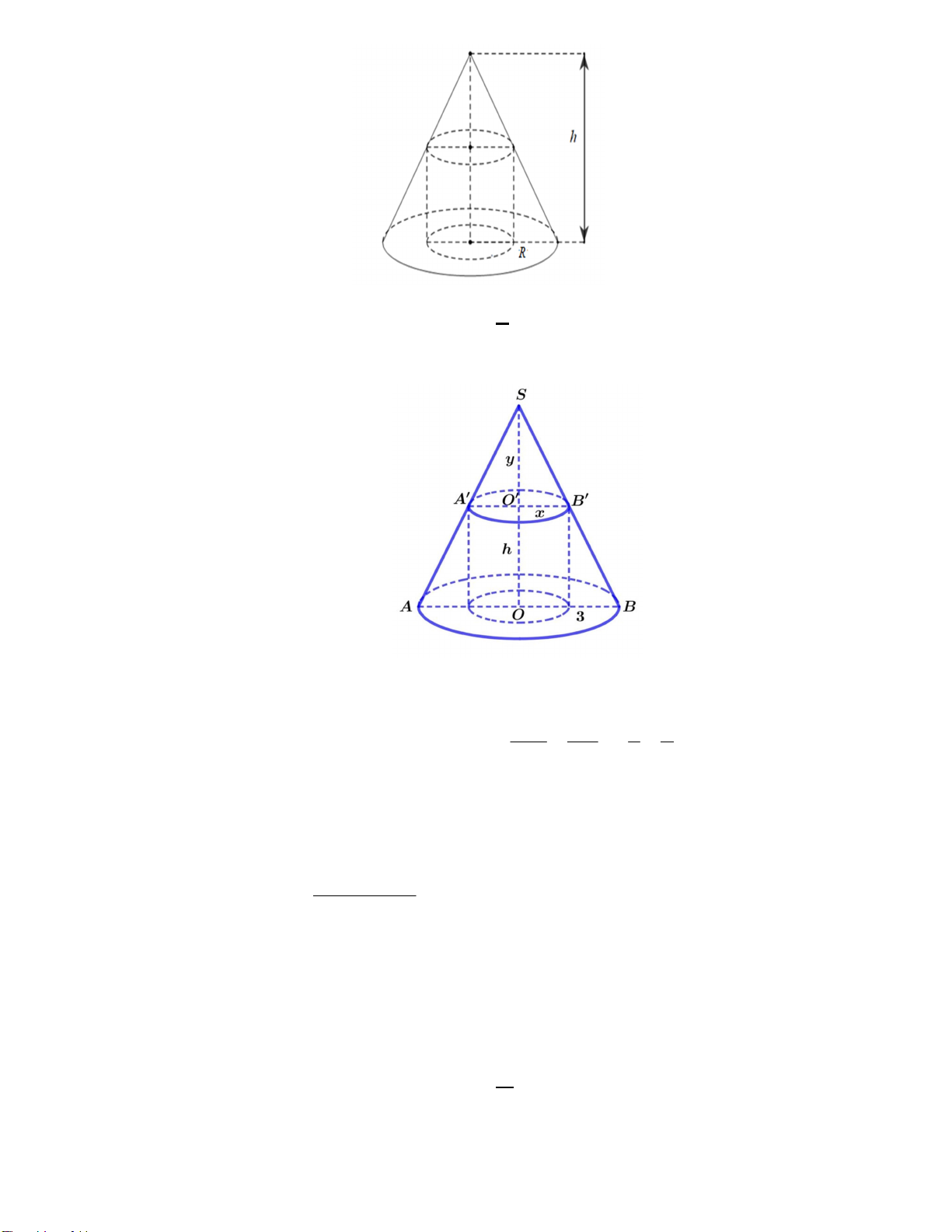
Câu 23. Cho hình nón có bán kính đáy bằng 3 và chiều cao bằng 6 , một khối trụ có bán kính đáy thay đổi
nội tiếp khối nón đã cho (như hình vẽ). Thể tích lớn nhất của khối trụ bằng A. 6 . B. 8 . C. 4 . D. 10 . 1
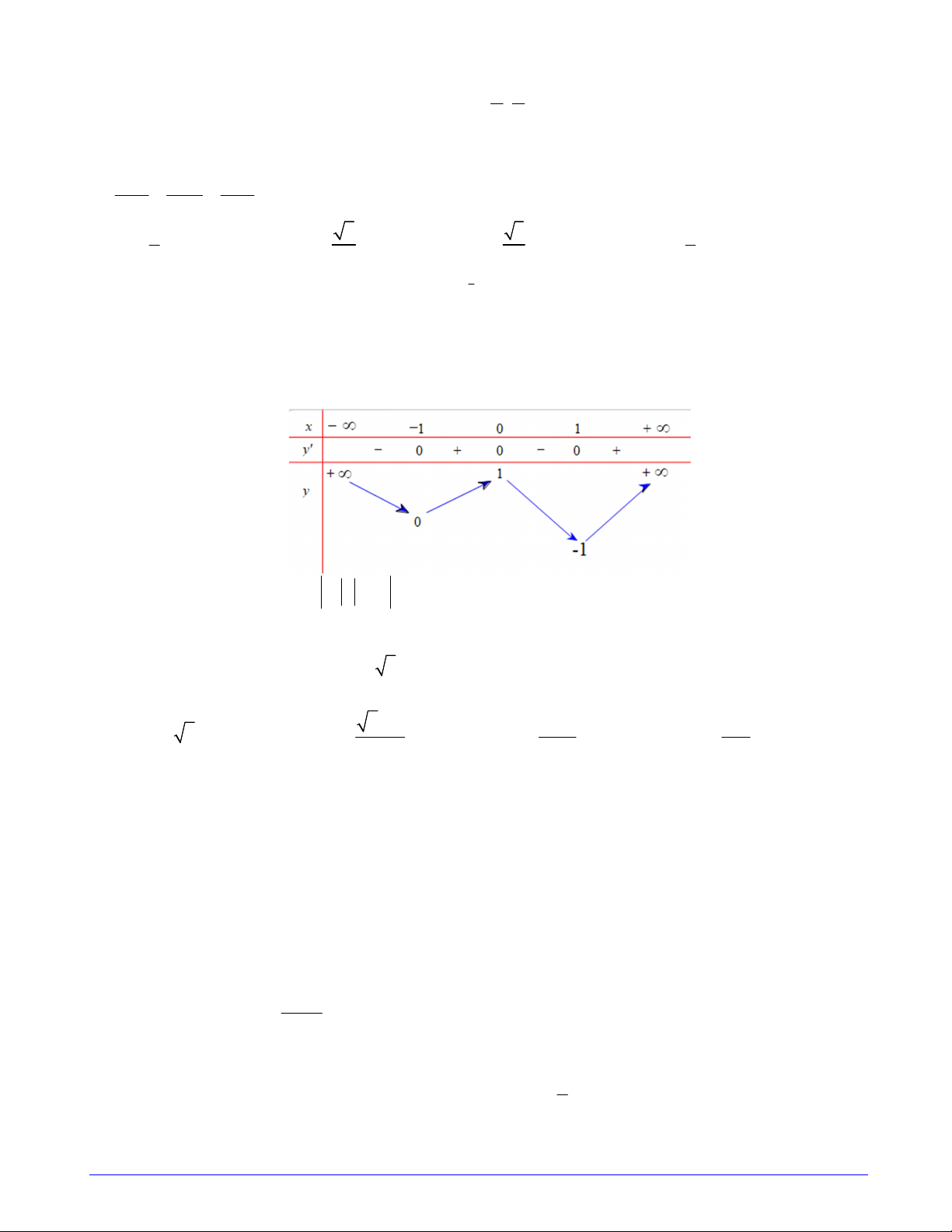
Câu 24. Tập xác định của hàm số  y  3 x    2x3 1 là A. D  ;  1  1; B. D  1;  1 \   0 C. D  0;  1 D. D  1;  1
Câu 25. Biến cố A liên quan đến một phép thử ngẫu nhiên T có hữu hạn kết quả đồng khả năng xuất hiện.
Khẳng định nào sau đây là đúng? n A A. P     A  . B.    1 P A . n    P   A n  n  \ A C. P     A  . D. P     A  . n   A n    Trang 3/7 - Mã đề 101  2 3x khi x  1 3 Câu 26. Cho hàm số  f(x)   . Tính tích phân f x   1dx . 4  x khi x   1 1 3 5 7 A. . B. . C. 1. D. . 2 2 2
Câu 27. Tính thể tích của một hình hộp chữ nhật biết rằng ba mặt của hình này có diện tích là 2 20cm , 2 10cm , 2 8cm . A. 3 1600cm B. 3 80cm C. 3 40cm D. 3 38cm
Câu 28. Cho hàm số f (x) liên tục trên [a; b] và số thực k tùy ý. Trong các khẳng định sau, khẳng định nào sai? a b a A. kf t dt   ( ) 0 B. f(x)dx     f(x)dx a a b b 2b b b C. f(2x)dx   2 f(x)dx D. kf(x)dx   k f(t)dt a 2a a a
Câu 29. Quay xung quanh trục Ox hình phẳng giới hạn bởi đồ thị của hàm số y  (x  3) log x  1 , trục 0,5
Ox , và đường thẳng x  1 ta thu được khối tròn xoay có thể tích bằng 3 3 A. (x   2 3) (log x+1)dx . B.  (x  2 3) (log x+1)dx . 0,5  0,5 2 1 2 2 C.  (x   2 3) (log x+1)dx . D. (x  2 3) (log x+1)dx . 0,5  0,5 1 1
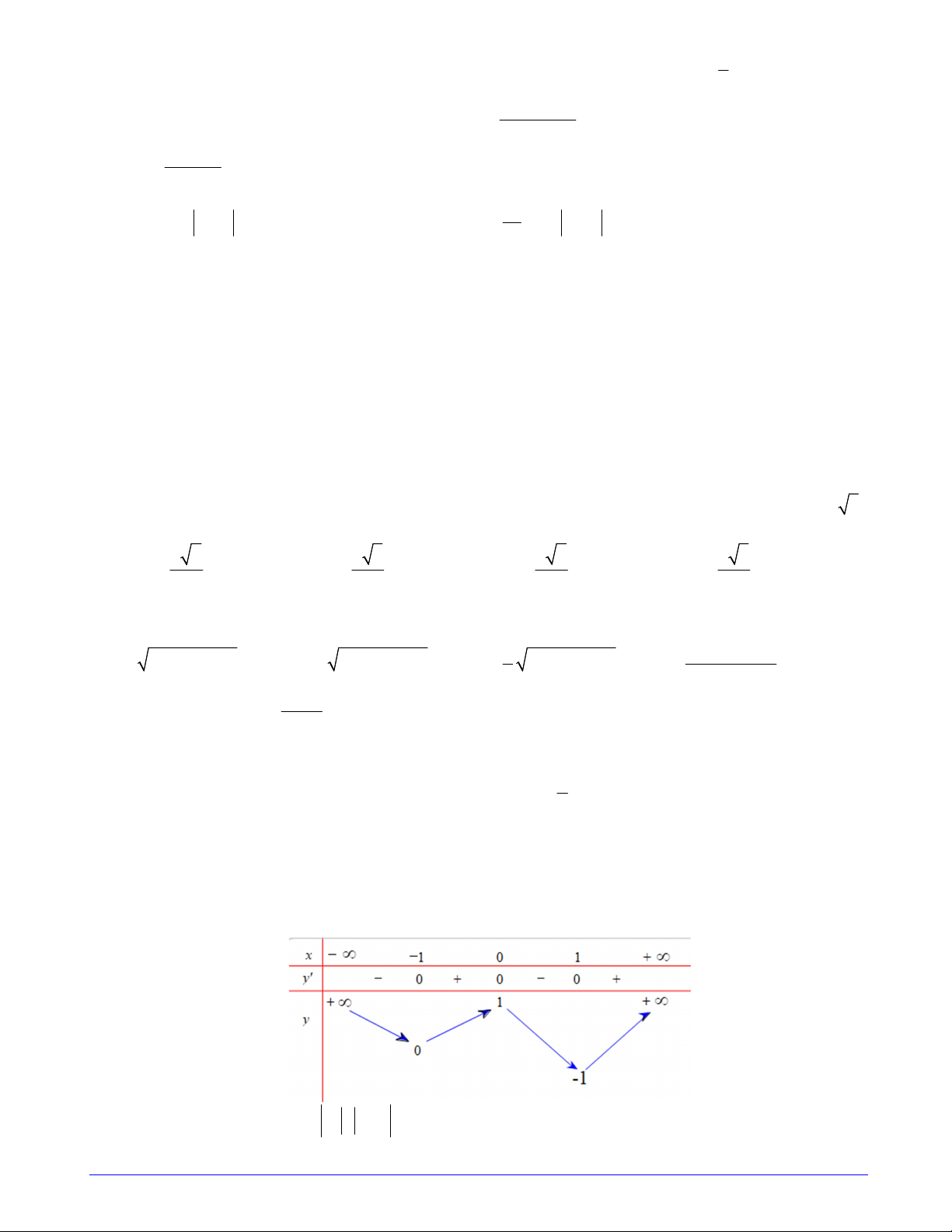
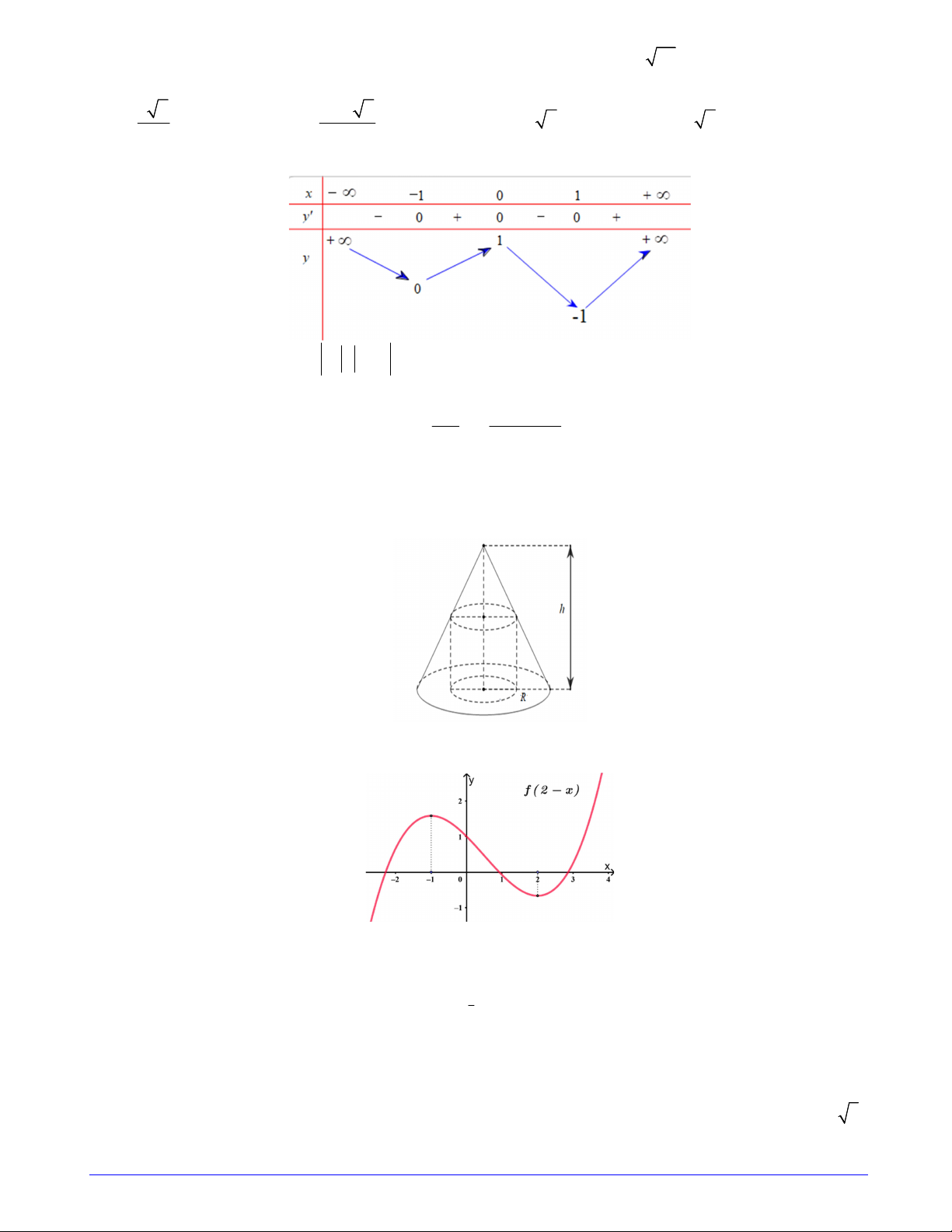
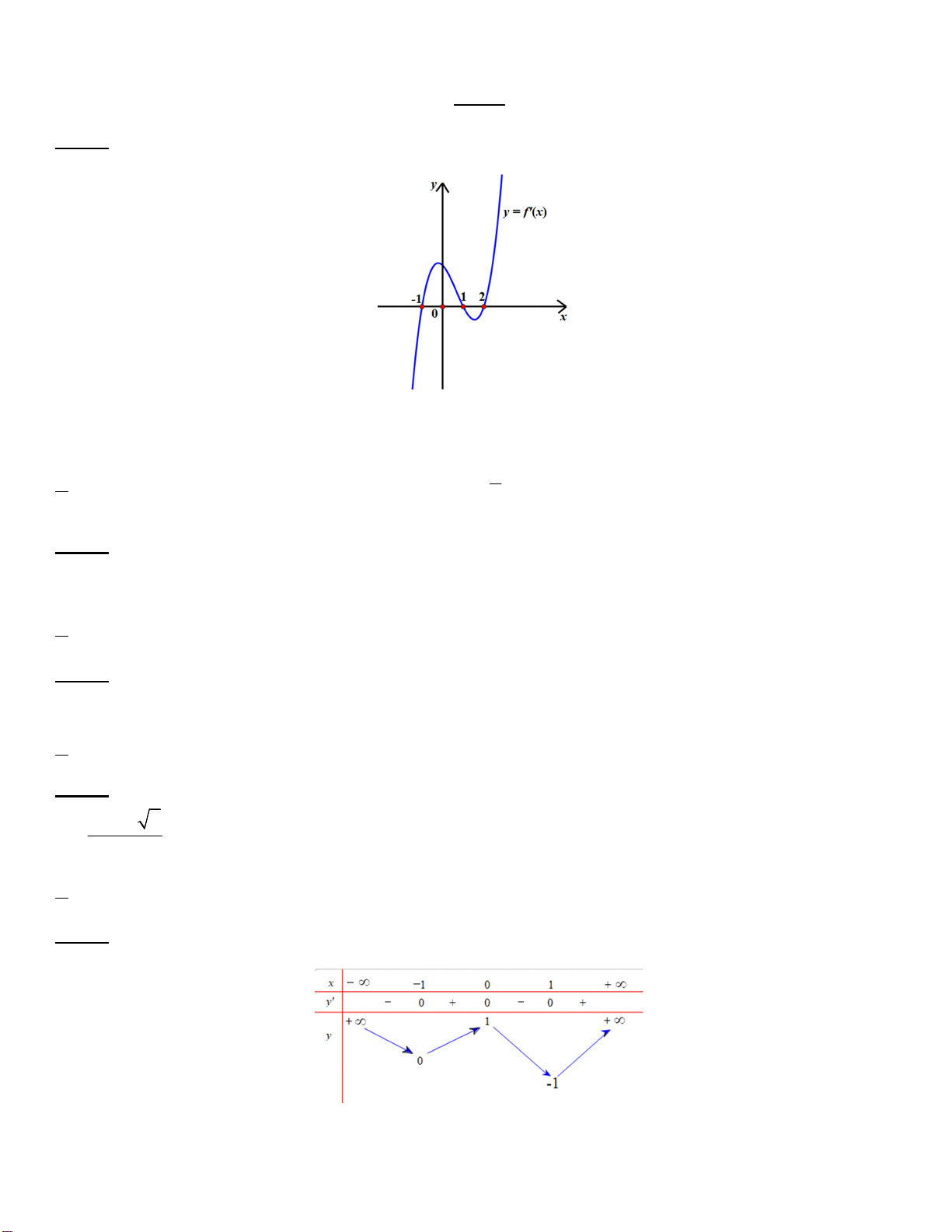
Câu 30. Cho hàm số y  f x có đồ thị hàm số y  f 'x như hình vẽ
Hàm số g x  f 1 2xđạt cực đại tại điểm nào? 1 A. x  1; B. x  0 C. x  1;x  2 D. x  ;x  1 2 2 x    2 1 x  1
Câu 31. Tổng các nghiệm của phương trình  log      2 2 x là 2  x    A. 4 B. 1 C. 5 D. 3
Câu 32. Cho hàm số bậc ba f x có đồ thị hàm số như hình vẽ bên. Biết hàm số f x đạt cực trị tại hai điểm
x ,x thỏa mãn x  x  4 và f x f x
2 . Gọi S ,S là diện tích của hai hình phẳng được cho 1    2   1 2 2 1 1 2 S
trong hình vẽ bên. Tính tỉ số 1 . S2 Trang 4/7 - Mã đề 101 3 3 5 8 A. . B. . C. . D. . 5 8 3 5
Câu 33. Gọi S là tập tất cả các giá trị nguyên của m để bất phương trình  2   x m m e  mx  2 2 2
m  2m  0nghiệm đúng với mọi x thuộc  . Tổng giá trị tất cả các phần tử của S bằng A. 2 B. 0 C. 5 D. 4
Câu 34. Cho hàm số y  f x  3 x  2
bx  cx  3 thỏa mãn min f x f 1
1. Giá trị lớn nhất của 0;2      
hàm số g x  f  1x  1 x  là A. 17 B. 55 C. 3  2 D. 5
Câu 35. Cho hàm số y  f x có f x  3 x  2 '
3x 10x; x   . Có bao nhiêu giá trị nguyên dương của
m để hàm số g x  f  2x 2mx m 2  3 có 13 điểm cực trị? A. 5 B. 2 C. 3 D. 4  ex  2 3 5 cos x cosx sinx    Câu 36. Cho tích phân I  dx  a.eb  c 
, với a , b , c là các số thực. Tính 2 cos x 0
giá trị của biểu thức P  a  b  c ?. A. 10. B. 2. C. 4. D. 16.
Câu 37. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB  1, AD  10 , SA  SB ,
SC  SD . Biết mặt phẳng SAB và SCD vuông góc nhau đồng thời tổng diện tích của hai tam giác
SAB và SCD bằng 2 . Thể tích khối chóp S.ABCD bằng 3 1 A. 2 . B. 1. C. . D. . 2 2
Câu 38. Cho hình trụ có đáy là hai đường tròn tâm O và O , bán kính đáy bằng chiều cao và bằng R . Trên
đường tròn đáy có tâm O lấy điểm A , trên đường tròn tâm O lấy điểm B . Đặt  là góc giữa AB và đáy.
Biết rằng thể tích khối tứ diện OOAB đạt giá trị lớn nhất. Khẳng định nào sau đây đúng? A.   1 tan . B.   1 tan . C. tan   1 . D. tan   2 . 2 2
Câu 39. Cho hàm số f (x) xác định, có đạo hàm, liên tục và đồng biến trên [1;4] thỏa mãn x  xf x  f  2 x x  f  3 2 ( ) [ ( )] , [1;4], (1) . Giá trị f (4) bằng 2 391 361 381 371 A. . B. . C. . D. . 18 18 18 18
Câu 40. Cho hình chóp S.ABC có SA ABC    AB  a BC  a ABC  0 ; 2 2, 3 , 45 . Gọi I là trực tâm
của tam giác SBC . Giá trị lớn nhất của thể tích khối chóp I.ABC bằng 3 a 3 a 3 a 2 A. . B. . C. 3 a . D. . 2 4 2 Trang 5/7 - Mã đề 101
Câu 41. Có bao nhiêu giá trị nguyên của m để hàm số y  4 x  2
mx  64x có đúng 5 điểm cực trị? A. 5 B. 19 C. 6 D. 24
Câu 42. Cho hình tứ diện đều ABCD . Trên mỗi cạnh của tứ diện, ta đánh dấu 3 điểm chia đều cạnh tương
ứng thành các phần bằng nhau. Gọi S là tập hợp các tam giác có ba đỉnh lấy từ 18 điểm đã đánh dấu. Lấy ra
từ S một tam giác, xác suất để mặt phẳng chứa tam giác đó song song với đúng một cạnh của tứ diện đã cho bằng 2 9 2 4 A. . B. . C. . D. 45 34 5 15
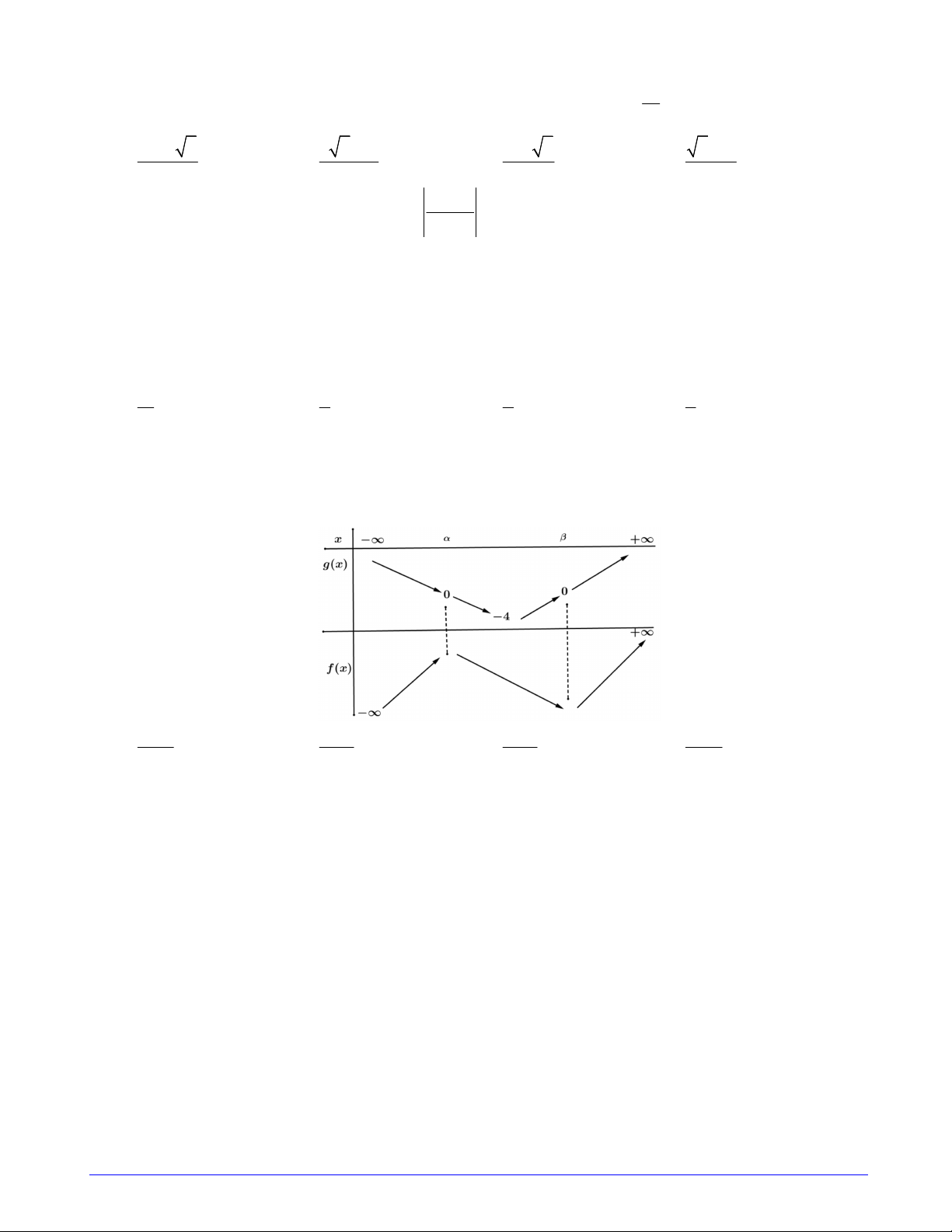
Câu 43. Cho các hàm số y  f x;y  g xliên tục và có đạo hàm trên  , trong đó hàm số
g x  f 2 x 'là hàm số bậc ba có đồ thị như hình vẽ. Hàm số y  f  2 x   3x  2 2
2x  x  2023 nghịch biến trên khoảng nào dưới đây? 1   1 A.    ;       1 B. 1;2 C.   ;  D. 2;0 3     3 4x 7
Câu 44. Cho các hàm số f x  ;g x ax bx cx a b g 3   ;g 9  81 x
  5  3    0;  0 4  2 và     3 .
Số giá trị nguyên của m để phương trình f g   x  f   2 1 2
1 m  2g x  4  1 có 3 nghiệm phân biệt là A. 15 B. 17 C. 19 D. 0 Câu 45. Cho hàm số y f x x   2 e   2
ln x  4x  5. Có bao nhiêu cặp số x;y với x  ;y   thỏa mãn f  2 x  2 y   f 2x  4y? A. 12 B. 11 C. 8 D. 4
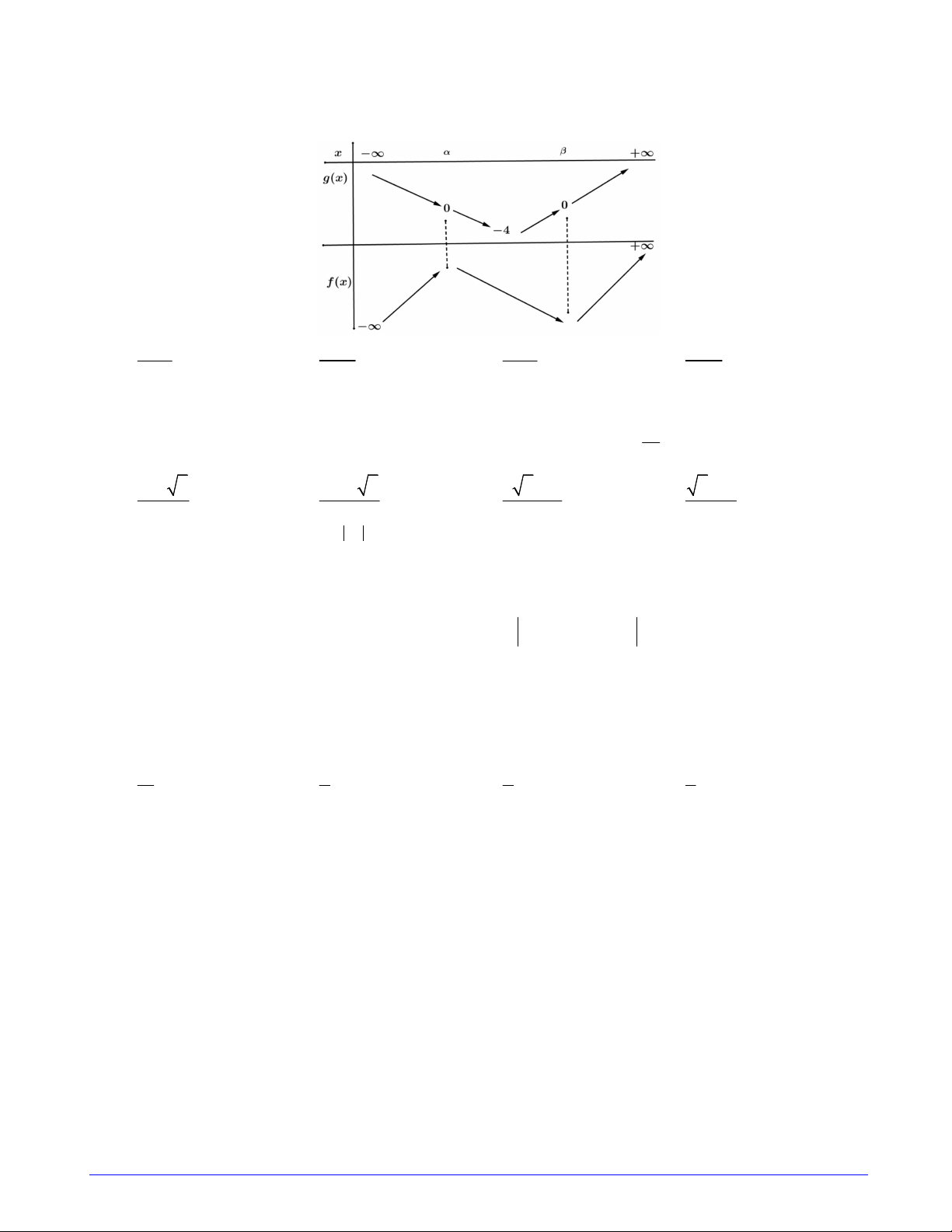
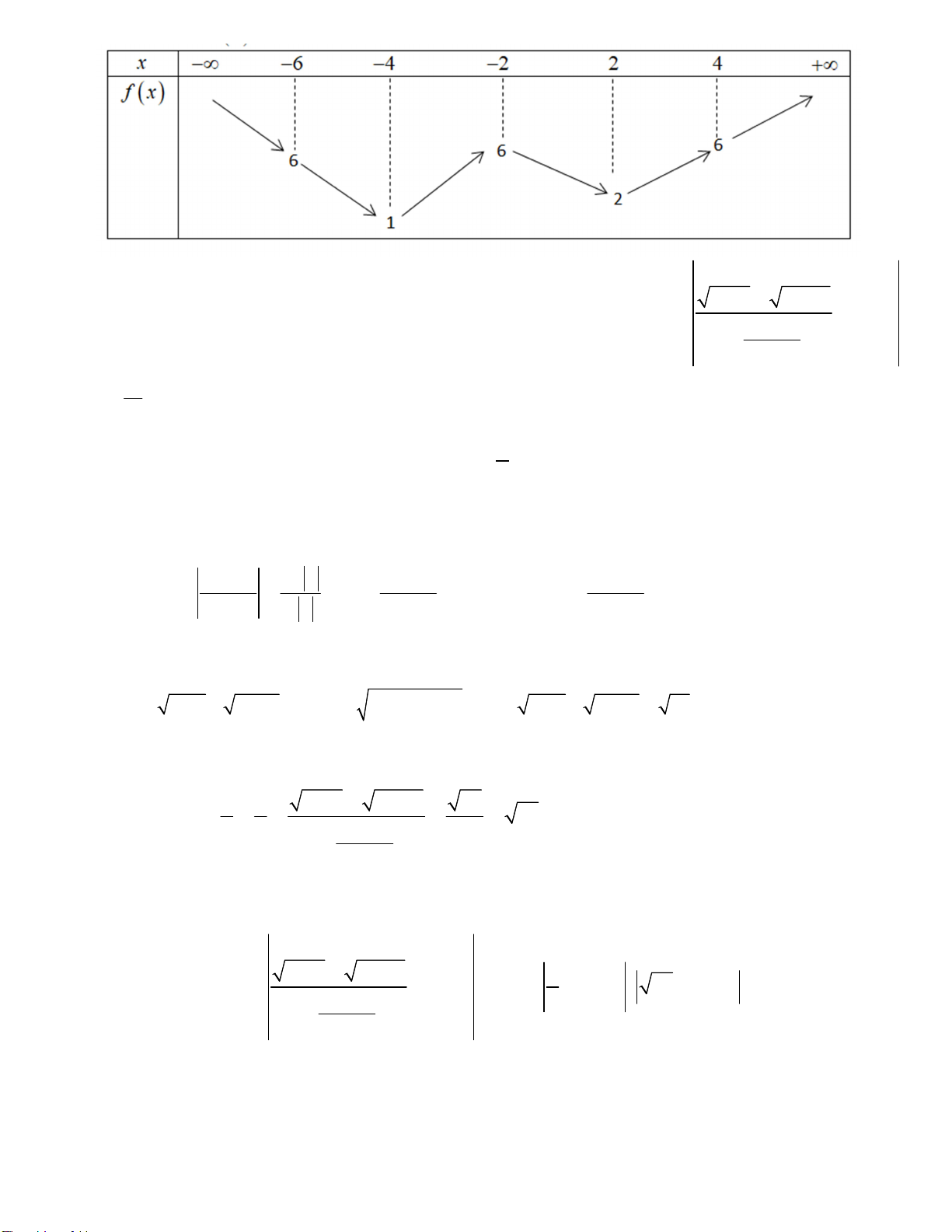
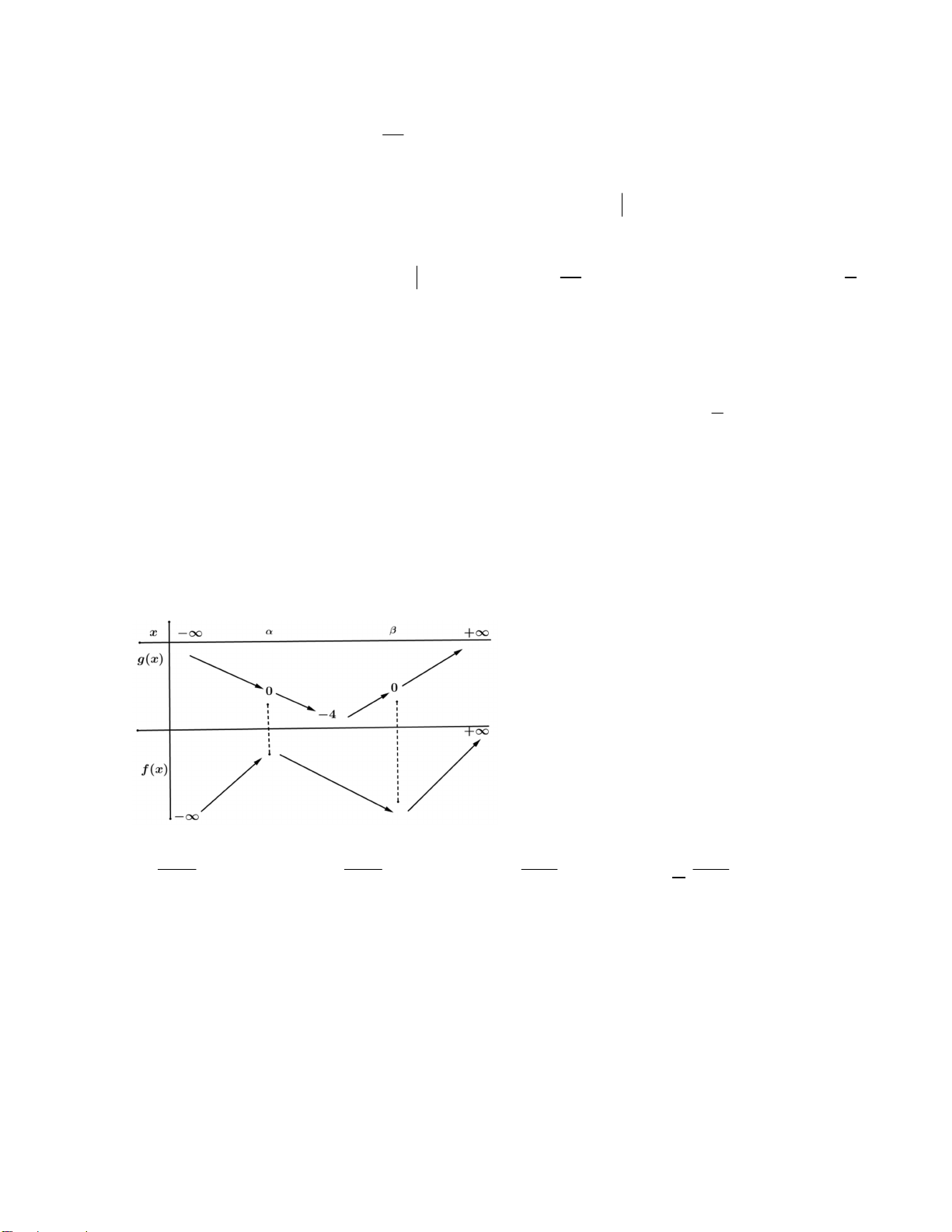
Câu 46. Cho hàm số f x liên tục trên  , có bảng biến thiên như sau
Có tất cả bao nhiêu giá trị nguyên của tham số m để giá trị lớn nhất của hàm số 4  x  12   x y  f m 16  nhỏ hơn ? 32x    f 3    2  x 16 A. 8 . B. 10 . C. 11. D. 9 . Trang 6/7 - Mã đề 101
Câu 47. Cho mặt cầu S có bán kính R không đổi, hình trụ T  bất kì nội tiếp mặt cầu S. Thể tích khối V
trụ T  là V ; và thể tích phần còn lại của khối cầu là V . Giá trị lớn nhất của 1 bằng bao nhiêu? 1 2 V2 1  2 3 2 3 1 1  3 3 1 A. . B. . C. . D. . 2 2 2 2 x mx m m 2
Câu 48. Cho phương trình 22 4 3  3  2 
. Có bao nhiêu số nguyên m để phương trình có đúng x  m
hai nghiệm phân biệt thuộc đoạn 6;0   ? A. 3. B. 1. C. 2. D. 0.
Câu 49. Cho hàm số y  f  x có đạo hàm liên tục trên 0;   1 , thỏa mãn 1 f  2 2  x   4. 2x  1    
f x với mọi x thuộc đoạn 0;   1 và f  
1  2 . Giá trị I   xf xdx bằng 0 11 4 3 5 A. . B. . C. . D. . 4 3 4 3
Câu 50. Cho hai hàm số f x  3 ax  2
3x bx  1  2d và g x  2
cx  2x  d có bảng biến thiên như
hình vẽ. Biết rằng đồ thị của hai hàm số đã cho cắt nhau tại ba điểm phân biệt có hoành độ x ,x ,x thỏa mãn 1 2 3 2 x  2 x  2
x  30 . Diện tích hình phẳng giới hạn bởi các đường y  f x,y  gx,x  3,x  6 bằng 1 2 3 1123 1231 1321 2113 A. . B. . C. . D. . 12 12 12 12
------------- HẾT -------------
Thí sinh không được sử dụng bất cứ tài liệu gì.
Cán bộ coi thi không giải thích gì thêm. Trang 7/7 - Mã đề 101 SỞ GD VÀ ĐT BẮC NINH
ĐỀ THI GIAO LƯU HỌC SINH GIỎI THPT
CỤM TRƯỜNG THPT GIA BÌNH, NĂM HỌC 2022 - 2023 THUẬN THÀNH, LƯƠNG TÀI Môn: Toán - Lớp 12
Ngày thi: 8 tháng 01 năm 2023 ( Đề thi gồm 7 trang)
Thời gian: 90 phút (không kể thời gian phát đề) Mã đề thi
Họ và tên thí sinh:.............................................................................. SBD:..................... 102
Câu 1. Cho hai khối trụ có cùng thể tích; bán kính đáy và chiều cao của hai khối trụ lần lượt là R ,h và 1 1 R ,h R 3 h
. Biết rằng 1  . Tỉ số 1 bằng 2 2 R 2 h 2 2 3 9 2 4 A. . B. . C. . D. . 2 4 3 9
Câu 2. Cho khối chóp S.ABC có SA  SB  SC  a và    ASB  2  0 , BSC  3  0 , CSA  40. Mặt
phẳng  bất kì qua A cắt SB , SC tại B , C . Tìm giá trị nhỏ nhất của chu vi ABC  . A. 2a . B. a 3 . C. a 2 . D. a .
Câu 3. Cho đồ thị hàm số y  f 2  x có đồ thị như hình vẽ
Hàm số g x  f  2
x  3 nghịch biến trên khoảng nào dưới đây? A. 1;0 B. 0;  1 C. 1;3 D. ;  1 Câu 4. Gọi ,
m n lần lượt là số đường tiệm cận đứng và số đường tiệm cận ngang của đồ thị hàm số x  1 x y 
. Giá trị của m  n bằng 3 x  x A. 3 B. 5 C. 2 D. 4
Câu 5. Cho dãy số a thỏa mãn a  1 và a  10a 1, n  2. Tìm giá trị nhỏ nhất của n để n  1 n n1 loga  100 n A. 102 . B. 103 . C. 100 . D. 101.
Câu 6. Cho hàm số y  f x có đồ thị hàm số y  f 'x như hình vẽ
Hàm số g x  f 1 2xđạt cực đại tại điểm nào? Trang 1/7 - Mã đề 102 1 A. x  1; B. x  0 C. x  1;x  2 D. x  ;x  1 2 2 x  x  1
Câu 7. Tìm họ tất cả các nguyên hàm của hàm số f (x)  . x 1 1 A. 1  C. B. 2 x  ln(x  1) C. (x  2 1) 2 x C. 2 x  ln x  1 C. D.  ln x  1 C. 2
Câu 8. Trong không gian Oxyz , cho hình hộp ABC . D 
A BC D biết A1;0; 1, B2;1;2, D1;1; 1,
C 4;5;5. Tọa độ của điểm  A là: A. A3;5;6. B. A3;5;6. C. A4;6;5. D. A3;4;  1 .
Câu 9. Cho hàm số f (x) liên tục trên [a; b] và số thực k tùy ý. Trong các khẳng định sau, khẳng định nào sai? a b a A. kf t dt   ( ) 0 B. f(x)dx     f(x)dx a a b b 2b b b C. f(2x)dx   2 f(x)dx D. kf(x)dx   k f(t)dt a 2a a a
Câu 10. Cho hình lăng trụ đứng ABC. 
A BC  có đáy là tam giác vuông và AB  BC  a , A  A  a 2 ,
M là trung điểm của BC . Tính khoảng cách d của hai đường thẳng AM và BC . a a a a A. d  7 . B. d  2 . C. d  3 . D. d  2 . 7 2 3 2
Câu 11. Trong không gian, cho hình chóp S.ABC cóSA, AB , BC đôi một vuông góc với nhau và
SA  a , AB  b , BC  c . Mặt cầu đi qua S , A , B , C có bán kính bằng 1 2a b c A. 2  2  2 a b c . B. 2  2  2 2 a b c . C. 2 a  2 b  2 c . D. . 2 3 x  1 Câu 12. Cho hàm số y 
(C) và d : y  2x  m 1 (m là tham số thực). Gọi k , k là hệ số góc x  2 1 2
của tiếp tuyến của C  tại giao điểm của d và C . Tính k .k . 1 2 1 A. k .k  3 . B. k .k  4 . C. k .k  . D. k .k  2 . 1 2 1 2 1 2 4 1 2 m
Câu 13. Cho hàm y  f x có f x  2 x x    3 '
1 x  x;x   . Có bao nhiêu giá trị nguyên của m  1;9  
9 để hàm sốy  f xnghịch biến trên ;2? A. 44 B. 50 C. 99 D. 49
Câu 14. Cho hàm số y  f xlà hàm đa thức bậc 4, có bảng biến thiên như sau
Số nghiệm của phương trình f x 1  1 là A. 6 B. 5 C. 3 D. 4 Trang 2/7 - Mã đề 102
Câu 15. Cho hình nón có bán kính đáy bằng 3 và chiều cao bằng 6 , một khối trụ có bán kính đáy thay đổi
nội tiếp khối nón đã cho (như hình vẽ). Thể tích lớn nhất của khối trụ bằng A. 6 . B. 8 . C. 4 . D. 10 .
Câu 16. Xét các số thực dương a, b, x, y thỏa mãn a  1, b  1 và x y
a  b  ab . Giá trị nhỏ nhất của biểu thức P  x  2 y bằng 3 3 6 3  2 2 A. . B. . C. 3  2 2 . D. 2 2 . 2 2
Câu 17. Tính thể tích của một hình hộp chữ nhật biết rằng ba mặt của hình này có diện tích là 2 20cm , 2 10cm , 2 8cm . A. 3 1600cm B. 3 80cm C. 3 40cm D. 3 38cm
Câu 18. Quay xung quanh trục Ox hình phẳng giới hạn bởi đồ thị của hàm số y  (x  3) log x  1 , trục 0,5
Ox , và đường thẳng x  1 ta thu được khối tròn xoay có thể tích bằng 2 3 A. (x   2 3) (log x+1)dx . B. (x  2 3) (log x+1)dx . 0,5  0,5 1 2 3 2 C.  (x   2 3) (log x+1)dx . D.  (x  2 3) (log x+1)dx . 0,5  0,5 1 1
Câu 19. Cho hình chóp S. ABC có AB  3, AC  4,BC  5 và góc giữa các cạnh bên với đáy bằng  60 .
Thể tích của khối chóp đã cho bằng 5 3 5 A. 15 3 B. 5 3 C. D. 6 3
Câu 20. Trong không gian Oxyz , cho mặt cầu S  2 2 2
: x  y  z  2x  4 y  4z  5  0 và mặt phẳng
P:x  y  2z 1 0. Gọi M là một điểm bất kì trên mặt cầu S. Khoảng cách từ M đến P có giá trị nhỏ nhất bằng 4 6 A. 2 6  2. B. 6  2 . C. 0 . D.  2 . 3
Câu 21. Trong không gian với hệ trục tọa độ Oxyz, gọi  là góc hợp bởi đường thẳng x  3 y  4 z  3 d :  
và mặt phẳng P : 2x  y  z 1  0 . Khi đó, giá trị cos bằng bao nhiêu 1 2 1 1 1 3 A. . B.  . C.  3 . D. . 2 2 2 2 Câu 22. Cho phương trình 2
2 cos 3x  3 2mcos3x  m  2  0. Số giá trị nguyên của tham số m để   
phương trình đã cho có đúng 3 nghiệm thuộc khoảng     ;     . là  6 3 A. 1 B. 4 C. 3. D. 2 Trang 3/7 - Mã đề 102
Câu 23. Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình thang vuông tại A và B , AB  BC  a ,
AD  2a , SA  ABCD và SA  a 2 . Gọi E là trung điểm củaAD . Kẻ EK  SD tại K . Tính thể
tích của khối cầu đi qua sáu điểm S , A , B , C , E , K ?  3 4 a  3 3 a  3 a A. V  . B. V   3 6 a . C. V  . D. V  . 3 2 6  2 3x khi x  1 3 Câu 24. Cho hàm số  f(x)   . Tính tích phân f x   1dx . 4  x khi x   1 1 7 3 5 A. 1. B. . C. . D. . 2 2 2
Câu 25. Có bao nhiêu giá trị nguyên của m để tập nghiệm của bất phương trình   3x 2x x m  0 chứa
không quá 8 giá trị nguyên? A. 8 B. 17 C. 15 D. 16
Câu 26. Gọi M,m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  x  2 x  3 trên 0;2   . Giá trị của M  m bằng A. 0 B. 3 C. 4 D. 2 1
Câu 27. Tập xác định của hàm số  y  3 x    2x3 1 là A. D  ;  1  1; B. D  0;  1 C. D  1;  1 D. D  1;  1 \   0
Câu 28. Biến cố A liên quan đến một phép thử ngẫu nhiên T có hữu hạn kết quả đồng khả năng xuất hiện.
Khẳng định nào sau đây là đúng? n  \ A A. P     A  . B.    1 P A . n    P   A n  n A C. P     A  . D. P     A  . n   A n     9    m.ab n
Câu 29. Cho a  log 3;b  log 2; và log
( m,n là các số nguyên tố). Giá trị của 12    2 5   125 . p ab q.b m  n  p  q bằng A. 6 B. 4 C. 8 D. 2
Câu 30. Tổng các nghiệm của phương trình log    1 .log 2x x  7  0 là 2 2 A. 1  log 7 B. 3 C. 4 D. 5 2
Câu 31. Cho hình trụ có đáy là hai đường tròn tâm O và O , bán kính đáy bằng chiều cao và bằng R . Trên
đường tròn đáy có tâm O lấy điểm A , trên đường tròn tâm O lấy điểm B . Đặt  là góc giữa AB và đáy.
Biết rằng thể tích khối tứ diện OOAB đạt giá trị lớn nhất. Khẳng định nào sau đây đúng? A.   1 tan . B. tan   1 . C. tan   2 . D.   1 tan . 2 2
Câu 32. Cho hàm số f (x) xác định, có đạo hàm, liên tục và đồng biến trên [1;4] thỏa mãn x  xf x  f  2 x x  f  3 2 ( ) [ ( )] , [1;4], (1) . Giá trị f (4) bằng 2 371 391 361 381 A. . B. . C. . D. . 18 18 18 18 Trang 4/7 - Mã đề 102
Câu 33. Cho hàm số y  f x  3 x  2
bx  cx  3 thỏa mãn min f x f 1
1. Giá trị lớn nhất của 0;2      
hàm số g x  f  1x  1 x  là A. 5 B. 55 C. 3  2 D. 17  ex  2 3 5 cos x cosx sinx    Câu 34. Cho tích phân I  dx  a.eb  c 
, với a , b , c là các số thực. Tính 2 cos x 0
giá trị của biểu thức P  a  b  c ?. A. 4. B. 16. C. 10. D. 2.
Câu 35. Cho hàm số bậc ba f x có đồ thị hàm số như hình vẽ bên. Biết hàm số f x đạt cực trị tại hai điểm
x ,x thỏa mãn x  x  4 và f x f x
2 . Gọi S ,S là diện tích của hai hình phẳng được cho 1    2   1 2 2 1 1 2 S
trong hình vẽ bên. Tính tỉ số 1 . S2 3 3 5 8 A. . B. . C. . D. . 5 8 3 5
Câu 36. Cho hình chóp S.ABC có SA ABC    AB  a BC  a ABC  0 ; 2 2, 3 , 45 . Gọi I là trực tâm
của tam giác SBC . Giá trị lớn nhất của thể tích khối chóp I.ABC bằng 3 a 2 3 a 3 a A. . B. . C. 3 a . D. . 2 4 2
Câu 37. Cho hàm số y  f x có f x  3 x  2 '
3x 10x; x   . Có bao nhiêu giá trị nguyên dương của
m để hàm số g x  f  2x 2mx m 2  3 có 13 điểm cực trị? A. 4 B. 5 C. 2 D. 3 2 x    2 1 x  1
Câu 38. Tổng các nghiệm của phương trình  log      2 2 x là 2  x    A. 1 B. 3 C. 4 D. 5
Câu 39. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB  1, AD  10 , SA  SB ,
SC  SD . Biết mặt phẳng SAB và SCD vuông góc nhau đồng thời tổng diện tích của hai tam giác
SAB và SCD bằng 2 . Thể tích khối chóp S.ABCD bằng 3 1 A. . B. . C. 2 . D. 1. 2 2
Câu 40. Gọi S là tập tất cả các giá trị nguyên của m để bất phương trình  2   x m m e  mx  2 2 2
m  2m  0nghiệm đúng với mọi x thuộc  . Tổng giá trị tất cả các phần tử của S bằng A. 4 B. 0 C. 5 D. 2
Câu 41. Cho hàm số f x liên tục trên  , có bảng biến thiên như sau Trang 5/7 - Mã đề 102
Có tất cả bao nhiêu giá trị nguyên của tham số m để giá trị lớn nhất của hàm số 4  x  12   x y  f m 16  nhỏ hơn ? 32x    f 3    2  x 16 A. 11. B. 9 . C. 8 . D. 10 .
Câu 42. Cho hàm số y  f  x có đạo hàm liên tục trên 0;   1 , thỏa mãn 1 f  2 2  x   4. 2x  1    
f x với mọi x thuộc đoạn 0;   1 và f  
1  2 . Giá trị I   xf xdx bằng 0 4 3 5 11 A. . B. . C. . D. . 3 4 3 4 x mx m m 2
Câu 43. Cho phương trình 22 4 3  3  2 
. Có bao nhiêu số nguyên m để phương trình có đúng x  m
hai nghiệm phân biệt thuộc đoạn 6;0   ? A. 3. B. 1. C. 2. D. 0. Câu 44. Cho hàm số y f x x   2 e   2
ln x  4x  5. Có bao nhiêu cặp số x;y với x  ;y   thỏa mãn f  2 x  2 y   f 2x  4y? A. 11 B. 8 C. 4 D. 12
Câu 45. Cho hai hàm số f x  3 ax  2
3x bx  1  2d và g x  2
cx  2x  d có bảng biến thiên như
hình vẽ. Biết rằng đồ thị của hai hàm số đã cho cắt nhau tại ba điểm phân biệt có hoành độ x ,x ,x thỏa mãn 1 2 3 2 x  2 x  2
x  30 . Diện tích hình phẳng giới hạn bởi các đường y  f x,y  gx,x  3,x  6 bằng 1 2 3 1231 1321 2113 1123 A. . B. . C. . D. . 12 12 12 12
Câu 46. Cho các hàm số y  f x;y  g xliên tục và có đạo hàm trên  , trong đó hàm số
g x  f 2 x 'là hàm số bậc ba có đồ thị như hình vẽ. Trang 6/7 - Mã đề 102 Hàm số y  f  2 x   3x  2 2
2x  x  2023 nghịch biến trên khoảng nào dưới đây? 1   1 A. 2;0 B.    ;       1 C. 1;2 D.   ;  3     3
Câu 47. Cho mặt cầu S có bán kính R không đổi, hình trụ T  bất kì nội tiếp mặt cầu S. Thể tích khối V
trụ T  là V ; và thể tích phần còn lại của khối cầu là V . Giá trị lớn nhất của 1 bằng bao nhiêu? 1 2 V2 1  2 3 2 3 1 1  3 3 1 A. . B. . C. . D. . 2 2 2 2 4x 7
Câu 48. Cho các hàm số f x  ;g x ax bx cx a b g 3   ;g 9  81 x
  5  3    0;  0 4  2 và     3 .
Số giá trị nguyên của m để phương trình f g   x  f   2 1 2
1 m  2g x  4  1 có 3 nghiệm phân biệt là A. 17 B. 19 C. 0 D. 15
Câu 49. Cho hình tứ diện đều ABCD . Trên mỗi cạnh của tứ diện, ta đánh dấu 3 điểm chia đều cạnh tương
ứng thành các phần bằng nhau. Gọi S là tập hợp các tam giác có ba đỉnh lấy từ 18 điểm đã đánh dấu. Lấy ra
từ S một tam giác, xác suất để mặt phẳng chứa tam giác đó song song với đúng một cạnh của tứ diện đã cho bằng 2 9 2 4 A. . B. . C. . D. 45 34 5 15
Câu 50. Có bao nhiêu giá trị nguyên của m để hàm số y  4 x  2
mx  64x có đúng 5 điểm cực trị? A. 19 B. 6 C. 24 D. 5
------------- HẾT -------------
Thí sinh không được sử dụng bất cứ tài liệu gì.
Cán bộ coi thi không giải thích gì thêm. Trang 7/7 - Mã đề 102 SỞ GD VÀ ĐT BẮC NINH
ĐỀ THI GIAO LƯU HỌC SINH GIỎI THPT
CỤM TRƯỜNG THPT GIA BÌNH, NĂM HỌC 2022 - 2023 THUẬN THÀNH, LƯƠNG TÀI Môn: Toán - Lớp 12
Ngày thi: 8 tháng 01 năm 2023 ( Đề thi gồm 7 trang)
Thời gian: 90 phút (không kể thời gian phát đề) Mã đề thi
Họ và tên thí sinh:.............................................................................. SBD:..................... 103 Câu 1. Cho phương trình 2
2 cos 3x  3 2mcos3x  m 2  0. Số giá trị nguyên của tham số m để   
phương trình đã cho có đúng 3 nghiệm thuộc khoảng     ;     . là  6 3 A. 2 B. 1 C. 4 D. 3.
Câu 2. Quay xung quanh trục Ox hình phẳng giới hạn bởi đồ thị của hàm số y  (x  3) log x  1 , trục 0,5
Ox , và đường thẳng x  1 ta thu được khối tròn xoay có thể tích bằng 3 3 A. (x   2 3) (log x+1)dx . B.  (x  2 3) (log x+1)dx . 0,5  0,5 2 1 2 2 C.  (x   2 3) (log x+1)dx . D. (x  2 3) (log x+1)dx . 0,5  0,5 1 1
Câu 3. Cho hình chóp S. ABC có AB  3, AC  4,BC  5 và góc giữa các cạnh bên với đáy bằng  60 .
Thể tích của khối chóp đã cho bằng 5 3 5 A. 5 3 B. C. D. 15 3 6 3
Câu 4. Gọi m,n lần lượt là số đường tiệm cận đứng và số đường tiệm cận ngang của đồ thị hàm số x  1 x y 
. Giá trị của m  n bằng 3 x  x A. 5 B. 4 C. 3 D. 2
Câu 5. Có bao nhiêu giá trị nguyên của m để tập nghiệm của bất phương trình   3x 2x x m  0 chứa
không quá 8 giá trị nguyên? A. 8 B. 17 C. 15 D. 16  2 3x khi x  1 3 Câu 6. Cho hàm số  f(x)   . Tính tích phân f x   1dx . 4  x khi x   1 1 7 3 5 A. . B. . C. . D. 1. 2 2 2
Câu 7. Trong không gian với hệ trục tọa độ Oxyz, gọi  là góc hợp bởi đường thẳng x  3 y  4 z  3 d :  
và mặt phẳng P : 2x  y  z 1  0 . Khi đó, giá trị cos bằng bao nhiêu 1 2 1 3 1 1 A.  3 . B. . C. . D.  . 2 2 2 2
Câu 8. Trong không gian, cho hình chóp S.ABC cóSA, AB , BC đôi một vuông góc với nhau và SA  a ,
AB  b , BC  c . Mặt cầu đi qua S , A , B , C có bán kính bằng 1 2a b c A. 2  2  2 a b c . B. 2  2  2 2 a b c . C. 2 a  2 b  2 c . D. . 2 3 Trang 1/7 - Mã đề 103
Câu 9. Tính thể tích của một hình hộp chữ nhật biết rằng ba mặt của hình này có diện tích là 2 20cm , 2 10cm , 2 8cm . A. 3 80cm B. 3 40cm C. 3 38 cm D. 3 1600cm 2 x  x  1
Câu 10. Tìm họ tất cả các nguyên hàm của hàm số f (x)  . x 1 1 A. 1  C. B. 2 x  ln(x  1) C. (x  2 1) 2 x C. 2 x  ln x  1 C. D.  ln x  1 C. 2
Câu 11. Cho khối chóp S.ABC có SA  SB  SC  a và    ASB  2  0 , BSC  3  0 , CSA  4  0 . Mặt
phẳng  bất kì qua A cắt SB , SC tại B , C . Tìm giá trị nhỏ nhất của chu vi ABC  . A. a 2 . B. a . C. 2a . D. a 3 .
Câu 12. Cho hàm số y  f x có đồ thị hàm số y  f 'x như hình vẽ
Hàm số g x  f 1 2xđạt cực đại tại điểm nào? 1 A. x  1; B. x  0 C. x  1;x  2 D. x  ;x  1 2
Câu 13. Cho dãy số a thỏa mãn a  1 và a  10a 1, n  2. Tìm giá trị nhỏ nhất của n để n  1 n n1 loga  100 n A. 103 . B. 100 . C. 101. D. 102 .
Câu 14. Cho hai khối trụ có cùng thể tích; bán kính đáy và chiều cao của hai khối trụ lần lượt là R ,h và 1 1 R ,h R 3 h
. Biết rằng 1  . Tỉ số 1 bằng 2 2 R 2 h 2 2 3 9 2 4 A. . B. . C. . D. . 2 4 3 9 x  1 Câu 15. Cho hàm số y 
(C) và d : y  2x  m 1 (m là tham số thực). Gọi k , k là hệ số góc x  2 1 2
của tiếp tuyến của C  tại giao điểm của d và C . Tính k .k . 1 2 1 A. k .k  3 . B. k .k  4 . C. k .k  . D. k .k  2 . 1 2 1 2 1 2 4 1 2
Câu 16. Gọi M,m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  x  2 x  3 trên 0;2   . Giá trị của M  m bằng A. 3 B. 4 C. 2 D. 0 Trang 2/7 - Mã đề 103
Câu 17. Xét các số thực dương a, b, x, y thỏa mãn a  1, b  1 và x y
a  b  ab . Giá trị nhỏ nhất của biểu thức P  x  2 y bằng 3 3 6 3  2 2 A. . B. . C. 3  2 2 . D. 2 2 . 2 2
Câu 18. Cho hàm số y  f xlà hàm đa thức bậc 4, có bảng biến thiên như sau
Số nghiệm của phương trình f x 1  1 là A. 4 B. 5 C. 3 D. 6  9    m.ab n
Câu 19. Cho a  log 3;b  log 2; và log
( m,n là các số nguyên tố). Giá trị của 12    2 5   125 . p ab  q.b m  n  p  q bằng A. 6 B. 4 C. 8 D. 2
Câu 20. Cho hình nón có bán kính đáy bằng 3 và chiều cao bằng 6 , một khối trụ có bán kính đáy thay đổi
nội tiếp khối nón đã cho (như hình vẽ). Thể tích lớn nhất của khối trụ bằng A. 4 . B. 10 . C. 6 . D. 8 .
Câu 21. Cho đồ thị hàm số y  f 2  x có đồ thị như hình vẽ
Hàm số g x  f  2
x  3 nghịch biến trên khoảng nào dưới đây? A. ;  1 B. 1;0 C. 0;  1 D. 1;3 1
Câu 22. Tập xác định của hàm số  y  3 x    2x3 1 là A. D  1;  1 \   0 B. D  0;  1 C. D  1;  1 D. D  ;  1  1;
Câu 23. Cho hình lăng trụ đứng ABC. 
A BC  có đáy là tam giác vuông và AB  BC  a , A  A  a 2 ,
M là trung điểm của BC . Tính khoảng cách d của hai đường thẳng AM và BC . Trang 3/7 - Mã đề 103 a a a a A. d  3 . B. d  7 . C. d  2 . D. d  2 . 3 7 2 2
Câu 24. Trong không gian Oxyz , cho mặt cầu S  2 2 2
: x  y  z  2x  4 y  4z  5  0 và mặt phẳng
P:x  y  2z 1 0. Gọi M là một điểm bất kì trên mặt cầu S. Khoảng cách từ M đến P có giá trị nhỏ nhất bằng 4 6 A. 2 6  2. B. 0 . C.  2. D. 6  2. 3
Câu 25. Cho hàm số f (x) liên tục trên [a; b] và số thực k tùy ý. Trong các khẳng định sau, khẳng định nào sai? b b a A. kf(x)dx   k f(t)dt B. kf t dt   ( ) 0 a a a b a b 2b C. f(x)dx     f(x)dx D. f(2x)dx   2 f(x)dx a b a 2a
Câu 26. Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình thang vuông tại A và B , AB  BC  a ,
AD  2a , SA  ABCD và SA  a 2 . Gọi E là trung điểm củaAD . Kẻ EK  SD tại K . Tính thể
tích của khối cầu đi qua sáu điểm S , A , B , C , E , K ?  3 4 a  3 3 a  3 a A. V  . B. V   3 6 a . C. V  . D. V  . 3 2 6
Câu 27. Biến cố A liên quan đến một phép thử ngẫu nhiên T có hữu hạn kết quả đồng khả năng xuất hiện.
Khẳng định nào sau đây là đúng? n  \ A A. P     A  . B.    1 P A . n    P   A n  n A C. P     A  . D. P     A  . n   A n   
Câu 28. Tổng các nghiệm của phương trình log    1 .log 2x x  7  0 là 2 2 A. 1  log 7 B. 3 C. 4 D. 5 2 m
Câu 29. Cho hàm y  f x có f x  2 x x    3 '
1 x  x;x   . Có bao nhiêu giá trị nguyên của m  1;9  
9 để hàm sốy  f xnghịch biến trên ;2? A. 49 B. 50 C. 99 D. 44
Câu 30. Trong không gian Oxyz , cho hình hộp ABCD. 
A BC D biết A1;0; 1, B2;1;2, D1;1; 1,
C 4;5;5. Tọa độ của điểm  A là: A. A3;4;  1 . B. A3;5;6. C. A3;5;6. D. A4;6;5.
Câu 31. Cho hàm số y  f x có f x  3 x  2 '
3x  10x; x   . Có bao nhiêu giá trị nguyên dương của
m để hàm số g x  f  2x 2mx m 2  3 có 13 điểm cực trị? A. 5 B. 2 C. 3 D. 4
Câu 32. Cho hàm số bậc ba f x có đồ thị hàm số như hình vẽ bên. Biết hàm số f x đạt cực trị tại hai điểm
x ,x thỏa mãn x  x  4 và f x f x
2 . Gọi S ,S là diện tích của hai hình phẳng được cho 1    2   1 2 2 1 1 2 S
trong hình vẽ bên. Tính tỉ số 1 . S2 Trang 4/7 - Mã đề 103 3 3 5 8 A. . B. . C. . D. . 5 8 3 5
Câu 33. Cho hình chóp S.ABC có SA ABC    AB  a BC  a ABC  0 ; 2 2, 3 , 45 . Gọi I là trực tâm
của tam giác SBC . Giá trị lớn nhất của thể tích khối chóp I.ABC bằng 3 a 2 3 a 3 a A. 3 a . B. . C. . D. . 2 2 4
Câu 34. Cho hàm số f (x) xác định, có đạo hàm, liên tục và đồng biến trên [1;4] thỏa mãn x  xf x  f  2 x x  f  3 2 ( ) [ ( )] , [1;4], (1) . Giá trị f (4) bằng 2 371 361 381 391 A. . B. . C. . D. . 18 18 18 18
Câu 35. Cho hàm số y  f x  3 x  2
bx  cx  3 thỏa mãn min f x f 1
1. Giá trị lớn nhất của 0;2      
hàm số g x  f  1x  1 x  là A. 17 B. 5 C. 55 D. 3  2  ex  2 3 5 cos x cosx sinx    Câu 36. Cho tích phân I  dx  a.eb  c 
, với a , b , c là các số thực. Tính 2 cos x 0
giá trị của biểu thức P  a  b  c ?. A. 2. B. 4. C. 16. D. 10. 2 x    2 1 x  1
Câu 37. Tổng các nghiệm của phương trình  log      2 2 x là 2  x    A. 1 B. 3 C. 4 D. 5
Câu 38. Gọi S là tập tất cả các giá trị nguyên của m để bất phương trình  2   x m m e  mx  2 2 2
m  2m  0nghiệm đúng với mọi x thuộc  . Tổng giá trị tất cả các phần tử của S bằng A. 2 B. 4 C. 0 D. 5
Câu 39. Cho hình trụ có đáy là hai đường tròn tâm O và O , bán kính đáy bằng chiều cao và bằng R . Trên
đường tròn đáy có tâm O lấy điểm A , trên đường tròn tâm O lấy điểm B . Đặt  là góc giữa AB và đáy.
Biết rằng thể tích khối tứ diện OOAB đạt giá trị lớn nhất. Khẳng định nào sau đây đúng? A. tan   1 . B. tan   2 . C.   1 tan . D.   1 tan . 2 2
Câu 40. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB  1, AD  10 , SA  SB ,
SC  SD . Biết mặt phẳng SAB và SCD vuông góc nhau đồng thời tổng diện tích của hai tam giác
SAB và SCD bằng 2 . Thể tích khối chóp S.ABCD bằng 3 1 A. . B. . C. 2 . D. 1. 2 2 Trang 5/7 - Mã đề 103 x mx m m 2
Câu 41. Cho phương trình 22 4 3  3  2 
. Có bao nhiêu số nguyên m để phương trình có đúng x  m
hai nghiệm phân biệt thuộc đoạn 6;0   ? A. 3. B. 1. C. 2. D. 0.
Câu 42. Cho hàm số f x liên tục trên  , có bảng biến thiên như sau
Có tất cả bao nhiêu giá trị nguyên của tham số m để giá trị lớn nhất của hàm số 4  x  12   x y  f m 16  nhỏ hơn ? 32x    f 3    2  x 16 A. 10 . B. 11. C. 9 . D. 8 . 4x 7
Câu 43. Cho các hàm số f x  ;g x ax bx cx a b g 3   ;g 9  81 x
  5  3    0;  0 4  2 và     3 .
Số giá trị nguyên của m để phương trình f g   x  f   2 1 2
1 m  2g x  4  1 có 3 nghiệm phân biệt là A. 0 B. 15 C. 17 D. 19
Câu 44. Cho các hàm số y  f x;y  g xliên tục và có đạo hàm trên  , trong đó hàm số
g x  f 2 x 'là hàm số bậc ba có đồ thị như hình vẽ. Hàm số y  f  2 x   3x  2 2
2x  x  2023 nghịch biến trên khoảng nào dưới đây?  1 1  A. 1;2 B.     ;       C. 2;0 D.  ;  1  3   3 
Câu 45. Cho hình tứ diện đều ABCD . Trên mỗi cạnh của tứ diện, ta đánh dấu 3 điểm chia đều cạnh tương
ứng thành các phần bằng nhau. Gọi S là tập hợp các tam giác có ba đỉnh lấy từ 18 điểm đã đánh dấu. Lấy ra
từ S một tam giác, xác suất để mặt phẳng chứa tam giác đó song song với đúng một cạnh của tứ diện đã cho bằng 9 2 4 2 A. . B. . C. D. . 34 5 15 45 Trang 6/7 - Mã đề 103
Câu 46. Cho hai hàm số f x  3 ax  2
3x bx  1  2d và g x  2
cx  2x  d có bảng biến thiên như
hình vẽ. Biết rằng đồ thị của hai hàm số đã cho cắt nhau tại ba điểm phân biệt có hoành độ x ,x ,x thỏa mãn 1 2 3 2 x  2 x  2
x  30 . Diện tích hình phẳng giới hạn bởi các đường y  f x,y  gx,x  3,x  6 bằng 1 2 3 1321 1123 1231 2113 A. . B. . C. . D. . 12 12 12 12
Câu 47. Cho mặt cầu S có bán kính R không đổi, hình trụ T  bất kì nội tiếp mặt cầu S. Thể tích khối V
trụ T  là V ; và thể tích phần còn lại của khối cầu là V . Giá trị lớn nhất của 1 bằng bao nhiêu? 1 2 V2 1  3 1  2 3 2 3 1 3 1 A. . B. . C. . D. . 2 2 2 2 Câu 48. Cho hàm số y f x x   2 e   2
ln x  4x  5. Có bao nhiêu cặp số x;y với x  ;y   thỏa mãn f  2 x  2 y   f 2x  4y? A. 4 B. 12 C. 11 D. 8
Câu 49. Có bao nhiêu giá trị nguyên của m để hàm số y  4 x  2
mx  64x có đúng 5 điểm cực trị? A. 5 B. 19 C. 6 D. 24
Câu 50. Cho hàm số y  f  x có đạo hàm liên tục trên 0;   1 , thỏa mãn 1 f  2 2  x   4. 2x  1    
f x với mọi x thuộc đoạn 0;   1 và f  
1  2 . Giá trị I   xf xdx bằng 0 11 4 3 5 A. . B. . C. . D. . 4 3 4 3
------------- HẾT -------------
Thí sinh không được sử dụng bất cứ tài liệu gì.
Cán bộ coi thi không giải thích gì thêm. Trang 7/7 - Mã đề 103 SỞ GD VÀ ĐT BẮC NINH
ĐỀ THI GIAO LƯU HỌC SINH GIỎI THPT
CỤM TRƯỜNG THPT GIA BÌNH, NĂM HỌC 2022 - 2023 THUẬN THÀNH, LƯƠNG TÀI Môn: Toán - Lớp 12
Ngày thi: 8 tháng 01 năm 2023 ( Đề thi gồm 7 trang)
Thời gian: 90 phút (không kể thời gian phát đề) Mã đề thi
Họ và tên thí sinh:.............................................................................. SBD:..................... 104
Câu 1. Cho hình nón có bán kính đáy bằng 3 và chiều cao bằng 6 , một khối trụ có bán kính đáy thay đổi nội
tiếp khối nón đã cho (như hình vẽ). Thể tích lớn nhất của khối trụ bằng A. 6 . B. 8 . C. 4 . D. 10 .
Câu 2. Trong không gian, cho hình chóp S.ABC cóSA, AB , BC đôi một vuông góc với nhau và SA  a ,
AB  b , BC  c . Mặt cầu đi qua S , A , B , C có bán kính bằng 1 2a b c A. 2 a  2 b  2 c . B. 2  2  2 a b c . C. 2  2  2 2 a b c . D. . 2 3
Câu 3. Cho hàm số y  f x có đồ thị hàm số y  f 'x như hình vẽ
Hàm số g x  f 1 2xđạt cực đại tại điểm nào? 1 A. x  0 B. x  1;x  2 C. x  ;x  1 D. x  1; 2
Câu 4. Cho đồ thị hàm số y  f 2  x có đồ thị như hình vẽ
Hàm số g x  f  2
x  3 nghịch biến trên khoảng nào dưới đây? A. 1;0 B. 0;  1 C. 1;3 D. ;  1 Trang 1/7 - Mã đề 104
Câu 5. Trong không gian Oxyz , cho mặt cầu S  2 2 2
: x  y  z  2x  4 y  4z  5  0 và mặt phẳng
P:x  y  2z 1 0. Gọi M là một điểm bất kì trên mặt cầu S. Khoảng cách từ M đến P có giá trị nhỏ nhất bằng 4 6 A. 2 6  2. B. 6  2. C. 0 . D.  2. 3 2 x  x  1
Câu 6. Tìm họ tất cả các nguyên hàm của hàm số f (x)  . x 1 1 A. 1  C. B. 2 x  ln(x 1) C. (x  2 1) 2 x C. 2 x  ln x  1 C. D.  ln x 1 C. 2
Câu 7. Cho hình lăng trụ đứng ABC. 
A BC  có đáy là tam giác vuông và AB  BC  a , A  A  a 2 , M
là trung điểm của BC . Tính khoảng cách d của hai đường thẳng AM và BC . a a a a A. d  2 . B. d  2 . C. d  3 . D. d  7 . 2 2 3 7
Câu 8. Cho hàm số f (x) liên tục trên [a; b] và số thực k tùy ý. Trong các khẳng định sau, khẳng định nào sai? b a b 2b A. f(x)dx     f(x)dx B. f(2x)dx   2 f(x)dx a b a 2a b b a C. kf(x)dx   k f(t)dt D. kf t dt   ( ) 0 a a a
Câu 9. Quay xung quanh trục Ox hình phẳng giới hạn bởi đồ thị của hàm số y  (x  3) log x  1 , trục 0,5
Ox , và đường thẳng x  1 ta thu được khối tròn xoay có thể tích bằng 3 3 A. (x   2 3) (log x+1)dx . B.  (x  2 3) (log x+1)dx . 0,5  0,5 2 1 2 2 C.  (x   2 3) (log x+1)dx . D. (x  2 3) (log x+1)dx . 0,5  0,5 1 1
Câu 10. Cho hình chóp S. ABC có AB  3, AC  4,BC  5 và góc giữa các cạnh bên với đáy bằng  60 .
Thể tích của khối chóp đã cho bằng 5 5 3 A. B. 15 3 C. 5 3 D. 3 6 m
Câu 11. Cho hàm y  f x có f x  2 x x    3 '
1 x  x;x   . Có bao nhiêu giá trị nguyên của m  1;9  
9 để hàm sốy  f xnghịch biến trên ;2? A. 44 B. 49 C. 50 D. 99
Câu 12. Xét các số thực dương a, b, x, y thỏa mãn a  1, b  1 và x y
a  b  ab . Giá trị nhỏ nhất của biểu thức P  x  2 y bằng 3 3 6 3  2 2 A. 3  2 2 . B. 2 2 . C. . D. . 2 2
Câu 13. Trong không gian Oxyz , cho hình hộp ABC . D 
A BC D biết A1;0; 1, B2;1;2, D1;1; 1,
C 4;5;5. Tọa độ của điểm  A là: A. A3;4;  1 . B. A3;5;6. C. A3;5;6. D. A4;6;5. Trang 2/7 - Mã đề 104 Câu 14. Cho phương trình 2
2 cos 3x  3 2mcos3x  m  2  0. Số giá trị nguyên của tham số m để   
phương trình đã cho có đúng 3 nghiệm thuộc khoảng     ;     . là  6 3 A. 4 B. 3. C. 2 D. 1
Câu 15. Trong không gian với hệ trục tọa độ Oxyz, gọi  là góc hợp bởi đường thẳng x  3 y  4 z  3 d :  
và mặt phẳng P : 2x  y  z 1  0 . Khi đó, giá trị cos bằng bao nhiêu 1 2 1 1 1 A.  3 . B.  3 . C. . D. . 2 2 2 2 1
Câu 16. Tập xác định của hàm số  y  3 x    2x3 1 là A. D  1;  1 \   0 B. D  0;  1 C. D  1;  1 D. D  ;  1  1;
Câu 17. Cho hàm số y  f xlà hàm đa thức bậc 4, có bảng biến thiên như sau
Số nghiệm của phương trình f x 1  1 là A. 6 B. 5 C. 3 D. 4
Câu 18. Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình thang vuông tại A và B , AB  BC  a ,
AD  2a , SA  ABCD và SA  a 2 . Gọi E là trung điểm củaAD . Kẻ EK  SD tại K . Tính thể
tích của khối cầu đi qua sáu điểm S , A , B , C , E , K ?  3 3 a  3 4 a  3 a A. V   3 6 a . B. V  . C. V  . D. V  . 2 3 6
Câu 19. Tính thể tích của một hình hộp chữ nhật biết rằng ba mặt của hình này có diện tích là 2 20cm , 2 10cm , 2 8cm . A. 3 80cm B. 3 40cm C. 3 38 cm D. 3 1600cm
Câu 20. Gọi M,m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  x  2 x  3 trên 0;2   . Giá trị của M  m bằng A. 0 B. 3 C. 4 D. 2
Câu 21. Tổng các nghiệm của phương trình log    1 .log 2x x  7  0 là 2 2 A. 3 B. 4 C. 5 D. 1  log 7 2 x  1 Câu 22. Cho hàm số y 
(C) và d : y  2x  m 1 (m là tham số thực). Gọi k , k là hệ số góc x  2 1 2
của tiếp tuyến của C  tại giao điểm của d và C . Tính k .k . 1 2 1 A. k .k  3 . B. k .k  4 . C. k .k  . D. k .k  2 . 1 2 1 2 1 2 4 1 2 Trang 3/7 - Mã đề 104  2 3x khi x  1 3 Câu 23. Cho hàm số  f(x)   . Tính tích phân f x   1dx . 4  x khi x   1 1 7 3 5 A. . B. . C. . D. 1. 2 2 2
Câu 24. Gọi m,n lần lượt là số đường tiệm cận đứng và số đường tiệm cận ngang của đồ thị hàm số x  1 x y 
. Giá trị của m  n bằng 3 x  x A. 2 B. 4 C. 3 D. 5
Câu 25. Cho dãy số a thỏa mãn a  1 và a  10a 1, n  2. Tìm giá trị nhỏ nhất của n để n  1 n n1 loga  100 n A. 103 . B. 100 . C. 101. D. 102 .
Câu 26. Cho hai khối trụ có cùng thể tích; bán kính đáy và chiều cao của hai khối trụ lần lượt là R ,h và 1 1 R h R ,h 3
. Biết rằng 1  . Tỉ số 1 bằng 2 2 R 2 h 2 2 9 2 4 3 A. . B. . C. . D. . 4 3 9 2
Câu 27. Biến cố A liên quan đến một phép thử ngẫu nhiên T có hữu hạn kết quả đồng khả năng xuất hiện.
Khẳng định nào sau đây là đúng? n  n  \ A A. P     A  . B. P     A  . n   A n    n A C. P     A  . D.    1 P A . n    P A
Câu 28. Có bao nhiêu giá trị nguyên của m để tập nghiệm của bất phương trình   3x 2x x m  0 chứa
không quá 8 giá trị nguyên? A. 17 B. 16 C. 8 D. 15
Câu 29. Cho khối chóp S.ABC có SA  SB  SC  a và    ASB  2  0 , BSC  3  0 , CSA  4  0 . Mặt
phẳng  bất kì qua A cắt SB , SC tại B , C . Tìm giá trị nhỏ nhất của chu vi ABC . A. a 3 . B. a 2 . C. a . D. 2a .  9    m.ab n
Câu 30. Cho a  log 3;b  log 2; và log
( m,n là các số nguyên tố). Giá trị của 12    2 5   125 . p ab q.b m  n  p  q bằng A. 4 B. 8 C. 2 D. 6
Câu 31. Cho hàm số y  f x có f x  3 x  2 '
3x  10x; x   . Có bao nhiêu giá trị nguyên dương của
m để hàm số g x  f  2x 2mx m 2  3 có 13 điểm cực trị? A. 5 B. 3 C. 4 D. 2
Câu 32. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB  1, AD  10 , SA  SB ,
SC  SD . Biết mặt phẳng SAB và SCD vuông góc nhau đồng thời tổng diện tích của hai tam giác
SAB và SCD bằng 2 . Thể tích khối chóp S.ABCD bằng 3 1 A. . B. . C. 2 . D. 1. 2 2 Trang 4/7 - Mã đề 104
Câu 33. Cho hình chóp S.ABC có SA ABC    AB  a BC  a ABC  0 ; 2 2, 3 , 45 . Gọi I là trực tâm
của tam giác SBC . Giá trị lớn nhất của thể tích khối chóp I.ABC bằng 3 a 2 3 a 3 a A. 3 a . B. . C. . D. . 2 2 4
Câu 34. Cho hàm số y  f x  3 x  2
bx  cx  3 thỏa mãn min f x f 1
1. Giá trị lớn nhất của 0;2      
hàm số g x  f  1x  1 x  là A. 5 B. 55 C. 3  2 D. 17 2 x    2 1 x  1
Câu 35. Tổng các nghiệm của phương trình  log      2 2 x là 2  x    A. 1 B. 5 C. 3 D. 4
Câu 36. Cho hình trụ có đáy là hai đường tròn tâm O và O , bán kính đáy bằng chiều cao và bằng R . Trên
đường tròn đáy có tâm O lấy điểm A , trên đường tròn tâm O lấy điểm B . Đặt  là góc giữa AB và đáy.
Biết rằng thể tích khối tứ diện OOAB đạt giá trị lớn nhất. Khẳng định nào sau đây đúng? A.   1 tan . B. tan   1 . C. tan   2 . D.   1 tan . 2 2
Câu 37. Cho hàm số bậc ba f x có đồ thị hàm số như hình vẽ bên. Biết hàm số f x đạt cực trị tại hai điểm
x ,x thỏa mãn x  x  4 và f x f x
2 . Gọi S ,S là diện tích của hai hình phẳng được cho 1    2   1 2 2 1 1 2 S
trong hình vẽ bên. Tính tỉ số 1 . S2 3 3 5 8 A. . B. . C. . D. . 5 8 3 5
Câu 38. Cho hàm số f (x) xác định, có đạo hàm, liên tục và đồng biến trên [1;4] thỏa mãn x  xf x  f  2 x x  f  3 2 ( ) [ ( )] , [1;4], (1) . Giá trị f (4) bằng 2 391 361 381 371 A. . B. . C. . D. . 18 18 18 18  ex  2 3 5 cos x cosx sinx    Câu 39. Cho tích phân I  dx  a.eb  c 
, với a , b , c là các số thực. Tính 2 cos x 0
giá trị của biểu thức P  a  b  c ?. A. 2. B. 16. C. 10. D. 4.
Câu 40. Gọi S là tập tất cả các giá trị nguyên của m để bất phương trình  2   x m m e  mx  2 2 2
m  2m  0nghiệm đúng với mọi x thuộc  . Tổng giá trị tất cả các phần tử của S bằng A. 5 B. 2 C. 4 D. 0 Trang 5/7 - Mã đề 104 4x 7
Câu 41. Cho các hàm số f x  ;g x ax bx cx a b g 3   ;g 9  81 x
  5  3    0;  0 4  2 và     3 .
Số giá trị nguyên của m để phương trình f g   x  f   2 1 2
1 m  2g x  4  1 có 3 nghiệm phân biệt là A. 15 B. 19 C. 0 D. 17
Câu 42. Cho hàm số f x liên tục trên  , có bảng biến thiên như sau
Có tất cả bao nhiêu giá trị nguyên của tham số m để giá trị lớn nhất của hàm số 4  x  12   x y  f m 16  nhỏ hơn ? 32x    f 3    2  x 16 A. 8 . B. 10 . C. 11. D. 9 .
Câu 43. Cho hàm số y  f  x có đạo hàm liên tục trên 0;   1 , thỏa mãn 1 f  2 2  x   4. 2x  1    
f x với mọi x thuộc đoạn 0;   1 và f  
1  2 . Giá trị I   xf xdx bằng 0 4 5 11 3 A. . B. . C. . D. . 3 3 4 4 Câu 44. Cho hàm số y f x x   2 e   2
ln x  4x  5. Có bao nhiêu cặp số x;y với x  ;y   thỏa mãn f  2 x  2 y   f 2x  4y? A. 4 B. 12 C. 11 D. 8
Câu 45. Cho mặt cầu S có bán kính R không đổi, hình trụ T  bất kì nội tiếp mặt cầu S. Thể tích khối V
trụ T  là V ; và thể tích phần còn lại của khối cầu là V . Giá trị lớn nhất của 1 bằng bao nhiêu? 1 2 V2 1  2 3 2 3 1 1  3 3 1 A. . B. . C. . D. . 2 2 2 2
Câu 46. Cho hình tứ diện đều ABCD . Trên mỗi cạnh của tứ diện, ta đánh dấu 3 điểm chia đều cạnh tương
ứng thành các phần bằng nhau. Gọi S là tập hợp các tam giác có ba đỉnh lấy từ 18 điểm đã đánh dấu. Lấy ra
từ S một tam giác, xác suất để mặt phẳng chứa tam giác đó song song với đúng một cạnh của tứ diện đã cho bằng 4 9 2 2 A. B. . C. . D. . 15 34 5 45
Câu 47. Cho hai hàm số f x  3 ax  2
3x bx  1  2d và g x  2
cx  2x  d có bảng biến thiên như
hình vẽ. Biết rằng đồ thị của hai hàm số đã cho cắt nhau tại ba điểm phân biệt có hoành độ x ,x ,x thỏa mãn 1 2 3 2 x  2 x  2
x  30 . Diện tích hình phẳng giới hạn bởi các đường y  f x,y  gx,x  3,x  6 bằng 1 2 3 Trang 6/7 - Mã đề 104 2113 1123 1231 1321 A. . B. . C. . D. . 12 12 12 12
Câu 48. Có bao nhiêu giá trị nguyên của m để hàm số y  4 x  2
mx  64x có đúng 5 điểm cực trị? A. 19 B. 6 C. 24 D. 5 x mx m m 2
Câu 49. Cho phương trình 22 4 3  3  2 
. Có bao nhiêu số nguyên m để phương trình có đúng x  m
hai nghiệm phân biệt thuộc đoạn 6;0   ? A. 1. B. 2. C. 3. D. 0.
Câu 50. Cho các hàm số y  f x;y  g xliên tục và có đạo hàm trên  , trong đó hàm số
g x  f 2 x 'là hàm số bậc ba có đồ thị như hình vẽ. Hàm số y  f  2 x   3x  2 2
2x  x  2023 nghịch biến trên khoảng nào dưới đây?  1 1  A. 1;2 B.     ;       C. 2;0 D.  ;  1  3   3 
------------- HẾT -------------
Thí sinh không được sử dụng bất cứ tài liệu gì.
Cán bộ coi thi không giải thích gì thêm. Trang 7/7 - Mã đề 104
ĐÁP ÁN CÁC MÃ ĐỀ
------------------------ Mã đề [101]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
B D B B D A D A A A C D A D B A C D D B A C B B D
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
D C C C B C A D D B C B A A A C D B B B A C A C C Mã đề [102]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
D C B C A B D A C A C B D A B B C D B B D D A B C
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
C D A C B D B A A A D C D D A C B A A B C C A D B Mã đề [103]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
A C A D C A B C B D A B D D B B B D C D C A B D D
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
A A B A B B A C D B B D B C D A D C A C A A C C C Mã đề [104]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
B A A B B D D B C C B D B C C A A C B C A B A A D
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
C B D B B D D C A B D A A D C D A D C C A D B C A
CÂU HỎI ĐỀ HSG CỤM 12 NĂM 2022 Mức 2
Câu 1: Cho hàm số y  f  x có đồ thị hàm số y  f ' x như hình vẽ
Hàm số g  x  f 1 2x đạt cực đại tại điểm nào? 1
A. x  0 B. x  1; x  2 C. x  ; x  1 D. x  1  ; 2
Câu 2: Cho hàm y  f  x có   2    m f x x x  3 ' 1 x  x; x
 . Có bao nhiêu giá trị nguyên của m1;99
để hàm số y  f  x nghịch biến trên  ;  2   ? A. 49 B. 50 C. 99 D. 44
Câu 3: Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  x  2
x  3 trên 0;2 . Giá trị của M  m bằng A. 4 B. 2 C. 0 D. 3
Câu 4: Gọi m, n lần lượt là số đường tiệm cận đứng và số đường tiệm cận ngang của đồ thị hàm số x  1 x y 
. Giá trị của m  n bằng 3 x  x A. 2 B. 4 C. 3 D. 5
Câu 5: Cho hàm số y  f  x là hàm đa thức bậc 4, có bảng biến thiên như sau 1
Số nghiệm của phương trình f  x  1 1 là A. 6 B. 5 C. 3 D. 4
Câu 6: Tập xác định của hàm số y x     x 1 3 2 3 1 là A. D   1  ;  1 \  0 B. D  0;  1 C. D   1  ;  1 D. D   ;    1  1;  9  . m ab  n
Câu 7: Cho a  log 3;b  log 2; và log 
( m, n là các số nguyên tố). Giá trị của 2 5 12   125  . p ab  . q b m  n  p  q bằng A. 8 B. 2 C. 6 D. 4
Câu 8: Xét các số thực dương a, b, x, y thỏa mãn a  1, b  1 và x y
a  b  ab . Giá trị nhỏ nhất của biểu thức P  x  2 y bằng 3 3 6 3  2 2 A. 3  2 2 . B. 2 2 . C. . D. . 2 2
Câu 9: Tổng các nghiệm của phương trình log 1 .log 2x x   7  0 là 2   2   A. 3 B. 4 C. 5 D. 1 log 7 2
Câu 10: Có bao nhiêu giá trị nguyên của m để tập nghiệm của bất phương trình   3x  2x x m   0 chứa không quá 8 giá trị nguyên? A. 15 B. 16 C. 8 D. 17 Mức 3
Câu 1; Cho đồ thị hàm số y  f 2  x có đồ thị như hình vẽ
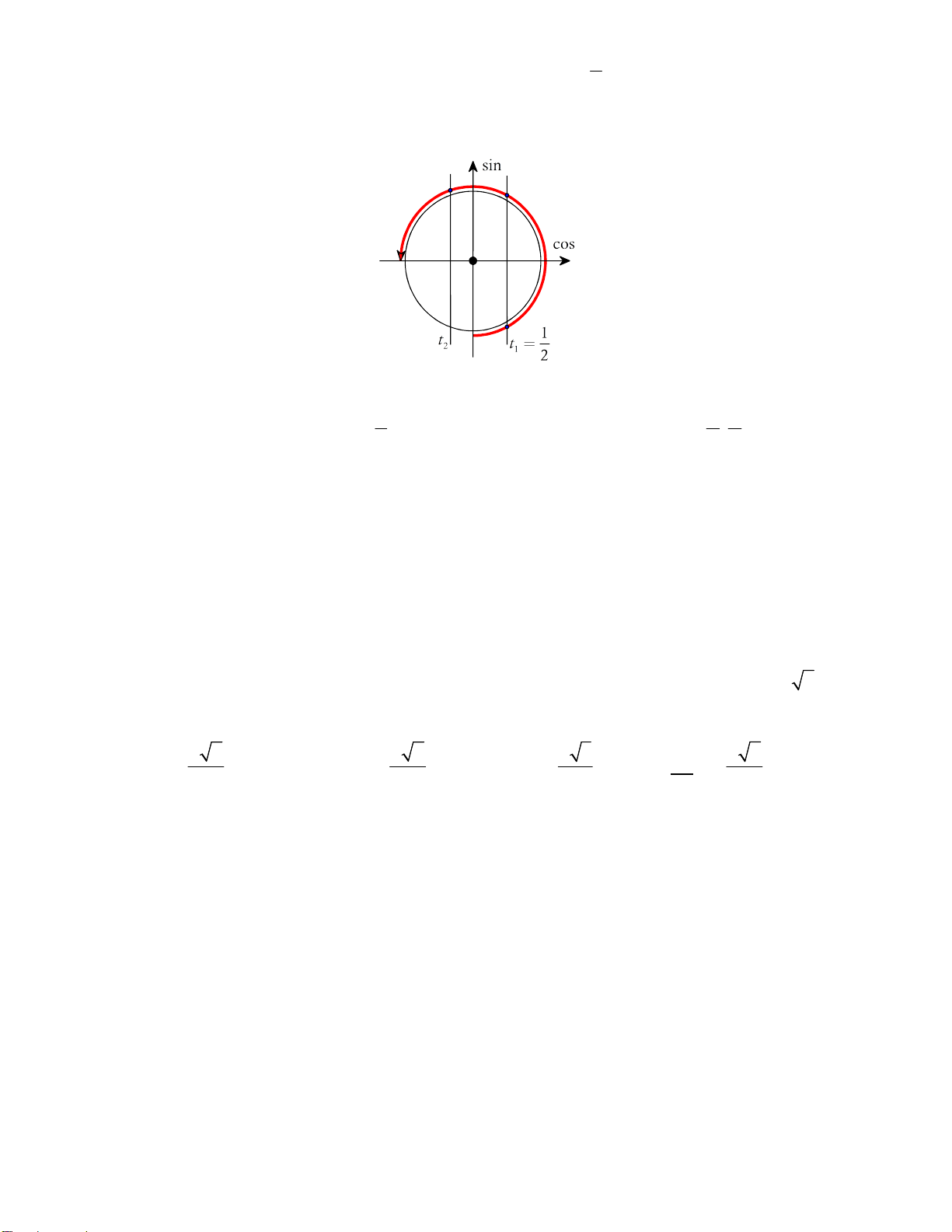
Hàm số g  x  f  2
x  3 nghịch biến trên khoảng nào dưới đây? A. 0;  1 B. 1;3 C.  ;    1 D.  1  ;0 Hướng dẫn 2
Gọi C là đồ thị hàm số y  gx  f 2  x .
Tịnh tiến C sang trái 2 đơn vị ta được đồ thị hàm số y  gx  2  f x.
Lấy đối xứng đồ thị hàm số y  f x qua Oy ta được đồ thị hàm số y  f x. x  0 x  0 x  0   Ta có y  f  2
x    y  x f 2 3
2 . x  3 ; y  0    2 x  3  0  x 3 2     . f   x  3  0  2  x  3   3 x    6 Bảng xét dấu y Vậy hàm số y  f  2
x  3nghịch biến trên khoảng 0;1.
Câu 2: Cho hàm số y  f  x có f  x 3 2 '  x  3x 10 ; x x
 . Có bao nhiêu giá trị nguyên dương của m để
hàm số g  x  f  2
x  2mx  m  2  3 có 13 điểm cực trị? A. 2 B. 3 C. 4 D. 5 Hướng dẫn + f  x 3 2 '
 0  x  3x 10x  0  x  0; x  5; x  2  u(x).u '(x) + đặt 2
u(x)  x  2mx  m  2 . Ta có g '(x)   f  u(x)  3'  . f ' u(x)  3 u(x) 3  u(x)  3  0 u(x)  3  u(x)  0 f ' u(x) 3  u(x) 3 2   
    u(x)  1(1)  ; u(x).u '(x)  0    u '(x)  0 u(x)  3  5 u(x)  8  
+Do vậy số điểm cực trị của hàm g  x  f  2
x  2mx  m  2  3 bằng số nghiệm bội lẻ của u(x)  0; 1  ; 3  ; 
8 +số điểm cực trị của u(x)
Ta có bảng biến thiên của hàm u(x) : m 2  ;  3  2  1 5 m  m  6  0 
Dựa vào bảng biến thiên, ta có: 2  8      2  3     m ycbt m m   2 2 m  m 1 0   1 5 m   2  1 5   1 5   m  2;    ;3;m     m2;  3 2   2    
Câu 3: Cho hàm số y  f x  3 x  2
bx  cx  3 thỏa mãn min f x f 1
1. Giá trị lớn nhất của hàm số 0;2      
g x  f  1x  1x  là A. 5 B. 55 C. 3  2 D. 17 Hướng dẫn: + min f  x  f  
1  1 nên suy ra hàm đạt cực tiểu tại x=1 0;2  f '(1)  0 3   2b  c  0 b   0 3        f (x)  x  3x  3  f (1) 1 b   c  4  1 c  3
Dễ dàng lập được bảng biến thiên của 3 f (x)  x  3x  3
+ Xét hàm g  x  f  1 x  1 x  ; Nhận xét: 2 2
t  1 x  1 x  t  2  2 1 x  2  t  2  min t  2, khi x  1;max t  2, khi x  0
Dựa vào bbt của f(x), suy ra max g(x)  f (2)  5 4 2 x 2 1  x 1
Câu 4: Tổng các nghiệm của phương trình 2 log    2 x là 2 x   A. 5 B. 3 C. 4 D.1 Hướng dẫn: Điều kiện: x>0 2 x 1 1 1 t 1  t 1  Đặt t  , phương trình có dạng 2 2 log t  2  log t  2  0 x 2 2 1 1 1 t 1  1 1 t 1  1 1 t 1  Xét f (t)  log t  2  f '(t) 
 .2 .ln 2  f '(t)    .2 .ln 22 2 2 2  0; t   0 2 2 t.ln 2 2 t .ln 2 4
Suy ra f’(t) có không quá 1 nghiệm, suy ra f(t) có không quá 2 nghiệm. 2  x 1  2 2 t  2  x  2x 1  0 x  1 Nhận xét ( )  0 x f t        
. Vậy tổng tất cả các nghiệm của 2 2 t  4  x 1 x  4x 1  0 x  2  3  4  x phương trình là 5.
Câu 5: Gọi S là tập tất cả các giá trị nguyên của m để bất phương trình  2 m  m x 2 2 e  2mx  m  2m  0
nghiệm đúng với mọi x thuộc  . Tổng giá trị tất cả các phần tử của S bằng A. 4 B. 0 C. 5 D. 2 Hướng dẫn: + Đặt f x   2 m  m x 2 ( ) 2
e  2mx  m  2m , nhận xét f 0  0nên yêu cầu tương đương f (x)  f (0);x   ,
suy ra x=0 là điểm cực tiểu của hàm số  f '(0)  0 + f x   2 m  m x 2 '( ) 2
e  2m  f '(0)  m  4m  0  m  0, m  4
+ Với m  0  f (x)  0;x   ( thỏa mãn) + Với
 4  ( )  8 x  8  8  8 x m f x e x e   x  
1   0;x   ( do đường thẳng y=x+1 là tiếp tuyến của đồ thị hàm số x
y  e tại x=0 ) hoặc có thể vẽ bbt của f(x) để suy ra f  x  0; x
  , suy ra m=4 thỏa mãn Vậy m=0 hoặc m=4.
Câu 6: Cho hàm số f (x) xác định, có đạo hàm, liên tục và đồng biến trên [1; 4] thỏa mãn 2 3
x  2xf (x)  [f (x)] , x
 [1;4], f (1)  . Giá trị f (4) bằng 2 5 391 361 381 371 A. . B. . C. . D. . 18 18 18 18 Hướng dẫn: Ta có: 2 2 x  2xf(x)  [f ( ) x ]  ( x 1 2 f (x))  [f ( ) x ] 2 4 4 [f (x)] f (x) f (x)   x   x  dx  xdx 1    2 f (x) 1 2 f (x) 1 1 2 f (x) 1 4 14 14 391  1 2 f (x)   1 2 f (4)  2   f (4)  1 3 3 18  ex  2 3 5cos x cos x sin x    Câu 7: Cho tích phân I  dx  . a eb  c 
, với a , b , c là các số thực. Tính giá trị của 2 cos x 0
biểu thức P  a  b  c . A. 4. B. 16. C. 10. D. 2. Lời giải Chọn A    3 3 x  x  3 ex.cos x  ex x x .sin x x cos sin I  5 e dx  e . dx   3  5e  dx  2 cos x 2 0 cos x 0 0 0      3 x x    3     x  x ex x ex .cos ex.cos  x e 3  5e  dx  3  5e  dx  3 3 3  5e   7e  6 . 2   0 cos x 0  cos x 0 cos x 0 0  0
Do đó a  7 , b  3 , c  6
 . Vậy P  a  b  c  4 .
Câu 8: Cho hàm số bậc ba f  x có đồ thị hàm số như hình vẽ bên. Biết hàm số f  x đạt cực trị tại hai điểm x , x thỏa 1 2
mãn x  x  4 và f  x  f x  2 . Gọi S , S là diện tích của hai hình phẳng được cho trong hình vẽ 1   2 2 1 1 2 S bên. Tính tỉ số 1 . S2 6 8 3 3 5 A. . B. . C. . D. . 5 5 8 3 . Lời giải
Không mất tính tổng quát, tịnh tiến đồ thị hàm bậc ba y  f  x sao cho điểm uốn của đồ thị thuộc
trục tung  x  x  0 . Lại có x  x  4 nên x  2, x  2 . 1 2 2 1 1 2
Theo giả thiết, ta có f  x  k  x  x    k  2 ' 2 2 x  4 với k  0 . 3  x  Suy ra f  x  k   4x C .  3  k k Do f    f   16 16 2 2  2   C   C  2  C  1 3 3 3  x  16k Suy ra f  x  k 
 4x  1 và f x  f 2   1. 2     3  3 7 0 0 3  x  20k
Ta có S   f x 1 dx  k      4xdx  . 2    3  3 2  2 32k S S  S BC.IC 2. 1 f 2 3 Xét 1 IABC 2 3   1  1  1  . S S S S 20k 5 2 2 2 2 3
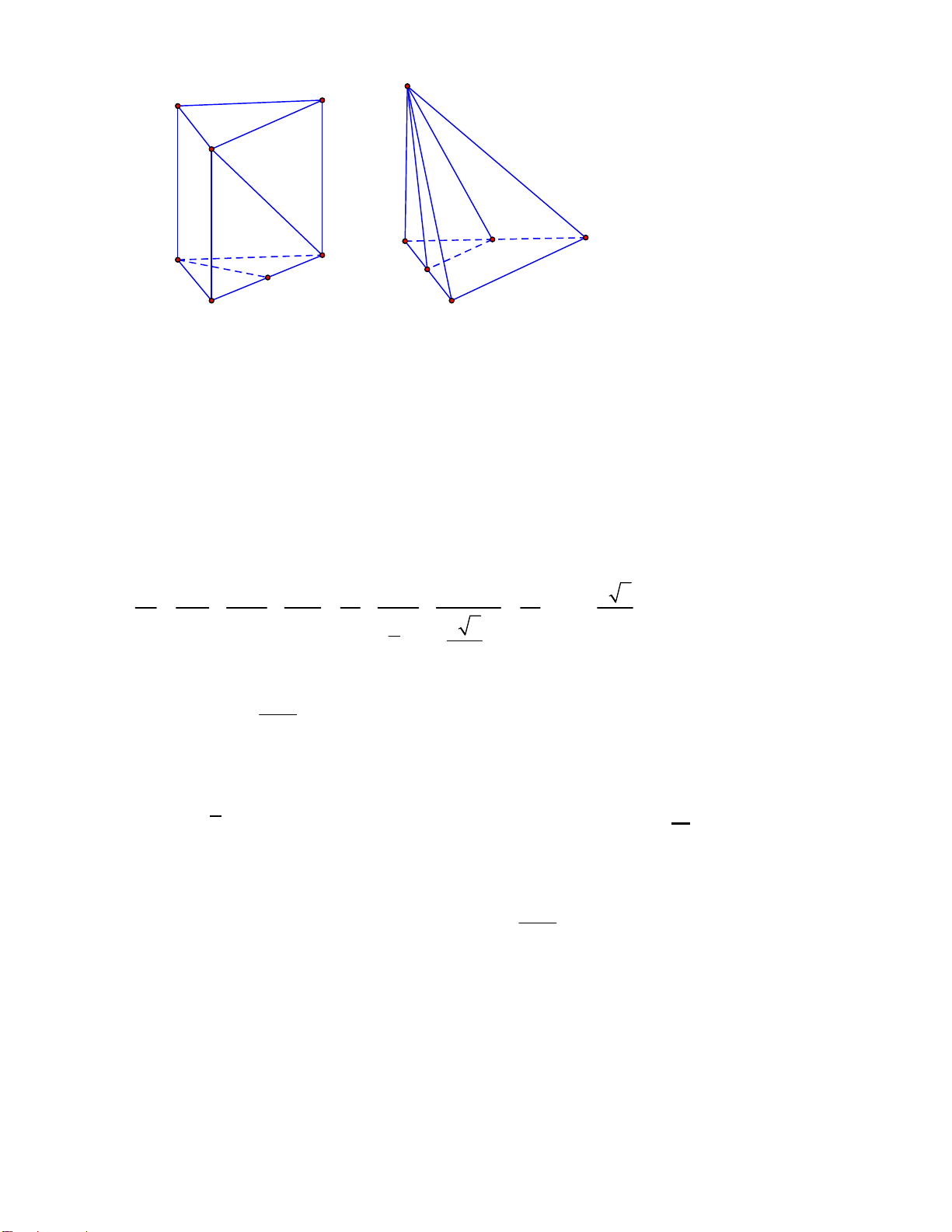
Câu 9: Cho hình chóp S.ABC có SA   ABC  0
; AB  2a 2, BC  3a, ABC  45 . Gọi I là trực tâm của tam giác
SBC . Giá trị lớn nhất của thể tích khối chóp I.ABC bằng 3 a 3 a 3 a 2 A. . B. . C. 3 a . D. . 2 4 2 Hướng dẫn
+ Gọi H là trực tâm của tam giác , K  AH  BC , ta chứng minh được HI  SBC  , suy ra trong
mặt phẳng SAK  có  0
KIH  90  I thuộc đường tròn đường kính HK . 1
+ Gọi E là hình chiếu vuông góc của I lên AK  IE  ABC  V  IE.S I .ABC 3 ABC 1 1 2 + 0 2 S  A . B BC.sin 45  3 . a 2a 2.  3a 2  V
 IE.a , suy ra thể tích I.ABC lớn nhất khi ABC 2 2 2 I .ABC HK
và chỉ khi IE lớn nhất. Do I thuộc nửa đường tròn đường kính HK nên IE  , suy ra IE lớn 2 HK  nhất bằng
khi I là điểm chính giữa của cung HK . 2
+ Chọn hệ trục như hình vẽ với tam giác ABC , ta có  0
AB  2a 2; ABC  45  AO  BO  2a  OC  a   A0;2a; B 2
 a;0;C a;0 : H 0; x  AC  a;2a; BH  2a; x. 8   a 3 a a Ta có 2 AC.BH  0  2a  2 .
a x  0  x  a  HK  a  IE  2  maxV  a  max 2 I .ABC 2 2
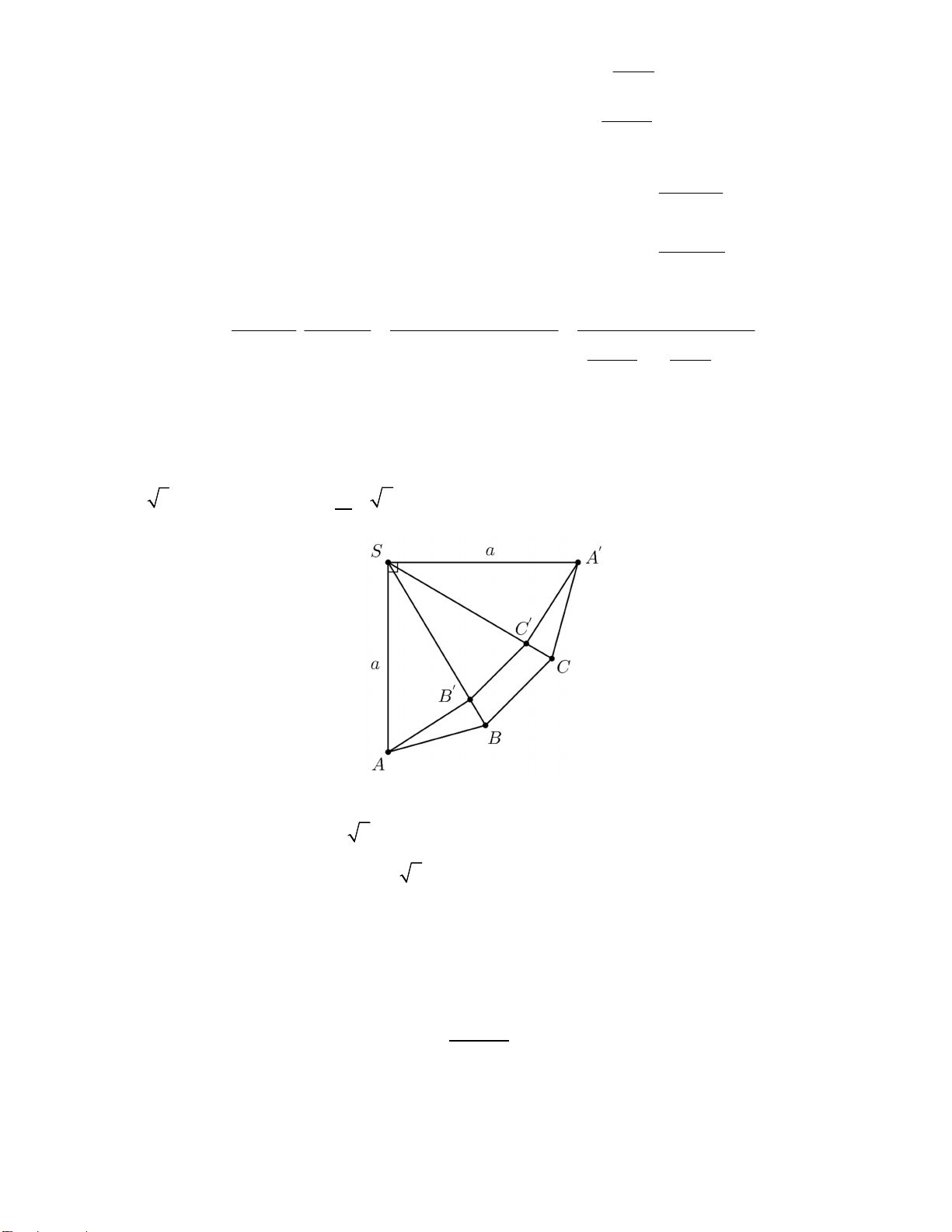
Câu 10: Cho hình trụ có đáy là hai đường tròn tâm O và O , bán kính đáy bằng chiều cao và bằng R . Trên
đường tròn đáy có tâm O lấy điểm A , trên đường tròn tâm O lấy điểm B . Đặt  là góc giữa AB và đáy. Biết
rằng thể tích khối tứ diện OO A
 B đạt giá trị lớn nhất. Khẳng định nào sau đây đúng? 1 1 A. tan   2 . B. tan  . C. tan  . D. tan  1. 2 2 Lời giải O' B A' O I B' A
+ Gọi A là hình chiếu của A lên mặt phẳng chứa đường tròn tâm O .
+ Gọi B là hình chiếu của B lên mặt phẳng chứa đường tròn tâm O .
+ Gọi R là bán kính của đường tròn tâm O , Ta có:    BAB . R Suy ra: AB 
. Gọi I là trung điểm của AB  OI  AB . tan R 1 + Ta có: 2 2 OI  OB  IB  4  . 2 2 tan  2 1 R 1 Và: S     .   OI. AB 4 OAB 2 2 4 tan tan  9 3 1 1 R 1 1 Suy ra: V       V    OO .S .   . . 4 OO AB OAB .O A B OAB 2 3 3 36 tan tan  1 1 + Ta có: V . 4 
đạt giá trị lớn nhất. OO A 
đạt giá trị lớn nhất khi và chỉ khi B 2 tan tan  Xét hàm số f t 2
 t. 4  t với t 0;2 1
Qua bảng biến thiên, ta có V khi t  2 hay tan  . max 2 3 1 R Cách 2: V    O . A OA'.d (O , A OA').sin(O . A OA') sin(O . A OA') OO AB 6 6 AA' 1 Vậy thể tích max khi 0 (O .
A OA')  90  AB '  R 2  tan   AB ' 2 Mức 4
Câu 1: Cho hàm số y  f  x x2  e   2
ln x  4x  5 . Có bao nhiêu cặp số x; y với x ;  y thỏa mãn f  2 2
x  y   f 2x  4y ? A. 12 B. 11 C. 8 D. 4 Hướng dẫn: Ta nhận thấy: + y  f  x x2  e   2 ln x  4x  5 x2  e
 ln  x  22  1 nên hàm số có đồ thị đối xứng nhau qua đường thẳng x  2 . x  2  x 2x 4 + 2 y '  e 
nên hàm số đồng biến trên 2; , nghịch biến trên ;2 2 x  2 x  4x  5 m  n m  n
Từ đó suy ra f m f n    m  n     2 m  n  4  2 2 2
x  y  2x  4y  0(1) Suy ra f  2 2
x  y   f 2x  4y   2 2
x  y  2x  4y  4  0(2)
+ (1) x  y  x  y    x  2   y  2 2 2 2 4 0 1
2  5  x 1  5  x 1;0;1;2;  3 10 x  1 x  0 Với  y  1 y  3  ; Với  y  0  y  4 
; Với x    y  2 0 2  5(l) x  3 x  2
+(2) x  y  x  y     x  2   y  2 2 2 2 4 4 0 1
2  9  x 1  3  x 4;3; 2  ; 1;0;1;  2 x  4 x  3 x  2 Với  y  2   ; Với  
 y  22  5(l) ; Với    y  22  8(l) x  2 x  1 x  0 Với x  1   y 1; y  5 
Vậy có 11 cặp thỏa mãn
Câu 2: Có bao nhiêu giá trị nguyên của m để hàm số 4 2
y  x  mx  64x có đúng 5 điểm cực trị? A. 19 B. 6 C. 24 D. 5 Hướng dẫn + xét 4 2 f x  x  mx  x  x  3 ( ) 64 x  mx  64 32 32 3 2
f '(x)  4.x  2mx  64; f '(x)  0  m  2x   g(x) ; g '(x)  4x  ; g '(x)  0  x  2  x 2 x x  2 0  g '(x)  0   g(x)    2 4 
TH1: Nếu m  24 thì f '(x)  0 có 1 nghiệm bội lẻ, suy ra f(x) có một điểm cực trị dương , suy ra f(x) có tối đa 2
nghiệm nên y  f (x) có tối đa 3 điểm cực trị (loại)
TH2: Nếu m  24 , khi đó f’(x) có 3 nghiệm bội lẻ, suy ra f(x) có 3 điểm cực trị.
Khi đó, để y  f (x) có 5 điểm cực trị  f  x  0 có 2 nghiệm bội lẻ 3
 x  mx  64  0 có đúng 1 nghiệm bội lẻ khác 0 64 3 2
x  mx  64  0  m  x   h(x) x Ta có bbt x  3  32 0  h '(x)  0   11 h(x)    3 0 , 2 
Suy ra, m  30 . Vậy 25  m  30 , có 6 giá trị nguyên của m 4x 7
Câu 3: Cho các hàm số f  x 
; g x  ax  bx  cx a  b  g 3   ; g 9  81 x   5 3  0; 0 . Số giá trị 4  và     2 3
nguyên của m để phương trình f  g   x  f  2 1 2
1 m  2g  x  4  1 có 3 nghiệm phân biệt là A. 17 B. 19 C. 0 D. 15 Hướng dẫn
Nhận xét, f(x) đồng biến trên R và thỏa mãn f (x)  f (1 x)  1  1 f (x)  f (1 x) Pt 2 2
 f g  x   f  m  g x 
 f g  x  f m  g x 
 g   x  g x   2 ( (1 2 )) 1 (1 2 ( 4)) ( (1 2 )) ( 2 ( 4)) 1 2 2 4  m
Đặt h(x)  g 1 2x  2g(x  4)  h (x)  2
 .g1 2x  2g (x  4)
Do g’(x) là hàm bậc 4 trùng phương có 1 điểm cực trị nên đồ thị hàm số đối xứng nhau qua Oy và đồng biến khi   x  x 
x>0. Suy ra h x   g   x 1 2 4 '( ) 0 ' 1 2  g '(x  4)   x  1  ; x  5 1    2x  x  4
h(1)  g(3)  2.g(3)  3g(3)  7; h(5)  g(9)  2g(9)  g(9)  81 ( do hàm g(x) là hàm lẻ nên g(-9)=-g(9)) Ta có bbt x  1 5  h '(x)  0  - h(x)  81 - 7 
Dựa vào bbt, để phương trình có 3 nghiệm phân biệt 2  7   m  81  m 8  ; 7  ;....;  8 . Có 17 giá trị nguyên thỏa mãn
Câu 4: Cho các hàm số y  f  x; y  g  x liên tục và có đạo hàm trên , trong đó hàm số g  x   f 2  x'
là hàm số bậc ba có đồ thị như hình vẽ. 12 Hàm số y  f  2 x   3 2
2  x  2x  x  2023 nghịch biến trên khoảng nào dưới đây?  1  1 A.    1; 2 B.  ;    C.  2  ;0 D. ;1    3   3  Hướng dẫn
Hàm số gx là hàm số bậc 3 nên có dạng:
gx   f 2x '  ax4x 1x4,a  0 f '2x  a  x4x  1 x4
Đặt t  2  x  f 't  at  6t  2t  1
Đạo hàm của hàm số y  f  2 x   3 2
2  x  2x  x 2021 là y  xf  2 x    2 x  x   ax 2 x   2 x   2 1 ' 2 ' 2 3 4 1 2 4 4 x 1   3x    1 x       3  Lập bảng xét dấu
Dựa vào bảng xét dấu trên ta có hàm số đã cho nghịch biến trên 1; 2.
Câu 5: Cho hàm số f  x liên tục trên  , có bảng biến thiên như sau 13 4  x  12  x
Có tất cả bao nhiêu giá trị nguyên của tham số m để giá trị lớn nhất của hàm số y   f m  32x  f  2   x 16  16 nhỏ hơn ? 3 A. 11. B. 9 . C. 8. D. 10. Lời giải Chọn C 32x 32 x 32x  32x  + Ta có   4   4  ;4 1 f  6. 2 2    2  x 16 8 x x 16  x 16 
Dấu = xảy ra tương ứng khi x=-4 và x=4 2 +   x   x     x  2 4 12 16 2 64
4  4  4  x  12  x  32
Dấu bằng xảy ra tương ứng khi x=4 và x=-4 2 4 4  x  12  x 32 Vậy suy ra     32 . 3 6  32x  1 f  2   x 16 
Dấu bằng xảy ra tương ứng khi x=4 và x=-4. 4  x  12  x  2  Từ đó ta có: max
 f m  max   f m ; 32  f m   32x   3 f   2   x 16  14  f m 2 16    3 3 16 Yêu cầu bài toán     32  f m  6.  3 f m 16  32   3
Dựa và bảng biến thiên của hàm số f(x) ta có m  5  ; 4  ;3; 1  ;0;1;2;  3 . CÁC CÂU HỎI THI CỤM 2 x  x 1
Câu 1. Tìm họ tất cả các nguyên hàm của hàm số f (x)  . x 1 1 2 x A. 1  C. B. 2 x  ln(x 1)  C. C. 2 x  ln x 1  C. D.  ln x 1  C. 2 (x 1) 2 2 3  x khi x 1 3 Câu 2. Cho hàm số f (x)  
. Tính tích phân f x   1d x . 4  x khi x 1 1 7 3 5 A. 1. B. . C. . D. . 2 2 2 Lời giải 3 3 2 f  x 1dx  f
 x 1dx 1  f  tdt 1 1 0 1 2 3 2 t 1 2 t 2 3 7 2
 3t dt  4  tdt  3.  4t  1 4     . 3 0 1 2 1 2 2 0 1 Câu 3.
Cho hàm số f (x) liên tục trên [a; b] và số thực k tùy ý. Trong các khẳng định sau, khẳng định nào sai ? b a b 2b A. f (x)dx   f (x)dx   B. f (2x)dx  2 f (x)dx   a b a 2a b b a C. kf (x)dx  k f (t)dt   D. kf (t)dt  0  a a a
Câu 4. Quay xung quanh trục Ox hình phẳng giới hạn bởi đồ thị của hàm số y  (x  3) log x 1 , trục Ox 0,5
, và đường thẳng x 1 ta thu được khối tròn xoay có thể tích bằng 15 3 3 A. 2 (x 3) (log x+1)dx  . B. 2  (x 3) (log x+1)dx 0,5  . 0,5 2 1 2 2 C. 2  (x 3) (log x+1)dx  . D. 2 (x 3) (log x+1)dx 0,5  . 0,5 1 1 Câu 5.
Tính thể tích của một hình hộp chữ nhật biết rằng ba mặt của hình này có diện tích là 2 20cm , 2 10cm , 2 8cm . A. 3 40cm B. 3 38cm C. 3 1600cm D. 3 80cm Lời giải  . a b  20 
Giả sử hình chữ nhật có ba kích thước là a , b , c . Ta có  . a c  10 2 2 2  a .b .c  1600  . a . b c  40 .  .bc  8 
Vậy thể tích khối hộp chữ nhật là 3 40cm . Câu 6.
Cho hai khối trụ có cùng thể tích; bán kính đáy và chiều cao của hai khối trụ lần lượt là R , h và R , h 1 1 2 2 R 3 h
. Biết rằng 1  . Tỉ số 1 bằng R 2 h 2 2 9 2 4 3 A. . B. . C. . D. . 4 3 9 2 Lời giải
Gọi V ,V lần lượt là thể tích của khối trụ thứ nhất và thứ hai. 1 2 2 h  R  4 Ta có: 2 2 1 2
V  V   R h   R h      . 1 2 1 1 2 2 h R 9 2  1  Câu 7.
Trong không gian, cho hình chóp S.ABC có SA , AB , BC đôi một vuông góc với nhau và SA  a ,
AB  b , BC  c . Mặt cầu đi qua S , A , B , C có bán kính bằng 2a  b  c 1 A. . B. 2 2 2 a  b  c . C. 2 2 2 2 a  b  c . D. 2 2 2 a  b  c . 3 2 Câu 8.
Cho hình chóp S. ABC có AB  3, AC  4, BC  5 và góc giữa các cạnh bên với đáy bằng 60 . Thể
tích của khối chóp đã cho bằng 5 3 5 A. 5 3 B. C. D. 15 3 6 3 16 Câu 9.
Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình thang vuông tại A và B , AB  BC  a ,
AD  2a , SA   ABCD và SA  a 2 . Gọi E là trung điểm của AD . Kẻ EK  SD tại K . Tính thể
tích của khối cầu đi qua sáu điểm S , A , B , C , E , K ? 3  a 3 3 a 3 4 a A. V  . B. 3 V  6 a . C. V  . D. V  . 6 2 3 Lời giải
Vì E là trung điểm AD nên ABCE là hình vuông cạnh a , nên CE  AD .
Mặt khác SA   ABCD  CE  SA .
Từ đó chứng minh được SK  KC . Dễ thấy có  SEC   SKC   SAC  
SBC  90 . Suy ra A , B , E , K luôn nhìn SC dưới 1 góc vuông
nên S , A , B , C , E , K nằm trên mặt cầu đường kính SC . SC
Gọi I là trung điểm SC thì mặt cầu đi qua qua sáu điểm S , A , B , C , E , K có bán kính R  . 2
Ta có ABCE là hình vuông cạnh a , nên AC  a 2 . SC
Tam giác SAC vuông cân tại A , cạnh AC  SA  a 2 nên SC  2a , suy ra R   a . 2 3 4 a
Vậy thể tích mặt cầu đi qua sáu điểm S , A , B , C , E , K là: V  3
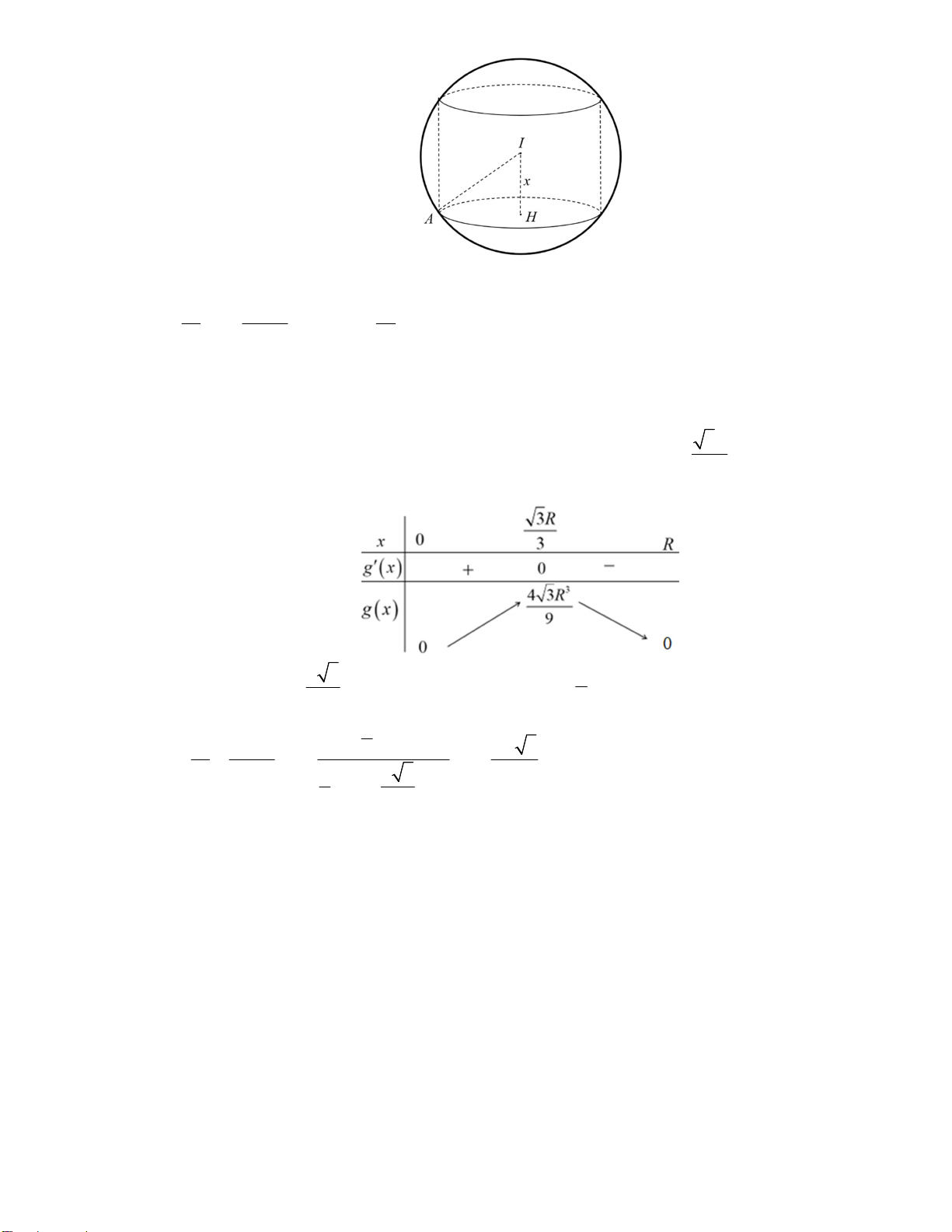
Câu 10. Cho hình nón có bán kính đáy bằng 3 và chiều cao bằng 6 , một khối trụ có bán kính đáy thay đổi nội
tiếp khối nón đã cho (như hình vẽ). Thể tích lớn nhất của khối trụ bằng 17 A. 10 . B. 6 . C. 8 . D. 4 . Lời giải Đặt OO  l , B O
   x , SO  h  6 và SO  y . O B   SO x y
Áp dụng định lý Talet vào tam giác SOB ta được     y  2x . OB SO 3 6
Ta có l  6  y  6  2x . Suy ra 2
V   .x .6  2x   . . x . x 6  2x .
Áp dụng bất đẳng thức Cô-si cho 3 số x , x và 6  2x ta được 3        x x   x x x 6 2x V . . . 6 2    8   .  3  Vậy V  8 khi x  2 . max
Câu 11. Trong không gian Oxyz , cho hình hộp ABCD.AB C  D
  biết A1;0;1, B 2;1;2 , D1; 1  ;  1 ,
C4;5; 5 . Tọa độ của điểm A là: A. A4;6;5 . B. A 3  ;4;  1 . C. A3;5; 6   . D. A3;5;6 . 18 Lời giải Gọi Aa;b;c
   
   
ABCD.A ' B 'C ' D ' là hình hộp  AC  AB  AD  AA  AA  AC  AB  AD  (2;5;  7) a 1  2 a  3   
AA  a 1;b;c   1  b   5  b   5 Vậy: A3;5; 6   . c 1 7     c  6  
Câu 12. Trong không gian Oxyz , cho mặt cầu S  2 2 2
: x  y  z  2x  4 y  4z  5  0 và mặt phẳng
P:x  y  2z 1 0. Gọi M là một điểm bất kì trên mặt cầu S. Khoảng cách từ M đến P có
giá trị nhỏ nhất bằng 4 6 A. 6  2 . B. 0 . C.  2 . D. 2 6  2. 3 Giải
Mặt cầu S  có tâm I 1; 2;2 và bán kính R  2 .
d I,P  6  R suy ra mặt phẳng P không cắt mặt cầu S  .
Điểm M S  thỏa mãn d M ,P nhỏ nhất bằng d I,P  R  6  2 . x  3 y  4 z  3
Câu 24. Trong không gian với hệ trục tọa độ Oxyz, gọi  là góc hợp bởi đường thẳng d :   1 2 1 
và mặt phẳng P : 2x  y  z 1  0 . Khi đó, giá trị cos bằng bao nhiêu 1 1 A.  3 . B.  3 . C. . D. . 2 2 2 2 Giải  
d có VTCP là u  1;2; 
1 và P có VTPT là n  2;1;  1 .   u.n 1.2  2.11.1 1 3
Vì  là góc không tù nên từ sin       cos  . u . n 6. 6 2 2
Câu 14. Biến cố A liên quan đến một phép thử ngẫu nhiên T có hữu hạn kết quả đồng khả năng xuất hiện.
Khẳng định nào sau đây là đúng ? n A 1 n  n  \ A A. P A    . B. P  A  . C. P  A    . D. P A    . n P  A n A n 19
Câu 15. Cho hình tứ diện đều ABCD . Trên mỗi cạnh của tứ diện, ta đánh dấu 3 điểm chia đều cạnh tương ứng
thành các phần bằng nhau. Gọi S là tập hợp các tam giác có ba đỉnh lấy từ 18 điểm đã đánh dấu. Lấy
ra từ S một tam giác, xác suất để mặt phẳng chứa tam giác đó song song với đúng một cạnh của tứ diện đã cho bằng 2 9 2 4 A. . B. . C. . D. 45 34 5 15 Lời giải Cách 1: A M1 N1 P1 M2 N2 M3 P2 N3 Q1 Q2 Q3 B D P3 E1 F1 E2 F2 E3 F3 C
Gọi các điểm được đánh dấu để chia đều các cạnh của tứ diện đều ABCD như hình vẽ.
+ Gọi S là tập hợp các tam giác có ba đỉnh lấy từ 18 điểm đã đánh dấu.
Số phần tử của S là số cách chọn ra 3 điểm không thẳng hàng trong số 18 điểm đã cho.
Chọn ra 3 điểm trong 18 điểm trên: có 3 C18 cách.
Chọn ra 3 điểm thẳng hàng trong 18 điểm trên có 3 6.C  6 cách. 3
Suy ra số tam giác thỏa mãn là 3 C  6  810 18
+ Gọi T là tập hợp các tam giác lấy từ S sao cho mặt phẳng chứa tam giác đó song song với đúng một
cạnh của tứ diện ABCD .
- Chọn 1 cạnh của tứ diện để mặt phẳng chứa tam giác chỉ song song với đúng cạnh đó: có 1 C  6 6 cách.
Xét các tam giác mà mặt phẳng chứa nó chỉ song song với cạnh BD , suy ra tam giác đó phải có một cạnh song song với BD .
- Có 6 cách chọn cạnh song song với BD là M N , M N , M N , E F , E F , E F . 1 1 2 2 3 3 1 1 2 2 3 3 20
- Giả sử ta chọn cạnh M N là cạnh của tam giác. Cần chọn đỉnh thứ 3 của tam giác trong 16 điểm còn 2 2 lại.
Do M N  ABD mà mặt phẳng chứa tam giác song song với BD nên đỉnh thứ 3 không thể là 7 2 2  
điểm còn lại nằm trong mp  ABD .
Do mặt phẳng chứa tam giác chỉ song song với BD nên đỉnh thứ 3 không được trùng với một trong ba
điểm E , F , P . Vậy đỉnh thứ 3 chỉ được chọn trong 16  7  3  6 điểm còn lại. 2 2 2
Suy ra có 6 tam giác có 1 cạnh là M N và mặt phẳng chứa nó chỉ song song với BD . 2 2
Vậy số tam giác mà mặt phẳng chứa nó chỉ song song với cạnh BD là: 6.6  36 .
Tương tự cho các trường hợp khác, ta có số tam giác mà mặt phẳng chứa nó chỉ song song với đúng
một cạnh của tứ diện ABCD là: 36.6  216 . nT  216 4
Vậy xác suất cần tìm là   . n S  810 15 Cách 2
+) Gọi S là tập hợp các tam giác có ba đỉnh lấy từ 18 điểm đã đánh dấu.
Chọn ra 3 điểm trong 18 điểm trên: có 3 C18 cách. Trong số 3
C đó, có 6 cách chọn ra 3 điểm thẳng hàng trên các cạnh. 18 Suy ra nS  3  C  6  810 18
+) Xét phép thử: “Lấy ngẫu nhiên một phần thử thuộc S ”. Ta có n  810 . 21
+) Gọi T là biến cố: “Mặt phẳng chứa tam giác được chọn song song với đúng một cạnh của tứ diện đã cho”.
Chọn một cạnh của tứ diện: 6 cách, (giả sử chọn AB ).
Chọn đường thẳng song song với AB : 6 cách, (giả sử chọn PQ ).
Chọn đỉnh thứ 3: 6 cách, M , N , E, K , F, I  . n T  216 4
Suy ra nT   6.6.6  216. Vậy   . n  810 15
Câu 16. Cho dãy số a thỏa mãn a 1 và a 10a 1, n  2 . Tìm giá trị nhỏ nhất của n để log a  100 n  1 n n 1  n A. 100. B. 101. C. 102 . D. 103 . Lời giải. 1  1 
a  10a 1  a   10 a  (1) . n n 1  n  n 1  9   9  1 1 8 Đặt b
 a   b  a   . Từ (1)  b 10b , n   2 n n 1 1 9 9 9 n n 1  n 8
Dãy b là cấp số nhân với công bội là q 10 . Nên 1 n 1 b b .q  .10    . n  n 1 9 1 8 n 1 Do đó 1 a  b   10  , n  1,2,... . n n 9 9 9 n 8 n 1 Ta có 100 1 100 log a  100  a  10  10  10 . n 9 9
Vậy giá trị nhỏ nhất của n để log a  100 là n  102 . n Câu 17. Cho phương trình 2
2cos 3x 32mcos3x m2  0. Số giá trị nguyên của tham số m để phương   
trình đã cho có đúng 3 nghiệm thuộc khoảng  ;     . là  6 3 A. 3. B. 2 C. 1 D. 4 Lời giải.       Với x  ;    3x   ; .  6 3     2 
Đặt t  cos3x 1 t  
1 . Phương trình trở thành 2
2t 32mt m2  0. 22  1 t1  Ta có    m  2 2 5 
 phương trình có hai nghiệm  2 . t m 2 2    O 1   
Ta thấy ứng với một nghiệm t thì cho ta hai nghiệm  ; . 1  x thuộc khoảng   2  6 3 1 t 0 2 
Do đó yêu cầu bài toán   (tham khảo hình vẽ) t 1 2  
1 m2  0 1 m  2      m 2 1 m    3
Câu 18. Cho hình lăng trụ đứng ABC.AB C
  có đáy là tam giác vuông và AB  BC  a , AA  a 2 , M là
trung điểm của BC . Tính khoảng cách d của hai đường thẳng AM và B C  . a 2 a 2 a 3 a 7 A. d  . B. d  . C. d  . D. d  . 2 2 3 7 Lời giải 23 A C' A' B' M B C A C M N B B'
Tam giác ABC vuông và AB  BC  a nên A
 BC chỉ có thể vuông tại B . AB  BC Ta có   AB  BCB . AB  BB ' Kẻ MN // B C   B C  //  AMN   d  d B C  , MN   d B C
 , AMN   d C, AMN   d B, AMN  .
Vì tứ diện BAMN là tứ diện vuông nên 1 1 1 1 1 1 1 7 a 7         d  . 2 2 2 2 2 2 2 2 d BA BM BN a  a    a 7 a 2   2     2   x 1 Câu 19. Cho hàm số y  (C) và d : y  2
 x  m 1 ( m là tham số thực). Gọi k , k là hệ số góc của tiếp x  2 1 2
tuyến của C tại giao điểm của d và C . Tính k .k . 1 2 1 A. k .k  . B. k .k  2 . C. k .k  3 . D. k .k  4 . 1 2 4 1 2 1 2 1 2 Lời giải x 1
Xét phương trình hoành độ giao điểm 2x  m 1  (1) . x  2 2
 f (x)  2x  (m  6)x  2m  3  0
Phương trình (1) có hai nghiệm phân biệt   có hai nghiệm phân  x  2   f ( 2  )  0 biệt    m R . 2
  m  4m 12  0 24  m  6 x  x   1 2 
Gọi x , x là hai nghiệm của phương trình (1) , khi đó 2 . 1 2  3  2m  x .x  1 2  2  1 k   1  x  2 1 2
Hệ số góc của tiếp tuyến của C tại giao điểm của d và C là  . 1 k  2  x  22 2 1 1 1 1 Ta có k .k  .    4 . 1 2
x  22 x  22 x .x  2(x  x ) 42 2 3 2m m  6  1 2 1 2 1 2  2.  4  2 2   
Câu 20. Cho khối chóp S.ABC có SA  SB  SC  a và  ASB  20 ,   BSC  30 ,  
CSA  40 . Mặt phẳng  
bất kì qua A cắt SB , SC tại B , C . Tìm giá trị nhỏ nhất của chu vi A  B C   . A. a 3 . B. a 2 . C. a . D. 2a .
Trải các tam giác SAB , SBC , SCA trên một mặt phẳng như hình trên. Tam giác SAC trở thành tam giác SAC . Khi đó C  AB  B C    C A
   AA  a 2 . Dấu “=” xảy ra khi A , B, C , A thẳng hàng. Vậy chu vi tam giác A  B C
  nhỏ nhất bằng a 2 . MỨC 4 25    m  x mx m 2
Câu 21. Cho phương trình 2 2 4 3 3  2 
. Có bao nhiêu số nguyên m để phương trình có đúng hai x  m
nghiệm phân biệt thuộc đoạn  6  ;  0 ? A. 0. B. 1. C. 2. D. 3. Lời giải    m  2 2     m  x mx m 2 Với điều kiện trên 2 2 4 3 3  2  x m m 2 1 2  3  2  . x  m x  m 2     m 2
Đặt t  x  m , t  0 ta được: t m 22 1 3  2    * . t 2
Nhận thấy: Hàm số f t t m22 1 3  
 2 đồng biến trên khoảng 0; . m  Hàm số g t 2 
nghịch biến trên khoảng 0; . t
Và f  m  2   g  m  2  . Vậy  
* có nghiệm duy nhất t  m  2 . x  2 
Khi đó x  m  m  2   . x  2  2m  6   2  2m  0 1   m  4
Để phương trình có đúng hai nghiệm phân biệt thuộc đoạn  6  ;  0     . 2  2m  2  m  2
Do m nguyên nên m1;3;  4 .
Câu 22. Cho hàm số y  f  x có đạo hàm liên tục trên 0;  1 , thỏa mãn 1  f    x 2  2   4. 2x 1 f  x  
 với mọi x thuộc đoạn 0;  1 và f   1  2 . Giá trị I xf  xdx bằng 0 3 5 11 4 A. . B. . C. . D. . 4 3 4 3 Hướng dẫn 2 2 2 Ta có  f    x    x   f  x   f    x  f  x     2 4. 2 1 4 4. 2x   1 . 26 1 2 1
Lấy tích phân hai vế từ 0 đến 1 ta được  f   x 4 f  x d    x  4.     2 2x 1 dx 0  0  1   f    x 2 1  x  f   x 20 d 4 dx  . (*) 0 0 3 1 u   f (x) du  f '(x)dx 1 1 Xét I  f  xdx . Đặt     I  xf (x)  xf '  xd .x 0 dv  dx v  x 0 0 1 2 1 1 20 1 2 1 4 Khi đó (*)   f    x dx 4  xf (x)  4xf '   xdx    f    x dx 4xf '   xdx   0 0 0 0 3 0 0 3 2 1   f    x 2 1  dx  4xf '   x 1 1 2 dx  4x dx  0   f  
  x 2x dx  0  f   x  2x 0 0 0 0 2 1  3
f (x)  x  C . Vì f (1)  2 nên 2 C 1 f ( ) x  x 1. Vậy xf  xdx  . 0 4
Câu 23. Cho hai hàm số f  x 3 2
 ax  3x  bx 1 2d và g  x 2
 cx  2x  d có bảng biến thiên như hình vẽ.
Biết rằng đồ thị của hai hàm số đã cho cắt nhau tại ba điểm phân biệt có hoành độ x , x , x thỏa mãn 1 2 3 2 2 2
x  x  x  30 . Diện tích hình phẳng giới hạn bởi các đường y  f  x, y  g  x, x  3, x  6 bằng 1 2 3 2113 1123 1231 1321 A. . B. . C. . D. . 12 12 12 12 Lời giải Ta có f  x 2  3ax  6x  b
Từ BBT suy ra f  x và g  x có chung hai nghiệm là  và  27  2 6       c 3a a  c    d b  b  3d .    c 3a  1 
Từ BBT suy ra đồ thị hàm số g  x có đỉnh I ; 4   và c  0  c  1 2 1 3 12c  . c   d  4   d   4  b  2 c c c c Xét f  x  g  x 3   ax    c 2 0 3
x  b  2 x 1 3d  0 *
Từ giả thiết suy ra phương trình (*) có 3 nghiệm phân biệt x , x , x thỏa mãn 1 2 3
x  x  x  30   x  x  x 2 2 2 2
 2 x x  x x  x x  30 1 2 3 1 2 3  1 2 2 3 3 1 3 12c 2 2  2  c  3  b  2  c  3    2.  30   2. c  30      a  a  c  c
 c  32  2310c 2 2
 30c  0  29c  26c  3  0 c 1 tm   3 c   loai  29  c 1;a 1;b  9  ;d  3  6 6 1321  f  x  g  x 3 2
 x  4x  7x 10  S  f  x  g  x 3 2 dx  x  4x  7x 10dx    12 3  3 
Câu 24. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB 1, AD  10 , SA  SB , SC  SD . Biết
mặt phẳng SAB và SCD vuông góc nhau đồng thời tổng diện tích của hai tam giác S  AB và S  CD bằng 2
. Thể tích khối chóp S.ABCD bằng 3 1 A. 2 . B. 1. C. . D. . 2 2 Lời giải 28 S x A D N M O B C 2 Ta có V  2V  d  , A SCD.S S.ABCD . A SCD 3 SCD
Ta có SAB  SCD  Sx // AB . Gọi M là trung điểm của CD, N là trung điểm của AB .
 SM  CD , SN  AB  SM  Sx , SN  Sx .
Mặt khác SAB  SCD  SN  SCD tại S ,  NSM  90 2 1 d  ,
A SCD  d  N,SCD  SN V  .SN. .SM.CD . S.ABCD 3 2 2 2 2 2
SN  SM  MN  AD 10 . 1 1 1 2  S S
 SN.AB  SM.CD  AB SN  SM  SN  SM  4 SAB SCD   2 2 2 2 1 2 2
 SN  SM  2SN.SM 16  SN.SM  3. Vậy V  . .3.1 1. S.ABCD 3 2
Câu 25. Cho mặt cầu S  có bán kính R không đổi, hình trụ T  bất kì nội tiếp mặt cầu S  . Thể tích khối trụ  V
T  là V ; và thể tích phần còn lại của khối cầu là V . Giá trị lớn nhất của 1 bằng bao nhiêu? 1 2 V2 3 1 1 2 3 2 3 1 1 3 A. . B. . C. . D. . 2 2 2 2 Lời giải 29
Gọi I là tâm mặt cầu. Gọi H là tâm đường tròn đáy của hình trụ. V V V Ta có 1 1 
. Do đó để 1 đạt GTLN thì V đạt GTLN. V V V V 1 2 1 2
Đặt IH  x 0  x  R . Ta có 2
V   HA .2IH    2 2 R  x .2x    3 2 2x  2xR  1 Đặt g  x 3 2  2x  2xR . 3R Ta có g x 2 2  6x  2R gx 2 2  0  6  x  2R  0  x  3 Bảng biến thiên 4 3 4 Suy ra V có GTLN là 3
 R . Thể tích khối cầu là 3 V   R 1 9 3 4 3  V V R 1 3 Khi đó 1  1 3  1  . V V V 4 4 3 2 2 1 3 3  R   R 3 9 30
Document Outline

  • MÃ 101
  • MÃ 102
  • MÃ 103
  • MÃ 104
  • Dap an Word
  • hướng dẫn giải một số câu - hoàn thiện