Đề giao lưu HSG tỉnh Toán 11 năm 2019 – 2020 trường Bá Thước – Thanh Hóa

SỞ GIÁO DỤC & ĐÀO TẠO
ĐỀ THI GIAO LƯU HỌC SINH GIỎI CẤP TỈNH THANH HÓA NĂM HỌC 2019 - 2020
TRƯỜNG THPT BÁ THƯỚC
Môn thi: Toán - Lớp 11
Thời gian làm bài: 180 phút (không kể thời gian giao đề )
Ngày thi: 28 tháng 12 năm 2019
(Đề thi có 01 trang, gồm 05 câu) Câu I (4.0 điểm).
1. Lập bảng biến thiên và vẽ đồ thị ( P) của hàm số 2
y = ax + bx − 3 , biết rằng ( P) có đỉnh I (2; ) 1 .
2. Giải bất phương trình: ( x + ) x + + ( x + ) 2 1 2 6
x + 7 ≥ x + 7x +12 . Câu II (4.0 điểm). x ( + x) x 2 2 3 sin . 1 cos − 4cos . x sin − 3
1. Giải phương trình: 2 = 0 . 2sin x −1 (  y − 6x −  ) 1
y + 2 + (4x + 2) 2x +1 = 0
2. Giải hệ phương trình:  ( ; x y ∈ ) . 2 2
x + 2 + x + x − y −1 = 3 x + y −1 + y −1  Câu III (4.0 điểm).
1. Cho x, y, z là các số thực dương thay đổi thỏa mãn điều kiện xyz + x + z = y . Tìm giá trị 2 2 4z 3z
lớn nhất của biểu thức: P = − − + . 2 2 2 2 2 x +1 y +1 z +1 (z +1) z +1
2. Cho dãy số (u thỏa mãn điều kiện u = 2 và 2
u + u + u + ... + u = n u , n ∀ = 1,2,... n ) 1 1 2 3 n n
Tìm công thức số hạng tổng quát u của dãy số (u . n ) n Câu IV (4.0 điểm).
1. Một hộp đựng 50 chiếc thẻ được đánh số từ 1 đến 50 . Chọn ngẫu nhiên từ hộp hai thẻ.
Tính xác suất để hiệu bình phương số ghi trên hai thẻ là số chia hết cho 3.
2. Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác ABC cân tại A, M là trung điểm  4 7 
của AB . Đường thẳng CM : x − 2 y + 7 = 0 và K ; 
 là trọng tâm tam giác ACM . Đường  3 2 
thẳng AB đi qua điểm D (3;− )
1 . Tìm tọa độ các đỉnh của tam giác ABC , biết điểm M có hoành
độ nguyên và tâm đường tròn ngoại tiếp tam giác ABC thuộc đường thẳng x + 6y − 26 = 0. Câu V (4.0 điểm).
1. Cho hình chóp S.ABCD có đáy là hình thoi cạnh 3a , SA = SD = 3a , SB = SC = 3a 3 .
Gọi M , N lần lượt là trung điểm của các cạnh SA và SD , P là điểm thuộc cạnh AB sao cho
AP = 2a . Tính diện tích thiết diện của hình chóp khi cắt bởi mặt phẳng (MNP) .
2. Cho tứ diện ABCD , G là trọng tâm tam giác BCD và M là điểm di động bên trong
tam giác BCD sao cho khi M khác G thì MG không song song với CD . Đường thẳng qua
M và song song với GA cắt các mặt phẳng ( ABC ) , ( ACD) , ( ABD) lần lượt tại P,Q, R . Tìm
giá trị lớn nhất của tích . MP . MQ MR .
-------------------- Hết -------------------- 1
ĐÁP ÁN VÀ HƯỚNG DẪN CHẤM Nội dung Điể Câu Ý m
Lập bảng biến thiên và vẽ đồ thị (P) của hàm số 2
y = ax + bx − 3 , biết rằng 1 ( 2,0
P) có đỉnh I (2; ) 1 .  b − = 2 4a + b = 0 a = 1 −
Từ giả thiết ta có:  2a ⇔  ⇔   4a + 2b = 4 b  = 4  0,5
4a + 2b − 3 = 1 Vậy ( P) : 2
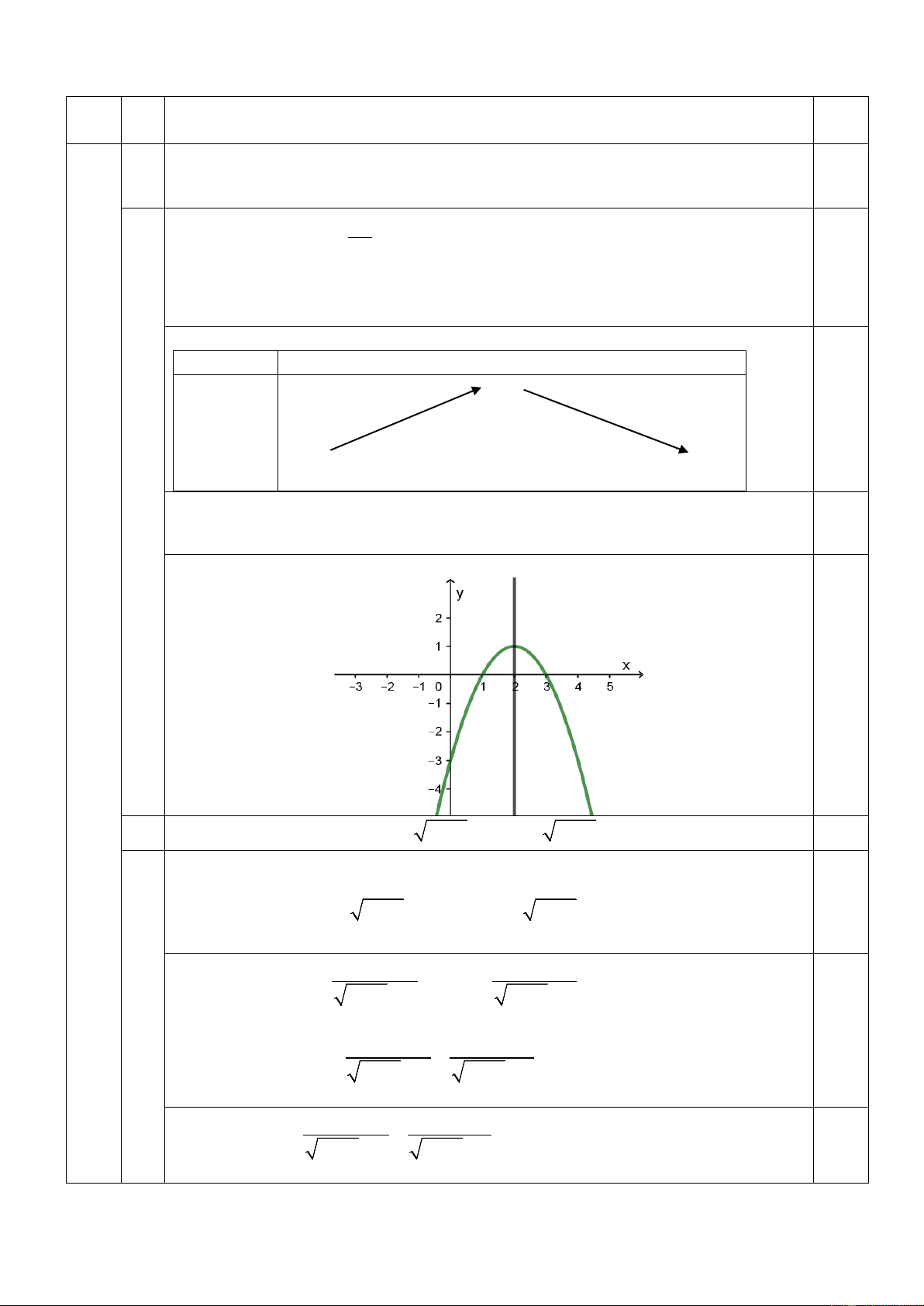
y = −x + 4x − 3 Bảng biến thiên: x −∞ 2 +∞ 1 0,5 y −∞ −∞
Đồ thị hàm số có đỉnh I (2; ), trục đối xứng 1 x = 2
Đồ thị hàm số cắt trục tung tại ( 0,5 0; 3
− ) và cắt trục hoành tại (1;0), (3;0)
Đồ thị hàm số như hình vẽ I 0,5 2
Giải bất phương trình: ( x + ) x + + ( x + ) 2 1 2 6
x + 7 ≥ x + 7x +12 . 2,0 Đk: x ≥ 2. − 0,5
BPT ⇔ ( x + )( x + − ) + ( x + )( x + − ) 2 1 2 2 6 7
3 ≥ x + 2x − 8 ( − −
⇔ x + ) x 2 + (x + ) x 2 1 6
≥ (x − 2)(x + 4) x + 2 + 2 x + 7 + 3 0,5 (  + +  ⇔ x − ) x 1 x 6 2 + −  (x + 4) ≥ 0   x + 2 + 2 x + 7 + 3  x +1 x + 6 Ta có + − (x + 4) x + 2 + 2 x + 7 + 3 0,5 2 x + 2 x + 2 x + 6 x + 6 1 = − + − − x + 2 + 2 2 x + 7 + 3 2 x + 2 + 2 (x + ) x +
(x + 6)( x +7 + )1 2 2 1 = − − − < 0, x ∀ ≥ 2 − x + 2 + 2 x + 7 + 3 x + 2 + 2
BPT ⇔ x − 2 ≤ 0 ⇔ x ≤ 2 0,5
Vậy tập nghiệm của bất phương trình là S = [ 2; − 2] x ( + x) x 2 2 3 sin . 1 cos − 4cos . x sin − 3 1 Giải phương trình 2,0 : 2 = 0 . 2sin x −1  π x ≠ + k2π  Đ 1  6
K: Điều kiện: sin x ≠ ⇔  , k ∈  (*). 0,25 2 5π x ≠ + k2π  6
Với điều kiện trên, phương trình đã cho tương đương: x ( + x) x 2 2 3 sin . 1 cos − 4cos . x sin − 3 = 0 2 0,5
⇔ 2 3 sin x + 2 3 sin .
x cos x − 2 cos x (1− cos x) − 3 = 0 ⇔ ( x − x) − ( 2 2 2 3 sin cos 3sin x − 2 3 sin .
x cos x + cos x) = 0  x − x = ⇔ ( x − x)( x − x − ) 3 sin cos 0 3 sin cos 3 sin cos 2 = 0 ⇔  0,25 II
 3 sin x − cos x = 2 π
TH1: 3 sin x − cos x = 0 ⇔ cot x = 3 ⇔ x =
+ kπ , k ∈ 0,25 6  π π   π 
TH2: 3 sin x − cos x = 2 ⇔ 2 sin x cos − cos xsin = 2 ⇔ sin x − = 1      6 6   6  0,25 π π 2π
⇔ x − = + k2π ⇔ x =
+ k2π , k ∈ 6 2 3
Đối chiếu điều kiện ta thấy phương trình đã cho có nghiệm 7π 2π 0,5 x = + k2π , x =
+ k2π , k ∈ 6 3 Giải hệ phương trình: (  y − 6x −  ) 1
y + 2 + (4x + 2) 2x +1 = 0 ( ) 1 2  ( ; x y ∈ ) 2,0 2 2
x + 2 + x + x − y −1 = 3 x + y −1 + y −1  (2) 3  1 x ≥ −  2  Điề  u kiện: y ≥ 1  2
x + x − y −1≥ 0  0,5
x + y −1≥ 0 Pt ( )
1 ⇔ ( y + 2) − (6x + 3) y + 2 + 2 
(2x + )1 2x +1 = 0
⇔ ( y + 2) y + 2 − 3(2x + ) 1
y + 2 + 2 (2x + ) 1 2x +1 = 0
Đặt a = y + 2;b = 2x +1;(a > 0;b ≥ 0) ta được:
a − ab + b = ⇔ (a − b)2 3 2 3 3 2 0
(a + 2b) = 0 ⇔ a = b 0,5
⇒ y + 2 = 2x +1 ⇔ y = 2x −1(⇒ 2x −1≥1 ⇔ x ≥ ) 1
Thay y = 2x −1 vào (2) ta được: 2 2 x + 2 +
x − x = 3 3x − 2 + 2x − 2 ⇔ ( 2
x − 3x + 2) + ( 2
x − x − 2x − 2 ) + 3(x − 3x − 2) = 0 0,5 ⇔ (  1 3  2
x − 3x + 2)1+ +  = 0 2 
x − x + 2x − 2 x + 3x − 2  x = 1 2
⇔ x − 3x + 2 = 0 ⇔  (t / m) x = 2 +x = 1⇒ y = 1 +x = 2 ⇒ y = 3 0,5 KL : T = 1;1 , 2;3 x; y ({ ) ( )} ( )
Cho x, y, z là các số thực dương thay đổi thỏa mãn điều kiện xyz + x + z = y .
Tìm giá trị lớn nhất của biểu thức: 1 2 2 4z 3z 2,0 P = − − + . 2 2 2 2 2 x +1 y +1 z +1 (z +1) z +1 Đặt π x = tan ,
A y = tan B, z = tan C, (0 < , A B, C < ) 2 Theo giả thiết ta có: y − z tan B − tan C 0,5 x = ⇔ tan A =
= tan(B − C) ⇒ A = B − C + kπ 1+ yz 1+ tan B tan C π III Do −
< A − B + C < π ⇒ k = 0 ⇒ A − B = C − . Khi đó: 2 1 1 4 tan C 3 tan C = − − + P 2( ) 2 2 2 2 2 1+ tan A 1+ tan B 1+ tan C
(1+ tan C) 1+ tan C 2 2 2 2 = 2( os c A − os c
B) − 4 sin C + 3sin C.cos C = cos 2 A − os
c 2B − 4 sin C + 3sin C.cos C = − ( 0,5 A − B) ( A+ B) 2 2sin sin
− 4sin C + 3sin C.cos C = = C ( A+ B) 2 2sin .sin
− 4sin C + 3sin C.cos C = 2 2 2
≤ 2sin C − 4sin C + 3sin C.cos C = sin C(3cos C − 2) = sin C(1− 3sin C) Nếu 3 sin C > ⇒ P < 0 . 0,5 3 4 Nếu 3 sin C ≤
. Áp dụng bất đẳng thức Côsi cho 3 số không âm 3 2 2 2
6 sin C(1− 3sin C)(1− 3sin C) 2 2 2 2
P = sin C(1− 3sin C) = 6 2 2 2
1 6 sin C +1− 3sin C +1− 3sin C 4 3 ≤ ( ) = 2 ⇒ P ≤ . 6 3 81 9
Dấu ‘’ = ‘’ xảy ra khi  1  2 sin C =  tan C = 3 4   2 2 s
 in(A + B) =1⇒ tan B = cot A ⇒ tan C = , tanA= , tan B = 2 4 2   0,5
A − B = C − tan A − tan B 2   = − 
1+ tan Atan B 4 2 2 ⇒ x = 2; y = ; z =
.Vậy giá trị lớn nhất của P bằng 2 . 2 4 9 Cho dãy số
(u thỏa mãn điều kiện u = 2 và n ) 1 2 2
u + u + u + ... + u = n u , n ∀ = 1,2,... 2,0 1 2 3 n n
Tìm công thức số hạng tổng quát u của dãy số (u . n ) n 2
Với n  2, ta có u  u  4u  u  . 1 2 2 2 3
Với mọi n  2, 3,..., ta có u  u ... u u  2 n u , 0,5 1 2  n 1 n n
u  u ... u  n 2 1 u . 1 2  n 1   n1 2
Trừ hai đẳng thức trên ta được u  2
n u n  1 u ,n  3 n n  n 1 n1 0,5  n  
1 u n 2 2
1 u ,n  3  u  u ,n  3 n  n 1 n  n  n 1 1 n1 n2 3 2 6u 4  u  . ... . u  2 , n 3. n 2 n 1 n 5 4 nn   1
nn      1 0,5
Với n = 1, n = 2 công thức trên vẫn đúng. 4 0,5 Vậy * u = n ∀ ∈  . n n (n + ) , 1
Một hộp đựng 50 chiếc thẻ được đánh số từ 1 đến 50. Chọn ngẫu nhiên từ 1
hộp hai thẻ. Tính xác suất để hiệu bình phương số ghi trên hai thẻ là số 2,0 chia hết cho 3. n (Ω) 2 = C50
Gọi A là biến cố hiệu bình phương số ghi trên hai thẻ là số chia hết cho 3
Giả sử 2 số được chọn là a,b . Theo giả thiết 0,5 IV (  a − b 3 2 2 a − b ) ( )
3 ⇔ (a − b)(a + b) ⇔ 3 
(a + b)3
Nếu (a − b)3 thì a, b phải đồng dư khi chia 3 ⇒ số cách chọn là: 2 2 2
C + C + C 0,5 16 17 17
Nếu (a + b)3 thì hoặc a và b cùng chia hết cho 3 hoặc một số chia 3 dư 1, 5
một số chia 3 dư 2 ⇒ số cách chọn là: 2 1 1
C + C .C 16 17 17 (  a − b  )3 a3 Lại có: ( ⇔  ⇒ số cách chọn là: 2 C 0,5  16 a + b  )3 b  3
Do đó: n( A) = ( 2 2 2
C + C + C ) + ( 2 1 1 C + C C ) 2 2 2 2 1 1
− C = C + C + C + C C 16 17 17 16 17 17 16 16 17 17 17 17
C + C + C + C C 681 0,5 Vậy P ( A) 2 2 2 1 1 16 17 17 17 17 = = 2 C 1225 50
Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác ABC cân tại A, M là trung điể  4 7 
m của AB . Đường thẳng CM : x − 2 y + 7 = 0 và K ;   là trọng  3 2  2 2,0
tâm tam giác ACM . Đường thẳng AB đi qua điểm D (3;− ) 1 . Tìm tọa độ các
đỉnh của tam giác ABC , biết điểm M có hoành độ nguyên và tâm đường
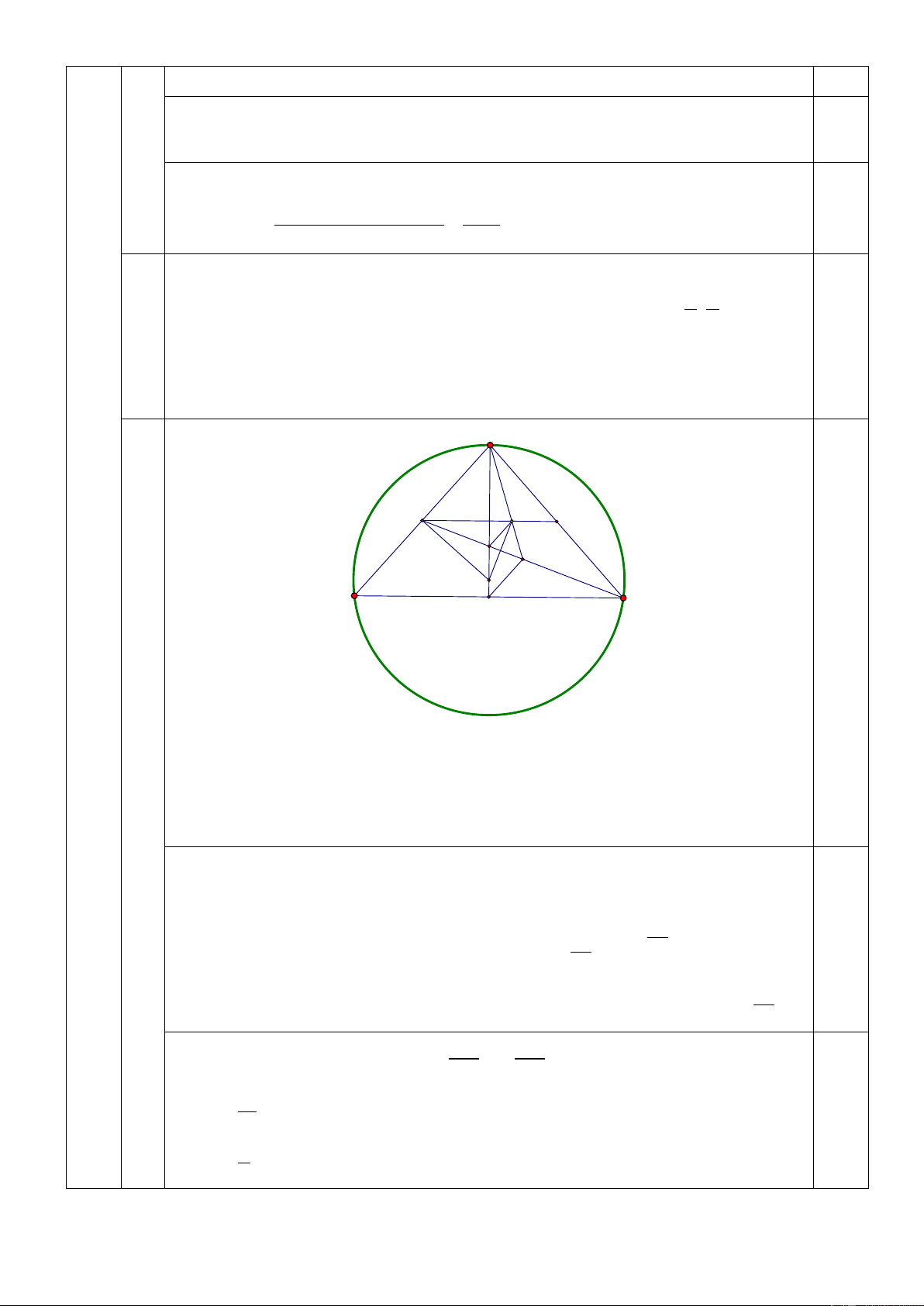
tròn ngoại tiếp tam giác ABC thuộc đường thẳng x + 6 y − 26 = 0. A K M N G E I B H C 0,5
Gọi I là tâm đường tròn ngoại tiếp tam giác ABC. Trước hết ta chứng minh
MC  IK. Thật vậy, gọi H , N lần lượt là trung điểm BC, AC; G  AH  CM .
Suy ra G là trọng tâm tam giác ABC. Mặt khác K là trọng tâm tam giác
ACM nên KG || HE . Suy ra KG || AB . Mà IM  AB nên KG  IM .
Rõ ràng AH  MK nên G là trực tâm tam giác MIK . Suy ra MC  IK .
Đường thẳng KI qua K và vuông góc với CM nên có phương trình:
12x  6 y 37  0. x 1 12
 x 6y37  0   25   Tọa độ       I thỏa mãn hệ 25 I 1;  .  0,5
x  6 y  26  0 y    6    6    
Gọi M 2 m7; m MC. Ta có DM   m   25 2
10; m 1 ; IM  2m  8;m   .   6    235 455 2
DM  IM  DM .IM  0  5m  m   0 6 6  13 m  (l)  0,5 3    7 m  (tm)  2 6   7  9 Suy ra    M 0;     , DM 3; 
. Từ đó suy ra AB : 3x  2y 7  0.    2  2
Gọi C 2c 7;c CM .  4 7  Do K ; 
 là trọng tâm ACM nên A112 ;
c 7  c . Mà A  AB suy ra c  5 0,5  3 2 
Từ đó A1; 2, B1;  5 , C 3; 
5 . Thử lại ta thấy AB = AC thỏa mãn bài toán.
Cho hình chóp S.ABCD có đáy là hình thoi cạnh 3a , SA = SD = 3a ,
SB = SC = 3a 3 . Gọi M , N lần lượt là trung điểm của các cạnh SA và SD , 1
P là điểm thuộc cạnh AB sao cho AP = 2a . Tính diện tích thiết diện của hình
chóp khi cắt bởi mặt phẳng (MNP) . S M N P A B F 0,5 E D C I
Do MN //AD ⇒ MN //BC . Vậy (MNP) cắt mặt phẳng ( ABCD) theo giao tuyến
đi qua P , song song BC và cắt DC tại điểm I . Thiết diện của khối chóp cắt
bởi mặt phẳng (MNP) chính là hình thang MNIP . V Do N ∆ DI = MA ∆
P nên MP = NI . Từ đó suy ra MNIP là hình thang cân.
Trong tam giác SAB , ta có  2 2 2 2 2 2 2
SA + AB − SB
9a + 9a − 27a 9a 1 cos SAB = = = − = − . 2 2.S . A AB 2.3 .3 a a 18a 2 0,5
Trong tam giác, MAP , ta có = + −  2 2 9a 3a 37a a 37 2 2 2 2 MP MA AP 2 . MA A . P cos MAP = + 4a + ⋅ 2a = ⇒ MP = 4 2 4 2
Từ M kẻ MF ⊥ PI , từ N kẻ NE ⊥ PI . Dễ thấy, tứ giác MNEF là hình chữ nhật và từ đó suy ra 3a 3a 0,5 MN = EF = ⇒ PF = EI = . 2 4 2 2 37a 9a a 139
Xét tam giác vuông MFP , ta có 2 2 MF = MP − FP = − = . 4 16 4  3a  a 139 0,5 ( + ⋅   MN + IP) 3a 2 .MF  2  4 9a 139 Ta có S = = = . MNIP 2 2 16
Cho tứ diện ABCD . G là trọng tâm tam giác BCD và M là điểm di động 2
bên trong tam giác BCD sao cho khi M khác G thì MG không song song
với CD . Đường thẳng qua M và song song với GA cắt các mặt phẳng 7
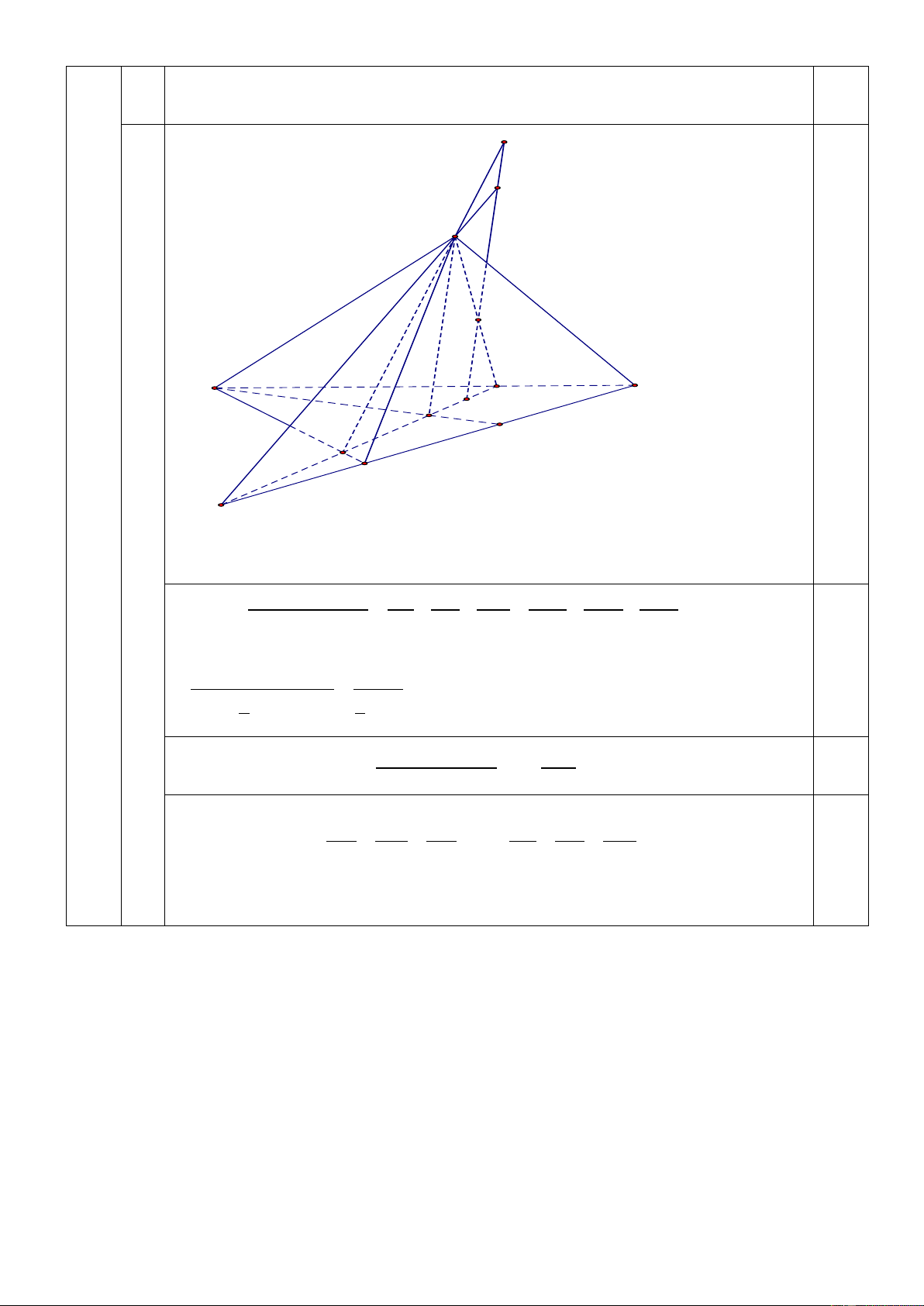
( ABC), ( ACD), ( ABD) lần lượt tại P,Q,R . Tìm giá trị lớn nhất của tích . MP . MQ MR . P Q A R 0,5 K B D M G I C J - Xét M trùng G thì 3 . MP . MQ M R = GA
- Xét M không trùng G, nêu cách kẻ P,Q, R đúng
MP + MQ + MR MI MJ MK S S S MBC MCD MBD = + + = + + Tính có: GA GI GJ GK S S S GBC GCD GCD 0,5 S + S + S MBC MCD MBD SABC = = = 3 1 1 S S 3 ABC 3 ABC 3 3
 MP + MQ + MR   3GA  Theo Côsi 3 . MP . MQ MR ≤ = = GA     0,5  3   3  Dấu bằng xảy ra khi MP MQ MR MI MJ MK
MP = MQ = MR ⇔ = = = 1 ⇔ = = = 1 GA GA GA GI GJ GK 0,5
⇔ M trùng trọng tâm G tam giác BCD
KL: Giá trị lớn nhất bằng 3
GA khi M là trọng tâm tam giác BCD 8
Document Outline

• Đề-giao-lưu-BT-HVM-lần-1