Đề giao lưu HSG Toán 7 năm 2022 – 2023 phòng GD&ĐT Lang Chánh – Thanh Hóa

UBND HUYỆN LANG CHÁNH
ĐỀ GIAO LƯU HỌC SINH GIỎI LỚP 7
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
CẤP HUYỆN NĂM HỌC: 2022 - 2023 Môn: TOÁN
Thời gian: 120 phút (không kể thời gian giao đề)
ĐỀ CHÍN H THỨC
Ngày thi: 01 tháng 4 năm 2023
(Đề thi gồm có 01 trang) Bài 1: (4,0 điểm)
a) Tính bằng cách hợp lí: A =  − 3 4  7  − 4 7  7  +  : +  +  :  7 11 11  7 11 11 b) Tính: 2022 2021 2020 B = 2 − 2 − 2 −...− 2 −1 30 7 13 27
c) Tính giá trị của biểu thức 2 ⋅5 + 2 ⋅5 C = 10 7 2 .5 .( 17 20 2 + 5 ) Bài 2: (4,0 điểm)
a) Tìm x, y, z biết x −1 y −3 z − 2 = =
và x −3y + 4z = 4. 2 4 3
b) Cho a,b,c thỏa mãn b − c c − a a − b + + = 2022
(a − b)(a − c) (b − a)(b − c) (c − a)(c − b)
Tính giá trị biểu thức 1 1 1 Q = + +
a − b b − c c − a Bài 3:(4,0 điểm)
a) Tìm các cặp số nguyên ( ;x y) thoả mãn: 2x + xy −3y −5x +3 = 0
b) Cho các số nguyên tố p và q thoả mãn: 2 2
p − 2q =17 . Tính 4
( p + q) +15 Bài 4:(6,0 điểm)
Cho tam giác ABC có góc A = 60° ( góc B và góc C nhọn). Tia phân giác của
góc B cắt AC tại D , tia phân giác của góc C cắt AB tại E . BD cắt CE tại I .Trên cạnh
BC lấy F sao cho BF = BE . Trên tia IF lấy M sao cho IM = IB + IC . a) Tính góc 
BIC và chứng minh ID = IF .
b) Chứng minh tam giác BCM là tam giác đều.
c) Tìm điều kiện của tam giác A
∆ BC để D và E cách đều đường thẳng BC . Bài 5: (2,0 điểm)
Cho các số không âm x, y, z thoả mãn: x +3z = 2022 và x + 2y = 2023
Tính giá trị lớn nhất của biểu thức: 1
A = x + y + z + . 2 HẾT!
Cán bộ coi thi không giải thích gì thêm
Họ và tên thí sinh: .................................................. SBD............
HƯỚNG DẪN CHẤM TOÁN 7 NĂM HỌC 2022-2023 Câu Ý Nội dung36 Điểm Bài
a). Tính bằng cách hợp lí: A =  − 3 4  7  − 4 7  7 4đ  +  : +  +  : 1: 4đ  7 11 11  7 11 11 b) Tính: 2022 2021 2020 S = 2 − 2 − 2 −...− 2 −1 30 7 13 27
c) Tính giá trị của biểu thức 2 ⋅5 + 2 ⋅5 C = 10 7 2 .5 .( 17 20 2 + 5 )
a a) A = −3 4  7 −4 7  7 −3 4  11 −4 7  11  +  : +  +  : =  + . +  + . 1đ  7 11 11  7 11 11  7 11 7  7 11 7 0,25 = − 3 4 − 4 7  11 11  + + + . = 0. = 0  7 11 7 11 7 7 Vậy A = 0 0,5 0,25 b b) 2022 2021 2020 S = 2 − 2 − 2 −...− 2 −1 1,5đ 2022 S = − ( 2021 2020 2 2 + 2 + ...+ 2 + ) 1 Đặt 2021 2020 P = 2 + 2 + ...+ 2 +1 2022 2021 2020 2P = 2 + 2 + 2 + ...+ 2 0,5 P − P = ( 2022 2021 2020 + + + + ) −( 2021 2020 2 2 2 2 ... 2 2 + 2 + ...+ 2 + ) 1 2022 2P − P = 2 −1 2022 P = 2 −1 Do đó: 0,5 2022 S = − ( 2022 2 2 − ) 1 =1 Vậy S =1 0,25 0,25
c c) Tính giá trị của biểu thức 1,5đ 30 7 13 27 2 ⋅5 + 2 ⋅5 C = 10 7 2 .5 .( 17 20 2 + 5 ) 13 7 2 ⋅5 .( 17 20 2 + 5 ) = 10 7 2 .5 .( 17 20 2 + 5 ) 36 0,5 13 7 2 ⋅5 = 10 7 2 .5 3 = 2 = 8 0,5 0,25 0,25 Bài
a) Tìm x, y, z biết x −1 y −3 z − 2 = =
và x −3y + 4z = 4. 4đ 2: 4đ 2 4 3
b) Cho a,b,c thỏa mãn b − c c − a a − b + + = 2022
(a − b)(a − c) (b − a)(b − c) (c − a)(c − b)
Tính giá trị biểu thức 1 1 1 Q = + +
a − b b − c c − a a
x −1 y − 3 z − 2 x −1 3y − 9 4z −8 x −1− 3y + 9 + 4z −8 = = = = = = = 2 0,75 2đ 2 4 3 2 12 12 2 −12 +12 x −1 y − 3 z − 2 = 2 ⇒ x = 5; = 2 ⇒ y =11; = 2 ⇒ z = 8 0,75 2 4 3
Vậy x = 5; y =11; z = 8 0,5 b b − c c − a a − b + + = 2022
2đ (a −b)(a −c) (b − a)(b −c) (c − a)(c −b)
(b − a) − (c− a) (c − b) − (a − b) (a − c) − (b − c) ⇒ + + = 2022 0,75
(a − b)(a − c)
(b − a)(b − c)
(c − a)(c − b) 1 1 1 1 1 1 ⇒ + + + + + = 2022
c − a a − b a − b b − c b − c c − a 0,5  1 1 1 0,5 2  ⇒ + + =   2022
 a − b b − c c − a  Vậy 1 1 1 + + =1011 0,25
a − b b − c c − a Bài 3:
a) Tìm các cặp số nguyên ( ;x y) thoả mãn: 2x + xy −3y −5x +3 = 0 4đ (4đ)
b) Cho các số nguyên tố p và q thoả mãn: 2 2
p − 2q =17 . Tính 4
( p + q) +15
a Ta có: 2x + xy−3y−5x+3= 0 2đ
Suy ra: 2x + xy − 2x −3y −3x + 6 = 3
⇒ x(x + y − 2) − 3(x + y − 2) = 3 0,5
⇒ (x − 3)(x + y − 2) = 3
Do x, y là số nguyên nên ta có: 0,5
(x − 3)(x + y − 2) = 3 =1.3 = 3.1 = ( 1 − )( 3 − ) = ( 3 − )( 1 − ) 0,5 x − 3 =1 x − = ⇒  hoặc 3 3 
x + y − 2 = 3
x + y − 2 = 1 0,25 hoặc x −3 = 1 − x − = − 0,25  hoặc 3 3 
x + y − 2 = 3 −
x + y − 2 = 1 −
Từ đó tìm được các cặp (x;y) là: (4;1), (6;-3), (2; -3), (0; 1) b Ta có: 2đ 2 2 p − 2q =17 2 2
⇒ p −1 = 2q +16 2
⇒ ( p −1)( p +1) = 2q +162 0,5
Mà p −1+ p +1= 2 ⇒ (p −1)(p +1)2 suy ra p −1; p +1 là hai số
chẵn liên tiếp⇒ (p −1)(p +1)8 0,5 2 2 2
⇒ 2q +168 ⇒ 2q 8 ⇒ q 4 ⇒ q2 0,5 Mà
q là số nguyên tố ⇒ q = 2 2 2 ⇒ p = 2.2 +17 = 25 Mà 0,25
p là số nguyên tố ⇒ p = 5. Ta có: 4 4
( p + q) +15 = (5 + 2) +15 = 2416 . 0,25 Vậy: 4
( p + q) +15 = 2416 Bài
Cho tam giác ABC có góc A = 60° ( góc B và góc C nhọn). Tia phân giác 6đ 4:
của góc B cắt AC tại D , tia phân giác của góc C cắt AB tại E . BD cắt (6đ)
CE tại I .Trên cạnh BC lấy F sao cho BF = BE . Trên tia IF lấy M sao
cho IM = IB + IC . a) Tính góc 
BIC và chứng minh ID = IF .
b) Chứng minh tam giác BCM là tam giác đều.
c) Tìm điều kiện của tam giác A
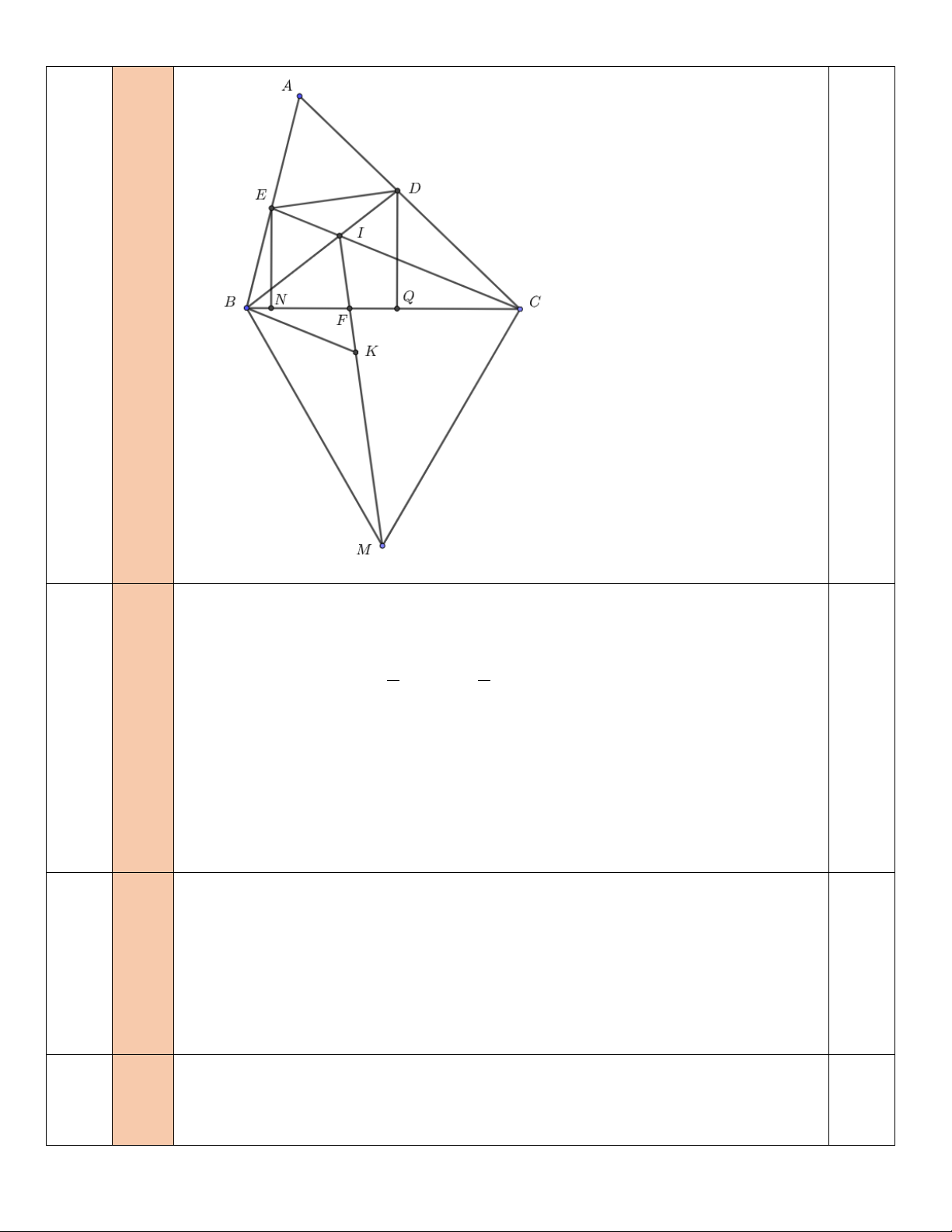
∆ BC để D và E cách đều đường thẳng BC . a 2đ A
∆ BC có  = ° ⇒  +  A 60 B C =120° 0,5 ⇒  +  1 =  +  IBC CCB (B C) 1 = .120° = 60° 2 2 0,5 ⇒  BIC =120° . Chứng minh B ∆ IF = B ∆ IE ( ) ⇒  =  c-g-c BIF BIE = 60° 0,5 ⇒  =  FIC DIC = 60° Chứng minh F ∆ IC = D
∆ IC (g-c-g) ⇒ ID = IF . 0,5 b
Trên đoạn thẳng IM lấy K sao cho IK = IB ⇒ IB ∆ K đều 0,5 2đ ⇒ IB = BK . Chứng minh I ∆ BC = K
∆ BM (c-g-c) ⇒ BC = BM ( ) 1 0,5 0,5 IB ∆ K đều ⇒ 
IBK = 60° mà  =  ⇒  IBC KBM CBM = 60° (2) Từ ( ) 1 và (2) ⇒ B
∆ CM là tam giác đều 0,5 c B ∆ IF = B
∆ IE ⇒ IF = IE , mà ID = IF ⇒ ID = IE . 0,5 2đ ⇒ ID
∆ E cân tại I , mà  = ° ⇒  DIE 120 IDE = 30° 0,5
Kẻ EN ⊥ BC và DQ ⊥ BC ⇒ EN // DQ = ⇔ ⇔  EN DQ ED // 3 BC DBC = 0° ( vì  IDE = 30° ) 0,5 ⇔  ABC = 60° ⇔ A
∆ BC là tam giác đều. 0,5 Bài
Cho các số không âm x, y, z thoả mãn: x +3z = 2022 và x + 2y = 2023. Tính 2đ 5: 2đ
trị lớn nhất của biểu thức: 1
A = x + y + z + . 2
Ta có: x + 3z = 2022 (1) và x + 2y = 2023 (2)
Từ (1) ⇒ x = 2022−3z
Trừ vế theo vế (2) cho (1), ta được: 2y −3z =1 1 3z y + ⇒ = 2 Khi đó: 0,5 1 1+ 3z 1
A = x + y + z + = (2022 − 3z) + + z + 2 2 2 1 1 3
= 2022 + + − 3z + z + z 2 2 2 1 0,5 = 2023− z 2 Vì 1 1
z ≥ 0 ⇒ − z ≤ 0 ⇒ 2023− z ≤ 2023 2 2 0,5 ⇒ A ≤ 2023
Dấu “=” xảy ra khi và chỉ khi:  z = 0  x = 2022 0,25  1 y =  2  z = 0 0,25
Vậy: GTLN của Abằng 2023⇔ x = 2022  1 y =  2
Lưu ý:-Nếu HS làm theo cách khác đúng vẫn cho điểm tối đa.
-Bài hình vẽ hình sai hoặc không vẽ hình không chấm điểm. các trường hợp
khác do tổ chấm thống nhất.
Document Outline

• ĐỀ GIAO LƯU HỌC SINH GIỎI LỚP 7
• UBND HUYỆN LANG CHÁNH
• CẤP HUYỆN NĂM HỌC: 2022 - 2023