Đề giao lưu HSG Toán 8 năm 2016 – 2017 phòng GD&ĐT Chí Linh – Hải Dương

Xin giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 8 đề giao lưu HSG Toán 8 năm 2016 – 2017 phòng GD&ĐT Chí Linh – Hải Dương; đề thi có đáp án và lời giải chi tiết.

Trích dẫn đề giao lưu HSG Toán 8 năm 2016 – 2017 phòng GD&ĐT Chí Linh – Hải Dương:
+ Cho hai số chính phương liên tiếp. Chứng minh rằng tổng của hai số đó cộng với tích của chúng là một số chính phương lẻ.
+ Cho tam giác ABC vuông tại A (AB > AC). Kẻ đường cao AH.
a) Chứng minh rằng AB2/AC2 = BH/CH.
b) Kẻ AD là tia phân giác của góc BAH (D thuộc BH). Chứng minh rằng: DH.DC = BD.HC.
c) Gọi M là trung điểm của AB, E là giao điểm của hai đường thẳng MD và AH. Chứng minh rằng CE // AD.

16 8 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 8

Môn: Toán 8

Thông tin:

5 trang 4 tháng trước

Tác giả:

Profile Mai Nguyệt
UBND THỊ XÃ CHÍ LINH
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ GIAO LƯU HỌC SINH GIỎI
NĂM HỌC 2016 - 2017
MÔN: TOÁN 8
Thời gian làm bài: 150 phút
(Đề gồm 01 trang)
Câu 1: (2,0 điểm)
a) Rút gọn biểu thức :
2 2
2 2 3 2
2 2 1 2
1
2 8 8 4 2
x x x
A
x x x x x x
với
0; 2
x x
.
b) Cho hai số x, y thỏa mãn x + y = 2 và x
2
+ y
2
= 10. Tính giá trị của biểu thức : M = x
3
+ y
3
.
Câu 2: (2,0 điểm)
a) Giải phương trình :
2
2
21
4 6
4 10
x x
x x
b) Giải bất phương trình :
2
2 3
4 1 2 5
1
1 1
y
y
y y y
Câu 3: (2,0 điểm)
a) Cho hai số chính phương liên tiếp. Chứng minh rằng tổng của hai số đó cộng với tích
của chúng là một số chính phương lẻ.
b) Giải phương trình nghiệm nguyên dương :
2
3 5 7
y
x x
.
Câu 4: (3,0 điểm)
Cho tam giác ABC vuông tại A (AB > AC). Kẻ đường cao AH.
a) Chứng minh rằng :
2
2
AB BH
AC CH
.
b) Kẻ AD là tia phân giác của góc BAH
( )
D BH
. Chứng minh rằng :
. .
DH DC BD HC
.
c) Gọi M là trung điểm của AB, E là giao điểm của hai đường thẳng MD và AH. Chứng minh
rằng CE // AD.
Câu 5: (1,0 điểm)
Cho
0 4
b a
và
2 3 4
ab a b
. Tìm giá trị lớn nhất của biểu thức
2 2
P a b
.
---------- HẾT ----------
------------- Giám thị không giải thích gì thêm --------------
UBND THỊ XÃ CHÍ LINH
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
HƯỚNG DẪN CHẤM ĐỀ GIAO LƯU HỌC SINH GIỎI
NĂM HỌC 2016 - 2017
MÔN: TOÁN - LỚP 8
(Hư
ớng dẫn chấm v
à bi
ểu điểm gồm 03
trang)
Câu
Phần
Nội dung đáp án Điểm
Câu 1
a
a) Ta có
2 2
2 2 3 2
2 2 1 2
A 1
2 8 8 4 2
x x x
x x x x x x
2 2 2
2 2 2
2 2 2
2( 4) 4(2 ) (2 )
x x x x x
x x x x x
2 2 2 2
2 2 2 2 2
2 2 ( 1)( 2) ( 2) 4 ( 1)( 2)
2( 4) ( 4)(2 ) 2( 2)( 4)
x x x x x x x x x x
x x x x x x x
3 2 2 2
2 2 2 2
4 4 4 1 ( 4)( 1)
.
2( 4) 2 ( 4)
x x x x x x x x
x x x x
1
2
x
x
. Vậy
1
A
2
x
x
với
0; 2
x x
.
0,25
0,25
0,25
0,25
b
+ Ta có
2 2 2
( ) 2
x y x y xy
+ Do đó
10 4 2 3
xy xy
+ Khi đó
3 3 3
( ) 3 ( )
M x y x y xy x y
+ Tính được
3
2 3.( 3).2 26
M
Vậy M = 26.
Chú ý
: N
ếu HS tính trực tiếp x v
à y
r
ồi thay v
ào M tính v
ẫn cho điểm tối đa.
0,25
0,25
0,25
0,25
Câu 2
a
Ta có
2 2
4 10 ( 2) 6 0
x x x x
. Phương trình trở thành :
2 2 2 2
( 4 6)( 4 10) 21 ( 4 8 2)( 4 8 2) 21
x x x x x x x x
2 2
2
2
2
2
( 4 8) 25
4 8 5
4 8 5
4 3 0 (1)
4 13 0 (2)
x x
x x
x x
x x
x x
- Giải PT (1) được nghiệm
1 2
1; 3
x x
.
- Giải PT (2) vô nghiệm vì
2 2
4 13 ( 2) 9 0
x x x x
Vậy tập nghiệm của PT là
{1;3}
S
.
0,25
0,25
0,25
0,25
b
b) ĐK : y
1
2 2 2
2 3 2 3
2
3 3 2
2
2
4 1 2 5 4(1 ) 1 2 5
0
1 1 1 (1 )(1 ) 1
3 3 3 ( 1) 3 ( 1)
0 0 0
1 1 (1 )(1 )
3
0 3 0 0 ( 1 0)
1
y y y y y
y y y y y y y y
y y y y y y
y y y y y
y
y y do y y
y y
Vậy nghiệm của bất phương trình đã cho là
0
1
y
y
0,25
0,25
0,25
0,25
Câu 3
a
+ Gọi hai số chính phương liên tiếp lần lượt là a
2
và (a +1)
2
(
a N
).
+ Theo bài ra ta có: a
2
+ (a + 1)
2
+ a
2
(a + 1)
2
= a
4
+ 2a
3
+ 3a
2
+ 2a + 1
= (a
4
+ 2a
3
+ a
2
) + 2(a
2
+ a) + 1 = (a
2
+ a)
2
+ 2(a + 1) + 1
= (a
2
+ a + 1)
2
= [a(a
+ 1) + 1]
2
+ Do a nguyên nên a(a + 1) là số chẵn
a
2
+ a + 1 là số lẻ.
+ Vậy [a(a
+ 1) + 1]
2
là một số chính phương lẻ. Suy ra đpcm.
0,25
0,25
0,25
0,25
b
Nếu
2
y
thì vế trái chia hết cho 9, ta chứng minh vế phải không chia hết
cho 9.
+ Thật vậy giả sử
2 2 2
5 7 9 5 7 3 2 1 3 6 3
x x x x x x x
2 2
2 1 3 ( 1) 3 ( 1) 3
x x x x
(vì 3 là số nguyên tố).
Suy ra x có dạng
3 1( )
x k k N
.
+ Khi đó
2 2 2
5 7 (3 1) 5(3 1) 7 9 9 3
x x k k k k
không chia hết cho 9
mâu thuẫn giả sử.
+ Do đó y < 2. Suy ra
{0;1}
y
.
- Với y = 0 thì
{2;3}
x
- Với y = 1 thì
{1;4}
x
+
V
ậy (x ; y) = (2; 0), (3; 0), (1; 1), (4; 1).
0,25
0,25
0,25
0,25
Câu 4
Hìn
h
vẽ
0,25
a
Chứng minh
HAB
( . )
HCA g g
AH HB AB
HC AH AC
2
2
AB AH HB HB
.
AC HC AH HC
Chú ý : HS có thể chứng minh AB
2
= BH.BC và AC
2
= CH.BC rồi chia vế.
0,25
0,25
0,25
M
E
N
D
H
C
B
A
2
1
b
+ Chứng minh được :
1
2
1 2
90
90
o
o
DAC A
ADC A DAC ADC
A A
=>
ADC
cân tại C
=> CA = CD.
+ Chứng minh được
DH AH
DB AB
(tính chất đường phân giác)
+ Chứng minh được
AH CH CH
AB AC CD
(tam giác đồng dạng và do CA = CD)
+ Suy ra được
. .
DH CH
DH DC BD HC
DB CD
0,25
0,25
0,25
0,25
c
+ Dựng N là điểm đối xứng của D qua M => AN = BD.
+ Ta có :
( )
DH HE
AN AE
DH DH CH
cmt
AN DB CD
HE CH HE CH
AE CD AH DH
+ Suy ra được
HCE
( . . )
HDA c g c
CEH DAH
+ Mà hai góc ở vị trí SLT nên CE // AD.
0,25
0,25
0,25
0,25
Câu 5
+ Với
0 3,0 4
b b a
thì
2 2 2 2
3 4 25
P a b
Đẳng thức xảy ra khi và chỉ khi a = 4; b = 3.
+ Chứng minh được bất đẳng thức
2 2 2 2 2
( ) ( )( )
ax by a b x y
(1)
+ Với
3 4
b a
thì
0 4 3 1
a b
. Do đó
2
( )
a b a b
2 2 2
( ) 2 2 (3 4 ) 4 3
P a b a b ab a b ab a b a b a b
(2)
Áp dụng (1) ta có
2 2 2 2 2 2 2
(3 4 ) (3 4 )( ) 25( )
a b a b a b
(3)
Từ (2) và (3) suy ra
2 2 2 2 2 2 2
( ) 25( ) 25
a b a b a b
+ Vậy Max(P) = 25 khi a = 4; b = 3.
0,25
0,25
0,25
0,25
| 1/5
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

UBND THỊ XÃ CHÍ LINH
ĐỀ GIAO LƯU HỌC SINH GIỎI
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO NĂM HỌC 2016 - 2017 MÔN: TOÁN 8
Thời gian làm bài: 150 phút (Đề gồm 01 trang) Câu 1: (2,0 điểm) 2 2  x  2x 2x  1 2 
a) Rút gọn biểu thức : A     1  với x  0; x  2 . 2 2 3  2 
 2x  8 8  4x  2x  x  x x 
b) Cho hai số x, y thỏa mãn x + y = 2 và x2 + y2 = 10. Tính giá trị của biểu thức : M = x3 + y3. Câu 2: (2,0 điểm) a) Giải phương trình : 21 2 x  4x  6  2 x  4x 10 2 4 1 2 y  5
b) Giải bất phương trình :   2 3 1  y  y 1  y y 1 Câu 3: (2,0 điểm)
a) Cho hai số chính phương liên tiếp. Chứng minh rằng tổng của hai số đó cộng với tích
của chúng là một số chính phương lẻ.
b) Giải phương trình nghiệm nguyên dương : y 2 3  x  5x  7 . Câu 4: (3,0 điểm)
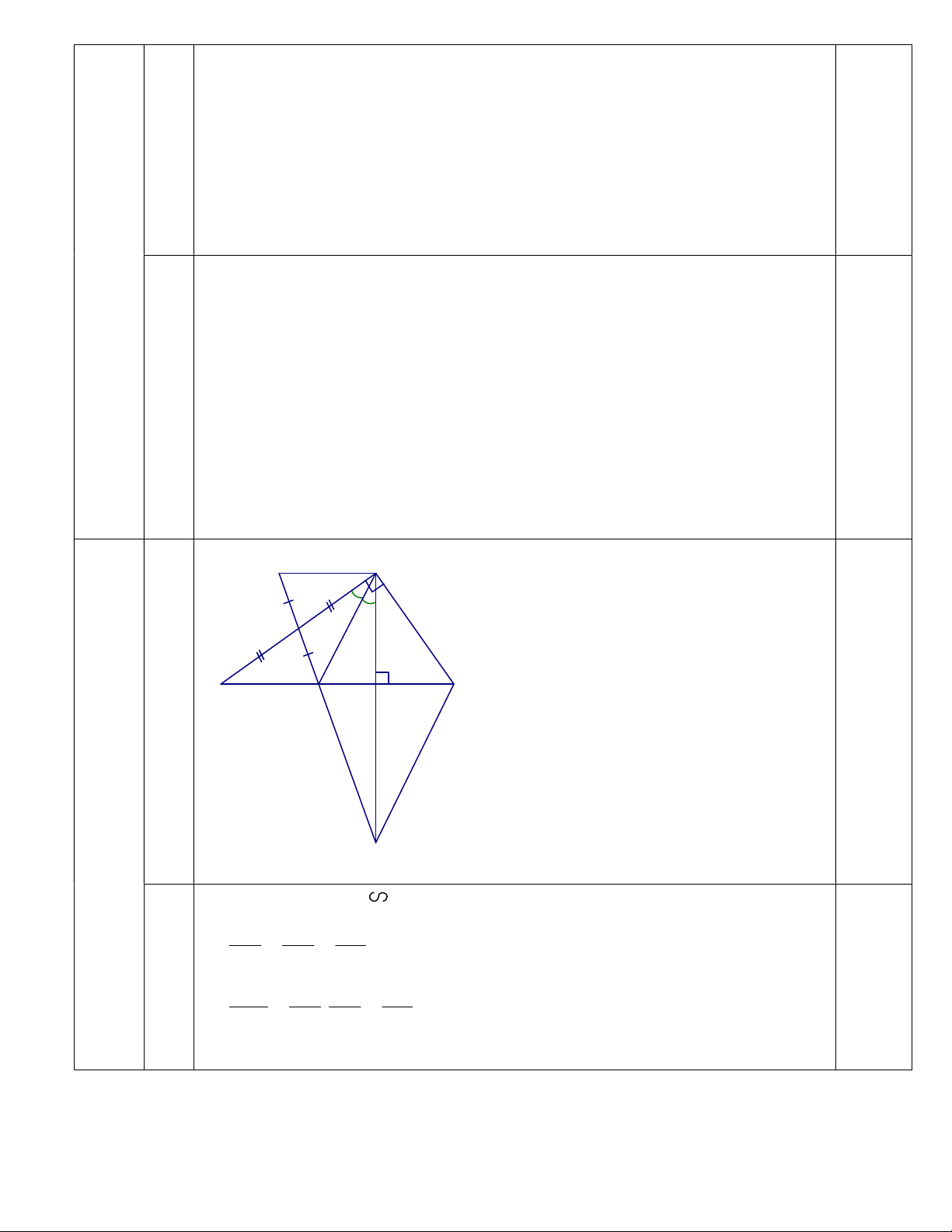
Cho tam giác ABC vuông tại A (AB > AC). Kẻ đường cao AH. 2 AB BH a) Chứng minh rằng :  . 2 AC CH
b) Kẻ AD là tia phân giác của góc BAH (D  BH ) . Chứng minh rằng : DH.DC  B . D HC .
c) Gọi M là trung điểm của AB, E là giao điểm của hai đường thẳng MD và AH. Chứng minh rằng CE // AD. Câu 5: (1,0 điểm)
Cho 0  b  a  4 và 2ab  3a  4b . Tìm giá trị lớn nhất của biểu thức 2 2 P  a  b . ---------- HẾT ----------
------------- Giám thị không giải thích gì thêm -------------- UBND THỊ XÃ CHÍ LINH
HƯỚNG DẪN CHẤM ĐỀ GIAO LƯU HỌC SINH GIỎI
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO NĂM HỌC 2016 - 2017 MÔN: TOÁN - LỚP 8
(Hướng dẫn chấm và biểu điểm gồm 03 trang) Câu Phần Nội dung đáp án Điểm 2 2  x  2x 2x  1 2  a) Ta có A     1  2 2 3  2 
 2x  8 8  4x  2x  x  x x  2 2 2  x  2x 2x  x  x  2  0,25    2 2  2 
 2(x  4) 4(2  x)  x (2  x)  x  a 2 2 2 2  x  2x 2x
 (x 1)(x  2)   x(x  2)  4x  (x 1)(x  2)  0,25      2 2  2   2  2 
 2(x  4) (x  4)(2  x)  x
  2(x  2)(x  4)  x  3 2 2 2 x  4x  4x  4x x 1 x(x  4)(x 1)  .  0,25 Câu 1 2 2 2 2 2(x  4) x 2x (x  4) x 1   . Vậy x 1 A  với x  0; x  2 . 0,25 2x 2x + Ta có 2 2 2 x  y  (x  y)  2xy 0,25
+ Do đó 10  4  2xy  xy  3       b + Khi đó 3 3 3 M x y (x y) 3xy(x y) 0,25 + Tính được 3 M  2  3.(3).2  26 0,25 Vậy M = 26. 0,25
Chú ý : Nếu HS tính trực tiếp x và y rồi thay vào M tính vẫn cho điểm tối đa. Ta có 2 2
x  4x 10  (x  2)  6  0 x
 . Phương trình trở thành : 2 2 2 2 0,25
(x  4x  6)(x  4x 10)  21  (x  4x  8  2)(x  4x  8  2)  21 2 2  (x  4x  8)  25 2  x  4x  8  5   2 x  4x  8  5  a 2 x  4x  3  0 (1)   0,25 2 x  4x 13  0 (2)
- Giải PT (1) được nghiệm x  1; x  3 . 1 2 0,25
- Giải PT (2) vô nghiệm vì 2 2
x  4x 13  (x  2)  9  0 x  Câu 2 0,25
Vậy tập nghiệm của PT là S  {1;3}. b) ĐK : y  1 2 2 2 4 1 2 y  5 4(1 y) 1 y  y 2 y  5      0 0,25 2 3 2 3 1 y  y 1 y y 1 (1 y  y )(1 y) 1 y 2 3y  3y 3y( y 1) 3y( y 1)   0   0   0 0,25 3 3 2 b 1 y 1 y (1 y)(1 y  y ) 3y 2 
 0  3y  0  y  0 (do 1 y  y  0) 0,25 2 1 y  y  y  0
Vậy nghiệm của bất phương trình đã cho là  0,25  y  1
+ Gọi hai số chính phương liên tiếp lần lượt là a2 và (a +1)2 ( a  N ). 0,25
+ Theo bài ra ta có: a2 + (a + 1)2 + a2(a + 1)2 = a4 + 2a3 + 3a2 + 2a + 1
= (a4 + 2a3 + a2) + 2(a2 + a) + 1 = (a2 + a)2 + 2(a + 1) + 1 a
= (a2 + a + 1)2 = [a(a + 1) + 1]2 0,25
+ Do a nguyên nên a(a + 1) là số chẵn  a2 + a + 1 là số lẻ. 0,25
+ Vậy [a(a + 1) + 1]2 là một số chính phương lẻ. Suy ra đpcm. 0,25
Nếu y  2 thì vế trái chia hết cho 9, ta chứng minh vế phải không chia hết Câu 3 cho 9. + Thật vậy giả sử 2 2 2
x  5x  79  x  5x  73  x  2x 1 3x  63 0,25 2 2
 x  2x 13  (x 1) 3  (x 1)3 (vì 3 là số nguyên tố).
Suy ra x có dạng x  3k 1(k  N ) . b + Khi đó 2 2 2
x  5x  7  (3k 1)  5(3k 1)  7  9k  9k  3 không chia hết cho 9 0,25 mâu thuẫn giả sử.
+ Do đó y < 2. Suy ra y {0;1} . 0,25 - Với y = 0 thì x {2;3} - Với y = 1 thì x {1;4} 0,25
+ Vậy (x ; y) = (2; 0), (3; 0), (1; 1), (4; 1). N A 1 2 M Hìn B D H C h vẽ 0,25 Câu 4 E Chứng minh HAB HC ( A g.g) 0,25 AH HB AB    0,25 HC AH AC a 2 AB AH HB HB 0,25   .  2 AC HC AH HC
Chú ý : HS có thể chứng minh AB2 = BH.BC và AC2 = CH.BC rồi chia vế.  DAC   A  90o  1  + Chứng minh được :  ADC   A  90o    DAC   ADC => A  DC cân tại C 2   A   A 1 2  0,25 => CA = CD. b DH AH + Chứng minh được 
(tính chất đường phân giác) 0,25 DB AB AH CH CH + Chứng minh được  
(tam giác đồng dạng và do CA = CD) 0,25 AB AC CD + Suy ra được DH CH   DH.DC  B . D HC 0,25 DB CD
+ Dựng N là điểm đối xứng của D qua M => AN = BD. 0,25 DH HE    + Ta có : AN AE HE CH HE CH      0,25 c DH DH CH AE CD AH DH (cmt)   AN DB CD  0,25 + Suy ra được H  CE HD ( A . c g.c)   CEH   DAH
+ Mà hai góc ở vị trí SLT nên CE // AD. 0,25
+ Với 0  b  3,0  b  a  4 thì 2 2 2 2
P  a  b  3  4  25 0,25
Đẳng thức xảy ra khi và chỉ khi a = 4; b = 3. 0,25
+ Chứng minh được bất đẳng thức 2 2 2 2 2
(ax  by)  (a  b )(x  y ) (1)
+ Với 3  b  a  4 thì 0  a  b  4  3 1. Do đó 2 (a  b)  a  b Câu 5 2 2 2
 P  a  b  (a  b)  2ab  a  b  2ab  a  b  (3a  4b)  4a  3b (2) 0,25 Áp dụng (1) ta có 2 2 2 2 2 2 2
(3a  4b)  (3  4 )(a  b )  25(a  b ) (3) Từ (2) và (3) suy ra 2 2 2 2 2 2 2
(a  b )  25(a  b )  a  b  25
+ Vậy Max(P) = 25 khi a = 4; b = 3. 0,25