UBND HUYỆN LANG CHÁNH
ĐỀ GIAO LƯU HỌC SINH GIỎI LỚP 8
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
CẤP HUYỆN NĂM HỌC: 2022 - 2023 ĐỀ CHÍ Môn:Toán NH THỨC
Thời gian: 150 phút (không kể thời gian giao đề)
(Đề thi có 01 trang; gồm 05 câu)
Bài 1.(4,0 điểm) 1. Rút gọn biểu thức:
𝐴𝐴 = �2𝑥𝑥3+𝑥𝑥2−𝑥𝑥 − 𝑥𝑥2+𝑥𝑥� : 2𝑥𝑥2+𝑥𝑥−1 + 𝑥𝑥 . với 𝑥𝑥 ≠ ±1, 𝑥𝑥 ≠ 1 𝑥𝑥3−1 𝑥𝑥2−1 𝑥𝑥2−1 2𝑥𝑥−1 2
2. Cho ba số x, y, z khác 0 và thoả mãn: 1 + 1 + 1 = 1 x y z x + y + z
Tính giá trị biểu thức = ( 2023 2023 + )( 2023 2023 + )( 2023 2023 P x y y z z + x )
Bài 2. (4,0 điểm) 2 1. Giải phương trình 2 9x x   40 x  2 3
2. Tìm x và y thỏa mãn đồng thời cả hai hệ thức sau:
x3 + y3 = 9 (1) và x2 + 2y2 = x + 4y (2)
Bài 3. (4,0 điểm)
1. Giải phương trình nghiệm nguyên dương: 2 2
x + y = 3 − x . y
2. Cho x, y là các số nguyên thỏa mãn đẳng thức ( 2x − ) = ( 2 3 1 2 y − ) 1 Chứng minh rằng 2 2
x − y chia hết cho 40
Bài 4. (6,0 điểm)
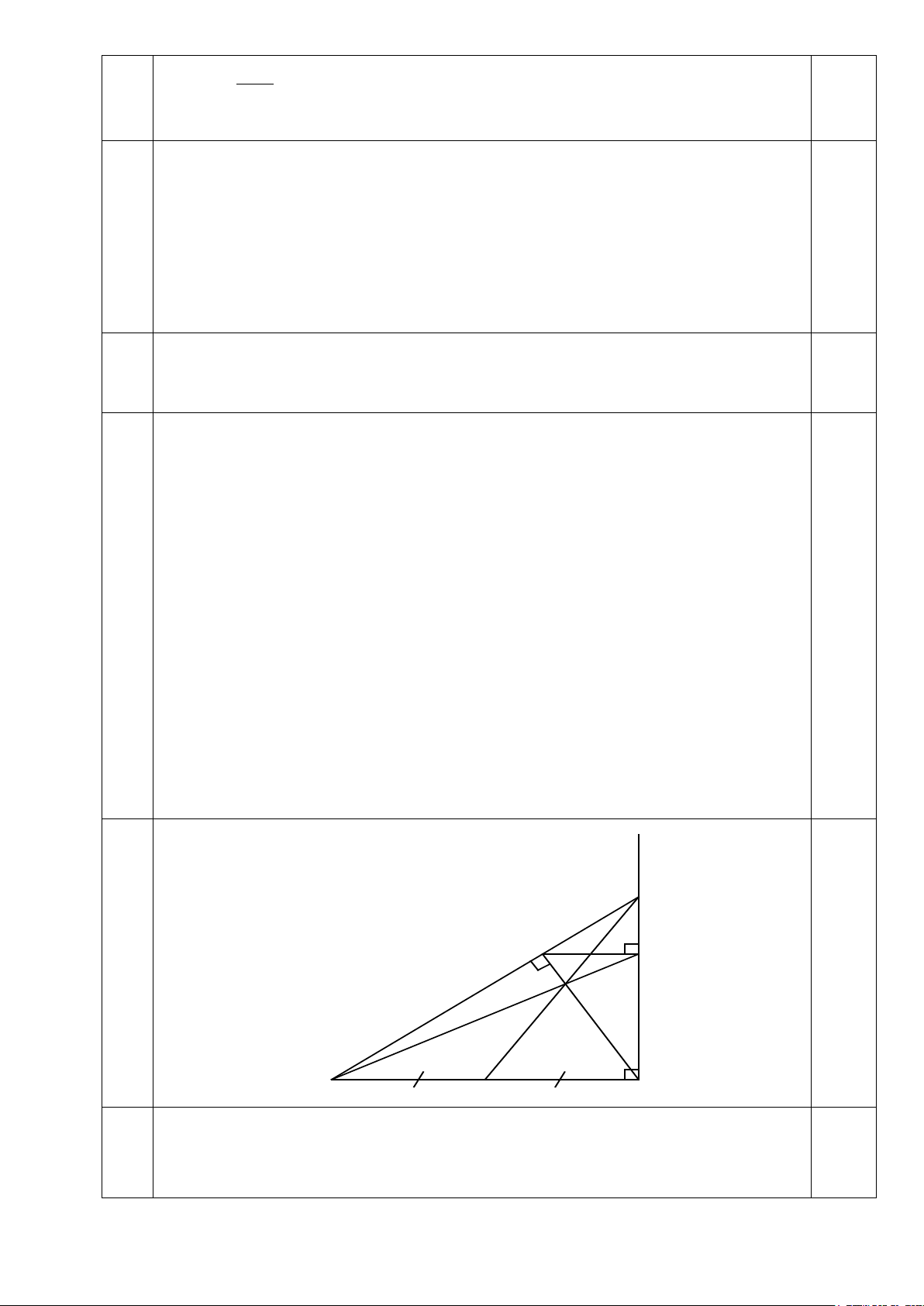
Cho đoạn thẳng AB. Kẻ tia Bx vuông góc với AB tại B. Trên tia Bx lấy điểm C
(C khác B). Kẻ BH vuông góc với AC (điểm H thuộc AC). Gọi M là trung điểm của
AB. 1. Chứng minh rằng: HA.HC = HB2
2. Kẻ HD vuông góc với BC (D thuộc BC). Gọi I là giao điểm của AD và BH.
Chứng minh rằng ba điểm C, I,M thẳng hàng.
3. Giả sử AB cố định, điểm C thay đổi trên tia Bx. Biết MI .CH . AB =1 IC HA BM
Tìm vị trí của điểm C trên tia Bx sao cho diện tích tam giác ABI lớn nhất.
Bài 5. (2,0 điểm)
Cho các số a,b,c không âm thỏa mãn a +b + c = 3
Tìm giá trị nhỏ nhất của biểu thức P = (a − )3 +(b − )3 +(c − )3 1 1 1 HẾT!
Cán bộ coi thi không giải thích gì thêm
Họ và tên thí sinh: .................................................. SBD............ HƯỚNG DẪN CHẤM Câu Hướng dẫn chấm Điểm 1 2đ 1. - Với 1 x ≠ 1,
± x ≠ , biểu thức A xác định nên ta có : 2  3 2x + 2 x − 2 x x + x  2 2x + x − A = 1 x  −  : +  3 2  x −1 x − 2 1 x −1 2x −   1  x( 2 2x + x − ) 1 2  x + 2 x x −   = − 1 x . +  3 0,5 x − 2 1 x −1  2
2x + x −1 2x −1   x ( 2 x − ) 1 2 x + = − x + x 0,5 3 x − 2 1
2x + x −1 2x −1
x(x −1)(x +1) x(x + = − 1) + x (x − 2
1)(x + x +1) (x +1)(2x −1) 2x −1 x(x + = 1) − x + x 2
(x + x +1) (2x −1) 2x −1 0,5 2 x + = x 2 x + x +1 0,5 2 x + x 1 Vậy : A = ( với x ≠ 1, ± x ≠ ) 2 x + x +1 2 2đ 2. Ta có: 1 1 1 1 + + =
⇔ ( yz + xz + xy)( x + y + z) = xyz
x y z x + y + z 0,5 2 2 2 2 2 2
⇔ xyz + x z + x y + y z + xyz + y x + z y + z x + xyz = xyz 2 2 2 2 2 2
⇔ x y + x z + y x + y z + z y + z x + 2xyz = 0
⇔ (x + y)(x + z)( y + z) = 0 0,5 2023 2023 2023 2023 x = − y x = − y x + y = 0    2023 2023 2023 2023
⇔ y = −z ⇔ y = −z ⇔ y + z =    0 0,5   2023 2023  2023 2023 z = −x z = −x z + x = 0   ⇒ P = ( 2023 2023 x + y )( 2023 2023 y + z )( 2023 2023 z + x ) = 0. 0,5 2 1. ĐKXĐ: x ≠ 3. 0,25 2  3 2 x  6 2 2 2 2 x  x  2 9x x x   40 ⇔  x +  − − 40 = 0 ⇔ − . 6 − 40 = 0 x  2 3  x − 3 x − 3  0,5  x − 3  x −  3 2 Đặt x t 
ta có phương trình t2 – 6t – 40 =0  (t −10)(t + 4) = 0 0,25 x  3 t = 10 ⇔  0,25 t = −4 2 = 10 ⇔ x t = 10 2
⇔ x −10x + 30 = 0 vô nghiệm; x − 3 0,5 2 x x = 2 0,25 2 t = 4 − ⇔ = 4
− ⇔ x + 4x −12 = 0 ⇔ (x − 2)(x + 6) = 0 <=> x − 3  x = 6 −
Vậy tập nghiệm của phương trình là S = {− ;6 } 2
2. Nhân hai vế phương trình (2) với 3, ta được 2 2 3x + 6y = 3x +12y (3). 0,5
Trừ hai phương trình (1) và (3) vế theo vế, ta được: 3 3
(x −1) = (2 − y) ⇔ y = 3 − x . 0,5
Thế y = 3− x vào (3), ta được 2
x − 3x + 2 = 0 ⇔ (x −1)(x − 2) = 0 0,5  x= 1 hoặc x = 2 . 0,5
Với x = 1thì y = 2. Với x = 2 thì y = 1.
Vậy ( x; y) = (2; 1), (1; 2). 3 1. Ta có: 2 2 2
(x − y) ≥ 0 ⇔ x + y ≥ 2xy ⇒ 3− xy ≥ 2xy ⇔ xy ≤1 0,75
Mà 𝑥𝑥, 𝑦𝑦 ∈ 𝑍𝑍+ ⇒ 0 < 𝑥𝑥𝑦𝑦 ≤ 1 ⇒ 𝑥𝑥𝑦𝑦 = 1 ⇒ 𝑥𝑥 = 𝑦𝑦 = 1 0,75
Vậy nghiệm nguyên dương của phương trình là (x, y) = (1;1) 0,5
2. Ta có ( 2x − ) = ( 2y − ) 2 2 3 1 2
1 ⇔ 3x − 2y =1(*) 0,5
Th1: Trước hết ta chứng minh 2 2 x − y 8 Ta có : 2 x ≡ 0;1;4(mod8) 2 3  x ≡   0;3;4(mod8) 2 2  ⇒ 
⇒ 3x − 2y ≡ 0;6;3;1;4;2(mod8) 2 y ≡ 0;1;4  (mod8) 2 2y ≡ 0;2  (mod8) Do đó từ (*) ta có : 2 2 x − y ≡ ( ) 2 2 3 2
1 mod8 ⇔ x ≡ y ≡1(mod8) 2 2 ⇔ x − y ≡ ⇒ ( 2 2 0(mod8) x − y )8( ) 1 0,5 Th2: Chứng minh 2 2 x − y 5 2 x ≡ 0;1;4(mod5) 2 3  x ≡   0;3;2(mod5) Ta có 2 2  ⇒ 
⇒ 3x − 2y ≡ 0;3;2;1;4(mod5) 2 y ≡ 0;1;4  (mod5) 2 2y ≡ 0;2;3  (mod5) Do đó từ ( *) ta có : 2 2 x − y ≡ ( ) 2 2 3 2
1 mod5 ⇒ x − y ≡1(mod5) 2 2
⇔ x − y ≡ ( ) 2 2
0 mod5 ⇒ x − y 5(2) 0,5
Từ (1) và (2) kết hợp với ( ) 2 2
5;8 =1⇒ x − y 40 ⇒ dfcm 0,5 4 x 0,5 (bao C gồm vẽ H K hình D và ghi I GT, KL) A M B
1. 1.Xét ∆AHB và ∆BHC có: 1,5 +) 𝐴𝐴𝐴𝐴𝐴𝐴 � = 𝐴𝐴𝐴𝐴𝐵𝐵 �(do BH⊥ AC) +) 𝐴𝐴𝐴𝐴𝐴𝐴 � =𝐴𝐴𝐴𝐴𝐵𝐵
� ( cùng phụ với 𝐴𝐴𝐴𝐴𝐴𝐴 �) ⇒ ∆ AHB ~∆BHC (g.g) ⇒ HA HB 2 = ⇒ . HA HC = HB HB HC
2. Giả sử đường thẳng CI cắt HD và AB lần lượt tại các điểm K và M’
*Áp dụng hệ quả định lý Ta lét vào các tam giác: CAM’, CM’B với HD // AB, ta có: HK CK = , KD CK = HK KD ⇒ = (1) 0,5 ' ' AM CM ' ' BM CM ' ' AM BM
*Áp dụng hệ quả định lý Ta lét vào các tam giác: IAM’, IM’B với HD // AB, ta có: HK KI = , KD KI = HK KD ⇒ = (2) 0,5 ' ' M B IM ' , AM IM ' ' M B AM Từ (1) và (2) suy ra: ' ' HK HK KD KD M B AM 2 ' ' 2 ' ' : = : ⇒ =
⇒ AM = M B ⇒ AM = BM 0,5 ' ' ' ' ' ' AM M B M B AM AM M B
⇒ M’ là trung điểm của AB. Mà M cũng là trung điểm của AB (gt) 0,5
⇒ M’ trùng với M. Vậy 3 điểm C, I, M thẳng hàng 3. Ta có: MI CH AB MI HA BM . HA.AB HA . . = 1 ⇒ = = = IC HA BM IC CH.AB CH 2 .AB CH 2 2 . HACH HB AB = = (1) ( Vì : BM = ; Theo câu a: 2 . HACH = HB ) 0,5 2 2 2CH 2CH 2
Mà ∆AHB ~∆BHC nên HB AB = (2) HC BC 2 2 2
Từ (1) và (2) suy ra MI AB a MI a = = ⇒ = 2 2 2 2 IC 2BC 2x MC a + 2x 0,5 2 Suy ra SIAB IM a = = . Mà 1 S = = CAB . ax AB BC 2 2 S + 2 2 CAB MC a 2x 1 3 3 3 3 2 ⇒ S = = ≤ = = IAB . a x a a a a 2 2 a + 2 2 2 2 x  a  a 4 2a 4 2 0,5 . 2 + 2x   4 .2x  x  x 2 2
Dấu „=” xảy ra khi: a = 2 2 a a x ⇔ x = ⇔ x = x 2 2 2
Vậy Khi C trên tia Bx sao cho a a BC =
thì giá trị lớn nhất của S = 0,5 2 IAB 4 2
5 Với các số a,b,c không âm thỏa mãn a +b + c = 3.Ta có : 2 ( − )3 3 2  2 9  3a  3  3a 3 *) 1 = − 3 + 3 −1 = − 3 + + −1 = − + −1 a a a a a a a a a a ≥ −     1( ) 1  4  4  2  4 4 0,5 2 ( − )3 3 2  2 9  3b  3  3b 3 *) 1 = − 3 + 3 −1 = − 3 + + −1 = − + −1 b b b b b b b b b b ≥ −     1(2)  4  4  2  4 4 2 ( − )3 3 2  2 9  3c  3  3c 3 *) 1 = − 3 + 3 −1 = − 3 + + −1 = − + −1 c c c c c c c c c c ≥ − 0,25     1(3)  4  4  2  4 4
Cộng theo vế (1), (2) và (3) ta được :
(a )3 (b )3 (c )3 3 (a b c) 3 3 3 1 1 1 3 .3 4 P − − + − + − ≥ + + − = − = − ⇒ ≥ 0,5 4 4 4 4
Dấu bằng xảy ra khi và chỉ khi : 2   3 a a  − =  0     (a b c)  3 3 2 ; ; 0; ;  =  2 2 2    3  b  b   − =  0   3 3  0,5   2  ⇔ (a; ; b c) =  ;0; 2 2     2    3 c c  − =   0   3 3  (a; ; b c) =    ; ;0 2    2 2 
a + b + c = 3 Vậy 3
Min P = − khi (a b c)  3 3 ; ; 0; ;  = và các hoán vị của nó 4 2 2    0,25
Lưu ý: Học sinh làm cách khác nếu đúng vẫn được điểm tối đa.
Document Outline

• ĐỀ GIAO LƯU HỌC SINH GIỎI LỚP 8
• UBND HUYỆN LANG CHÁNH
• CẤP HUYỆN NĂM HỌC: 2022 - 2023
• Môn:Toán