Đề giao lưu HSG Toán 8 năm 2024 – 2025 cụm chuyên môn số 1 Nga Sơn – Thanh Hóa

CỤM CHUYÊN MÔN SỐ 1
ĐỀ THI GIAO LƯU HỌC SINH GIỎI CỤM
THCS: AN - ĐIỀN - PHÚ - THÁI
Năm học: 2024 - 2025 Môn: Toán 8 Đề chính thức
Thời gian: 150 phút (không kể thời gian giao đề)
Ngày thi: 28 tháng 12 năm 2024
(Đề thi gồm có 01 trang) Câu I. (4 điểm) 1) Thu gọn biểu thức: 1 1 1 1 1 P = + + + + 2 2 2 2 2
x − x x − 3x + 2 x − 5x + 6 x − 7x +12 x − 9x + 20
(với x ≠ 0; x ≠ 1; x ≠ 2; x ≠ 3; x ≠ 4; x ≠ 5 ).
Tìm các giá trị của x nguyên để .xP đạt giá trị nguyên. 2) Các số ;    
x y; z khác 0 thỏa mãn x + y + z =1 và x y y z  z x  + + + + + =      2 −  .
 y x   z
y   x z 
Tính giá trị của biểu thức: 2023 2023 2023 P = x + y + z . Câu II. (4 điểm)
1) Tìm x , biết: 2x +5 2x + 2 3 − = (với x ≠ 4 − ; x ≠ 1; − x ≠ 2 ) 2 2
x + 5x + 4 x + 2x −8 2 2) Cho đa thức ( ) 3 2
f x = ax + bx + cx + d . Tìm a, b, c, d biết rằng khi chia đa thức f (x)
lần lượt cho các đa thức x −1; x − 2; x −3 đều có số dư là 6 và tại x =1 thì đa thức f (x) đó nhận giá trị bằng 18 − . Câu III. (4 điểm)
1) Tìm các số tự nhiên n để (n −8)2 2 + 36 là số nguyên tố.
2) Cho a, b, c, d là các số nguyên thỏa mãn ( 3 3 a + b ) = ( 3 3 5 13 c + d ) .
Chứng minh rằng: a + b + c + d chia hết cho 6 Câu IV. (6 điểm)
Cho hình vuông ABCD. Gọi E, K lần lượt là trung điểm của AB và CD; O là giao
điểm của AK và DE. Kẻ DM vuông góc với CE tại M.
1) Chứng minh rằng tam giác AKM vuông.
2) Gọi N là giao điểm của AK và BM. Chứng minh A
∆ DM cân và tính  ANB . 3) Tia phân giác của 
DCE cắt AD tại F. Chứng minh rằng: CF ≤ 2EF . Câu V. (2 điểm)
Cho a, b, c là các số thực dương thỏa mãn: ab +bc + ca = abc .
Tìm giá trị lớn nhất của biểu thức: a b c + + . bc(a + ) 1 ca(b + ) 1 ab(c + ) 1
.................................. Hết .....................................
Họ tên học sinh: .................................................; Số báo danh: .................................... HƯỚNG DẪN CHẤM Môn thi: TOÁN 8 Câu
Nội dung cần đạt Điểm
1) Với x ≠ 0; x ≠1; x ≠ 2; x ≠ 3; x ≠ 4; x ≠ 5 . Ta có: 1 1 1 1 1 P = + + + + 2 2 2 2 2
x − x x − 3x + 2 x − 5x + 6 x − 7x +12 x − 9x + 20 1 1 1 1 1 = + + + + x(x − ) 1 (x − )
1 (x − 2) (x − 2)(x −3) (x −3)(x − 4) (x − 4)(x −5) 0,5 điểm 1 1 1 1 1 1 1 1 1 1 = − + − + − + − + −
x −1 x x − 2 x −1 x − 3 x − 2 x − 4 x − 3 x − 5 x − 4 0,25 điểm 1 1 5 = − = 0,25 điểm
x − 5 x x(x −5) Ta có 5 5 .xP = .x =
x(x − 5) x − 5 0,25 điểm
Nên .xP đạt giá trị nguyên khi x −5 là ước của 5. 0,25 điểm Khi đó: x −5∈{ 1; − 1;5;− } 5 nên x∈{4;6;10; } 0 0,25 điểm
Kết hợp với đề bài x ≠ 0; x ≠ 1; x ≠ 2; x ≠ 3; x ≠ 4; x ≠ 5 ta được: Câu I 0,25 điểm x ∈{6;1 } 0 thì .xP nguyên. 4 điểm
2)  x y   y z   z x  + + + + + =      2 − 
 y x   z
y   x z   1 1   1 1   1 1  x + +  y + +   z + =   2 −   y z   z x   x y 
  1 1     1 1     1 1   x + +   1 +  y + +   1 +  z + +   1 = 1 0,25 điểm   y z     z x     x y    1 1 1   1 1 1   1 1 1  x + + + y + + + + z + + =       1  y z x   z x y   x y z  (  
x + y + z) 1 1 1 + + =   1  x y z  0,25 điểm 1 1 1 1 + + =
x y z x + y + z 1 1 1 1 + = −
y z x + y + z x 0,25 điểm
y + z x − ( x + y + z) = yz
x(x + y + z) 0,25 điểm y + z −( y + z) = yz
x(x + y + z) y + z y + z + = yz
x(x + y + z) 0 0,25 điểm (   y + z) 1 1  +  =  yz x(x y z) 0  + +  
( + ) x(x + y + z)+ yz y z . =
xyz (x + y + z) 0 ( + +
y + z) (x y)(x z) . =
xyz (x + y + z) 0
(x + y)(x + z)( y + z) = 0 0,25 điểm
- Nếu x + y = 0 thay vào x + y + z =1 ta được z =1 và x = −y Khi đó: 2023 2023 2023 P = x + y + z = (−y)2023 2023 2023 + y +1 = 1 0,25 điểm
Tương tự y + z = 0 và x + z = 0 ta có P =1. 0,25 điểm Vậy P =1. 1) Với x ≠ 4 − ; x ≠ 1; − x ≠ 2 . Ta có: 2x + 5 2x + 2 3 − = 2 2
x + 5x + 4 x + 2x −8 2 2x + 5 2x + 2 3 0,25 điểm ( − = x + )
1 (x + 4) (x − 2)(x + 4) 2  1 1   1 1  3 + − + = 
 x 1 x 4  
  x 2 x 4  + + − +  2 0,25 điểm 1 1 3 − = x +1 x − 2 2 0,25 điểm
x − 2 − x −1 3 ( = x + ) 1 (x − 2) 2 0,25 điểm 3 − 3 ( = x + ) 1 (x − 2) 2 0,25 điểm ( x + ) 1 (x − 2) = 2 − Câu II 0,25 điểm 2 − = 4 điểm x x 0 x(x − ) 1 = 0 0,25 điểm
x = 0 hoặc x =1
Vậy x = 0 hoặc x =1. 0,25 điểm 2)
Từ đề bài ta suy ra được f (x) −6 chia hết cho x −1; x − 2; x −3. 0,5 điểm
Vì f(x) là đa thức bậc 3 nên ta có: f (x) − 6 = . m (x − )
1 (x − 2)(x − 3) , trong đó m là hằng số khác 0. Lại có f (− ) 1 = 18 − nên 1 − 8 − 6 = . m ( 2 − ).( 3 − ).( 4 − ) 0,5 điểm ⇒ m =1
Vậy f (x) − 6 = (x − )
1 (x − 2)(x − 3) 0,5 điểm Suy ra f (x) 3 2
= x − 6x +11x Vậy 0,5 điểm a =1;b = 6
− ;c =11;d = 0.
1)(n −8)2 + = n − n + = (n +10)2 2 4 2 2 2 36 16 100 − 36n 0,5 điểm = ( 2 n − n + )( 2
6 10 n + 6n +10) Để (n −8)2 2
+ 36 là số nguyên tố thì: 2
n − 6n +10 =1 hoặc 2 n + 6n +10 =1 0,5 điểm - Nếu 2 n
− 6n +10 =1 thì (n − )2 3 = 0 . Suy ra n = 3 Khi đó (n −8)2 2
+ 36 = 37 là số nguyên tố (thoả mãn) 0,5 điểm - Nếu 2
n + 6n +10 =1 thì (n + )2 3 = 0 . Suy ra n = 3
− (loại do n là số tự nhiên)
Vậy n = 3 thoả mãn bài toán. 0,5 điểm 2) Ta có: ( 3 3 a + b ) = ( 3 3 5 13 c + d ) Câu III 3 3 3 3
a + b + c + d = ( 3 3 3 3
6 a + b − 2c − 2d ) 0,5 điểm 4 điểm Do ( 3 3 3 3
6 a + b − 2c − 2d ) chia hết cho 6 nên 3 3 3 3
a + b + c + d chia hết cho 6 0,5 điểm Xét hiệu ( 3 3 3 3
a + b + c + d ) −(a + b + c + d )
= ( 3 − )+( 3 − )+( 3 − )+( 3 a a b b c c d − d )
mà ( 3a − a) = a(a − )1(a + )1 là tích của ba số thự nhiên liên tiếp nên ( 0,5 điểm 3 a − a)3 Tương tự: ( 3
b − b)3; ( 3
c − c)3; ( 3 d − d )3 Mà 3 3 3 3
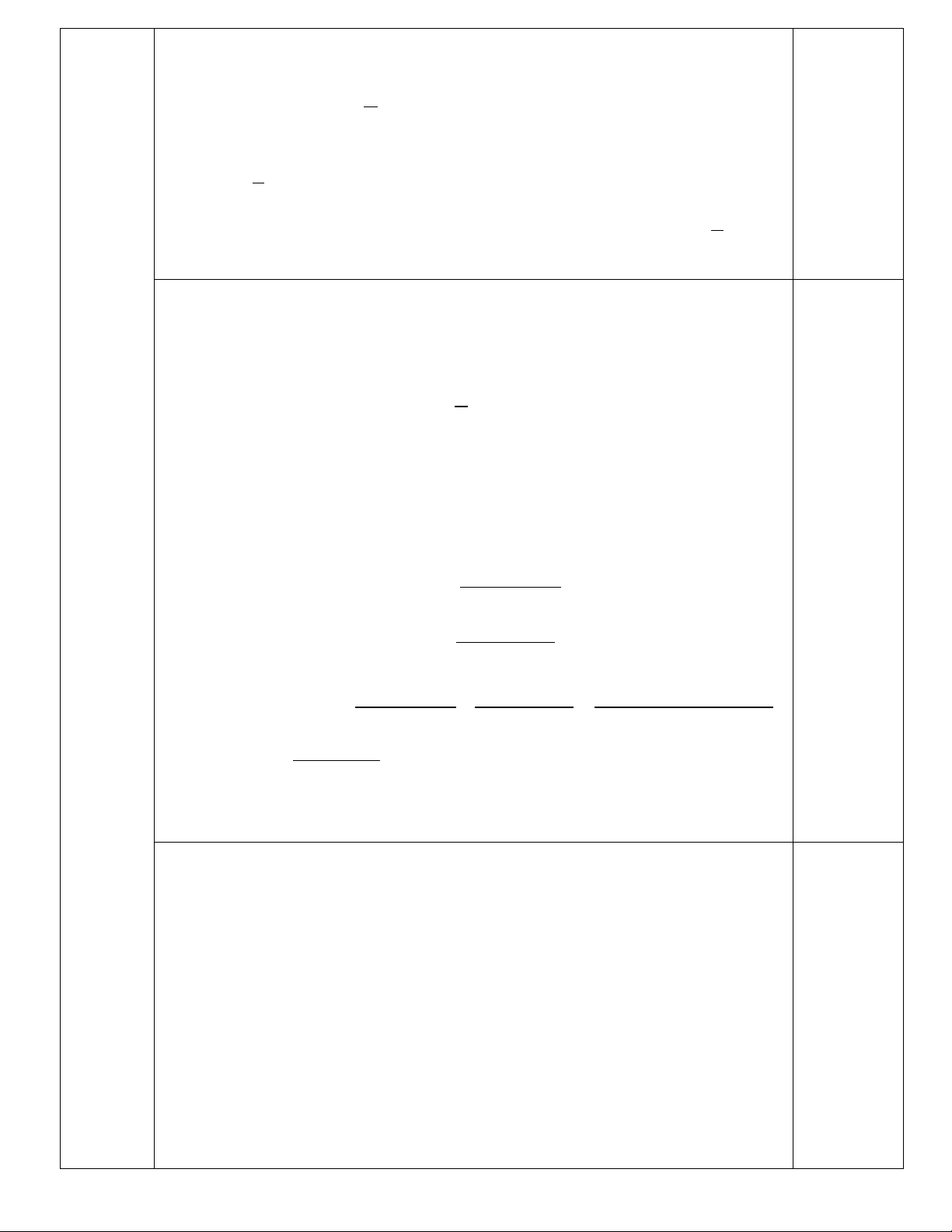
a + b + c + d chia hết cho 6 nên a + b + c + d chia hết cho 6. 0,5 điểm A E B F O Câu IV M 6 điểm H Q D K C N
1) Chứng minh được tứ giác AEKD là hình chữ nhật. 0,5 điểm
Khi đó O là trung điểm của DE. DE ∆
M vuông tại M có MO là đường trung tuyến ứng với cạnh DE 1 0,5 điểm
nên OM = OD = OE = DE 2
mà DE = AK (tứ giác AEKD là hình chữ nhật) nên 1 0,5 điểm OM = AK 2 A
∆ MK có MO là đường trung tuyến ứng với cạnh AK và 1 OM = AK 2 0,5 điểm Suy ra A
∆ MK vuông tại M.
2) Gọi H là giao điểm của AK và DM.
Chứng minh được tứ giác AECK là hình bình hành 0,25 điểm
nên AK / /MC mà DM ⊥ MC . Suy ra AK ⊥ DM tại H. Xét D
∆ MC vuông tại M có MK là đường trung tuyến ứng với cạnh huyền DC nên 1
KM = KD = KC = DC 0,25 điểm 2 Khi đó D
∆ MK cân tại K có KH ⊥ DM nên AK là đường trung trực của DM. 0,25 điểm
Do AK là đường trung trực của DM nên AD = AM. Khi đó A ∆ DM cân tại A. 0,25 điểm
mà AD = AM và AM = AB nên A ∆ BM cân tại A. 0 Do A
∆ DM cân tại A nên   180 MAD AMD − = 2 0,25 điểm 0 Do A
∆ BM cân tại A nên   180 MAB AMB − = 2 0 0 0
360 − MAD + MAB Suy ra  +  −  −    180 MAD 180 MAB ( ) AMD AMB = + = 2 2 2 0,25 điểm   0 0 360 90 0 AMD AMB − + = = 135 2 0,25 điểm Khi đó  0 HMN = 45 nên H
∆ MN vuông cân tại M Vậy  0,25 điểm 0 ANB = 45 .
3) Qua E kẻ đường vuông góc với CF cắt CD tại Q.
Do tứ giác AEKD là hình chữ nhật nên EK ⊥ KD nên E
∆ KQ vuông cân tại K. 0,5 điểm Xét E ∆ KQ và C ∆ DF có:
EK = AD = CD ;  =  0
EKQ CDF = 90 ;  = 
QEK FCD (cùng phụ  EQK ) 0,5 điểm Suy ra E ∆ KQ = CD ∆
F (cạnh góc vuông - góc nhọn kề) nên EQ = CF E
∆ CQ có CF vừa là đường cao vừa là đường phân giác nên E ∆ CQ cân
tại C. Suy ra: CQ = CE 0,5 điểm Xét C ∆ FQ và C ∆ FE có:
CE = CQ ;  =  ECF QCF ; FC chung Nên C ∆ FQ = C ∆ FE (c-g-c) 0,25 điểm
Khi đó: FE = FQ nên FE + FQ = 2EF
Áp dụng bất đẳng thức tam giác ta có:
QE ≤ FE + FQ = 2EF mà EQ = CF nên CF ≤ 2EF . 0,25 điểm
Do ab +bc + ca = abc nên 1 1 1 + + = 1 a b c Chứng minh được 4 1 1 ≤ + với mọi m, n dương. m + n m n 0,5 điểm Dấu "=" xảy ra khi m = n. Vận dung ta có: a a a a  1 1  = = ≤ + ; bc(a ) 1
abc bc ab bc ca bc 4  ab bc ca bc  + + + + + + + 
dấu " = " xảy ra khi b = c 0,5 điểm Tương tự: b b  1 1  ≤ + dấu "=" xảy ra khi c = a ca(b ) 1
4  ab ca bc ca  + + +  c c  1 1  ≤ + dấu "=" xảy ra khi a = b ab(c ) 1
4  ab bc ca ab  + + +  Câu V Suy ra 2 điểm a b c + + bc(a + ) 1 ca(b + ) 1 ab(c + ) 1 a  1 1  b  1 1  c  1 1  ≤ + + + + + 0,5 điểm
4  ab bc ca bc  4  ab ca bc ca  4  ab bc ca ab  + + + + + +  a b c + + bc(a + ) 1 ca(b + ) 1 ab(c + ) 1 1 1 ≤ (a + c) 1 1 + (a +b) 1 1 . . + . (b + c) 4 ab + bc 4 bc + ca 4 ca + ab a b c 1  1 1 1  + + ≤ + + bc(a ) 1 ca(b ) 1 ab(c ) 1 4  a b c  + + +   a b c 1 + + ≤ bc(a + ) 1 ca(b + ) 1 ab(c + ) 1 4 0,5 điểm
Vậy GTLN của biểu thức bằng 1 khi a = b = c = 3 4 Lưu ý:
- Điểm toàn bài làm tròn đến 0,25 đ;
- HS làm cách khác, nếu đúng vẫn cho điểm tối đa.
Xem thêm: ĐỀ THI HSG TOÁN 8
https://thcs.toanmath.com/de-thi-hsg-toan-8
Document Outline

• an dien phu thai TOÁN 8
  • HƯỚNG DẪN CHẤM
• HSG 8